Modelling Porous Cementitious Media with/without Integrated Latent Heat Storage: Application Scenario
Abstract
:1. Introduction
2. Experimental Database
3. Heat Conduction in Two-Phase Porous System
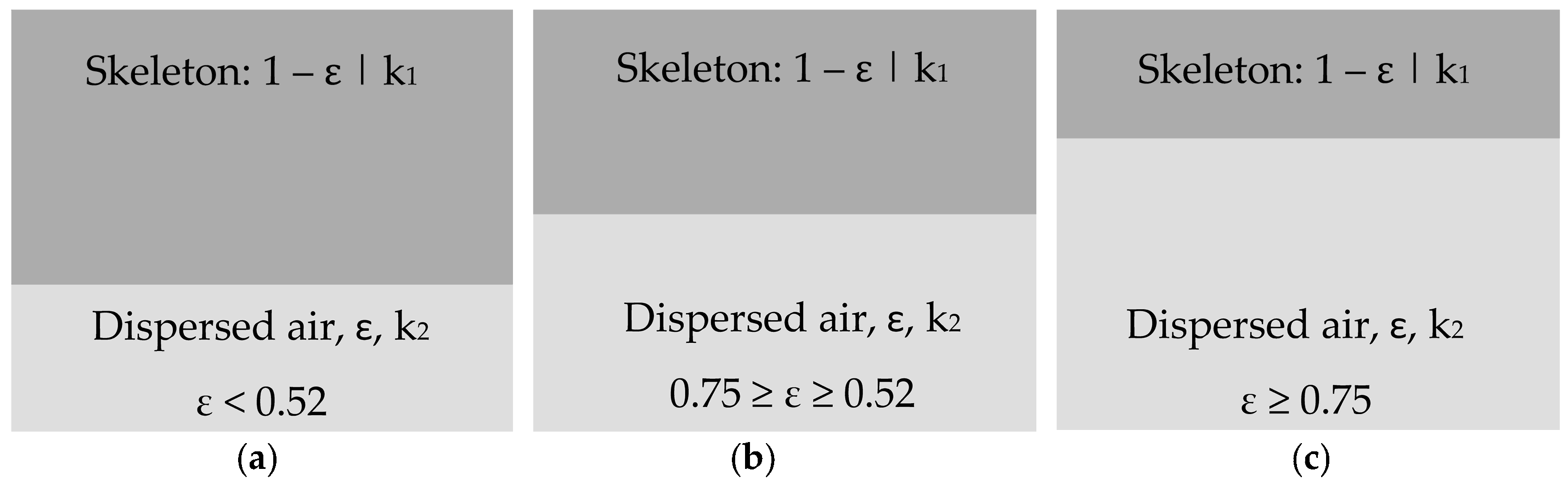
3.1. Modified Lewis-Nielsen Model for Conductivity of Porous Cementitious Composites
3.2. Fitting Parameters A and ψ for Porous Cementitious Composites
4. Analytical Predictions vs. Experimental Data
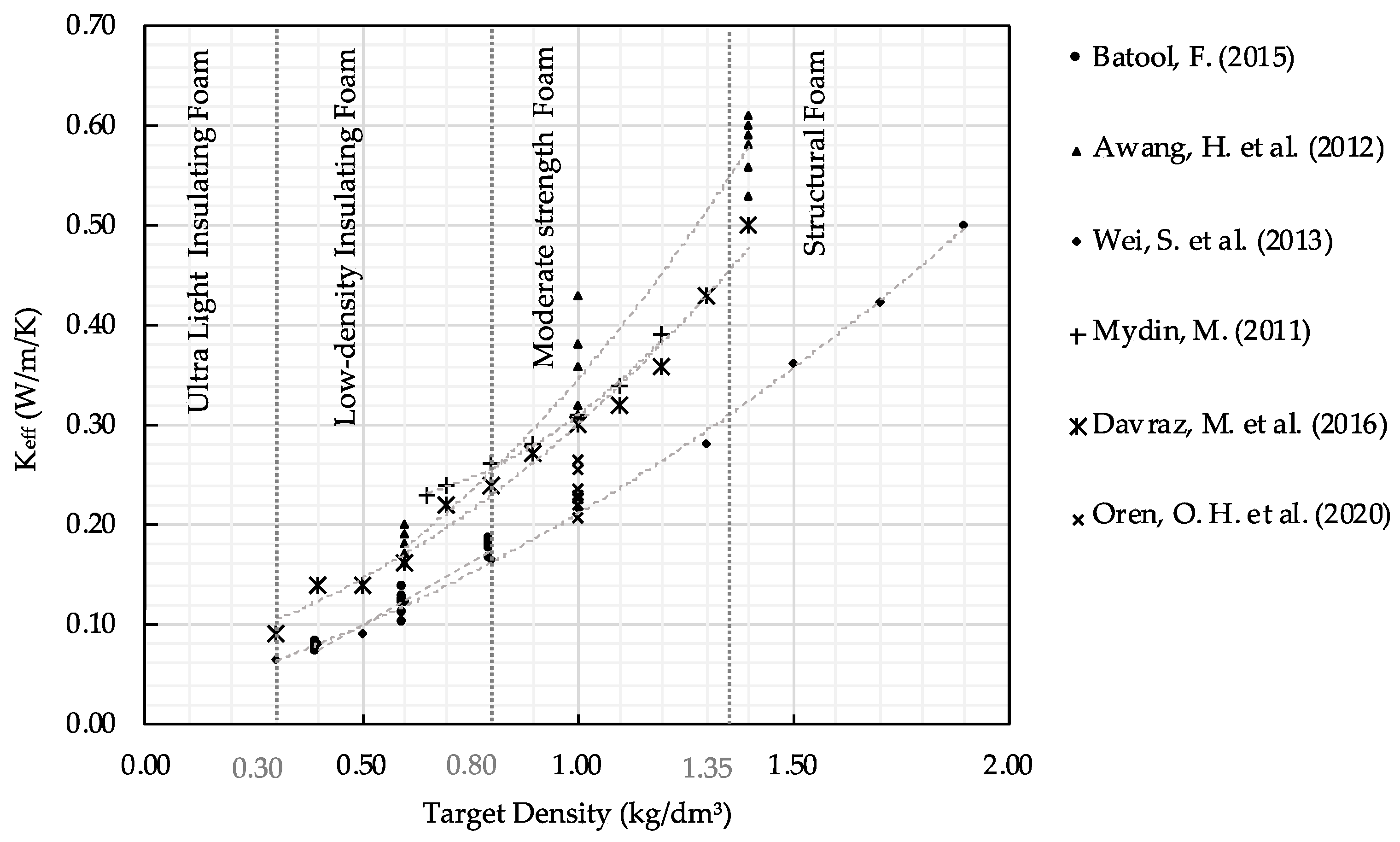
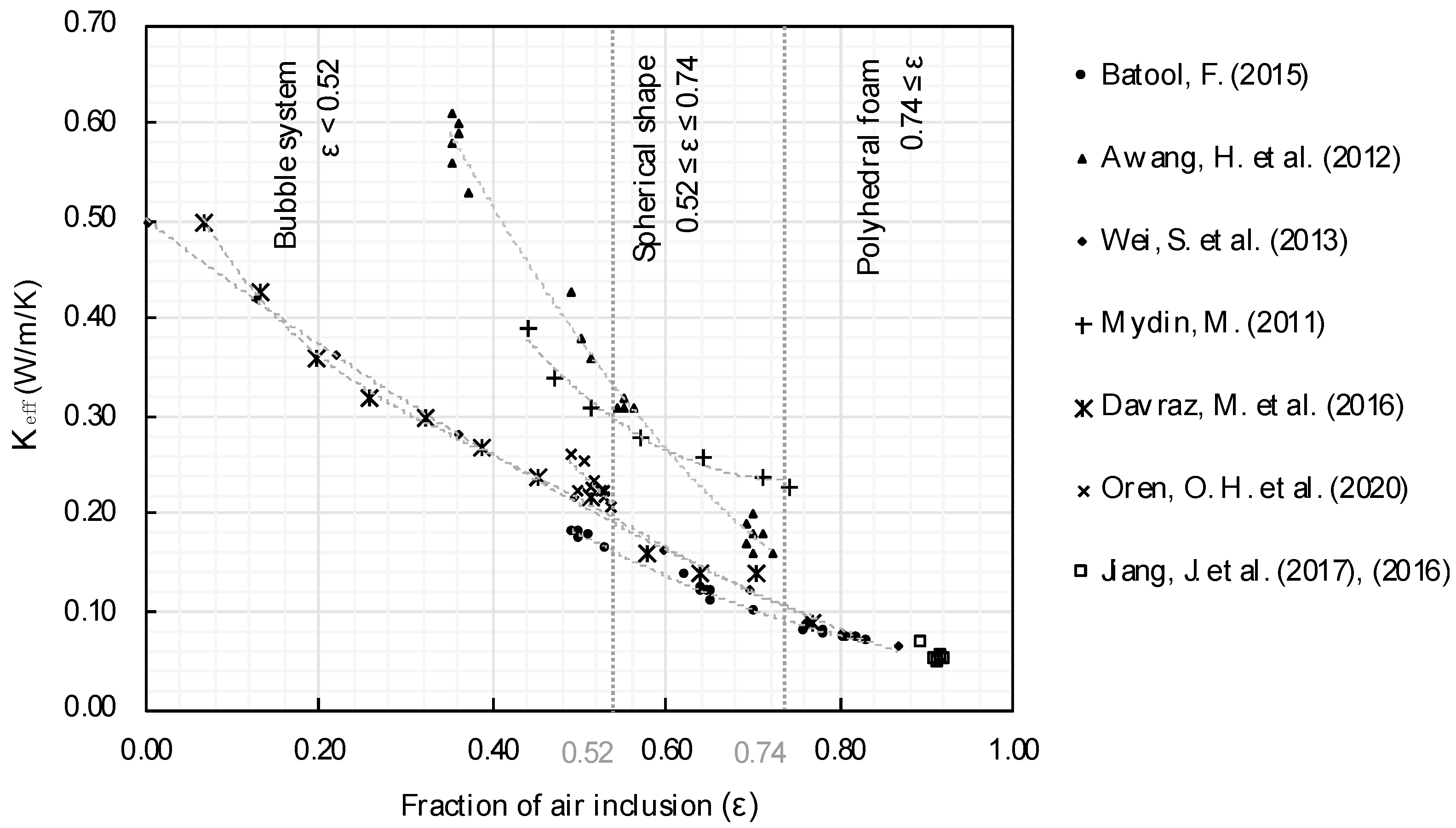
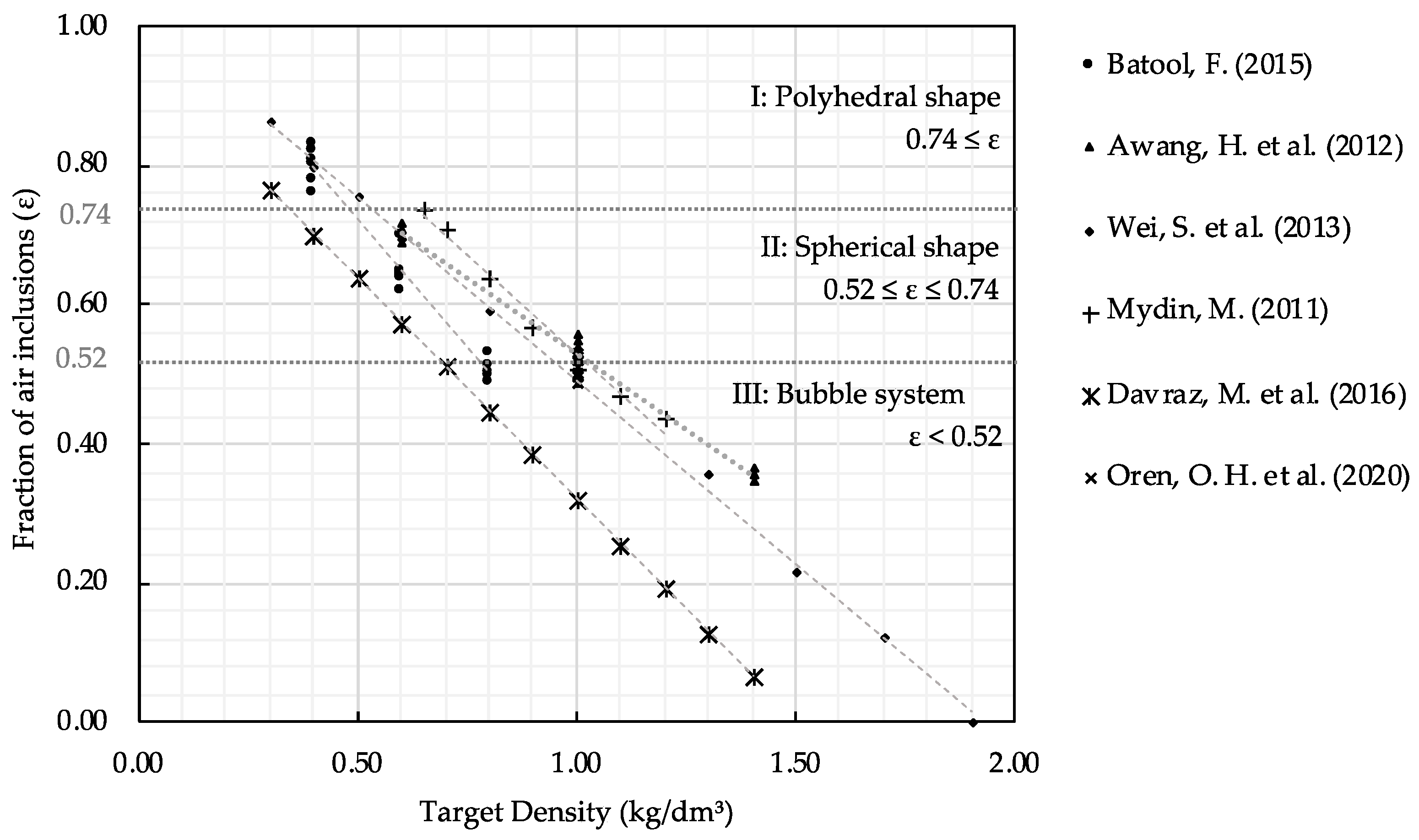
4.1. Classification of Test Data
4.2. Analytical Description vs. Experimental Measurements of Thermal Conductivity Keff
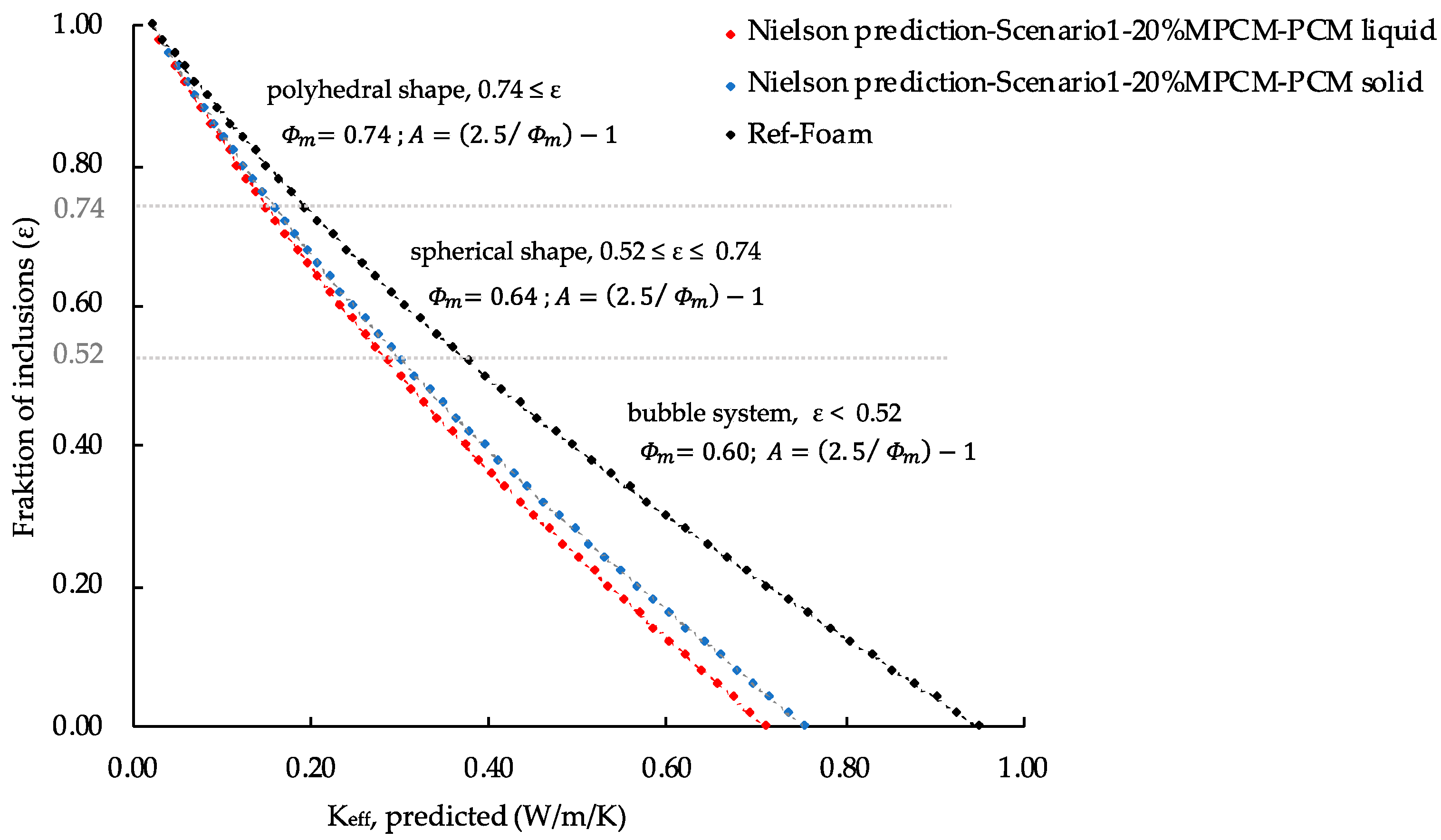
4.3. Extension of the Analytical Model for Porous LHTES-Systems (Mineral Foams)
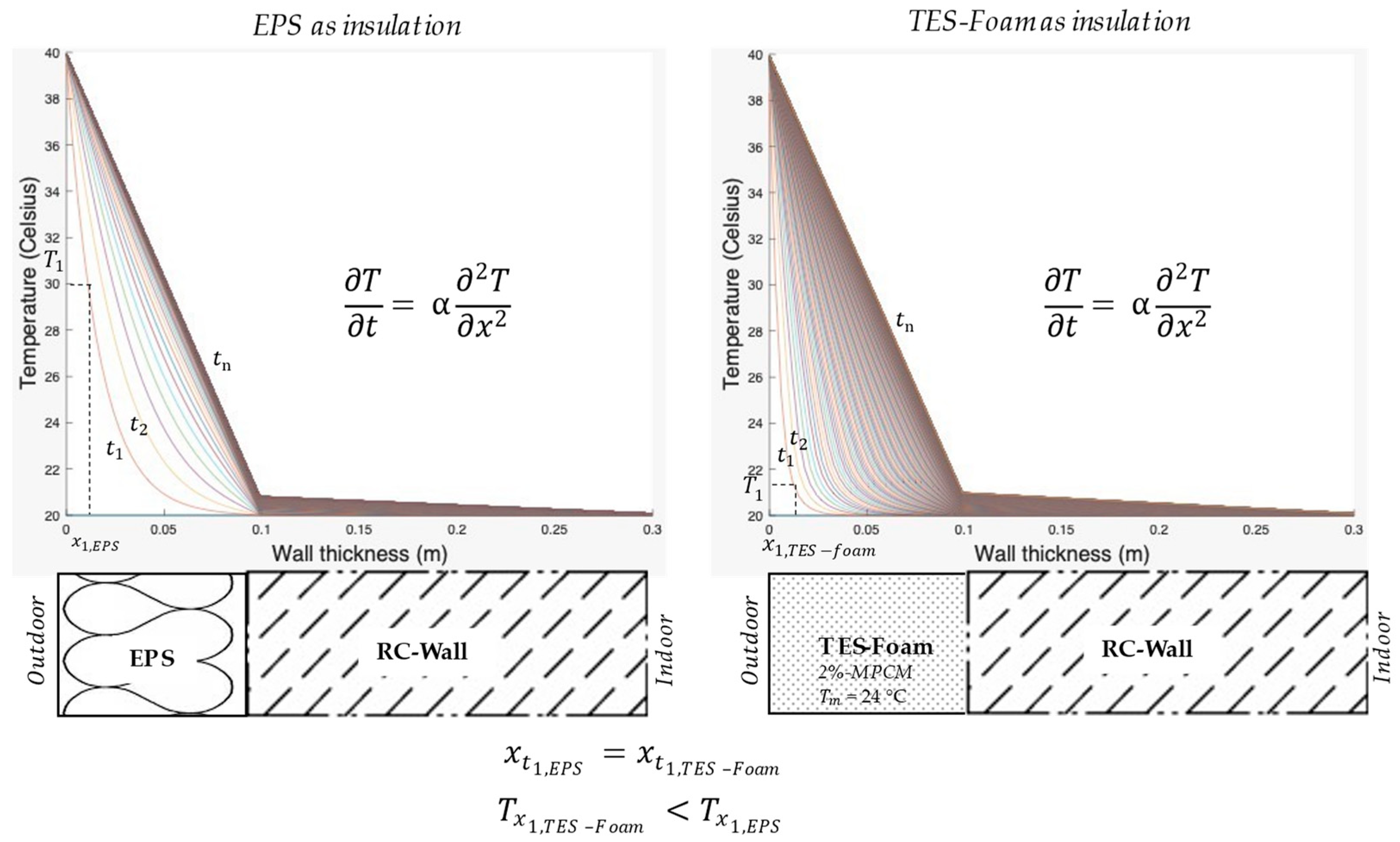
5. Integration of LHTES and Dynamic Envelopes: Application Scenario-1D Model Based on the First Law of Thermodynamics
Parametric Studies for Thermal Performance in Multi-Layer Structures (EPS vs. TES Foam Composites)
- “Summer” ;
- “Winter” ;
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miller, S.A.; Habert, G.; Myers, R.J.; Harvey, J.T. Achieving net zero greenhouse gas emissions in the cement industry via value chain mitigation strategies. One Earth 2021, 4, 1398–1411. [Google Scholar] [CrossRef]
- Chen, X.-S.; Li, Y.-P.; Jiang, Y.-L.; Liu, Y.-X.; Zhang, T. Theoretical research on gas seepage in the formations surrounding bedded gas storage salt cavern. Pet. Sci. 2022, 19, 1766–1778. [Google Scholar] [CrossRef]
- Xue, W.; Wang, Y.; Chen, Z.; Liu, H. An integrated model with stable numerical methods for fractured underground gas storage. J. Clean. Prod. 2023, 393, 136268. [Google Scholar] [CrossRef]
- Yang, T.; King, W.P.; Miljkovic, N. Phase change material-based thermal energy storage. Cell Rep. Phys. Sci. 2021, 2. [Google Scholar] [CrossRef]
- Lu, S.; Lin, Q.; Liu, Y.; Yue, L.; Wang, R. Study on thermal performance improvement technology of latent heat thermal energy storage for building heating. Appl. Energy 2022, 323, 119594. [Google Scholar] [CrossRef]
- Hassan, F.; Jamil, F.; Hussain, A.; Ali, H.M.; Janjua, M.M.; Khushnood, S.; Farhan, M.; Altaf, K.; Said, Z.; Li, C. Recent advancements in latent heat phase change materials and their applications for thermal energy storage and buildings: A state of the art review. Sustain. Energy Technol. Assess. 2021, 49, 101646. [Google Scholar] [CrossRef]
- Heim, D.; Pawłowski, M. The methodology of thermal energy management for nearly zero energy buildings. Period. Polytech. Civ. Eng. 2019, 63, 499–517. [Google Scholar] [CrossRef]
- Al-Yasiri, Q.; Szabó, M. Experimental study of PCM-enhanced building envelope towards energy-saving and decarbonisation in a severe hot climate. Energy Build. 2023, 279, 112680. [Google Scholar] [CrossRef]
- Piselli, C.; Prabhakar, M.; de Gracia, A.; Saffari, M.; Pisello, A.L.; Cabeza, L.F. Optimal control of natural ventilation as passive cooling strategy for improving the energy performance of building envelope with PCM integration. Renew. Energy 2020, 162, 171–181. [Google Scholar] [CrossRef]
- Saffari, M.; de Gracia, A.; Fernández, C.; Cabeza, L.F. Simulation-based optimization of PCM melting temperature to improve the energy performance in buildings. Appl. Energy 2017, 202, 420–434. [Google Scholar] [CrossRef]
- Park, J.H.; Berardi, U.; Chang, S.J.; Wi, S.; Kang, Y.; Kim, S. Energy retrofit of PCM-applied apartment buildings considering building orientation and height. Energy 2021, 222, 119877. [Google Scholar] [CrossRef]
- Ryms, M.; Klugmann-Radziemska, E. Possibilities and benefits of a new method of modifying conventional building materials with phase-change materials (PCMs). Constr. Build. Mater. 2019, 211, 1013–1024. [Google Scholar] [CrossRef]
- Marani, A.; Nehdi, M.L. Integrating phase change materials in construction materials: Critical review. Constr. Build. Mater. 2019, 217, 36–49. [Google Scholar] [CrossRef]
- Chihab, Y.; Bouferra, R.; Garoum, M.; Essaleh, M.; Laaroussi, N. Thermal inertia and energy efficiency enhancements of hollow clay bricks integrated with phase change materials. J. Build. Eng. 2022, 53, 104569. [Google Scholar] [CrossRef]
- Sawadogo, M.; Duquesne, M.; Belarbi, R.; Hamami, A.E.A.; Godin, A. Review on the integration of phase change materials in building envelopes for passive latent heat storage. Appl. Sci. 2021, 11, 9305. [Google Scholar] [CrossRef]
- Ben Romdhane, S.; Amamou, A.; Ben Khalifa, R.; Saïd, N.M.; Younsi, Z.; Jemni, A. A review on thermal energy storage using phase change materials in passive building applications. J. Build. Eng. 2020, 32, 101563. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; De Masi, R.F.; de’ Rossi, F.; Vanoli, G.P. Energy refurbishment of existing buildings through the use of phase change materials: Energy savings and indoor comfort in the cooling season. Appl. Energy 2014, 113, 990–1007. [Google Scholar] [CrossRef]
- Du, K.; Calautit, J.; Wang, Z.; Wu, Y.; Liu, H. A review of the applications of phase change materials in cooling, heating and power generation in different temperature ranges. Appl. Energy 2018, 220, 242–273. [Google Scholar] [CrossRef]
- Drissi, S.; Mo, K.H.; Falchetto, A.C.; Ling, T.-C. Understanding the compressive strength degradation mechanism of cement-paste incorporating phase change material. Cem. Concr. Compos. 2021, 124, 104249. [Google Scholar] [CrossRef]
- Bao, X.; Tian, Y.; Yuan, L.; Cui, H.; Tang, W.; Fung, W.; Qi, H. Development of high performance PCM cement composites for passive solar buildings. Energy Build. 2019, 194, 33–45. [Google Scholar] [CrossRef]
- Kishore, R.A.; Bianchi, M.V.; Booten, C.; Vidal, J.; Jackson, R. Optimizing PCM-integrated walls for potential energy savings in U.S. Buildings. Energy Build. 2020, 226, 110355. [Google Scholar] [CrossRef]
- Yang, Y.K.; Kim, M.Y.; Chung, M.H.; Park, J.C. PCM cool roof systems for mitigating urban heat island—An experimental and numerical analysis. Energy Build. 2019, 205, 109537. [Google Scholar] [CrossRef]
- Abouebeid, S.; Hany, N.; Mosaad, G. Towards enhancing indoor environmental quality: A case of smart adaptive building envelopes in a coastal city. F1000Research 2022, 11, 731. [Google Scholar] [CrossRef]
- Marszal-Pomianowska, A.J.; Johra, H.; Madsen, H.; Kazmi, H.S.; Knotzer, A.; Salom, J.; Lopes, R. Principles of Energy Flexible Buildings: Energy in Buildings and Communities Programme. 2020. Available online: https://www.annex67.org/media/1918/principles-of-energy-flexible-buildings.pdf (accessed on 15 August 2023).
- Hekimoğlu, G.; Nas, M.; Ouikhalfan, M.; Sarı, A.; Tyagi, V.; Sharma, R.; Kurbetci, S.; Saleh, T.A. Silica fume/capric acid-stearic acid PCM included-cementitious composite for thermal controlling of buildings: Thermal energy storage and mechanical properties. Energy 2020, 219, 119588. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Navarro, L.; Pisello, A.L.; Olivieri, L.; Bartolomé, C.; Sánchez, J.; Álvarez, S.; Tenorio, J.A. Behaviour of a concrete wall containing micro-encapsulated PCM after a decade of its construction. Sol. Energy 2020, 200, 108–113. [Google Scholar] [CrossRef]
- Omrany, H.; Chang, R.; Soebarto, V.; Zhang, Y.; Ghaffarianhoseini, A.; Zuo, J. A bibliometric review of net zero energy building research 1995–2022. Energy Build. 2022, 262, 111996. [Google Scholar] [CrossRef]
- Posani, M.; Veiga, M.D.R.; de Freitas, V.P. Towards resilience and sustainability for historic buildings: A review of envelope retrofit possibilities and a discussion on hygric compatibility of thermal insulations. Thermal Insulations. Int. J. Arch. Heritage 2019, 15, 807–823. [Google Scholar] [CrossRef]
- Gilka-Bötzow, A.; Folino, P.; Maier, A.; Koenders, E.A.B.; Caggiano, A. Triaxial failure behavior of highly porous cementitious foams used as heat insulation. Processes 2021, 9, 1373. [Google Scholar] [CrossRef]
- Vaou, V.; Panias, D. Thermal insulating foamy geopolymers from perlite. Miner. Eng. 2010, 23, 1146–1151. [Google Scholar] [CrossRef]
- Modesti, M.; Lorenzetti, A.; Besco, S. Influence of nanofillers on thermal insulating properties of polyurethane nanocomposites foams. Polym. Eng. Sci. 2007, 47, 1351–1358. [Google Scholar] [CrossRef]
- Gonçalves, M.C.; Margarido, F. Materials for Construction and Civil Engineering; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Arzumanyan, A. Technological peculiarities of non autoclaved foam concrete production on the base of volcanic pumice aggregates. In Materials Science. Mater. Sci. Forum 2019, 974, 206–210. [Google Scholar] [CrossRef]
- Puga, H.; Carneiro, V.; Jesus, C.; Pereira, J.; Lopes, V. Influence of particle diameter in mechanical performance of Al expanded clay syntactic foams. Compos. Struct. 2018, 184, 698–703. [Google Scholar] [CrossRef]
- Gao, H.; Liu, H.; Liao, L.; Mei, L.; Lv, G.; Liang, L.; Zhu, G.; Wang, Z.; Huang, D. Improvement of performance of foam perlite thermal insulation material by the design of a triple-hierarchical porous structure. Energy Build. 2019, 200, 21–30. [Google Scholar] [CrossRef]
- Rugele, K.; Lehmhus, D.; Hussainova, I.; Peculevica, J.; Lisnanskis, M.; Shishkin, A. Effect of fly-ash cenospheres on properties of clay-ceramic syntactic foams. Materials 2017, 10, 828. [Google Scholar] [CrossRef] [PubMed]
- Shishkin, A.; Bumanis, G.; Irtiseva, K.; Ozolins, J.; Korjakins, A. Clay Ceramic Hollow Sphere—Cement Syntactic Foam Composite for Building Applications. Key Eng. Mater. 2019, 800, 228–234. [Google Scholar] [CrossRef]
- Fernando, P.; Jayasinghe, M.; Jayasinghe, C. Structural feasibility of Expanded Polystyrene (EPS) based lightweight concrete sandwich wall panels. Constr. Build. Mater. 2017, 139, 45–51. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism Dover Publications, Unabriged 3rd ed.; Dover Publications, Inc.: New York, NY, USA, 1954; Volume 1. [Google Scholar]
- Wellander, N. Homogenization of the Maxwell Equations: Case II. Nonlinear Conductivity. Appl. Math. 2002, 47, 255–283. [Google Scholar] [CrossRef]
- Angell, T.S.; Kirsch, A. The conductive boundary condition for Maxwell’s equations. SIAM J. Appl. Math. 1992, 52, 1597–1610. [Google Scholar] [CrossRef]
- Nemilov, S.V. The review of possible interrelations between ionic conductivity, internal friction and the viscosity of glasses and glass forming melts within the framework of Maxwell equations. J. Non-Crystalline Solids 2011, 357, 1243–1263. [Google Scholar] [CrossRef]
- Goncharenko, A.V. Generalizations of the Bruggeman equation and a concept of shape-distributed particle composites. Phys. Rev. E 2003, 68, 041108. [Google Scholar] [CrossRef]
- Tjaden, B.; Cooper, S.J.; Brett, D.J.; Kramer, D.; Shearing, P.R. On the origin and application of the Bruggeman correlation for analysing transport phenomena in electrochemical systems. Curr. Opin. Chem. Eng. 2016, 12, 44–51. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, G.; Li, D.; Wang, C.; Bai, S.; Li, G.; Wang, G. Three-dimensional multi-phase simulation of cooling patterns for proton exchange membrane fuel cell based on a modified Bruggeman equation. Appl. Therm. Eng. 2020, 174, 115313. [Google Scholar] [CrossRef]
- Myers, M.T. Pore Modeling: Extending the Hanai-Bruggeman Equation. In Proceedings of the SPWLA 30th Annual Logging Symposium, Denver, CO, USA, 11–14 June 1989. [Google Scholar]
- Sanjaya, C.S. Pore Size Effect on Heat Transfer through Porous Medium. Ph.D. Thesis, National University of Singapore, Singapore, 2011. [Google Scholar]
- Skibinski, J.; Cwieka, K.; Ibrahim, S.H.; Wejrzanowski, T. Influence of pore size variation on thermal conductivity of open-porous foams. Materials 2019, 12, 2017. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, H.; Xie, P.; Najm, H. Analysis of thermal conductivity of porous concrete using laboratory measurements and microstructure models. Constr. Build. Mater. 2019, 218, 90–98. [Google Scholar] [CrossRef]
- Lewis, T.B.; Nielsen, L.E. Dynamic mechanical properties of particulate-filled composites. J. Appl. Polym. Sci. 1970, 14, 1449–1471. [Google Scholar] [CrossRef]
- Nielsen, L.E. The thermal and electrical conductivity of two-phase systems. Ind. Eng. Chem. Fundamentals 1974, 13, 17–20. [Google Scholar] [CrossRef]
- Pal, R. On the Lewis-Nielsen model for thermal/electrical conductivity of composites. Compos. Part A Appl. Sci. Manuf. 2008, 39, 718–726. [Google Scholar] [CrossRef]
- Kochetov, R.; Korobko, A.V.; Andritsch, T.; Morshuis, P.H.F.; Picken, S.J.; Smit, J.J. Three-phase lewis-nielsen model for the thermal conductivity of polymer nanocomposites. In Proceedings of the 2011 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Cancun, Mexico, 16–19 October 2011; pp. 338–341. [Google Scholar] [CrossRef]
- Montes-De-Oca, L.M.; Medina-Esquivel, R.; Zambrano-Arjona, M.; Martínez-Torres, P. Thermal detection of second critical micelle concentration in SDS and CTAB aqueous solutions using a modified Lewis-Nielsen effective thermal model. J. Mol. Liq. 2022, 363, 119864. [Google Scholar] [CrossRef]
- Pietrak, K.; Wiśniewski, T.S. A review of models for effective thermal conductivity of composite materials. J. Power Technol. 2015, 95, 14–24. [Google Scholar]
- Wang, X.J.; Niu, X.H.; Qiu, X.W.; Istikomah, N.; Wang, L.B. Thermal conductivity of porous polymer materials considering pore special-shape and anisotropy. Express Polym. Lett. 2021, 15, 319–328. [Google Scholar] [CrossRef]
- Javierre, E.; Vuik, C.; Vermolen, F.; van der Zwaag, S. A comparison of numerical models for one-dimensional Stefan problems. J. Comput. Appl. Math. 2006, 192, 445–459. [Google Scholar] [CrossRef]
- Visintin, A. Models of Phase Transitions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996; Volume 26. [Google Scholar]
- Gupta, S.C. The Classical Stefan Problem: Basic Concepts, Modelling and Analysis with Quasi-Analytical Solutions and Methods; Elsevier: Amsterdam, The Netherlands, 2017; Volume 45. [Google Scholar]
- Caggiano, A.; Mankel, C.; Koenders, E. Reviewing theoretical and numerical models for PCM-embedded cementitious composites. Buildings 2018, 9, 3. [Google Scholar] [CrossRef]
- Mankel, C.; Caggiano, A.; König, A.; Schicchi, D.S.; Sam, M.N.; Koenders, E. Modelling the thermal energy storage of cementitious mortars made with PCM-recycled brick aggregates. Materials 2020, 13, 1064. [Google Scholar] [CrossRef] [PubMed]
- Voller, V.R.; Swaminathan, C.R.; Thomas, B.G. Fixed grid techniques for phase change problems: A review. Int. J. Numer. Methods Eng. 1990, 30, 875–898. [Google Scholar] [CrossRef]
- Šavija, B.; Zhang, H.; Schlangen, E. Influence of microencapsulated phase change material (PCM) addition on (micro) mechanical properties of cement paste. Materials 2017, 10, 863. [Google Scholar] [CrossRef]
- Dobri, A.; Tsiantis, A.; Papathanasiou, T.; Wang, Y. Investigation of transient heat transfer in multi-scale PCM composites using a semi-analytical model. Int. J. Heat Mass Transf. 2021, 175, 121389. [Google Scholar] [CrossRef]
- Šavija, B.; Schlangen, E. Use of phase change materials (PCMs) to mitigate early age thermal cracking in concrete: Theoretical considerations. Constr. Build. Mater. 2016, 126, 332–344. [Google Scholar] [CrossRef]
- Fachinotti, V.; Peralta, I.; Toro, S.; Storti, B.; Caggiano, A. Automatic Generation of High-Fidelity Representative Volume Elements and Computational Homogenization for the Determination of Thermal Conductivity in Foamed Concretes. 2022. Available online: https://ssrn.com/abstract=4286262 (accessed on 15 August 2023).
- Batool, F. Effect of Microstructure on Thermal Conductivity of Cement-Based Foam. Ph.D. Thesis, University of Alberta Libraries, Edmonton, AB, Canada, 2015. [Google Scholar]
- Awang, H.; Mydin, M.A.O.; Roslan, A.F. Effect of additives on mechanical and thermal properties of lightweight foamed concrete. Adv. Appl. Sci. Res. 2012, 3, 3326–3338. [Google Scholar]
- Wei, S.; Yiqiang, C.; Yunsheng, Z.; Jones, M. Characterization and simulation of microstructure and thermal properties of foamed concrete. Constr. Build. Mater. 2013, 47, 1278–1291. [Google Scholar] [CrossRef]
- Mydin, M.A.O. Effective thermal conductivity of foamcrete of different densities. Concr. Res. Lett. 2011, 2, 181–189. [Google Scholar]
- Davraz, M.; Kilinçarslan, Ş.; Koru, M.; Tuzlak, F. Investigation of relationships between ultrasonic pulse velocity and thermal conductivity coefficient in foam concretes. Acta Phys. Pol. A 2016, 130, 469–470. [Google Scholar] [CrossRef]
- Oren, O.H.; Gholampour, A.; Gencel, O.; Ozbakkaloglu, T. Physical and mechanical properties of foam concretes containing granulated blast furnace slag as fine aggregate. Constr. Build. Mater. 2019, 238, 117774. [Google Scholar] [CrossRef]
- Jiang, J.; Lu, Z.; Niu, Y.; Li, J. Investigation of the properties of high-porosity cement foams containing epoxy resin. Constr. Build. Mater. 2017, 154, 115–122. [Google Scholar] [CrossRef]
- Jiang, J.; Lu, Z.; Niu, Y.; Li, J.; Zhang, Y. Investigation of the properties of high-porosity cement foams based on ternary Portland cement–metakaolin–silica fume blends. Constr. Build. Mater. 2016, 107, 181–190. [Google Scholar] [CrossRef]
- Neville, A.M.; Brooks, J.J. Concrete Technology; Longman Scientific & Technical: New York, NY, USA, 1987; Volume 438. [Google Scholar]
- Tran, N.P.; Nguyen, T.N.; Ngo, T.D.; Le, P.K.; Le, T.A. Strategic progress in foam Stabilization towards high-performance foam concrete for building sustainability: A state-of-the-art review. J. Clean. Prod. 2022, 375, 133939. [Google Scholar] [CrossRef]
- Kern, T. Neuses Verfahren zur experimentellen Untersuchung wässriger Schäume. Ph.D Thesis, University of Paderborn, Paderborn, Germany, 2002. [Google Scholar]
- Lohaus, L.; Pott, J.U. Konstruktionsleichtbeton unter Verwendung Vorgeschäumter Luftporen; Forschungsbericht; Institut für Baustoffe, Universität Hannover: Hanover, Germany, 2005; Available online: https://www.baustoff.uni-hannover.de/de/forschung/forschungsprojekte/forschungsprojekte-detailansicht/projects/konstruktionsleichtbeton-unter-verwendung-vorgeschaeumter-luftporen/ (accessed on 15 August 2023).
- Pott, J.U. Entwicklungsstrategien für zementgebundene Schäume. IfB. 2006. Available online: https://www.baustoff.uni-hannover.de/fileadmin/baustoff/publications/Heft05-Pott-ZemSchaum.pdf (accessed on 15 August 2023).
- Sam, M.; Caggiano, A.; Dubyey, L.; Dauvergne, J.-L.; Koenders, E. Thermo-physical and mechanical investigation of cementitious composites enhanced with microencapsulated phase change materials for thermal energy storage. Constr. Build. Mater. 2022, 340, 127585. [Google Scholar] [CrossRef]
- Available online: https://issuu.com/detail-magazine/docs/978-3-920034-18-8_bk_de_daemmstoffe (accessed on 15 August 2023).
- Schild, K. Wärmeschutz: Grundlagen-Berechnung-Bewertung; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]


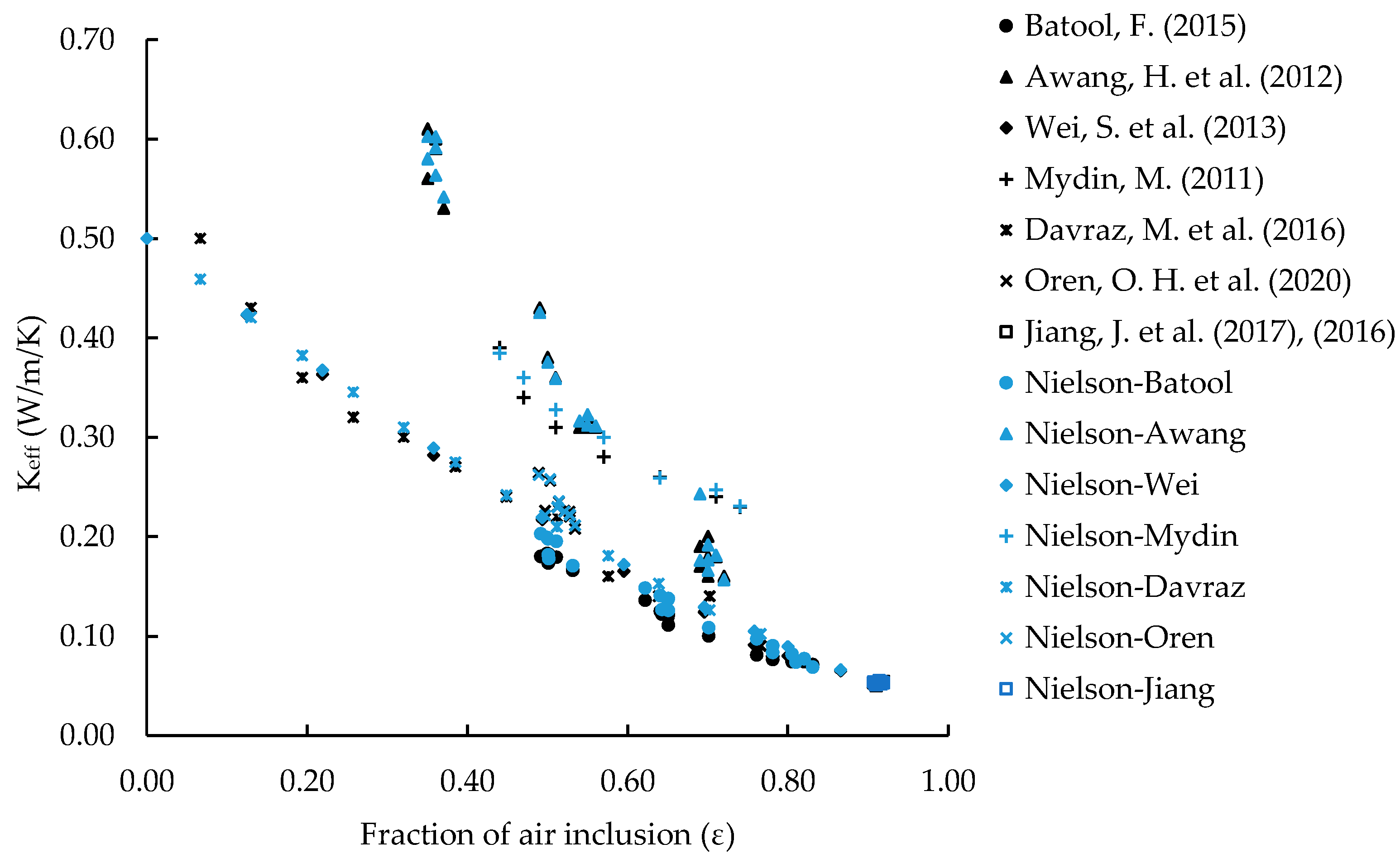
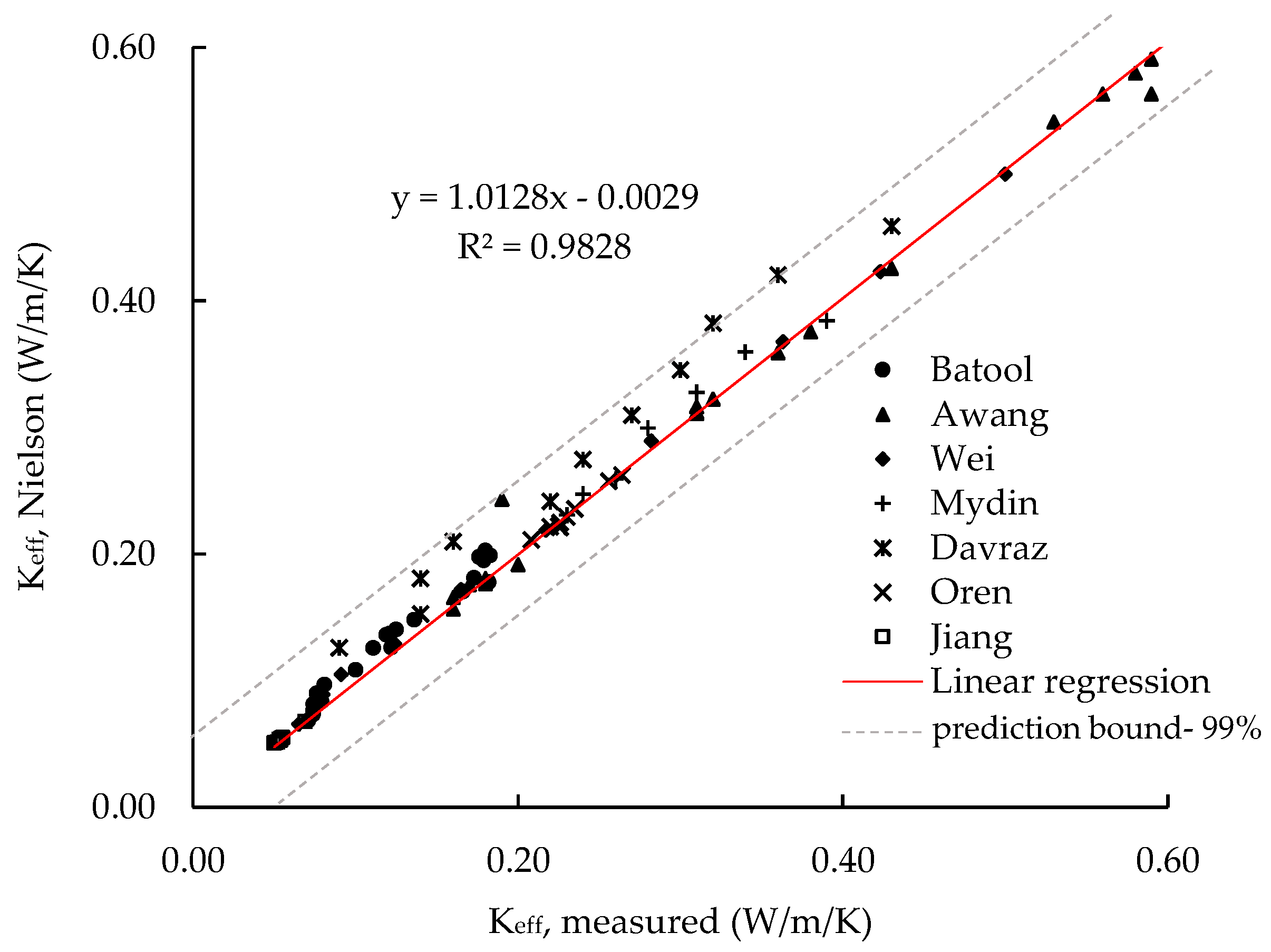



| Authors | Binder Type | Additive/Filler | W/b Ratio | Target Density ρ (kg/m3) | Dry Density ρ (kg/m3) | Matrix Conductivity (k/W/m) | Dispersed Air Content ꜫ | Foaming Agent | Foaming Method | Conductivity Measurnment Method | Foam Conductivity (k/W/m) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Batool, F. (2015) [1] | HE portland cement | Ref | 0.69 | 800 | 724 | 0.458 | 0.49 | Synthetic | Physical air-entraining | Transient plane source (TPS) | 0.180 |
| 600 | 492 | 0.458 | 0.64 | 0.125 | |||||||
| 400 | 303 | 0.458 | 0.78 | 0.076 | |||||||
| FA10 | 800 | 751 | 0.458 | 0.50 | 0.183 | ||||||
| 600 | 549 | 0.458 | 0.62 | 0.136 | |||||||
| 400 | 360 | 0.458 | 0.76 | 0.081 | |||||||
| FA20 | 800 | 710 | 0.407 | 0.50 | 0.182 | ||||||
| 600 | 499 | 0.407 | 0.64 | 0.122 | |||||||
| 400 | 273 | 0.407 | 0.81 | 0.074 | |||||||
| SF10 | 800 | 755 | 0.415 | 0.50 | 0.173 | ||||||
| 600 | 499 | 0.415 | 0.65 | 0.111 | |||||||
| 400 | 320 | 0.415 | 0.78 | 0.079 | |||||||
| SF20 | 800 | 750 | 0.416 | 0.53 | 0.166 | ||||||
| 600 | 474 | 0.416 | 0.70 | 0.100 | |||||||
| 400 | 270 | 0.416 | 0.83 | 0.071 | |||||||
| MK10 | 800 | 759 | 0.456 | 0.50 | 0.176 | ||||||
| 600 | 529 | 0.456 | 0.65 | 0.119 | |||||||
| 400 | 295 | 0.456 | 0.81 | 0.074 | |||||||
| MK20 | 800 | 756 | 0.461 | 0.51 | 0.179 | ||||||
| 600 | 533 | 0.461 | 0.65 | 0.121 | |||||||
| 400 | 276 | 0.461 | 0.82 | 0.074 | |||||||
| Awang, H. et al. (2012) [2] | SEM1 Portland cement/sand (1:1.5) | RefSa | 0.45 | 600 | n.a. | 1.400 | 0.69 | Protein-based | Physical air-entraining | Transient plane source (TPS) | 0.190 |
| 1000 | n.a. | 1.400 | 0.49 | 0.430 | |||||||
| 1400 | n.a. | 1.400 | 0.36 | 0.590 | |||||||
| FA15 | 600 | n.a. | n.a. | 0.69 | 0.170 | ||||||
| FA30 | 600 | n.a. | n.a. | 0.70 | 0.160 | ||||||
| RL15 | 600 | n.a. | n.a. | 0.72 | 0.160 | ||||||
| RL30 | 600 | n.a. | n.a. | 0.70 | 0.200 | ||||||
| PF20 | 600 | n.a. | n.a. | 0.70 | 0.180 | ||||||
| PF40 | 600 | n.a. | n.a. | 0.71 | 0.180 | ||||||
| FA15 | 1000 | n.a. | n.a. | 0.50 | 0.380 | ||||||
| FA30 | 1000 | n.a. | n.a. | 0.51 | 0.360 | ||||||
| RL15 | 1000 | n.a. | n.a. | 0.56 | 0.310 | ||||||
| RL30 | 1000 | n.a. | n.a. | 0.55 | 0.310 | ||||||
| PF20 | 1000 | n.a. | n.a. | 0.54 | 0.310 | ||||||
| PF40 | 1000 | n.a. | n.a. | 0.55 | 0.320 | ||||||
| FA15 | 1400 | n.a. | n.a. | 0.35 | 0.580 | ||||||
| FA30 | 1400 | n.a. | n.a. | 0.35 | 0.610 | ||||||
| RL15 | 1400 | n.a. | n.a. | 0.36 | 0.590 | ||||||
| RL30 | 1400 | n.a. | n.a. | 0.37 | 0.530 | ||||||
| PF20 | 1400 | n.a. | n.a. | 0.36 | 0.600 | ||||||
| PF40 | 1400 | n.a. | n.a. | 0.35 | 0.560 | ||||||
| Wei, S. et al. (2013) [3] | CEM I | FA20 | 0.40 | 1900 | 1870 | 0.500 | 0.00 | Protein-based | Physical air-entraining | Rapid-K Thermal Conductivity test | 0.500 |
| 1700 | 1636 | 0.500 | 0.13 | 0.423 | |||||||
| 1500 | 1461 | 0.500 | 0.22 | 0.363 | |||||||
| 1300 | 1201 | 0.500 | 0.36 | 0.282 | |||||||
| 1000 | 948 | 0.500 | 0.49 | 0.217 | |||||||
| 800 | 757 | 0.500 | 0.60 | 0.165 | |||||||
| 600 | 570 | 0.500 | 0.70 | 0.124 | |||||||
| 500 | 453 | 0.500 | 0.76 | 0.091 | |||||||
| 400 | 374 | 0.500 | 0.80 | 0.080 | |||||||
| 300 | 252 | 0.500 | 0.87 | 0.065 | |||||||
| Mydin, M. (2011) [4] | OPC cement/sand (2:1) | Ref | 0.50 | 650 | n.a. | n.a. | 0.74 | Protein-based | Physical air-entraining | Hot guarded plate test (HGP) | 0.230 |
| 700 | n.a. | n.a. | 0.71 | 0.240 | |||||||
| 800 | n.a. | n.a. | 0.64 | 0.260 | |||||||
| 900 | n.a. | n.a. | 0.57 | 0.280 | |||||||
| 1000 | n.a. | n.a. | 0.51 | 0.310 | |||||||
| 1100 | n.a. | n.a. | 0.47 | 0.340 | |||||||
| 1200 | n.a. | n.a. | 0.44 | 0.390 | |||||||
| Davraz, M. et al. (2016) [5] | CEM I 42.5 R Portland cement | PF/L | 0.30 | 300 | 364 | n.a. | 0.77 | Protein-based | Physical air-entraining | GHP/HFM-TS EN 12667 | 0.090 |
| 400 | 510 | n.a. | 0.70 | 0.140 | |||||||
| 500 | 563 | n.a. | 0.64 | 0.140 | |||||||
| 600 | 715 | n.a. | 0.58 | 0.160 | |||||||
| 700 | 837 | n.a. | 0.51 | 0.220 | |||||||
| 800 | 851 | n.a. | 0.45 | 0.240 | |||||||
| 900 | 965 | n.a. | 0.38 | 0.270 | |||||||
| 1000 | 1100 | n.a. | 0.32 | 0.300 | |||||||
| 1100 | 1272 | n.a. | 0.26 | 0.320 | |||||||
| 1200 | 1321 | n.a. | 0.19 | 0.360 | |||||||
| 1300 | 1429 | n.a. | 0.13 | 0.430 | |||||||
| 1400 | 1531 | n.a. | 0.07 | 0.500 | |||||||
| Oren, O. H. et al. (2020) [6] | CEM II 42.5R/sand | FA40/Sa | 0.91 | 1000 | 975 | n.a. | 0.53 | Protein-based | Physical air-entraining | Transient plane source (TPS) | 0.225 |
| 0.68 | 1000 | 1029 | n.a. | 0.51 | 0.235 | ||||||
| 0.55 | 1000 | 1033 | n.a. | 0.50 | 0.256 | ||||||
| FA40/Sa/GBS | 0.91 | 1000 | 949 | n.a. | 0.53 | 0.220 | |||||
| 0.68 | 1000 | 1004 | n.a. | 0.52 | 0.226 | ||||||
| 0.55 | 1000 | 1030 | n.a. | 0.51 | 0.230 | ||||||
| FA40/GBS | 0.91 | 1000 | 926 | n.a. | 0.53 | 0.208 | |||||
| 0.68 | 1000 | 996 | n.a. | 0.50 | 0.226 | ||||||
| 0.55 | 1000 | 1132 | n.a. | 0.49 | 0.264 | ||||||
| Jiang, J. et al. (2017) [7] (2016) [8] | CEM I 42.5 R Portland cement | ER0% | 0.60 | n.a. | n.a. | n.a. | n.a. | Protein-based | Physical air-entraining | Heat Flow Meter (HFM) | 0.059 |
| ER3% | 0.60 | n.a. | n.a. | n.a. | n.a. | 0.064 | |||||
| ER6% | 0.60 | n.a. | n.a. | n.a. | n.a. | 0.063 | |||||
| ER0% | 0.80 | n.a. | n.a. | n.a. | n.a. | 0.060 | |||||
| ER3% | 0.80 | n.a. | n.a. | n.a. | n.a. | 0.063 | |||||
| ER6% | 0.80 | n.a. | n.a. | n.a. | n.a. | 0.064 | |||||
| ER9% | 0.80 | n.a. | n.a. | n.a. | n.a. | 0.065 | |||||
| ER9% | 0.60 | n.a. | n.a. | n.a. | 0.89 | 0.069 | |||||
| Ref | 0.80 | n.a. | n.a. | n.a. | 0.92 | 0.052 | |||||
| C/SF6 | 0.80 | n.a. | n.a. | n.a. | 0.91 | 0.050 | |||||
| C/MK20 | 0.80 | n.a. | n.a. | n.a. | 0.92 | 0.054 | |||||
| C/MK20/SF6 | 0.80 | n.a. | n.a. | n.a. | 0.92 | 0.054 | |||||
| Ref | 1.00 | n.a. | n.a. | n.a. | 0.91 | 0.053 | |||||
| C/SF6 | 1.00 | n.a. | n.a. | n.a. | 0.91 | 0.051 | |||||
| C/MK20 | 1.00 | n.a. | n.a. | n.a. | 0.91 | 0.053 | |||||
| C/MK20/SF6 | 1.00 | n.a. | n.a. | n.a. | 0.91 | 0.055 |
| Air Fraction | Foam Class | Shape of Air Voids | Type of Packing | Maximum Packing Fraction (Φm) |
|---|---|---|---|---|
| ε ≥ 0.75 | I | Polyhedral | Hexagonal close | 0.74 |
| 0.75 ≥ ε ≥ 0.52 | II | Spherical | Random close | 0.64 |
| ε < 0.52 | III | Bubbles | Random loose | 0.60 |
| Air Fraction | Foam Class | A | Φm | ψ |
|---|---|---|---|---|
| ε ≥ 0.75 | I | 2.37 | 0.74 | 1.370 |
| 0.75 ≥ ε ≥ 0.52 | II | 2.90 | 0.64 | 1.563 |
| ε < 0.52 | III | 3.10 | 0.60 | 1.546 |
| Vol.- %MPCM in Paste | Keff Paste (w/b = 0.4) Solid Phase MPCM (W/m/K) | Keff Paste (w/b = 0.4) Liquid Phase MPCM (W/m/K) | |
|---|---|---|---|
| LHTES Paste | 40 | 0.600 | 0.464 |
| 20 | 0.754 | 0.759 | |
| Keff Ref Paste (W/m/K) | 0.89–0.93 | ||
| K Air(W/m/K) | 0.025 | ||
| Foam Class | Vol-. %MPCM in Paste | keff Foam Solid Phase PCM (W/m/K) | keff Foam Liquid Phase PCM (W/m/K) | |
|---|---|---|---|---|
| TES Polyhedral Foam | I | 40 | ≤0.14 | ≤0.10 |
| 20 | ≤0.17 | ≤0.15 | ||
| TES Spherical Foam | II | 40 | ≤0.24 | ≤0.20 |
| 20 | ≤0.30 | ≤0.28 | ||
| TES Polyhedral Foam | I | 0 | ≤0.2 | |
| TES Spherical Foam | II | 0 | ≤0.39 | |
| Paste [80] | Air | MPCM [80] | |
|---|---|---|---|
| Density, ρ (kg/m3) | 1708 | 1.2 | 760 |
| Sensible heat capacity, Cp (J/kg/K) | 1300 | 1000 | 2100 |
| Latent heat storage, h (kJ/kg) | 0 | 0 | 195 |
| TES-Foam 0% MPCM | TES-Foam 2% MPCM | RC-Wall | EPS [81,82] | |
|---|---|---|---|---|
| Density, ρ (kg/m3) | 200 | 90 | 2000 | 30 |
| Predicted effective conductivity, keff (W/m/K) | 0.07 * | 0.05 * | 2.1 | 0.04 |
| Volumetric heat capacity, Cp, sensible (kJ/m3/K) | 223.120 | 210.632 | 1760 | 45 |
| Latent heat storage, h (kJ/m3) | 0 | 2964 | 0 | 0 |
| TES-Foam 0% MPCM | TES-Foam 2% MPCM | RC-Wall | EPS | |
|---|---|---|---|---|
| Thermal diffusivity, α 10−5 (m2/S) | 0.0314 | 0.0237 | 0.15 | 0.08 |
| Heat penetration coefficient, b (J/(m2/k/S0.5) | 124.9 | 102.6 | 1922.5 | 42.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazari Sam, M.; Schneider, J.; Lutze, H.V. Modelling Porous Cementitious Media with/without Integrated Latent Heat Storage: Application Scenario. Energies 2023, 16, 6687. https://doi.org/10.3390/en16186687
Nazari Sam M, Schneider J, Lutze HV. Modelling Porous Cementitious Media with/without Integrated Latent Heat Storage: Application Scenario. Energies. 2023; 16(18):6687. https://doi.org/10.3390/en16186687
Chicago/Turabian StyleNazari Sam, Mona, Jens Schneider, and Holger V. Lutze. 2023. "Modelling Porous Cementitious Media with/without Integrated Latent Heat Storage: Application Scenario" Energies 16, no. 18: 6687. https://doi.org/10.3390/en16186687
APA StyleNazari Sam, M., Schneider, J., & Lutze, H. V. (2023). Modelling Porous Cementitious Media with/without Integrated Latent Heat Storage: Application Scenario. Energies, 16(18), 6687. https://doi.org/10.3390/en16186687