1. Introduction
South Africa has been ranked among several other developing and developed countries as one of the world’s leading contributors to greenhouse gas emissions; in fact, the country was ranked as the twelfth largest emitter of carbon dioxide worldwide as of 2006 [
1]. In recent years, updated rankings placed the country as the world’s fourteenth-largest greenhouse gas emitter [
2,
3]. This is because of the country’s high dependence on fossil fuels as the primary source of energy [
4,
5,
6]. At least eighty-three per cent of the coal produced in the country is produced in the Mpumalanga Province [
7]. This has led to constant complaints and cases of environmental and social issues in the region [
8]. Studies conducted in the area speak on the discontent of residents situated near plants and mines vulnerable to contracting respiratory and pulmonary sicknesses associated with the pollutants released from the plants and mines. Mines will often release particulate matter in the form of dust, which, when inhaled, can cause heart and breathing problems [
9]. In addition, the country intends to expand and open new coal plants in the region. Though this is meant to contribute to the current energy crises, it contradicts some of the country’s objectives in fulfilling its sustainable energy mandates. This triggers more concern for the future of energy in the country.
On the other hand, one can also easily look at the country’s potential in some of its green or sustainable energy sources. As the country attempts to transition to greener energy sources, the Northern Cape has been a forerunner for one of South Africa’s possible sustainable energy options, solar energy. The province has the highest number of renewable energy projects, housing about fifty-nine. Among these projects, forty-eight were identified in the 2019 Northern Cape Treasury Policy Brief (2019), where thirty-two of these projects are fully operational, one is fully operational, thirteen are awaiting construction, one is under construction, and one is halted. Most of these projects are funded by private entities or government initiatives. This ranges from banks, groups, organizations and companies [
6]. Seeing the evident contrast, specifically between the Northern Cape Province and the Mpumalanga Province, in the energy direction of the country, this research employs geostatistical techniques and the Geographical Information Systems (GIS) database tools to assess the regional solar energy potentials between the two provinces.
The Renewable Energy Independent Power Procurement Producer Programme (REIPPPP) was introduced in South Africa’s Integrated Resource Plan (IRP) of 2010 to promote collaboration between the public and private sectors in the energy market. This initiative aims to foster renewable energy production by creating a competitive environment for alternative energy, mainly through the involvement of independent producers. Despite some success, as noted by van der Merwe and Brent (2020) [
10], where over 2900 megawatts of renewable energy have been commissioned through privately funded projects worth approximately 13 billion US Dollars, the government’s slow policy implementation for integrating independent energy sources into the grid raises uncertainty among investors. This lack of clear policy and approach in the renewable energy sector, as highlighted by Kannan and Vakeesan (2016) [
11], has rendered the field less appealing. This underscores the importance of enhancing methods, data, and analytical techniques for energy assessments like the Photovoltaic Geographical Information Systems (PVGIS) [
12].
The country aims to improve the renewable energy market scene and reduce its greenhouse gas emissions as per the 2003 white paper and the Integrated Resource Plan of 2010, considering renewable energy sources such as solar energy is very important [
6,
13]. The country has also committed to reducing its greenhouse gas emissions from 398–614 metric tons of carbon dioxide emissions to about 350–420 metric tons of carbon dioxide by 2030 [
2]. This a commitment made by the country as part of its mitigation targets in the United Nations (UN) most recent National Determined Contribution (NDC). This climate action plan is part of the Paris Agreement and must be updated every five consecutive years. As such, there is a growing need to explore and invest in renewable energy sources. Analyzing the annual solar irradiance distribution and trends over the two provinces would give an idea of how South Africa can efficiently plan for the development of solar panels or technology in the most effective regions of the country for optimum solar energy harnessing.
South Africa’s “favorable” geographic positioning implies that it may have great potential in using solar energy. Through the development of geodatabases built upon years of remotely sensed data on solar energy, a web-based tool- PVGIS, (version 5.2) presents capabilities of monitoring and assessing the solar potential of different locations [
11,
14,
15]. In this regard, this research attempts to compare and assess the regional potential of solar energy between the two provinces, using data from the PVGIS tool and the Kriging technique, to study how the mentioned provinces could be suited for future solar technologies. To achieve this, this study, therefore, uses geostatistical techniques, specifically Kriging, to create spatially interpolated maps that represent the annual distribution and trends of optimum solar irradiation over the two regions, Mpumalanga and Northern Cape, based on the data acquired from the PVGIS tool (
https://re.jrc.ec.europa.eu/pvg_tools/en/) (accessed on 20 June 2022). The interpolated maps will enable the identification of sites that receive relatively high amounts of irradiation annually.
Modern-day advancements in Geographical Information Systems (GIS) and Remote Sensing (RS) techniques enable the effective and efficient analyses of such trends. Photovoltaic Geographical Information Systems (PVGIS) is one of these techniques. The PVGIS system is a web-based tool that assesses solar radiation trends daily, weekly, monthly and yearly [
10]. It uses interactive web applications for map-based queries of solar radiation databases and Photovoltaic (PV) performance assessments. The map-based query integrates a geographical database with a solar model, r.sun [
16].
The solar data are obtained from a method known as the Heliosat-2 method. The model estimates beam, diffuse, and reflected components of the clear-sky and real-sky global irradiance/irradiation on horizontal and inclined surfaces. The total daily irradiation (Wh/m
2) is computed by the integration of the irradiance values (W/m
2) that are calculated at a time step of 15 min from sunrise to sunset [
16,
17]. This database has become an essential part of a constantly developing energy assessment and monitoring sector. Lastly, since this database was developed based on remotely sensed data from satellites and model algorithms, it provides a basis for geographically monitoring and interacting with solar energy over small-scale to large-scale regions.
Using the PVGIS tool combined with geostatistical techniques, the spatial nature of solar radiation and its characteristics can be studied and presented qualitative and quantitatively. The geostatistical technique, Kriging, is used in this study. Kriging, a geostatistical method, estimates values in d-dimensional space while incorporating anisotropy [
17,
18]. It stands out for providing the best linear unbiased estimate of a variable, achieved through minimizing estimate variance based on statistical principles. This technique has proven advantageous for estimating highly variable spatial data and is particularly relevant for this study’s assessment of irradiation.
Mohd et al. (2021) [
17] mention that Kriging is the most successful for phenomena with a very strong random component or for the estimation of statistical characteristics (uncertainty). Its strength lies in countering bias through random functions and statistical techniques, leading to limited bias in estimates due to correlations derived from the semi-variogram pattern. While the user’s choice of theoretical semi-variogram function introduces some subjectivity, selecting functions closely aligned with the mean line of the variogram graph or with lower standard error and deviation can enhance predictions. It is also safe to mention that, in the attempt to predict and estimate highly spatially variable data, it is always safe to expect that specific results could potentially differ significantly and, therefore, be better predicted by a more anisotropic function [
19]. Although Kriging’s potential weakness lies in user discretion for function selection and assessing stationarity, it remains a powerful method for spatial data estimation, offering valuable insights for various applications.
Following this section of the article study are five sections: Study Area (
Section 2), Materials and Methods (
Section 3), Results (
Section 4), Discussion (
Section 5), and Conclusion (
Section 6). The Study Area is a regional and geographic background about the areas in the study. Following
Section 2 is the Materials and Methods section (
Section 3), where in-depth details about the data collection, PVGIS tool application, and spatial interpolation techniques used are explained.
Section 4, the Results section, compiles all the findings and outcomes obtained throughout the study. The Results section is followed by
Section 5, the Discussion section, where an assessment and breakdown of the findings in the Results section is made. Lastly, the Conclusion section is the final section, essentially a summarized round-up of the overall study and its findings.
2. Study Area
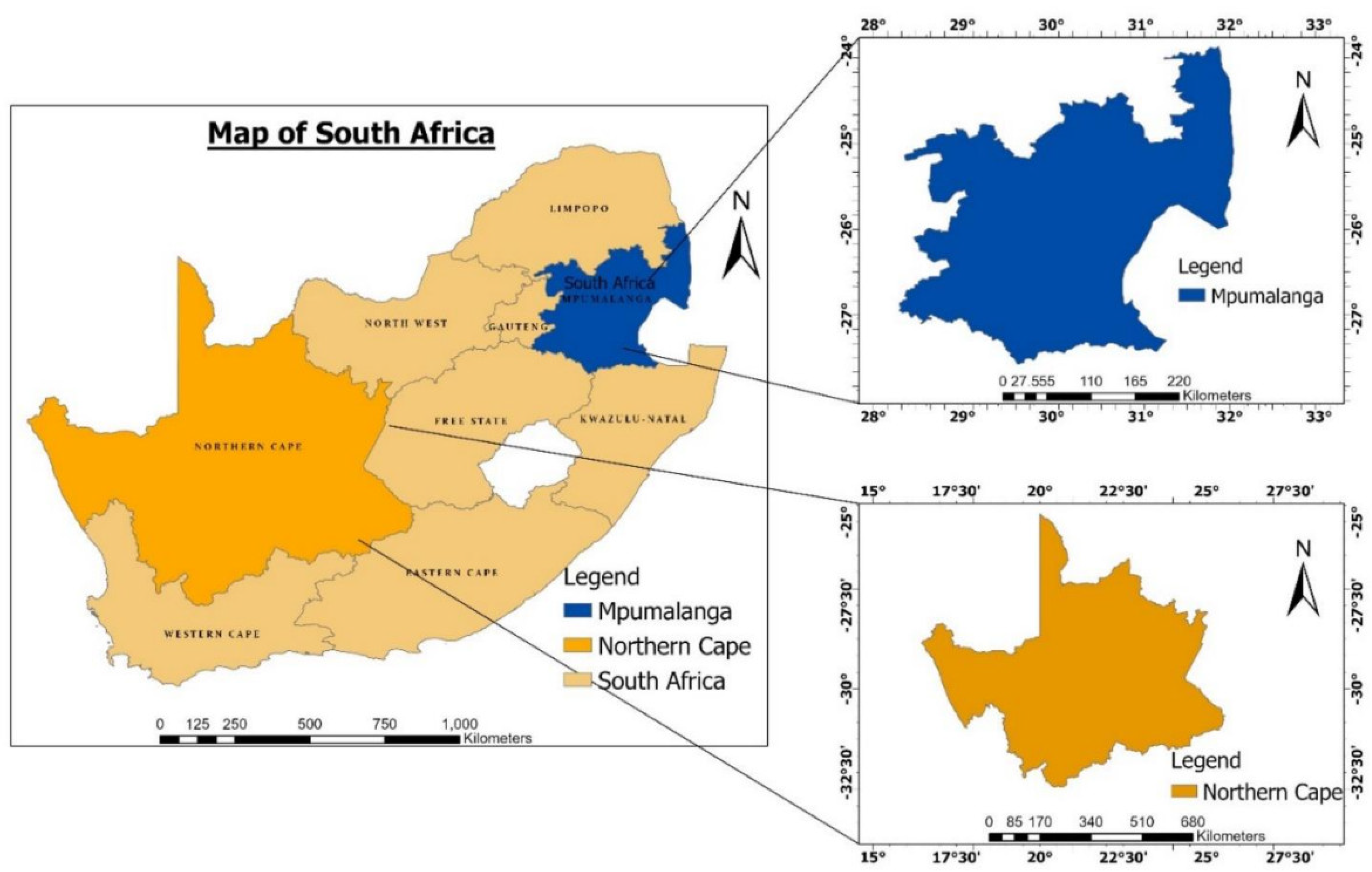
Figure 1 depicts the subjects of this study: the Mpumalanga Province and Northern Cape Province in South Africa, both situated at opposing ends of the country. Mpumalanga, located in the eastern region (25.5653° S, 30.5279° E), is characterized by mountainous terrain and divided into the Highveld and Bushveld. With an elevation ranging from 1700 to 2300 m, it experiences a varied climate, receiving most precipitation during warm, humid summers and minimal rainfall during cold, dry winters. The province houses eighty-five per cent of the country’s coal plants.
In contrast, the Northern Cape Province, South Africa’s largest, spans a vast area (29.0467° S, 21.8569° E) and is sparsely populated. It encompasses flat central regions, a hilly west coast, and the Kalahari Desert to the north. The province’s semiarid climate yields low average annual rainfall of around 200 millimeters, with varied patterns across its east and west. Known for Kimberlite diamonds, the Northern Cape has embraced renewable energy, particularly solar power, due to its favorable location, land cover, and solar exposure. This province’s inclusion in the study offers a comparative basis for assessing solar energy potential.
5. Discussion
5.1. Regional Irradiation Trends and Distribution between the Two Provinces
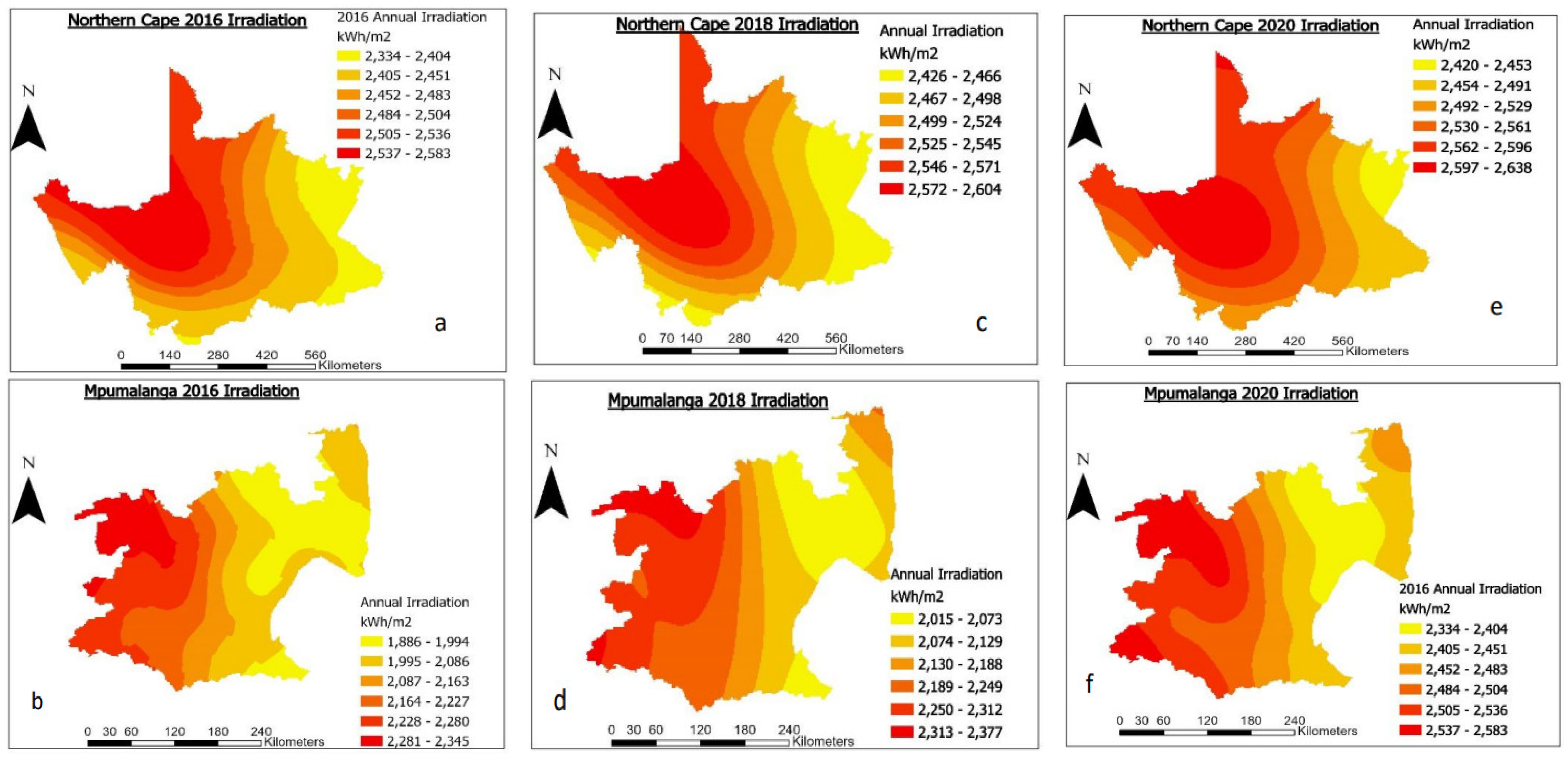
The study utilized PVGIS data to determine the optimal angles for surface placement to receive higher irradiation levels. The latitudinal positioning of the two provinces indicated an estimated optimum angle of 28° to 30° facing north (or toward the equator) for maximum annual irradiation. The Northern Cape Province exhibited greater annual optimum irradiance (ranging from 2300 kWh/m2 to 2638 kWh/m2), mainly from September to December. This region experienced the highest irradiance in its central to northwestern parts, corresponding with the Namib desert’s expanse. While generally having lower annual irradiance than the Northern Cape, Mpumalanga Province still reached significant highs. Its irradiance varied across regions; its highest areas were concentrated in the far west. Notably, Mpumalanga’s irradiance increased annually in 2018, showcasing comparable potential to the Northern Cape despite the latter’s higher average irradiance. This also implies that the region’s annual changes and irradiance fluctuations may favor potential solar energy harnessing as it may have periods of relatively higher irradiation experienced. Most importantly, the results of this study proved that both provinces have considerable solar energy potential comparable to worldwide standards despite both provinces having variable annual and regional irradiation totals.
Most of the world experiences annual irradiation ranging between 1500 kWh/m
2 and 1800 kWh/m
2 [
25]. This implies that the two study areas compare higher to most parts of the world. This supports Mpumalanga Province’s high solar energy potential for future solar technology. Based on the land use and land cover of the Mpumalanga Province, most of its built-up settings are situated toward the northwestern parts, while a considerable portion of the province’s central and eastern parts is characterized by thick forests/plantations and grasslands. These eastern parts are mostly mountainous and, therefore, have higher variability to the sun due to the shading effect [
26]. Therefore, in predicting how the Mpumalanga Province may fare for future solar systems, it can be suggested that panels could be placed on buildings or built structures. The existence of built environments at the irradiance hotspots of the province implies that building incorporated panels would be more efficient, while, in the less built areas, solar array farms can be built. However, as mentioned by Sinah et al. (2014) [
27], building incorporated panels are preferred over panel or array farms as they would require less environmental reconstruction to design and install.
5.2. Validation of PVGIS Data Quality and Interpolation Reliability
To validate the accuracy and reliability of the maps and results produced, a comparison of the optimum solar irradiation obtained for the Mpumalanga and Northern Cape provinces is made against the optimum tilted solar irradiation obtained from the Global Solar Atlas. The Global Solar Atlas is a web-based tool the World Bank Group developed to simulate different information about solar energy and regional photovoltaic potential. The Solar Atlas tool uses the Solargis database, a sophisticated model calculating solar radiation using Meteosat Prime and IODC satellite data from 1994 (2000). The annual average irradiance obtained for the three years of the two provinces in this research is compared with that of the Solar Atlas data. In this case, the optimum irradiation data from the Solar Atlas will be a comparative “ground truth” measurement to what was obtained using the PVGIS and Kriging technique in this paper.
The first agreement in both results (Kriging and PVGIS used in this research versus Solar Atlas) is that of the optimum angle estimated. Both tools and results estimate that the optimum angle for a plane within the two provinces should be between 28° and 30° north-facing. This is a good result, seeing that there is a common expectation as to what the orientation of a plane in either province should be to receive optimum irradiation.
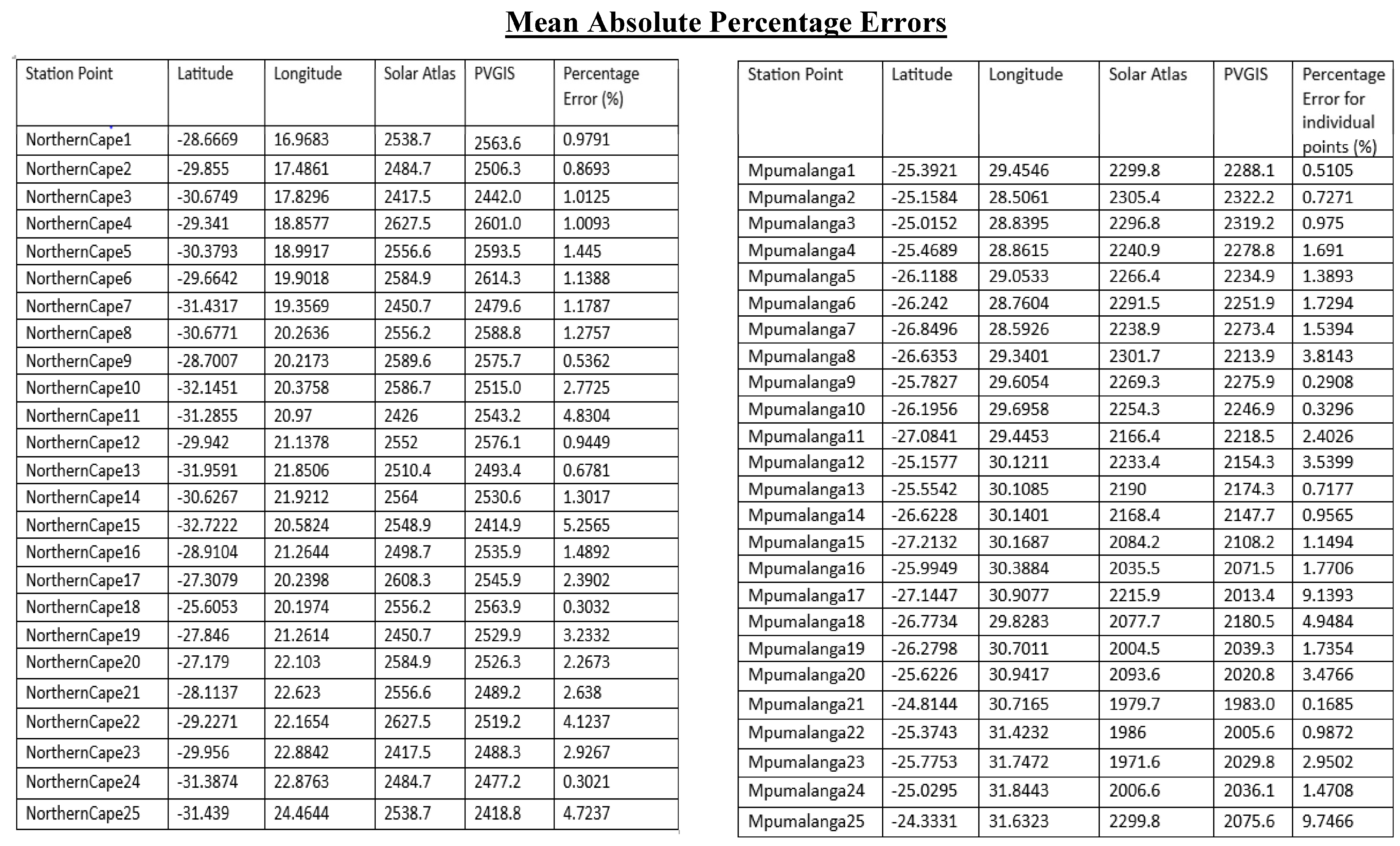
Two evaluation and comparison methods are used for validation: (1) Mean Absolute Percentage Error (MAPE) for the yearly optimum irradiation for the predicted regions; (2) visual comparison of the overall annual optimum irradiation over the 3-year maps between Kriging and PVGIS maps (used in this research) and the maps of the Solar Atlas. The mean absolute percentage error is a common metric that forecasts errors between predicted and actual datasets [
26]. The mean absolute percentage error is calculated using the equation:
where
n is the total number of points or stations used in the prediction for either province,
Ai Fi are the actual values (Solar Atlas) and forecasted or predicted values (PVGIS and Kriging), respectively. The mean optimum annual irradiation results obtained using Kriging and PVGIS in this research will form the predicted data of the equation, while the mean optimum annual irradiation obtained from the Solar Atlas will act as the observed or expected value. The table in
Appendix A shows the results of the optimum monthly irradiation from using PVGIS and Kriging for all the measured and predicted points, as well as their Solar Atlas monthly optimum irradiation and the individual percentage errors of those stations/points. The same percentages are summed and averaged to obtain the final and overall mean average percentage error.
Results after the application of the MAPE show that the PVGIS Kriging estimates and prediction used in this research performed very well when evaluated with the Solar Atlas optimum irradiation. This is confirmed by the overall annual error amounting to 1.98505% for the Northern Cape Province and 2.32625% for the Mpumalanga Province. Additionally, the MAPE of the individual stations or points used for the prediction in both provinces shows relatively low errors, ranging from the lowest of 0.3021% to the highest of 9.7466%. The complete tabular summary containing all the information relating to the MAPE of all the individual points can be accessed in
Appendix A. Generally, a mean absolute error between 0% and 5% is regarded as a very low error and an accurately acceptable result. In the case of this research, such results are achieved implying that not only are the achieved results closely accurate to that of the solar data, but it also means that the results of this paper associated with the kriging technique are well validated and present relatively minimal offset and reliable results. This further supports the reliability of the performance of the overall estimation conducted using Kriging and PVGIS. Essentially, the prediction algorithm used in this study performed accurately. Improvements to the reliability of the results can, in future, be compared with other databases, including ground-truth data.
Finally, it is also worth mentioning that since Kriging is essentially a spatial interpolation technique used to estimate the relative value of a specific feature in space based on already known points (or areas), slight offset errors may occur between predicted regions versus areas with already known data. However, the results presented in this research imply that the Stable Kriging interpolation method produced acceptable or relatively results since the final interpolation output bias ranged between 0.889721% and 1.679798% when cross-validated with points of known data.
Figure 6 illustrates consistent patterns in both sets of maps, indicating the highest and lowest optimum irradiation areas for the Northern Cape and Mpumalanga provinces. Results from PVGIS (version 5.2) and Kriging closely align with Solar Atlas data, demonstrating a high level of agreement. For Northern Cape, the highest irradiation values are nearly identical (2606 kWh/m
2 PVGIS vs. 2611 kWh/m
2 Solar Atlas), and lows show minimal variance (2434 kWh/m
2 PVGIS vs. 2376 kWh/m
2 Solar Atlas). Similarly, both maps exhibit similar spatial trends and closely matched high and low irradiation values for Mpumalanga. This alignment underscores the effectiveness of Kriging interpolation, reinforcing its utility in estimating spatial variables.
5.3. Limitations and Recommendations
The study examined annual optimum irradiation levels and their regional variations. Still, potential influencing factors like diffuse irradiation, temperature, sun exposure hours, and azimuth angle were not isolated due to their automatic deduction by PVGIS algorithms. Future research could benefit from incorporating these factors to enhance understanding of solar irradiance patterns. While solar irradiance reflects sun energy reaching Earth’s surface, it does not directly correspond to actual electrical output due to losses during conversion using different PV materials, energy transfer, and occasional anomalies. Moreover, solar irradiance fluctuates daily.
Interpolation, a method for representing spatial data, has inherent limitations tied to its purpose. The success of variable analysis using Kriging models relies on data quality relative to the semi-variogram, and changing models can yield diverse outcomes. There is not a universally superior model; the optimal choice may also depend on the data [
28]. Future studies could explore alternative interpolation techniques to minimize errors and variance, allowing for a more comprehensive representation of the data.
6. Conclusions
This study effectively employed Kriging interpolation to illustrate solar energy distribution and spatial variation in Northern Cape Province and Mpumalanga, generating maps depicting optimum annual irradiation with a low estimate error of 1.25% to 2.27%. The interpolation revealed moderate-to-strong spatial dependency, indicating meaningful autocorrelation among nearby values. In other words, attribute values of the points of data near one another are significantly influential and correlated to each other. This is good because it implies homogeneity of the output as opposed to high randomness. Furthermore, the validation process solidifies the reliability of PVGIS in regional solar irradiation assessment, with the overall Mean Absolute Percentage Error (MAPE) results falling within the range from 1.98505% to 2.32625% for the Northern Cape and Mpumalanga provinces when comparing the PVGIS tool to data from the Solar Atlas.
The annual optimum irradiation patterns offer insights into regional solar energy variability at an optimal angle (28° to 30°), providing estimated expectations for yearly irradiation in the provinces. Comparing both provinces, the Northern Cape exhibited higher irradiation, while Mpumalanga’s northwestern parts displayed comparable potential. Hotspots were identified in Mpumalanga’s western regions and Northern Cape’s central and northern areas, with Northern Cape showing minimal regional variation in optimum irradiation compared to Mpumalanga’s higher variability. Mpumalanga’s high spatial variation in irradiation in optimum irradiation ranges from relatively low to high, while Northern Cape’s spatial variation in irradiation ranges from moderately high to very high. It is for that very reason that the two have significant differences. For future recommendations, assessing actual PV outputs in these regions, potentially using the PVGIS tool, could enhance understanding of PV system performance based on irradiance, contributing to solar energy system insights in these provinces.