Massive Multi-Source Joint Outbound and Benefit Distribution Model Based on Cooperative Game
Abstract
:1. Introduction
- (1)
- An advanced three-party joint delivery operation model, integrating wind, photovoltaic, and thermal power, is established utilizing mixed-integer linear programming (MILP), and a novel improved ant lion algorithm is introduced to effectively solve this model;
- (2)
- To address the mathematical model presented in this paper, an enhanced ant lion optimization algorithm (MALO) is proposed. By incorporating the vortex convergence method into the modeling, the improved algorithm not only enhances the utilization ability compared to the original algorithm, but also aligns seamlessly with the biological mechanism of an ant lion preying on ants;
- (3)
- The incremental benefits derived from the joint operation of wind, photovoltaic, and thermal power are allocated using the M-Shapley value method, overcoming the limitations observed in the conventional Shapley value method. This leads to a more equitable and efficient benefit distribution strategy for the three-party joint operation.
2. Joint Wind, Photovoltaic, and Thermal Power Delivery Model
2.1. Optimal Target Function
2.2. Constraint Condition
2.2.1. Maximum Transmission Power Constraint
2.2.2. Transmission Power Stability Constraint
2.2.3. Thermal Power Unit Output Constraint
2.2.4. Start–Stop Time Constraint of Thermal Power Unit
2.2.5. Wind Farm and Solar Electric Field Output Constraints
2.2.6. Generation Reserve Constraint
3. Improved ALO Algorithms
3.1. The Original Ant Lion Optimization Algorithm
- ➀
- The ant population moves in a random manner following the guidelines specified by Equation (18). However, to guarantee that the ants traverse the feasible region in a randomized fashion, certain adjustments are applied based on Equation (20):
- ➁
- As the ant moves in a random manner, it becomes subject to the influence of the trap set by the ant lion. This interaction is mathematically expressed as follows:
- ➂
- If an ant falls into the trap, the ant lion will promptly respond by hurling sand towards the trap’s edge, effectively hindering the ant from escaping. As a consequence, the ant’s activity range progressively diminishes over time. This phenomenon can be mathematically represented as follows:
- ➃
- Each ant can only be captured by a single ant lion, and the specific ant lion to capture an ant is determined using the Roulette Wheel approach. Ant lions that are more fit have a higher likelihood of capturing ants. To make this determination, the individual fitness of each ant lion is compared to the individual fitness of the ant. If the individual fitness of the ant surpasses that of the ant lion, the ant lion preys on the ant, and its position is then replaced with the position of the ant. This process concludes with the update of the ant lion’s position. The mathematical formula representing this process is as follows:
- ➄
- The elite strategy of the ant lion involves the calculation of the fitness for each individual ant lion. The ant lion that exhibits the highest fitness value emerges as the elite ant lion. This winning ant lion is designated as the elite member of the population. The mathematical expression representing this process is as follows:
- ➅
- The update of the ant population is performed to preserve the global diversity of ants after each iteration. This update is carried out based on the mathematical expression (28).
3.2. Ant Lion Algorithm Enhancement
3.2.1. Improve the Roulette Selection Values
3.2.2. Vortex Convergence
3.3. Improved Antlion Algorithm Steps
- (1)
- Input the original data and various constraints, determine the size and dimension of ants and ant lions, randomly initialize the positions of ants and ant lions within the feasible region, and calculate their respective fitness values;
- (2)
- Select the ant lion with the highest fitness level in the ant lion population as the elite ant lion;
- (3)
- Conduct random walks for the chosen ant lion, optimizing the Roulette Wheel approach and the current optimal ant lion, and then update the position of the ant using Formula (30);
- (4)
- Calculate and compare the fitness of the ants after the position update with the fitness of the ant lion. If it is lower than the ant lion’s fitness, the ant lion is replaced, and the finest fitness ant lion within the ant lion population becomes the new elite ant lion. The new step update formula generates a new population, calculates the fitness values, directly compares them to the fitness of the elite ant lion, and selects the value with the best fitness as the elite ant lion;
- (5)
- Determine if the maximum number of iterations has been reached; if so, conclude the iteration; otherwise, continue with Step (3).
4. Cooperative Game and Profit Distribution Model
4.1. Cooperation Game Model
4.2. Shapley Profit Distribution Model
4.3. M-Shapley Profit Distribution Model
5. Example Analysis
5.1. Simulation Setup
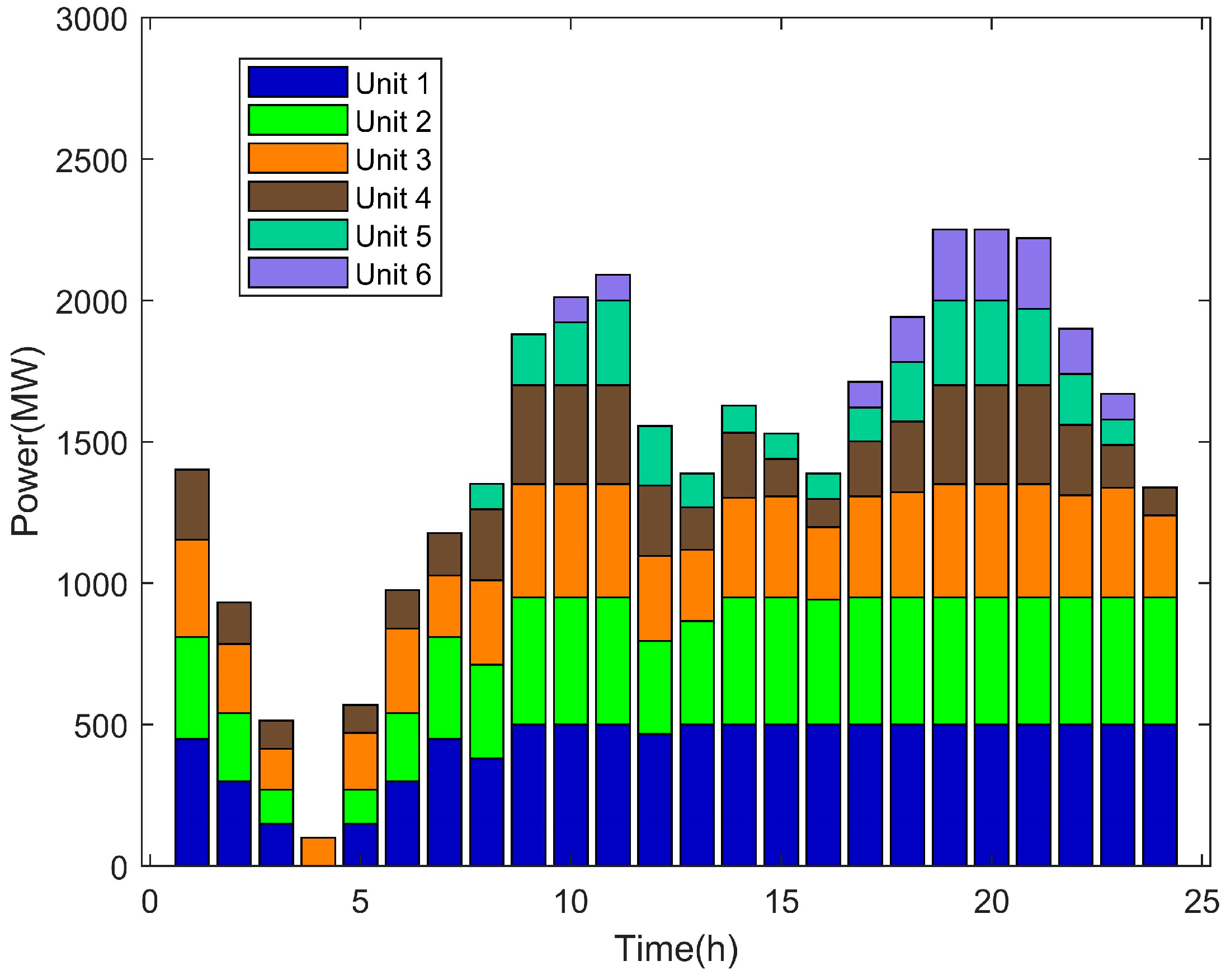
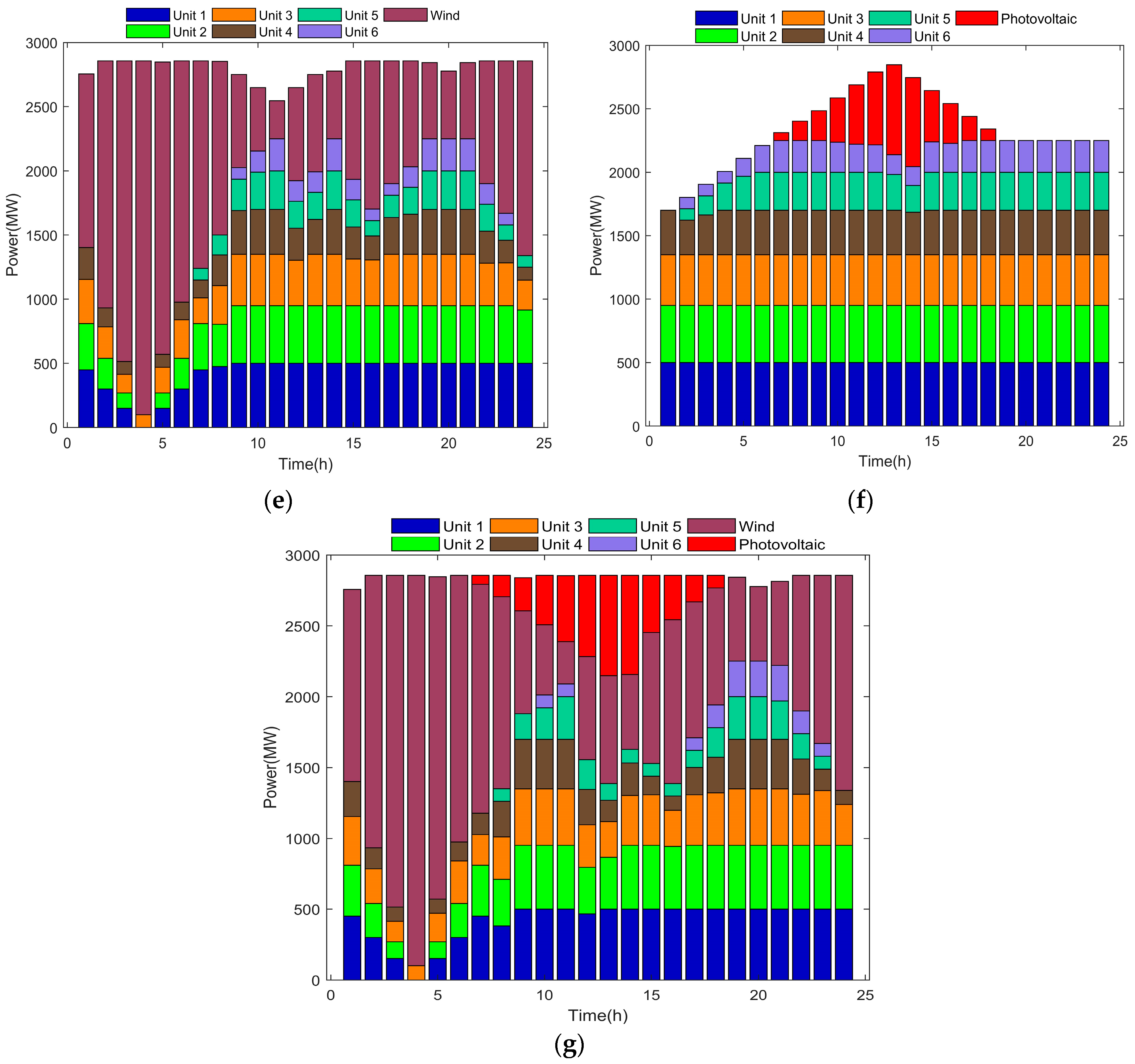
5.2. Power Transmission Simulation Results
5.3. M-Shapley Value Allocation Strategy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, Y.; Li, C.; Zhao, Y. Source-grid-load multi-period optimal scheduling method considering wind-photovoltaic-photothermal combined DC transmission. Proc. CSEE 2022, 42, 559–573. [Google Scholar]
- He, W.; Liu, M.; Wang, K.; Pan, B. Massive Multi-source Joint Outbound and Benefit Distribution Model Based on Cooperative Game. In Proceedings of the 2023 IEEE International Conference on Power Science and Technology (ICPST), Kunming, China, 5–7 May 2023; pp. 519–527. [Google Scholar]
- Shen, J.; Wang, Y.; Cheng, C. Research status and prospect of water-wind-solar multi-energy complementary power generation scheduling problem. Proc. CSEE 2022, 42, 3871–3885. [Google Scholar]
- Zhang, B.; Yu, J.; Huang, W. Challenges and thinking of large-scale new energy transmission power grid in Gansu. Grid. Clean. Energy 2020, 36, 81–89, 96. [Google Scholar]
- Mei, H.; Gao, B.; Cao, Z. Optimal configuration of wind-solar-thermal-storage combined delivery system with CSP power station. J. Solar. Energy 2022, 43, 124–133. [Google Scholar]
- Alassi, A.; Bañales, S.; Ellabban, O.; Adam, G.; MacIver, C. HVDC Transmission: Technology Review, Market Trends and Future Outlook. Renew. Sustain. Energy Rev. 2019, 112, 530–554. [Google Scholar] [CrossRef]
- Li, Q.; Zhao, D.; Yin, J. Sediment Instability Caused by Gas Production from Hydrate-bearing Sediment in Northern South China Sea by Horizontal Wellbore: Evolution and Mechanism. Nat. Resour. Res. 2023, 32, 1595–1620. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Jiang, B.; Zhuo, H.; Chen, W.; Chen, Y.; Li, X. Low-loading Pt nanoparticles combined with the atomically dispersed FeN4 sites supported by FeSA-N-C for improved activity and stability towards oxygen reduction reaction/hydrogen evolution reaction in acid and alkaline media. J. Colloid Interface Sci. 2023, 635, 514–523. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, C.; Yang, Y.; Ansari, U.; Han, Y.; Li, X.; Cheng, Y. Preliminary experimental investigation on long-term fracture conductivity for evaluating the feasibility and efficiency of fracturing operation in offshore hydrate-bearing sediments. Ocean Eng. 2023, 281, 114949. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, Y.; Pan, X. A short-term optimal scheduling model for wind- solar- hydro hybrid generation system with cascade hydropower considering regulation reserve and spinning reserve requirements. IEEE Access 2021, 9, 10765–10777. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, Y.; Xie, T.; Zhang, K.; He, X. Wind Power Consumption Model Based on the Connection between Mid- and Long-Term Monthly Bidding Power Decomposition and Short-Term Wind-Thermal Power Joint Dispatch. Energies 2022, 15, 7201. [Google Scholar] [CrossRef]
- Xu, D.; Guo, J.; Ding, X. Co-evolutionary genetic algorithm based joint economic dispatch of wind-solar-storage in distribution network. New Technol. Electr. Energy 2020, 39, 51–57. [Google Scholar]
- Li, F. Study on Improving Transient Stability of Wind-Thermal-Bundled System by Current-Limiting SSSC; Northeast Electric Power University: Jilin, China, 2021. [Google Scholar]
- Xu, J.; Liu, L.; Wang, F. Equilibrium strategybased economic- reliable approach for day ahead scheduling towards solar wind gas hybrid power generation system: A case study from China. Energy 2022, 240, 122728. [Google Scholar] [CrossRef]
- Rana, M.M.; Atef, M.; Sarkar, M.R.; Uddin, M.; Shafiullah, G. A Review on Peak Load Shaving in Microgrid—Potential Benefits, Challenges, and Future Trend. Energies 2022, 15, 2278. [Google Scholar] [CrossRef]
- Tan, Q.; Ding, Y.; Li, Y. Multi-objective optimization of wind-solar-thermal joint dispatch strategy considering economic-environmental balance. Power Const. 2020, 41, 129–136. [Google Scholar]
- Contreras, J. A Cooperative Game Theory Approach to Transmission Planning in Power Systems. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1997. [Google Scholar]
- Tan, Z.; Song, Y.; Zhang, H.; Shang, J. Large-scale wind power and thermal power combined delivery system and its profit distribution model. Power Syst. Auto 2013, 37, 63–70. [Google Scholar]
- Wu, D.; Yu, A. Profit allocation based on nucleolus theory in large-scale multi-source joint delivery coordination scheduling. Power System Technol. 2016, 40, 2975–2981. [Google Scholar]
- Chen, C.; Wu, C.; Kang, K.; Lin, X.; Ma, Y.; Sui, Q.; Xu, H. Optimal Strategy of Distributed Energy Storage Two-layer Cooperative Game Based on Improved Owen-Value Method. Proc. CSEE 2022, 42, 3924–3936. [Google Scholar]
- Ye, G.; Gao, F. Coordinated Optimization Scheduling of Data Center and Electricity Retailer Based on Cooperative Game Theory. CPSS Trans. Power Electr. App. 2022, 9, 273–282. [Google Scholar] [CrossRef]
- Owen, G. Values of Games with a Priori Unions. In Mathematical Economics and Game Theory; Springer: Berlin/Heidelberg, Germany, 1977; Volume 141, pp. 76–88. [Google Scholar]
- Shapley, L.S. A Value for n-Person Games. Contributions to the Theory of Games II; Princeton University Press: Princeton, NJ, USA, 1953; pp. 307–317. [Google Scholar]
- Xie, J.; Zhang, L.; Chen, X. Incremental benefit allocation for joint operation of multi-stakeholder wind-PV-hydro complementary generation system with cascade hydro-power: An Aumann-Shapley value method. IEEE Access 2020, 8, 68668–68681. [Google Scholar] [CrossRef]
- Ma, T.; Pei, W.; Xiao, H. Cooperative operation method for wind-solar-hydrogen multi-agent energy system based on Nash bargaining theory. Proc. CSEE 2021, 41, 25–39. [Google Scholar]
- Li, X.; Yang, Y. Joint optimal dispatch of wind power and cascade hydropower with hydrogen storage based on bi-directional electricity price compensation. Power Syst. Technol. 2020, 44, 3297–3305. [Google Scholar]
- Shandilya, S.K.; Izonin, I.; Singh, K.K. Modeling and Comparative Analysis of Multi-Agent Cost Allocation Strategies Using Cooperative Game Theory for the Modern Electricity Market. Energies 2022, 15, 2352. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, J.; Chen, X. Cooperative game-based synergistic gains allocation methods for wind-solar-hydro hybrid generation system with cascade hydropower. Energies 2020, 13, 3890. [Google Scholar] [CrossRef]
- Shi, H. Research on the Mechanism of Wind-Thermal Energy Delivery and Benefit Distribution Based on Cooperative Game; Xian University of Technology: Xi’an, China, 2019. [Google Scholar]
- Mirjalili, R. The ant lion optimizer. Adv. Eng. Soft. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, Y.; Zheng, Y. Remaining useful life prediction of lithium-ion battery based on ALO-SVR. China J. Electr. Eng. 2021, 41, 1445–1457. [Google Scholar]
- Liu, S.; Gao, Z.; Li, M. A closed-form logarithmic spiral method for seismic passive earth pressure in anisotropic sand. Comput. Geotech. 2022, 152, 105052. [Google Scholar] [CrossRef]
- Xie, Y.; Yao, Y.; Wang, Y.; Cha, W.; Zhou, S.; Wu, Y.; Huang, C. A Cooperative Game-Based Sizing and Configuration of Community-Shared Energy Storage. Energies 2022, 15, 8626. [Google Scholar] [CrossRef]
- Wu, W.; Zhu, J.; Chen, Y. Modified Shapley Value-Based Profit Allocation Method for Wind Power Accommodation and Deep Peak Regulation of Thermal Power. IEEE Trans. Ind. App. 2023, 59, 276–288. [Google Scholar] [CrossRef]
- Devi, N.N.; Thokchom, S.; Singh, T.D.; Panda, G.; Naayagi, R.T. Multi-Stage Bargaining of Smart Grid Energy Trading Based on Cooperative Game Theory. Energies 2023, 16, 4278. [Google Scholar] [CrossRef]
- Branzei, R.; Dimitrov, D.; Tijs, S. Models in Cooperative Game Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]

| Time Period | Utilization Ratio | Time Period | Utilization Ratio | Time Period | Utilization Ratio |
|---|---|---|---|---|---|
| 1 | 0.41 | 9 | 0.22 | 17 | 029 |
| 2 | 0.59 | 10 | 0.15 | 18 | 0.25 |
| 3 | 0.71 | 11 | 0.09 | 19 | 0.18 |
| 4 | 084 | 12 | o.22 | 20 | 0.16 |
| 5 | 0.69 | 13 | 0.23 | 21 | 0.18 |
| 6 | 0.57 | 14 | 0.16 | 22 | 0.29 |
| 7 | 0.49 | 15 | 0.28 | 23 | 0.36 |
| 8 | 0.41 | 16 | 0.35 | 24 | 0.46 |
| Mode of Operation | Abandoned Wind Rate/% | Photovoltaic Curtailment Ratio/% |
|---|---|---|
| Tripartite Union | 1.60 | 0 |
| Wind power independence | 37.82 | - |
| Photoelectric independence | - | 9.82 |
| Solving Algorithm | Profit | Literature |
|---|---|---|
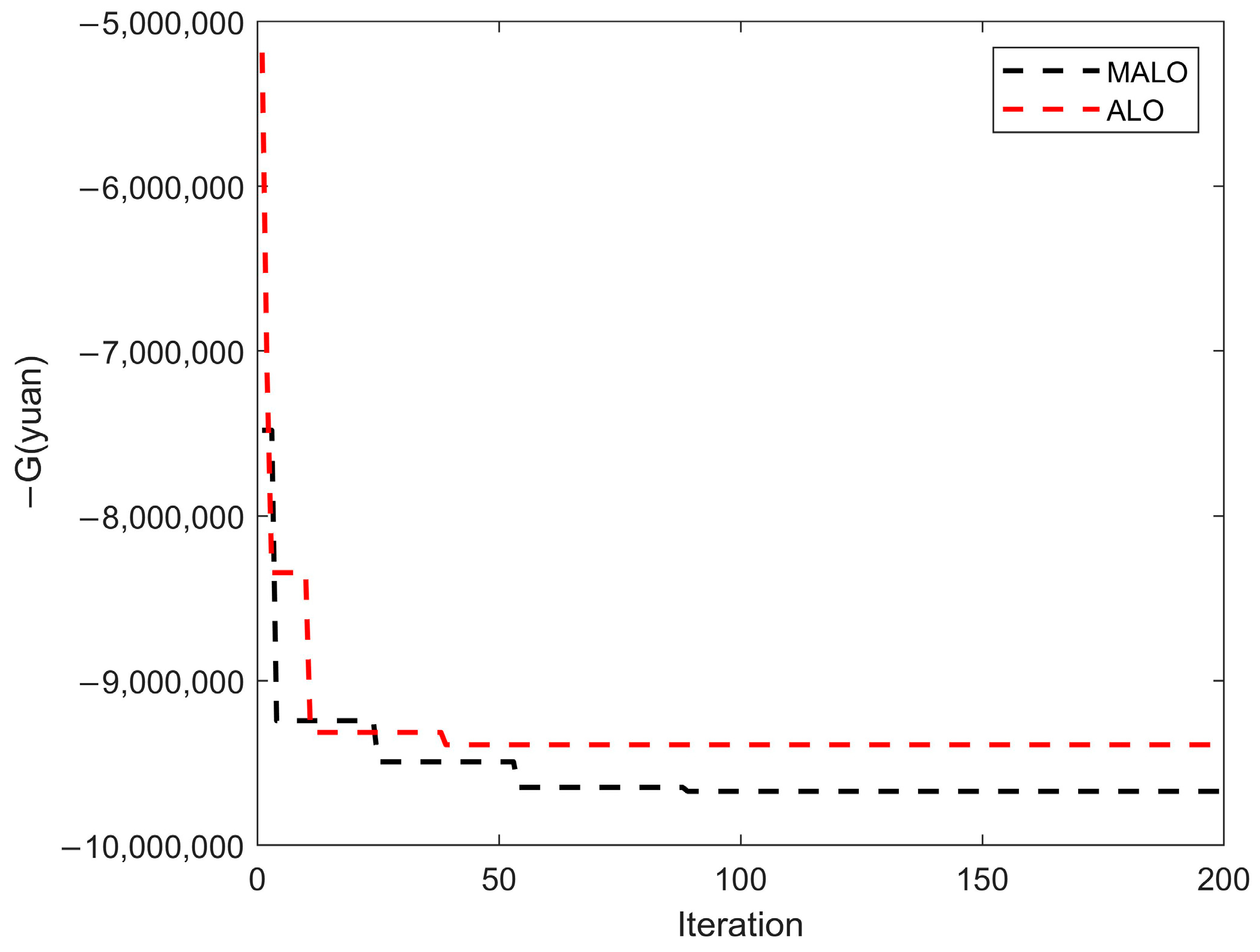
| ALO | 9,484,652/Yuan | -- |
| LINGO optimizer | 9,514,652/Yuan | Literature [19] |
| MALO | 9,669,273/Yuan | -- |
| Operating Mode | Tripartite Union | Combined Thermal and Wind Power | Combined Thermal Power and Photovoltaic | Wind Power, Photovoltaic Joint |
|---|---|---|---|---|
| Profit/Yuan | 9,669,273 | 8,856,441 | 3,276,310 | 4,165,790 |
| Operating mode | Thermal power independence | Wind power independence | Photoelectric independence | |
| Profit/Yuan | 2,521,129 | 1,936,098 | 629,670 |
| Distribution Mode | Wind Power | Photovoltaic | Thermal Power | |||
|---|---|---|---|---|---|---|
| Profit/Ten Thousand Yuan | Profit Ratio/Ten Thousand Yuan | Profit/Ten Thousand Yuan | Profit Ratio/Ten Thousand Yuan | Profit/Ten Thousand Yuan | Profit Ratio/Ten Thousand Yuan | |
| Direct distribution | 7,534,297.52 | 77.92% | 1,534,513.63 | 15.87% | 600,461.85 | 6.21% |
| M-Shapley strategy | 4,389,361.42 | 45.39% | 1,324,250.26 | 13.70% | 3,955,661.32 | 40.91% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, W.; Liu, M.; Zuo, C.; Wang, K. Massive Multi-Source Joint Outbound and Benefit Distribution Model Based on Cooperative Game. Energies 2023, 16, 6590. https://doi.org/10.3390/en16186590
He W, Liu M, Zuo C, Wang K. Massive Multi-Source Joint Outbound and Benefit Distribution Model Based on Cooperative Game. Energies. 2023; 16(18):6590. https://doi.org/10.3390/en16186590
Chicago/Turabian StyleHe, Wang, Min Liu, Chaowen Zuo, and Kai Wang. 2023. "Massive Multi-Source Joint Outbound and Benefit Distribution Model Based on Cooperative Game" Energies 16, no. 18: 6590. https://doi.org/10.3390/en16186590
APA StyleHe, W., Liu, M., Zuo, C., & Wang, K. (2023). Massive Multi-Source Joint Outbound and Benefit Distribution Model Based on Cooperative Game. Energies, 16(18), 6590. https://doi.org/10.3390/en16186590







