Drilling Deeper in Shallow Geoexchange Heat Pump Systems—Thermogeological, Energy and Hydraulic Benefits and Restraints
Abstract
:1. Introduction
2. Methods
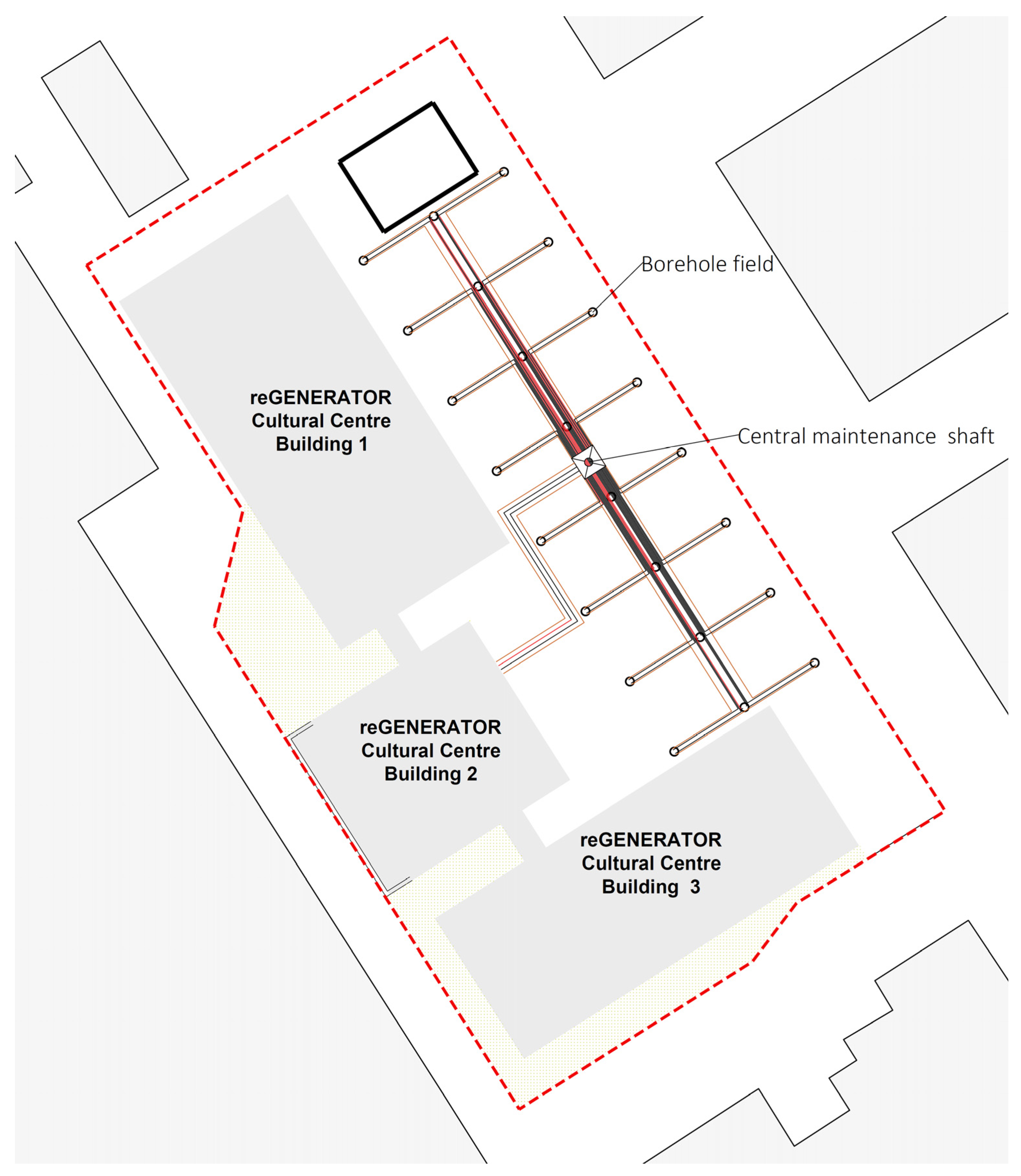
3. Case Study Project Data and Thermogeological Environment
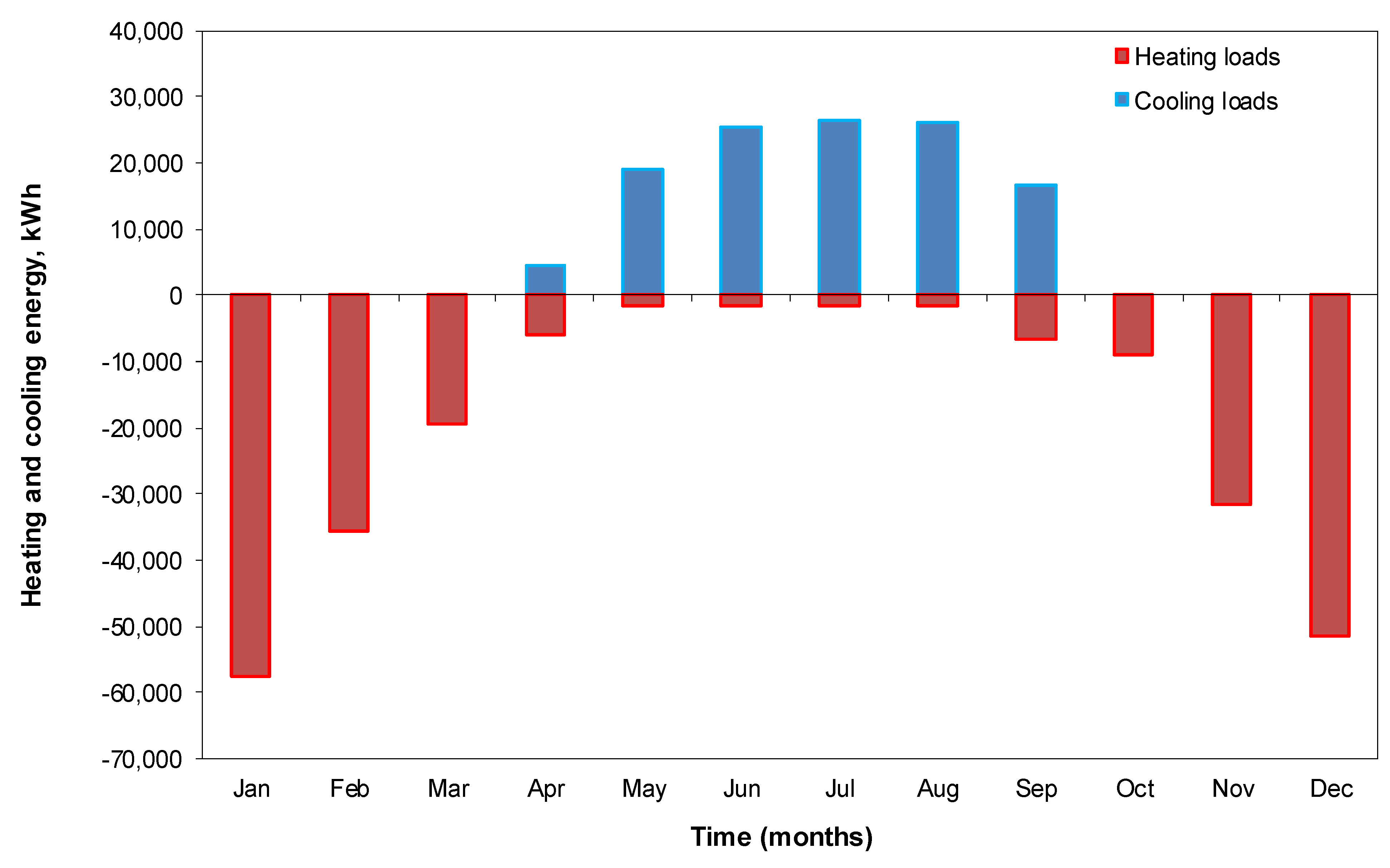
4. Results
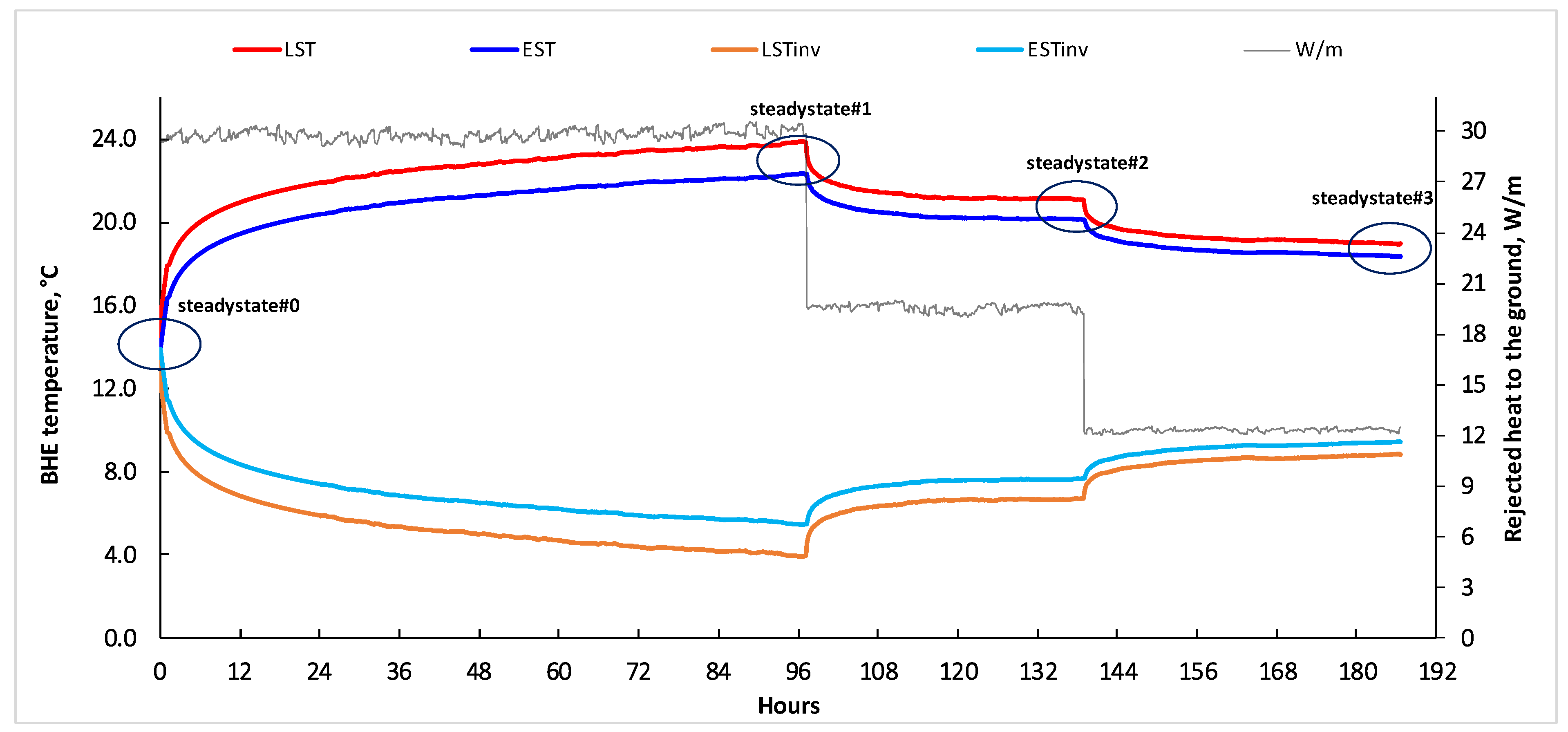
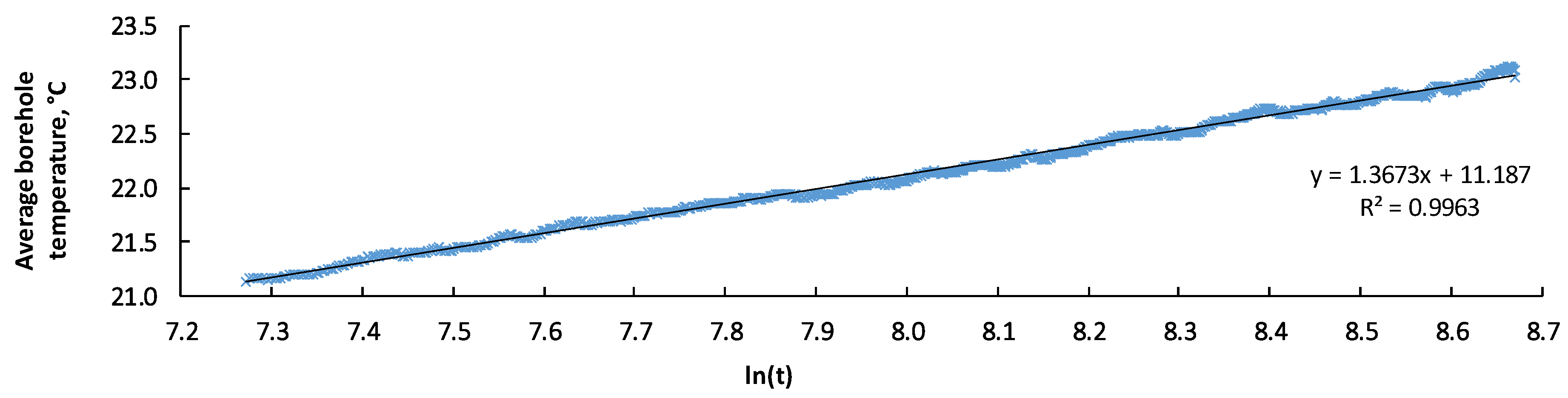
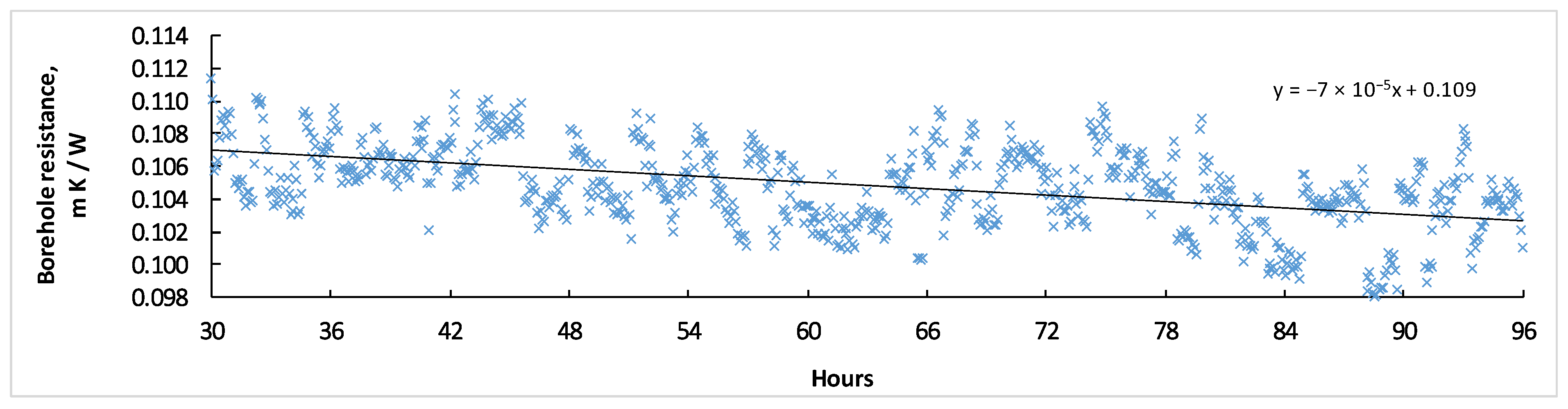
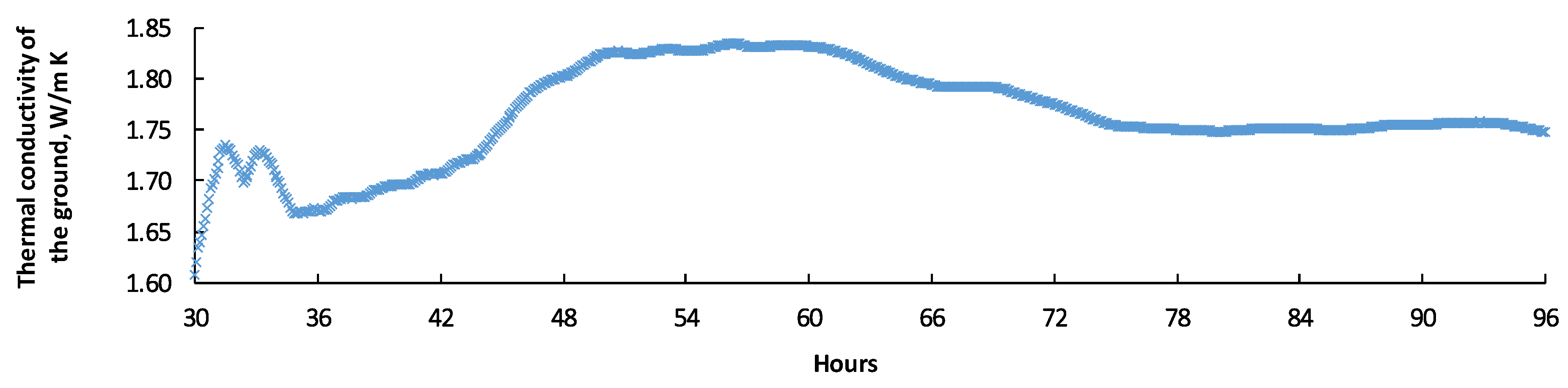
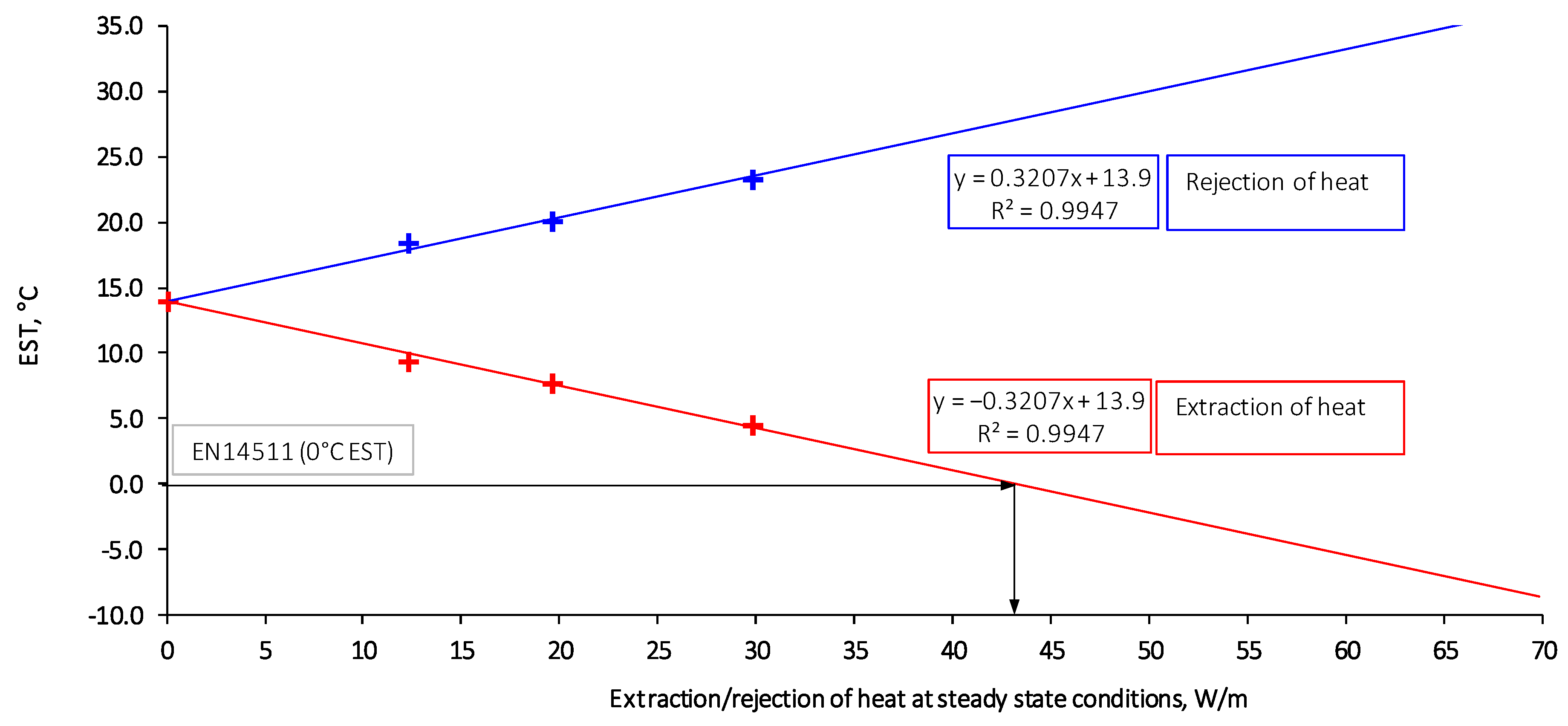
4.1. Results of Performing the Thermal Response Test (TRT) as the Project Groundwork
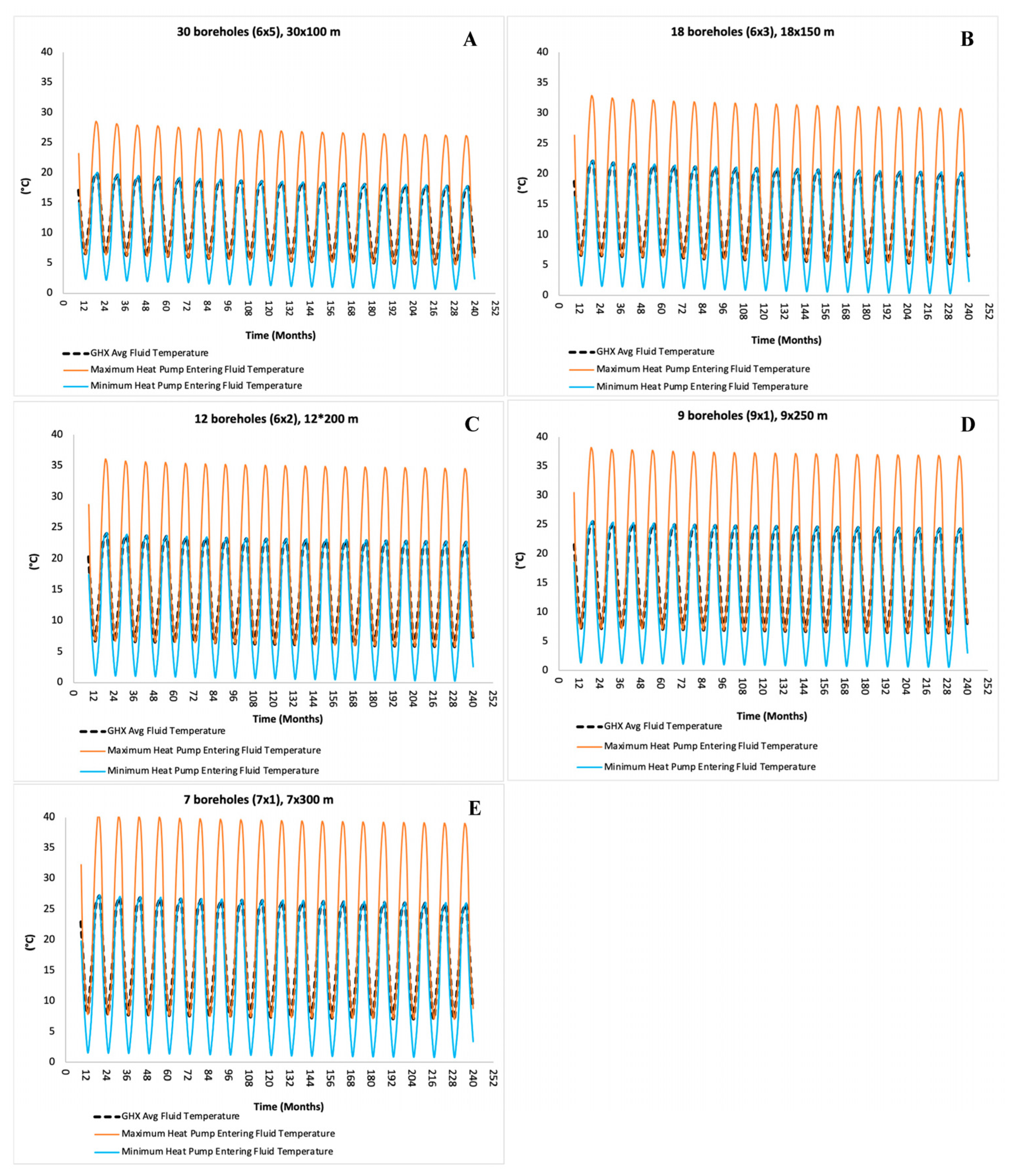
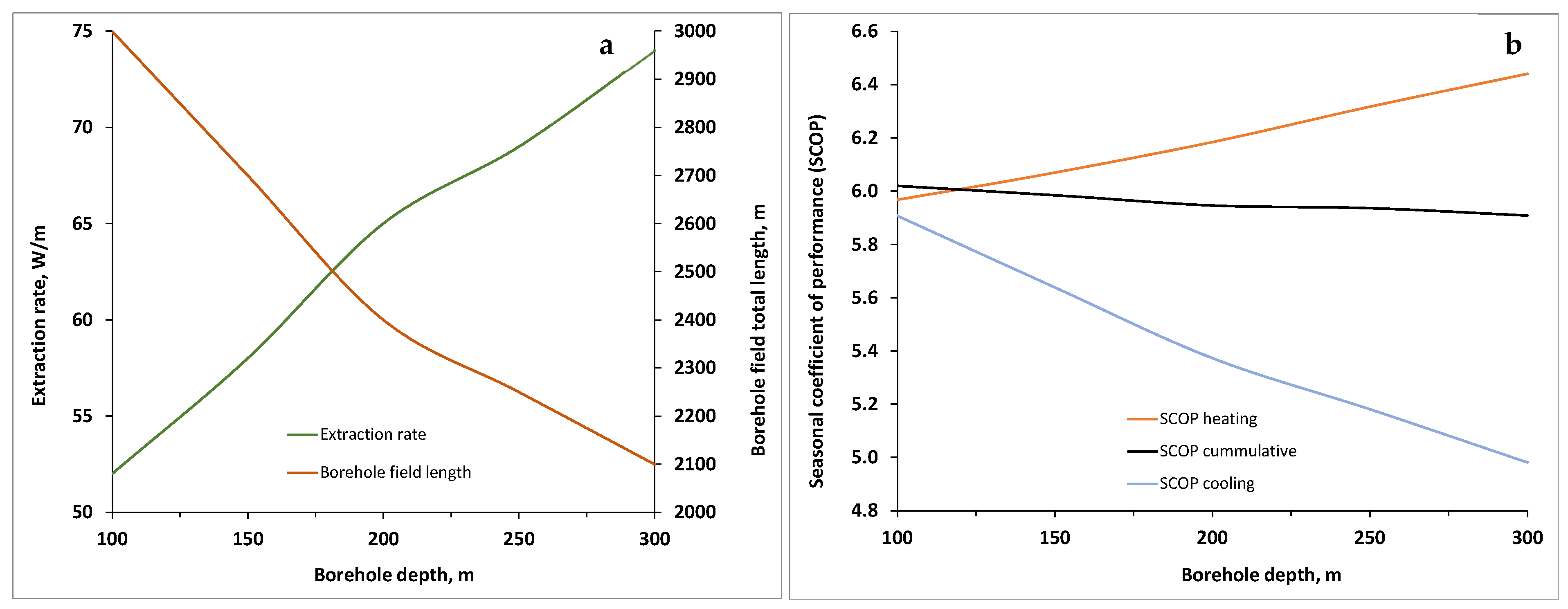
4.2. Sensitivity Analysis for Various BHE Depths
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Euler number (2.7183) | |
| exponential integral | |
| borehole heat exchanger diameter, (mm) | |
| borehole depth (m) | |
| heat power per meter of a borehole, (W/m) | |
| equivalent borehole thermal resistance, (m K/W) | |
| radius, (m) | |
| borehole radius, (m) | |
| time, (s) | |
| temperature in function of radius and time, (°C) | |
| temperature, (°C) | |
| initial borehole temperature, (°C) | |
| skin factor, (-) | |
| thermal diffusivity, (m2/s) | |
| temperature drop/rise due to skin effect, (°C) | |
| Euler’s constant () | |
| slope of the line | |
| thermal conductivity, (W/m K) |
References
- Kavadias, K.; Jimenez Navarro, J.; Thomassen, G. Decarbonising the EU Heating Sector: Integration of the Power and Heating Sector; EUR 29772 EN; Publications Office of the European Union: Luxembourg, 2019; ISBN 978-92-76-08386-3. JRC114758. [Google Scholar] [CrossRef]
- EHPA. Heat Pump Record: 3 Million Units Sold in 2022, Contributing to REPowerEU Targets. Available online: https://www.ehpa.org/press_releases/heat-pump-record-3-million-units-sold-in-2022-contributing-to-repowereu-targets/ (accessed on 4 April 2023).
- De Swardt, C.A.; Meyer, J.P. A performance comparison between an air-source and a ground-source reversible heat pump. Int. J. Energy Res. 2001, 25, 899–910. [Google Scholar] [CrossRef]
- Walch, A.; Mohajeri, N.; Gudmundsson, A.; Scartezzini, J.L. Quantifying the technical geothermal potential from shallow borehole heat exchangers at regional scale. Renew. Energy 2021, 165, 369–380. [Google Scholar] [CrossRef]
- Lee, S.M.; Park, S.H.; Jang, Y.S.; Kim, E.J. Proposition of Design Capacity of Borehole Heat Exchangers for Use in the Schematic-Design Stage. Energies 2021, 14, 822. [Google Scholar] [CrossRef]
- Letizia Fascì, M.; Lazzarotto, A.; Acuna, J.; Claesson, J. Analysis of the thermal interference between ground source heat pump systems in dense neighborhoods. Sci. Technol. Built Environ. 2019, 25, 1069–1080. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Sun, P.; Kong, X.; Sun, S. Effect of depth and fluid flow rate on estimate for borehole thermal resistance of single U-pipe borehole heat exchanger. Renew. Energy 2020, 147, 2399–2408. [Google Scholar] [CrossRef]
- Kurevija, T.; Macenić, M.; Sabolić, T.; Jovanović, D. Defining geoexchange extraction rates in the same geological envi-ronment for different borehole geometry settings–Pilot results from the HAPPEN-HORIZON 2020 project. Rud. Geološko-Naft. Zb. (Min. Geol. Pet. Eng. Bull.) 2021, 3, 99–113. [Google Scholar] [CrossRef]
- Casasso, A.; Sethi, R. Efficiency of closed loop geothermal heat pumps: A sensitivity analysis. Renew. Energy 2014, 62, 737–746. [Google Scholar] [CrossRef]
- Jun, L.; Xu, Z.; Jun, G.; Jie, Y. Evaluation of heat exchange rate of GHE in geothermal heat pump systems. Renew. Energy 2009, 34, 2898–2904. [Google Scholar] [CrossRef]
- Galgaro, A.; Farina, Z.; Emmi, G.; De Carli, M. Feasibility analysis of a Borehole Heat Exchanger (BHE) array to be installed in high geothermal flux area: The case of the Euganean Thermal Basin, Italy. Renew. Energy 2015, 78, 93–104. [Google Scholar] [CrossRef]
- Rybach, L. Global Status, Development and Prospects of Shallow and Deep Geothermal Energy. Int. J. Terr. Heat Flow Appl. Geotherm. 2022, 5, 20–25. [Google Scholar] [CrossRef]
- Piipponen, K.; Martinkauppi, A.; Korhonen, K.; Vallin, S.; Arola, T.; Bischoff, A.; Leppäharju, N. The deeper the better? A thermogeological analysis of medium-deep borehole heat exchangers in low-enthalpy crystalline rocks. Geotherm. Energy 2022, 10, 12. [Google Scholar] [CrossRef]
- Aničić, B.; Juriša, M. Basic Geological Map of SFRJ—Page Rogatec; Croatian Geological Survey: Zagreb, Croatia, 1984. [Google Scholar]
- Macenić, M.; Kurevija, T.; Medved, I. Novel geothermal gradient map of the Croatian part of the Pannonian Basin System based on data interpretation from 154 deep exploration wells. Renew. Sustain. Energy Rev. 2020, 132, 110069. [Google Scholar] [CrossRef]
- Nakić, Z.; Bačani, A.; Parlov, J.; Duić, Ž.; Perković, D.; Kovač, Z.; Tumara, D.; Mijatović, I.; Špoljarić, D.; Ugrina, I.; et al. Definiranje Trendova i Ocjena Stanja Podzemnih Voda na Području Panonskog Dijela Hrvatske; Expert study; Faculty of Mining, Geology and Petroleum Engineering: Zagreb, Croatia, 2016. [Google Scholar]
- Gehlin, S. Thermal Response Test: Method Development and Evaluation. Ph.D. Thesis, Lulea University of Technology, Lulea, Sweden, 2002. [Google Scholar]
- Kurevija, T.; Strpić, K.; Koščak-Kolin, S. Applying petroleum the pressure buildup well test procedure on thermal response test—A novel method for analyzing temperature recovery period. Energies 2018, 11, 366. [Google Scholar] [CrossRef]
- Kurevija, T.; Macenić, M.; Strpić, K. Steady-state heat rejection rates for a coaxial borehole heat exchanger during passive and active cooling determined with the novel step thermal response test method. Rud. Geološko-Naft. Zb. (Min. Geol. Pet. Eng. Bull.) 2018, 33, 61–71. [Google Scholar] [CrossRef]
- Kurevija, T.; Macenić, M.; Borović, S. Impact of grout thermal conductivity on the long-term efficiency of the ground-source heat pump system. Sustain. Cities Soc. 2017, 31, 1–11. [Google Scholar] [CrossRef]
- Kurevija, T.; Strpić, K. Hydraulic and thermogeological design differences between two-loop vertical and inclined coaxial borehole heat exchangers. Renew. Energy 2018, 117, 314–323. [Google Scholar] [CrossRef]
- Eklöf, C.; Gehlin, S. A Mobile Equipment for Thermal Response Test. Master’s Thesis, Luleå University of Technology, Luleå, Sweden, 1996. Available online: https://www.diva-portal.org/smash/get/diva2:1032479/FULLTEXT01.pdf (accessed on 17 July 2023).


| Propylene Glycol Vol. Conc., % | 15.0 | Depth, m | Re | pD, Bar | ΔT, °C | Extraction, kW | Flow, l/s Both Pipes | Flow, l/s per Pipe |
|---|---|---|---|---|---|---|---|---|
| Pipe sdr11 | 2U D40/32.7 mm | 100 | 2360 | 0.083 | 3.3 | 5.2 | 0.400 | 0.200 |
| Specific heat, kJ/kg °C | 3.986 | 150 | 2573 | 0.144 | 5.0 | 8.7 | 0.437 | 0.218 |
| Density, kg/m3 | 1019.8 | 200 | 3847 | 0.380 | 5.0 | 13.0 | 0.652 | 0.326 |
| Viscosity, mPas | 3.37 | 250 | 5110 | 0.771 | 5.0 | 17.3 | 0.866 | 0.433 |
| Freezing point, °C | −5.3 | 300 | 6573 | 1.427 | 5.0 | 22.2 | 1.114 | 0.557 |
| Propylene glycol vol. conc., % | 20.0 | Depth, m | Re | pD, bar | ΔT, °C | Extraction, kW | Flow, l/s both pipes | Flow, l/s per pipe |
| Pipe sdr11 | 2U D40/32.7 mm | 100 | 2367 | 0.120 | 2.8 | 5.2 | 0.480 | 0.240 |
| Specific heat, kJ/kg °C | 3.929 | 150 | 2367 | 0.180 | 4.6 | 8.7 | 0.480 | 0.240 |
| Density, kg/m3 | 1025.8 | 200 | 3264 | 0.414 | 5.0 | 13.0 | 0.662 | 0.331 |
| Viscosity, mPas | 4.05 | 250 | 4330 | 0.836 | 5.0 | 17.3 | 0.878 | 0.439 |
| Freezing point, °C | −7.3 | 300 | 5572 | 1.546 | 5.0 | 22.2 | 1.130 | 0.565 |
| Propylene glycol vol. conc., % | 25.0 | Depth, m | Re | pD, bar | ΔT, °C | Extraction, kW | Flow, l/s both pipes | Flow, l/s per pipe |
| Pipe sdr11 | 2U D40/32.7 mm | 100 | 2345 | 0.222 | 2.1 | 5.2 | 0.650 | 0.325 |
| Specific heat, kJ/kg °C | 3.861 | 150 | 2345 | 0.342 | 3.5 | 8.7 | 0.650 | 0.325 |
| Density, kg/m3 | 1031.0 | 200 | 2431 | 0.472 | 5.0 | 13.0 | 0.673 | 0.337 |
| Viscosity, mPas | 5.57 | 250 | 3225 | 0.951 | 5.0 | 17.3 | 0.894 | 0.447 |
| Freezing point, °C | −10.0 | 300 | 4148 | 1.753 | 5.0 | 22.2 | 1.150 | 0.575 |
| Propylene Glycol Vol. Conc., % | 15.0 | Depth, m | Re | pD, Bar | ΔT, °C | Extraction, kW | Flow, l/s per Pipe |
|---|---|---|---|---|---|---|---|
| Pipe sdr11 | 1U D45/36.8 mm | 100 | 2726 | 0.074 | 5.0 | 5.2 | 0.261 |
| Specific heat, kJ/kg °C | 3.986 | 150 | 4582 | 0.269 | 5.0 | 8.7 | 0.437 |
| Density, kg/m3 | 1019.8 | 200 | 6837 | 0.714 | 5.0 | 13.0 | 0.652 |
| Viscosity, mPas | 3.37 | 250 | 9081 | 1.458 | 5.0 | 17.3 | 0.866 |
| Freezing point, °C | −5.3 | 300 | 11,681 | 2.710 | 5.0 | 22.2 | 1.114 |
| Propylene glycol vol. conc., % | 20.0 | Depth, m | Re | pD, bar | ΔT, °C | Extraction, kW | Flow, l/s per pipe |
| Pipe sdr11 | 1U D45/36.8 mm | 100 | 2322 | 0.082 | 5.0 | 5.2 | 0.265 |
| Specific heat, kJ/kg °C | 3.929 | 150 | 3882 | 0.292 | 5.0 | 8.7 | 0.443 |
| Density, kg/m3 | 1025.8 | 200 | 5802 | 0.775 | 5.0 | 13.0 | 0.662 |
| Viscosity, mPas | 4.05 | 250 | 7695 | 1.576 | 5.0 | 17.3 | 0.878 |
| Freezing point, °C | −7.3 | 300 | 9903 | 2.928 | 5.0 | 22.2 | 1.130 |
| Propylene glycol vol. conc., % | 25.0 | Depth, m | Re | pD, bar | ΔT, °C | Extraction, kW | Flow, l/s per pipe |
| Pipe sdr11 | 1U D45/36.8 mm | 100 | 2372 | 0.159 | 3.6 | 5.2 | 0.370 |
| Specific heat, kJ/kg °C | 3.861 | 150 | 2891 | 0.333 | 5.0 | 8.7 | 0.451 |
| Density, kg/m3 | 1031.0 | 200 | 4314 | 0.877 | 5.0 | 13.0 | 0.673 |
| Viscosity, mPas | 5.57 | 250 | 5724 | 1.779 | 5.0 | 17.3 | 0.893 |
| Freezing point, °C | −10.0 | 300 | 7372 | 3.300 | 5.0 | 22.2 | 1.150 |
| Propylene Glycol Vol. Conc., % | 15.0 | Depth, m | Re | pD, Bar | ΔT, °C | Extraction, kW | Flow, l/s per Pipe |
|---|---|---|---|---|---|---|---|
| Pipe sdr11 | 1U TC50/40.9 mm | 100 | 2462 | 0.059 | 5.0 | 5.2 | 0.261 |
| Specific heat, kJ/kg °C | 3.986 | 150 | 4123 | 0.164 | 5.0 | 8.7 | 0.437 |
| Density, kg/m3 | 1019.8 | 200 | 6152 | 0.434 | 5.0 | 13.0 | 0.652 |
| Viscosity, mPas | 3.37 | 250 | 8171 | 0.884 | 5.0 | 17.3 | 0.866 |
| Freezing point, °C | −5.3 | 300 | 10,510 | 1.640 | 5.0 | 22.2 | 1.114 |
| Propylene glycol vol. conc., % | 20.0 | Depth, m | Re | pD, bar | ΔT, °C | Extraction, kW | Flow, l/s per pipe |
| Pipe sdr11 | 1U TC50/40.9 mm | 100 | 2366 | 0.061 | 4.4 | 5.2 | 0.300 |
| Specific heat, kJ/kg °C | 3.929 | 150 | 3493 | 0.178 | 5.0 | 8.7 | 0.443 |
| Density, kg/m3 | 1025.8 | 200 | 5220 | 0.471 | 5.0 | 13.0 | 0.662 |
| Viscosity, mPas | 4.05 | 250 | 6876 | 0.945 | 5.0 | 17.3 | 0.872 |
| Freezing point, °C | −7.3 | 300 | 8910 | 1.778 | 5.0 | 22.2 | 1.130 |
| Propylene glycol vol. conc., % | 25.0 | Depth, m | Re | pD, bar | ΔT, °C | Extraction, kW | Flow, l/s per pipe |
| Pipe sdr11 | 1U TC50/40.9 mm | 100 | 2365 | 0.115 | 3.3 | 5.2 | 0.410 |
| Specific heat, kJ/kg °C | 3.861 | 150 | 2601 | 0.203 | 5.0 | 8.7 | 0.451 |
| Density, kg/m3 | 1031.0 | 200 | 3882 | 0.533 | 5.0 | 13.0 | 0.673 |
| Viscosity, mPas | 5.57 | 250 | 5151 | 1.081 | 5.0 | 17.3 | 0.893 |
| Freezing point, °C | −10.0 | 300 | 6633 | 2.003 | 5.0 | 22.2 | 1.150 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurevija, T.; Macenić, M.; Tuschl, M. Drilling Deeper in Shallow Geoexchange Heat Pump Systems—Thermogeological, Energy and Hydraulic Benefits and Restraints. Energies 2023, 16, 6577. https://doi.org/10.3390/en16186577
Kurevija T, Macenić M, Tuschl M. Drilling Deeper in Shallow Geoexchange Heat Pump Systems—Thermogeological, Energy and Hydraulic Benefits and Restraints. Energies. 2023; 16(18):6577. https://doi.org/10.3390/en16186577
Chicago/Turabian StyleKurevija, Tomislav, Marija Macenić, and Martina Tuschl. 2023. "Drilling Deeper in Shallow Geoexchange Heat Pump Systems—Thermogeological, Energy and Hydraulic Benefits and Restraints" Energies 16, no. 18: 6577. https://doi.org/10.3390/en16186577
APA StyleKurevija, T., Macenić, M., & Tuschl, M. (2023). Drilling Deeper in Shallow Geoexchange Heat Pump Systems—Thermogeological, Energy and Hydraulic Benefits and Restraints. Energies, 16(18), 6577. https://doi.org/10.3390/en16186577








