A Graph-Theoretic Approach for Optimal Phasor Measurement Units Placement Using Binary Firefly Algorithm
Abstract
:1. Introduction
State-of-the-Art OPP Algorithms
- This paper proposes a Binary Firefly Algorithm (BFA) for optimal PMU placement in a degree centrality-ranked undirected graph search space. In this approach, the algorithm demonstrates the ability to locate the global minima through a descending node degree centrality score search manner.
- This paper investigates the possibility of finding a balance in PMU installation costs and observability reliability by a consideration of topological network issues coupled with practical contingencies using established observability performance metrics.
2. Power System Observability Analysis
2.1. Topological Observability Case Factors
2.1.1. Normal Operation without ZIB Effect
- A PMU installed at a given bus measures the voltage and current phasors of all incident branches; therefore, all incident branches are directly observable.
- Voltage and current phasors at one end of the branch can be calculated using Ohm’s law if the voltage at the other end of a branch current is known, resulting in all neighbouring buses being observable.
- If the voltage phasors of two connected buses are known, KCL is used to calculate the branch current phasor.
2.1.2. Normal Operation with ZIB Effect
- If there exists an observable ZIB with all adjacent buses being observable except only one of them, the unobservable bus, through the ZIB effect, becomes observable, as Kirchhoff’s current law can be used to calculate the unknown voltage phasor to the ZIB.
- For an unobservable ZIB that has neighbours with known voltage phasors, then the ZIB is deemed to be observable as its voltage phasors can be calculated using its node equation.
- For the unobservable ZIB group with voltage phasors of its neighbouring buses being known, the nodal equation can be used to calculate the voltage phasors of every unobservable ZIB, making them observable.
2.2. Practical Constraints Case Factors
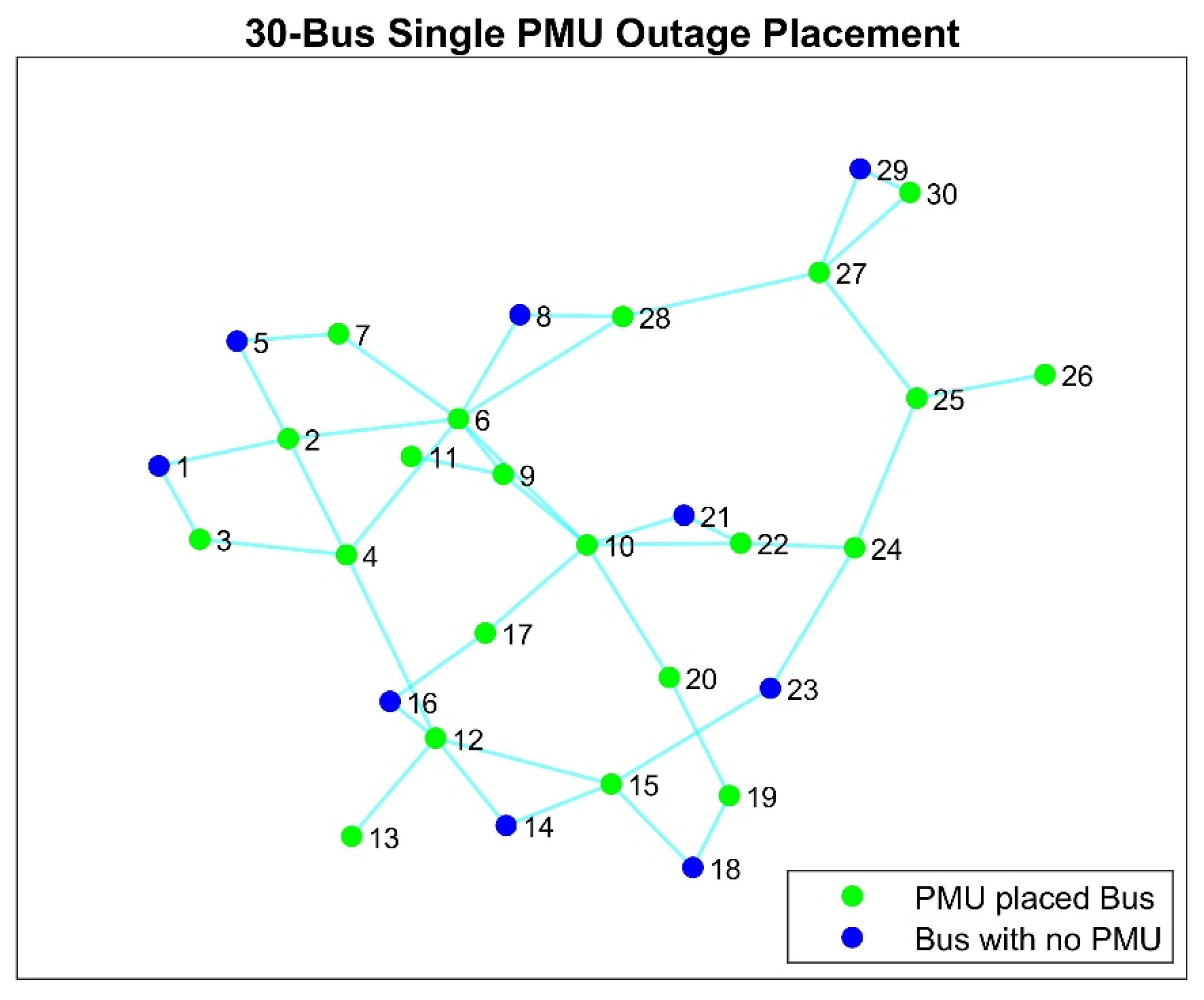
Single PMU Outage
3. Proposed Method
3.1. Graph Topological Observability
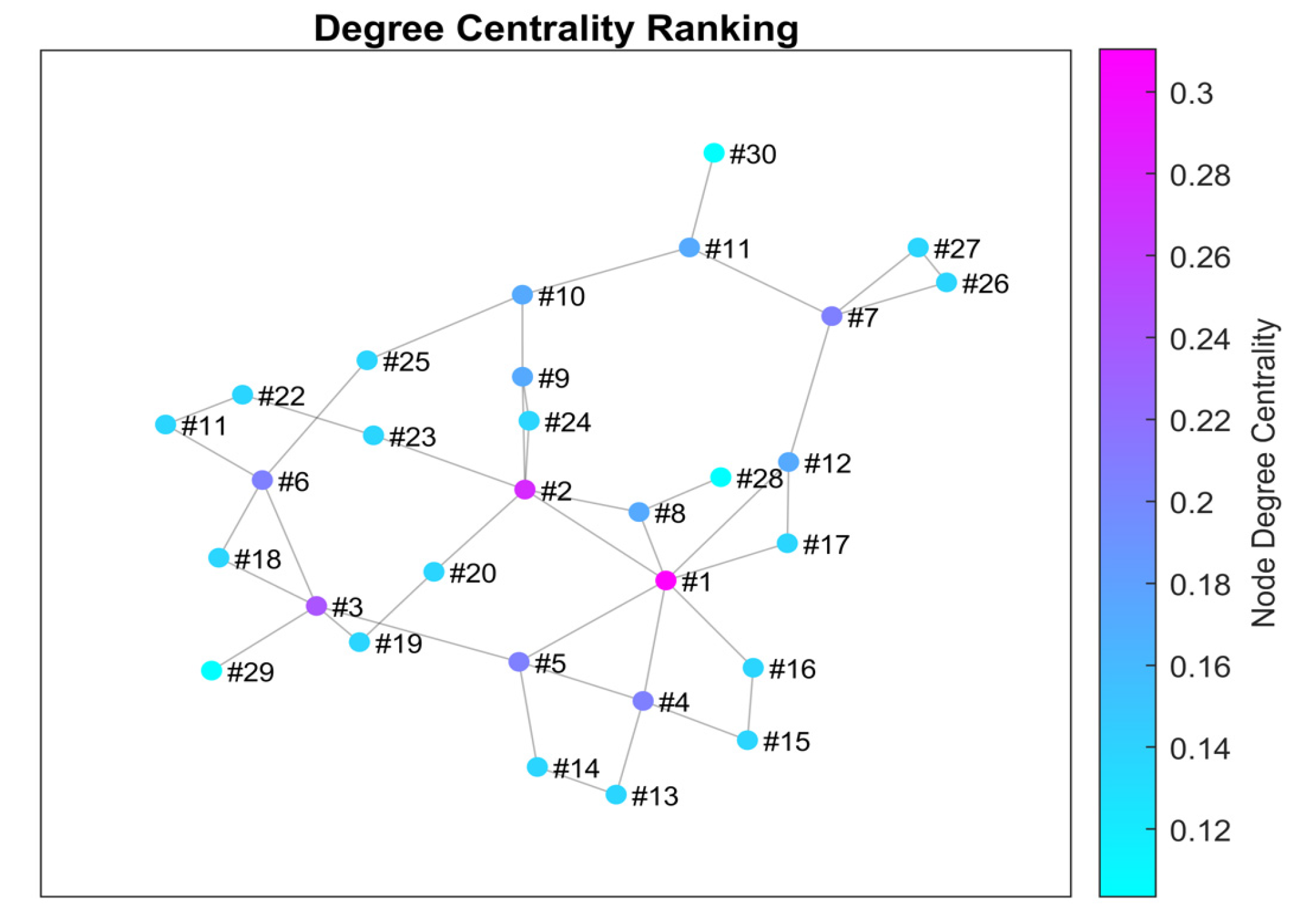
3.2. Search Space Visualization
3.3. Radial Buses Avoidance
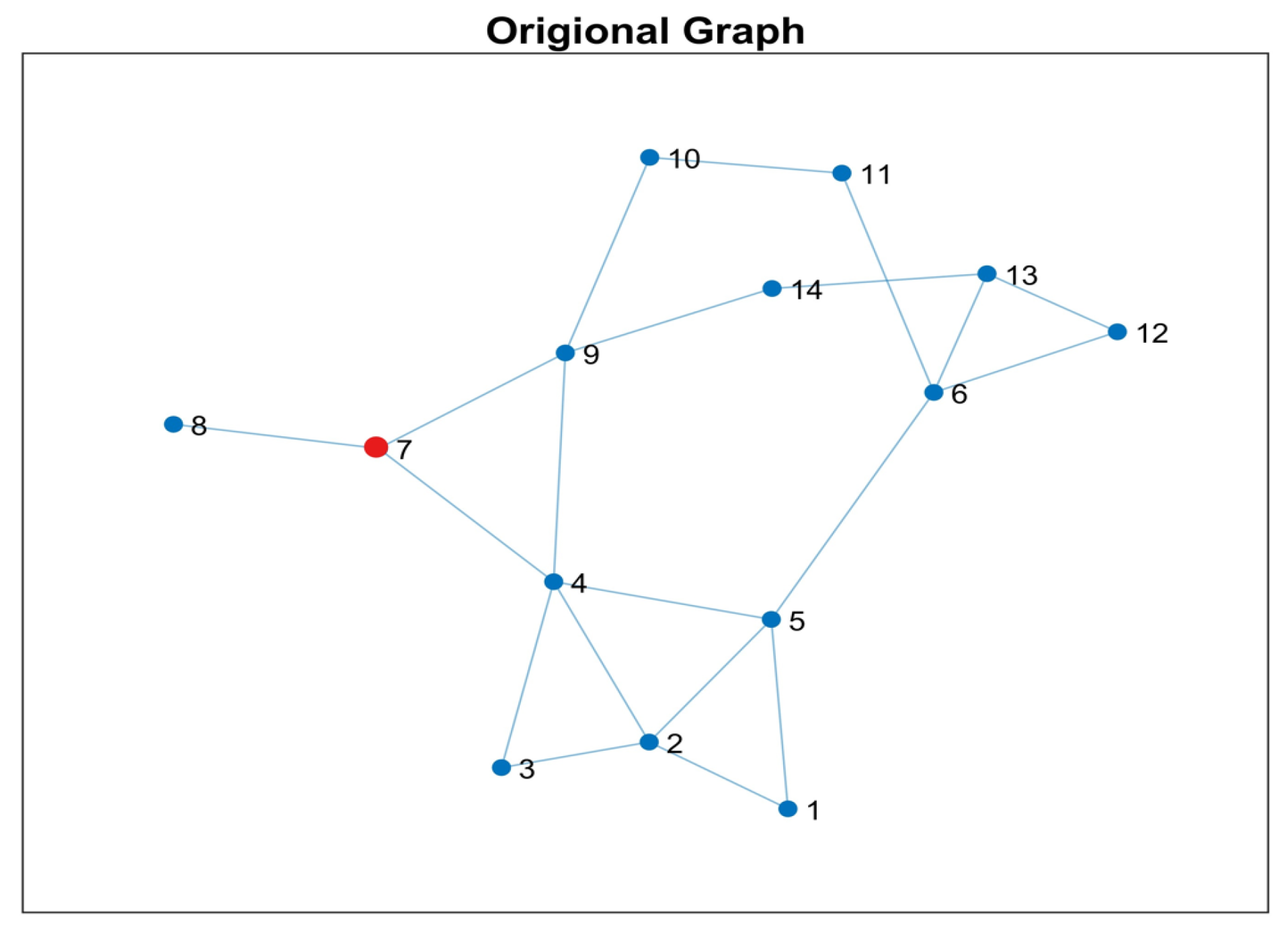
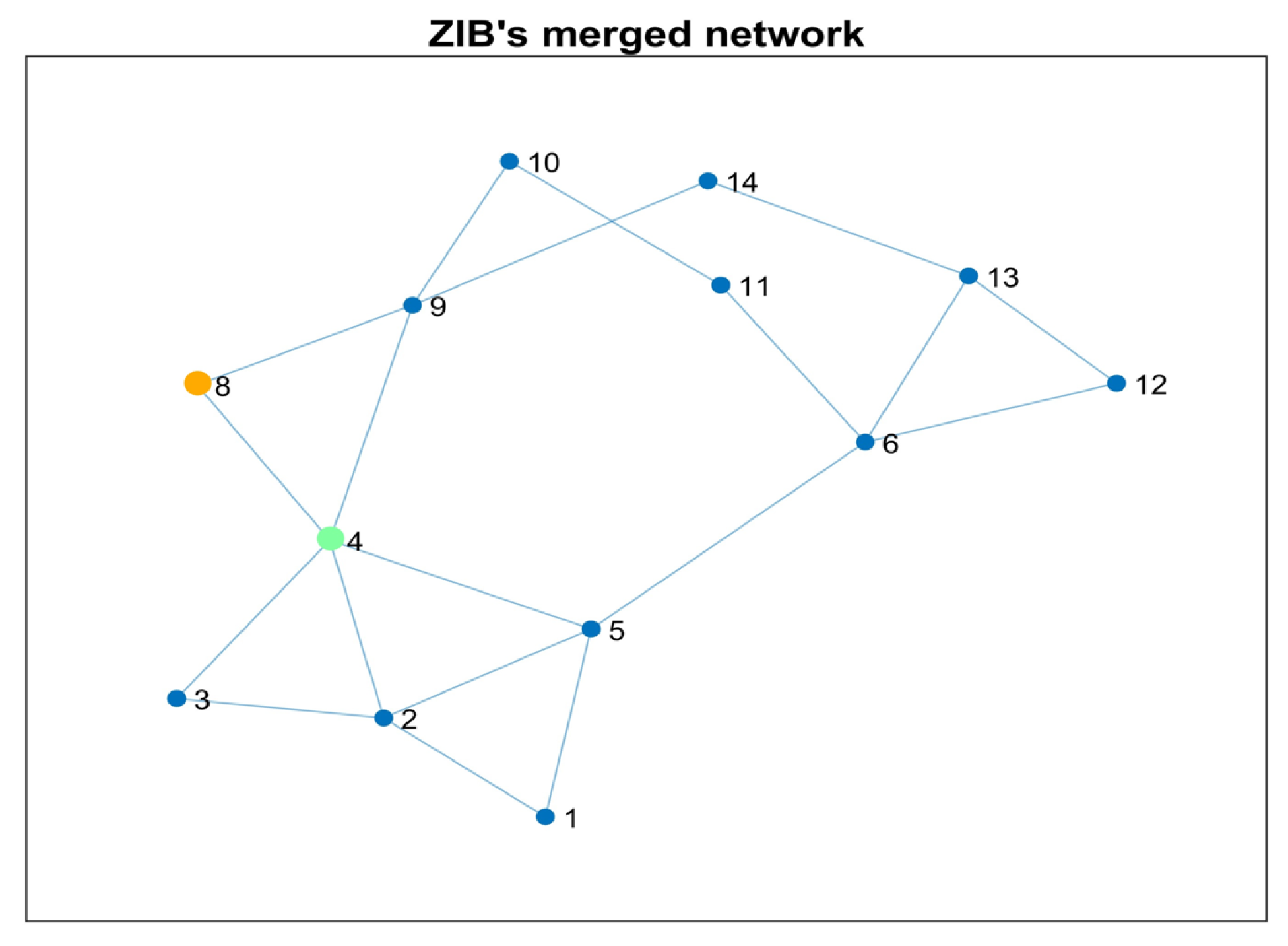
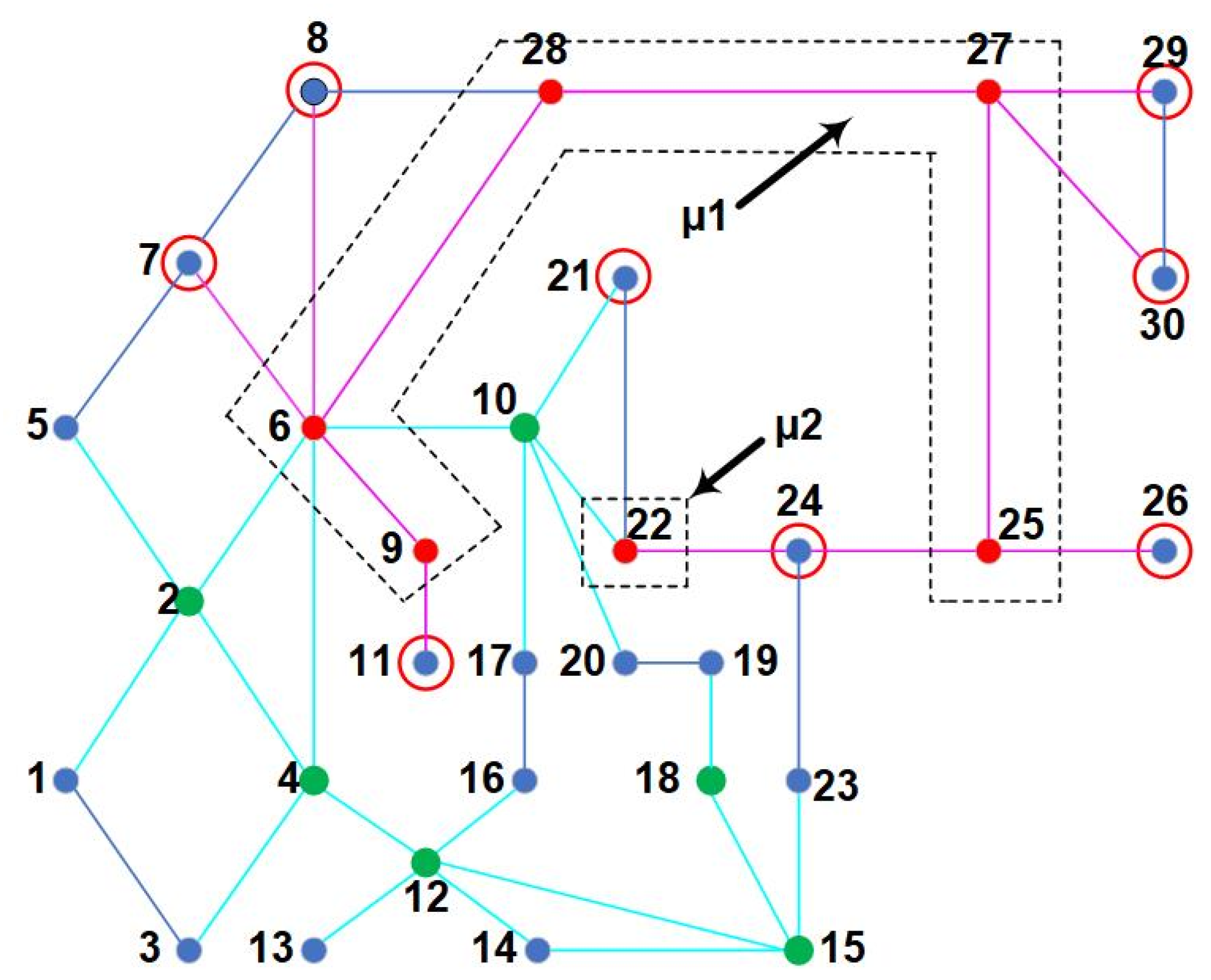
3.4. Topological Network Transformation with Consideration of ZIBs
3.5. Firefly Algorithm Overview
- In any given population of fireflies, they are all unisex, and, for mating purposes, any firefly will become attracted to a brighter firefly.
- A firefly flies randomly if there is no brighter firefly than itself, otherwise, a less bright firefly flies towards a brighter one because the attractiveness of a less bright firefly is proportional to the light intensity of a brighter firefly, and both attractiveness and light intensity are inversely proportional to the distance from the light receptor.
- The fitness function of the landscape determines the light intensity of each firefly.
3.6. Binary Firefly Algorithm (BFA)
- System observability constraint function is satisfied or;
- No bus is greater than , leading to the completion of a local search by the , where is the best solution given by Equation (14). However, the chances of the BFA reaching this point is rare as this will mean that the number of PMUs found is the same as .
| Algorithm 1: Binary Firefly Algorithm | ||||||
| Input Variables: A,, | ||||||
| Initialize: ,, | ||||||
| Output: Optimal Placement set | ||||||
| 1 | Randomly generate the initial population, | |||||
| 2 | Compute the Node degree of each bus by using (6) | |||||
| 3 | Compute the Node degree centrality of each bus by using (7) | |||||
| 4 | Compute difference between any bus andusing (10) as and initialize | |||||
| 5 | while t ≤ max iteration do | |||||
| 6 | for i = 1 to n do | |||||
| 7 | if then | |||||
| 8 | for j = 1 to do | |||||
| 9 | Find max | |||||
| 10 | Using (13) move to bus | |||||
| 11 | Place a PMU at bus | |||||
| 12 | Evaluate system Observability using (4) | |||||
| 14 | end for | |||||
| 15 | Rank buses without PMUs update position | |||||
| 16 | end if | |||||
| 17 | end for | |||||
| 18 | t = t + 1 | |||||
| 19 | end while | |||||
| 20 | if F() ≥ then | |||||
| 21 | Rank Placement sets based on SORI and find the optimal placement set with the highest SORI | |||||
| 22 | else | |||||
| 23 | Go to Step-5 | |||||
| 24 | end if | |||||
| 25 | ||||||
| 26 | Stop. | |||||
4. Tests and Simulation Studies
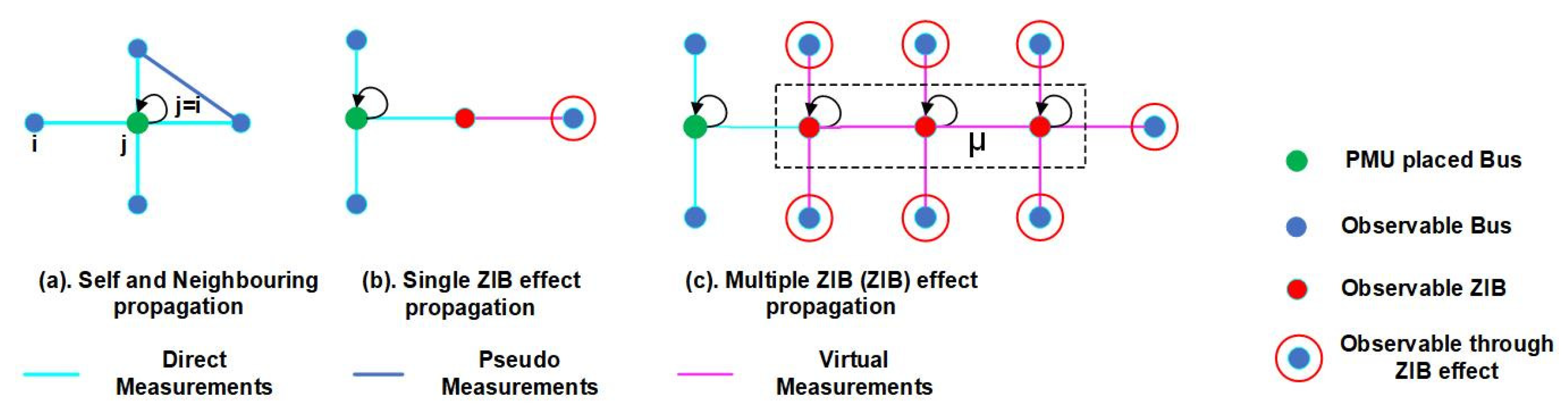
- Substation Measurements: These are measurements that are taken at the substation level by the PMU placed at that substation. In this paper, a power system is converted into an undirected graph; the self-propagations () signify this measurement.
- Direct Measurements: These are measurements that are collected by PMU from all branches linked to the bus it is installed at, otherwise referred to as neighbouring propagations.
- Pseudo Measurements: These kinds of measurements are voltage phasors and branch currents that are calculated from any two observable substations without PMUs installed on them.
- Virtual Measurements: Essentially, these are measurements obtained through the effect of ZIBs. These measurements are possible through the following ways:
- Single ZIB effect: One or more unobservable buses becoming observable through neighbouring an observable ZIB.
- Group ZIB effect: Multiple unobservable buses become observable through neighbouring an interconnected group of observable ZIBs, forming a super node.
Adopted Observability Performance Metrics
5. Illustrative Results and Discussions
5.1. Case 1: Normal Operation without ZIB Effect and Unlimited Channel Limits
5.2. Case 2: Normal Operation with ZIB Effect Consideration
5.3. Case 3: Single PMU Outage
5.4. Case 4: Single PMU Outage with ZIB Effect
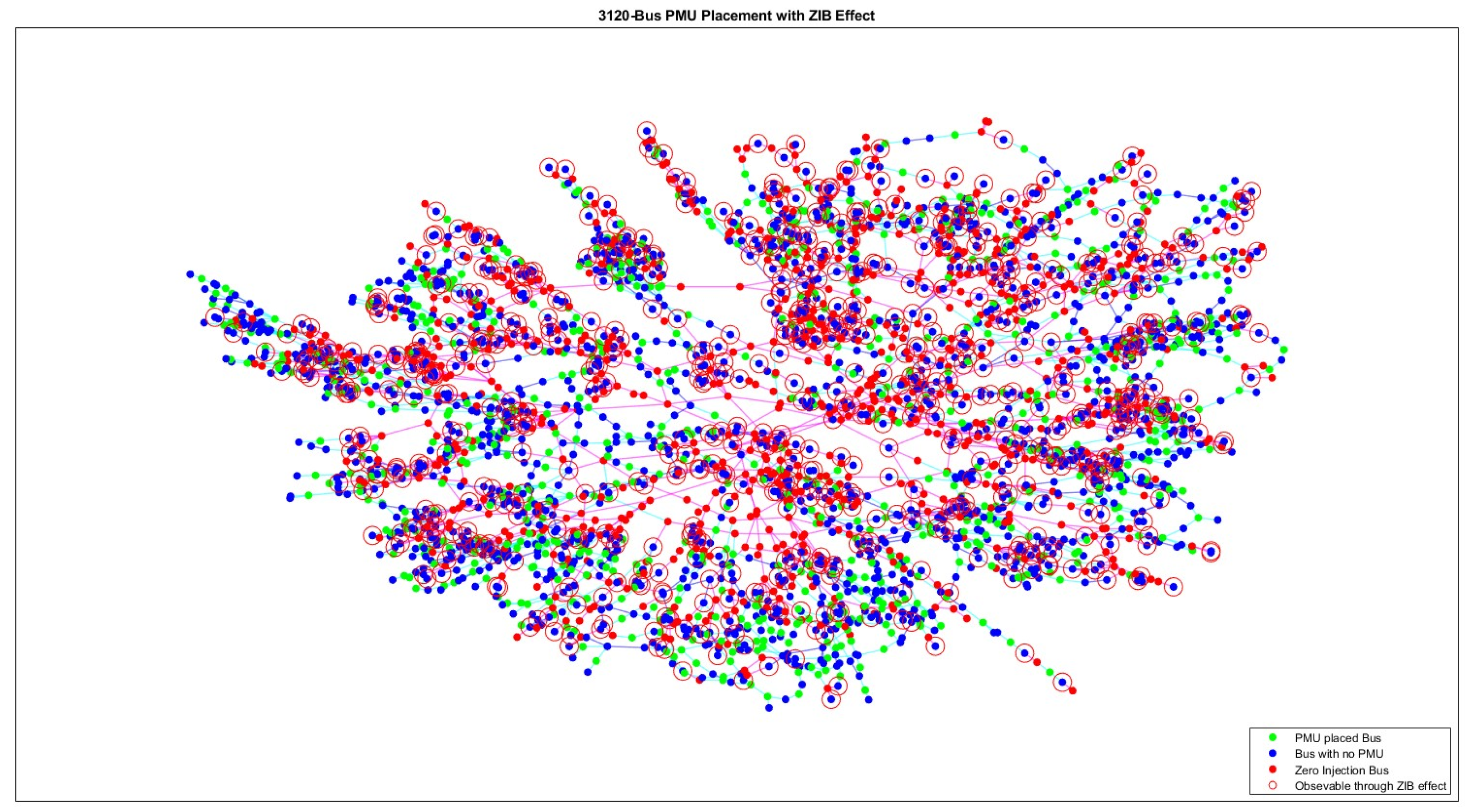
5.5. Algorithm Efficacy on Large-Sale Power Systems
5.6. ZIB Effect Propagation Evaluations
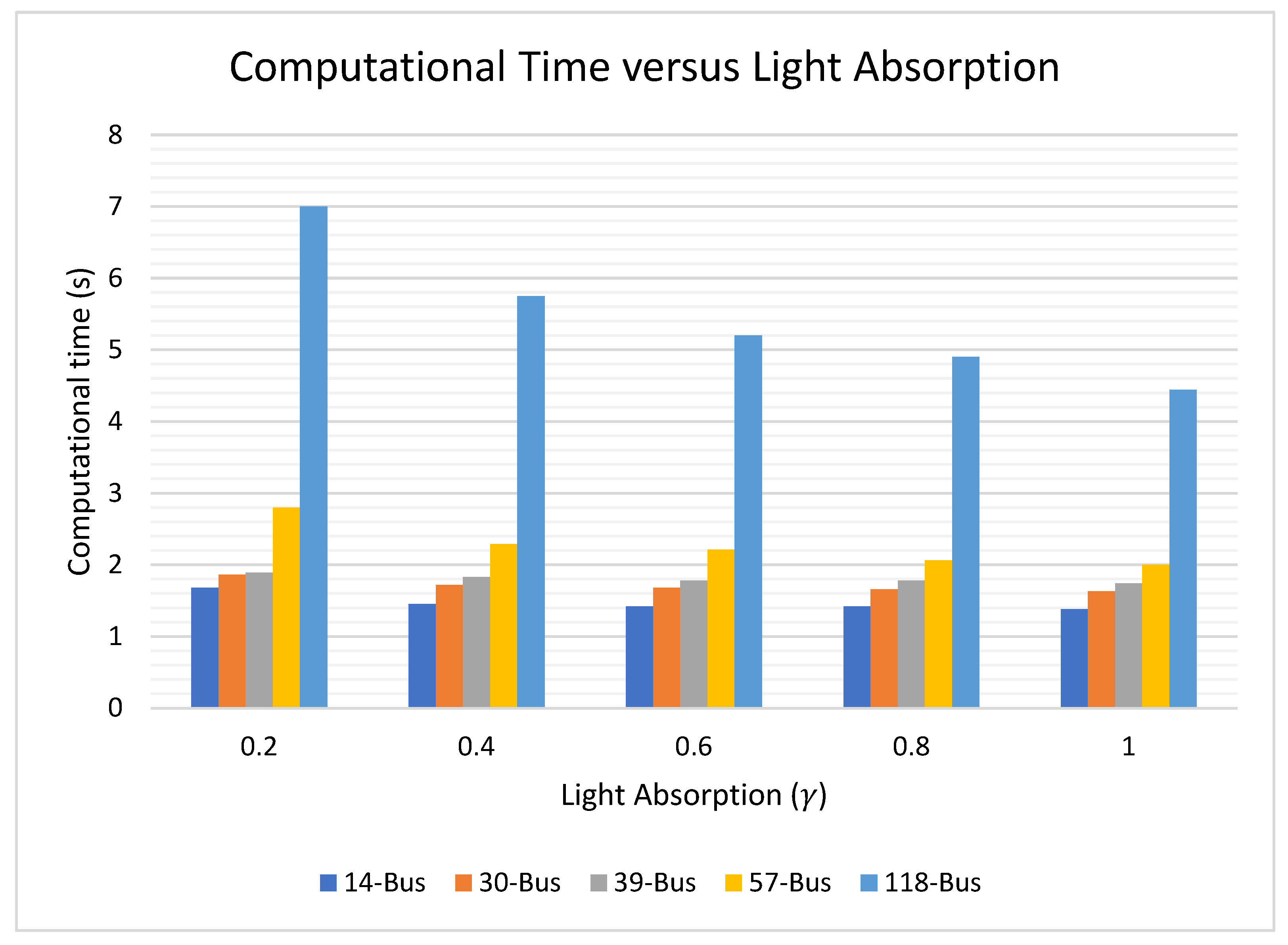
5.7. BFA Computational Time
5.8. BFA Sensitivity Analysis
5.9. BFA Comparison with Existing OPP Algorithms
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gamboa, S.; Orduña, E. Hierarchically Distributed Architecture for Large-Scale Integrated WAMPAC System. In Proceedings of the 2015 International Conference on Electronics, Communications and Computers (CONIELECOMP), Cholula, Mexico, 25–27 February 2015; pp. 16–20. [Google Scholar]
- Guo, X.-C.; Liao, C.-S.; Chu, C.-C. Decentralized PMU Placements in a Dynamic Programming Approach. In Proceedings of the 2019 IEEE Industry Applications Society Annual Meeting, Baltimore, MD, USA, 29 September–3 October 2019; pp. 1–8. [Google Scholar]
- Blair, S.M.; Syed, M.H.; Roscoe, A.J.; Burt, G.M.; Braun, J. Measurement and Analysis of PMU Reporting Latency for Smart Grid Protection and Control Applications. IEEE Access 2019, 7, 48689–48698. [Google Scholar] [CrossRef]
- IEEE Std C37.118.1a-2014 (Amendment to IEEE Std C37.118.1-2011); IEEE Standard for Synchrophasor Measurements for Power Systems—Amendment 1: Modification of Selected Performance Requirements. IEEE Standards Association: Piscataway, NJ, USA, 2014; pp. 1–25. [CrossRef]
- Specialized Protection/Control. Available online: https://www.gegridsolutions.com/multilin/catalog/p847.htm (accessed on 21 October 2022).
- Maji, T.K.; Acharjee, P. Multiple Solutions of Optimal PMU Placement Using Exponential Binary PSO Algorithm for Smart Grid Applications. IEEE Trans. Ind. Appl. 2017, 53, 2550–2559. [Google Scholar] [CrossRef]
- Xu, J.; Wen, M.H.F.; Li, V.O.K.; Leung, K.-C. Optimal PMU Placement for Wide-Area Monitoring Using Chemical Reaction Optimization. In Proceedings of the 2013 IEEE PES Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 24–27 February 2013; pp. 1–6. [Google Scholar]
- Bombieri, N.; Pravadelli, G.; Fujita, M.; Austin, T.; Reis, R. VLSI-SoC: Design and Engineering of Electronics Systems Based on New Computing Paradigms: 26th IFIP WG 10.5/IEEE International Conference on Very Large Scale Integration, VLSI-SoC 2018, Verona, Italy, 8–10 October 2018, Revised and Extended Selected Papers; Springer: Berlin/Heidelberg, Germany, 2019; ISBN 978-3-030-23425-6. [Google Scholar]
- Shalini; Samantaray, S.R.; Sharma, A. Enhancing Performance of Wide-Area Back-Up Protection Scheme Using PMU Assisted Dynamic State Estimator. IEEE Trans. Smart Grid 2019, 10, 5066–5074. [Google Scholar] [CrossRef]
- Johnson, T.; Moger, T. A Critical Review of Methods for Optimal Placement of Phasor Measurement Units. Int. Trans. Electr. Energy Syst. 2021, 31, e12698. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Amjad, M.; Qureshi, M.A.; Imran, K.; Haider, Z.M.; Khan, M.O. A Critical Review of State-of-the-Art Optimal PMU Placement Techniques. Energies 2022, 15, 2125. [Google Scholar] [CrossRef]
- Gharani Khajeh, K.; Bashar, E.; Mahboub Rad, A.; Gharehpetian, G.B. Integrated Model Considering Effects of Zero Injection Buses and Conventional Measurements on Optimal PMU Placement. IEEE Trans. Smart Grid 2017, 8, 1006–1013. [Google Scholar] [CrossRef]
- Nagananda, K.G.; Kishore, S.; Blum, R.S. A PMU Scheduling Scheme for Transmission of Synchrophasor Data in Electric Power Systems. IEEE Trans. Smart Grid 2015, 6, 2519–2528. [Google Scholar] [CrossRef]
- Manousakis, N.M.; Korres, G.N. A Weighted Least Squares Algorithm for Optimal PMU Placement. IEEE Trans. Power Syst. 2013, 28, 3499–3500. [Google Scholar] [CrossRef]
- Joshi, P.M.; Verma, H.K. Synchrophasor Measurement Applications and Optimal PMU Placement: A Review. Electr. Power Syst. Res. 2021, 199, 107428. [Google Scholar] [CrossRef]
- Aminifar, F.; Lucas, C.; Khodaei, A.; Fotuhi-Firuzabad, M. Optimal Placement of Phasor Measurement Units Using Immunity Genetic Algorithm. IEEE Trans. Power Deliv. 2009, 24, 1014–1020. [Google Scholar] [CrossRef]
- Milosevic, B.; Begovic, M. Nondominated Sorting Genetic Algorithm for Optimal Phasor Measurement Placement. IEEE Trans. Power Syst. 2003, 18, 69–75. [Google Scholar] [CrossRef]
- Andreoni, R.; Macii, D.; Brunelli, M.; Petri, D. Tri-Objective Optimal PMU Placement Including Accurate State Estimation: The Case of Distribution Systems. IEEE Access 2021, 9, 62102–62117. [Google Scholar] [CrossRef]
- Theodorakatos, N.P. Optimal Phasor Measurement Unit Placement for Numerical Observability Using Branch-and-Bound and a Binary-Coded Genetic Algorithm. Electr. Power Compon. Syst. 2019, 47, 357–371. [Google Scholar] [CrossRef]
- Li, W.; Deka, D.; Chertkov, M.; Wang, M. Real-Time Faulted Line Localization and PMU Placement in Power Systems through Convolutional Neural Networks. IEEE Trans. Power Syst. 2019, 34, 4640–4651. [Google Scholar] [CrossRef]
- Rezaeian Koochi, M.H.; Dehghanian, P.; Esmaeili, S. PMU Placement with Channel Limitation for Faulty Line Detection in Transmission Systems. IEEE Trans. Power Deliv. 2020, 35, 819–827. [Google Scholar] [CrossRef]
- Shi, Y.; Tuan, H.D.; Duong, T.Q.; Poor, H.V.; Savkin, A.V. PMU Placement Optimization for Efficient State Estimation in Smart Grid. IEEE J. Sel. Areas Commun. 2020, 38, 71–83. [Google Scholar] [CrossRef]
- Bonavolontà, F.; Noia, L.P.D.; Liccardo, A.; Tessitore, S.; Lauria, D. A PSO-MMA Method for the Parameters Estimation of Interarea Oscillations in Electrical Grids. IEEE Trans. Instrum. Meas. 2020, 69, 8853–8865. [Google Scholar] [CrossRef]
- Rahman, N.H.A.; Zobaa, A.F. Integrated Mutation Strategy with Modified Binary PSO Algorithm for Optimal PMUs Placement. IEEE Trans. Ind. Inform. 2017, 13, 3124–3133. [Google Scholar] [CrossRef]
- Appasani, B.; Mohanta, D.K. Co-Optimal Placement of PMUs and Their Communication Infrastructure for Minimization of Propagation Delay in the WAMS. IEEE Trans. Ind. Inform. 2018, 14, 2120–2132. [Google Scholar] [CrossRef]
- Arpanahi, M.K.; Alhelou, H.H.; Siano, P. A Novel Multiobjective OPP for Power System Small Signal Stability Assessment Considering WAMS Uncertainties. IEEE Trans. Ind. Inform. 2020, 16, 3039–3050. [Google Scholar] [CrossRef]
- Johnson, T.; Moger, T. Security-Constrained Optimal Placement of PMUs Using Crow Search Algorithm. Appl. Soft Comput. 2022, 128, 109472. [Google Scholar] [CrossRef]
- Guo, X.-C.; Liao, C.-S.; Chu, C.-C. Enhanced Optimal PMU Placements with Limited Observability Propagations. IEEE Access 2020, 8, 22515–22524. [Google Scholar] [CrossRef]
- Rezaeian Koochi, M.H.; Hemmatpour, M.H. A General PMU Placement Approach Considering Both Topology and System Aspects of Contingencies. Int. J. Electr. Power Energy Syst. 2020, 118, 105774. [Google Scholar] [CrossRef]
- Chen, X.; Wei, F.; Cao, S.; Soh, C.B.; Tseng, K.J. PMU Placement for Measurement Redundancy Distribution Considering Zero Injection Bus and Contingencies. IEEE Syst. J. 2020, 14, 5396–5406. [Google Scholar] [CrossRef]
- Shafiullah, M.; Hossain, M.I.; Abido, M.A.; Abdel-Fattah, T.; Mantawy, A.H. A Modified Optimal PMU Placement Problem Formulation Considering Channel Limits under Various Contingencies. Measurement 2019, 135, 875–885. [Google Scholar] [CrossRef]
- Babu, R.; Bhattacharyya, B. Strategic Placements of PMUs for Power Network Observability Considering Redundancy Measurement. Measurement 2019, 134, 606–623. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.; Ma, M.; Shen, R.; Yu, Y. An Optimal PMU Placement with Reliable Zero Injection Observation. IEEE Access 2018, 6, 54417–54426. [Google Scholar] [CrossRef]
- Koutsoukis, N.C.; Manousakis, N.M.; Georgilakis, P.S.; Korres, G.N. Numerical Observability Method for Optimal Phasor Measurement Units Placement Using Recursive Tabu Search Method. IET Gener. Transm. Amp; Distrib. 2013, 7, 347. [Google Scholar] [CrossRef]
- Wang, B.; Liu, D.; Li, X. An Improved Ant Colony System in Optimizing Power System PMU Placement Problem. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009; pp. 1–3. [Google Scholar]
- Shahraeini, M.; Alvandi, A.; Khormali, S. Behavior Analysis of Random Power Graphs for Optimal PMU Placement in Smart Grids. In Proceedings of the 2020 10th International Conference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 29–30 October 2020; pp. 107–112. [Google Scholar]
- Rios, M.A.; Gómez, O. Identification of Coherent Groups and PMU Placement for Inter-Area Monitoring Based on Graph Theory. In Proceedings of the 2011 IEEE PES CONFERENCE ON INNOVATIVE SMART GRID TECHNOLOGIES LATIN AMERICA (ISGT LA), Medellin, Colombia, 19–21 October 2011; pp. 1–7. [Google Scholar]
- von Meier, A.; Stewart, E.; McEachern, A.; Andersen, M.; Mehrmanesh, L. Precision Micro-Synchrophasors for Distribution Systems: A Summary of Applications. IEEE Trans. Smart Grid 2017, 8, 2926–2936. [Google Scholar] [CrossRef]
- Li, J.; Wei, X.; Li, B.; Zeng, Z. A Survey on Firefly Algorithms. Neurocomputing 2022, 500, 662–678. [Google Scholar] [CrossRef]
- Nuqui, R.F.; Phadke, A.G. Phasor Measurement Unit Placement Techniques for Complete and Incomplete Observability. IEEE Trans. Power Deliv. 2005, 20, 2381–2388. [Google Scholar] [CrossRef]
- Guo, X.-C.; Liao, C.-S.; Chu, C.-C. Optimal PMU Placements under Propagation Depth Constraints by Mixed Integer Linear Programming. In Proceedings of the 2016 IEEE International Conference on Smart Grid Communications (SmartGridComm), Sydney, NSW, Australia, 6–9 November 2016; pp. 656–661. [Google Scholar]
- Awon, M.; Butt, H.Z.; Abdullah Khalid, H.; Janjua, A.K. System Redundancy Index Based Optimized Phasor Measurement Unit Placement for Complete Network Observability. In Proceedings of the 2018 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Islamabad, Pakistan, 10–12 September 2018; pp. 1–5. [Google Scholar]
- Sushma, G.C.; Jyothsna, T.R. Observability Constrained GA Approach for Optimal PMU Placement Considering Zero Injection Modeling. In Proceedings of the 2018 International Conference on Control, Power, Communication and Computing Technologies (ICCPCCT), Kannur, India, 23–24 March 2018; pp. 174–178. [Google Scholar]
- Abdulrahman, I.; Radman, G. ILP-Based Optimal PMU Placement with the Inclusion of the Effect of a Group of Zero-Injection Buses | SpringerLink. Available online: https://link.springer.com/article/10.1007/s40313-018-0389-4 (accessed on 22 August 2022).
- Yuvaraju, V.; Thangavel, S. Optimal Phasor Measurement Unit Placement for Power System Observability Using Teaching–Learning Based Optimization. Int. J. Electr. Power Energy Syst. 2022, 137, 107775. [Google Scholar] [CrossRef]
- Kiio, M.N.; Wekesa, C.W.; Kamau, S.I. Evaluating Performance of a Linear Hybrid State Estimator Utilizing Measurements from RTUs and Optimally Placed PMUs. IEEE Access 2022, 10, 63113–63131. [Google Scholar] [CrossRef]
- Huang, L.; Sun, Y.; Xu, J.; Gao, W.; Zhang, J.; Wu, Z. Optimal PMU Placement Considering Controlled Islanding of Power System. IEEE Trans. Power Syst. 2014, 29, 742–755. [Google Scholar] [CrossRef]
- Abdelsalam, A.A.; Hassanin, K.M.; Abdelaziz, A.Y.; Alhelou, H.H.; Abdelsalam, A.A.; Hassanin, K.M.; Abdelaziz, A.Y.; Alhelou, H.H. Optimal PMUs Placement Considering ZIBs and Single Line and PMUs Outages. AIMSE 2020, 8, 122–141. [Google Scholar] [CrossRef]
- Xia, N.; Gooi, H.B.; Chen, S.X.; Wang, M.Q. Redundancy Based PMU Placement in State Estimation. Sustain. Energy Grids Netw. 2015, 2, 23–31. [Google Scholar] [CrossRef]


| Refs. | Year | Contributions | Techniques | Test Systems | Topology and Sensor Issues | Observability Metrics | Contingencies Considered | Achievements |
|---|---|---|---|---|---|---|---|---|
| [27] | 2022 | New meta-heuristic approach in solving the OPP presenting multiple solution sets. Solves contingencies with and without ZIB consideration. | Crow Search Algorithm (CSA) | 14-bus, 30-bus, 57-bus, 72-bus | Effect of ZIB, and channel limits | Total System Observability Redundancy Index (TSORI) | N-1 PMU loss, N-1 line loss with and without ZIB effect | CSA solves the OPP for multiple PMU placement sets for the same optimal PMU number, allowing for better redundancy set to be selected. |
| [28] | 2020 | Modifications of observability propagation rules. Formulated the OPP problem with bounded OPDs. | Mathematical programming | 39-bus, 57-bus, 118-bus | Effect of ZIB, conventional measurements, and channel limits | Observability Propagation Depth (OPD) | N-1 PMU loss, N-1 line loss, and N-1 PMU or N-1 line loss | Exposes the risk of unlimited observability propagations under different contingencies. |
| [29] | 2020 | Novel formulations of various topological and contingencies. | Mathematical formulations based on topology and system disturbances effects | 68-bus, and 140-bus | Effect of parallel lines, effect of ZIB, PMU channel limits, and pre-existing measurements | None | N-1 line loss | The proposed methodology demonstrates the ability to find fewer optimal PMUs under the largest single line outages possible. |
| [30] | 2020 | Modelling of linear observability constraints using channel limits, ZIB effect, and existing measurements. | Integer Linear Programming (ILP) | 14-bus, 30-bus, New England 39-bus, 57-bus, and 118-bus | Effect of ZIB, and channel limitations | None | N-1 and N-2 PMU loss | Introduction of linear and compact forms of observability constraints. |
| [31] | 2019 | Novel use of a meta-heuristic algorithm with modifications of classic OPP formulation. | Constriction Factor Particle Swarm Optimization (CF-PSO) and Mixed Integer Linear Programming (MILP) | 14-bus, 30-bus, New England 39-bus, 118-bus, Polish 2383-bus, Polish 2736-bus, and Polish-3120-bus | Channel limitations under various contingencies | TSORI and Bus Observability Index (BOI) | N-1 and N-2 PMU loss | Demonstrates the power of meta-heuristic methods in finding more than one solution for the same number of optimal PMU, thereby increasing the chances of finding high measurement redundancy. |
| [32] | 2019 | Solves MINLP framework using a two-phase Branch-and-Bound algorithm (BBA), starting with PMUs pre-assigned to each bus to a radial bus. | Mixed Integer Nonlinear Programming (MINLP) formulation solved by Branch-and-Bound Algorithm (BBA) | 14-bus, 30-bus, New England 39-bus, 118-bus, and 246-bus | Effect of ZIB, and channel limitations | None | N-1 PMU loss and N-1 line loss | Radial buses are excluded from optimal design as two-phased Branch-and-Bound finds several optimum points. |
| [33] | 2018 | OPP model that considers ZIB, proposed a new ZIB-based metric. | Integer Linear Programming (ILP) | 14-bus, 30-bus, 39-bus, 118-bus, 300-bus, Polish 2383-bus, Polish | Channel limitations | Zero Injection Utilization Rate (ZIUR) Zero Injection Observability Depth (ZIOD) | N-1 PMU loss, and N-1 line loss | The proposed ZIOD metric is a reliable measure of system reliability. |
| IEEE-Bus System | ZIB Locations | Radial Buses Locations | Bus with the Maximum Number of Branches |
|---|---|---|---|
| 14-Bus | 7 | 8 | 4 |
| 30-Bus | 6, 9, 22, 25, 27, 28 | 11, 13, 26 | 6 |
| 39-Bus | 1, 2, 5, 6, 9, 10, 11, 13, 14, 17, 19, 22 | 30, 31, 32, 33, 34, 36, 37, 38 | 16 |
| 57-Bus | 4, 7, 11, 21, 22, 24, 26, 34, 36, 37, 39, 40, 45, 46,48 | 33 | 9 |
| 118-Bus | 5, 9, 30, 37, 38, 63, 64, 68, 71, 81 | 10, 73, 87, 111, 112, 116, 117 | 49 |
| IEEE Test System | Optimal Number of PMUs | Optimal PMU Locations | Best BOI from Placement Sets | Maximum Redundancy | Best SORI | CPU Time |
|---|---|---|---|---|---|---|
| 14-bus | 4 | 2, 6, 7, 9 | 1, 1, 1, 3, 2, 1, 2, 1, 2, 1, 1, 1, 1, 1 | 3 | 19 | 0.847 s |
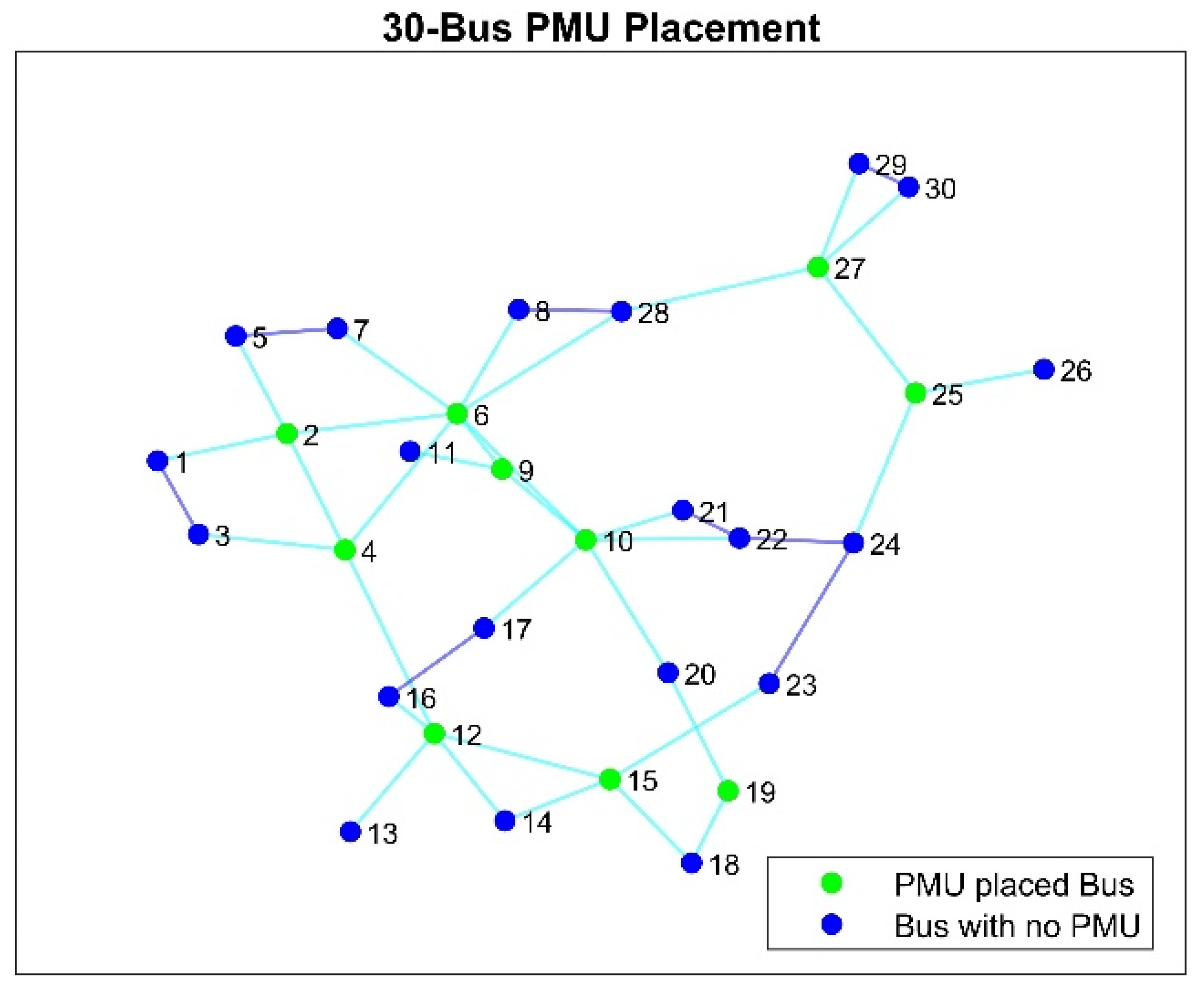
| 30-bus | 10 | 2, 4, 6, 9, 10, 12, 15, 19, 25, 27. 1, 7, 9, 10, 12, 18, 24, 25, 27, 28. 1, 2, 6, 9, 10, 12, 15,20, 25, 29. | 1, 3, 1, 4, 1, 5, 1, 1, 3, 3, 1, 3, 1, 2, 2, 1, 1, 2, 1, 2, 1, 1, 1, 1, 2, 1, 2, 2, 1, 1 | 5 | 52 | 0.761 s |
| 39-bus | 13 | 2, 6, 9, 10, 13, 14, 17, 19, 20, 22, 23, 25, 29. 2, 6, 9, 10, 12,14,17,19, 20, 22, 23, 25, 29. | 1, 2, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 3, 2, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 | 3 | 52 | 1.418 s |
| 57-bus | 17 | 1, 4, 9, 15, 20, 24, 26, 28, 29, 31, 32, 36, 38, 41, 47, 51, 53, 57. 1, 4, 9, 20, 22, 25, 26, 29, 32, 36, 39, 41, 45, 46, 49, 51, 53. | 2, 1, 2, 1, 1, 1, 1, 1, 1, 2, 2, 1, 2, 1, 2, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 2, 1 | 2 | 72 | 3.892 s |
| 118-bus | 32 | 2, 6, 9, 11, 12, 17, 21, 24, 26, 28, 34, 37, 41, 45, 49, 52, 56, 62, 64, 68, 71, 75, 77, 80, 85, 86, 91, 94, 101, 104, 107, 108, 110, 114 | 1, 2, 3, 1, 1, 1, 1, 2, 1, 1, 3, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2, 1, 1, 2, 1, 3, 1, 1, 2, 1, 1, 1, 4, 1, 2, 1, 1, 3, 1, 1, 1, 1, 2, 1, 2, 1, 1, 1, 2, 3, 1, 1, 4, 3, 1, 2, 1, 1, 2, 1, 4, 1, 1, 2, 2, 1, 1, 1, 2, 2, 1, 1, 3, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 | 4 | 164 | 2896.1 s |
| 300-bus | 91 | 1, 2, 3, 11, 12, 15, 17, 20, 22, 23, 25, 29, 31, 33, 35, 36, 37, 38, 43, 48, 49, 53, 54, 55, 58, 59, 60, 62, 64, 65, 71, 79, 83, 85, 86, 88, 89, 90, 98, 99, 101, 103, 109, 111, 112, 113, 116, 118, 119, 124, 132, 133, 138, 143, 145, 152, 157, 163, 167, 173, 175, 177, 183, 185, 189, 190, 193, 196, 198, 199, 203, 204, 208, 210, 211, 213, 216, 217, 219, 224, 225, 228, 267, 268, 269, 270, 272, 273, 274, 276, 294 | 2, 2, 3, 2, 1, 1, 2, 3, 1, 2, 1, 1, 1, 1, 3, 1, 1, 1, 1, 2, 2, 3, 2, 2, 1, 1, 1, 1, 3, 1, 1, 1, 1, 1, 1, 4, 3, 2, 3, 1, 2, 2, 1, 1, 1, 1, 2, 2, 3, 1, 1, 1, 2, 2, 2, 2, 1, 2, 3, 3, 2, 1, 1, 3, 2, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 1, 2, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 1, 1, 1, 2, 1, 2, 2, 2, 1, 2, 1, 2, 1, 1, 3, 2, 1, 2, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2, 1, 2, 1, 1, 2, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 2, 1, 1, 2, 1, 1, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 2, 1, 2, 2, 2, 1, 2, 3, 1, 1, 1, 3, 2, 1, 1, 1, 1, 1, 1, 1, 3, 1, 1, 3, 2, 1, 2, 2, 1, 3, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 4, 2, 1, 2, 3, 2, 3, 3, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2, 1, 1, 1, 1, 1, 1 | 4 | 465 | 4320.2 s |
| IEEE Test System | Optimal Number of PMUs | Optimal PMU Locations | Best BOI from Placement Sets | Maximum Redundancy | Best SORI | CPU Time |
|---|---|---|---|---|---|---|
| 14-bus | 3 | 2, 6, 9 | 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1,1, 1 | 2 | 15 | 2.58 s |
| 30-bus | 6 | 2, 4, 10, 12, 15, 20. 2, 4, 8, 10, 13, 17. 2, 4, 8, 10, 13, 16. 1, 6, 8, 10, 13, 16. 3, 5, 8, 10, 16, 20. 2, 4, 8, 10, 13, 18. 3, 5, 8, 10, 13, 16. | 1, 3, 1, 4, 1, 3, 3, 4, 3, 3, 1, 2, 2, 1, 1, 1, 1, 2, 1, 1, 3, 3, 3, 3 | 4 | 51 | 3.04 s |
| 39-bus | 7 | 1, 8, 16, 20, 23, 25, 29. 1, 5, 11, 13, 15, 17, 19. 1, 5, 9, 11, 13, 15, 19. 1, 5, 10, 11, 13, 15,19. | 2, 2, 1, 1, 1, 1, 1, 2, 2, 1, 2, 2, 1, 2, 2, 2, 1, 1, 1, 2, 1, 1, 2, 1, 1, 1, 1, 1, 1 | 2 | 40 | 2.64 s |
| 57-bus | 12 | 1, 9, 10, 15, 18, 20, 25, 29, 32, 49, 53, 56. 1, 7, 8, 12, 15, 17, 19, 22, 25, 34, 38, 41. 1, 8, 12, 15, 17, 19, 22, 25, 31, 34, 39, 41. 1, 4, 7, 8, 12, 16, 19, 22, 25, 34, 38, 41. | 2, 1, 2, 1, 2, 2, 2, 2, 2, 3, 1, 2, 1, 1, 1, 2 , 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 3, 2, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1 | 2 | 59 | 2.73 s |
| 118-bus | 28 | 3, 8, 12, 15, 19, 21, 27, 31, 32, 34, 42, 45, 49, 53, 56, 62, 72, 75, 77, 80, 83, 86, 89, 92, 96, 100, 105, 110 3, 7, 10, 13, 17, 19, 25, 28, 29, 31, 37, 40, 44, 48, 51, 57, 63, 66,68, 71,73, 76,79, 82,86, 90, 95, 100 | 1, 1, 3, 2, 2, 1, 3, 1, 3, 2, 1, 2, 2, 1, 4, 1, 3, 2, 1, 1, 1, 1, 1, 2, 2, 1, 1, 2, 3, 3, 3, 2, 1, 2, 3, 1, 2, 1, 1, 2, 1, 1, 1, 3, 1, 1, 1, 1, 3, 1, 1, 1, 1, 1, 1, 1, 1, 3, 2, 1, 4, 2, 1, 1, 1, 2, 1, 3, 1, 1, 3, 3, 1, 1, 3, 1, 1, 1, 2, 1, 1, 3, 1, 3, 1, 2, 2, 2, 2, 2, 1, 1, 3, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 | 4 | 174 | 440.50 s |
| 300-bus | 65 | 1, 2, 3, 11, 14, 17, 22, 25, 26, 37, 38, 42, 43, 48, 49, 53, 55, 58, 59, 60, 64, 76, 77, 80, 85, 88, 91, 92, 98, 99, 104, 118, 121, 124, 125, 131, 133, 136, 140, 141, 155, 158, 160, 163, 167, 169, 171, 177, 183, 185, 193, 196, 202, 208, 210, 211, 213, 217, 225, 228, 267, 268, 269, 274, 294 | 2, 2, 11, 2, 2, 3, 1, 2, 1, 1, 1, 11, 1, 1, 2, 1, 1, 2, 2, 2, 9, 4, 1, 1, 10, 3, 10, 2, 2, 1, 1, 1, 1, 2, 2, 3, 1, 1, 9, 10, 2, 3, 10, 10, 9, 9, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 2, 3, 1, 2, 1, 1, 2, 1, 1, 1, 1, 1, 2, 2, 2, 1, 2, 1, 1, 1, 3, 2, 1, 1, 3, 2, 1, 3, 1, 1, 11, 2, 2, 1, 1, 1, 1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 3, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 10, 1, 1, 10, 1, 9, 9, 2, 1, 9, 1, 2, 1, 1, 3, 2, 1, 11, 2, 1, 9, 2, 1, 1, 1, 9, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 9, 1, 9, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 9, 1, 1, 1, 1, 1, 9, 1, 1, 1, 1, 4, 4, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 3, 3, 3, 1 | 11 | 528 | 1845 s |
| IEEE Test System | Optimal Number of PMUs | Optimal PMU Locations | Best BOI | Maximum Redundancy | SORI | CPU Time |
|---|---|---|---|---|---|---|
| 14-bus | 9 | 2, 4, 5, 6, 7, 8, 9, 11, 13. | 2, 3, 2, 5, 4, 4, 4, 2, 3, 2, 2, 2, 2, 2 | 4 | 39 | 0.79 s |
| 30-bus | 21 | 2, 3, 4, 6, 7, 9, 10, 11, 12, 13, 15, 17, 19, 20, 22, 24, 25, 26, 27, 28, 30. | 2, 3, 2, 5, 2, 7, 2, 2, 4, 6, 2, 4, 2, 2, 2, 2, 2, 2, 2, 3, 2, 3, 2, 3, 4, 2, 4, 3, 2, 2 | 7 | 85 | 0.73 s |
| 39-bus | 28 | 2, 3, 6, 8, 9, 10, 11, 13, 14, 16, 17, 19, 20, 22, 23, 25, 26, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39 | 2, 4, 2, 2, 2, 3, 2, 2, 3, 4, 3, 2, 3, 2, 2, 3, 2, 2, 4, 3, 2, 3, 3, 2, 4, 3, 2, 2, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 | 4 | 96 | 0.83 s |
| 57-bus | 36 | 1, 3, 4, 6, 9, 10, 11, 12, 14, 15, 18, 20, 21, 22, 24, 25, 27, 28, 29, 31, 32, 33, 35, 36, 37, 38, 41, 45, 47, 48, 49, 51, 53, 54, 56, 57 | 2, 2, 3, 5, 2, 2, 2, 2, 4, 4, 3, 3, 6, 2, 5, 2, 2, 3, 2, 2, 3, 3, 2, 3, 3, 2, 2, 3, 2, 2, 2, 3, 2, 2, 2, 3, 3, 5, 2, 2, 3, 2, 2, 2, 2, 2, 2, 4, 3, 2, 2, 2, 2, 2, 2, 3, 2 | 6 | 148 | 1.1 s |
| 118-bus | 68 | 2, 3, 5, 7, 9, 10, 11, 12, 15, 17, 19, 21, 22, 24, 25, 27, 29, 30, 31, 32, 34, 36, 37, 40, 42, 44, 45, 46, 49, 51, 53, 54, 56, 57, 59, 62, 64, 65, 66, 68, 70, 71, 73, 75, 77, 79, 80, 83, 85, 86, 87, 89, 90, 92, 94, 96, 100, 102, 105, 106, 109, 110, 111, 112, 115, 116, 117, 118 | 2, 2, 3, 2, 3, 2, 2, 3, 2, 2, 3, 6, 2, 2, 3, 2, 4, 2, 3, 2, 2, 2, 4, 2, 2, 2, 4, 2, 2, 2, 4, 3, 2, 4, 2, 2, 3, 3, 2, 3, 2, 4, 2, 2, 4, 2, 2, 2, 9, 2, 2, 2, 2, 6, 3, 5, 2, 2, 4, 2, 3, 2, 2, 2, 4, 5, 2, 3, 5, 4, 3, 2, 2, 2, 4, 2, 4, 2, 2, 5, 2, 3, 2, 2, 4, 3, 2, 2, 6, 3, 2, 6, 2, 4, 2, 3, 2, 2, 2, 4, 2, 2, 3, 2, 2, 3, 2, 2, 2, 4, 2, 2, 2, 2, 2, 2, 2, 2 | 9 | 323 | 3.72 s |
| 300-bus | 204 | 1, 2, 3, 5, 7, 8, 11, 12, 15, 16, 17, 19, 20, 22, 23, 25, 27, 29, 31, 33, 35, 36, 37, 38, 39, 41, 43, 44, 47, 48, 49, 51, 53, 54, 55, 57, 58, 59, 60, 62, 64, 65, 68, 69, 71, 73, 78, 79, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 93, 97, 98, 99, 100, 101, 102, 103, 105, 109, 111, 112, 113, 115, 116, 118, 119, 122, 124, 125, 132, 134, 135, 137, 138, 143, 144, 145, 148, 149, 150, 152, 153, 155, 157, 158, 160, 162, 163, 164, 167, 168, 171, 173, 175, 177, 179, 183, 184, 185, 189, 190, 192, 193, 194, 196, 198, 199, 201, 202, 203, 204, 206, 208, 209, 210, 211, 212, 213, 215, 216, 217, 218, 219, 220, 223, 224, 225, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 267, 268, 269, 270, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 292, 293, 294, 295, 296, 297, 298, 299, 300 | 4, 4, 5, 2, 3, 2, 4, 3, 2, 2, 3, 4, 2, 2, 4, 3, 3, 2, 2, 4, 2, 3, 5, 2, 2, 2, 2, 2, 3, 2, 4, 4, 3, 2, 6, 4, 2, 6, 3, 3, 2, 2, 5, 3, 2, 2, 3, 4, 4, 2, 2, 2, 4, 3, 3, 2, 2, 3, 4, 5, 3, 4, 2, 6, 3, 3, 2, 3, 2, 2, 3, 2, 3, 2, 2, 2, 2, 2, 5, 2, 5, 3, 5, 3, 4, 4, 3, 4, 4, 4, 2, 2, 2, 2, 2, 2, 3, 5, 3, 3, 2, 3, 2, 3, 4, 2, 2, 3, 3, 2, 4, 4, 2, 2, 2, 6, 2, 2, 4, 3, 2, 2, 2, 4, 3, 2, 3, 2, 2, 2, 2, 2, 2, 3, 2, 3, 3, 2, 2, 2, 2, 2, 2, 2, 3, 2, 2, 3, 2, 2, 3, 3, 2, 3, 2, 2, 2, 2, 2, 2, 2, 2, 3, 2, 2, 2, 2, 2, 3, 2, 2, 2, 4, 2, 2, 3, 3, 2, 2, 2, 2, 2, 2, 3, 2, 2, 2, 2, 5, 3, 2, 2, 3, 2, 2, 3, 3, 4, 3, 2, 2, 2, 3, 3, 2, 2, 3, 2, 2, 4, 3, 2, 3, 2, 2, 6, 3, 2, 2, 2, 2, 2, 2, 2, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 5, 10, 4, 6, 3, 4, 4, 4, 2, 4, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 2, 2, 2, 2, 2, 2 | 10 | 788 | 69.29 s |
| IEEE Test System | Optimal Number of PMUs | Optimal PMU Locations | Best BOI | Maximum Redundancy | SORI | CPU Time |
|---|---|---|---|---|---|---|
| 14-bus | 7 | 2, 4, 5, 6, 9, 11, 13 | 2, 3, 2, 4, 4, 4, 2, 2, 2, 2, 2, 2, 2 | 4 | 33 | 1.38 s |
| 30-bus | 12 | 2, 4, 5, 6, 9, 11, 13, 15, 17, 19, 20, 24 | 2, 5, 2, 7, 2, 5, 5, 7, 5, 4, 2, 2, 2, 2, 2, 2, 2, 3, 2, 2, 5, 5, 5, 5 | 5 | 85 | 1.63 s |
| 39-bus | 16 | 1, 3, 8, 15, 16, 20, 21, 23, 25, 26, 29, 34, 36, 37, 38, 39 | 4, 3, 3, 2, 2, 2, 2, 3, 4, 2, 3, 3, 3, 2, 5, 3, 2, 2, 3, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2 | 5 | 74 | 1.74 s |
| 57-bus | 23 | 1, 3, 6, 9, 10, 12, 13, 15, 18, 20, 25, 27, 29, 31, 32, 33, 38, 41, 49, 51, 53, 54, 56 | 2, 2, 4, 3, 4, 3, 5, 4, 4, 6, 2, 4, 2, 2, 3, 2, 2, 4, 2, 2, 2, 2, 2, 2, 3, 2, 3, 4, 4, 2, 3, 2, 2, 3, 2, 2, 2, 2, 2, 2, 3, 2 | 6 | 115 | 2.0 s |
| 118-bus | 60 | 2, 3, 6, 8, 10, 11, 12, 15, 17, 19, 21, 22, 26, 27, 29, 31, 32, 34, 35, 40, 42, 44, 45, 46, 49, 51, 53, 54, 56, 57, 59, 62, 65, 66, 70, 72, 75, 77, 79, 80, 83, 85, 86, 87, 89, 91, 92, 94, 96, 100, 102, 105, 106, 109, 110, 111, 112, 115, 117, 118 | 2, 2, 5, 4, 4, 2, 11, 2, 5, 5, 2, 2, 3, 2, 9, 2, 3, 2, 2, 2, 2, 2, 2, 7, 3, 2, 2, 4, 3, 8, 8, 7, 2, 7, 8, 2, 3, 2, 2, 4, 2, 2, 2, 6, 2, 2, 2, 2, 5, 3, 4, 2, 2, 4, 2, 3, 2, 10, 4, 2, 6, 3, 2, 2, 2, 4, 2, 3, 2, 2, 5, 3, 2, 2, 4, 3, 2, 2, 3, 2, 2, 6, 2, 4, 2, 3, 2, 2, 2, 4, 2, 2, 3, 2, 2, 3, 2, 2, 2, 4, 2, 2, 2, 2, 2, 2, 2, 2 | 11 | 339 | 4.44 s |
| 300-bus | 143 | 1, 2, 3, 5, 8, 11, 15, 17, 19, 20, 22, 25, 27, 31, 37, 38, 41, 43, 44, 47, 48, 49, 51, 53, 55, 58, 59, 60, 64, 66, 78, 79, 83, 84, 85, 86, 87, 88, 89, 90, 93, 98, 99, 101, 103, 105, 115, 116, 118, 119, 122, 124, 125, 132, 134, 135, 136, 141, 152, 155, 157, 158, 160, 162, 163, 164, 167, 168, 169, 171, 175, 177, 179, 184, 185, 190, 192, 193, 194, 196, 199, 202, 203, 204, 206, 208, 209, 210, 211, 212, 213, 215, 217, 218, 224, 225, 228, 229, 230, 232, 233, 235, 236, 237, 238, 239, 241, 243, 244, 247, 248, 249, 250, 252, 253, 256, 257, 258, 259, 260, 262, 264, 265, 267, 268, 269, 274, 275, 277, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 294, 300 | 4, 4, 23, 6, 6, 3, 2, 6, 3, 2, 2, 16, 3, 2, 9, 2, 3, 2, 2, 2, 14, 6, 3, 2, 17, 2, 18, 2, 2, 4, 2, 2, 2, 3, 4, 4, 2, 2, 16, 16, 3, 4, 16, 17, 14, 17, 3, 2, 2, 2, 2, 2, 2, 5, 4, 2, 8, 6, 3, 4, 4, 2, 3, 3, 3, 2, 2, 2, 2, 3, 4, 2, 2, 2, 3, 2, 7, 6, 2, 2, 9, 2, 2, 4, 3, 2, 15, 4, 3, 2, 3, 2, 2, 2, 2, 3, 2, 3, 3, 2, 3, 3, 5, 5, 5, 2, 2, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 4, 4, 2, 2, 5, 3, 5, 4, 4, 2, 2, 2, 2, 3, 2, 2, 4, 2, 16, 2, 3, 15, 2, 15, 15, 3, 2, 14, 2, 4, 3, 2, 3, 3, 2, 18, 3, 2, 15, 2, 2, 3, 2, 14, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 4, 2, 2, 2, 2, 2, 14, 2, 14, 2, 2, 2, 2, 2, 2, 5, 2, 2, 2, 14, 2, 2, 2, 2, 2, 14, 2, 5, 2, 2, 6, 13, 5, 4, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 4, 4, 5, 4, 4, 4, 4, 4, 2 | 18 | 979 | 73.44 s |
| Optimal Number of PMUs | ||||
|---|---|---|---|---|
| IEEE Test System | Case 1 | Case 2 | Case 3 | Case 4 |
| 14-bus | 4 | 3 | 9 | 7 |
| 30-bus | 10 | 6 | 21 | 12 |
| 39-bus | 13 | 7 | 28 | 16 |
| 57-bus | 17 | 12 | 36 | 23 |
| 118-bus | 32 | 28 | 68 | 60 |
| 300-bus | 91 | 65 | 204 | 143 |
| Case 1 | Case 2 | Case 3 | Case 4 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | Test System | Number of PMUs | SORI | Number of PMUs | SORI | Number of PMUs | SORI | Number of PMUs | SORI |
| Proposed | Polish 2383 | 829 | 3325 | 515 | 9049 | 1719 | 6020 | 1110 | 27,138 |
| Polish 3120 | 1131 | 4281 | 699 | 19,225 | 2263 | 7759 | 1444 | 63,216 | |
| [44] | Polish 2383 | - | - | 559 | - | - | - | - | - |
| [28] | Polish 2383 | - | - | 556 | - | - | - | - | - |
| Test System | PMU Placement |
|---|---|
| Polish 2838 | 105, 125, 187, 192, 207, 213, 217, 218, 223, 226, 229, 230, 233, 235, 237, 239, 240, 245, 246, 247, 249, 255, 257, 259, 265, 267, 273, 277, 278, 279, 282, 285, 287, 288, 295, 299, 300, 314, 315, 316, 319, 320, 324, 325, 326, 334, 339, 347, 350, 353, 360, 365, 366, 368, 370, 377, 378, 380, 384, 385, 388, 392, 393, 394, 404, 408, 409, 411, 424, 425, 431, 432, 434, 437, 438, 442, 443, 444, 445, 446, 448, 456, 459, 462, 464, 468, 472, 475, 476, 481, 486, 488, 493, 494, 497, 502, 505, 508, 510, 511, 512, 514, 515, 523, 525, 527, 529, 530, 533, 535, 544, 547, 548, 550, 553, 563, 567, 579, 583, 584, 589, 591, 593, 594, 595, 601, 602, 603, 605, 618, 621, 624, 636, 637, 643, 646, 648, 649, 650, 653, 661, 666, 668, 671, 676, 678, 679, 680, 685, 690, 691, 694, 695, 703, 704, 710, 718, 720, 721, 723, 724, 728, 733, 742, 745, 747, 749, 750, 752, 755, 756, 758, 762, 763, 765, 768, 774, 775, 776, 778, 781, 785, 794, 796, 798, 802, 834, 835, 839, 849, 852, 858, 859, 860, 862, 870, 871, 877, 883, 891, 892, 895, 899, 908, 910, 913, 914, 920, 943, 949, 954, 957, 961, 964, 968, 973, 978, 979, 995, 996, 997, 998, 1024, 1058, 1059, 1077, 1079, 1082, 1097, 1104, 1107, 1117, 1138, 1140, 1141, 1143, 1149, 1154, 1155, 1168, 1169, 1179, 1183, 1184, 1190, 1191, 1192, 1201, 1206, 1207, 1216, 1217, 1229, 1234, 1240, 1241, 1245, 1250, 1251, 1278, 1284, 1285, 1308, 1326, 1328, 1329, 1330, 1337, 1345, 1346, 1351, 1366, 1374, 1375, 1389, 1393, 1402, 1410, 1415, 1416, 1418, 1421, 1426, 1427, 1430, 1450, 1453, 1454, 1462, 1469, 1475, 1476, 1483, 1486, 1489, 1500, 1505, 1512, 1513, 1514, 1517, 1518, 1528, 1533, 1534, 1536, 1540, 1543, 1546, 1552, 1553, 1556, 1565, 1566, 1576, 1579, 1580, 1584, 1585, 1594, 1598, 1605, 1610, 1616, 1617, 1619, 1620, 1622, 1623, 1625, 1639, 1641, 1642, 1643, 1652, 1656, 1658, 1660, 1661, 1668, 1674, 1675, 1676, 1680, 1683, 1688, 1690, 1691, 1697, 1700, 1702, 1703, 1717, 1728, 1733, 1734, 1739, 1743, 1752, 1755, 1757, 1760, 1761, 1766, 1772, 1784, 1786, 1787, 1793, 1794, 1796, 1801, 1809, 1825, 1826, 1829, 1836, 1837, 1838, 1844, 1845, 1847, 1860, 1867, 1871, 1873, 1882, 1883, 1884, 1886, 1889, 1891, 1894, 1900, 1918, 1921, 1924, 1926, 1934, 1946, 1949, 1950, 1957, 1963, 1970, 1976, 1983, 1985, 1986, 1991, 1993, 1998, 2006, 2007, 2011, 2013, 2018, 2021, 2023, 2032, 2036, 2037, 2042, 2043, 2044, 2045, 2047, 2048, 2052, 2054, 2056, 2058, 2085, 2087, 2088, 2091, 2093, 2095, 2096, 2099, 2100, 2105, 2106, 2119, 2122, 2124, 2127, 2132, 2137, 2140, 2145, 2146, 2151, 2152, 2154, 2155, 2160, 2167, 2168, 2172, 2173, 2175, 2190, 2191, 2195, 2196, 2199, 2202, 2203, 2204, 2209, 2212, 2217, 2218, 2224, 2229, 2231, 2232, 2233, 2235, 2240, 2242, 2244, 2245, 2247, 2251, 2255, 2265, 2267, 2268, 2270, 2271, 2274, 2281, 2283, 2286, 2288, 2293, 2298, 2304, 2305, 2306, 2310, 2311, 2313, 2323, 2324, 2331, 2336, 2339, 2342, 2350, 2372, 2374, 2375 |
| Polish 3120 | 20, 35, 42, 46, 48, 59, 63, 69, 72, 74, 78, 83, 89, 95, 97, 98, 101, 107, 110, 111, 117, 121, 124, 129, 130, 133, 138, 150, 153, 154, 156, 160, 163, 167, 169, 173, 174, 177, 179, 184, 185, 187, 194, 196, 201, 208, 210, 215, 219, 222, 225, 229, 235, 236, 240, 241, 243, 245, 248, 249, 252, 260, 264, 270, 274, 278, 281, 282, 287, 289, 291, 292, 297, 299, 302, 303, 304, 306, 308, 310, 311, 312, 313, 318, 321, 327, 328, 333, 336, 338, 343, 345, 348, 350, 353, 363, 364, 365, 366, 367, 369, 373, 374, 378, 379, 382, 385, 388, 390, 392, 393, 394, 396, 401, 407, 409, 410, 414, 415, 421, 422, 429, 435, 438, 440, 442, 443, 446, 450, 452, 455, 461, 463, 464, 467, 470, 472, 474, 478, 479, 483, 485, 486, 488, 489, 491, 492, 497, 499, 501, 505, 506, 509, 511, 513, 514, 516, 518, 520, 522, 526, 533, 536, 541, 548, 550, 565, 567, 569, 570, 575, 580, 583, 585, 590, 594, 605, 608, 609, 612, 615, 617, 619, 627, 629, 635, 638, 639, 641, 642, 647, 648, 650, 651, 656, 658, 661, 667, 669, 671, 676, 678, 681, 682, 685, 687, 694, 696, 700, 701, 702, 706, 709, 714, 722, 723, 733, 739, 740, 741, 742, 743, 744, 750, 752, 754, 760, 761, 763, 764, 766, 767, 768, 773, 774, 780, 785, 786, 789, 790, 796, 800, 805, 807, 811, 813, 815, 818, 820, 822, 830, 832, 838, 839, 841, 842, 845, 848, 850, 852, 853, 858, 865, 868, 871, 874, 875, 878, 883, 887, 891, 896, 902, 903, 910, 915, 923, 932, 935, 939, 940, 945, 947, 949, 950, 952, 956, 963, 966, 969, 971, 972, 986, 989, 991, 1010, 1012, 1013, 1020, 1022, 1033, 1034, 1035, 1036, 1040, 1043, 1044, 1048, 1050, 1054, 1055, 1060, 1069, 1073, 1074, 1085, 1090, 1093, 1095, 1096, 1098, 1102, 1105, 1106, 1110, 1116, 1117, 1125, 1126, 1127, 1131, 1134, 1139, 1146, 1149, 1152, 1153, 1154, 1155, 1157, 1158, 1163, 1165, 1166, 1169, 1171, 1180, 1181, 1184, 1187, 1190, 1192, 1194, 1198, 1201, 1202, 1205, 1211, 1213, 1217, 1221, 1225, 1230, 1237, 1239, 1241, 1245, 1246, 1248, 1252, 1253, 1255, 1258, 1260, 1261, 1271, 1273, 1277, 1280, 1285, 1289, 1290, 1291, 1292, 1299, 1302, 1307, 1310, 1311, 1314, 1320, 1322, 1326, 1327, 1331, 1335, 1347, 1348, 1353, 1354, 1356, 1357, 1359, 1360, 1364, 1367, 1370, 1375, 1377, 1378, 1380, 1382, 1383, 1384, 1385, 1386, 1389, 1391, 1414, 1415, 1417, 1419, 1424, 1425, 1426, 1432, 1433, 1434, 1435, 1436, 1442, 1443, 1445, 1447, 1448, 1449, 1452, 1456, 1459, 1464, 1467, 1469, 1470, 1478, 1486, 1490, 1491, 1492, 1500, 1504, 1508, 1510, 1511, 1515, 1518, 1519, 1526, 1527, 1530, 1535, 1539, 1541, 1543, 1545, 1547, 1548, 1550, 1551, 1553, 1555, 1559, 1562, 1569, 1574, 1576, 1579, 1586, 1587, 1588, 1589, 1590, 1592, 1595, 1596, 1609, 1612, 1613, 1614, 1615, 1619, 1621, 1625, 1627, 1628, 1629, 1634, 1639, 1641, 1645, 1648, 1655, 1662, 1664, 1680, 1681, 1685, 1687, 1690, 1692, 1698, 1699, 1708, 1716, 1719, 1730, 1731, 1733, 1736, 1743, 1744, 1752, 1753, 1755, 1760, 1766, 1769, 1770, 1781, 1789, 1790, 1791, 1792, 1793, 1796, 1802, 1803, 1812, 1819, 1824, 1829, 1832, 1833, 1834, 1835, 1836, 1837, 1840, 1845, 1847, 1849, 1856, 1861, 1862, 1863, 1865, 1866, 1867, 1869, 1871, 1877, 1883, 1885, 1886, 1889, 1893, 1898, 1899, 1901, 1907, 1908, 1910, 1911, 1914, 1916, 1925, 1927, 1929, 1930, 1937, 1940, 1942, 1944, 1952, 1953, 1957, 1959, 1961, 1964, 1967, 1969, 1971, 1972, 1976, 1980, 1981, 1988, 1989, 1992, 1993, 1994, 1997, 2000, 2001, 2010, 2011, 2014, 2015, 2016, 2019, 2020, 2021, 2029, 2030, 2038, 2042, 2044, 2046, 2047, 2050, 2053, 2060, 2073, 2074, 2075, 2082, 2083, 2086, 2100, 2101, 2107, 2108, 2109, 2114, 2122, 2123, 2132, 2133, 2134, 2141, 2143, 2147, 2149, 2150, 2152, 2155, 2159, 2161, 2162, 2166, 2168, 2169, 2170, 2174, 2178, 2181, 2184, 2187, 2188, 2195, 2199, 2202, 2204, 2205, 2219, 2223, 2224, 2225, 2226, 2230, 2232, 2233, 2236, 2243, 2244, 2245, 2246, 2249, 2252, 2253, 2255, 2256, 2257, 2259, 2262, 2263, 2265, 2269, 2274, 2277, 2278, 2279, 2286, 2288, 2297, 2299, 2300, 2301, 2302, 2307 |
| Case | Test Systems | Number of ZIB Buses | Optimal Number of PMUs | Buses Observable through Both Direct PMU Measurement and ZIB Effect | Buses Observable through ZIB Effect Only | Max ZIOD | Deepest Propagation Path through ZIIR | ZIUR (%) |
|---|---|---|---|---|---|---|---|---|
| 2 | 14-Bus | 1 | 3 | - | 8 | 2 | 4:7:8 | 100 |
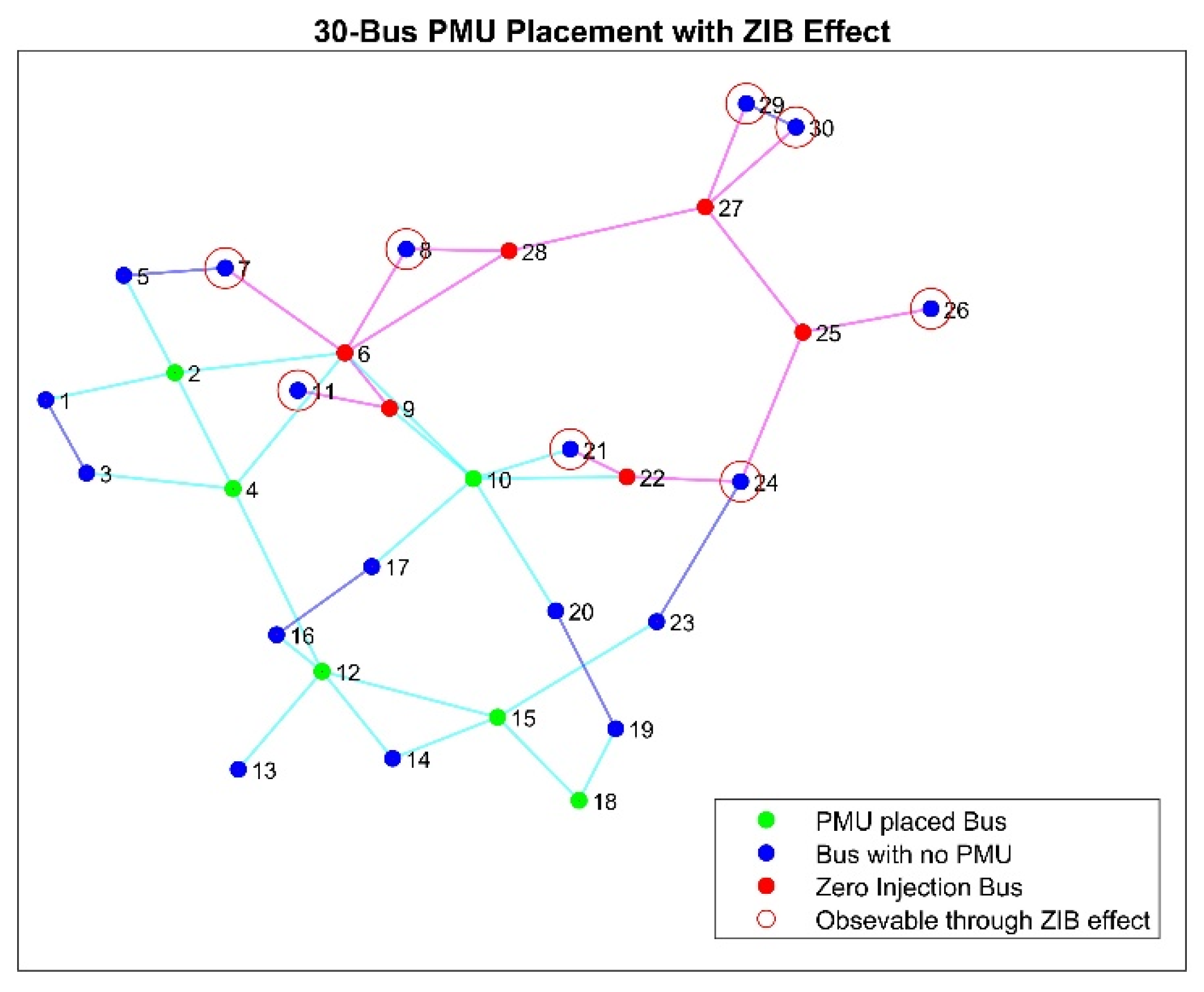
| 30-Bus | 6 | 6 | 21 | 7, 8, 11, 24, 26, 29, 30 | 6 | 10:9, 6, 28, 27, 25:26 | 116.6 | |
| 39-Bus | 10 | 7 | 7,21,15 | 3, 4, 12, 18, 27, 30, 33.35 | 7 | 8:4, 6, 11, 10, 13, 14:4 | 80 | |
| 57-Bus | 15 | 12 | 8, 13, 14, 38, 41, 57 | 5, 6, 23, 27, 35, 43, 47 | 5 | 27:26, 24:23 | 46.6 | |
| 4 | 14-Bus | 1 | 7 | - | 8 | 2 | 4:7:8 | 100 |
| 30-Bus | 6 | 12 | 21 | 8, 11, 26, 29, 30 | 6 | 10:9, 6, 28, 27, 25:26 | 83.3 | |
| 39-Bus | 10 | 16 | 4, 7, 18, 27 | 12, 30, 31, 32, 33, 35 | 6 | 15:14, 13, 10, 11, 6:31 | 60 | |
| 57-Bus | 15 | 23 | 5, 8, 14, 43, 44, 57 | 23, 35, 47 | 3 | 38:37, 36:35 | 20 |
| Case 1: Normal Operation without ZIB Effect and Unlimited Channel Limits | ||||||||
| Refs. | 14-Bus | 30-Bus | 39-Bus | 57-Bus | 118-Bus | 300-Bus | Polish 2383-Bus | Polish 3120-Bus |
| Proposed | 0.847 s | 0.761 s | 1.418 s | 3.892 s | 2896.1 s | 1015 s | 3625.7 s | 7989.3 s |
| [27] | 1.11 s | 3.53 s | - | 24.87 s | - | - | - | - |
| [45] | 1.855 s | 7.886 s | - | 16.425 s | 38.347 s | - | - | - |
| [32] | 0.008 s | 0.013 s | 0.014 s | 0.071 s | 0.036 s | 0.189 s | - | - |
| Case 2: Normal Operation with ZIB Effect Consideration | ||||||||
| Refs. | 14-Bus | 30-Bus | 39-Bus | 57-Bus | 118-Bus | 300-Bus | Polish 2383-Bus | Polish 3120-Bus |
| Proposed | 2.58 | 3.04 | 2.64 | 2.73 | 440.5 | 3252.9 s | 6298.1 s | |
| [27] | 1.2 | 3.0 | - | 53.4 | - | - | - | - |
| [44] | 0.1101 | 0.1547 | 0.2084 | - | 0.1984 | - | 2.5888 | - |
| [45] | 1.664 s | 4.572 s | - | 11.243 s | 34.136 s | |||
| Case 3: Single PMU Outage | ||||||||
| Refs. | 14-Bus | 30-Bus | 39-Bus | 57-Bus | 118-Bus | 300-Bus | Polish 2383-Bus | Polish 3120-Bus |
| Proposed | 0.79 | 0.73 | 0.83 | 1.1 | 3.72 | 69.3 | 4116.5 s | 5331.1 s |
| [27] | 1.9 | 4156.1 | - | 37,050.2 | - | - | - | - |
| [46] | 2.357 s | 3.450 s | - | 7.216 s | - | - | - | - |
| [47] | - | - | - | - | - | - | 0.062 s | - |
| Case 4: Single PMU Outage with ZIB Effect | ||||||||
| Refs. | 14-Bus | 30-Bus | 39-Bus | 57-Bus | 118-Bus | 300-Bus | Polish 2383-Bus | Polish 3120-Bus |
| Proposed | 1.38 s | 1.63 s | 1.74 s | 2.0 s | 4.44 s | 73.44 s | 3003.2 s | 4528 s |
| [27] | 1.4 s | 153.3 s | - | 37,050.2 s | - | - | - | - |
| [44] | 0.1 s | 0.2 s | 0.2 s | - | 0.2 s | - | 3.1 s | - |
| [47] | 0.014 s | 0.098 s | 0.247 s | - | 0.862 s | - | 4889 s | - |
| Year | Refs. | Optimal Number of PMUs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 | ||||||||||||
| 14-Bus | 30-Bus | 39-Bus | 57-Bus | 118-Bus | 300-Bus | 14-Bus | 30-Bus | 39-bus | 57-Bus | 118-Bus | 300-Bus | ||
| N/A | Proposed | 14-Bus | 30-Bus | 39-bus | 57-Bus | 118-Bus | 300-Bus | 14-Bus | 30-Bus | 39-bus | 57-Bus | 118-Bus | 300-Bus |
| 2022 | [27] | 4 (19) | 10 (52) | 13 (52) | 17 (72) | 32 (164) | 96 (419) | 3 (15) | 6 (51) | 7 (40) | 12 (59) | 28 (174) | 65 (528) |
| 2020 | [28] | 4 (16) | 10 (48) | - | 17 (69) | - | - | 3 | 7 | - | 12 | - | - |
| 2020 | [48] | - | - | 13 | 17 | 32 | - | - | - | 8 | 11 | 28 | - |
| 2020 | [30] | 4 (17) | 10 (51) | 13 (52) | 17 (71) | 32 (157) | - | 3 (15) | 7 (29) | 8 (32) | 12 (49) | 29 (143) | - |
| 2019 | [32] | 4 | 10 | 13 | 17 | 32 | - | 3 | 6 | 8 | 11 | 28 | - |
| 2018 | [44] | 4 (19) | 10 (52) | 13 (52) | - | 32 (163) | - | 3 (16) | 6 (37) | 8 (45) | - | 28 (156) | - |
| 2018 | [33] | 4 | 10 | 13 | - | 32 | - | 3 | 7 | 8 | - | 28 | - |
| 2018 | [33] | - | - | - | - | - | - | 3 | 7 | 9 | 12 | 29 | - |
| 2015 | [49] | - | - | - | - | - | - | 3 | 7 | 9 | 12 | 29 | 74 |
| Year | Refs. | Optimal Number of PMUs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 3 | Case 4 | ||||||||||||
| 14-Bus | 30-Bus | 39-bus | 57-Bus | 118-Bus | 300-Bus | 14-Bus | 30-Bus | 39-bus | 57-Bus | 118-Bus | 300-Bus | ||
| N/A | Proposed | 9 (39) | 21 (85) | 28 (96) | 36 (148) | 68 (323) | 204 (788) | 7 (33) | 12 (85) | 16 (74) | 23 (115) | 60 (339) | 143 (979) |
| 2022 | [27] | 9 | 21 | - | 25 | - | - | 7 | 15 | - | 25 | - | -- |
| 2020 | [28] | - | - | - | - | - | - | - | - | - | - | - | - |
| 2020 | [48] | 9 (39) | 21 (83) | 29 (99) | 33 (129) | 69 (313) | - | - | - | - | - | - | - |
| 2020 | [30] | - | - | - | - | - | - | 7 | 14 | 17 | 22 | 61 | - |
| 2019 | [32] | - | - | - | - | - | - | - | - | - | - | - | - |
| 2018 | [44] | - | - | - | - | - | - | 7 | 14 | 19 | - | 64 | - |
| 2018 | [33] | - | - | - | - | - | - | 7 | 16 | 19 | 27 | 62 | - |
| 2018 | [33] | - | - | - | - | - | - | - | - | - | - | - | - |
| 2015 | [49] | - | - | - | - | - | - | - | - | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tshenyego, O.; Samikannu, R.; Mtengi, B.; Mosalaosi, M.; Sigwele, T. A Graph-Theoretic Approach for Optimal Phasor Measurement Units Placement Using Binary Firefly Algorithm. Energies 2023, 16, 6550. https://doi.org/10.3390/en16186550
Tshenyego O, Samikannu R, Mtengi B, Mosalaosi M, Sigwele T. A Graph-Theoretic Approach for Optimal Phasor Measurement Units Placement Using Binary Firefly Algorithm. Energies. 2023; 16(18):6550. https://doi.org/10.3390/en16186550
Chicago/Turabian StyleTshenyego, Onkemetse, Ravi Samikannu, Bokani Mtengi, Modisa Mosalaosi, and Tshiamo Sigwele. 2023. "A Graph-Theoretic Approach for Optimal Phasor Measurement Units Placement Using Binary Firefly Algorithm" Energies 16, no. 18: 6550. https://doi.org/10.3390/en16186550
APA StyleTshenyego, O., Samikannu, R., Mtengi, B., Mosalaosi, M., & Sigwele, T. (2023). A Graph-Theoretic Approach for Optimal Phasor Measurement Units Placement Using Binary Firefly Algorithm. Energies, 16(18), 6550. https://doi.org/10.3390/en16186550











