Developed and Intelligent Structure of a Control for PV Water Treatment System
Abstract
:1. Introduction
- Detailed study and development of a water treatment system with different control approaches;
- Verification and simulation;
- The establishment and implementation of an experimental test bench for the PV water treatment system based on a PVG, a chopper, inverter, motor pump, UV lamp, sensors, etc.;
- Interpretation of the results.
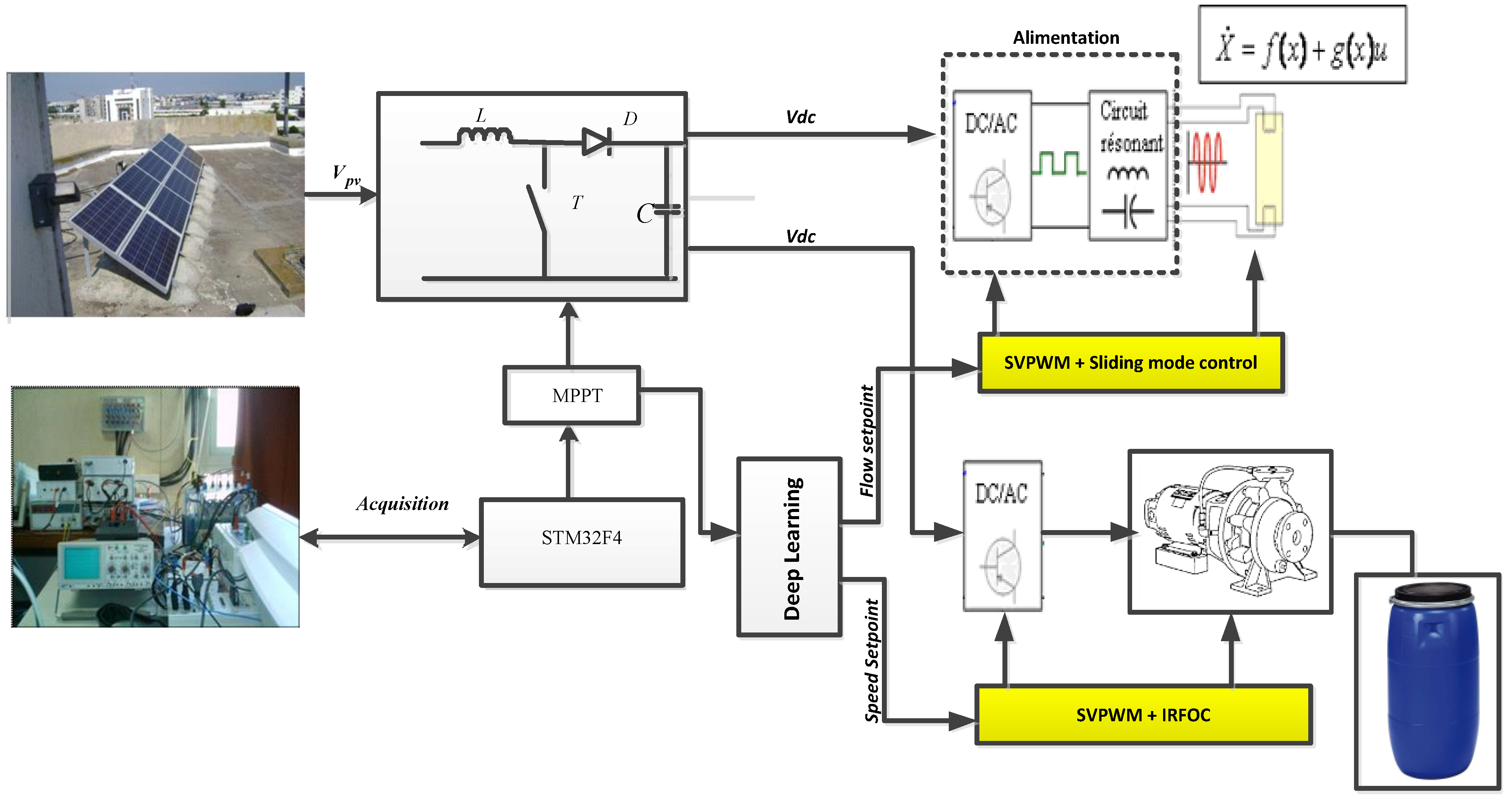
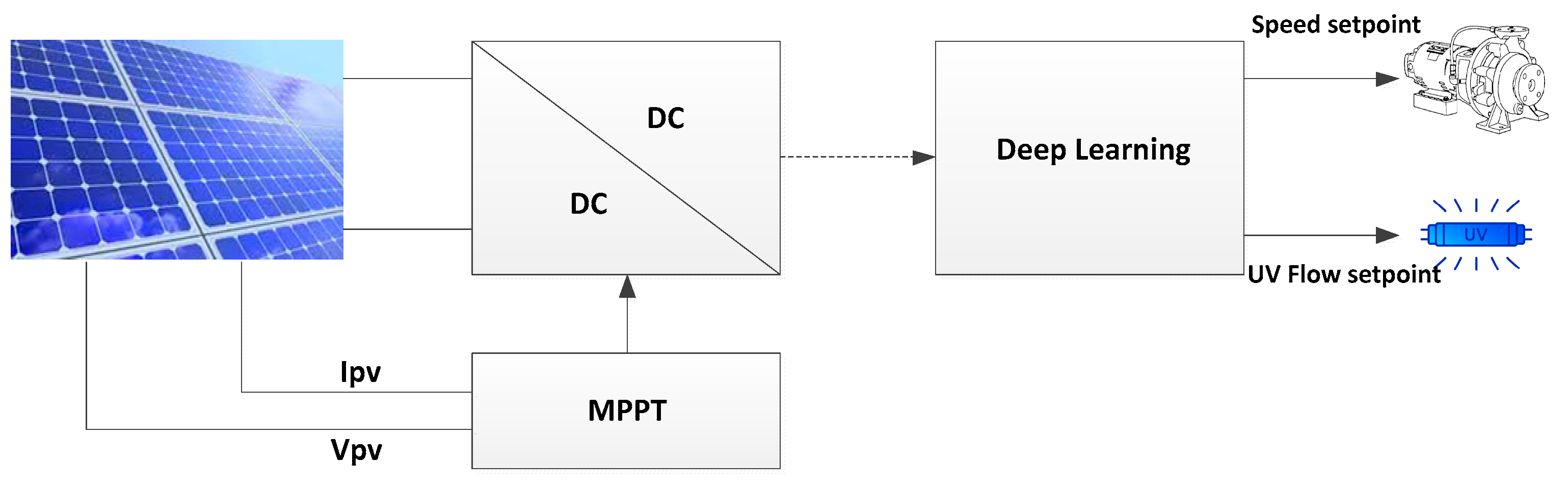
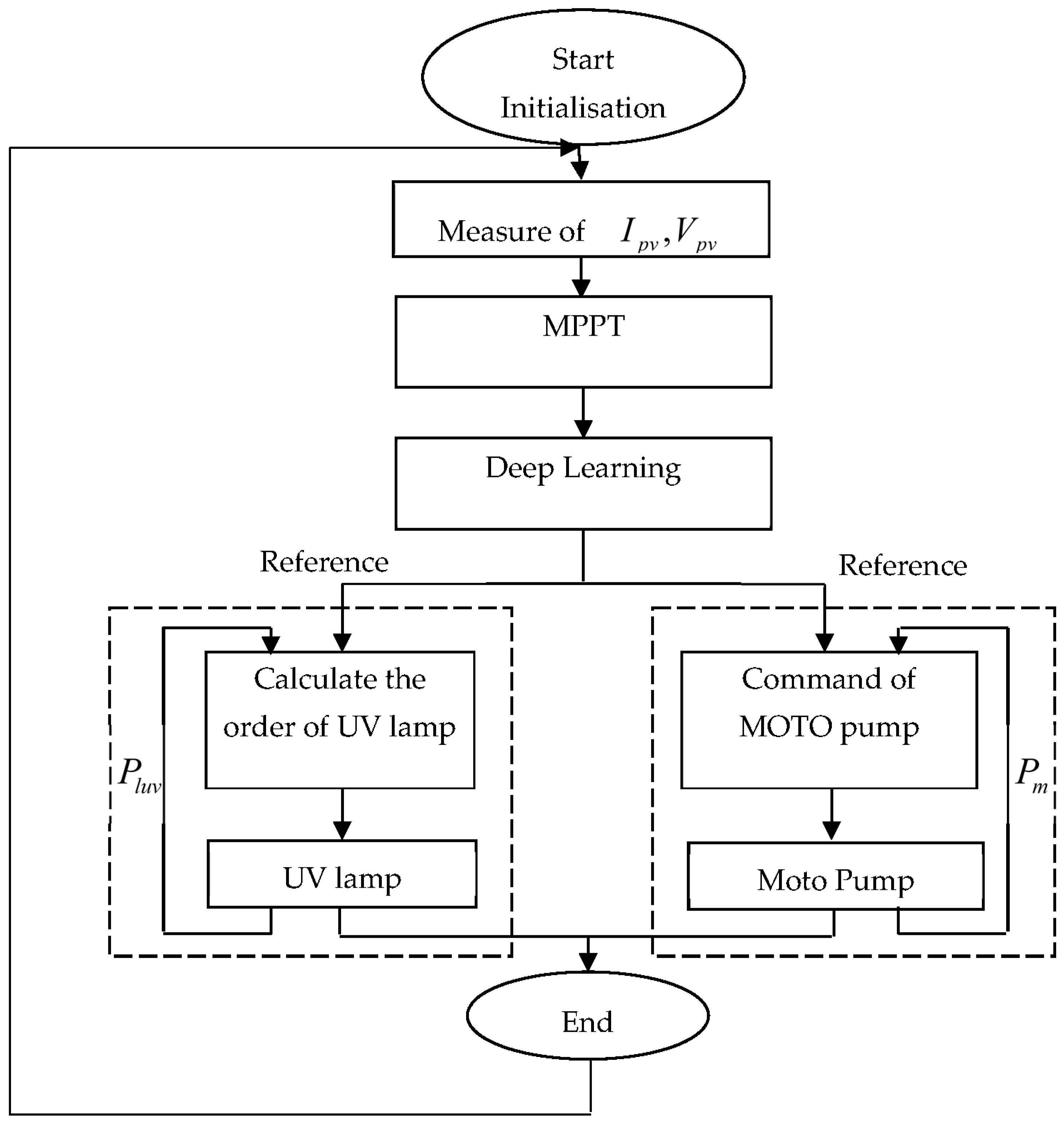
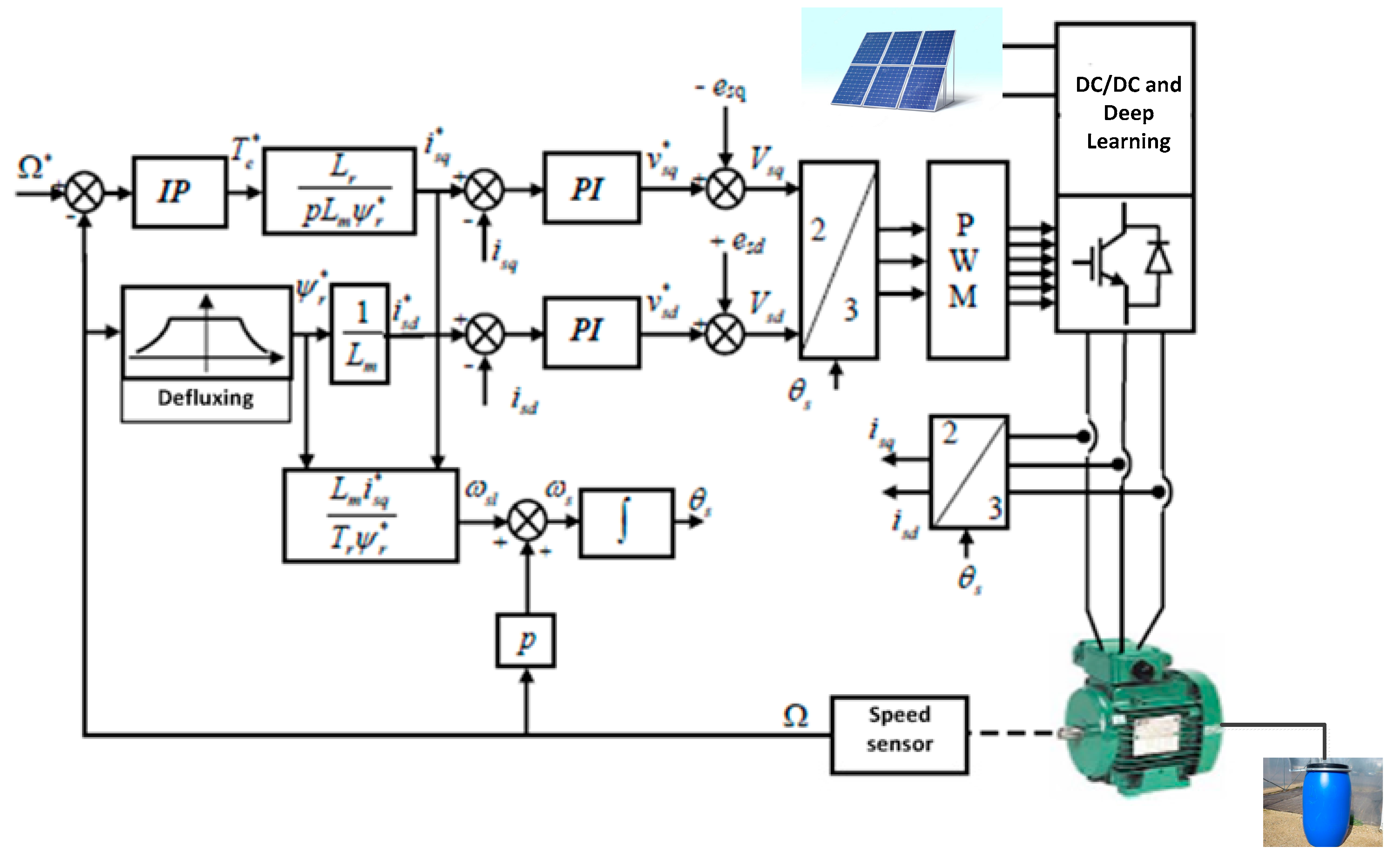
2. General Structure of PV Water Treatment System
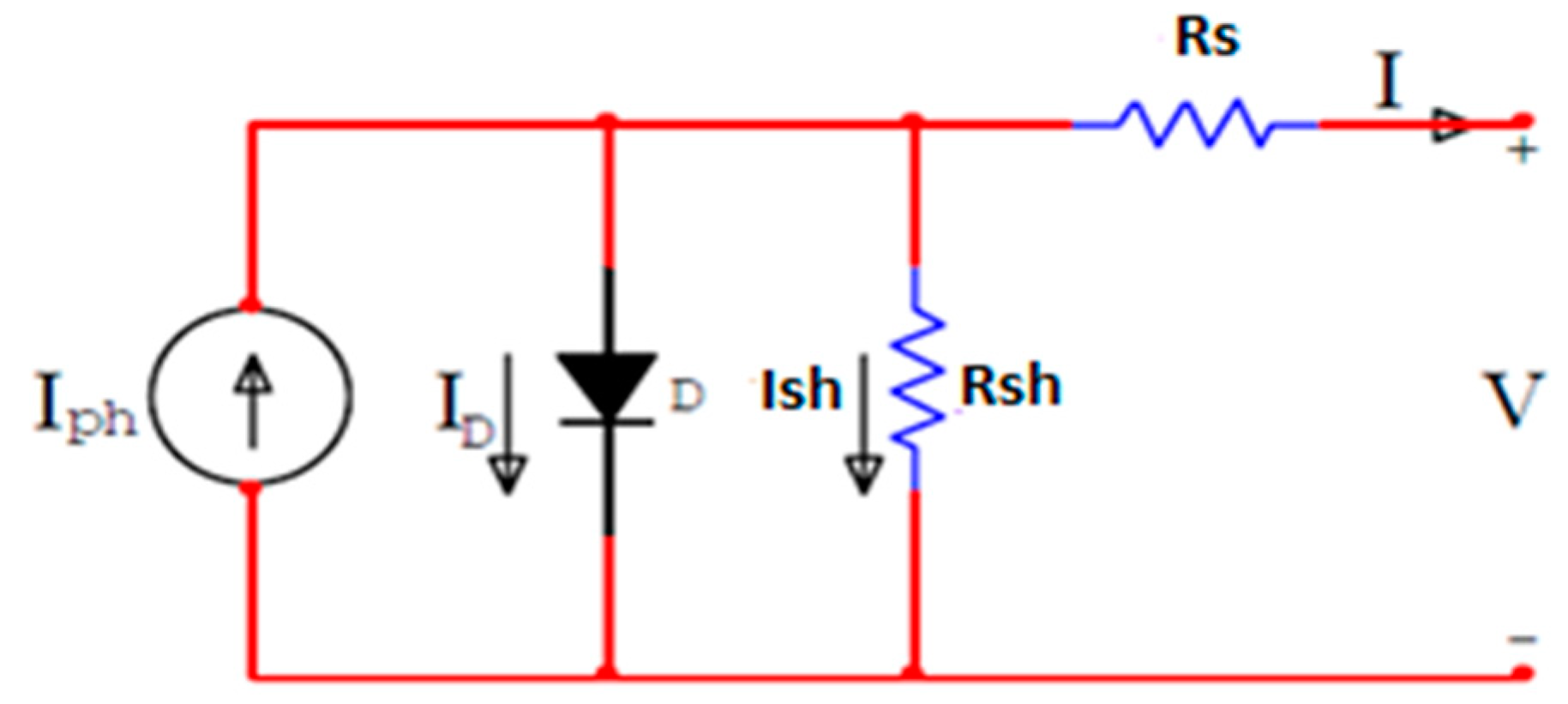
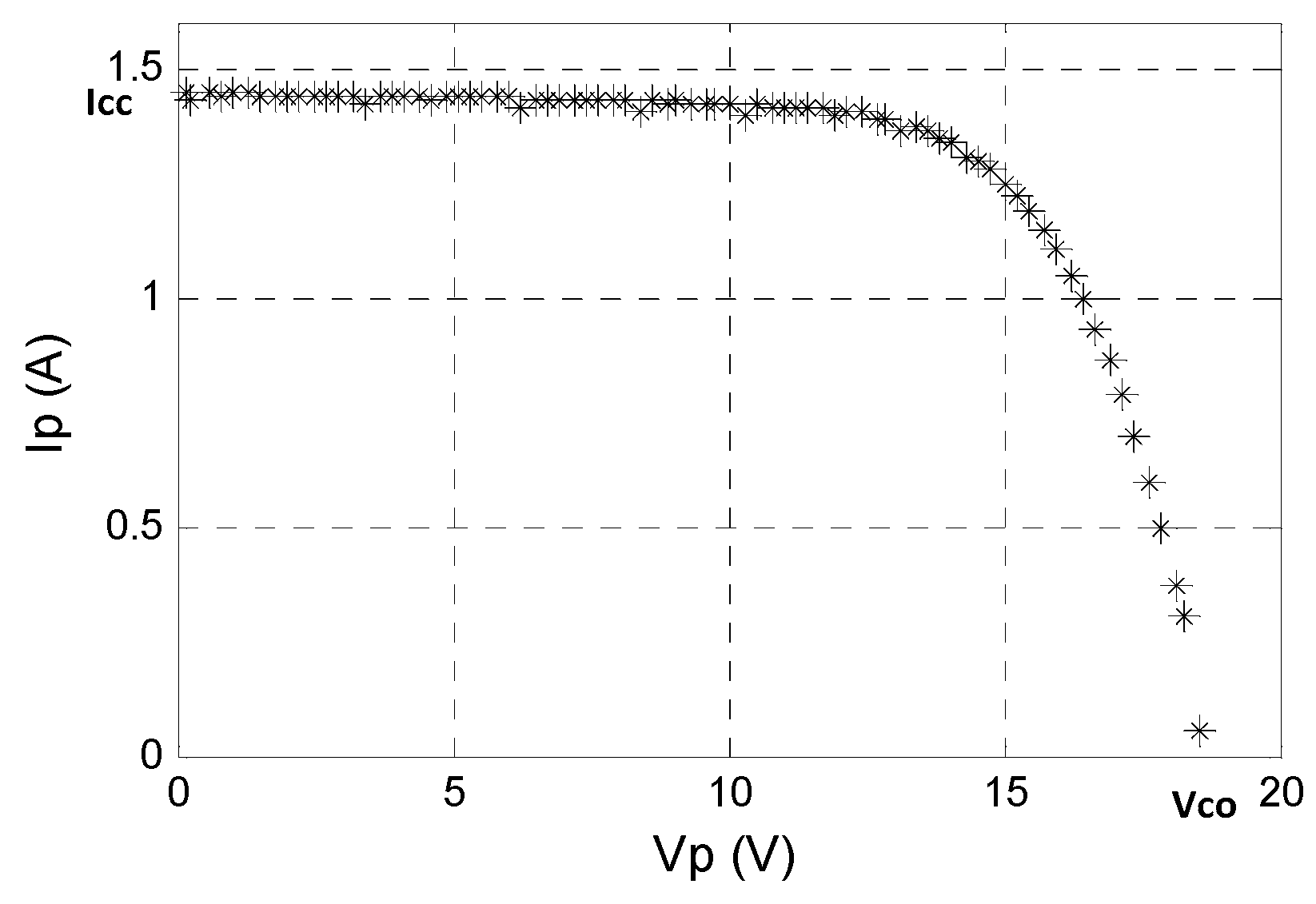
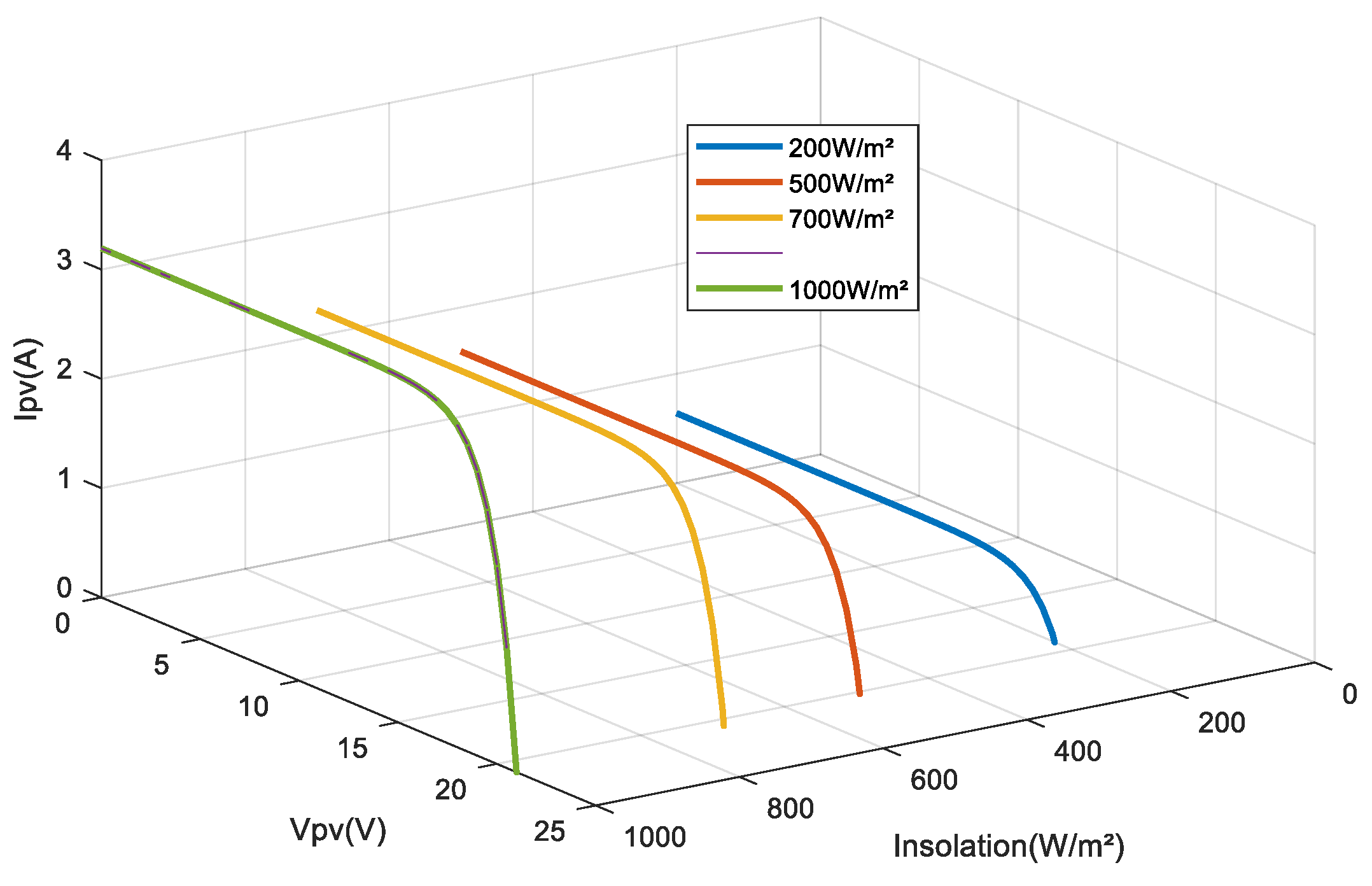
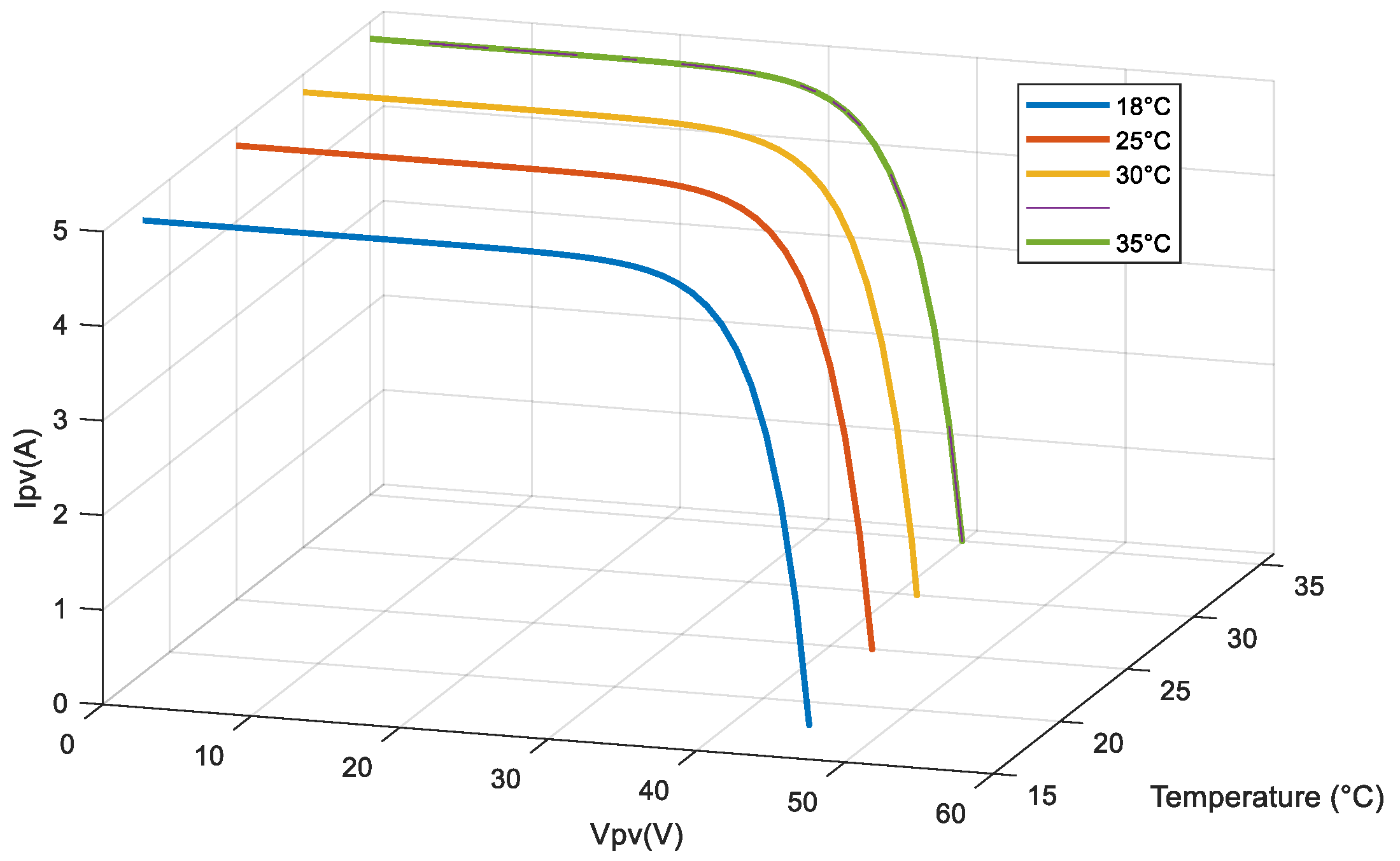
2.1. PVG Model
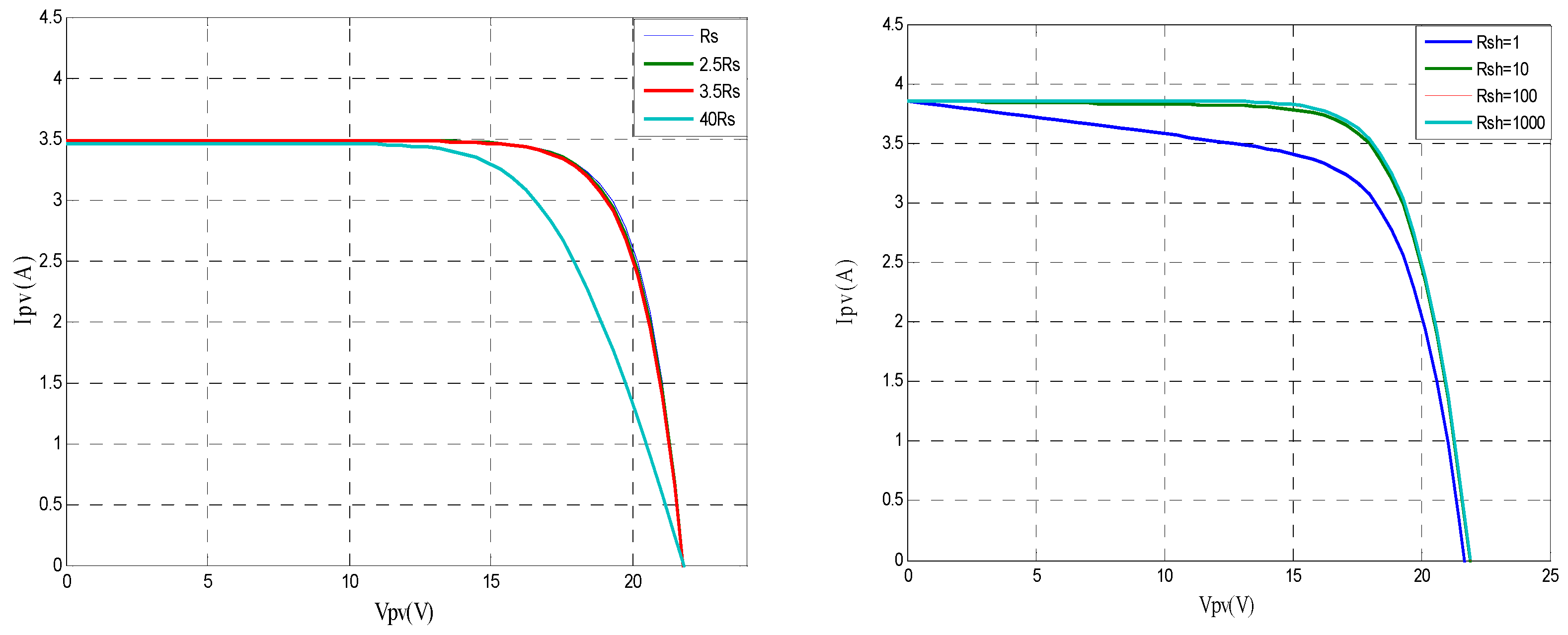
2.1.1. Effect of Series and Shunt Resistances
2.1.2. Estimation of Series and Shunt Resistances
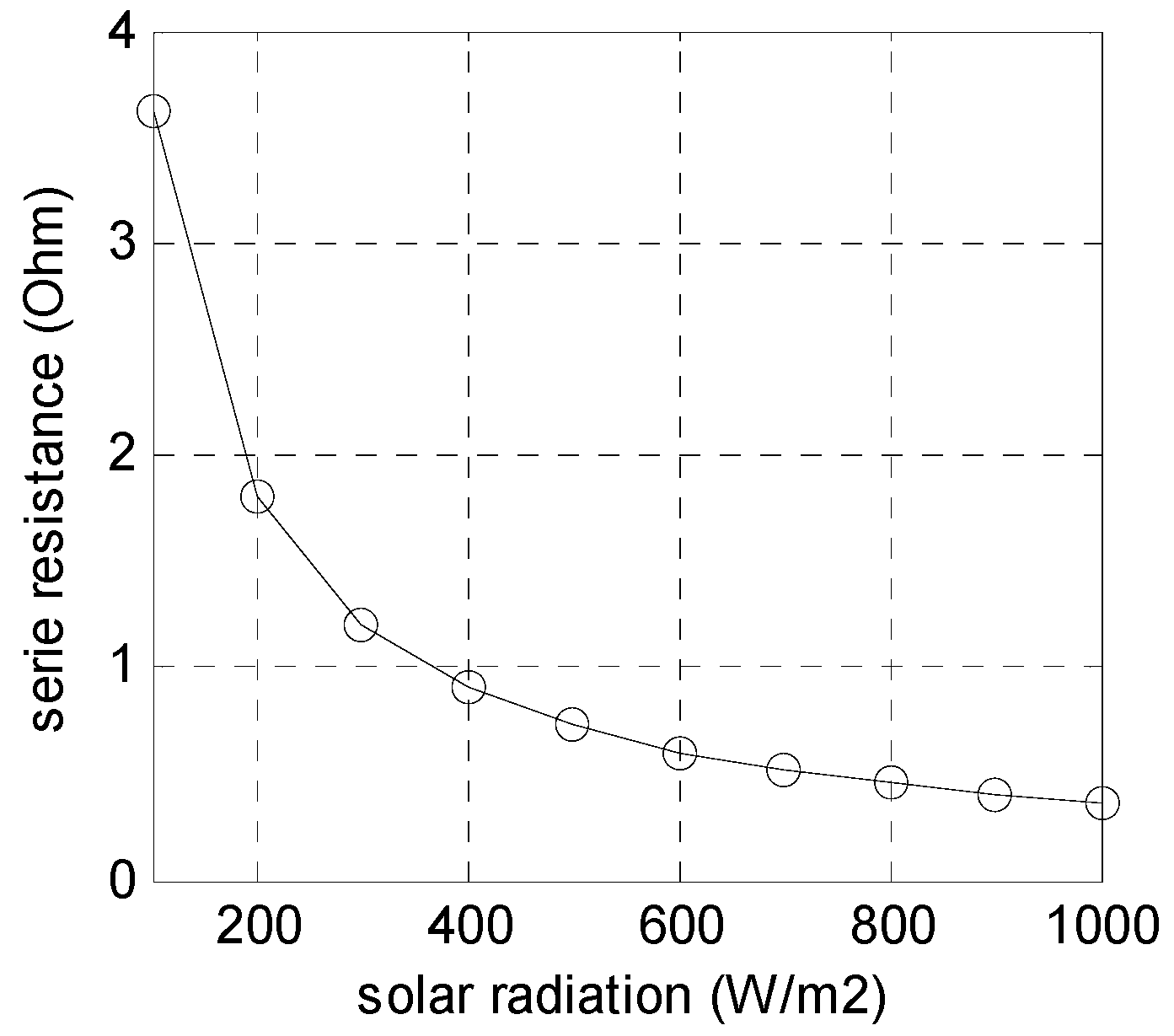
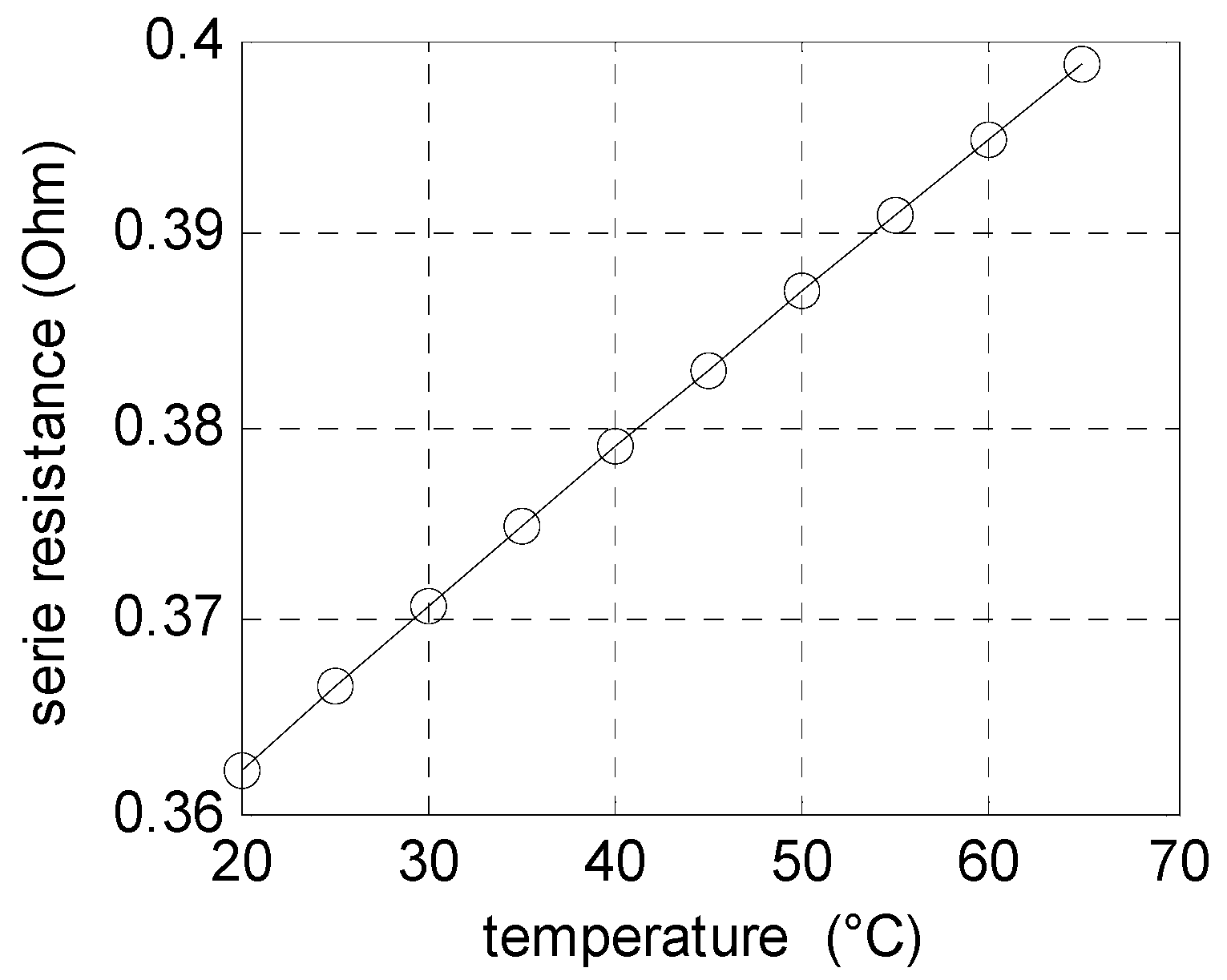
2.1.3. Influence of Illumination and Temperature on the Estimated Series Resistance
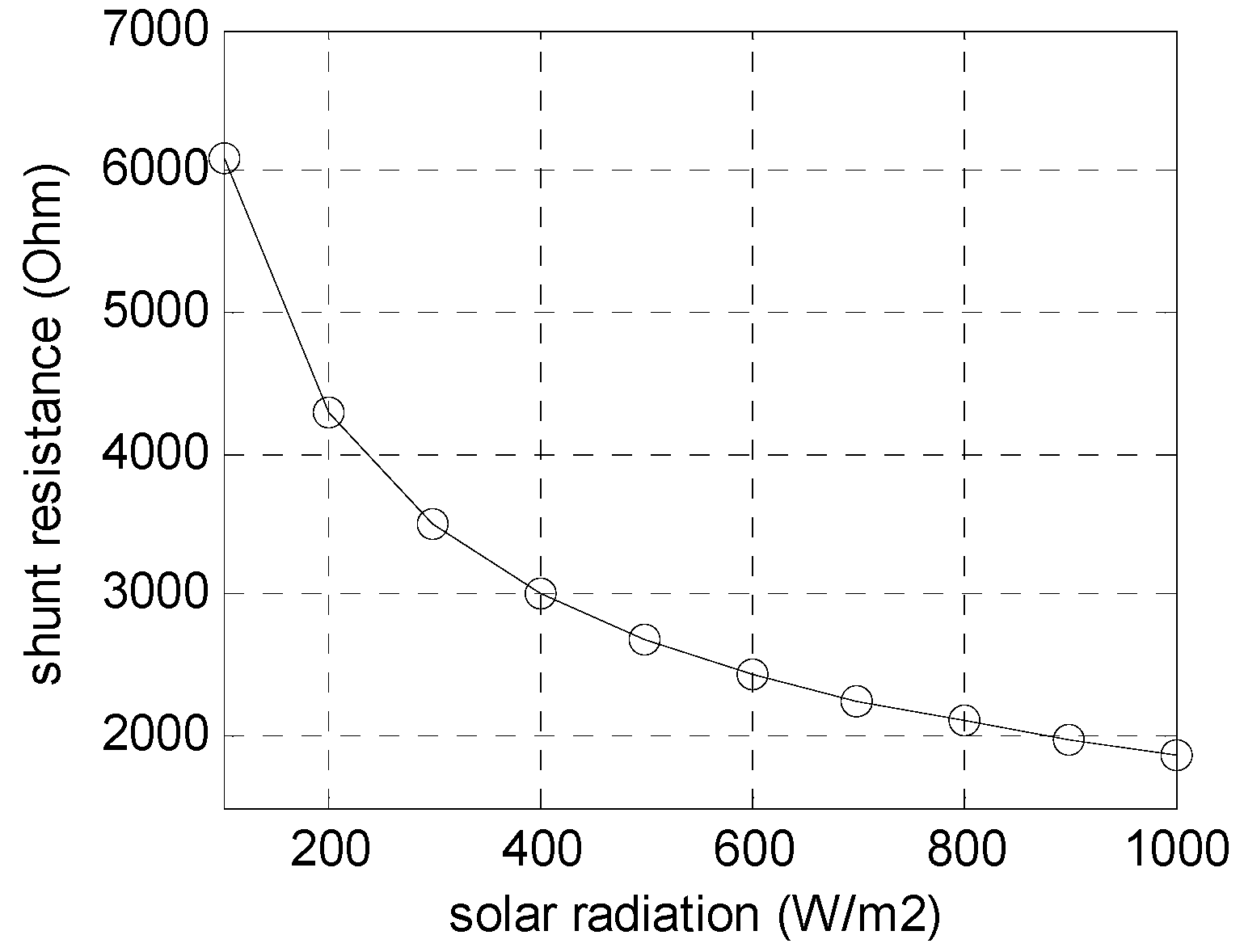
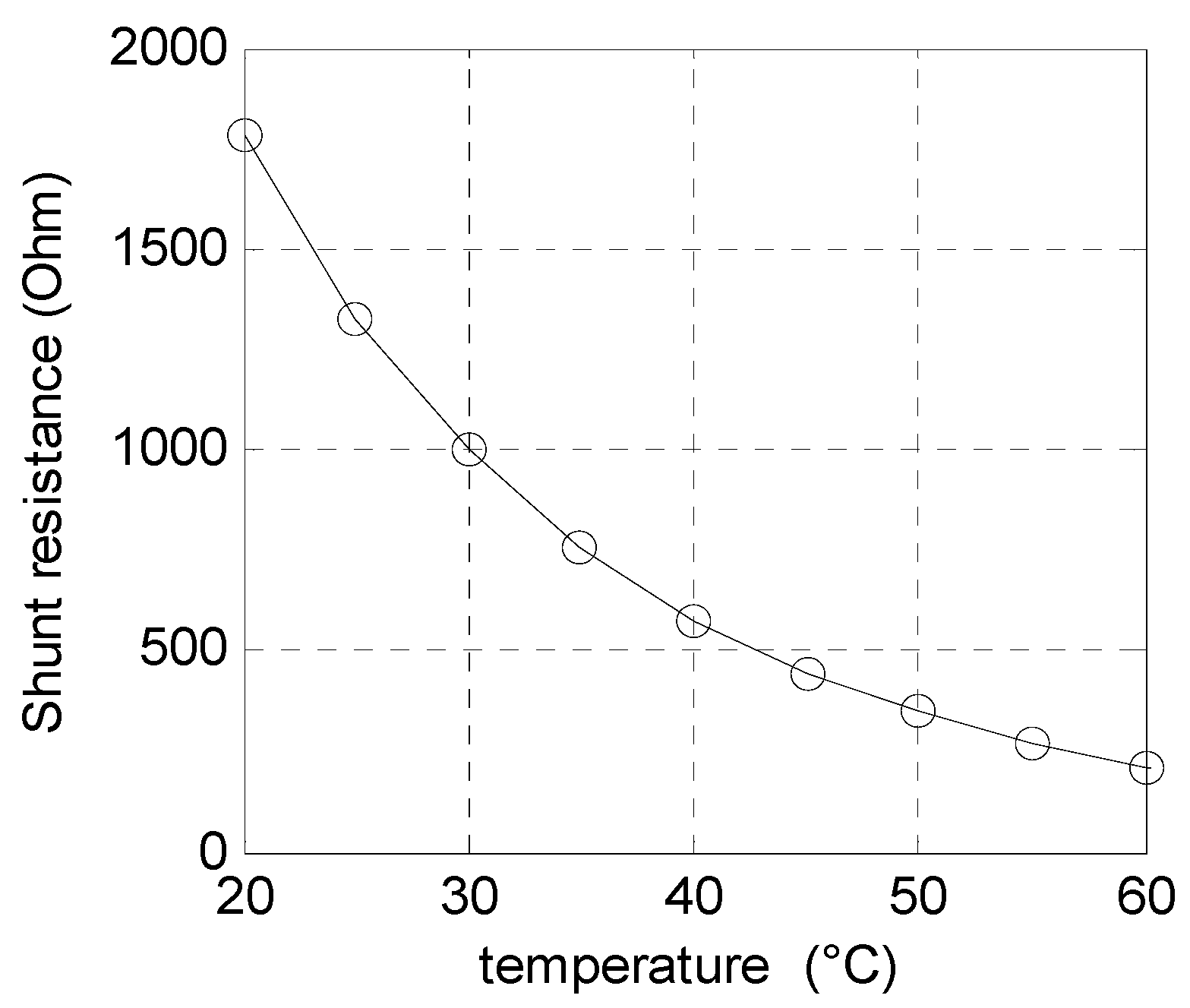
2.1.4. Influence of Illumination and Temperature on the Estimated Shunt Resistance
2.2. Optimal Operation of PV System
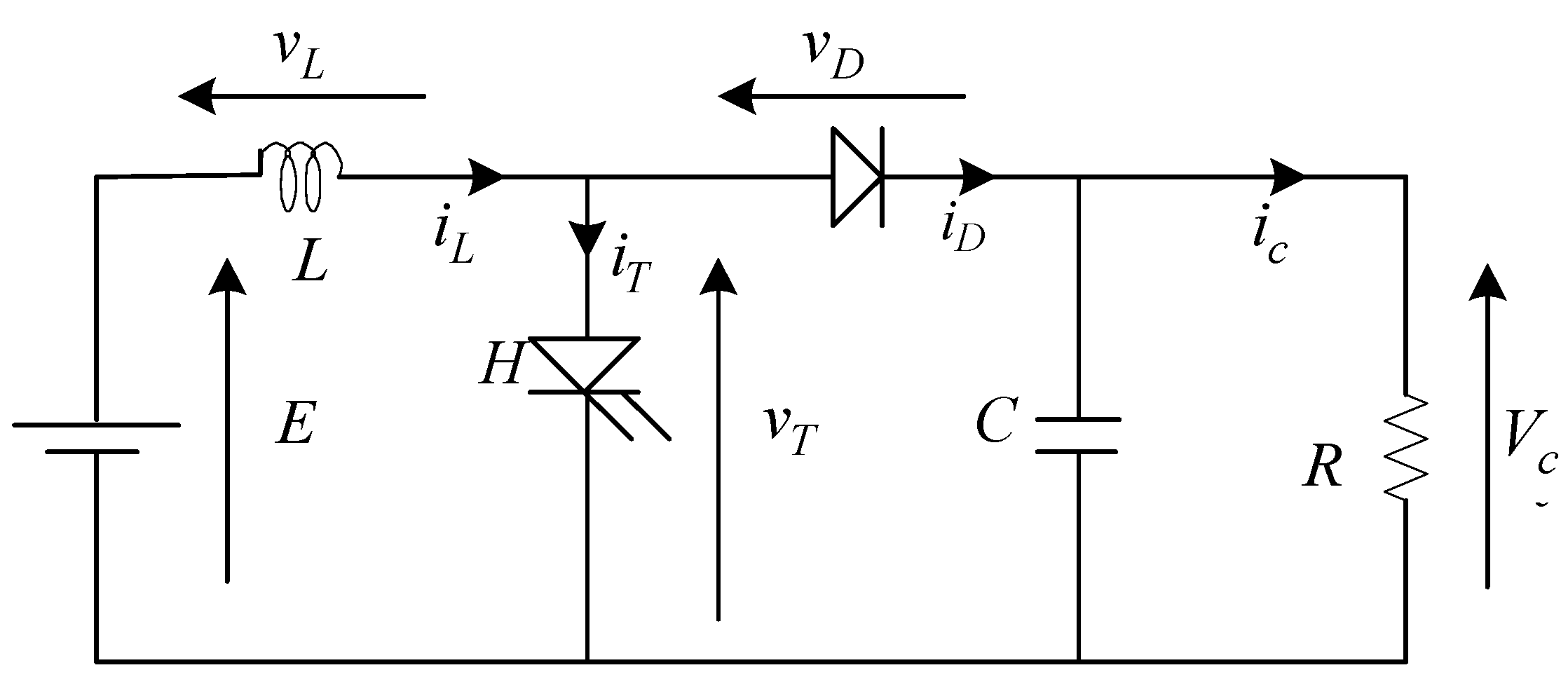
2.2.1. Adaptation Stage: DC/DC Converter
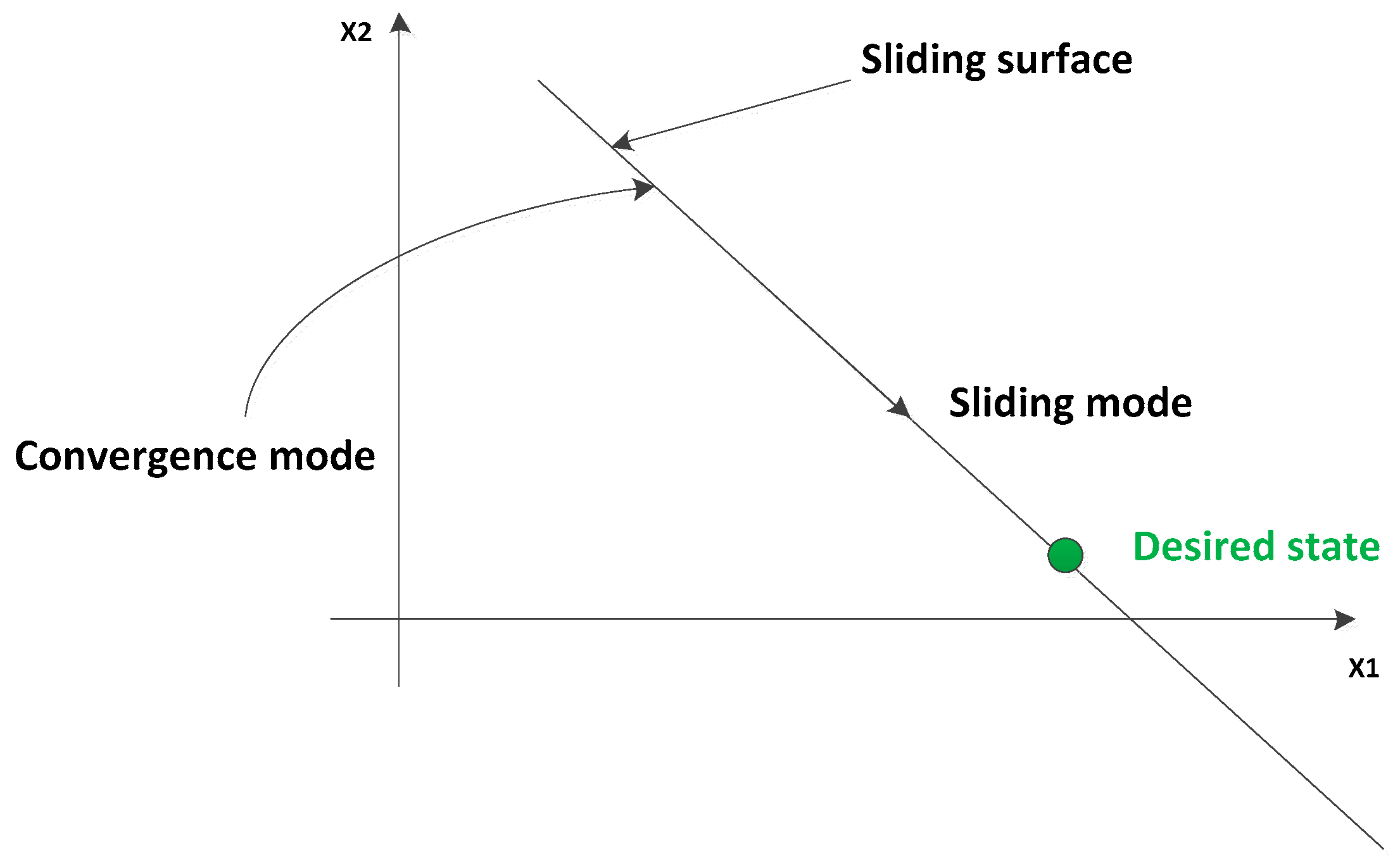
2.2.2. Adopted MPPT Technique: Sliding Mode Control
- Convergence towards the sliding surface;
- Sliding along it.
2.3. Kinetic Modeling of Water Disinfection
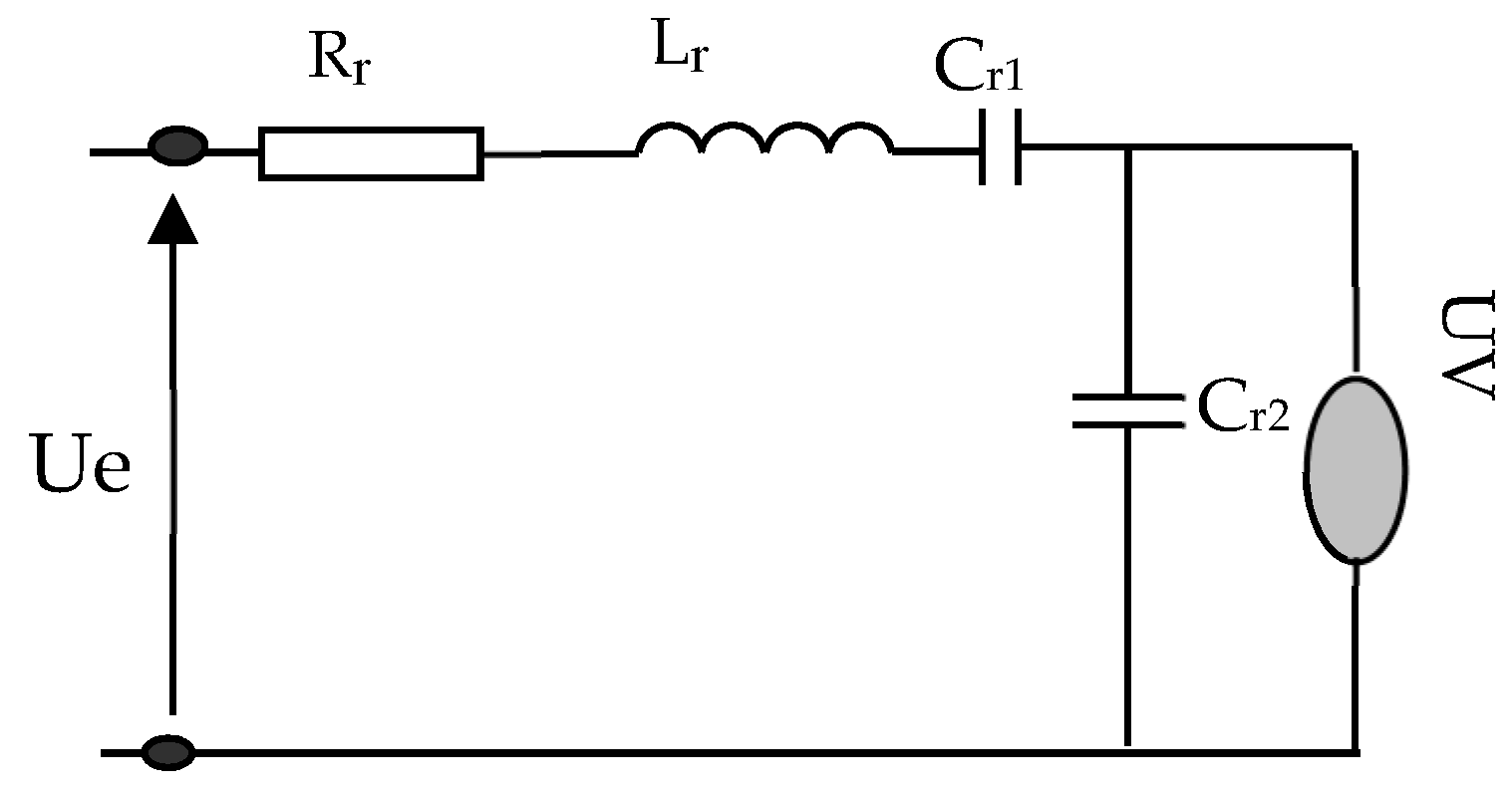
Discharge Lamp Model
2.4. Deep Learning
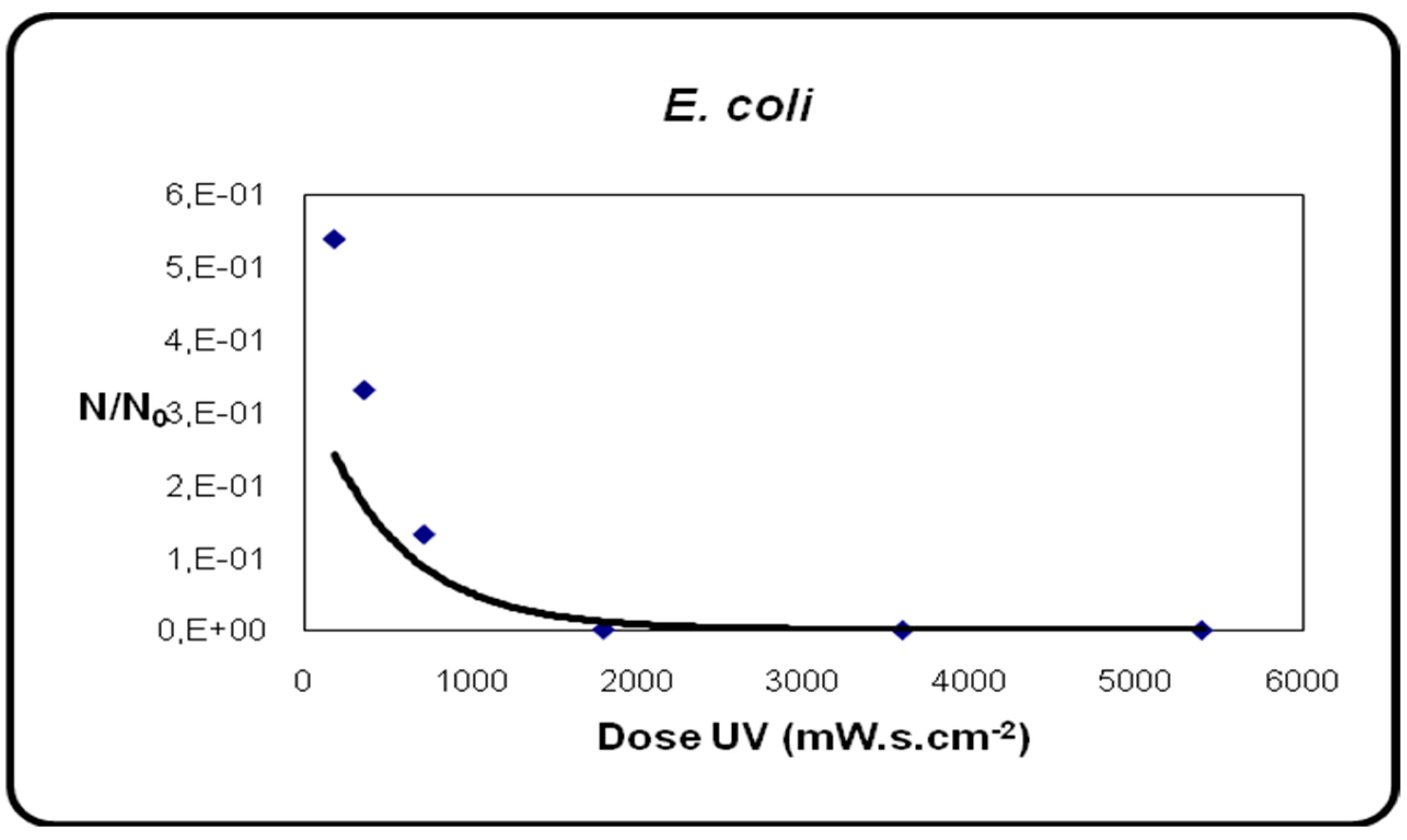
Investigating the Effect of Different Flow Rates on Disinfection Efficiency
2.5. Description of the Pilot Unit
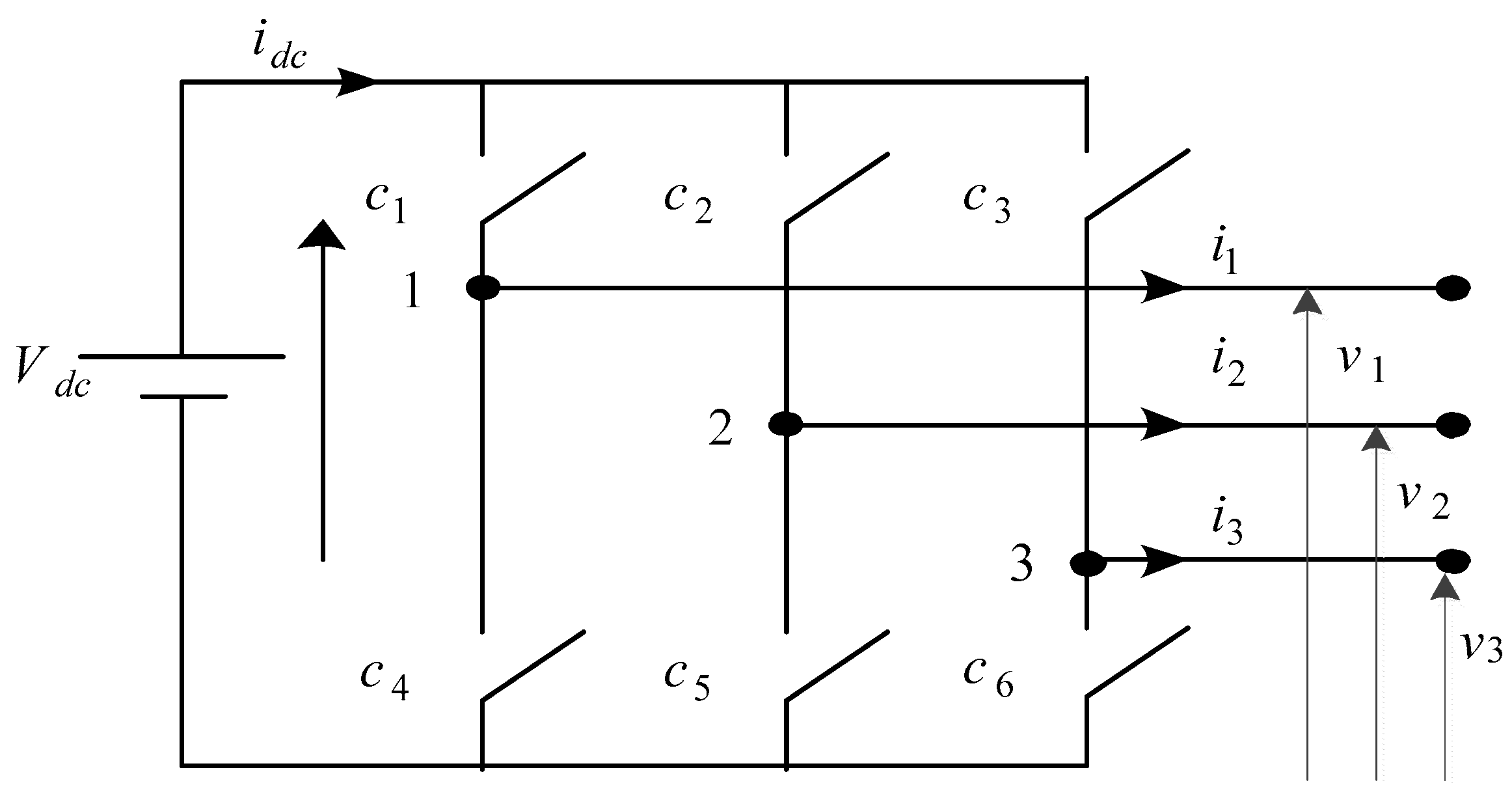
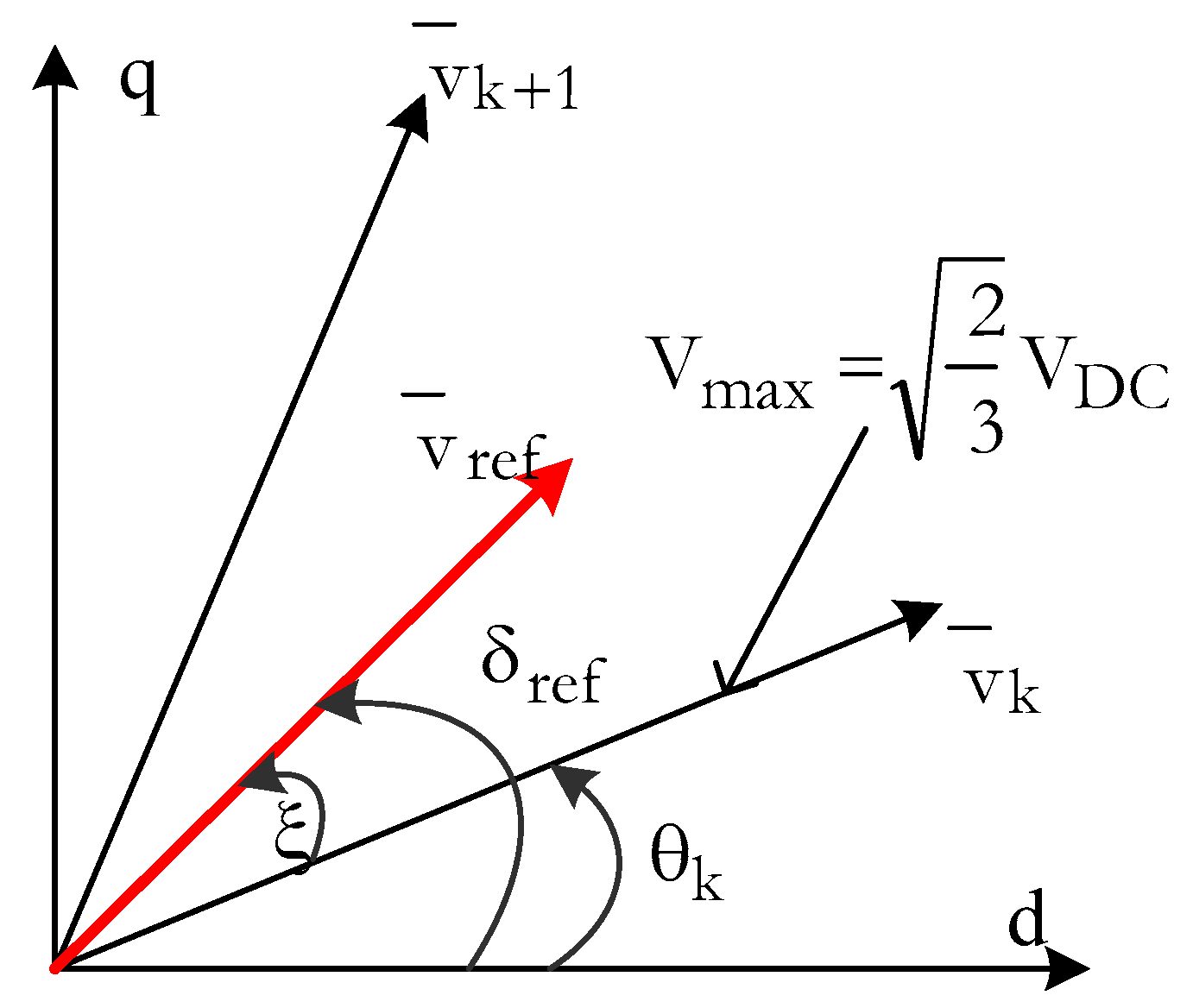
2.6. SVPWM Technique for Inverter
2.7. Asynchronous Machine and Vector Control by Orientation of the Rotor Flux
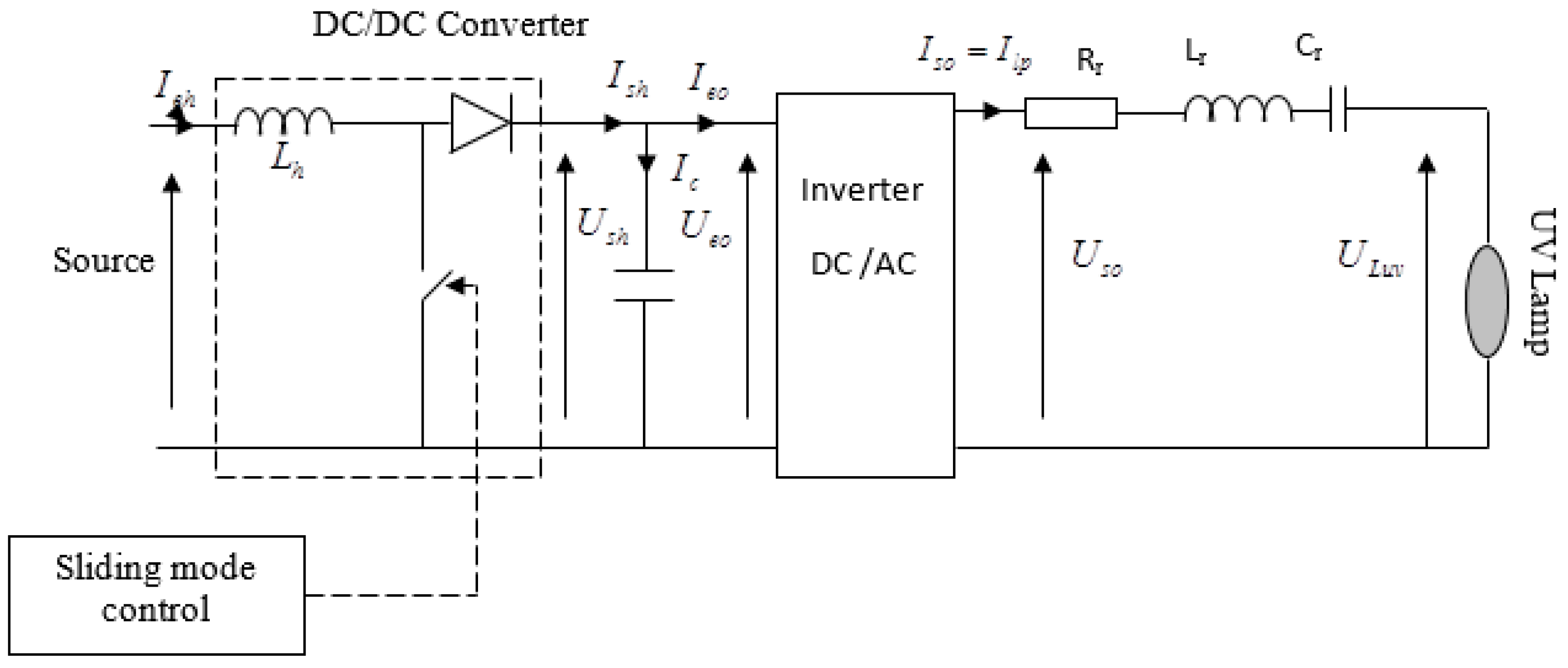
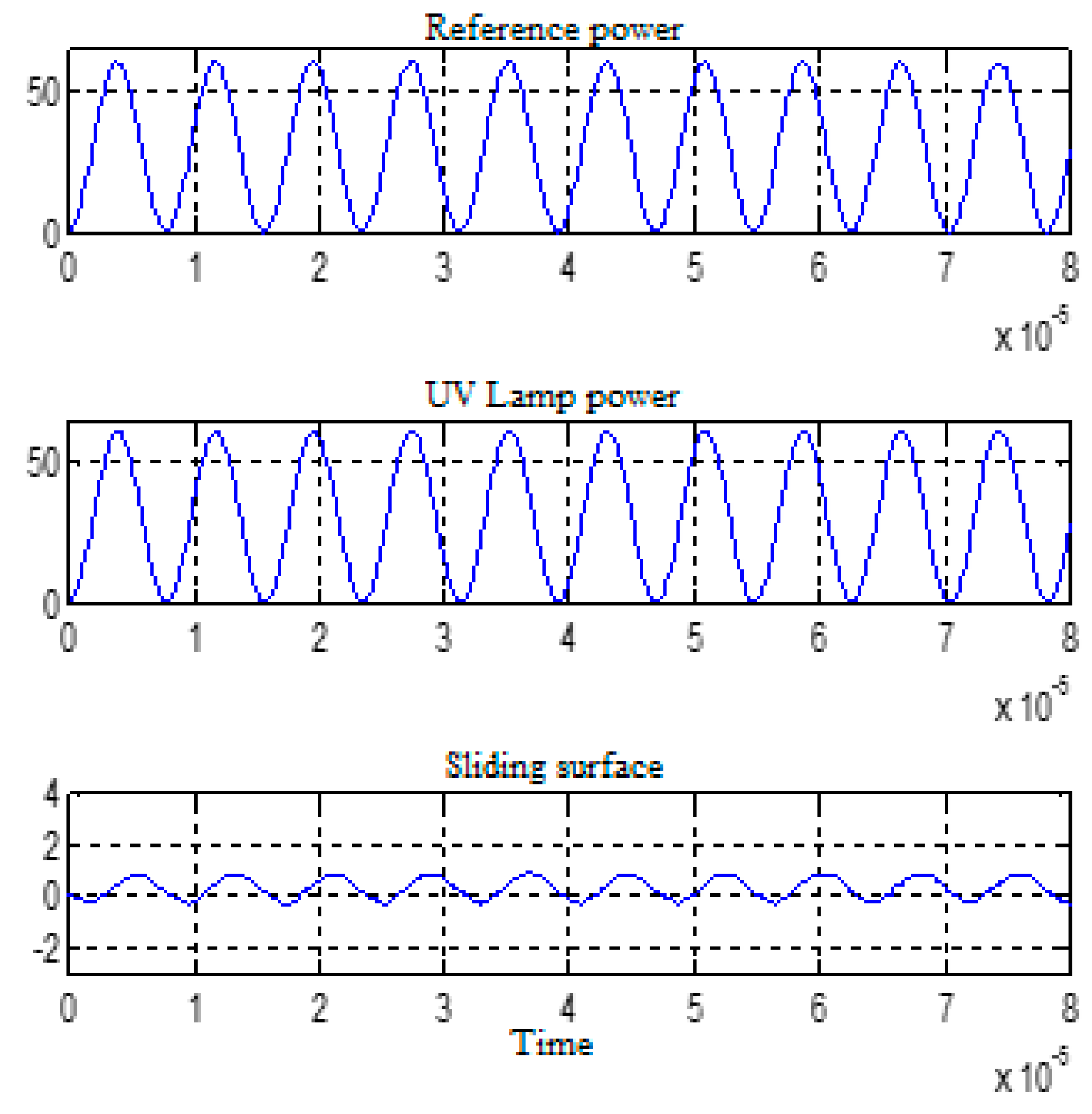
2.8. Sliding Mode UV Lamp Control; Simulation Results
2.8.1. Nonlinear Control via Sliding Mode
2.8.2. Calculation of UV Lamp Control
2.8.3. Nonlinear Component
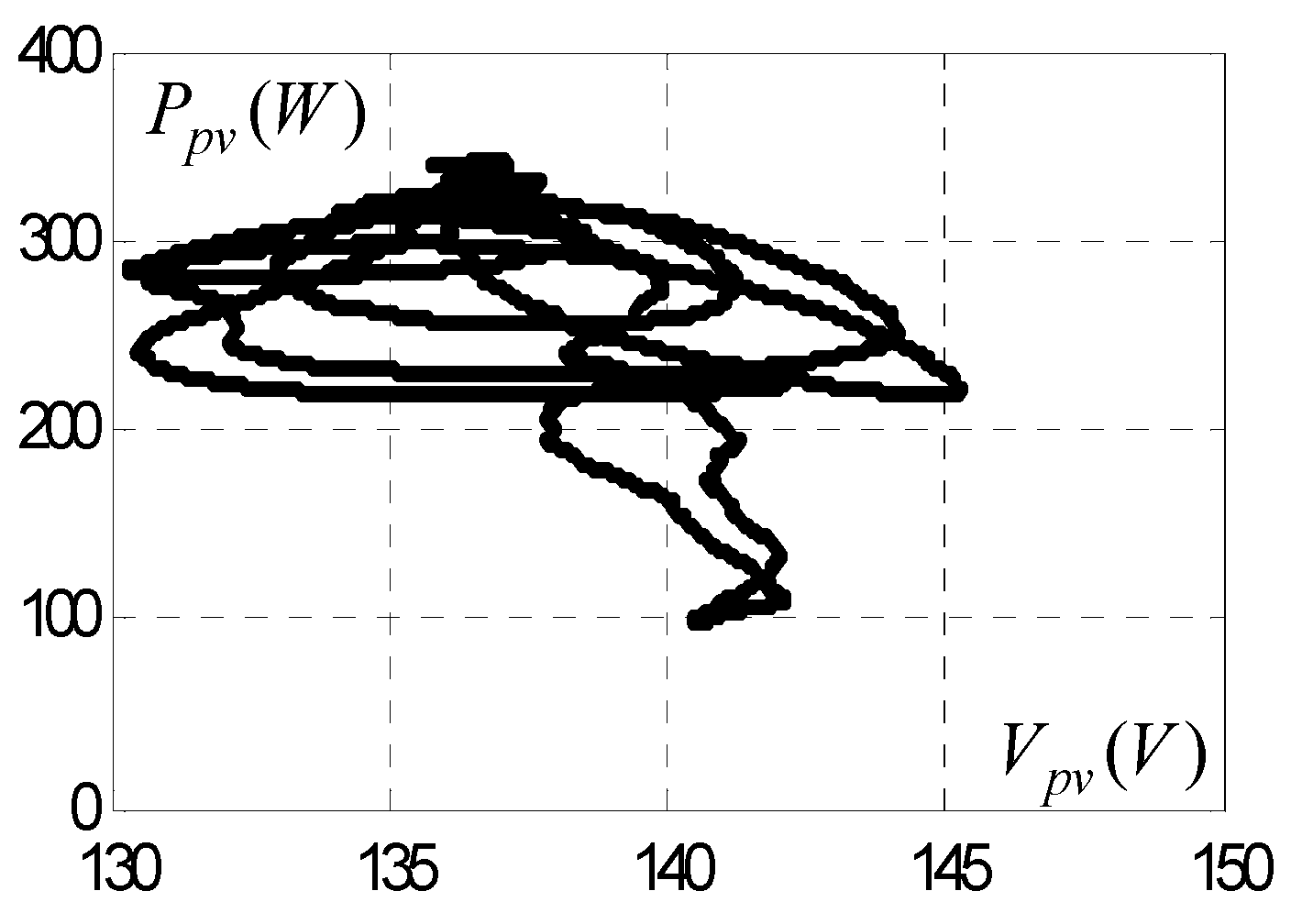
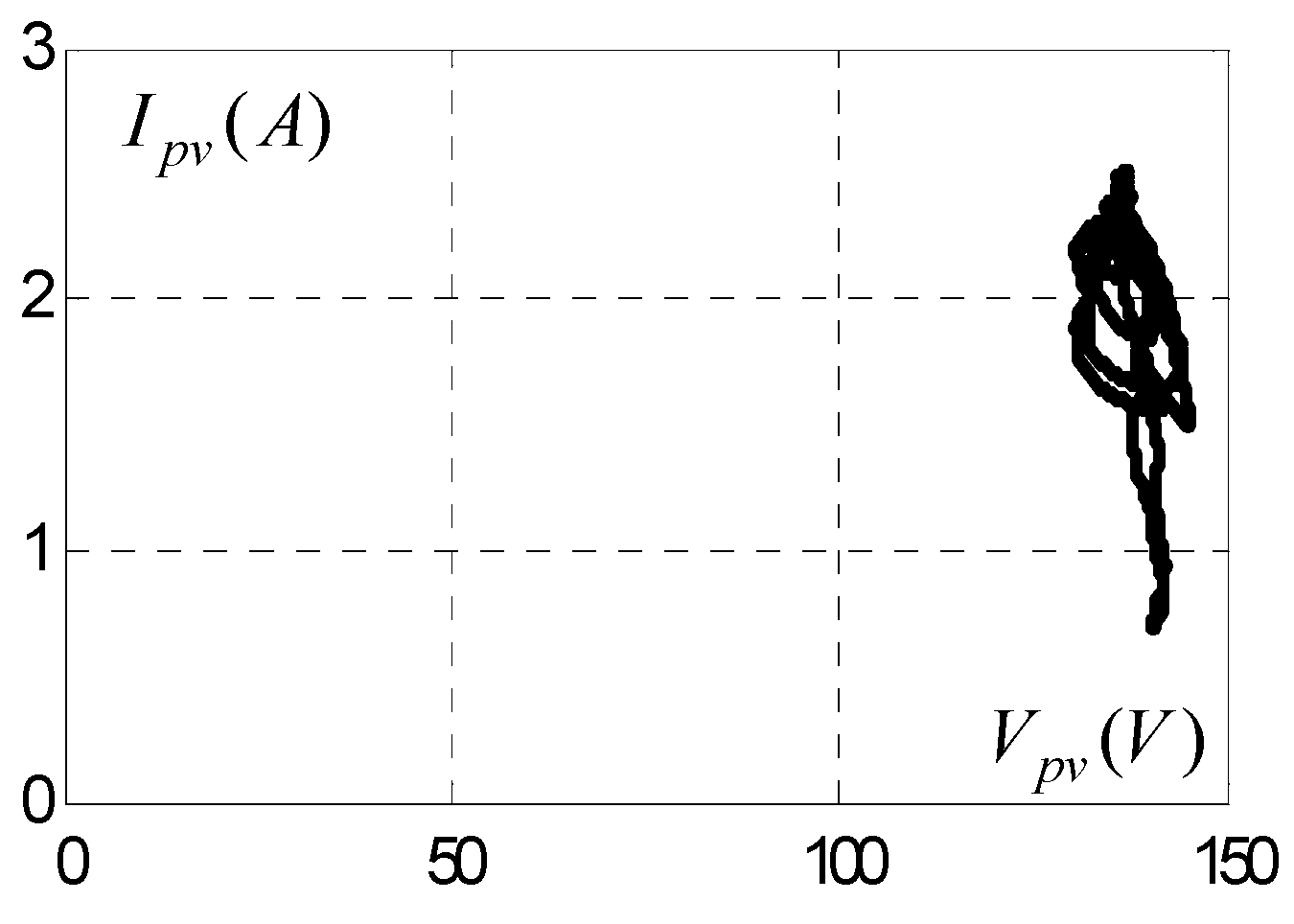
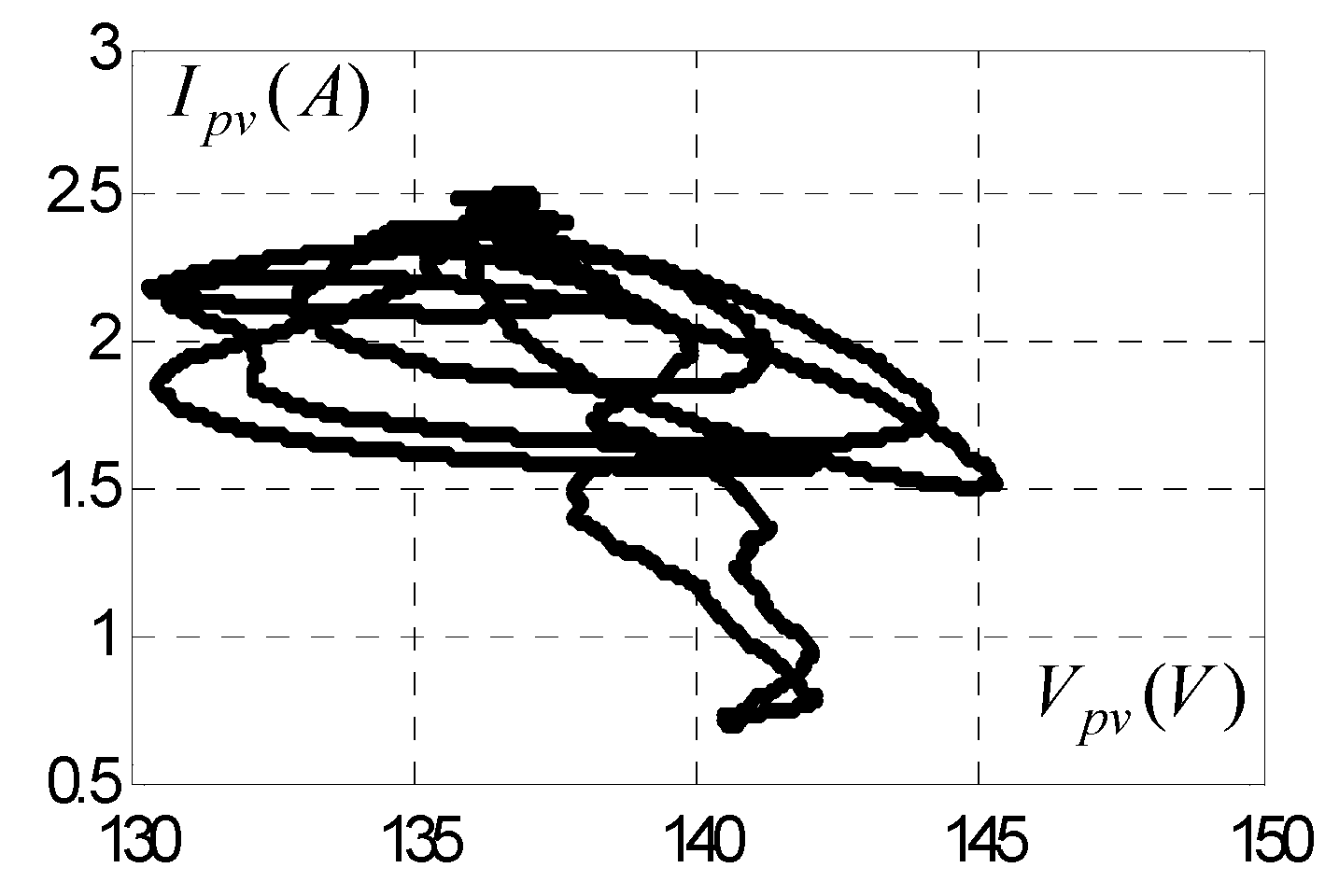
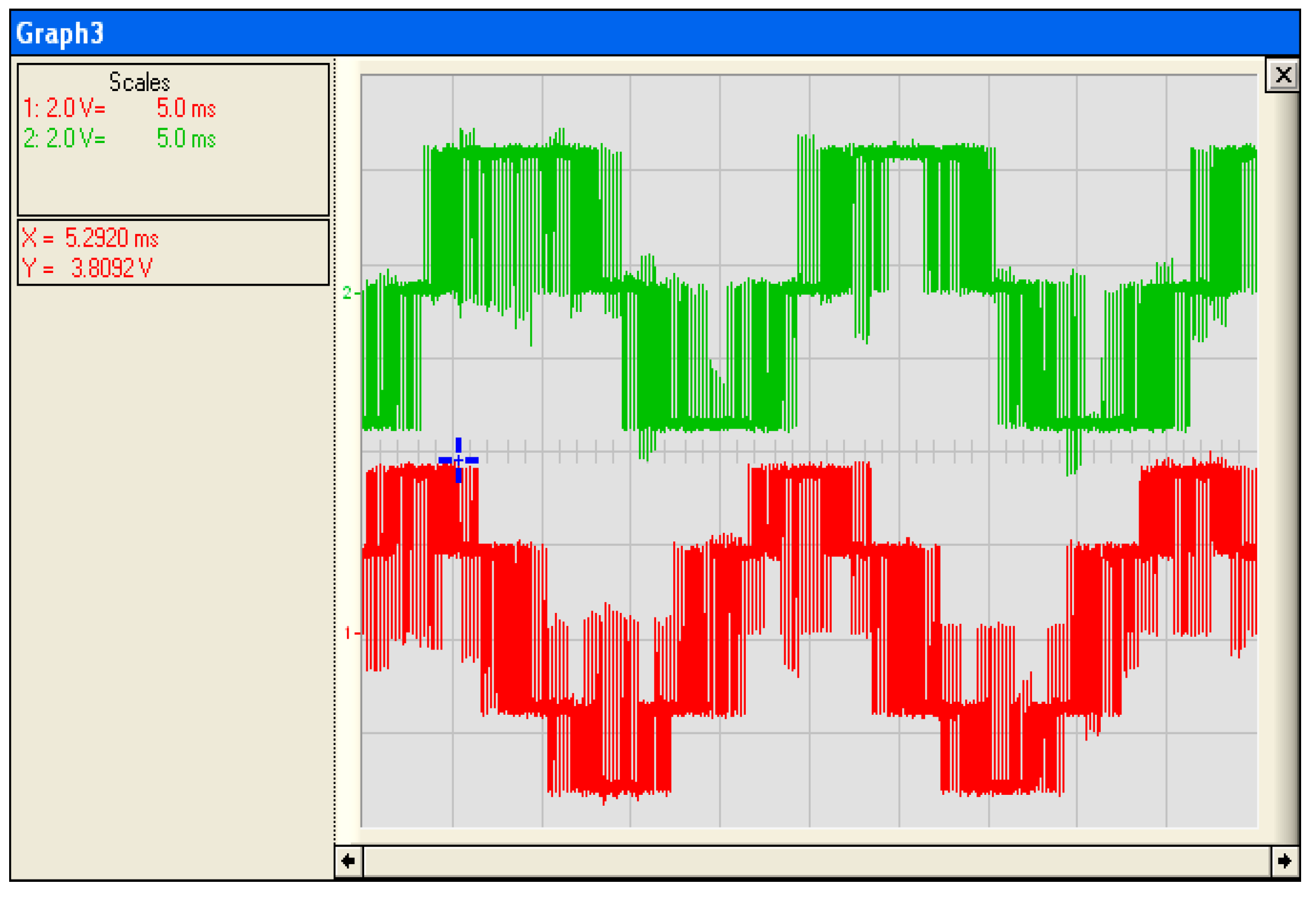
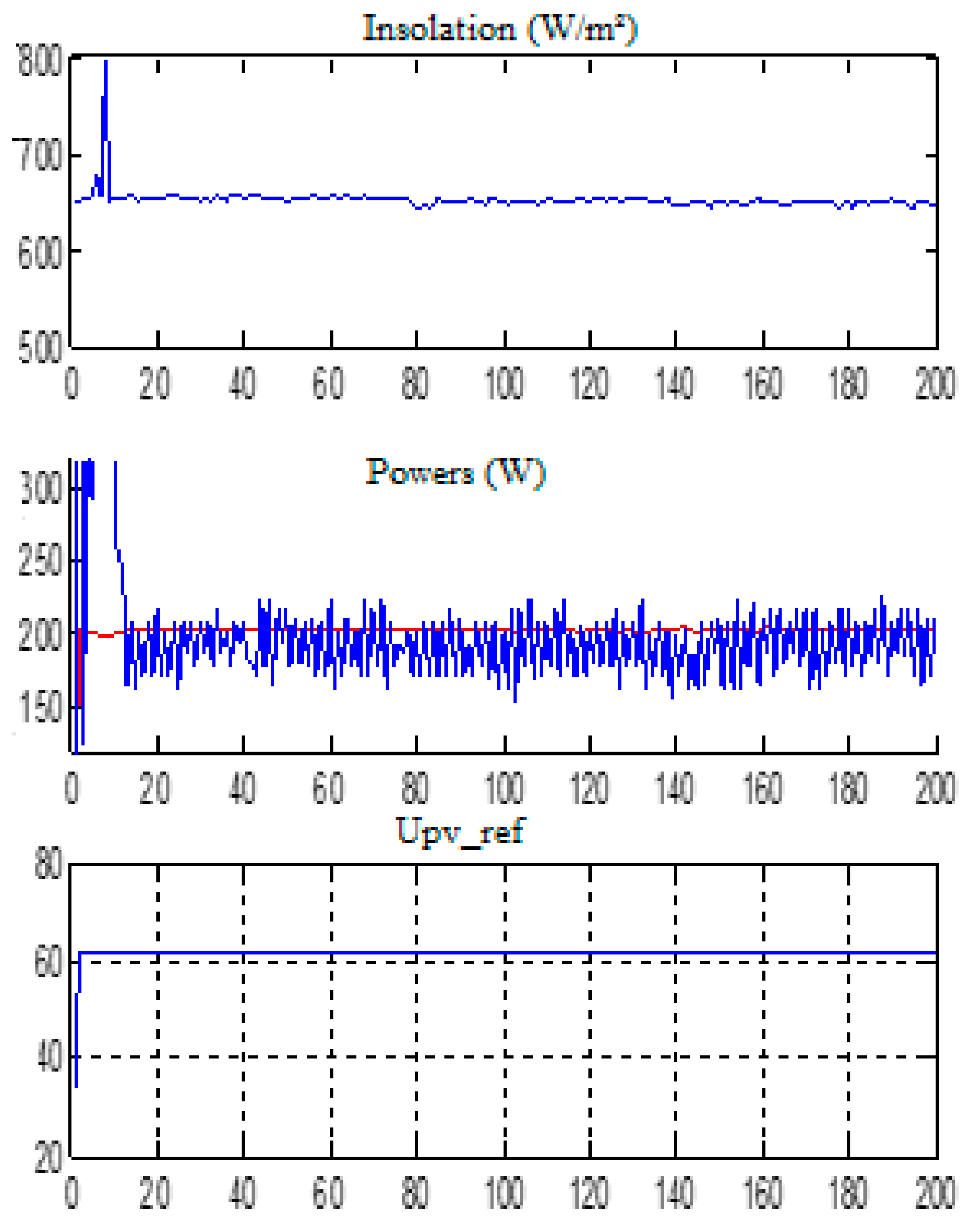
3. Experimental Results
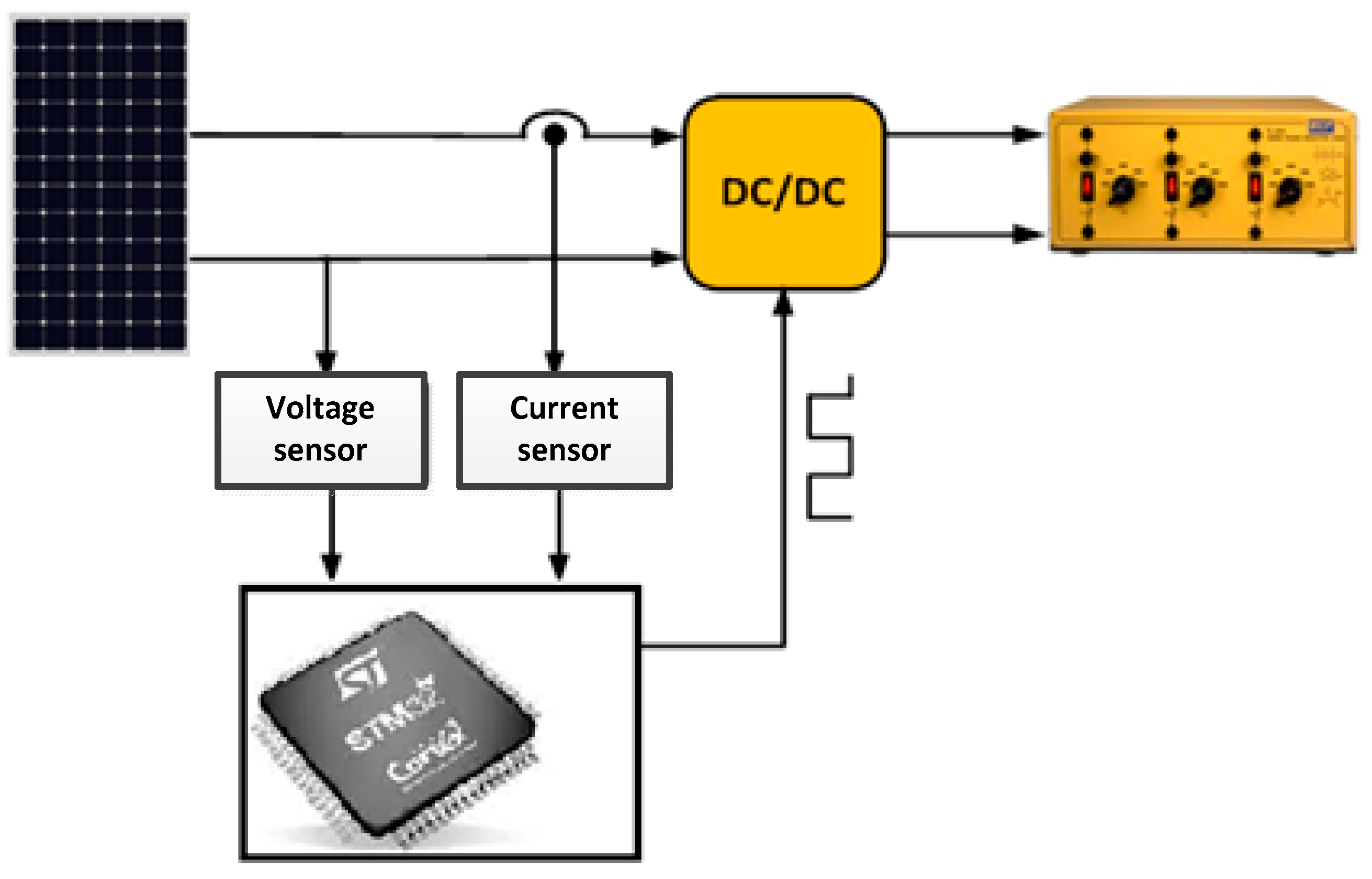
3.1. Material Description of the Experimental Device
3.2. Test of Sliding Mode (MPPT) Command with Resistive Load
- STM microcontroller;
- A photovoltaic generator consisting of ten panels, type TITAN-12-50;
- A SEMIKRON-type DC/DC converter;
- A resistive load of 400 W power;
- A Metrix OX7104 type digital oscilloscope;
- A voltage sensor type LV-25-P, a current sensor type LA-25-NP, a temperature sensor and a sensor.
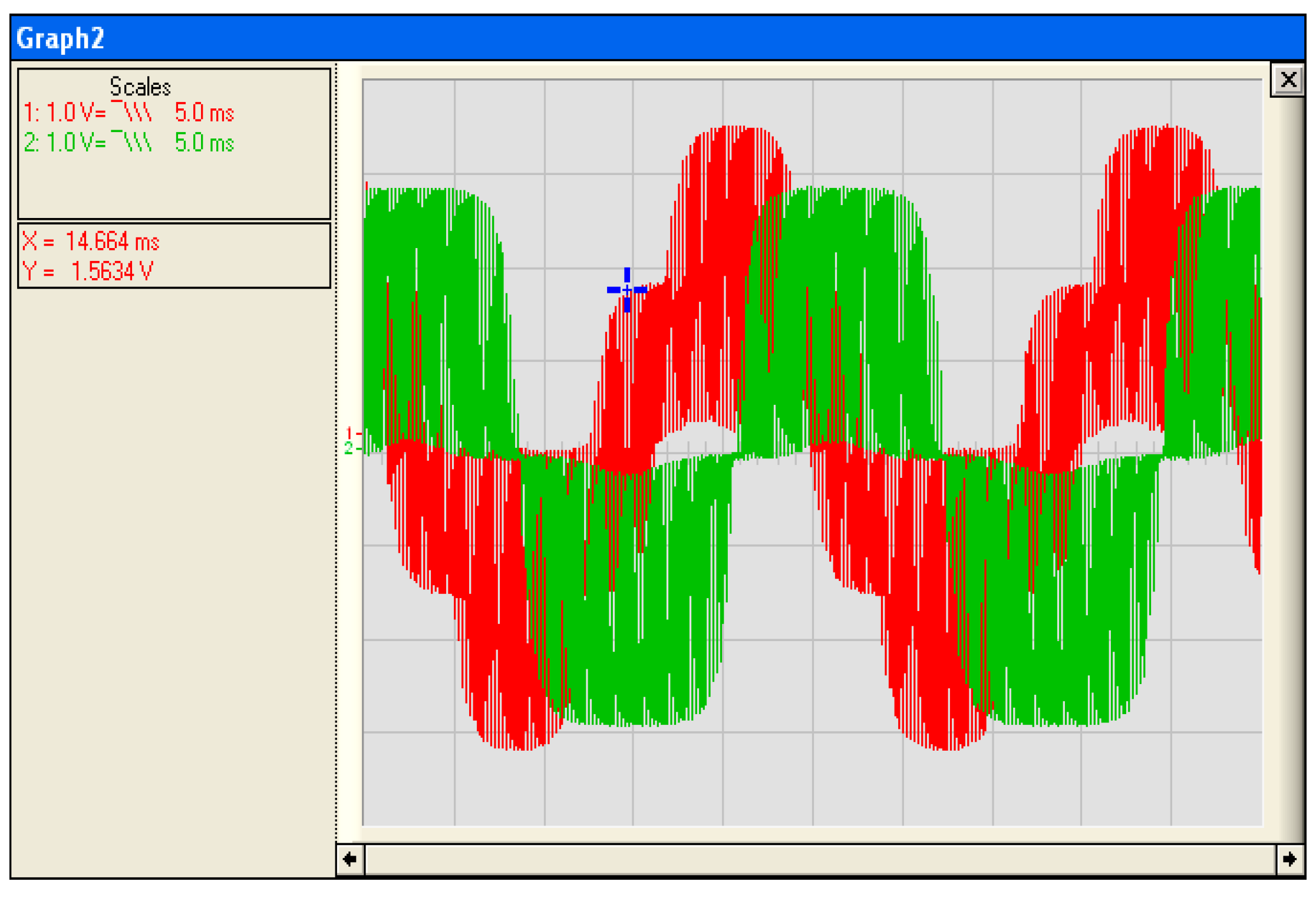
3.3. Test of SVPWM Technique for Inverter
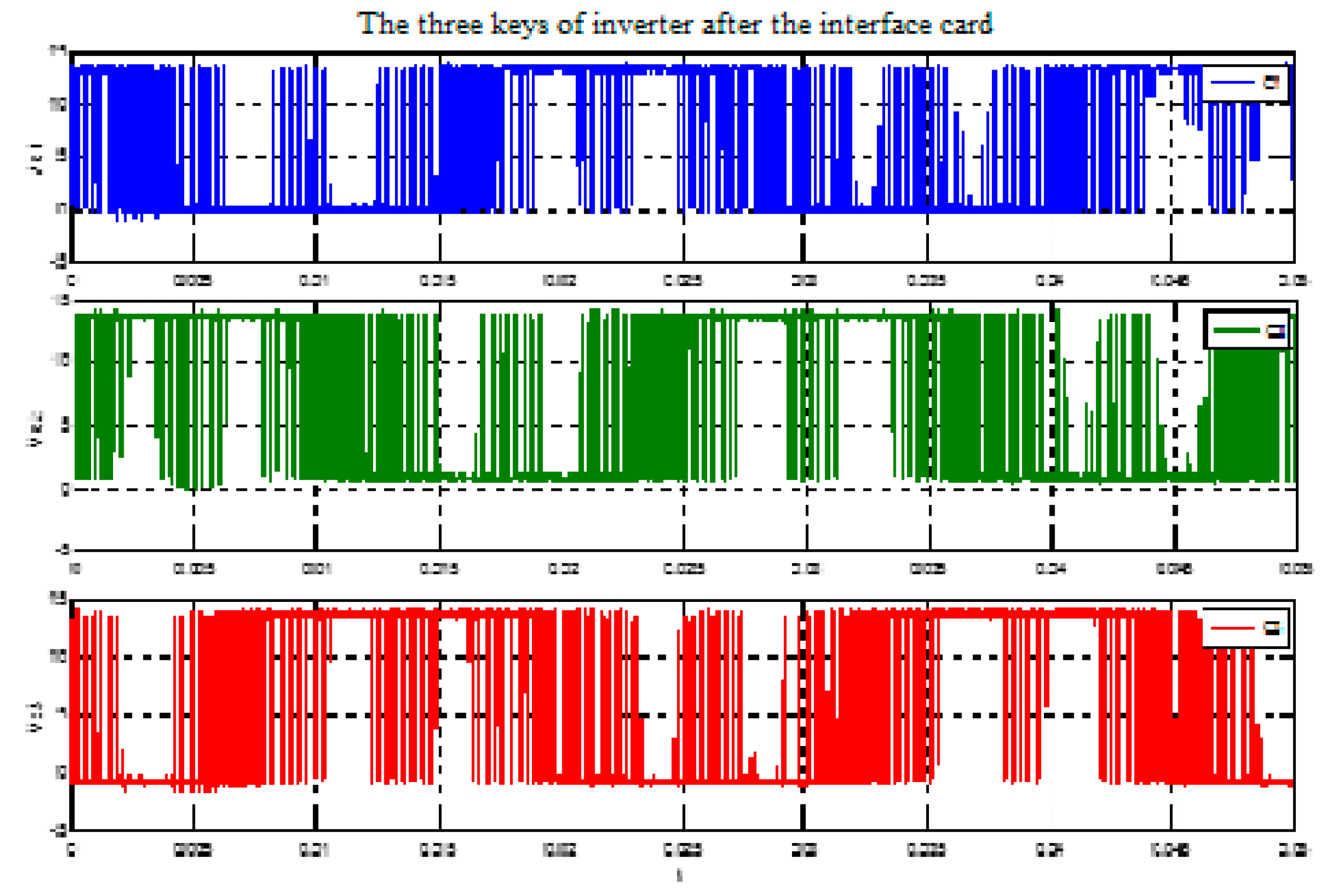
3.3.1. Interface Board between STM32F4 and Inverter
3.3.2. Inverter Forward and Quadrature Voltage Generation Board
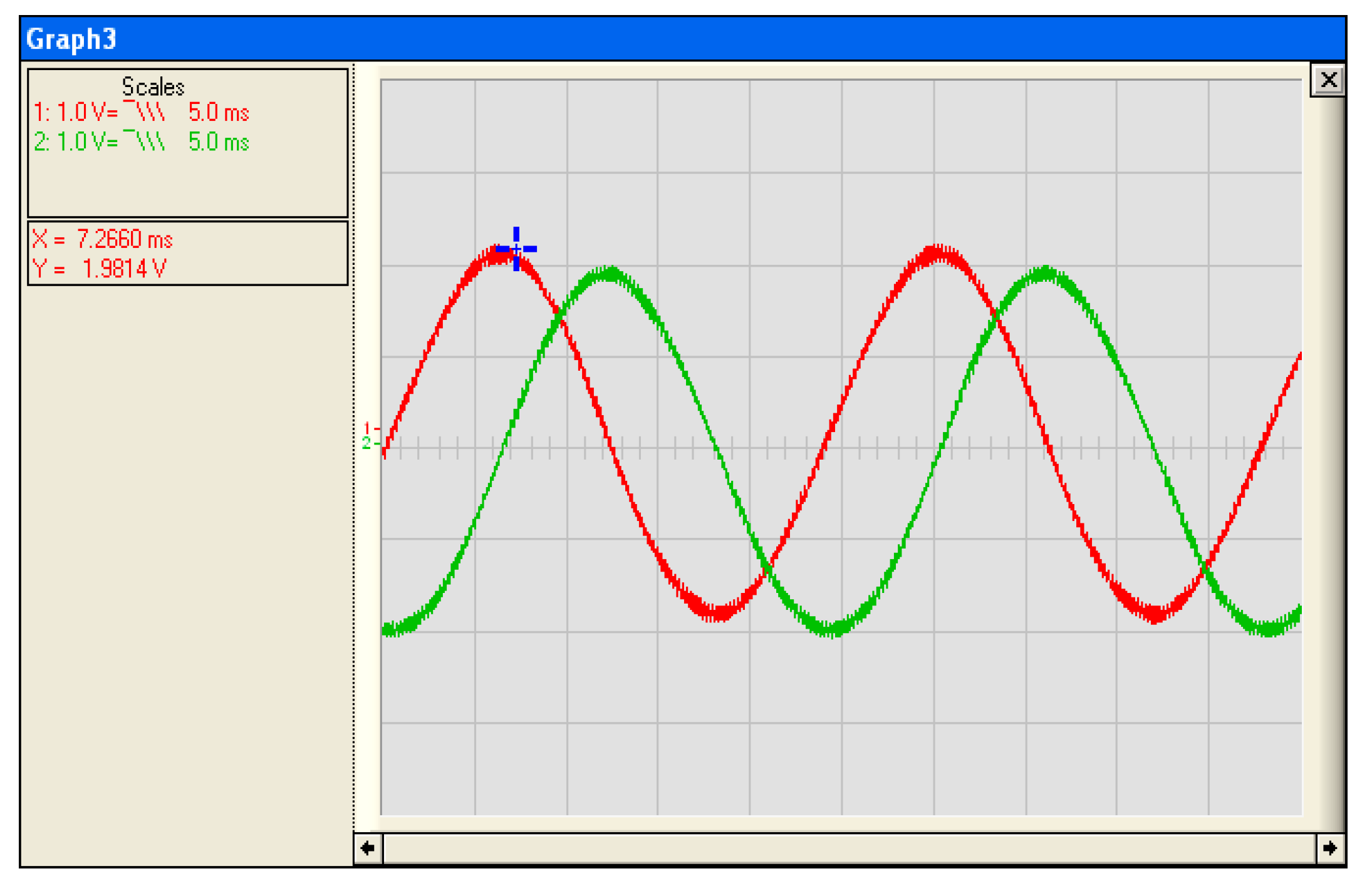
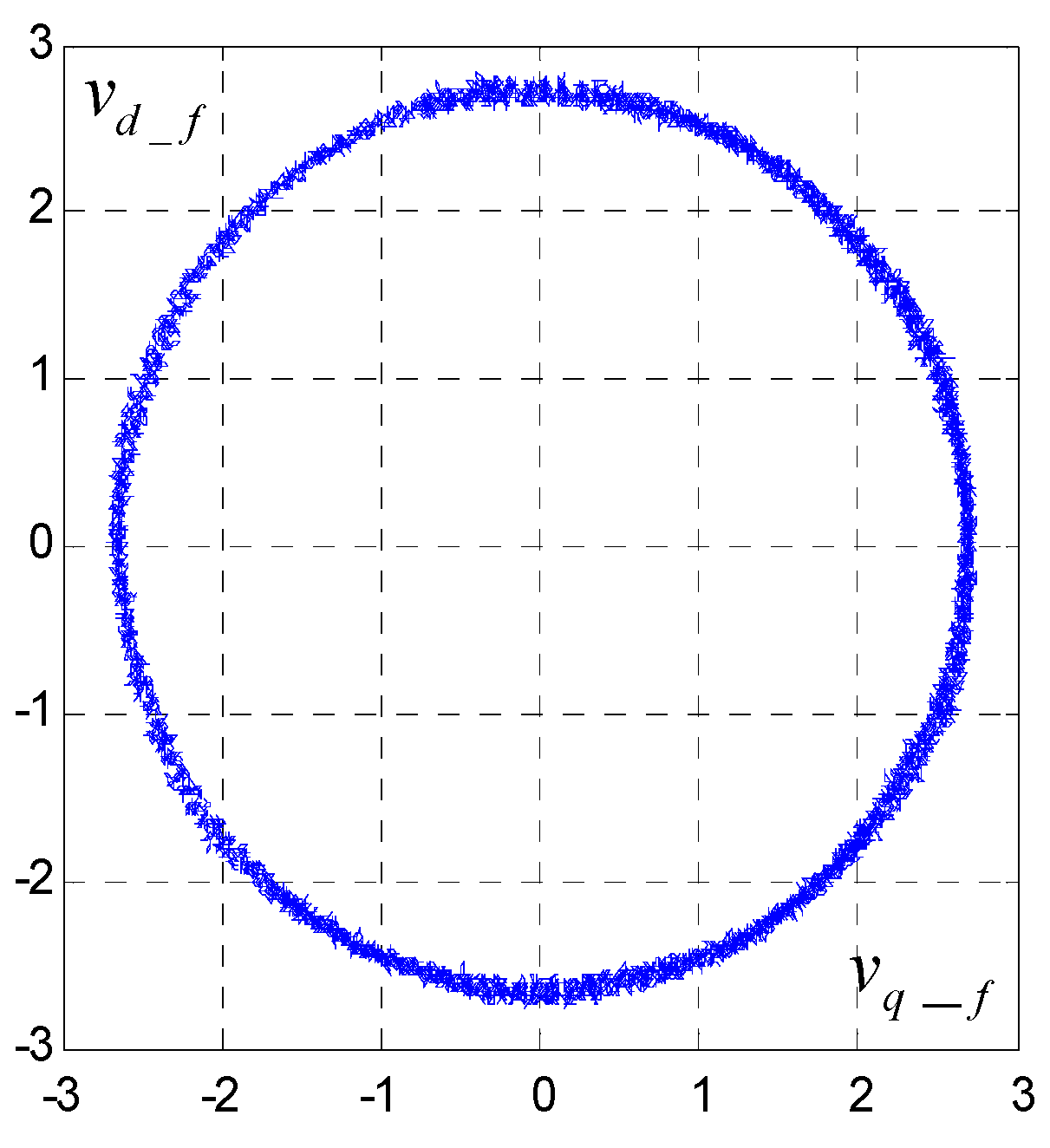
3.4. Implementation and Test of Vector Control by Orientation of the Rotor
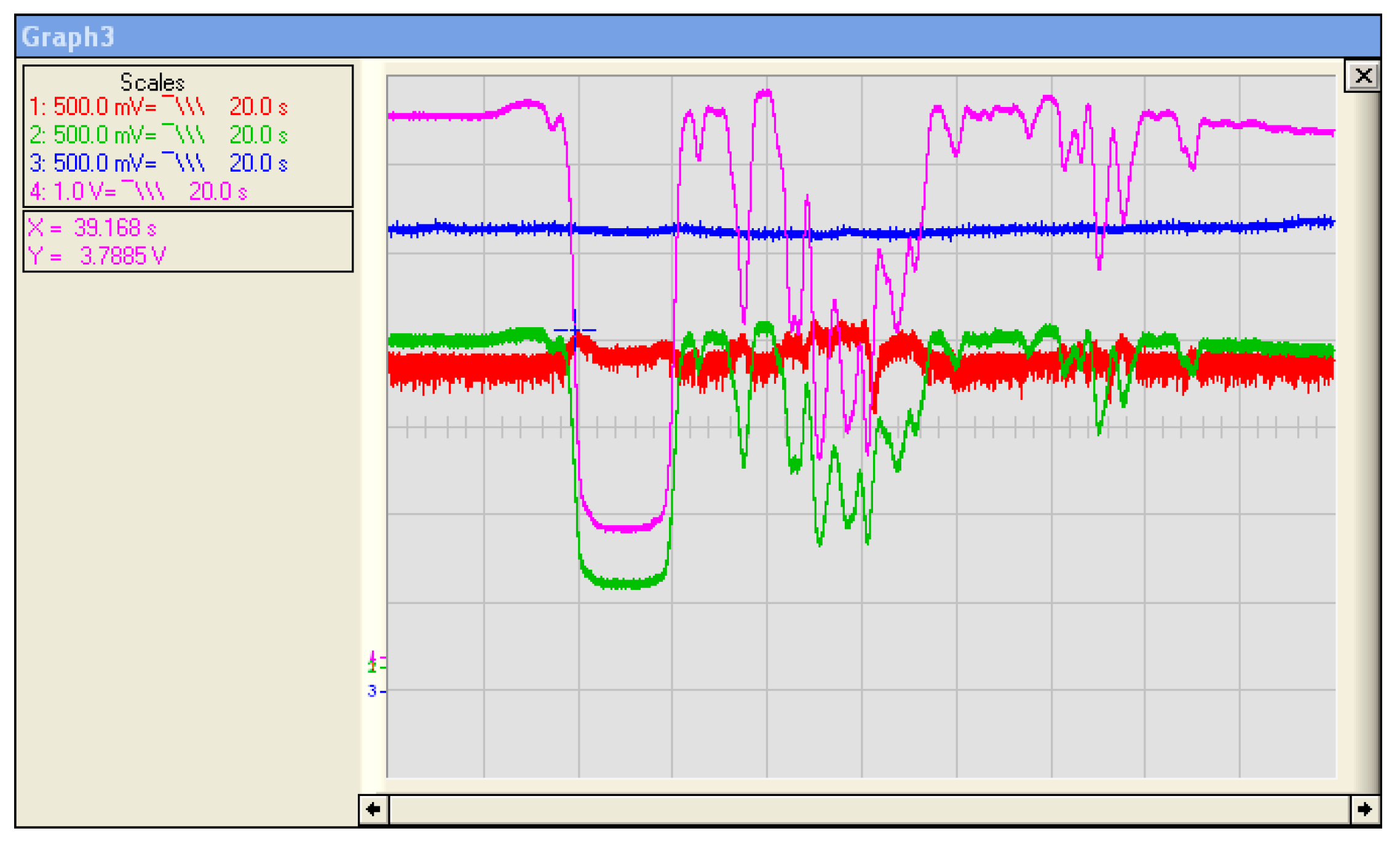
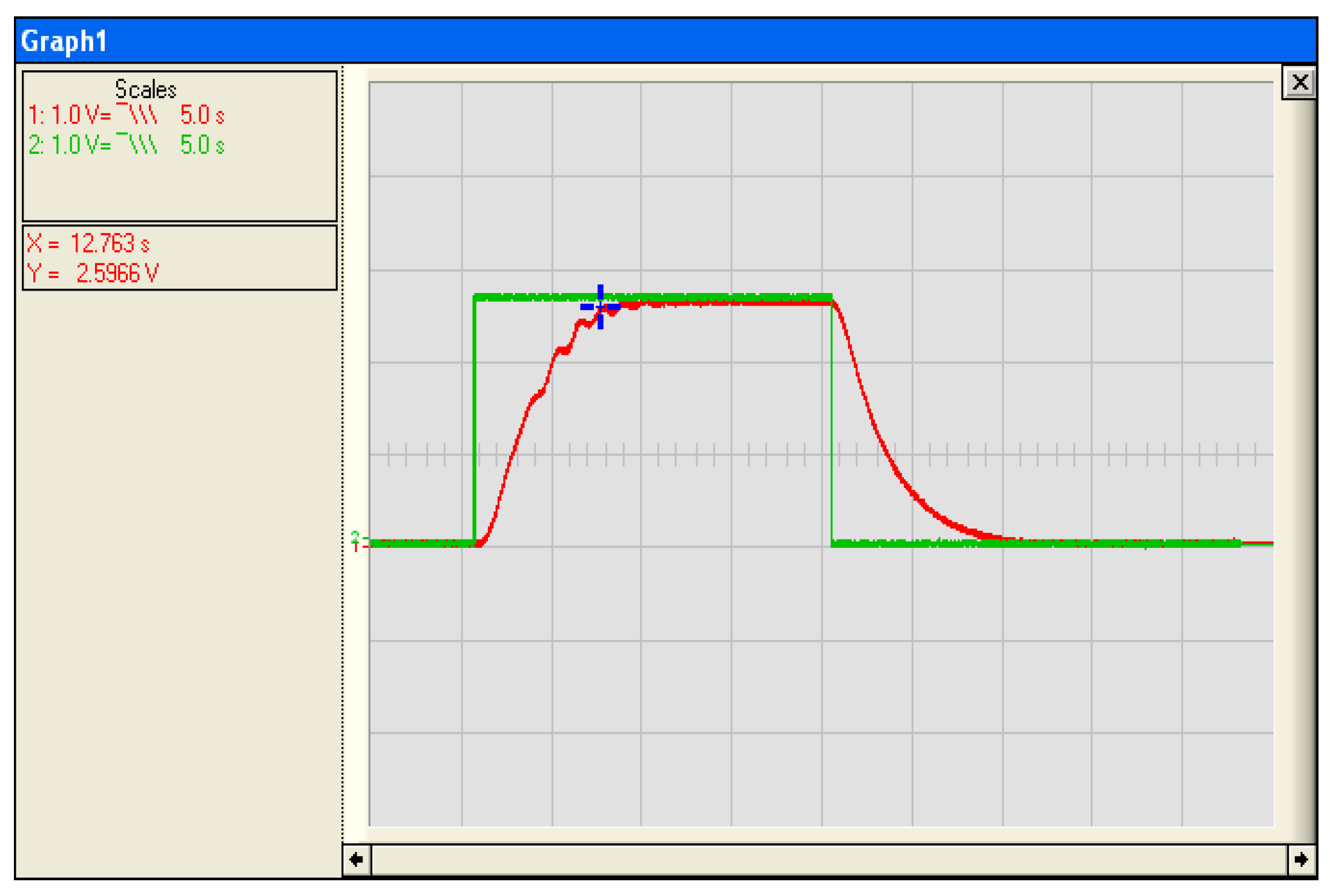
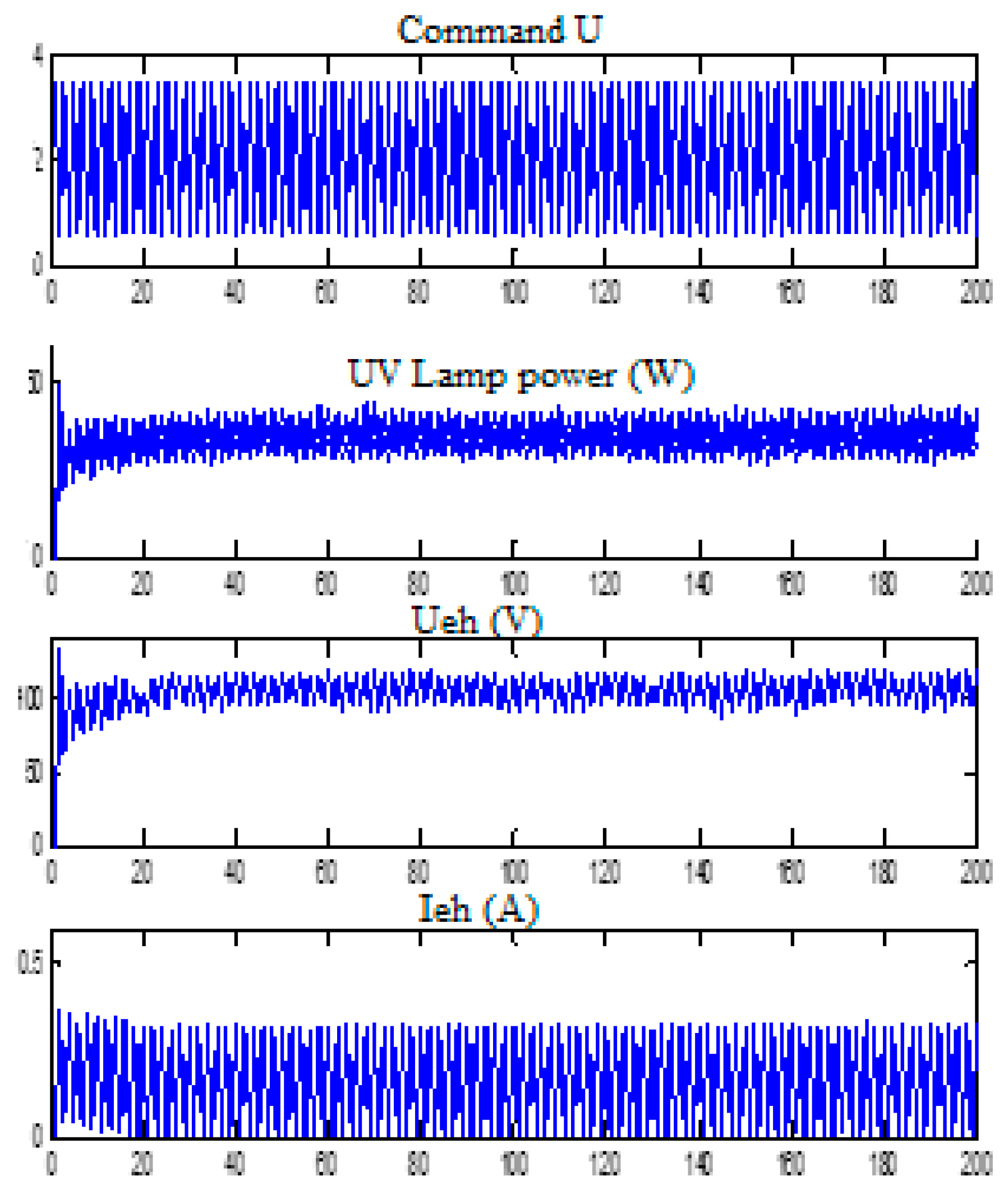
3.5. Implementation and Test of UV Lamp Control
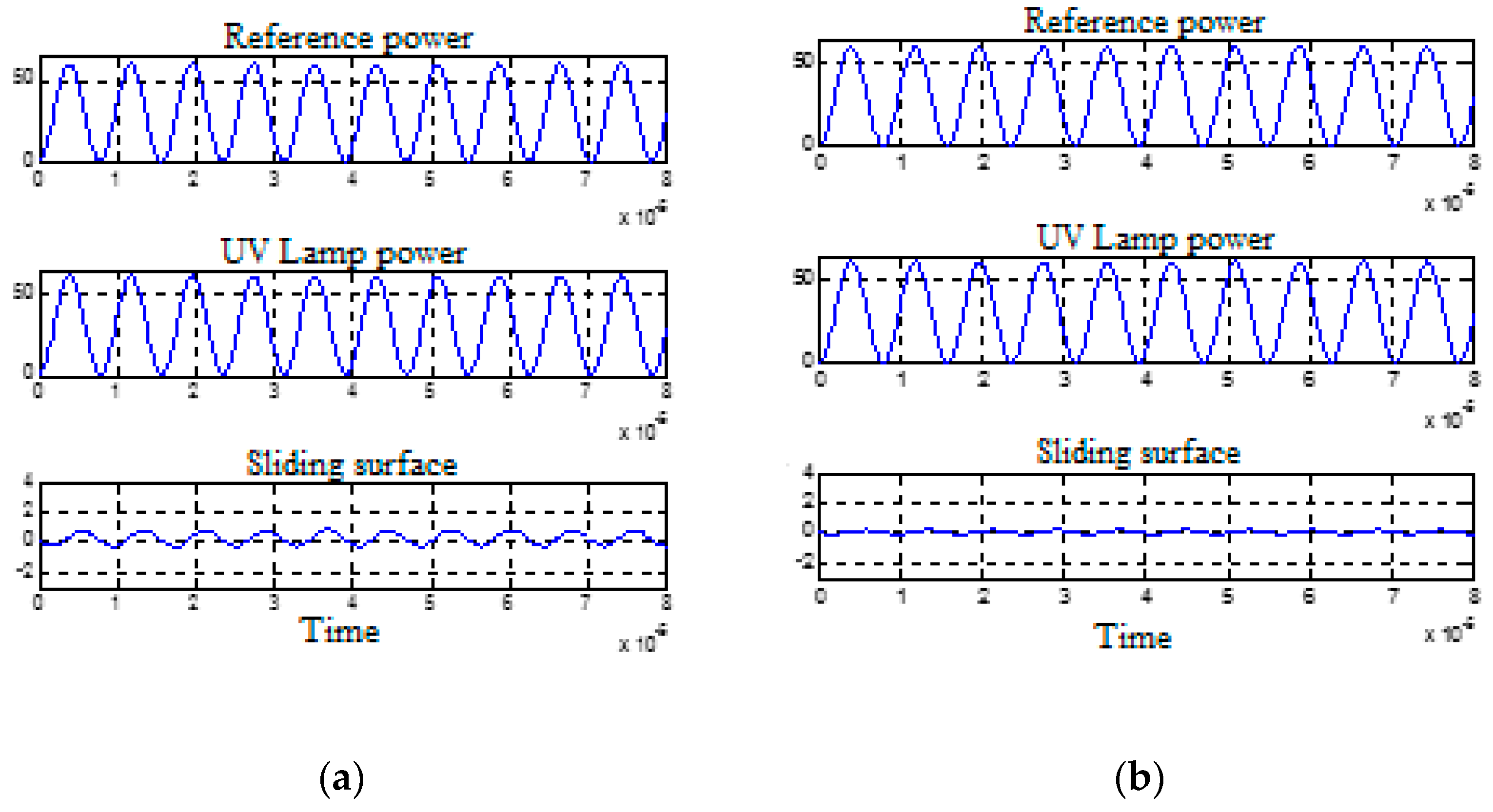
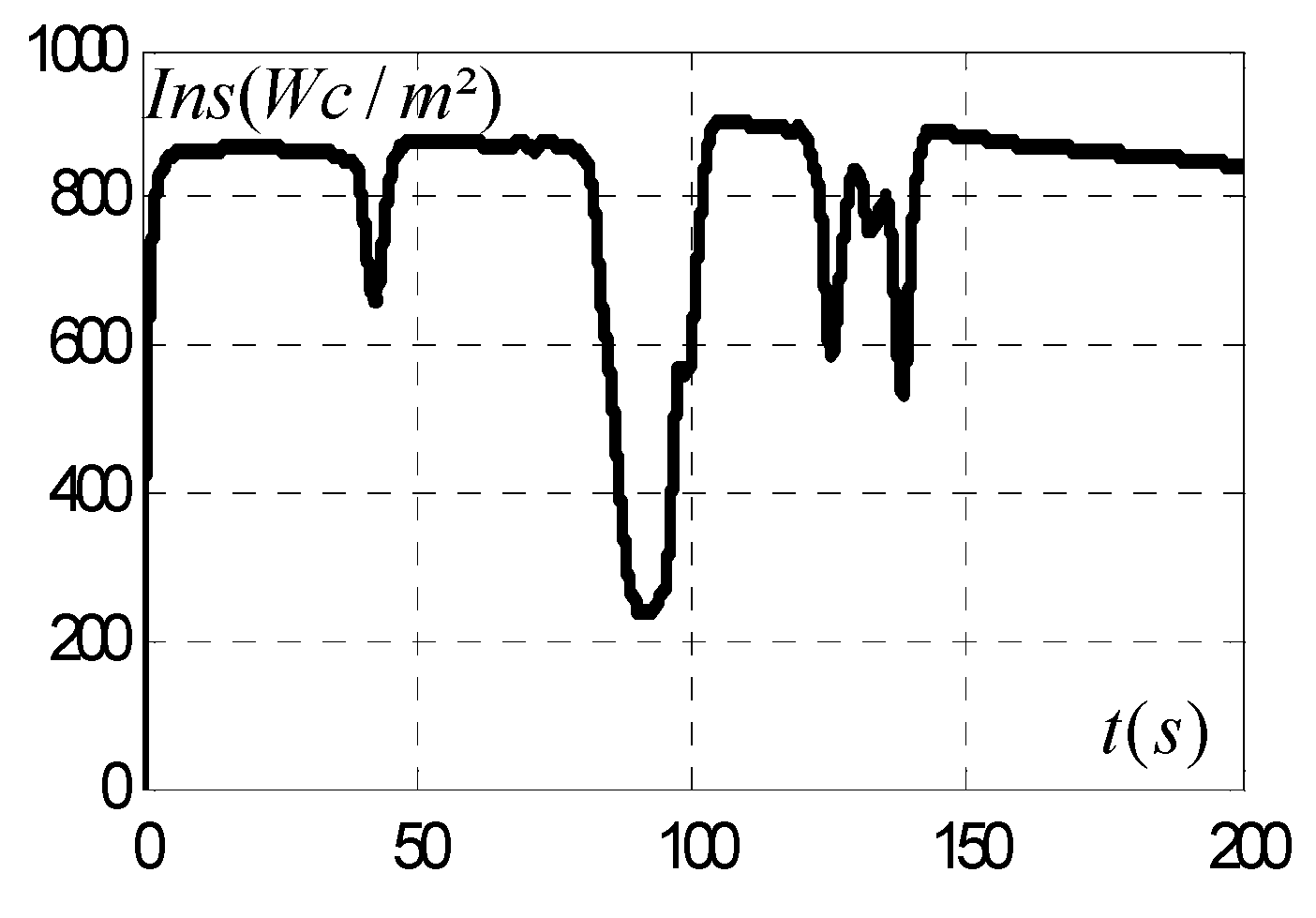
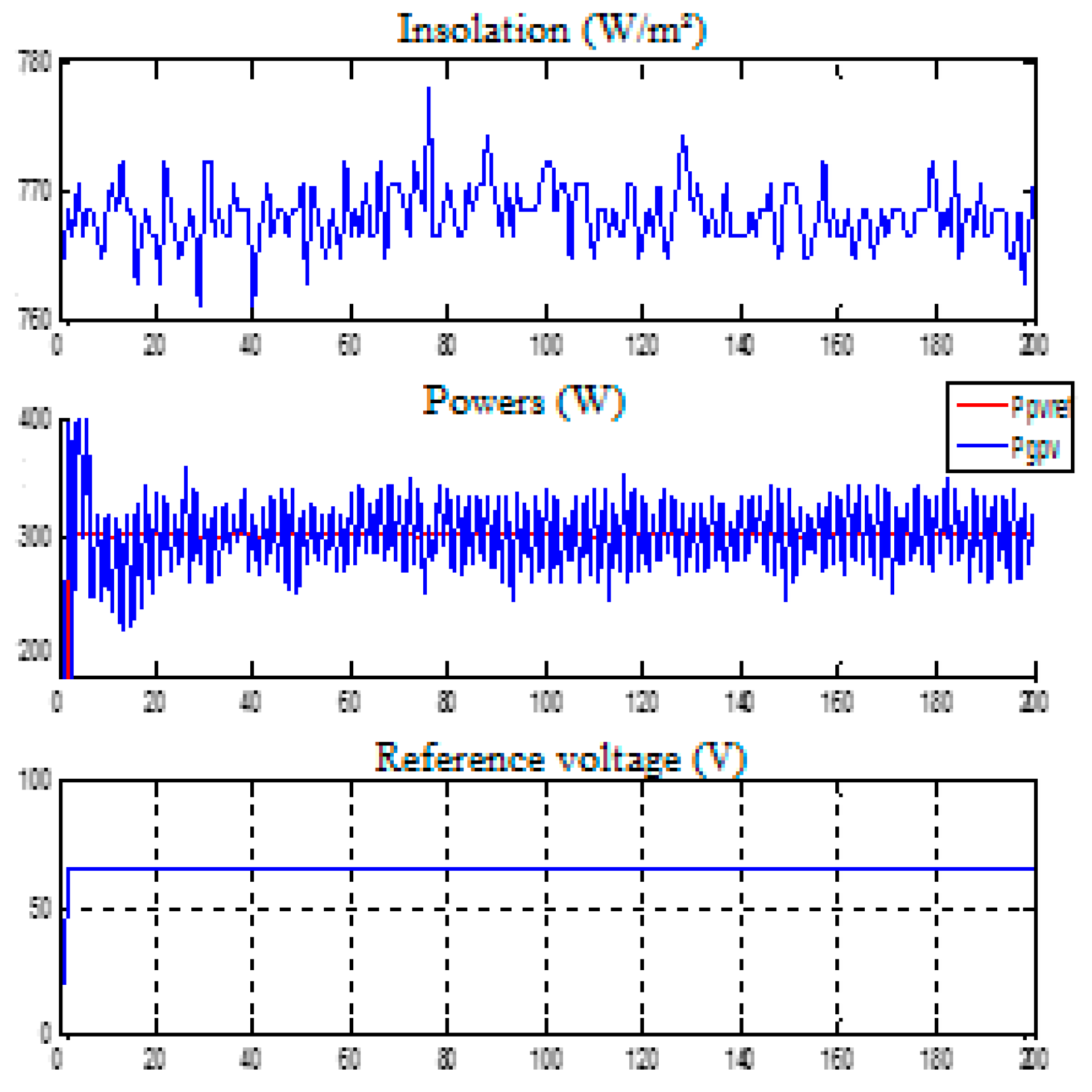
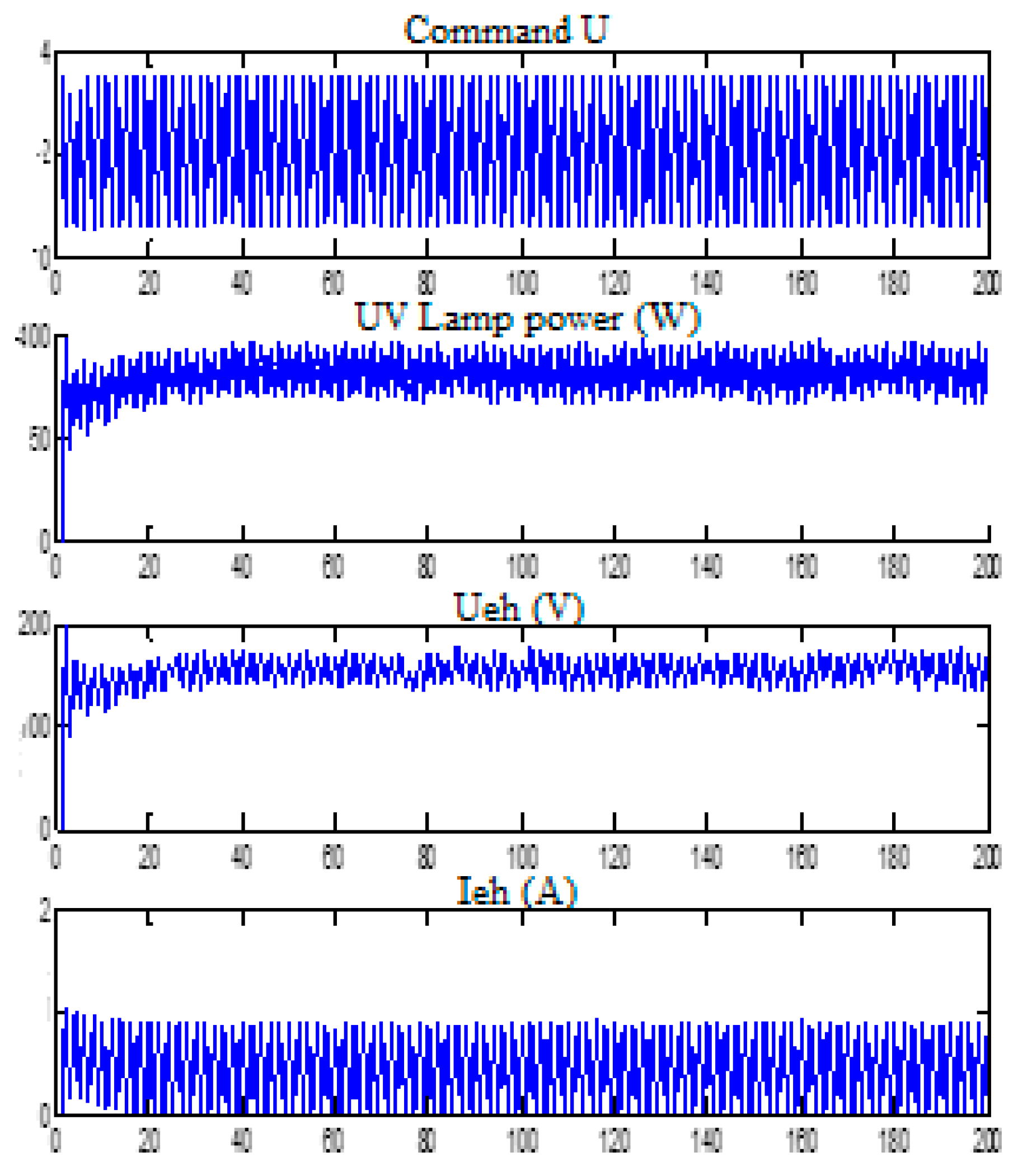
3.6. Comparative Study of Simulation Results and Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gammoudi, R.; Brahmi, H.; Dhifaoui, R. Estimation of Climatic Parameters of a PV System Based on Gradient Method. Complexity 2019, 2019, 7385927. [Google Scholar] [CrossRef]
- Alayi, R.; Sevbitov, A.; Assad, M.E.H. Investigation of energy and economic parameters of photovoltaic cells in terms of different tracking technologies. Int. J. Low-Carbon Technol. 2022, 17, 160–168. [Google Scholar] [CrossRef]
- Almallahi, M.N.; Assad, M.E.H.; Alshihabi, S.; Alayi, R. Multi-criteria decision-making approach for the selection of cleaning method of solar PV panels in United Arab Emirates based on sustainability perspective. Int. J. Low-Carbon Technol. 2022, 17, 380–393. [Google Scholar] [CrossRef]
- Gorji, S.A.; Ektesabi, M.; Zheng, J. Isolated switched-boost push-pull DC-DC converter for step-up applications. Electron. Lett. 2017, 53, 177–1796. [Google Scholar] [CrossRef]
- Hemza, A.; Abdeslam, H.; Chenni, R.; Narimene, D. Photovoltaic system output simulation under various environmental conditions. In Proceedings of the 2016 International Renewable and Sustainable Energy Conference IRSEC, Marrakech, Morocco, 16–17 November 2016; pp. 722–726. [Google Scholar]
- AlShabi, M.; Ghenai, C.; Bettayeb, M.; Ahamad, F.F.; Assad, M.E.H. Multi-group grey wolf optimizer (MG-GWO) for estimating photovoltaic solar cell model. J. Therm. Anal. Calorim. 2021, 144, 1655–1670. [Google Scholar] [CrossRef]
- Carreño-Ortega, A.; Galdeano-Gómez, E.; Pérez-Mesa, J.C.; Del Galera-Quiles, M.C. Policy and environmental implications of photovoltaic systems in farming in southeast Spain: Can greenhouses reduce the greenhouse effect. Energies 2017, 10, 761. [Google Scholar] [CrossRef]
- Zitouni, N.; Gammoudi, R.; Hamrouni, N. An ANN–Constant power generation control for LVRT of grid-connected PVG. Energy Explor. Exploit. SAGE J. 2022, 41, 1150528. [Google Scholar] [CrossRef]
- Balamurugan, T.; Manoharan, S.; Sheeba, P.; Hafaifa, A. design a photovoltaic array with boost converter using fuzzy logic controller. Int. J. Electr. Eng. Technol. 2012, 3, 444–456. [Google Scholar]
- Ralik, A.; Jusoh, A.; Sutikno, T. A review on perturb and observe maximum power point tracking in photovoltaic system. Indones. J. Electr. Eng. Comput. Sci. 2015, 13, 745–751. [Google Scholar]
- Li, C.; Chen, Y.; Zhou, D.; Liu, J.; Zeng, J. A high-performance adaptive incremental conductance MPPT algorithm for photovoltaic systems. Energies 2016, 9, 288. [Google Scholar] [CrossRef]
- Bao, X.; Tan, P.; Zhuo, F.; Yue, X. Low voltage ride through control strategy for high-power grid-connected photovoltaic inverter. In Proceeding of the 28th Conference on Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 97–100. [Google Scholar]
- Hejri, M.; Mokhtari, H.; Azizian, M.R.; Ghandhari, M.; Soder, L. On the parameter extraction of a fiveparameter double-diode model of photovoltaic cells and modules. IEEE J. Photovolt. 2014, 4, 915–923. [Google Scholar] [CrossRef]
- Chu, Y.M.; Shankaralingappa, B.M.; Gireesha, B.J.; Alzahrani, F.; Khan, M.; Khan, S.U. Combined impact of Cattaneo-Christov double diffusion and radiative heat flux on bio-convective flow of Maxwell liquid configured by a stretched nanomaterial surface. Appl. Math. Comput. 2022, 419, 126883. [Google Scholar] [CrossRef]
- Mares, O.P.; Badescu, M.V. A simple but accurate procedure for solving the five-parameter model. Energy Convers. Manag. 2015, 105, 139–148. [Google Scholar] [CrossRef]
- Allani, M.Y.; Mezghani, D.; Tadeo, F.; Mami, A. FPGA Implementation of a Robust MPPT of a Photovoltaic System Using a Fuzzy Logic Controller Based on Incremental and Conductance Algorithm. Eng. Technol. Appl. Sci. Res. 2019, 9, 4322–4328. [Google Scholar] [CrossRef]
- Zissis, G.; Damelincourt, J.J.; Bezanahary, T. Modelling discharge lamps for electronic circuit designers: A review of the existing methods. IEEE Ind. Appl. Soc. 2001, 2, 1260–1262. [Google Scholar]
- Silva, E.A.; Bradaschia, F.; Cavalcanti, M.C.; Nascimento, A.J. Parameter estimation method to improve the accuracy of photovoltaic electrical model. IEEE J. Photovolt. 2016, 6, 278–285. [Google Scholar] [CrossRef]
- Labidi, Z.R.; Schulte, H.; Mami, A. A Model-Based Approach of DC-DC Converters Dedicated to Controller Design Applications for Photovoltaic Generators. Eng. Technol. Appl. Sci. Res. 2019, 9, 4371–4376. [Google Scholar] [CrossRef]
- Huang, M.; Ma, Y.; Wan, J.; Wang, Y. Simulation of a paper mill wastewater treatment using a fuzzy neural network. Expert Syst. Appl. 2009, 36, 5064–5070. [Google Scholar]
- Andoulsi, R.; Mami, A.; Dauphin-Tanguy, G.; Annabi, M. Modelling and simulation by bond graph technique of a DC motor fed from a photovoltaic source via MPPT boost converter. In Proceedings of the Conference of Particle Accelerator (CSSC’99), New York, NY, USA, 16–19 March 1987; pp. 4181–4187. [Google Scholar]
- Zitouni, N.; Gammoudi, R. Database for control a complex water treatment system powered by photovoltaic generator for deep learning. In Proceedings of the International Conference on Electrical, Computer and Energy Technologies (ICECET 2022), Prague, Czech Republic, 20–22 July 2022. [Google Scholar]
- Maged, M.H.; Khalafallah, M.G.; Hassanien, E.A. Prediction of wastewater treatment plant performance using artificial neural networks. Environ. Model. Softw. 2004, 19, 919–928. [Google Scholar]





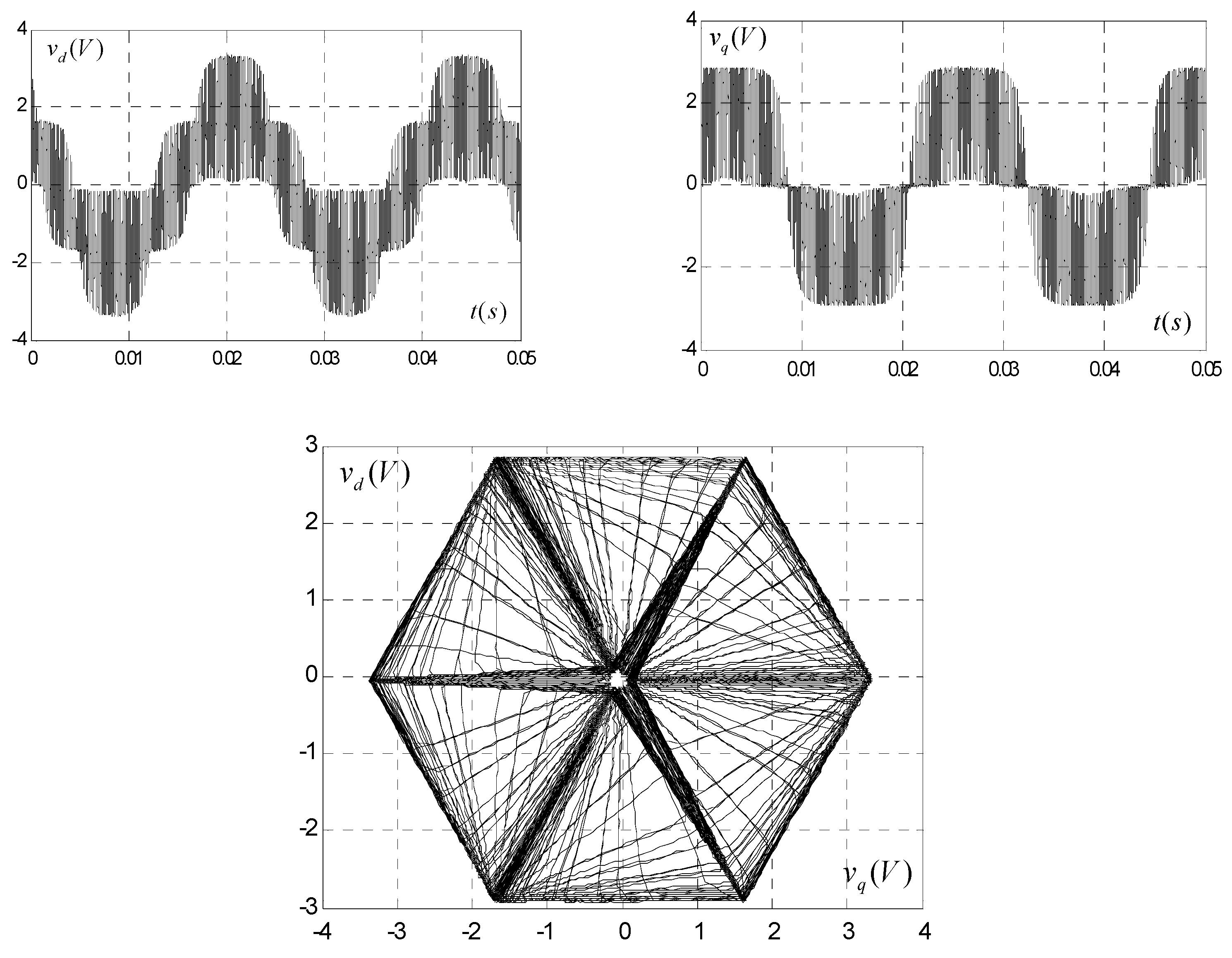



| D1 | D2 | D3 | D4 | D5 | |
|---|---|---|---|---|---|
| Debits (m3/h) | 0.023 | 0.039 | 0.081 | 0.15 | 0.25 |
| Depression U-Log10 | 4.3 | 3.7 | 2.39 | 1.67 | 1.18 |
| Efficiency (%) | 99.99 | 99.9 | 99.6 | 97.9 | 93.39 |
| Water quality | Adequate | Good | Not acceptable | Not acceptable | Not acceptable |
| UV Flux | Debits | Depression | Residence Time | Water Quality |
|---|---|---|---|---|
| 3.5 | 0.023 | 4.3 | 0.13 | Adequate |
| 3.65 | 0.031 | 4.28 | 0.096 | Adequate |
| 3.8 | 0.061 | 4.29 | 0.049 | Adequate |
| 4 | 0.072 | 4.31 | 0.041 | Adequate |
| 4.2 | 0.079 | 4.3 | 0.037 | Adequate |
| 4.35 | 0.086 | 4.28 | 0.033 | Adequate |
| 4.5 | 0.092 | 4.29 | 0.031 | Adequate |
| 4.65 | 0.101 | 4.27 | 0.029 | Adequate |
| 4.75 | 0.16 | 4.3 | 0.018 | Adequate |
| 5 | 0.21 | 4.29 | 0.014 | Adequate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zitouni, N.; Gammoudi, R.; Attafi, R.; Mezgahni, D. Developed and Intelligent Structure of a Control for PV Water Treatment System. Energies 2023, 16, 6540. https://doi.org/10.3390/en16186540
Zitouni N, Gammoudi R, Attafi R, Mezgahni D. Developed and Intelligent Structure of a Control for PV Water Treatment System. Energies. 2023; 16(18):6540. https://doi.org/10.3390/en16186540
Chicago/Turabian StyleZitouni, Naoufel, Rabiaa Gammoudi, Rim Attafi, and Dhafer Mezgahni. 2023. "Developed and Intelligent Structure of a Control for PV Water Treatment System" Energies 16, no. 18: 6540. https://doi.org/10.3390/en16186540
APA StyleZitouni, N., Gammoudi, R., Attafi, R., & Mezgahni, D. (2023). Developed and Intelligent Structure of a Control for PV Water Treatment System. Energies, 16(18), 6540. https://doi.org/10.3390/en16186540





