Reliability of Microinverters for Photovoltaic Systems: High-Temperature Accelerated Testing with Fixed and Cyclic Power Stresses
Abstract
:1. Introduction
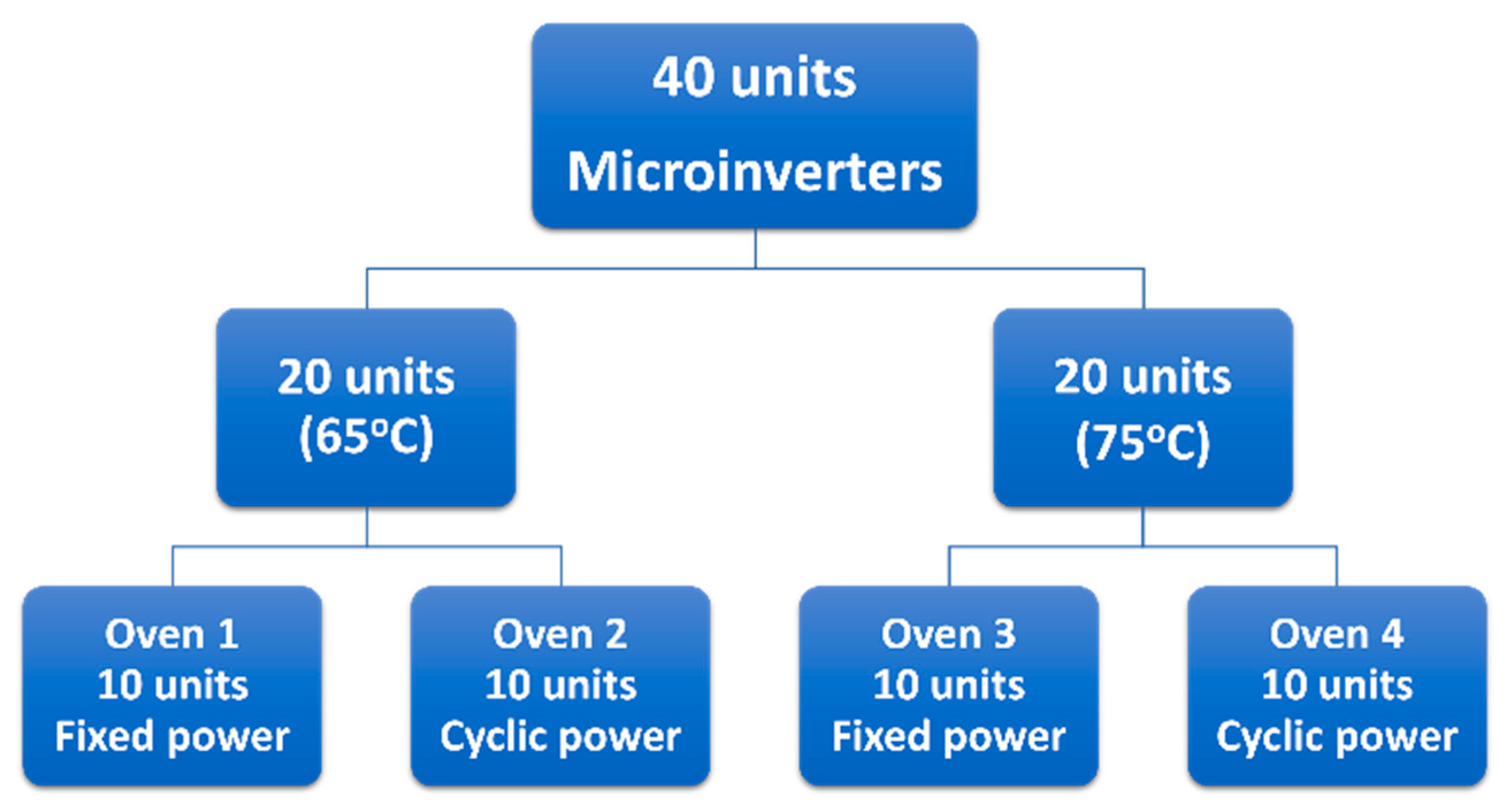
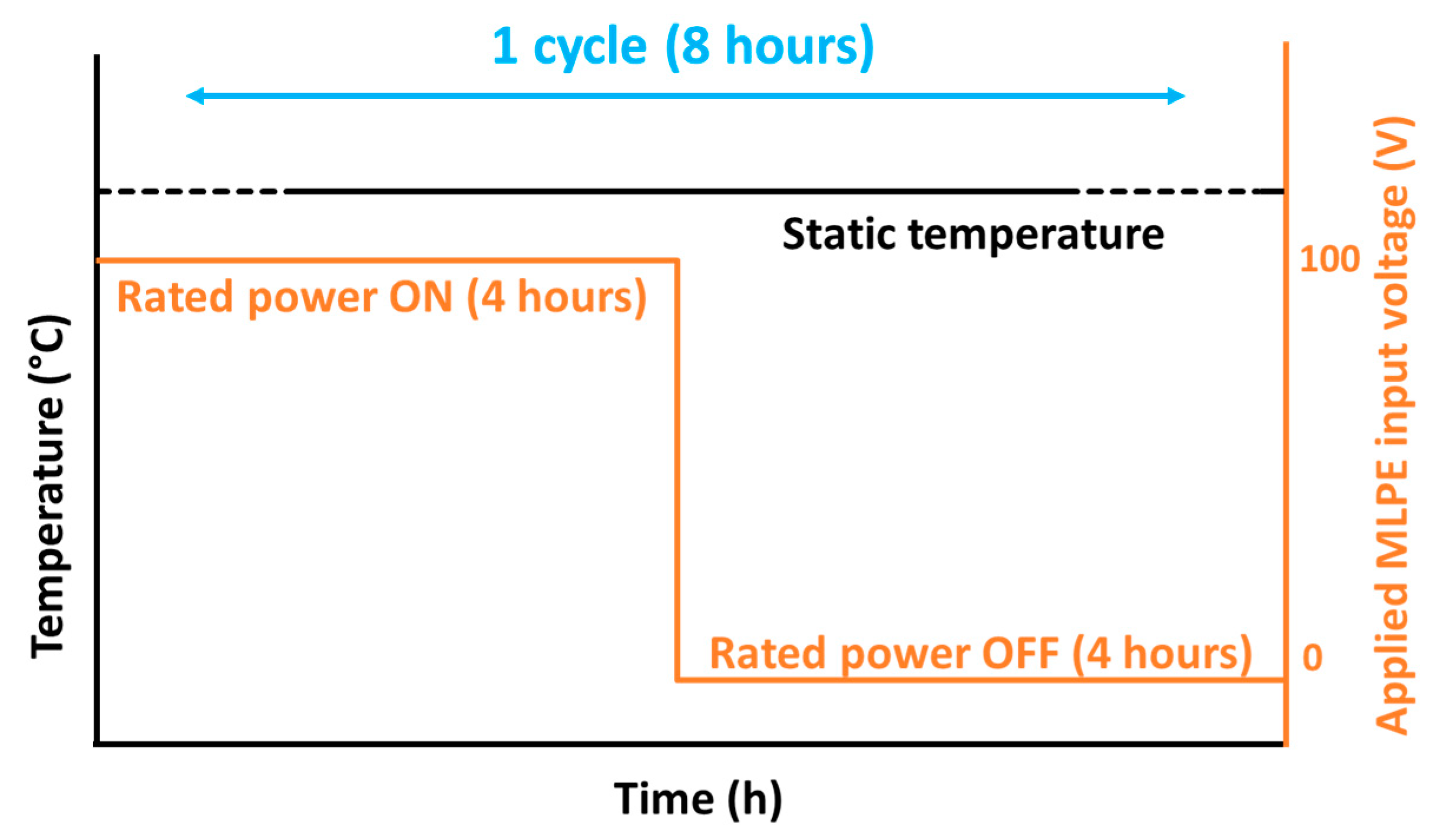
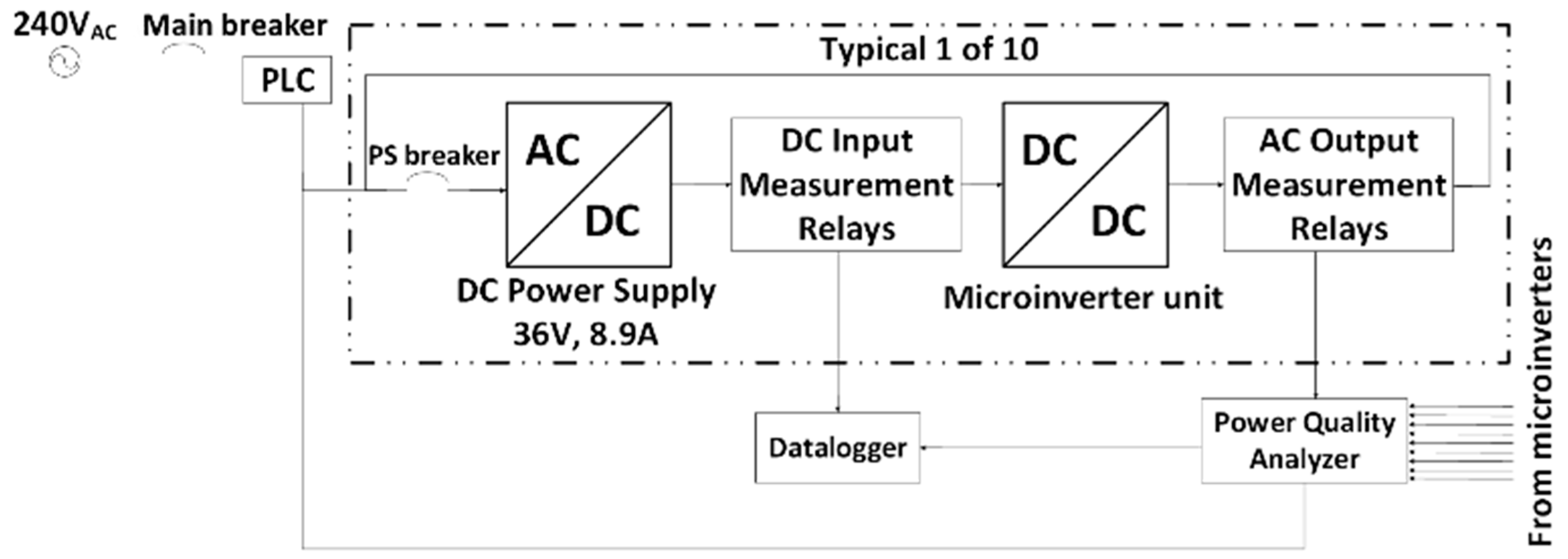
2. Experimental Testing Setup
3. Results and Discussion
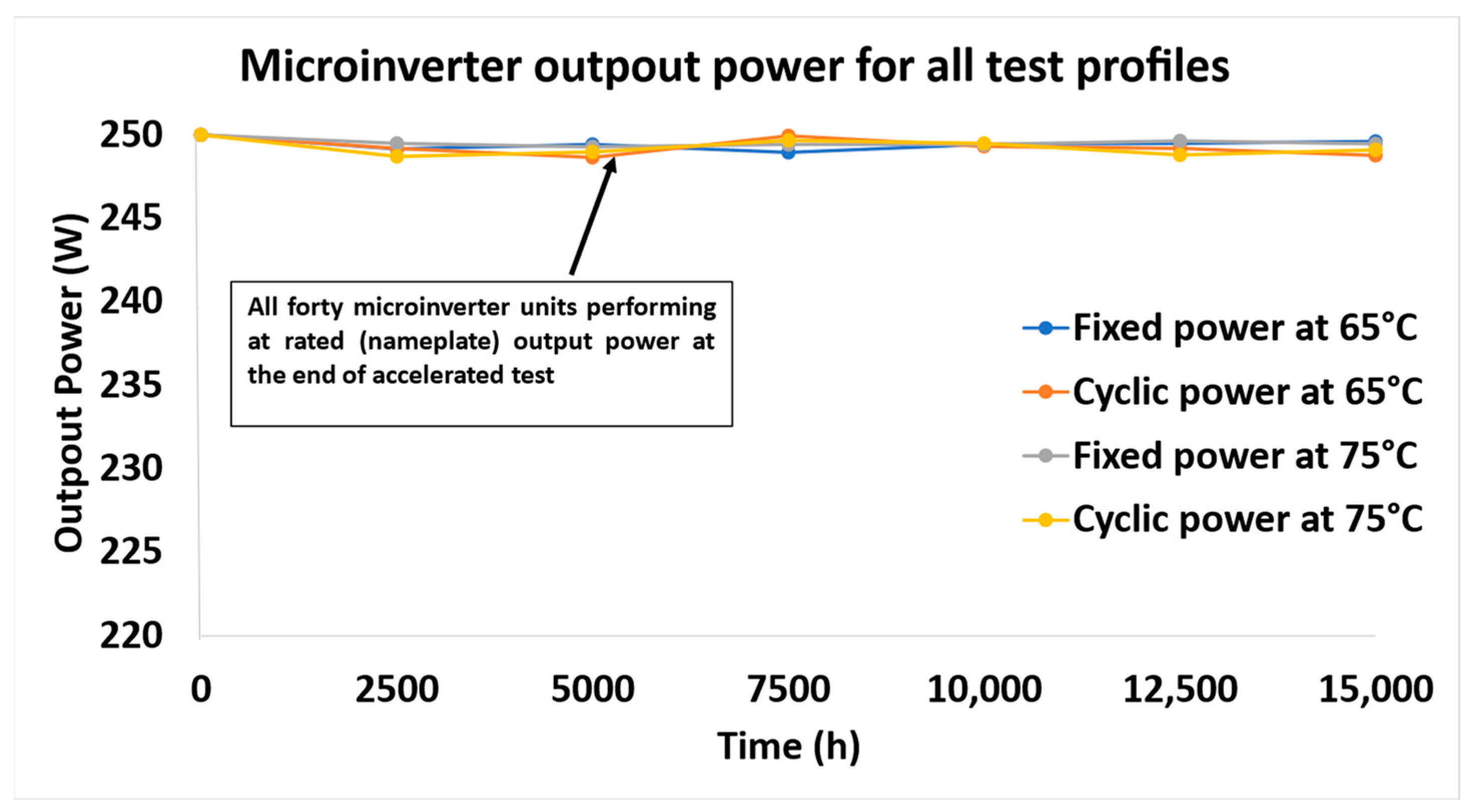
3.1. High Static Temperature Testing for the Microinverters
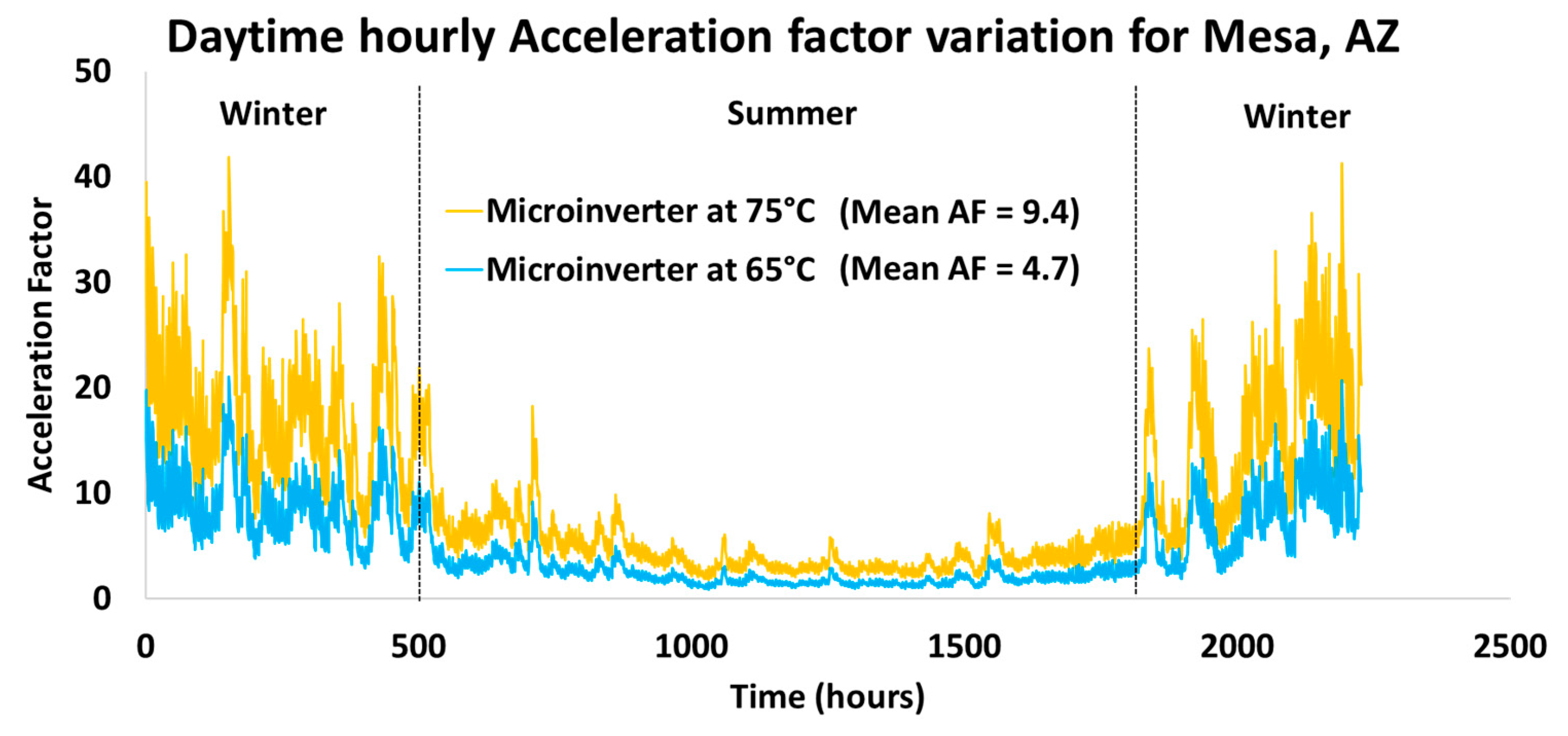
3.2. Estimated Field-Use Lifetime for the Microinverters
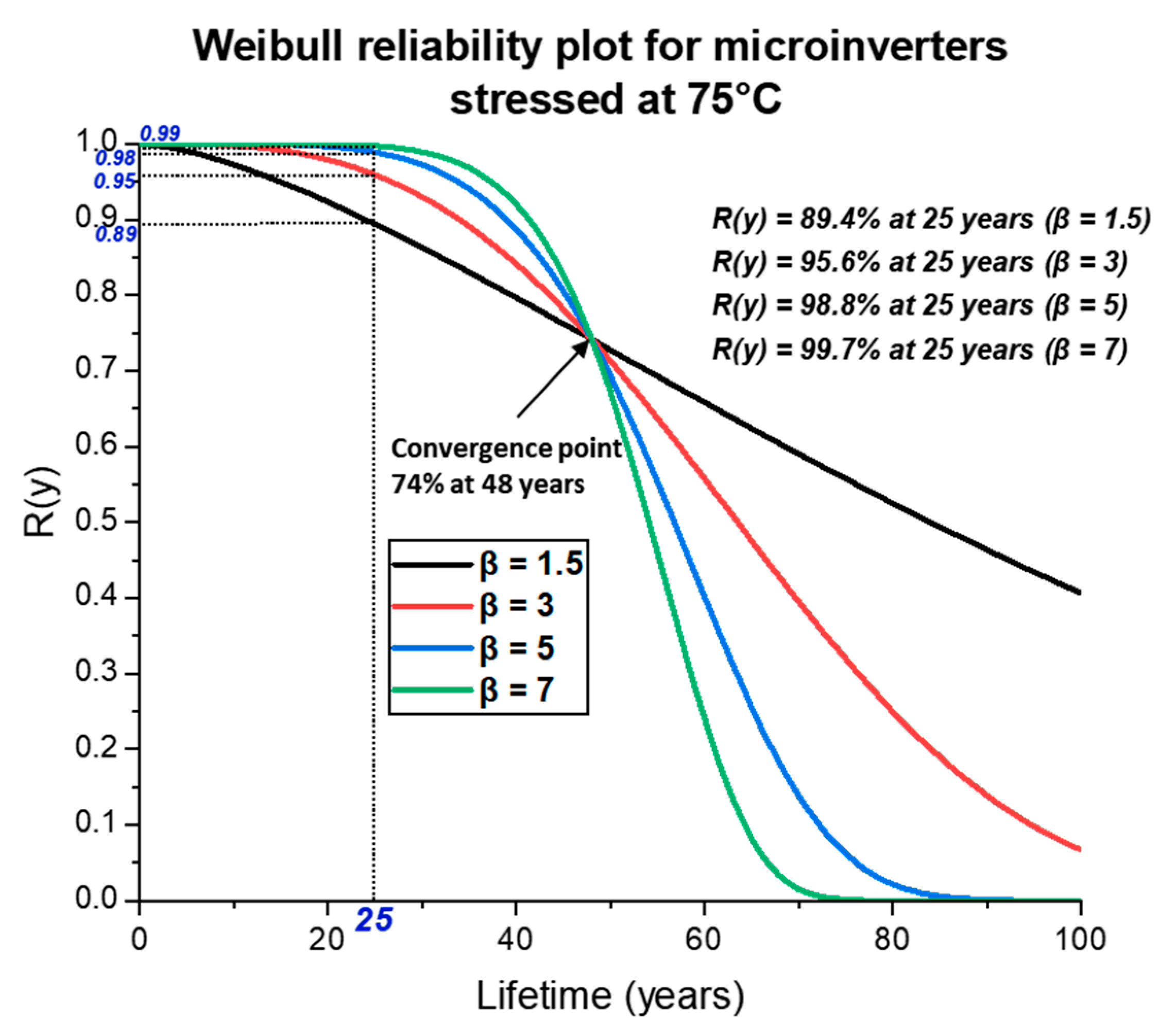
3.3. Reliability Analysis Using the Weibull Distribution Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Photovoltaic Systems with Module-Level Power Electronics. U.S. Department of Energy. 2015. Available online: https://www.nrel.gov/docs/fy15osti/64876.pdf (accessed on 9 March 2023).
- IEA. Solar PV, IEA, Paris. 2022. Available online: https://www.iea.org/reports/solar-pv (accessed on 8 March 2023).
- Feldman, D.; Dummit, K.; Zuboy, J.; Heeter, J.; Xu, K.; Margolis, R. Spring 2022 Solar Industry Update. 2022. Available online: https://www.nrel.gov/docs/fy22osti/82854.pdf (accessed on 8 March 2023).
- Shaunagh, M.; Siqi, H.; Cormac, G. Module Level Power Electronics. 2022. Available online: https://cdn.ihsmarkit.com/www/pdf/0822/Module-Level-Power-Electronics.pdf (accessed on 9 March 2023).
- Module Level Power Electronics (MLPE) Market Growth Analysis and Industry Research Report to 2030|Solar Edge, Enphase, Tigo/SMA. 31 July 2023. Available online: https://www.marketwatch.com/press-release/module-level-power-electronics-mlpe-market-growth-analysis-and-industry-research-report-to-2030-solar-edge-enphase-tigosma-2023-03-08?mod=search_headline (accessed on 9 March 2023).
- Afridi, M.; Kumar, A.; ibne Mahmood, F.; Tamizhmani, G. Hotspot testing of glass/backsheet and glass/glass PV modules pre-stressed in extended thermal cycling. Sol. Energy 2023, 249, 467–475. [Google Scholar] [CrossRef]
- Afridi, M.A.; Arbab, M.; Bilal, M.; Ullah, H.; Ullah, N. Determining the effect of soiling and dirt particles at various tilt angles of photovoltaic modules. Int. J. Eng. Work. 2017, 4, 143–146. [Google Scholar]
- Kumar, A.L.; Alexander, S.A.; Rajendran, M. Power Electronic Converters for Solar Photovoltaic Systems; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Afridi, M.; Kumar, A.; Mahmood, F.I.; TamizhMani, G. Comparative Analysis of Hotspot Stress Endurance in Pristine and Thermal Cycled Prestressed Glass–Glass Photovoltaic Modules. Sustainability 2023, 15, 12131. [Google Scholar] [CrossRef]
- Deline, C.; Meydbray, J.; Donovan, M. Photovoltaic Shading Testbed for Module-Level Power Electronics: 2016 Performance Data Update. 2016. Available online: https://www.nrel.gov/docs/fy16osti/62471.pdf (accessed on 9 March 2023).
- Deline, C.; Marion, B.; Granata, J.; Gonzalez, S. Performance and Economic Analysis of Distributed Power Electronics in Photovoltaic Systems. 2011. Available online: https://www.nrel.gov/docs/fy11osti/50003.pdf (accessed on 9 March 2023).
- ibne Mahmood, F.; Kumar, A.; Afridi, M.; TamizhMani, G. Potential induced degradation in c-Si glass-glass modules after extended damp heat stress. Sol. Energy 2023, 254, 102–111. [Google Scholar] [CrossRef]
- Ma, M.; Wang, H.; Xiang, N.; Yun, P.; Wang, H. Fault diagnosis of PID in crystalline silicon photovoltaic modules through IV curve. Microelectron. Reliab. 2021, 126, 114236. [Google Scholar] [CrossRef]
- Plante, R.H. Solar Energy, Photovoltaics, and Domestic Hot Water: A Technical and Economic Guide for Project Planners, Builders, and Property Owners; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Dogga, R.; Pathak, M. Recent trends in solar PV inverter topologies. Sol. Energy 2019, 183, 57–73. [Google Scholar] [CrossRef]
- Cha, W.-J.; Kwon, J.-M.; Kwon, B.-H. Highly efficient step-up dc–dc converter for photovoltaic micro-inverter. Sol. Energy 2016, 135, 14–21. [Google Scholar] [CrossRef]
- Day, N.U.; Reinhart, C.C.; DeBow, S.; Smith, M.K.; Sailor, D.J.; Johansson, E.; Wamser, C.C. Thermal effects of microinverter placement on the performance of silicon photovoltaics. Sol. Energy 2016, 125, 444–452. [Google Scholar] [CrossRef]
- Bilal, M.; Arbab, M.N.; Afridi, M.Z.U.A.; Khattak, A. Increasing the output power and efficiency of solar panel by using concentrator photovoltaics (CPV). Int. J. Eng. Work. 2016, 3, 98–102. [Google Scholar]
- Parker, T.P.; Chapman, P.L.; Gilchrist, P. Dominant factors affecting reliability of alternating current photovoltaic modules. In Proceedings of the 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015; pp. 1–6. [Google Scholar]
- De Leon, S.; Calleja, H.; Mina, J. Reliability of photovoltaic systems using seasonal mission profiles and the FIDES methodology. Microelectron. Reliab. 2016, 58, 95–102. [Google Scholar] [CrossRef]
- Krauter, S.; Bendfeld, J. Cost, performance, and yield comparison of eight different micro-inverters. In Proceedings of the 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015; pp. 1–4. [Google Scholar]
- Armijo, K.M.; Yang, B.B.; Riley, D.; Lavrova, O.; Gonzalez, S.; Lomasney, H. Predictive reliability for AC photovoltaic modules based on electro-thermal phenomena. In Proceedings of the IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015; pp. 1–6. [Google Scholar]
- Flicker, J.; Tamizhmani, G.; Moorthy, M.K.; Thiagarajan, R.; Ayyanar, R. Accelerated Testing of Module-Level Power Electronics for Long-Term Reliability. IEEE J. Photovolt. 2017, 7, 259–267. [Google Scholar] [CrossRef]
- Afridi, M.; Tatapudi, S.; Flicker, J.; Srinivasan, D.; Tamizhmani, G. Reliability evaluation of DC power optimizers for photovoltaic systems: Accelerated testing at high temperatures with fixed and cyclic power stresses. Eng. Fail. Anal. 2023, 152, 107484. [Google Scholar] [CrossRef]
- Lakshminarayanan, V.; Sriraam, N. The effect of temperature on the reliability of electronic components. In Proceedings of the 2014 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 6–7 January 2014; pp. 1–6. [Google Scholar]
- Ristow, A.; Begovic, M.; Pregelj, A.; Rohatgi, A. Development of a methodology for improving photovoltaic inverter reliability. IEEE Trans. Ind. Electron. 2008, 7, 2581–2592. [Google Scholar] [CrossRef]
- Sastry, A.; Kulasekaran, S.; Flicker, J.; Ayyanar, R.; TamizhMani, G.; Roy, J.; Srinivasan, D.; Tilford, I. Failure modes and effect analysis of module level power electronics. In Proceedings of the 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015; pp. 1–3. [Google Scholar]
- Luko, S.N.; Neubauer, D.V. Building on Reliability: Reliability Test Planning. ASTM Standardization News, January/February 2021. Available online: https://sn.astm.org/data-points/building-reliability-reliability-test-planning-jf21.html (accessed on 10 July 2023).
- Flicker, J. Reliability of Module Level Power Electronics and Standards Development. p. 2015. Available online: https://www.researchgate.net/profile/Jack-Flicker/publication/279448898_Poster_Module_Level_Power_Electronics_Reliability_and_Standards_Development/links/5592f1bf08ae16f493ee495a/Poster-Module-Level-Power-Electronics-Reliability-and-Standards-Development.pdf (accessed on 10 July 2023).
- Tatapudi, S.; Flicker, J.; Srinivasan, D.; Upadhyaya, J.; Selvarangan, K.; Nandakumar, L.; Leslie, J.; Tamizhmani, G. Design of Experimental Test Setup for Large-scale Reliability Evaluation of Module Level Power Electronics (MLPE). In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 1347–1351. [Google Scholar]
- Hacke, P.; Clemens, D.; Thiagarajan, R.; Flicker, J.; Igarashi, H. Evaluation of the DC bus link capacitors and power transistor modules in the qualification testing of PV inverters. Prog. Photovolt. Res. Appl. 2021, 29, 675–683. [Google Scholar] [CrossRef]
- Flicker, J. Capacitor Reliability in Photovoltaic Inverters. 2015. Available online: https://www.researchgate.net/publication/279448671_Capacitor_Reliability_in_Photovoltaic_Inverters (accessed on 9 March 2023).
- Kozak, J.P.; Ngo, K.D.; DeVoto, D.J.; Major, J.J. Impact of accelerated stress-tests on SiC MOSFET precursor parameters. In Proceedings of the International Symposium on 3D Power Electronics Integration and Manufacturing (3D-PEIM), College Park, MD, USA, 25–27 June 2018; pp. 1–5. [Google Scholar]
- IEC 62093-2021; Power Conversion Equipment for Photovoltaic Systems—Design Qualification Testing. International Electrotechnical Commission: London, UK, 2021.
- Afridi, M.Z.U.A. Module Level Power Electronics and Photovoltaic Modules: Thermal Reliability Evaluation. Doctoral Dissertation, Arizona State University, Tempe, AZ, USA, 2023. [Google Scholar]
- Tariq, M.S.; Butt, S.A.; Khan, H.A. Impact of module and inverter failures on the performance of central-, string-, and micro-inverter PV systems. Microelectron. Reliab. 2018, 88, 1042–1046. [Google Scholar] [CrossRef]
- Kim, K.-S.; Jeong, S.-G.; Kwon, B.-H. Single power-conversion DAB microinverter with safe commutation and high efficiency for PV power applications. Sol. Energy 2019, 193, 676–683. [Google Scholar] [CrossRef]
- Watson, J.; Castro, G. A review of high-temperature electronics technology and applications. J. Mater. Sci. Mater. Electron. 2015, 26, 9226–9235. [Google Scholar] [CrossRef]
- Military Handbook: Reliability Prediction of Electronic Equipment; Department of Defense: Washington, DC, USA, 1991.
- Flicker, J.; Lavrova, O.; Tamizhmani, G. Co-located Accelerated Testing of Module Level Power Electronics and Associated PV Panels. In Proceedings of the IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 1273–1277. [Google Scholar]
- Luko, S.N. Attribute Reliability and the Success Run: A Review. SAE Trans. 1997, 106, 251–261. [Google Scholar] [CrossRef]
- Luko, S.N. Weibull Analysis with Assumed Weibull Slope Where NO Failures are Observed. SAE Trans. 1998, 107, 347–352. [Google Scholar] [CrossRef]
- Nelson, W. Applied Life Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1982. [Google Scholar]
- Nelson, W. Weibull analysis of reliability data with few or no failures. J. Qual. Technol. 1985, 17, 140–146. [Google Scholar] [CrossRef]
- Luko, S.N.; Neubauer, D.V. Building on Reliability: Reliability Test Planning, Part 2. ASTM Standardization News, May/June 2021. Available online: https://sn.astm.org/data-points/building-reliability-reliability-test-planning-part-2-mj21.html (accessed on 10 July 2023).



| Microinverters | ||
|---|---|---|
| Testing hours (h) | 15,000 | |
| Temperature | 65 °C | 75 °C |
| Average acceleration factor | 4.7 | 9.4 |
| Equivalent field operational time hours (h) based on 24 h per day MLPE operation | 70,470 (8 years) | 140,500 (16 years) |
| Equivalent field operational time (years) based on 8 h per day MLPE operation | 24 | 48 |
| Confidence Level (%) | Reliability (%) |
|---|---|
| 60 | 91.24 |
| 70 | 88.65 |
| 80 | 85.13 |
| 90 | 79.43 |
| 95 | 74.11 |
| 99 | 63.09 |
| Microinverters at 65 °C (Fixed and Cyclic Power) | ||||
|---|---|---|---|---|
| Field-equivalent operational time (years) | 24 | |||
| Shape factor | 1.5 | 3 | 5 | 7 |
| Scale factor (years) | 53.6 | 35.9 | 30.5 | 28.5 |
| L10 lifetime (years) | 12 | 17 | 19.5 | 20.7 |
| L50 (Median) lifetime (years) | 42 | 31.7 | 28.4 | 27 |
| 25-year survival probability (%) | 72.7 | 71.3 | 69.3 | 67.1 |
| Microinverters at 75 °C (Fixed and Cyclic Power) | ||||
| Field-equivalent operational time (years) | 48 | |||
| Shape factor | 1.5 | 3 | 5 | 7 |
| Scale factor (years) | 107 | 71.7 | 61 | 57 |
| L10 lifetime (years) | 24 | 34 | 39 | 41.4 |
| L50 (Median) lifetime (years) | 84 | 63.5 | 57 | 54 |
| 25-year survival probability (%) | 89.4 | 95.9 | 98.8 | 99.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afridi, M.; Tatapudi, S.; Flicker, J.; Srinivasan, D.; Tamizhmani, G. Reliability of Microinverters for Photovoltaic Systems: High-Temperature Accelerated Testing with Fixed and Cyclic Power Stresses. Energies 2023, 16, 6511. https://doi.org/10.3390/en16186511
Afridi M, Tatapudi S, Flicker J, Srinivasan D, Tamizhmani G. Reliability of Microinverters for Photovoltaic Systems: High-Temperature Accelerated Testing with Fixed and Cyclic Power Stresses. Energies. 2023; 16(18):6511. https://doi.org/10.3390/en16186511
Chicago/Turabian StyleAfridi, Muhammad, Sai Tatapudi, Jack Flicker, Devarajan Srinivasan, and Govindasamy Tamizhmani. 2023. "Reliability of Microinverters for Photovoltaic Systems: High-Temperature Accelerated Testing with Fixed and Cyclic Power Stresses" Energies 16, no. 18: 6511. https://doi.org/10.3390/en16186511
APA StyleAfridi, M., Tatapudi, S., Flicker, J., Srinivasan, D., & Tamizhmani, G. (2023). Reliability of Microinverters for Photovoltaic Systems: High-Temperature Accelerated Testing with Fixed and Cyclic Power Stresses. Energies, 16(18), 6511. https://doi.org/10.3390/en16186511






