European Green Deal: Improving the Efficiency of Using Planetary Hydraulic Machines

Abstract

Research is devoted to the use of energy-efficient hydraulic motors in running modules for mechatronic systems of construction, road, municipal, agricultural, railway and other self-propelled machines; robots are used in various branches of the European economy and can contribute to the practical implementation of the philosophy of the “European Green Deal”. As a result of this research, design schemes and a mathematical apparatus have been developed that allow determining the rational force in the contact zone of the movable and fixed distributors. In order to determine the geometric parameters of the stepped surfaces of the movable and fixed distributors, which ensure the formation of an oil film in the contact zone, a structural-functional diagram of the mathematical model has been developed, which makes it possible to obtain a quantitative estimate of the increase in the productivity of the distribution system. The conducted studies have established that with rational design of the distribution system elements by reducing the clamping force by 3...5% in the distribution system, leakage through the end gap is reduced by 26%. Reduction of leakage in the contact zone allows an increase in productivity of the distribution system of 2.4% by increasing the volumetric efficiency (reducing losses).

1. Introduction

Modern industry in the civilized world cannot be imagined without the application of innovations and effective use of existing technologies and technical structures. Technical progress, which reduces economic and energy costs and negative environmental consequences, and increases the efficiency of the use of technical means, is foreseen by many economic and industrial development programs of various countries, for example, the “European Green Deal” [1]. Some of the relevant scientific and practical directions are research devoted to running modules [2], mechatronic systems of self-propelled and industrial machines [3], robots [4,5], etc., which require the use of efficient hydraulic motors.

During the development of hydraulic drives of active working bodies and running modules of mechatronic systems of self-propelled vehicles, a tendency was determined to use low-speed high-torque hydraulic motors instead of high-speed ones with gearboxes [6,7,8]. Gerotor [9], orbital [10] and planetary [11] hydromotors have found application as such hydraulic motors. Planetary-type hydraulic motors (HM) are mainly used to drive running modules and working bodies of mechatronic systems of self-propelled vehicles [12].

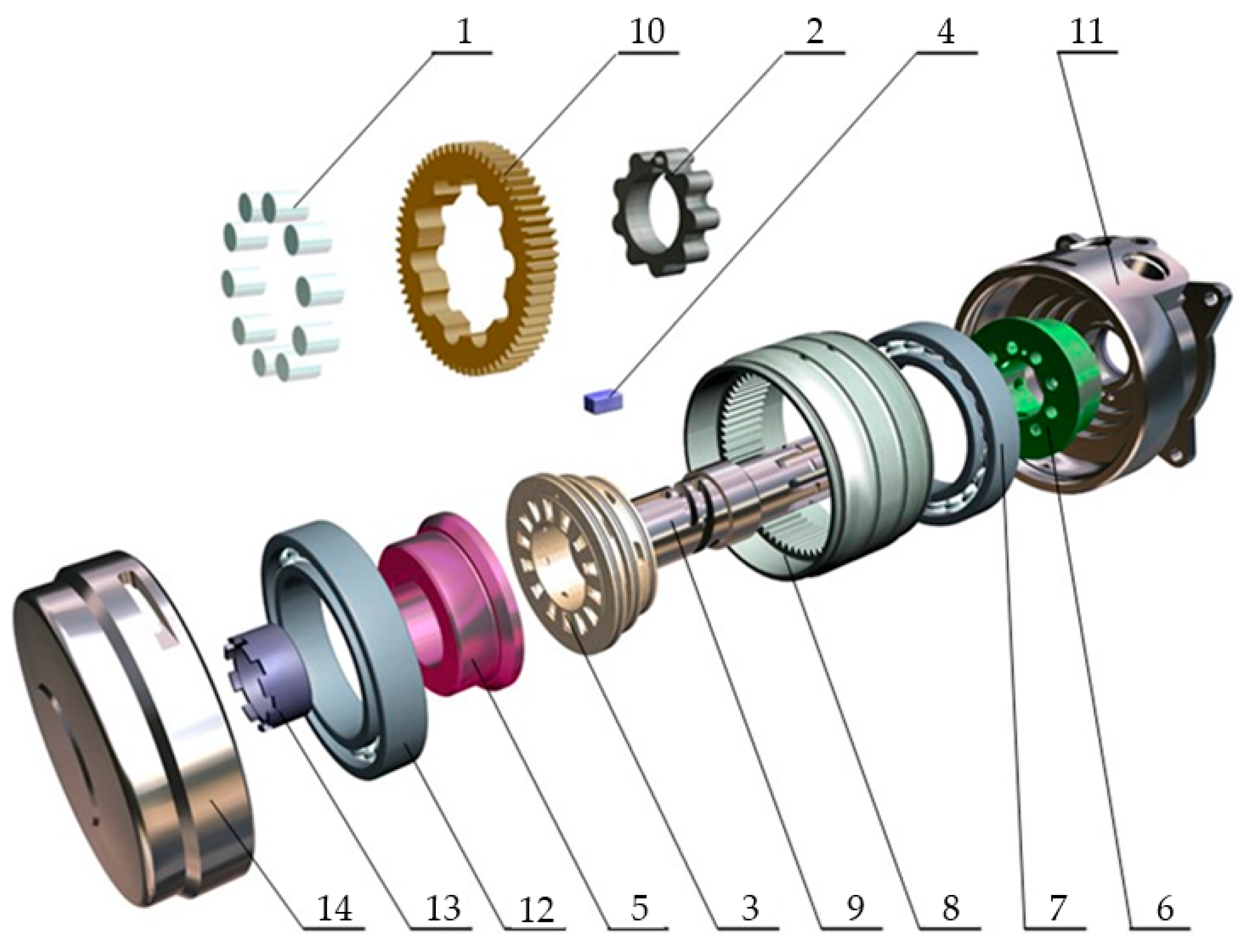
The main systems of the planetary HM (Figure 1), which ensure its performance, are the system of rotors [13,14] and the distribution system [15,16]. The system of rotors is represented by an external rotor 10 with inserted teeth (rollers) 1 and an internal rotor 2, forming a hypocycloidal engagement [14]. The distribution system is represented by a movable distributor 3 and a fixed distributor 6. Shaft 9 and front cover 11 are also involved in the distribution system, which serve to supply (remove) the working fluid.

To ensure the operation of the hypocycloidal engagement, it is necessary to have a rotating hydraulic field created by the working fluid distribution system [15,16]. The hydraulic field (Figure 2) is formed by contacting the end surfaces of the movable 3 and fixed 6 distributors on the contact surfaces of which distribution windows are made [17]. During the operation of the distribution system, the injection zone 4 is replaced by the drain zone 5, i.e., there is a rotation (turn) of the hydraulic field [17]. The principle of operation of the end distribution system of a planetary HM, shown in Figure 2, is described in detail in [16].

The main disadvantage of planetary hydraulic machines (PHM) is the unevenness of their output characteristics due to the presence of hydraulic and volumetric losses in the distribution system. These losses are due to the irrational design of the elements of the distribution system, the geometric parameters of which set the necessary force for constant contact between the movable and fixed distributors. Constant high-quality contact between distributors is the basis for stabilizing the output characteristics of PHM.

Therefore, the study of the working processes occurring in the butt distribution system of a planetary-type HM in order to justify the rational geometric parameters of the elements of the hydraulic fluid distribution system, which ensure an increase in the efficient use of PHM, is an urgent task.

Increasing requirements for the performance of hydraulic drives of active working bodies and running systems [8,18] in various fields of mechanical engineering are determined by the presence of hydraulic machines. To determine the technical level of hydraulic machines and hydraulic drives, even at the design stage, much attention is paid to the development of criteria for their evaluation [19]. Today, hydraulic machines with gerotor technologies [18], which are used in gerotor [20], orbital [21] and planetary [22] hydraulic machines, deserve special attention.

The authors of [18] carried out a thorough analysis of gerotor technologies in hydraulic machines, for which they developed a search strategy that included sources of information from published open and accessible articles, as well as articles and texts from their personal library. The number of sources reviewed is 166, with the earliest article dated 1968 and the latest publication published in February 2019. It should be noted that in conducting that search, a more complete review of the literature is reflected by the authors of [18] over the past decade (i.e., since 2009), with special attention paid to the articles published in the last five years (2015–2019). Analyzing the citation of this work [18], I would like to note that in that article, only in one section, the design, calculation and operating conditions of orbital HM are considered, and all this is stated in 17 sources (which is only 10% of all references). This indirectly confirms the practical absence of publications on planetary (orbital) HM, as the authors directly write about [18]: ... “Very little published work was available on HM, especially the orbital rotor low-speed high-torque type in which epitrochoid and its associated envelope are used as rotor-stator...”.

If we consider the published literature over the past 15 years, then attention should be paid to the hydrodynamic analysis of gerotor pumps [23] and methods for increasing their load capacity [24], as well as the design of the rotor using cycloidal curves [25] with the rationale for the optimal tooth profile for cycloidal gears [26], calculation of forces and moments between contacting rotors [27]. The profiles of a complex gear profile [28] were substantiated and a kinematic analysis was performed [29]. Using the GeroLAB application package, the gap modulus between the gear profiles of the rotors associated with the leakage phenomenon was substantiated [30]; an analysis of leakages for hydraulic pumps of various types was carried out [31]. The effect of pressure [32], specific feed rate and rotational speed [33] on the overall efficiency of a gear motor has been studied. Using a genetic algorithm, multicriteria optimization of the gear profile [34] and the gerotor port [35] was carried out. as well as optimization of the gerotor pump using the evolutionary strategy algorithm [36]. However, issues related to the interaction of the rotor system and the working fluid distribution system were not considered.

Much attention is paid to mathematical modeling. The theory of gearing is considered; a mathematical model is proposed that takes into account the profiles of the internal (cycloidal) and external (hypocycloidal) rotors [37]. Based on the mathematical model of the rotor, a hypocycloidal tooth profile was constructed [38], the effect of the tooth profile on the performance of the gerotor pump was studied [39], the instantaneous flow rate was numerically calculated [40] and the displacement analysis [41] of the gerotor pump was performed. A mathematical model has been developed [42] and numerical simulation [43] of the vibration-aspiration separation process has been carried out. The possibility of carrying out hydrodynamic calculations in hydraulic machines using CFD software packages [44] was considered and a three-dimensional CFD transitional model for an orbital engine was proposed [45], as well as a computational model of a gear train, which allows the finite element method to determine the effect of mechanical and hydraulic loads on strength [46]. A program has been developed for designing such gears, taking into account the equations of hydrodynamics [47]. A parametric design of the cycloidal transmission profile was performed using the NX10.0 software [48]. Modeling of the working fluid flow [49] based on the solution of the RANS equations with the SST turbulence model [50] was carried out, cavitation phenomena [51] and fluid aeration [52] were studied using computer simulation, and guidelines for setting up models were developed using a reduced number of computational simulations hydrodynamics [53]. The effect of air dissolved and entrained in the working fluid on the performance of a gerotor pump was studied by simulating cavitation using the PumpLinx^® CFD software [54]. A numerical model has been developed that can be applied to orbital-type HM, which makes it possible to quantitatively measure wear [55]. Modeling of work processes occurring in the distribution systems of the working fluid was not carried out.

The effect of aerated and non-aerated fluids [56], viscosity of Bingham fluids [57] and fluid compressibility [58,59] on the functional parameters of pumps, as well as the gas content of the working fluid on the parameters of HM [60], was studied. The influence of the interaction between the liquid and the mechanical parts of the gear pump on leakages was considered [61], and the influence of the fluid flow dynamics inside the channels of the gerotor pump on leakages and its performance was also studied [62]. Studies of the effect of leakage and viscosity of the working fluid on the output characteristics of the distribution systems of PHM have not been carried out.

The systematization and comparative analysis of schemes of mechanisms of planetary rotary hydraulic machines [63] were carried out, the issues of improving the planetary rotary hydraulic machine were considered [64], and computational and constructive methods for expanding the supply channels in hydraulic machines with a planetary rotor were proposed [65]. To improve the performance of a rotary planetary pump, a loading model has been proposed that makes it possible to determine the pressure distribution in each of the working chambers [66]. However, it should be noted that the supply of working fluid and the principle of operation of PHM (orbital) differ from hydraulic machines with a planetary rotor.

An analysis of the reasons for the unsatisfactory operation of PHM (orbital) made it possible to identify two main units that limit their effective operation: the rotor system [13,14] and the distribution system [16,17]. In the system of rotors, the kinematics of the movement of the outer rotor was studied [13,14] and the effect of changing the gap between the inner and outer rotors on the change in the functional parameters of the planetary HM was determined [67]. The dynamic processes occurring in the system of rotors are described [10,12,22]; an experimental assessment of the influence of the design features of the system of rotors on the functional characteristics of planetary HM is carried out [68]. Methods and tools have been developed to control the error in the form of manufacturing rotors [69], and the methodology for automating the control of the toothed surface of rotors has been substantiated [70]. Studies related to the influence of the geometric parameters of distribution systems on the functional parameters of hydraulic machines have not been carried out.

The distribution system is a complex unit, which is a device for supplying and draining the working fluid into the working chambers [15,16], formed by the outer and inner rotors, in a certain sequence [13,14]. The rational kinematic schemes of the distribution system [16] and the rational geometrical parameters of the distribution windows [71] were substantiated, allowing to reduce the pulsations of the working fluid flow; the influence of the shape of the windows made in the form of a segment [15,17], a circle [15,72] and a groove [15,73] on the throughput of the distribution system justified the angular arrangement of the windows [74]. The dynamic processes occurring in the distribution systems were investigated [10,12,75] and experimental studies of the throughput of the distribution systems of planetary HM were carried out [76]. The issues of ensuring the operability of the distribution system were not considered.

However, one must take into account the fact that the planetary (orbital) HM is a structure consisting of a gearbox and a liquid distribution device [14,16]. In this case, the gearbox has a special cycloidal gearing that forms the working chambers, and the distribution device ensures the supply of the working fluid to these chambers. An analysis of literary sources shows that if scientific publications can still be found on the gearboxes of planetary (orbital) HM, then there are simply no publications on the distribution systems of these HM. In the 17 sources of literature analysis given [18], there is not a single source considering the operation of the hydraulic fluid distribution system of a planetary (orbital) HM, and this is an almost complete analysis for 50 years.

Having analyzed the available literary space in order to appropriately substantiate the issue under study based on the current state of knowledge, it can be argued that today (starting from 2018) the publications of Ukrainian researchers A. Panchenko, A. Voloshina, S. Kiurchev and their colleagues are the most numerous sources of information on the calculation, design and operation of planetary (orbital) HM.

The operability of the distribution system, as a rule, determines the operability and resource of the hydraulic machine as a whole. The main condition that determines the operability of the distribution system is to ensure the conditions for pressing (creating constant contact) of the movable distributor to the stationary one. Therefore, increasing the efficiency of using PHM by substantiating the rational geometric parameters of the elements of the distribution system and ensuring its operable state (fulfillment of the condition for pressing the movable distributor to the stationary one) is an urgent problem requiring urgent study.

The purpose of the work is to substantiate the rational geometric parameters of the elements of the distribution system, which provide an increase in the efficiency of the use of PHM by studying the working processes occurring in the distribution system of a planetary HM.

To achieve the goal of the study, it is necessary to perform the following tasks:

−

To develop calculation schemes and mathematical apparatus to determine the rational contact force of the elements of the distribution system, which ensures an increase in its productivity;

−

To develop a structural and functional diagram of a mathematical model for studying the working processes that are observed in the distribution system of the working fluid during the operation of a planetary HM;

−

To study the influence of the design features of the elements of the end distribution system on the change in the output parameters of the planetary-type HM.

2. Materials and Methods

During the operation of the planetary HM, its operable state is determined by the qualitative operation of the distribution system [72,73], which creates a rotating hydraulic field that ensures the interaction of the movable and stationary rotors [13,14]. The stability (uniqueness) of the output parameters of the planetary HM during the operation of the power hydraulic drive of self-propelled equipment depends on the stability of the interaction of the elements of its distribution system. The main elements of the distribution system of the planetary HM are fixed (Figure 3a) and movable (Figure 3b) distributors, which form a contact zone with their end surfaces H₁ and H₂, on which distribution windows are located [17].

To draw up a diagram of the forces acting in the end distribution system of a planetary-type HM (Figure 3c), the calculation scheme was taken as a basis for determining leaks in the gap formed by the “opening” of the contact surfaces of the movable and fixed (stationary) distributors, given in [17]. The diagram of the forces acting in the end gap shows (Figure 3c) that the pressing force ensures the contact interaction of the end surfaces H₁ and H₂ of the stationary and movable distributors in the planetary HM and is set by the pressure of the working fluid on the stepped surfaces of the stationary distributor. Thus, the pressing force provides high-quality interaction of the contact surfaces H₁ and H₂, which is necessary to start the operation (start-up) of the planetary HM.

At the beginning of the movement (at start-up) of the planetary HM, the stationary distributor, under the action of the resulting pressure force of the working fluid on the stepped surfaces of the stationary distributor, is pressed against the movable distributor. The pressing (resulting) force F₁ counteracts the repulsive (resulting) force F₂ of the pressure of the working fluid on the stepped surfaces of the fixed distributor located in the contact zone.

To determine the resulting forces F₁ and F₂, we assume that the working fluid is supplied through channel C₁, and the outlet is through channel C₂ (Figure 3c). We will assume that the resulting pressure force of the working fluid, acting from left to right, is the pressing force F₁, and from right to left-the repulsive force F₂.

The pressing (resulting) force F₁ formed by a significant liquid on the stepped surfaces of the surface precipitation can be expressed:

$$F_1=\frac{\pi }{4}\cdot \left(p_1\cdot \left({D^{\prime }}_1^2-D_1^2\right)+p_2\cdot \left(D_3^2-{D^{\prime }}_1^2\right)+p_3\cdot \left(D_4^2-D_3^2\right)+p_4\cdot \left(D_5^2-D_4^2\right)\right)$$

(1)

where p₁ is the drainage pressure; p₂, p₄ are discharge pressures; p₃ is drain pressure; and D₁, D’₁, D₃, D₄, D₅ are diameters of the stepped surfaces of the fixed distributor.

Then, the repulsive (resulting) force F₂ acting on the fixed distributor will be equal to:

$$F_2=\frac{\pi }{4}\cdot p_5\cdot \left(D_5^2-D_2^2\right)+p_6\cdot A_1+p_7\cdot A_2+F_h$$

(2)

where p₅ is the discharge pressure; p₆, p₇ are discharge and drain pressures in distribution windows, respectively; D₂ is the diameter of the stepped surface of the fixed distributor; A₁, A₂ are overlapping areas of distribution windows in the pressures and unloading zones, respectively; and F_h is the force required to create an oil film of height h in the contact zone between the annular surfaces H₁ and H₂ (Figure 3c).

The contact zone of the end distribution system of a planetary-type HM is represented by surfaces H₁ and H₂, and limited by diameters D₁ and D₂ (Figure 3c), for the fixed and movable distributors, respectively. On the annular contact surface H₁ of the fixed distributor, the injection and drain windows are alternately located (Figure 4) [15,16,17]. On the contact surface H₂ of the movable distributor, also made in the form of a ring, there are working and unloading windows (Figure 4) [15,16,17]. Moreover, distribution windows can be made both in the form of a segment [15,17], and in the form of a circle [15,72] and a groove [15,73]. During the operation of the distribution system, these surfaces overlap, forming the overlapping areas of the distribution windows A₁ and A₂ in the pressures and unloading zones, respectively (Figure 4) [15].

The developed calculation scheme for determining the overlapping areas of the distribution windows in the contact zone shows the angular symmetry of the location of the distribution windows of the movable and fixed distributors (Figure 4). Therefore, the distribution window overlap areas for the pressure zone A₁ and the unloading zone A₂ are numerically equal to each other and are determined from the expression:

$$A_1\left(t\right)=A_2\left(t\right)={\displaystyle \sum {\phi }_i}\left(t\right)\cdot \pi \cdot \left[{\left(\frac{D_2^0}{2}\right)}^2-{\left(\frac{D_1^0}{2}\right)}^2\right]$$

(3)

where φ_i is the angle limiting the geometrical parameters of the windows of the movable distributor; D⁰₁, D⁰₂ are inner and outer diameters limiting the geometrical parameters of distribution windows.

The angle φ_i, which limits the geometric parameters of the windows of the movable distributor with the injection (drain) windows of the fixed distributor, participating in the overlap (Figure 4), is equal to:

$${\phi }_i\left(t\right)={\tau }_i\left(t\right)+{\gamma }_i\left(t\right)+{\psi }_i\left(t\right)$$

(4)

where τ_i and ψ_i are the angles limiting the windows of the movable and fixed distributors participating in the overlap, respectively; γ_i is the angle characterizing the overlap zone of the windows of the movable and fixed distributors.

It has been established that the angles τ_i and ψ_i are always equal, i.e., τ_i = ψ_i. The sum of the angles τ_i (ψ_i)) and γ_i is the angle ε, which limits the geometric parameters of the distribution windows of the movable and fixed distributors, i.e., ε = τ_i(ψ_i)) + γ_i. It should be noted that ε = π/Z₂, where Z₂ is the number of windows of the fixed distributor. The window overlap angle γ_i of the fixed distributor is defined as the difference between the angle ε, which limits the geometrical parameters of the distribution windows, and the angle σ_i between the current centers of the windows of the movable and fixed distributors, i.e., γ_i = π/Z₂ − σ_i(t).

The angle σ_i between the current centers of the windows of the movable and fixed distributors located in the overlap is determined by the expression [15,17]

$${\sigma }_i=|{\beta }_i–{\alpha }_i(t)|$$

(5)

where α_i(t) is the current angle of location of the windows of the movable distributor; β_i is the current angle of location of the windows of the fixed distributor, and the odd windows are taken as pressure (delivery) windows and the even ones as drain windows.

Then, taking into account all the assumptions, formula (5) and expression (4), for determining the angle φ_i limiting the geometric parameters of the windows of the movable distributor, can be written as follows:

$${\phi }_i\left(t\right)=\frac{\pi }{Z_2}+\left|{\beta }_i-{\alpha }_i(t)\right|$$

(6)

At the moment of starting the planetary HM, during the rotation of the movable distributor, an oil film is formed in the gap h between the contact surfaces H₁ and H₂ (Figure 3c). The formation of an oil film makes it possible to eliminate dry friction in the contact zone of the elements of the distribution system of a planetary-type HM. At the same time, the formation of an oil film generates a repulsive force F_h, which can lead to a violation of the quality of contact between the surfaces H₁ and H₂.

The repulsive force F_h required to create an oil film of height h in the contact zone between the annular surfaces H₁ and H₂ (Figure 3c) is determined from the expression

$$F_h=\frac{\pi }{4}\cdot p_h\cdot \left(D_2^2-D_1^2\right)$$

(7)

where p_h is the pressure formed in the contact zone between the rotating surfaces H₁ and H₂ of the fixed and movable distributors.

The value of pressure p_h formed in the contact zone between the rotating surfaces H₁ and H₂ of the fixed and movable distributors depends on a number of factors (Figure 3c). The determining factor is the geometric parameters (dimensions) of the ring formed by the rotating surfaces H₁ and H₂ of the fixed and movable distributors. The next important factor is the manufacturing accuracy of the contact surfaces of the movable and fixed distributors, determined by the perpendicularity of their ends to the axis of rotation. Important factors are the materials from which the distributors are made, as well as the technical characteristics of the working fluid. Then, the pressure p_h formed in the contact zone after the corresponding transformations is determined from the expression [14]:

$$p_h=\frac{12{\mu }^{\prime }}{h^3}\cdot \frac{Q_{\mathit{leak}}}{{\displaystyle \sum \left({\phi }_1+{\phi }_2\right)}}\cdot \left(\mathit{ln}\frac{D_2^0}{D_2}+\mathit{ln}\frac{D_1}{D_1^0}\right)+\frac{3\rho \cdot {\omega }_{hm}^2}{160}\cdot \left(D_2^2-D_1^2+D_2^{0^2}-D_1^{0^2}\right),$$

(8)

where μ′ is the coefficient of dynamic viscosity of the working fluid; h is the gap formed between the contact surfaces of the fixed and movable distributors during their rotation (Figure 3c); Q_leak is leakage of the working fluid in the zone of the injection and drain, respectively; ρ is the density of the working fluid; and ω_hm is the angular velocity of the hydraulic motor shaft.

Substituting expressions (7) and (8) into (2) and performing the appropriate transformations, we obtain the dependence for determining the repulsion force F₂ of the fixed distributor:

$$\begin{array}{l}{F}_2=\frac{\pi }{4}\cdot p_5\cdot \left(D_5^2-D_2^2\right)+\left(p_6\cdot {\displaystyle \sum {\phi }_1}+p_7\cdot {\displaystyle \sum {\phi }_2}\right)\cdot \frac{\pi }{4}\cdot \left(D_2^{0^2}-D_1^{0^2}\right)+\left[\frac{12\mu }{h^3}\cdot \frac{Q_{\mathit{leak}}}{{\displaystyle \sum \left({\phi }_1+{\phi }_2\right)}}\cdot \left(\mathit{ln}\frac{D_2^0}{D_2}+\mathit{ln}\frac{D_1}{D_1^0}\right)\right.+\\ \left.+\frac{3\rho \cdot {\omega }_{Ƨм}^2}{160}\cdot \left(D_2^2-D_1^2+D_1^0{}^{{}^2}-D_2^0{}^{{}^2}\right)\right]\cdot \frac{\pi }{4}\cdot \left(D_2^2-D_1^2\right).\end{array}$$

(9)

The stability of the output parameters of the planetary-type HM in the steady state of operation depends on the quality of its distribution system, which is ensured by the interaction of the contact surfaces H₁ and H₂ of its distributors. The steady-state mode of operation of the planetary HM is characterized by the presence of a hydrodynamic force F_d that occurs during the rotation of the movable distributor. Therefore, in the gap h (Figure 3c) on the sealing bands b₁ and b₂ (Figure 4) of the movable and fixed distributors, an oil wedge forms from the oil film. Then, the performance of the distribution system of the planetary-type HM is ensured by the stability of the preload of the fixed distributor to the movable one, when the condition F₁ > F₂ is met.

However, excess of the resulting force F₁ over F₂ causes increased friction and wear of the contact surfaces H₁ and H₂ of the distributors. Thus, the pressing force F₁ must balance between the values that provide the conditions for creating an oil film in the gap h and the values that provide high-quality contact between the surfaces H₁ and H₂. Therefore, the sum of the pressing force F₂ and the hydrodynamic force F_d must balance the pressing force F₁, i.e., F₁ = F₂ + F_d. In general, most distribution systems of hydraulic machines are designed with incomplete hydrostatic unloading of the pressing force F₁, when the excess pressing force F₁–F₂ is balanced by the hydrodynamic force F_d.

To determine the hydrodynamic force F_d, the following assumptions are made:

−

The gap between the contact surfaces of the movable and fixed distributors is wedge-shaped;

−

The contact surfaces of the movable and fixed distributors are represented by the annular surfaces of the outer and inner sealing bands and are replaced by an equal square;

−

The law of oil wedge height change is assumed to be exponential;

−

The value of the coefficient of dynamic viscosity of the working fluid is taken to be constant.

Taking into account the assumptions made, the hydrodynamic force F_d is equal to:

$$F_d=\frac{{\mu }^{\prime }\cdot V^{\prime }\cdot {\left(L+l\right)}^3}{h_{\min }^2}\cdot K,$$

(10)

where V’ is the linear sliding speed of the center of gravity of the movable distributor, V’ = π/2 · n · (D₂ – D₁); L is the length of the side of the square of the outer sealing band, L = {π/4 · [(D₂)² – (D⁰₂)²]}^0.5; l is the length of the side of the square of the inner sealing band, l = {π/4 · [(D₁)² – (D⁰₁)²]}^0.5; and K is dimensionless coefficient of bearing capacity of the oil wedge:

$$\begin{array}{l}K=\frac{{\pi }^4}{4}\cdot e^{0.75\cdot \ln \frac{h_{\min }}{h_{\max }}}\cdot {\displaystyle \sum _{m,n=1,2,\dots }^{m=4,n=4}\frac{m\cdot \left[1-{\left(-1\right)}^n\right]\cdot \left[1-{\left(-1\right)}^m\cdot e^{-1.5\cdot \ln \frac{h_{\min }}{h_{\max }}}\right]}{n\cdot {\pi }^2\cdot \left[2.25\cdot {\left(\ln \frac{h_{\min }}{h_{\max }}\right)}^2+m^2\cdot {\pi }^2\right]}}\times \\ \times \frac{-4m\cdot e^{0.25\cdot \ln \frac{h_{\min }}{h_{\max }}}\cdot {\pi }^2\cdot \frac{\left(D_2-D_1\right)}{4}\cdot \left[1-{\left(-1\right)}^n\right]\cdot \left[1-{\left(-1\right)}^m\cdot e^{-0.5\cdot \ln \frac{h_{\min }}{h_{\max }}}\right]}{2n\cdot {\pi }^2\cdot \left(0.25\cdot {\left(\ln \frac{h_{\min }}{h_{\max }}\right)}^2+m^2\cdot {\pi }^2\right)\cdot \left[m^2+n^2\cdot \frac{2.25\cdot {\left(\ln \frac{h_{\min }}{h_{\max }}\right)}^2}{\pi }\right]\cdot \left(L+l\right)\cdot \frac{h_{\max }}{h_{\min }}}\cdot \ln \frac{h_{\min }}{h_{\max }}\end{array}$$

(11)

where e, m and n are dimensionless coefficients that determine the physical state of the oil wedge (determined experimentally); h_max, h_min are the maximum and minimum gaps between the contact surfaces H₁ and H₂ of the movable and fixed distributors.

Knowing the pressing force F₁ and repulsion F₂, it is possible to determine the minimum gap between the surfaces of the movable and fixed distributors:

$$h_{\min }=\sqrt{\frac{{\mu }^{\prime }\cdot \frac{\pi }{2}\cdot n\cdot \left(D_2-D_1\right)\cdot {\left(\sqrt{\frac{\pi }{4}\cdot \left(D_2^2-D_2^0{}^{{}^2}\right)}+\sqrt{\frac{\pi }{4}\cdot \left(D_1^0{}^{{}^2}-D_1^2\right)}\right)}^3}{F_1-F_2}\cdot K}$$

(12)

As a result of the action of the hydrodynamic force F_d, the performance of the distribution system of the planetary-type HM is determined by the leaks Q_leak in the end gap between the contact surfaces H₁ and H₂ of its distributors. Leaks Q_leak in the contact zone of the movable and fixed distributors arising from the formation of an oil wedge are determined from the expression [14], taking into account the corresponding transformations:

$$Q_{\mathit{leak}}=\frac{h^3}{12{\mu }^{\prime }}{\displaystyle \sum \left({\phi }_1+{\phi }_2\right)}\cdot \left[p_h\left(t\right)\cdot \frac{\left(\mathit{ln}\frac{D_1}{D_1^0}-\mathit{ln}\frac{D_2^0}{D_2}\right)}{\mathit{ln}\frac{D_1}{D_1^0}\cdot \mathit{ln}\frac{D_2^0}{D_2}}-\frac{3\rho \cdot {\omega }_{hm.}^2}{80}\cdot \left(\frac{\left(D_1^0{}^2-D_1^2\right)}{\mathit{ln}\frac{D_1}{D_1^0}}+\frac{\left(D_2^2-D_2^0{}^{{}^2}\right)}{\mathit{ln}\frac{D_2^0}{D_2}}\right)\right]$$

(13)

Then, the losses in the distribution system of the planetary-type HM can be defined as a change in its volumetric efficiency:

$${\eta }_{vol}=1-\frac{\frac{h^3}{12{\mu }^{\prime }}{\displaystyle \sum \left({\phi }_1+{\phi }_2\right)}\cdot \left[p_h\left(t\right)\cdot \frac{\left(\mathit{ln}\frac{D_1}{D_1^0}-\mathit{ln}\frac{D_2^0}{D_2}\right)}{\mathit{ln}\frac{D_1}{D_1^0}\cdot \mathit{ln}\frac{D_2^0}{D_2}}-\frac{3\rho \cdot {\omega }_{hm.}^2}{80}\cdot \left(\frac{\left(D_1^0{}^2-D_1^2\right)}{\mathit{ln}\frac{D_1}{D_1^0}}+\frac{\left(D_2^2-D_2^0{}^{{}^2}\right)}{\mathit{ln}\frac{D_2^0}{D_2}}\right)\right]}{\mu \cdot {\displaystyle \sum \left[\frac{\pi }{Z_2}-\left|{\beta }_i-{\alpha }_i\left(t\right)\right|\right]\cdot \frac{\left[{\left(\frac{D_2^0}{2}+b_2\right)}^2-{\left(\frac{D_1^0}{2}+b_1\right)}^2\right]}{2}\cdot \sqrt{\frac{2\cdot \left(p_6-p_7\right)}{\rho }}}}$$

(14)

Thus, to maintain the stability of the output parameters of the planetary-type HM in the steady state of operation, it is necessary to form the ratio of the pressing F₁ and repulsive F₂ forces, which ensures a qualitative interaction of the contacting surfaces H₁ and H₂ of its distributors. The required ratio of F₁ and F₂ is determined by the justification of the geometrical parameters of the annular surfaces of the movable and fixed distributors in order to form an oil film in the contact zone between the rotating surfaces H₁ and H₂. The substantiation of rational geometric parameters of the annular surfaces of the movable and fixed distributors provides an increase in the productivity of the distribution systems of PHM.

The steady-state mode of operation of the planetary HM is characterized by the presence of a hydrodynamic force F_d, that occurs during the rotation of the movable distributor. Therefore, modeling the steady-state operation of a planetary HM using the obtained mathematical apparatus will make it possible to quantify the increase in the productivity of its distribution system by substantiating the design parameters of the fixed and movable distributors.

3. Results

For rotary hydraulic machines, the force F₁ is 10–20% higher than F₂. According to experimental data obtained during the operation of planetary HM of the PRG series, the force F₁ exceeds F₂ by 10–11%. Therefore, in order to improve the performance of the planetary HM distribution system, the geometric parameters of the stepped surfaces of the movable and fixed distributors were determined by modeling the steady-state operating conditions of the HM.

The distribution system of planetary HM of the PRG series is structurally designed in such a way that the inner diameter D₁ of the movable distributor is limited by the dimensions of the HM shaft, and the outer diameter D₂ is limited by the dimensions of the bearing in which it rotates. Thus, the diameters D₁ and D₂ are determined taking into account the design features of a particular HM and limit the contact zone formed by the end surfaces H₁ and H₂ of the fixed and movable distributors (Figure 3c).

Knowing the diameters D₁ and D₂, as well as the size of the sealing belts b₁ and b₂, the inner and outer diameters are determined, which limit the dimensions of the distribution windows: D⁰₁ = D₁ + 2 · b₁, D⁰₂ = D₂ + 2 × b₂. For planetary HM, it is recommended to take the width of the sealing belts within 1.5–5 mm.

To ensure the reverse movement of the shaft of a planetary-type HM, the working fluid (under discharge pressure) can be supplied to the fixed distributor both through channel C₁ and through channel C₂. Therefore, when reversing the hydraulic motor shaft, in order to ensure the same clamping force of the fixed distributor, the areas of the annular surfaces on which the discharge pressure applied through the channels C₁ or C₂ must be equal. The equality of the areas of the stepped annular surfaces of the fixed distributor formed by the diameters D₃, D₄ and D₅, respectively, is achieved when the condition (D₅)² − (D₄)² = (D₄)² − (D₃)² is fulfilled. Hence, the diameter D₅, which determines the overall dimensions of the fixed distributor, will be equal to: D₅ = [(D₄)² − (D₃)²]^0.5. The diameters D₃, D₄ and D₅ of the stepped surfaces of the fixed distributor are calculated when determining the clamping force F₁ (Figure 3c).

Modeling of the distribution system operation was carried out on the example of a planetary HM of the PRG series, with serial and modernized distribution systems, based on the obtained mathematical apparatus, taking into account the set of geometric parameters of its distributors.

The developed mathematical model (Figure 5), which describes the steady-state operation of the planetary HM, makes it possible to simulate the ongoing processes depending on the design features of the elements of its distribution system using the VisSim dynamic simulation system.

The initial data are given in block 1 (Figure 5), which is standard for introducing the initial conditions of the simulation [73,75]. Block 2 allows you to determine the relative position of the windows of the movable and fixed distributors, as well as the angles that limit the overlap zone of the distribution windows [15,73,75]. Block 3 allows you to determine the angles φi, limiting the geometric parameters of the windows of the movable and fixed distributors involved in the overlap, described by expression (6). The determination of the change in leakage in the end gap of the distribution system in block 4 is implemented using expression (13). The change in volumetric efficiency, described by expression (14) at any time, is determined in block 5.

For modeling, the characteristics and design parameters of the elements of the distribution system of a serial planetary HM of the PRG-22 series with a working volume V equal to 160 cm³ were selected. Below are the initial conditions and initial data for describing the processes occurring in the distribution system of the planetary-type HM in steady state.

The modernized HM differs from the serial one only in the distribution system. At the same time, the number of windows of the movable and fixed distributors (kinematic scheme [47]) remained unchanged. The flow rate Q_p of the working fluid passing through the hydraulic motor (pump delivery) was Q_p = 100 l/min = const. The pressure at the inlet to the hydraulic motor (at the outlet of the pump), as well as at the inlet to the safety valve, is equal to the nominal pressure, i.e., p_p(out) = p_hm(in) = p_v(in) = p_nom = 16 MPa [75]. The pressure at the outlet (at the outlet) of the HM and the pressure at the outlet (at the outlet) of the safety valve, equal to zero, i.e., p_hm(out) = p_v(out) = 0 MPa [75]. The load Mload on the shaft of the planetary hydraulic motor was assumed to be constant and equal to M_load = 365 N·m = const; the inertial component is absent [75].

In the serial planetary HM of the PRG-22 series, the pressing force F₁ in the contact zone (Figure 3c) exceeded the repulsive force F₂ by 10–11%, i.e., F₁ = 1.1–1.11 F₂. The geometric dimensions of the stepped annular surfaces of the fixed distributor of the modernized planetary HM, which form the given clamping force F1, were calculated from the condition that F₁ = 1.06–1.07 × F₂. This relationship between pressing and pressing forces was determined experimentally for distributors with different contact surfaces. Therefore, the condition for increasing the productivity of the distribution system and maintaining its performance for planetary HM of the PRG-22 series will look like this:

$$1.06\le \frac{F_1}{F_2}\le 1.07$$

(15)

At the first stage of the comparative studies of serial and modernized HM, dependencies were obtained that characterize the change in leakage through the end clearance in the contact zone of the planetary HM distribution system. Analysis of the results of the studies (Figure 6a) shows that a decrease in clamping force by 3–5% in the modernized distribution system allows to reduce leakage through the end gap from 147 to 109 cm³/s, while maintaining the oil film between the contact surfaces of the distributors. The decrease in leakage by 26% in the distribution system is explained by the reduction of the oil wedge in the contact zone in the steady-state operation of the planetary HM, which ensures constant contact between the end surfaces of the movable and fixed distributors.

At the second stage of the research, the task was to determine the quantitative value of increasing the productivity of the modernized distribution system of the planetary HM by reducing its volumetric losses expressed through volumetric efficiency. Analysis of the obtained research results (Figure 6b) shows that the reduction of leakages in the end gap of the contact zone of a planetary-type HM distribution system allows to increase its volumetric efficiency from 0.912 to 0.934. The increase in the volumetric efficiency of the distribution system determines the increase in the productivity of the distribution system of a planetary-type HM by 2.4%.

Thus, it can be stated that the steady-state mode of operation of the planetary HM is characterized by the presence of a hydrodynamic force F_d that occurs during the rotation of the movable distributor. At the same time, the stability of the output parameters of the planetary-type HM in the steady state of operation depends on the quality of the contact between the rotating surfaces H₁ and H₂ of the fixed and movable distributors. Substantiation of rational geometric parameters of the annular surfaces of the movable and fixed distributors provides an increase in the productivity of the distribution systems of PHM.

In this regard, the results of the studies have shown that with rational design of the elements of the distribution system of a planetary-type HM, reducing the clamping force by 3–5% in the modernized distribution system can reduce leakage through the end clearance by 26%. Reducing leakage in the contact zone allows you to increase the performance of the distribution system by 2.4% by increasing its volumetric efficiency (reducing losses).

4. Discussion

In energy-efficient mechatronic systems of self-propelled vehicles, which correspond to modern innovative programs of technological development, planetary orbital and gerotor hydraulic machines are increasingly used as HM. The output characteristics of these hydraulic machines allow them to be used without additional gearboxes.

One of the main disadvantages of orbital and PHM is the instability (unevenness) of their output characteristics, caused by the imperfection of their distribution systems, which are a device for forming a hydraulic field (Figure 2) by supplying and draining the working fluid into the working chambers in a certain sequence. The imperfection of distribution systems, determined by the presence of hydraulic and volumetric losses caused by irrational pressing of a fixed distributor to a movable one, is considered in the example of planetary HM of the PRG series.

An analysis of literary sources has shown that there is a very limited number of studies aimed at ensuring the stability of the output parameters of PHM (orbital). Therefore, another objective of this work is to popularize ongoing research related to the use of gerotor technologies in hydraulic drives of mechatronic systems of self-propelled vehicles in order to promote this exciting field of research for young researchers and graduate students around the world. However, one must take into account the fact that the planetary (orbital) HM is a structure consisting of a gearbox and a liquid distribution device. In this case, the gearbox has a special cycloidal gearing that forms the working chambers, and the distribution device ensures the supply of the working fluid to these chambers. Therefore, if you can still find scientific publications about the gearboxes of planetary (orbital) HM, then there are simply no publications about the distribution systems of these HM.

In support of the above, it is necessary to add that the largest European manufacturer of orbital HMs is Danfoss, which has been producing these hydraulic machines for more than 50 years. However, at the same time, we did not find a single scientific publication (except for commercial catalogs) related to the calculation, design and operation of the hydraulic machines produced by them, as well as the authors [18]. We assume that this information is a trade secret and therefore is not “advertised”.

It should also be noted that over the entire period under review, the manufactured hydraulic machines have not changed structurally, which indicates both a monopoly on the market for manufactured products and a monopoly on scientific research. This is confirmed by the “policy” of such a global manufacturer as China, which managed to “copy” and produce thousands of products, but today there are no planetary (orbital) HM under the brand of a Chinese manufacturer; only licensed HM are produced. This is despite the fact that the entire world’s mechanical engineering annually consumes thousands of these HM to drive the active working bodies of all manufactured self-propelled equipment. I would like to note that issues related to the calculation, design and operation of planetary (orbital) hydraulic machines and their elements are practically a “pioneer” direction in the development of a modern hydraulic drive.

The substantiation of rational geometrical parameters of the elements of the distribution system, providing an increase in its productivity, included three stages. At the first stage, design schemes, mathematical apparatus, restrictions and assumptions were developed to determine the rational contact force of the elements of the distribution system, which ensures an increase in its productivity. At the second stage, a structural and functional diagram of a mathematical model was developed to study the processes occurring in the distribution system during the operation of a planetary HM. At the third stage, the influence of the design features of the elements of the distribution system on the change in the output parameters of the planetary-type HM was studied.

The result of the development of the scheme of forces acting in the distribution system of the planetary-type HM (Figure 3c) and the calculation scheme for determining the overlap areas of the distribution windows in the contact zone (Figure 4) are the obtained mathematical dependencies. The developed mathematical apparatus makes it possible to determine the rational pressing forces F₁ and repulsion F₂ formed by the action of the working fluid on the stepped surfaces of the fixed distributor. The interaction of the forces of pressing F₁ and repulsion F₂ determines the stability of the output characteristics of the planetary-type HM in the steady state of operation, providing a high-quality interaction of the contact surfaces H₁ and H₂ of its distributors.

It should be noted that in the steady-state operation of the planetary HM, when the movable distributor rotates, a hydrodynamic force F_d acting in the gap h (Figure 3c) arises. Due to the action of the hydrodynamic force F_d, an oil wedge is formed on the sealing bands b₁ and b₂ (Figure 4) of the movable and fixed distributors. Then, the performance of the distribution system of the planetary-type HM is ensured by the stability of the compression of the fixed distributor to the movable one, subject to the condition F₁ > F₂. Therefore, the sum of the repulsive force F₂ and the hydrodynamic force F_d must balance the pressing force F₁, i.e., F₁ = F₂ + F_d, which was not taken into account in previous studies.

The next stage of the study was to determine the leakage rate Q_leak in the gap between the contact surfaces H₁ and H₂ (Figure 3c) of the elements of the distribution system, as well as changes in the volumetric efficiency of the planetary HM. Moreover, the gap between the contact surfaces of the movable and fixed distributors was determined taking into account the bearing capacity coefficient of the oil wedge, and the leakage in the contact zone that occurs during the formation of the oil wedge was determined taking into account the action of the hydrodynamic force F_d. A quantitative assessment of the increase in the productivity of the distribution system of a planetary-type HM was obtained as a result of modeling a steady-state operation using the developed mathematical apparatus and a mathematical model for determining volumetric losses in the end distribution system.

As a result of the research, it was found that the rational design of the elements of the distribution system makes it possible to reduce the clamping force by 3...5%, provided that the condition 1.06 ≤ F₁/F₂ ≤ 1.07 is met. Such a ratio of pressing F₁ and repulsive F₂ forces made it possible to reduce leakage through the gap h in the distribution system of the planetary HM by 26%. Such a reduction in the Q_leak flow rate in the gap between the contact surfaces H₁ and H₂ made it possible to increase the performance of the distribution system by 2.4% by reducing losses (increasing volumetric efficiency) of the planetary HM.

5. Conclusions

The functioning of many branches of modern industry is regulated by various development programs that involve the use of innovative technologies and optimization of existing approaches, which contributes to the sustainable, energy-efficient development of related industries and the economy. The use of energy-efficient hydraulic motors in mechatronic systems and running modules of self-propelled machines, industrial machines, robots, etc., which are used in various sectors of the European economy, will contribute to the practical implementation of the philosophy of the “European Green Deal”.

In order to determine the geometric parameters of the stepped surfaces of the movable and fixed distributors to ensure the formation of an oil film in the contact zone, design schemes, a mathematical apparatus and a structural-functional scheme of the mathematical model have been developed. The developed measures make it possible to determine the rational force in the contact zone of the movable and fixed distributors during their design. Rational force in the contact zone provides an increase in the performance of the distribution system and the efficiency of the HM as a whole.

The conducted studies have established that with the rational design of the elements of the distribution system due to the reduction of the clamping force by 3–5% in the distribution system, the leakage through the end gap is reduced by 26%. Reducing the leakage in the contact zone allows to increase the productivity of the distribution system by 2.4% due to the increase in volumetric efficiency (reduction of losses) of the planetary HM.