Advances in the Co-Simulation of Detailed Electrical and Whole-Building Energy Performance

Abstract

This article describes recent co-simulation advances for the simultaneous modeling of detailed building electrical distribution systems and whole-building energy performance. The co-simulation architecture combines the EnergyPlus^® engine for whole-building energy modeling with a new Modelica library for building an electrical distribution system model that is based on harmonic power flow. This new library allows for a higher-fidelity modeling of electrical power flows and losses within buildings than is available with current building electrical modeling software. We demonstrate the feasibility of the architecture by modeling a simple, two-zone thermal chamber with internal power electronics converters and resistive loads, and we validate the model using experimental data. The proposed co-simulation capability significantly expands the capabilities of building electrical distribution system models in the context of whole-building energy modeling, thus enabling more complex analyses than would have been possible with individual building performance simulation tools that are used to date.

1. Introduction

The value of using building performance simulation to understand and optimize the mechanical and thermal performance of buildings is well established. Recent trends in building performance simulation research have increased the interest in similar high-fidelity models for building electrical performance, such as detailed electrical load behavior and distribution system efficiency. Grid-interactive efficient building applications require energy-consumption trends at hourly or subhourly time steps, rather than at monthly or annual intervals [1]. Similarly, utility planning activities—such as energy efficiency incentive planning, transmission and distribution planning, and policy and rate design—often need 15 min interval data and energy consumption estimates by end use [2]. In these applications, the ability to accurately represent the electrical performance of building loads and the building distribution system complements the thermal and mechanical system models currently in use.

Accurate and detailed building electrical distribution system models provide a variety of benefits, both for traditional energy efficiency analysis and grid-interactive efficient building applications [3]. Modelers are able to compare the efficiency of different distribution topologies; this capability is useful in evaluating the benefits of direct current (DC) distribution systems with and without on-site photovoltaic (PV) generation [4,5,6,7]. Electrical simulation also more accurately models reactive power consumption (useful for grid planning; (confer [2]) and provides granular insight into the building-scale impacts of utility control strategies, such as conservation voltage reduction, which are usually only analyzed at the utility scale [8,9].

Finally, electrical distribution system models enable investigation of the interaction between electrical systems and heating, ventilation, and air conditioning (HVAC) systems, allowing researchers to answer the following question: can higher-efficiency electrical distribution systems reduce building cooling load, thereby contributing to additional energy savings? In high-performing buildings, the magnitude and timing of heat gains from electrical loads have a substantial impact on building performance [10]. The same is true for data centers: increasing the efficiency of energy delivery substantially reduces cooling load and HVAC consumption [11,12]. Research of other building types has found that, in cooling-dominated climates, the reduction in cooling energy attributable to more efficient electrical distribution outweighs the increase in heating energy, thus delivering more energy savings overall than the electrical distribution savings alone [13]. These research efforts all required some degree of sequential or co-simulation to evaluate the combined electrical and thermal performance of the buildings studied.

A rich body of research has leveraged the Modelica language [14,15] to enable co-simulations of building systems. Implementations have evolved from bespoke, engine-to-engine translators to middleware-based architectures [16,17] to interoperable modules that are based on the open Functional Mock-up Interface (FMI) standard for co-simulation and model exchange [18,19]. To date, these efforts have focused on robust co-simulations of the building envelope, HVAC, other mechanical systems, and building control algorithms [20,21,22]. The Modelica Standard Library provides a basic set of electrical component models. The Modelica Buildings Library also includes an electrical package [23]; however, the simplified models used are better suited to traditional utility-scale transmission and distribution system analysis than to detailed performance evaluation of building electrical distribution systems.

In this article, we describe an advance in co-simulation capability that combines the existing strengths of EnergyPlus^® [24] for whole-building energy simulations with the Building Electrical Efficiency Analysis Model (BEEAM), a newly developed Modelica library for the harmonic power-flow simulation of building electrical distribution systems [25,26]. The co-simulation capability leverages the FMI standard and is compatible with any Modelica-based co-simulation workflow. It unlocks more detailed modeling and co-simulations of building electrical distribution system performance than has previously been available. We first describe the technical implementation of the co-simulation workflow. We then demonstrate the workflow using a simple two-zone thermal chamber with internal power electronics converters and resistive loads. We present the model architecture, a demonstration model, simulation results, and validation using experimental measurements.

2. Methods

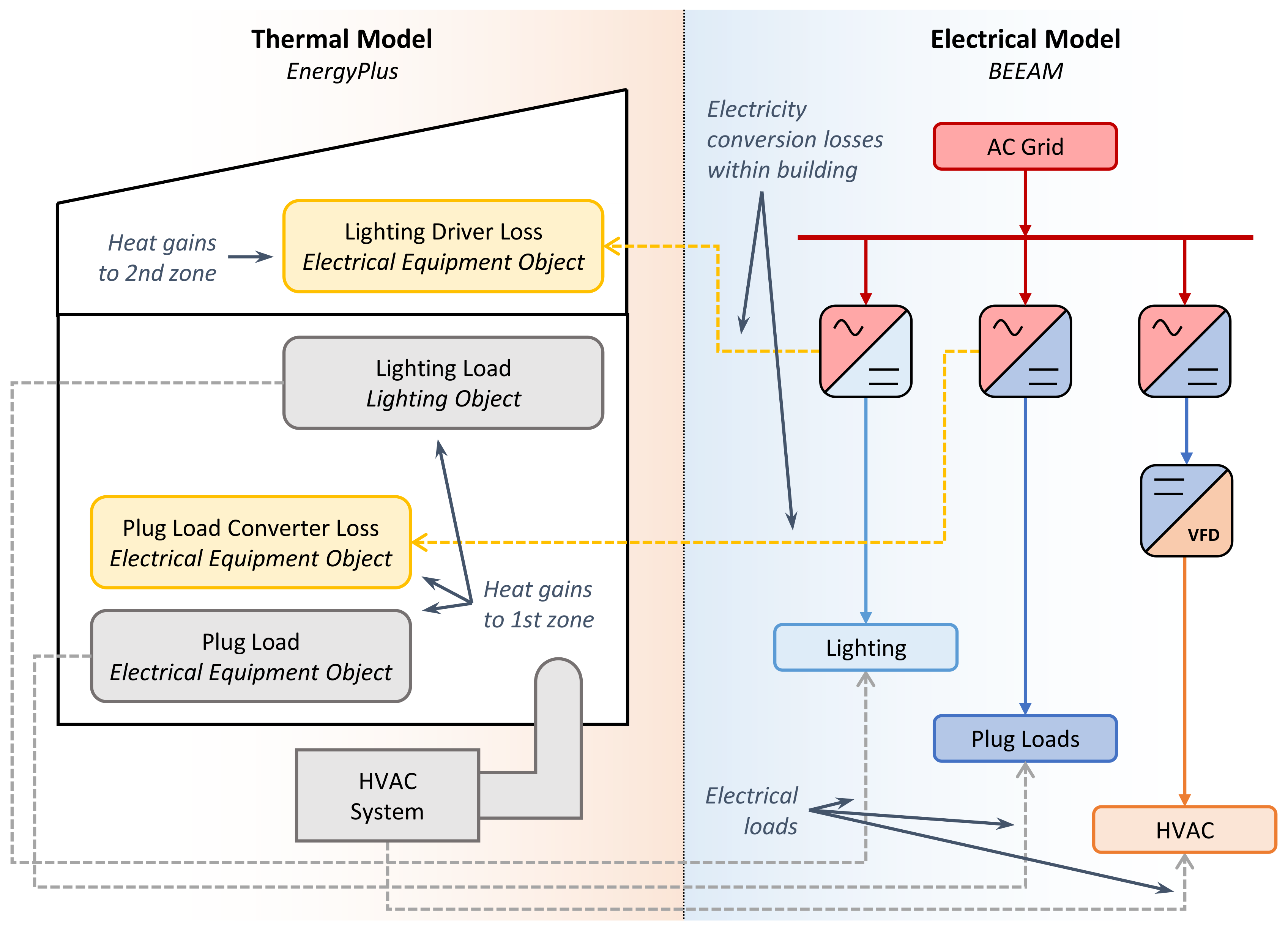
2.1. Model Architecture

In co-simulations, multiple simulation engines, or simulators, are coupled such that they exchange data via state variables. The purpose of co-simulation is to allow each engine to simulate, in detail, those aspects of the model that they are best suited to represent. The proposed co-simulation capability couples a recent version of EnergyPlus [27] with the newly developed BEEAM Modelica library [26]. EnergyPlus can model most aspects of whole-building energy performance, such as heat gains from building loads, heat transfer, and HVAC system performance. The BEEAM models the details of building electrical distribution system performance, including power flows, harmonics, and system efficiency.

In EnergyPlus, lighting and miscellaneous electrical loads are typically driven by schedules, whereas HVAC system loads (both thermal and electrical) are calculated based on the building’s internal heat gains, heat exchange with the surrounding environment, and the HVAC equipment’s performance characteristics. Like loads, electrical losses within the building distribution system contribute internal heat gains to the building. However, electrical distribution losses are rarely incorporated into whole-building energy models, in part because few tools exist which accurately predict such losses. In the proposed co-simulation architecture (Figure 1), calculated electrical distribution system loads are an output from EnergyPlus and an input to the BEEAM, while calculated electrical distribution system losses are an output from the BEEAM and an input to EnergyPlus. Data exchange is performed using the FMI standard version 2.0 [19]; see Section 2.1.3.

The proposed architecture captures the zone-level interaction among the building internal loads, the heating and cooling demand placed on the HVAC system, electricity demand, and losses in the building electrical distribution system. These quantities are interdependent; electrical distribution losses affect HVAC load, HVAC load affects electricity demand, and electrical demand affects electrical distribution losses. For certain electrical distribution topologies, distribution system losses are non-trivial, and failing to model them degrades the accuracy of the building energy-consumption estimates [4]. Co-simulation allows the modeler to simultaneously represent both the electrical and thermal behavior of the building accurately and in detail. This increases model accuracy and enables higher-fidelity analyses of building performance. Examples of questions that can be answered with the proposed architecture include the following:

• How does the coincidence of on-site PV generation and building load influence the efficiency of energy delivery?
• What is the impact of Power-over-Ethernet switch and cabling losses on zone cooling demand?
• What is the overall energy efficiency of AC versus DC distribution for data centers?

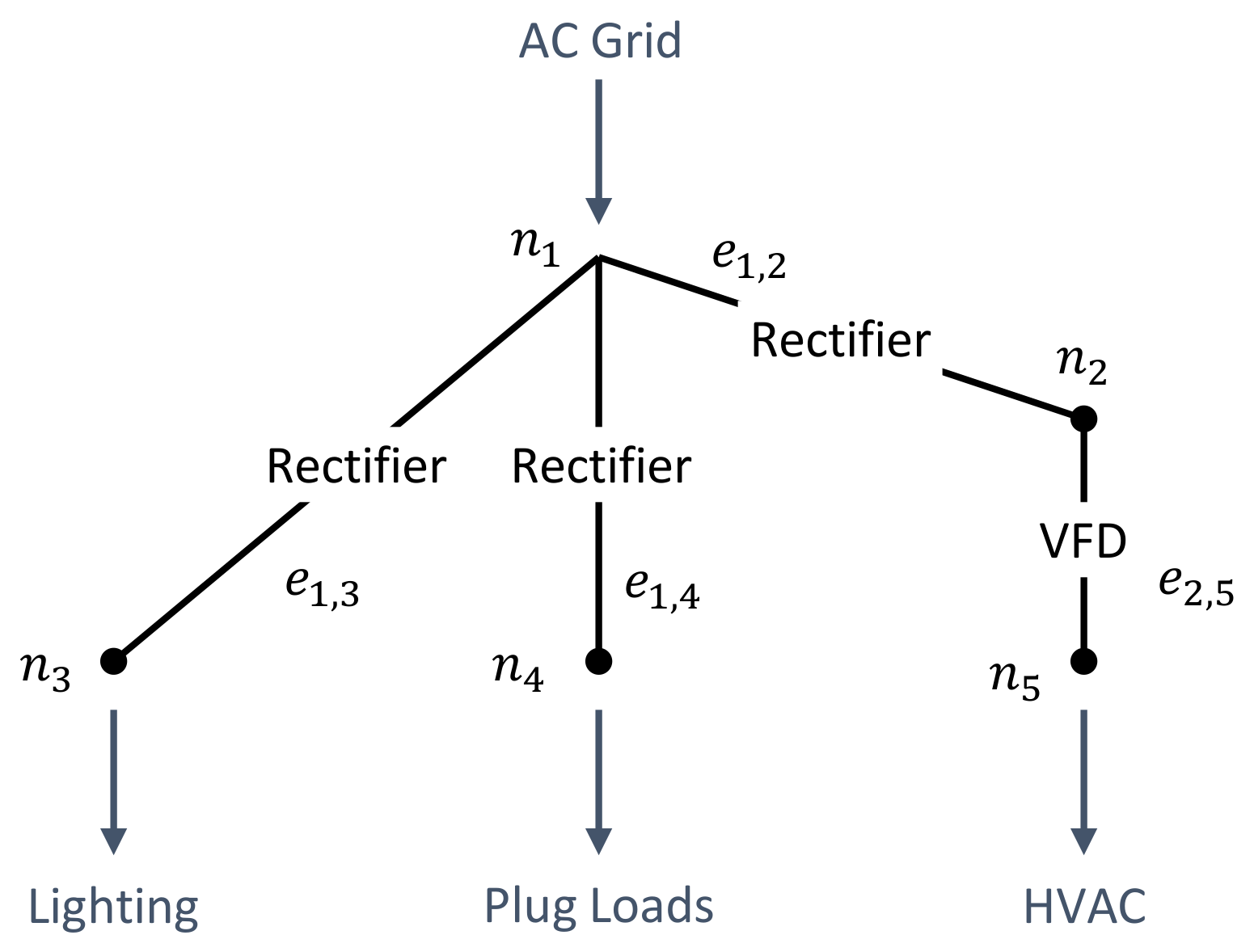
2.1.1. Electrical Simulation

The components of the proposed electrical distribution system were modeled using the BEEAM library, which was developed by several contributing authors [26]. The BEEAM models electrical distribution systems in buildings, including conventional alternating current (AC), direct current (DC), and hybrid systems. A major focus of the library is the accurate modeling of the behavior of distribution systems containing nonlinear power electronic loads and sources. Conventional power-system analysis techniques do not adequately model nonlinear loads because their underlying assumption is that the devices in the distribution system are linear (no waveform distortion): existing tools for modeling building electrical distribution systems, such as the electrical package of the Modelica Buildings Library [23] or the conventional power flow model in ESP-r [28], model AC power system voltages and currents at the fundamental frequency only (typically 50 Hz or 60 Hz). In contrast, a realistic representation of the power of electronic devices requires modeling of the nonlinear (distorted) waveforms they produce and the downstream effects on electrical distribution system equipment. Harmonic power flow (HPF) models capture these nonlinear effects by modeling system voltage and currents not only at the fundamental frequency, but also at its multiples, or “harmonics”, through using a Fourier transformation to accurately represent the distorted waveforms in the frequency domain. The BEEAM’s representation of an electrical distribution system is an extension of HPF. In addition, the BEEAM constructs electrical distribution models with interconnected 2-port and 1-port networks. This is a more flexible representation than existing tools, which typically assume a pre-determined network topology (single-phase, balanced three-phase, etc.).

In comparison to existing tools, the BEEAM therefore provides the following benefits:

• Ability to flexibly model arbitrary electrical distribution topologies (AC or DC, or single-phase or multi-phase) alone or in combination;
• Ability to flexibly model arbitrary power flows between the electric grid, loads, on-site PV generation, and on-site storage;
• Robust and accurate modeling of harmonic voltage and currents;
• Accurate representation of the highly nonlinear behavior of power electronics converters;
• Ability to compute component-level losses throughout the building electrical distribution system.

Conceptually, the BEEAM models a building electrical distribution system as a directed graph consisting of electrical buses (nodes) and branches (edges). For example, Figure 2 shows a graph with five nodes and four edges, which captures the topology of the five-bus, four-branch electrical distribution system shown in Figure 1.

The power-flow relationships within such a system may be summarized by the pair of equations as follows:

$$\begin{array}{cc}\hfill \sum _{s\in {\mathcal{S}}_i}{P}_{\mathrm{Source},s}-\sum _{\ell \in {\mathcal{L}}_i}{P}_{\mathrm{Load},\ell }& =\sum _{i,k\in {\mathcal{B}}_i}{P}_{\mathrm{Branch},i\to k}\forall i\in \mathcal{N}\hfill \end{array}$$

(1)

$$P_{\mathrm{Branch},i\to k}+P_{\mathrm{Branch},k\to i}=P_{\mathrm{Loss},i,k}\left(P_{\mathrm{Branch},i\to k},P_{\mathrm{Branch},k\to i},\dots \right)\forall i,k\in \mathcal{B}$$

(2)

Sets $\mathcal{N}$ and $\mathcal{B}$ represent all buses and branches in the power system, respectively. The bus power balance Equation (1) states that for each bus $i\in \mathcal{N}$, the total generated power $P_{\mathrm{Source},s}$ entering the node from sources $s\in {\mathcal{S}}_i$ is connected at the bus minus the total consumed power $P_{\mathrm{Load},\ell }$, thus leaving the node to loads $\ell \in {\mathcal{L}}_i$, which are connected at the bus and are equal to the sum of power leaving the node via the system branches. In (1), $P_{\mathrm{Branch},i\to k}$ (which may be positive or negative) describes the power at bus i flowing toward bus k, which is leaving bus i and entering branch $i,k$, and ${\mathcal{B}}_i$ describes the set of branches $i,k$ that are connected to node i. Equation (2) states that the branch electrical loss $P_{\mathrm{Loss},i,k}$, which is a function of the power flows associated with the branch and other variables, equals the sum of power flows entering each end of the branch. These equations omit many modeling details, such as voltage, current, reactive power, harmonics, and the electrical laws that define the behavior of linear and nonlinear system branches. Although greatly simplified, Equations (1) and (2) are sufficient to describe the relationships needed for co-simulation (see Section 2.1.3). Othee et al. [25] provided a full mathematical treatment of the BEEAM, including equations for voltage-current relationships, power balance, transformer ratios, and converter losses (AC/DC, DC/DC, and DC/AC).

The BEEAM leverages the HPF technique to solve the system of equations that define the distribution system behavior. Prior research by contributing authors has shown that HPF strikes a balance between accuracy and computational efficiency in modeling electrical systems that contain power electronics converters and other nonlinear loads [29]. Like conventional power flow, HPF models the electrical distribution system in the frequency domain through using a set of complex algebraic equations (recall that whereas conventional power flow models the system fundamental frequency, HPF models multiple frequencies). Systems of nonlinear algebraic equations can be solved with nonlinear iterative techniques, such as Newton–Raphson, without requiring numeric integration (Figure 3).

Therefore, power flow (both conventional and HPF) enjoys a substantial advantage in computational efficiency compared to the time-domain simulation of AC systems. The BEEAM uses adjacent equations to represent the nonlinear device behavior and conversion efficiency as the voltage, current, and power interactions among the harmonic frequencies. This enables the library to accurately represent highly nonlinear waveforms such as those produced by single-phase power electronics converters. The BEEAM includes models for a variety of power electronics converters, include rectifiers, inverters, bi-directional AC/DC converters, and DC/DC converters.

The BEEAM is implemented as a Modelica library. Modelica is an object-oriented, equation-based modeling language that describes the physical systems to be simulated as a collection of simultaneous equations [14]. Typically, these equations represent the underlying physics of the system and are organized hierarchically using a set of interconnected blocks. The equations in these blocks result in a system of differential-algebraic equations, which are solved using various numerical methods. The advantage of using Modelica is that the modeler can focus on the fundamental physics of the system (in this case, the HPF equations) and offload the task of providing a numerical solution to the model for a specific Modelica implementation. The BEEAM has been tested with both the open-source OpenModelica [30] and commercial Dymola [31] implementations of Modelica.

2.1.2. Building Energy Simulation

EnergyPlus is a whole-building energy simulation program developed by the U.S. Department of Energy., and it was first released in 2001 [24]. EnergyPlus includes several algorithms for simulating heat and mass balance, and it allows for the detailed simulation of building thermal envelopes, HVAC systems (e.g., fans, heating coils, and cooling coils), and central plant components (e.g., boilers, chillers, and pumps). EnergyPlus has been validated using ASHRAE Standard 140 [32].

EnergyPlus describes the energy balance of building thermal zones via

$$C_z\frac{d{T}_z}{dt}=\sum _{\ell =1}^{N_{\mathrm{Loads}}}{\dot{Q}}_{\ell }+\sum _{s=1}^{N_{\mathrm{Surf}}}{h}_s{A}_s\left(T_s-T_z\right)+\sum _{i=1}^{N_{\mathrm{Zones}}}{\dot{m}}_i{C}_p\left(T_i-T_z\right)+{\dot{m}}_{\infty }{C}_p\left(T_{\infty }-T_z\right)+{\dot{Q}}_{\mathrm{sys}}$$

(3)

in which $T_z$ is the zone temperature, $C_z\frac{d{T}_z}{dt}$ represents the energy stored in the zone air, ${\dot{Q}}_{\ell }$ represents the internal heat gains from loads in the zone, $h_s{A}_s\left(T_s-T_z\right)$ represents the convective heat transfer from zone surfaces, ${\dot{m}}_i{C}_p\left(T_i-T_z\right)$ represents heat transfer due to interzone air mixing, ${\dot{m}}_{\infty }{C}_p\left(T_{\infty }-T_z\right)$ represents heat transfer due to outside air infiltration, and ${\dot{Q}}_{\mathrm{sys}}$ represents the heat energy delivered by zone air systems (adapted from Equation (2.1) [33]). Heat gains from internal loads ${\dot{Q}}_{\ell }$ are a function of building services and occupant behavior, ${\dot{Q}}_{\mathrm{sys}}$ is a function of the building’s HVAC system performance and is related to the HVAC input energy, and the other expressions represent the heat transfer between zones. Similar equations exist for radiative forcing. EnergyPlus also models many other relationships within the building, but the zone energy balance is most relevant for understanding co-simulations with the BEEAM.

2.1.3. Co-Simulation Implementation and Data Exchange

The electrical loads and losses in a building’s distribution system relate directly to the heat gains in the building zones. Co-simulation requires mapping the electrical model to the thermal model and vice versa:

$$P_{\mathrm{Load},\ell }=f\left({\dot{Q}}_{\ell },{\dot{Q}}_{\mathrm{sys}},\dots \right)$$

(4)

$${\dot{Q}}_{\ell }=g\left(P_{\mathrm{Load},\ell },P_{\mathrm{Loss},i,k},\dots \right)$$

(5)

Equations (4) and (5) are conceptual; their exact implementation varies by building and component. For example, the energy consumption from electrical lights in a zone driven by a schedule in the whole-building energy model (EnergyPlus) might be mapped to the load imposed on a particular lighting circuit in the electrical distribution model (BEEAM). Similarly, the same lighting load might induce driver losses (modeled in the BEEAM), which correspond to the heat gains in the plenum above the building zone that the lights serve (modeled in EnergyPlus). These interdependencies in turn affect the thermal (heating or cooling) load on the building’s HVAC system.

The FMI standard [34] allows for the exchange of this information between simulation tools via co-simulation, in which each model has a built-in solver, or via model-through-model exchange, in which the models require an external solver. A simulation or model exported using this standard is called an a functional mockup unit (FMU). A co-simulation FMU is, in essence, a black box executable program that computes model outputs when given the correct input connections and is driven by a controlling simulation manager. This has the advantage in that complicated simulation workflows and numerical solvers can be pre-packaged or compiled into an FMU, which are then used within an equation-oriented environment such as Modelica. The beauty of this approach is that mapping functions f and g may be tailored as needed to the specifics of the building being modeled without a need for re-imagining the internal implementation of either simulation engine.

The specific co-simulation configuration used for this work was an electrical model created within Dymola with an embedded EnergyPlus FMU. Figure 4 depicts this arrangement for the demonstration model described in the following section. Appendix A describes the technical implementation of the co-simulation.

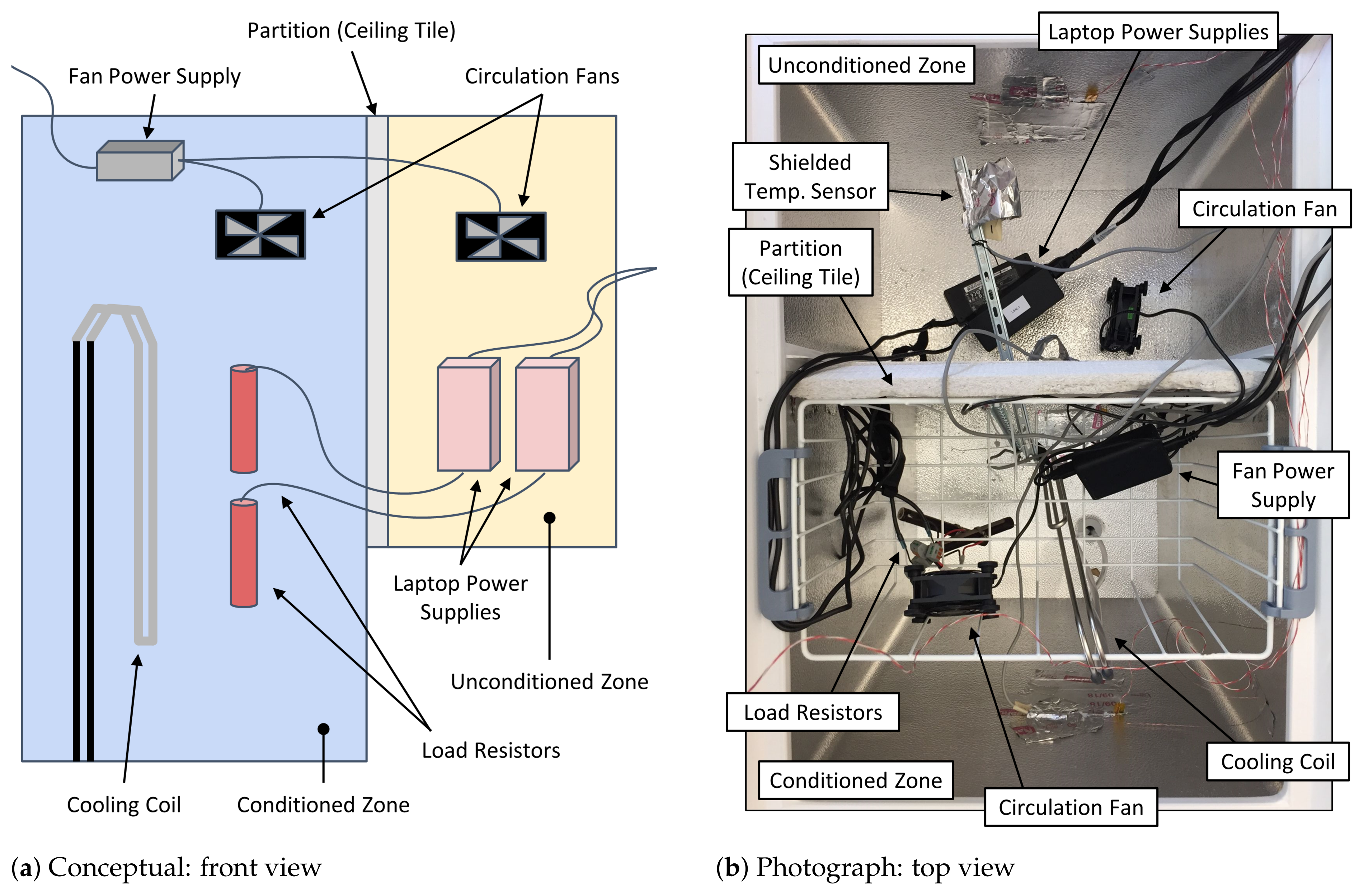
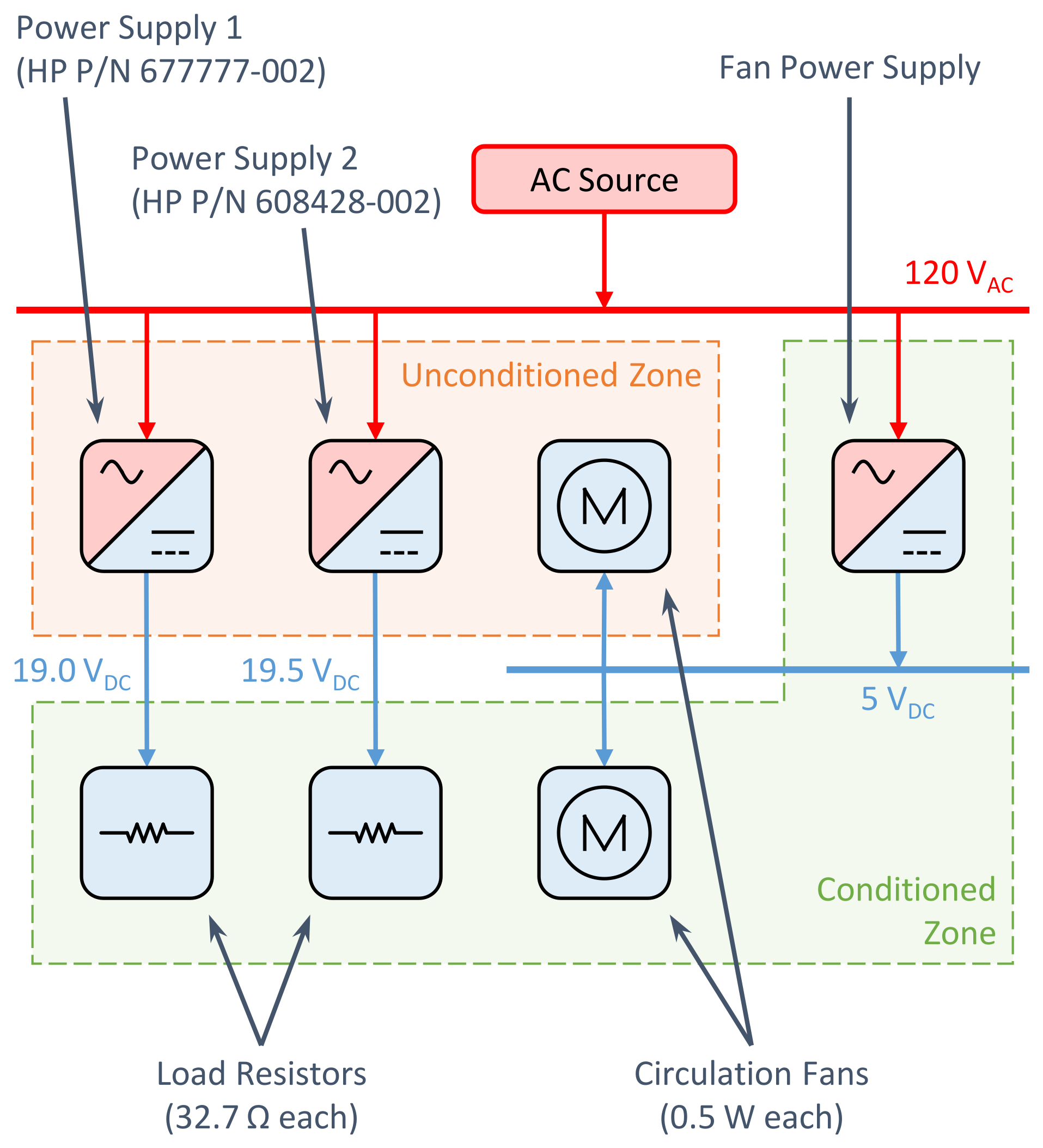
2.2. Validation Experiment

To demonstrate the proposed co-simulation capability and to validate the accuracy of the data exchange mechanism, we modeled the behavior of a two-zone thermal chamber with internal electrical loads, as well as validated the model using a series of laboratory experiments. Although simple, the experiment provides concrete examples of mapping functions f and g, which are described by (4) and (5), and therefore demonstrate a complete electrical–thermal co-simulation model.

The experimental thermal chamber used was a Steca PF-166 chest refrigerator. The chamber was partitioned internally into conditioned and unconditioned zones. The conditioned zone was cooled via a simple cooling water loop and coil; the unconditioned zone had no direct cooling. Both zones had internal heat gains produced by a simple electrical distribution system consisting of power electronic converters, fans, and resistive loads. Figure 5 displays the physical layout of the experiment. We modeled the thermal chamber and cooling loop using EnergyPlus, and the electrical devices were modeled using the BEEAM. Section 2.2.1 and Section 2.2.2 describe the electrical and thermal models, respectively.

The configuration of the electrical devices approximately mimics the configuration of a building with loads in a conditioned space (e.g., light-emitting diode [LED] lighting in an occupied room) and power electronics conversion equipment in an adjacent, unconditioned space (e.g., LED drivers in a plenum). The load in the conditioned zone consisted of two  $32.7$ $\mathsf{\Omega }$ load resistors; each load resistor was connected to the output of a laptop power supply (AC/DC converter), which was located in the unconditioned zone. The two power supplies used in the experiment were Hewlett Packard (HP) models 677777-002 and 608428-002, each rated at 90 W and with nominal output voltages of $19.5$ VDC and $19.0$ VDC, respectively. The load resistors consumed approximately 11 W each. Each zone was well mixed using a small 5 VDC fan; each fan consumed approximately $0.5$ W. The two fans were fed from a small, dedicated AC/DC power supply located in the conditioned zone. A Chroma 66205 digital power meter measured the total electrical input power.

Similar to a building, the thermal chamber’s internal thermal mass and insulation (R-value) vary across the physical space. The aggregate R-value of the chamber envelope was approximately 2.9 m${}^2$K/W, and the R-value of the ceiling tile used as a vertical partition was approximately 0.26 m${}^2$K/W. The conditioned zone used a liquid cooling system, with water pumped through a cooling coil from a cooling water reservoir. The cooling water reservoir contained a fixed mass of water that was continually cycled through the cooling coil, causing the cooling water temperature to rise as it absorbed heat energy from the thermal chamber. During the experiments, an Endress-Hauser Picomag flow meter measured the cooling water flow rate, and an Onset HOBO data logger with multiple temperature probes recorded the air temperatures of the conditioned and unconditioned zones, the ambient temperature, as well as the water inlet and outlet temperatures. The air temperature probes were shielded to minimize the effects of radiative gains on the measured temperatures. The pump was external to the thermal chamber, and its energy consumption was not recorded.

We conducted four experiments: three to calibrate the properties of the thermal chamber model, and one to validate the final coupled model. The first three experiments characterized the chamber envelope, cooling coil and cooling water loop, and the properties of the partition between the conditioned and unconditioned zones, respectively. The model properties calibrated during each experiment were set to fixed values in later experiments. These calibration experiments are not described in detail in this article; however, Section 2.2.2 provides the chamber model’s calibrated properties. The fourth and final experiment provided measurements so as to validate the co-simulation model.

Prior to the validation (fourth) experiment, we opened the thermal chamber and allowed it to reach equilibrium with the laboratory ambient environment. The validation experiment then proceeded in two stages. In the first stage, we closed the chamber and activated the electric loads but not the cooling water loop. Internal heat gains from the electric loads caused the thermal chamber to heat up: the internal temperature of the conditioned chamber rose to approximately 65 ${}^{\circ }\mathrm{C}$ over the course of 40 h. After 40 h, we activated the cooling system, thus allowing the internal air temperature to rapidly decrease to a steady-state value of approximately 39 ${}^{\circ }\mathrm{C}$. The experiment concluded after 52 h. Charts of the experimental results with comparisons to the modeled data are provided in Section 3.

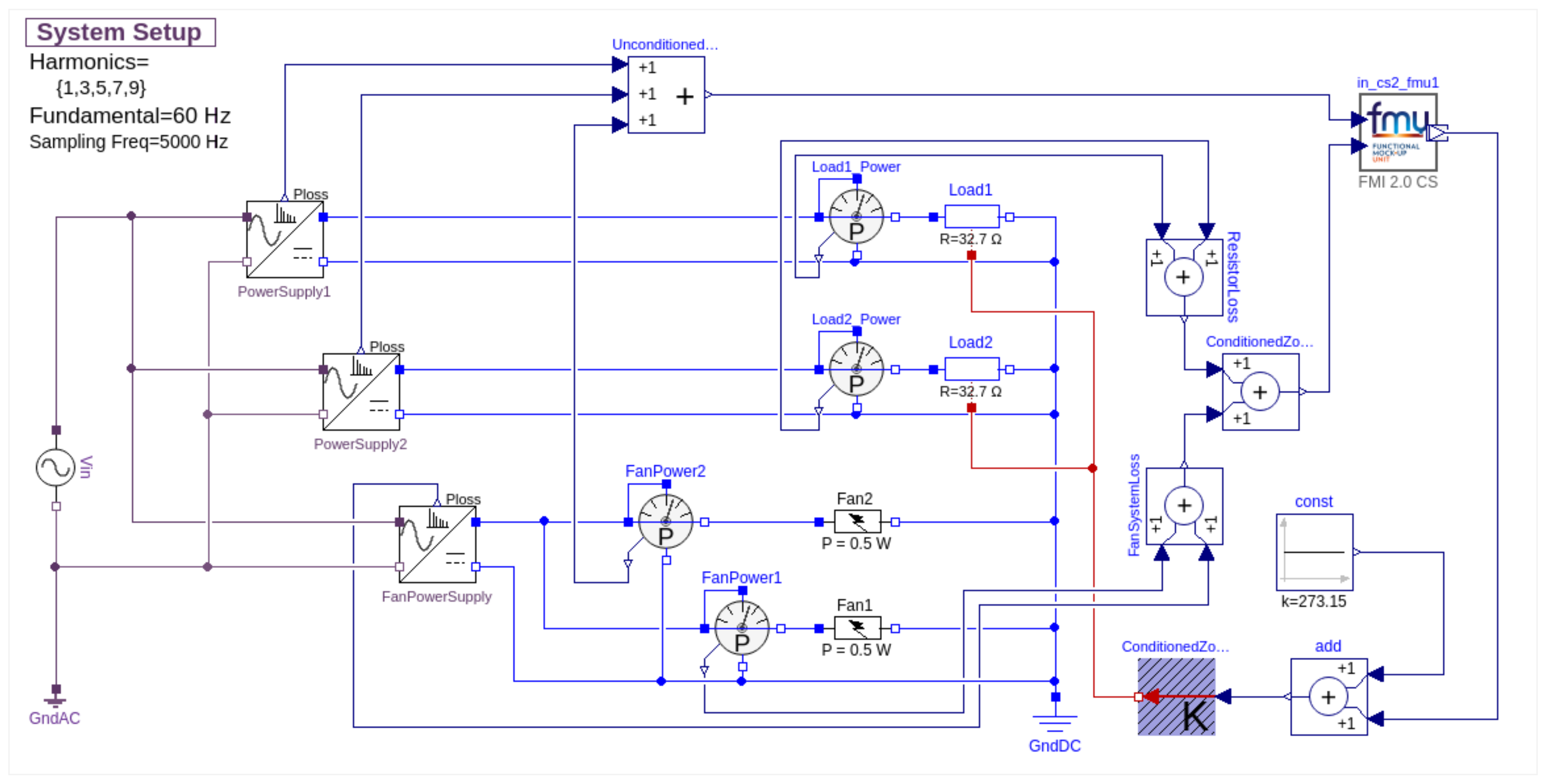
2.2.1. Electrical Model

Figure 6 provides a single-line diagram of the electrical distribution system used in the validation experiment. The electrical model consists of three AC/DC power electronics converters (the two HP laptop power supplies plus the small DC fan power supply), two fixed-load resistors ( $32.7$ $\mathsf{\Omega }$ each), and two small DC circulation fans modeled as fixed $0.5$ W DC loads. We obtained independent efficiency and harmonic characterization data for each of the HP laptop power supplies via laboratory measurement; we used these to construct AC/DC converter models as described in [25]. The characterization data showed that the actual power supply output voltage varied slightly with load. Therefore, we modeled the power supply output voltages at their measured values for 10% loading (approximately  9 W): $19.92$ VDC for the HP 677777-002 and $19.51$ VDC for the HP 608428-002. We modified the BEEAM to vary the power supply voltage as a function of load, which is a recommended enhancement. Characterization data for the fan power supply were not available. Therefore, we modeled this power supply using the efficiency curve of a generic 24 VDC, 25 W LED driver, but with the output voltage scaled to 5 VDC.

The EnergyPlus model was embedded in the BEEAM model as an FMU, as described in Section 2.1.3. The BEEAM model independently summed the measured load power and converter losses for the conditioned and unconditioned zones (see Figure 6), as well as provided these values as inputs to the EnergyPlus FMU. This data transfer represents the mapping function g of Equation (5).

To demonstrate bidirectional data exchange, we modeled the load resistors with a temperature coefficient of resistance derived from the experimental data, such that their resistance (and therefore power consumption) varied slightly with the conditioned zone temperature. The modeled effect of zone temperature on the load power was small and had negligible impact on the validation results; furthermore, it was included primarily to demonstrate the data export from EnergyPlus to the BEEAM, that is, the mapping function f of Equation (4).

2.2.2. Thermal Model

We modeled the thermal chamber and cooling system in EnergyPlus. The geometry of the model (Figure 7) followed the refrigerator unit manufacturer’s documentation. The unit’s single internal chamber was partitioned into a conditioned zone (left) and an unconditioned zone (upper-right). The small chamber at the lower-right of the unit contained the compressor in the original refrigerator. The compressor was not in operation during the experiment, and the compressor chamber was modeled as a thermal zone at the laboratory ambient temperature.

The thermal properties of the chamber envelope were based on the material properties specified by the manufacturer: an outer housing of $0.7$ mm painted steel, 100 mm of insulation with an insulation value of 19 mW/K, and an inner housing of $0.7$ mm aluminum. In the experimental thermal chamber (Figure 5b), the barrier between the conditioned and unconditioned zones was penetrated by a metal rod (which provides structure for sensors) and several small holes were created. To model the effect of these discontinuities, we added an airflow mixing-rate variable that captures the additional heat transfer between the two zones. This approach enabled us to achieve alignment between the modeled and measured zone temperature values without requiring a detailed thermal bridge model. The envelope thermal properties and the properties of the partition were experimentally calibrated via a set of three experiments:

• We removed the chamber partition and cooling system, then introduced a known, fixed internal heat source to produce a response in the chamber internal temperature. We used the steady-state temperature to calibrate the insulation properties, and the transient response was used to calibrate the chamber’s overall thermal mass.
• We introduced the cooling water loop to the chamber (still with the partition removed), heated the chamber, and allowed the cooling loop to cool the chamber to a steady-state temperature. We used this experiment to calibrate the properties of the cooling model.
• We introduced the partition between the thermal zones, then performed a heating/cooling cycle with a fixed internal heat source in one zone only. We enabled the cooling loop only after the chamber had heated to a steady-state temperature. With this experiment, we calibrated the insulation properties of the inner partition, the thermal mass of each zone, and the air mixing between the zones.

These experiments yielded a well-calibrated thermal model for the chamber and cooling loop.

Table 1. Thermal Model Calibrated Properties.

Description	Value	Unit
Thermal transmittance of the chamber envelope	0.38	W/(m2K)
Thermal transmittance of the interior partition	2.316	W/(m2K)
Effective surface area of the thermal mass in the conditioned zone	0.02	m2
Effective thickness of the thermal mass in the conditioned zone	0.04	m
Effective surface area of the thermal mass in the unconditioned zone	0.03	m2
Effective thickness of the thermal mass in the unconditioned zone	0.11	m
Airflow mixing rate between zones	0.003	m3/s
Zone thermal capacitance multiplier	21
Air-to-water thermal resistance of the cooling coil	0.75	W/K

lists the final calibrated values.

The internal heat gains from the loads and power supplies were modeled as Electric-Equipment objects with values driven by the EnergyPlus external interface, as described in Appendix A.1. Because the experiment used mixing fans, we assumed a uniform internal air temperatures in each chamber and assigned each load object a convection ratio of 1.0. Because the chamber was closed (no external air is delivered from an HVAC system, that is, no ${\dot{Q}}_{\mathrm{sys}}$), and because we lacked the characterization data for the cooling coil required to implement a full-fidelity coil model in EnergyPlus, we represented the delivered cooling, $\dot{Q}$, as a “negative load” rather than a built-up cooling coil. We described the heat transfer using a simple thermal resistance equation between the water and air “reservoirs”,

$$\dot{Q}=\frac{T_{\mathrm{Air}}-T_{\mathrm{Water}}}{R_{\mathrm{Coil}}}$$

(6)

in which $T_{\mathrm{Air}}$ is the modeled temperature of the conditioned zone air, $T_{\mathrm{Water}}$ is the measured entering temperature of the cooling water, and $R_{\mathrm{Coil}}$ is a thermal resistance for the cooling water coil, calibrated to $0.75$ W/K. This simple cooling model performed well because the coil temperature remained consistently above the dew point, and because the coil entering and leaving water temperatures were nearly identical throughout the entire experiment. We implemented this model as a negative heat gain using EnergyPlus Energy Management System code, which allows for the customization of EnergyPlus internal behavior.

The Energy Management System code also overrode the normal weather input so as to set the ambient temperature to the measured temperature of the laboratory, as well as to set the wind speed and solar irradiance to zero (which is consistent with an indoor laboratory environment). Ambient temperature and the measured temperature of the cooling water were provided as model inputs via schedules.

2.2.3. Model Summary

The coupled electrical and thermal models accepted ambient conditions, operating schedules, and rated loads as inputs, and they predicted the total electrical input power and thermal chamber internal temperatures as outputs.

Table 2. Model Inputs, Parameters, and Outputs.

Model	Inputs	Calibrated Parameters	Outputs
Electrical	Load resistance Fan power	Converter efficiency curves Temperature coefficient of load resistors	Electrical input power
Thermal	Ambient temperature Cooling water temperature Cooling on/off schedule	Envelope insulation Partition insulation Thermal mass Air exchange Cooling coil thermal resistance	Conditioned zone temperature Unconditioned zone temperature

summarizes the model inputs, model outputs, and calibrated model parameters for both the electrical and thermal models. The model inputs comprise the measured values imposed as schedules or fixed values in the models, while the model outputs comprise the simulated values that were compared to the experimental data so as to validate the accuracy of the co-simulation (see Section 3). The calibrated model parameters were derived from or calibrated based on independent laboratory experiments, as described in Section 2.2.1 and Section 2.2.2, except for the temperature coefficient of the load resistances, which was estimated directly from the measured power in the validation experiment. This last parameter had a negligible impact on the model outputs, and it was included primarily to demonstrate bidirectional data exchange (see Section 2.2.1). The model parameters that were not calibrated, such as the converter power and voltage ratings, are not listed in the table.

3. Results

We simulated the coupled model using Dymola with an explicit Euler integration method and a fixed time step of 60 s. The model inputs from the measured data were as documented in Table 2. The FMU used the FMI 2.0 standard. Under this configuration, the simulation was numerically stable. (However, we note that an initial attempt to simulate both models as compiled FMUs when using Dymola required a first-order lag block between the FMUs in order for the simulation to be stable. This limitation is an artifact of the Dymola solver and was therefore abandoned in favor of the single-FMU configuration of Figure 4.)

Figure 8 displays the time-series results of the validation experiments, including comparisons with the model outputs for conditioned zone temperature, unconditioned zone temperature, and electrical input power. As described in Section 2.2, the cooling system was disabled (off) during hours 0–40 and enabled (on) during hours 40–52. The conditioned and unconditioned zones reached the modeled steady-state temperature rises of 65 ${}^{\circ }\mathrm{C}$ and  63 ${}^{\circ }\mathrm{C}$, respectively, by hour 25. Shortly after cooling began, both zones reached a second steady-state temperature of approximately 39 ${}^{\circ }\mathrm{C}$, and remained at that temperature until the conclusion of the experiment.

The modeled outputs closely tracked the measured data. The BEEAM model underpredicted the electrical input power by approximately 1 W. We did not verify the load resistances (the model uses the nominal values), nor did we characterize the AC/DC converter powering the DC fans. These are two potential sources of the error in predicted power. The EnergyPlus model also slightly underpredicted the total temperature rise of the conditioned zone during the unconditioned period; this is expected given the underprediction of the internal gains. The thermal dynamics of the model aligned well with the measured data.

To quantify the accuracy of the model, we calculated the normalized mean bias error (NMBE) and the coefficient of variation in the root-mean-square error (CV(RMSE)) per the formulas defined in ASHRAE Guideline 14 [35],

$$\begin{array}{cc}\hfill \mathrm{NMBE}& =\frac{{\sum }_{i=1}^n\left(y_i-{\widehat{y}}_i\right)}{\left(n-p\right)\times \overline{y}},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \mathrm{CV}\left(\mathrm{RMSE}\right)& =\frac{\sqrt{\frac{{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{\left(n-p\right)}}}{\overline{y}},\hfill \end{array}$$

(8)

in which n is the number of observations, $y_i$ represent the measured observations, ${\widehat{y}}_i$ represent the modeled observations, $\overline{y}$ is the arithmetic mean of the measured data, and $p=1$ for the calibrated simulations. (Although we reference ASHRAE Guideline 14 for the NMBE and CV(RMSE) formulas, it does not otherwise directly apply to the model validation performed in this work.) Because the raw measured and modeled data were not fully time-aligned, the NMBE and CV(RMSE) calculations used 15 min averages for each time series.

Table 3. Validation Results.

Modeled Quantity	NMBE a	CV(RMSE) b
Conditioned zone temperature	1.4%	2.0%
Unconditioned zone temperature	−1.1%	2.8%
Electrical input power	3.4%	3.4%

^a Normalized mean bias error. ^b Coefficient of variation in the root-mean-square error.

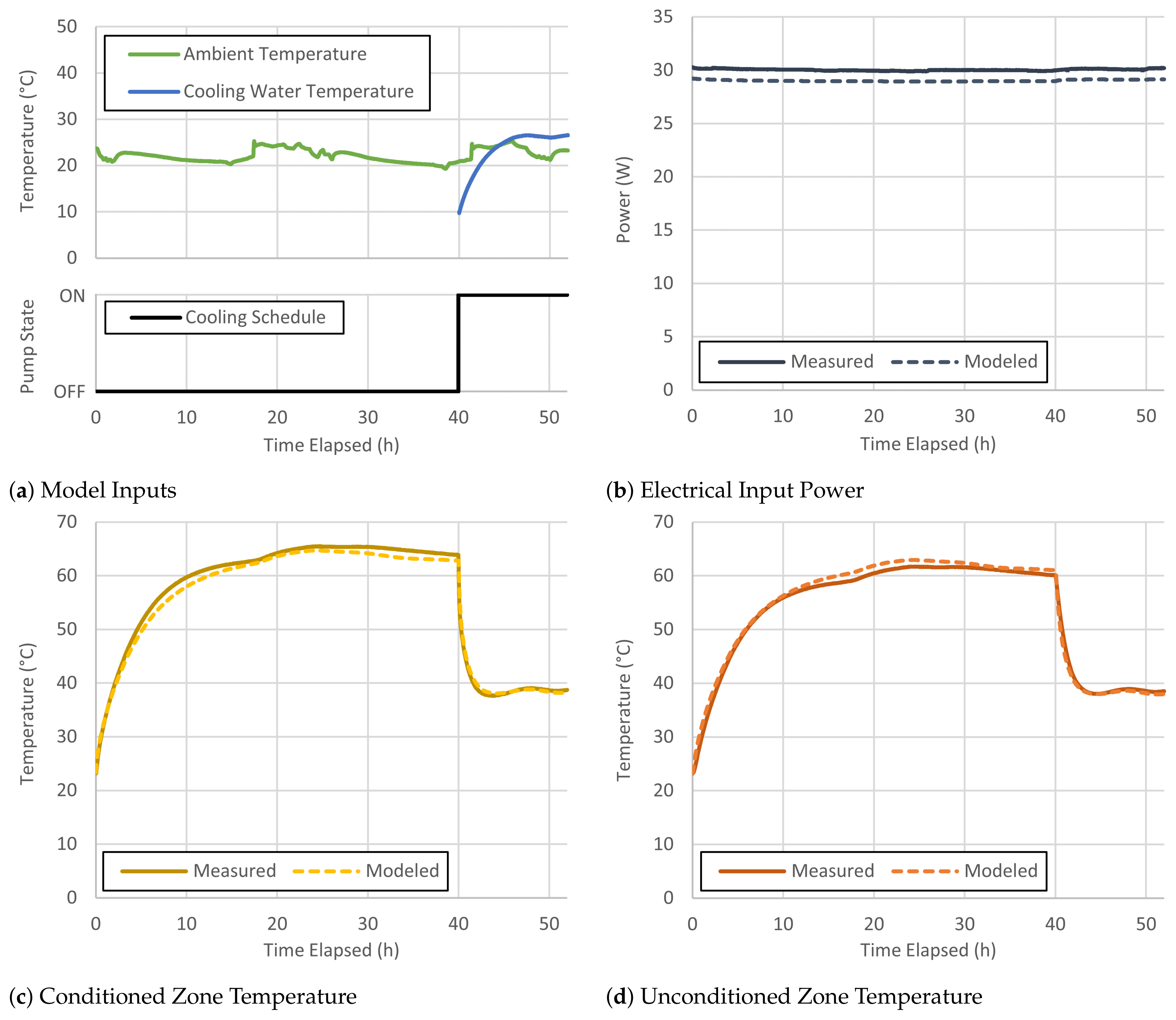
provides the values of the validation metrics for each model output of interest. Note that the negative value for NMBE for the unconditioned zone temperatures indicated that the model underpredicts the measured values.

4. Discussion

The simulation results demonstrate the stable co-simulation of a whole-building energy model (EnergyPlus) with a detailed electrical distribution system performance model (BEEAM). When given well-calibrated input models, the co-simulation can also be highly accurate. In this case, the demonstration model closely replicated the results of the validation experiment, including electrical input power and zone temperatures.

More importantly, the validation experiment demonstrated the validity of the data exchange between the electrical and thermal models. In the experiment, approximately 6 W of the modeled 29 W of internal heat gains (21%) represented the losses associated with the power electronics converters. Had these losses not been included in the model, the internal temperature and cooling load prediction errors would have been substantial. The same principle extends to whole-building models with many thermal zones, many loads, and complex electrical distribution systems. By capturing the interaction between the behavior of a building’s electrical and thermal systems, the proposed co-simulation framework enabled more complex, comprehensive analyses of the energy efficiency, as well as allowed for the co-optimization of building electrical and thermal performance.

This validation study model uses a simple Euler integration method. Although variable-step and adaptive-step methods can exhibit improved performance, co-simulation using an EnergyPlus FMU requires fixed, predetermined time steps (implying a fixed-step integration method). In addition, the selected integration method has minimal impact on the model performance in this case because the harmonic power-flow equations are algebraic, not differential. However, the integration method is an important consideration for more complex models.

4.1. Limitations

The proposed co-simulation capability shows significant promise but is, at present, subject to several practical limitations. Presently, each co-simulation requires bespoke modeling, with simulation settings and interconnections between the BEEAM and EnergyPlus model being individually enumerated by the modeler. Little automation infrastructure for FMU-based co-simulation currently exists within the building performance simulation space. These limitations should be addressed in future work.

The experimental validation also had several limitations:

• As previously mentioned, the AC/DC power supply serving the circulation fans was not characterized. Therefore, its efficiency curve remains unknown. This was a potential source of error in the prediction of electrical input power.
• The high circulation rate of the cooling water relative to the load and the coil characteristics resulted in nearly identical coil entering and leaving water temperatures. Because the temperature difference was very small, random errors and/or biases in the measured water temperatures frequently resulted in a calculated cooling energy that was physically impossible (such as negative cooling or steady-state cooling that significantly exceeded the thermal chamber’s internal heat gains). As a result, the experimental cooling energy data were unusable, and we did not attempt to compare them to the modeled cooling energy.
• Because accuracy specifications were not available for all the of the instrumentation used in the experiment, we did not perform an uncertainty analysis. It is therefore unknown whether the model outputs match the measured data within the experimental uncertainty. Nevertheless, the calculated error metrics were low.

The scope of the experimental validation was limited by laboratory-access restrictions related to the COVID-19 pandemic. We recommend that future work include more extensive experimental validation.

4.2. Future Work

We recommend future work to further validate the accuracy of the BEEAM and of the co-simulation models that incorporate the BEEAM so as to investigate the scalability of such co-simulation models, and, in particular, to provide automation that enables the use of co-simulation in large-scale analyses. For validation, co-simulation demonstrations using real building systems should be considered. In addition, the capability should be validated for a diversity of building types, system configurations, and electrical components. Full-building distribution systems also require much larger, more complex electrical distribution models. Future work should investigate the scalability of the BEEAM to accommodate such models. Finally, without advances in automation, Modelica- and FMU-based co-simulation models have limited application in large-scale analyses. Future work for co-simulation automation should include developing common model architecture and data exchange standards to allow for the programmatic construction of the BEEAM models; developing model articulation capabilities for Modelica; and implementing Modelica-based workflows for large-scale parametric analyses, including FMU-based simulation, as recommended by [36]. These capabilities will enable the use of co-simulation models at the same level of sophistication that single-engine physics-based building models are used today.

5. Conclusions

We describe and demonstrate an advance in co-simulation capability that combines the BEEAM—a Modelica library for detailed modeling of building electrical distribution systems—with the whole-building energy modeling capabilities of EnergyPlus. The BEEAM library is also compatible with other Modelica libraries, permitting more complex co-simulations. We verified the stability of the demonstration model and validated its accuracy compared to a laboratory demonstration by using a simple two-zone thermal chamber with internal electrical equipment. The proposed capability significantly expands the fidelity of building electrical distribution system modeling in the context of whole-building energy modeling, thus enabling more complex analyses than would have been possible with the individual building performance simulation tools that are used to date.