Modelling and Performance Analysis of a Tidal Current Turbine Connected to the Grid Using an Inductance (LCL) Filter

Abstract

Nowadays, integrating renewable energy sources, such as tidal power, into the existing power grids of turbines is crucial for sustainable energy generation. However, tidal turbine energy transforms the potential energy of moving water into electrical energy. When both nonlinear load and dynamic load harmonics are present, the tide speed variance causes serious power quality issues such as low power factor, unstable voltage, harmonic distortions, frequency fluctuations, and voltage sags. The integration of an LCL-filter-based connection scheme can address these challenges by improving power quality and the overall performance of the tidal current turbine grid system. This study shifts LCL filter research from its conventional wind energy emphasis to the emerging field of tidal stream generation systems. The LCL filter analysed in this paper is modelled to exhibit adequate mechanical, electrical, and hydrodynamic characteristics. This model accounts for tidal current variations, turbine speed control, and power extraction dynamics. The LCL filter is evaluated for its effectiveness in reducing harmonic distortions, voltage fluctuations, and reactive power fluctuations. This system is composed of a 1.5 MW/C, a 1.2 MW three-level inverter with a nominal voltage of 600 V, and an inductance (LCL) filter. The results show that the inverter produces a harmonic distortion of less than 0.5%, which demonstrates the effectiveness of the filter in improving total harmonic distortion, reactive power consumption, and voltage control.

1. Introduction

Nowadays, renewable energy sources are being increasingly utilised in electrical systems to mitigate the impacts of climate change. It is anticipated that a significant portion of the future energy mix will comprise renewable sources of energy, which can play an important role given their enormous potential, particularly wave and tidal stream generation [1]. Similarities between offshore wind and tidal stream turbines include the usage of electric machinery, system structure, and control strategies [2]. It has been found that, globally, sources of marine energy are extensive when compared to other renewable energy sources such as wind, solar, geothermal, etc. [3]. However, tidal energy developers have shifted their focus to tidal streams, which offer the major advantage of being near coastal cities and grids [4]. It is noted that tidal power is a predictable energy resource, whose accuracy has been within 98% for decades. This predictability allows tidal power generation to be successfully integrated into electrical grids [4,5,6,7,8]. The typical behaviour of the power system has changed because of the increasing use of renewable energy sources. As a result, the weak grid inertia of the future is likely to be dominated by power electronic interfaces [9]. However, tidal energy generation comes with many challenges, and its integration into the grid presents numerous operational and control difficulties that limit the grids’ ability to run steadily and dependably. Therefore, it is important to maintain the stability of voltage and frequency in the power network by ensuring that harmonic distortions are kept as low as possible [7,10]. In power converters with a rectifier input stage, LCL filters are specially designed to cut down on harmonic current absorption (frequency converters for UPS, motors, etc.). They primarily consist of a parallel-series configuration of inductors and capacitors designed to lower the total harmonic distortions (THDs) of rectifiers [9,11,12]. The tidal energy generation system is connected to the grid via an inverter using an LCL filter that maintains the high quality of grid current by decreasing the frequency harmonics to a lower level, thereby presenting a better dynamic performance [13]. It can be mentioned that LCL is one of the most frequently employed filters in grid-connected filters [14]. The design of LCL filters is the subject of many studies, which either suggest various methods and algorithms to discover the ideal values for the filter’s components or various damping circuits to achieve the necessary attenuation [15].

For this study, an LCL filter was integrated into an offshore power system between a VSI and the grid (Figure 1). This filter is necessary to reduce the output of current harmonics and ensure dynamic performance for feedback control. It is possible to use a straightforward series inductor; however, the harmonic attenuation is not very noticeable. In addition, these systems have a significant voltage drop, necessitating the design of a large inductor [11].

Various standards related to harmonic emissions have been adopted by national and international organisations due to the widespread usage of electronics in power systems [16]. As a result, the IEEE and IEC have specified the quality of voltage that a utility grid should be able to provide to a consumer at any point in a distribution system and proposed limitations on harmonic currents injected via nonlinear loads [17]. As long as the harmonic currents introduced by generators and consumers are constrained, a utility grid should be able to offer a certain quality of voltage, as specified in a previous paper [1].

The modelling of tidal power plant components is the subject of numerous scholarly articles. However, extensive research has not been conducted on the use of filters in tidal generation systems [18]. Several filter design methodologies and applications have also been described in the literature, although only for grid-connected inverters for wind and solar systems [19]. However, the application of such filters and their harmonic analysis in tidal energy conversion systems is not documented. Reznik used a line controller to adjust the active and reactive power [11]. Nevertheless, the relative saturation blocks serve as a limitation for determining active and reactive power systems. The ripple of the switching frequency is minimised using an LCL filter. On the other hand, the PI-based controllers of the PCC allow for the selection of the desired reference measurements, and the obtained values are then compared with those of the frame. Therefore, common techniques for tuning such filters are explored and adjusted to meet the needs of a particular test scenario. Thus, a set of specifications for an LCL filter of a 3.6 MW grid-connected wind turbine with a full-scale power electronic converter were established. The frequency domain analysis of LCL filters focuses on passive damping techniques and changes in the capacitive branch that may enhance the features of such filters. In this study, the LCL filter designs were employed and subsequently compared for their harmonic characteristics and losses. It is explored the impact of incorporating extra branches on reducing both harmonic content and losses. The examination was conducted using an open-loop converter control system. Most of the research on LCL filter integration applications using wind and solar energy systems is due to advances in solar and wind technologies and their competitiveness with offshore energy, which is still in the development stage. However, a tidal energy system was used in this study that captures mechanical energy from tidal speeds to generate electrical power, which may be supplied to the nearest coastal part of the grid.

The objective of this paper was to create a Simulink model power generation system and incorporate a designed LCL filter into the system. Additionally, the study involves an analysis of the performance of the overall tidal current turbine connected to a grid with the integration of the LCL filter. LCL filters are integrated into the renewable energy system to minimise these harmonics due to several advantages over traditional L filters. The inverter is expected to generate harmonic distortions of less than 0.5% and the simulation as well as the analysis findings confirm the efficiency of the developed LCL filters in attenuating harmonics. Besides the grid, the system consists of a 1.5 MW three-level diode clamped inverter with a nominal voltage of 600 V, a 1.3 MW inductance–capacitance–inductance–inductance (LCL) filter, and a 1.5 MW tidal generator.

This paper is structured as follows: In Section 1, the background and objectives of this paper are presented. Section 2 provides a description of the main components of the tidal generation system: the tidal turbine, the PMSG machine, the LCL filter, and the control scheme. Section 3 provides details of the mathematical model of all tidal generation systems. Section 4 presents the control scheme, and the modelling of the entire tidal generation system connected to the grid is presented in Section 5. Section 6 is dedicated to the simulation model of the proposed system and the results, and Section 7 provides the discussion as well as the analysis. Section 8 consists of the conclusions and recommendations as well as suggestions for future work.

2. Tidal Overview

Tidal movements result from the gravitational attraction of celestial bodies such as the sun and moon towards terrestrial planets, particularly impacting planet Earth’s energy [20,21]. The power of tidal stream can be calculated using the same equation as applied to wind energy systems, referred to as Equation (1), with the utilization of Equation (2) [22]. We can ascertain the portion of available tidal power that a tidal turbine can capture. This amount of power depends on the type of turbine and its efficiency and is represented by the power coefficient $C_p$, which is significantly less than one. Consequently, the expression for the power harnessed by the tidal turbine from the tides can be formulated as follows:

$$\mathrm{P}=\frac{1}{2}{C}_p\mathrm{A}\rho V_{wind}^3$$

(1)

$$\mathrm{P}=\frac{1}{2}{C}_P\mathrm{A}\rho V_{tide}^3$$

(2)

where $C_p$ is the theoretical maximum amount of the power coefficient. This constraint is relative to the Betz limit, or more precisely to the Lanchester–Betz limit. In practice, this limitation cannot be achieved, and the maximum amounts of the $C_p$ of real turbines are usually in around the 0.4–0.5 range.

In practice, the typical power coefficient is 35–45%. ρ is the seawater density and is estimated at around 1025 kg/m³ [23]. The $C_p$ variations depend on the pitch angle of the blades $\left(\beta \right)$ and the tip-speed ratio λ, defined as the ratio between the rotor tip speed and the tides’ velocity $C_p(\lambda ,\beta )$ curve [23].

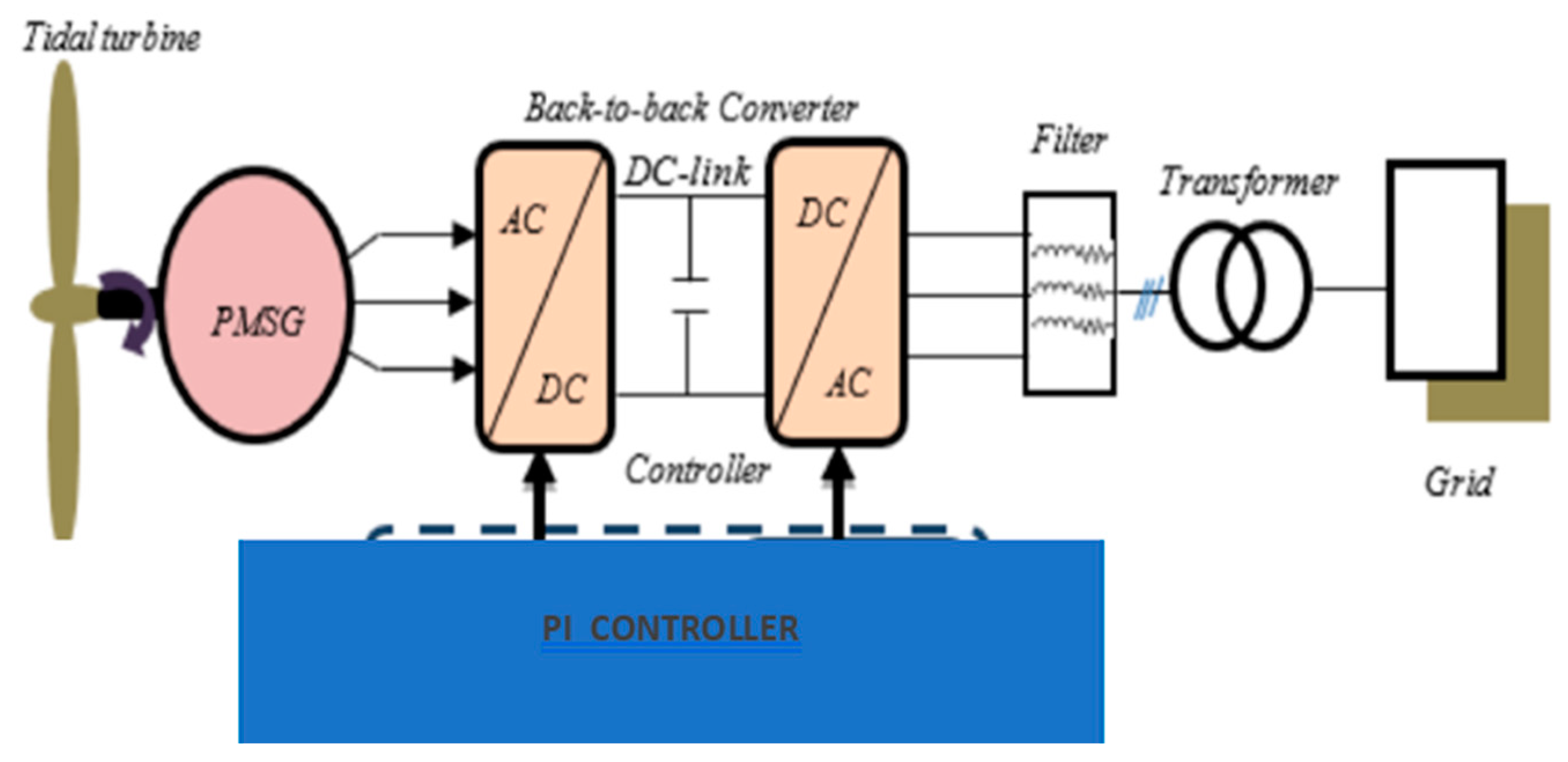
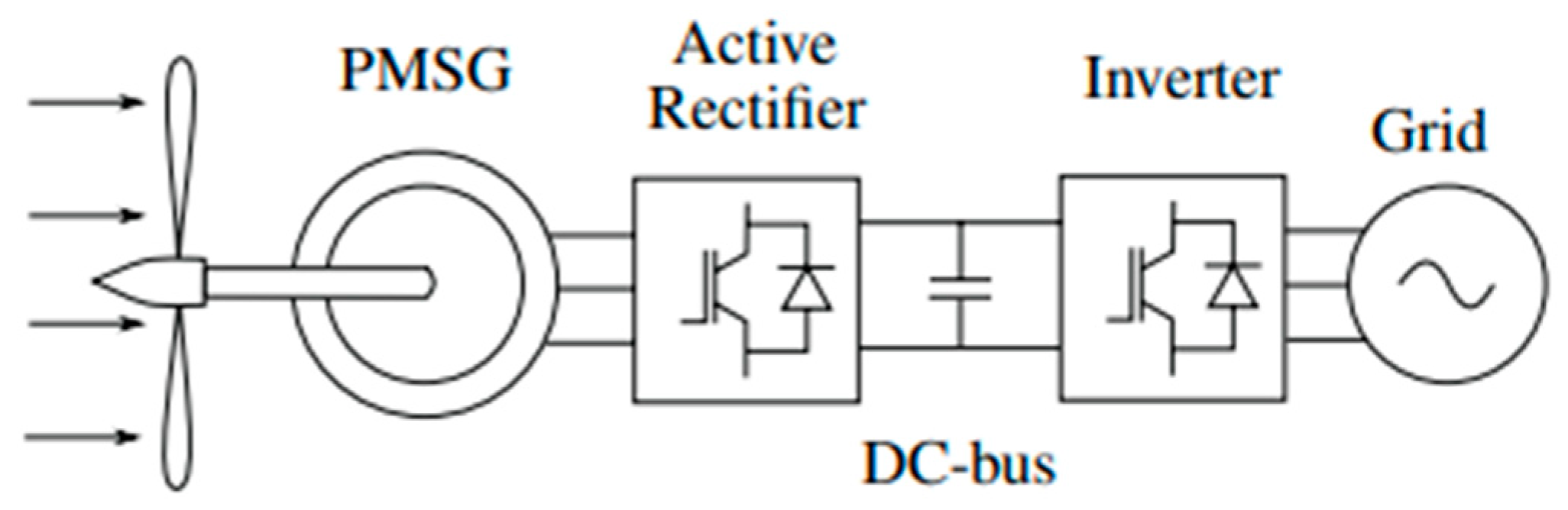
3. Modelling of Tidal Generation Connected to Grid Using LCL Filter

The block diagram presents a grid-connected tidal energy generation system, as shown in Figure 2. The AC output of the PMSG was rectified, and the DC-link voltage was then adjusted to obtain constant voltage by means of a PI controller, and the constant DC-link voltage was inverted to obtain the AC voltage recommended [24,25]. The LCL filter model is shown in Figure 2, where $L_1$ is the inverter-side inductor, $L_2$ is the grid-side inductor, ρ is a capacitor with a series $R_f$ damping resistor, $R_1$ and $R_2$ are inductor resistances, and voltages vi and vg are the input and output (inverter voltage and output system voltage). A three-phase power grid with current-controlled technology utilising PLL and CP transformation, a tidal current and turbine profile, a filter for power factor correction, a DC-to-AC converter, and an LCL filter for harmonic reduction constitute the entire system. Tidal energy by its own nature produces fluctuating voltage [26].

4. Control Scheme

In this study, the system performance was managed using the voltage-oriented control methods illustrated in Figure 3. The system controls the output DC voltage by doubling the current and rapidly responding to changes in its loop configuration. The inner current references are produced by the outer loop’s DC-link voltage control [19].

4.1. Modelling of Phase-Locked Loop (PLL)

In this work, the transformation’s phase angle was determined using a phase-locked loop (PLL). The PLL circuit consists of a phase detector, a loop filter, and a voltage-controlled oscillator. The closed-loop transfer function of the PLL depicted in (Figure 4) is expressed using the following equation [27]:

$$G_{\mathrm{P}\mathrm{L}\mathrm{L}}\left(S\right)=\frac{{\theta }^{*}}{\theta }=\frac{K_{1S}+K_2}{S^2+K_{1S}+K_2}$$

(3)

where $K_1$ is the proportional PI loop filter, and $K_2$ is the equivalent proportional integral gain.

The following phrase can be used to assess a PLL’s parameters $K_1$ and $K_2$.

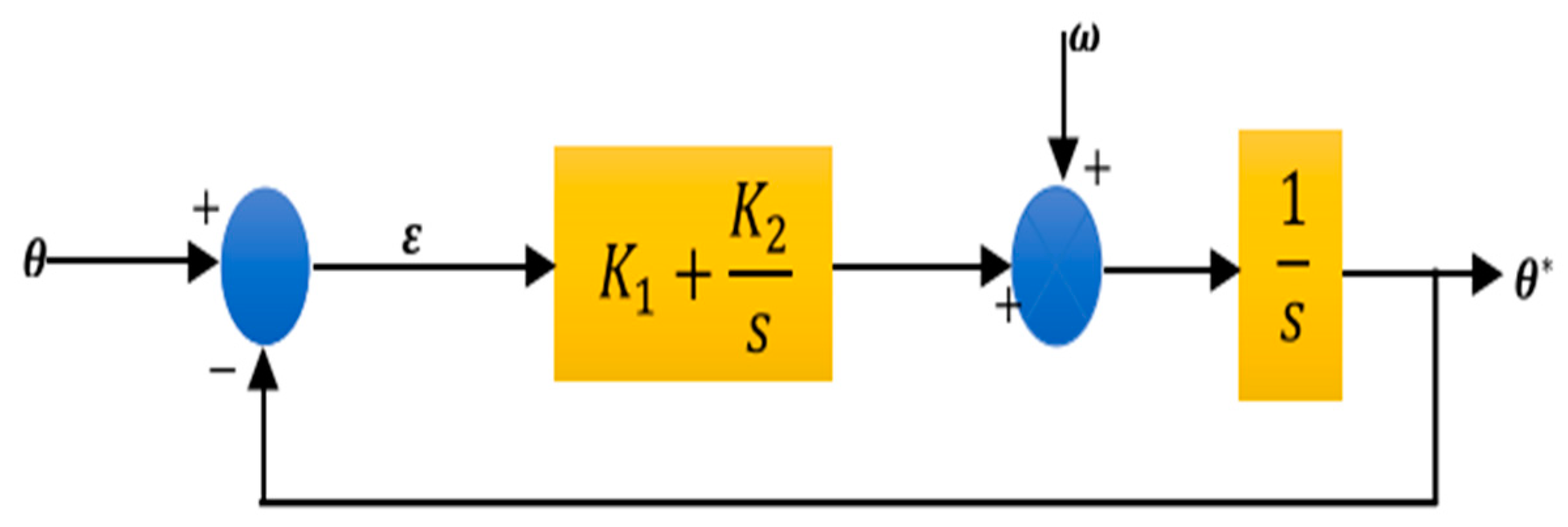
4.1.1. Outer-Loop Controller

The outer-loop controller ensures that the DC-link voltage remains near the predetermined DC reference voltage. This reference voltage needs to be substantially higher than the peak voltage of the generator to keep the converter’s diode from conduction. Equation (4) represents the transfer function of the outer-loop controller [11].

$${\mathrm{T}\mathrm{F}}_{\mathrm{v}}={\mathrm{k}}_{\mathrm{p}\mathrm{v}}+\frac{{\mathrm{k}}_{\mathrm{p}\mathrm{v}}}{{\mathrm{s}\mathrm{T}}_{\mathrm{i}\mathrm{v}}}$$

(4)

The method to estimate the tuning parameters is as follows:

$$\left\{\begin{array}{c}{\mathrm{k}}_{\mathrm{p}\mathrm{v}}=0.12\frac{{\mathrm{C}}_{\mathrm{d}\mathrm{c}}}{{\mathrm{T}}_{\mathrm{s}}}\\ {\mathrm{T}}_{\mathrm{i}\mathrm{v}}=17{\mathrm{T}}_{\mathrm{s}}\end{array}\right.$$

(5)

where the proportional gain is denoted as ${\mathrm{k}}_{\mathrm{p}\mathrm{v}}$, along with the outer voltage loop time integrator is denoted as ${\mathrm{T}}_{\mathrm{i}\mathrm{v}}$, and the sampling period, ${\mathrm{T}}_{\mathrm{s}}$, is expressed as follows:

$${\mathrm{T}}_{\mathrm{s}}=\frac{1}{{\mathrm{f}}_{\mathrm{s}}}$$

(6)

4.1.2. Inner-Loop Control

The transfer function of the inner-loop controller is provided below. In this loop, the current parameters $i_d$ and $i_q$ are obtained by applying the dq0 generator transformation to the currents ${\mathrm{I}}_{\mathrm{a}}, {\mathrm{I}}_{\mathrm{b}}, \mathrm{a}\mathrm{n}\mathrm{d} {\mathrm{I}}_{\mathrm{c}}$. These currents are then compared with the reference values $i_{d-ref}$ generated at the outer loop and $i_{q-ref}$ in the outer loop; $i_{q-ref}$ is set to zero.

$${\mathrm{T}\mathrm{F}}_{\mathrm{i}}={\mathrm{k}}_{\mathrm{p}\mathrm{i}}+\frac{{\mathrm{k}}_{\mathrm{p}\mathrm{i}}}{{\mathrm{s}\mathrm{T}}_{\mathrm{i}\mathrm{i}}}$$

(7)

where ${\mathrm{k}}_{\mathrm{p}\mathrm{i}}$ and ${\mathrm{T}}_{\mathrm{i}\mathrm{i}}$ are re-estimated with the equation below:

$$\left\{\begin{array}{c}{\mathrm{k}}_{\mathrm{p}\mathrm{i}}=\frac{{\mathrm{L}}_{\mathrm{s}}}{3{\mathrm{T}}_{\mathrm{s}}}\\ {\mathrm{T}}_{\mathrm{i}\mathrm{i}}=\frac{{\mathrm{L}}_{\mathrm{s}}}{{\mathrm{R}}_{\mathrm{s}}}\end{array}\right.$$

(8)

where ${\mathrm{k}}_{\mathrm{p}\mathrm{i}}$ represents the proportionality factor, while ${\mathrm{T}}_{\mathrm{i}\mathrm{i}}$ indicates an integration time constant for inner-loop control. In

Table 1. Rectifier control design parameters.

Control Loop Parameters	Value
${\mathrm{K}}_{\mathrm{p}\mathrm{v}}$	133.5
${\mathrm{K}}_{\mathrm{i}\mathrm{v}}$	133,500

and

Table 2. Rectifier control design parameters.

Control Loop Parameters	Value
${\mathrm{K}}_{\mathrm{p}\mathrm{i}}$	3.24
${\mathrm{K}}_{\mathrm{i}\mathrm{i}}$	50.625

, the tuning parameters for the outer- and inner-loop controls are presented.

4.2. Modulation Control

The modulation signals ${\mathrm{m}}_{\mathrm{d}}$ and ${\mathrm{m}}_{\mathrm{q}}$ are used to generate the PWM signals to drive the rectifier switches based on Equation (9) [28] as follows:

$$\left\{\begin{array}{c}{{\mathrm{m}}^{\mathrm{*}}}_{\mathrm{d}}=\frac{2}{{\mathrm{V}}_{\mathrm{d}\mathrm{c}}}({\mathrm{V}}_{\mathrm{g}\mathrm{d}}+{\mathrm{L}}_{\mathrm{s}}\mathsf{\omega }{\mathrm{I}}_{\mathrm{d}}+{\mathrm{u}}_{\mathrm{d}})\\ {{\mathrm{m}}^{\mathrm{*}}}_{\mathrm{q}}=\frac{2}{{\mathrm{V}}_{\mathrm{d}\mathrm{c}}}({\mathrm{V}}_{\mathrm{g}\mathrm{q}}-{\mathrm{L}}_{\mathrm{s}}{\mathsf{\omega }\mathrm{I}}_{\mathrm{q}}+{\mathrm{u}}_{\mathrm{q}})\end{array}\right.$$

(9)

where ${\mathrm{V}}_{\mathrm{g}\mathrm{d}}$ and ${\mathrm{V}}_{\mathrm{g}\mathrm{q}}$ are disturbances from input power transmission, and u_d and u_q are the current errors output signals.

4.3. Modelling of Permanent Magnet Synchronous

A full-scale back-to-back converter allows a link to be established between the PMSG and the load. The converter is configured by a generator-side converter and a load-side converter [29]. The load-side inverter ensures the conversion of the DC voltage to the AC voltage, and the LCL filter reduces the output voltage harmonics [30]. The composition of back-to-back converters linked to the PMSG tidal energy system is illustrated in Figure 5. Using a supplementary inverter with a PMSG can provide AC power to the grid with constant frequency and voltage [31].

This section highlights the connection of a Permanent Magnet Synchronous Generator (PMSG) model with back-to-back IGBT converters [32] Within the PMSG model, the following equation is employed to ascertain the stator voltage in a fixed reference frame:

$$\left[V_{abc}\right]=\left[R\right]\left[i_{abc}\right]+\left[L\right]\frac{d\left(i_{abc}\right)}{dt}+\frac{\lambda abc}{dt}$$

(10)

where

$$\left[L\right]=\left[\begin{array}{ccc}{L}_{xx}& M_s& M_s\\ M_s& L_{xx}& M_s\\ M_s& M_s& L_{ss}\end{array}\right]$$

(11)

Given these assumptions, the generator model operates consistently in its fixed state (stator), overseeing all its conditions. By using Equations (10) and (11), we can derive a simplified model suitable for simulation, modelling, and control using rotor coordinates (d–q coordinates). The transformation between (a, b, c) and d–q coordinates can be represented by ${\mathrm{J}}_{\mathrm{r}\mathrm{o}\mathrm{t}}$, ${\mathrm{T}}_{\mathrm{r}\mathrm{o}\mathrm{t}}$, and ${\mathrm{T}}_{\mathrm{g}\mathrm{e}\mathrm{n}}$, with the low-speed shaft gearbox, high-speed shaft, and generator denoted by ${\mathrm{T}}_{\mathrm{r}\mathrm{o}\mathrm{t}}$ 1: ɳ gear, and ${\mathrm{T}}_{\mathrm{g}\mathrm{e}\mathrm{n}}$, respectively [3]. Utilising this transformation, the d–q PMSG (permanent magnet synchronous generator) voltages are obtained as follows [33]:

$$\left\{\begin{array}{c}{\mathrm{V}}_{\mathrm{d}}={\mathrm{R}}_{\mathrm{i}\mathrm{d}}+{\mathrm{L}}_{\mathrm{d}}\frac{{\mathrm{d}\mathrm{i}}_{\mathrm{d}}}{\mathrm{d}\mathrm{t}}-{\mathrm{L}}_{\mathrm{q}}{\mathrm{i}}_{\mathrm{q}}{\mathsf{\omega }}_{\mathrm{s}}\\ {\mathrm{V}}_{\mathrm{q}}={\mathrm{R}\mathrm{i}}_{\mathrm{q}}+{\mathrm{L}}_{\mathrm{q}}\frac{{\mathrm{d}\mathrm{i}}_{\mathrm{d}}}{\mathrm{d}\mathrm{t}}+({\mathrm{L}}_{\mathrm{d}}{\mathrm{i}}_{\mathrm{d}}+{\mathrm{ɸ}}_{\mathrm{m}}){\mathsf{\omega }}_{\mathrm{s}}\end{array}\right.$$

(12)

The electromagnetic magnet torque is presented as follows:

$${\mathrm{T}}_{\mathrm{e}\mathrm{m}}=\frac{3}{2}\mathrm{P}\left({\mathrm{ɸ}}_{\mathrm{d}}.{\mathrm{i}}_{\mathrm{d}}-{\mathrm{ɸ}}_{\mathrm{q}}{\mathrm{i}}_{\mathrm{d}}\right)=\frac{3}{2}\mathrm{P}\left[{\mathrm{ɸ}}_{\mathrm{m}}{\mathrm{i}}_{\mathrm{q}}+({\mathrm{L}}_{\mathrm{d}}-{\mathrm{L}}_{\mathrm{q}}){\mathrm{i}}_{\mathrm{d}}{\mathrm{i}}_{\mathrm{q}}\right]$$

(13)

If the permanent magnets are mounted on the rotor surface, then ${\mathrm{L}}_{\mathrm{d}}={\mathrm{L}}_{\mathrm{q}}$, and the electromagnetic torque is obtained as follows:

$${\mathrm{T}}_{\mathrm{e}\mathrm{m}}=\frac{3}{2}\mathrm{P}{\mathrm{ɸ}}_{\mathrm{m}}{\mathrm{i}}_{\mathrm{q}}$$

(14)

$$\mathrm{J}=\frac{2{N^2}_p\mathrm{H}{\mathrm{P}}_{\mathrm{n}\mathrm{o}\mathrm{m}}}{{\mathsf{\omega }}_{\mathrm{n}\mathrm{o}\mathrm{m}}}$$

(15)

where $N_p$ represents the count of pole pairs, while H signifies the inertia constant. The system’s input is the electromagnetic torque, and its output is the active power, denoted as P. The design of the controller relies on the system’s response characteristics during step changes in the generator torque, specifically for a fixed tidal speed, as exemplified in the following equations [16]:

$$\left\{-\left(\mathrm{R}+{\mathrm{L}}_{\mathrm{d}\mathrm{s}}\right){\mathrm{i}}_{\mathrm{d}}={\mathrm{V}}_{\mathrm{d}}-{\mathrm{ɸ}}_{\mathrm{q}}{\mathsf{\omega }}_{\mathrm{s}}\right\}$$

(16)

$$\left\{-\left(\mathrm{R}+{\mathrm{L}}_{\mathrm{d}\mathrm{s}}\right){\mathrm{i}}_{\mathrm{q}}={\mathrm{V}}_{\mathrm{q}}+{\mathrm{ɸ}}_{\mathrm{d}}{\mathsf{\omega }}_{\mathrm{s}}\right\}$$

(17)

The mechanical equation is presented as follows: Here, $\mathsf{\Omega }=\frac{{\mathsf{\omega }}_{\mathrm{s}}}{\mathrm{P}}$ represents the mechanical speed, ${\mathrm{T}}_{\mathrm{g}\mathrm{e}\mathrm{n}}$ is the mechanical torque delivered to the generator shaft, either via the gearbox or directly from the turbine in a directly driven system. On the other hand, the turbine defines the electromagnetic torque ${\mathrm{T}}_{\mathrm{e}\mathrm{m}}$.

$${\mathrm{T}}_{\mathrm{g}\mathrm{e}\mathrm{n}}-{\mathrm{T}}_{\mathrm{e}\mathrm{m}}=\left({\mathrm{J}}_{\mathrm{s}}+\mathrm{h}\right) {\mathsf{\Omega }}_{\mathrm{g}\mathrm{e}\mathrm{n}}$$

(18)

$${\mathrm{T}}_{\mathrm{e}\mathrm{m}}=\frac{3}{2}\left[{\mathrm{ɸ}}_{\mathrm{m}}{\mathrm{i}}_{\mathrm{q}}+({\mathrm{L}}_{\mathrm{d}}-{\mathrm{L}}_{\mathrm{q}}){\mathrm{i}}_{\mathrm{d}}{\mathrm{i}}_{\mathrm{q}}\right]$$

(19)

$$\mathrm{W}\mathrm{i}\mathrm{t}\mathrm{h} \left\{\begin{array}{c}{\mathrm{ɸ}}_{\mathrm{d}}={\mathrm{L}}_{\mathrm{d}}+{\mathrm{ɸ}}_{\mathrm{m}}\\ {\mathrm{ɸ}}_{\mathrm{q}}={\mathrm{L}}_{\mathrm{q}}{\mathrm{i}}_{\mathrm{q}}\end{array}\right\}$$

(20)

The electro magmatic torque ${\mathrm{T}}_{\mathrm{e}\mathrm{m}}$ can be simplified as follows:

$${\mathrm{T}}_{\mathrm{e}\mathrm{m}}=\frac{3}{2}\mathrm{P}{\mathrm{ɸ}}_{\mathrm{m}}{\mathrm{i}}_{\mathrm{q}}$$

(21)

The PMSG-driven turbine replicates varying tidal speeds to demonstrate the functioning of the control system. The specific parameters for modelling the permanent magnet synchronous tidal generator are provided in

Table 3. Generator modelling parameters.

Parameters	Values
${\mathrm{P}}_{\mathrm{n}\mathrm{o}\mathrm{m}}$	1.5 MW
${\mathrm{V}}_{\mathrm{n}\mathrm{o}\mathrm{m}}$	600 V
${\mathrm{R}}_{\mathrm{s}}$	0.006
${\mathrm{L}}_{\mathrm{d}\mathrm{q}}$	0.3 × 10−3
Φ	1.48
J	35,000

and

Table 4. Generator modelling parameters.

Parameters	Values
Viscous Damping	0.01
Friction	0
$N_p$	48

.

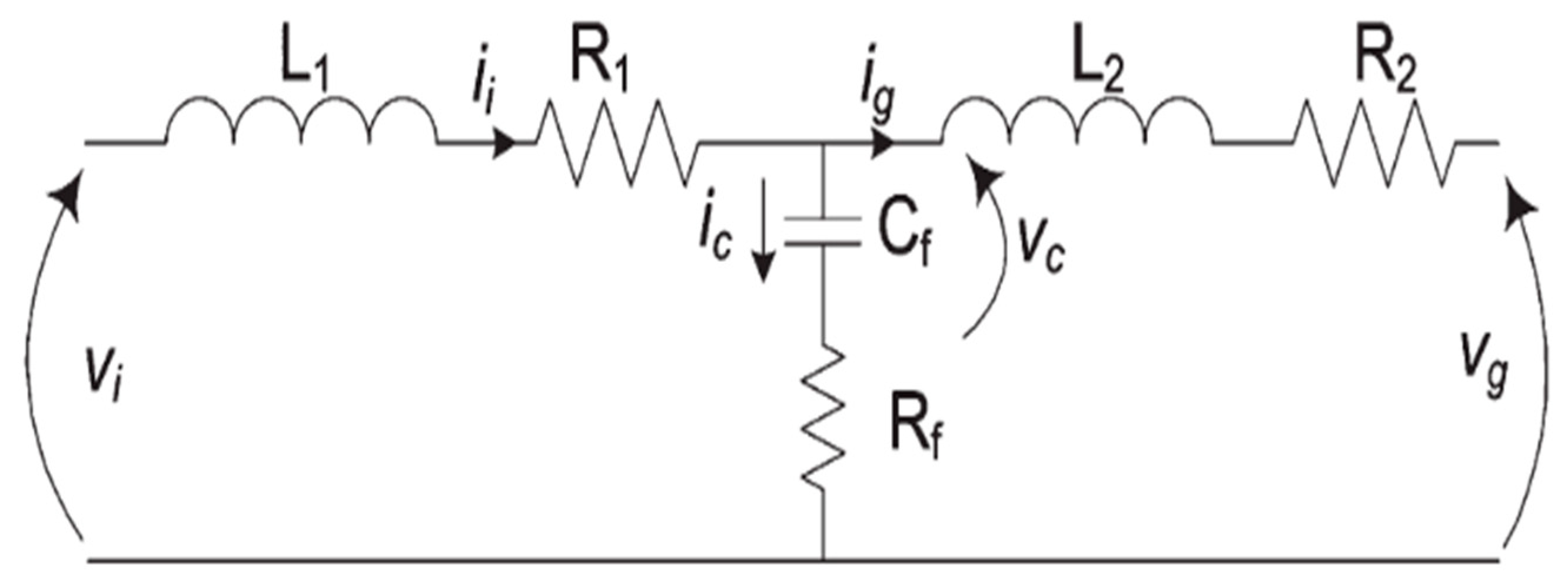
4.4. Modelling of LCL Filter

Due to several advantages over conventional L filters, upgraded filters of higher orders, such as LCL filters, are now utilised to reduce these harmonics rather than the typical L filters [34]. The harmonic attenuation of higher orders is accomplished at a higher rate of resonance frequency at 60 dB/decade [11]. The fact that the LCL filter generates enough resonance frequency to saturate the grid with distorted currents is one of its main drawbacks [35]. Therefore, active or passive dampening techniques are needed to remove the resonance frequency’s effects [36]. The following criteria were used to determine an LCL filter’s parameter range: (1) capacitance range of an LCL filter; (2) power factor reduction; (3) reactive power compensation limit; (4) net inductance range of an LCL filter; (5) inductance ranges on the inverter side (${\mathrm{L}}_{\mathrm{i}}$) and the grid side (${\mathrm{L}}_{\mathrm{g}}$); (6) harmonic limitations as per IEEE-519 Std; and (7) voltage drop across filter or DC bus availability. The LCL filter’s parameters were customised from an existing Simulink model [11], which are given in

Table 5. LCL filter parameters.

Parameters	Values
$\mathrm{Inverter-side} \mathrm{inductor} ({\mathrm{L}}_{\mathrm{i}}$)	0.9 mH
$\mathrm{Capacitor} \mathrm{filter} ({\mathrm{C}}_{\mathrm{f}}$)	531 μF

. The reasons for this are the proposed filter’s specified design characteristics and requirements, such as IEEE-519 standard [16],for harmonic current attenuations, the maximum voltage difference permitted between the filter’s two sides to prevent switching losses, and the cap on reactive power compensation [16].

The three-phase LCL filter was modelled by incorporating the inverter power rating ${\mathrm{P}}_{\mathrm{n}}$, the DC-link voltage, VDC, the grid frequency ${\mathrm{f}}_{\mathrm{g}}$, the switching frequency ${\mathrm{f}}_{\mathrm{s}\mathrm{w}}$, and the sampling frequency ${\mathrm{f}}_{\mathrm{s}\mathrm{a}\mathrm{m}\mathrm{p}}$.

4.5. Filter Capacitor

The impedance ${\mathrm{Z}}_{\mathrm{b}}$ and base capacitance are determined using the following equations [37]:

$${\mathrm{Z}}_{\mathrm{b}}=\frac{{{\mathrm{U}}_{\mathrm{n}}}^2}{{\mathrm{P}}_{\mathrm{n}}}$$

(22)

$${\mathrm{C}}_{\mathrm{b}}=\frac{1}{{\mathrm{W}}_{\mathrm{g}}{\mathrm{Z}}_{\mathrm{b}}}$$

(23)

In Equation (22), the voltage of the grid is denoted by Un, and the frequency of the grid is represented as in ${\mathrm{W}}_{\mathrm{g}}$ radians per second. The estimated value of the LCL filter capacitor ${\mathrm{C}}_{\mathrm{f}}$ is approximately 5% of the base capacitance [8]:

$${\mathrm{C}}_{\mathrm{f}}=0.05{\mathrm{C}}_{\mathrm{b}}$$

(24)

4.6. Current Ripple

The following equation is used to determine the maximum current variation at the inverter output [11]:

$${∆\mathrm{I}}_{\mathrm{L}\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{{2\mathrm{V}}_{\mathrm{D}\mathrm{C}}}{{3\mathrm{L}}_{\mathrm{i}}}\left(1-\mathrm{m}\right)\mathrm{m}{\mathrm{T}}_{\mathrm{S}\mathrm{W}}$$

(25)

where ${\mathrm{L}}_{\mathrm{i}}$ denotes the inductance of the inverter side, and ${\mathrm{T}}_{\mathrm{S}\mathrm{W}}$ corresponds to the switching period. The parameter “m” represents the inverter modulation index, which was estimated to be approximately 0.57 [13]. This study suggests that the inverter-side current ripple should be maintained within the range of 10–25% of the maximum current. Thus, the value for the maximum current ripple ${∆\mathrm{I}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ can be expressed as follows:

$${∆\mathrm{I}}_{\mathrm{L}\mathrm{m}\mathrm{a}\mathrm{x}}=\left(1\%-5\%\right){\mathrm{I}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(26)

The primary objective of the LCL filter is to reduce the anticipated current by approximately 20%, leading to an output current ripple of approximately 2%. Equation (28) pertains to the harmonic current [11]:

$${\mathrm{L}}_{\mathrm{g}}=\frac{\sqrt{\frac{1}{{{\mathrm{K}}_{\mathrm{a}}}^2}+1}}{{\mathrm{C}}_{\mathrm{f}}{{\mathsf{\omega }}_{\mathrm{S}\mathrm{W}}}^2}$$

(27)

where ${\mathrm{K}}_{\mathrm{a}}$ denotes the desired attenuation level, ${\mathsf{\omega }}_{\mathrm{S}\mathrm{W}}$ indicates the switching frequency in radians per second, and r represents the ratio of inductances on the inverter side and the grid side [38]. The resonant frequency ${\mathsf{\omega }}_{\mathrm{r}\mathrm{e}\mathrm{s}}$ in radians per second and the damping ratio (ζ) of the LCL filter are expressed using Equations (28) and (29), respectively.

$${\mathsf{\omega }}_{\mathrm{r}\mathrm{e}\mathrm{s}}=\sqrt{\frac{{\mathrm{L}}_{\mathrm{i}}+{\mathrm{L}}_{\mathrm{g}}}{{\mathrm{L}}_{\mathrm{i}}{\mathrm{L}}_{\mathrm{g}}{\mathrm{C}}_{\mathrm{f}}}}$$

(28)

$$\mathrm{ç}=\frac{{\mathrm{C}}_{\mathrm{f}}{\mathsf{\omega }}_{\mathrm{r}\mathrm{e}\mathrm{s}}{\mathrm{R}}_{\mathrm{d}}}{2}$$

(29)

The damping resistor parameter is denoted by Rd. To achieve an approximately sized resonant frequency for the LCL filter, it can be expressed in the following manner [38]:

$${\mathrm{f}}_{\mathrm{r}\mathrm{e}\mathrm{s}}=\frac{1}{2\mathsf{\pi }}\sqrt{\frac{{\mathrm{L}}_{\mathrm{i}}+{\mathrm{L}}_{\mathrm{g}}}{{\mathrm{L}}_{\mathrm{i}}{\mathrm{L}}_{\mathrm{g}}{\mathrm{C}}_{\mathrm{f}}}}$$

(30)

$${10\mathrm{f}}_{\mathrm{g}}<{\mathrm{f}}_{\mathrm{r}\mathrm{e}\mathrm{s}}<{0.5\mathrm{f}}_{\mathrm{S}\mathrm{W}}$$

(31)

The filter’s inductive reactance compensates for this to a great extent, and the converter offers control over the reactive power sent to the grid. Therefore, the suggested solution design models, for example, LCL filters, are those listed in Table 5 and

Table 6. LCL filter parameters.

Parameters	Values
Damping resistor (${\mathrm{R}}_{\mathrm{d}}$)	0.118 Ω
Resonant frequency (${\mathrm{f}}_{\mathrm{r}\mathrm{e}}\mathrm{e}$)	845 $\mathrm{H}\mathrm{z}$
Grid-side inductor (${\mathrm{L}}_{\mathrm{g}}$)	0.00761 Ω
Sampling frequency ${\mathrm{f}}_{\mathrm{s}}$	10,000 $\mathrm{H}\mathrm{z}$
Crossover frequency ${\mathrm{f}}_{\mathrm{c}}$	254 $\mathrm{H}\mathrm{z}$

. With these parameters, the filter resonance occurs at 769.5 Hz [39].

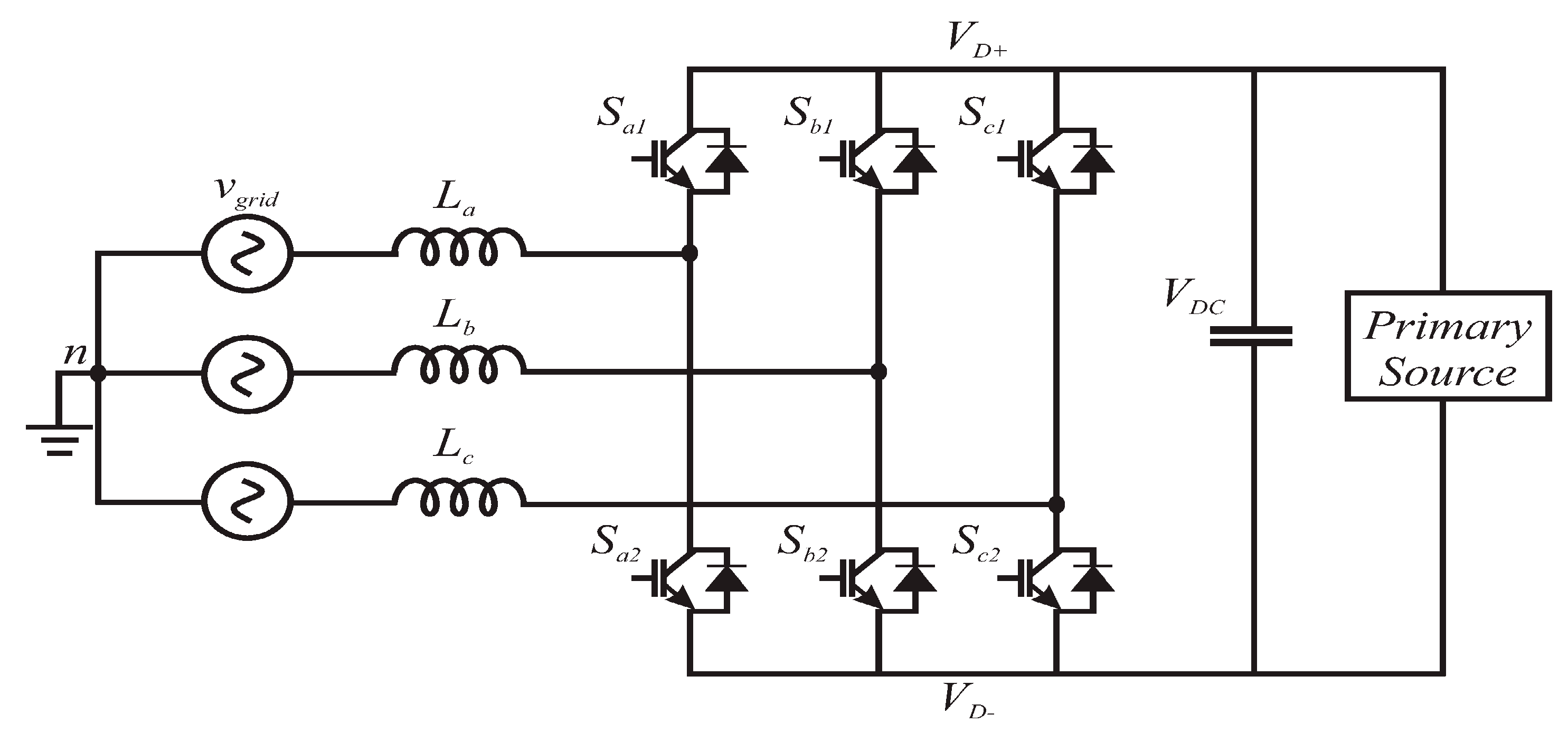
4.7. Modelling of Back-to-Back Converters

The back-to-back converter topology, shown in Figure 6, is the TCS under consideration. Tidal turbines drive a permanent magnet synchronous generator (PMSG), which produces an AC current with variable frequency and amplitude. This “wild” AC is transformed into a DC current by an active rectifier and sent to the DC bus with voltage V_dc. A grid-coupled inverter changes the DC electricity back into a fixed-frequency AC current [40]. The inverter can separately control the reactive and active power that is injected, and it can also balance the active power by adjusting the DC bus voltage. The active rectifier is a three-phase IGBT voltage source converter that employs field-oriented control (FOC) to adjust the generator current based on the alignment of the stator current with the electromotive force (EMF).

The power converter controller on the generator side adjusts the speed and/or torque of the electric generator based on the FOC vector parameters evaluated using a higher-level controller [28], as shown in Figure 7.

In the realm of vector control, the adjustment of instantaneous voltage, current, and flux space vectors takes center stage, grounded in the relationship established for optimal transients [41]. As a result, the system is controlled by shifting the position of the space vectors and ensuring their precise orientation for both steady-state and transient conditions. Consequently, this approach governs the system by strategically shifting space vectors to achieve precise alignment, catering to both steady-state and transient scenarios. Among the methodologies harnessing current control loops in a synchronous reference framework, voltage-oriented control (VOC) and flux-oriented control (FOC) emerge as notable strategies. Notably, virtual flux-oriented control (VFOC) offers advantages over VOC, particularly in optimizing rectifier performance under non-ideal line voltage conditions [42].

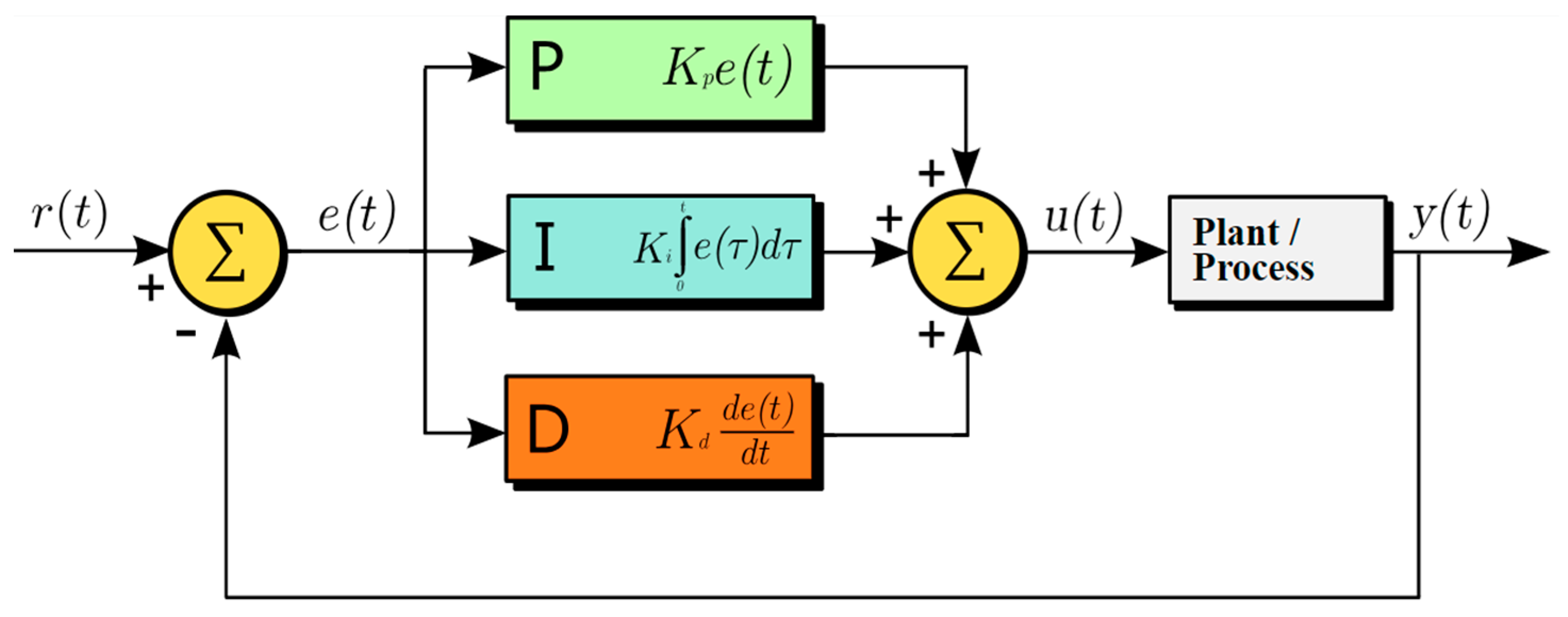
4.8. PID Controller

To achieve our objectives, a methodology based on the typical closed-loop system, illustrated in Figure 7, was adopted. In this system, the controller and plant transfer functions are represented by $G_c\left(S\right)$ and by $G_p\left(S\right)$, respectively. The system can receive both setpoint inputs (r(t)) and disturbance inputs (p(t)). Our approach for designing PID controllers is detailed below.

Initially, the specific type of PID controller employed in the simulations is described. Subsequently, the optimisation algorithm used is outlined [42]. Applying this methodology, the various plant transfer functions were examined, and the results were compared with those obtained using alternative tuning techniques. Through this process, it is demonstrated that the closed-loop system remains robust to gain fluctuations when adjusted using our suggested methods. Furthermore, the step responses exhibit an iso-damping property [43].

Figure 7. A PID controller with a feedback loop block diagram [44].

Figure 7. A PID controller with a feedback loop block diagram [44].

A proportional–integral–derivative controller, often known as a PID controller, is a feedback-based control loop mechanism that is frequently used in industrial control systems and other applications that call for constantly modulated control. The name PID comes from the fact that a PID controller continually determines an error value, e(t), as the difference between a desired setpoint (SP) and a measured process variable (PV), and then corrects the error based on proportional, integral, and derivative terms (denoted P, I, and D, respectively) [44]. PID systems automatically rectify the control function with accuracy and responsiveness. A common example is the cruise control on a car, which would slow down if engine power was applied continuously while it ascended a slope.

In Figure 7, $K_p$ is a tuning parameter for proportional gain, $K_i$ is a tuning parameter for integral gain,$K_d$ is a tuning parameter for derivative gain, $e\left(t\right)=SP-PV\left(t\right)$ e(t) is indicating the error $SP$ is the setpoint, PV(t) is the process variable), and $t$ is the time or instantaneous time [44].

4.9. Generic Three-Phase VSC Electrical Topology

Figure 8 illustrates a generic three-phase VSC electrical topology [30]. The system configuration is shown. The setup consists of a voltage source rectifier with a line inductance on the AC side (L_s, R_s), six separate IGBT switches, and a DC-link capacitor C on the DC side.

An active rectifier refers to a voltage source converter that utilises three-phase IGBT technology to regulate generator current. It accomplishes this by drawing power from a balanced three-phase voltage source (represented by ${\mathrm{V}}_{\mathrm{a}}, {\mathrm{V}}_{\mathrm{b}}{, \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{V}}_{\mathrm{c}}$) and obtaining currents ${\mathrm{I}}_{\mathrm{a}}, {\mathrm{I}}_{\mathrm{b}}$, and ${\mathrm{I}}_{\mathrm{c}}$. The PWM rectifier equation can be effectively formulated using Park’s transformation [45] as follows:

$$\left[\begin{array}{c}{\mathrm{V}}_{\mathrm{d}}\\ {\mathrm{V}}_{\mathrm{q}}\end{array}\right]={\mathrm{L}}_{\mathrm{s}}\left[\begin{array}{c}\frac{{\mathrm{d}\mathrm{I}}_{\mathrm{d}}}{\mathrm{d}\mathrm{t}}\\ \frac{{\mathrm{d}\mathrm{I}}_{\mathrm{q}}}{\mathrm{d}\mathrm{t}}\end{array}\right]+\left[\begin{array}{cc}{\mathrm{R}}_{\mathrm{s}}& {-\mathsf{\omega }\mathrm{L}}_{\mathrm{s}}\\ {\mathsf{\omega }\mathrm{L}}_{\mathrm{s}}& {\mathrm{R}}_{\mathrm{s}}\end{array}\right]\left[\begin{array}{c}{\mathrm{I}}_{\mathrm{d}}\\ {\mathrm{I}}_{\mathrm{q}}\end{array}\right]+\left[\begin{array}{c}{\mathrm{V}}_{\mathrm{r}\mathrm{d}}\\ {\mathrm{V}}_{\mathrm{r}\mathrm{q}}\end{array}\right]$$

(32)

In the context of a d–q rotating reference frame, we can represent the voltages and currents as follows: ${\mathrm{I}}_{\mathrm{d}}$ and ${\mathrm{I}}_{\mathrm{q}}$ denote the voltage components along the d-axis and q-axis, respectively. Similarly, ${\mathrm{V}}_{\mathrm{d}}$, ${\mathrm{V}}_{\mathrm{q}}$, and ${\mathrm{V}}_{\mathrm{r}\mathrm{d}}$ represent the corresponding voltage components in the rotating d–q frame. Additionally, ${\mathrm{I}}_{\mathrm{d}}$ and ${\mathrm{I}}_{\mathrm{q}}$ refer to the current components along the d-axis and q-axis, while ${\mathrm{I}}_{\mathrm{r}\mathrm{a}}$, ${\mathrm{I}}_{\mathrm{r}\mathrm{b}}$, and ${\mathrm{I}}_{\mathrm{r}\mathrm{c}}$ are the respective currents in the d–q frame. To express the equation in this rotating reference frame, we utilise the transformation presented in Equation (31). This allows us to reframe the equation appropriately as follows [30]:

$$\left\{\begin{array}{c}{\mathrm{V}}_{\mathrm{d}}={\mathrm{L}}_{\mathrm{s}}\frac{\mathrm{d}\mathrm{I}}{\mathrm{d}\mathrm{t}}+{\mathsf{\omega }\mathrm{L}}_{\mathrm{s}}{\mathrm{i}}_{\mathrm{q}}+{\mathrm{u}}_{\mathrm{d}}\\ 0={\mathrm{L}}_{\mathrm{s}}\frac{\mathrm{d}\mathrm{I}}{\mathrm{d}\mathrm{t}}-{\mathsf{\omega }\mathrm{L}}_{\mathrm{s}}{\mathrm{i}}_{\mathrm{d}}+{\mathrm{u}}_{\mathrm{q}}\end{array}\right.$$

(33)

4.10. Modelling of DC-Link Voltage

The functionality of the rectifier hinges on the minimum DC-link voltage. This value is determined by the peak of the line-to-line voltage, as indicated in Equation (34) below [46].

$${\mathrm{V}}_{(\mathrm{D}\mathrm{C}-\mathrm{m}\mathrm{i}\mathrm{n})}>\sqrt{2}\sqrt{3}{\mathrm{V}}_{\mathrm{L}\mathrm{N}\left(\mathrm{r}\mathrm{m}\mathrm{s}\right)}=\sqrt{3}{\mathrm{E}}_{\mathrm{m}}$$

(34)

The minimum DC-link voltage, denoted as ${\mathrm{V}}_{(\mathrm{D}\mathrm{C}-\mathrm{m}\mathrm{i}\mathrm{n})}$, is calculated based on the line-to-ground voltage, represented as ${\mathrm{V}\mathrm{L}\mathrm{N}}_{\left(\mathrm{r}\mathrm{m}\mathrm{s}\right)}$. Equation (35) is used to determine this minimum DC link and ${\mathrm{V}\mathrm{L}\mathrm{N}}_{\left(\mathrm{r}\mathrm{m}\mathrm{s}\right)}$, taking into account the maximum reference voltage $\frac{{\mathrm{V}}_{\mathrm{D}\mathrm{C}}}{2}$ as shown in Equation (36) [47].

$${\mathrm{V}}_{\left(\mathrm{L}\mathrm{N}\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}\right)}=\frac{{\mathrm{V}}_{\mathrm{D}\mathrm{C}}}{2}$$

(35)

$${\mathrm{V}}_{(\mathrm{D}\mathrm{C}-\mathrm{m}\mathrm{i}\mathrm{n})}>{2\mathrm{V}}_{\mathrm{L}\mathrm{N}\left(\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}\right)}=\frac{2\sqrt{2}}{\sqrt{3}}{\mathrm{V}}_{\mathrm{L}\mathrm{N}\left(\mathrm{r}\mathrm{m}\mathrm{s}\right)}=1.663\mathrm{V}\mathrm{L}\mathrm{L}\left(\mathrm{r}\mathrm{m}\mathrm{s}\right)$$

(36)

The voltage across the DC link does not comply with Equation (37). The capacitance of the DC-link capacitor can be determined using the following equation:

$${\mathrm{C}}_{\mathrm{D}\mathrm{C}}=\frac{\mathrm{P}}{2\mathsf{\pi }\mathrm{f}{\mathrm{V}}_{\mathrm{D}\mathrm{C}}{∆\mathrm{V}}_{\mathrm{D}\mathrm{C}}}$$

(37)

where the term “${∆\mathrm{V}}_{\mathrm{D}\mathrm{C}}$” denotes the peak ripple DC voltage, which is approximately 5% of the supply voltage (${\mathrm{V}}_{\mathrm{D}\mathrm{C}}$). In this context, “P” stands for active power, and “f” represents the generator frequency.

5. Case System Description

The filters were positioned between the step-down transformer and the voltage source converter (VSC). However, a generator-side controller was used to regulate the PMG’s variable speed. The initial stage on the network side was filtration using the CLC filter, converter, and rectifier, as shown in Figure 9. The tidal conversion systems were simulated with these improvements using the MATLAB/Simulink program to assess the system’s operational performance with the design parameters indicated in Table 1, Table 3, Table 4, Table 5 and Table 6.

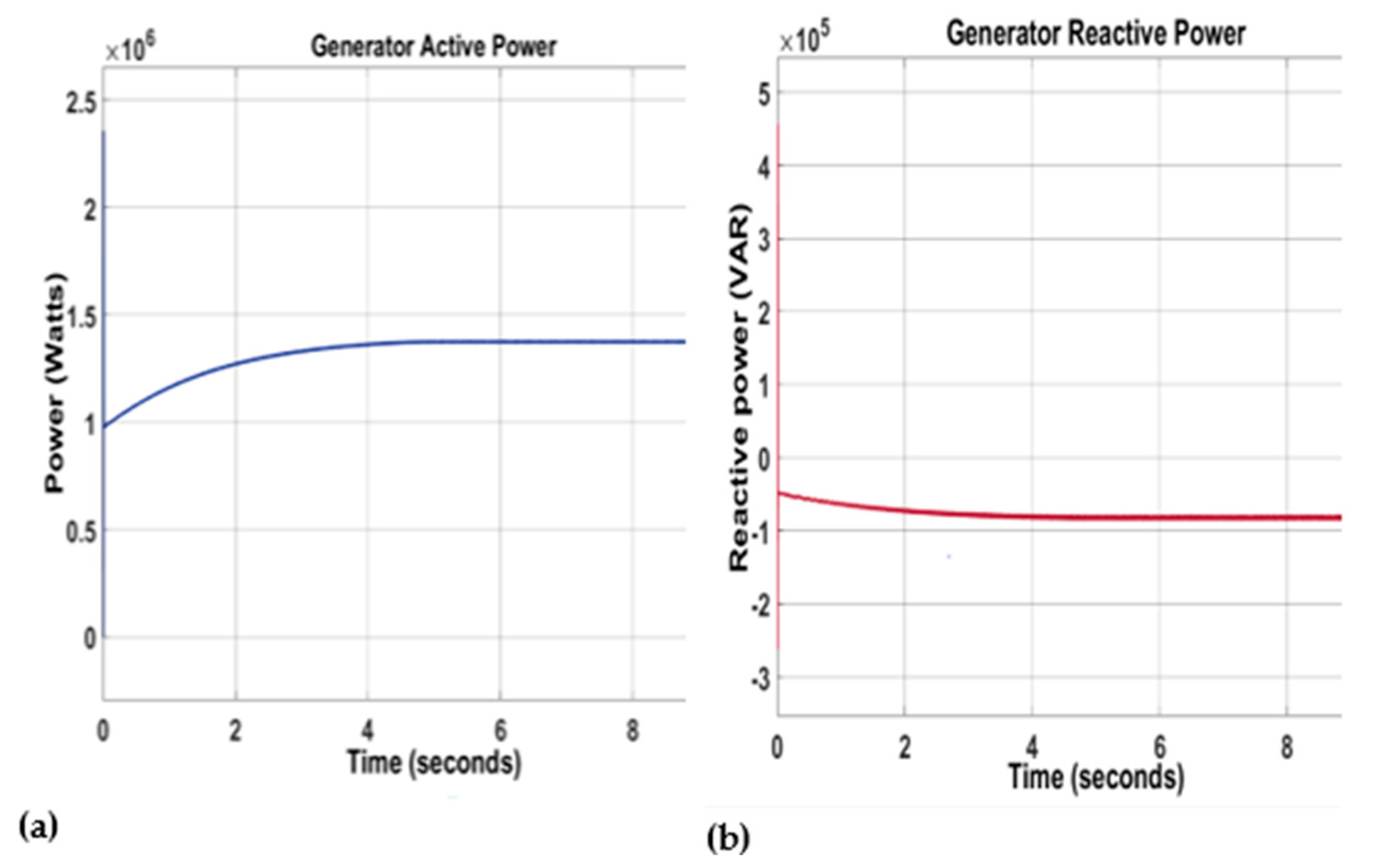
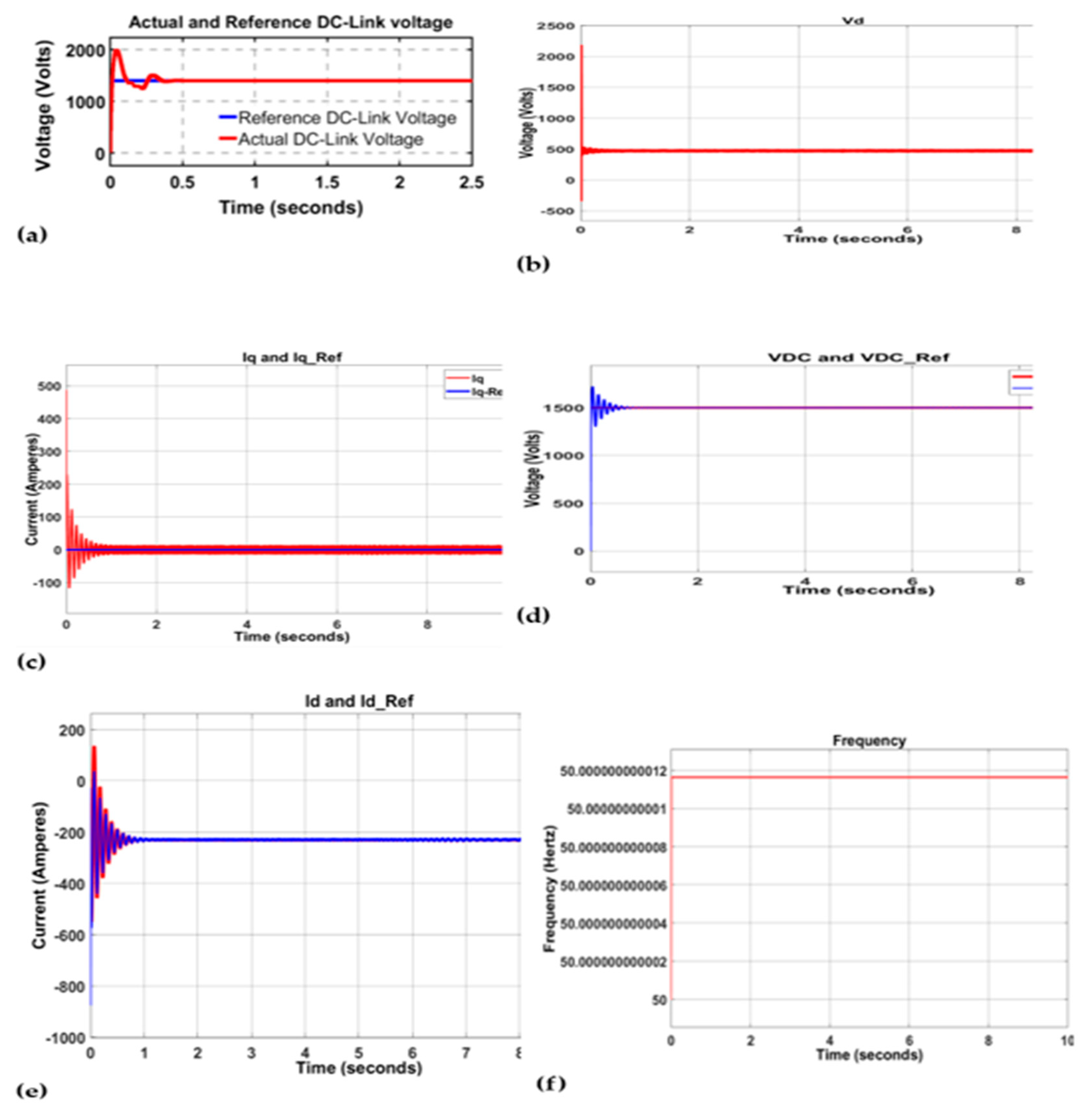
6. Results and Analysis

To determine how well the LCL filters can enhance the power quality of a small coastal village load supplied by a grid-connected tidal turbine, the suggested approach was tested using the simplified network shown in Figure 5 and Figure 6. This power system consists of a full-scale power converter connected to the grid using PMSG and a tidal turbine shaft attached to the PMG rotor. Through lengthy three-phase submarine cables, the MV generator output (6.6 KV) is transmitted over land. Typically, an onshore transformer is used to convert the level of voltage tidal transmission LV (690 V). The speed required to run the tidal generator is predicted to remain constant at 12 m/s. At a rotational speed of 7.7 rad/sec, it can be noted that the tidal rotor speed reaches 24 r/min when the tidal current velocity increases to 12 m/s after 10 s. Figure 10 shows that the generator torque eventually reached its maximum of 600 KNm.

Figure 11a,b indicate that the tidal generator’s active power output was approximately 1.324 MW, and the reactive power of the tidal energy generation is also shown. At the beginning of the simulation, the signal had an overshoot of 233%, a positive undershoot of around 1.055%, and a negative undershoot of about 69.62%.

6.1. Control

The concept behind the voltage control approach is to compare the DC-link voltage to a reference voltage that is set at 1500 volts. The currents of ${\mathrm{I}}_{\mathrm{q}}$ and the ${\mathrm{I}}_{\mathrm{q}}$ reference -${\mathrm{I}}_{\mathrm{d}\mathrm{r}\mathrm{e}\mathrm{f}}$ were compared using the current PI controller on the q-axis, and the error found in the difference between the two currents generates the voltage $V_q$. The $V_q$ reference has a value of zero ${\mathrm{I}}_{\mathrm{d}}$ reference -${\mathrm{I}}_{\mathrm{d}\mathrm{r}\mathrm{e}\mathrm{f}}$ In Figure 12e, the DC link is shown. Figure 12d displays the DC link’s actual and reference voltages. The results demonstrate that the model control yields better results since the difference in inaccuracy between the two signals is very small. However, there are overshoots in 14, 688, and 15 of the 24 simulation states, following which both voltages remain at the same level. The current (${\mathrm{I}}_{\mathrm{d}})$ and the current reference (${\mathrm{I}}_{\mathrm{d}\mathrm{r}\mathrm{e}\mathrm{f}}$) are compared in Figure 12e.

The current PI controller generates the voltage ($V_q$) on the q-axis by comparing the two currents. The $I_q$ reference value is set to be close to zero. However, the grid voltage in the dq0 frame must generate the voltage required to identify the modulation signal. Because the grid regulates its reactive power, the voltage in the d-axis is 500 V, and the voltage in the q-axis is zero. As demonstrated in Figure 12b, the voltages in the dq0 frame $({\mathrm{V}}_{\mathrm{d}} \mathrm{a}\mathrm{n}\mathrm{d} {\mathrm{V}}_{\mathrm{q}})$ assist in the evaluation of the modulation signal in the dq0 frame. Their d-axis and q-axis values are estimated. A magnitude of 0.7 determines the modulation signal results on both axes. Firstly, the modulation signals undergo conversion from the dq0 to the ABC frame before being sent to the pulse width generator. This generator produces twelve pulses required for operating the three-level inverter. The phase-locked loop (PLL) plays a crucial role in generating an output signal dependent on the input signal’s phase. In this case, the PLL uses an internal frequency oscillator to track the frequency and phase of a sinusoidal three-phase signal. To ensure synchronisation, the control system regulates the internal oscillator, minimising any phase difference. Figure 12 illustrates the frequency of the PLL(f), set at 50 Hz, which is like the grid frequency, with a slight variation around 50 Hz. By employing the dq0 frame current control synchronisation, the PLL accurately determines the grid voltage and phase angle, facilitating the proper synchronisation of the inverter with the grid.

This control technique is anticipated to control the grid-tied operating mode’s current injected by a grid-connected inverter. In this study, this was accomplished by a PI controller-based dual-current control loop. The dq0 reference frame was used to implement the current control. The frequency and phase of the grid-tied inverter at the common point PLL were used to synchronise the PCC with the grid. The analysis of the results suggests a strong system response. The fact that there was almost no difference between the DC-link voltage and the outer loop’s reference voltage indicates that the power going to the inverter is well regulated and has a quick response time.

Similarly, the inner control loop results show that a unity power factor is attained by properly regulating and phasing the current injected into the grid. However, the PLL analysis demonstrates that the inverter’s frequency conforms with the PCC’s frequency concerning the grid.

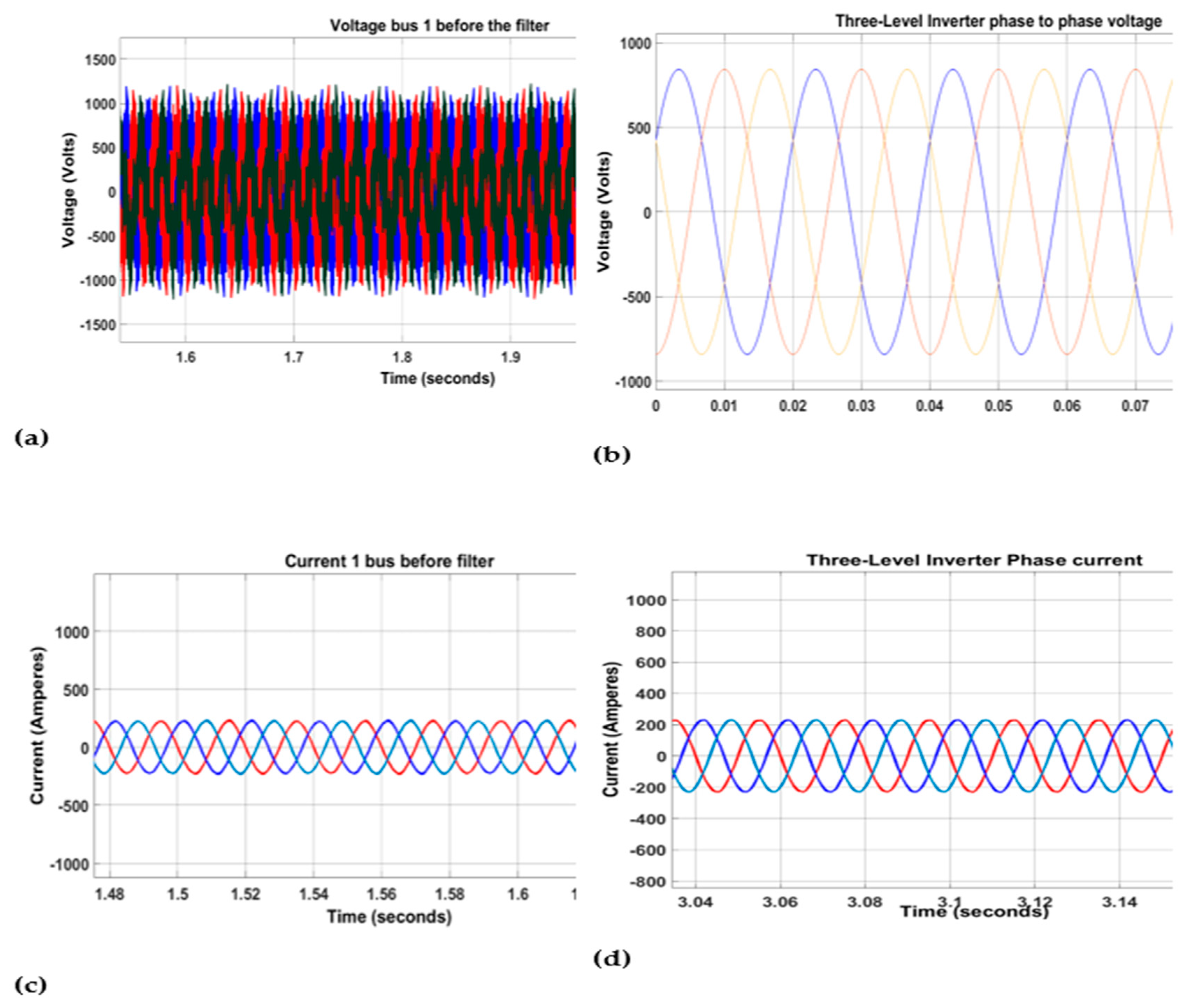
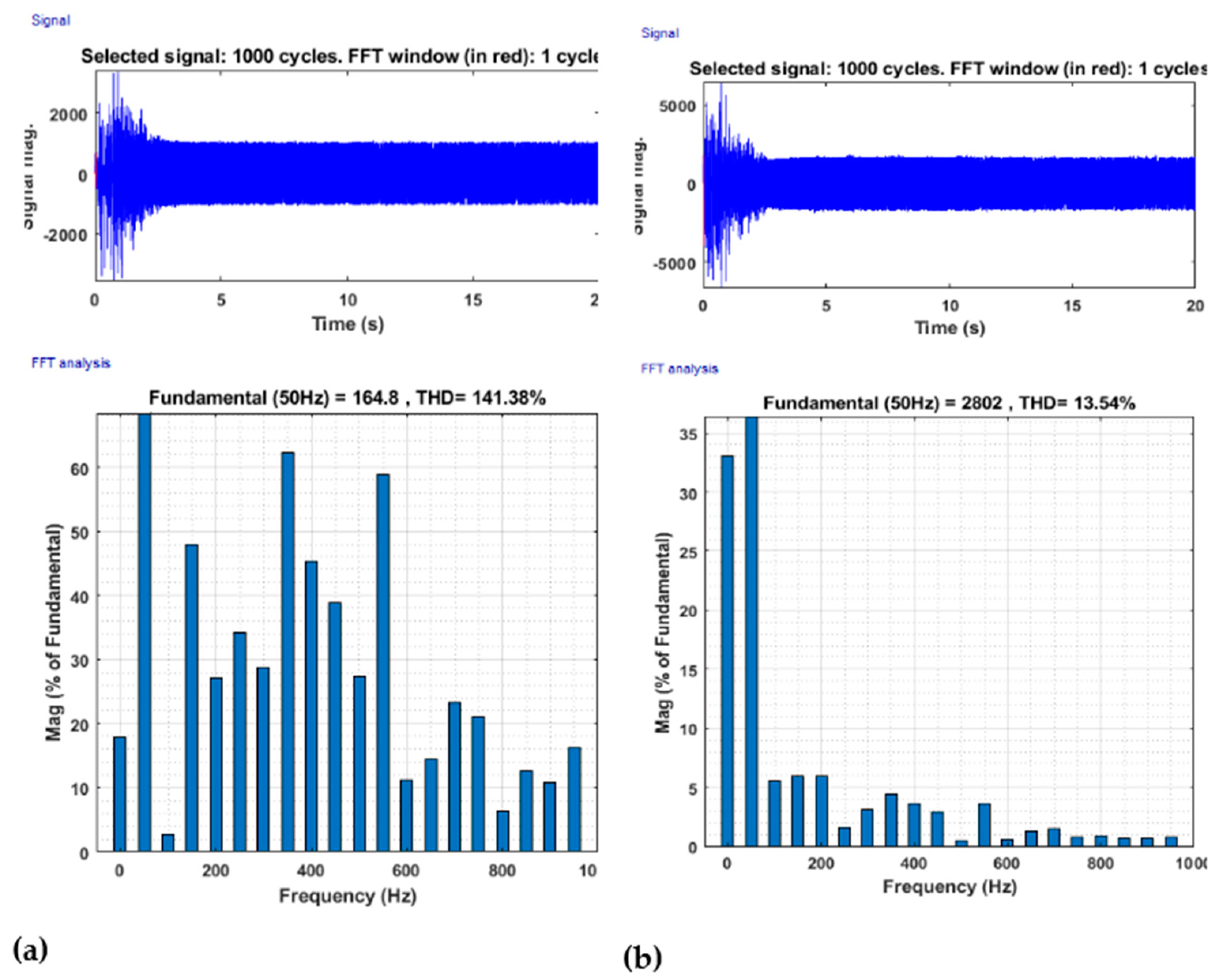
6.2. Inverter Characteristics

The grid-connected applications for tidal energy conversion systems (TCSs) have frequently used multilevel voltage-source inverter (VSI) technology. Due to VSI’s inherent buck characteristics, a boost converter, which is used to step up the DC-link voltage, must be included when using it as the power conversion circuit in TCS, increasing the cost and complexity of the entire conversion system [48]. As the dual component of VSI, the current-source inverter (CSI) has advantages over VSI in terms of built-in boosting and short-circuit protection, direct control of the output current, and extended storage unit lifetime [48,49].

Figure 13a depicts the phase-to-phase voltage of a three-level inverter, showing the presence of harmonics induced by the inverter switching. These harmonics can adversely affect the system’s efficiency by causing issues such as poor power factors and transient effects. To maintain system performance within acceptable limits, the overall harmonic distortion for voltages ranging from 1 to 68 kV should not exceed 5%. Additionally, the total harmonic distortion of the voltage is approximately 45.01% for frequencies up to 5 kHz, as indicated in Figure 14. In contrast, the current harmonic distortion constraint is set at a higher level (Figure 13c), with a minimum threshold of 1000 A and an expected level above 20%, as shown in Figure 13c.

To mitigate these harmonics, an LCL filter was installed between the inverter and the grid. This filter effectively eliminated unwanted harmonics. Consequently, in the output of the LCL filter, the current is indicated in Figure 13d.

Both signals exhibited harmonics that were greater than the 50 Hz standard system frequency. In Figure 13, the output of the LCL filter is depicted, displaying the phase-to-phase voltages and currents. The voltage magnitudes measured approximately 600 V (Figure 13b), and the phase currents were approximately 1213 A (Figure 13d). The phase-to-phase voltage exhibited a rise time of approximately 5.853 milliseconds, followed by a fall time of 5.837 milliseconds. The voltage also had an overshot of 0.324% and an undershot of 1.985%. Similarly, the phase current had a rise time of 5.819 milliseconds and a fall time of 5.823 milliseconds, with overshoot and undershoot values of 1.99% each.

Figure 15 shows the phase-to-ground voltage wave, which had a total harmonic distortion of 141.38%, and the phase current signal had a total harmonic distortion of 13.54%. The total harmonic distortions for current and voltage illustrated in Figure 15a,b decreased by 0.07% and 0.12%, respectively.

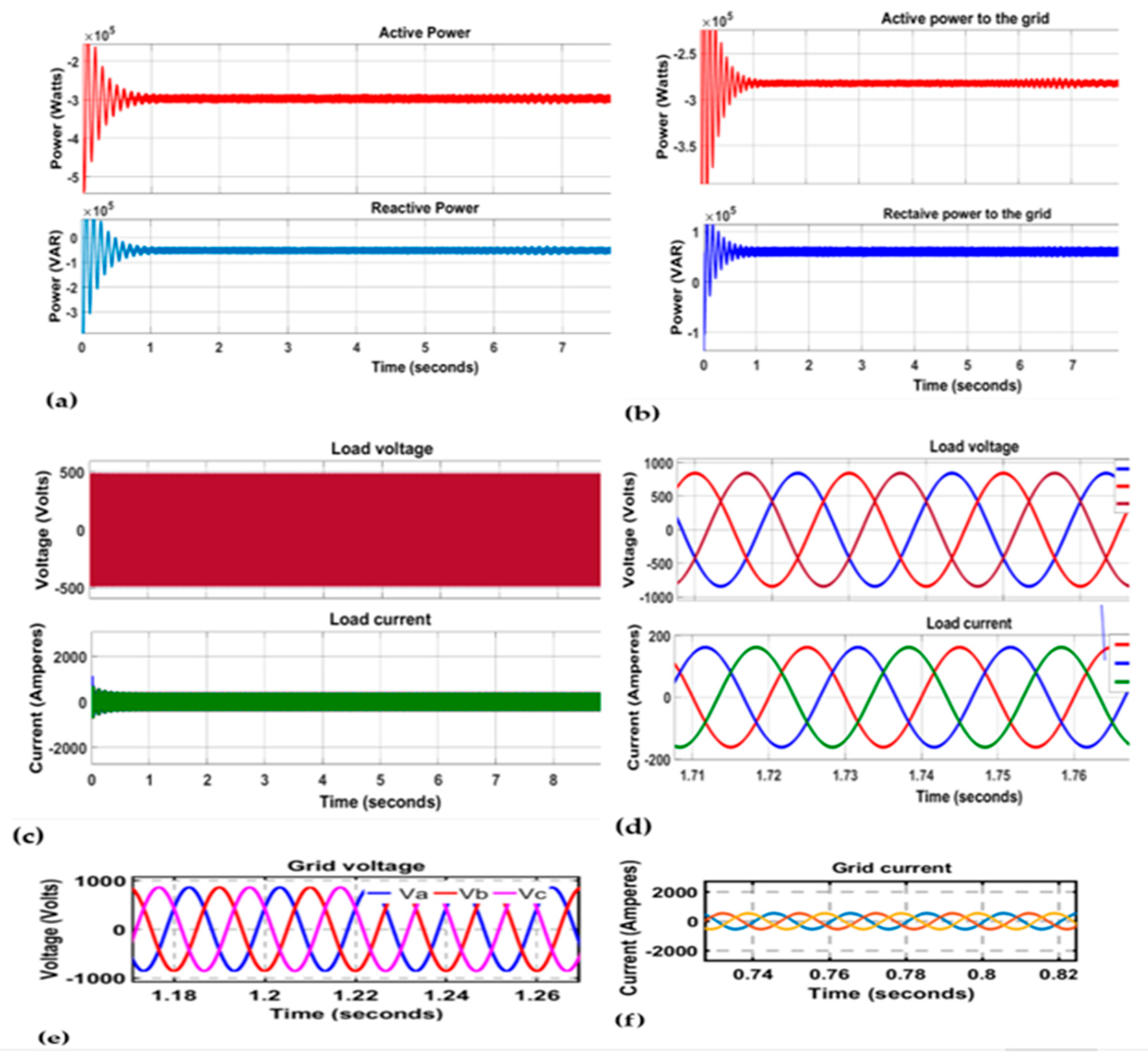
6.3. Case Studies

To assess the performance of the tidal generation system depending on the load value, two case studies were taken into consideration. In the first scenario, the load was less than the power produced by the tidal energy generation system, whereas, in the second scenario, the load was greater than the power created by the tidal generation. In these instances, the active and reactive power as well as the loads and the grid’s voltage and currents were investigated, and the results are shown in Figure 16a,b.

These two scenarios were analysed to determine the operation strategy based on the load quantity value. The load in the first scenario was less powerful than the power generated by the tidal energy-generating equipment. The characteristics provided in Figure 16 were used in this case study for the active power, reactive power, voltage, and current of the load and the grid. The output terminals of the grid-connected tidal energy generation system had a 2.5 MW load. Due to the tidal energy generation’s limited output of 1.54 MW, the system imported power from the grid to handle the 2.5 MW load. Only a load of about 1.23 MW could be received from the grid-tied inverter due to the inverter’s efficiency of 88%; the remainder must be supplied by the grid, as indicated in Figure 16a,f. Figure 16 displays the active and reactive power curves as observed at the load’s output terminals. The reactive power fluctuated to about zero (1.865 × 10⁻⁷ VAR), whereas the active power was 2.5 MW. Between t = 0 and t = 0.3 s, the active power signal overshoots were 14.557%, while between t = 0.3 and t = 0.4 s, the value fell short by approximately 1.998% at time t = 0.6 s according to Equation (18) presented in Energies Standard 2021, volume 14 (page 688).

Subsequently, this response was maintained, resulting in a consistent and stable calculation of 917 kW. The active and reactive power rates exported to the grid are illustrated in Figure 16 a,b. The tidal energy system drew approximately 573.9 kW of active power from the grid and was expected to have a reactive power of about 508.4 KVAR from the grid-connected inverter. It is worth noting that the active power signal had an increased time of approximately 61.950 milliseconds, with an overshoot of 10.92% and an undershoot of 8.35%. However, reactive power took around 29.842 milliseconds, resulting in an overrun of 55% and an undershoot of 1.986%. Figure 16c,d depict the phase currents and phase-to-phase voltages at the load’s ends as pure sinusoidal waves. The voltage (RMS) was approximately 600 V, while the currents were around 874.4 A. The voltage rise time was roughly 5.854 milliseconds, and the voltage die time was about 5.858 milliseconds. Additionally, the voltage had a 1.983% overshoot and a 1.983% undershoot. As for the current, the rising time was approximately 5.858 milliseconds, and the fall time was close to 5.855 milliseconds. The current overshoot was 0.312%, and the current undershoot was around 1.984% or approximately 0.310%.

The tidal generator terminals combined the phase current and phase-to-ground voltage, as shown in Figure 14. The RMS magnitude of the phase-to-phase voltage was approximately 951 volts. Meanwhile, the current phase of the generator measured around 1082 amps, as indicated in Figure 16. Incorporating the rectifier and filter in the generator’s output is crucial to avoid excessive voltage and frequency. Similar findings have been reported in previous research [50,51,52]. The RMS magnitude measurements for voltages and currents were approximately 600 V and 425 A, respectively. The voltage signals experienced a boost lasting about 5.867 milliseconds, followed by a drop lasting 5.866 milliseconds. The overshoot and undershoot values were 0.211% and 1.987%, respectively. For current signals, the enhanced period lasted roughly 5.459 milliseconds, while the drop period was expected to be around 5.381 milliseconds. Other factors, such as overshoot and undershoot, were found to be 6.19% and 1.983%, respectively.

7. Discussion

The integration of the distribution system power unit into the utility grid raises several challenging problems, such as poor power quality and harmonic distortion (THD), which can disrupt the grid and result in significant financial losses. Grid-tied distributed units’ operations must comply with grid codes and standards, which is one of the process’s key issues. It should be highlighted that one of the characteristics considered for power quality assessment is harmonic distortion (THD). Along with their role in lowering weak harmonics, filters can also change the impedance paths of the greatest harmonics, which escape damping and may result in urges at the machine’s terminals from voltage waves reflecting in the cables. The harmonic element is not filtered unless a frequency element has a level path with a low impedance that passes through the filter. These circumstances will help in identifying the system’s undesirable resonance frequencies. Regardless of whether the grid features are unknown or not, filter design can be guided by the given harmonic current constraints, but in this work, the existing CL filter Simulink model was employed. A purely inductive filter requires an inductance value that is too high for an MW converter’s grid connection, resulting in an undesirable voltage drop across it. A large inductor might also cause poor control bandwidth. Therefore, the harmonics are nonetheless reduced to levels that are acceptable for the generator side with the inclusion of a passive filter. The maximum voltage THD for a range of voltages from 1 to 68 kV was 5%, and the maximum THD for currents more than 1000 A was 20%. The simulation outcomes, however, demonstrated that the inverter control program successfully converted the tidal DC power to AC power with total harmonic distortions calculated at 2.44% for the voltage and 0.16% for the current value. Less than 15 mv exhibited a decrease in the number of waves. Even when the generator output changed in either amplitude or frequency, it remained stable. According to the IEEE Standard 1547-2003, it is less than 5%. It was observed that the generator’s output voltage produced less energy than the grid voltage despite the input AC voltage having experienced a significant range of variations. Jayalakshmi [53] used the preferred inverter reactive power output that is fed into the grid to design the q-axis reference current. The inverter terminals of the model used in this investigation had a voltage source that was just sinusoidally controlled. This study shows how crucial it is for generation systems to be connected to the grid to reduce harmonic distortion. After the simulation and control, the harmonic distortion level was roughly maintained at 3% to 3.5%. This satisfies the requirements perfectly. Both the inverter output current and the active power wind generation system output decreased. Therefore, the power utility would experience a power shortage to meet the load demand. However, the reference voltage and the filter output were tied to the control signal. For the PI controller to reduce the error, it depended on the input parameters. The PWM signal, which was fed as a gate signal to the IGBT switch, was then generated through a comparison with the saw-tooth waveform. The voltage source converter, as can be seen, inverted the DC voltage to the sinusoid AC voltage waveform, maintaining the unity power factor.

8. Conclusions

The increasing awareness of environmental issues and the rapid rise in electric power consumption have sparked a heightened interest in renewable energy sources. Among these sources, tidal energy stands out as a promising option to power coastal areas due to its abundance, affordability, and eco-friendliness. Given the significant role of energy in the modern economy, this paper focused on modelling, simulating, and analysing the performance of a tidal current turbine connected to a grid. The study particularly emphasised the integration of an LCL Filter, which was thoroughly modelled, simulated, and examined to enhance the system’s overall efficiency and stability. Voltage-oriented control techniques used in wind turbine systems have been utilised to control tidal energy systems and the functioning of weak and extremely weak grids. It was observed that LCL filters were the most popular option. Thus, an advanced control is required for the control structure to maintain the plant’s stability and effective regulation. Also mentioned was passive and active damping regarding resonance-peak damping for higher-order filters. Therefore, the tidal turbine generating algorithm was effectively implemented, and the all-system block system was simulated using MATLAB/Simulink. The system imported electricity from the grid to satisfy the 2.5 MW load because tidal energy generation had a limited output of 1.54 MW. Due to the grid-tied inverter’s 88% efficiency, only a load of roughly 1.23 MW could be received from it; any further power must come from the grid. The active power was 2.5 MW, whereas the reactive power varied in a range around zero (1.865 × 10⁻⁷ VAR) from t = 0 to t = 0.3 s. There were some harmonics at the PMSG output restrictions and some with voltage sag in the tidal power generation. The LCL filter lowered the switching frequency ripple and aided in coupling with a current-like performance to the utility grid, and the intermediate circuit’s voltage ripples were reduced and stabilised at the predetermined value. Therefore, it meets industry standards and allows for the occurrence of a THD within. The outcomes of the simulation demonstrate that the controller’s operation presents no issues and offers a superior dynamic and steady-state performance of the grid-connected tidal energy system with low overall harmonic distortion, which was around 0.12% for voltage and 0.07% for current. To prevent over-modulation, its minimum operating voltage was higher than the grid peak voltage. However, during this investigation, 85% efficiency was attained. The goal of future studies should be to validate these results with a test bench setup and conduct a sensitivity analysis to measure how the system responds to changes in its parameters. Furthermore, future analysis should focus on more advanced and intelligent control strategies to enhance the performance of single-stage inverters. Another factor that needs to be investigated in the framework of smart grids is how to incorporate two-way communication into these systems.