Experimental and DEM Simulation Study on the Mechanical Characteristic and Strain Energy Evolution of Longmaxi Shale under a Confining Pressure Unloading Path
Abstract
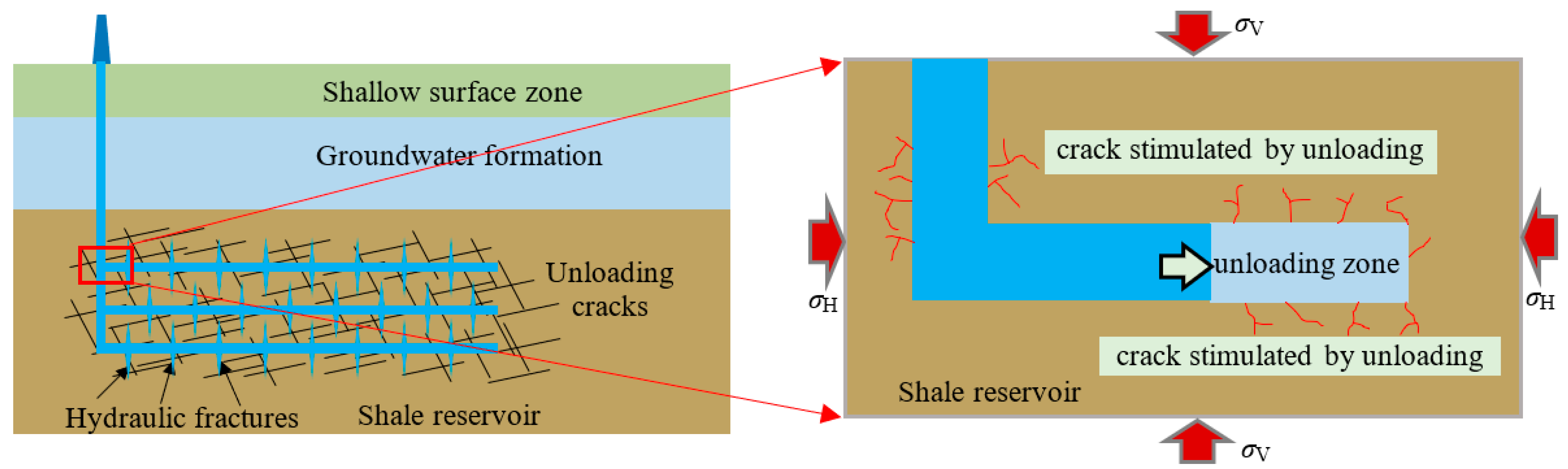
:1. Introduction
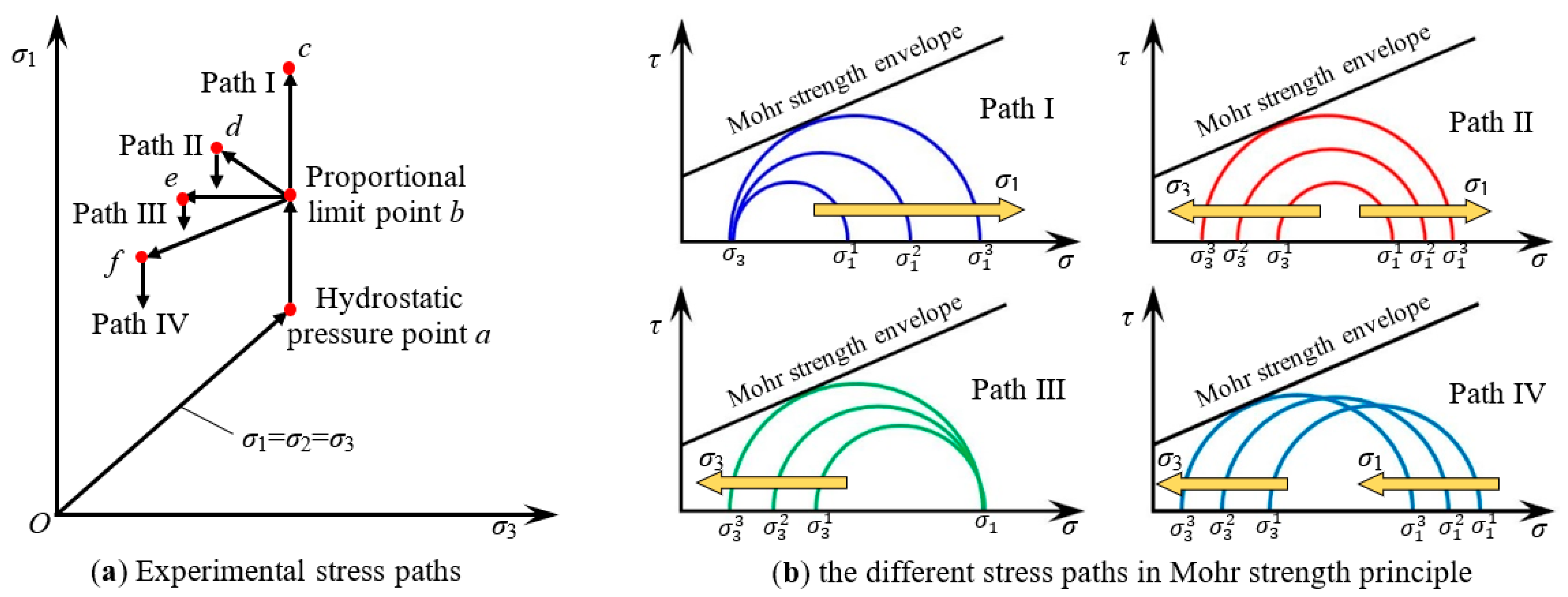
2. Experimental Methodology and Procedures
2.1. Specimen Preparation and Description
2.2. Experimental Program
3. Experimental Results of Confining Pressure Unloading Tests on Shale
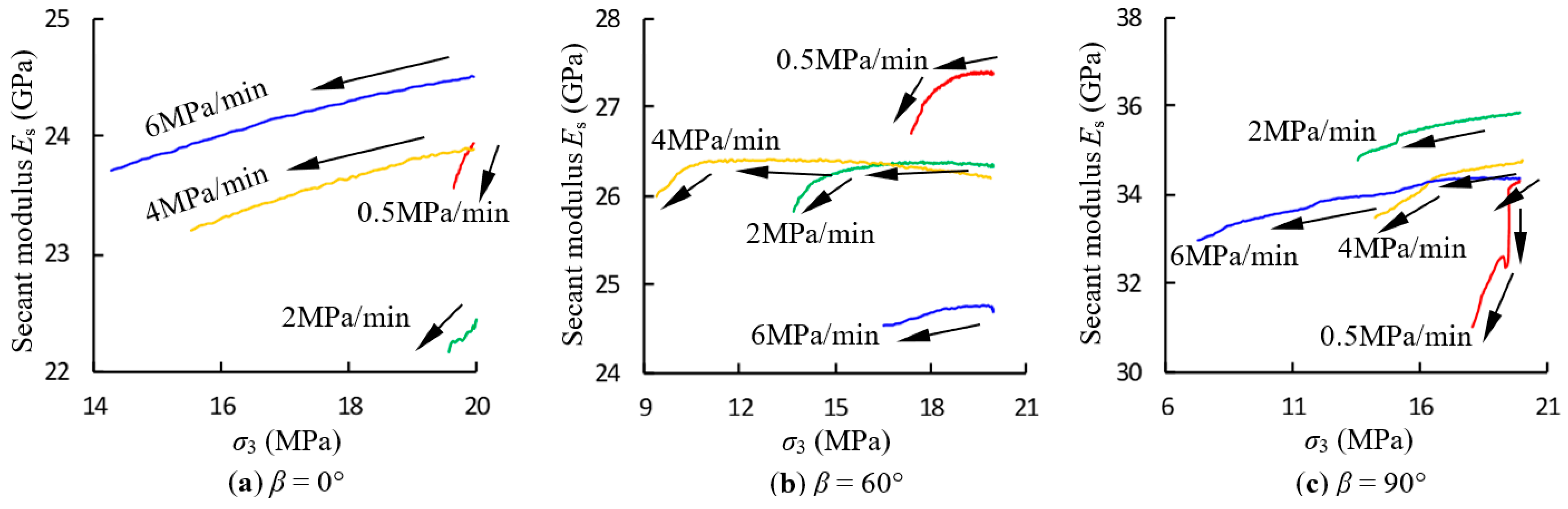
3.1. Analysis of Strength and Deformation Parameters
3.2. Analysis of the Failure Mode
4. DEM Simulation of Confining Pressure Unloading Tests on Shale
4.1. DEM Simulation Model and Procedure
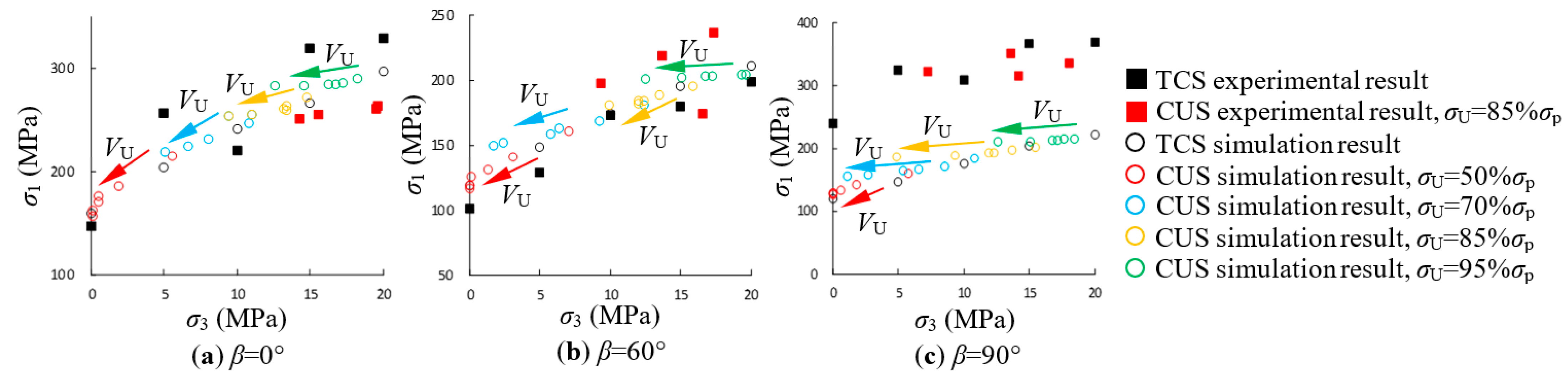
4.2. Results Comparison of the DEM Simulation with Laboratory Tests
4.3. DEM Simulation Results of Unloading Confining Pressure Tests on Shale
4.4. Discussion on the Failure Mechanism of Unloading Confining Pressure Tests on Shale
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| DEM | discrete element method |
| PFC | particle flow code |
| XRD | X-ray diffraction |
| TCS | triaxial compression strength |
| CUS | confining pressure unloading strength |
| PB | Parallel bond model |
| SJ | Smooth joint model |
| β | bedding inclination of shale specimen, ° |
| σ3 | confining pressure, MPa |
| σp | peak stress, MPa |
| E | elasticity modulus, GPa |
| v | Poisson’s ratio |
| C | cohesion, MPa |
| φ | friction angle, ° |
| VU | confining pressure unloading rate, MPa/min |
| σU | Unloading initial point, MPa |
| ∆σ3 | confining pressure reduction, MPa |
| U1 | axial strain energy, MJ/m3 |
| U3 | radial strain energy, MJ/m3 |
| Ue | elastic strain energy, MJ/m3 |
| Ud | dissipated energy, MJ/m3 |
References
- Yu, M. Chemical and Thermal Effects on Wellbore Stability of Shale Formations. Ph.D. Dissertation, The University of Texas at Austin, Austin, TX, USA, 2002. [Google Scholar]
- Liu, X.; Zeng, W.; Liang, L.; Lei, M. Wellbore stability analysis for horizontal wells in shale formations. J. Nat. Gas Sci. Eng. 2016, 31, 1–8. [Google Scholar] [CrossRef]
- Jin, X.; Shah, S.N.; Roegiers, J.C.; Zhang, B. Fracability evaluation in shale reservoirs-an integrated petrophysics and geomechanics approach. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, Society of Petroleum Engineers, The Woodlands, TX, USA, 4–6 February 2014. [Google Scholar]
- Jin, X.; Shah, S.N.; Truax, J.A.; Roegiers, J.C. A Practical petrophysical approach for brittleness prediction from porosity and sonic logging in shale reservoirs. In Proceedings of the SPE Annual Technical Conference And Exhibition, Society of Petroleum Engineers, Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar]
- Rybacki, E.; Meier, T.; Dresen, G. What controls the mechanical properties of shale rocks?—Part II: Brittleness. J. Pet. Sci. Eng. 2016, 144, 39–58. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.C.; Ranjith, P.G.; Perera, M.S.A. The brittleness indices used in rock mechanics and their application in shale hydraulic fracturing: A review. J. Pet. Sci. Eng. 2016, 143, 158–170. [Google Scholar] [CrossRef]
- Kivi, I.R.; Ameri, M.; Molladavoodi, H. Shale brittleness evaluation based on energy balance analysis of stress-strain curves. J. Pet. Sci. Eng. 2018, 167, 1–19. [Google Scholar] [CrossRef]
- Yang, S.Q.; Yin, P.F.; Ranjith, P.G. Experimental study on mechanical behavior and brittleness characteristics of Longmaxi formation shale in Changning, Sichuan Basin, China. Rock Mech. Rock Eng. 2020, 53, 2461–2483. [Google Scholar] [CrossRef]
- Duan, K.; Ji, Y.L.; Wu, W.; Kwok, C.Y. Unloading-induced failure of brittle rock and implications for excavation-induced strain burst. Tunn. Undergr. Space Technol. 2019, 84, 495–506. [Google Scholar] [CrossRef]
- Ren, F.Q.; Chang, Y.; He, M.C. A systematic analysis method for rock failure mechanism under stress unloading conditions: A case of rock burst. Environ. Earth Sci. 2020, 79, 370. [Google Scholar] [CrossRef]
- Dokhani, V.; Yu, M.; Bloys, B. A wellbore stability model for shale formations: Accounting for strength anisotropy and fluid induced instability. J. Nat. Gas Sci. Eng. 2016, 32, 174–184. [Google Scholar] [CrossRef]
- Ma, T.S.; Chen, P.; Zhang, Q.B.; Zhao, J. A novel collapse pressure model with mechanical-chemical coupling in shale gas formations with multi-weakness planes. J. Nat. Gas Sci. Eng. 2016, 36, 1151–1177. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, D.Y.; Ren, S.; Yang, C.H. Comparison of the characteristics of rock salt exposed to loading and unloading of confining pressures. Acta Geotech. 2016, 11, 221–230. [Google Scholar] [CrossRef]
- Liang, Y.P.; Li, Q.M.; Gu, Y.L.; Zou, Q.L. Mechanical and acoustic emission characteristics of rock: Effect of loading and unloading confining pressure at the postpeak stage. J. Nat. Gas Sci. Eng. 2017, 44, 54–64. [Google Scholar] [CrossRef]
- Niandou, H.; Shao, J.F.; Henry, J.P.; Fourmaintraux, D. Laboratory investigation of the mechanical behavior of Tournemire shale. Int. J. Rock Mech. Min. Sci. 1997, 34, 3–16. [Google Scholar] [CrossRef]
- Kuila, U.; Dewhurst, D.N.; Siggins, A.F.; Raven, M.D. Stress anisotropy and velocity anisotropy in low porosity shale. Tectonophysics 2011, 503, 34–44. [Google Scholar] [CrossRef]
- Masri, M.; Sibai, M.; Shao, J.F.; Mainguy, M. Experimental investigation of the effect of temperature on the mechanical behavior of Tournemire shale. Int. J. Rock Mech. Min. Sci. 2014, 70, 185–191. [Google Scholar] [CrossRef]
- Rybacki, E.; Reinicke, A.; Meier, T.; Makasi, M.; Dresen, G. What controls the mechanical properties of shale rocks?—Part I: Strength and young’s modulus. J. Pet. Sci. Eng. 2015, 135, 702–722. [Google Scholar] [CrossRef]
- Heng, S.; Guo, Y.; Yang, C.; Daemen, J.J.K.; Li, Z. Experimental and theoretical study of the anisotropic properties of shale. Int. J. Rock Mech. Min. Sci. 2015, 74, 58–68. [Google Scholar] [CrossRef]
- Yang, S.Q.; Yin, P.F.; Huang, Y.H. Experiment and discrete element modelling on strength, deformation and failure behaviour of shale under Brazilian compression. Rock Mech. Rock Eng. 2019, 52, 4339–4359. [Google Scholar] [CrossRef]
- Yang, S.Q.; Yin, P.F.; Li, B.; Yang, D.S. Behavior of transversely isotropic shale observed in triaxial tests and Brazilian disc tests. Int. J. Rock Mech. Min. Sci. 2020, 133, 104435. [Google Scholar] [CrossRef]
- Gui, J.C.; Guo, J.C.; Sang, Y.; Chen, Y.X.; Ma, T.S.; Ranjith, P.G. Evaluation on the anisotropic brittleness index of shale rock using geophysical logging. Petroleum 2022, in press. [CrossRef]
- Zhai, M.Y.; Xue, L.; Bu, F.C.; Yang, B.C.; Huang, X.L.; Liang, N.; Ding, H. Effects of bedding planes on progressive failure of shales under uniaxial compression: Insights from acoustic emission characteristics. Theor. Appl. Fract. Mech. 2022, 119, 103343. [Google Scholar] [CrossRef]
- Guo, X.L.; Tan, Z.S.; Wang, X.; Li, A.; Ma, Z.J.; Wu, Y.S. Effect of bedding angle and mineral composition on mechanical properties and fracture behavior of phyllite under unloading confining pressures. Geotech. Geol. Eng. 2020, 38, 3611–3621. [Google Scholar] [CrossRef]
- Wang, J.J.; Liu, M.N.; Jian, F.X.; Chai, H.J. Mechanical behaviors of a sandstone and mudstone under loading and unloading conditions. Environ. Earth Sci. 2019, 78, 30. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Cheng, Y.P.; Jin, K.; Tu, Q.G.; Zhao, W.; Zhang, R. Effect of confining pressure unloading on strength reduction of soft coal in borehole stability analysis. Environ. Earth Sci. 2017, 76, 173. [Google Scholar] [CrossRef]
- Huang, R.Q.; Huang, D. Evolution of rock cracks under unloading condition. Rock Mech. Rock Eng. 2014, 47, 453–466. [Google Scholar] [CrossRef]
- Gong, H.L.; Luo, Y.; Xu, K.; Huang, J.H.; Wang, G.; Li, X.P. Failure behaviors of fractured granite during loading and unloading under high confining pressure based on acoustic emission multi-parameter analysis. Theor. Appl. Fract. Mech. 2022, 121, 103442. [Google Scholar] [CrossRef]
- Huang, D.; Li, Y.R. Conversion of strain energy in triaxial unloading tests on marble. Int. J. Rock Mech. Min. Sci. 2014, 66, 160–168. [Google Scholar] [CrossRef]
- Dai, B.; Zhao, G.Y.; Dong, L.J.; Yang, C. Mechanical characteristics for rocks under different paths and unloading rates under confining pressures. Shock Vib. 2015, 2015, 578748. [Google Scholar] [CrossRef]
- Zhang, L.M.; Cong, Y.; Meng, F.Z.; Wang, Z.Q.; Zhang, P.; Gao, S. Energy evolution analysis and failure criteria for rock under different stress paths. Acta Geotech. 2020, 16, 569–580. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Y.J.; Ma, D.P. Mechanical characteristics of coal samples under triaxial unloading pressure with different test paths. Shock Vib. 2020, 2020, 8870821. [Google Scholar] [CrossRef]
- Hou, Z.Y.; Hao, C.B.; Xiao, F.K.; Liu, G. Research on energy conversion and damage features of unloading instability of sandstone under high stress. Adv. Civ. Eng. 2021, 3, 6655968. [Google Scholar] [CrossRef]
- Xie, H.P.; Peng, R.D.; Ju, Y. Energy dissipation of rock deformation and fracture. Chin. J. Rock Mech. Eng. 2004, 23, 3565–3570. [Google Scholar]
- Zhang, L.M.; Gao, S.; Wang, Z.Q.; Ren, M.Y. Analysis on deformation characteristics and energy dissipation of marble under different unloading rates. Teh. Vjesn.—Tech. Gaz. 2014, 21, 987–993. [Google Scholar]
- Zhao, G.Y.; Dai, B.; Dong, L.J.; Yang, C. Energy conversion of rocks in process of unloading confining pressure under different unloading paths. Trans. Nonferrous Met. Soc. China 2015, 25, 1626–1632. [Google Scholar] [CrossRef]
- Li, D.Y.; Sun, Z.; Xie, T.; Li, X.B.; Ranjith, P.G. Energy evolution characteristics of hard rock during triaxial failure with different loading and unloading paths. Eng. Geol. 2017, 228, 270–281. [Google Scholar] [CrossRef]
- Yang, R.; Ma, D.P.; Yang, Y.J. Experimental Investigation of Energy Evolution in Sandstone Failure during Triaxial Unloading Confining Pressure Tests. Adv. Civ. Eng. 2019, 2019, 7419752. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.N.; Zhang, L.M.; Cong, Y.; Song, Y.D.; He, K.Q. The meso-fracturing mechanism of marble under unloading confining pressure paths and constant axial stress. Sci. Rep. 2021, 11, 17835. [Google Scholar] [CrossRef]
- Hao, X.J.; Yuan, L.; Sun, Z.W.; Zhao, W.P.; Ren, B.; Zhao, D.F.; Xue, J.H.; Zhang, X.Y.; Yu, G.F.; Zhang, Q. An integrated study of physical and numerical modelling on the stability of underground tunnel influenced by unloading rate. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2022, 129, 104602. [Google Scholar] [CrossRef]
- Sun, B.W.; Yang, S.Q.; Xu, J.; Yin, P.F. Discrete element simulation on failure mechanical behavior of transversely isotropic shale under two kinds of unloading paths. Theor. Appl. Fract. Mech. 2022, 121, 103466. [Google Scholar] [CrossRef]
- Yin, Q.; Wu, S.S.; Wu, J.Y.; Jing, H.W.; Zhang, J.; Zhang, Y.C. Experiment and particle flow simulation of unloading induced shearing properties for jointed sandstone materials. Case Stud. Constr. Mater. 2023, 18, e02012. [Google Scholar] [CrossRef]
- Cundall, P.A. A Computer Model for Simulating Progressive Large Scale Movements in Blocky Rock Systems. In Proceedings of the Symposium of the International Society of Rock Mechanics, Nancy, France, 4–6 October 1971; Volume 1. Paper No. II-8. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A Discrete Numerical Model for Granular Assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Itasca Consulting Group, Inc. PFC 5.0 Documentation; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2018. [Google Scholar]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Xie, H.P.; Ju, Y.; Li, L.Y. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles. Chin. J. Rock Mech. Eng. 2005, 24, 3003–3010. [Google Scholar]












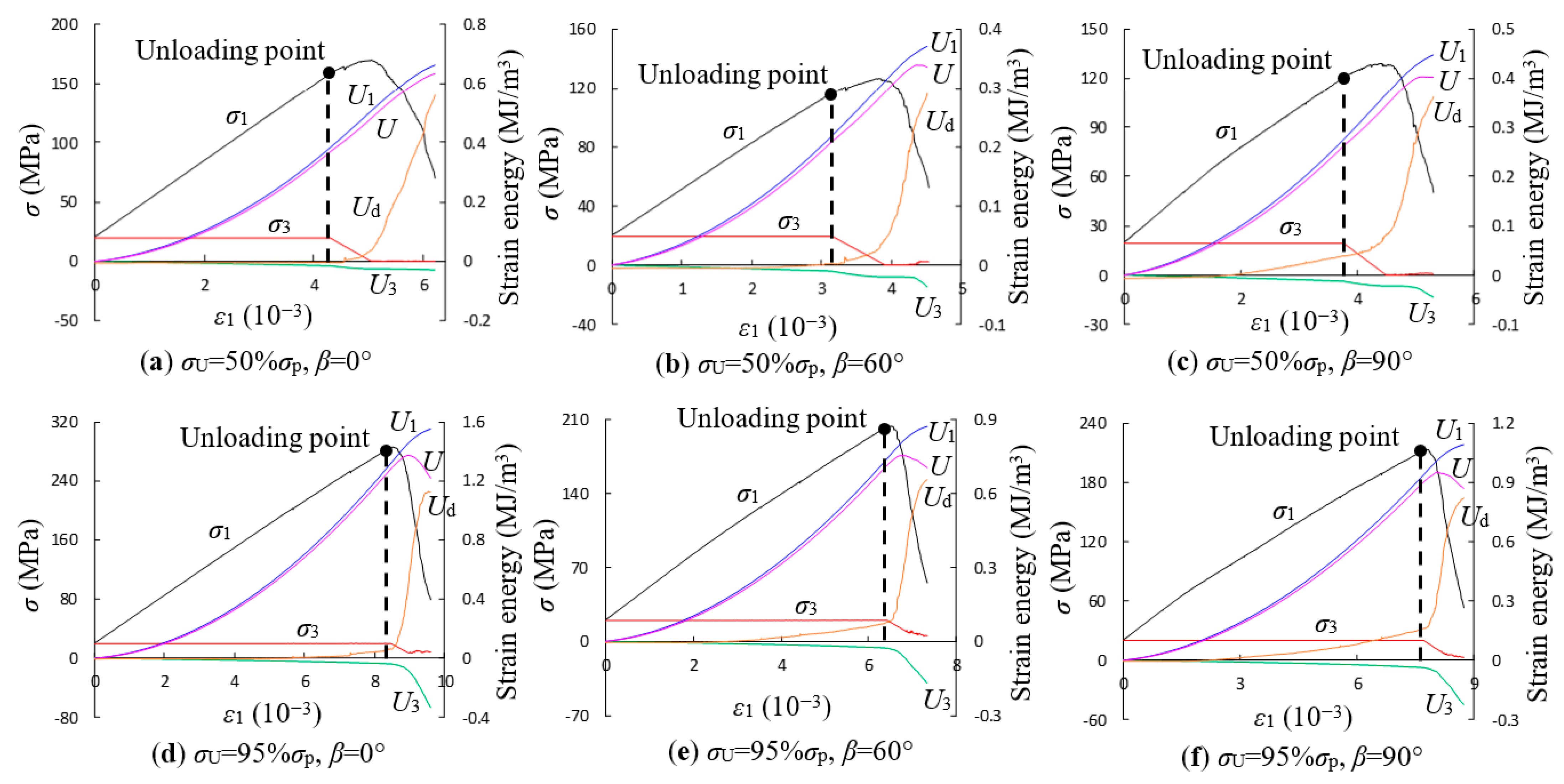
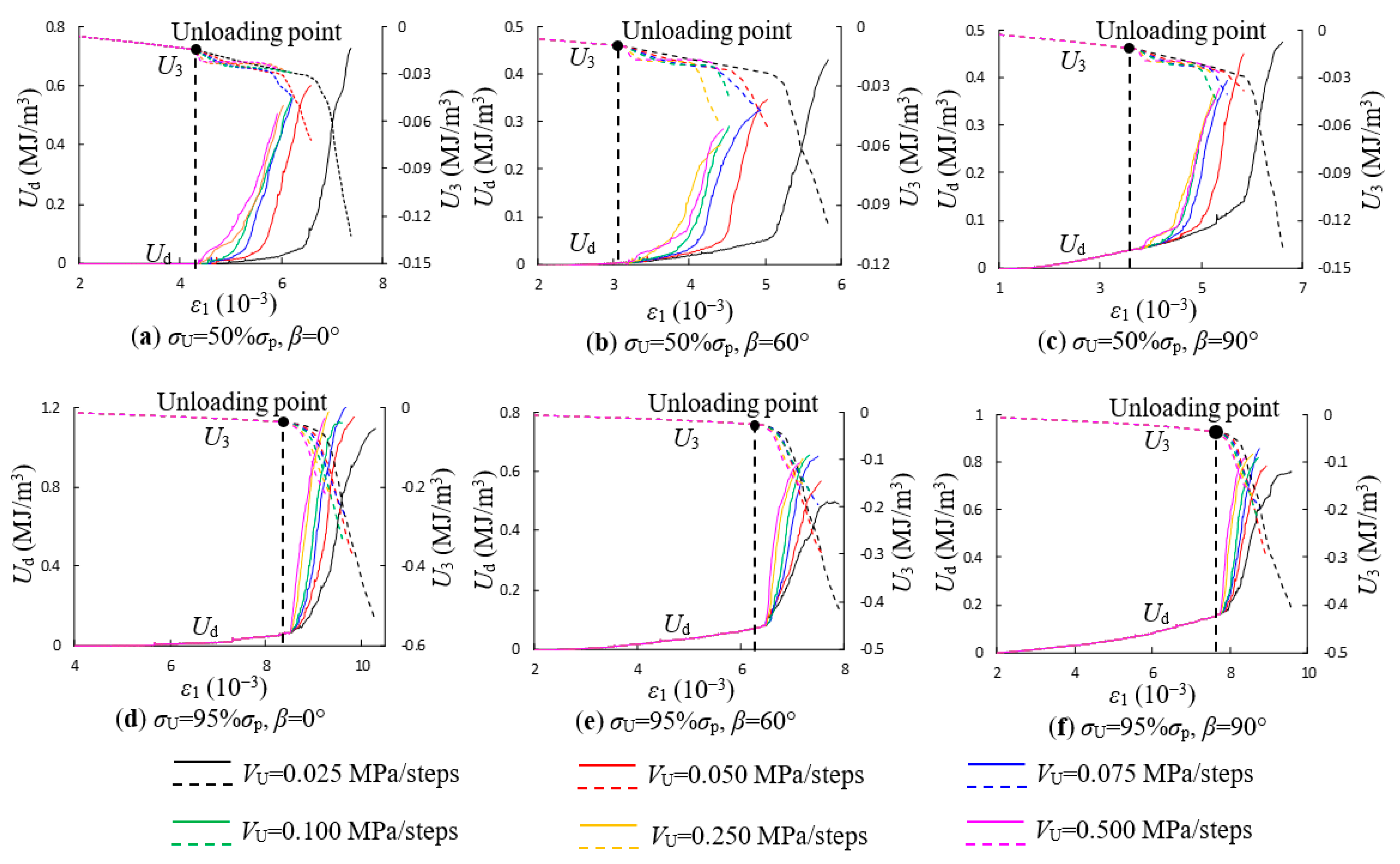
| β | σ3/MPa | σ1/MPa | E/GPa | v | C/MPa | φ |
|---|---|---|---|---|---|---|
| 0° | 0 | 146.41 | 25.09 | 0.111 | 28.88 | 52.3° |
| 5 | 257.43 | 32.70 | 0.212 | |||
| 10 | 220.98 | 26.81 | 0.204 | |||
| 15 | 320.07 | 35.31 | 0.193 | |||
| 20 | 329.42 | 34.37 | 0.158 | |||
| 60° | 0 | 100.52 | 23.79 | 0.113 | 23.96 | 41.7° |
| 5 | 128.98 | 23.72 | 0.115 | |||
| 10 | 173.45 | 26.75 | 0.108 | |||
| 15 | 180.56 | 26.56 | 0.121 | |||
| 20 | 198.99 | 26.55 | 0.109 | |||
| 90° | 0 | 229.33 | 37.35 | 0.136 | 53.35 | 45.6° |
| 5 | 325.20 | 37.91 | 0.135 | |||
| 10 | 308.78 | 36.79 | 0.103 | |||
| 15 | 365.99 | 37.71 | 0.127 | |||
| 20 | 369.03 | 37.55 | 0.136 |
| β | VU (MPa/min) | σU (MPa) | σ1–σ3 (MPa) | σ3` (MPa) | σ1 (MPa) | ∆σ3 (MPa) | ∆σ3/σ3 (%) |
|---|---|---|---|---|---|---|---|
| 0° | 0.5 | 239.1 | 244.1 | 19.64 | 263.7 | 0.36 | 1.80 |
| 2 | 240.8 | 241.9 | 19.57 | 261.5 | 0.43 | 2.15 | |
| 4 | 232.8 | 239.8 | 15.53 | 255.3 | 4.47 | 22.35 | |
| 6 | 230.9 | 236.4 | 14.26 | 250.7 | 5.74 | 28.70 | |
| 60° | 0.5 | 150.4 | 219.8 | 17.37 | 237.2 | 2.63 | 13.15 |
| 2 | 163.5 | 204.8 | 13.69 | 218.5 | 6.31 | 31.55 | |
| 4 | 153.5 | 188.2 | 9.34 | 197.5 | 10.66 | 53.30 | |
| 6 | 151.2 | 157.7 | 16.53 | 174.2 | 3.47 | 17.35 | |
| 90° | 0.5 | 283.4 | 318.2 | 18.03 | 336.2 | 1.97 | 9.85 |
| 2 | 289.8 | 337.9 | 13.56 | 351.5 | 6.44 | 32.20 | |
| 4 | 282.6 | 302.2 | 14.18 | 316.4 | 5.82 | 29.10 | |
| 6 | 289.2 | 315.4 | 7.25 | 322.7 | 12.75 | 63.75 |
| Parallel Bond | Smooth Joint | ||
|---|---|---|---|
| Parameters | Value | Parameters | Value |
| Particle minimum radius, Rmin (mm) | 0.8 | SJ normal stiffness, sj_kn (GPa) | 100,000 |
| Particle radius ratio, Rrat | 1.25 | SJ shear stiffness, sj_ks (GPa) | 50,000 |
| Particle density, ρ (Kg/m3) | 2500 | SJ friction coefficient, sj_fric | 2.0 |
| PB friction coefficient, pb_fric | 0.7 | SJ tensile strength, sj_ten (MPa) | 42 |
| PB radius multiplier | 1.0 | SJ cohesion, sj_coh (MPa) | 100 |
| PB effective modulus, pb_emod (GPa) | 16.5 | Loading rate (m/s) | 0.05 |
| PB normal-to-shear stiffness ratio, pb_krat | 2 | ||
| PB tensile strength, pb_ten (MPa) | 50 | ||
| PB cohesion, pb_coh (MPa) | 250 | ||
| Loading Path | Initial Confining Pressure (MPa) | Bedding Inclination | Unloading Point σU | Unloading Rate VU (MPa/100 Steps) | Loading Rate |
|---|---|---|---|---|---|
| Increase axial stress and decrease confining pressure | 20 | 0°, 15°, 30°, 45°, 60°, 75°, 90° | 50% σp, 70% σp, 85% σp, 95% σp | 0.025, 0.05, 0.075, 0.1, 0.25, 0.5 | 0.05 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, P.; Yang, S.; Gao, F.; Tian, W. Experimental and DEM Simulation Study on the Mechanical Characteristic and Strain Energy Evolution of Longmaxi Shale under a Confining Pressure Unloading Path. Energies 2023, 16, 5960. https://doi.org/10.3390/en16165960
Yin P, Yang S, Gao F, Tian W. Experimental and DEM Simulation Study on the Mechanical Characteristic and Strain Energy Evolution of Longmaxi Shale under a Confining Pressure Unloading Path. Energies. 2023; 16(16):5960. https://doi.org/10.3390/en16165960
Chicago/Turabian StyleYin, Pengfei, Shengqi Yang, Feng Gao, and Wenling Tian. 2023. "Experimental and DEM Simulation Study on the Mechanical Characteristic and Strain Energy Evolution of Longmaxi Shale under a Confining Pressure Unloading Path" Energies 16, no. 16: 5960. https://doi.org/10.3390/en16165960
APA StyleYin, P., Yang, S., Gao, F., & Tian, W. (2023). Experimental and DEM Simulation Study on the Mechanical Characteristic and Strain Energy Evolution of Longmaxi Shale under a Confining Pressure Unloading Path. Energies, 16(16), 5960. https://doi.org/10.3390/en16165960







