Large-Eddy Simulation of Utility-Scale Wind Farm Sited over Complex Terrain
Abstract
1. Introduction
1.1. Surface Roughness
1.2. Form-Induced Dispersive Stress
1.3. Outline
2. Numerical Methods
2.1. Large-Eddy Simulation (LES)
2.2. The Actuator Line and the Actuator Disk
2.3. Near-Surface Model
2.4. Remark
3. Results and Discussions
3.1. Simulation Setup
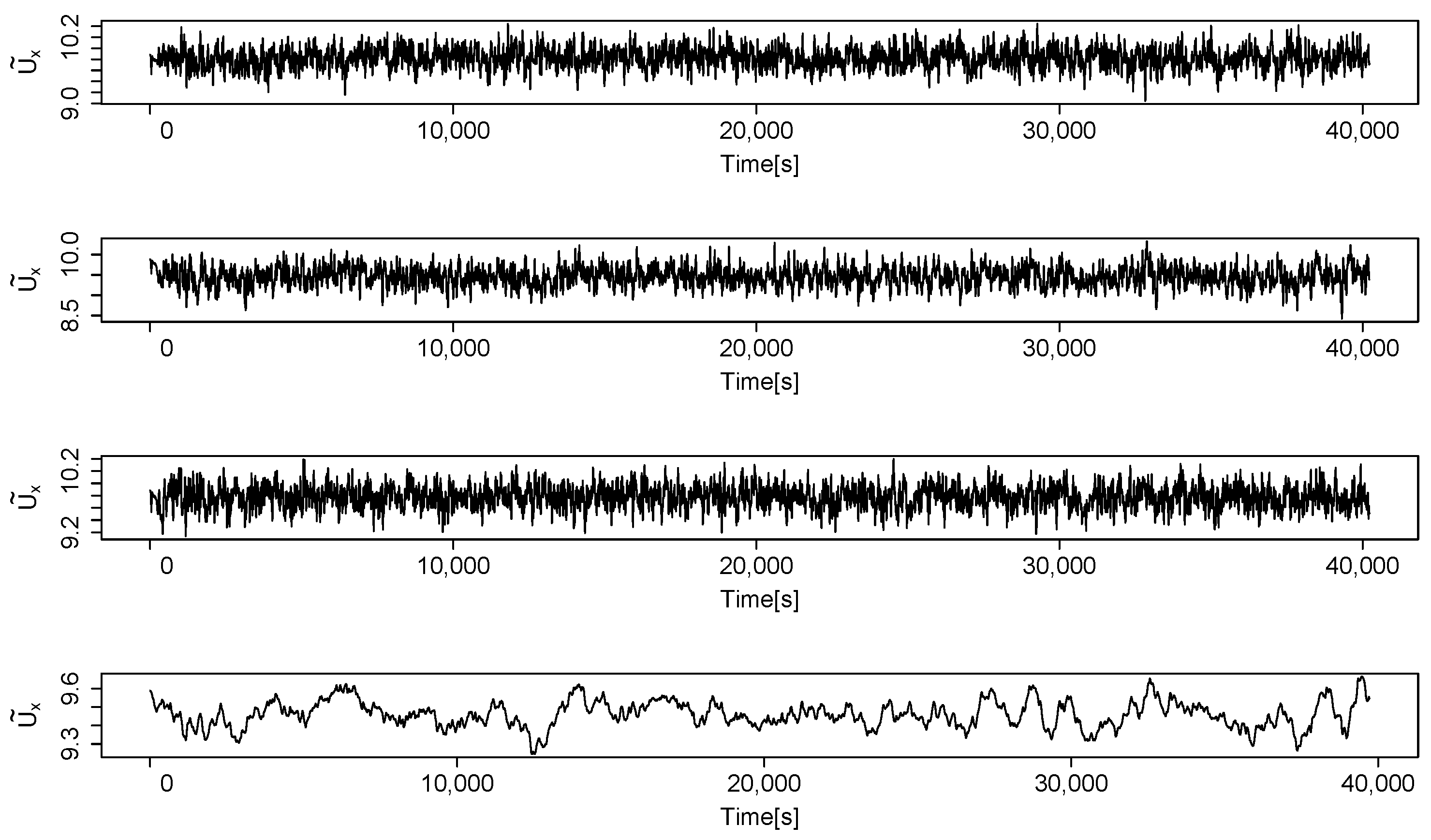
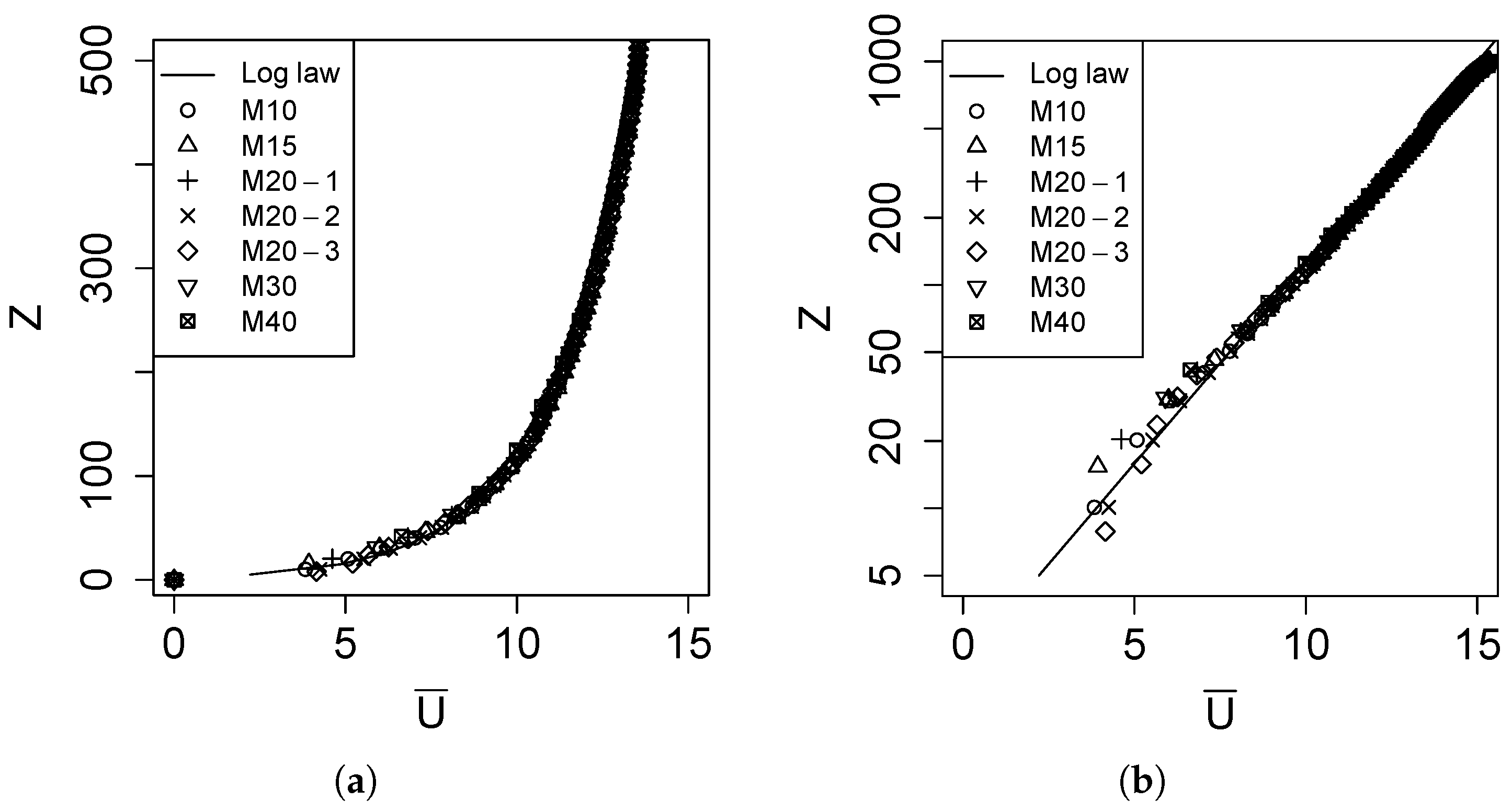
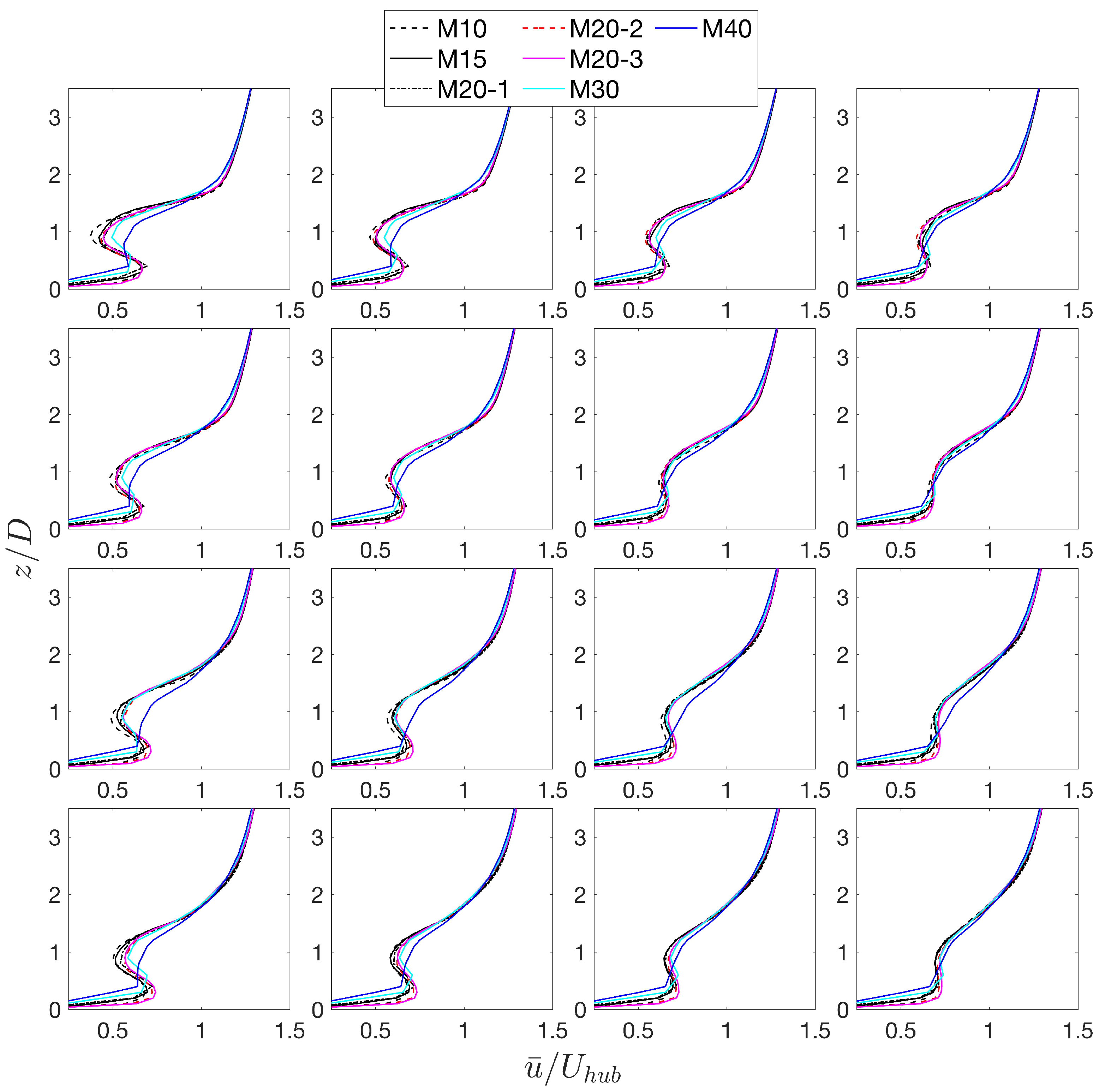
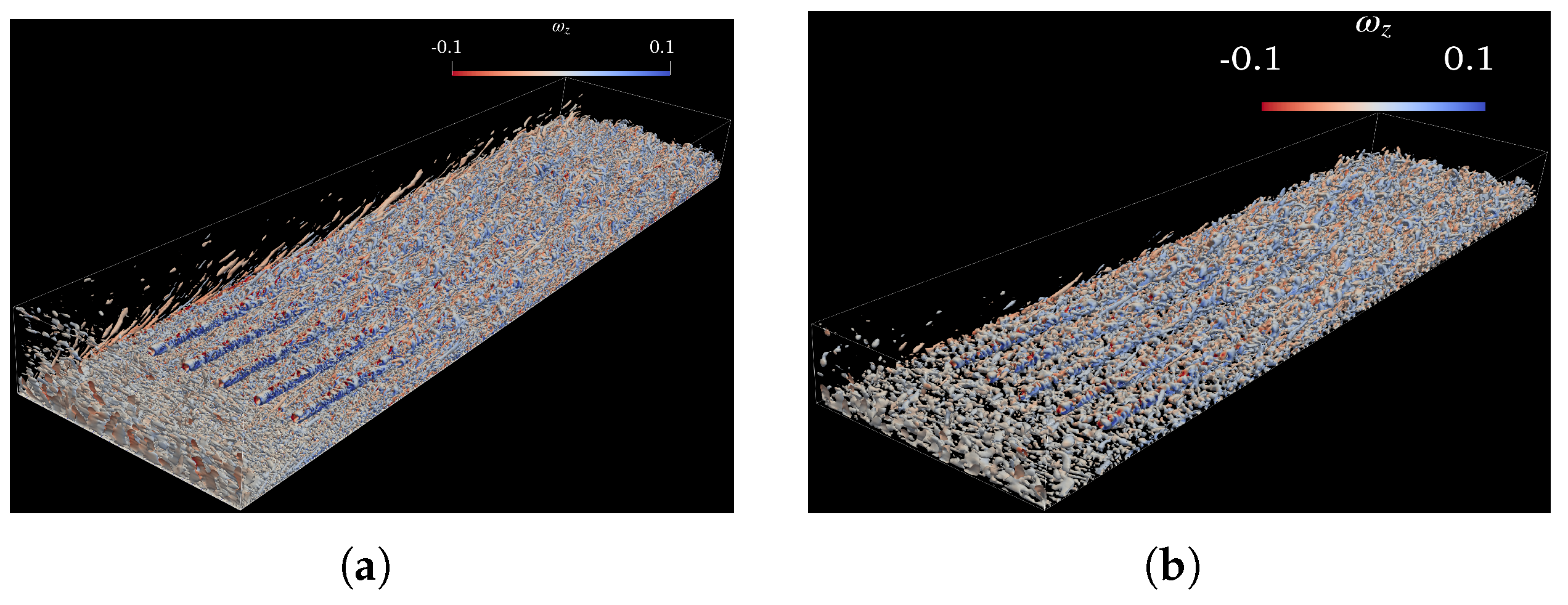
3.2. Effect of Mesh Resolution
3.2.1. Mean Profiles and Turbulence
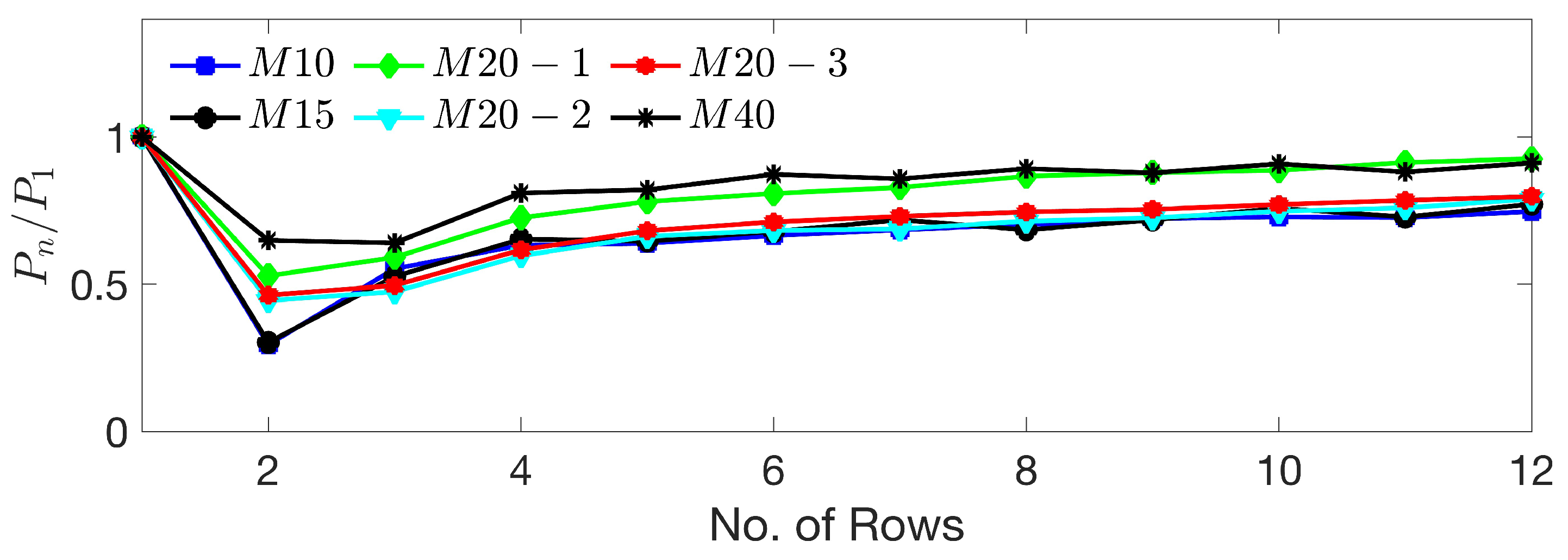
3.2.2. Effects of Resolution on the Power Output of the Wind Farm
3.3. Effect of Vertical Mixing on Wind Farms in Complex Terrain
3.4. Relation between the Power and the Drag Coefficient
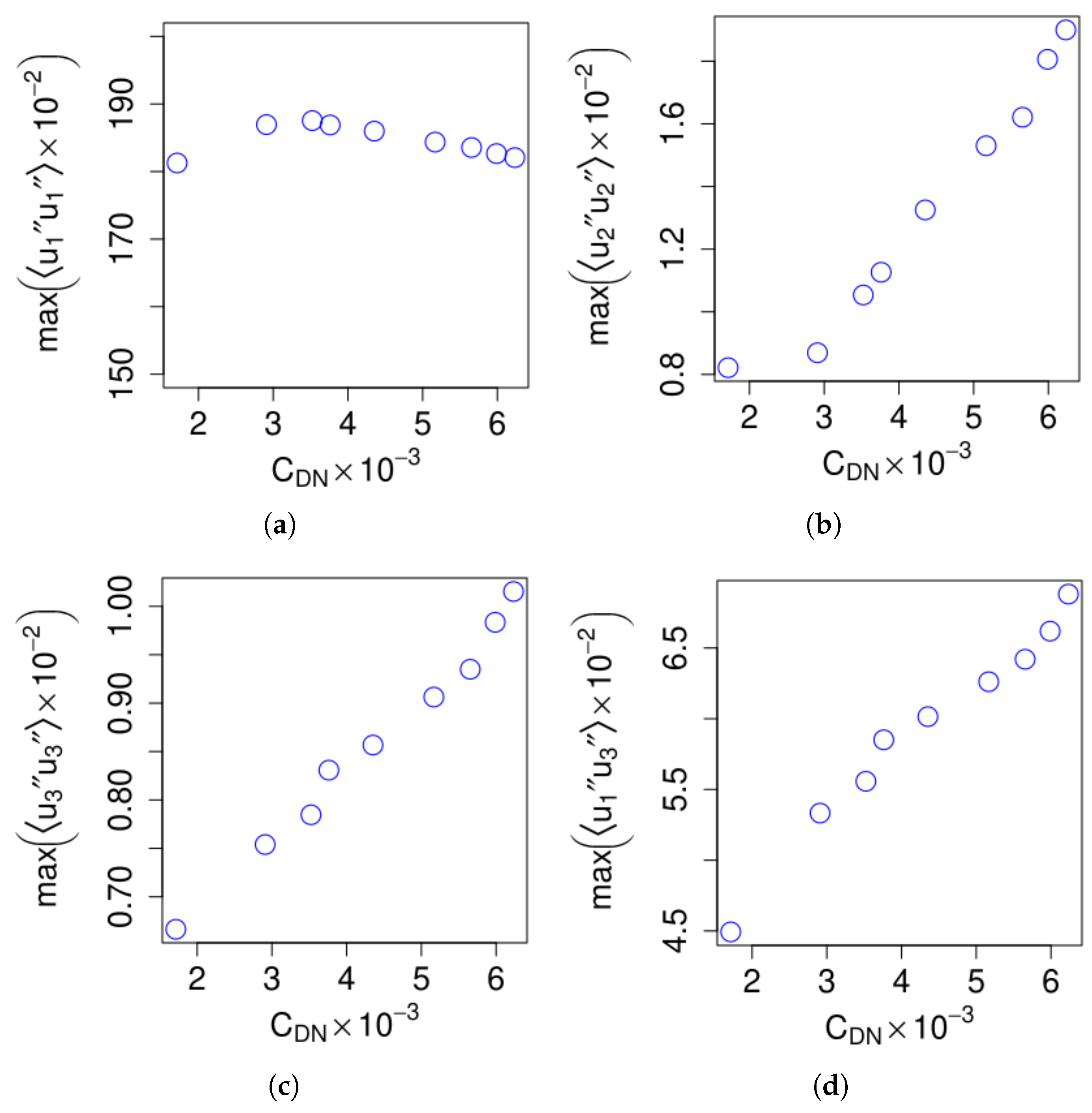
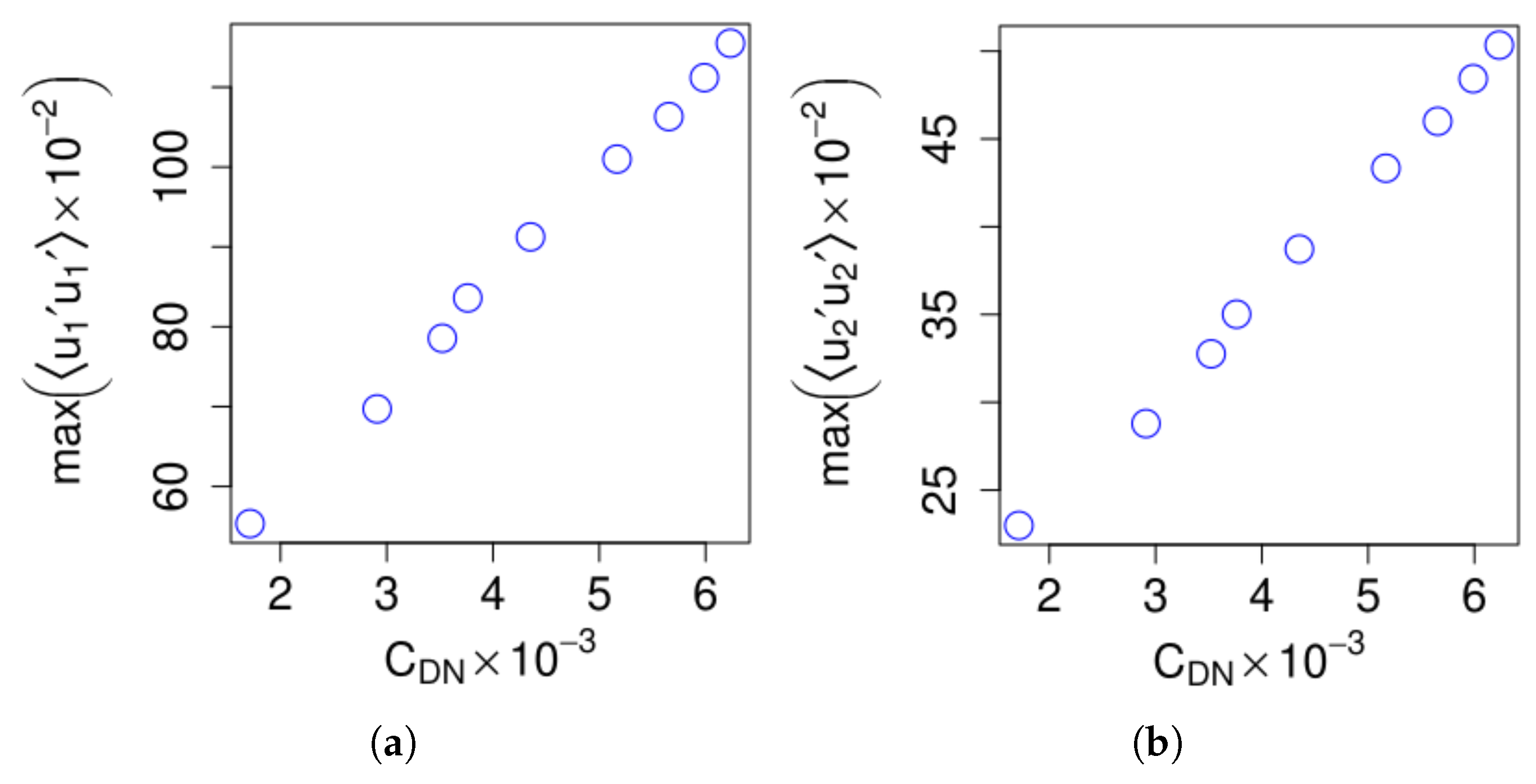
3.5. Dispersive Stress Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Churchfield, M.J.; Lee, S.; Michalakes, J.; Moriarty, P.J. A numerical study of the effects of atmospheric and wake turbulence on wind turbine dynamics. J. Turbul. 2012, 13, N14. [Google Scholar] [CrossRef]
- Vanderwende, B.; Lundquist, J.K. Could crop height affect the wind resource at agriculturally productive wind farm sites? Bound.-Layer Meteorol. 2016, 158, 409–428. [Google Scholar] [CrossRef]
- Pan, Y.; Archer, C.L. A Hybrid Wind-Farm Parametrization for Mesoscale and Climate Models. Bound.-Layer Meteorol. 2018, 168, 469–495. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-turbine and wind-farm flows: A review. Bound.-Layer Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef]
- Alfredsson, P.H.; Segalini, A. Introduction Wind farms in complex terrains: An introduction. Philos. Trans. R. Soc. A 2017, 375, 20160096. [Google Scholar] [CrossRef]
- Tian, W.; Ozbay, A.; Yuan, W.; Sarakar, P.; Hu, H.; Yuan, W. An experimental study on the performances of wind turbines over complex terrain. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Yang, X.; Pakula, M.; Sotiropoulos, F. Large-eddy simulation of a utility-scale wind farm in complex terrain. Appl. Energy 2018, 229, 767–777. [Google Scholar] [CrossRef]
- Liu, L.; Stevens, R.J. Enhanced wind-farm performance using windbreaks. Phys. Rev. Fluids 2021, 6, 074611. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, P.; Bitsuamlak, G.; Cao, S. Large-eddy simulation of wind-turbine wakes over two-dimensional hills. Phys. Fluids 2022, 34, 065123. [Google Scholar] [CrossRef]
- Calaf, M.; Meneveau, C.; Meyers, J. Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 2010, 22, 015110. [Google Scholar] [CrossRef]
- Tobin, N.; Chamorro, L.P. Windbreak effects within infinite wind farms. Energies 2017, 10, 1140. [Google Scholar] [CrossRef]
- Mahrer, Y. An improved numerical approximation of the horizontal gradients in a terrain-following coordinate system. Mon. Weather Rev. 1984, 112, 918–922. [Google Scholar] [CrossRef]
- Lundquist, K.A.; Chow, F.K.; Lundquist, J.K. An Immersed Boundary Method for the Weather Research and Forecasting Model. Mon. Weather Rev. 2010, 138, 796–817. [Google Scholar] [CrossRef]
- Lundquist, K.A.; Chow, F.K.; Lundquist, J.K. An immersed boundary method enabling large-eddy simulations of flow over complex terrain in the WRF model. Mon. Weather Rev. 2012, 140, 3936–3955. [Google Scholar] [CrossRef]
- Arthur, R.S.; Mirocha, J.D.; Lundquist, K.A.; Street, R.L. Using a canopy model framework to improve large-eddy simulations of the neutral atmospheric boundary layer in the Weather Research and Forecasting Model. Mon. Weather Rev. 2019, 147, 31–52. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.S.; Alam, J.M. Scale-adaptive turbulence modeling for LES over complex terrain. Eng. Comput. 2020, 38, 1995–2007. [Google Scholar] [CrossRef]
- Alam, J. Interaction of vortex stretching with wind power fluctuations. Phys. Fluids 2022, 34, 075132. [Google Scholar] [CrossRef]
- Stevens, R.; Meneveau, C. Flow structure and turbulence in wind farms. Annu. Rev. Fluid Mech. 2017, 49, 311–339. [Google Scholar] [CrossRef]
- Xie, S.; Archer, C.L. A numerical study of wind-turbine wakes for three atmospheric stability conditions. Bound.-Layer Meteorol. 2017, 165, 87–112. [Google Scholar] [CrossRef]
- Abedi, H. Assessment of flow characteristics over complex terrain covered by the heterogeneous forest at slightly varying mean flow directions (a case study of a Swedish wind farm). Renew. Energy 2023, 202, 537–553. [Google Scholar] [CrossRef]
- Bao, J.; Chow, F.K.; Lundquist, K.A. Large-eddy simulation over complex terrain using an improved immersed boundary method in the Weather Research and Forecasting Model. Mon. Weather Rev. 2018, 146, 2781–2797. [Google Scholar] [CrossRef]
- Moeng, C.H. A large-eddy-simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 1984, 41, 2052–2062. [Google Scholar] [CrossRef]
- Moeng, C.H.; Sullivan, P.P. A comparison of shear-and buoyancy-driven planetary boundary layer flows. J. Atmos. Sci. 1994, 51, 999–1022. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Meneveau, C.; Parlange, M.B. A scale-dependent dynamic model for large-eddy simulation: Application to a neutral atmospheric boundary layer. J. Fluid Mech. 2000, 415, 261–284. [Google Scholar] [CrossRef]
- Bose, S.T.; Park, G.I. Wall-modeled large-eddy simulation for complex turbulent flows. Annu. Rev. Fluid Mech. 2018, 50, 535–561. [Google Scholar] [CrossRef] [PubMed]
- Chow, F.K.; Schär, C.; Ban, N.; Lundquist, K.A.; Schlemmer, L.; Shi, X. Crossing Multiple Gray Zones in the Transition from Mesoscale to Microscale Simulation over Complex Terrain. Atmosphere 2019, 10, 274. [Google Scholar] [CrossRef]
- Goodfriend, E.; Katopodes Chow, F.; Vanella, M.; Balaras, E. Large-Eddy Simulation of Flow Through an Array of Cubes with Local Grid Refinement. Bound.-Layer Meteorol. 2016, 159, 285–303. [Google Scholar] [CrossRef]
- Mason, P.J.; Thomson, D.J. Stochastic backscatter in large-eddy simulations of boundary layers. J. Fluid Mech. 1992, 242, 51–78. [Google Scholar] [CrossRef]
- Senocak, I.; Ackerman, A.S.; Kirkpatrick, M.P.; Stevens, D.E.; Mansour, N.N. Study of near-surface models for large-eddy simulations of a neutrally stratified atmospheric boundary layer. Bound.-Layer Meteorol. 2007, 124, 405–424. [Google Scholar] [CrossRef]
- Johnson, P.L. On the role of vorticity stretching and strain self-amplification in the turbulence energy cascade. J. Fluid Mech. 2021, 922, A3. [Google Scholar] [CrossRef]
- Hossen, M.K.; Mulayath Variyath, A.; Alam, J.M. Statistical Analysis of Dynamic Subgrid Modeling Approaches in Large Eddy Simulation. Aerospace 2021, 8, 375. [Google Scholar] [CrossRef]
- Garratt, J. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Stull, R.B.; Ahrens, C.D. Meteorology for Scientists and Engineers; Brooks/Cole: Pacific Grove, CA, USA, 2000. [Google Scholar]
- Blom, J.; Wartena, L. The influence of changes in surface roughness on the development of the turbulent boundary layer in the lower layers of the atmosphere. J. Atmos. Sci. 1969, 26, 255–265. [Google Scholar] [CrossRef]
- Nickerson, E.C.; Smiley, V.E. Surface layer and energy budget parameterizations for mesoscale models. J. Appl. Meteorol. 1975, 14, 297–300. [Google Scholar] [CrossRef]
- Ye, C.; Liu, X.N.; Wang, X.K. Effects of roughness elements distribution on overland flow resistance. J. Mt. Sci. 2015, 12, 1145–1156. [Google Scholar] [CrossRef]
- Tani, I.; Sato, H. Boundary-layer transition by roughness element. J. Phys. Soc. Jpn. 1956, 11, 1284–1291. [Google Scholar] [CrossRef]
- Irwin, J.S. A theoretical variation of the wind profile power-law exponent as a function of surface roughness and stability. Atmos. Environ. 1979, 13, 191–194. [Google Scholar] [CrossRef]
- Essa, K.S.; Embaby, M.; Etman, S.M. A notional variation of the wind profile power-law exponent as a function of surface roughness and stability. Atmos. Environ. 2004, 13, 191–194. [Google Scholar]
- Cao, S.; Wang, T.; Ge, Y.; Tamura, Y. Numerical study on turbulent boundary layers over two-dimensional hills—Effects of surface roughness and slope. J. Wind. Eng. Ind. Aerodyn. 2012, 104, 342–349. [Google Scholar] [CrossRef]
- De Paepe, W.; Pindado, S.; Bram, S.; Contino, F. Simplified elements for wind-tunnel measurements with type-III-terrain atmospheric boundary layer. Measurement 2016, 91, 590–600. [Google Scholar] [CrossRef]
- Finnigan, J.; Ayotte, K.; Harman, I.; Katul, G.; Oldroyd, H.; Patton, E.; Poggi, D.; Ross, A.; Taylor, P. Boundary-layer flow over complex topography. Bound.-Layer Meteorol. 2020, 177, 247–313. [Google Scholar] [CrossRef]
- Tobin, N.; Hamed, A.M.; Chamorro, L.P. Fractional flow speed-up from porous windbreaks for enhanced wind-turbine power. Bound.-Layer Meteorol. 2017, 163, 253–271. [Google Scholar] [CrossRef]
- Zhang, Y. Ground Surface Effects in Wind Farms: A Micro Wind Farm Model Study. Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 2018. [Google Scholar]
- Mattuella, J.; Loredo-Souza, A.; Oliveira, M.; Petry, A. Wind tunnel experimental analysis of a complex terrain micrositing. Renew. Sustain. Energy Rev. 2016, 54, 110–119. [Google Scholar] [CrossRef]
- Cheng, S.; Elgendi, M.; Lu, F.; Chamorro, L.P. On the wind turbine wake and forest terrain interaction. Energies 2021, 14, 7204. [Google Scholar] [CrossRef]
- Yang, D.; Meneveau, C.; Shen, L. Large-eddy simulation of offshore wind farm. Phys. Fluids 2014, 26, 025101. [Google Scholar] [CrossRef]
- Modesti, D.; Pirozzoli, S.; Orlandi, P.; Grasso, F. On the role of secondary motions in turbulent square duct flow. J. Fluid Mech. 2018, 847, R1. [Google Scholar] [CrossRef]
- Moltchanov, S.; Shavit, U. A phenomenological closure model of the normal dispersive stresses. Water Resour. Res. 2013, 49, 8222–8233. [Google Scholar] [CrossRef]
- Raupach, M.R.; Shaw, R. Averaging procedures for flow within vegetation canopies. Bound.-Layer Meteorol. 1982, 22, 79–90. [Google Scholar] [CrossRef]
- Raupach, M.; Coppin, P.; Legg, B. Experiments on scalar dispersion within a model plant canopy part I: The turbulence structure. Bound.-Layer Meteorol. 1986, 35, 21–52. [Google Scholar] [CrossRef]
- Böhm, M.; Finnigan, J.; Raupach, M. Dispersive fluxes and canopy flows: Just how important are they? In Proceedings of the 24th Conference on Agricultural and Forest Meteorology, 14th Conference on Biometeorology and Aerobiology: Third Symposium on the Urban Environment, Davis, CA, USA, 14–18 August 2000; American Meteorological Society: Boston, MA, USA, 2000. [Google Scholar]
- Poggi, D.; Katul, G.; Albertson, J. A note on the contribution of dispersive fluxes to momentum transfer within canopies. Bound.-Layer Meteorol. 2004, 111, 615–621. [Google Scholar] [CrossRef]
- Coceal, O.; Thomas, T.; Castro, I.; Belcher, S. Mean flow and turbulence statistics over groups of urban-like cubical obstacles. Bound.-Layer Meteorol. 2006, 121, 491–519. [Google Scholar] [CrossRef]
- Giménez-Curto, L.A.; Lera, M.A.C. Oscillating turbulent flow over very rough surfaces. J. Geophys. Res. Ocean. 1996, 101, 20745–20758. [Google Scholar] [CrossRef]
- Cheng, H.; Castro, I.P. Near wall flow over urban-like roughness. Bound.-Layer Meteorol. 2002, 104, 229–259. [Google Scholar] [CrossRef]
- Santiago, J.L.; Martilli, A.; Martín, F. CFD simulation of airflow over a regular array of cubes. Part I: Three-dimensional simulation of the flow and validation with wind-tunnel measurements. Bound.-Layer Meteorol. 2007, 122, 609–634. [Google Scholar] [CrossRef]
- Pokrajac, D.; Campbell, L.J.; Nikora, V.; Manes, C.; McEwan, I. Quadrant analysis of persistent spatial velocity perturbations over square-bar roughness. Exp. Fluids 2007, 42, 413–423. [Google Scholar] [CrossRef]
- Manes, C.; Pokrajac, D.; Coceal, O.; McEWAN, I. On the significance of form-induced stress in rough wall turbulent boundary layers. Acta Geophys. 2008, 56, 845–861. [Google Scholar] [CrossRef]
- Jelly, T.O.; Busse, A. Reynolds number dependence of Reynolds and dispersive stresses in turbulent channel flow past irregular near-Gaussian roughness. Int. J. Heat Fluid Flow 2019, 80, 108485. [Google Scholar] [CrossRef]
- Toussaint, D.; Chedevergne, F.; Léon, O. Analysis of the different sources of stress acting in fully rough turbulent flows over geometrical roughness elements. Phys. Fluids 2020, 32, 075107. [Google Scholar] [CrossRef]
- Alam, J.M.; Fitzpatrick, L.P. Large eddy simulation of flow through a periodic array of urban-like obstacles using a canopy stress method. Comput. Fluids 2018, 171, 65–78. [Google Scholar] [CrossRef]
- Borue, V.; Orszag, S.A. Local energy flux and subgrid-scale statistics in three-dimensional turbulence. J. Fluid Mech. 1998, 366, 1–31. [Google Scholar] [CrossRef]
- Johnson, P.L. Energy Transfer from Large to Small Scales in Turbulence by Multiscale Nonlinear Strain and Vorticity Interactions. Phys. Rev. Lett. 2020, 124, 104501. [Google Scholar] [CrossRef]
- Stevens, R.J.A.M.; Martínez-Tossas, L.A.; Meneveau, C. Comparison of wind farm large eddy simulations using actuator disk and actuator line models with wind tunnel experiments. Renew. Energy 2018, 116, 470–478. [Google Scholar] [CrossRef]
- Gharaati, M.; Xiao, S.; Wei, N.J.; Martínez-Tossas, L.A.; Dabiri, J.O.; Yang, D. Large-eddy simulation of helical- and straight-bladed vertical-axis wind turbines in boundary layer turbulence. J. Renew. Sustain. Energy 2022, 14, 053301. [Google Scholar] [CrossRef]
- Singh, J.; Alam, J. Vortex-Stretching based Large Eddy Simulation Framework for Wind Farms. arXiv 2022, arXiv:2205.01526. [Google Scholar]
- Wurps, H.; Steinfeld, G.; Heinz, S. Grid-resolution requirements for large-eddy simulations of the atmospheric boundary layer. Bound.-Layer Meteorol. 2020, 175, 179–201. [Google Scholar] [CrossRef]
- Sullivan, P.P.; McWilliams, J.C.; Moeng, C.H. A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Bound.-Layer Meteorol. 1994, 71, 247–276. [Google Scholar] [CrossRef]
- Basu, S.; Lacser, A. A cautionary note on the use of Monin-Obukhov similarity theory in very high-resolution large-eddy simulations. Bound.-Layer Meteorol. 2017, 163, 351–355. [Google Scholar] [CrossRef]
- Lopez-Villalobos, C.; Martínez-Alvarado, O.; Rodriguez-Hernandez, O.; Romero-Centeno, R. Analysis of the influence of the wind speed profile on wind power production. Energy Rep. 2022, 8, 8079–8092. [Google Scholar] [CrossRef]
- Townsend, A. The Structure of Turbulent Shear Flow; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Pope, S.B. Turbulent Flows; IOP Publishing: Bristol, UK, 2001. [Google Scholar]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Meneveau, C. Big wind power: Seven questions for turbulence research. J. Turbul. 2019, 20, 2–20. [Google Scholar] [CrossRef]
- Schumann, U. Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli. J. Comput. Phys. 1975, 18, 376–404. [Google Scholar] [CrossRef]
- Bhuiyan, M.; Samad, A.; Alam, J.M. Large Eddy Simulation of Turbulent Flow Over a Hill Using a Canopy Stress Model. In Proceedings of the Recent Advances in Mathematical and Statistical Methods: IV AMMCS International Conference, Waterloo, ON, Canada, 20–25 August 2017; Springer: Cham, Switzerland, 2017; pp. 151–160. [Google Scholar]
- Elgendi, M.; AlMallahi, M.; Abdelkhalig, A.; Selim, M.Y. A review of wind turbines in complex terrain. Int. J. Thermofluids 2023, 17, 100289. [Google Scholar] [CrossRef]
- Medici, D.; Ivanell, S.; Dahlberg, J.Å.; Alfredsson, P.H. The upstream flow of a wind turbine: Blockage effect. Wind Energy 2011, 14, 691–697. [Google Scholar] [CrossRef]
- Simley, E.; Angelou, N.; Mikkelsen, T.; Sjöholm, M.; Mann, J.; Pao, L.Y. Characterization of wind velocities in the upstream induction zone of a wind turbine using scanning continuous-wave lidars. J. Renew. Sustain. Energy 2016, 8, 013301. [Google Scholar] [CrossRef]
- Strickland, J.M.; Stevens, R.J. Investigating wind farm blockage in a neutral boundary layer using large-eddy simulations. Eur. J. Mech.-B/Fluids 2022, 95, 303–314. [Google Scholar] [CrossRef]
- Davidson, P.A. Turbulence: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Chow, F.K.; Moin, P. A further study of numerical errors in large-eddy simulations. J. Comput. Phys. 2003, 184, 366–380. [Google Scholar] [CrossRef]
- Celik, I.; Cehreli, Z.; Yavuz, I. Index of resolution quality for large eddy simulations. J. Fluids Eng. 2005, 127, 949–958. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Modeling turbine wakes and power losses within a wind farm using LES: An application to the Horns Rev offshore wind farm. Renew. Energy 2015, 75, 945–955. [Google Scholar] [CrossRef]
- Frandsen, S.; Barthelmie, R.; Pryor, S.; Rathmann, O.; Larsen, S.; Højstrup, J.; Thøgersen, M. Analytical modelling of wind speed deficit in large offshore wind farms. Wind Energy 2006, 9, 39–53. [Google Scholar] [CrossRef]
- Liu, L.; Stevens, R.J. Effects of two-dimensional steep hills on the performance of wind turbines and wind farms. Bound.-Layer Meteorol. 2020, 176, 251–269. [Google Scholar] [CrossRef]











| Cases | ||||
|---|---|---|---|---|
| M10 | 10 | 10 | 10 | |
| M15 | 15 | 6 | 6 | |
| M20-1 | 20 | 5 | 5 | |
| M20-2 | 10 | 5 | 10 | |
| M20-3 | 8 | 5 | 12 | |
| M30 | 30 | 3 | 3 | |
| M40 | 40 | 2 | 2 |
| Cases | Classification | ||
|---|---|---|---|
| A | sea | ||
| B | beaches, morass | ||
| C | grass prairie | ||
| D | airports, heather | ||
| E | low crops | ||
| F | high crops | ||
| G | scattered obstacles | ||
| H | trees, hedgerows | ||
| I | mixed farm fields | ||
| J | suburban houses, regular coverage of obstacles |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, J.; Alam, J.M. Large-Eddy Simulation of Utility-Scale Wind Farm Sited over Complex Terrain. Energies 2023, 16, 5941. https://doi.org/10.3390/en16165941
Singh J, Alam JM. Large-Eddy Simulation of Utility-Scale Wind Farm Sited over Complex Terrain. Energies. 2023; 16(16):5941. https://doi.org/10.3390/en16165941
Chicago/Turabian StyleSingh, Jagdeep, and Jahrul M Alam. 2023. "Large-Eddy Simulation of Utility-Scale Wind Farm Sited over Complex Terrain" Energies 16, no. 16: 5941. https://doi.org/10.3390/en16165941
APA StyleSingh, J., & Alam, J. M. (2023). Large-Eddy Simulation of Utility-Scale Wind Farm Sited over Complex Terrain. Energies, 16(16), 5941. https://doi.org/10.3390/en16165941






