A Turn-Ratio-Changing Half-Bridge CLLC DC–DC Bidirectional Battery Charger Using a GaN HEMT

Abstract

This paper presents a 250 kHz bidirectional battery charger circuit using a GaN HEMT. The charger is subjected to a high-/low-side constant voltage at 200 V/20 V. The charger circuit is a hybrid of the LLC and flyback circuit topologies. Both the power output analysis and efficiency control of this circuit are simplified when the magnetization current is minimized using the low-resistance GaN HEMT. The switching frequency is controlled to match the series resonance in a way that is analogous to conventional LLC circuit controls, while the duty ratio that determines the power output and the dead time, which determines the zero voltage switching, is controlled in an analogous manner to the flyback circuit control. The charging and discharging modes were altered by applying a double-throw relay that changes the transformer turn ratio, which is different from conventional LLC designs using the switching frequency adjustment. A nominal turn ratio with N_p = 35 and N_s = 3.5 for a 200 V/20 V converter can only produce an internal series resonance with no current flowing in any charging direction. The proposed circuit using a transformer with multiple windings (N_p = 35, N_s,F = 4, and N_s,R = 3) was fabricated to deliver 125 W output power from the power grid battery to the vehicle battery in the forward (charging) mode and 90 W in the reverse (discharging) mode. The conversion efficiency was calculated to be as high as 97% in the forward mode and 95% in the reverse mode. The high conversion efficiency is due to the characteristics of the GaN HEMT, including low resistive and switching losses. The equations derived in this paper associate these losses with the series resonant frequency and power conversion rate, which highlight the advantages of using a GaN HEMT in this CLLC design.

1. Introduction

The need for high power density, high efficiency, and bidirectional operation is the trend of power conversion systems for EV charger, charging station, and energy storage applications [1]. Resonant converters [2] are good candidates, with high power and high efficiency that can perform soft switching operations using resonance, and they are also suitable for high switching operations to decrease the passive components, thereby increasing the high power density.

There are various DC/DC resonant power converter topologies, such as the LLC converter, CLLC converter, phase-shifted full bridge (PSFB), and dual active bridge (DAB) [2]. Among these converter topologies, CLLC is a promising topology for high efficiency in a bidirectional operation owing to its characteristics of zero-voltage switching (ZVS) and zero-current switching (ZCS), and it is suitable for the requirement of a wide range of output voltages [3,4,5,6,7,8]. Many studies have adopted CLLC circuits to obtain a good performance. A full-bridge CLLC resonant topology was selected to achieve both high efficiency and wide voltage regulation [3], and synchronous rectification (SR) is an effective method to obtain high efficiency [4,5,6,7,8]. An SR scheme based on resonant inductor voltage was proposed in [4] without current sensors. In [5], the SR drive action was enabled without any additional hardware. Phase tracking for SR was proposed in [6]. A natural SR feature was used for a full-bridge CLLC converter [7], and an optimized digital SR control strategy was proposed in [8]. In addition to ZVS, ZCS, and SR operation, a much better efficiency can be obtained using dead-time control [9] and wide-bandgap transistors, such as SiC [10,11] and GaN [12,13], due to their material characteristics [10,11,12,13]. However, dead-band control is necessary to ensure the zero crossing of the resonant current that occurs within the dead time. A tradeoff between the dead time and power conversion efficiency as well as the constant voltage regulation needs to be considered.

For improving the power density, an integrated transformer structure integrating resonant inductances and a transformer was proposed in [14]. Moreover, there are many methods to achieve a wide output voltage range, such as implementing phase-shift control [15], adding an extra buck/boost converter [16], using a relay-based control transformer turn ratio [11], or changing the mode between full-bridge and half-bridge for a flexible gain control scheme [17]. In addition, a current-fed CLLC converter with additional inductance was proposed to maximize the ZVS for the entire load range [18], and the sliding mode control was proposed to improve the dynamic response [19].

The most recent review of bidirectional onboard chargers for electric vehicles [20] showed several works in the specialized literature that achieved around 90% power efficiency for higher levels of power with similar characteristics and functions. One of the important elements of the considered converters is the transformer. In DC/DC converters, not only iron losses but also losses occurring in the core depend on the material. Other parameters, such as the Steinmetz frequency, have been taken into account and modeled in the recent literature, including the inductor core [21], the transformer core loss [22], and the off-resonance loss [23]. The modeling of power electronics dynamics using a discrete model simulation that is useful for analyzing the power loss was also introduced in [24].

This paper introduces a new circuit topology for a half-bridge CLLC DC–DC converter with a D-mode GaN HEMT for high-speed switching, which can operate in both charging and discharging modes. In this CLLC charger, the mode switching between charging and discharging is achieved using a double-throw relay instead of controlling the switching frequency as in the previously proposed CLLC. A feature of the proposed CLLC circuit topology is the use of a relay to switch the transformer turn ratio in order to change the direction of the current flow. The purpose of this paper is to propose a circuit model based on adjusting the switching frequency and the duty cycle to achieve the best efficiency according to the ZVS as well as the ZCS control, along with the design methodology being presented. The paper is organized as follows: Section 2 introduces the half-bridge CLLC DC–DC converter circuit. Based on the introduction of the CLLC DC–DC converter and transformer, the proposed model is introduced. Moreover, the charging and discharging modes are discussed. Section 3 discusses zero-current switching control, the core loss of the transformer, and the dead-time control. The proposed circuit and model are verified by the simulation and experiment presented in Section 4. Section 5 concludes the paper.

The main reasons why the wide-bandgap device GaN HEMT is well-suited for CLLC DC–DC converter applications are that it can perform high-frequency switching with a low switching loss and it involves low Ciss and Coss variation between the turn-on and turn-off modes [25,26]. The Ciss and Coss variations of a MOSFET can be as high as several hundred times between the turn-on and turn-off modes. As for the GaN HEMT, the parasitic capacitances are nearly one-third of the MOSFET and the parasitic capacitance variation differs only five times between the turn-on and turn-off modes. Thus, the LC tank resonance is not considerably affected by the parasitic capacitance change. In addition, the GaN HEMT has high breakdown voltage in nature, which is useful for 500 W high-power—for instance, 400 V/48 V—applications.

2. Half-Bridge CLLC DC–DC Converter Circuit

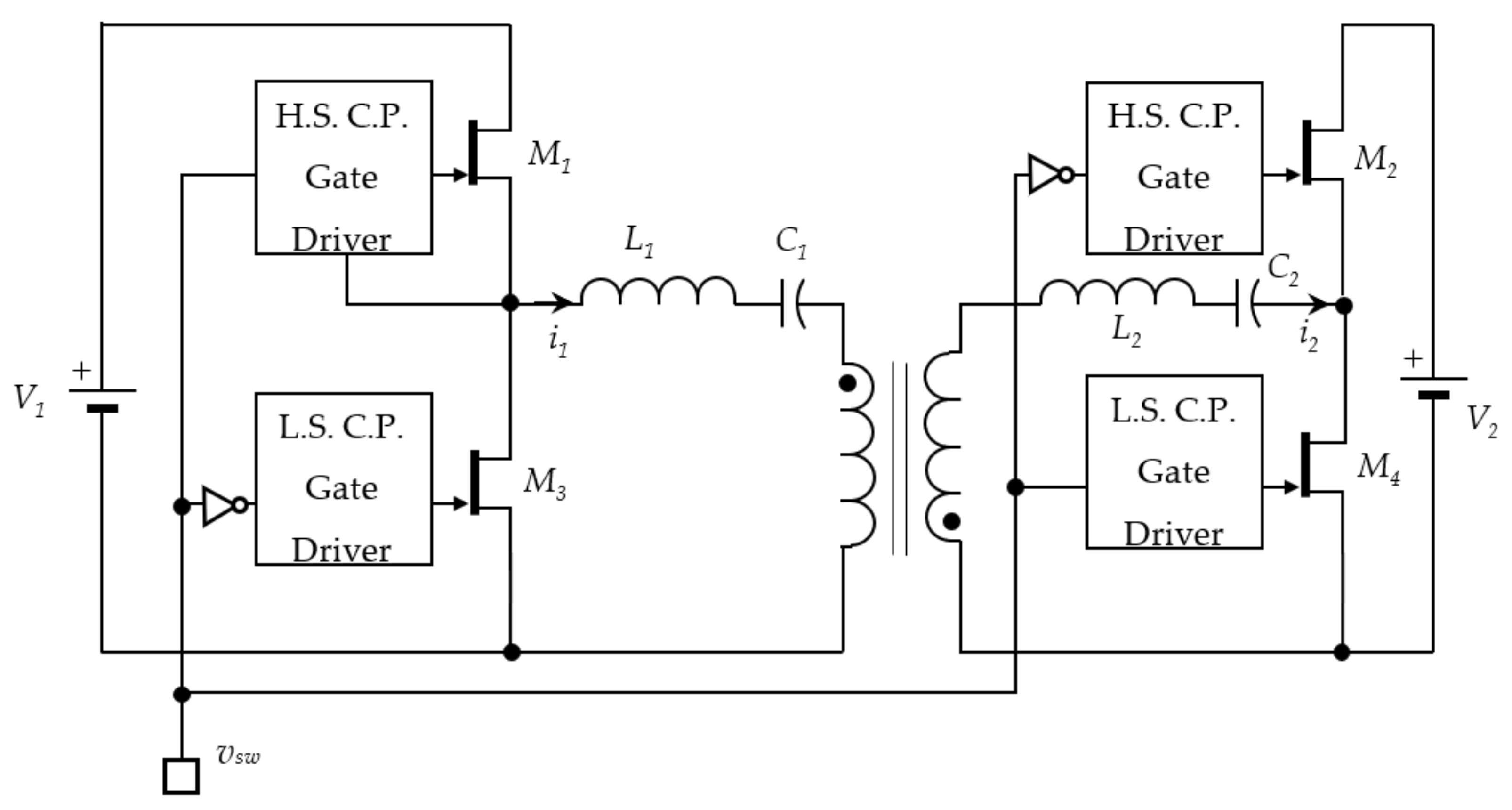
2.1. Previous Work

The CLLC is an extension of the LLC circuit topology [27] that uses the “first harmonic approximation” (FHA) technique to enable the analysis of resonant converters by means of a classical complex AC circuit analysis. In order to reduce the complexity of the analysis, an earlier version of a half-bridge CLLC DC–DC converter circuit was presented by Zou et al. [28]. They specifically defined the voltage source on the primary side as the grid voltage and the battery on the secondary side to be the vehicle battery. When the magnetization current and the core loss of the transformer are ignored, the circuit mode can be simplified, as shown in Figure 1; it consists of two capacitors on both the grid side, simplified by a voltage source V_in, and the vehicle side, simplified by an output resistance R_o. However, in the circuit model, there are multiple conducting paths of circulating current in the secondary side, as it has two capacitors. If the gate pulse of M₄ achieves zero-current switching (ZCS) early, the secondary-side resonant current partially circulates through M₄, discharging the battery, which lowers the conversion efficiency. Therefore, in order to minimize the circulating current in the secondary side, an extra dead-band control is necessary to ensure the zero crossing of the resonant current occurs within the dead time. This made the control system dependent on the loading condition while charging or discharging. The dead time needs to be long enough for handling the worst case within the desired switching frequency range; however, the increase in the dead time lowers the power conversion efficiency and the regulation in constant voltage control.

2.2. The Proposed Circuit Model

The proposed circuit topology of the CLLC circuit is shown in Figure 2, which has only one capacitor on either side of the circuit. The dead-time control is required only to avoid the shoot-through problem between the high- and low-side transistors, as shown in Figure 3. Figure 3a shows the waveform for the dead time subjected to the switching period $T$ and duty cycle δ, while Figure 3b depicts the dead-time generator circuit. The circuit comprises a fast-switching Schottky diode in parallel with a trimmer resistor, which helps to bypass the RC delay. A gate driver with an integrated dead-time controller can be found in standard ICs, such as the STDRIVEG600 half-bridge gate driver. We can also add a resistor to delay the turn-on time of the transistor in the gate driver circuit for high-voltage applications, as shown in Figure 3b.

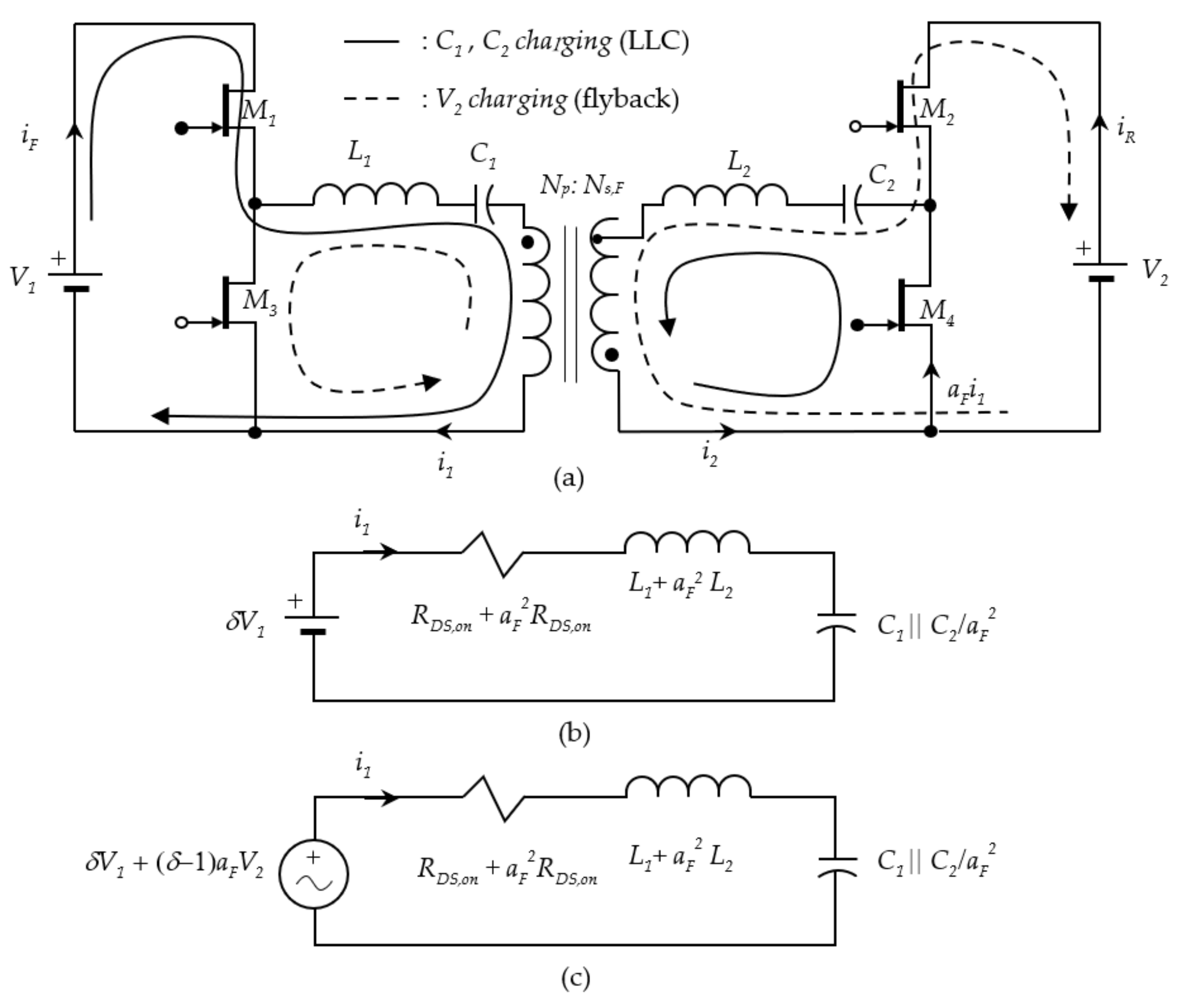
2.3. Transformer Model

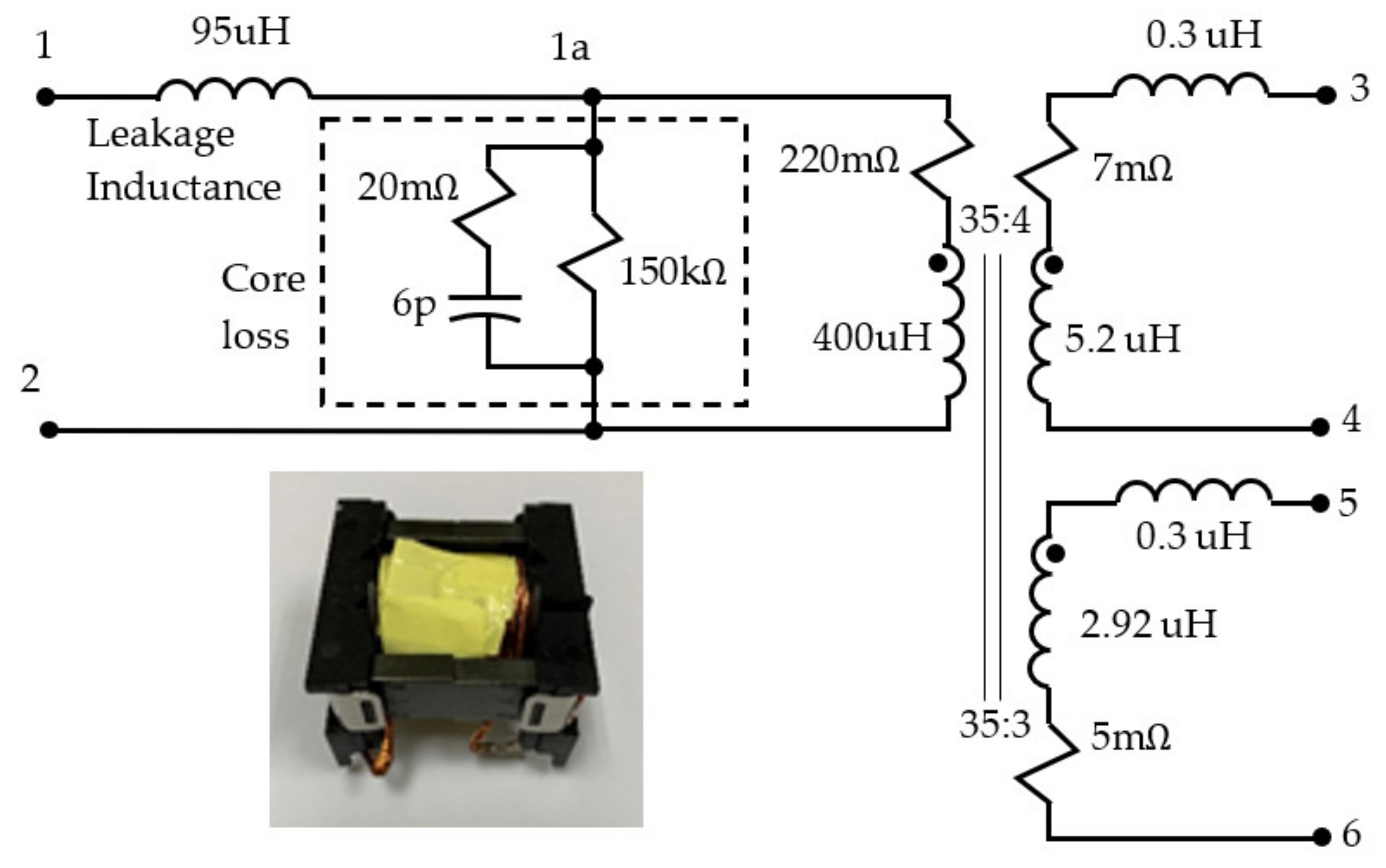
Reducing the magnetization current is necessary to improve the efficiency of the CLLC circuit and simplify its model into a second-order oscillation system. The magnetization current, which is not directly related to the power rating, can significantly impact the CLLC power-conversion efficiency. The switching frequency is used to match the series resonance, accounting for environmental changes, LC component variation, and stray impedance. By using a simple second-order resonant model, the duty cycle can be easily adjusted to achieve ZCS (zero-current switching) and further enhance the power conversion efficiency. The Steinmetz equivalent circuit, as shown in Figure 4, is a practical representation of a transformer’s physical behavior through an equivalent circuit model incorporating an ideal transformer. Ignoring the core loss of the transformer due to the air gap introduced into the transformer core design, the magnetizing inductance is still present between two LC tanks and results in a fourth-order system that consists of both series resonance and parallel resonance. 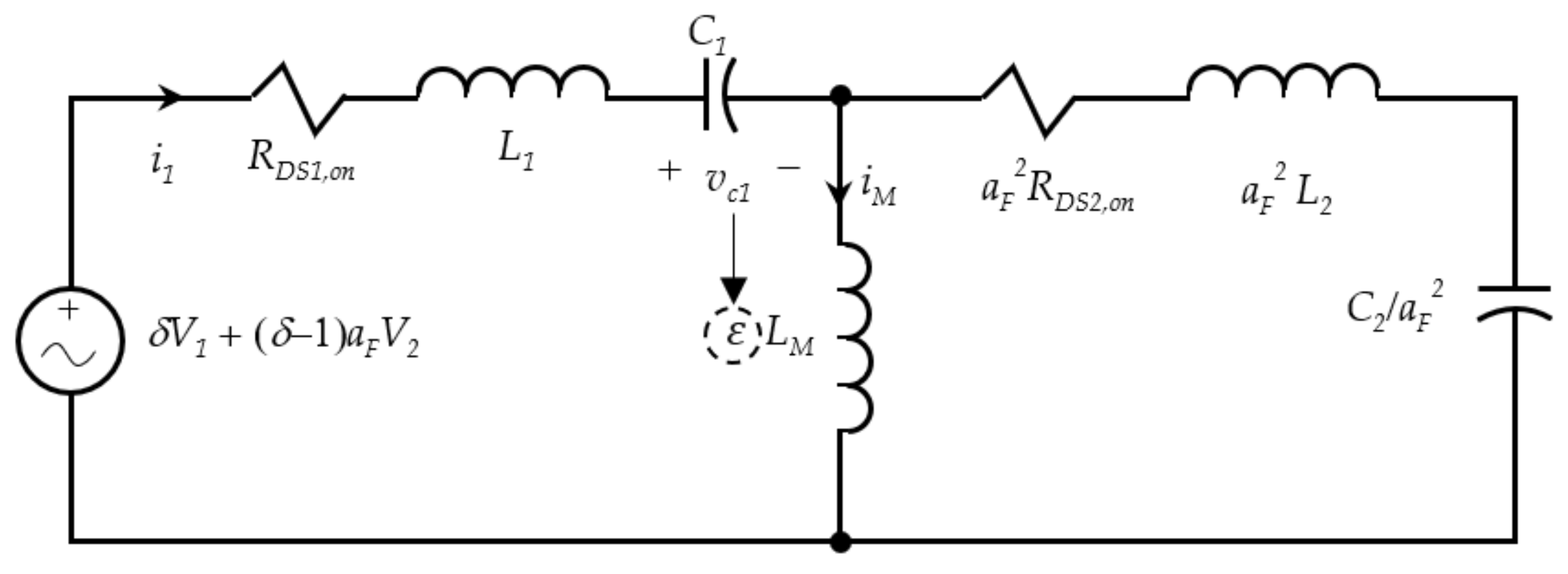The equivalent circuit model of the half-bridge CLLC is shown in Figure 5. In this paper, we used $a_F$ to denote the transformer turn ratio in the forward (charging) mode, $a_R$ to denote the transformer turn ratio in the reverse (discharging) mode, and $b$ to denote the nominal transformer turn ratio. A nominal turn ratio with $a_F=b$ can only result an internal series resonance with no current flowing in any charging direction. The half-bridge CLLC circuit uses the turn ratio $a_F<b$ during the forward (charging) mode and the turn ratio $a_R>b$ during the reverse (discharging) mode.

The LC tank’s series resonance on both sides of the transformer is identical, allowing for the use of a single switching frequency to produce the series resonance on both sides of the transformer.

$$L_1=b^2{L}_2, C_1=C_2/b^2$$

(1)

For the series resonance design, the nominal transformer turn ratio $b$ was used to determine both the inductance and capacitance ratios and to keep the inductors and capacitors the same without replacement in different (charging/discharging) modes. In that case, the magnetization current $i_M$ from the circuit shown in Figure 5 can be ignored. The switching frequency ${\omega }_0$ is preferable to match the series resonance of the LC tank on both sides of the transformer.

$${\omega }_0=\frac{1}{\sqrt{({a_F}^2+b^2)L_2\left(\frac{1}{{a_F}^2+b^2}\right)C_2}}=\frac{1}{\sqrt{L_2{C}_2}}=\frac{1}{\sqrt{L_1{C}_1}}$$

(2)

Considering that the magnetization current $i_M$ can or cannot be ignored from the equivalent circuit, we first assumed the switch frequency is tuned to eliminate the series impedance of the LC tank, and the remaining switch resistance ${a_F}^2{R}_{DS2,on}$ was used to compare with the magnetization inductance as follows. As shown in Figure 5, the on-resistance ${a_F}^2{R}_{DS2,on}$ of transistors is outside of the LC tank when the transformer is inside of the LC tank. Therefore, when the perfect series resonance is assumed, the AC voltage experienced by the on-resistance ${a_F}^2{R}_{DS2,on}$ is equivalent to the difference between the input voltage and the transformed output voltage as $\delta V_1+{(\delta -1)a}_F{V}_2$, which is much smaller than that of the transformer coils which oscillates with the capacitor voltage $v_{c1}$ with peak-to-peak voltage swing $V_{c1,pp}$. Therefore, a correction factor ${\epsilon }_F$ for the forward (charging) mode was introduced to equalize the different voltages in one equivalent circuit.

$${\epsilon }_F=\frac{V_{c1,pp}}{\delta V_1+{(\delta -1)a}_F{V}_2}$$

(3)

The magnetization current is a branch current derived from the current divider circuit consisting of magnetization inductance and the switch on-resistance as follows.

$$\frac{I_{M,F,max}}{I_{1,max}}=\frac{{a_F}^2{R}_{DS2,on}}{{\epsilon }_F{{\omega }_{0}L}_{M,F}+{a_F}^2{R}_{DS2,on}}$$

(4)

The inductance $L_M$ is the primary inductance, excluding the leakage inductance during the forward (charging) mode. Similarly, the magnetization current required in the reverse (discharging) mode can also be expressed as follows.

$$\frac{I_{M,R,max}}{I_{2,max}}=\frac{R_{DS1,on}/{a_R}^2}{{\epsilon }_R{{\omega }_{0}L}_{M,R}+R_{DS1,on}/{a_R}^2}$$

(5)

Since the turn ratio between the primary winding and the secondary winding becomes $a_R$ in the reverse (discharging) mode, the magnetization inductance ratio between the forward (charging) mode and the reverse (discharging) mode is expressed in the reverse (discharging) mode as follows.

$$\frac{L_{M,F}}{L_{M,R}}={a_R}^2$$

(6)

Equation (5) can be re-written as follows.

$$\frac{I_{M,R,max}}{I_{2,max}}=\frac{R_{DS1,on}}{{\epsilon }_R{{\omega }_{0}L}_{M,F}+R_{DS1,on}}$$

(7)

Equation (7) states that the resistance of $R_{DS1,on}$ in the similar range of ${a_F}^2{R}_{DS2,on}$ ignores magnetization. High-breakdown-voltage GaN HEMTs were applied to the CLLC as $M_1$ and $M_3$, and the low-resistance GaN HEMTs were applied as $M_2$ and $M_4$. It was a challenging task for the high-breakdown-voltage GaN transistor to have a low resistance. According to Equation (7), we need only a high ${a_F}^2$ to balance the resistance between high-/low-voltage GaN. The task for reducing the effect of the magnetization current from the CLLC circuit analysis is then transformed into the task of increasing $\epsilon {{\omega }_{0}L}_{M,F}$, as shown in Equations (5) and (7). In order to achieve this, we need to (1) use the higher turns of the coils on both of the primary and secondary windings to increase both $L_{M,F}$ and $L_{M,R}$ and (2) increase the switching frequency ${\omega }_0$. The latter solution has a side effect: the switching loss can also be amplified due to a high switching frequency. The former solution has also a side effect, which is that it increases the transformer size. A hybrid solution was adopted in which we increased both the turns and the switching frequency to their limits.

If the magnetization current can be ignored through the use of low-resistance GaN HEMTs, the series resonant circuit can then be simplified by combining both the inductances and the capacitances into a single inductor and single capacitor. The resonance mechanism can be simplified into a secondary differential equation, which is useful for the forward (charging) and reverse (discharging) mode analysis in the following sections.

2.4. Forward (Charging) Mode

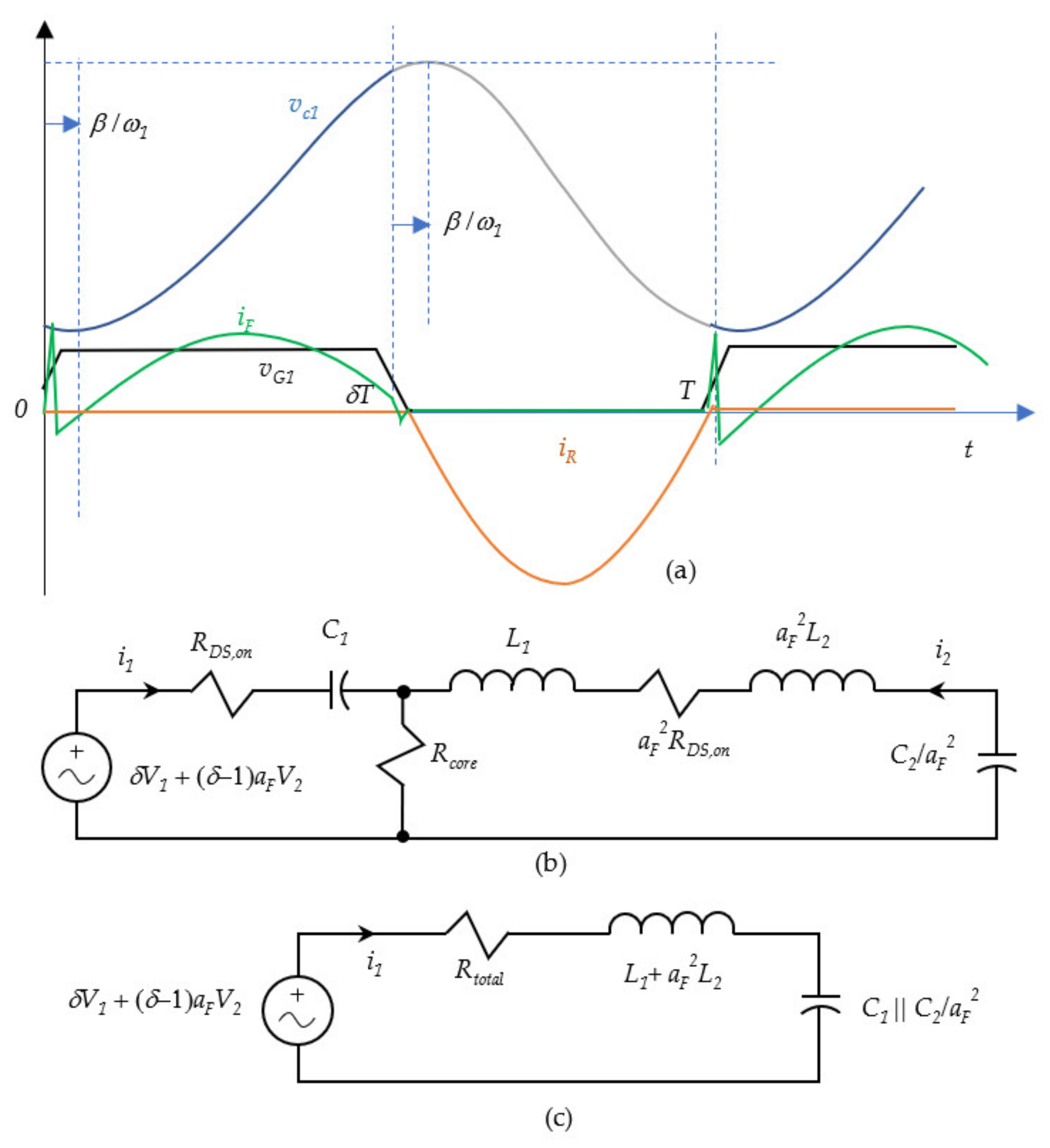
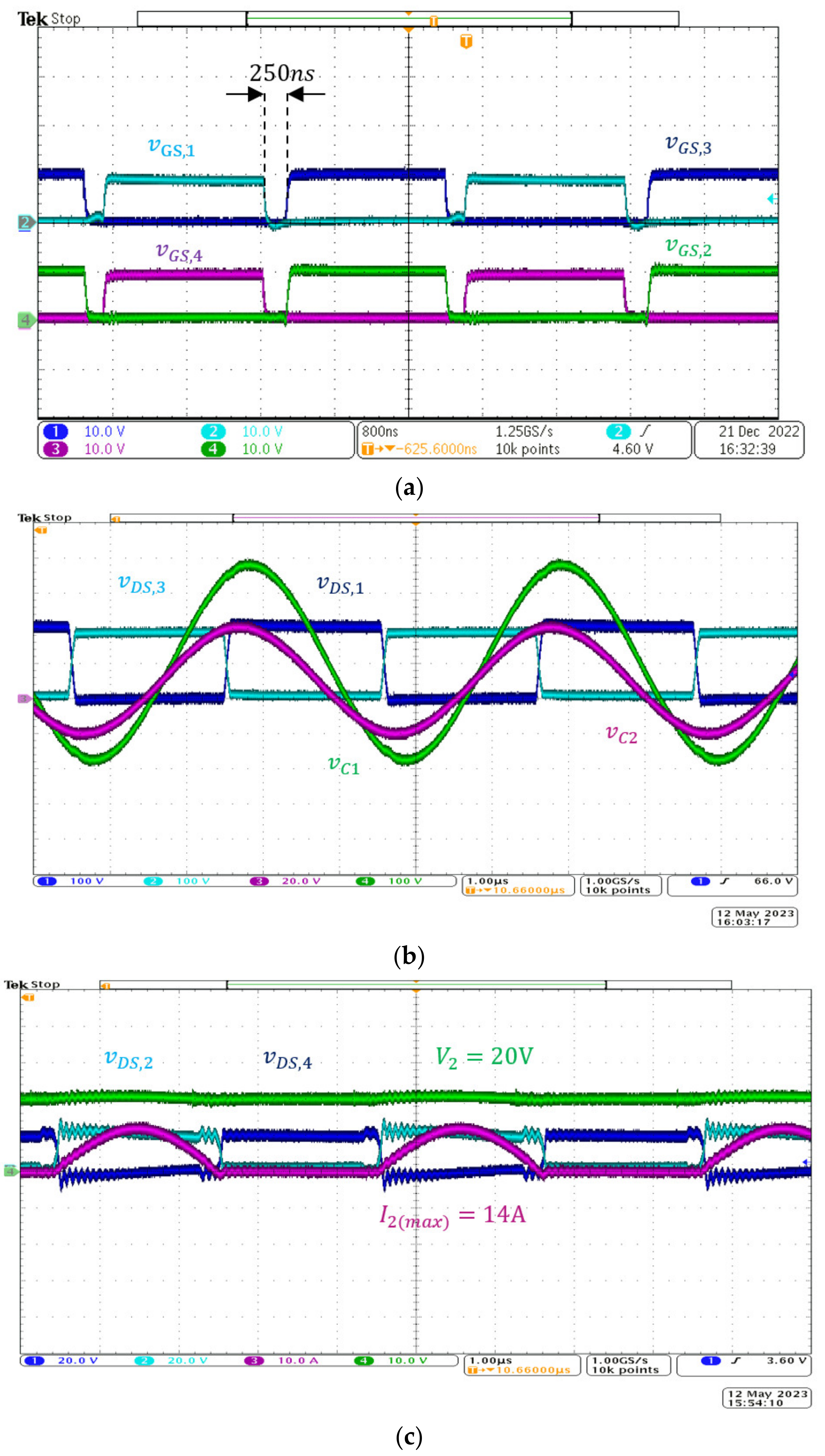
As shown in Figure 6a, there are two sessions for the charging mode. The first session, indicated by a solid line, is for charging the resonant capacitors C₁ and C₂ during the turn-on time of transistors M₁ and M₄. The second session, indicated by a dash line, is for transferring the electrical energy stored in both C₁ and C₂ to the battery V₂ on the secondary side during the turn-on time of transistors M₂ and M₃. During the second session, the same resonant voltage on C₁ must be transformed using the transformer into a voltage level higher than V₂ in order to yield a charging current flow into the battery V₂; therefore, we used the turn ratio $a_F<b$.

The equivalent model from the circuit as shown in Figure 6a can be converted into either Figure 6b or Figure 6c depending on the view of the DC component and the AC swing analysis, respectively. The DC component and AC swing analyses both share the same series RLC circuit topology, which are different only in the source type and the mismatched loop resistance. The magnetization inductance was assumed to be considerably large and can be ignored in the analyses. Ignoring the core loss, parasitic capacitance of the coils of the transformer, and magnetization current, we can simplify the CLLC circuit when v_sw is high by assuming that the coupling coefficient of the transformer is the unity.

$$\frac{d^2{i}_1}{d{t}^2}+2{\xi }_1{\omega }_1\frac{{di}_1}{dt}+{{\omega }_1}^2{i}_1=0$$

(8)

The equation above is applicable for both DC component and AC swing analyses, because the voltage source vanishes. The Heaviside step function $u_s(t)$ sets the time as zero when M₁ and M₄ turn on. In Equation (8), the natural frequency ${\omega }_1$ is a function of primary inductor L₁ that can simply be the transformer leakage inductance, the secondary inductance L₂ that can also be the secondary leakage inductance, and primary capacitor C₁ or the secondary capacitor C₂. The transformer turn ratio $a_F$ during the forward mode is expressed as follows.

$$a_F=\frac{N_p}{N_{s,F}}$$

(9)

$N_p$ denotes the turns on the primary winding and $N_{s,F}$ denotes the turns on the secondary winding of the transformer windings in the forward (charging) mode. The natural frequency ${\omega }_1$ is then defined as follows.

$${\omega }_1=\frac{1}{\sqrt{(L_1+{a_F}^2{L}_2)(C_1||C_2/{a_F}^2)}}$$

(10)

The natural frequencies in Equation (10) can be simplified when the following conditions are satisfied.

$$L_1=b^2{L}_2, C_1=C_2/b^2$$

(11)

Equation (11) then yields the relation that eliminates both factors $a_F$ and $b$ as follows.

$${\omega }_1=\frac{1}{\sqrt{({a_F}^2+b^2)L_2\left(\frac{1}{{a_F}^2+b^2}\right)C_2}}={\omega }_0$$

(12)

${\omega }_0$ denotes the base frequency, and the impedance on both sides of the transformer vanishes under the base-frequency switching condition.

$${\omega }_0=\frac{1}{\sqrt{L_2{C}_2}}=\frac{1}{\sqrt{L_1{C}_1}}$$

(13)

The damping ratio ${\xi }_1$ of the current oscillation is derived as follows, providing that the transistor on-resistances are identical.

$${\xi }_1=\frac{R_{DS,on}(1+{a_F}^2)}{2}\sqrt{\frac{\left(\frac{1}{{a_F}^2+b^2}\right)C_2}{({a_F}^2+b^2)L_2}}=\frac{R_{DS,on}(1+{a_F}^2)}{2(1+{a_F}^2/b^2)}\sqrt{\frac{C_1}{L_1}}$$

(14)

The series resonant quality factor is derived as follows.

$$Q_1=\frac{1}{2{\xi }_1}$$

(15)

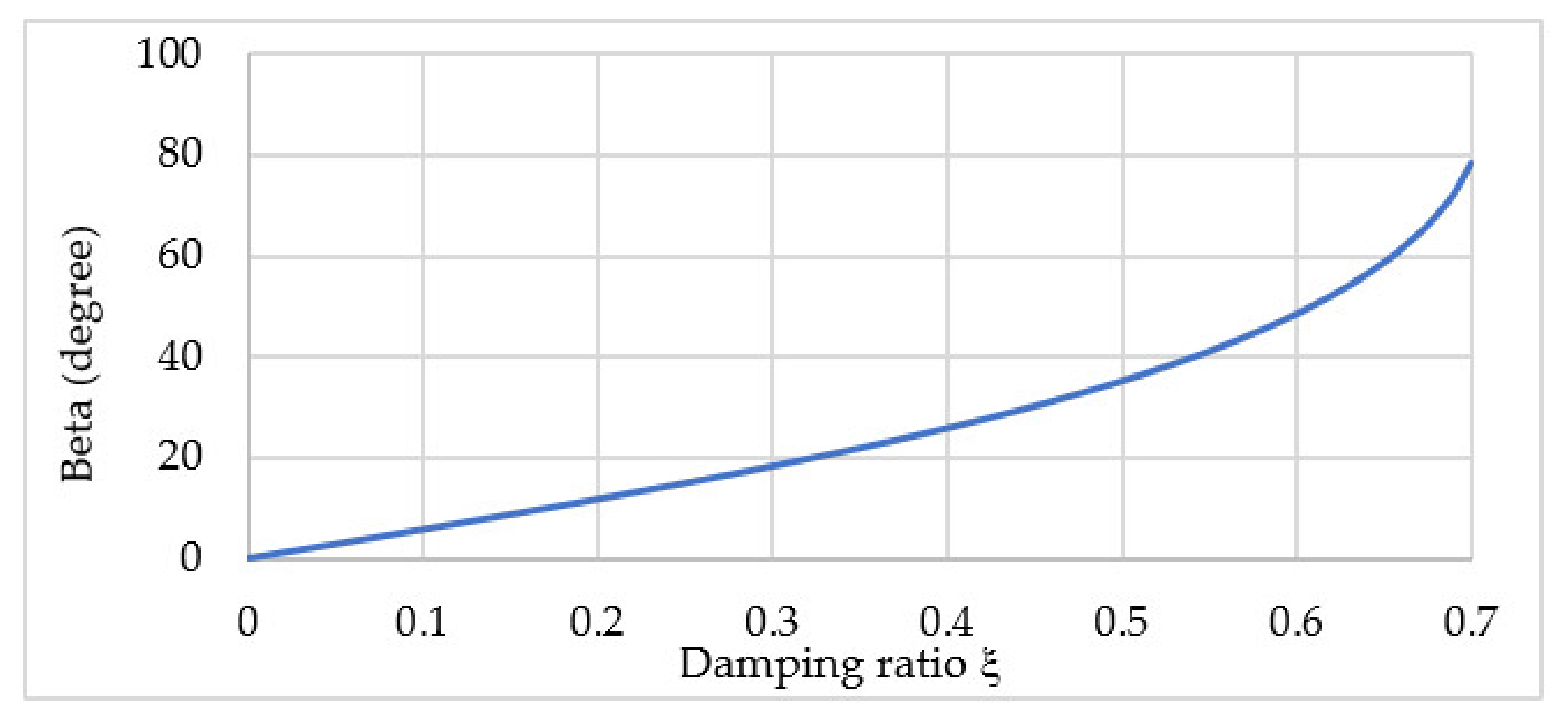
Equation (8) shows that the damping ratio and series resonant quality factor of the circuit are a function of Rayleigh energy dissipation in the second-order term of the RHS. In Equation (14), we modeled only the resistive loss of the transistor as the energy dissipation source, which is not entirely accurate when the drain–source voltage is high during turn-off. The reverse recovery charge Q_rr stored in the output parasitic capacitance C_oss of the transistor can produce a larger energy dissipation than the resistive loss.

To address this issue, using the GaN HEMT instead of MOSFET or IGBT can be beneficial because the C_oss of a GaN HEMT is only one tenth of that of the MOSFET or IGBT. This can result in a very small switching loss compared to the resistive loss under 250 kHz switching frequency. The damping ratio and quality factor of the series resonant circuit is calculated as shown in

Table 1. Parameters used to estimate the damping ratio and quality factor in the forward (charging) mode.

Symbol	Abbreviation	Unit	Value	Equation
C1	Primary resonant capacitance	nF	4.22
L1	Primary leakage inductance	μH	95
f0 = ω0/2π	Switching frequency	kHz	250
aF	Transformer turn ratio		8.75	(9)
RDS,on	Transistor on-resistance	$\mathsf{\Omega }$	0.15
b	Inductance ratio		8
${\xi }_1$	Damping ratio		0.0177	(14)
Q1	Series resonant quality factor		28.32	(15)

, according to Equations (14) and (15).

When the on-resistances of the transistors are in the range of 100 mΩ, the capacitance of C₁ is in the range of pF, and the inductance is 100 μH. The damping ratio is very small for a turn ratio a_F lower than 10, making the system in Equation (8) lightly damped or even undamped. In the perfect tuning of the resonance, the initial condition of the current i₁(0) is zero; provided there is still some charge remaining in the capacitors C₁ and C₂, the current response can then be expressed as follows.

$$i_1=I_{1,max}sin({\omega }_{1}t-\beta )$$

(16)

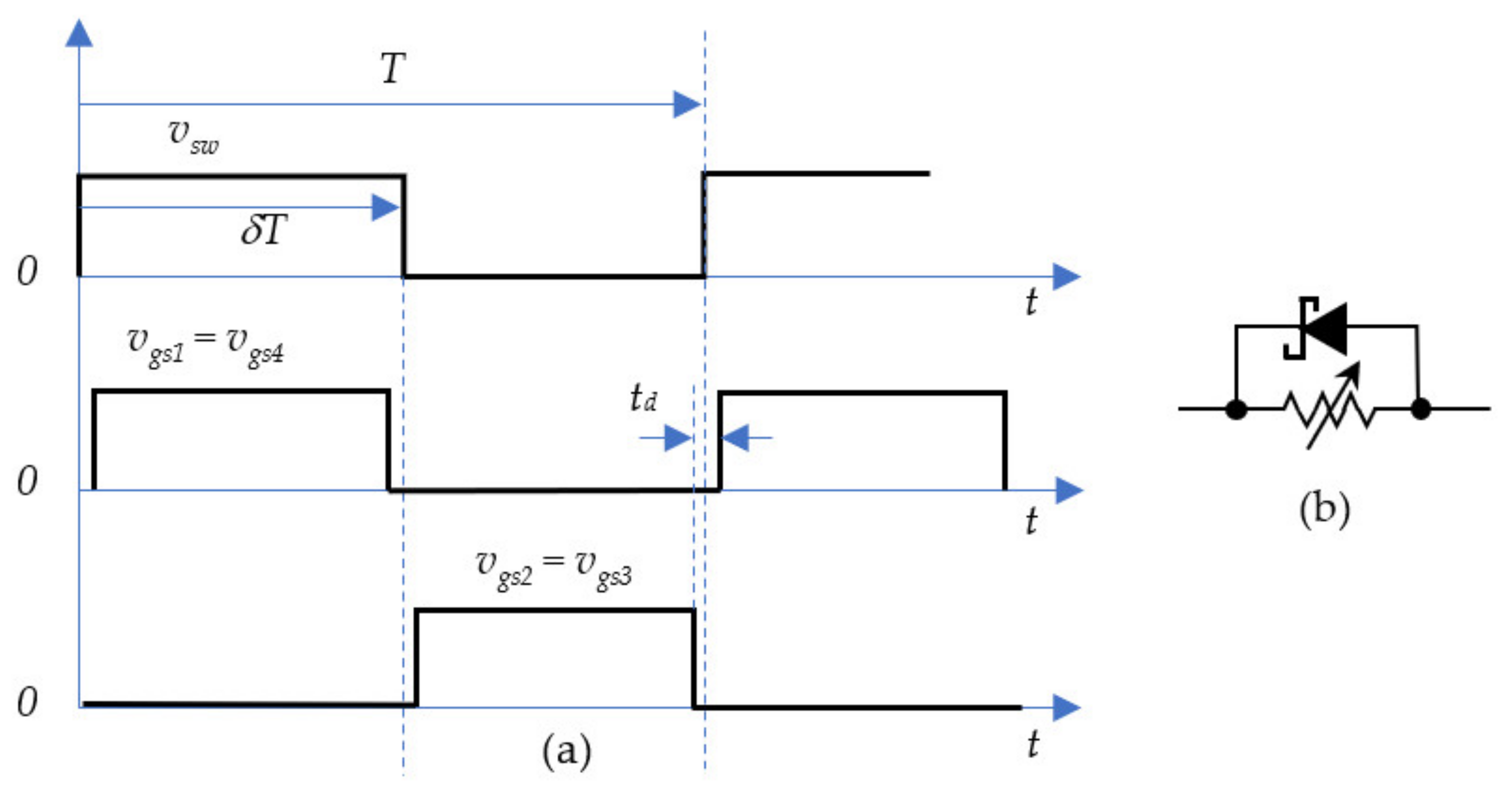
The phase lag $\beta$ between the switching time and the zero-current $i_1=0$ time is dependent on both the switching frequency and the duty cycle δ of the switching control. The ideal switching operation is when the current $i_1$ becomes zero at $t=\frac{\pi }{{\omega }_1}$; under the current resonance, the current on the inductor L₂ located on the secondary side of the transformer is also zero. At the same time, the capacitors C₁ and C₂ are filled with their maximum charges, and both reach the highest voltage under the LC resonance. This is, then, the best moment to turn off the transistors M₁ and M₄ as well as turn on transistors M₂ and M₃ to achieve the zero-current switching (ZCS) operation, which yields $\beta =0$. If the switching performed a perfect ZCS, the switching frequency of the transistors must be identical to the resonance frequency of the LC tank.

As a result, as shown in Figure 7, the voltage $v_{c1}$ is able to swing from $V_{c1,min}$ as its minimum voltage at time $t=0$ to the maximum voltage $v_{c1}=V_{c1,max}$ at time $t=\frac{\pi }{{\omega }_1}$. The capacitor voltage swings on a bias voltage $\delta V_1$, which is the DC component that depends on the duty of the transistor switching control, as shown in Figure 7. The reason for the bias voltage to exist is that the capacitor is subjected to an average voltage due to the input voltage $V_1$ under the switching operation, as shown in Figure 6b. The capacitor voltage may be written as follows.

$$v_{c1}\left(t\right)=\delta V_1+\frac{V_{c1(pp)}}{2}cos({\omega }_{1}t)$$

(17)

$V_{c1(pp)}$ denotes the peak-to-peak voltage, which is obtained as follows.

$$V_{c1(pp)}=V_{c1,max}-V_{c1,min}$$

(18)

We can obtain the voltage on the same capacitor C₁, holding a relation in the middle time $t=\frac{\pi }{2{\omega }_1}$, as follows.

$$v_{c1}(\frac{\pi }{2{\omega }_1})-v_{c1}(0)=\frac{V_{c1(pp)}}{2}=\frac{1}{C_1}{\int }_0^{\frac{\pi }{{2\omega }_1}}{i}_{1}dt=\frac{I_{1,max}}{{\omega }_1{C}_1}$$

(19)

The maximum current on the primary side is then obtained as follows.

$$I_{1,max}=\frac{{\omega }_1{C}_1{V}_{c1(pp)}}{2}=\frac{V_{c1(pp)}}{2}\sqrt{\frac{C_1}{L_1}}$$

(20)

The power transferred from the primary-side grid battery to the capacitors during the first session of the charging mode when the transistors M₁ and M₄ turn on can be derived for the primary side as follows.

$$P_{prim}=-V_1\frac{{\omega }_1}{2\pi }{\int }_0^{\frac{\pi }{{\omega }_1}}{i}_{1}dt$$

(21)

The peak-to-peak voltage $V_{c1(pp)}$ was determined by the series resonance quality factor $Q_1$, which can be directly measured from the experiments or obtained through simulation. As shown in Figure 6c, the switching of AC voltage is based on the voltage difference between the grid DC voltage and the vehicle DC voltage during the entire forward mode as follows.

$$P_{prim}=\frac{I_{1,max}{V}_1}{\pi }=\frac{V_1{V}_{c1(pp)}}{2\pi }\sqrt{\frac{C_1}{L_1}}$$

(22)

According to Equation (22), the output power can increase by increasing the capacitance and reducing the primary leakage capacitance simultaneously, without changing the switching frequency. The output power of a particular design was calculated as shown in

Table 2. Parameters used to estimate the charging power.

Symbol	Abbreviation	Unit	Value	Equation
δ	Duty cycle	-	0.5
V1	Grid DC voltage	V	200
V2	Vehicle DC voltage	V	20
Q1	Series resonant quality factor		28.32
aF	Transformer turn ratio		8.75
C1	Primary resonant capacitance	nF	4.22
L1	Primary leakage inductance	μH	95
Vc1(pp)	Peak-to-peak voltage of vc1	V	265	(18)
I1,max	Maximum current of i1	A	0.89	(20)
Pprim	Grid power transfer	W	56	(22)

.

2.5. Reverse (Discharging) Mode

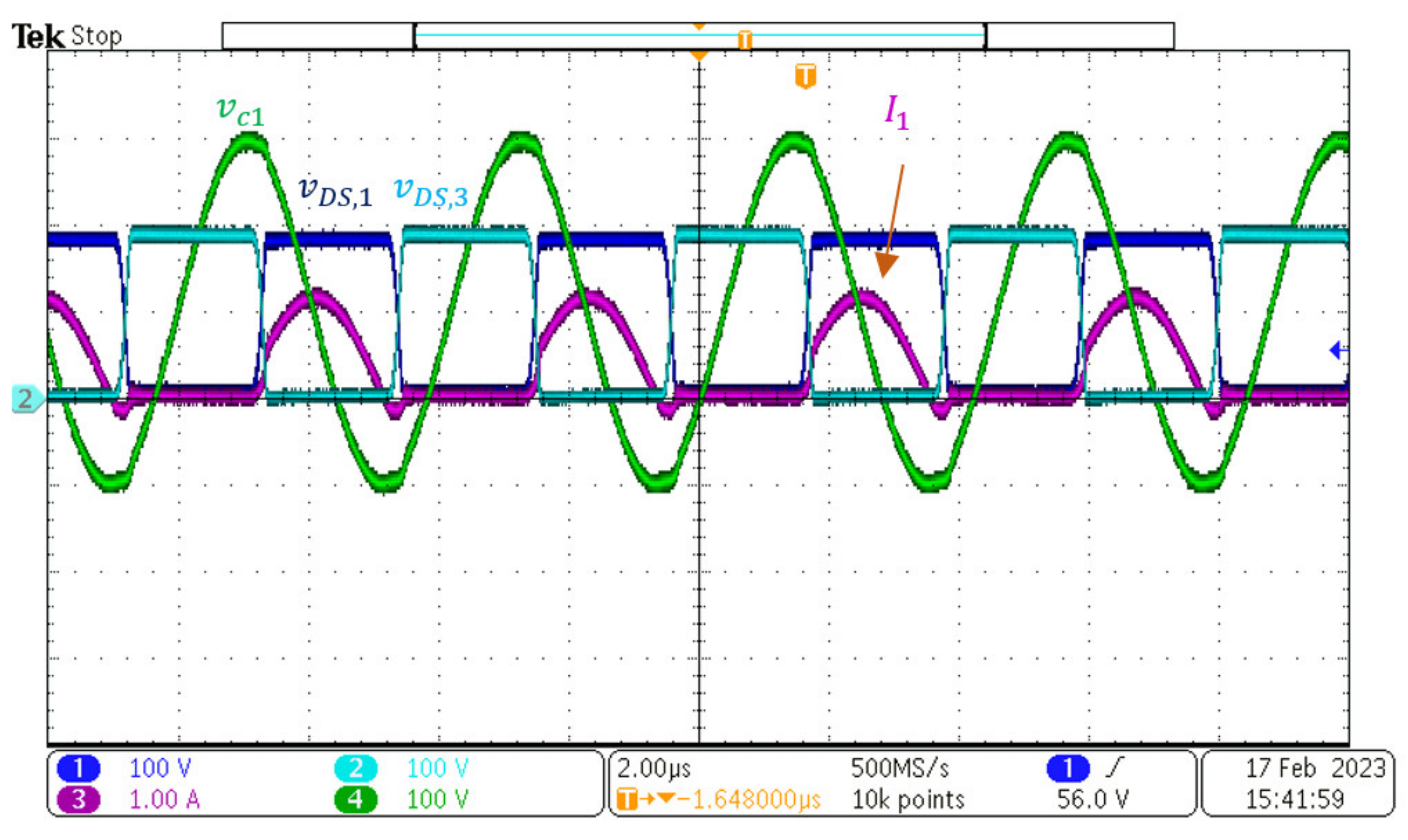
As shown in Figure 8a, there are also two sessions for the discharging mode. The first session with a current flow indexed using a solid line is to charge the resonant capacitors C₁ and C₂ during the turn-on time of transistors M₂ and M₃. The second session is to convey the increased electrical energy stored in both C₁ and C₂ into the battery V₁ on the primary side during the turn-on time of transistors M₁ and M₄, whose current path is marked as a dashed line. Depending on DC component and AC swing analyses, the circuit depicted in Figure 8a can be converted into either Figure 8b or Figure 8c. The transformer turn ratio between the primary side and secondary side during the reverse mode is provided as follows.

$$a_R=\frac{N_p}{N_{s,R}}$$

(23)

$N_p$ denotes the turns on the primary winding and $N_{s,R}$ denotes the turns on the secondary winding of the transformer windings in the reverse (discharging) mode.

Analogous to Equation (14), the damping ratio ${\xi }_2$ of the current i₂ oscillation is derived as follows, providing that the transistor on-resistances are identical.

$${\xi }_2=\frac{R_{DS,on}(1+1/{a_R}^2)}{2(1+b^2/{a_R}^2)}\sqrt{\frac{C_2}{L_2}}=\frac{R_{DS,on}(b^2+b^2/{a_R}^2)}{2(1+b^2/{a_R}^2)}\sqrt{\frac{C_1}{L_1}}$$

(24)

The series resonant quality factor is derived as follows.

$$Q_2=\frac{1}{2{\xi }_2}$$

(25)

The damping ratio and quality factor of the series resonant circuit was calculated as shown in

Table 3. Parameters used to estimate the damping ratio and quality factor in the reverse (discharging) mode.

Symbol	Abbreviation	Unit	Value	Equation
C1	Primary resonant capacitance	nF	4.22
L1	Primary leakage inductance	μH	95
aR	Transformer turn ratio (reverse mode)		11.67
RDS,on	Transistor on-resistance	$\mathsf{\Omega }$	0.2
b	Inductance ratio		8
${\xi }_2$	Damping ratio		0.0293	(24)
Q2	Series resonant quality factor		17	(25)

, according to Equations (24) and (25).

Analogous to Equation (25), the maximum current on the secondary side due to the switching frequency ${\omega }_2=\frac{1}{\sqrt{L_2{C}_2}}$ is then obtained as follows.

$$I_{2,max}=\frac{{\omega }_2{C}_2{V}_{c2(pp)}}{2}=\frac{V_{c2(pp)}}{2}\sqrt{\frac{C_2}{L_2}}$$

(26)

The power transferred from the secondary side battery to the primary capacitor during the first session of the charging mode, when the transistors M₂ and M₃ turn on, can be derived for the secondary side as follows.

$$P_{sec}=-V_2\frac{{\omega }_2}{2\pi }{\int }_0^{\frac{\pi }{{\omega }_2}}{i}_{2}dt=\frac{I_{2,max}{V}_2}{\pi }=\frac{V_2{V}_{c2(pp)}}{2\pi }\sqrt{\frac{C_2}{L_2}}$$

(27)

The peak-to-peak voltage $V_{c2(pp)}$ is determined by the series resonant quality factor $Q_2$, which is derived as follows. As shown in Figure 8c, the switching of the AC voltage is based on the voltage difference between the grid DC voltage and the vehicle DC voltage during the entire forward mode as follows.

$$V_{c2(pp)}=Q_2((\delta -1)V_1/a_R+\delta V_2)$$

(28)

The series resonant quality is crucial to the power conversion rate. The higher the series resonant quality, the higher the peak-to-peak voltage $V_{c2(pp)}$ in capacitor $C_2$. According to Equation (24), we may select a very-low dynamic RON resistance to reduce the damping ratio and increase the series resonant quality. This yields a reason for the GaN HEMT to be used when it is known that the electron mobility of 2DEG of AlGaN/GaN is high and the resistance of the GaN HEMT can be made very low. The calculation of the output power of a particular design is shown in

Table 4. Parameters used to estimate the discharging power.

Symbol	Abbreviation	Unit	Value	Equation
δ	Duty cycle	-	0.5
V1	Grid DC voltage	V	200
V2	Vehicle DC voltage	V	20
Q2	Series resonant quality factor		17
b	Inductance ratio		8
aR	Transformer turn ratio (reverse mode)		11.67
C1	Primary resonant capacitance	nF	4.22
L1	Primary leakage inductance	μH	95
Vc2(pp)	Peak-to-peak voltage of vc2	V	24.3	(28)
I2,max	Maximum current of i1	A	5.2	(26)
Psec	Vehicle power transfer	W	33	(27)

. Comparing the results of Table 2 with that of Table 4, we can find that the charging power to the vehicle during the charging mode is almost as twice the discharging power from the vehicle. The difference can be made smaller by redesigning the transformer turn ratio.

3. Zero-Current Switching Control

3.1. Core Loss of the Transformer

System variations, including the leakage inductance L₁ of the transformer, the resistance of the vehicle battery, and the grid, can affect the resonance frequencies of the forward (charging) and reverse (discharging) modes. Additionally, an under-modeled parasitic capacitor and core loss in the transformer can also influence the actual resonance frequency. Even with the zero-current switching (ZCS) control of the vehicle current during charging, improperly switching the current can still lead to imperfect ZCS and zero β, causing the grid current $i_F$ to ring on the transistor $M_1$, as shown in Figure 9a. Figure 9b depicts the equivalent circuit to which the core resistance was added, which is further simplified in Figure 9c under the resonance condition.

Assuming that the vehicle battery charging current $i_R$ is synchronized with the switching signal, the grid current $i_F$ lags behind the current $i_R$ by a phase lag $\beta$. Integrating the grid current $i_F$ from Equation (16), we obtained the voltage on the capacitor $C_1$ that is $90°$ ahead of the current $i_F$ as follows.

$$v_{c1}(t)=\delta V_1-\frac{V_{c1(pp)}}{2}cos({\omega }_{1}t-\beta )$$

(29)

In the previous section, it was explained that there are two sessions for the charging mode. The first session is to charge the resonant capacitors $C_1$ and $C_2$ during the turn-on time of transistors M₁ and M₄. The second session is to convey the electrical energy stored in both $C_1$ and $C_2$ to the battery V₂ on the secondary side during the turn-on time of transistors M₂ and M₃. Each session forms a part of the sinusoidal resonant voltage as shown in Figure 9a, but the mismatch of the resonant frequencies causes a non-zero phase lag $\beta$ and simultaneously reduces the voltage gain. Furthermore, the core loss of the transformer, as shown in Figure 4, can divide the grid current $i_F$ into two parts, one going through the core loss shunt and the other to $i_2$, which can cause a phase difference between the vehicle current $i_R$ and the grid current $i_F$. Using Equation (14), we integrated the dynamic resistance into the total resistance $R_{total}$.

$${\xi }_2=\frac{R_{total}}{2(1+{a_F}^2/b^2)}\sqrt{\frac{C_1}{L_1}}$$

(30)

The total resistance $R_{total}$ is defined in the forward (charging) mode and derived as follows.

$$R_{total}=R_{dynamic}+R_{DS,on}(1+{a_F}^2)$$

(31)

where

$$R_{dynamic}=\frac{L_1}{R_{core}{C}_1}$$

(32)

Derived from the frequency response of the second-order system in Equation (7), the phase lag is formulated as follows.

$$\beta ={tan}^{-1}({\xi }_2/\sqrt{1-2{{\xi }_2}^2})$$

(33)

The phase lag is plotted in terms of the damping ratio ${\xi }_2$ in Figure 10. The damping ratio is in a reciprocal relation with the core loss resistance.

3.2. Dead-Time Control—Drain–Source Voltage Rising Phase

During the forward mode, when the switch M₁ on the upper arm of the vehicle side and the switch M₄ on the lower arm of the battery side are simultaneously turned off, we assumed that the switches M₃ and M₂ were both turned off to prevent the shoot-through problem between the upper and lower arms. The interval in which all switches are off is known as the dead time. To calculate the dead time required, an equivalent circuit as shown in Figure 11b is required to understand the turn-off mechanism. The dead-time period is reserved for the charging/discharging in the drain–source capacitors $C_{DS}$ together with the bootstrap capacitor during the reverse recovery time.

When the switch M₁ is turned off from its turned-on state, the drain–source voltage is nearly zero and the bootstrap capacitor subjected to the gate-drive power supply voltage $V_{GG}$ has a voltage as follows.

$$v_{boot}=V_{GG}-v_{DS,on}<V_{GG}$$

(34)

The charges in the bootstrap capacitor have to be refilled into $V_{GG}$ during the reverse recovery time. The KVL equation due to the transistor M₁ in the reverse recovery time is derived as follows.

$$V_1-V_{c1,min}=L_1\frac{d{i}_1}{dt}+v_{DS}$$

(35)

where

$$i_F=C_{oss}\frac{d{v}_{DS}}{dt}=(C_{DS}+C_{GD})\frac{d{v}_{DS}}{dt}$$

(36)

Part of the current $i_F$ surging into the bootstrap capacitor further decreases the capacitor voltage $\Delta v_{boot}=\alpha \Delta v_{DS}$, which is formulated as follows.

$$i_{boot}=C_{boot}\frac{d{v}_{boot}}{dt}=\alpha C_{boot}\frac{d{v}_{DS}}{dt}$$

(37)

Due to the current flowing between capacitors being much faster than through the choke $L_1$, the fraction $\alpha$ can be evaluated from the charge redistribution law as follows.

$$\alpha =\frac{C_{oss}}{C_{boot}+C_{oss}}$$

(38)

The KCL equation can be expressed as follows.

$$i_1-i_{boot}=i_F$$

(39)

From Equation (35), we obtain the following equation.

$$V_1-V_{c1,min}=L_1\frac{d(i_F+i_{boot})}{dt}+v_{DS}$$

(40)

Substituting Equations (36) and (37) into Equation (40), we obtain

$$L_1{(C}_{oss}+\alpha C_{boot})\frac{d^2{v}_{DS}}{d{t}^2}+v_{DS}=V_1-V_{c1,min}$$

(41)

It is then expressed in the standard form of the second-order system equation as follows.

$$\frac{d^2{v}_{DS}}{d{t}^2}+{{\omega }_{rising}}^2{v}_{DS}={{\omega }_{rising}}^2{V}_{DD}$$

(42)

where the resonant frequency is

$$f_{rising}=\frac{1}{2\pi \sqrt{L_1{(C}_{oss}+\alpha C_{boot})}}$$

(43)

Due to the very low damping ratio of the second-order differential Equation (41), the rise time is assumed to be one quarter of the oscillation cycle time, approximately 90 degrees forward in the phase.

$$t_{rising}=\frac{1}{4f_{rising}}=\frac{\pi \sqrt{L_1{(C}_{oss}+\alpha C_{boot})}}{2}$$

(44)

The nominal values of the parameters and the calculation result are shown in

Table 5. Nominal parameters used to estimate the dead time.

Symbol	Unit	Value
$\alpha$		0.01
$L_1$	μH	95
$C_{oss}$	pF	130 @ $V_{DS}=200 \mathrm{V}$
$C_{boot}$	nF	50	10
$f_{rising}$	kHz	645	1065
$t_r$	ns	388	234

. It is preferable to use a bootstrap with a small capacitance; however, a larger bootstrap capacitor can yield a better stable high-side gate control.

4. Simulation and Experiment

4.1. Circuit Simulation

A circuit simulation was conducted using OrCAD Pspice to guide and compare the practical circuit used in the experiment. In the simulation, the transistor parameters with VTO = 7.0 V and a gate signal of 0/10 V matched the actual circuit in the experiment using the Transphorm high-voltage cascode GaN and low-voltage EPC E-mode GaN as mentioned in Section 1. The relay-controlled transformer is shown in Figure 4. The transistors used in the simulation emulate the gate drive and the transistor characteristics from the experiment data. The proposed circuit using a transformer with multiple windings $a_F$ 8.75 and $a_R$ = 11.67 was provided empirically. Controlling the voltage of Vrelay as shown in Figure 12a, we were able to obtain a transformer turn ratio of 35:4 in the forward (charging) mode and 35:3 in the reverse (discharging) mode. In practice, the primary winding and secondary winding are isolated. The dead-time control was conducted using a rise time of 200 ns and falling time of 200 ns in Figure 12a, which leads the gate signal to increase/decrease a 7 V spacing with 160 ns as shown in Figure 12b. The dead-time control is necessary to avoid the shoot-through problem on the half-bridge of each individual side. The initial voltages inside the B1 and B2 capacitors were set to 200 V and 20 V, respectively.

This section discusses the behavior of the CLLC circuit in both the forward (charging) and reverse (discharging) modes. In the forward mode, as shown in Figure 12b, the capacitors C₁ and C₂ are in the resonant mode with a small phase lag β and damping ratio of 0.1 to 0.2, resulting in a current ripple, as discussed in Section 3.1 and Figure 9. Notably, the forward current (green line) has a larger ripple when the transistor M1 turns on compared to when M3 turns on. In contrast, the reverse current (red line), despite being 35/4 times larger than the forward current, presents a lower current ripple due to a better ZCS, as observed on the battery side B2 in Figure 12a. In the reverse mode, as shown in Figure 12c, the voltages of capacitors C₁ (yellow line) and C₂ (purple line) have smaller amplitudes of swings with phase lag of 15 degrees and a higher damping ratio, above 0.2, due to the excitation required. Additionally, the core loss increases when the CLLC is used in the reverse (discharging) mode. It can be observed that the reverse current (red line) has a larger ripple when the transistor M2 turns on compared to M4. The current ripple of forward current (green line) is still larger than the reverse current ripple. This is due to the large phase lag on the voltage of the capacitor C₁ (yellow line) than capacitor C₂ (purple line). In the simulation, it was observed that, for 50% duty switching, there are unbalanced ZCS situations in either the forward (charging) or the reverse (discharging) side due to the asymmetric circuits stated in Equations (14) and (24). Assuming a duty cycle of 0.5 is quite risky because it does not correspond with real circuits/systems; therefore, the actual duty cycle must be verified against the actual circuit, which had a value of 46~48% in the experiments. It is essential to adjust the switching frequency to reduce the phase lag and increase power efficiency, as the phase lag directly affects current ripples and switching loss.

In

Table 6. Comparisons between the analytical solution and simulation results.

Symbol	Unit	Table 3	Charging Simulation	Table 4	Discharging Simulation
f0	kHz	250	256	250	256
δ		0.5	0.5	0.5	0.5
$t_r$	ns	0	160	0	160
Vc1(pp)	V	265	380
I1,max	A	0.89	1.1
PF	W	56	48
Vc2(pp)	V			24.3	36
I2,max	A			5.2	5.7
Psec	W			33	37.6

, we compare the analytical solution with no dead-time control, $t_r=0$, to the simulation with significant dead-time control, $t_r=160 \mathrm{n}\mathrm{s}$, which is about 8% of the pulse time of switching. The difference is shown on the peak-to-peak voltage on the resonant capacitors. A smaller dead time allows the higher resonant voltage and larger conduction current on both grid and vehicle sides to exist because the extra dead time $t_r$ can reduce the power delivery time.

We conducted a comprehensive scan of the switching frequency and duty cycle, as depicted in Figure 13a. The results show that the power delivery is relatively insensitive to the duty cycle δ of switching, except for the case of the power conversion decreasing rapidly around 256 kHz, switching with a duty of 46%.

4.2. Experiment

In accordance with the design specification, as shown in

Table 7. Design specification.

Direction	Rated Power	High-Voltage Side	Low-Voltage Side	Output
Forward	100 W	200 V	20 V	$I_{average}$ = 5 A

, the PCB was fabricated, which features a double-throw relay to alter the transformer turn ratio, as shown in Figure 14. The turn ratio of 35:4 was used in the forward mode, while a high turn ratio of 35:3 was used in the reverse mode. The key components of the circuit are listed in

Table 8. Circuit components.

Component	Description	Quantity
Cascode GaN	TPH3208PS (primary high-voltage side)	2
E-mode GaN	EPC-2304 (secondary low-voltage side)	2
C1	Film cap 4.4 n, 630 V	1
C2	Film cap 270 n, 630 V	1
L2	Power inductor 1.5 μ, 14.7 A	1
Transformer	Wound type; turn ratio 35:3; primary Lm = 300 μH, leakage L1 = 95 μH; core material: SIFERRIT N87	1

. The grid side and vehicle side were connected to a Chroma 63206A-600-420 DC electronic load depending on the charging direction of the setting. The series resonant circuit inductances include the transformer’s leakage inductance L1 and L2, as shown in Table 8. The series resonant capacitors of two film capacitors are C₁ = 4.4 nF and C₂ = 270 nF, respectively. The transformer is made in-house with SIFERRIT N87 core material and measured using a GW Instek LCR-819 RLC meter, as shown in Table 8. Two STDRIVEG600 high-voltage half-bridge gate drivers hold a dead time of 250 ns to separately control the high-/low-side GaN HEMTs.

The experiment’s charging waveforms are shown in Figure 15. Figure 15a shows that the gate signals have a 250 ns dead-time control at V_GS = 12 V under f_s = 250 kHz and 50% duty. The capacitor voltage waveforms $v_{c1}$ and $v_{c2}$ are shown in Figure 15b, with $V_{c1(pp)}$= 600 V and $V_{c2(pp)}$ = 68 V, respectively. The drain–source voltage of the transistors $v_{DS,1}$ and $v_{DS,3}$ are nicely separated without shoot-through problems. Figure 15c shows the waveforms of the vehicle-side (electronic load) current $i_2$ and the associated voltage $v_2$, with $I_{2(max)}$ = 14.3 A. As shown in Figure 15d, the grid-side current $i_1$ from the DC power supply CHROMA 62012P-600-8 yielded $I_{1(max)}$ = 1.75 A, and the associated capacitor voltage had a phase lag $\beta =$ 18°. The phase lag $\beta$ causes a switching loss and reduces the power conversion efficiency. The critical issue in the practical implementation is to reduce the EMI by carefully selecting the bootstrap capacitor, dead-time duration, and switching frequency adjustment. To reduce ringing, it is important to carefully select the bootstrap capacitors and gate resistance for the gate–source response. The ideal dead time can be determined by comparing the sinusoidal wave form of the resonant capacitor voltages $v_{c1}$ and $v_{c2}$. A perfect sinusoidal wave form indicates a better resonance mechanism, resulting in a better power factor and efficiency. Increasing the magnitude of the resonance is critical for higher power transfer efficiency.

Table 9. Comparison of the equations and experimental results.

Symbol	Theoretical Value	Equation	Measurement
$V_{c1\left(pp\right)}$	600 V	(18)	600 V
$I_{1max}$	2 A	(20)	1.74 A
$I_{2max}$	14.4 A	(26)	13.2 A
${\xi }_2$	0.166	(30)	0.3
$P_{prim}$	127 W	(22)	100 W

summarizes the experimental results. In the forward mode, the operational parameters are $V_1=200 \mathrm{V}$, $V_2=20 \mathrm{V}$, $f_0=248 \mathrm{k}\mathrm{H}\mathrm{z}$, and $\delta =50\%$. The power transferred to the DC electronic load $P_{Foward}$ is 127 W at the resonant frequency. The experimental results match the theoretical values closely, except for the damping ratios, which are 55% lower than the theoretical values.

The results of the experiments on power efficiencies are shown in Figure 16. There are three different kinds of power losses, including resistive, switching, and core losses. The average power conversion efficiency in the forward mode is 95% for an output power between 70 and 100 W, and the average power efficiency is 92% in the reverse mode, occurring in the range between 35 and 85 W. The best forward (charging) mode efficiency of 97% occurred at 90 W output. The best reverse (discharging) mode efficiency of 95% occurred at 40 W output. The efficiency difference in the two opposite charging directions is due to an impedance difference, as shown in Figure 6b and Figure 8b, which resulted in two different resonant frequencies. The selected switching frequency can match the forward (charging) mode, which can also deviate from the actual series resonant frequency of the reverse (discharging) mode. The mismatch of the series resonances caused the voltage gain in the reverse (discharging) mode to be lower than that in the forward (charging) mode. The reverse (discharging) mode is shown in Figure 17.

5. Discussion

This research work showed the open-loop control characteristics. In order to conduct further closed-loop control, one may need to know the voltage gain vs. switching frequency. The sensitivity of the power conversion to both switching frequency and the duty ratio are nonlinear, as shown in Figure 13. As shown in Figure 13, the duty does not affect the power conversion or the voltage gain as the switching frequency does. We can linearize the voltage-gain sensitivity due to the switching frequency change according to the experimental data, as shown in Figure 18. The dots are from experiments under an input voltage V_in = 200 V and switching frequency at different ratios of 250 kHz when the duty ratio was set to 50%. The voltage gain is approximately 7%, increasing for every 1% increment of switching frequency. For different ranges of the power conversion, one can use the gain-scheduling techniques to fit different ranges of voltages.

Our experiments recorded the transient response, as shown in Figure 19. It can also be seen that the open-loop control transient response of the CLLC charger yields a voltage overshoot around 25% in Figure 19a and the current overshoot is 200% in Figure 19b. The soft-starting method [29] may be used in the closed-loop control system, which we have not yet implemented. It can also be seen from Figure 19b that the settling time is about 100 ms, which is fast enough to allow for the soft-starting procedures which take around 500 ms to 1 s to initialize. When the load changes, the voltage gain only slightly changes and the currents at both input and output significantly change. Figure 20 shows the result when the load is increased by 100% in the forward (charging) mode; it can be observed that the input voltage V1 remains 200 V when the output voltage V2 drops from 20 V to 17 V, which is a 15% decrement. Thus, the power conversion rate increases to 200% and the input and output currents also increase to 70%, which is identical to the current rises from the experiment, as shown in Figure 20.

For the closed-loop control, we need to first know the battery rating and to feedback the battery status according to AI techniques [30] and/or the battery modeling techniques [31]. The health of the battery (SOH) and the voltage to SOC characteristics are important to achieve the most suitable charging current when fast charging is preferable. SOC determines the proper charging and discharging current, especially when the battery strings are charged in a parallel connection; the batteries can be deemed as capacitors with different capacitances, and the one with the largest capacitance always has the higher current. The anomaly condition as well as the cell inconsistency of the cells in the battery pack may be detected according to these four parameters obtained from the SOC-VOC model fitting [32]. The charging current is directly related to the power conversion, as shown in Figure 13, and the voltage gain versus switching frequency, as shown in Figure 18, is applicable to the power conversion via a constant current control.

In a real-time application, a microprocessor must be integrated into the closed-loop control system to both control the relay to change the transformer turn ratio and maintain a stable output voltage or current. The proposed real-time control scheme, excluding the soft start, is shown in Figure 21. The parameters L₁, C₁, L₂, C₂, and transformer turn ratio were designed according to the rated voltages and power based on Equations (14), (24), (21) and (27). In the control scheme, we can use the same equations to generate a different voltage and power. The critical issue for the control is to maintain zero-current switching (ZCS) in order to obtain the best power conversion efficiency. The real-time measurement on the capacitor voltage as well as the battery voltage for state estimation and SOC state detection is also critical, and requires high-frequency AD/DA data-acquired ICs. An alternative manner to achieve ZCS is the formation of an inner feedback control loop to maximize the power efficiency via duty adjustment under the same switching frequency. The actual implementation will need cost-based evaluations.

The electrical double-pole double-throw relay, as shown in Figure 13, is connected to the two secondary windings of the transformer, as shown in Figure 4, with eight pins. One power pin is connected to 12 V/0 V and one to the ground. One pole pin switches between terminals 3 and 5, as is labeled in Figure 4. The other pole pins switch between terminals 4 and 6, as is labeled in Figure 4. The pole pin connection is determined by the voltage of the power pin. When the power pin is engaged to the 12 V source, the transformer uses terminals 3 and 4 as the secondary winding to the vehicle side. When the power pin goes to the ground, the transformer uses terminals 5 and 6 as the secondary winding to the vehicle side. The control of the state of the power pin can be implemented using a common-source circuit with a gate voltage control with a MOSFET switch. The turn ratios are different when the power pins have different voltages.

6. Conclusions

We presented a half-bridge CLLC circuit topology that can perform either the charging or discharging of batteries. The comparisons between the theoretical derivations and the experimental results show good consistencies, which indicate that the theoretical derivations can be used as design guidelines for future CLLC circuit designs. The feature of this CLLC circuit topology is its use of a relay to switch the transformer turn ratio in order to change the direction of the current flow. The sinusoidal wave form of voltage presented on either the primary winding in the forward (charging) mode or the secondary winding in the reverse (discharging) mode from the DC voltage is achieved by the resonance network from the conventional LLC circuit concept. In order to achieve a bidirectional current flow and, thus, to enable the possibility of charging/discharging together, the CLLC circuit proposed in this paper returns the magnetic energy to the resonant capacitors C₁ and C₂ in one phase and conveys the energy from the resonant capacitors to the vehicle batteries or grid load in the other phase. The proposed CLLC converter can achieve only half of the power conversion that the half-bridge LLC converter does. However, the comparison between the CLLC converter and conventional LLC converter is equivalent to the comparison of a half-wave rectifier with the full-wave rectifier; the former one allows for charging/discharging in only half of the time period. The results obtained from the CLLC show good power efficiencies, which are almost all above 90%. The power efficiency reaches the best values at a certain power in the forward (charging) mode when the power efficiency drops along the output power in the reverse (discharging) mode. In order to achieve a higher power conversion and higher efficacy using the proposed CLLC in high-power applications, we will still need to reduce the coil resistance of the transformer, the transistor on-resistance, and the switching loss of transistors in the future. These improvements can be achieved through reconfiguring the GaN transistor epi layout design and finding innovative methods with which to cool down the circuit from the external apparatus, such as using an inexpensive cryocooler, which are the current research focuses in NYCU.