A Survey on Multi-Active Bridge DC-DC Converters: Power Flow Decoupling Techniques, Applications, and Challenges
Abstract
1. Introduction
2. Principles of the MAB Converter
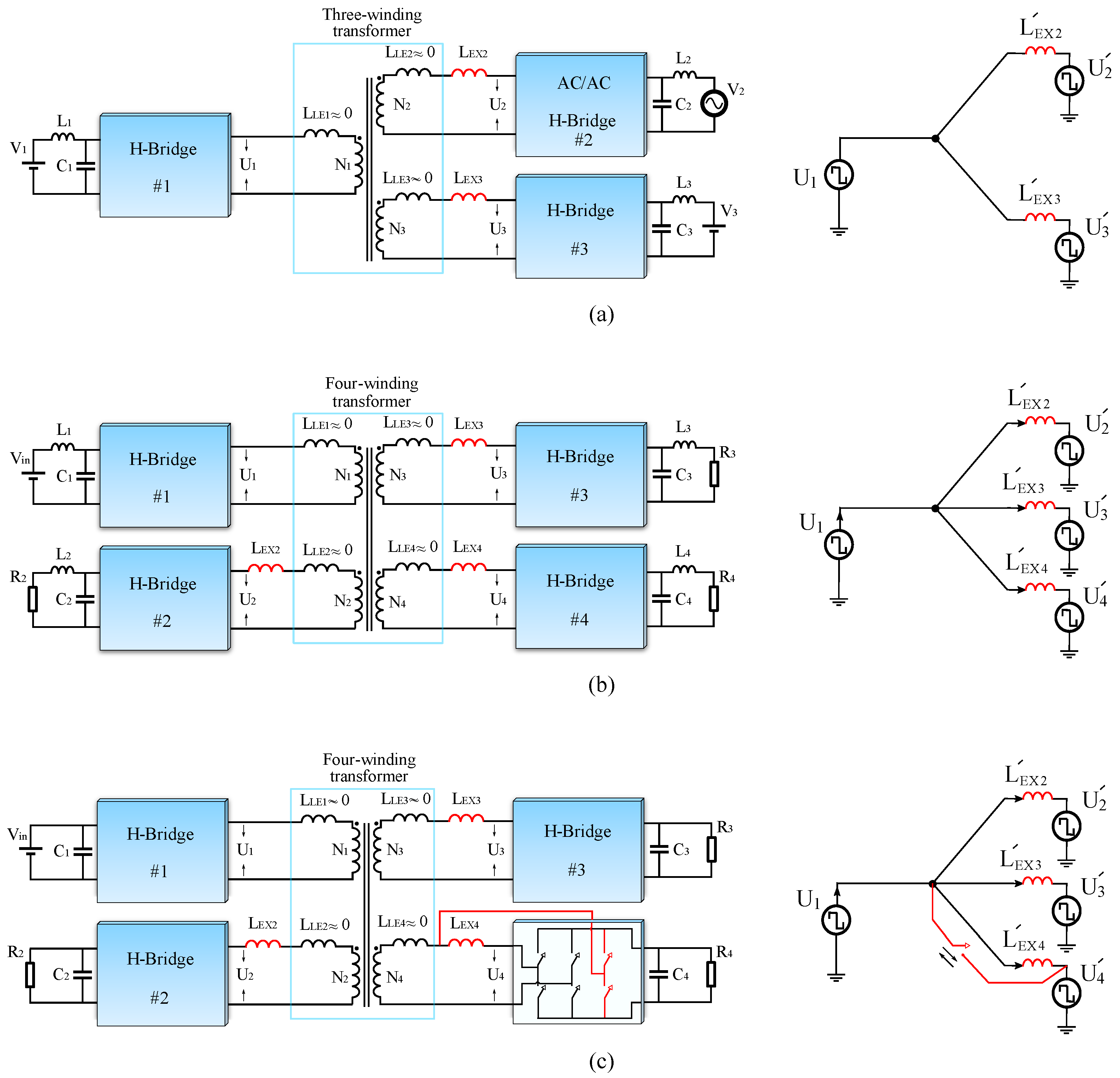
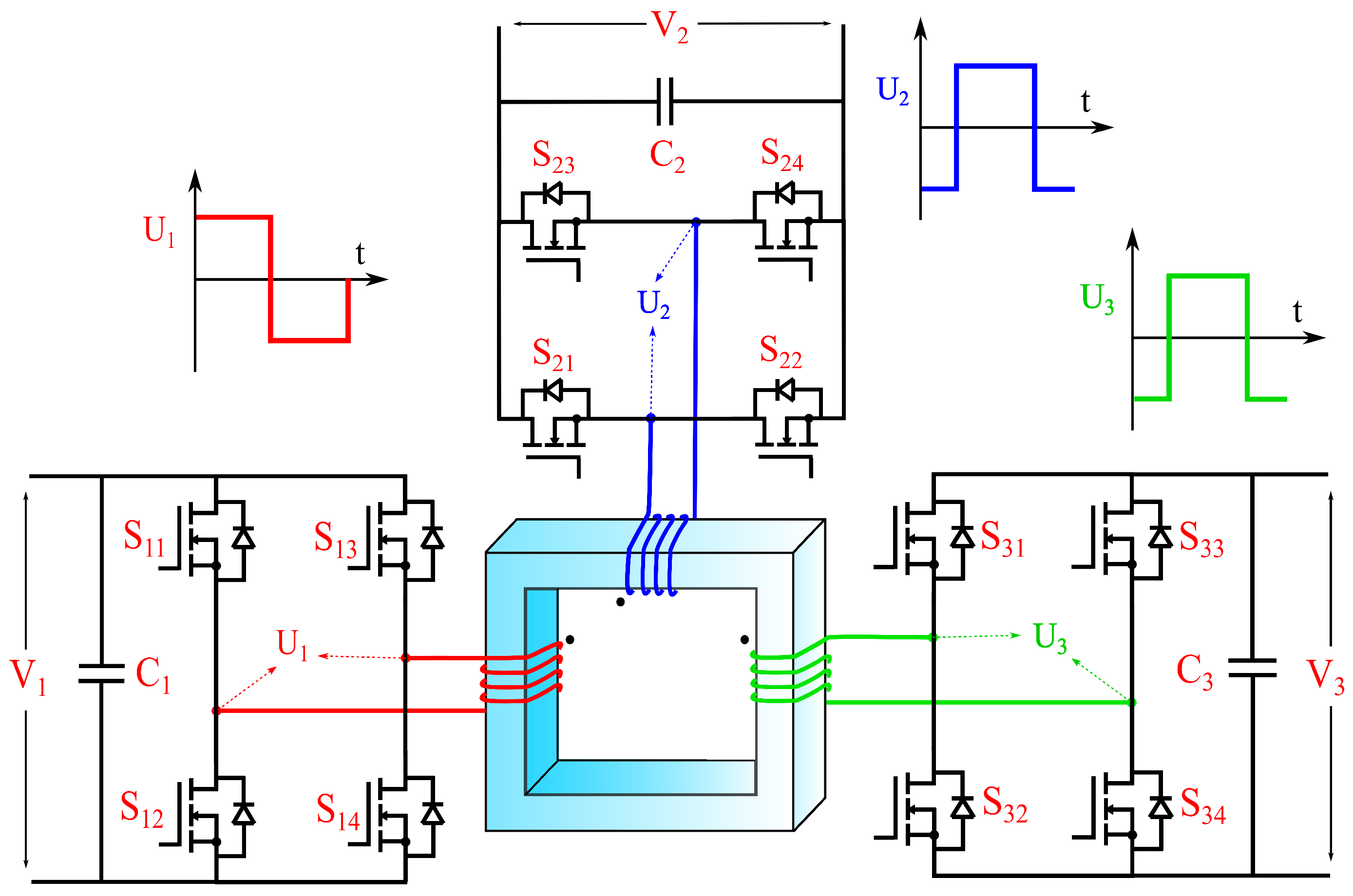
2.1. Topology of the MAB Converter
2.2. Equivalent Circuit Model of MAB Converter
- MWHFT is replaced by one of the extended T, Pi, or cantilever ECMs.
- Each H-bridge replaced by an AC voltage source ().
- Magnetizing inductance can be eliminated since it is much greater than the leakage inductance, and by referring parameters to the primary side, ideal transformers can be neglected, so a Star-type (Y-type) ECM will be achieved.
- In order to directly link voltage sources to each other, a star to delta ) transformation should be applied to achieve -type ECM.
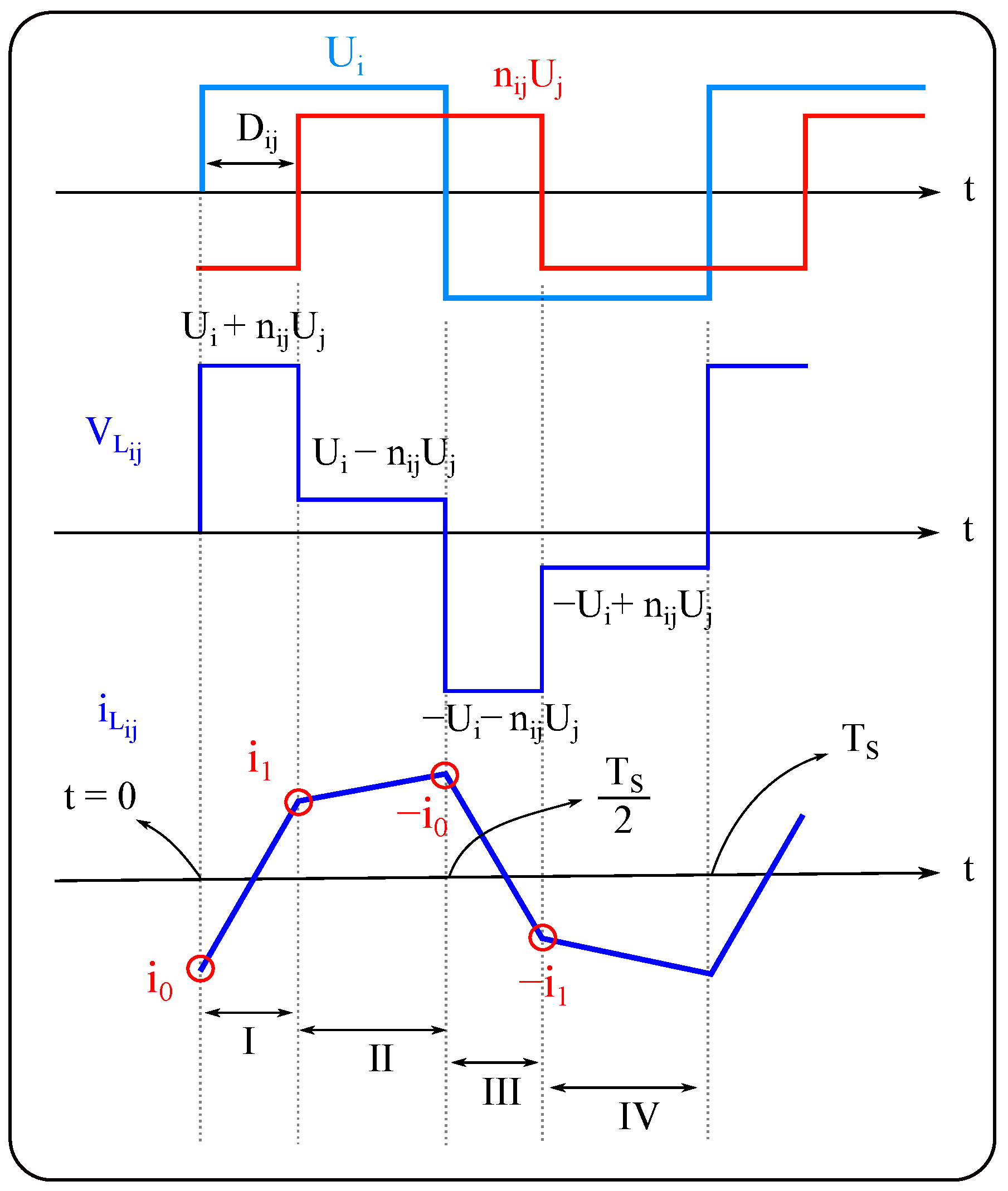
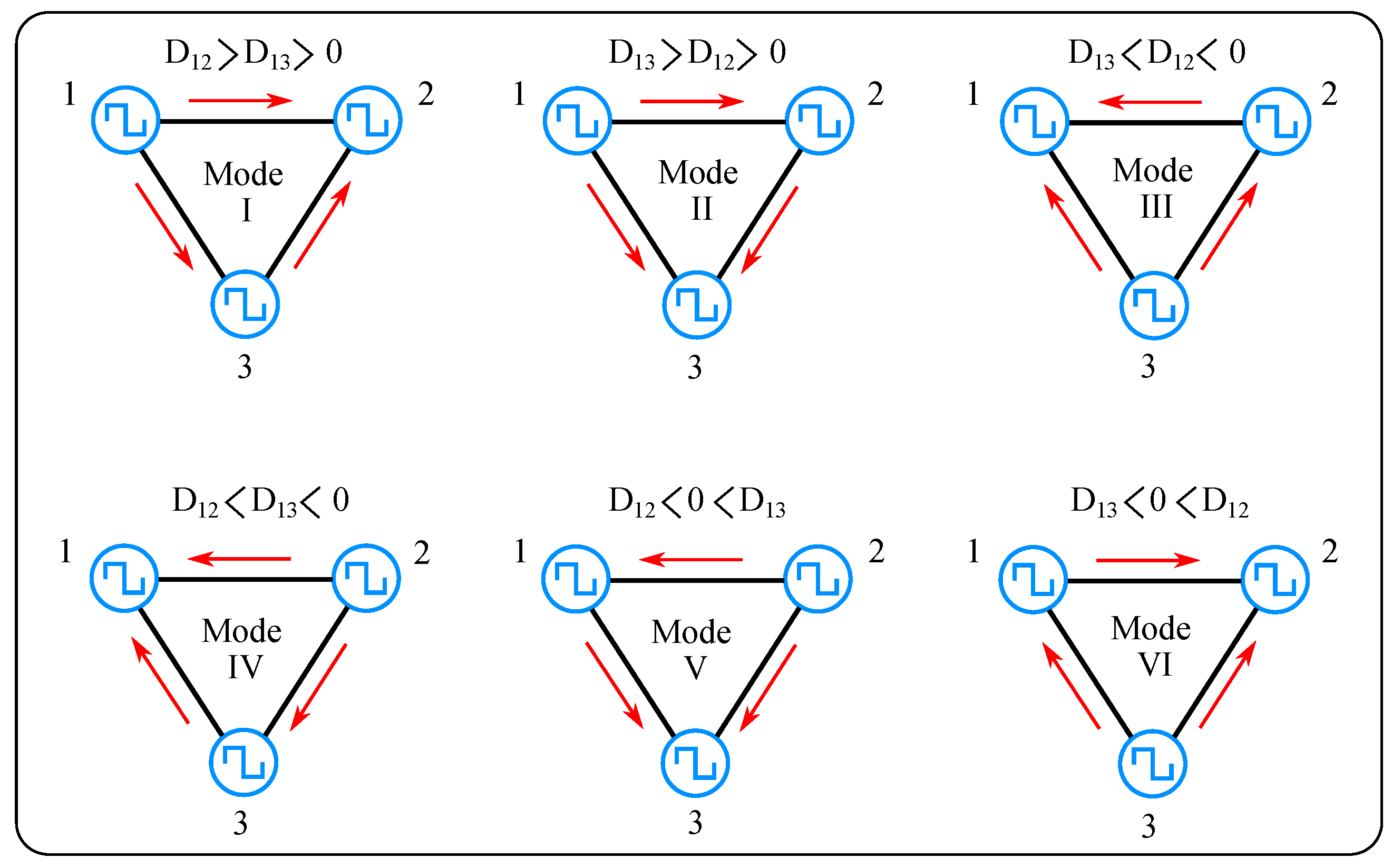
2.3. Power Flow Analysis
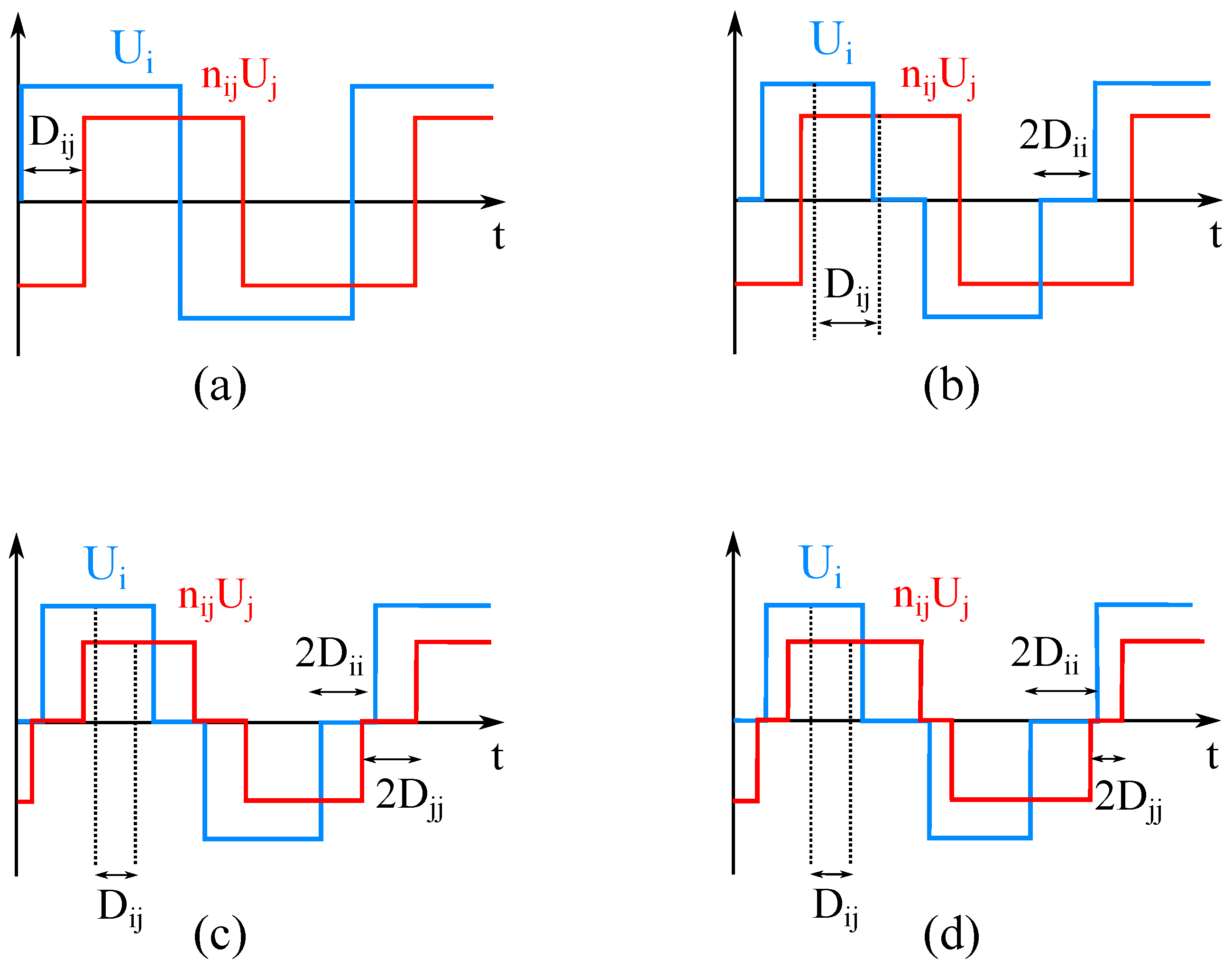
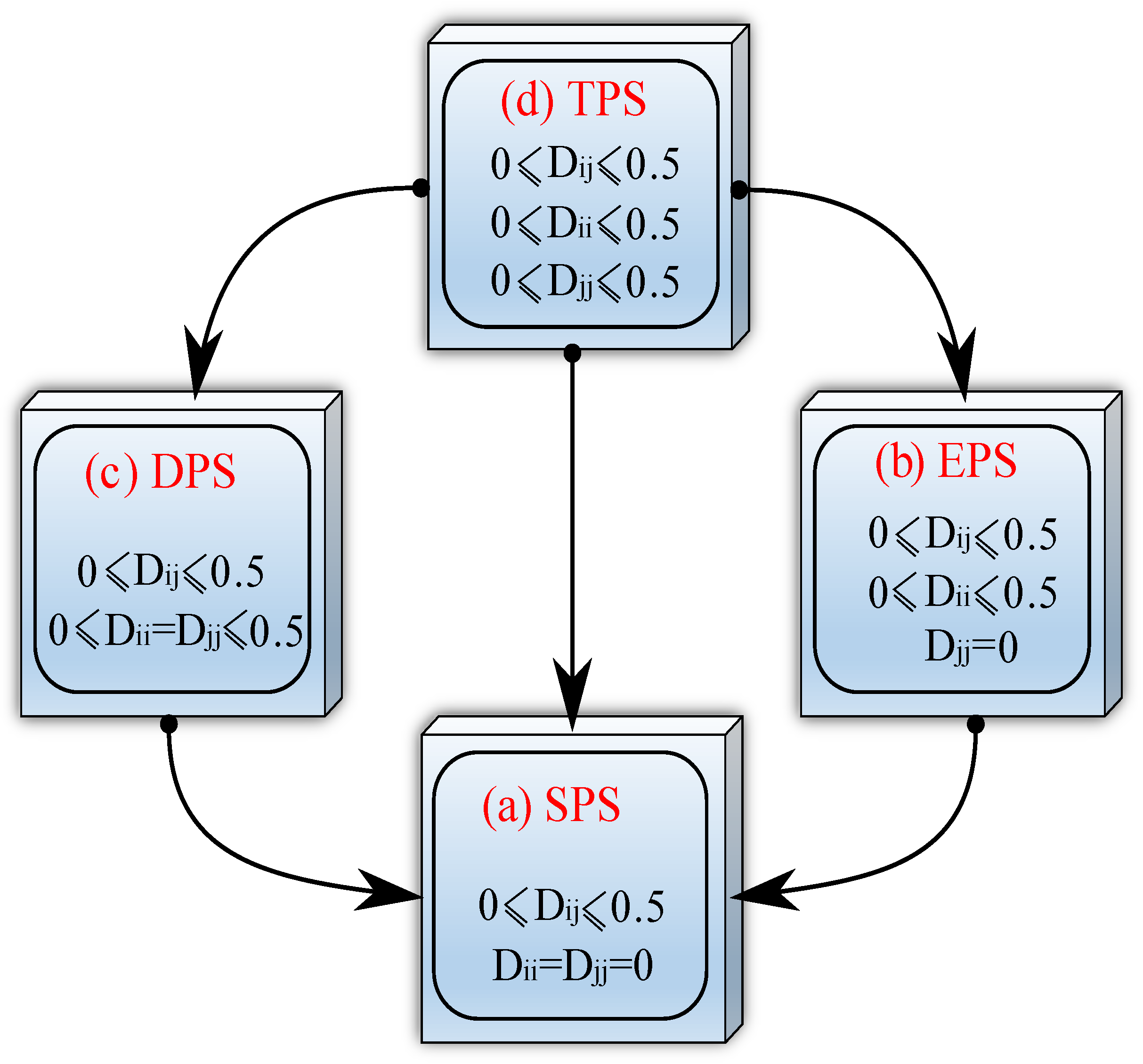
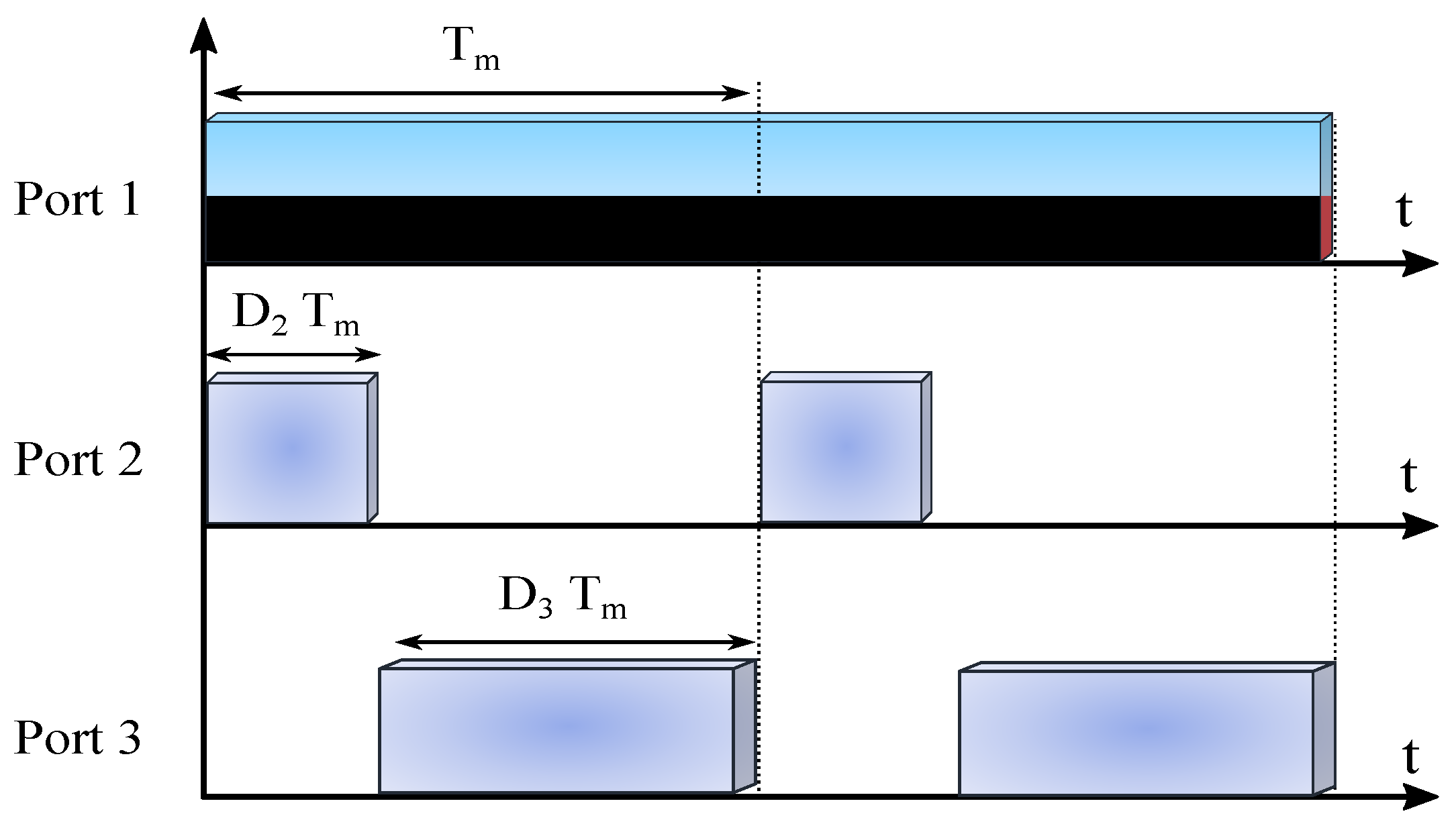
2.3.1. Introduction to Modulation Techniques
- If the DC voltages are not equal (e.g.,: ), using SPS modulation leads to unequal RMS value of the square AC voltages, which leads to reactive power, and more conduction losses. GPS modulation can modify and equalize the RMS values of the generated AC voltages and reduce or fully eliminate the reactive power. As a result, conduction losses are decreased [79,120,122,160].
- Reduces peak value of the inductor current and provides lower current stress in components [53].
- Under conventional SPS modulation, a DC offset appears in the AC current during transients (which decays slowly due to transformer resistance) and increases the settling time during transients. Advanced modulation techniques are capable of eliminating the inductor current DC offset in one switching cycle [43].
- Advanced modulation strategies have more control freedom and can provide a more satisfactory transient response in comparison with conventional SPS modulation.
- Using a small inner phase shift in GPS modulation can reduce high-frequency oscillations of the AC voltages and currents during the switching transient, and reduce the EMI [136].
- In comparison with SPS modulation, GPS can increase the power flow capability between two ports by almost [157].
2.3.2. Modelling Approaches to Derive Power Flow Relationships
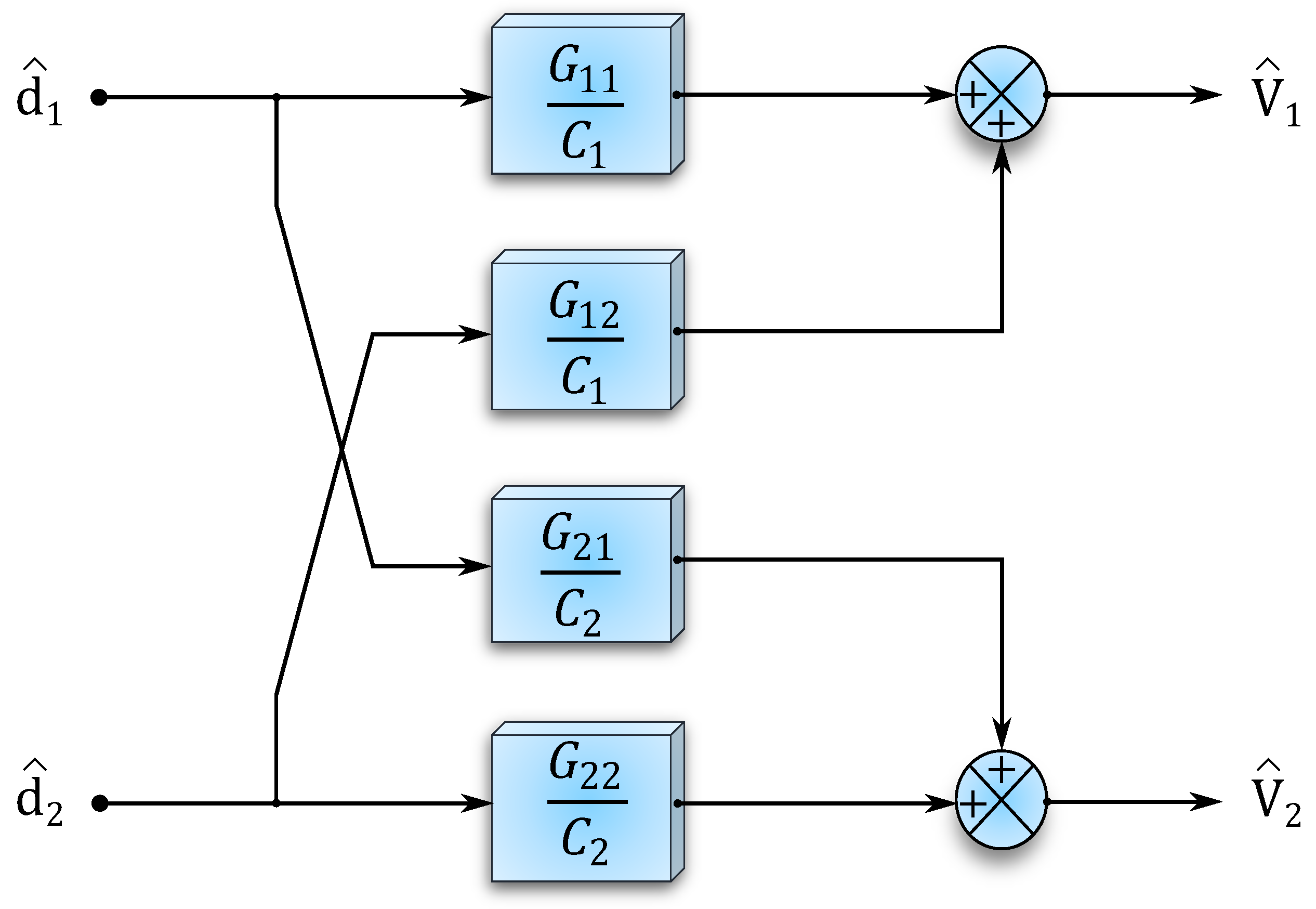
3. Dynamics and Small Signal Modelling
Cross-Coupling Behavior
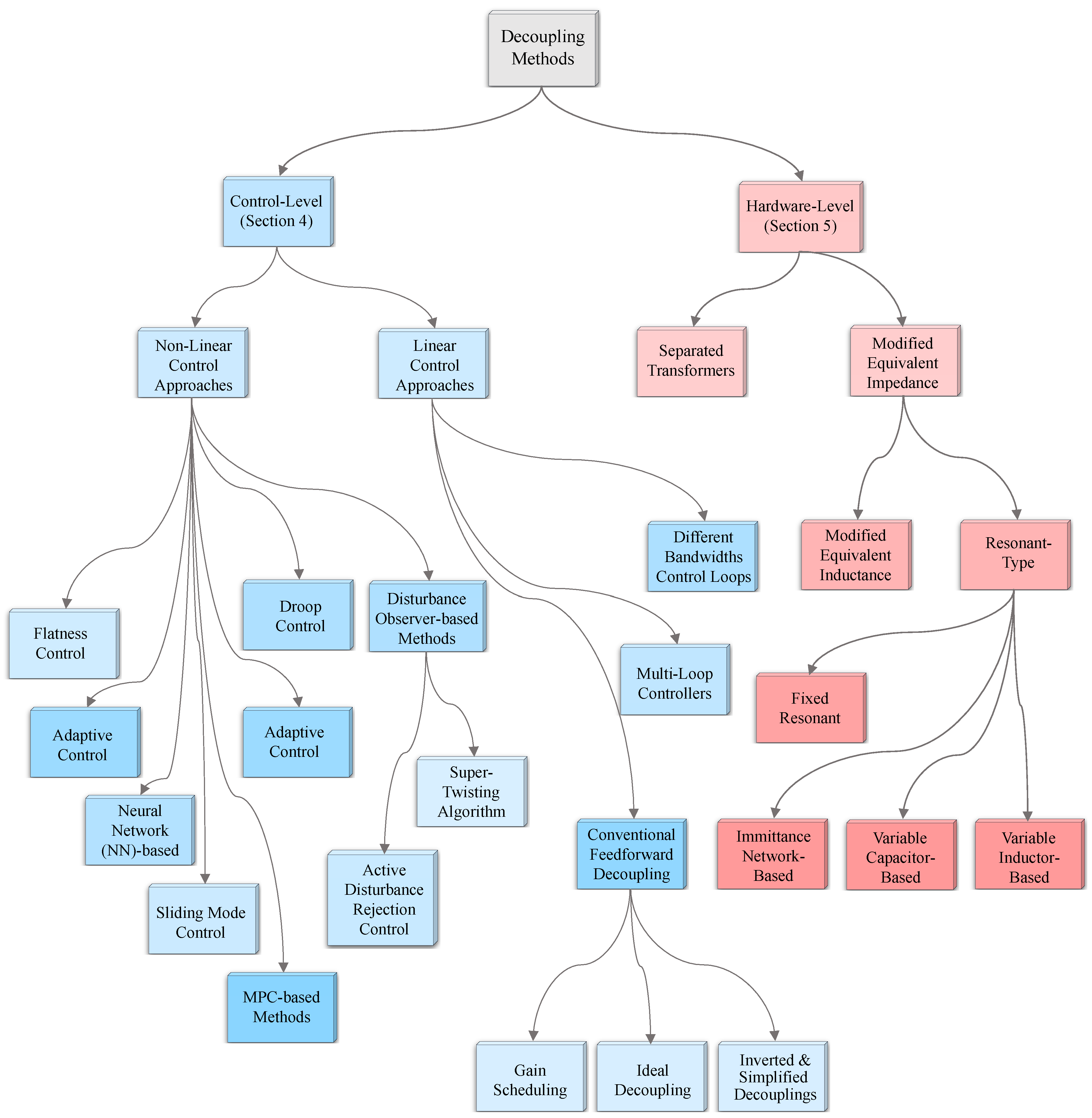
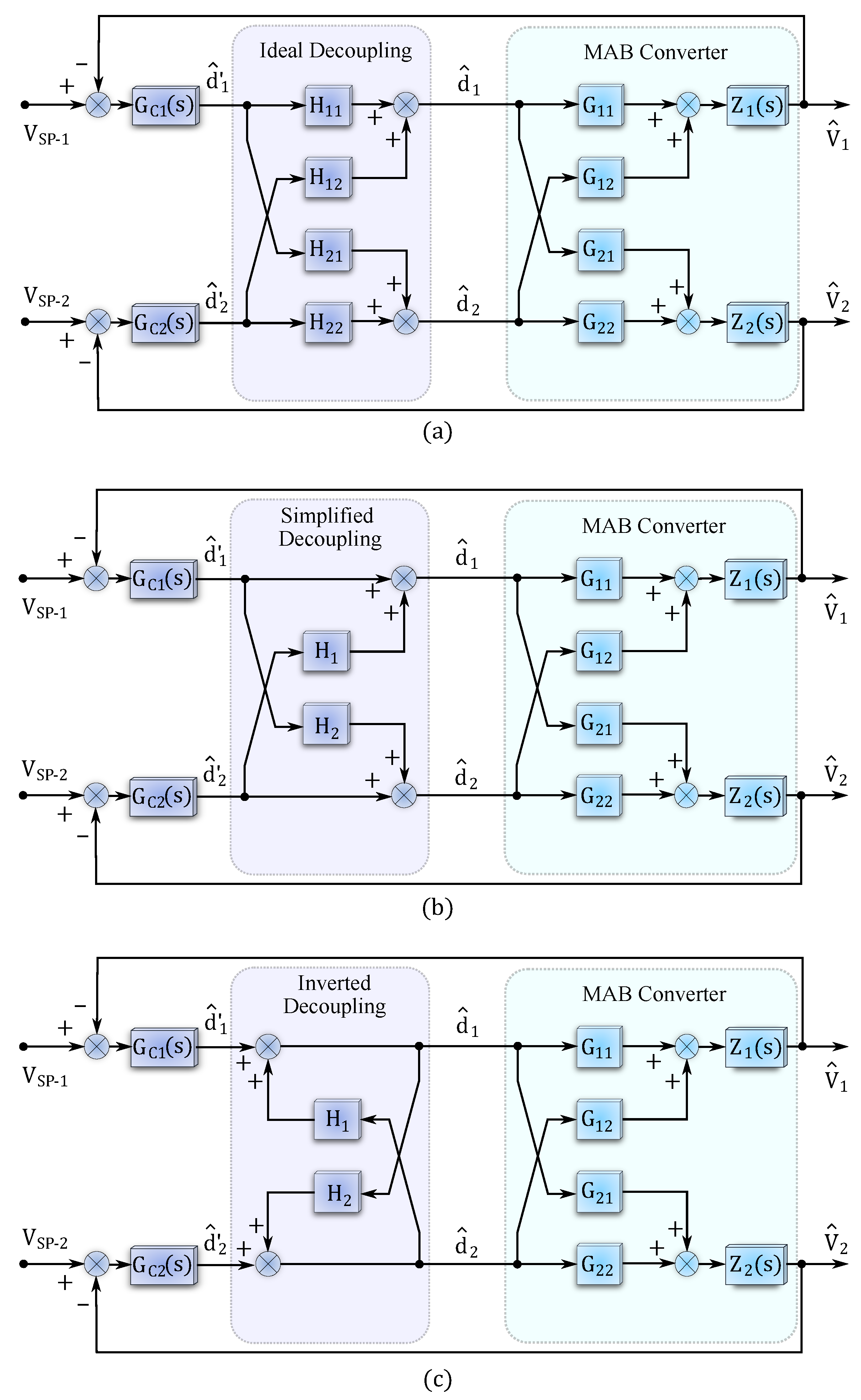
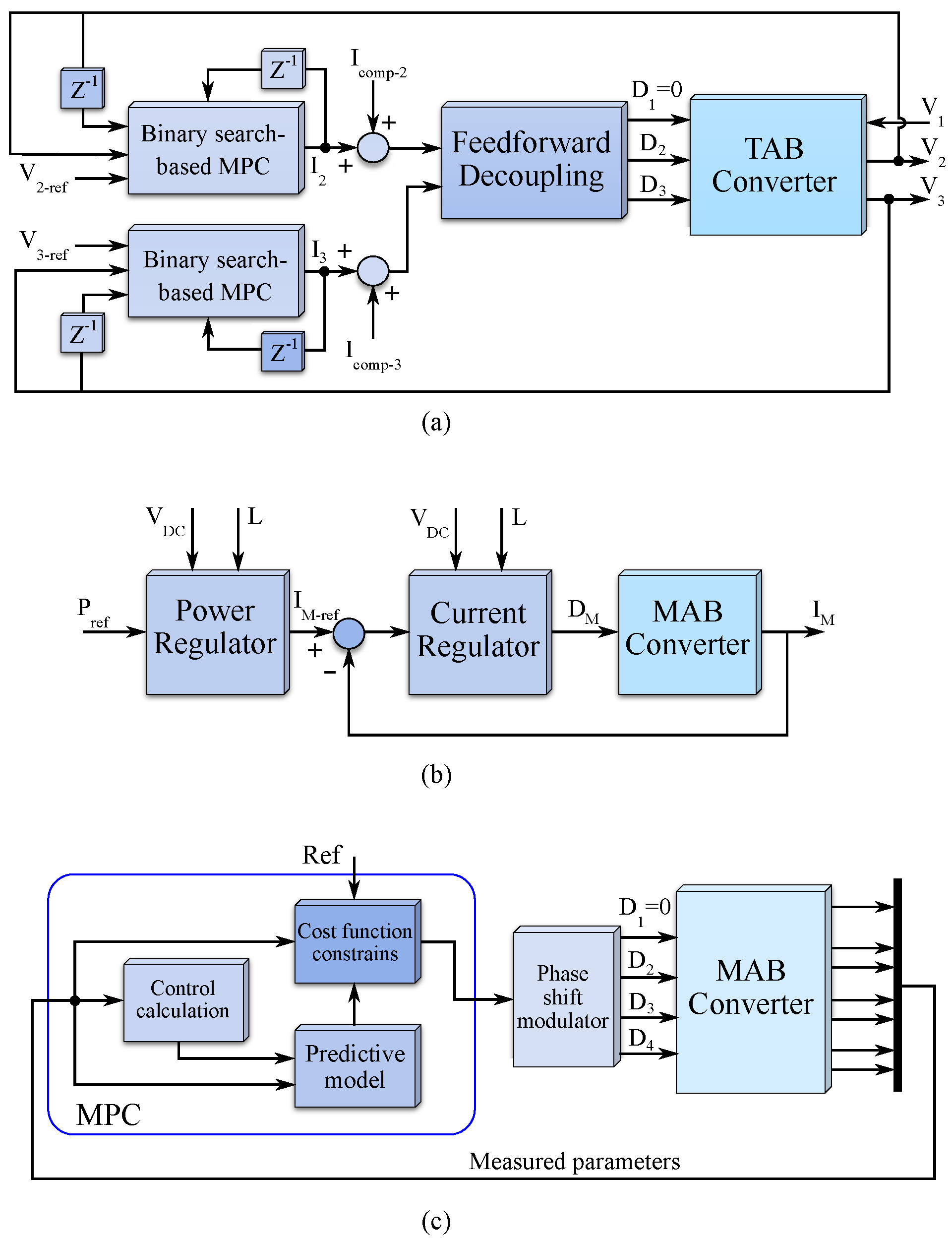
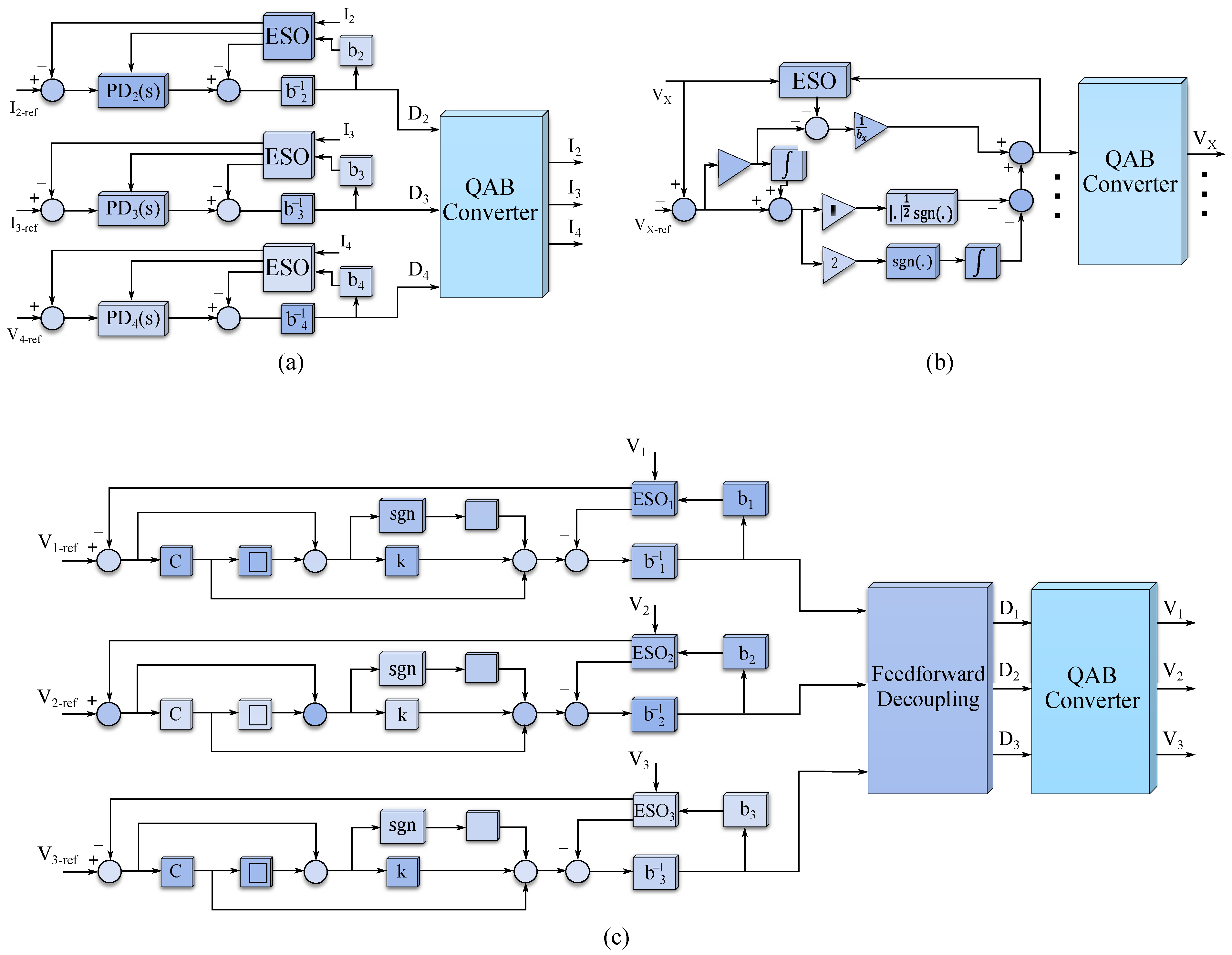
4. Control-Level Decoupling
4.1. Conventional Feedforward Decoupling Approaches
- Ideal decoupling can lead to complex expressions for the decoupling terms and is difficult to realize [169].
- The conventional decoupling has a centralized control structure, which means the number and complexity of the decoupling terms will increase with the number of ports, especially in applications with multi-directional power flow requirements.
- Effective performance of the feedforward linear control-based decoupling methods, requires a precise dynamic model of the converter [169].
- The control-to-output behaviour of the MAB converter with large phase shift values is highly non-linear. In general, linear control-based feedforward decouplers are not capable of dealing with significant non-linearity, and hence their desired performance is limited to the specific operating points in linear regions, and, the maximum power rating is restricted [170].
- Taking the RHP zero caused by the inductor dynamics into account, can make the decoupling design complicated [15].
- It can reduce the overall dynamic performance of the MAB converter [101].
4.2. Other Linear Control Approaches for Decoupling
4.3. Nonlinear Control Approaches
5. Hardware-Level Decoupling
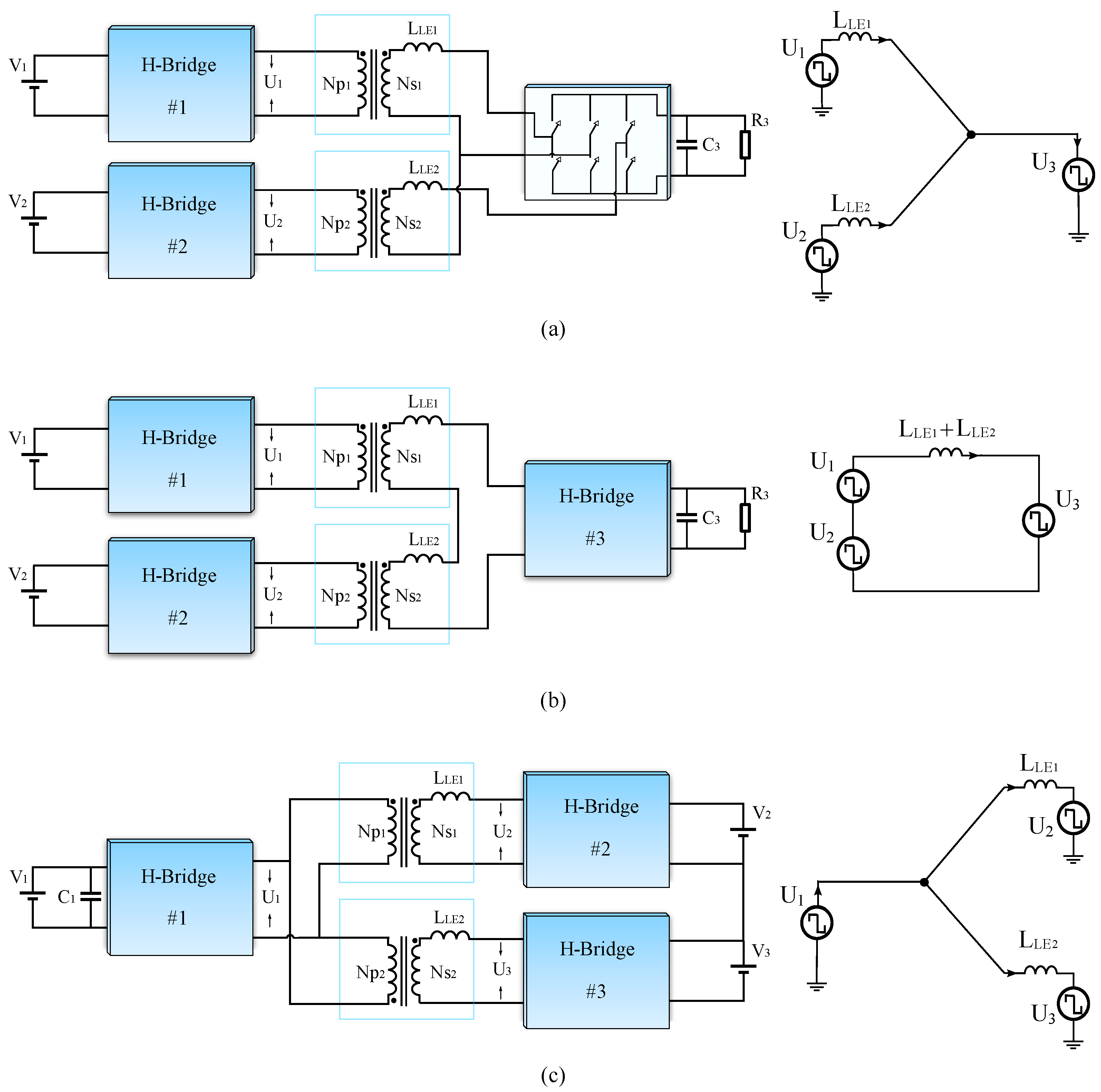
5.1. Modified Inductance Type MAB
5.2. Separate Multiple Transformers
- Two winding transformers are much easier to design, manufacture, and optimize [183]. Moreover, desired leakage inductances are easier to achieve.
- Since two windings can be wound on different arms of the magnetic core, two-winding transformers can provide better galvanic isolation for high-voltage applications, especially when the voltage difference between two connected ports is considerable.
- The magnetic coupling between two transformers is neglected, hence, the cross-coupling effect can be reduced or fully eliminated (depending on the connection of the transformers).
- In a multi-winding transformer-based MAB converter with two inputs, a small deviation or disturbance in their voltages or the phase shift between them can cause circulating power and higher conduction losses, while an implementation with multiple two-winding transformers can overcome this problem.
- In the conventional MAB converter, with unequal phase shifts at the input ports, two voltages oppose each other (for part of the period), and this leads to a reduction in the slope of the sum of the produced magnetic flux. As a consequence of the lower rate of change in magnetic flux, the back electromagnetic force (EMF) will be reduced which causes high inrush currents from input ports. In the worst-case scenario when , a magnetic short circuit occurs [109]. Using two-winding transformers can address the magnetic short-circuit drawback of conventional MAB converters.
- In [41], it was suggested that an MWHFT in a MAB converter can have problems with saturation which are exacerbated as the number of ports (windings) increases - although the mechanism for this effect was not fully explained or discussed.
- Two-winding transformers can provide better heat dissipation than multi-winding transformers [184].
- Using two-winding transformers, the scalability of the converter is greater, since the implementation of a multi-winding transformer does not do not allow retrospective addition of another port (isolated active bridge) [104].
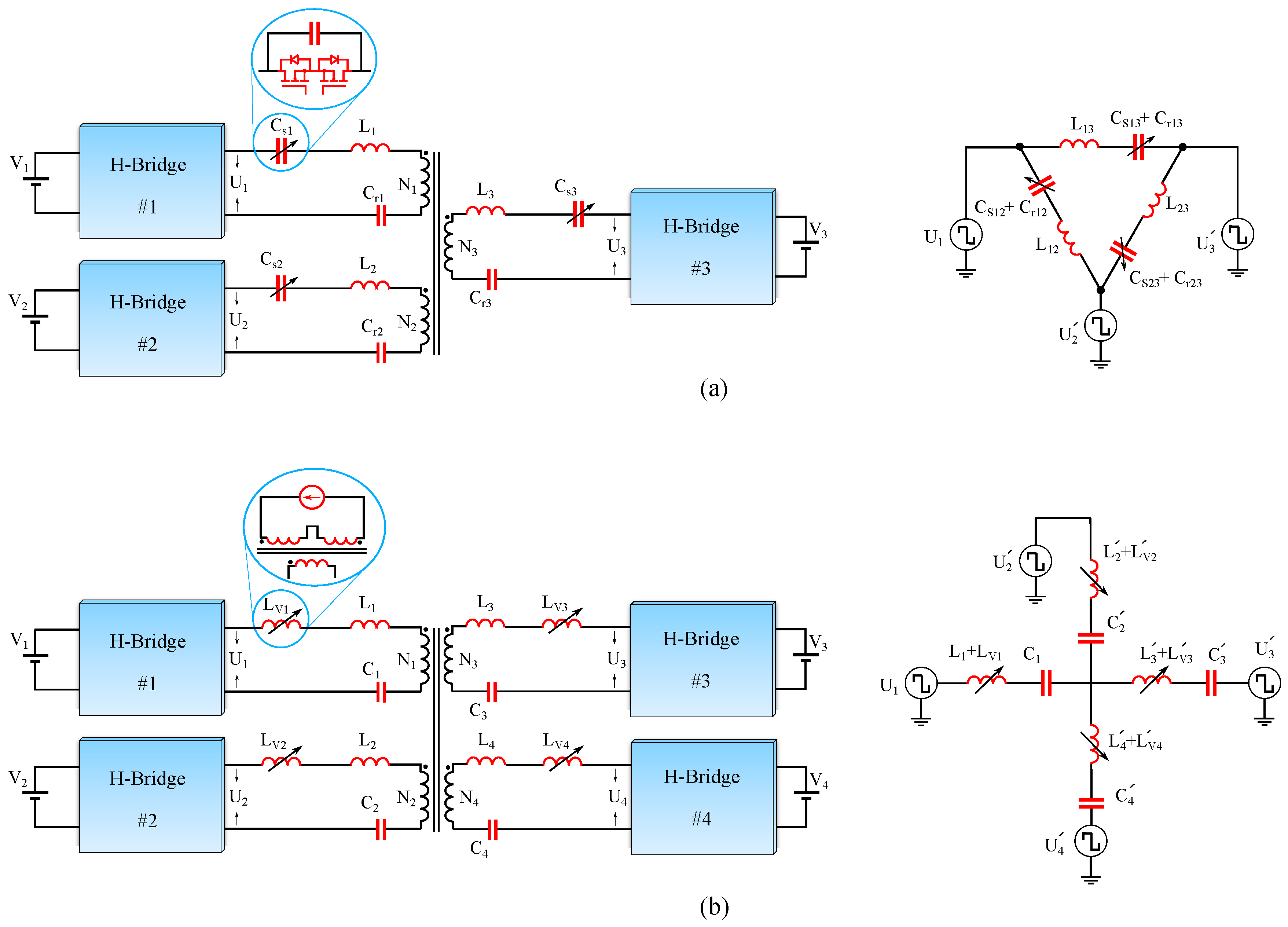
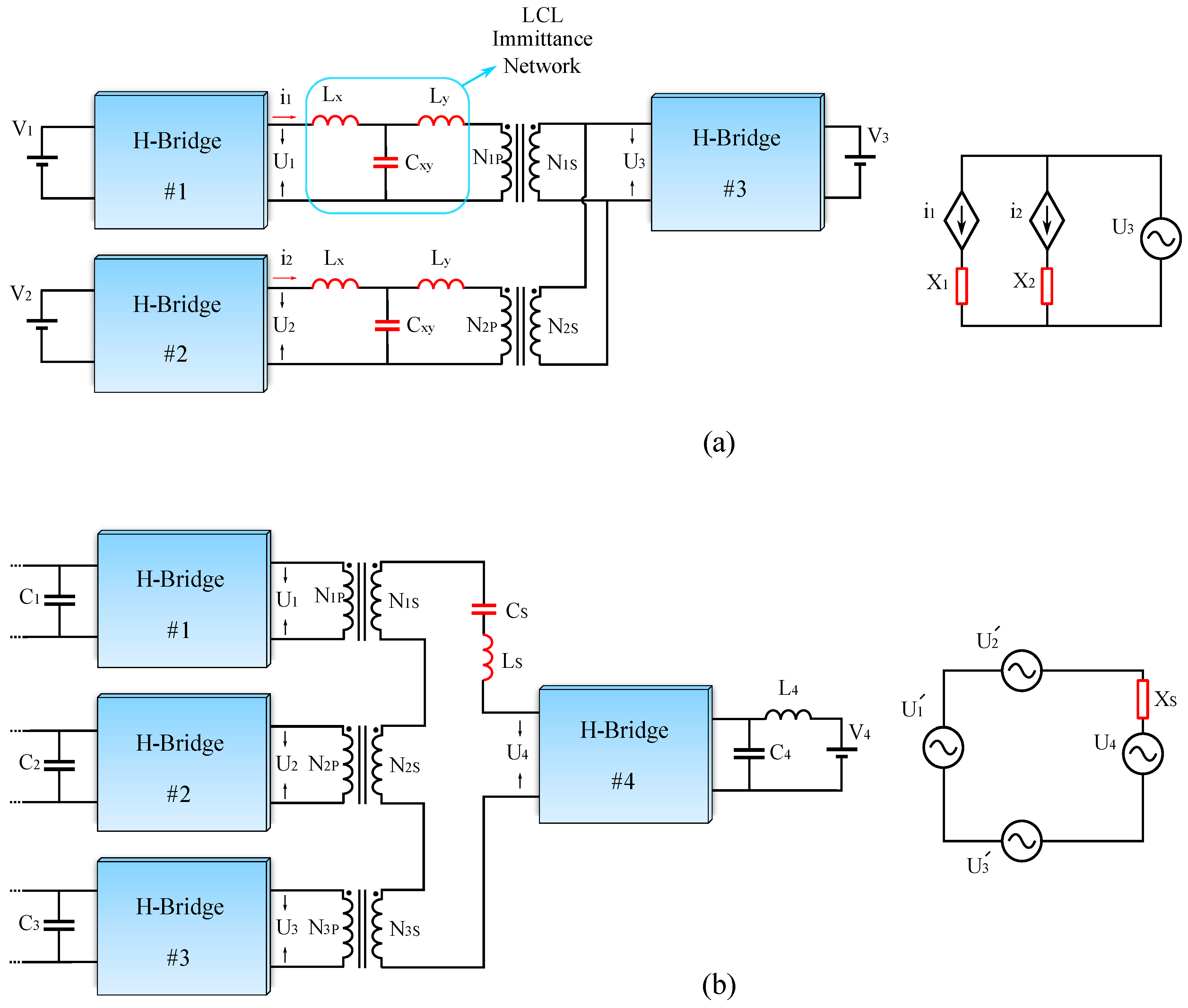
5.3. Resonant-Type Decoupling Approaches
6. Discussion, Outlook, and Conclusions
- Steady-state modelling: More control variables are offered by the MAB converter, which complicates the time-domain analysis. FCA, which approximates the waveforms and considers only the fundamental component in the frequency domain, greatly simplifies the analysis but reduces its precision. Using GHA and taking into account higher odd-order components of the waveforms can compensate for the lack of precision without sacrificing simplicity.
- Optimisation: Many researchers aimed to reduce both switching losses and conduction losses to flatten the efficiency curve for the entire operating range. Advanced modulation such as GPS can reduce the switching losses by expanding ZVS criteria and reducing the conduction losses by eliminating the reactive power. Others employed wide band-gap power semiconductors such as SiC-MOSFETs or used resonant circuits to reduce the conduction losses.
- Transformer design and modelling: The leakage inductance plays a key role in the operation of the MAB converter. However, designing the MWHFT is more complicated than conventional two-winding HFTs. In addition, deriving a simple and accurate ECM with measurable parameters is another challenge with MWHFTs.
- Reliability and fault tolerance: Fault detection and ride-through become increasingly important in MAB converters, as a fault in one port can impact the operation of the other ports. Several research papers sought to analyze the fault ride-through in MAB converters by bypassing the faulty port or attempting to remove DC current bias using advanced modulation techniques.
- Application-oriented research: Many authors focused on specific applications, then adapted or modified the fundamental topology of the MAB converter or integrated it with other types of converters, such as DC/AC inverters, to satisfy the requirements of the applications considered.
- Power flow decoupling control: Since cross-regulation in the MAB converter is the most unique challenge that complicates the control structure, and it does not exist in the DAB converter, it is the most extensively researched topic among other related MAB converter research gaps.
Author Contributions
Funding
 This project has received funding from the European Union’s EU Framework Programme for Research and Innovation Horizon 2020 under Grant Agreement No 955646.
This project has received funding from the European Union’s EU Framework Programme for Research and Innovation Horizon 2020 under Grant Agreement No 955646.Conflicts of Interest
Abbreviations
| MAB | Multi-Active Bridge |
| DAB | Dual Active Bridge |
| MMAB | Modular Multi-Active Bridge |
| TAB | Triple Active Bridge |
| QAB | Quadruple Active Bridge |
| PS | Phase Shift |
| SPS | Single Phase Shift |
| GPS | General Phase Shift |
| EPS | Extended Phase Shift |
| DPS | Dual Phase Shift |
| TPS | Triple Phase Shift |
| ADRC | Active Disturbance Rejection Control |
| MPC | Model Predictive Control |
| SMC | Sliding Mode Control |
| STA | Super-Twisting Algorithm |
| ESO | Extended State Observer |
| TDA | Time Domain Analysis |
| FDA | Frequency-Domain Analysis |
| FCA | Fundamental Component Analysis |
| GHA | General Harmonics Analysis |
| RCC | Ripple Correlation Control |
| FFT | Fast Fourier Transformation |
| NN | Neural Network |
| RES | Renewable Energy System |
| EV | Electric Vehicle |
| ESS | Energy Storage System |
| HESS | Hybrid Energy Storage System |
| FC | Fuel Cell |
| SC | Super Capacitor |
| UPQC | Unified Power Quality Conditioner |
| MEA | More Electric Aircraft |
| SST | Solid State Transformer |
| DFIG | Doubly Fed Induction Generator |
| UPS | Uninterruptible Power Supply |
| MIMO | Multi-Input Multi-Output |
| FHS | First Harmonic Synchronized |
| ZVS | Zero Voltage Switching |
| HFT | High Frequency Transformer |
| MWHFT | Multi-Winding High-Frequency Transformer |
| RHP | Right Half Plane |
| PI | Proportional Integral |
| PD | Proportional Differential |
| PIR | Proportional Integral Resonant |
| PR | Proportional Resonant |
| EMF | Electromagnetic Force |
| ECM | Equivalent Circuit Model |
| MMC | Modular Multilevel Converters |
| LUT | Look-Up Table |
References
- Singh, A.K.; SinghPatel, C.R.B. Global Warming Dataset and Analysis. In Proceedings of the 2022 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COM-IT-CON), Faridabad, India, 26–27 May 2022; IEEE: Manhattan, NY, USA, 2022; Volume 1, pp. 441–447. [Google Scholar]
- Bhattacharjee, A.K.; Kutkut, N.; Batarseh, I. Review of multiport converters for solar and energy storage integration. IEEE Trans. Power Electron. 2018, 34, 1431–1445. [Google Scholar] [CrossRef]
- Zhao, C.; Kolar, J. A novel three-phase three-port UPS employing a single high-frequency isolation transformer. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 6, pp. 4135–4141. [Google Scholar] [CrossRef]
- Michon, M.; Duarte, J.; Hendrix, M.; Simoes, M. A three-port bi-directional converter for hybrid fuel cell systems. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 6, pp. 4736–4742. [Google Scholar] [CrossRef]
- Yang, W.; Ma, J.; Zhu, M.; Hu, C. Fault Diagnosis and Tolerant Method of Open-Circuit Fault for Triple Active-Bridge DC-DC Converter. In Proceedings of the 2022 IEEE Industry Applications Society Annual Meeting (IAS), Las Vegas, NV, USA, 7–11 October 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Zhang, X.; Liu, H.; Wheeler, P.; Wu, F. Research on Power Decoupling and Parameter Mismatch of Three-Port Isolated Resonant DC-DC Converter Applied Switch Controlled Capacitor. IEEE Trans. Ind. Electron. 2022, 70, 8098–8107. [Google Scholar] [CrossRef]
- Biswas, I.; Kastha, D.; Bajpai, P. Small signal modeling and decoupled controller design for a triple active bridge multiport DC–DC converter. IEEE Trans. Power Electron. 2020, 36, 1856–1869. [Google Scholar] [CrossRef]
- Wang, K.; Liu, W.; Wu, F. Topology-level power decoupling three-port isolated current-fed resonant DC-DC converter. IEEE Trans. Ind. Electron. 2021, 69, 4859–4868. [Google Scholar]
- Liu, D.; Li, H. A ZVS bi-directional DC–DC converter for multiple energy storage elements. IEEE Trans. Power Electron. 2006, 21, 1513–1517. [Google Scholar] [CrossRef]
- Kurm, S.; Agarwal, V. Interfacing Standalone Loads with Renewable Energy Source and Hybrid Energy Storage System Using a Dual Active Bridge Based Multi-Port Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 4738–4748. [Google Scholar]
- Karami, M.; Baranwal, R. Optimal Control of Triple Active Bridge Based on Deep Machine Learning Techniques. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–7. [Google Scholar]
- Pereira, T.; Wei, Y.; Pascal, Y.; Mantooth, H.A.; Liserre, M. Self-Tuning Multiport Resonant DC/DC Converter Based on Actively-Controlled Inductors for Hybrid Storage System Integration. IEEE Trans. Power Electron. 2022. [Google Scholar]
- Mitra, S.K.; Karanki, S.B. An SOC Based Adaptive Energy Management System for Hybrid Energy Storage System Integration to DC Grid. IEEE Trans. Ind. Appl. 2022, 38, 4787–4804. [Google Scholar]
- Tao, H.; Kotsopoulos, A.; Duarte, J.L.; Hendrix, M.A.M. Transformer-Coupled Multiport ZVS Bidirectional DC–DC Converter with Wide Input Range. IEEE Trans. Power Electron. 2008, 23, 771–781. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Li, H. Asymmetrical Duty Cycle Control and Decoupled Power Flow Design of a Three-port Bidirectional DC-DC Converter for Fuel Cell Vehicle Application. IEEE Trans. Power Electron. 2012, 27, 891–904. [Google Scholar] [CrossRef]
- Duarte, J.L.; Hendrix, M.; Simoes, M.G. Three-Port Bidirectional Converter for Hybrid Fuel Cell Systems. IEEE Trans. Power Electron. 2007, 22, 480–487. [Google Scholar] [CrossRef]
- Buticchi, G.; Costa, L.F.; Barater, D.; Liserre, M.; Amarillo, E.D. A Quadruple Active Bridge Converter for the Storage Integration on the More Electric Aircraft. IEEE Trans. Power Electron. 2018, 33, 8174–8186. [Google Scholar] [CrossRef]
- Al-Jafeary, I.M.K.; Tan, N.M.L.; Mansor, M.B.; Buticchi, G. A Multi-Pulse Phase-Modulation/Duty Cycle Control for a Triple Active Bridge Converter. In Proceedings of the 2022 IEEE 31st International Symposium on Industrial Electronics (ISIE), Anchorage, AK, USA, 1–3 June 2022; pp. 388–393. [Google Scholar] [CrossRef]
- Rahrovi, B.; Mehrjardi, R.T.; Ehsani, M. On the analysis and design of high-frequency transformers for dual and triple active bridge converters in more electric aircraft. In Proceedings of the 2021 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2–5 February 2021; IEEE: Manhattan, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Gu, C.; Yan, H.; Yang, J.; Sala, G.; De Gaetano, D.; Wang, X.; Galassini, A.; Degano, M.; Zhang, X.; Buticchi, G. A multiport power conversion system for the more electric aircraft. IEEE Trans. Transp. Electrif. 2020, 6, 1707–1720. [Google Scholar] [CrossRef]
- Buticchi, G.; Farjudian, A.; Oh, J.; Tarisciotti, L. An ANN-Assisted Control for the Power Decoupling of a Multiple Active Bridge DC-DC Converter. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Cai, Y.; Gu, C.; Li, J.; Yang, J.; Buticchi, G.; Zhang, H. Dynamic Performance Enhancement of a Triple Active Bridge with Power Decoupling-Based Configurable Model Predictive Control. IEEE Trans. Transp. Electrif. 2022, 9, 3338–3349. [Google Scholar] [CrossRef]
- Yang, J.; Buticchi, G.; Gu, C.; Günter, S.; Zhang, H.; Wheeler, P. A generalized input impedance model of multiple active bridge converter. IEEE Trans. Transp. Electrif. 2020, 6, 1695–1706. [Google Scholar] [CrossRef]
- Karanayil, B.; Ciobotaru, M.; Agelidis, V.G. Power Flow Management of Isolated Multiport Converter for More Electric Aircraft. IEEE Trans. Power Electron. 2017, 32, 5850–5861. [Google Scholar] [CrossRef]
- Liu, R.; Xu, L.; Kang, Y.; Hui, Y.; Li, Y. Decoupled TAB converter with energy storage system for HVDC power system of more electric aircraft. J. Eng. 2018, 2018, 593–602. [Google Scholar] [CrossRef]
- Purgat, P.; Mackay, L.; Schulz, M.; Han, Y.; Qin, Z.; März, M.; Bauer, P. Design of a power flow control converter for bipolar meshed LVDC distribution grids. In Proceedings of the 2018 IEEE 18th International Power Electronics and Motion Control Conference (PEMC), Budapest, Hungary, 26–30 August 2018; IEEE: Manhattan, NY, USA, 2018; pp. 1073–1078. [Google Scholar]
- Liao, J.; Guo, C.; He, D.; Zhou, N.; Wang, Q.; Wang, Y. Decoupling Control of Triple Active Bridge-Power Flow Controller in Meshed Bipolar DC Distribution Grids. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 7569–7580. [Google Scholar] [CrossRef]
- Byun, H.J.; Kim, S.H.; Yi, J.; Won, C.Y. Triple-Active-Bridge converter Coupling Power control method for Voltage Balancing in Bipolar DC Distribution. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Naseem, N.; Cha, H. Triple-active-bridge converter with automatic voltage balancing for bipolar DC distribution. IEEE Trans. Power Electron. 2022, 37, 8640–8648. [Google Scholar] [CrossRef]
- Lee, J.Y.; Jung, J.H. Modified three-port DAB converter employing voltage balancing capability for bipolar DC distribution system. IEEE Trans. Ind. Electron. 2021, 69, 6710–6721. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, J.; Zhu, M.; Dai, N. A DC-DC converter with input full active bridge and output semi active bridge for bipolar LVDC systems. In Proceedings of the 2022 IEEE Industry Applications Society Annual Meeting (IAS), Detroit, MI, USA, 9–14 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Teng, B.; Ma, J.; Zhu, M.; Cai, X. Dynamic fault reconfiguration of multiport active bridge converter for reliable bipolar DC system. In Proceedings of the 18th International Conference on AC and DC Power Transmission (ACDC 2022), Online, 2–3 July 2022; Volume 2022, pp. 482–487. [Google Scholar] [CrossRef]
- Lai, J.; Yin, X.; Wang, Y.; Jiang, L.; Ullah, Z.; Yin, X. Isolated Bipolar Modular Multilevel DC-DC Converter with Self-balancing Capability for Interconnection of MVDC and LVDC Grids. CSEE J. Power Energy Syst. 2023, 9, 365–379. [Google Scholar] [CrossRef]
- Bempah, K.O.; Heo, K.W.; Jung, J.H. Power flow decoupling method of triple-active-bridge converter for islanding mode operation in DC microgrid systems. J. Power Electron. 2023, 23, 58–67. [Google Scholar]
- Gu, C.; Zheng, Z.; Xu, L.; Wang, K.; Li, Y. Modeling and control of a multiport power electronic transformer (PET) for electric traction applications. IEEE Trans. Power Electron. 2015, 31, 915–927. [Google Scholar] [CrossRef]
- Lin, Z.; Pan, S.; Wang, M.; Lin, W.; Gong, J.; Yao, L.; Jain, P. A Three-Port LCC Resonant Converter for the 380-V/48-V Hybrid DC System. IEEE Trans. Power Electron. 2022, 37, 10864–10876. [Google Scholar] [CrossRef]
- Oluwasogo, E.S.; Cha, H. Self-current sharing in dual-transformer-based triple-port active bridge DC–DC converter with reduced device count. IEEE Trans. Power Electron. 2020, 36, 5290–5301. [Google Scholar]
- Wu, H. A Feedforward Decoupling Control Method for Multi-ports DC Transformer. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Philadelphia, PA, USA, 2021; Volume 1732, p. 012155. [Google Scholar]
- Costa, L.F.; Hoffmann, F.; Buticchi, G.; Liserre, M. Comparative analysis of multiple active bridge converters configurations in modular smart transformer. IEEE Trans. Ind. Electron. 2018, 66, 191–202. [Google Scholar]
- El Shafei, A.; Ozdemir, S.; Altin, N.; Jean-Pierre, G.; Nasiri, A. Design and implementation of a medium voltage, high power, high frequency four-port transformer. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; IEEE: Manhattan, NY, USA, 2020; pp. 2352–2357. [Google Scholar]
- Rahman, M.A.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. Modeling and control of sic-based high-frequency magnetic linked converter for next generation solid state transformers. IEEE Trans. Energy Convers. 2019, 35, 549–559. [Google Scholar]
- Feng, M.; Gao, C.; Xu, J.; Zhao, C.; Li, G. Modeling for complex modular power electronic transformers using parallel computing. IEEE Trans. Ind. Electron. 2022, 70, 2639–2651. [Google Scholar] [CrossRef]
- Gao, S.; Yuan, L.; Dai, Y.; Mou, D.; Chen, K.; Zhao, Z. High-Frequency Current Predictive Control Method for Multiactive-Bridge Converter. IEEE Trans. Power Electron. 2022, 37, 10144–10148. [Google Scholar] [CrossRef]
- Buticchi, G.; De Carne, G.; Pereira, T.; Wang, K.; Gao, X.; Yang, J.; Ko, Y.; Zou, Z.; Liserre, M. A Multi-port Smart Transformer for Green Airport Electrification. In Proceedings of the 2022 24th European Conference on Power Electronics and Applications (EPE’22 ECCE Europe), Hanover, Germany, 5–9 September 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–8. [Google Scholar]
- Pan, Y.; Teng, J.; Yang, C.; Bu, Z.; Wang, B.; Li, X.; Sun, X. Capacitance Minimization and Constraint of CHB Power Electronic Transformer Based on Switching Synchronization Hybrid Phase-Shift Modulation Method of High Frequency Link. IEEE Trans. Power Electron. 2023, 38, 6224–6242. [Google Scholar]
- Li, X.; Cheng, L.; He, L.; Wang, C.; Zhu, Z. Decoupling Control of an LLC-Quad-Active-Bridge Cascaded Power Electronic Transformer Based on Accurate Small-Signal Modeling. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 4115–4127. [Google Scholar]
- El Shafei, A.; Ozdemir, S.; Altin, N.; Jean-Pierre, G.; Nasiri, A. Development of a Medium Voltage, High Power, High Frequency Four-Port Solid State Transformer. CES Trans. Electr. Mach. Syst. 2022, 6, 95–104. [Google Scholar] [CrossRef]
- Naseem, N.; Cha, H. Quad-Active-Bridge Converter with Current Balancing Coupled Inductor for SST Application. IEEE Trans. Power Electron. 2021, 36, 12528–12539. [Google Scholar] [CrossRef]
- Costa, L.F.; Buticchi, G.; Liserre, M. Quad-Active-Bridge DC–DC Converter as Cross-Link for Medium-Voltage Modular Inverters. IEEE Trans. Ind. Appl. 2017, 53, 1243–1253. [Google Scholar] [CrossRef]
- Wu, H. A fault ride through strategy of multi-ports DC transformer. In Proceedings of the 2020 5th International Conference on Automation, Control and Robotics Engineering (CACRE), Dalian, China, 19–20 September 2020; pp. 416–421. [Google Scholar] [CrossRef]
- Falcones, S.; Ayyanar, R.; Mao, X. A DC–DC Multiport-Converter-Based Solid-State Transformer Integrating Distributed Generation and Storage. IEEE Trans. Power Electron. 2013, 28, 2192–2203. [Google Scholar] [CrossRef]
- Rashidi, M.; Altin, N.N.; Ozdemir, S.S.; Bani-Ahmed, A.; Nasiri, A. Design and Development of a High-Frequency Multiport Solid-State Transformer with Decoupled Control Scheme. IEEE Trans. Ind. Appl. 2019, 55, 7515–7526. [Google Scholar] [CrossRef]
- Sha, D.; Jia, X.; Yao, H.; Liu, D.; Gu, H. A DAB-Based DC Transformer for Multiterminal HVdc Dynamic Simulation Platform with Short Circuit Tolerance. IEEE Trans. Power Electron. 2022, 38, 1948–1957. [Google Scholar]
- Pereira, T.; Wei, Y.; Mantooth, H.A.; Liserre, M. Analysis and Design of a Multiport Resonant DC-Transformer for Solid-State Transformer Applications. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–8. [Google Scholar]
- Ozdemir, S.; Altin, N.; El Shafei, A.; Rashidi, M.; Nasiri, A. A decoupled control scheme of four-port solid state transformer. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; IEEE: Manhattan, NY, USA, 2019; pp. 5009–5015. [Google Scholar]
- Rahman, M.A.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. Data-driven coordinated control of converters in a smart solid-state transformer for reliable and automated distribution grids. IEEE Trans. Ind. Appl. 2020, 56, 4532–4542. [Google Scholar]
- Teng, B.; Ma, J.; Zhu, M.; Cai, X. Fault Reconfiguration of Series-Connected Dual-Transformer Active Bridge Converter for Reliable Shipboard DC System. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–5. [Google Scholar]
- Rahman, M.A.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. A magnetic linked multiport fractional converter for application to variable speed wind power generating systems. IEEE J. Emerg. Sel. Top. Ind. Electron. 2021, 3, 321–331. [Google Scholar] [CrossRef]
- Yang, R.H.; Jin, J.X.; Mu, S.; Zhang, M.S.; Jiang, S.; Chen, X.Y. Battery-energy-storage-based triple-active-bridge DC unified power quality conditioner for energy management and power quality enhancement of DC renewable sources. Int. J. Electr. Power Energy Syst. 2022, 143, 108442. [Google Scholar] [CrossRef]
- Han, J.; Li, X.; Sun, Y.; Gong, S.; Huang, S. Optimal design and decoupling control of series DC-link voltages for quadruple-active-bridge based UPQC. Int. J. Electr. Power Energy Syst. 2022, 140, 108038. [Google Scholar] [CrossRef]
- Han, J.; Li, X.; Sun, Y.; Gong, S.; Huang, S.; Peng, Y.; Jiang, Y. Optimal operation of QAB-based unified power quality conditioner integrated with PV arrays under VA capacity constraints. Int. J. Electr. Power Energy Syst. 2022, 143, 108495. [Google Scholar] [CrossRef]
- Han, J.; Li, X.; Sun, Y.; Gong, S.; Huang, S. Quadruple-active-bridge based unified power quality conditioner-L with fault current limiting capability. Electr. Power Syst. Res. 2022, 206, 107780. [Google Scholar]
- Chandwani, A.; Mallik, A. Phase-Duty Modulated Loop Decoupling and Design Optimization for a Triple Active Bridge Converter for Light Electric Vehicle Charging. IEEE J. Emerg. Sel. Top. Ind. Electron. 2023, 4, 357–367. [Google Scholar] [CrossRef]
- Dao, N.D.; Lee, D.C.; Phan, Q.D. High-efficiency SiC-based isolated three-port DC/DC converters for hybrid charging stations. IEEE Trans. Power Electron. 2020, 35, 10455–10465. [Google Scholar] [CrossRef]
- Ling, Z.; Wang, H.; Yan, K.; Gan, J. Optimal isolation control of three-port active converters as a combined charger for electric vehicles. Energies 2016, 9, 715. [Google Scholar] [CrossRef]
- Kougioulis, I.; Pal, A.; Wheeler, P.; Ahmed, M.R. An Isolated Multiport DC-DC Converter for Integrated Electric Vehicle On-board Charger. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 4178–4198. [Google Scholar] [CrossRef]
- Pham, V.L.; Wada, K. Normalization design of inductances in triple active bridge converter for household renewable energy system. IEEJ J. Ind. Appl. 2020, 9, 227–234. [Google Scholar]
- Santoro, D.; Kortabarria, I.; Toscani, A.; Concari, C.; Cova, P.; Delmonte, N. PV Modules Interfacing Isolated Triple Active Bridge for Nanogrid Applications. Energies 2021, 14, 2854. [Google Scholar] [CrossRef]
- Alajmi, B.N.; Marei, M.I.; Abdelsalam, I. A multiport DC–DC converter based on two-quadrant inverter topology for PV systems. IEEE Trans. Power Electron. 2020, 36, 522–532. [Google Scholar] [CrossRef]
- Malekjamshidi, Z.; Jafari, M. Design and development of a cascaded modular multi-level converter based on current-fed quadruple-active bridge converters for grid integration of photovoltaic systems. IET Energy Syst. Integr. 2021, 3, 26–38. [Google Scholar] [CrossRef]
- Wang, P.; Lu, X.; Wang, W.; Xu, D. Hardware decoupling and autonomous control of series-resonance-based three-port converters in DC microgrids. IEEE Trans. Ind. Appl. 2019, 55, 3901–3914. [Google Scholar] [CrossRef]
- Haque, M.M.; Wolfs, P.J.; Alahakoon, S.; Blaabjerg, F. High-Frequency-Linked Three-Port Converter with Optimized Control Strategies Based on Power System Load Flow Concepts for PV-Battery Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 1032–1045. [Google Scholar] [CrossRef]
- Karami, M.; Zhu, G.; Baranwal, R.; Bhavaraju, V.; Ganger, D.W.; Luo, C. Optimal Design of Multi-port DC/DC Converters for Low Power and High Frequency Applications. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Virtual, 10–14 October 2021; IEEE: Manhattan, NY, USA, 2021; pp. 267–273. [Google Scholar]
- Rasheed, M.; Wang, H.; Zane, R. Analysis of a Five-Port Differential Power Processing Triple Active Bridge Converter for Active Cell Balancing in Lithium-ion Battery Packs. In Proceedings of the 2022 IEEE 23rd Workshop on Control and Modeling for Power Electronics (COMPEL), Tel Aviv, Israel, 20–23 June 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–8. [Google Scholar]
- Wang, P.; Chen, Y.; Elasser, Y.; Chen, M. Small signal model for very-large-scale multi-active-bridge differential power processing (MAB-DPP) architecture. In Proceedings of the 2019 20th Workshop on Control and Modeling for Power Electronics (COMPEL), Toronto, ON, Canada, 17–20 June 2019; IEEE: Manhattan, NY, USA, 2019; pp. 1–8. [Google Scholar]
- Zhao, C.; Round, S.D.; Kolar, J.W. An Isolated Three-Port Bidirectional DC-DC Converter with Decoupled Power Flow Management. IEEE Trans. Power Electron. 2008, 23, 2443–2453. [Google Scholar] [CrossRef]
- Pham, V.L.; Wada, K. Applications of triple active bridge converter for future grid and integrated energy systems. Energies 2020, 13, 1577. [Google Scholar] [CrossRef]
- Qi, Z.; Rahman, M.A.; Islam, M.R. Model Predictive Control for Magnetic Linked Multiport Converter. In Proceedings of the 2022 IEEE Global Conference on Computing, Power and Communication Technologies (GlobConPT), New Delhi, India, 23–25 September 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Dey, S.; Mallik, A. Switching Network Loss Minimization through Multivariable Modulation in a Multi-Active Bridge Converter. IEEE Trans. Ind. Electron. 2022, 70, 10833–10847. [Google Scholar] [CrossRef]
- Sal y Rosas, D.; Chavez, D.; Frey, D.; Ferrieux, J.P. Single-Stage Isolated and Bidirectional Three-Phase Series-Resonant AC–DC Converter: Modulation for Active and Reactive Power Control. Energies 2022, 15, 8070. [Google Scholar]
- Wei, S.; Mou, D.; Wen, W.; Zhao, Z.; Li, K. Transient DC Bias and Universal Dynamic Modulation of Multiactive Bridge Converters. IEEE Trans. Power Electron. 2022, 37, 11516–11522. [Google Scholar] [CrossRef]
- Costa, L.F.; Buticchi, G.; Liserre, M. Optimum Design of a Multiple-Active-Bridge DC–DC Converter for Smart Transformer. IEEE Trans. Power Electron. 2018, 33, 10112–10121. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, P.; Li, H.; Chen, M. Power Flow Control in Multi-Active-Bridge Converters: Theories and Applications. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1500–1507. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Qin, Z.; Bauer, P. Decoupling Control of Multiactive Bridge Converters Using Linear Active Disturbance Rejection. IEEE Trans. Ind. Electron. 2021, 68, 10688–10698. [Google Scholar] [CrossRef]
- Hebala, O.M.; Aboushady, A.A.; Ahmed, K.H.; Abdelsalam, I. Generalized Active Power Flow Controller for Multiactive Bridge DC–DC Converters with Minimum-Current-Point-Tracking Algorithm. IEEE Trans. Ind. Electron. 2022, 69, 3764–3775. [Google Scholar] [CrossRef]
- Gong, S.; Li, X.; Han, J.; Sun, Y.; Xu, G.; Jiang, Y.; Huang, S. Sliding mode control-based decoupling scheme for quad-active bridge DC–DC converter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 1153–1164. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Purgat, P.; Qin, Z.; Bauer, P. A multiactive bridge converter with inherently decoupled power flows. IEEE Trans. Power Electron. 2020, 36, 2231–2245. [Google Scholar] [CrossRef]
- Koohi, P.; Watson, A.J.; Soeiro, T.B.; Clare, J.C.; Rivera, M.; Venugopal, P.; Wheeler, P.W. A Hardware-Based Bidirectional Power Flow Decoupling Approach for Multi-Active-Bridge Converters. In Proceedings of the 2023 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Venice, Italy, 28–31 March 2023; IEEE: Manhattan, NY, USA, 2023; pp. 1–7. [Google Scholar]
- Rahman, M.A.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. A modular magnetic linked converter station for offshore power transfer through HVDC link. IEEE Trans. Ind. Electron. 2022, 70, 9067–9077. [Google Scholar] [CrossRef]
- Han, J.; Li, X.; Jiang, Y.; Gong, S. Three-phase UPQC topology based on quadruple-active-bridge. IEEE Access 2020, 9, 4049–4058. [Google Scholar] [CrossRef]
- Liao, M.; Li, H.; Wang, P.; Sen, T.; Chen, Y.; Chen, M. Machine Learning Methods for Feedforward Power Flow Control of Multi-Active-Bridge Converters. IEEE Trans. Power Electron. 2022, 38, 1692–1707. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, P.; Elasser, Y.; Chen, M. LEGO-MIMO architecture: A universal multi-input multi-output (MIMO) power converter with linear extendable group operated (LEGO) power bricks. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; IEEE: Manhattan, NY, USA, 2019; pp. 5156–5163. [Google Scholar]
- Chen, Y.; Wang, P.; Elasser, Y.; Chen, M. Multicell reconfigurable multi-input multi-output energy router architecture. IEEE Trans. Power Electron. 2020, 35, 13210–13224. [Google Scholar] [CrossRef]
- Rahman, M.A.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. Design of a multiloop control structure for load-disturbance attenuation and power-mismatch mitigation in isolated multiport power converters. IEEE Trans. Ind. Electron. 2021, 69, 8984–8996. [Google Scholar]
- Phattanasak, M.; Gavagsaz-Ghoachani, R.; Martin, J.P.; Nahid-Mobarakeh, B.; Pierfederici, S.; Davat, B. Control of a hybrid energy source comprising a fuel cell and two storage devices using isolated three-port bidirectional DC–DC converters. IEEE Trans. Ind. Appl. 2014, 51, 491–497. [Google Scholar] [CrossRef]
- Purgat, P.; Bandyopadhyay, S.; Qin, Z.; Bauer, P. Power Flow Decoupling Controller for Triple Active Bridge Based on Fourier Decomposition of Transformer Currents. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 1201–1208. [Google Scholar] [CrossRef]
- Smith, Z.T.; Beddingfield, R.B.; Grainger, B.M. Power Flow Control for Decoupled Load Performance of Current-Fed Triple Active Bridge Converter. IEEE Open J. Power Electron. 2023, 4, 319–329. [Google Scholar] [CrossRef]
- Phattanasak, M.; Gavagsaz-Ghoachani, R.; Martin, J.P.; Pierfederici, S.; Davat, B. Flatness based control of an isolated three-port bidirectional DC-DC converter for a fuel cell hybrid source. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; IEEE: Manhattan, NY, USA, 2011; pp. 977–984. [Google Scholar]
- Ibrahim, A.A.; Zilio, A.; Younis, T.; Biadene, D.; Caldognetto, T.; Mattavelli, P. Optimal Modulation of Triple Active Bridge Converters by an Artificial-Neural-Network Approach. IEEE Trans. Ind. Electron. 2023, 1–10. [Google Scholar]
- Zhao, H.; Qi, Y.; Li, W. Decentralized Power Management for Multi-active Bridge Converter. In Proceedings of the IECON 2022–48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Wu, F.; Liu, W.; Wang, K.; Wang, G. Modeling and Closed-Loop Control of Three-Port Isolated Current-Fed Resonant DC-DC Converter. IEEE Trans. Transp. Electrif. 2022, 9, 1341–1349. [Google Scholar] [CrossRef]
- Wu, F.; Wang, K.; Su, J. TAB Series-Resonant DC-DC Converter and Multi-Phase-Shift Based Global Optimization Modulation. Appl. Sci. 2022, 12, 6783. [Google Scholar] [CrossRef]
- Wu, J.; Yan, X.; Sun, X.; Su, X.; Du, H.; Wang, X. A Series Resonant Three-Port DC–DC Converter with Decoupling Function and Magnetic Integration. IEEE Trans. Power Electron. 2022, 37, 14720–14737. [Google Scholar] [CrossRef]
- Cao, L.; Lin, J.; Jiang, X.; Wong, C.S.; Loo, K. An Immittance-Network-Based Multiport ZVS Bidirectional Converter with Power Decoupling Capability. IEEE Trans. Power Electron. 2022, 37, 12729–12740. [Google Scholar] [CrossRef]
- Tang, X.; Wu, H.; Hua, W.; Yu, Z.; Xing, Y. Three-port bidirectional series-resonant converter with first-harmonic-synchronized PWM. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 1410–1419. [Google Scholar] [CrossRef]
- Kimura, Y.; Yanagi, Y.; Iwaya, K.; Miyazaki, T. A Method for Decoupling Current Control of Three-port Isolated Converter. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; IEEE: Manhattan, NY, USA, 2018; pp. 895–900. [Google Scholar]
- Kim, D.U.; Byen, B.; Jeong, B.; Kim, S. Design of Triple-Active Bridge Converter with Inherently Decoupled Power Flows. In Proceedings of the 2022 24th European Conference on Power Electronics and Applications (EPE’22 ECCE Europe), Hanover, Germany, 5–9 September 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–9. [Google Scholar]
- Kiran, R.; Kalpana, R. An Isolated Dual-Input Half-Bridge DC–DC Boost Converter with Reduced Circulating Power between Input Ports. IEEE Can. J. Electr. Comput. Eng. 2022, 45, 68–76. [Google Scholar]
- Jakka, V.N.S.R.; Shukla, A.; Demetriades, G.D. Dual-transformer-based asymmetrical triple-port active bridge (DT-ATAB) isolated DC–DC converter. IEEE Trans. Ind. Electron. 2017, 64, 4549–4560. [Google Scholar] [CrossRef]
- Yu, X.; Lan, Z.; Zeng, J.; Tu, C.; He, D. Time-domain based Superposition Analysis for Triple Active Bridge and its Application for ZVS and Current Stress Optimization. IEEE Trans. Power Electron. 2023, 38, 5844–5857. [Google Scholar] [CrossRef]
- Takanobu, O.; Hoshi, N. A new control method for triple-active bridge converter with feed forward control. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; IEEE: Manhattan, NY, USA, 2018; pp. 971–976. [Google Scholar]
- Kim, S.Y.; Song, H.S.; Nam, K. Idling port isolation control of three-port bidirectional converter for EVs. IEEE Trans. Power Electron. 2011, 27, 2495–2506. [Google Scholar] [CrossRef]
- Romero-Cadaval, E.; Barrero-González, F.; González-Romera, E.; Milanés-Montero, M.I.; Roncero-Clemente, C. Improved Operation Strategy for the High Voltage Input Stage of a Multi-Port Smart Transformer. Energies 2022, 15, 3778. [Google Scholar] [CrossRef]
- Zou, S.; Lu, J.; Khaligh, A. Modelling and control of a triple-active-bridge converter. IET Power Electron. 2020, 13, 961–969. [Google Scholar] [CrossRef]
- Chattopadhyay, R.; Gohil, G.; Acharya, S.; Nair, V.; Bhattacharya, S. Efficiency improvement of three port high frequency transformer isolated triple active bridge converter. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; IEEE: Manhattan, NY, USA, 2018; pp. 1807–1814. [Google Scholar]
- Uttam, V.; Kudaravalli, V.R.; Iyer, V.M. Generalised Harmonic Model for a Triple Active Bridge DC-DC Converter. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–7. [Google Scholar]
- Dey, S.; Mallik, A.; Akturk, A. Investigation of ZVS criteria and Optimization of Switching Loss in a Triple Active Bridge Converter using Penta-Phase-Shift Modulation. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 7014–7028. [Google Scholar] [CrossRef]
- Ibrahim, A.A.; Caldognetto, T.; Biadene, D.; Mattavelli, P. Multidimensional Ripple Correlation Technique for Optimal Operation of Triple Active-Bridge Converters. IEEE Trans. Ind. Electron. 2022, 70, 8032–8041. [Google Scholar] [CrossRef]
- Koneh, N.N.; Ko, J.S.; Kim, D.K. Simulations of the Comparative Study of the Single-Phase Shift and the Dual-Phase Shift-Controlled Triple Active Bridge Converter. Electronics 2022, 11, 3274. [Google Scholar] [CrossRef]
- Koneh, N.N.; Ko, J.S.; Kim, D.K. Simulations to Eliminate Backflow Power in an Isolated Three-Port Bidirectional DC–DC Converter. Energies 2023, 16, 450. [Google Scholar] [CrossRef]
- Ibrahim, A.A.; Caldognetto, T.; Mattavelli, P. Conduction loss reduction of isolated bidirectional dc-dc triple active bridge. In Proceedings of the 2021 IEEE Fourth International Conference on DC Microgrids (ICDCM), Arlington, VA, USA, 18–21 July 2021; IEEE: Manhattan, NY, USA, 2021; pp. 1–8. [Google Scholar]
- Xiao, X.; Wu, K.; Wang, H.; Zhang, X. Efficiency Optimization Scheme for Isolated Triple Active Bridge DC-DC Converter Based on Minimized Reactive Power. In Proceedings of the 2022 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Xiamen, China, 4–7 November 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1398–1403. [Google Scholar]
- Karbozov, A.; Majumder, M.G.; Krishnamoorthy, H.S.; Rajashekara, K. A Novel Control Strategy for Extending the ZVS Range of Triple Active Bridge Converter. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Li, J.; Luo, Q.; Luo, T.; Mou, D.; Liserre, M. Efficiency Optimization Scheme for Isolated Triple Active Bridge DC–DC Converter with Full Soft-Switching and Minimized RMS Current. IEEE Trans. Power Electron. 2022, 37, 9114–9128. [Google Scholar] [CrossRef]
- Minami, K.; Okutani, S.; Ohura, M.; Huang, P.Y.; Kado, Y. Machine Learning Aided Optimized Modulation in Triple Active Bridge Converter. In Proceedings of the IECON 2022–48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Purgat, P.; Bandyopadhyay, S.; Qin, Z.; Bauer, P. Zero voltage switching criteria of triple active bridge converter. IEEE Trans. Power Electron. 2020, 36, 5425–5439. [Google Scholar] [CrossRef]
- Ibrahim, A.A.; Caldognetto, T.; Biadene, D.; Mattavelli, P. Online Loss Reduction of Isolated Bidirectional DC-DC Quad-Active Bridge Converters. In Proceedings of the 2023 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Venice, Italy, 29–31 March 2023; IEEE: Manhattan, NY, USA, 2023; pp. 1–6. [Google Scholar]
- Wu, Y.; Mahmud, M.H.; Christian, S.; Fantino, R.A.; Gomez, R.A.; Zhao, Y.; Balda, J.C. A 150-kW 99% Efficient All-Silicon-Carbide Triple-Active-Bridge Converter for Solar-Plus-Storage Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 10, 3496–3510. [Google Scholar] [CrossRef]
- Wang, Z.; Castellazzi, A. SiC-based Triple Active Bridge Converter for Shipboard Micro-grid Applications with Efficient Energy Storage. In Proceedings of the 2018 International Conference on Smart Grid (icSmartGrid), Nagasaki, Japan, 4–6 December 2018; pp. 39–45. [Google Scholar] [CrossRef]
- Wang, C.S.; Li, W.; Wang, Y.F.; Han, F.Q.; Chen, B. A high-efficiency isolated LCLC multi-resonant three-port bidirectional DC-DC converter. Energies 2017, 10, 934. [Google Scholar] [CrossRef]
- Wang, C.S.; Li, W.; Wang, Y.F.; Han, F.Q.; Meng, Z.; Li, G.D. An isolated three-port bidirectional DC-DC converter with enlarged ZVS region for HESS applications in DC microgrids. Energies 2017, 10, 446. [Google Scholar] [CrossRef]
- Chen, B.; Wang, P.; Wang, Y.; Li, W.; Han, F.; Zhang, S. Comparative analysis and optimization of power loss based on the isolated series/multi resonant three-port bidirectional DC-DC converter. Energies 2017, 10, 1565. [Google Scholar] [CrossRef]
- Chandwani, A.; Mallik, A.; Akturk, A. Steady-State Model Derived Multi-variable Loss Optimization for Triple Active C 3 L 3 Resonant Converter. IEEE Trans. Transp. Electrif. 2023. [Google Scholar] [CrossRef]
- Suzuki, K.; Iyasu, S.; Hayashi, Y.; Handa, Y. Continuous Power Transfer Control of Triple Active Bridge Converter during Magnetic Saturation. In Proceedings of the 2022 11th International Conference on Renewable Energy Research and Application (ICRERA), Istanbul, Turkey, 18–21 September 2022; IEEE: Manhattan, NY, USA, 2022; pp. 96–100. [Google Scholar]
- Thönnessen, A.; Fronczek, C.; Bündgen, D.; Kowalewski, P.; De Doncker, R.W. Eliminating DC-Bias Currents in Multi-Active Bridge Converters with an Open-Loop Control Algorithm. In Proceedings of the 2022 IEEE 7th Southern Power Electronics Conference (SPEC), Nadi, Fiji, 5–8 December 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–5. [Google Scholar]
- Wei, S.; Wen, W. High-Frequency Oscillation of the Active-Bridge-Transformer-Based DC/DC Converter. Energies 2022, 15, 3311. [Google Scholar] [CrossRef]
- Narayanaswamy, J.; Mandava, S. Non-Isolated Multiport Converter for Renewable Energy Sources: A Comprehensive Review. Energies 2023, 16, 1834. [Google Scholar] [CrossRef]
- Dhananjaya, M.; Pattnaik, S. Review on multi-port DC–DC converters. IETE Tech. Rev. 2022, 39, 586–599. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, Q.; Wei, Y.; Mou, D.; Lu, X.; Sun, P. Topology analysis and review of three-port DC–DC converters. IEEE Trans. Power Electron. 2020, 35, 11783–11800. [Google Scholar] [CrossRef]
- Affam, A.; Buswig, Y.M.; Othman, A.K.B.H.; Julai, N.B.; Qays, O. A review of multiple input DC-DC converter topologies linked with hybrid electric vehicles and renewable energy systems. Renew. Sustain. Energy Rev. 2021, 135, 110186. [Google Scholar]
- Gevorkov, L.; Domínguez-García, J.L.; Romero, L.T.; Martínez, À.F. Modern MultiPort Converter Technologies: A Systematic Review. Appl. Sci. 2023, 13, 2579. [Google Scholar] [CrossRef]
- Haque, M.M.; Wolfs, P.; Alahakoon, S.; Islam, M.A.; Nadarajah, M.; Zare, F.; Farrok, O. Three-Port Converters for Energy Conversion of PV-BES Integrated Systems—A Review. IEEE Access 2023. [Google Scholar] [CrossRef]
- Zhang, N.; Sutanto, D.; Muttaqi, K.M. A review of topologies of three-port DC–DC converters for the integration of renewable energy and energy storage system. Renew. Sustain. Energy Rev. 2016, 56, 388–401. [Google Scholar] [CrossRef]
- Pereira, T.; Hoffmann, F.; Zhu, R.; Liserre, M. A comprehensive assessment of multiwinding transformer-based DC–DC converters. IEEE Trans. Power Electron. 2021, 36, 10020–10036. [Google Scholar] [CrossRef]
- Mukherjee, S.; Sarkar, I. A Brief Review on Triple Active Bridge DC-DC Converter. In Proceedings of the 2023 IEEE International Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 19–20 February 2022; IEEE: Manhattan, NY, USA, 2023; pp. 1–6. [Google Scholar]
- Ibrahim, A.A.; Zilio, A.; Younis, T.; Biadene, D.; Caldognetto, T.; Mattavelli, P. Artificial Neural Networks Approach for Reduced RMS Currents in Triple Active Bridge Converters. In Proceedings of the IECON 2022–48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Ortega, L.; Zumel, P.; Fernández, C.; López-López, J.; Lázaro, A.; Barrado, A. Power distribution algorithm and steady-state operation analysis of a modular multiactive bridge converter. IEEE Trans. Transp. Electrif. 2020, 6, 1035–1050. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, Y.; Ji, S.; Zhao, Z.; Yuan, L.; Mo, X. ZVS Soft Switching Operation Region Analysis of Modular Multi Active Bridge Converter Under Single Phase Shift Control. IEEE Trans. Ind. Electron. 2022, 70, 6865–6875. [Google Scholar] [CrossRef]
- Zumel, P.; Fernandez, C.; Lazaro, A.; Sanz, M.; Barrado, A. Overall analysis of a modular multi active bridge converter. In Proceedings of the 2014 IEEE 15th Workshop on Control and Modeling for Power Electronics (COMPEL), Santander, Spain, 22–25 June 2014; IEEE: Manhattan, NY, USA, 2014; pp. 1–9. [Google Scholar]
- Wen, W.; Li, K.; Zhao, Z.; Yuan, L.; Mo, X.; Cai, W. Analysis and control of a four-port megawatt-level high-frequency-bus-based power electronic transformer. IEEE Trans. Power Electron. 2021, 36, 13080–13095. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. A multiple-winding magnetics model having directly measurable parameters. In Proceedings of the PESC 98 Record. 29th Annual IEEE Power Electronics Specialists Conference (Cat. No. 98CH36196), Fukuoka, Japan, 22–22 May 1998; IEEE: Manhattan, NY, USA, 1998; Volume 2, pp. 1472–1478. [Google Scholar]
- Hsu, S.P. Problems in Analysis and Design of Switching Regulators: I. Pole Placement Technique for dc-to-dc Switching Regulators. ii. Transformer Modelling. iii. Cross-Regulation of the Two-Output Cuk Converter; California Institute of Technology: Pasadena, CA, USA, 1980. [Google Scholar]
- Hanson, A.J.; Perreault, D.J. Modeling the magnetic behavior of n-winding components: Approaches for unshackling switching superheroes. IEEE Power Electron. Mag. 2020, 7, 35–45. [Google Scholar]
- Qin, H.; Zhang, H.; Liu, M.; Ma, C. Comparison of Different Multi-winding Transformer Models in Multi-port AC-coupled Converter Application. In Proceedings of the IECON 2021–47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; IEEE: Manhattan, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Uttam, V.; Iyer, V.M. A Unified Modeling Approach for a Multi-Active Bridge Converter. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022-ECCE Asia), Himeji, Japan, 15–19 May 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1614–1620. [Google Scholar]
- Zhao, B.; Yu, Q.; Sun, W. Extended-phase-shift control of isolated bidirectional DC–DC converter for power distribution in microgrid. IEEE Trans. Power Electron. 2011, 27, 4667–4680. [Google Scholar] [CrossRef]
- Bai, H.; Mi, C. Eliminate reactive power and increase system efficiency of isolated bidirectional dual-active-bridge DC–DC converters using novel dual-phase-shift control. IEEE Trans. Power Electron. 2008, 23, 2905–2914. [Google Scholar] [CrossRef]
- Wu, K.; de Silva, C.W.; Dunford, W.G. Stability analysis of isolated bidirectional dual active full-bridge DC–DC converter with triple phase-shift control. IEEE Trans. Power Electron. 2011, 27, 2007–2017. [Google Scholar] [CrossRef]
- Hou, N.; Li, Y.W. Overview and comparison of modulation and control strategies for a nonresonant single-phase dual-active-bridge DC–DC converter. IEEE Trans. Power Electron. 2019, 35, 3148–3172. [Google Scholar] [CrossRef]
- Dey, S.; Mallik, A. Multi-variable control-based conduction loss optimization in dual active bridge converter considering generalized harmonic approximation oriented steady-state model. In Proceedings of the 2022 IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 20–24 March 2022; IEEE: Manhattan, NY, USA, 2022; pp. 245–250. [Google Scholar]
- Zha, D.; Wang, Q.; Cheng, M.; Deng, F.; Buja, G. Regulation Performance of Multiple DC Electric Springs Controlled by Distributed Cooperative System. Energies 2019, 12, 3422. [Google Scholar] [CrossRef]
- Liu, D.; Li, H.; Marlino, L.D. Design of a 6 kW multiple-input bi-directional dc-dc converter with decoupled current sharing control for hybrid energy storage elements. In Proceedings of the APEC 07-Twenty-Second Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 25 February–1 March 2007; IEEE: Manhattan, NY, USA, 2007; pp. 509–513. [Google Scholar]
- Ohno, T.; Hoshi, N. Transient Response Improvement Method with State Space Control for Triple Active Bridge DC/DC Converter. In Proceedings of the 2019 8th International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019; IEEE: Manhattan, NY, USA, 2019; pp. 657–662. [Google Scholar]
- Shubnaya, A.; Ibanez, F.M.; Cortes, P.R. Compensating measurement delays in decoupling blocks of dq control technique for multiple active bridge converter. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Langbauer, T.; Connaughton, A.; Vollmaier, F.; Pajnic, M.; Krischan, K. Closed-Loop Control of a Three-Port Series Resonant Converter. In Proceedings of the 2021 IEEE 22nd Workshop on Control and Modelling of Power Electronics (COMPEL), Aalborg, Denmark, 9–12 November 2020; IEEE: Manhattan, NY, USA, 2021; pp. 1–7. [Google Scholar]
- Karbozov, A.; Majumder, M.G.; Krishnamoorthy, H.S.; Rajashekara, K. Triple Active Bridge based Multiport Energy Router for Subsea-Renewable Interconnection. IEEE Trans. Ind. Appl. 2023, 59, 4528–4538. [Google Scholar] [CrossRef]
- Zhao, C. Isolated Three-Port Bidirectional DC-DC Converter. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2010. [Google Scholar]
- Wang, Q.G. Decoupling Control; Springer Science & Business Media: Berlin, Germany, 2002; Volume 285. [Google Scholar]
- Liu, L.; Tian, S.; Xue, D.; Zhang, T.; Chen, Y.; Zhang, S. A review of industrial MIMO decoupling control. Int. J. Control. Autom. Syst. 2019, 17, 1246–1254. [Google Scholar] [CrossRef]
- Wang, P.; Chen, Y.; Yuan, J.; Pilawa-Podgurski, R.C.; Chen, M. Differential power processing for ultra-efficient data storage. IEEE Trans. Power Electron. 2020, 36, 4269–4286. [Google Scholar] [CrossRef]
- Bempah, K.O.; Heo, K.W.; Jung, J.H. Real-time Power Flow Decoupling of Triple-Active-Bridge Converter for DC Microgrid System Applications. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022-ECCE Asia), Himeji, Japan, 15–19 May 2022; IEEE: Manhattan, NY, USA, 2022; pp. 1865–1872. [Google Scholar]
- Ma, F.; Wang, X.; Deng, L.; Zhu, Z.; Xu, Q.; Xie, N. Multiport railway power conditioner and its management control strategy with renewable energy access. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 1405–1418. [Google Scholar] [CrossRef]
- Yu, H.; Wang, Y.; Chen, Z. A Renwable Electricity-Hydrogen-Integrated Hybrid DC Traction Power System. In Proceedings of the 2021 IEEE Southern Power Electronics Conference (SPEC), Kigali, Rwanda, 6–9 December 2021; IEEE: Manhattan, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Hoffmann, F.; Person, J.; Andresen, M.; Liserre, M.; Freijedo, F.D.; Wijekoon, T. A multiport partial power processing converter with energy storage integration for EV stationary charging. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 7950–7962. [Google Scholar] [CrossRef]
- Kado, Y.; Okutani, S.; Katagiri, K.; Huang, P.Y. Autonomous DC microgrid consisting of triple active bridge converters. In Proceedings of the 2019 IEEE Third International Conference on DC Microgrids (ICDCM), Matsue, Japan, 20–23 May 2019; IEEE: Manhattan, NY, USA, 2019; pp. 1–5. [Google Scholar]
- Katagiri, K.; Nishimoto, K.; Nakagawa, S.; Okutani, S.; Kado, Y.; Wada, K. Decoupling Power Flow Control of Triple-Active Bridge Converter with Voltage Difference between Each Port for Distributed Power Supply System. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018; IEEE: Manhattan, NY, USA, 2018; p. P–1. [Google Scholar]
- Ohno, T.; Hoshi, N. Current Tracking Control of Triple Active Bridge DC/DC Converter Under Varying DC-Bus Voltage Conditions. IEEE Open J. Power Electron. 2022, 3, 834–845. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef]
- Qi, Y.; Liu, X.; Li, W.; Zhou, Z.; Liu, W.; Rajashekara, K. Decentralized Control for a Multi-active Bridge Converter. IEEE Trans. Ind. Electron. 2022, 70, 11412–11421. [Google Scholar] [CrossRef]
- Liu, X.; Liu, J.; Zhen, Y. Flat Control Strategy of Three-port DC-DC Converter for Renewable Energy and Energy Storage. In Proceedings of the 2021 5th CAA International Conference on Vehicular Control and Intelligence (CVCI), Tianjin, China, 29–31 October 2021; IEEE: Manhattan, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Kulkarni, S.V.; Khaparde, S.A. Transformer Engineering: Design, Technology, and Diagnostics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Beiranvand, H.; Hoffmann, F.; Pascal, Y.; Hahn, F.; Liserre, M. Multiwinding Transformer Leakage Inductance Optimization for Power Flow Decoupling in Multiport DC-DC Converters. In Proceedings of the 2021 IEEE 15th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Florence, Italy, 14–16 July 2021; IEEE: Manhattan, NY, USA, 2021; pp. 1–8. [Google Scholar]
- Mou, D.; Dai, Y.; Yuan, L.; Luo, Q.; Wang, H.; Wei, S.; Zhao, Z. Reactive Power Minimization for Modular Multi-Active-Bridge Converter with Whole Operating Range. IEEE Trans. Power Electron. 2023, 38, 8011–8015. [Google Scholar] [CrossRef]
- Sippola, M.; Sepponen, R.E. Accurate prediction of high-frequency power-transformer losses and temperature rise. IEEE Trans. Power Electron. 2002, 17, 835–847. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, Y.; Cui, S.; Mortimer, B.J.; De Doncker, R.W. Three-Port Bidirectional Operation Scheme of Modular-Multilevel DC–DC Converters Interconnecting MVDC and LVDC Grids. IEEE Trans. Power Electron. 2021, 36, 7342–7348. [Google Scholar] [CrossRef]
- Krishnaswami, H.; Mohan, N. Three-port series-resonant DC–DC converter to interface renewable energy sources with bidirectional load and energy storage ports. IEEE Trans. Power Electron. 2009, 24, 2289–2297. [Google Scholar] [CrossRef]
- Madawala, U.K.; Thrimawithana, D.J. A bidirectional inductive power interface for electric vehicles in V2G systems. IEEE Trans. Ind. Electron. 2011, 58, 4789–4796. [Google Scholar] [CrossRef]
- Wang, Y.; Han, F.; Yang, L.; Xu, R.; Liu, R. A three-port bidirectional multi-element resonant converter with decoupled power flow management for hybrid energy storage systems. IEEE Access 2018, 6, 61331–61341. [Google Scholar]
- Hazra, S.; Bhattacharya, S.; Chakraborty, C. A novel control principle for a high frequency transformer based multiport converter for integration of renewable energy sources. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; IEEE: Manhattan, NY, USA, 2013; pp. 7984–7989. [Google Scholar]
- Keshmiri, N.; Mudiyanselage, G.A.; Chakkalakkal, S.; Kozielski, K.; Pietrini, G.; Emadi, A. Design and Control Methodology of a Three-Port Resonant Converter for Electric Vehicles. IEEE Open J. Ind. Electron. Soc. 2022, 3, 650–662. [Google Scholar] [CrossRef]




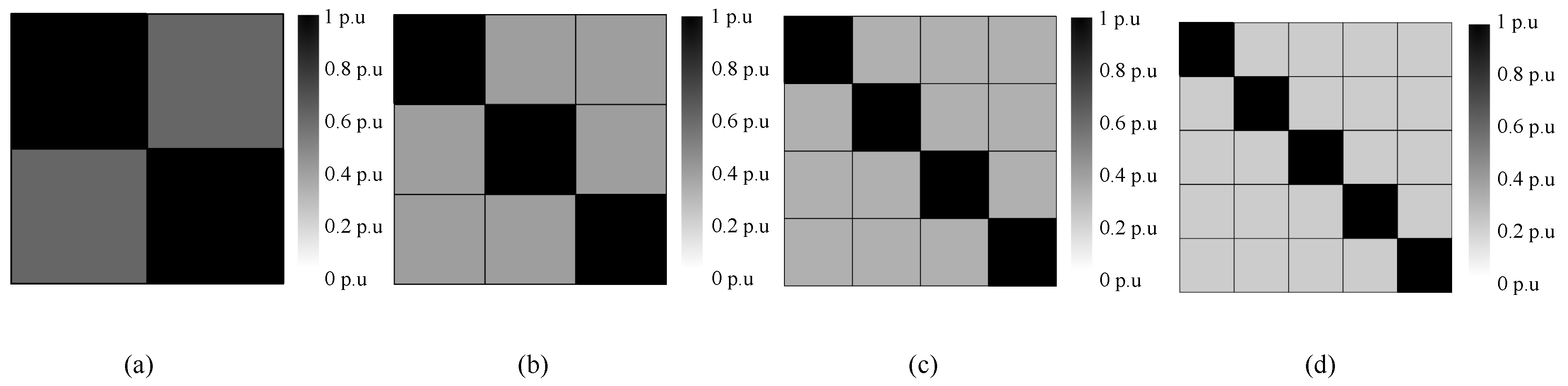


| Approach | Advantages | Disadvantages | References |
|---|---|---|---|
| TDA | The most accurate method. Provides the most information and insight about steady-state operation. | The high computational effort with increasing numbers of freedom in power flow control. | [15,22,35,43,60,78,84,86,110] [13,14,21,24,34,52,68,94,161] [83,89,162] |
| FCA | Easy to implement. Low computational cost. The best approach for resonant-type MAB converters. | Low accuracy (especially for higher value of the inner phase shifts). | [76,85,100,111,163,164] [3,65,112,113] |
| GHA | The most convenient method, with sufficient accuracy. | Relatievly high computation effort to achieve higher accuracy. | [79,114,115,116,117,124,160] [63,72,96,165,166] |
| Model-free (black-box) | Easy to implement. Robust to uncetenities. | Is not a general method. Does not demonstrates the inner operation principles of the converter | [91,99,118] |
| Ref. | N | App | M | Model | Control Approach | Decoupling Performance | Complexity | P [kW] | V [v] | f [kHz] | Year |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [58] | 4 | DFIG | SPS | TDA | Multi-loop (PIR voltage control) | Moderate | High | 1 | 200, 500, 500, 500 | 20 | 2022 |
| [59] | 3 | UPQC | SPS | TDA | PI Voltage control | Low | Low | 1.5 | 48, 48, 48 | 10 | 2022 |
| [94] | 4 | MV grid integration | SPS | TDA | Multi-loop controllers | High | High | 1 | 100, 150, 150, 150 | 20 | 2022 |
| [68] | 3 | PV modules | SPS | TDA | PI voltage controller + MPPT algorithm | Low | Low | 0.1 | 50, 50, 12 | 250 | 2021 |
| [14] | 3 | HESS | SPS + Duty Cycle | TDA | PI voltage controller | Low | Low | 1 | 54, 400, 42 | 20 | 2008 |
| [89] | 4 | Offshore power transfer through HVDC | SPS | TDA | Multi-loop PI controller | Moderate | Moderate | 5 | 300, 100, 1500 | 10 | 2023 |
| [93] | 12 | Energy router | Time-sharing +SPS | TDA | Time-sharing + PI voltage controller | High | Low | 0.5 | 72∼90 | 200 | 2020 |
| [83] | 4 | LVDC in smart homes | Time-sharing +SPS | TDA | Time-sharing + PI voltage controller | High | Low | 0.4 | 400, 48, 15, 5 | 100 | 2019 |
| [162] | 3 | HESS | SPS | TDA | Feedforward + Multi-loop PI controllers | Moderate | Moderate | 6 | 18, 18, 430 | 20 | 2007 |
| [63] | 3 | EV charging station | GPS | GHA | Feedforward + PI voltage controller | Low | Moderate | 0.3 | 80, 80, 12 | 100 | 2022 |
| [172] | 3 | Railway traction system | GPS | TDA | Feedforward + Multi-loop PI controllers | Moderate | Moderate | 20 | 300, 300, 300 | 10 | 2020 |
| [20] | 4 | MEA | SPS | . | Feedforward + PI voltage controller | Low | Moderate | 1 | 50, 50 50, 50 | 10 | 2020 |
| [165] | 3 | On-board Charger | SPS | GHA | Feedforward + PI power controller | Low | Moderate | 1 | 400, 400, 60 | 100 | 2021 |
| [27] | 3 | Bipolar DC grid | SPS | . | Feedforward + Multi-loop PI controllers | Moderate | Moderate | 0.03 | 12,12, 11.6 | . | 2022 |
| [34] | 3 | Isolated DC microgrid | SPS | FCA | Feedforward with gain schedualing + PI voltage controller | Moderate | High | 2 | 380, 380, 380 | 50 | 2023 |
| [7] | 3 | HESS | GPS | GHA | Feedforward + Multi-loop PI controllers | Moderate | Moderate | 1 | 55, 48, 100 | 25 | 2021 |
| [164] | 3 | . | SPS + dutycycle | FCA | Feedforward + Multi-loop PI controllers (in dq frame) | Moderate | High | . | . | . | 2022 |
| [174] | 3 | EV charging station | SPS | TDA | Feedforward with gain scheduling + PI voltage controller | Moderate | High | 3 | 400, 200, 140 | 20 | 2022 |
| [38] | 3 | DC transformer | SPS | TDA | Feedforward + PI voltage controller | Low | Moderate | . | . | . | 2021 |
| [111] | 3 | . | SPS | FCA | Feedforward + PI power controller | Low | Moderate | 1 | 100, 75, 75 | 20 | 2018 |
| [76] | 3 | UPS | SPS + duty cycle | FCA | Feedforward with gain scheduling + multi-loop PI controllers | Moderate | High | 1.5 | 300, 42, 14 | 100 | 2008 |
| [15] | 3 | HESS | SPS + duty cycle | TDA | Multi-loop controllers with different bandwidths | Moderate | Moderate | 2.5 | 300, 12, 16 | 20 | 2012 |
| [17] | 4 | HESS in MEA | SPS | TDA | Feedforward + multi-loop PI controllers with different bandwidth | Moderate | High | 3 | 270, 270, 270, 270 | 20 | 2018 |
| [52] | 4 | Solid-state Transformer | SPS + duty cycle | TDA | Multi-loop phase shift + duty cycle control | Moderate | Moderate | 20 | 200∼400 | 100 | 2019 |
| [171] | 3 | DC microgrid | SPS | FCA | Feedforward with gain scheduling + PI voltage controller | Moderate | High | 2 | 380, 380, 200 | 50 | 2022 |
| [95] | 3 | HESS | SPS | TDA | Multi-loop controllers with different bandwidths | Moderate | Moderate | 0.6 | 60, 60, 13 | 20 | 2015 |
| [175] | 3 | DC microgrid | SPS | TDA | Feedforward + PI voltage controller | Low | Moderate | 10 | 400, 400, 48 | 20 | 2019 |
| [176] | 3 | DC microgrid | SPS | TDA | Feedforward + PI voltage controller | Low | Moderate | 10 | 400, 400, 49 | 20 | 2018 |
| [75] | 10 | Differential power processing | SPS | TDA | PI voltage controller | Moderate | Low | 0.03 | 5 for all | 100 | 2019 |
| [166] | 3 | Energy router | GPS | GHA | Feedforward + Multi-loop PI controllers | Moderate | Moderate | . | . | . | 2023 |
| Ref. | N | App | M | Model | Control Approach | Decoupling Performance | Control Structure | Complexity | P [kW] | V [v] | f [kHz] | Year |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [22] | 3 | MEA | SPS | TDA | MPC | High | D | High | . | 50, 70 60 | 50 | 2023 |
| [86] | 4 | . | SPS | TDA | SMC+ feedforward | High | C | High | 0.7 | 180, 48 48, 48 | 100 | 2022 |
| [78] | 4 | . | SPS | TDA | MPC | High | C | High | . | . | . | 2022 |
| [43] | 4 | SST | SPS+ duty cycle | TDA | MPC | High | C | High | . | . | . | 2022 |
| [84] | 4 | ESS & RES integration | SPS | TDA | ADRC | High | D | Moderate | 2 | 200 for all | 100 | 2021 |
| [60] | 4 | UPQC | SPS | TDA | STA | High | D | high | 1.4 | 150 for all | 100 | 2022 |
| [98] | 3 | HESS | SPS | TDA | Flatness Control | Moderate | C | high | 1 | 60, 13, 60 | 10 | 2011 |
| [35] | 12 | SST for locomotive traction | GPS | TDA | Off-line Newton Iteration + multi-loop controllers | Moderate | C | High | 6 | 16∼25 | 20 | 2016 |
| [163] | 3 | RES and ESS integration | SPS | FCA | NSS | Moderate | C | High | 20 | . | 1 | 2019 |
| [21] | 4 | MEA | SPS | TDA | Hybrid NN + linearized model | Moderate | C | Moderate | . | . | . | 2022 |
| [91] | 6 | . | SPS | Model- free | Machine learning | High | C | Moderate | 0.05 | 12 for all | 0.5 | 2023 |
| [161] | 3 | DC electric springs | SPS | TDA | Feedforward +adaptive droop control | Moderate | C | High | . | . | . | 2019 |
| [24] | 3 | MEA | SPS | TDA | Feedforward + droop control | Moderate | C | Moderate | 2 | 200 | 20 | 2017 |
| [52] | 4 | SST | SPS+ duty cycle | TDA | Online calculation | Moderate | C | High | 20 | 200∼ 400 | 100 | 2019 |
| [96] | 3 | . | SPS | GHA | Online calculation | High | C | High | . | . | 20 | 2020 |
| [97] | 3 | DC microgrid | SPS | TDA | Online calculation | Moderate | C | High | 150, 75, 50 | 2023 | ||
| [100] | 3 | Grid forming | SPS + frequency control | FCA | Adaptive frequency control | Moderate | D | Moderate | 1 | 100 for all | 20 | 2022 |
| [13] | 3 | HESS | SPS | TDA | Multi-loop adaptive + droop control | Low | C | High | 0.5 | 48, 48, 250 | 50 | 2023 |
| [85] | 4 | . | GPS | FCA | Adaptive perturb & observe + feedforward | Moderate | C | Moderate | . | 100 | 2.5 | 2022 |
| [179] | 3 | . | SPS | TDA | Adaptive frequency control | Low | D | Moderate | 0.5 | 100 for all | 20 | 2022 |
| [99] | 3 | . | GPS | Model- free | NN-based + feedforward | High | C | Moderate | 5 | 400 | 40 | 2023 |
| Ref. | N | App | M | Decoupling Approach | N Switches | HFT | N Inductor | N Capacitor | P [kW] | V [v] | f [kHz] | Year |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [106] | 3 | Integration of HVDC, AC grid and ESS | GPS | Modified inductance | 16 | 3- windings | 5 (3 for filter) | 3 (for filter) | . | 141, 48, 380 | . | 2018 |
| [87] | 4 | . | SPS | Modified inductance | 16 | 4- windings | 7 (4 for filter) | 4 (for filter) | 2 | 160 for all | 100 | 2021 |
| [107] | 3 | . | SPS | Modified inductance | 12 | 3- windings | 2 | 3 (for filter) | 2 | 200,100, 100 | . | 2022 |
| [88] | 4 | . | SPS | Modified inductance | 18 | 4- windings | 3 | 4 (for filter) | . | . | . | 2023 |
| [182] | 3 | . | SPS | Modified inductance | 12 | 3- windings | . | 3 (for filter) | . | 50,50, 70 | 20 | 2021 |
| [188] | 3 | . | SPS | Multiple- resonant (for 2 ports) | 12 | 3- windings | 4 | 7 (3 for filter) | 0.75 | 230, 92, 115 | 95 | 2018 |
| [71] | 3 | RES and HESS integration | SPS | Resonant | 10 | 3- windings | 3 | 4 (3 for filter) | 0.3 | 12, 24, 110 | 40 | 2019 |
| [105] | 3 | ESS | FHS- PWM | FHS-PWM +Resonant | 12 | 3- windings | 4 | 5 (3 for filter) | 1 | 110 for all | 100 | 2021 |
| [101] | 3 | . | SPS + duty cycle | Resonant | 12 | 3- windings | 7 (4 for filter) | 6 (3 for filter) | 1 | 200, 120, 150 | 50 | 2022 |
| [102] | 3 | . | GPS | Resonant | 12 | 3- windings | 3 | 3 (1 for filter) | 2 | 60, 150, 60 | 50 | 2022 |
| [103] | 3 | RES | SPS | Resonant | 8 | 3- windings | 2 | 8 (2 for resonant) | 0.74 | 400, 60, 200 | 50 | 2022 |
| [8] | 3 | . | SPS + duty cycle | Resonant | 12 | 33- windings | 6 (4 for filter) | 4 (2 for filter) | . | 60, 72, 200 | 50 | 2022 |
| [46] | 4 | SST | SPS | Resonant + PR controllers | 16 | 4- windings | 3 | 7 (4 for filter) | 2 | 380 | 16 | 2022 |
| [190] | 3 | HESS in EVs | SPS + duty Cycle | Resonant + feedforward | 12 | 3- windings | 2 | 5 (3 for filter) | 6 | 14,46, 800 | 10 | 2022 |
| [6] | 3 | HESS | GPS | Variable resonant | 16 | 3- windings | 3 | 6 | 1.5 | 62,72, 110 | 50 | 2022 |
| [12] | 4 | HESS | SPS + duty Cycle | Variable resonant | 16 | 4- windings | 4 (variable inductors) | 8 | 15 | . | 200 | 2023 |
| [104] | 3 | RES and HESS integration | GPS | Resonant (Immittance network) | 12 | 3- windings | 4 | 5 (3 filter) | 1 | 96, 72, 300 | 100 | 2022 |
| [80] | 4 | EV charger | SPS + duty cycle | Resonant + separated HFTs | 16 | Triple HFT | 3 | 7 (4 for filter) | 2 | 400 | 120 | 2022 |
| [189] | 3 | RES | SPS | Negative inductance emulation | 12 | 3- windings | 3 | 3 for filter | 2.6 | 50, 100, 170 | 1 | 2013 |
| [109] | 3 | . | SPS + duty cycle | Separated HFTs | 14 | Dual HFT | 0 | 3 | . | 40∼60 for all | 15 | 2017 |
| [108] | 3 | RES | SPS | Separated HFTs | 10 | Dual HFT | 0 | 5 (1 for filter) | 1 | 48, 230, 300 | 20 | 2022 |
| [30] | 3 | Bipolar DC system | SPS + duty cycle | Separated HFTs | 8 | Dual HFTs | 0 | 5 | 2 | 380 | 50 | 2022 |
| [37] | 3 | SST | SPS | Separated HFTs | 12 | Dual HFT | 0 | 1 | 1 | 70, 70, 100 | 20 | 2021 |
| [131] | 3 | HESS | SPS | Resonant | 12 | 3- windings | 2 | 5 (3 for filter) | 1 | 85, 100, 200 | 20 | 2017 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koohi, P.; Watson, A.J.; Clare, J.C.; Soeiro, T.B.; Wheeler, P.W. A Survey on Multi-Active Bridge DC-DC Converters: Power Flow Decoupling Techniques, Applications, and Challenges. Energies 2023, 16, 5927. https://doi.org/10.3390/en16165927
Koohi P, Watson AJ, Clare JC, Soeiro TB, Wheeler PW. A Survey on Multi-Active Bridge DC-DC Converters: Power Flow Decoupling Techniques, Applications, and Challenges. Energies. 2023; 16(16):5927. https://doi.org/10.3390/en16165927
Chicago/Turabian StyleKoohi, Peyman, Alan J. Watson, Jon C. Clare, Thiago Batista Soeiro, and Patrick W. Wheeler. 2023. "A Survey on Multi-Active Bridge DC-DC Converters: Power Flow Decoupling Techniques, Applications, and Challenges" Energies 16, no. 16: 5927. https://doi.org/10.3390/en16165927
APA StyleKoohi, P., Watson, A. J., Clare, J. C., Soeiro, T. B., & Wheeler, P. W. (2023). A Survey on Multi-Active Bridge DC-DC Converters: Power Flow Decoupling Techniques, Applications, and Challenges. Energies, 16(16), 5927. https://doi.org/10.3390/en16165927