Optimization with Neural Network Feasibility Surrogates: Formulations and Application to Security-Constrained Optimal Power Flow

Abstract

In many areas of constrained optimization, representing all possible constraints that give rise to an accurate feasible region can be difficult and computationally prohibitive for online use. Satisfying feasibility constraints becomes more challenging in high-dimensional, non-convex regimes which are common in engineering applications. A prominent example that is explored in the manuscript is the security-constrained optimal power flow (SCOPF) problem, which minimizes power generation costs, while enforcing system feasibility under contingency failures in the transmission network. In its full form, this problem has been modeled as a nonlinear two-stage stochastic programming problem. In this work, we propose a hybrid structure that incorporates and takes advantage of both a high-fidelity physical model and fast machine learning surrogates. Neural network (NN) models have been shown to classify highly non-linear functions and can be trained offline but require large training sets. In this work, we present how model-guided sampling can efficiently create datasets that are highly informative to a NN classifier for non-convex functions. We show how the resultant NN surrogates can be integrated into a non-linear program as smooth, continuous functions to simultaneously optimize the objective function and enforce feasibility using existing non-linear solvers. Overall, this allows us to optimize instances of the SCOPF problem with an order of magnitude CPU improvement over existing methods.

1. Introduction

The security-constrained optimal power flow (SCOPF) problem is an important tool in day-to-day power grid operations. Independent system operators (ISOs) solve the SCOPF problem frequently (every few hours [1]) to obtain operational policies that are considered N-1 secure (i.e., resilient against contingencies where any one transmission line or generator may fail without loss of service to power consumers). The most common practice involves solving a linearized form of the OPF problem without contingencies, and then use of heuristics to obtain safe (but potentially sub-optimal) SCOPF solutions using a subset of contingencies. Thus, further improvements in computational cost are necessary for increased adoption of the more accurate non-linear formulation. More recent approaches have formulated and solved the SCOPF problem using stochastic programming formulations that capture thousands of contingencies using parallel interior point solvers with high-performance computing hardware [2]. Some parallel solutions of the SCOPF problem are scalable and can be computed in a timely manner (about 10 min for thousands of contingencies) if the computing resources are available. Several other methods for managing the computational tractability of SCOPF problems include problem decomposition [3], learning active constraint sets [4], and identifying umbrella constraints [5].

Other work has looked at parallelization of the ACOPF [6], which may be extended to SCOPF in the future. There are excellent literature sources [7,8] that survey all formulations, linearizations, and relaxations that are common in the OPF problem and, by extension, the SCOPF problem. Recent work has also shown that many convex relaxations to these problems can produce infeasible solutions [9], and that determining AC system feasibility is an NP hard problem [10]. As the problem is of key interest to critical infrastructure systems, there have been research competitions dedicated to solving the SCOPF efficiently. This includes the ARPA-E Grid Optimization competition [11,12,13]. This contest focused on solving large cases of this problem and successful teams used convex relaxations, contingency-screening heuristics, problem decompositions and various solvers (IPOPT, KNITRO, Gurobi). While this work focuses on the economic dispatch problem, there have been some studies into using surrogate models for the unit commitment problem as well [14].

Surrogate modeling techniques are widely used across engineering disciplines owing to their ability to produce tractable computational models that capture complex phenomena [15,16]. A key aspect of such data-driven techniques is their ability to incorporate diverse, large-scale datasets (e.g., operational and/or simulation data) into flexible, accurate, and fast prediction models. In the context of data science, surrogate modeling techniques can harness new hardware and algorithmic advances to utilize massive amounts of data with access to scalable training architectures [17].

Neural networks have received particular interest with respect to surrogate modeling [18] due their excellent approximation properties and arbitrary degree of accuracy with enough activation neurons [19]. Deep neural networks have specifically garnered attention for their ability to represent complex non-linear relationships between inputs and outputs and learn significant features while utilizing training data efficiently [20]. In the context of the machine learning (ML) literature, however, the optimization aspects commonly refer to the training of the neural network model [21], as opposed to embedding [22] the surrogate model within a mathematical optimization problem in the form of an algebraic function. The latter embedded NN differs from its more commonplace predictive applications (e.g., image classification) in that its algebraic representation permits design and control problems that are often concerned with enforcing physical constraints. By representing only a subset of the optimization formulation with an ML model, physics-based knowledge, which may be implicitly defined on the inputs and outputs, can be incorporated, and this allows for hybrid models that still maintain a first-principles relationships between the model variables.

This manuscript explores hybrid modeling for the well-known, yet challenging, SCOPF problem and demonstrates both the promise and research challenges associated with incorporating deep NNs into large-scale non-linear programming formulations (NLPs). We describe a novel sampling scheme that utilizes an equation-based sampling method of the SCOPF problem to generate a diverse dataset containing balanced points of safe and unsafe operating modes. Subsequently, a deep NN is trained to learn the classification boundary between these spaces. We then introduce a new optimization formulation that uses the surrogate model to enforce secure operation in a traditional AC optimal power flow (ACOPF) formulation. As opposed to fully black-box methods, this approach allows the constraint to be agnostic to objective function parameters and have mathematical guarantees of feasibility in the nominal state variables. We compare the scalability and accuracy of our proposed formulation against the equivalent extensive SCOPF problem and discuss future enhancements.

The rest of the paper is organized as follows: Section 2 summarizes previous relevant work. Section 3 describes the mathematical formulation of SCOPF and how certain constraints can be handled with surrogates. Section 4 examines accurate sampling in the high-dimensional security space. Section 5 shows how trained NN models can be embedded into optimization models. Section 6 shows the numerical results, and Section 7 summarizes the key findings.

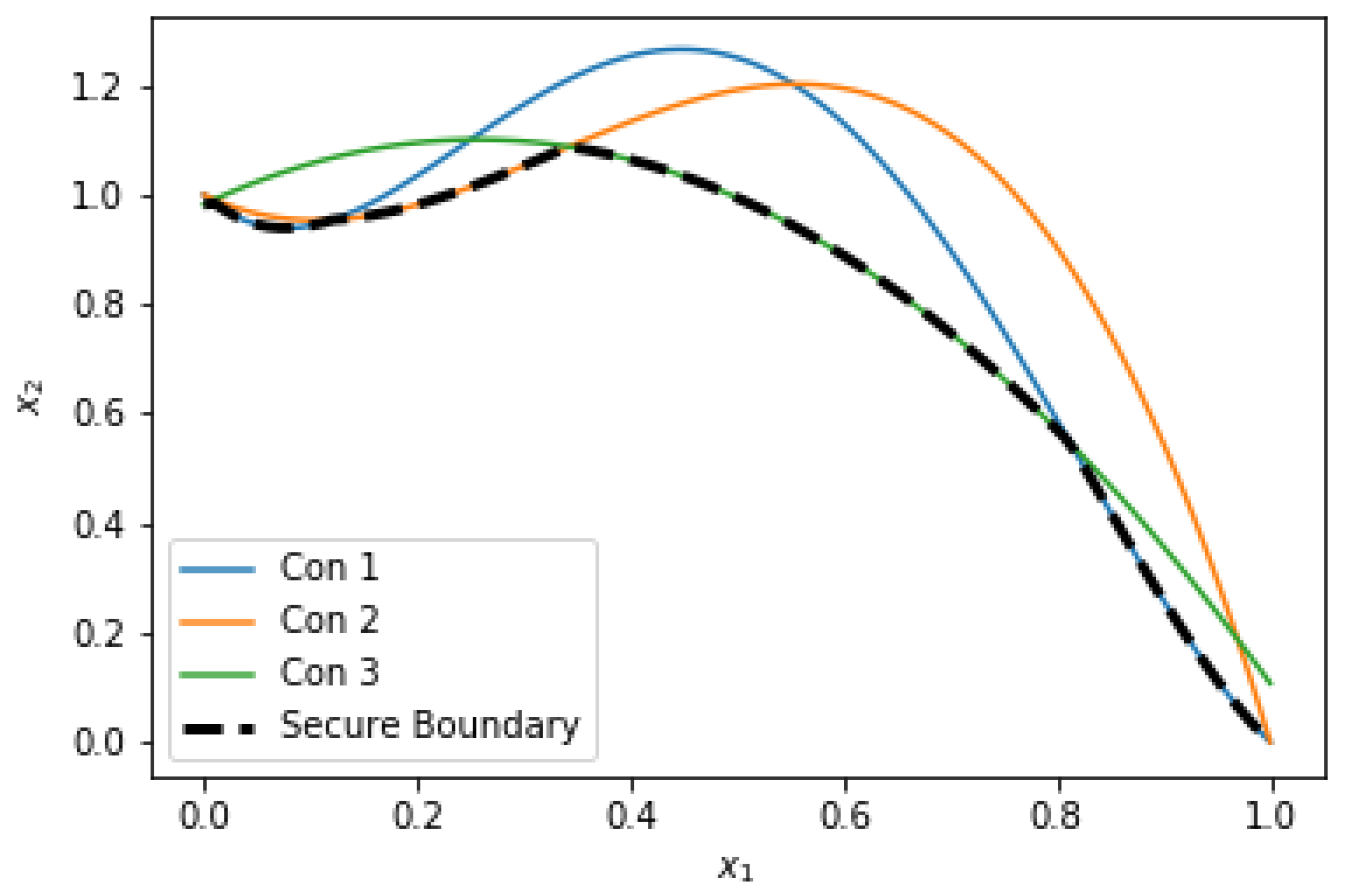
The key advances and research contributions can be outlined in three methodological sections, shown in Figure 1. The novel sampling approach is shown to be highly effective for characterizing non-convex boundary functions; algebraic reformulations of NN functions are detailed and discussed with respect to their use in large NLPs; and the hybrid solution method allows for quick and accurate solution of the SCOPF. These contributions with respect to related literature are further detailed below in Related Work.

2. Related Work

In this work, the SCOPF problem is solved using a hybrid surrogate-based approach, where a deep neural network (DNN) surrogate is used as the feasibility classifier within the overall SCOPF formulation. This approach tackles the issue of tractability by using computational resources a priori (offline) to map the secure space of the problem and train the surrogate. It also allows for a more compact representation of the feasibility space into a single NN constraint. Previous work [23] trained non-linear regression models and single-layer NN models to find the security boundary of a given load profile for the worst case contingency. More recent work [24] has trained NN classifiers for various criteria of power grid security with ReLU activation functions. These constraints were then added to the ACOPF problem as a set of linear constraints with binary variables to generate a mixed-integer non-linear program (MINLP). The power equations are then linearized to convert this to a mixed integer linear problem (MILP). Our work builds on this by using deep NN models to map the secure and insecure space of all contingencies of interest, variable in-load demand, and higher dimensional representations of the security boundary. We focus on ML representations that maintain non-linearity but avoid discrete variables, which ultimately maintains their representation as an NLP problem that can be solved using powerful interior point solvers.

Other related work has, instead, replaced the entire optimal power flow problem with a surrogate model, using optimal solutions to train it [25]. In [26], the authors look at verification of neural networks that predict optimal power flow solutions, showing that well-trained networks have good bounds on output error. These approaches have the advantage of learning the full problem which makes forward prediction faster, but can make the model inflexible to changing objective function parameters and requires some post-processing to guarantee even pre-contingency state feasibility. In [27], the authors use a distance metric from the boundary to quantify historical data points’ security even when most are not near to the boundary, which also requires knowledge of the exact feasibility space. We, instead, use the model to map out boundary points where the constraints become active, using an optimization-based approach described in detail in Section 4. One advantage of our approach is that the classification model can learn the feasibility boundary in the higher dimensional space of the nominal variables instead of learning a single distance metric. We build on our previous work in [28] by introducing (a) a model-based sampling algorithm that can accurately find data points without the need for an iterative “guess and check” procedure, (b) exploring various neural network formulations/facilitated Python implementations, and (c) applying our approach to much larger grid problems with more contingencies.

3. Security-Constrained Optimal Power Flow

3.1. Full Formulation

SCOPF is a non-linear, non-convex formulation based on the AC power flow equations. It seeks to find an economically optimal setting for the control variables, such that they balance all load demands in the network and can still provide power under outage events. A general form of the preventative SCOPF problem can be written compactly as the following non-linear program:

$$\begin{array}{ccc}\hfill \mathrm{(1a)}& \min {\displaystyle \sum _{g\in \mathbf{G}}}C\left(p_0^g\right)\hfill & \mathrm{s}.\mathrm{t}.\hfill & & \\ \hfill \mathrm{(1b)}& P_{i,c}(v,\delta )=p_{i,c}^G-p_{i,c}^L\hfill & \hfill \forall i\in \mathbf{N},\forall c\in \mathcal{C}\hfill \mathrm{(1c)}& Q_{i,c}(v,\delta )=q_{i,c}^G-q_{i,c}^L\hfill & \hfill \forall i\in \mathbf{N},\forall c\in \mathcal{C}\hfill \mathrm{(1d)}& p_i^{G,\min }\le p_{i,c}^G\le p_i^{G,\max }\hfill & \hfill \forall i\in \mathbf{G},\forall c\in \mathcal{C}\hfill \mathrm{(1e)}& q_i^{G,\min }\le q_{i,c}^G\le q_i^{G,\max }\hfill & \hfill \forall i\in \mathbf{G},\forall c\in \mathcal{C}\hfill \mathrm{(1f)}& v_i^{\min }\le v_{i,c}\le V_i^{\max }\hfill & \hfill \forall i\in \mathbf{N},\forall c\in \mathcal{C}\hfill \mathrm{(1g)}& {\delta }_i^{\min }\le {\delta }_{i,c}\le {\delta }_i^{\max }\hfill & \hfill \forall i\in \mathbf{N},\forall c\in \mathcal{C}\end{array}$$

where $\mathcal{C}$ represents the set of contingencies, including the nominal case ($\mathcal{C}=0$), constraints (1b) and (1c) model the power flow equations, and the Equations (1d)–(1g) model operational limits (e.g., on generation, voltage magnitude, voltage angle, etc.). Indices $\mathbf{G}$, $\mathbf{N}$, $\mathbf{R}$ and $\mathbf{L}$ represent system generators, buses (nodes), reference bus and loads, respectively. The objective function is to minimize the operating costs for the nominal case while ensuring secure network operation across all contingency states. The cost function is given by empirical coefficients that relate generator power to operating cost and is typically quadratic.

A common representation for $P_{i,c}$ in (1b) and $Q_{i,c}$ in (1c) is given, respectively, by the following set of equations:

$$\begin{array}{}\hfill \mathrm{(2a)}& v_i\sum _{k=1}^N{v}_k\left(g_{ik}cos({\delta }_i-{\delta }_k)+b_{ik}sin({\delta }_i-{\delta }_k)\right)\hfill & \hfill \forall i\in \mathbf{N}\hfill \mathrm{(2b)}& v_i\sum _{k=1}^N{v}_k\left(g_{ik}sin({\delta }_i-{\delta }_k)-b_{ik}cos({\delta }_i-{\delta }_k)\right)\hfill & \hfill \forall i\in \mathbf{N}\end{array}$$

Here, the net power injections are calculated given voltage magnitudes (v), angles ($\delta$) and admittance parameters (g,b). If $\mathcal{C}=\left[0\right]$, the overall formulation is solved only for the nominal variables and the resulting problem is the non-convex ACOPF. It has been shown that solutions to this ACOPF problem are not robust to system failures and many operating points are not N-1 secure. Therefore, explicit outages are added to $\mathcal{C}$ to guarantee robustness to anticipated contingency events. Equations (1b)–(1g) show that the power flow equations must be satisfied under each contingency, essentially duplicating the nominal model with an outage event. This problem is referred to as SCOPF, or the extensive formulation; more mathematical details on this formulation can be found in [2]. When seeking a more secure solution (i.e., including more contingency constraints), the problem space grows quickly: for example, the small IEEE Case 30 has 449 variables in the original ACOPF and 18,409 variables when considering all 41 line contingencies (all detailed parameters of grid case studies can be found in [29]). This shows how tractability quickly becomes challenging when considering contingencies.

Within the SCOPF problem, we can categorize power grid variables into state (x) and control (y) variables to align with the general NLP formulation shown in Section 3.2.

$$\begin{array}{}\hfill \mathrm{(3a)}& x=[v^L,{\delta }^L,q^G,{\delta }^G,p^R,q^R]\hfill \hfill \mathrm{(3b)}& y=[p^L,q^L,p^G,v^G,v^R,{\delta }^R]\hfill \end{array}$$

3.2. Representing Secure Region Using NN Classifier

Instead of solving the full contingency-constrained optimization problem, we propose a hybrid modeling formulation where the security constraints are captured using an NN that predicts the security of the solution space.

$$\begin{array}{}\hfill \mathrm{(4a)}& \hfill \underset{x,y}{min}& f\left(y\right)\hfill \hfill \mathrm{(4b)}& \hfill \mathrm{s}.\mathrm{t}.& g(x,y)=0\hfill \hfill \mathrm{(4c)}& & y_L\le y\le y_U\hfill \hfill \mathrm{(4d)}& & x_L\le x\le x_U\hfill \hfill \mathrm{(4e)}& & y_{sec}=NN(x,y)\hfill \hfill \mathrm{(4f)}& & y_{sec}\le \alpha \hfill \end{array}$$

Formulations (4a)–(4f) shows the general form of an optimization problem with an embedded NN model to represent a subset of the problem formulation. In the case of SCOPF, constraint (4e) provides a mapping from our nominal state solutions to the N-1 contingency space and, specifically, whether they constitute a feasible point. It can be thought of as a non-linear algebraic constraint similar to (4b). Equation (4f) enforces a security threshold for the classifier using parameter $\alpha$, set between 0 and 1. Higher $\alpha$ values result in more false negatives, while lower $\alpha$ values result in more false positives. A false positive refers to a situation where the NN classifies a feasible point as infeasible. Conversely, a false negative occurs when the NN classifies an infeasible point as feasible. In this problem structure, $\alpha$ can be a tunable parameter depending on how conservative a solution we want. If constraint (4e) can be represented without integer variables, the full problem can be solved with interior point methods, which have proven to be fast and accurate for large NLPs [30,31].

When considering the link between Formulations (1a)–(1g) and this general NLP, Equation (4a) corresponds to Equation (1a) for the objective function. Equation (4b) corresponds to Equations (1b) and (1c) for $\mathcal{C}=\left[0\right]$, or the ACPF equations for nominal operation. The remainder of the problem constraints in $\mathcal{C}$ are captured with the NN classifier.

4. Efficient Sampling for Security Training Set

4.1. Optimization-Based Sampling Algorithm

The first challenge towards training an accurate security classifier surrogate is obtaining diverse and informative samples of the operational space. Here, we introduce an optimization-based adaptive sampling technique [32,33] which aims to find informative sampling locations for the NN classifier (i.e., points close to the boundary, where constraints become active/inactive). Most grids are operated close to the security boundary [34], so we might expect many of these points to be consistent with historical data points. This is distinct from existing sampling approaches for this problem, which use hyperspheres [35] to reduce absolute bounds on system variables, which is particularly amenable to global solution methods. Our optimization-based sampling scheme uses a non-linear programming formulation that targets boundary samples, which are key to improving classification accuracy.

The formulation we seek to solve is presented as follows:

$$\begin{array}{}\hfill \mathrm{(5a)}& \underset{x_0,y_0,x_{\mathcal{C}},y_{\mathcal{C}}}{max}SF\hfill \hfill \mathrm{(5b)}& \mathrm{s}.\mathrm{t}.\left(1\mathrm{b}\right)–\left(1\mathrm{g}\right)\hfill \hfill \mathrm{(5c)}& p^L=p_{nom}SF\hfill \hfill \mathrm{(5d)}& P{F}_i^2=\frac{{\left(p_i^L\right)}^2}{{\left(p_i^L\right)}^2+{\left(q_i^L\right)}^2},\forall i\in \mathbf{N}\hfill \end{array}$$

In Equations (5a)–(5d), $SF$ represents the scaling factor, $p_{nom}$ represents an initial feasible vector of loads, $p_d$ represents the scaled load vector, and $PF$ is the power factor ratio between the real and reactive power at each load. This problem is solved via non-linear local optimization techniques (Algorithm 1) with several sampled grid profiles, targeting multiple and diverse boundary points where security constraints become active. Initial load conditions and ramping directions are sampled via a Latin-hypercube (LHS) design to maximize the spatial coverage of the space. This approach leads to many points on the security boundary of the system and allows us to characterize points between initial loads and the final solution as N-1 secure. Points corresponding to a higher $SF$ can be labeled as insecure. In Algorithm 1, state and control variables are calculated for both nominal operation ($x_0$,$y_0$) and under each contingency ($x_c$,$y_c$) to explicitly calculate whether each point is secure or insecure with the nominal variables saved for the ML training dataset (step 7). We include Figure 2 to show a simple visualization of a single initial load profile and corresponding load direction.

Algorithm 1: Sampling the Security Boundary

1:  Initialize nominal loads $IL:=\{p_1,...,p_{N_l}\}$   2:  Initilize load directions $LD:=\{l{d}_1,...,l{d}_{N_d}\}$   3:  for $i=1,...,N_l$ do   4:   for $j=1,...,N_d$ do   5:    $p_{nom}\leftarrow p_i\ast l{d}_j$   6:    $(\widetilde{x_0},\widetilde{y_0},\widetilde{x_{\mathcal{C}}},\widetilde{y_{\mathcal{C}}})\leftarrow$ Formulation (5)   7:    $\{p^L,p^G\}\leftarrow (\widetilde{x_0},\widetilde{y_0})$   8:   end for   9:  end for

This sampling framework allows us to find classification points at any arbitrary distance from the true boundary, significantly reduces training data demands, and provides the basis for a balanced dataset. The above are existing challenges in the training of high-dimensional, non-convex classification models, which is the expected nature of security-based power flow classifiers. Although offline sampling costs may increase, each data point added to the training set contains targeted and rich information regarding the representation of the underlying space. Furthermore, this algorithm is parallelized, such that each contingency scenario can be sampled individually. During this process, the worst-case scenario is recorded, and this feature is expected to be particularly useful in even larger grids. The worst-case scenario corresponds to the smallest SF as this represents the smallest load profile that would cause N-1 feasibility constraints to become active. Parallelization is also possible for various load-direction vectors ($l{d}_j$) and starting points. The proposed sampling formulation is much faster (>10×) than its SCOPF counterpart since its objective is the maximization of a single scaling parameter, allowing us to collect several samples in the time it would take to solve a single instance of SCOPF. Algorithm 1 is solved with the interior point solver IPOPT [30], with linear solver MA27, and 3000 maximum iterations.

4.2. Toy Example to Visualize Optimization-Based Sampling

Figure 3 illustrates the approach with a simple 2-d space, where the overall secure region is given by three non-linear constraints, two of which are non-convex constraints, leading to an overall feasible region that is non-convex. When using a Latin-hypercube (LHS) design to map the feasibility boundary, many more points would be required. Instead, if the LHS samples are used as initial guesses to our optimization-based sampling framework, the identified samples all lie around the security boundary and this leads to a very accurate classifier (Figure 4).

Figure 4 shows 15 samples generated using Latin-hypercube samples (LHS) and using the model-guided algorithm. Model-guided samples are shown with $\pm 5\%$ L2 distance from the boundary.

Table 1. Naive Sampling Classifier Accuracy.

Samples	1%	5%	10%	20%	LHS
5	50.5	52.7	55.4	61.0	79.9
10	50.6	54.7	56.1	72.8	86.6
15	50.8	54	62	74.6	82.4
25	51.6	62.5	82.3	93.7	93.5
50	60.5	99.5	100	100	97.7

shows the accuracy results for LHS sampling with increasing training data size. The accuracy metric of the classifier is defined as the percentage of test points correctly classified, $(TP+TN)/(TP+TN+FP+FN)$. TP, TN, FP and FN refer to true positives, true negatives, false positives and false negatives respectively. The accuracy is assessed for randomly generated test points at set distances from the boundary and for a set of test points spaced throughout the explored region drawn again from an LHS distribution. This allows us to quantify the accuracy of classifiers in different regions: from very close to the boundary, to further from the boundary, to an average metric from samples spaced out in the entire region (which is a common metric used). We note that the accuracy increases as we add more samples and that the accuracy is better the further we are from the boundary, which is not surprising. We also observe that this type of analysis enables us to realize that the accuracy of the classifier at the boundary is only 50–60%, but the average accuracy over the entire space is 80–90%, which is misleading if it is important to accurately classify non-convex boundaries.

Table 2. Model-Based Sampling Classifier Accuracy.

Samples	1%	5%	10%	20%	LHS
5	74.6	94.8	99.5	100	98.7
10	88.4	97.5	100	100	99.1
15	87.9	99.5	100	100	99.1
25	91.4	99.3	100	100	99.1
50	88.5	99.2	100	100	99.1

shows the contrasting performance of the model-guided training set, which is trained with samples at 5% distance from the boundary. We note that the classifier performs much better on random test points with as few as five training points. It can generalize very well to test points 5% and greater with fewer training points than the naive approach. It also performs significantly better when extrapolating to test points that are even closer to the active constraints (1% distance). This is important for sharp boundaries since most optimal solutions will have at least one active security constraint. Overall, the model-guided sampling approach is shown to be superior to an LHS method for surrogate accuracy, with further improvements in regions that are challenging to classify.

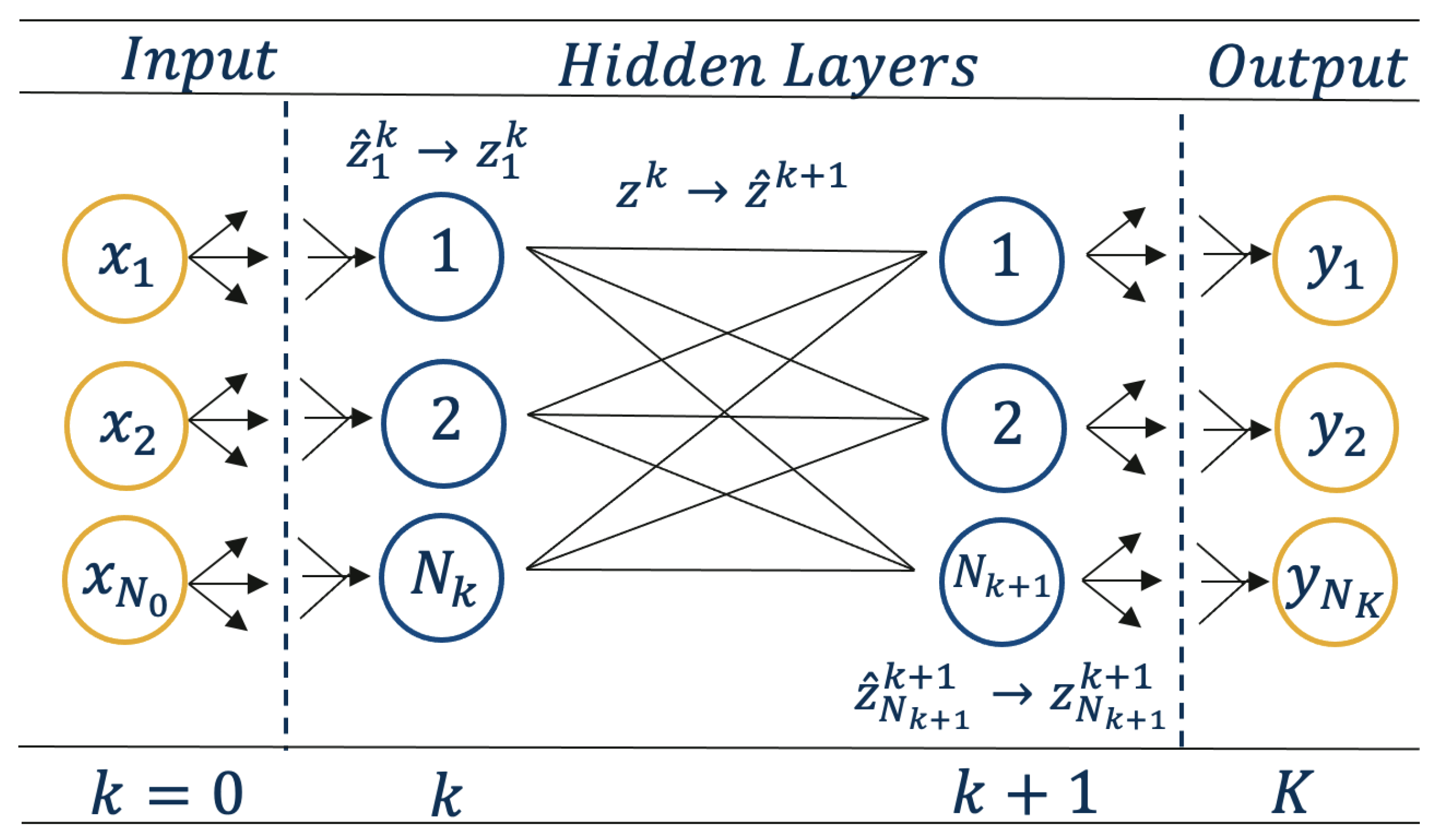
5. Neural Network Representation

Implementing the security classifier in Equation (4e) requires formulating the neural network in terms of optimization variables and constraints. The choice of NN formulation affects the fundamental form of the surrogate model and the resulting optimization problem. A major thread of research has developed surrogate formulations for machine learning surrogates and includes mixed-integer linear representations for ReLU networks [36,37,38,39], full-space and reduced-space representations for smooth activation functions [22], as well as complementarity representations for ReLU functions [40]. For our application, we assume a simple feed-forward NN described by Formulations (6a)–(6d) that contains $k=\{1,\dots ,K\}$ layers where each layer contains $N_k$ nodes (depicted by Figure 5). It is also important to note that the OPF problem we are applying this approach to is an NLP, so the inclusion of mixed integers for the NN representation would result in an MINLP problem more difficult to solve than the extensive form. Thus, we focus on three constraint formulations that implement the NN as a smooth, non-linear function that are compatible with large NLP solvers and provide a comparison between them when used in an optimization context.

We denote the input vector by $x\in {\mathbb{R}}^{N_0}$ and the output vector by $y\in {\mathbb{R}}^{N_K}$. The input vector to each layer ${\widehat{z}}^{k-1}$ is a linear combination of the output of the previous layer, i.e., ${\widehat{z}}^{k+1}=W^k{z}^k+b^k$, where $W^k$ is a $N^{k+1}\times N^k$ weight matrix and $b^k$ is a $N^{k+1}\times 1$ bias vector between layers k and $k+1$. Each hidden layer incorporates an activation function $z=\sigma \left(\widehat{z}\right)$, which usually applies a non-linear transformation to each element of the vector input. We denote the vector x as $z^0$ to represent the input layer to the neural network (the input layer is usually not considered a layer). The pre-activation values ${\widehat{z}}^k$ at each layer k are given by (6b) and the post-activation values $z^k$ are denoted by (6c). Finally, the output layer produces the vector y as a linear combination of the final hidden layer given by (6d).

$$\begin{array}{}\hfill \mathrm{(6a)}& z^0=x\hfill & \hfill \mathrm{(6b)}& {\widehat{z}}^k=W^k{z}^{k-1}+b^k,\hfill & \hfill \forall k\in \{1,...,K-1\}\hfill \mathrm{(6c)}& z^k=\sigma \left({\widehat{z}}^k\right),\hfill & \hfill \forall k\in \{1,...,K-1\}\hfill \mathrm{(6d)}& y=W^K{z}^K+b^K\hfill \end{array}$$

It is helpful to express Formulations (6a)–(6d) element-wise to demonstrate different neural network representations for the security-constrained optimization problem. Formulations (7a)–(7d) is analogous to (6a)–(6d), but it additionally unfolds the inner layer nodes.

$$\begin{array}{}\hfill \mathrm{(7a)}& x_n=z_n^0\hfill & \hfill \forall n\in \{1,...,N_0\}\hfill \mathrm{(7b)}& {\widehat{z}}_n^k=\sum _{i=1}^{N_{k-1}}{W}_{i,n}^k{z}_n^{k-1}+b_n^k,\hfill & \hfill \forall n\in \{1,...,N_k\},\forall k\in \{1,...,K-1\}\hfill \mathrm{(7c)}& z_n^k=\sigma \left({\widehat{z}}^k\right),\hfill & \hfill \forall n\in \{1,...,N_k\},\forall k\in \{1,...,K-1\}\hfill \mathrm{(7d)}& y_n=\sum _{i=1}^{N_{K-1}}{W}_{i,n}^K{z}_n^{K-1}+b_n^K\hfill & \hfill \forall n\in \{1,...,N_K\}\end{array}$$

The choice of the best activation function used for Equation (7c) generally falls to the problem of training a neural network, although the ReLU function has been commonly selected for its favorable properties [41]. In the optimization problem, (7a)–(7d) can be implemented using the different aforementioned algebraic representations. As this manuscript utilizes the non-linear ACPF equations, we choose to examine the three following smooth NN representations.

• Full Space Representation (Non-linear)

The variables and constraints described by (7a)–(7d) are formulated explicitly in the problem. The activation constraints can be any smooth function (e.g., tanh, sigmoid, softplus). Intermediate variables (e.g., $z^k,{\widehat{z}}^k$) are formulated in IPOPT and related through sequential constraints.

• Reduced Space Representation (Non-linear)

The reduced-space representation is similar to the full space, but the NN variables and constraints are captured as one expression that connects the input and output variables. Here, intermediate variables (e.g., $z^k,{\widehat{z}}^k$) are not explicitly formulated in IPOPT and the problem variable size is reduced. Previous research has shown that reduced-space representations may have advantages when embedded in optimization formulations [22]; thus, we implement this formulation to access the advantages over a full-space formulation.

• ReLU with Complementarity Representation

While we can formulate ReLU within full- and reduced-space representations, the resulting constraints are not smooth (ReLU is given by $z=max(0,\widehat{z})$). To handle this, ReLU can be formulated using complementarity conditions, where we substitute (7c) with (8) for each node in the NN to generate a mathematical program with complementarity constraints (MPCC) [42].

$$\begin{array}{cc}0\le (z_n^k-{\widehat{z}}_n^k)\perp z_n^k\ge 0\hfill & \hfill \forall n\in \{1,...,N_k\},\forall k\in \{1,...,K-1\}\end{array}$$

(8)

The complementarity constraints in (8) permit smooth transformations, which have been studied extensively with respect to regularity properties [43]. This manuscript uses a simple component-wise formulation initially presented in [44] given by (9). This representation introduces a non-linear constraint for each node (complementarity) in the neural network and uses the regularization parameter $ϵ\ge 0$ to satisfy NLP constraint qualifications. This formulation is implemented within pyomo.mpec [45] and is used in the neural network package OMLT [46].

$$\begin{array}{cc}(z_n^k-{\widehat{z}}_n^k)z_n^k\le ϵ\hfill & \hfill \forall n\in \{1,...,N_k\},\forall k\in \{1,...,K-1\}\end{array}$$

(9)

Other variations of (9) can be found in the literature and include different regularization techniques, NCP functions, and objective penalties [47]. Overall, this Section provides a general mathematical framework for embedding NN models from various ML libraries into a non-linear program. Open source code for the tool OMLT can be found online (github.com/cog-imperial/OMLT, accessed on 11 July 2023) for implementing all of the discussed formulations in Python.

6. Results

We apply this overall framework to three case study examples: IEEE-118 system with 6 considered contingencies, IEEE-118 with 33 contingencies, and IEEE-300 with 10 contingencies. IEEE-118 has 99 loads, 54 generators, and 186 branches. IEEE-300 has 201 loads, 69 generators, and 411 branches. Increasing the number of buses affects the size of the nominal state model for both baseline and hybrid approaches, while increasing the number of contingencies affects the size and complexity of the security region we want to represent with the NN surrogate.

6.1. Sampling and NN Training

Below, we discuss the training specifications and results with respect to the feasibility classifiers and their accuracy. An NN with two hidden layers and 20 neurons is trained using ADAM in Tensorflow. The output layer is a softmax function, which converts the outputs to a probability between 0 and 1. This is commonly used in NN architectures used for binary classification. Specifically, we plot the receiver operating characteristic (ROC) curve, which is useful for showing the expected trade-off between the conservativeness and accuracy of classification models. An ideal ROC for a classifier would show a right-angle in the upper left corner corresponding to a high true positive rate and a low false positive rate. While a high true positive rate provides the most confidence in grid security, the accuracy trade-off would be important to tailor to the specific grid application.

These test points are drawn from the same distribution as is described in Section 4, so they are closer to the boundary and, thus, more difficult to classify. We show the effect of doubling the training dataset on accuracy for IEEE Case 118 with six contingencies. Figure 6 shows the model performance for testing data points with differing amounts of training data available: 5500 and 2750 training points, respectively. For an $\alpha$ value of 0.5, the model accuracy is 89% with the larger training set compared to 81% with the smaller set. One advantage of our approach is that sampling and fitting can be performed once and offline, so this would not increase the computational cost of the optimization formulation that needs to be solved routinely, but there are diminishing returns with further samples. Overall, the sampling costs for the Case 118 take, on average, 0.4 s per sample and the Case 300 takes, on average, 1.2 s per sample. The networks are trained for 5000 epochs, with restoration of the best weights for validation accuracy.

We observe in Figure 7 (blue line, more constrained Case 118) that, when increasing the number of contingencies, the classification boundary becomes harder to accurately predict with the same amount of points. In this case, we must increase our training set to 11,000 points in order to achieve a test accuracy of 85%, again using a two-layer NN with 20 nodes in each layer. Figure 7 shows the classifier performance for this highly constrained case study. The overall shape of the ROC is highly symmetric due to the balanced dataset provided by the sampling approach and shows that secure and insecure points are equally difficult to classify.

In Figure 7 (red line, larger bus system Case 300), we show the results for using our methodology on the IEEE Case 300. As the dimensionality of the problem is increased, the training set is increased to 25,000 points and the hidden layers are increased to 50 nodes per layer. The accuracy for the test points is found to be 81%. In this case, the training data accuracy is less ideal than the previous cases as it only reaches an accuracy of 96%. Larger NN models are able to increase this training accuracy as universal approximators; however, there is an important trade-off between model complexity and the resultant hybrid optimization results, which is discussed below.

6.2. Optimization Results and Comparison of Hybrid versus Extensive Formulations

After we train the security surrogate, we embed it as a constraint into the original ACOPF formulation, which is a non-linear and non-convex problem. The final formulation is a hybrid model (i.e., comprised of both physics-based and data-based constraints) described by (4a)–(4f). First, we show a comparison of our method and the traditional extensive SCOPF for the 118 case study with six included contingencies.

In

Table 3. Comparison of SCOPF Formulations: Case 118 (6 Contingencies).

Formulation	MAE ($\mathit{x},{\mathit{x}}_{\mathit{sc}}$)	Avg CPU [s]	Variables
SCOPF	-	5.27	6502
SI: tanh (full-space)	0.85%	0.40	1334
SI: tanh (reduced-space)	0.85%	0.32	1172
SI: relu	0.76%	0.61	1354

, we show a complete comparison of Formulations (1a)–(1g) and (4a)–(4f), including various NN formulations, as described in Section 5. Here $MAE(x,x_{sc})$ refers to the mean absolute error between the solution vector found with the hybrid approach and the corresponding solution vector with the full SCOPF formulation, presented in Section 3.1. These values are normalized to represent the average percent error across each variable and unique solution. All hybrid formulations result in a small difference compared to the extensive solution when comparing optimal generator set points for various load profile inputs. This comparison allows us to quantify how close the hybrid optimization method gets to the baseline with respect to optimality. The baseline SCOPF solution is found by solving the full problem with all relevant contingencies using IPOPT. As the NN architectures have similar accuracy, it is not surprising that they perform similarly with respect to the fidelity of the solution. Furthermore, all the hybrid formulations achieve a significant reduction in CPU time (8–16×) compared to the extensive formulation, which is our primary motivation. We see some differences amongst these formulations in variable size and time, but would expect the reduced space formulation to further distinguish itself as the size of the network increases.

Next in

Table 4. Comparison of SCOPF Formulations: Case 118 (33 Contingencies).

Formulation	MAE ($\mathit{x},{\mathit{x}}_{\mathit{sc}}$)	Avg CPU [s]	Variables
SCOPF	-	39.03	43,262
SI: tanh (full-space)	1.95%	1.40	1334
SI: tanh (reduced-space)	2.63%	1.21	1172
SI: relu	4.32%	1.13	1384

, we show the scalability of the method to highly constrained problems, where we consider 33 separate line contingencies.

For this case, the variable size of the problem increases significantly for the extensive version, while the hybrid models stay much closer to the smaller case study above. The results show that the extensive formulation scales poorly as more contingencies constraints are added, increasing the problem variable space by 6x and the average CPU time by a similar amount. The hybrid formulation presented maintains the same problem size as in the smaller contingency since the embedded networks are of equal size. Although the CPU time is increased, due to this being a harder optimization problem with a tighter feasible space, it scales much better than the traditional formulation and allows for secure solutions in fractions of the time (20× speedup).

Finally, we present the results for the IEEE 300 Case study in

Table 5. Comparison of SCOPF Formulations: Case 300 (10 Contingencies).

Formulation	MAE ($\mathit{x},{\mathit{x}}_{\mathit{sc}}$)	Avg CPU [s]	Variables
SCOPF	-	54.48	26,434
SI: tanh (full-space)	9.9%	7.24	2949
SI: tanh (reduced-space)	9.9%	1.99	2618
SI: relu	9.7%	1.95	2989

. A similar pattern is seen with respect to the CPU time with about an order of magnitude reduction. A higher error is seen between the full SCOPF solution and the hybrid approximation, but still less than 10%. As with most data-driven approaches, increasing the problem dimensionality requires further sampling and considerations of the model size and complexity. Some prediction error is expected, but the method proves to be highly informative to the ACOPF solver when constraining the solution space to the secure region of the NN prediction. Importantly, this formulation also maintains the nominal case variables for the ACOPF problem allowing for guarantees on feasibility of the pre-contingency space. This allows for the solution of the non-linear, non-convex ACOPF formulation without relaxations.

With respect to the NN representation, we see that full-space, reduced-space, and ReLU with complementarity, all have similar accuracy in their solutions ($MAE(x,x_{sc})$). This is expected as these networks were trained on the same data with equivalent hyperparameters. In terms of the variable size, the reduced-space formulation is the most compact but the full-space and ReLU are both much smaller than the extensive formulation. There is a small but significant improvement in CPU time by using the reduced space formulation across each case. These differences may become more exaggerated as the size of the NN increases.

7. Discussion and Conclusions

Overall, we have provided a general approach to representing non-linear feasibility regions with NN models and integrating these models back into challenging optimization problems to reduce online computational costs. We present promising results with respect to the accuracy of NN-based classifiers for security, especially when carefully collecting samples of high value to our classifier using optimized-based sampling. The model-based sampling approach proves to be much more effective at characterizing non-convex boundary functions, such as feasibility, than existing space-filling designs of experiments. The positive results for this sampling approach motivates future studies looking into how it might perform in other modeling contexts that include feasibility functions. Mapping the feasibility space is useful in many engineering problems, including studies of system operability and flexibility, that arise in several industrial processes. We have shown how NNs can be included as algebraic constraints into the baseline AC optimal power flow problem, resulting in tractable hybrid models. We have observed that the hybrid model can be solved very fast (5×–20× speedup) and still give similar results to the extensive formulation. The facility and adaptability of the NN formulations discussed, along with open source software, allows for many future studies that integrate data-driven functions with first-principles models.

As seen by the results, the ML classification error increases with the dimensionality and the number of contingencies. This can be tackled by increased sampling, and use of adaptive sampling techniques that focus sampling in regions that balance exploration and exploitation of the feasibility boundary. The main advantage of this approach is that all of the sampling effort can be performed only once and offline. Moreover, as the size of the problem increases, it is expected that the size of the ML model will also increase. This may lead to increased CPU costs for optimization of the hybrid formulation, especially if dense NN architectures are used. This risk can be mitigated by taking advantage of modern sparsification techniques, as well as reduced-space formulations and customized NLP algorithms, to optimize NLP formulations with embedded ML models [22]. Finally, as decomposition and parallelization techniques advance, this will lower the optimization times for extensive formulations with the use of high-performance computing. However, an approach for mapping complex feasible regions using ML models may have many applications beyond the one described here, such as fast computation and visualization of security feasibility, or for sensitivity analyses to identify critical contingencies.

There are several future directions that may be pursued that could further improve and extend this work. The ML model errors can be more accurately quantified using verification approaches. This is an important area of research that can provide bounds on the worst-case predictions of NN models, which would be useful to guarantee the accuracy of trained models and to promote their adoption by system operators. These bounds are especially informative in cases outside of the training data regime where NN extrapolation errors may be much higher. These studies also may assuage ethical/implementation challenges surrounding the black-box nature of NNs and the lack of formal guarantees of optimality. Network sparsification techniques could lead to equally accurate networks with reduced model complexity. This may be an important way to further speed up hybrid solutions, as sparser NN functions decrease the variable size of the problem. In this work, we have used and compared different forms of feed-forward NNs, but, for larger or more complex feasibility functions, other ML techniques can be considered. For example, an interesting future direction is to look at more complicated neural network architectures and training routines that can embed system physics into the surrogate. While this has been shown to improve extrapolation in regression models, no current work has looked at physics-informed neural networks for black-box-feasibility. One other future direction is to combine an ML screening model that can target important contingencies a priori to the sampling and hybrid solution method. This may allow for many low-risk contingencies to be eliminated. Many of these directions must be considered when scaling up the approach even further to larger case studies.