Next Article in Journal
Optimizing Hybrid Microgrid Power Systems for Local Power Distribution: A Study on Combined Photovoltaic and Fuel Cell Systems in the Philippines
Previous Article in Journal
Impact Assessment of Hydrate Cuttings Migration and Decomposition on Annular Temperature and Pressure in Deep Water Gas Hydrate Formation Riserless Drilling
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 16
Issue 16
10.3390/en16165904
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Overview of Intelligent Inverters and Associated Cybersecurity Issues for a Grid-Connected Solar Photovoltaic System

by
Sai Nikhil Vodapally
and
Mohd Hasan Ali
*
Department of Electrical and Computer Engineering, The University of Memphis, Memphis, TN 38152, USA
*
Author to whom correspondence should be addressed.
Energies 2023, 16(16), 5904; https://doi.org/10.3390/en16165904
Submission received: 26 June 2023 / Revised: 3 August 2023 / Accepted: 7 August 2023 / Published: 10 August 2023
(This article belongs to the Section A: Sustainable Energy)
Browse Figures
Versions Notes

Abstract

:
The major problem associated with the grid-connected solar photovoltaic (PV) system is the integration of the generated DC power into the AC grid and maintaining the stability of the system. With advancements in research on these PV inverters, artificial intelligence (AI)-based control models are replacing the existing linear methods. These smart PV systems are prone to a variety of attacks, ranging from physical attacks on the PV plants to data integrity attacks and communication-based attacks. This paper provides an overview of the cybersecurity issues with smart PV inverters, their impacts on the grids, and control methods that exist to detect and identify cyber-attacks on a smart PV grid system. An extensive bibliography is provided on grid-forming and grid-following inverters with a variety of control techniques like Proportional–Integral–Derivative (PID) control, fuzzy-based control, and their performances under different fault situations. Multi-level inverter design approaches with various intelligent control techniques to overcome switching failures and other system faults are reviewed. Moreover, some recommendations for future research on intelligent inverters for grid-connected PV systems are proposed. This work will benefit researchers, scientists, and engineers who are working in the field of intelligent inverters for the grid-connected PV system.

1. Introduction

With the reduction in the material cost of making solar photovoltaic (PV) panels and the sustainability of solar energy, the usage of PV systems has been increasing in the recent past across the globe [1,2,3]. These are extensively used in distributed power generation and exclusively in stand-alone power systems [4]. Many equivalent circuit representations of solar panels exist in which single-diode and two-diode models are widely used [5]. The voltage and current ratings of these solar PV panels depend on the number of cells connected in series and parallel [6]. Moreover, a battery energy storage system (BESS) in conjunction with the PV system is used to maintain the stability of the system during power fluctuations in the PV system, thereby delivering constant power to the load [7,8,9,10]. The ramp rate control algorithm combined with BESS is the most commonly employed algorithm by solar PV plants to maintain stability and to better manage energy [11,12].
The DC energy obtained through the PV systems is converted and fed to an AC system with the help of converters. One way of achieving this is by first using a boost converter for increasing the voltage and an inverter for converting this DC voltage to AC [13,14,15]. The boost converter is controlled by the maximum power point tracking (MPPT) algorithm, where it tracks and operates at the maximum power point (MPP) of the connected PV system [15]. Though many MPPT algorithms are proposed, Perturb and Observe (P&O), Incremental Conductance (IC), and Constant Voltage (CV) algorithms are the most popular [16]. It is noteworthy that the IC algorithm has better control over the MPP in comparison with the other common MPPT algorithms and has smaller voltage oscillations when compared with the P&O algorithm [17,18]. Non-linear controllers like fuzzy logic controllers and artificial intelligence (AI)-based controllers can be used to accurately track the MPP [19,20,21,22,23].
Most of the DC to AC converters are controlled by using phase-locked loops (PLL), where the controllers are provided with the magnitude, frequency, and phase angle of the grid voltage. This type of control logic-based inverter is generally known as grid-following inverter (GFLI). The control method for these inverters is based on the current injection to the grid. Therefore, this type of voltage-source inverter (VSI) simply acts as a current source with a large impedance to the grid [24]. The major disadvantages of GFLIs are that they are found to become unstable during the off-grid mode of operation or weak grid conditions and affect the inertia of the total system when connected in a large amount [25,26]. Also, these types of inverters lack the capability of handling the system during blackouts and are not able to restore the system after faults or cyber-attacks [27]. Several control methods are proposed to overcome the drawbacks of GFLIs in [28,29,30,31]. The other type of inverter is the grid-forming inverter (GFMI), where the control techniques of these inverters are designed to control the output voltage and frequency without relying on the PLL [24,25,27,32,33,34,35]. They are capable of black starting the system independently by forming the voltage and frequency during a blackout [27,36]. Typically, GFMIs are not supposed to use the PLL, but recent research has focused on using the PLL for the frequency and angle references to operate in parallel and in synchronization with the grid [27,32,35].
Also, a cascaded multi-level inverter (MLI) design approach has been used to make the system fault-tolerant, and various control strategies for it have been proposed to improve system stability and power quality and to reduce harmonics distortions [37,38,39]. MLIs are a system design approach where the output voltage signal of these converters is built by stepping through many voltage levels. Different voltage levels in the output signal can be obtained by connecting capacitors across the DC bus. When compared with a conventional two-level inverter, the output voltage generated from these MLIs has reduced harmonic distortions at a given frequency [37]. The greater the number of levels, the less harmonic content there will be. A comparative study of the available types of MLIs is presented in [38,39].
With the use of machine-learning (ML)- and deep-learning (DL)-based algorithms, the smart grids systems are smart enough to handle all the tasks autonomously, like tracking the MPP, handling the faults, maintaining the stability, and so on [40,41,42]. To implement these AI-based systems, these smart grids need a large number of Internet of Things (IoT) devices that are continuously exchanging information with the supervisory control and data acquisition (SCADA) system for remote calculation. Various wired or wireless communications like power line communication (PLC), 2G, 3G, and 4G [43,44,45,46,47,48] are used for data transfer between the systems. These communication lines are prone to cyber-attacks that can lead to catastrophic disasters. So, there is a need to protect these communications lines and devices to operate the smart PV system safely. Moreover, a PV inverter is comprised of power electronic devices that exhibit low inertia. When many PV inverters are connected, the overall inertia of the grid is reduced, thereby making these grids more susceptible to faults. All these factors challenge researchers to develop smart, intelligent inverters that are capable of following the grid and forming the grid when needed [35,49]. An intelligent inverter incorporates AI and smart control strategies to optimize the operation, enhance efficiency, reduce harmonics, handle various faults, and adapt to changing environments. Unlike traditional inverters that merely perform basic DC to AC conversions, intelligent inverters utilize sophisticated control algorithms and data-driven approaches to improve their performance.
Most of the literature reviews available on intelligent control of PV systems have been focused on developing algorithms and techniques for smooth control of GFLI and GFMI. In [50], a review of AI applications is discussed with a focus on converters and their faults, but the authors have not mentioned the cybersecurity-related issues associated with intelligent converters. In [51], cyber security-based issues in the control of grid-tied power electronic converters have been discussed. In [52], state-of-the-art smart grid cybersecurity architectures have been discussed without a clear picture of intelligent techniques for controlling the converter.
Based on the above background, this paper presents an extensive overview of GFLI and GFMI (and their associated controllers) of a grid-connected PV system. An in-depth review of the different control methods proposed for both GFLI and GFMI and their advantages and disadvantages are also provided. Various control designs to overcome the faults in a grid-connected solar PV system and intelligent control methods for the inverters that can handle these faults are provided. A review of the cyber-attacks on a grid-connected PV system and their impacts are discussed. Also, a review of the detection and identification methods of these cyber-intrusions proposed by researchers is provided. Some recommendations for future research on intelligent inverters for grid-connected PV systems are proposed. It is hoped that the paper will help readers, researchers, and engineers by serving as a basic reference for developing future technology in the field of intelligent inverters for the grid-connected PV system.
This paper is organized as follows. Section 2 discusses the GFMIs, GFLIs, and their control methods. In Section 3, intelligent control methods for smart inverters are presented. Section 4 reviews the cybersecurity issues associated with smart PV inverters. Section 5 provides recommendations for future research on intelligent inverters for PV systems. In Section 6, the conclusions of the paper are presented.

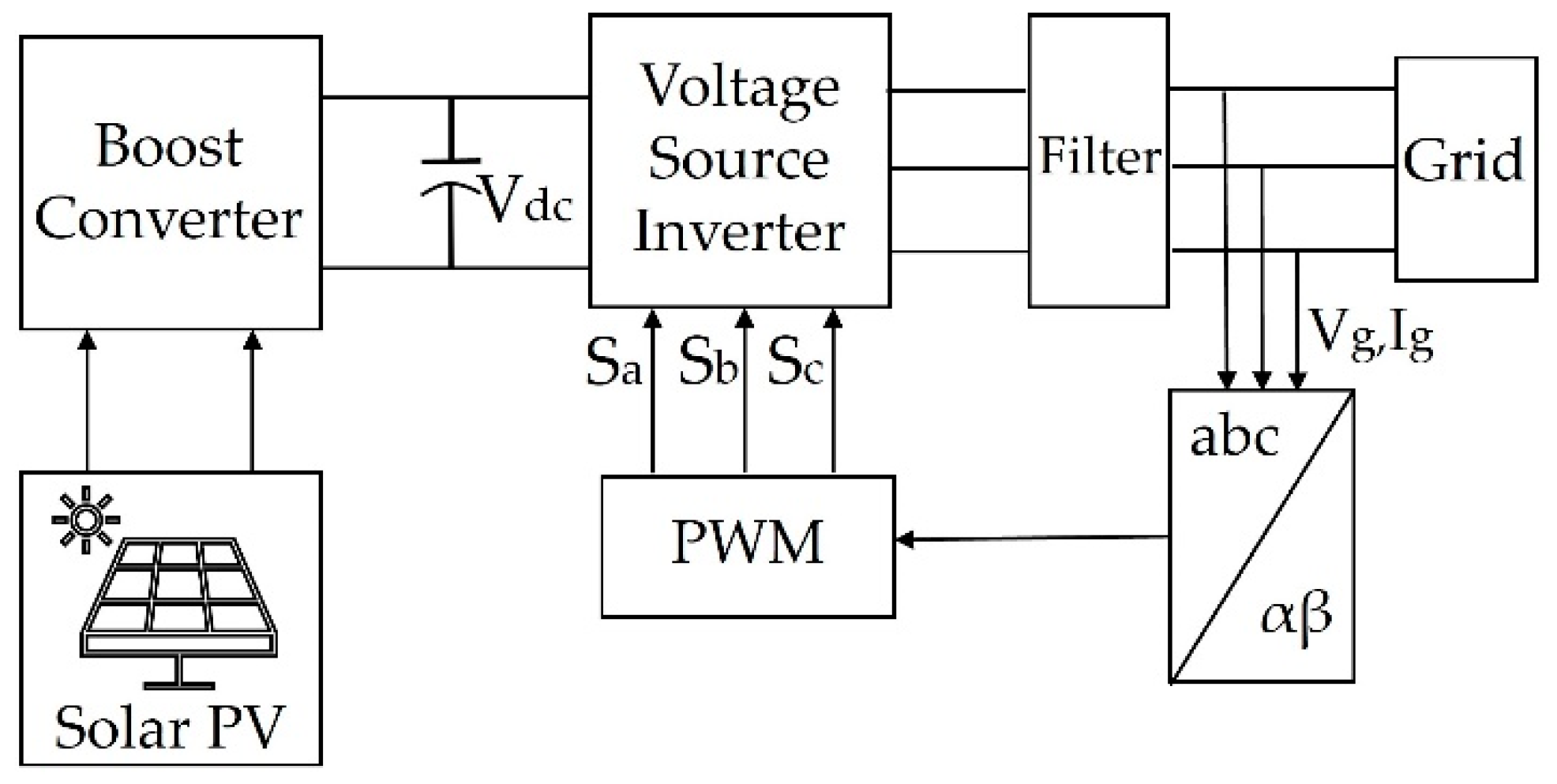
2. Grid-Following Inverters (GFLIs) and Grid-Forming Inverters (GFMIs) of PV Systems

PWM-based inverters are employed to convert the DC energy from PV panels to AC energy. The most common pulse width modulation (PWM) technique in use is sinusoidal PWM (SPWM), where the output pulses generated are in the form of a sinusoidal signal. The harmonics in the output voltage waveform depend on the frequency of the carrier signal (fc) and the modulation index. A detailed review of the effects of modulation index and fc is provided in [53]. For a closed-loop system, these reference signals are generated based on the feedback from the output voltage signals. These inverters can be interfaced either in parallel to or in series with the grid. These topologies with control methods are depicted in [54,55]. The grid interactive intelligent inverters need to be smart enough to handle the faults, should be self-healing, should adapt to the situation, and should be able to defend themselves against hacking [56]. Based on the control approach, whether they are independent or dependent on the utility grid, inverters can be broadly classified into two main groups such as GFMIs and GFLIs. An overview of the available control schemes for the GFLIs and GFMIs is given below.

2.1. Grid-Following Inverters

The primary function of the GFLI is to inject the generated power produced from the DC system into the AC grid and to provide control over active and reactive powers. The voltage magnitude, its frequency, and the phase angle (θ) of the synchronous machines-based utility grid are used as a primary input for the d-q reference frame-based current control technique to control active and reactive powers by employing PLL and current control loops. These inverters can regulate the current quickly and depend solely on the AC grid to maintain the voltage magnitude and frequency stability, as represented in Figure 1. Several methods are proposed to implement the GFLI control techniques. A brief review of these control methods is provided below.

2.1.1. Conventional d-q Frame-Based PI Control Technique

Conventional d-q frame-based controllers have two control loops, an active and reactive power control loop and the DC bus voltage control loop [57]. These two loops help maintain a constant stable DC bus voltage and control the active and reactive power feeding into the AC grid. This is illustrated in Figure 2.
The PI controller is used to regulate the current in the control system. Though the PI controller’s start-up transient is very fast, due to the disadvantages of unregulated steady-state errors, researchers are focusing on other control methods. A proportional resonant (PR) control for a three-phase inverter is proposed in [58] to reduce the steady-state errors at the fundamental frequency. A novel proportional complex integral (PCI) control is also proposed in [59] in theoretical comparison with the PI and PR control methods under balanced conditions.

2.1.2. PLL-Less Modified Voltage-Modulated Direct Power Control (VM-DPC) Method

The major drawback of the conventional d-q frame-based control techniques is that it relies on PLL for the point of connection (PoC) voltage, its frequency, and phase angle. Because of its non-linear nature, which causes unstable damping modes, the PLL cannot be used during weak or ultraweak grid conditions, which has driven researchers to focus on PLL-less control techniques for GFLIs [30].
The most common approach is based on the Direct Power Control (DPC) method, where the Voltage-Modulated DPC (VM-DPC) has several advantages in comparison with the other available DPC-based control methods. But the only drawback with this method is that it uses PoC voltage to control the injection of active and reactive powers to the grid. A modified VM-DPC is proposed in [28], which does not use a PLL or PoC voltage. It uses the GFLI output voltage and current to provide a decoupled real/reactive power control. This makes the proposed system work in a weak and stiff grid.

2.1.3. PLL-Less Active and Reactive Control Method

A single loop, PLL-less active and reactive power control for a single-phase GFLI is proposed in [30]. In this method, the PI controller is used to generate feedback terms from the active and reactive reference values, which are, in turn, used to find the error dynamics of the powers to calculate the modulation index. Additional conditions for maintaining steady-state voltage stability with weak resistive and inductive grids are provided. Even though this method is less complex to implement and can be easily implemented in weak grids, it lacks a control loop for DC bus voltage.

2.1.4. Resonance Suppression in Weak Grids Based on the Predictive Control Method

An LCL filter is used in series with the inverters to reduce the harmonics generated in the output signals. One of the major problems associated with the weak grid is the resonance of this LCL filter which affects the stability of the inverters. Based on the predictive control, an effective resonance suppression in weak grids is proposed in [29]. A dual-mode adaptive model predictive control (MPC) is proposed to toggle between the inverter current feedback (ICF) and the grid current feedback (GCF) for resonance suppression based on the operating conditions. This proposed model can also be used in stiff grids or ultra-weak grids. The only drawback of this control method is that it uses the MPC-based control method, which results in excessive computations [28].

2.1.5. Power Synchronization-Based Control Approach for High Voltage DC

In a weak grid, GFLIs will not be able to maintain the stability of the system as they are dependent on PLL. This is one of the major drawbacks of the GFLIs, as they are inoperable in weak/ultra-weak grid conditions. Though several PLL-independent methods are proposed for GFLIs [28,30], a power-synchronization-based control method with backup PLL is proposed in [60], where a high amount of DC power is available in the system. In this method, a fundamental control loop based on a power-synchronization control approach is described. But due to its inoperable condition during the severe faults on the AC system, a backup PLL loop with PI control is used. Based on the operating conditions, a selector block is designed to switch between these loops. This control method can be used for any grid-connected converter and can also maintain voltage stability in weak/ultra-weak grid conditions.

2.1.6. Modified Instantaneous Active Reactive Control (IARC) Method for Unbalanced Grid Conditions

Imbalances in the grid are caused due to short circuit faults, which affect the performance of the GFLIs. The unbalanced grid conditions cause ripples in the DC-link voltage with a frequency of twice the line frequency. Various control methods are proposed for GFLIs, such as Instantaneous Active Reactive Control (IARC), Instantaneously Controlled Positive Sequence (ICPS), and Positive–Negative Sequence Compensation (PNSC) to eliminate these ripples. Though the IARC method has proven effective in controlling the DC-link voltage and is able to eliminate the ripples generated, it does not eliminate the 3rd harmonic distortions on the output current. A modified IARC method to overcome the drawback of the conventional IARC method is proposed and an extensive comparison of the other available methods is provided in [31]. A feed-forward scheme for the conventional IARC method is suggested to eliminate the 3rd harmonic distortion components.

2.2. Grid-Forming Inverters

The primary control schemes of the GFMIs are based on stabilizing the magnitude and frequency of the output voltage signal. Typically, the output electrical frequency of synchronous machine (SM)-based power sources is dependent on their rotational speeds, which is similar to a grid-forming source controlling its frequency and magnitude [61]. An overview of GFMIs, their ideal characteristics, challenges, drawbacks in implementation, and a commercial view are presented in [33]. A typical structure of GFMI is represented in Figure 3.
GFMIs have a fault-ride-through capability as they are completely independent of the grid voltage and frequency and can generate the voltage at synchronous speed autonomously. A detailed research roadmap on GFMIs is discussed in [27], and an in-detail review of the types of control methods in GFMIs, their control schemes, implementation, and real-world applications are provided in [32,34,62,63,64,65]. A review of some of the control methods for special conditions is provided below.

2.2.1. PLL-Free, PI Control-Based Grid-Forming Control Method

Unlike GFLIs, which depend on PLL for the magnitude, frequency, and phase angle of the grid, GFMIs are generally independent and autonomous in maintaining the magnitude and frequency of the output signal. They must be robust with respect to the transients in the system, and they should be able to control the frequency and the magnitude at the Point of Coupling (PoC). One of the major problems with GFMIs is the overcurrent issues during load changes and unusual conditions [61].
A PLL-independent, PI control-based grid-forming control method with current limitation control is proposed in [25]. Results from the experimental setup and simulations are presented for different test cases. Moreover, an adaptive inertia constant algorithm is also proposed to provide system stability in case of any large events.

2.2.2. Matching of SM Control Method

The main goal of the GFMIs is to mimic the operational characteristics of the SMs. Based on the structural similarities between the SM and GFMIs, a novel control strategy is proposed in [66], which uses the DC-side measurements to drive the frequency of the converter with a virtual oscillator to match the characteristics of the SM. Simulation results are shown for a three-phase system to prove the proposed model is yielding the predicted behavior.
An in-detail background description of the proposed model in [66] with necessary mathematical equations and models is provided in [67]. It also addresses the problems in designing control strategies for GFMIs for weak grid conditions, as the utility grid is too weak to regulate the frequency of the system.

2.2.3. Dynamic Phasor-Based Modelling (DPM) Approach for Stability Analysis

SMs are well known for their robustness and comparatively high-inertia nature. When the inverter-based microgrids are connected to the system, it affects the stability of the system as the power converters may show low-inertia nature. So, the calculation of the system’s overall stability in designing and modelling the control parameters is a key factor in inverter-dominated systems. A small signal model analysis can be used to estimate the dynamics and stability of the system [68]. But the major drawback of this small-signal model analysis is the increase of complexity in estimating the stability as the number of converters connected to the system increases. To overcome this problem, a novel modelling strategy is proposed in [69] based on dynamic phasors to perfectly estimate the stability parameters of the system. This DPM approach is discussed for droop-controlled inverters. A comparison of the proposed method with the other analysis methods is also provided. Though this proposed approach is accurate and less complex than the reduced-order small signal analysis for the multi-inverter-based system, the complexity of the proposed approach increases if the microgrids have different generation sources integrated into the grid.

2.2.4. Tuning of Power Converter through AI

Due to the low-inertia nature of the power converters, when they are integrated into the microgrid system, they affect the stability of the system. Among them, rotor angle stability is one of the major concerns. To reduce these electromechanical oscillations that occur through the integration of these converters, power system stabilizers are used to dampen oscillatory modes for a small zone of operation level. An AI-based power oscillations damper for GFMIs is proposed in [70] by increasing the gain of the power control loop at the oscillation frequency. In this method, a random forest (RF)-based decision-tree AI algorithm is used in which the results from the simulations are used to train the RF-based AI algorithm in Python using the scikit-learn package.

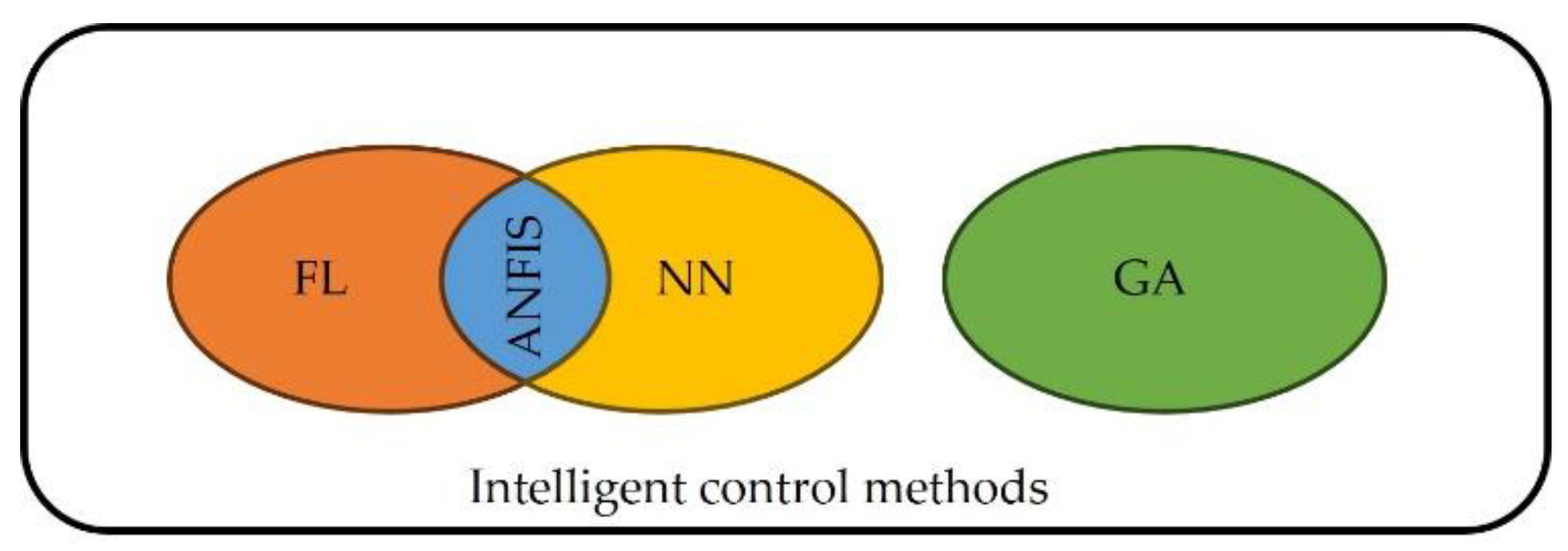
3. Intelligent Control Methods

With the advancements in intelligent non-linear control methods, control structures based on fuzzy logic (FL), neural networks (NN), neuro-fuzzy, and genetic algorithm (GA), as shown in Figure 4, have been implemented for the inverter structures to accomplish tasks that may not be possible through the traditional control structures. With the new research trend in the development of AI-based control approaches for grid-connected PV systems, many new control approaches can be developed. Integration of non-linear controllers in combination with artificial NN (ANN) can provide very good dynamic performance for the controller. These ANN-based approaches can be used to track the MPP, optimize the PV power output, and reduce harmonic distortions [41,71]. A review showing that a few of the authors proposed intelligent control methods for the inverters is presented below, along with a quick summary of control structures presented in Table 1.

3.1. Fuzzy Logic (FL)-Based Control Strategies

A fuzzy logic controller (FLC) is the simplest type of non-linear control system based on fuzzy logic or fuzzy rules that can handle uncertainty and imprecision in decision making. Due to the fast and better responses, FL-based controls are used for the converters in AC and DC systems. Many authors worked on FL-based intelligent control strategies not just pertaining to the normal operation of the system but for handling the faults more quickly and accurately than the traditional controllers [72]. Many FL-based approaches were presented to optimize the power in PV systems [19,20]. A novel FL-based inverter control was proposed for a three-phase grid-connected solar PV system in [73], which was tested on an experimental testbed under different fault scenarios using a digital signal processor (DSP). A novel FL-based control approach is also proposed for MLIs in [74] for a single-phase PV system. In this method, an FL-based algorithm is designed and implemented using a field programmable gate array (FPGA) module. The usage of FPGA helps in controlling the converters at a very high speed. In [75], the authors proposed a fuzzy PQ inverter control strategy, which enhanced the low-voltage ride-through capability of the grid-connected solar PV system.
Table 1. A review of intelligent control methods for inverters.
Table 1. A review of intelligent control methods for inverters.
MethodologyAdvantagesLimitationsRef.Type of ControllerMajor Findings
FLSimplest non-linear controllerAssigning weights to fuzzy rules to achieve the desired output[73]Novel FL-based inverter controlLower harmonic distortion than conventional PI-based inverter controllers
[74]Novel FL controller for MLILower harmonic distortions, number of levels and phases can be modified without significant burden, reduces output filter dimensions
[75]Fuzzy PQ inverter controlEnhancement of low-voltage ride-through capability
NNAbility to learn and approximate almost any complex relationNo definite rules in determining the number of hidden layers and cells in those layers[76]ANN-based SVPWM for 3-level inverterSimple and quick computations
[77]MPC-based ANN controller for 3-phase inverterReduces the computational cost and reduces the THD when compared to traditional MPC
[41]ANN controller for 15-level MLIReduces THD by adjusting switching angle
[78]Deep CNN-based control for 3-phase inverterFault diagnosis effectively identifies noise signals without any additional device
[40]ANN-based detection and mitigationConnects an auxiliary inverter to the system for fault mitigation
[42]NN-based faulty switch detection and mitigationNN decided to isolate faulty switch or to continue operation based on fault type
[79]Cascaded feed-forward NN based on droop controlNon-linear relations between input and output can be replaced, while linear relations stay intact
ANFISHas the learning capability of NN and human-like inference ability of FLHigh training time and tend to overfit[80]Neuro-fuzzy control for grid-connected inverterFaster dynamic response and better performance than PI controller
[81]ANFIS controller for 5-level MLI of grid-connected solar PV systemReduces the THD of output signal
[82]ANFIS for MPCParameter estimation of MPC using ANFIS
GAEfficiently explores large parameter space and finds the optimal parametersHigh convergence speed[83]GA for NN-based PID control schemeOptimizes the initial weights of NN to reduce the suppression time and overshoot
[84]GA-based controller for grid-connected solar PV inverterOptimizes the inverter structure considering the power losses, its volume, and its cost
[85]GA for optimization of PI for grid-connected inverterOptimizes the PI control parameters to improve active power control

3.2. Neural Network (NN)-Based Control Strategies

One of the major advantages of the NNs is their ability to learn and approximate almost any complex, non-linear relation between an input and output. They possess parallel processing capabilities and non-linear and adaptive structures. Moreover, they can be designed without being reliant on the system parameters. This motivated researchers to adapt the concept of NN for complex inverter control structures, which can significantly reduce the computation burden and operate the inverter at a faster rate. In [76], a novel ANN-based space vector (SV) PWM technique for the three-level inverter is proposed. This proposed method can overcome the drawback of the traditional SVPWM, where the control structure requires complex and time-consuming computations. Another NN based on model predictive control (MPC) has been proposed in [77]; this ANN based on MPC can generate the switching signals for the inverter without the need for any mathematical model and significantly reduces the computational cost. Furthermore, the proposed method has significantly reduced the total harmonic distortion (THD) of the inverter output signal when compared with the traditional MPC. An ANN technique to reduce the harmonic distortions is presented in [41] with other intelligent techniques like genetic algorithm (GA) and particle swarm optimization (PSO) for a 15-level MLI. In the ANN-based approach, datasets with different voltage levels and switching angles are used to train the AI model. Once trained, the model is used to control the output voltage of the inverter to reduce the harmonic distortions by adjusting the switching angle.
NNs can also be helpful in identifying and detecting faults in inverters. Many approaches like power probe units (PPU) and differential protection strategies exist for identifying and locating the type of fault that occurred to take the right action to prevent the system from further damaging [86]. These methods use the mathematical model of the system, which increases the system complexity due to their non-linear factors. An AI-based approach can help in identifying, detecting, and diagnosing these faults avoiding mathematical complexity. A deep convolution NN (CNN) with global max pooling has been proposed in [78] for the fault diagnosis in a three-phase inverter. This CNN-based strategy has proven effective in identifying noise signals accurately without the use of any additional noise reduction processing. The ANN-based control approach is proposed in [40] to detect and mitigate the faults of MLIs in a solar PV system. In this proposed approach, 70% of the 1500 datasets obtained from simulation and experimental setup of 20 different types of faults are used to train the AI-based model using an advanced back propagation (BP) algorithm to identify the fault. During the fault mitigation process, an intelligent control algorithm is used to connect an auxiliary inverter to the system. Based on the output voltage, the AI-based model will be able to identify and locate the fault, and the auxiliary inverter setup will be used to mitigate it. An AI-based neural network (NN) classification is proposed for a cascaded MLI system in [42]. Data obtained from the simulations and the experimental setup are used to train the model. Based on the output voltage from the cascaded MLI, the fault and its location are detected. A corrective action is taken by the AI model to either isolate the faulty switch or to continue to operate the system during the fault based on the fault type. This AI-based approach takes about six cycles to detect and mitigate the open-switch and short-switch faults and about nine cycles to mitigate the short-switch fault. This method ensures a smooth and continuous operation of MLIs during switching device failures.
NNs can also be combined together to form cascaded NN structures in the traditional control structures. With the help of cascaded NNs, the non-linear relations between input and output can be replaced by multiple neural networks leaving the linear relations intact. A cascaded feed-forward NN (CFNN) based on droop control is proposed for a bidirectional inverter in [79], which is evaluated for different operational scenarios using a real-time power hardware-in-the-loop (PHIL) experimental testbed. This PHIL testbed is developed using a MATLAB/Simulink environment and Opal-RT systems. The experimental results indicate the effectiveness of the system and also reduce the computational burden.

3.3. Adaptive Neuro-Fuzzy Inference System (ANFIS)-Based Control Strategies

One of the drawbacks associated with fuzzy-based control is the assigning of weight to the fuzzy rules to achieve the desired objective or output. Moreover, NNs pose limitations, such as not having any definite rules in determining the number of hidden layers, the number of cells in these layers, and not being able to solve steady-state errors [87,88]. These drawbacks can be overcome by using an adaptive neuro-fuzzy inference system (ANFIS) introduced by Jang in 1993 [89]. These neuro-fuzzy controllers are derived by blending the strengths of FLCs and NN control methods. It combines the NNs’ capabilities of learning and parallel processing with the human-like inference abilities of FL. This results in more powerful and adaptive control systems. A MATLAB/Simulink simulation of a neuro-fuzzy control for a grid-connected inverter is proposed in [80], where the simulation results indicated that the developed ANFIS model has a faster dynamic response and better performance than the conventional PI controller. In [81], an ANFIS control model is developed for a three-phase five-level MLI of a grid-connected solar PV system. This developed model is evaluated on an experimental testbed using FPGA modules, where the results show the effectiveness of the ANFIS model in reducing the THD of the output signals. An ANFIS-based control strategy for a novel transformerless inverter is proposed in [90]. In [91], an adaptive neuro-fuzzy control model is proposed for the inverters in a microgrid, and in [82], an ANFIS model for parameter estimation for MPC is proposed.

3.4. Genetic Algorithm (GA)-Based Control Strategies

The concept of genetic algorithm (GA) can be employed for inverter control strategies to optimize the parameters and settings for better performance of the system. GA offers the advantage of efficiently exploring a large parameter space and finding the optimal parameters/settings, making them a valuable tool for enhancing the performance and efficiency of the inverters [83]. In [84], the GA is proposed for the optimization of a grid-connected solar PV system inverter, considering the power losses of the grid-tied inverter, its volume, and its cost. GA for optimization of the PI controller parameters of a grid-connected inverter to improve the active power control is proposed in [85]. To reduce the suppression time and overshoot in the backpropagation NN-based PID control scheme, GA has been used in [83] to optimize the initial weights of the NN for a transformerless grid-connected PV inverter system.

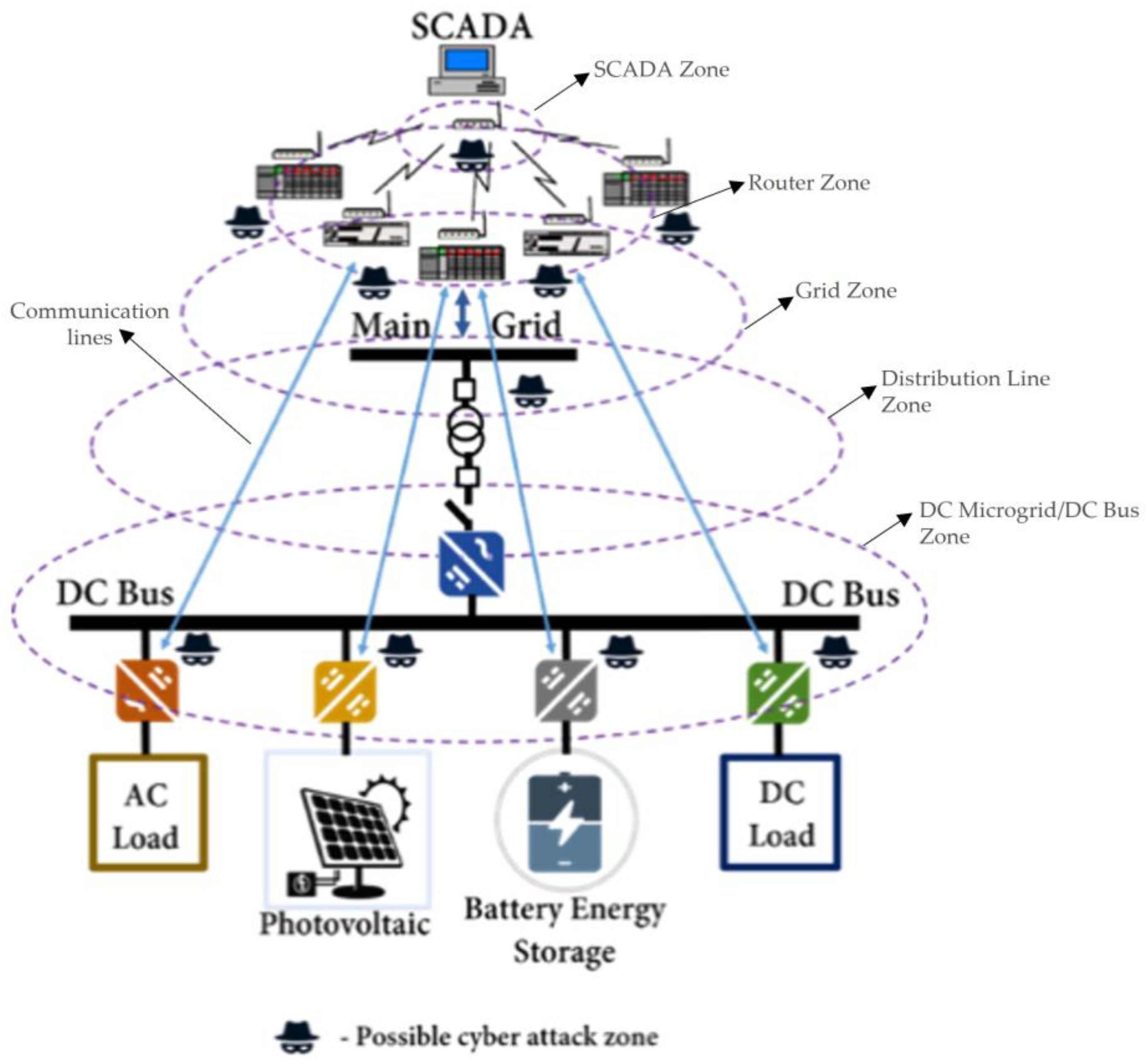
4. Cybersecurity Issues with Smart PV Inverters

Smart PV inverters comprise sophisticated power electronic devices such as microcontrollers, digital signal processors, and integrated circuits (ICs) and are becoming vulnerable to a variety of cyber-attacks ranging from data integrity attacks to communication-based attacks. Moreover, abnormal behaviors in these inverters, like unintended power factor adjustments, voltage fluctuation, etc., are observed due to the improper firmware upgrades of the PV plants [92]. Cybersecurity is one of the major concerns with the increase of information and communication-based control approaches. In the modern control approaches, these converters in the system are remotely controlled by a SCADA system that communicates mainly through ethernet or other wireless communications [93,94]. These communication lines are prone to cyber intrusions that result in loss of control over the converters in the system and gaining access to the entire system by the intruder [95,96]. The work in [97] demonstrated a communication attack on a testbed environment that can cause adverse physical damage to the PV system when the power limits are manipulated, which aggravates the operation of PV inverters. Some major attack incidents include Stuxnet (2010) [98], where Iran’s nuclear system’s SCADA and programmable logic controllers (PLCs) were targeted; the Night Dragon attack (2011), which affected 71 organizations in China; and a ransomware attack in June 2017, which targeted many organizations in Ukraine, including the electricity company. These incidents show what cyber-attackers can do to a smart grid system. These factors have drawn the interest of researchers to study cyber–physical security for a smart PV grid-connected system [99,100,101]. Studies on the cybersecurity challenges and vulnerability analysis on PV inverters are discussed in [51,102,103].

4.1. Types of Cyber-Attacks

It is observed that cyber-attacks cause more damage to the smart grid with power electronics-based inverters due to their low-inertia nature [104]. Due to this, when traditional grids exhibiting a high-inertia nature are coupled with these power electronics-based inverter systems, they create a vulnerable point for the attackers and damage the systems very quickly before a cyber-attack is even detected [12,104,105].
Figure 5 shows the vulnerable points in a PV-connected DC smart grid system where the system is prone to attack. Out of all the types of attacks [96,106] on smart grid systems, Distributed Denial of Signal (DDoS) attacks and False Data Injection (FDI) attacks are considered to be the predominant attacks [107,108]. In a DDoS attack, the attacker tries to disrupt the communication lines or networks by blocking or jamming the flow of signals through them at the vulnerable points shown in Figure 5. The impacts of DDoS attacks can be considered similar to time delay issues in the smart PV-connected grid system, where a delay more than the tolerance level can lead to devastating effects. In the FDI attack, false data are injected into the SCADA system through the communication lines, where the control signal from the SCADA system is altered, leading to catastrophic disasters.

4.2. AI in Detecting Cyber-Attacks

Communications have been the essential part of the smart grid system where the converters are controlled by the SCADA system to exchange data, send alarms, or correct errors across the system using wired communications networks like power line communications, optical fiber, or wireless communication networks like ZigBee, 3G (CELLULAR), or 4G (LTE) [43,44,45,46,47,48]. Security against cyber-attacks on communication lines is inevitable for the safe and better operation of smart grids. Based on factors like grid architecture and control mode, different protection schemes were proposed in [109] for communication-based cyber-attacks. Studies performed in [110] suggest that cyber-attack propagation can be limited better in a decentralized PV system than in a centralized connection. This suggests that the communication layer requires a redundant security system.
With the increase of Internet of Things (IoT) devices in smart grids and with more advancements in control strategies, patterns during cyber-attacks can be observed and detected. Any change in the known system parameters that do not match up with the other parameters within the system can be identified as a cyber-attack. Many detection methodologies were proposed by the researchers to detect and identify cyber-attacks [100,111,112]. In [103], Support Vector Machine (SVM), Long-Short Term Memory (LSTM)-based AI algorithms were proposed to detect the FDI cyber-attack using the data obtained from the Phasor Measuring Units (PMUs). Based on the patterns observed from the waveform data obtained at the point of common coupling (PCC), a multi-layer LSTM model was developed in [113] to detect the FDI-based attacks. Detection of deception attacks on inverter controllers using an active synchronous detection method is proposed in [114].

5. Discussion

Intelligent inverters will lead the future of PV grid-connected systems due to their capability to handle faults and cyber-attacks and maintain stability. For the development of these intelligent inverters, extensive research in the following areas is recommended.

5.1. Mitigation of Cyber-Attacks

Though numerous studies have been conducted on detecting and identifying cyber-attacks using ML and DL algorithms [111,115], more research needs to be performed to mitigate these intrusions. Photovoltaic-based grids need to be cyber-attack tolerant. As mentioned earlier, cyber-attacks may be related to communication lines, inverter controls, and data centers. Cyber-attacks often result in data robbery and system shutdown by controlling the converters. With modern photovoltaic systems remotely controlled, the orientation of the photovoltaic panels can also be controlled by intruders, which may result in a reduction in power generated which can be overlooked by the user. Besides affecting the stability of the grid, a cyber-attack of any level can lead to disruption of electric power availability and hence the reliability of the grid. To overcome this, multi-level protection is to be provided to ensure better safety of the system. Moreover, keeping in view the high chances of attacking grids with a high-inertia nature, future research must be in the area of developing inverter controllers which can control the inertia.
Supervised learning, where the control models are trained with the existing/historical measured data, is used to identify the faults in a PV system. The performance accuracy of these models depends on the quantity and quality of the available data. But with the development of new control approaches, the historical data may not be sufficient enough or may not be available immediately, so the AI models have to be self-learning and should be able to adapt to new environments. Also, reinforcement learning-based approaches, where the control model learns from the environment by obtaining a reward when a corrective action is taken and penalizes when a wrong action is taken, are to be employed.
Besides detecting and identifying cyber-attacks, research should be focused on developing AI controllers which can mitigate cyber-attacks. Further research is also needed in developing test bed environments to field validate the proposed methods for detection, identifying, and mitigating cyber-intrusions.

5.2. 5G-Enabled Communication Considerations

As mentioned earlier, communications are an integral part of smart grids. The current communication networks implemented in smart grids are ZigBee, 3G, and 2G networks. But the major concern with these communication networks is that they fail to operate fully autonomously with frequent data transmission for longer durations. With the 5G networks available across the globe and 6G coming in the future, it is time to move on to more efficient next-generation networks. The future 5G network can overcome these barriers by providing a higher speed of up to 20 Gbps and a higher bandwidth network that is more reliable with low latency [116,117]. This will enable faster data exchange and effective control of PV-connected electric grids. It should also be ensured that the 5G networks are provided with suitable protection against cyber-attacks.

5.3. Time Delay Issues and Solutions

Delays in the flow of information between the SCADA and the smart grid can significantly impact the performance of the controllers. These delays can possibly be caused by the signal transmissions through the power line communications like optical fiber or by wireless communications networks. Cyber-attacks like DDoS attacks at the vulnerable points in Figure 5 can also create time delays. Time delays in the system can also be introduced by time synchronization of the measured signals by global positioning system (GPS) and the analog-to-digital (A/D) conversions by the signal measuring units like Remote Terminal Units (RTUs) and Phasor Measurement Units (PMUs) [106,118,119,120]. Communication delays can also be associated with the opening and closing operations of the circuit breakers on the transmission and distribution lines following a fault in smart grid systems. Future research in the direction of investigating the causes and effects of time delays and exploring the time delay tolerance level of the smart PV-connected grid system for proper functioning will help find the means to minimize the adverse effects of these delays on the system.

5.4. Impacts of Geomagnetically Induced Current (GIC) on PV Inverters/Converters

Due to the variations in the Earth’s static magnetic field (nT/minute), quasi-DC currents with a very low frequency, typically less than 1 Hz, are induced in the power conductors like transmission lines. These currents, which are commonly referred to as Geomagnetically Induced Currents (GIC), have an adverse effect on the power system network, which results in damage to the transformers and other critical equipment [121,122]. Due to the effects of GIC on 13–14 March of 1989, the entire Québec hydropower grid system collapsed in 25 s, which resulted in the tripping of the interconnections to Montréal and damaging of a large transformer [123]. The harmonics generated in the system due to the impact of GIC can result in the heating of the transformers and generators and the tripping of the reactive power support components like capacitor banks, STATic synchronous COMpensator (STATCOM), or Static Var Compensators (SVCs) [124,125,126,127]. Due to the interconnection of these vulnerable equipment to the PV system, the impact of GIC can be seen on the inverters/converters in the PV system. A controlled ground resistance model is proposed in [128,129] to stabilize the system under the impacts of GIC and also during the unsymmetrical faults. Further extensive research is to be focused on the adverse impacts of GIC and the possible mitigation methods for the inverters and controllers of the PV-connected grid system.

6. Conclusions

This paper provides an overview of advanced intelligence control-based inverters that are capable of identifying, detecting, and mitigating faults and associated cybersecurity issues. The conclusions that can be drawn from the review conducted in this paper are as follows.
  • Though there are advantages and disadvantages of both grid-following and grid-forming inverters, control methods that are capable of operating the converters in either mode to overcome the disadvantages of these inverters based on the situation are needed;
  • An extensive bibliography on the existing control methods of these inverters suggests that intelligent control methods are the future of PV systems that are self-learning, self-sustaining, and fault-tolerant;
  • Communication of these intelligent converters with the SCADA is an important feature and technique in making these lines more secure, and fast transfer speeds are needed;
  • More advanced ML- and DL-based methods with field validation are needed to detect, identify, and mitigate the cyber-attacks on the PV system inverters.
This article serves as a guideline for further investigation of technology development for inverters and benefits the researchers, readers, and engineers who deal with research in the field of inverters of grid-connected PV systems.

Author Contributions

Conceptualization, S.N.V. and M.H.A.; resources, M.H.A.; writing—original draft preparation, S.N.V.; writing—review and editing, M.H.A. and S.N.V.; supervision, M.H.A.; project administration, M.H.A.; funding acquisition, M.H.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ul-Haq, A.; Alammari, R.; Iqbal, A.; Jalal, M.; Gul, S. Computation of Power Extraction from Photovoltaic Arrays under Various Fault Conditions. IEEE Access 2020, 8, 47619–47639. [Google Scholar] [CrossRef]
  2. Walker, G.R. Evaluating MPPT Converter Topologies Using a Matlab PV Model. Aust. J. Electr. Electron. Eng. 2001, 21, 49–55. [Google Scholar]
  3. Hohm, D.P.; Ropp, M.E. Comparative Study of Maximum Power Point Tracking Algorithms Using an Experimental, Programmable, Maximum Power Point Tracking Test Bed. In Proceedings of the Conference Record of the Twenty-Eighth IEEE Photovoltaic Specialists Conference, Anchorage, AK, USA, 15–22 September 2000; pp. 1699–1702. [Google Scholar] [CrossRef]
  4. Patel, H.; Agarwal, V. MATLAB-Based Modeling to Study the Effects of Partial Shading on PV Array Characteristics. IEEE Trans. Energy Convers. 2008, 23, 302–310. [Google Scholar] [CrossRef]
  5. Ding, K.; Bian, X.; Liu, H.; Peng, T. A MATLAB-Simulink-Based PV Module Model and Its Application under Conditions of Nonuniform Irradiance. IEEE Trans. Energy Convers. 2012, 27, 864–872. [Google Scholar] [CrossRef]
  6. Ibrahim, A.W.; Shafik, M.B.; Ding, M.; Sarhan, M.A.; Fang, Z.; Alareqi, A.G.; Almoqri, T.; Al-Rassas, A.M. PV Maximum Power-Point Tracking Using Modified Particle Swarm Optimization under Partial Shading Conditions. Chin. J. Electr. Eng. 2020, 6, 106–121. [Google Scholar] [CrossRef]
  7. Chiang, H.C.; Ma, T.T.; Cheng, Y.H.; Chang, J.M.; Chang, W.N. Design and Implementation of a Hybrid Regenerative Power System Combining Grid-Tie and Uninterruptible Power Supply Functions. IET Renew. Power Gener. 2010, 4, 85–99. [Google Scholar] [CrossRef]
  8. Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
  9. Liu, X.; Wang, P.; Loh, P.C. A Hybrid AC/DC Microgrid and Its Coordination Control. IEEE Trans. Smart Grid 2011, 2, 278–286. [Google Scholar] [CrossRef] [Green Version]
  10. Hong, I.; Kang, B.; Park, S. Design and Implementation of Intelligent Energy Distribution Management with Photovoltaic System. IEEE Trans. Consum. Electron. 2012, 58, 340–346. [Google Scholar] [CrossRef]
  11. Alam, M.J.E.; Muttaqi, K.M.; Sutanto, D. A Novel Approach for Ramp-Rate Control of Solar PV Using Energy Storage to Mitigate Output Fluctuations Caused by Cloud Passing. IEEE Trans. Energy Convers. 2014, 29, 507–518. [Google Scholar] [CrossRef] [Green Version]
  12. Ye, J.; Giani, A.; Elasser, A.; Mazumder, S.K.; Farnell, C.; Mantooth, H.A.; Kim, T.; Liu, J.; Chen, B.; Seo, G.S.; et al. A Review of Cyber-Physical Security for Photovoltaic Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 4879–4901. [Google Scholar] [CrossRef]
  13. Walker, G.R.; Sernia, P.C. Cascaded DC-DC Converter Connection of Photovoltaic Modules. IEEE Trans. Power Electron. 2004, 19, 1130–1139. [Google Scholar] [CrossRef]
  14. Strache, S.; Wunderlich, R.; Heinen, S. A Comprehensive, Quantitative Comparison of Inverter Architectures for Various PV Systems, PV Cells, and Irradiance Profiles. IEEE Trans. Sustain. Energy 2014, 5, 813–822. [Google Scholar] [CrossRef]
  15. Wu, T.F.; Chen, Y.K. Modeling PWM DC/DC Converters out of Basic Converter Units. IEEE Trans. Power Electron. 1998, 13, 870–881. [Google Scholar] [CrossRef]
  16. De Brito, M.A.G.; Galotto, L.; Sampaio, L.P.; De Azevedo Melo, G.; Canesin, C.A. Evaluation of the Main MPPT Techniques for Photovoltaic Applications. IEEE Trans. Ind. Electron. 2013, 60, 1156–1167. [Google Scholar] [CrossRef]
  17. Qin, S.; Wang, M.; Chen, T.; Yao, X. Comparative Analysis of Incremental Conductance and Perturb-and-Observation Methods to Implement MPPT in Photovoltaic System. In Proceedings of the 2011 International Conference on Electrical and Control Engineering, Yichang, China, 16–18 September 2011; pp. 5792–5795. [Google Scholar] [CrossRef]
  18. Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of the Incremental Conductance Maximum Power Point Tracking Algorithm. IEEE Trans. Sustain. Energy 2013, 4, 108–117. [Google Scholar] [CrossRef]
  19. Louzazni, M.; Aroudam, E. Intelligent PID-Fuzzy Logic Control for Three-Phase Grid-Connected Photovoltaic Inverter. In Proceedings of the 2014 9th International Conference on Intelligent Systems: Theories and Applications, Rabat, Morocco, 7–8 May 2014. [Google Scholar] [CrossRef]
  20. Thao, N.G.M.; Dat, M.T.; Binh, T.C.; Phuc, N.H. PID-Fuzzy Logic Hybrid Controller for Grid-Connected Photovoltaic Inverters. In Proceedings of the 2010 International Forum on Strategic Technology, Ulsan, Republic of Korea, 13–15 October 2010; pp. 140–144. [Google Scholar] [CrossRef]
  21. Wang, Y.; Ding, L.; Li, N. The Application of Fuzzy Parameters Self-Tuning PID Controller in MPPT of Photovoltaic Power System. In Proceedings of the 2011 International Conference on Transportation, Mechanical, and Electrical Engineering, Changchun, China, 16–18 December 2011; pp. 1129–1132. [Google Scholar] [CrossRef]
  22. Mozaffari Niapour, S.A.K.; Danyali, S.; Sharifian, M.B.B.; Feyzi, M.R. Brushless DC Motor Drives Supplied by PV Power System Based on Z-Source Inverter and FL-IC MPPT Controller. Energy Convers. Manag. 2011, 52, 3043–3059. [Google Scholar] [CrossRef]
  23. Basilio, J.C.; Matos, S.R. Design of PI and PID Controllers with Transient Performance Specification. IEEE Trans. Educ. 2002, 45, 364–370. [Google Scholar] [CrossRef]
  24. Du, W.; Tuffner, F.K.; Schneider, K.P.; Lasseter, R.H.; Xie, J.; Chen, Z.; Bhattarai, B. Modeling of Grid-Forming and Grid-Following Inverters for Dynamic Simulation of Large-Scale Distribution Systems. IEEE Trans. Power Deliv. 2021, 36, 2035–2045. [Google Scholar] [CrossRef]
  25. Qoria, T.; Rokrok, E.; Bruyere, A.; François, B.; Guillaud, X. A PLL-Free Grid-Forming Control with Decoupled Functionalities for High-Power Transmission System Applications. IEEE Access 2020, 8, 197363–197378. [Google Scholar] [CrossRef]
  26. Lasseter, R.H.; Chen, Z.; Pattabiraman, D. Grid-Forming Inverters: A Critical Asset for the Power Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 925–935. [Google Scholar] [CrossRef]
  27. Lin, Y.; Eto, J.H.; Johnson, B.B.; Flicker, J.D.; Lasseter, R.H.; Villegas Pico, H.N.; Seo, G.-S.; Pierre, B.J.; Ellis4, A.; Miller, J.; et al. Research Roadmap on Grid-Forming Inverters with Editing and Support from Hariharan Krishnaswami. Available online: https://www.nrel.gov/docs/fy21osti/73476.pdf (accessed on 30 July 2023).
  28. Bahrani, B. Power-Synchronized Grid-Following Inverter without a Phase-Locked Loop. IEEE Access 2021, 9, 112163–112176. [Google Scholar] [CrossRef]
  29. Umar, M.F.; Khan, A.; Easley, M.; D’Silva, S.; Nun, B.; Shadmand, M.B. Resonance Suppression Based on Predictive Control of Grid-Following Inverters with LCL Filter in Weak Grid Condition. In Proceedings of the ECCE 2020—IEEE Energy Conversion Congress and Exposition, Detroit, MI, USA, 11–15 October 2020; pp. 4742–4748. [Google Scholar] [CrossRef]
  30. Khan, A.; Easley, M.; Hosseinzadehtaher, M.; Shadmand, M.B.; Abu-Rub, H.; Fajri, P. PLL-Less Active and Reactive Power Controller for Grid-Following Inverter. In Proceedings of the ECCE 2020—IEEE Energy Conversion Congress and Exposition, Detroit, MI, USA, 11–15 October 2020; pp. 4322–4328. [Google Scholar] [CrossRef]
  31. Zarei, S.F.; Mokhtari, H.; Ghasemi, M.A.; Peyghami, S.; Davari, P.; Blaabjerg, F. Control of Grid-Following Inverters under Unbalanced Grid Conditions. IEEE Trans. Energy Convers. 2020, 35, 184–192. [Google Scholar] [CrossRef]
  32. Unruh, P.; Nuschke, M.; Strauß, P.; Welck, F. Overview on Grid-Forming Inverter Control Methods. Energies 2020, 13, 2589. [Google Scholar] [CrossRef]
  33. Matevosyan, J.; Badrzadeh, B.; Prevost, T.; Quitmann, E.; Ramasubramanian, D.; Urdal, H.; Achilles, S.; Macdowell, J.; Huang, S.H.; Vital, V.; et al. Grid-Forming Inverters: Are They the Key for High Renewable Penetration? IEEE Power Energy Mag. 2019, 17, 89–98. [Google Scholar] [CrossRef]
  34. Rathnayake, D.B.; Akrami, M.; Phurailatpam, C.; Me, S.P.; Hadavi, S.; Jayasinghe, G.; Zabihi, S.; Bahrani, B. Grid Forming Inverter Modeling, Control, and Applications. IEEE Access 2021, 9, 114781–114807. [Google Scholar] [CrossRef]
  35. Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-Forming Converters: An Overview of Control Approaches and Future Trends. In Proceedings of the ECCE 2020—IEEE Energy Conversion Congress and Exposition, Detroit, MI, USA, 11–15 October 2020; pp. 4292–4299. [Google Scholar] [CrossRef]
  36. Seo, G.S.; Colombino, M.; Subotic, I.; Johnson, B.; Gros, D.; Dorfler, F. Dispatchable Virtual Oscillator Control for Decentralized Inverter-Dominated Power Systems: Analysis and Experiments. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 561–566. [Google Scholar] [CrossRef] [Green Version]
  37. Newton, C.; Sumner, M.; Alexander, T. Multi-Level Converters: A Real Solution to High Voltage Drives? Power Eng. J. 1997, 12, 21–26. [Google Scholar] [CrossRef]
  38. Bhuvaneswari, G. Nagaraju Multi-Level Inverters—A Comparative Study. IETE J. Res. 2015, 51, 141–153. [Google Scholar] [CrossRef]
  39. Sruthi, R.; Reddy, P.N. Comparitive Study of Conventional Inverter Topologies for Stand-Alone PV System. In Proceedings of the 2021 2nd International Conference for Emerging Technology, Belagavi, India, 21–23 May 2021. [Google Scholar] [CrossRef]
  40. Stonier, A.A.; Lehman, B. An Intelligent-Based Fault-Tolerant System for Solar-Fed Cascaded Multilevel Inverters. IEEE Trans. Energy Convers. 2018, 33, 1047–1057. [Google Scholar] [CrossRef]
  41. Alexander, S.A.; Manigandan, T. Power Quality Improvement in Solar Photovoltaic System to Reduce Harmonic Distortions Using Intelligent Techniques. J. Renew. Sustain. Energy 2014, 6, 043127. [Google Scholar] [CrossRef]
  42. Khomfoi, S.; Tolbert, L.M. Fault Diagnosis and Reconfiguration for Multilevel Inverter Drive Using AI-Based Techniques. IEEE Trans. Ind. Electron. 2007, 54, 2954–2968. [Google Scholar] [CrossRef]
  43. Terashmila, L.K.A.; Iqbal, T.; Mann, G. A Comparison of Low Cost Wireless Communication Methods for Remote Control of Grid-Tied Converters. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Windsor, ON, Canada, 30 April–3 May 2017. [Google Scholar] [CrossRef]
  44. Gozde, H.; Taplamacioglu, M.C.; Ari, M.; Shalaf, H. 4G/LTE Technology for Smart Grid Communication Infrastructure. In Proceedings of the 2015 3rd International Istanbul Smart Grid Congress and Fair, Istanbul, Turkey, 29–30 April 2015. [Google Scholar] [CrossRef]
  45. Baimel, D.; Tapuchi, S.; Baimel, N. Smart Grid Communication Technologies—Overview, Research Challenges and Opportunities. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Capri, Italy, 22–24 June 2016; pp. 116–120. [Google Scholar] [CrossRef]
  46. Chang, K.H.; Mason, B. The IEEE 802.15.4g Standard for Smart Metering Utility Networks. In Proceedings of the 2012 IEEE 3rd International Conference on Smart Grid Communications, Tainan, Taiwan, 5–8 November 2012; pp. 476–480. [Google Scholar] [CrossRef]
  47. Wang, W.; Xu, Y.; Khanna, M. A Survey on the Communication Architectures in Smart Grid. Comput. Netw. 2011, 55, 3604–3629. [Google Scholar] [CrossRef]
  48. Parikh, P.P.; Kanabar, M.G.; Sidhu, T.S. Opportunities and Challenges of Wireless Communication Technologies for Smart Grid Applications. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar] [CrossRef]
  49. Yao, Z.; Xiao, L.; Yan, Y. Seamless Transfer of Single-Phase Grid-Interactive Inverters between Grid-Connected and Stand-Alone Modes. IEEE Trans. Power Electron. 2010, 25, 1597–1603. [Google Scholar] [CrossRef]
  50. Kurukuru, V.S.B.; Haque, A.; Khan, M.A.; Sahoo, S.; Malik, A.; Blaabjerg, F. A Review on Artificial Intelligence Applications for Grid-Connected Solar Photovoltaic Systems. Energies 2021, 14, 4690. [Google Scholar] [CrossRef]
  51. Sahoo, S.; Dragicevic, T.; Blaabjerg, F. Cyber Security in Control of Grid-Tied Power Electronic Converters—Challenges and Vulnerabilities. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5326–5340. [Google Scholar] [CrossRef]
  52. Tuyen, N.D.; Quan, N.S.; Linh, V.B.; Van Tuyen, V.; Fujita, G. A Comprehensive Review of Cybersecurity in Inverter-Based Smart Power System Amid the Boom of Renewable Energy. IEEE Access 2022, 10, 35846–35875. [Google Scholar] [CrossRef]
  53. Al-Adwan, I.M.; Al Shiboul, Y.A. Effect of the Modulation Index and the Carrier Frequency on the Output Vol Tage Waveform of the Spwm Voltage Source Inverter. In Proceedings of the 17th International Multi-Conference on Systems, Signals and Devices, Monastir, Tunisia, 20–23 July 2020; pp. 960–968. [Google Scholar] [CrossRef]
  54. Dasgupta, S.; Sahoo, S.K.; Panda, S.K. Single-Phase Inverter Control Techniques for Interfacing Renewable Energy Sources with Microgrid-Part I: Parallel-Connected Inverter Topology with Active and Reactive Power Flow Control along with Grid Current Shaping. IEEE Trans. Power Electron. 2011, 26, 717–731. [Google Scholar] [CrossRef]
  55. Dasgupta, S.; Sahoo, S.K.; Panda, S.K.; Amaratunga, G.A.J. Single-Phase Inverter-Control Techniques for Interfacing Renewable Energy Sources with Microgrid-Part II: Series-Connected Inverter Topology to Mitigate Voltage-Related Problems along with Active Power Flow Control. IEEE Trans. Power Electron. 2011, 26, 732–746. [Google Scholar] [CrossRef]
  56. Mirafzal, B.; Adib, A. On Grid-Interactive Smart Inverters: Features and Advancements. IEEE Access 2020, 8, 160526–160536. [Google Scholar] [CrossRef]
  57. Ali, M.H.; Thotakura, N.L. Smart Inverters and Controls for Grid-Connected Renewable Energy Sources. In Advances in Control Techniques for Smart Grid Applications; Springer Nature: Singapore, 2022; pp. 201–266. [Google Scholar] [CrossRef]
  58. Park, S.Y.; Lai, J.S.; Lee, W.C. An Easy, Simple, and Flexible Control Scheme for a Three-Phase Grid-Tie Inverter System. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, ECCE 2010—Proceedings 2010, Atlanta, GA, USA, 12–16 September 2010; pp. 599–603. [Google Scholar] [CrossRef]
  59. Guo, X.Q.; Wu, W.Y. Improved Current Regulation of Three-Phase Grid-Connected Voltage-Source Inverters for Distributed Generation Systems. IET Renew. Power Gener. 2010, 4, 101–115. [Google Scholar] [CrossRef]
  60. Zhang, L.; Harnefors, L.; Nee, H.P. Power-Synchronization Control of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
  61. Pattabiraman, D.; Lasseter, R.H.; Jahns, T.M. Comparison of Grid Following and Grid Forming Control for a High Inverter Penetration Power System. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018. [Google Scholar] [CrossRef]
  62. Vandoorn, T.L.; De Kooning, J.D.M.; Meersman, B.; Vandevelde, L. Review of Primary Control Strategies for Islanded Microgrids with Power-Electronic Interfaces. Renew. Sustain. Energy Rev. 2013, 19, 613–628. [Google Scholar] [CrossRef]
  63. Han, H.; Hou, X.; Yang, J.; Wu, J.; Su, M.; Guerrero, J.M. Review of Power Sharing Control Strategies for Islanding Operation of AC Microgrids. IEEE Trans. Smart Grid 2016, 7, 200–215. [Google Scholar] [CrossRef] [Green Version]
  64. Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-Forming Converters: Control Approaches, Grid-Synchronization, and Future Trends—A Review. IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]
  65. Mohiuddin, S.M.; Qi, J. A Unified Droop-Free Distributed Secondary Control for Grid-Following and Grid-Forming Inverters in AC Microgrids. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020. [Google Scholar] [CrossRef]
  66. Jouini, T.; Arghir, C.; Dörfler, F. Grid-Friendly Matching of Synchronous Machines by Tapping into the DC Storage. IFAC-PapersOnLine 2016, 49, 192–197. [Google Scholar] [CrossRef]
  67. Arghir, C.; Jouini, T.; Dörfler, F. Grid-Forming Control for Power Converters Based on Matching of Synchronous Machines. Automatica 2018, 95, 273–282. [Google Scholar] [CrossRef] [Green Version]
  68. Katiraei, F.; Iravani, M.R.; Lehn, P.W. Small-Signal Dynamic Model of a Micro-Grid Including Conventional and Electronically Interfaced Distributed Resources. IET Gener. Transm. Distrib. 2007, 1, 369–378. [Google Scholar] [CrossRef] [Green Version]
  69. Guo, X.; Lu, Z.; Wang, B.; Sun, X.; Wang, L.; Guerrero, J.M. Dynamic Phasors-Based Modeling and Stability Analysis of Droop-Controlled Inverters for Microgrid Applications. IEEE Trans. Smart Grid. 2014, 5, 2980–2987. [Google Scholar] [CrossRef] [Green Version]
  70. Baltas, G.N.; Lai, N.B.; Marin, L.; Tarrasó, A.; Rodriguez, P. Grid-Forming Power Converters Tuned through Artificial Intelligence to Damp Subsynchronous Interactions in Electrical Grids. IEEE Access 2020, 8, 93369–93379. [Google Scholar] [CrossRef]
  71. Ma, S.; Chen, M.; Wu, J.; Huo, W.; Huang, L. Augmented Nonlinear Controller for Maximum Power-Point Tracking with Artificial Neural Network in Grid-Connected Photovoltaic Systems. Energies 2016, 9, 1005. [Google Scholar] [CrossRef] [Green Version]
  72. Hannan, M.A.; Ghani, Z.A.; Hoque, M.M.; Ker, P.J.; Hussain, A.; Mohamed, A. Fuzzy Logic Inverter Controller in Photovoltaic Applications: Issues and Recommendations. IEEE Access 2019, 7, 24934–24955. [Google Scholar] [CrossRef]
  73. Hannan, M.A.; Ghani, Z.A.; Mohamed, A.; Uddin, M.N. Real-Time Testing of a Fuzzy Logic Controller Based Grid-Connected Photovoltaic Inverter System. In Proceedings of the 2014 IEEE Industry Application Society Annual Meeting, Vancouver, BC, Canada, 5–9 October 2014. [Google Scholar] [CrossRef]
  74. Cecati, C.; Ciancetta, F.; Siano, P. A Multilevel Inverter for Photovoltaic Systems with Fuzzy Logic Control. IEEE Trans. Ind. Electron. 2010, 57, 4115–4125. [Google Scholar] [CrossRef]
  75. Chandran, P.; Madhura, R.S.; Roselyn, J.P.; Devaraj, D.; Gopal, V.; Ravi, A. Development of Intelligent Fuzzy PQ-FRT Control Strategy for Grid-Connected Solar PV System. In Proceedings of the 2019 IEEE International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS), Tamilnadu, India, 11–13 April 2019. [Google Scholar] [CrossRef]
  76. Hassan, A.A.; El-Habrouk, M.; Abdelhamid, T.H.; Deghedie, S. A Novel Neural Network-Based Method for the Implementation of Space Vector PWM for Three-Level Voltage-Source Inverters. In Proceedings of the 2020 8th International Conference on Control, Mechatronics and Automation, Moscow, Russia, 6–8 November 2020; pp. 172–178. [Google Scholar] [CrossRef]
  77. Mohamed, I.S.; Rovetta, S.; Do, T.D.; Dragicevic, T.; Diab, A.A.Z. A Neural-Network-Based Model Predictive Control of Three-Phase Inverter with an Output LC Filter. IEEE Access 2019, 7, 124737–124749. [Google Scholar] [CrossRef]
  78. Zhang, S.; Wang, R.; Si, Y.; Wang, L. An Improved Convolutional Neural Network for Three-Phase Inverter Fault Diagnosis. IEEE Trans. Instrum. Meas. 2022, 71, 3510915. [Google Scholar] [CrossRef]
  79. Alzayed, M.; Lemaire, M.; Zarrabian, S.; Chaoui, H.; Massicotte, D. Droop-Controlled Bidirectional Inverter-Based Microgrid Using Cascade-Forward Neural Networks. IEEE Open J. Circuits Syst. 2022, 3, 298–308. [Google Scholar] [CrossRef]
  80. Altin, N.; Sefa, I. Simulation of Neuro-Fuzzy Controlled Grid Interactive Inverter. In Proceedings of the 2011 23rd International Symposium on Information, Communication and Automation Technologies, Sarajevo, Bosnia and Herzegovina, 27–29 October 2011. [Google Scholar] [CrossRef]
  81. Karuppusamy, P.; Natarajan, A.M.; Vijeyakumar, K.N. An Adaptive Neuro-Fuzzy Model to Multilevel Inverter for Grid Connected Photovoltaic System. J. Circuits Syst. Comput. 2015, 24, 1550066. [Google Scholar] [CrossRef]
  82. Babayomi, O.; Zhang, Z.; Li, Y.; Kennel, R. Adaptive Predictive Control with Neuro-Fuzzy Parameter Estimation for Microgrid Grid-Forming Converters. Sustainability 2021, 13, 7038. [Google Scholar] [CrossRef]
  83. Michalewicz, Z.; Janikow, C.Z.; Krawczyk, J.B. A Modified Genetic Algorithm for Optimal Control Problems. Comput. Math. Appl. 1992, 23, 83–94. [Google Scholar] [CrossRef] [Green Version]
  84. Ammous, A.; Alahdal, A.; Ammous, K. Optimization of an On-Grid Inverter for PV Applications Using Genetic Algorithms. J. Eng. 2020, 2020, 7063243. [Google Scholar] [CrossRef] [Green Version]
  85. Yang, Q.; Dai, N. Genetic Algorithm for PI Controller Design of Grid-Connected Inverter Based on Multilayer Perceptron Model. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC): Energy Transition for Carbon Neutrality, Nanjing, China, 23–25 December 2021; pp. 2770–2775. [Google Scholar] [CrossRef]
  86. Dhar, S.; Patnaik, R.K.; Dash, P.K. Fault Detection and Location of Photovoltaic Based DC Microgrid Using Differential Protection Strategy. IEEE Trans. Smart Grid 2018, 9, 4303–4312. [Google Scholar] [CrossRef]
  87. Uddin, M.N.; Abido, M.A.; Rahman, M.A. Development and Implementation of a Hybrid Intelligent Controller for Interior Permanent-Magnet Synchronous Motor Drives. IEEE Trans. Ind. Appl. 2004, 40, 68–76. [Google Scholar] [CrossRef]
  88. Mitra, S.; Hayashi, Y. Neuro-Fuzzy Rule Generation: Survey in Soft Computing Framework. IEEE Trans. Neural Netw. 2000, 11, 748–768. [Google Scholar] [CrossRef] [Green Version]
  89. Jang, J.S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
  90. Khan, M.A.; Haque, A.; Kurukuru, V.S.B. Intelligent Control of a Novel Transformerless Inverter Topology for Photovoltaic Applications. Electr. Eng. 2020, 102, 627–641. [Google Scholar] [CrossRef]
  91. Kamal, T.; Karabacak, M.; Perić, V.S.; Hassan, S.Z.; Fernández-Ramírez, L.M. Novel Improved Adaptive Neuro-Fuzzy Control of Inverter and Supervisory Energy Management System of a Microgrid. Energies 2020, 13, 4721. [Google Scholar] [CrossRef]
  92. Benkraouda, H.; Chakkantakath, M.A.; Keliris, A.; Maniatakos, M. SNIFU: Secure Network Interception for Firmware Updates in Legacy PLCs. In Proceedings of the 2020 IEEE 38th VLSI Test Symposium (VTS), San Diego, CA, USA, 5–8 April 2020. [Google Scholar] [CrossRef]
  93. Pong, P.W.T.; Annaswamy, A.M.; Kroposki, B.; Zhang, Y.; Rajagopal, R.; Zussman, G.; Poor, H.V. Cyber-Enabled Grids: Shaping Future Energy Systems. Adv. Appl. Energy 2021, 1, 100003. [Google Scholar] [CrossRef]
  94. Liu, C.C.; Stefanov, A.; Hong, J.; Panciatici, P. Intruders in the Grid. IEEE Power Energy Mag. 2012, 10, 58–66. [Google Scholar] [CrossRef]
  95. Dumitrache, I.; Dogaru, D.I. Smart Grid Overview: Infrastructure, Cyber-Physical Security and Challenges. In Proceedings of the 2015 20th International Conference on Control Systems and Computer Science, Bucharest, Romania, 27–29 May 2015; pp. 693–699. [Google Scholar] [CrossRef]
  96. Hossain, M.M.; Peng, C. Cyber–Physical Security for on-Going Smart Grid Initiatives: A Survey. IET Cyber-Phys. Syst. Theory Appl. 2020, 5, 233–244. [Google Scholar] [CrossRef]
  97. Kang, B.J.; Maynard, P.; McLaughlin, K.; Sezer, S.; Andrén, F.; Seitl, C.; Kupzog, F.; Strasser, T. Investigating Cyber-Physical Attacks against IEC 61850 Photovoltaic Inverter Installations. In Proceedings of the 2015 IEEE 20th Conference on Emerging Technologies & Factory Automation (ETFA), Luxembourg, 8–11 September 2015. [Google Scholar] [CrossRef] [Green Version]
  98. Karnouskos, S. Stuxnet Worm Impact on Industrial Cyber-Physical System Security. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 4490–4494. [Google Scholar] [CrossRef]
  99. Sahoo, S.; Dragicevic, T.; Blaabjerg, F. Resilient Operation of Heterogeneous Sources in Cooperative DC Microgrids. IEEE Trans. Power Electron. 2020, 35, 12601–12605. [Google Scholar] [CrossRef]
  100. Sargolzaei, A.; Yen, K.K.; Abdelghani, M.N.; Sargolzaei, S.; Carbunar, B. Resilient Design of Networked Control Systems under Time Delay Switch Attacks, Application in Smart Grid. IEEE Access 2017, 5, 15901–15912. [Google Scholar] [CrossRef]
  101. Basnet, M.; Poudyal, S.; Ali, M.H.; Dasgupta, D. Ransomware Detection Using Deep Learning in the SCADA System of Electric Vehicle Charging Station. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Conference—Latin America, ISGT Latin America, Lima, Peru, 15–17 September 2021. [Google Scholar] [CrossRef]
  102. Zhang, J.; Ye, J.; Guo, L.; Li, F.; Song, W. Vulnerability Assessments for Power-Electronics-Based Smart Grids. In Proceedings of the ECCE 2020—IEEE Energy Conversion Congress and Exposition, Detroit, MI, USA, 11–15 October 2020; pp. 1702–1707. [Google Scholar] [CrossRef]
  103. Zhang, J.; Li, Q.; Ye, J.; Guo, L. Cyber-Physical Security Framework for Photovoltaic Farms. In Proceedings of the 2020 IEEE CyberPELS, Miami, FL, USA, 3 October 2020. [Google Scholar] [CrossRef]
  104. Khan, A.; Hosseinzadehtaher, M.; Shadmand, M.B.; Bayhan, S.; Abu-Rub, H. On the Stability of the Power Electronics-Dominated Grid: A New Energy Paradigm. IEEE Ind. Electron. Mag. 2020, 14, 65–78. [Google Scholar] [CrossRef]
  105. Abu-Rub, O.H.; Fard, A.Y.; Umar, M.F.; Hosseinzadehtaher, M.; Shadmands, M.B. Towards Intelligent Power Electronics-Dominated Grid via Machine Learning Techniques. IEEE Power Electron. Mag. 2021, 8, 28–38. [Google Scholar] [CrossRef]
  106. Dogaru, D.I.; Dumitrache, I. Robustness of Power Systems in the Context of Cyber Attacks. In Proceedings of the 2017 21st International Conference on Control Systems and Computer Science (CSCS), Bucharest, Romania, 29–31 May 2017; pp. 506–512. [Google Scholar] [CrossRef]
  107. Sahoo, S.; Peng, J.C.H. A Localized Event-Driven Resilient Mechanism for Cooperative Microgrid against Data Integrity Attacks. IEEE Trans. Cybern. 2021, 51, 3687–3698. [Google Scholar] [CrossRef]
  108. Liu, S.; Siano, P.; Wang, X. Intrusion-Detector-Dependent Frequency Regulation for Microgrids under Denial-of-Service Attacks. IEEE Syst. J. 2020, 14, 2593–2596. [Google Scholar] [CrossRef]
  109. Memon, A.A.; Kauhaniemi, K. A Critical Review of AC Microgrid Protection Issues and Available Solutions. Electr. Power Syst. Res. 2015, 129, 23–31. [Google Scholar] [CrossRef]
  110. Gunduz, H.; Jayaweera, D. Reliability Assessment of a Power System with Cyber-Physical Interactive Operation of Photovoltaic Systems. Int. J. Electr. Power Energy Syst. 2018, 101, 371–384. [Google Scholar] [CrossRef]
  111. Isozaki, Y.; Yoshizawa, S.; Fujimoto, Y.; Ishii, H.; Ono, I.; Onoda, T.; Hayashi, Y. Detection of Cyber Attacks against Voltage Control in Distribution Power Grids with PVs. IEEE Trans. Smart Grid 2016, 7, 1824–1835. [Google Scholar] [CrossRef]
  112. Basnet, M.; Ali, M.H. Deep Learning-Based Intrusion Detection System for Electric Vehicle Charging Station. In Proceedings of the 2020 2nd International Conference on Smart Power & Internet Energy Systems (SPIES), Bangkok, Thailand, 15–18 September 2020; pp. 408–413. [Google Scholar] [CrossRef]
  113. Li, F.; Li, Q.; Zhang, J.; Kou, J.; Ye, J.; Song, W.Z.; Mantooth, H.A. Detection and Diagnosis of Data Integrity Attacks in Solar Farms Based on Multilayer Long Short-Term Memory Network. IEEE Trans. Power Electron. 2021, 36, 2495–2498. [Google Scholar] [CrossRef]
  114. Li, Y.; Zhang, P.; Zhang, L.; Wang, B. Active Synchronous Detection of Deception Attacks in Microgrid Control Systems. IEEE Trans. Smart Grid 2017, 8, 373–375. [Google Scholar] [CrossRef]
  115. Li, Q.; Li, F.; Zhang, J.; Ye, J.; Song, W.; Mantooth, A. Data-Driven Cyberattack Detection for Photovoltaic (PV) Systems through Analyzing Micro-PMU Data. In Proceedings of the ECCE 2020—IEEE Energy Conversion Congress and Exposition, Detroit, MI, USA, 11–15 October 2020; pp. 431–436. [Google Scholar] [CrossRef]
  116. Abrahamsen, F.E.; Ai, Y.; Cheffena, M. Communication Technologies for Smart Grid: A Comprehensive Survey. Sensors 2021, 21, 8087. [Google Scholar] [CrossRef]
  117. Borenius, S.; Costa-Requena, J.; Lehtonen, M.; Kantola, R. Providing Network Time Protocol Based Timing for Smart Grid Measurement and Control Devices in 5G Networks. In Proceedings of the 2019 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids, Beijing, China, 21–23 October 2019. [Google Scholar] [CrossRef] [Green Version]
  118. Zhou, Y.; Ghosh, S.; Ali, M.H.; Wyatt, T.E. Minimization of Negative Effects of Time Delay in Smart Grid System. In Proceedings of the 2013 Proceedings of IEEE Southeastcon, Jacksonville, FL, USA, 4–7 April 2013. [Google Scholar] [CrossRef]
  119. Macana, C.A.; Mojica-Nava, E.; Quijano, N. Time-Delay Effect on Load Frequency Control for Microgrids. In Proceedings of the 2013 10th IEEE International Conference on Networking, Sensing and Control, Evry, France, 10–12 April 2013; pp. 544–549. [Google Scholar] [CrossRef]
  120. Musleh, A.S.; Muyeen, S.M.; Al-Durra, A.; Kamwa, I.; Masoum, M.A.S.; Islam, S. Time-Delay Analysis of Wide-Area Voltage Control Considering Smart Grid Contingences in a Real-Time Environment. IEEE Trans. Ind. Inf. 2018, 14, 1242–1252. [Google Scholar] [CrossRef]
  121. North American Electric Reliability Corporation (NERC). 2012 Special Reliability Assessment Interim Report: Effects of Geomagnetic Disturbances on the Bulk Power System. 2012. Available online: https://www.nrc.gov/reading-rm/doc-collections/commission/slides/2012/20120615/lauby-20120615.pdf (accessed on 30 July 2023).
  122. Marti, L.; Rezaei-Zare, A.; Narang, A. Simulation of Transformer Hotspot Heating Due to Geomagnetically Induced Currents. IEEE Trans. Power Deliv. 2013, 28, 320–327. [Google Scholar] [CrossRef]
  123. High-Impact, Low-Frequency Risk to the North American Bulk Power System (June 2010)|Department of Energy. Available online: https://www.energy.gov/ceser/downloads/high-impact-low-frequency-risk-north-american-bulk-power-system-june-2010 (accessed on 19 December 2022).
  124. Chandrasena, W.; McLaren, P.G.; Annakkage, U.D.; Jayasinghe, R.P. Modeling GIC Effects on Power Systems: The Need to Model Magnetic Status of Transformers. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 2, pp. 981–986. [Google Scholar] [CrossRef]
  125. Rezaei-Zare, A. Reactive Power Loss versus GIC Characteristic of Single-Phase Transformers. IEEE Trans. Power Deliv. 2015, 30, 1639–1640. [Google Scholar] [CrossRef]
  126. Shetye, K.; Overbye, T. Modeling and Analysis of GMD Effects on Power Systems: An Overview of the Impact on Large-Scale Power Systems. IEEE Electrif. Mag. 2015, 3, 13–21. [Google Scholar] [CrossRef]
  127. Overbye, T.J.; Shetye, K.S.; Hutchins, T.R.; Qiu, Q.; Weber, J.D. Power Grid Sensitivity Analysis of Geomagnetically Induced Currents. IEEE Trans. Power Syst. 2013, 28, 4821–4828. [Google Scholar] [CrossRef]
  128. Hussein, A.A.; Ali, M.H. Fuzzy Logic Controlled Variable Resistor for Suppressing GIC in Transformers. IET Gener. Transm. Distrib. 2017, 11, 1494–1501. [Google Scholar] [CrossRef]
  129. Hussein, A.A.; Ali, M.H. Mitigation of Adverse Effects of Gics on Transformers Using Look-up Table Controlled Ground Resistance. In Proceedings of the 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016. [Google Scholar] [CrossRef]
Energies 16 05904 g001
Figure 1. Control structure of GFLI.
Figure 1. Control structure of GFLI.
Energies 16 05904 g001
Energies 16 05904 g002
Figure 2. Structure of conventional d-q frame-based PI control technique.
Figure 2. Structure of conventional d-q frame-based PI control technique.
Energies 16 05904 g002
Energies 16 05904 g003
Figure 3. Control structure of GFMI.
Figure 3. Control structure of GFMI.
Energies 16 05904 g003
Energies 16 05904 g004
Figure 4. Intelligent control methods for inverters.
Figure 4. Intelligent control methods for inverters.
Energies 16 05904 g004
Energies 16 05904 g005
Figure 5. PV-connected DC smart grid supervised by the SCADA system.
Figure 5. PV-connected DC smart grid supervised by the SCADA system.
Energies 16 05904 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Vodapally, S.N.; Ali, M.H. Overview of Intelligent Inverters and Associated Cybersecurity Issues for a Grid-Connected Solar Photovoltaic System. Energies 2023, 16, 5904. https://doi.org/10.3390/en16165904

AMA Style

Vodapally SN, Ali MH. Overview of Intelligent Inverters and Associated Cybersecurity Issues for a Grid-Connected Solar Photovoltaic System. Energies. 2023; 16(16):5904. https://doi.org/10.3390/en16165904

Chicago/Turabian Style

Vodapally, Sai Nikhil, and Mohd Hasan Ali. 2023. "Overview of Intelligent Inverters and Associated Cybersecurity Issues for a Grid-Connected Solar Photovoltaic System" Energies 16, no. 16: 5904. https://doi.org/10.3390/en16165904

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop