Challenges and Opportunities for Lithium Extraction from Geothermal Systems in Germany—Part 3: The Return of the Extraction Brine
Abstract
:1. Introduction
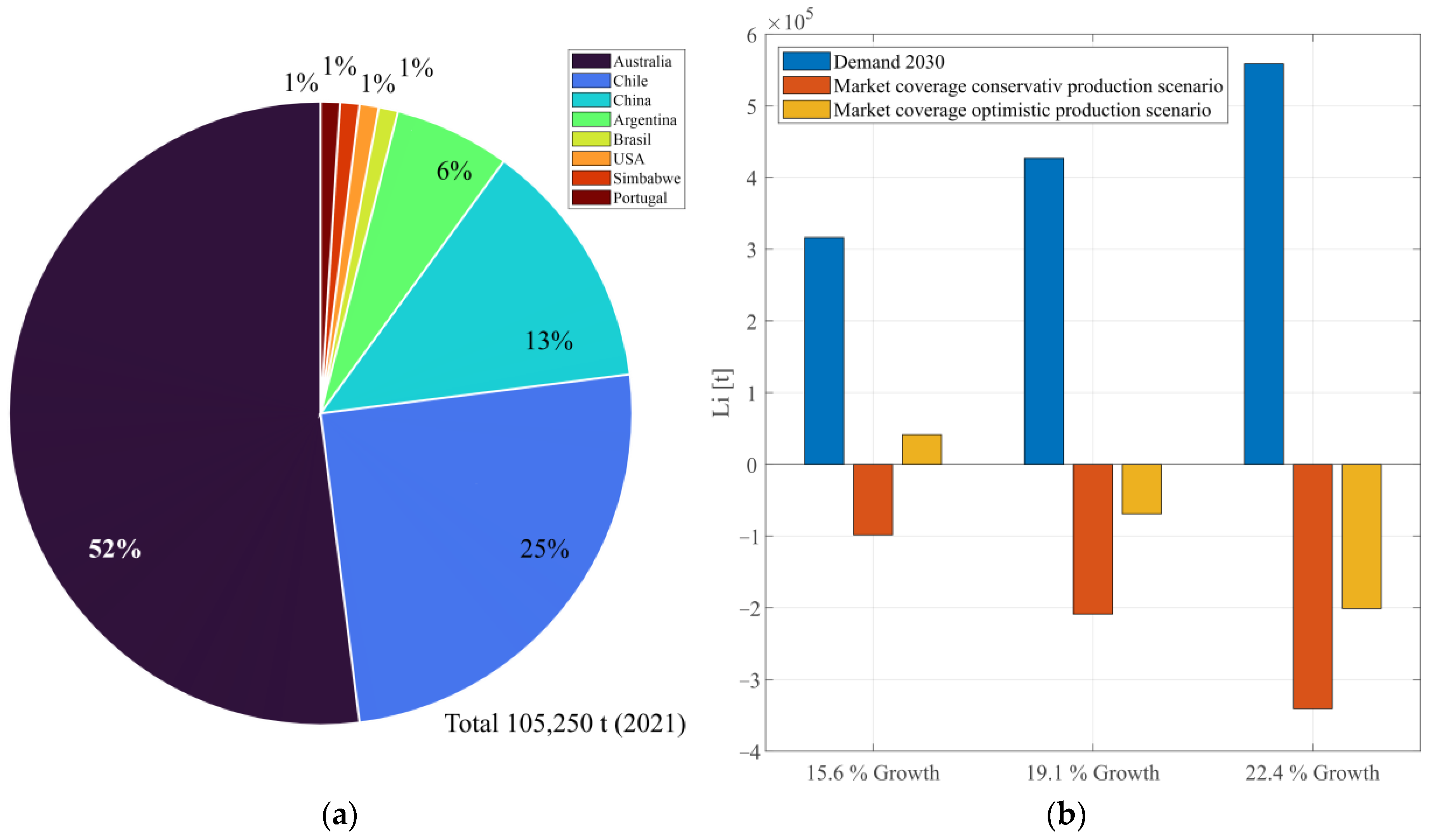
1.1. The Market and Projections
1.2. Geothermal Reservoirs in the Upper Rhine Graben
1.3. Li Extraction from Geothermal Fluids
2. Methods
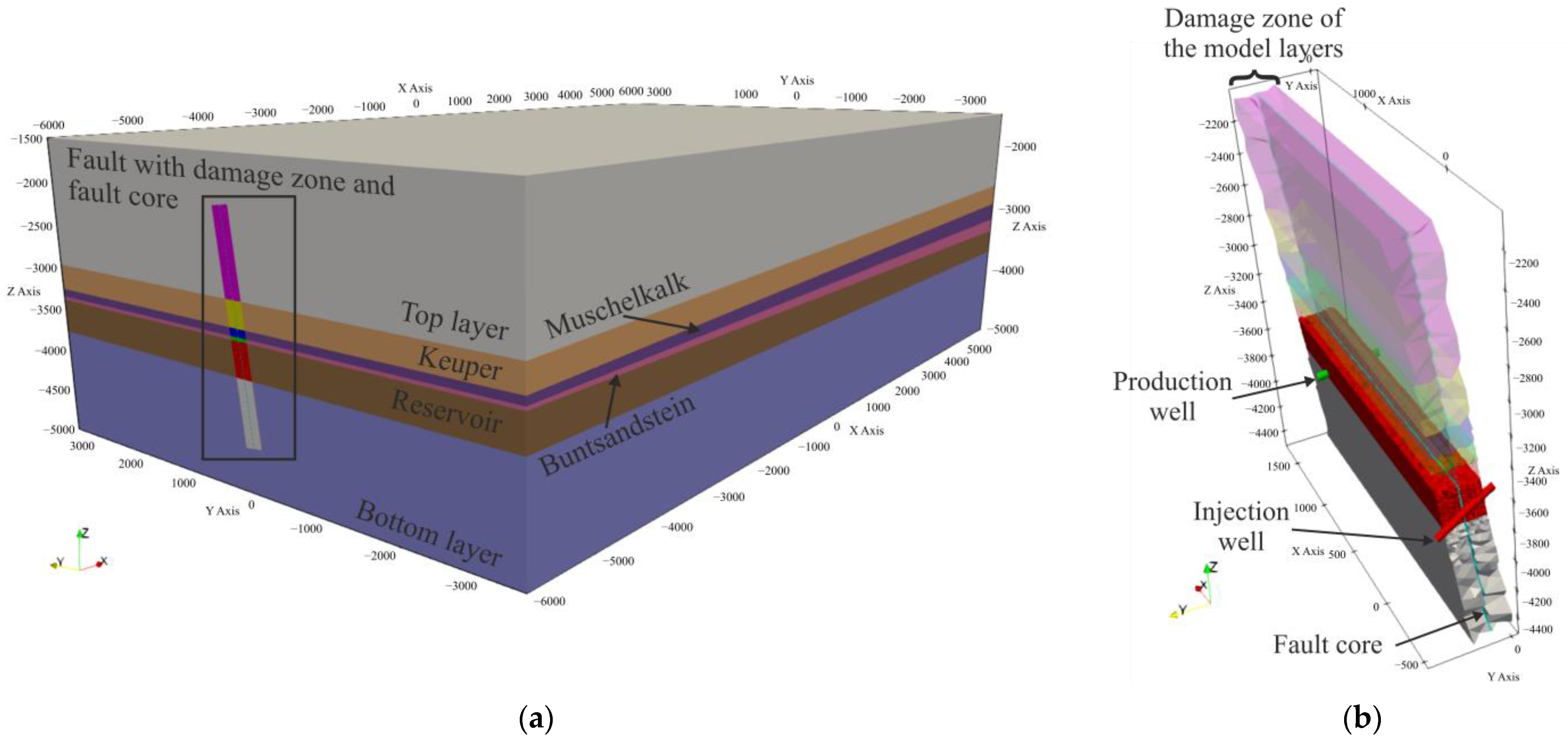
2.1. Geological Model
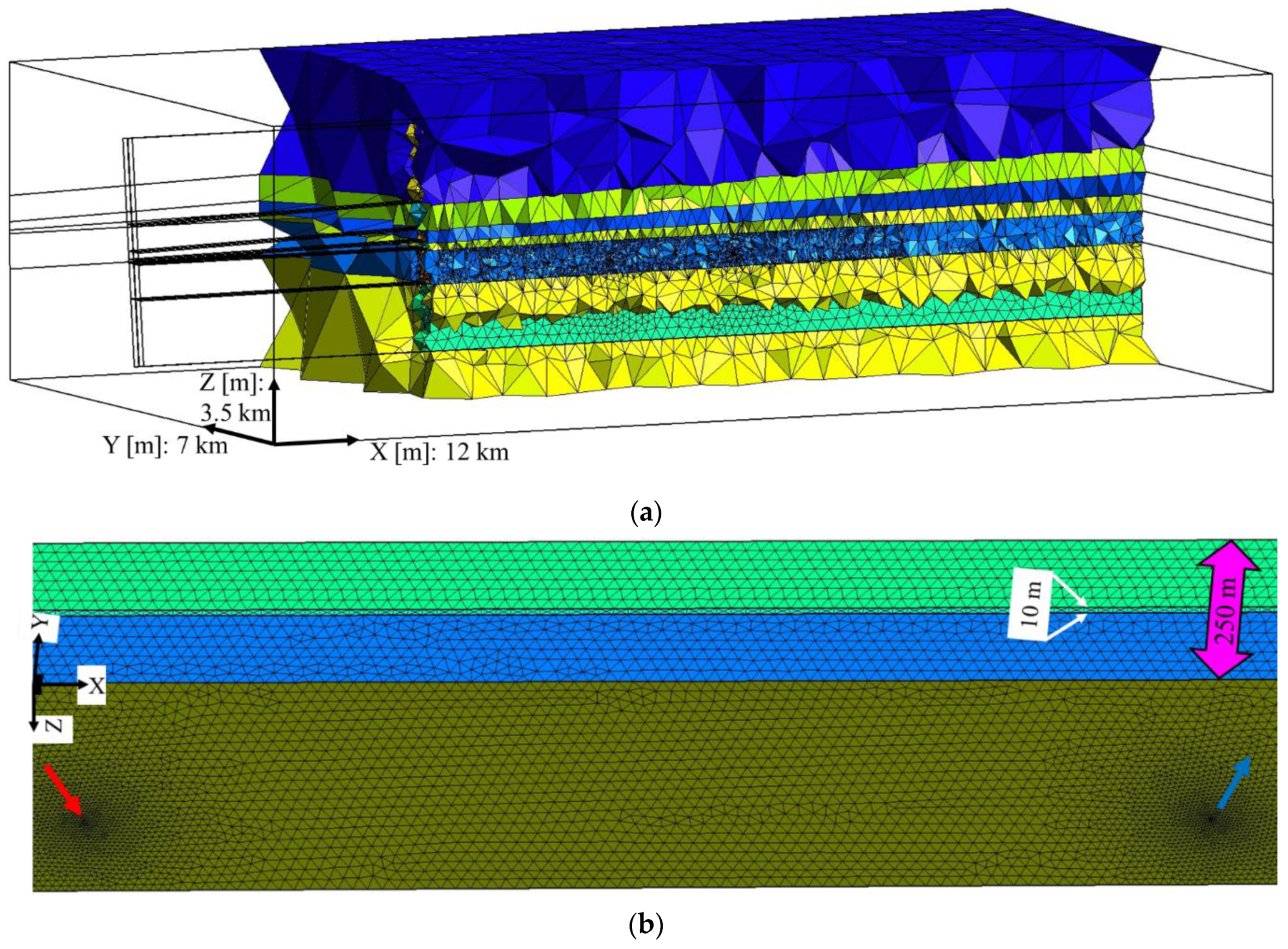
2.2. Mesh Generation
2.3. Parametrization
2.4. Numerical Modeling
2.5. Governing Equations
2.6. Model Scenarios
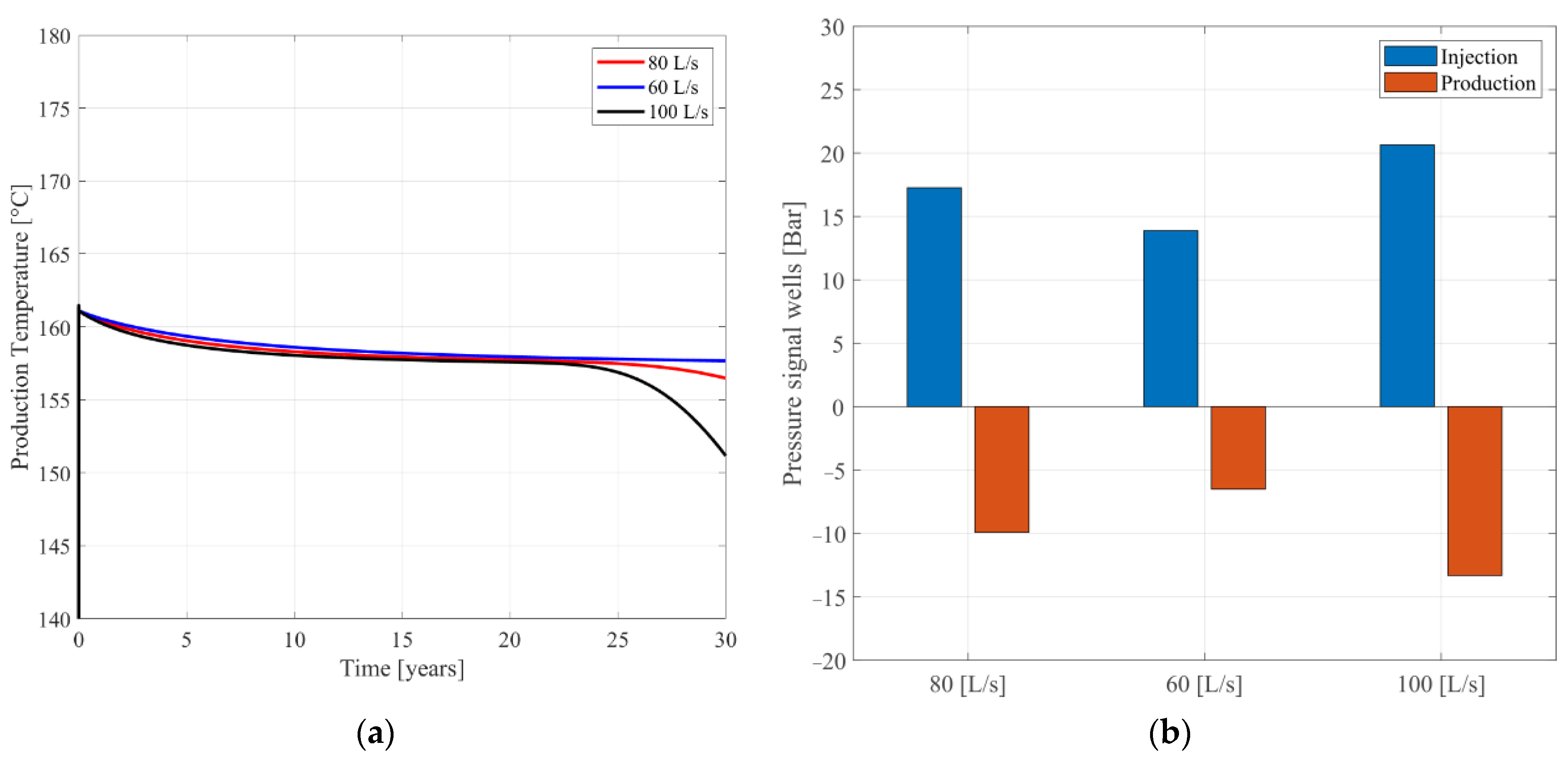
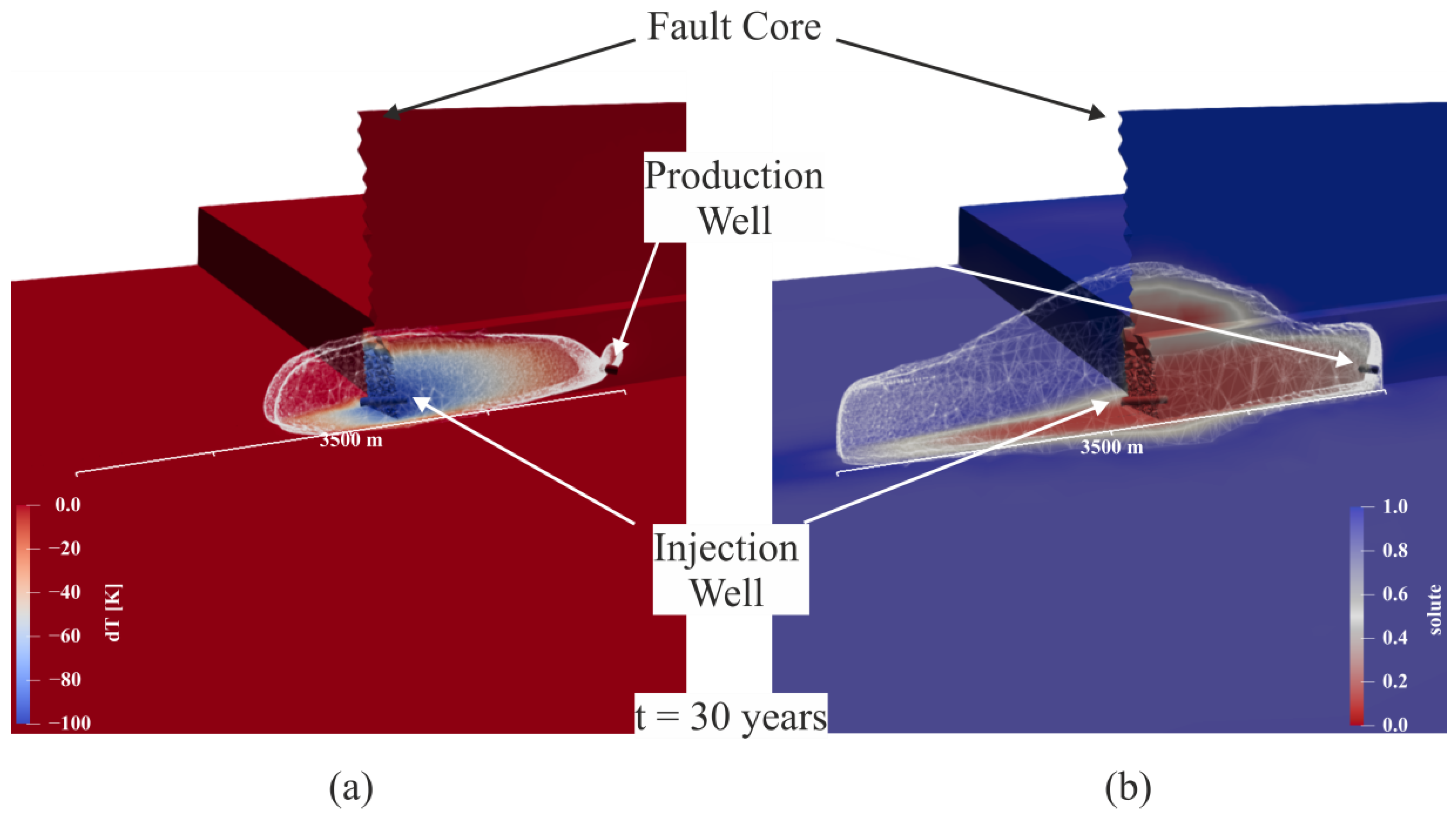
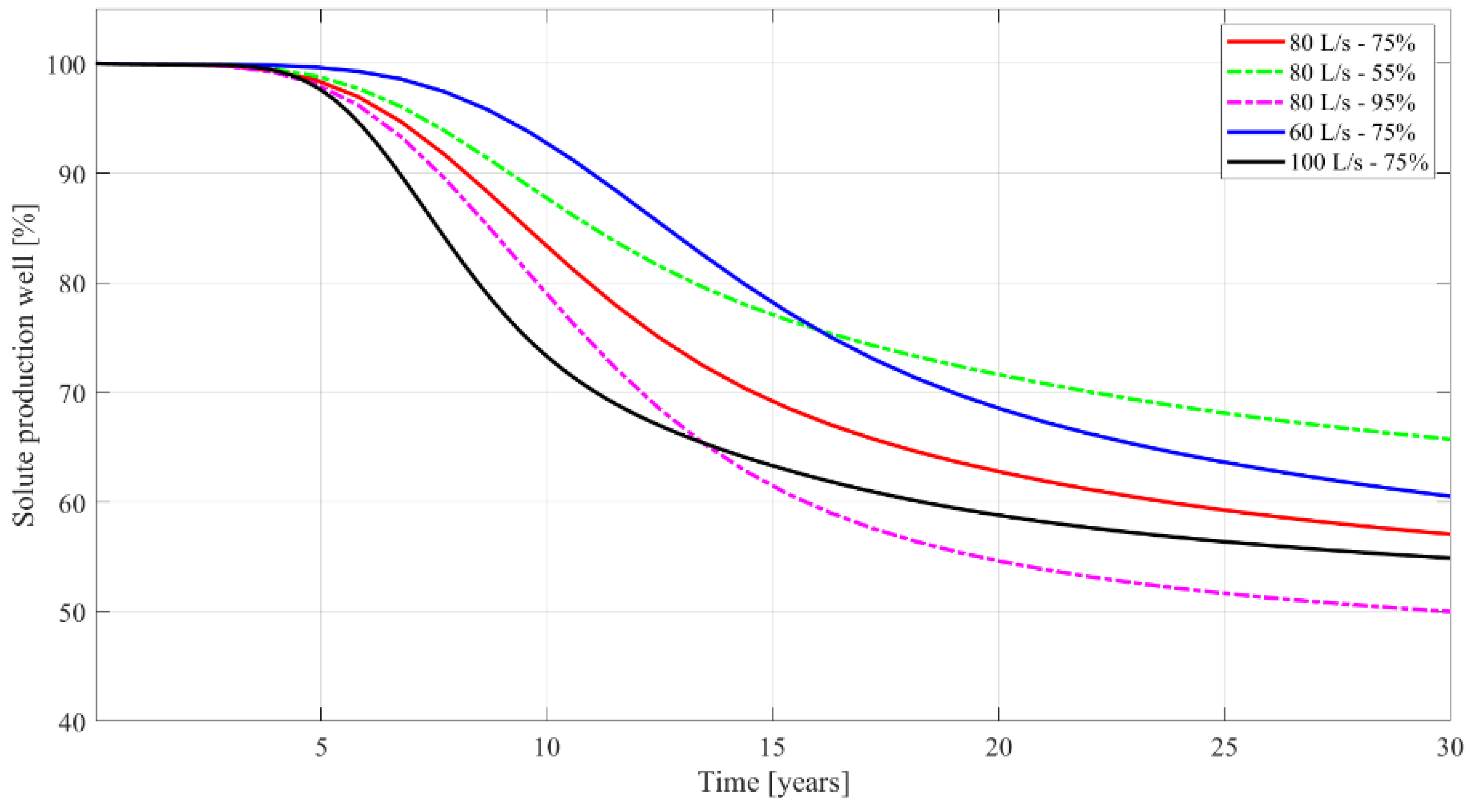
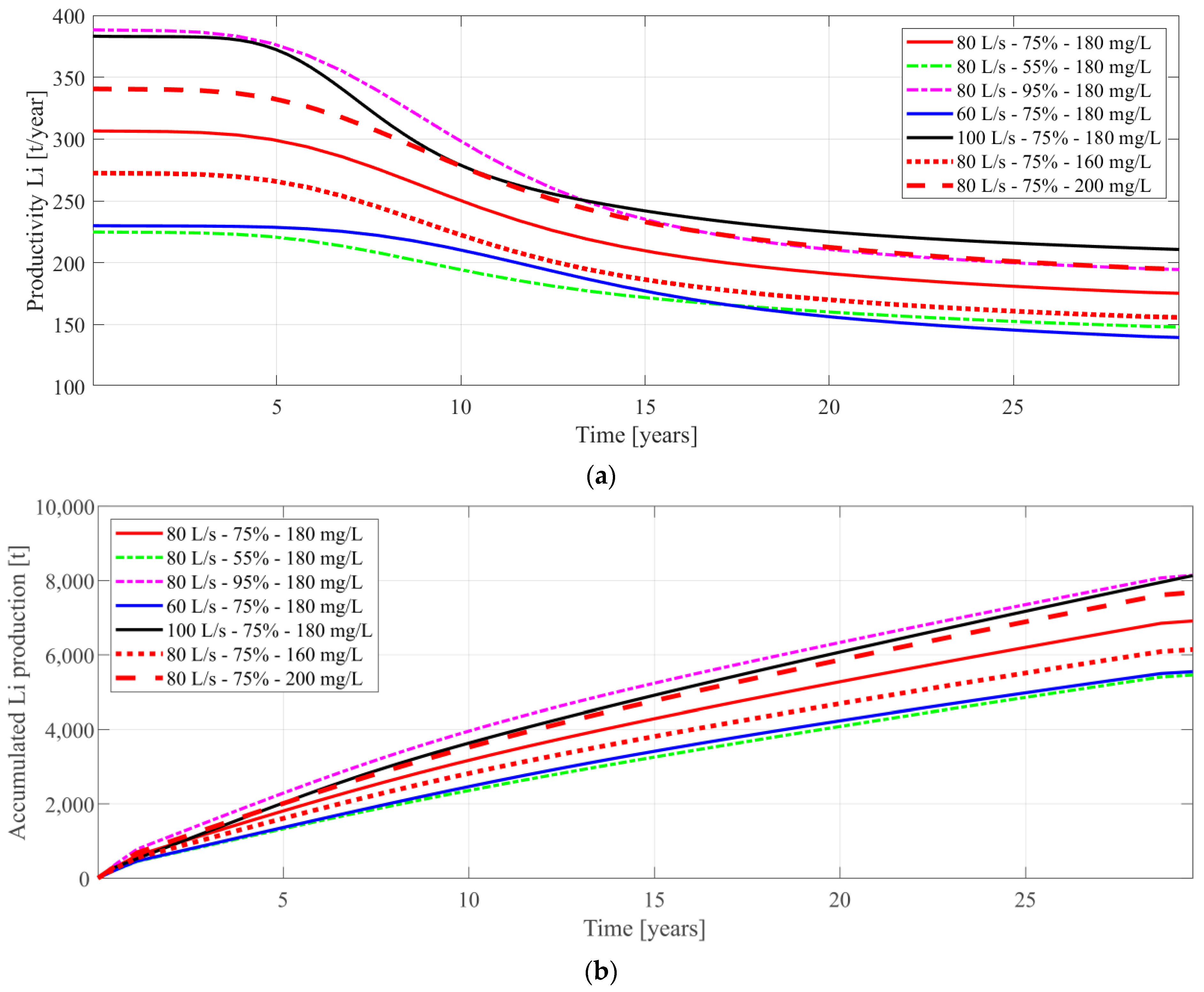
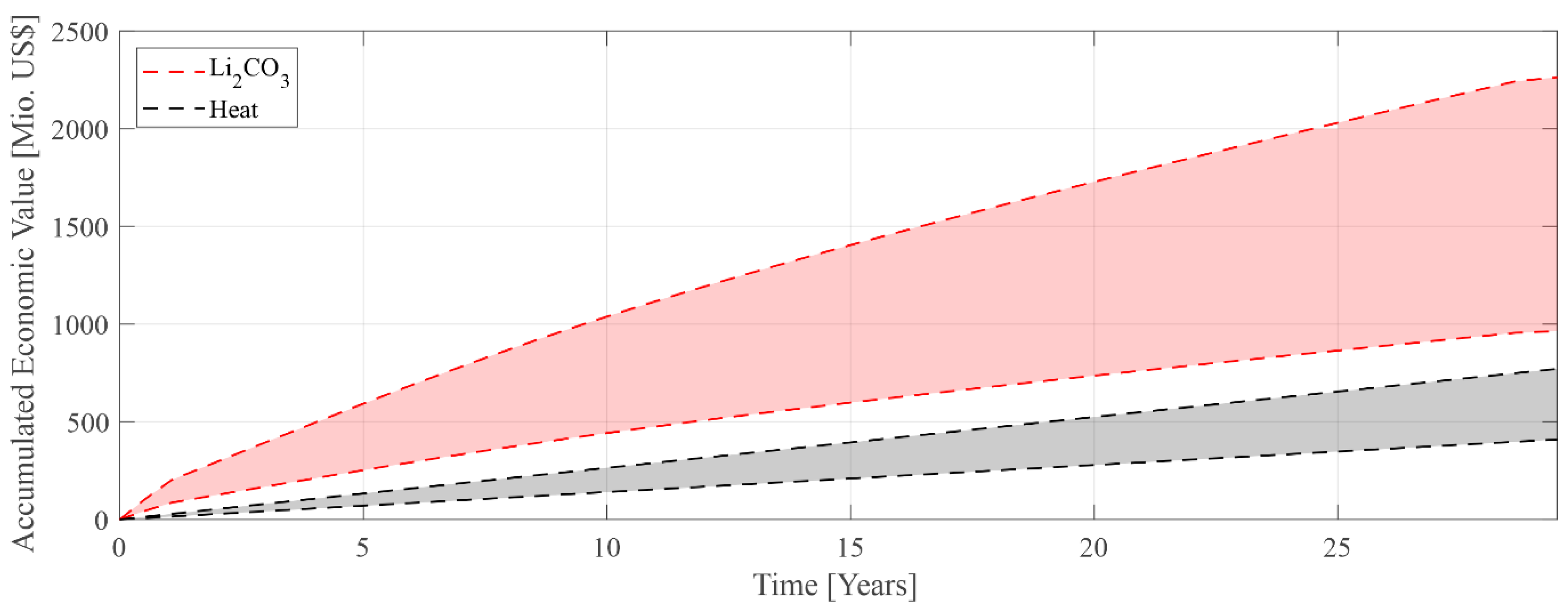
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schmidt, M. Rohstoffrisikobewertung—Lithium: Rohstoffinformationen 33; DERA-Deutsche Rohstoffagentur in der Bundesanstalt für Geowissenschaften und Rohstoffe: Berlin, Germany, 2017. [Google Scholar]
- Schmidt, M. Rohstoffrisikobewertung—Lithium: Rohstoffinformationen 54; DERA-Deutsche Rohstoffagentur in der Bundesanstalt für Geowissenschaften und Rohstoffe: Berlin, Germany, 2023; ISBN 9783943566031. [Google Scholar]
- Martin, G.; Rentsch, L.; Höck, M.; Bertau, M. Lithium market research—Global supply, future demand and price development. Energy Storage Mater. 2017, 6, 171–179. [Google Scholar] [CrossRef]
- Meng, F.; McNeice, J.; Zadeh, S.S.; Ghahreman, A. Review of Lithium Production and Recovery from Minerals, Brines, and Lithium-Ion Batteries. Miner. Process. Extr. Met. Rev. 2021, 42, 123–141. [Google Scholar] [CrossRef]
- Goldberg, V.; Nitschke, F.; Kluge, T. Herausforderungen und Chancen für die Lithiumgewinnung aus geothermalen Systemen in Deutschland—Teil 2: Potenziale und Produktionsszenarien in Deutschland. Grundwasser 2022, 27, 261–275. [Google Scholar] [CrossRef]
- Europäisches Parlament. Fit Für 55: Abgeordnete Unterstützen Ziel der Emissionsneutralität Für neue Autos und Lieferwagen ab 2035. 2022. Available online: https://www.europarl.europa.eu/news/de/press-room/20220603IPR32129/fit-fur-55-emissionsneutralitat-fur-neue-pkw-und-lieferwagen-ab-2035 (accessed on 1 March 2023).
- Europäische Kommission. Widerstandsfähigkeit der EU bei kritischen Rohstoffen: Einen Pfad hin zu größerer Sicherheit und Nachhaltigkeit abstecke; Mitteilung der Kommission an das Europäische Parlament, den Rat, den Europäischen Wirtschafts- und Sozialausschuss und den Ausschuss der Regionen; Version COM(2020) 474 final; Europäische Kommission: Brussels, Belgium, 3 September 2020. [Google Scholar]
- DERA. Batterierohstoffe Für die Elektromobilität; DERA Themenheft: Berlin, Germany, 2021. [Google Scholar]
- Reich, R.; Slunitschek, K.; Danisi, R.M.; Eiche, E.; Kolb, J. Lithium Extraction Techniques and the Application Potential of Different Sorbents for Lithium Recovery from Brines. Miner. Process. Extr. Met. Rev. 2022, 44, 261–280. [Google Scholar] [CrossRef]
- Stringfellow, W.T.; Dobson, P.F. Technology for the Recovery of Lithium from Geothermal Brines. Energies 2021, 14, 6805. [Google Scholar] [CrossRef]
- Sanjuan, B.; Gourcerol, B.; Millot, R.; Rettenmaier, D.; Jeandel, E.; Rombaut, A. Lithium-rich geothermal brines in Europe: An up-date about geochemical characteristics and implications for potential Li resources. Geothermics 2022, 101, 102385. [Google Scholar] [CrossRef]
- Rettenmaier, D.; Millot, R.; Blandine, G.; Sanjuan, B.; Elodie, J.; Sophie, L.; Clement, B.; Zorn, R. Rohstoff Lithium aus Geothermie—Und aus Europa (EuGeLi—European Geothermal Lithium); Der Geothermie Kongress: Essen, Germany, 2021. [Google Scholar]
- Bauer, M.; Freeden, W.; Jacobi, H.; Neu, T. Handbuch Tiefe Geothermie; Springer Spektrum: Berlin/Heidelberg, Germany, 2014; ISBN 9783642545108. [Google Scholar]
- Goldberg, V.; Kluge, T.; Nitschke, F. Herausforderungen und Chancen für die Lithiumgewinnung aus geothermalen Systemen in Deutschland—Teil 1: Literaturvergleich bestehender Extraktionstechnologien. Grundwasser 2022, 27, 239–259. [Google Scholar] [CrossRef]
- Dilger, G.; Deinhardt, A.; Reimer, D.; Link, K.; Zwicklhuber, K.; Götzl, G. Tiefe Geothermie-Projekte in Deutschland 2021/2022. Geotherm. Energ. Fachz. Für Geotherm. Forsch. Anwend. Dtschl. Osterr. Der Schweiz 2021, 30, 100. [Google Scholar]
- Bridge, G.; Faigen, E. Towards the lithium-ion battery production network: Thinking beyond mineral supply chains. Energy Res. Soc. Sci. 2022, 89, 102659. [Google Scholar] [CrossRef]
- Fraunhofer ISI. Geplante Gesamte Batteriezellproduktionskapazität [GWh]. BMBF-Geförderten Begleitmaßnahme BEMA 2020 II. 2022. Available online: https://www.isi.fraunhofer.de/de/presse/2022/presseinfo-17-Batteriezellfertigung-Verzehnfachung-2030.html (accessed on 15 March 2023).
- Trading Economics. Lithium. 2022. Available online: https://tradingeconomics.com/commodity/lithium (accessed on 14 November 2022).
- Trading Economics. Lithium Carbonate Prices. 2023. Available online: https://tradingeconomics.com/commodity/lithium (accessed on 15 March 2023).
- Steiger, K.; Hilgers, C.; Kolb, J. Lithiumbedarf Für Die Batteriezellen-Produktion in Deutschland Und Europa Im Jahr 2030; KIT: Karlsruhe, Germany, 2022. [Google Scholar]
- Geyer, O.F.; Gwinner, M.; Simon, T. Geologie von Baden-Württemberg, 5, Völlig neu Bearbeitete Auflage; Schweizerbart: Stuttgart, Germany, 2011; ISBN 978-3-510-65267-9. [Google Scholar]
- Eisbacher, G.H.; Fielitz, W. Karlsruhe und seine Region. In Sammlung Geologischer Führer Band 103; Gebrüder Borntraeger Verlagsbuchhandlung: Stuttgart, Germany, 2010. [Google Scholar]
- Grimmer, J.C.; Ritter, J.R.R.; Eisbacher, G.H.; Fielitz, W. The Late Variscan control on the location and asymmetry of the Upper Rhine Graben. Int. J. Earth Sci. 2017, 106, 827–853. [Google Scholar] [CrossRef]
- Sanjuan, B.; Millot, R.; Innocent, C.; Dezayes, C.; Scheiber, J.; Brach, M. Major geochemical characteristics of geothermal brines from the Upper Rhine Graben granitic basement with constraints on temperature and circulation. Chem. Geol. 2016, 428, 27–47. [Google Scholar] [CrossRef]
- Vidal, J.; Genter, A. Overview of naturally permeable fractured reservoirs in the central and southern Upper Rhine Graben: Insights from geothermal wells. Geothermics 2018, 74, 57–73. [Google Scholar] [CrossRef]
- Vulcan Energy Vulcan Zero Carbon LithiumTM Project Phase One DFS Results and Resources-Reserves Update. 2023. Available online: https://v-er.eu/vulcan-zero-carbon-lithium-project-phase-one-dfs-results-and-resources-reserves-update/ (accessed on 15 March 2023).
- Q-con GmbH; Deutsche Erdwärme GmbH Seismische Gefährdungsstudie für das Geothermieprojekt. 2020. Available online: https://www.graben-neudorf.de/index.php?id=382 (accessed on 15 March 2023).
- Moeck, I.S. Catalog of geothermal play types based on geologic controls. Renew. Sustain. Energy Rev. 2014, 37, 867–882. [Google Scholar] [CrossRef] [Green Version]
- Eggeling, L.; Herr, K.; Goldberg, V.; Siefert, D.; Köhler, J.; Kölbel, T.; Reith, S. Schlussbericht zum Verbundprojekt ANEMONA. Anlagenmonitoring als Schlüsseltechnologie für den erfolgreichen Betrieb von Geothermiekraftwerken in Deutschland; EnBW AG: Karlsruhe, Germany, 2018. [Google Scholar]
- Uhde, J. Welcome to the Geothermal Power Plant Insheim. In Proceedings of the 9th European Geothermal Workshop, Karlsruhe, Germany, 23–24 September 2021. [Google Scholar]
- Drüppel, K.; Stober, I.; Grimmer, J.C.; Mertz-Kraus, R. Experimental alteration of granitic rocks: Implications for the evolution of geothermal brines in the Upper Rhine Graben, Germany. Geothermics 2020, 88, 101903. [Google Scholar] [CrossRef]
- Bąbel, M.; Schreiber, B.C. Geochemistry of Evaporites and Evolution of Seawater. In Treatise on Geochemistry; Elsevier: Amsterdam, The Netherlands, 2014; Volume 9, pp. 483–560. ISBN 9780080983004. [Google Scholar]
- Burisch, M.; Walter, B.F.; Gerdes, A.; Lanz, M.; Markl, G. Late-stage anhydrite-gypsum-siderite-dolomite-calcite assemblages record the transition from a deep to a shallow hydrothermal system in the Schwarzwald mining district, SW Germany. Geochim. et Cosmochim. Acta 2018, 223, 259–278. [Google Scholar] [CrossRef]
- Aquilina, L.; Ladouche, B.; Doerfliger, N.; Seidel, J.L.; Bakalowicz, M.; Dupuy, C.; Le Strat, P. Origin, evolution and residence time of saline thermal fluids (Balaruc springs, southern France): Implications for fluid transfer across the continental shelf. Chem. Geol. 2002, 192, 1–21. [Google Scholar] [CrossRef]
- Egert, R.; Gholami Korzani, M.; Held, S.; Kohl, T. Implications on large-scale flow of the fractured EGS reservoir Soultz inferred from hydraulic data and tracer experiments. Geothermics 2020, 84, 101749. [Google Scholar] [CrossRef]
- Sanjuan, B.; Scheiber, J.; Gal, F.; Touzelet, S.; Genter, A.; Villadangos, G. Inter-well chemical tracer testing at the Rittershoffen geothermal site (Alsace, France). In Proceedings of the European Geothermal Congress 2016, Strasbourg, France, 19–24 September 2016. [Google Scholar]
- Regenspurg, S.; Feldbusch, E.; Norden, B.; Tichomirowa, M. Fluid-rock interactions in a geothermal Rotliegend/Permo-Carboniferous reservoir (North German Basin). Appl. Geochem. 2016, 69, 12–27. [Google Scholar] [CrossRef]
- Palmer, T.D.; Howard, J.H.; Lande, D.P. Geothermal Development of the Salton Trough, California and Mexico, UCRL-51775; U.S. Department of Commerce: Livermore, CA, USA, 1975. [Google Scholar]
- Bertold, C.E.; Baker, D.H. Lithium recovery from geothermal fluids, in: Lithium resources and requirements by the year 2000. Geol. Surv. Prof. Pap. 1976, 1005, 61–66. [Google Scholar]
- Liu, G.; Zhao, Z.; Ghahreman, A. Novel approaches for lithium extraction from salt-lake brines: A review. Hydrometallurgy 2019, 187, 81–100. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Lee, M.S. A review on the separation of lithium ion from leach liquors of primary and secondary resources by solvent extraction with commercial extractants. Processes 2018, 6, 55. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.; Jing, Y.; Xiao, J.; Wang, X.; Yao, Y.; Jia, Y. Solvent extraction of lithium from aqueous solution using non-fluorinated functionalized ionic liquids as extraction agents. Sep. Purif. Technol. 2017, 172, 473–479. [Google Scholar] [CrossRef]
- Xiang, W.; Liang, S.; Zhou, Z.; Qin, W.; Fei, W. Extraction of lithium from salt lake brine containing borate anion and high concentration of magnesium. Hydrometallurgy 2016, 166, 9–15. [Google Scholar] [CrossRef]
- Xiang, W.; Liang, S.; Zhou, Z.; Qin, W.; Fei, W. Lithium recovery from salt lake brine by counter-current extraction using tributyl phosphate/FeCl3 in methyl isobutyl ketone. Hydrometallurgy 2017, 171, 27–32. [Google Scholar] [CrossRef]
- Yu, X.; Fan, X.; Guo, Y.; Deng, T. Recovery of lithium from underground brine by multistage centrifugal extraction using tri-isobutyl phosphate. Sep. Purif. Technol. 2019, 211, 790–798. [Google Scholar] [CrossRef]
- Swain, B. Recovery and recycling of lithium: A review. Sep. Purif. Technol. 2017, 172, 388–403. [Google Scholar] [CrossRef]
- Zhang, Z.; Jia, Y.; Liu, B.; Sun, H.; Jing, Y.; Zhang, Q.; Shao, F.; Qi, M.; Yao, Y. Study on behavior of lithium ion in solvent extraction and isotope separation. J. Mol. Liq. 2021, 324, 114709. [Google Scholar] [CrossRef]
- Park, J.; Jung, Y.; Kusumah, P.; Lee, J.; Kwon, K.; Lee, C.K. Application of ionic liquids in hydrometallurgy. Int. J. Mol. Sci. 2014, 15, 15320–15343. [Google Scholar] [CrossRef] [PubMed]
- Reich, R.; Danisi, R.M.; Kluge, T.; Eiche, E.; Kolb, J. Structural and compositional variation of zeolite 13X in lithium sorption experiments using synthetic solutions and geothermal brine. Microporous Mesoporous Mater. 2023, 359, 112623. [Google Scholar] [CrossRef]
- Battistel, A.; Palagonia, M.S.; Brogioli, D.; La Mantia, F.; Trócoli, R. Electrochemical Methods for Lithium Recovery: A Comprehensive and Critical Review. Adv. Mater. 2020, 32, 1905440. [Google Scholar] [CrossRef] [Green Version]
- Calvo, E.J. Electrochemical methods for sustainable recovery of lithium from natural brines and battery recycling. Curr. Opin. Electrochem. 2019, 15, 102–108. [Google Scholar] [CrossRef]
- Romero, V.C.E.; Llano, K.; Calvo, E.J. Electrochemical extraction of lithium by ion insertion from natural brine using a flow-by reactor: Possibilities and limitations. Electrochem. commun. 2021, 125, 106980. [Google Scholar] [CrossRef]
- Li, X.; Mo, Y.; Qing, W.; Shao, S.; Tang, C.Y.; Li, J. Membrane-based technologies for lithium recovery from water lithium resources: A review. J. Memb. Sci. 2019, 591, 117317. [Google Scholar] [CrossRef]
- Adionics Adionics. 2021. Available online: http://www.adionics.com/en/homepage/markets/Lithium (accessed on 31 January 2022).
- Eramet Eramet. 2021. Available online: https://www.eramet.com/en/eramet-and-electricite-de-strasbourg-announce-success-first-pilot-test-extract-lithium-geothermal (accessed on 31 January 2022).
- Geolith Geolith. 2021. Available online: https://en.geolith.fr/copie-de-technologies (accessed on 31 January 2022).
- Unlimited Unlimited. 2021. Available online: https://www.geothermal-lithium.org/ (accessed on 31 January 2022).
- Wedin, F. Vulcan Energy Resources 2022 Corporate presentation Q1 2022. Available online: www.v-er.eu (accessed on 15 July 2022).
- Goldberg, V.; Winter, D.; Nitschke, F.; Held, S.; Groß, F.; Pfeiffle, D.; Uhde, J.; Morata, D.; Koschikowski, J.; Kohl, T. Development of a continuous silica treatment strategy for metal extraction processes in operating geothermal plants. Desalination 2023, 564, 116775. [Google Scholar] [CrossRef]
- Leiter, C.; Elsner, M. Geologische Vorausprofile der Bohrungen GN-Th-1 & GN-Th-2, Graben-Neudorf. Hauptbetriebsplan—Geotherm. Graben-neud. 2020. Available online: https://www.graben-neudorf.de/index.php?id=382 (accessed on 15 March 2023).
- Bauer, J.F.; Meier, S.; Philipp, S.L. Architecture, fracture system, mechanical properties and permeability structure of a fault zone in Lower Triassic sandstone, Upper Rhine Graben. Tectonophysics 2015, 647, 132–145. [Google Scholar] [CrossRef]
- Choi, J.H.; Edwards, P.; Ko, K.; Kim, Y.S. Definition and classification of fault damage zones: A review and a new methodological approach. Earth Sci. Rev. 2016, 152, 70–87. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Stricker, K.; Grimmer, J.C.; Egert, R.; Bremer, J.; Korzani, M.G.; Schill, E.; Kohl, T. The potential of depleted oil reservoirs for high-temperature storage systems. Energies 2020, 13, 6510. [Google Scholar] [CrossRef]
- Evans, J.P.; Forster, C.B.; Goddard, J.V. Permeability of fault-related rocks, and implications for hydraulic structure of fault zones. J. Struct. Geol. 1997, 19, 1393–1404. [Google Scholar] [CrossRef]
- Francke, H.; Thorade, M. Density and viscosity of brine: An overview from a process engineers perspective. Geochemistry 2010, 70, 23–32. [Google Scholar] [CrossRef] [Green Version]
- Ramalingam, A.; Arumugam, S. Experimental study on specific heat of hot brine for salt gradient solar pond application. Int. J. ChemTech Res. 2012, 4, 956–961. [Google Scholar]
- Toner, J.D.; Catling, D.C. A Low-Temperature Thermodynamic Model for the Na-K-Ca-Mg-Cl System Incorporating New Experimental Heat Capacities in KCl, MgCl2, and CaCl2 Solutions. J. Chem. Eng. Data 2017, 62, 995–1010. [Google Scholar] [CrossRef]
- Schneider, M. Geothermie Macht Unterhaching Unabhängig: Ein Dorf Braucht Keinen Gaspreisdeckel. Available online: https://www.merkur.de/wirtschaft/unterhaching-geothermie-germering-kosten-waerme-heizen-heizung-bayern-energiekrise-gaspreisdeckel-92017391.html (accessed on 17 March 2023).
- Gholami Korzani, M.; Held, S.; Kohl, T. Numerical based filtering concept for feasibility evaluation and reservoir performance enhancement of hydrothermal doublet systems. J. Pet. Sci. Eng. 2020, 190, 106803. [Google Scholar] [CrossRef]
- Permann, C.J.; Gaston, D.R.; Andrš, D.; Carlsen, R.W.; Kong, F.; Lindsay, A.D.; Miller, J.M.; Peterson, J.W.; Slaughter, A.E.; Stogner, R.H.; et al. MOOSE: Enabling massively parallel multiphysics simulation. SoftwareX 2020, 11, 100430. [Google Scholar] [CrossRef]
- Yan, G.; Busch, B.; Egert, R.; Esmaeilpour, M.; Stricker, K.; Kohl, T. Transport mechanisms of hydrothermal convection in faulted tight sandstones. EGUsphere 2022. [Google Scholar] [CrossRef]
- Egert, R.; Gholami Korzani, M.; Held, S.; Kohl, T. Thermo-hydraulic Modeling of an Enhanced Geothermal System in the Upper Rhine Graben Using MOOSE/TIGER. In Proceedings of the World Geothermal Congress (WGC 2021), Reykjavík, Iceland, 21–26 May 2021. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier (Environmental science series): New York, NY, USA, 1972. [Google Scholar]
- Dashti, A.; Gholami Korzani, M.; Geuzaine, C.; Egert, R.; Kohl, T. Impact of structural uncertainty on tracer test design in faulted geothermal reservoirs. Geothermics 2023, 107, 102607. [Google Scholar] [CrossRef]
- Baujard, C.; Genter, A.; Dalmais, E.; Maurer, V.; Hehn, R.; Rosillette, R.; Vidal, J.; Schmittbuhl, J. Hydrothermal characterization of wells GRT-1 and GRT-2 in Rittershoffen, France: Implications on the understanding of natural flow systems in the rhine graben. Geothermics 2017, 65, 255–268. [Google Scholar] [CrossRef] [Green Version]
- Held, S.; Genter, A.; Kohl, T.; Kölbel, T.; Sausse, J.; Schoenball, M. Economic evaluation of geothermal reservoir performance through modeling the complexity of the operating EGS in Soultz-sous-Forêts. Geothermics 2014, 51, 270–280. [Google Scholar] [CrossRef]
- Faltlhauser, M. Zahlen und Fakten zur Stromversorgung in Deutschland 2016; Wirtschaftsbeirat Bayern: München, Germany, 2016; pp. 1–24. [Google Scholar]
- Ghergut, J.; Wiegand, B.; Behrens, H.; Sauter, M. Model-Independent, and Model- Dependent Aspects of ‘Geothermal Solute’ Co-Production Forecast for Hydrothermal vs. Petrothermal Reservoirs. In Proceedings of the 48th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 6–8 February 2023; pp. 1–9. [Google Scholar]
- Calvo, G.; Mudd, G.; Valero, A.; Valero, A. Decreasing Ore Grades in Global Metallic Mining: A Theoretical Issue or a Global Reality? Resources 2016, 5, 36. [Google Scholar] [CrossRef] [Green Version]
- Höök, M.; Davidsson, S.; Johansson, S.; Tang, X. Decline and depletion rates of oil production: A comprehensive investigation. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20120448. [Google Scholar] [CrossRef]
- Destatis. Energiepreisentwicklung. 2023. Available online: https://www.destatis.de/DE/Themen/Wirtschaft/Preise/Publikationen/Energiepreise/energiepreisentwicklung-pdf-5619001.html (accessed on 15 March 2023).
- Xu, C.; Dai, Q.; Gaines, L.; Hu, M.; Tukker, A.; Steubing, B. Future material demand for automotive lithium-based batteries. Commun. Mater. 2020, 1, 10. [Google Scholar] [CrossRef]
| Layers | Porosity [%] | Permeability [m2] | Thermal Conductivity [W/(m.K)] | Matrix Density [kg/m3] | Specific Heat Capacity [J/(kg.K)] |
|---|---|---|---|---|---|
| Top layer | 4 | * 7 × 10−14 | 2.5 | 2400 | 730 |
| Top layer damage zone | * 2.71 × 10−13 | ||||
| Keuper | 4 | 5.42 × 10−16 | 2.5 | 2400 | 730 |
| Keuper damage zone | 2.71 × 10−15 | ||||
| Muschelkalk | 3 | 1.29 × 10−15 | 2 | 2400 | 730 |
| Muschelkalk damage zone | 6.46 × 10−15 | ||||
| Upper Buntsandstein | 9 | 2.3 × 10−15 | 3 | 2300 | 710 |
| Upper Buntsandstein damage zone | 1.15 × 10−14 | ||||
| Buntsandstein (reservoir) | 9 | 2.3 × 10−15 | 3 | 2300 | 710 |
| Reservoir damage zone | 1.21 × 10−13 | ||||
| Basement | 0.5 | 3.45 × 10−18 | 3.4 | 2600 | 900 |
| Basement damage zone | 1.73 × 10−17 | ||||
| Core zone | ** 0.5 | ** 3.45 × 10−18 | ** 2.5 | ** 2400 | ** 730 |
| Model Name | Extraction Efficiency [%] | Flow Rate [kg/s] | Li Concentration [mg/s] |
|---|---|---|---|
| Reference Model | 75 | 80 | 180 |
| 55% Ex | 55 (−27%) | 80 | 180 |
| 95% Ex | 95 (+27%) | 80 | 180 |
| 60 L/s | 75 | 60 (−25%) | 180 |
| 100 L/s | 75 | 100 (+25%) | 180 |
| 160 mg/L | 75 | 80 | 160 (−11%) |
| 200 mg/L | 75 | 80 | 200 (+11%) |
| Model Name | Initial Productivity [t/a] | Final Productivity [t/a] | Accumulated Li Production [t] | Mean Output over 30 Years [t/a] |
|---|---|---|---|---|
| Reference Model | 307 | 175 | 6920 | 234 |
| 55% Ex | 225 (−27%) | 148 (−15%) | 5465 (−21%) | 185 (−21%) |
| 95% Ex | 388 (+27%) | 194 (+11%) | 8148 (+18%) | 275 (+18%) |
| 60 L/s | 230 (−25%) | 139 (−21%) | 5554 (−20%) | 188 (−20%) |
| 100 L/s | 383 (+25%) | 210 (+20%) | 8150 (+18%) | 275 (+18%) |
| 160 mg/L | 272 (−11%) | 156 (−11%) | 6151 (−11%) | 208 (−11%) |
| 200 mg/L | 340 (+11%) | 195 (+11%) | 7689 (+11%) | 260 (+11%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goldberg, V.; Dashti, A.; Egert, R.; Benny, B.; Kohl, T.; Nitschke, F. Challenges and Opportunities for Lithium Extraction from Geothermal Systems in Germany—Part 3: The Return of the Extraction Brine. Energies 2023, 16, 5899. https://doi.org/10.3390/en16165899
Goldberg V, Dashti A, Egert R, Benny B, Kohl T, Nitschke F. Challenges and Opportunities for Lithium Extraction from Geothermal Systems in Germany—Part 3: The Return of the Extraction Brine. Energies. 2023; 16(16):5899. https://doi.org/10.3390/en16165899
Chicago/Turabian StyleGoldberg, Valentin, Ali Dashti, Robert Egert, Binil Benny, Thomas Kohl, and Fabian Nitschke. 2023. "Challenges and Opportunities for Lithium Extraction from Geothermal Systems in Germany—Part 3: The Return of the Extraction Brine" Energies 16, no. 16: 5899. https://doi.org/10.3390/en16165899
APA StyleGoldberg, V., Dashti, A., Egert, R., Benny, B., Kohl, T., & Nitschke, F. (2023). Challenges and Opportunities for Lithium Extraction from Geothermal Systems in Germany—Part 3: The Return of the Extraction Brine. Energies, 16(16), 5899. https://doi.org/10.3390/en16165899







