Small-Signal Modeling and Stability Analysis of a Grid-Following Inverter with Inertia Emulation
Abstract
:1. Introduction
- How does the synthetic inertia control interact with other control loops in small-signal dynamics?
- How can the inverter-grid stability be guaranteed by understanding the relation between the synthetic inertia control and grid characteristics?
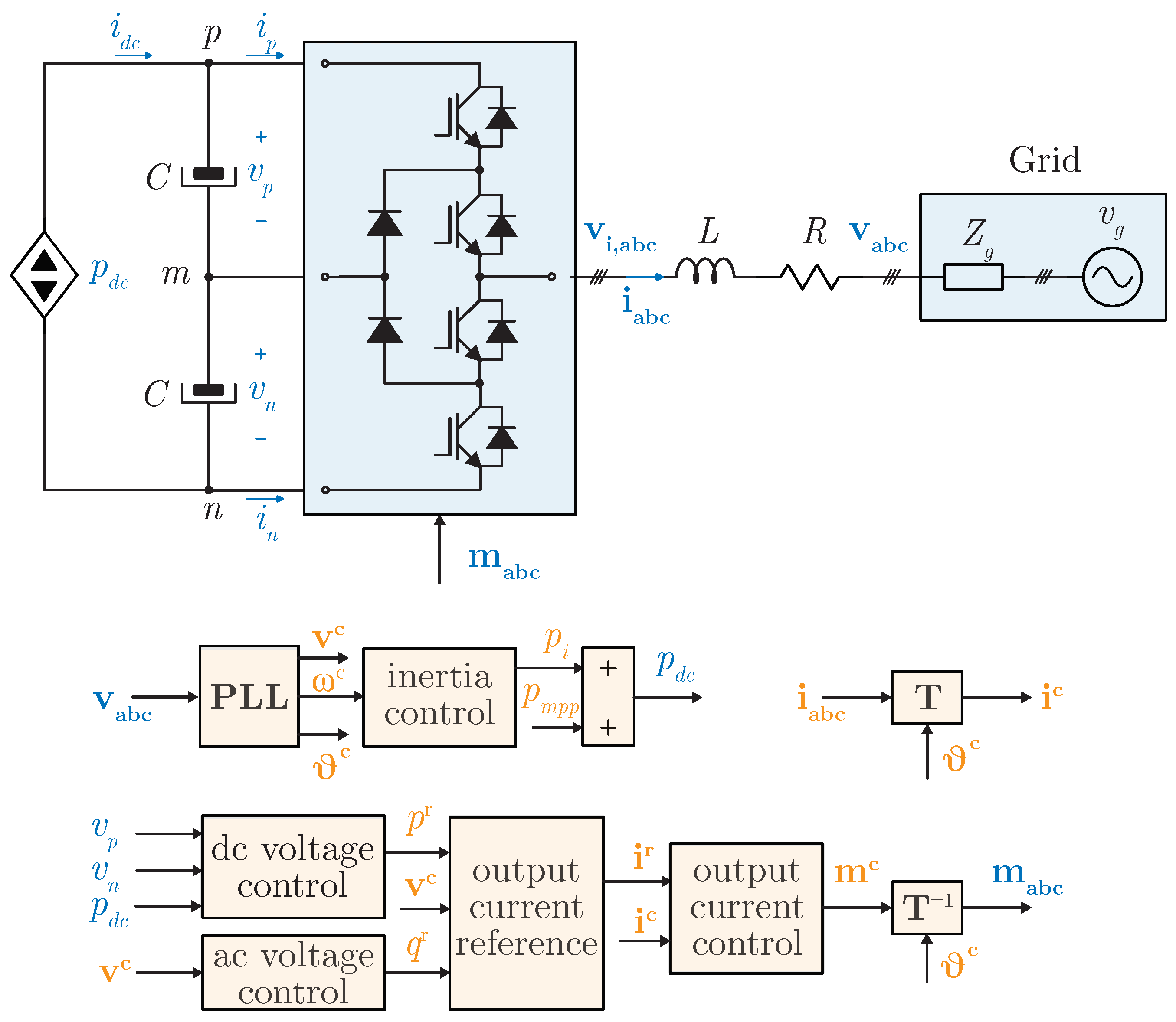
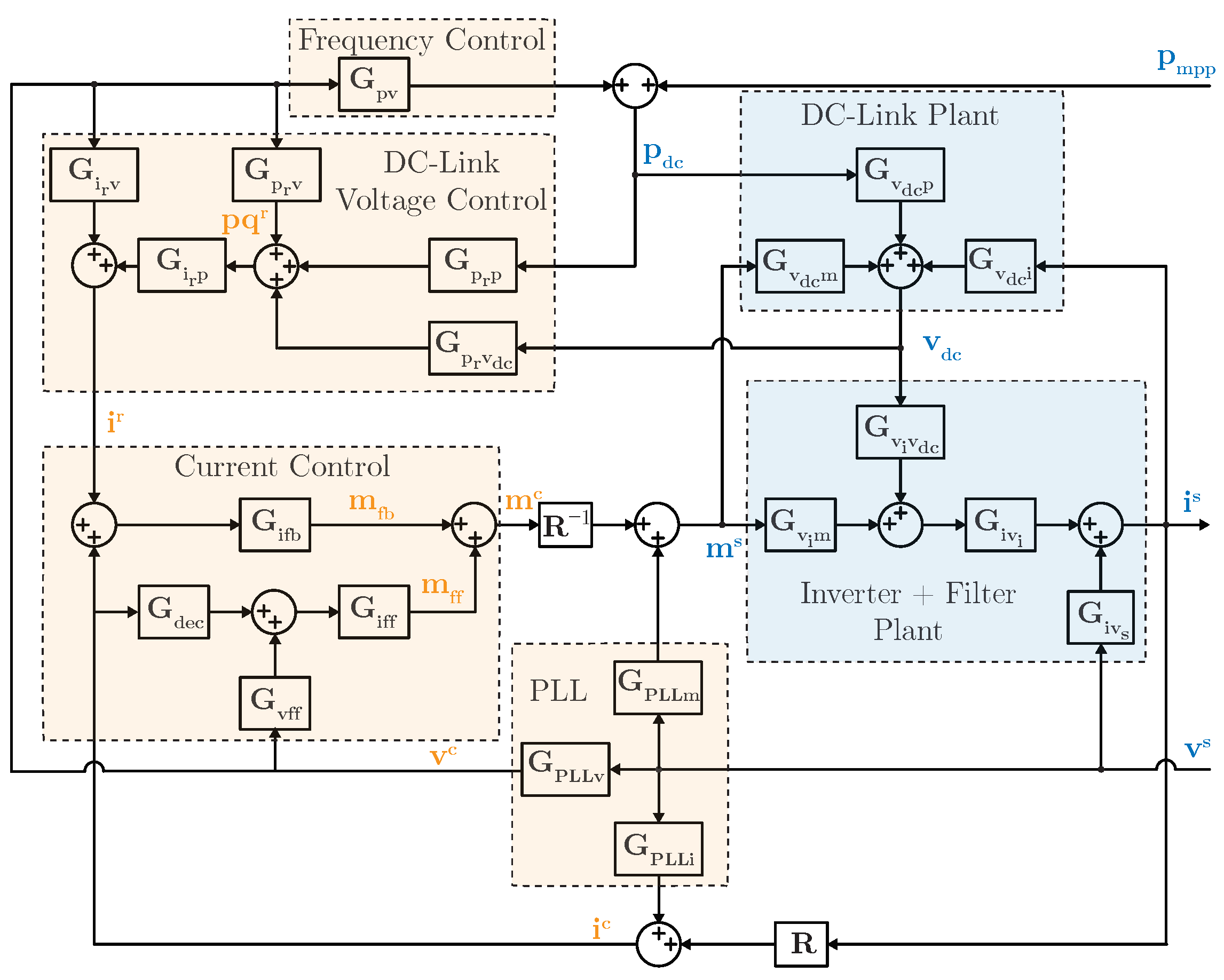
2. System Modeling
2.1. Inverter
2.2. Modulation and Delay
2.3. Phase-Locked Loop
2.4. Current Control
2.5. DC-Link Dynamic Modeling
2.6. Voltage Control
2.7. Frequency Control Support
2.8. Model Validation
3. Control Design
3.1. Current Control
3.2. DC Voltage Control
4. Grid-Connection Stability Analysis
4.1. Inverter and Grid Equivalent Models
4.2. Inverter Output Admittance
4.3. Connection to an RL Grid
5. Conclusions
- An increase in the synthetic inertia control gain leads to an overall degradation of small-signal stability.
- Power and voltage feedforward loops should have limited bandwidth to avoid interference with the effects of the synthetic inertia control.
- The bandwidth of the PLL should be restricted since it is cascaded in the synthetic inertia control loop.
- The maximum value for the synthetic inertia is inversely proportional to the grid equivalent short circuit ratio.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations and Symbols
| Abbreviation | Description | |
| BESS | Battery Energy Storage System | |
| ESS | Energy Storage System | |
| FLL | Frequency-Locked Loop | |
| GFL | Grid-Following | |
| GFM | Grid-Forming | |
| MPPT | Maximum Power Point Tracking | |
| PCC | Point of Common Coupling | |
| PI | Proportional-Integral | |
| PID | Proportional-Integral-Derivative | |
| PLL | Phase-Locked Loop | |
| PS | Power Synchronization | |
| RES | Renewable Energy Source | |
| ROCOF | Rate of Change of Frequency | |
| ROCOP | Rate Of Change of Power | |
| SCR | Short-Circuit Ratio | |
| SRF | Synchronous Reference Frame | |
| WECS | Wind Energy Conversion System | |
| Symbol | Description | Unit |
| C | DC-Link capacitance | F |
| Difference between PLL and system angles | rad | |
| i | Output current | A |
| DC-link current delivered by the input stage | A | |
| Negative DC-link current drained from the inverter stage | A | |
| Positive DC-link current drained from the inverter stage | A | |
| Derivative gain of the current controller | s/A | |
| Synthetic inertia gain | s | |
| Integral gain of the current controller | 1/As | |
| Integral gain of the PLL controller | 1/Vs | |
| Integral gain of the voltage controller | W/Vs | |
| Proportional gain of the current controller | 1/A | |
| Proportional gain of the PLL controller | 1/Vs | |
| Proportional gain of the voltage controller | W/V | |
| L | Output filter inductance | H |
| Equivalent grid inductance | H | |
| m | Modulation function | - |
| Modulation function reference from the feedback control | - | |
| Modulation function reference from the feedforward control | - | |
| Power delivered by the DC-link input stage | W | |
| Synthetic inertia control power reference | W | |
| Inverter active power reference | W | |
| Transfer function of the PI controller of the PLL | 1/Vs | |
| Proportional-integral DC-link voltage controller | W/V | |
| Vector of active and reactive power references | VA | |
| Proportional-integral-derivative current controller | 1/A | |
| Inverter reactive power reference | var | |
| Center value of the reactive power reference | var | |
| R | Output filter resistance | |
| Rotating matrix | - | |
| Equivalent grid resistance | ||
| Inverter droop gain | V/var | |
| Park transformation matrix | - | |
| Digital control time delay | s | |
| Time constant of the derivative current controller | s | |
| Cut-off frequency of the synthetic inertia control | s | |
| Sampling period | s | |
| Park transformation angle | rad | |
| Unitary vector | - | |
| v | Point-of-Common-Coupling voltage | V |
| DC-link voltage | V | |
| Grid voltage | V | |
| Voltage between common ground and DC-link middle point | V | |
| Inverter output voltage referred to the DC-link middle point | V | |
| Voltage across the DC-link lower capacitor | V | |
| Inverter rated output line voltage | V | |
| Voltage across the DC-link upper capacitor | V | |
| Angular frequency | rad/s | |
| Voltage feedforward cut-off frequency | rad/s | |
| Power feedforward cut-off frequency | rad/s | |
| Vector of variables in the DQ system frame | - | |
| Vector of variables in the DQ control frame | - | |
| Vector of reference variables in the DQ control frame | - | |
| Vector of variables in synchronous reference frame | - | |
| Vector of variables in stationary reference frame | - | |
| Inverter admittance matrix | S | |
| Grid impedance matrix |
References
- Yaramasu, V.; Wu, B.; Sen, P.C.; Kouro, S.; Narimani, M. High-power wind energy conversion systems: State-of-the-art and emerging technologies. Proc. IEEE 2015, 103, 740–788. [Google Scholar] [CrossRef]
- Carrasco, J.; Franquelo, L.; Bialasiewicz, J.; Galvan, E.; PortilloGuisado, R.; Prats, M.; Leon, J.; Moreno-Alfonso, N. Power-Electronic Systems for the Grid Integration of Renewable Energy Sources: A Survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]
- Vazquez, S.; Lukic, S.M.; Galvan, E.; Franquelo, L.G.; Carrasco, J.M. Energy Storage Systems for Transport and Grid Applications. IEEE Trans. Ind. Electron. 2010, 57, 3881–3895. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.; Chowdhury, T.A.; Dhar, A.; Al-Ismail, F.S.; Choudhury, M.; Shafiullah, M.; Hossain, M.; Ullah, A.; Rahman, S.M.; Hossain, A. Solar and Wind Energy Integrated System Frequency Control: A Critical Review on Recent Developments. Energies 2023, 16, 812. [Google Scholar] [CrossRef]
- Tielens, P.; Hertem, D.V. The relevance of inertia in power systems. Renew. Sustain. Energy Rev. 2016, 55, 999–1009. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2130–2146. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw Hill: New York, NY, USA, 1994. [Google Scholar]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar] [CrossRef]
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.P.; Hansen, T.M.; Tonkoski, R. Virtual inertia: Current trends and future directions. Appl. Sci. 2017, 7, 654. [Google Scholar] [CrossRef] [Green Version]
- Eriksson, R.; Modig, N.; Elkington, K. Synthetic inertia versus fast frequency response: A definition. Inst. Eng. Technol. 2018, 12, 507–514. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.; Kling, W.L.; Ferreira, J.A. Wind turbines emulating inertia and supporting primary frequency control. IEEE Trans. Power Syst. 2006, 21, 433–434. [Google Scholar] [CrossRef]
- Mauricio, J.M.; Marano, A.; Gomez-Exposito, A.; Martinez Ramos, J.L. Frequency Regulation Contribution Through Variable-Speed Wind Energy Conversion Systems. IEEE Trans. Power Syst. 2009, 24, 173–180. [Google Scholar] [CrossRef]
- Van de Vyver, J.; De Kooning, J.D.M.; Meersman, B.; Vandevelde, L.; Vandoorn, T.L. Droop Control as an Alternative Inertial Response Strategy for the Synthetic Inertia on Wind Turbines. IEEE Trans. Power Syst. 2016, 31, 1129–1138. [Google Scholar] [CrossRef]
- Bolzoni, A.; Perini, R. Feedback Couplings Evaluation on Synthetic Inertia Provision for Grid Frequency Support. IEEE Trans. Energy Convers. 2021, 36, 863–873. [Google Scholar] [CrossRef]
- Arani, M.F.M.; Mohamed, Y.A.R.I. Analysis and mitigation of undesirable impacts of implementing frequency support controllers in wind power generation. IEEE Trans. Energy Convers. 2016, 31, 174–186. [Google Scholar] [CrossRef]
- Fini, M.H.; Golshan, M.E.H.; Marti, J.R.; Ketabi, A. Determining the Required Frequency Control Reserve and Capacity and Location of Synchronous and Virtual Inertial Resources. IEEE Trans. Sustain. Energy 2023, 14, 27–38. [Google Scholar] [CrossRef]
- Alsharafi, A.S.; Besheer, A.H.; Emara, H.M. Primary Frequency Response Enhancement for Future Low Inertia Power Systems Using Hybrid Control Technique. Energies 2018, 11, 699. [Google Scholar] [CrossRef] [Green Version]
- Ochoa, D.; Martinez, S. Analytical Approach to Understanding the Effects of Implementing Fast-Frequency Response by Wind Turbines on the Short-Term Operation of Power Systems. Energies 2021, 14, 3660. [Google Scholar] [CrossRef]
- Duckwitz, D.; Fischer, B. Modeling and Design of df/dt -Based Inertia Control for Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1553–1564. [Google Scholar] [CrossRef]
- Fang, J.; Deng, H.; Tashakor, N.; Blaabjerg, F.; Goetz, S.M. State-Space Modeling and Control of Grid-Tied Power Converters with Capacitive/Battery Energy Storage and Grid-Supportive Services. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 234–250. [Google Scholar] [CrossRef]
- Fu, R.; Wang, X.; Zhang, Y.; Li, L. Inertial and Primary Frequency Response of PLL Synchronized VSC Interfaced Energy Resources. IEEE Trans. Power Syst. 2022, 37, 2998–3013. [Google Scholar] [CrossRef]
- Khazaei, J.; Tu, Z.; Liu, W. Small-Signal Modeling and Analysis of Virtual Inertia-Based PV Systems. IEEE Trans. Energy Convers. 2020, 35, 1129–1138. [Google Scholar] [CrossRef]
- Fang, J.; Lin, P.; Li, H.; Yang, Y.; Tang, Y. An improved virtual inertia control for three-phase voltage source converters connected to a weak grid. IEEE Trans. Power Electron. 2019, 34, 8660–8670. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Gu, Y.; Green, T.C. Revisiting Grid-Forming and Grid-Following Inverters: A Duality Theory. IEEE Trans. Power Syst. 2022, 37, 4541–4554. [Google Scholar] [CrossRef]
- Du, W.; Tuffner, F.K.; Schneider, K.P.; Lasseter, R.H.; Xie, J.; Chen, Z.; Bhattarai, B. Modeling of Grid-Forming and Grid-Following Inverters for Dynamic Simulation of Large-Scale Distribution Systems. IEEE Trans. Power Deliv. 2021, 36, 2035–2045. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Gong, H.; Wang, X.; Harnefors, L. Rethinking Current Controller Design for PLL-Synchronized VSCs in Weak Grids. IEEE Trans. Power Electron. 2022, 37, 1369–1381. [Google Scholar] [CrossRef]
- Harnefors, L.; Bongiorno, M.; Lundberg, S. Input-admittance calculation and shaping for controlled voltage-source converters. IEEE Trans. Ind. Electron. 2007, 54, 3323–3334. [Google Scholar] [CrossRef]
- Alawasa, K.M.; Mohamed, Y.A.R.I.; Xu, W. Modeling, analysis, and suppression of the impact of full-scale wind-power converters on subsynchronous damping. IEEE Syst. J. 2013, 7, 700–712. [Google Scholar] [CrossRef]
- Mansour, M.Z.; Mohammed, N.; Ravanji, M.H.; Bahrani, B. Output Impedance Derivation and Small-Signal Stability Analysis of a Power-Synchronized Grid Following Inverter. IEEE Trans. Energy Convers. 2022, 37, 2696–2707. [Google Scholar] [CrossRef]
- Tu, Y.; Liu, J.; Liu, Z.; Xue, D.; Cheng, L. Impedance-Based Analysis of Digital Control Delay in Grid-Tied Voltage Source Inverters. IEEE Trans. Power Electron. 2020, 35, 11666–11681. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Small-Signal Stability Assessment of Power Electronics Based Power Systems: A Discussion of Impedance-and Eigenvalue-Based Methods. IEEE Trans. Ind. Appl. 2017, 53, 5014–5030. [Google Scholar] [CrossRef]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Hoffmann, N.; Fuchs, F.W.; Kazmierkowski, M.P.; Schroder, D. Digital Current Control in a Rotating Reference Frame—Part I: System Modeling and the Discrete Time-Domain Current Controller with Improved Decoupling Capabilities. IEEE Trans. Power Electron. 2016, 31, 5290–5305. [Google Scholar] [CrossRef]
- Busada, C.A.; Jorge, S.G.; Solsona, J.A. Comments on ‘Digital Current Control in a Rotating Reference Frame—Part I: System Modeling and the Discrete Time-Domain Current Controller with Improved Decoupling Capabilities’. IEEE Trans. Power Electron. 2019, 34, 2980–2984. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, J.; Zhou, L.; Zhang, Y. DQ Current Control of Voltage Source Converters with a Decoupling Method Based on Preprocessed Reference Current Feed-forward. IEEE Trans. Power Electron. 2017, 32, 8904–8921. [Google Scholar] [CrossRef]
- Cvetanovic, R.; Petric, I.Z.; Mattavelli, P.; Buso, S. Small-Signal Modeling of Phase-Shifted Digital PWM in Interleaved and Multilevel Converters. IEEE Trans. Power Electron. 2023, 38, 3057–3068. [Google Scholar] [CrossRef]
- Jeong, S.; Jang, G. Stability Analysis of a Weak-Grid-Connected Voltage-Sourced Rectifier Considering the Phase-Locked Loop Dynamics. IEEE Trans. Power Syst. 2023, 38, 436–446. [Google Scholar] [CrossRef]
- Chung, S.K. A Phase Tracking System for Three Phase Utility Interface Inverters. IEEE Trans. Power Electron. 2000, 15, 431. [Google Scholar] [CrossRef] [Green Version]
- Park, R.H. Two-reaction theory of synchronous machines generalized method of analysis—Part I. Trans. Am. Inst. Electr. Eng. 1929, 48, 716–727. [Google Scholar] [CrossRef]
- Zhang, X.; Spencer, J.W.; Guerrero, J.M. Small-Signal Modeling of Digitally Controlled Grid-Connected Inverters with LCL Filters. IEEE Trans. Ind. Electron. 2013, 60, 3752–3765. [Google Scholar] [CrossRef] [Green Version]


























| Ref. | Analysis Method | Output Filter | Sync. | Digital Control Delay | Voltage Feedforward | DC Voltage Control | Power Feedforward | AC Voltage Control | Power Control | Synthetic Inertia |
|---|---|---|---|---|---|---|---|---|---|---|
| Proposed | Impedance | L | PLL | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ |
| [19] | Eigenvalue | LCL | PLL | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ |
| [20] | Eigenvalue | LCL | PLL | ✓ | ✗ | ✓ | ✗ | ✓ | ✓ | ✓ |
| [14] | Eigenvalue | LCL | FLL | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ |
| [21] | Phasor | L | PLL | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ |
| [22] | Eigenvalue | L | PLL | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ |
| [23] | Eigenvalue | L | PLL | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ |
| [26] | Impedance | L | PLL | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ |
| [27] | Impedance | L | PLL | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ |
| [28] | Impedance | L | PLL | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ |
| [29] | Impedance | L | PLL | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ |
| [30] | Impedance | L | PS | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ |
| [31] | Impedance | LCL | PLL | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| Parameter | Symbol | Value |
|---|---|---|
| Output inductance | L | 0.1 pu |
| Output resistance | R | 0.005 pu |
| Proportional gain | 0.1 pu | |
| Integrator gain | 2.0 pu | |
| Derivative gain | 0.0001 pu | |
| Derivative time constant | 0.0015 s | |
| Direct current reference | 1.0 pu | |
| Quadrature current reference | 0.0 pu | |
| Computational time delay | 0.001 s | |
| Dc-link voltage | 2.5 pu |
| Parameter | Symbol | Value |
|---|---|---|
| DC-link capacitance | C | 7.7 pu |
| Proportional gain | 3.3 pu | |
| Integral gain | 5.5 pu | |
| Active power reference | 1.0 pu | |
| Reactive power reference | 0.0 pu | |
| Cut-off frequency of power feedforward | rad/s |
| Parameter | Symbol | Value |
|---|---|---|
| PLL proportional gain | 377 pu/s | |
| PLL integral gain | 71,060 s | |
| Reactive power reference | 0 pu | |
| Output voltage amplitude | 1 pu | |
| Droop gain | 0.1 pu | |
| Inertia control gain | 1 s | |
| Inertia control time constant | 0.1 s | |
| Short-Circuit Ratio | SCR | 20 pu |
| Line R/L ratio | R/L | 0.1 pu |
| Output voltage feedforward cut-off frequency | rad/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schramm Dall’Asta, M.; Brunelli Lazzarin, T. Small-Signal Modeling and Stability Analysis of a Grid-Following Inverter with Inertia Emulation. Energies 2023, 16, 5894. https://doi.org/10.3390/en16165894
Schramm Dall’Asta M, Brunelli Lazzarin T. Small-Signal Modeling and Stability Analysis of a Grid-Following Inverter with Inertia Emulation. Energies. 2023; 16(16):5894. https://doi.org/10.3390/en16165894
Chicago/Turabian StyleSchramm Dall’Asta, Matheus, and Telles Brunelli Lazzarin. 2023. "Small-Signal Modeling and Stability Analysis of a Grid-Following Inverter with Inertia Emulation" Energies 16, no. 16: 5894. https://doi.org/10.3390/en16165894
APA StyleSchramm Dall’Asta, M., & Brunelli Lazzarin, T. (2023). Small-Signal Modeling and Stability Analysis of a Grid-Following Inverter with Inertia Emulation. Energies, 16(16), 5894. https://doi.org/10.3390/en16165894







