Abstract
With the increasing application of lithium-ion batteries, accurate estimation of the state of health (SOH) of lithium-ion batteries is of great significance for the safe operation of lithium-ion battery systems and the reduction of operation and maintenance costs. The complex physical and chemical reactions inside the lithium battery and the complex external working conditions make it challenging to achieve an accurate health-state estimation and life prediction. Therefore, the accurate estimation of the SOH of lithium-ion batteries is an important issue. At present, electrochemical impedance spectroscopy (EIS) is widely used in the study of battery-power impedance characteristics and battery-state estimation due to its advantage of nondestructive measurement. For this reason, this paper summarizes the research progress of lithium-ion SOH estimation based on EIS in recent years and details it layer by layer, mainly from two aspects: first, the quantitative relationship model between the characteristic parameters and SOH is established by constructing a frequency domain-equivalent circuit model. Secondly, we construct a quantitative relationship model between EIS data and SOH using the data-driven method. Finally, the advantages and disadvantages of different methods and estimation accuracy are analyzed and compared, and the future estimation of SOH based on EIS is prospected.
1. Introduction
In recent years, transportation electrification has developed rapidly worldwide, which helps to reduce greenhouse gas emissions and alleviate global warming. The lithium-ion battery (LIB), as the main energy-storage device, is one of the key components of electric transport systems.
In the practical application of lithium-ion batteries, the SOH of the battery is particularly important. As one of the important performance parameters of the electric vehicle battery, when the parameter shows that it has dropped to meet the normal demand, it is necessary to replace it with a new lithium battery in time to ensure the safe use of the electric vehicle [1,2,3,4]. Because the process of battery degradation to failure is very complex, there are many internal and external factors that affect lithium battery SOH, which brings many difficulties to the research of lithium battery SOH [5,6,7].
At present, SOH-estimation methods for lithium-ion batteries can be roughly divided into battery-model-based estimation methods and data-driven estimation methods [8,9,10,11]. The commonly used battery SOH-estimation methods rarely take into account the electrode–interface reaction information and usually only estimate based on the external characteristics of the battery or the DC internal resistance [12]. However, when lithium-ion batteries are charged and discharged, complex electrochemical reactions will occur at the internal electrode interface, and the reaction results are closely related to the battery’s SOH [13]. This shows that the SOH of the battery can also be estimated by studying the relationship between the electrode–interface information inside the battery and the battery state [14,15,16,17,18]. EIS, which contains rich information on material properties, interface phenomena, and electrochemical reactions within the battery, can reflect the aging state of the battery from multiple perspectives and is considered an effective means of achieving SOH estimation [19,20,21,22]. Table 1 compares the advantages and disadvantages of different methods.

Table 1.
Common SOH-prediction methods for lithium batteries.
However, few studies have summarized the research progress of the SOH estimation of lithium-ion batteries from the perspective of EIS. Therefore, this paper summarizes the literature in this field in recent years from model-based and data-driven perspectives, respectively, and then analyses and compares each method.
The structure of this paper is as follows: Section 2 summarizes the concept of SOH and the commonly used estimation methods; Section 3 summarizes the theory of EIS; Section 4 summarizes the current research progress in estimating SOH based on EIS from two perspectives; Section 5 makes a comparative analysis of the two methods and puts forward a prospect for the future SOH estimation.
2. Overview of SOH
The SOH of the battery, reflecting the capacity of the battery used to store electric energy relative to the initial battery, is an important parameter to characterize the current life of the battery and is widely used in battery-management systems [23]. The battery-power SOH can quantitatively describe the current life information of the battery and represent the life status of the battery from initial life to end of life, given as a percentage [24,25,26,27,28]. The higher the value, the better the current health of the battery and the longer the remaining life cycle [29]. The SOH of the original ex-factory new battery can be defined as 100%, and then, its value gradually decreases to 0% with the increase of battery cycle charge and discharge times and service time [30,31,32,33,34]. Because there are many performance indicators to characterize the battery, the definition of SOH lacks unity [35,36,37]. There are many ways to express the definition of SOH in the domestic and foreign literature. After reading a large number of documents, was found that it is most common to define SOH through internal resistance, the number of remaining cycles, and the capacity of the battery [38,39,40].
2.1. Define SOH with Battery Internal Resistance
The internal resistance of the battery will gradually increase with the aging of the battery [41,42]. Many documents have pointed out that there is an obvious relationship between the change of battery internal resistance and aging, so it is also common to use internal resistance to define battery SOH [43,44]. The definition formula is as follows:
where is the internal resistance at the end of battery life; is the current internal resistance of the battery; is the internal resistance of the new battery.
2.2. Define SOH with the Number of Remaining Battery Cycles
The number of battery cycles is also closely related to the aging state of the battery [45,46]. Some studies believe that when the number of battery cycle reaches a fixed value or a certain range, the battery service life can be considered to be over [47,48,49]. SOH is defined by the number of remaining cycles of the battery, and the expression is as follows:
where is the number of remaining cycles of the battery, and is the total number of cycles of the battery.
2.3. Define SOH with Battery Capacity
Capacity is one of the most important performance parameters of battery power, and its attenuation degree is often used to define SOH in the literature [50,51,52]. The rated capacity of the battery power is clearly defined in the national standard GBT31486-2015: the capacity released when the battery power is fully charged at room temperature, discharges at 1C, and reaches the termination voltage [53,54,55]. The SOH is defined by the battery capacity, that is, the ratio of the capacity () discharged by the current battery from the fully charged state to the cut-off voltage at the rate of 1C and the rated capacity () of the power battery [56]. The definition expression is as follows:
The end of life (EOL) of the battery power in the life-cycle aging test is: when the number of battery cycles reaches a certain number, the usable capacity cannot be less than 80% of the initial capacity [57,58,59]. This shows that the SOH changes from 100% to 0% when the battery power has never been used until it has gradually aged to its end of life. Therefore, in order to take the battery SOH range as 0–100%, Formula (3) is changed to the following form:
The subsequent calculation of SOH in this paper adopts Formula (4).
3. Theoretical Basis of EIS
3.1. Basic Principle of EIS
EIS is an important method to study the electrochemical interface process [60]. Since the measurement process will not cause damage to the battery, this method belongs to non-destructive measurement [61]. EIS measurement can deeply elucidate the electrochemical process occurring in the battery within a wide frequency range and can be used to identify the parameters of the battery model and study the dynamic behavior [62,63,64]. For a certain linear time-invariant system, the transfer function can usually be used to describe the system disturbance and response [65,66]. The frequency response function of the system is as follows:
where is the frequency-response function, which can reflect the frequency-response characteristics of the physical system with frequency change; is a sine wave electrical signal with an angular frequency of , that is, an excitation signal; is the output electrical signal of the system with an angular frequency of , that is, the response signal. When the excitation signal is a sine wave current signal, and the response signal is a sine wave voltage signal, the frequency-response function is called the impedance of the physical system.
When a series of disturbance signals at different angular frequencies is applied to an electrode system, a group of frequency-response functions can be measured. This series of frequency-response functions, namely impedance values, is arranged according to the frequency to form the electrochemical impedance spectrum [67,68,69]. Therefore, the electrochemical impedance spectrum is the impedance spectrum of the electrode system when it meets the basic conditions of resistance [70,71,72].
The electrochemical impedance spectrum is usually represented by Nyquist diagram [73,74,75]. The Nyquist diagram is a complex plane diagram of the EIS with the real part Re of impedance Z as the horizontal axis and the imaginary part Im as the vertical axis [76,77,78]. Admittance Y is also plotted in the same way. The Nyquist diagram of the electrochemical impedance spectrum of a certain lithium-ion battery measured in a 25 ℃ experimental environment is shown in Figure 1.
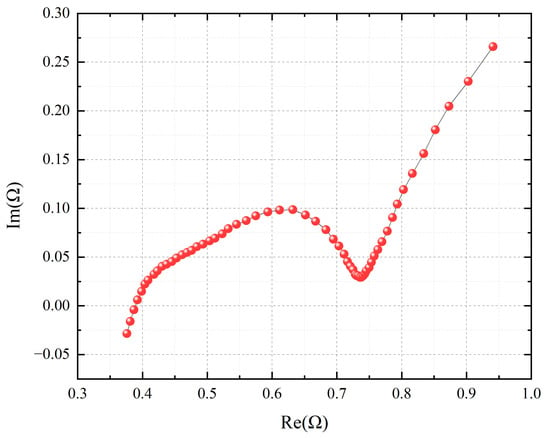
Figure 1.
Nyquist plot of electrochemical impedance spectroscopy.
3.2. Analyze the Principle of Battery Capacity Attenuation from EIS
The aging of LIBs is caused by many physical and chemical mechanisms, mainly including three common aging modes: loss of lithium ions, damage to anodic active substances, and damage to cathodic active substances. During battery aging, parasitic reaction, chemical decomposition (SEI layer decomposition and electrolyte decomposition), and SEI layer growth will lead to lithium-ion consumption, making the lithium ions insufficient to support the cycle between cathode and anode, leading to capacity degradation. The main reasons for the damage of the anode active material are structural disorder, particle cracking, graphite peeling, and loss of electrical contact or blockage of the active site, which makes the anode-active material of the battery unusable and also leads to the reduction of battery capacity and power attenuation. Similarly, these damages can also occur at the cathode and form a cathode–electrolyte interface (CEI) on the surface, causing damage to the cathode’s highly active material. The reactions caused by these aging mechanisms will act on different regions of the EIS, as shown in Figure 2.
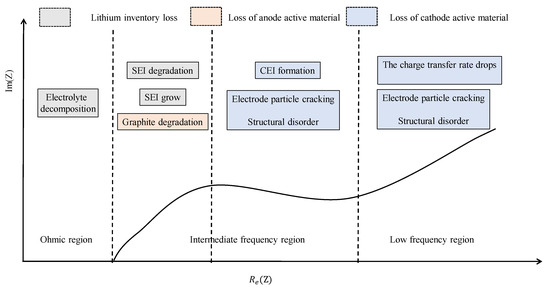
Figure 2.
The relationship between battery EIS curve and common aging mechanisms.
From Figure 2, it can be seen that the decomposition of the electrolyte during battery aging mainly affects the high-frequency impedance region; the degradation and growth of SEI films as well as the degradation of the graphite mainly affect the first half-circle in the mid-frequency region; the formation of CEI film and the impact of electrode particle cracking or structural disorder mainly affect the second semicircle in the mid-frequency region; the impact of the decrease in charge transfer rate mainly affects the low-frequency region. It is worth noting that electrode particle cracking or structural disorder can also affect the low-frequency region.
4. Summary of SOH Estimation Based on EIS
Currently, there are few studies about estimating SOH based on EIS, so each article is a valuable asset in this field. The commonly used SOH-estimation methods are usually based on the external characteristics of the battery and rarely use electrochemical theory to analyze the changes in the battery [79]. Therefore, the model parameters established lack physical significance and cannot accurately reflect the impact of a complex working environment and battery aging on battery-state estimation, resulting in limited estimation accuracy [18]. Daniel I. Stroe et al., 2014 studied the applicability of EIS technology for the diagnosis of monomer degradation of lithium-ion batteries, conducted accelerated aging tests in the laboratory, and determined that the increase of ohmic resistance in the aging process is related to the decline of the pulse-power capacity of lithium-ion batteries. Finally, it was proven that EIS technology can be used to detect SOH in lithium-ion batteries.
At present, when using EIS data to estimate SOH, there are mainly two methods: one is to establish the quantitative relationship model between characteristic parameters and SOH by building the frequency domain-equivalent circuit model [6]. The second is to construct a quantitative relationship model between EIS data and SOH using the data-driven method (Table 2). The following two main methods are summarized:
4.1. ECM-Based Approach
Lithium-ion battery models can be divided into electrochemical models, equivalent circuit models, and empirical model according to different modeling methods and the factors considered [80]. Because the method based on the electrochemical model is designed to represent the aging mechanism of the battery based on the internal mechanism of the battery and a certain feature [81], the construction of the electrochemical model needs to involve complex partial differential equations, which requires large computational resources and is not suitable for practical application [82]. The empirical model is generally based on the analysis of a large number of experimental data, fitting the capacity-decay curve, and then updating the model parameters through filtering algorithms to achieve real-time capacity estimation [83]. However, this method relies too much on the laboratory battery test accuracy, and its generalization performance is poor in practical applications. The equivalent circuit model does not need to consider the electrochemical reaction inside the battery but only describes the voltage response of the battery power with ideal electrical components according to the external electrical characteristics of the battery, describes the static voltage characteristics of the battery power with the voltage source, describes dynamic voltage characteristics such as polarization of the power battery with RC network, and has simple parameter identification, necessity of only a small amount of model calculations, and good real-time performance [36]. Therefore, when performing SOH estimation, the equivalent circuit model is often used.
For the measured electrochemical impedance spectra of lithium batteries, the equivalent circuit method can intuitively and concretely represent the dynamic behavior of the electrode-reaction process of lithium batteries. This method can represent the physical phenomena in the electrode-reaction process through different equivalent elements and fit the EIS curve of each frequency band through composite elements composed of equivalent elements. When the frequency-response curve of the circuit composed of composite components is consistent with the measured battery EIS curve, the circuit is called the equivalent circuit of the battery system.
- (1)
- Based on a single equivalent circuit model:
Xiong et al. established the mapping relationship between residual capacity and resistance based on the equivalent circuit model to estimate the SOH [84]. First, by analyzing the EIS test results under different SOHs, the degradation level can be detected by EIS measurement; then, using fractional order theory, an online parameter identification method based on the fractional order impedance model can be proposed, and the correlation between the change of parameters and degradation level can be discussed. The SEI (solid electrolyte–interface phase) resistance is extracted by selecting the appropriately fitting function to predict residual capacity. Finally, the effectiveness of this method is verified by experimental data. Matteo Galeotti et al. first constructed an equivalent circuit model to fit the impedance spectrum, used the parameters of the equivalent circuit model to reproduce the discharge curve of the battery, and then found the relationship between the ohmic internal resistance of the battery and the available capacity to evaluate the SOH [85].
However, the above two methods ignore the influence of temperature and SOC on the evaluation. Therefore, Wang et al. considered the influence of temperature and charge state on charge-transfer resistance [86] and proposed a calculation model of charge-transfer resistance:
, , , and are the parameter to be measured; T is the temperature of lithium-ion battery. Using this calculation model, a calculation model of SOH is proposed:
is the charge-transfer resistance at the end of the battery life, and is the reference value for calculating the growth rate of the charge-transfer resistance. Converting the randomly selected charge and charge-transfer resistance under temperature state to standard state can be used for health-state estimation, but it is difficult to find a suitable charge-transfer resistance.
On this basis, Qunming Zhang et al. [87] introduced an equivalent circuit model (ECM) in which the solid electrolyte–interface resistance and charge-transfer resistance are used to map their relationship with SOH under changing temperature and SOC, and the model parameters are determined by Hamilton Monte Carlo (HMC) sampling method. Finally, the charge-transfer resistance, temperature, and SOC are used as input variables for LIB SOH estimation. The estimation flow chart is shown in Figure 3.
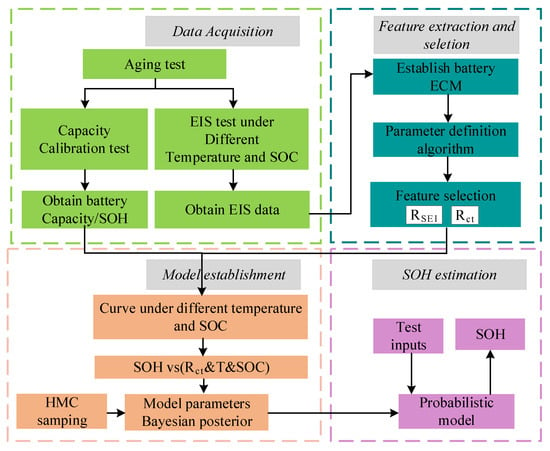
Figure 3.
Estimation flow chart.
- (2)
- Based on multiple equivalent circuit models:
However, the above methods only consider one circuit model in circuit fitting, which makes the fitting accuracy poor. The prediction of the equivalent circuit through EIS can determine the equivalent circuit model with the highest fitting accuracy, which can fundamentally improve the accuracy and robustness of the prediction model. On this basis, Pietro Iurilli et al. first summarized the relationship between general ECM and EIS [88] and described the degradation mechanism of each part, as shown in Figure 4. The model includes a resistor for ohmic region, two Zarc elements for intermediate frequency region (one element for each half-bow), and a Warburg element for the low-frequency region. The figure is described in three parts:
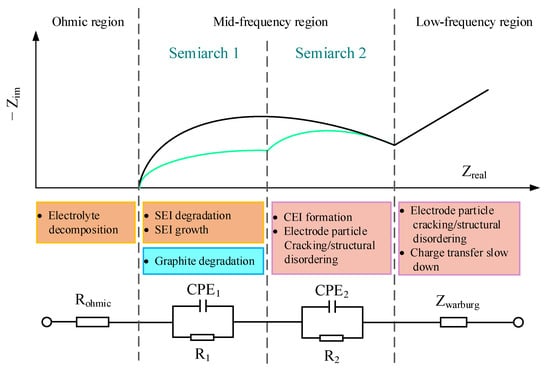
Figure 4.
Representation of typical EIS spectra of lithium-ion batteries.
Ohmic region: The high-frequency band is the inductive reactance behavior generated by the electron through the wire and the winding of the internal electrode, which can be expressed by the equivalent element Ls. For the intersection of the curve end and the real axis, it represents the ohmic resistance of the ion and electron from the electrode interface to the solution and through the active carbon pore, which can be expressed by the element .
Mid-frequency region: The first half-arc in the middle frequency band is related to the loss of lithium ions (mainly SEI growth and SEI layer decomposition mechanism), and the second half-arc is related to the loss of cathode active material.
Low-frequency region: The low-band oblique line is generated by the diffusion process of Li+ near the electrode interface and in the active material.
Next, Yang et al. proposed a health-assessment method based on multi-model probability fusion to improve the accuracy and reliability of SOH estimation [89].
Later, during the construction of ECM, Li et al. proposed the method of selecting ECM according to the shape of the impedance curve on a Nyquist diagram and subsequent complex nonlinear least-squares fitting. The selection of circuit components during the construction usually depends on the complexity of the impedance curve. The ECM generally includes resistors and inductors for ohmic region or parallel circuits of the corresponding inductors and resistors when there is an inductor tail. However, due to the change of the working state of the battery itself, the selection of circuit elements to describe the cathode and anode process of the battery has become the biggest problem in ECM construction. Then, a measurement method based on multiple ECMs was proposed to find the ECM with the highest fitting accuracy, which can fundamentally improve the accuracy and robustness of the prediction model [14]. According to the general equivalent circuit model, five ECM variants are herein proposed. As shown in Figure 5, these ECMs were verified to have good accuracy. Then, the ECM is fitted by nonlinear least-squares regression of the circuit model and impedance data. Finally, the ECM in Figure 5b is selected to estimate the SOH by comparing the fitting error. Finally, compared with the basic ECM, the SOH estimation error is reduced by 17.9%, making a major breakthrough.
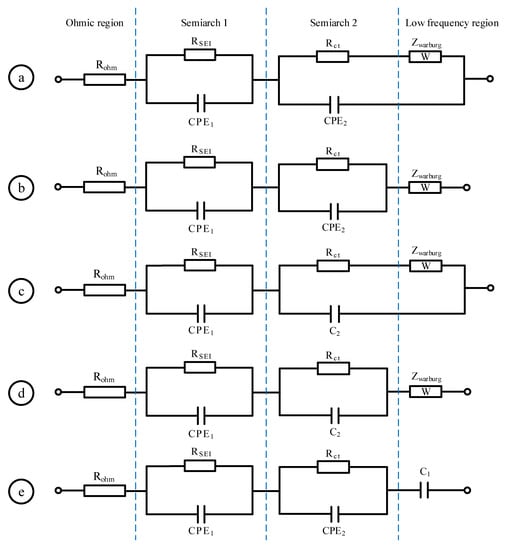
Figure 5.
(a–e) Different equivalent circuit models of lithium-ion batteries.

Table 2.
Summary of studies on estimating SOH based on EIS.
Table 2.
Summary of studies on estimating SOH based on EIS.
| Author(s) | Models | F (Hz) for Model | SOH Errors |
|---|---|---|---|
| Xiong Rui et al. [84] | ECM | 0.02–5000 Hz | Error < 3% |
| Matteo Galeotti et al. [85] | ECM | 0.2 Hz–5 kHz | Maximum error = 3.73% |
| Wang Xue yuan et al. [86] | ECM | 0.01 Hz–1 kHz | Absolute error < 15% |
| Zhang et al. [87] | ECM | 0.1 Hz–5 kHz | Error < 4% |
| Pietro Iurilli et al. [88] | ECM | 0.1–1000 Hz | - |
| Yang et al. [89] | ECM | 50 mHz–10 kHz | Accuracy increased by 46.38% |
| De zhi Li et al. [14] | ECM | 0.02 Hz–20 kHz | RMSE = 0.0497 |
| Akram Eddahech et al. [90] | RNN | 0.01 Hz–10 kHz | MSE = 0.462 |
| GENG Meng Meng et al. [91] | BP | 10 mHz–10 kHz | MAPE = 1.36%, RMSE = 1.57% |
| LIU Jia hao et al. [92] | LSTM | 0.01 Hz–10 kHz | RMSE = 3.981% |
| Zhang et al. [93] | GPR | 0.02 Hz–20 kHz | RMSE = 5.03% |
| Chun Chang et al. [94] | CS–Elman model | 20 mHz–20 kHz | R2 = 99.89% |
| T. K. Pradyumna et al. [95] | CNN | 0.1–1 kHz | RMSE = 0.233% |
| Li De zh et al. [14] | IPSO-CNN-BiLSTM model | 0.02 Hz–20 kHz | RMSE = 0.0183 |
| Chen, X. et al. [96] | SFS-GPR model | 0.02 Hz–20 kHz | RMSE = 0.042 |
4.2. Data-Driven Approach
The data-driven method uses SOH as the output of the machine learning model and highly correlated features as the input of the model. This method has high accuracy in the field of SOH estimation, but it is difficult to select appropriate input features.
- (1)
- Based on a single-network mode:
Akram Eddahech et al. first used cyclic neural network RNN to predict SOH based on EIS data [90]. In order to improve the speed and accuracy of the health-state estimation of retired batteries, GENG et al. selected eight of the square lithium iron phosphate batteries retired from an electric bus to continue the cyclic aging test and conducted the electrochemical impedance test after different cycles. According to the impedance characteristics of lithium-ion batteries, the real part, imaginary part, and mode value at 300 Hz, 60 Hz, and 1 Hz were extracted as the characteristic parameters and as the input parameters combined with the BP neural network algorithm; a fast estimation model of the health status of retired batteries based on electrochemical impedance and BP neural network was built, and 19 groups of data not participating in model training were used to verify the model [91]. LIU et al. proposed a lithium battery health-state estimation method based on the virtual part of the electrochemical impedance spectrum and the long- and short-term memory (LSTM) neural network [92]. The cycle number, frequency, SOC, and AC impedance virtual part at a specific frequency were used as the model input, and SOH was used as the output of the prediction model to predict.
Zhang et al. [93] conducted the aging test and published the 45 mAh commercial button battery (positive and negative active materials are lithium cobaltate and graphite, respectively) aging electrochemical impedance dataset in Nature Communications. They set three different temperatures (25 °C, 35 °C, and 45 °C). When the aging ambient temperature was 25 °C, the battery number was 25C01~25C08. When the aging ambient temperature was 35 °C, the battery number was 35C01~35C02, When the aging ambient temperature was 4 °C, the battery number was 45C01~45C02. Each aging cycle included two stages of charging and discharging: in the charging stage, the constant current was charged to the cut-off voltage of 4.2 V at the rate of 1C, and then, the constant voltage was charged until the current decayed to 0.1C, and finally, it was allowed to stand for 15 min. In the discharge stage, it was first discharged to the cut-off voltage of 3 V at the constant current of 2C and then left to stand for 15 min, as shown in Figure 6. In order to obtain the impedance data of the battery under different states of charge, each charge and discharge cycle process was divided into nine states, and the impedance data were tested, respectively, (a) before charging; (b) at the beginning of charging; (c) after 20 min of charging (50% SOC); (d) when fully charged (100% SOC); (e) 15 min after charging; (f) at the beginning of discharge; (g) after 10 min of discharge (50% SOC); (h) at the end of discharge; and (i) after letting stand for 15 min after discharge. The electrochemical impedance spectrum test was carried out in even number of charge–discharge cycles; the frequency range is 0.02 Hz–20 kHz, and the excitation current amplitude is 5 mA. This dataset is the largest lithium-ion battery impedance and corresponding aging dataset in China. It made a breakthrough contribution to the prediction of SOH and RUL in the field of impedance spectra. Then, they used the Gaussian process regression (GPR) method to take the real part and imaginary part of the impedance with the frequency range of 0.02–2000 Hz as the model input in order to make the model still achieve accurate prediction at different temperatures. Combining the training data collected at three temperatures (25 °C, 35 °C and 45 °C), the SOH and remaining useful life (RUL) of LIBs were estimated accurately.
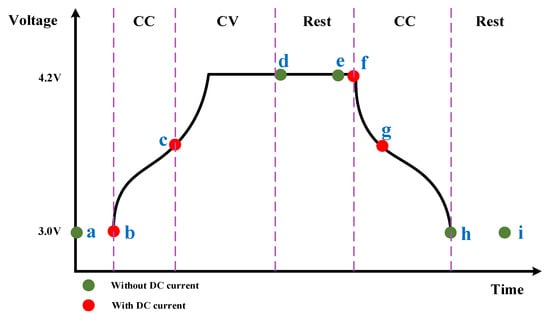
Figure 6.
EIS data collected in nine different states.
On the basis of the dataset published by Zhang et al., Chun Chang et al. proposed an SOH-estimation method for lithium-ion batteries based on the combination of EIS and Elman neural network and cuckoo search (CS–Elman) [94].
The methods mentioned above all need to manually process the input data. Sometimes, the manually processed data are unreasonable in many models, so T.K. Pradyumna et al. proposed the method of estimating SOH by automatically extracting input features from CNN [95], which avoids the problem of unreasonable feature extraction and missing important features. CNN is one of the most widely used algorithms in the field of deep learning. Because of its efficient feature-extraction ability, it is applied in the field of power system research [21]. Because EIS data contain rich information content, using CNN can greatly reduce the complexity of data processing and ensure that important information is not lost. The basic structure of CNN is shown in Figure 7. The filter is used to extract important features in the whole range of input data in the convolution layer. Convolution can be expressed by Equation (7).
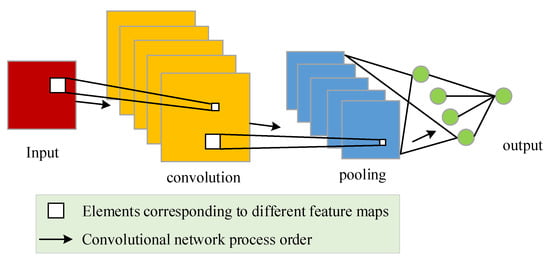
Figure 7.
CNN basic structure diagram.
The nonlinear mapping of the output of the convolution layer is realized in the activation layer. Common excitation functions are as follows:
- (2)
- Multi-network model based on automatic feature extraction:
However, the performance of traditional CNN needs to be improved, so it is a research direction to improve the CNN network or combine it with other prediction models. Therefore, Li et al. [14] proposed a new method to predict the SOH of lithium-ion batteries. First, the real part, imaginary part, modulus, and phase at 60 different frequencies under each charge-discharge cycle were used as inputs, and then, CNN was used to extract important features. Finally, it was combined with the bidirectional long- and short-term memory neural network (BiLSTM) model to predict SOH. In addition, an improved particle swarm optimization algorithm (PSO) was proposed to optimize the model on this basis, which has higher accuracy compared with traditional methods. The prediction model structure is shown in Figure 8.
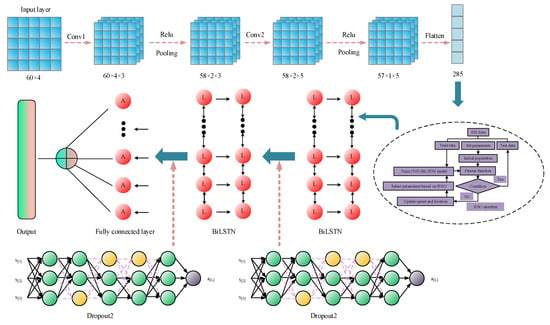
Figure 8.
Schematic diagram of the IPSO-CNN-BiLSTM model.
Similarly, Josue Obregon et al. explored a method for extracting overcomplete features from electrochemical impedance spectroscopy (EIS) data using convolutional autoencoders (CAEs). The extracted potential data representation was fed into a deep neural network (DNN) for battery-capacity maintenance and SOH estimation.
However, it takes a lot of time to carry out full-band EIS tests, and there are some difficulties in practical application. Therefore, how to select the impedance characteristic subset closely related to SOH from the full-band EIS data is a key problem to be solved urgently. In view of this, Chen Xiaoyu et al. proposed a SOH-estimation method based on feature selection and Gaussian process regression, which can gradually search the impedance feature subset [96] through the sequential forward search strategy combined with the cross-validation root mean square error index. Based on this, the multi-objective visual decision-making method based on the level chart was adopted, aiming at balancing the complexity and accuracy of the model, comprehensively considering the number of features and the root mean square error of cross validation, and implementing the impedance feature subset optimization. The proposed method was successfully applied to the published dataset, and the prediction flow chart is shown in Figure 9. Compared with the full-band EIS modeling method, this method can significantly improve the accuracy of SOH estimation, significantly reduce the EIS test time, and provide theoretical and technical support for the application of electrochemical impedance technology to online SOH estimation.
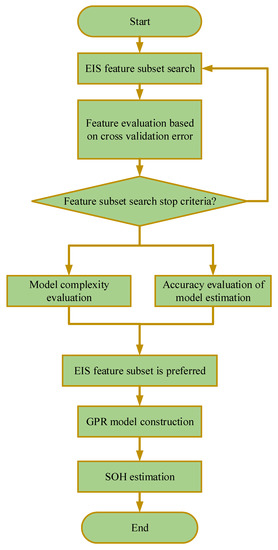
Figure 9.
Schematic diagram of algorithm flow.
5. Conclusions
In this paper, the definition of SOH and the theory of EIS are summarized, and then, the cause of the battery-capacity degradation is analyzed from the perspective of EIS. Finally, the research progress of predicting the SOH of lithium-ion batteries based on EIS in recent years is reviewed.
5.1. Summary
(1) Compared with the time–domain current and voltage-response curve data, the frequency-domain EIS can reflect the aging state of the battery from multiple perspectives because it contains rich information about material characteristics, interface phenomena, and electrochemical reactions inside the battery. Moreover, by measuring the impedance, the rich electrode–interface structure information inside the battery can be obtained, and it has the advantage of nondestructive measurement. It is thus an effective means to achieve SOH estimation;
(2) The model-based method uses the impedance spectrum measured at different temperatures and SOC conditions to fit with the built equivalent circuit so as to obtain the parameters of the equivalent circuit, reconstruct the discharge curve, study their cycle performance, and understand whether they have abnormal aging during operation. The physical effects occurring in any electrochemical system can be correlated with the electrical parameters of the ECM, which is helpful to quantify the phenomena occurring in the process of charging and discharging and the aging of the lithium-ion battery. The internal process of the lithium battery in the aging cycle process can be quantified by electrical parameters. The relationship between general ECM and EIS is established. By measuring the impedance data of the battery during aging and fitting the impedance data with the proposed equivalent circuit model, the parameters that have the highest correlation with the health status of the lithium-ion battery are extracted as the estimation index of SOH.
The quality of the model built by the model-based method is directly related to the accuracy of the lithium battery SOH prediction. The advantage of the ECM method is that the amount of calculations is relatively small, and it can directly simulate the dynamic behavior of the electrode-reaction process, but it is only applicable to the working environment in which the model parameters are identified. In the case of environmental temperature change, battery aging, etc., the accuracy of the model will significantly decline. This is mainly due to the lack of actual physical and chemical significance of the equivalent circuit model parameters, and it is difficult to maintain high accuracy in different environments and working conditions;
(3) The difference between the data-driven method and model-based method is that the data-driven method does not need to consider the electrochemical mechanism of LIBs but focuses on the historical data of batteries. The SOH prediction of LIBs using machine learning methods usually requires a large amount of historical data, and the EIS data are processed and correlated. The features with high correlation are extracted as the input of the machine learning model, and the SOH of LIBs is used as the output of the model. Through the adaptive iteration of the model for the data, high prediction accuracy is achieved.
The data-driven method does not need to consider the chemical reaction mechanism inside the lithium battery and can effectively avoid solving the complex nonlinear optimization problem of building the frequency domain-equivalent circuit model. This method is relatively simple and accurate, but this method usually extracts the eigenvectors of the indicators needed for prediction from the battery-degradation data, so the selection of the eigenvectors is also the key of the data-driven method, and it particularly depends on the quality of the data. In addition, due to the nonlinear correlation between different frequency impedance data, the accuracy of the SOH-estimation model is usually limited by directly using full-band EIS data. Moreover, it takes a lot of time to carry out full-band EIS tests, and there are certain difficulties in practical application. In addition, the EIS data used in some current studies are directly measured by an electrochemical workstation. However, due to operation error, conductor influence, or other accidents, EIS data may be damaged, which will affect the accuracy of subsequent experiments.
5.2. Outlook
(1) For the model method, the ECM with a higher fitting degree or better method can be found for parameter identification in the follow-up research, and combination with the data-driven method can also be considered for research;
(2) For the data-driven method, how to select the impedance feature subset closely related to SOH from the full-band EIS data is the key problem to be solved urgently;
(3) It is a good direction to consider the application of EIS in the field of lithium-ion batteries under low-temperature environments. In addition, it is also necessary to adopt appropriate methods to verify the reliability of the data measured from the electrochemical station.
Author Contributions
Writing—original draft, X.S.; methodology, Y.Z. (Yang Zhang); investigation, Y.Z. (Yongcheng Zhang); writing—review and editing, K.W.; project administration, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Youth Fund of Shandong Province Natural Science Foundation (No. ZR2020QE212), Key Projects of Shandong Province Natural Science Foundation (No. ZR2020KF020), the Guangdong Provincial Key Lab of Green Chemical Product Technology (GC202111), Zhejiang Province Natural Science Foundation (No. LY22E070007), and National Natural Science Foundation of China (No. 52007170).
Data Availability Statement
The data and materials used to support the results of this study cannot be obtained due to privacy reasons.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Huang, S.; Liu, C.; Sun, H.; Liao, Q. State of health estimation of lithium-ion batteries based on the regional frequency. J. Power Sources 2022, 518, 230773. [Google Scholar] [CrossRef]
- Sun, H.; Sun, J.; Zhao, K.; Wang, L.; Wang, K. Data-Driven ICA-Bi-LSTM-Combined Lithium Battery SOH Estimation. Math. Probl. Eng. 2022, 2022, 9645892. [Google Scholar] [CrossRef]
- Meng, J.; Cai, L.; Stroe, D.-I.; Huang, X.; Peng, J.; Liu, T.; Teodorescu, R. An Automatic Weak Learner Formulation for Lithium-Ion Battery State of Health Estimation. IEEE Trans. Ind. Electron. 2022, 69, 2659–2668. [Google Scholar] [CrossRef]
- Yi, Z.; Chen, Z.; Yin, K.; Wang, L.; Wang, K. Sensing as the key to the safety and sustainability of new energy storage devices. Prot. Control. Mod. Power Syst. 2023, 8, 23. [Google Scholar] [CrossRef]
- Yang, N.; Song, Z.; Hofmann, H.; Sun, J. Robust State of Health estimation of lithium-ion batteries using convolutional neural network and random forest. J. Energy Storage 2022, 48, 103857. [Google Scholar] [CrossRef]
- Zhang, C.; Cao, C.; Chen, R.; Jiang, J. Three-Leg Quasi-Z-Source Inverter with Input Ripple Suppression for Renewable Energy Application. Energies 2023, 16, 4393. [Google Scholar] [CrossRef]
- Yu, X.; Li, Y.; Li, X.; Wang, L.; Wang, K. Research on Outdoor Mobile Music Speaker Battery Management Algorithm Based on Dynamic Redundancy. Technologies 2023, 11, 60. [Google Scholar] [CrossRef]
- Yi, Z.; Zhao, K.; Sun, J.; Wang, L.; Wang, K.; Ma, Y. Prediction of the Remaining Useful Life of Supercapacitors. Math. Probl. Eng. 2022, 2022, 7620382. [Google Scholar] [CrossRef]
- Sun, H.; Yang, D.; Wang, L.; Wang, K. A method for estimating the aging state of lithium-ion batteries based on a multi-linear integrated model. Int. J. Energy Res. 2022, 46, 24091–24104. [Google Scholar] [CrossRef]
- Li, Q.; Li, D.; Zhao, K.; Wang, L.; Wang, K. State of health estimation of lithium-ion battery based on improved ant lion optimization and support vector regression. J. Energy Storage 2022, 50, 104215. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, D.; Du, J.; Sun, H.; Li, L.; Wang, L.; Wang, K. A Review of SOH Prediction of Li-Ion Batteries Based on Data-Driven Algorithms. Energies 2023, 16, 3167. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, W.L.; Xia, G.T.; Wang, L.C.; Wang, K. Self-Powered Electronic Skin for Remote Human-Machine Synchronization. Acs. Appl. Electron. Mater. 2023, 5, 498–508. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Y.; Sun, J.; Cui, Z.; Wang, K. Stacked bidirectional LSTM RNN to evaluate the remaining useful life of supercapacitor. Int. J. Energy Res. 2022, 46, 3034–3043. [Google Scholar] [CrossRef]
- Li, D.; Yang, D.; Li, L.; Wang, L.; Wang, K. Electrochemical Impedance Spectroscopy Based on the State of Health Estimation for Lithium-Ion Batteries. Energies 2022, 15, 6665. [Google Scholar] [CrossRef]
- Jiang, B.; Zhu, J.; Wang, X.; Wei, X.; Shang, W.; Dai, H. A comparative study of different features extracted from electrochemical impedance spectroscopy in state of health estimation for lithium-ion batteries. Appl. Energy 2022, 322, 119502. [Google Scholar] [CrossRef]
- Fu, Y.; Xu, J.; Shi, M.; Mei, X. A Fast Impedance Calculation-Based Battery State-of-Health Estimation Method. IEEE Trans. Ind. Electron. 2022, 69, 7019–7028. [Google Scholar] [CrossRef]
- Deng, Z.; Lin, X.; Cai, J.; Hu, X. Battery health estimation with degradation pattern recognition and transfer learning. J. Power Sources 2022, 525, 231027. [Google Scholar] [CrossRef]
- Yu, X.; Ma, N.; Zheng, L.; Wang, L.; Wang, K. Developments and Applications of Artificial Intelligence in Music Education. Technologies 2023, 11, 42. [Google Scholar] [CrossRef]
- Itagaki, M.; Honda, K.; Hoshi, Y.; Shitanda, I. In-situ EIS to determine impedance spectra of lithium-ion rechargeable batteries during charge and discharge cycle. J. Electroanal. Chem. 2015, 737, 78–84. [Google Scholar] [CrossRef]
- Lyu, C.; Zhang, T.; Luo, W.; Wei, G.; Ma, B.; Wang, L. SOH Estimation of Lithium-ion Batteries Based on Fast Time Domain Impedance Spectroscopy. In Proceedings of the 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 2142–2147. [Google Scholar]
- Messing, M.; Shoa, T.; Habibi, S. Estimating battery state of health using electrochemical impedance spectroscopy and the relaxation effect. J. Energy Storage 2021, 43, 103210. [Google Scholar] [CrossRef]
- Xu, Z.; Li, H.; Yazdi, M.; Ouyang, K.; Peng, W. Aging Characteristics and State-of-Health Estimation of Retired Batteries: An Electrochemical Impedance Spectroscopy Perspective. Electronics 2022, 11, 3863. [Google Scholar] [CrossRef]
- Liu, D.; Pang, J.; Zhou, J.; Peng, Y.; Pecht, M. Prognostics for state of health estimation of lithium-ion batteries based on combination Gaussian process functional regression. Microelectron. Reliab. 2013, 53, 832–839. [Google Scholar] [CrossRef]
- Sui, X.; He, S.; Vilsen, S.B.; Meng, J.; Teodorescu, R.; Stroe, D.-I. A review of non-probabilistic machine learning-based state of health estimation techniques for Lithium-ion battery. Appl. Energy 2021, 300, 117346. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Yu, Q. Fractional-Order Model-Based Incremental Capacity Analysis for Degradation State Recognition of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2019, 66, 1576–1584. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, L.; Zou, C.; Dorrell, D.D. State-of-health estimation for Li-ion batteries by combing the incremental capacity analysis method with grey relational analysis. J. Power Sources 2019, 410, 106–114. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, G.; Lin, M.; Wu, J.; Zheng, G. A Novel Estimation Method for the State of Health of Lithium-Ion Battery Using Prior Knowledge-Based Neural Network and Markov Chain. IEEE Trans. Ind. Electron. 2019, 66, 7706–7716. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Xia, Q.; Li, X.; Wang, K.; Li, Z.; Liu, H.; Wang, X.; Ye, W.; Li, H.; Teng, X.; Pang, J.; et al. Unraveling the Evolution of Transition Metals during Li Alloying- Dealloying by In-Operando Magnetometry. Chem. Mater. 2022, 34, 5852–5859. [Google Scholar] [CrossRef]
- Chaoui, H.; Ibe-Ekeocha, C.C. State of Charge and State of Health Estimation for Lithium Batteries Using Recurrent Neural Networks. IEEE Trans. Veh. Technol. 2017, 66, 8773–8783. [Google Scholar] [CrossRef]
- Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.G.; Park, J. A single particle model with chemical/mechanical degradation physics for lithium ion battery State of Health (SOH) estimation. Appl. Energy 2018, 212, 1178–1190. [Google Scholar] [CrossRef]
- Hu, X.; Feng, F.; Liu, K.; Zhang, L.; Xie, J.; Liu, B. State estimation for advanced battery management: Key challenges and future trends. Renew. Sustain. Energy Rev. 2019, 114, 109334. [Google Scholar] [CrossRef]
- Vidal, C.; Malysz, P.; Kollmeyer, P.; Emadi, A. Machine Learning Applied to Electrified Vehicle Battery State of Charge and State of Health Estimation: State-of-the-Art. IEEE Access 2020, 8, 52796–52814. [Google Scholar] [CrossRef]
- Ge, M.-F.; Liu, Y.; Jiang, X.; Liu, J. A review on state of health estimations and remaining useful life prognostics of lithium-ion batteries. Measurement 2021, 174, 109057. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The Co-estimation of State of Charge, State of Health, and State of Function for Lithium-Ion Batteries in Electric Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 92–103. [Google Scholar] [CrossRef]
- Wang, K.; Li, L.; Yin, H.; Zhang, T.; Wan, W. Thermal Modelling Analysis of Spiral Wound Supercapacitor under Constant-Current Cycling. PLoS ONE 2015, 10, 138672. [Google Scholar] [CrossRef]
- Wang, W.; Yang, D.; Huang, Z.; Hu, H.; Wang, L.; Wang, K. Electrodeless Nanogenerator for Dust Recover. Energy Technol. 2022, 10, 699. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Hoque, M.M.; Ker, P.J.; Saad, M.H.M.; Ayob, A. A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles: Challenges and recommendations. J. Clean. Prod. 2018, 205, 115–133. [Google Scholar] [CrossRef]
- Ma, N.; Yang, D.; Riaz, S.; Wang, L.; Wang, K. Aging Mechanism and Models of Supercapacitors: A Review. Technologies 2023, 11, 38. [Google Scholar] [CrossRef]
- Wang, W.; Yang, D.; Yan, X.; Wang, L.; Hu, H.; Wang, K. Triboelectric nanogenerators: The beginning of blue dream. Front. Chem. Sci. Eng. 2023, 17, 635–678. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, K.; Zhu, C.; Zhang, X.; Zhang, D. Co-Estimation of State-of-Charge and State-of- Health for Lithium-Ion Batteries Using an Enhanced Electrochemical Model. IEEE Trans. Ind. Electron. 2022, 69, 2684–2696. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Li, P.; Lin, X.; Bian, X. Data-Driven Battery State of Health Estimation Based on Random Partial Charging Data. IEEE Trans. Power Electron. 2022, 37, 5021–5031. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. A review of supercapacitor modeling, estimation, and applications: A control/management perspective. Renew. Sustain. Energy Rev. 2018, 81, 1868–1878. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Khaleghi, S.; Karimi, D.; Beheshti, S.H.; Hosen, M.S.; Behi, H.; Berecibar, M.; Van Mierlo, J. Online health diagnosis of lithium-ion batteries based on nonlinear autoregressive neural network. Appl. Energy 2021, 282, 116159. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Ojha, U.; Baronti, F.; Chow, M.-Y. Battery Management System an Overview of Its Application in the Smart Grid and Electric Vehicles. IEEE Ind. Electron. Mag. 2013, 7, 4–16. [Google Scholar] [CrossRef]
- Bian, X.; Wei, Z.G.; Li, W.; Pou, J.; Sauer, D.U.; Liu, L. State-of-Health Estimation of Lithium-Ion Batteries by Fusing an Open Circuit Voltage Model and Incremental Capacity Analysis. IEEE Trans. Power Electron. 2022, 37, 2226–2236. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, G.; Zhen, D.; Gu, F.; Ball, A. A review on online state of charge and state of health estimation for lithium-ion batteries in electric vehicles. Energy Rep. 2021, 7, 5141–5161. [Google Scholar] [CrossRef]
- Tran, M.-K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Tian, H.; Qin, P.; Li, K.; Zhao, Z. A review of the state of health for lithium -ion batteries: Research status and suggestions. J. Clean. Prod. 2020, 261, 120813. [Google Scholar] [CrossRef]
- Feng, X.; Weng, C.; He, X.; Han, X.; Lu, L.; Ren, D.; Ouyang, M. Online State-of-Health Estimation for Li-Ion Battery Using Partial Charging Segment Based on Support Vector Machine. IEEE Trans. Veh. Technol. 2019, 68, 8583–8592. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. Remaining Useful Life Prediction and State of Health Diagnosis for Lithium-Ion Batteries Using Particle Filter and Support Vector Regression. IEEE Trans. Ind. Electron. 2018, 65, 5634–5643. [Google Scholar] [CrossRef]
- Cui, Z.; Dai, J.; Sun, J.; Li, D.; Wang, L.; Wang, K. Hybrid Methods Using Neural Network and Kalman Filter for the State of Charge Estimation of Lithium-Ion Battery. Math. Probl. Eng. 2022, 2022, 9616124. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, Y.; Zhang, L.; Chen, J.; Wang, X.; Wang, X. Dig information of nanogenerators by machine learning. Nano Energy 2023, 114, 108656. [Google Scholar] [CrossRef]
- Guo, Y.; Yu, P.; Zhu, C.; Zhao, K.; Wang, L.; Wang, K. A state-of-health estimation method considering capacity recovery of lithium batteries. Int. J. Energy Res. 2022, 46, 23730–23745. [Google Scholar] [CrossRef]
- Hu, X.; Che, Y.; Lin, X.; Onori, S. Battery Health Prediction Using Fusion-Based Feature Selection and Machine Learning. IEEE Trans. Transp. Electrif. 2021, 7, 382–398. [Google Scholar] [CrossRef]
- Weng, C.; Feng, X.; Sun, J.; Peng, H. State-of-health monitoring of lithium-ion battery modules and packs via incremental capacity peak tracking. Appl. Energy 2016, 180, 360–368. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Hu, X.; Yuan, H.; Zou, C.; Li, Z.; Zhang, L. Co-Estimation of State of Charge and State of Health for Lithium-Ion Batteries Based on Fractional-Order Calculus. IEEE Trans. Veh. Technol. 2018, 67, 10319–10329. [Google Scholar] [CrossRef]
- Li, D.; Wang, L.; Duan, C.; Li, Q.; Wang, K. Temperature prediction of lithium-ion batteries based on electrochemical impedance spectrum: A review. Int. J. Energy Res. 2022, 46, 10372–10388. [Google Scholar] [CrossRef]
- Cui, Z.; Kang, L.; Li, L.; Wang, L.; Wang, K. A hybrid neural network model with improved input for state of charge estimation of lithium-ion battery at low temperatures. Renew. Energy 2022, 198, 1328–1340. [Google Scholar] [CrossRef]
- Mingant, R.; Bernard, J.; Sauvant-Moynot, V.; Delaille, A.; Mailley, S.; Hognon, J.L.; Huet, F. EIS Measurements for Determining the SoC and SoH of Li-ion Batteries. In Proceedings of the 218th Meeting of the Electrochemical-Society (ECS)/Symposium of the Battery/Energy Technology Joint General Session/Symposium on Electronics and 3D Packaging 4, Las Vegas, NV, USA, 10–15 October 2010; pp. 41–53. [Google Scholar]
- Xia, Z.; Abu Qahouq, J.A. Evaluation of Parameter Variations of Equivalent Circuit Model of Lithium-ion Battery under Different SOH Conditions. In Proceedings of the 12th Annual IEEE Energy Conversion Congress and Exposition (IEEE ECCE), Detroit, MI, USA, 10–15 October 2020; pp. 1519–1523. [Google Scholar]
- Zhang, Q.; Wang, D.; Schaltz, E.; Stroe, D.-I.; Gismero, A.; Yang, B. Degradation mechanism analysis and State-of-Health estimation for lithium-ion batteries based on distribution of relaxation times. J. Energy Storage 2022, 55, 105386. [Google Scholar] [CrossRef]
- Zhang, K.; Xiong, R.; Li, Q.; Chen, C.; Tian, J.; Shen, W. A novel pseudo-open-circuit voltage modeling method for accurate state-of-charge estimation of LiFePO4 batteries. Appl. Energy 2023, 347, 121406. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, D.; Zhang, Y.; Wang, L.; Wang, K. Online estimation of SOH for lithium-ion battery based on SSA-Elman neural network. Prot. Control. Mod. Power Syst. 2022, 7, 40. [Google Scholar] [CrossRef]
- Dehghani, A.; Bahlakeh, G.; Ramezanzadeh, B.; Ramezanzadeh, M. Potential of Borage flower aqueous extract as an environmentally sustainable corrosion inhibitor for acid corrosion of mild steel: Electrochemical and theoretical studies. J. Mol. Liq. 2019, 277, 895–911. [Google Scholar] [CrossRef]
- Sanaei, Z.; Ramezanzadeh, M.; Bahlakeh, G.; Ramezanzadeh, B. Use of Rosa canina fruit extract as a green corrosion inhibitor for mild steel in 1 M HCl solution: A complementary experimental, molecular dynamics and quantum mechanics investigation. J. Ind. Eng. Chem. 2019, 69, 18–31. [Google Scholar] [CrossRef]
- Nara, H.; Mukoyama, D.; Yokoshima, T.; Momma, T.; Osaka, T. Impedance Analysis with Transmission Line Model for Reaction Distribution in a Pouch Type Lithium-Ion Battery by Using Micro Reference Electrode. J. Electrochem. Soc. 2016, 163, A434–A441. [Google Scholar] [CrossRef]
- Ciucci, F. Modeling electrochemical impedance spectroscopy. Curr. Opin. Electrochem. 2019, 13, 132–139. [Google Scholar] [CrossRef]
- Li, Y.; Dong, B.; Zerrin, T.; Jauregui, E.; Wang, X.; Hua, X.; Ravichandran, D.; Shang, R.; Xie, J.; Ozkan, M.; et al. State-of-health prediction for lithium-ion batteries via electrochemical impedance spectroscopy and artificial neural networks. Energy Storage 2020, 2, e186. [Google Scholar] [CrossRef]
- Milojevic, Z.; Attidekou, P.S.; Muhammad, M.; Ahmeid, M.; Lambert, S.; Das, P.K. Influence of orientation on ageing of large-size pouch lithium-ion batteries during electric vehicle life. J. Power Sources 2021, 506, 230242. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.-S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gabers, M.; et al. Application of electrochemical impedance spectroscopy to commercial Li-ion cells: A review. J. Power Sources 2020, 480, 228742. [Google Scholar] [CrossRef]
- Perry, D.; Mamlouk, M. Probing mass transport processes in Li-ion batteries using electrochemical impedance spectroscopy. J. Power Sources 2021, 514, 23057. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, L.; Zhang, Y.; Wang, X.; Qiao, Y.; Sun, S.-G. Reliable impedance analysis of Li-ion battery half-cell by standardization on electrochemical impedance spectroscopy (EIS). J. Chem. Phys. 2023, 158, 054202. [Google Scholar] [CrossRef] [PubMed]
- Hsissou, R.; Abbout, S.; Safi, Z.; Benhiba, F.; Wazzan, N.; Guo, L.; Nouneh, K.; Briche, S.; Erramli, H.; Touhami, M.E.; et al. Synthesis and anticorrosive properties of epoxy polymer for CS in 1 M HCl solution: Electrochemical, AFM, DFT and MD simulations. Constr. Build. Mater. 2021, 270, 121454. [Google Scholar] [CrossRef]
- Shahmoradi, A.R.; Ranjbarghanei, M.; Javidparvar, A.A.; Guo, L.; Berdimurodov, E.; Ramezanzadeh, B. Theoretical and surface/electrochemical investigations of walnut fruit green husk extract as effective inhibitor for mild-steel corrosion in 1M HCl electrolyte. J. Mol. Liq. 2021, 338, 116550. [Google Scholar] [CrossRef]
- Balasurya, S.K.; Okla, M.K.; Mohebaldin, A.; Al-ghamdi, A.A.; Abdel-Maksoud, M.A.; Almunqedhi, B.; AbdElgawad, H.; Thomas, A.M.; Raju, L.L.; Khan, S.S. Self-assembling of 3D layered flower architecture of BiOI modified MgCr2O4 nanosphere for wider spectrum visible-light photocatalytic degradation of rhodamine B and malachite green: Mechanism, pathway, reactive sites and toxicity prediction. J. Environ. Manag. 2022, 308, 114614. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, K.; Zhou, Y.-t. Online State of Charge Estimation of Lithium-Ion Cells Using Particle Filter-Based Hybrid Filtering Approach. Complexity 2020, 2020, 8231243. [Google Scholar] [CrossRef]
- Wang, L.; Xie, L.; Yang, Y.; Zhang, Y.; Wang, K.; Cheng, S.j. Distributed Online Voltage Control with Fast PV Power Fluctuations and Imperfect Communication. IEEE Trans. Smart Grid 2023, 1–14. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.; Li, D.; Cui, X.; Wang, L.; Li, L.; Wang, K. Electrochemical Impedance Spectroscopy: A New Chapter in the Fast and Accurate Estimation of the State of Health for Lithium-Ion Batteries. Energies 2023, 16, 1599. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, L.; Li, Q.; Wang, K. A comprehensive review on the state of charge estimation for lithium-ion battery based on neural network. Int. J. Energy Res. 2022, 46, 5423–5440. [Google Scholar] [CrossRef]
- Cui, Z.; Kang, L.; Li, L.; Wang, L.; Wang, K. A combined state-of-charge estimation method for lithium-ion battery using an improved BGRU network and UKF. Energy 2022, 259, 124933. [Google Scholar] [CrossRef]
- Xiong, R.; Tian, J.; Mu, H.; Wang, C. A systematic model-based degradation behavior recognition and health monitoring method for lithium-ion batteries. Appl. Energy 2017, 207, 372–383. [Google Scholar] [CrossRef]
- Galeotti, M.; Cina, L.; Giammanco, C.; Cordiner, S.; Di Carlo, A. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy. Energy 2015, 89, 678–686. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Dai, H. Estimation of state of health of lithium-ion batteries based on charge transfer resistance considering different temperature and state of charge. J. Energy Storage 2019, 21, 618–631. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, C.-G.; Li, H.; Feng, G.; Peng, W. Electrochemical Impedance Spectroscopy Based State-of-Health Estimation for Lithium-Ion Battery Considering Temperature and State-of-Charge Effect. IEEE Trans. Transp. Electrif. 2022, 8, 4633–4645. [Google Scholar] [CrossRef]
- Iurilli, P.; Brivio, C.; Wood, V. On the use of electrochemical impedance spectroscopy to characterize and model the aging phenomena of lithium-ion batteries: A critical review. J. Power Sources 2021, 505, 229860. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, W.C.; Xie, C.J.; Du, B.H.; Zhao, B.; Deng, Z.F.; Li, Y.; Shi, Y.; Li, W.B.; Zhang, L.Q.; et al. Health degradation assessment of proton exchange membrane fuel cell based on multi-model probability fusion. Int. J. Energy Res. 2022, 46, 14174–14190. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Bertrand, N.; Deletage, J.Y.; Vinassa, J.M. Behavior and state-of-health monitoring of Li-ion batteries using impedence spectroscopy and recurrent neural networks. Int. J. Electr. Power Energy Syst. 2012, 42, 487–494. [Google Scholar] [CrossRef]
- Geng, M.; Fan, M.; Yang, K.; Zhao, G.; Tan, Z.; Gao, F.; Zhang, M. Fast estimation method for state-of-health of retired batteries based on electrochemical impedance spectroscopy and neural network. Energy Storage Sci. Technol. 2022, 11, 673–678. [Google Scholar]
- Liu, J.; Zhang, H.; Yuan, Y. Health state estimation of lithium battery based on LSTM and EIS. Transducer Microsyst. Technol. 2021, 40, 59–61, 65. [Google Scholar]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef]
- Chang, C.; Wang, S.; Jiang, J.; Gao, Y.; Jiang, Y.; Liao, L. Lithium-Ion Battery State of Health Estimation Based on Electrochemical Impedance Spectroscopy and Cuckoo Search Algorithm Optimized Elman Neural Network. J. Electrochem. Energy Convers. Storage 2022, 19, 030912. [Google Scholar] [CrossRef]
- Pradyumna, T.K.; Cho, K.; Kim, M.; Choi, W. Capacity estimation of lithium-ion batteries using convolutional neural network and impedance spectra. J. Power Electron. 2022, 22, 850–858. [Google Scholar] [CrossRef]
- Chen, X.; Geng, M.; Wang, Q.; Shen, J.; He, Y.; Ma, Z. Electrochemical impedance feature selection and gaussian process regression based on the state-of-health estimation method for lithium-ion batteries. Energy Storage Sci. Technol. 2022, 11, 2995–3002. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).