The Influence of Electric Arc Plasma Turbulence on Heat Transfer Processes Involving Powder Materials

Abstract

The paper presents an analysis of the heat transfer processes in electric arc plasma conditions between the powder material and the plasma jet in different convective states. The heat transfer processes in the plasma jet generated for coating deposition are considered based on varying the conditions for the jet–powder interaction. The formed coating deposited onto the substrate acts as an indicator of the heat transfer efficiency. The heat transfer between the plasma jet and the powder material is facilitated by the turbulent nature of the plasma jet. The presented calculation results demonstrate the influence of the plasma flow turbulence on the motion of the fine powder and heating of the generated jet at the outlet of the plasma torch. An analysis of the influence of plasma flow turbulence on the acceleration and heating of fine powder particles was carried out. The experimental results allowed for the determination of the effect of the plasma jet turbulence degree on the heat transfer processes between the plasma and fine powder: the technological efficiency of the device with varying parameters of the spraying process and the flow rates of the material supply and plasma-forming gas were presented. The values of the plasma-forming gas supply rate, the material supply rate, and the Reynolds number were obtained while the other process parameters were fixed. The research was carried out within the state assignment of the Ministry of Science and Higher Education of the Russian Federation (theme No. FSEG-2023-0012).

1. Introduction

The gas thermal (electric arc) spraying of coatings has become widespread as a method for the restoration of worn parts and the formation of protective layers, including self-fluxing materials and other coatings produced by DC plasma torches. However, the low efficiency of the interaction between a generated plasma jet and a powder material at the outlet of the plasma torch [1] significantly limits the range of applications of this technology [2,3], as the energy consumption of the technological process increases.

Throughout the existence of this technology, scientists have been trying to modernize the technological process of plasma spraying, working on the improvement of the equipment. Plasma spraying technology uses a plasma jet to melt a powder material for deposition onto the working surface (see Figure 1). One of the disadvantages of plasma spraying technology is the low electrical efficiency of the generated plasma jet at the outlet of the plasma torch, as well as the significant technological consumption of the sprayed powder material.

The papers of well-known scientists are devoted to increasing the efficiency of plasma spraying [1,2,3,4,5,6,7,8]. Considerable attention has been paid to the study of the heat transfer issues in a plasma flow and the numerical modeling in the papers of J. P. Trelles, V. Rat, Z. Duan, J. F. Coudert, J. J. Gonzales, and C. Baudry [9,10,11,12,13,14,15,16]. In these papers, it was noted that the heat transfer in the plasma is, to a large degree, governed by the stability of the plasma flow and the development of instabilities, leading to the turbulence of the plasma outflow from the nozzle part of the plasma torch.

A significant acceleration of the plasma flow in the nozzle part of the plasma torch, as well as the temperature gradient of the forming electric arc channel of the plasma torch and the electromagnetic Lorentz force, are the main reasons for the development of flow instability, leading to turbulence. The plasma jet, flowing from the plasma torch nozzle, interacts with the dense cold environment that increases the turbulence of the heated plasma flow [2,3].

An instability arises in an environment with variable conductivity σ = σ(T), which is associated with a fluctuation of the internal energy (with a temperature gradient), leading to a perturbation of the Joule dissipation, which enhances the fluctuation of the internal energy [17,18]. The spatial distribution of the Joule dissipation calculated in the simulation differs significantly from the distribution of the volume force. In particular, the source of dissipation is more concentrated near the edge of the outer electrode (nozzle) of the plasma torch. Studies have also shown that the unstable state of the plasma at the outlet of the plasma torch depends on the character of the change in the conductivity near the nozzle part and at its slight distance, where the instability criteria change depending on the plasma temperature. In connection with this circumstance, it becomes more difficult to set the boundary conditions when modeling a plasma jet.

The main attribute of the turbulence occurrence, which is distinctive for plasma [17,18], is an appearance of transverse and longitudinal pulsations, in contrast to an incompressible liquid medium where only transverse vortex pulsations are possible. In the case of plasma, the powder material is loaded into the plasma jet just in the region of the increasing plasma flow velocity and maximum temperature, due to the concentration of the dissipation source at the edge of the plasma torch nozzle. In this case, the plasma outflow characteristics are sensitive to a small change in the initial conditions.

The presence of a thermal field with a large temperature gradient at the outlet of the plasma torch and the properties of the sprayed material lead to various modes of hydrodynamic, thermal, and electromagnetic instabilities during the interaction of the arc discharges with the ambient environment.

The most important factor of the occurrence of turbulence in the jet of a DC plasma torch is the occurrence of transverse flows (Kelvin–Helmholtz) of instability, which appear at the interface between parallel gas flows with markedly different velocities, as well as plasma properties (for example, density and viscosity), which takes place at the exit boundary of the plasma torch nozzle into the environment.

The usage of turbulence models for the simulation of plasma flows is significantly more difficult than their use for most other industrial applications due to their inherent characteristics.

A more accurate description of the flow turbulence adds a much higher degree of complexity in the case of plasma flow modeling. There is a sufficient number of papers on the use of RANS (Reynolds-averaged Navier–Stokes equations) turbulence models for the analysis of thermal plasma jets, such as [19], and others devoted to 2D jet modeling using a two-fluid model to describe the heat transfer between the plasma jet and ambient cold gas, as well as the paper of Li and Chen [20] about the 3D modeling of a plasma jet using the k-ε turbulence model (which adequately describes open space turbulence). Non-stationary 3D models are more suitable for describing the essence and dynamics of the three-dimensional flow of a DC plasma jet. In most cases, the concept of the critical value of the Reynolds number (about 2000–2500) is introduced where the plasma flow changes from a laminar regime to a turbulent one at the outlet of the plasma torch. However, the calculations of the critical values of the Reynolds number by different authors do not always coincide, which, in our opinion, is conditioned by the difference in the initial design of the plasma torch, the flow rate of the plasma-forming gas, the change in the velocity of the plasma flow in the nozzle part of the plasma torch, and other factors.

The intention of scientists to develop a comprehensive mathematical model of an arc plasma torch is reflected in the papers [21,22,23,24,25,26] and represents a combination of gas dynamics, electromagnetic, and thermal energy dissipation problems, where the corresponding equations are implicitly coupled by thermodynamic and transport properties and explicitly coupled through Joule heating.

The results of the numerical simulation of a non-stationary mathematical model demonstrate the formation of thermal and dynamic boundary layers between a high-velocity plasma flow and a low-velocity loaded flow of powder material (about ten times slower), which prevents the efficient heating of particles [27,28].

An analysis of the results of a turbulent non-isothermal flow numerical simulation demonstrates chaotically occurring velocity and pressure pulsations, which lead to intensive mixing of the medium and more efficient heat transfer. The efficiency of the heat transfer processes in laminar and turbulent flows can be assessed by the average temperature of the heated body. During the heating time, the average temperature of the heated body in the laminar non-isothermal plasma flow increases by 13.1 °C and in the turbulent flow by 25.9 °C [28], which indicates a more efficient heat transfer in the turbulent flow. In this case, the main fluctuations of the plasma flow are recorded at a frequency of 300 Hz [29,30].

Modern software makes it possible to carry out numerical simulations of the physical processes in a plasma torch, thereby reducing the costs and time of novel device design for plasma-spraying technology. However, the necessity of justifying the choice of geometry and characteristics of a plasma torch does not allow us to fully depart from the empirical nature of the development.

In connection with the foregoing, this paper presents a new method for establishing the regularities of the influence of the flow turbulence degree of a plasma torch jet on the heat transfer processes between the plasma and the powder material supplied to the nozzle exit of the plasma torch. Herein, the indicator of an improvement in the heat transfer processes is fixed concerning the formation of a coating on the substrate, providing good adhesion. For this, with a change in the degree of turbulence, the following conditions of the plasma jet generation remain unchanged: the flow rate of the plasma-forming gas, the design of the plasma torch with inter-electrode inserts [2,3], the initial velocity of the powder with accompanying gas from a feeder and its mass rate (the initial powder is aluminum with the most prepared identical fraction), a DC plasma torch power supply, the distance to the substrate, and the coating time. A method of producing the plasma flow turbulence degree by increasing the supplied powder volume with the help of a refractory powder of the same fraction is also applied. Only the powder that reaches the temperature necessary for the formation of the coating is deposited to the substrate during the spraying, and the refractory powder falls off, reflecting off the substrate. Based on the obtained results, the amount of deposited powder is estimated, and the technological efficiency is determined for the known powder mass rate. Thus, with an increase in the flow turbulence degree (according to the Reynolds number), an increase in the deposited powder mass is observed. In addition, the results of the coating formation lead to a determination of the generalized heat transfer coefficient, which can be used for an adaptive method for heat transfer process simulation in a plasma jet at the plasma-forming gas flow rates considered in the paper.

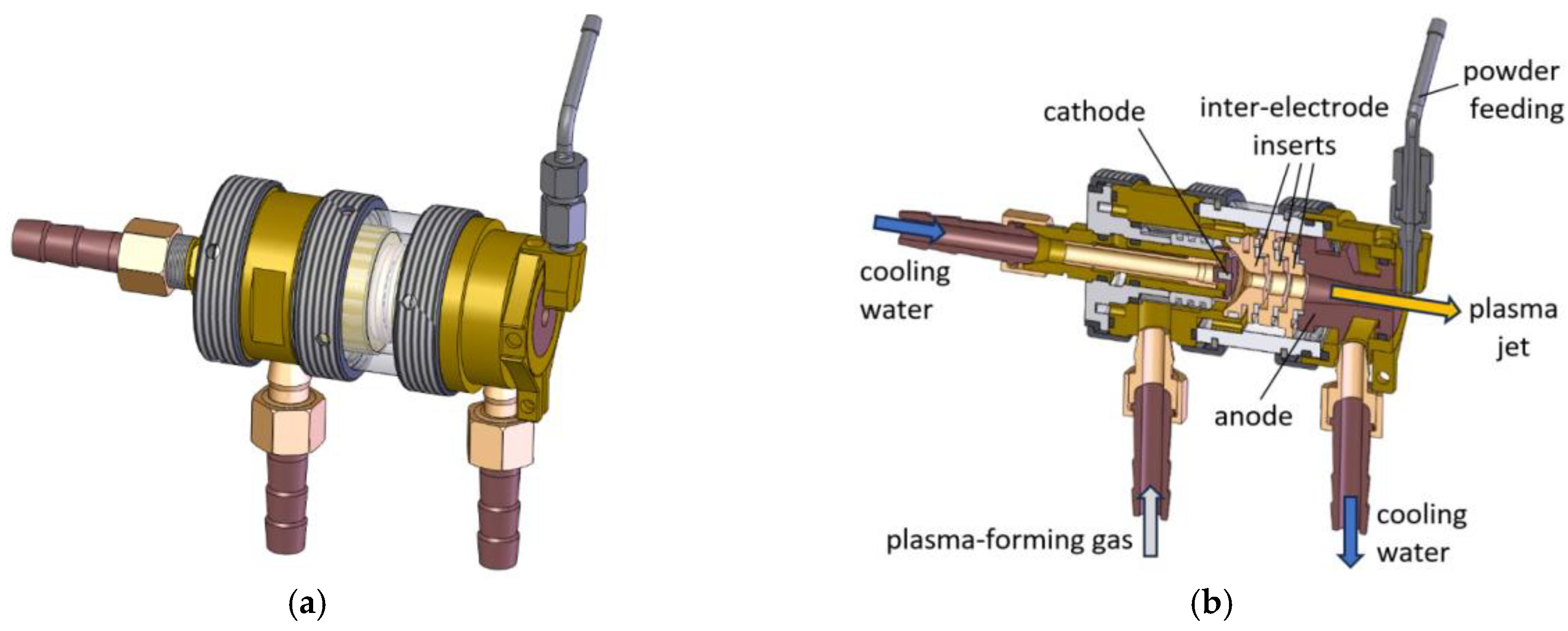
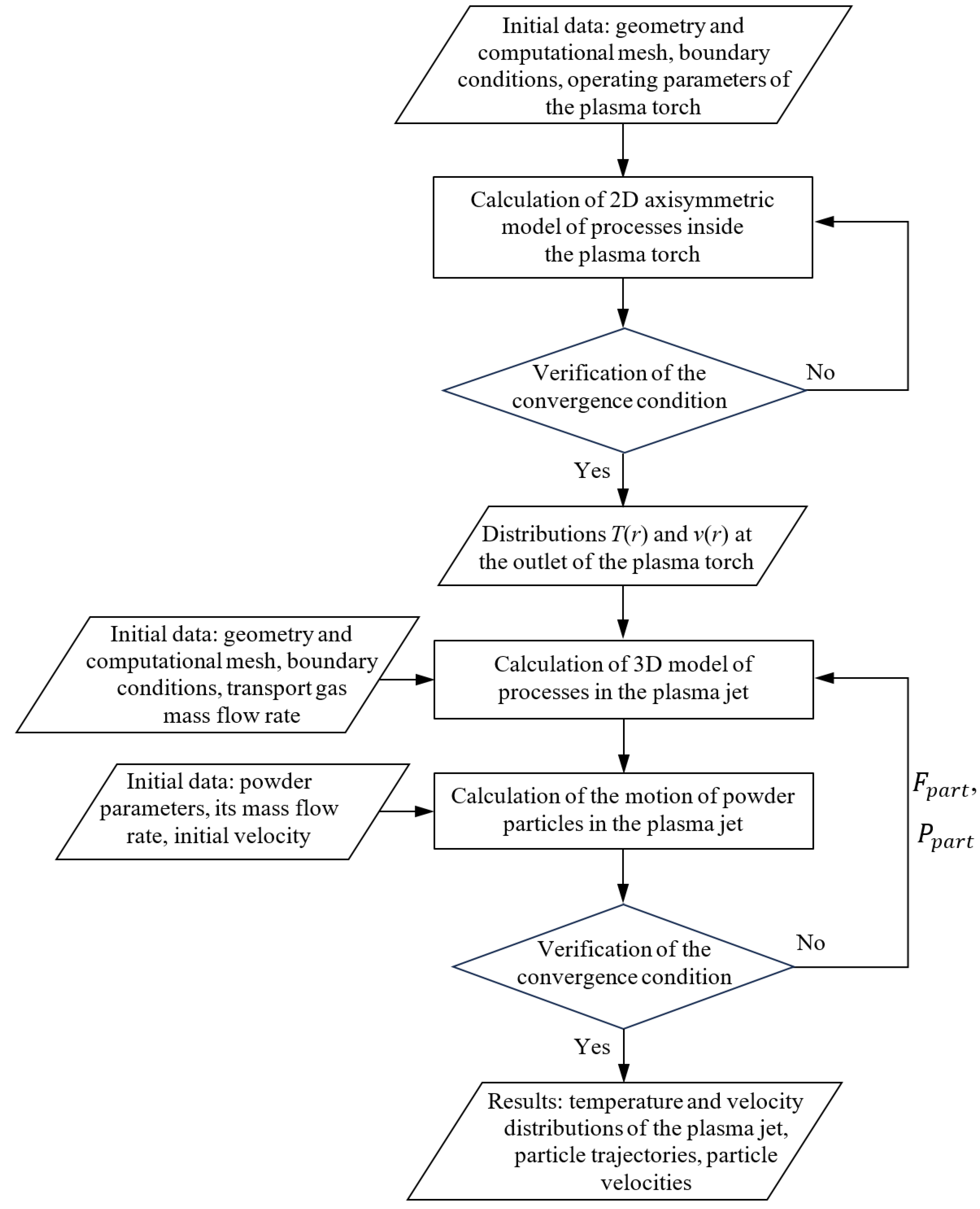
2. Mathematical Model of Powder Motion in a Plasma Jet

In order to establish the desirable rate of powder supply with the transporting gas for submersion in the axial region of the generated plasma jet (Figure 1), it is necessary to develop a mathematical model describing the processes under consideration.

From the description, it follows that the mathematical model of the process under consideration is quite complex, and should include both processes inside the arc plasma torch and processes in the area of the plasma jet. At the same time, the arc plasma torch with IEI as a whole has an axial symmetry. Therefore, for simplicity, the task is divided into two parts. A flowchart of the numerical model is shown in Figure 2.

Initially, the plasma processes inside the arc plasma torch were calculated (the problem was solved in a 2D axisymmetric formulation).

An electric arc closes inside the plasma torch, so the model included thermal, gas dynamic, and electromagnetic processes.

The basic equations of the used model are written in the following form [31,32]:

–

Energy equation:

$$\nabla ·\left[\overrightarrow{v}\left(\varrho h+\frac{\varrho v^2}{2}\right)\right]=\nabla \left(\lambda \nabla T\right)+P_h,$$

(1)

where $\overrightarrow{v}$ is the velocity, $\varrho$ is the density, h is the enthalpy related to the temperature T, $\lambda$ is the thermal conductivity, and $P_h$ is a source term for the energy equation.

In the case of the plasma conditions, the source term takes into account the Joule heating $\sigma E^2$ and power losses $u_{rad}$ due to radiation:

$$P_h=\sigma E^2-u_{rad},$$

(2)

where $\sigma$ is the electrical conductivity and $E$ is the electric field intensity.

–

Motion equation:

$$\nabla ·\left(\varrho \overrightarrow{v}\overrightarrow{v}\right)=-\nabla p+\mathsf{\Delta }·\left(\overline{\overline{\tau }}\right)+\varrho \overrightarrow{g}+\overrightarrow{F_B},$$

(3)

where p is the static pressure, $\overline{\overline{\tau }}$ is the stress tensor, $\overrightarrow{g}$ is the acceleration of gravity, and $\overrightarrow{F_B}$ is the electromagnetic force.

The stress tensor $\overline{\overline{\tau }}$ is defined by the following expression:

$$\overline{\overline{\tau }}=\mu \left[\left(\nabla \overrightarrow{v}+\nabla {\overrightarrow{v}}^{\mathrm{T}}\right)-\frac{2}{3}\nabla ·\overrightarrow{v}I\right].$$

(4)

The electromagnetic force is defined by the following expression:

$$\overrightarrow{F_B}=\overrightarrow{J}\times \overrightarrow{B},$$

(5)

where $\overrightarrow{J}$ is the current density and $\overrightarrow{B}$ is the magnetic induction.

–

Continuity equation:

$$\nabla ·\left(\varrho \overrightarrow{v}\right)=0.$$

(6)

–

The equations of the electromagnetic task for the magnetic vector potential $\overrightarrow{A}$ and the electric scalar potential $\phi$ were obtained from the system of the electromagnetic equations of Maxwell [32]:

$$\nabla ·\overrightarrow{A}={\mu }_0\overrightarrow{J},$$

(7)

$$\nabla ·\left(\sigma \nabla \phi \right)=0.$$

(8)

The problem was solved using the ANSYS Fluent software. The transition SST model was used to take into account the plasma turbulence.

Unfortunately, ANSYS Fluent software does not have built-in features for solving electromagnetic problems. On the other hand, ANSYS Fluent software allows the user to solve their own equations. Therefore, the solution of Equations (7) and (8) was performed through user-defined functions (UDF) [33].

A general view of the arc plasma torch for the calculation and its cut are shown in Figure 3. The mode of the operation and design of the plasma torch were set as identical to the ones in the experimental setup (for which experimental data were obtained).

The computational domain for the torch calculation is presented in Figure 4. It can be seen that the computational domain includes not only the region inside the arc plasma torch, but also the region of the plasma jet. This is performed in order to exclude the influence of the boundary condition on the plasma temperature and velocity distributions in the outlet section of the plasma torch.

The boundary conditions for the torch calculation are given in

Table 1. Boundary conditions for the arc plasma torch calculations.

Boundary (See Figure 4)	Physical Quantity
	T	${\mathit{v}}_{\mathit{z}}$	${\mathit{v}}_{\mathit{r}}$	p	${\mathit{A}}_{\mathit{z}}$	${\mathit{A}}_{\mathit{r}}$	$\mathit{\phi }$
AB	$T_c\left(r\right)$	0	0	–	$\frac{\partial A_z}{\partial n}=0$	$\frac{\partial A_r}{\partial n}=0$	$-{\phi }_c$
BC	300 K	$v_{z in}$	0	–	$\frac{\partial A_z}{\partial n}=0$	$\frac{\partial A_r}{\partial n}=0$	$\frac{\partial \phi }{\partial n}=0$
CD, DE	300 K	0	0	–	$\frac{\partial A_z}{\partial n}=0$	$\frac{\partial A_r}{\partial n}=0$	$\frac{\partial \phi }{\partial n}=0$
EF	300 K	0	0	–	$\frac{\partial A_z}{\partial n}=0$	$\frac{\partial A_r}{\partial n}=0$	$\frac{\partial \phi }{\partial n}=0$
FG	$\frac{\partial T}{\partial n}=0$	$\frac{\partial v_z}{\partial n}=0$	$\frac{\partial v_r}{\partial n}=0$	1 atm	0	0	$\frac{\partial \phi }{\partial n}=0$
GH	$\frac{\partial T}{\partial n}=0$	$\frac{\partial v_z}{\partial n}=0$	$\frac{\partial v_r}{\partial n}=0$	1 atm	$\frac{\partial A_z}{\partial n}=0$	$\frac{\partial A_r}{\partial n}=0$	$\frac{\partial \phi }{\partial n}=0$
AH	$\frac{\partial T}{\partial n}=0$	$\frac{\partial v_z}{\partial n}=0$	0	–	$\frac{\partial A_z}{\partial n}=0$	$\frac{\partial A_r}{\partial n}=0$	$\frac{\partial \phi }{\partial n}=0$
DL	–	–	–	–	–	–	0

Note: n is the direction perpendicular to a boundary.

.

At the cathode (the boundary AB), the temperature $T_c\left(r\right)$ was set according to a parabolic law with a maximum value of 10,000 K on the torch axis, with a temperature of 300 K for the radial coordinate r > 2 mm.

The value of the electric scalar potential at the cathode $-{\phi }_c$ was selected during the calculation so that the Joule heating power released in the plasma was equal to the specified value (24 kW).

The axial velocity at the inlet was set based on the mass flow rate $G$ of the plasma-forming gas:

$$v_{z in}=\frac{G}{\rho \left(300 K\right)·S_{in}},$$

(9)

where $S_{in}$ is the area of the inlet section.

It should be noted that, within the framework of the 2D axisymmetric model, it is impossible to correctly set the anode spot of the electric arc on the cylindrical surface of the anode. Therefore, it was assumed that the anode is the line DL (see Figure 4), on which the following condition for the electric scalar potential is set:

$${\left.\phi \right|}_{DL}=0.$$

(10)

The plasma gas is air. The dependences of the thermodynamic and transport properties of the air on temperature were calculated according to the method described in the book [34].

In the calculation, the power dissipated in the plasma was set to 24 kW. Three cases were calculated for different mass flow rates of the plasma-forming gas: 0.75 g/s; 1.0 g/s; and 1.4 g/s.

The mesh for the calculations consists of 117,306 triagonal cells.

A grid independence test was carried out for the model. It showed that an increase in the number of mesh elements by a factor of 2 led to a change in the maximum temperature by 3%, which seems to be a rather low value.

As a result of the calculation, two-dimensional distributions of the temperature, velocity, and other values were obtained. Examples of the obtained results for the case of the plasma gas flow rate G = 1.0 g/s are shown in Figure 5.

The main results of the first stage of calculations, namely the radial distributions of the temperature and plasma velocity in the outlet section of the plasma torch (see Figure 6), were chosen as the initial data for the model of the processes in a plasma jet.

Further, in the 3D formulation, the model of the processes in a plasma jet was considered, taking into account the motion of the particles of the processed powder and taking into account the reverse effect of the powder on the behavior of the plasma jet [31]:

• – Energy equation for a particle:

$$m_{part}·c_{p part}·\frac{d{T}_{part}}{dt}=\alpha ·S_{part}·\left(T-T_{part}\right)-{\epsilon }_{part}·S_{part}·{\sigma }_{SB}·T_{part}^4$$

(11)

where $m_{part}$ is the particle mass, $c_{p part}$ is the specific heat of the particle material, $T_{part}$ is the particle temperature, $\alpha$ is the convective heat transfer coefficient, $S_{part}$ is the surface area of the particle, ${\epsilon }_{part}$ is the particle emissivity, and ${\sigma }_{SB}$ is the Stefan–Boltzmann constant.

–

Motion equation for a particle:

$$\frac{d\overrightarrow{v_{part}}}{dt}=F_D·\left(\overrightarrow{v}-\overrightarrow{v_{part}}\right)+\frac{{\rho }_{part}-\rho }{{\rho }_{part}}·\overrightarrow{g},$$

(12)

where $\overrightarrow{v_{part}}$ is the particle velocity, ${\rho }_{part}$ is the particle density, and $F_D$ is the drag force defined by the following expression:

$$F_D=\frac{18\mu }{{\rho }_{part}·d_{part}^2}·\frac{C_D·Re}{24}.$$

(13)

–

Energy equation for the plasma:

$$\nabla ·\left[\overrightarrow{v}\left(\varrho h+\frac{\varrho v^2}{2}\right)\right]=\nabla \left(\lambda \nabla T\right)+P_h-P_{part},$$

(14)

where $P_{part}$ is the power losses for the plasma due to the powder heating. In the conditions of the plasma jet, the source term $P_h$ takes into account only the power losses $u_{rad}$ due to radiation:

$$P_h=-u_{rad},$$

(15)

–

Motion equation for the plasma:

$$\nabla ·\left(\varrho \overrightarrow{v}\overrightarrow{v}\right)=-\nabla p+\mathsf{\Delta }·\left(\overline{\overline{\tau }}\right)+\varrho \overrightarrow{g}-\overrightarrow{F_{part}},$$

(16)

where $\overrightarrow{F_{part}}$ is the momentum losses for the plasma due to the powder acceleration.

–

Continuity equation for the plasma:

$$\nabla ·\left(\varrho \overrightarrow{v}\right)=0.$$

(17)

The mesh for the calculation consisted of 999,068 polygonal cells, as shown in Figure 7.

The principles of setting the boundary conditions for this step are the same as in the calculation of the processes inside the plasma torch. At the inlet of the computational domain (blue circle in Figure 7b), the plasma temperature and axial velocity distributions obtained from the calculations inside the plasma torch (see Figure 6) are set.

The problem was solved using the ANSYS Fluent software.

The input data for the calculation:

• The nozzle diameter was 6 mm and the charge pipeline diameter was 1.6 mm;
• The flow rate of the plasma-forming gas (air) was 0.75 g/s; 1.0 g/s; and 1.4 g/s;
• The transporting gas flow rate was 0.08 g/s (which corresponds to an initial velocity through a charge pipeline of 34.5 m/s); the powder consumption was 0.07 g/s; and the powder material was aluminum with a powder diameter of 50–60 microns and an average diameter of 55 microns;
• The initial velocity of the powder varied from 3 m/s to 34.5 m/s.

The results are shown in Figure 8, Figure 9 and Figure 10 for variants with plasma-forming air flow rates of 0.75 g/s; 1.0 g/s; and 1.4 g/s, respectively.

The presented calculation results correspond to the experimental data for the temperature and plasma flow rate parameters [2,35]. The data for calculating the rate of the powder supply for immersion in the plasma jet are confirmed visually by a laboratory test arranged similarly to Figure 1.

Table 2. Plasma jet parameters.

Plasma Parameters	Plasma-Forming Gas Flow Rate, g/s
	0.75	1.0	1.4
Maximum plasma temperature, K	8460	7030	6656
Maximum plasma velocity, m/s	872	1192	1414

, containing the results of the calculation, shows the maximum temperatures and velocities of the plasma jet at different flow rates of the plasma-forming gas. Clearly, with an increase in the flow rate, the maximum velocity of the plasma jet increases (which is obvious), and the maximum temperature decreases (which is due to the fact that, with an increasing velocity, the gas moves inside the plasma torch at a higher velocity and does not have time to heat up to the same temperature, as it does with a low flow rate).

In addition, from the results of the calculations, it can be seen that the initial velocity of the powder has a significant impact on its trajectory. At high initial velocities, the powder passes through the plasma jet, and at low velocities, it moves approximately in its axial region, which leads to a longer time the powder spends in the plasma jet.

Table 3. Maximum powder velocity in various modes.

Initial Velocity, m/s	Plasma-Forming Gas Flow Rate, g/s
	0.75	1.0	1.4
3	131	178	201
5	131	179	203
10	131	184	211
17	126	185	219
34.5	92.5	145	182

shows the maximum velocities of the powder in various modes of operation. It is clear that, with an increase in the flow rate of the plasma-forming gas, the velocity of the powder increases. The decrease in the maximum velocity at the initial velocity of the powder of 34.5 m/s is due to the fact that the powder passes through the plasma jet.

The obtained data of the calculation of the powder supply to the jet, confirmed experimentally, act as the initial data for further experimental studies.

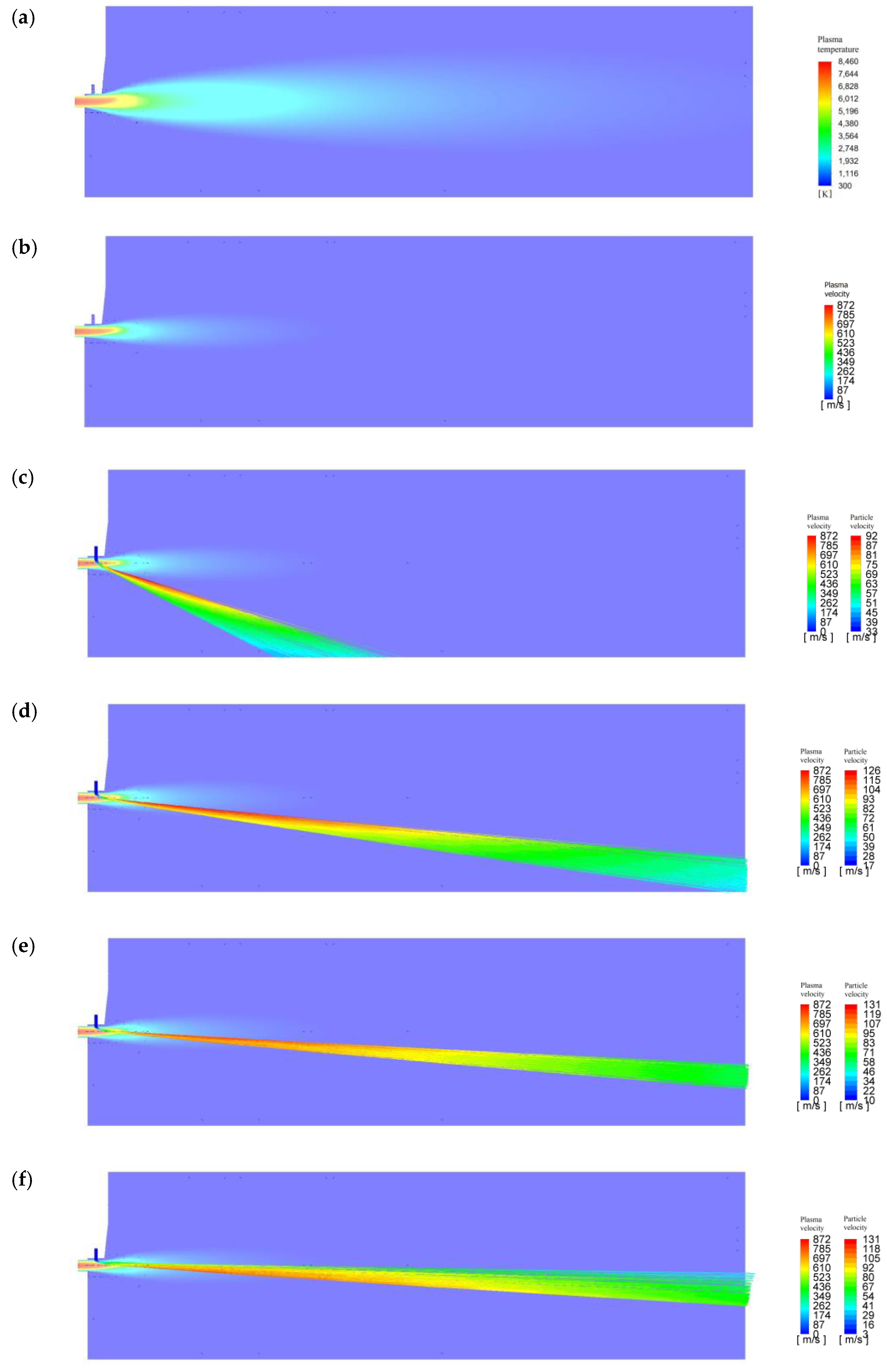
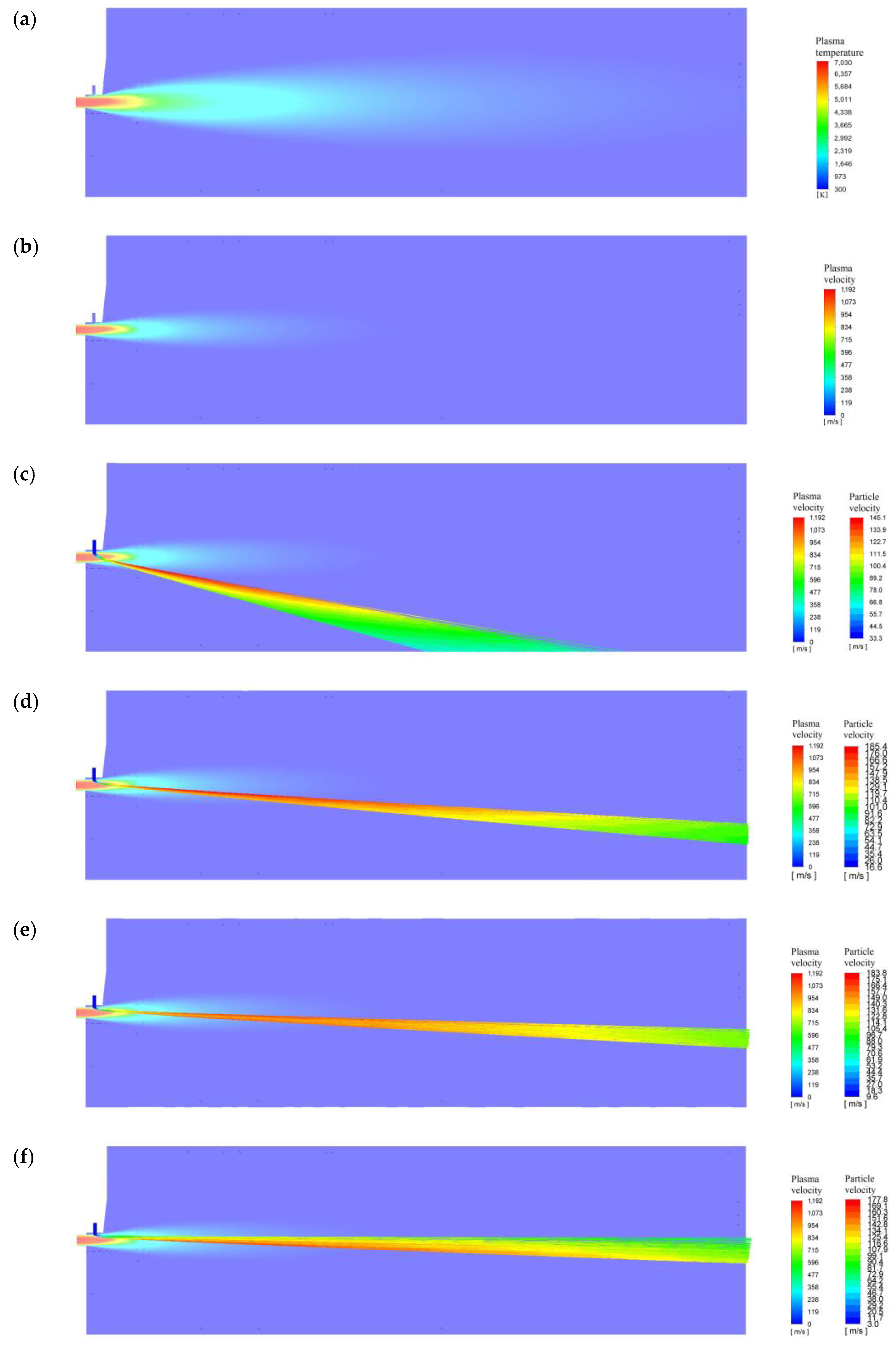
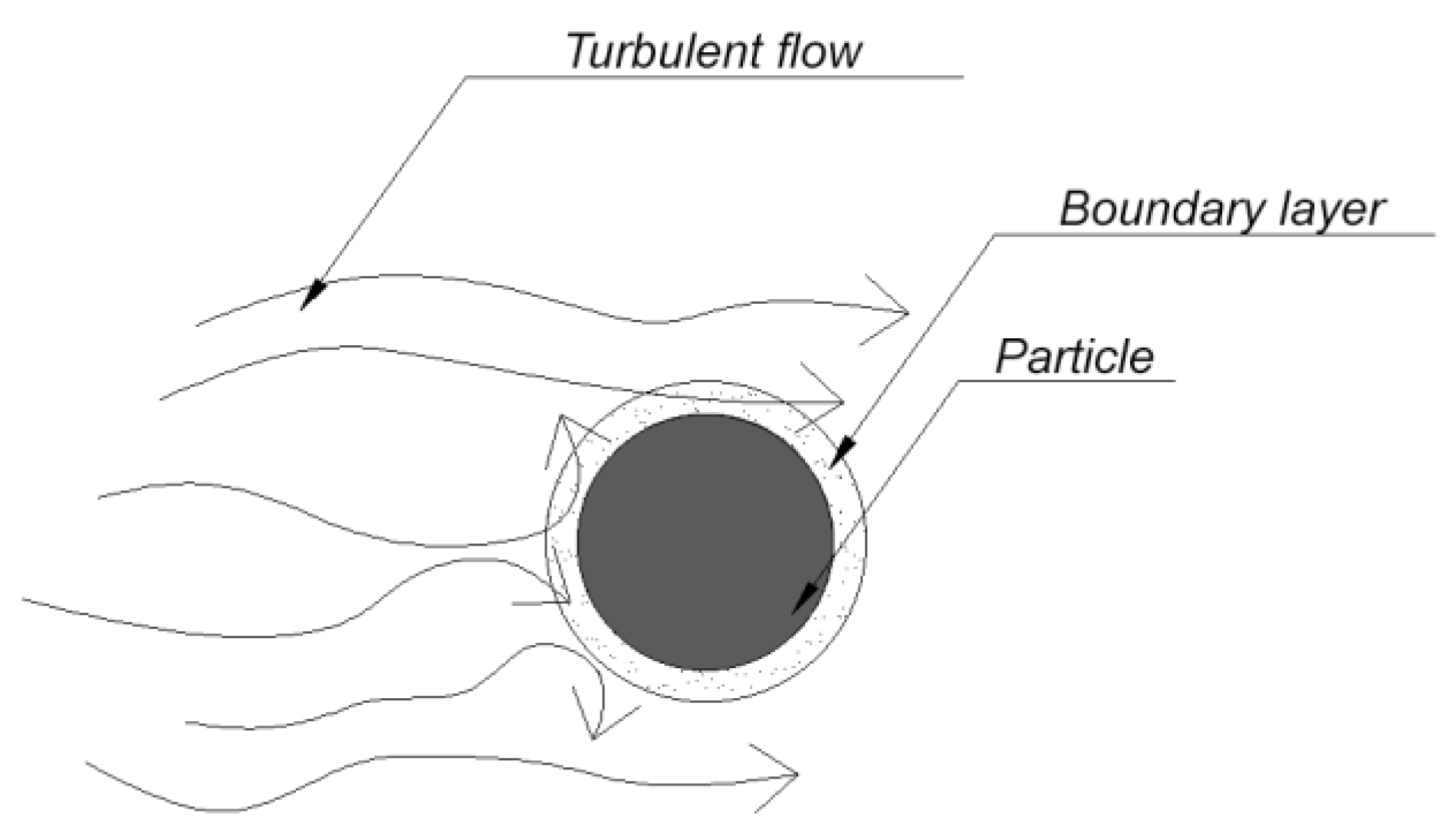
3. Influence of the Turbulent Nature of the Plasma-Forming Gas on the Heat Transfer between the Thermal Energy of the Plasma and the Powder Material

The turbulent nature of the heat transfer of the plasma-forming gas with the arc leads to the emergence of high-frequency pulsations, the amplitude and frequency of which depend on the flow rate, composition, temperature of the gas, and the dynamics of shunting the arc. These pulsations cause fluctuations in the enthalpy, velocity, and temperature of the plasma jet, with frequencies up to several kilohertz. There is an assumption that, during heat exchange in a turbulent flow, the heat transfer coefficient α increases, since the boundary layer of the particles, which complicates their heat exchange with the plasma, as a result of a several-times increase in the viscosity and a decrease in the thermal conductivity in this area, is dissipated to a greater extent than that during laminar flow under the influence of multidirectional forces.

The purpose of experimental studies is to determine the influence of the plasma flow turbulence degree at the outlet of the plasma torch on the heat exchange processes between the plasma and the powder material. In this case, the change in the conditions of the heat exchange processes is carried out by changing the degree of the plasma jet turbulence, and the remaining parameters of the process are left unchanged. The novelty of the solution lies in the fact that this process will be assessed by its result: the coating formation on the surface of a workpiece.

An increase in the degree of the turbulence of the flow can lead to an increase in the dissipation of the heat energy of the plasma on the powder material. Figure 11 shows the physical interpretation of the heat exchange processes between the plasma and the particle of the material immersed in the plasma.

With an improvement in the heat exchange conditions, it is possible to achieve a significant increase in the productivity of the technological process (increase in efficiency).

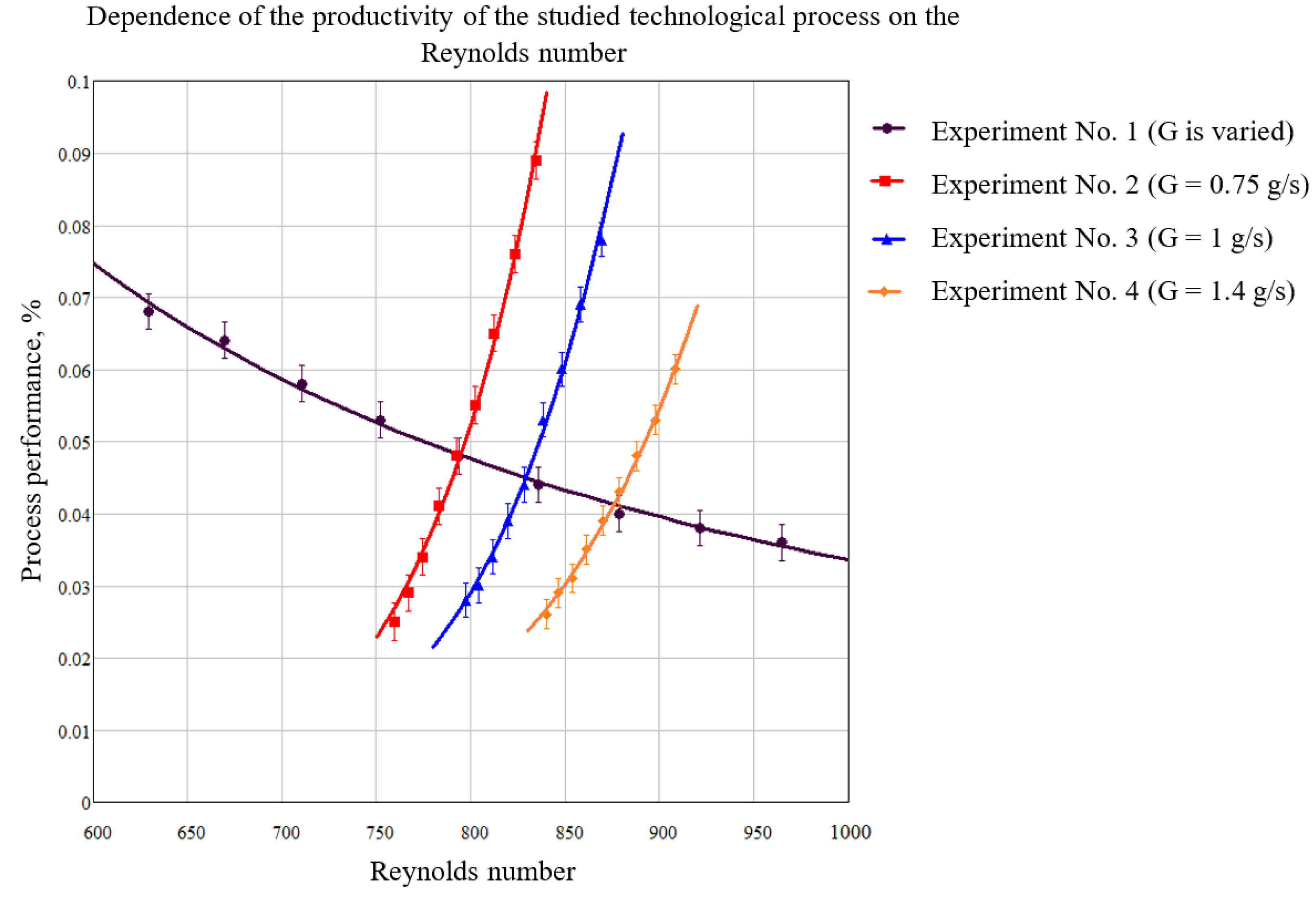
4. Laboratory Experiment to Determine the Effect of the Plasma Jet Turbulence Degree on the Intensity of Heating of the Particles of the Sprayed Material

To draw a conclusion on the expediency of the above concept, it is necessary to conduct a series of experiments, the methodology of which is based on solving the problem of the engineering optimization of the plasma-spraying process.

A dimensionless quantity called the Reynolds number is a similarity criterion of gas dynamic flows and, in this case, is defined as [2]:

$$\mathrm{Re}=\frac{\rho ·v_n·d_n}{\mu },$$

(18)

where $v_n$ is the plasma velocity at the outlet of the nozzle, $d_n$ is the diameter of the nozzle, and μ is the dynamic viscosity of the plasma.

According to [2], the occurrence of turbulence of the flow inside the cylindrical tube (the shape of the plasma torch channel) corresponds to the Reynolds number value ≈ 800.

The Prandtl number is defined based on the physical properties of the medium—the specific heat $c_p$, the thermal conductivity $\lambda$, and the dynamic viscosity $\mu$—and is a characteristic of the thermophysical properties of the heat transfer medium:

$$\mathrm{Pr}=\frac{\mu ·c_p}{\lambda }$$

(19)

The Reynolds number and the Prandtl number determine the dimensions of the dynamic boundary layer ${\delta }_v$ (the layer in which the velocity of the medium varies from the velocity of the jet at the outer boundary with the plasma to 0 at the outer boundary with the particle) and the temperature boundary layer ${\delta }_T$ (the layer in which the temperature of the medium varies from the temperature of the jet at the outer boundary with the plasma to the temperature of the particle at the outer boundary with the particle):

$${\delta }_v=\frac{d_{part}}{\sqrt{\mathrm{Re}}},$$

(20)

$${\delta }_T=\frac{d_{part}}{\sqrt{\mathrm{Re}}·\sqrt{\mathrm{Pr}}},$$

(21)

where $d_{part}$ is the diameter of the particle.

To formulate and solve the optimization problem, a mathematical apparatus is available that allowed us to vary all the available parameters that the experimental setup was able to change.

The choice criterion in the process of solving the optimization problem in the mathematical modeling will be the maximum value of the efficiency. Based on [1], it follows:

$$\eta =\frac{P_{pow}}{k_{jet}·P_{el}}=\frac{\alpha ·\Delta T·S_{part}·\frac{G_{pow}}{m_{part}}·\frac{l_{jet}}{v_r}}{k_{jet}·U·I}=\frac{\alpha ·\Delta T·S_{part}·G_{pow}·l_{jet}}{k_{jet}·U·I·m_{part}·\left|\overrightarrow{v_{pow}}-\overrightarrow{v}\right|}$$

(22)

where $P_{\mathrm{pow}}$ is the plasma jet power expended to heat the powder, $P_{el}$ is the total electric power expended, k_jet is the empirical coefficient that determines the fraction of the input power that is carried out by the plasma jet, $\Delta T$ is the difference between the plasma temperature and particle temperature, $G_{pow}$ is the mass rate of the powder feeding, $l_{jet}$ is the length of the thermal active zone of the plasma jet, $v_r$ is the relative velocity of the powder, and $\overrightarrow{v_{pow}}$ is the powder velocity.

The choice criterion In the process of solving the optimization problem In the laboratory experiment will be the maximum value of the process performance:

$$W=\frac{\mathsf{\Delta }{m}_{sb}}{t_{spr}},$$

(23)

where $\mathsf{\Delta }{m}_{sb}$ is the increase in the mass of the substrate after coating and $t_{spr}$ is the time of the spraying operation.

The technological efficiency of the process was also determined according to the following formula:

$${\eta }_t=\frac{W}{G_{pow}}.$$

(24)

For the convenience of correlating the results of the experiments, the same parameters were varied in each of the tasks and the same functional constraints were imposed on the tasks.

Likewise, in the case of choosing the design variables for the implementation of the experiment in the laboratory, it is possible to vary the following parameters:

• $G_{pow}={\rho }_{part}·v_{pow}·S_{tube}$, the mass flow rate of the powder, then the velocity of the powder $v_{pow}$ is in the range from 10 to 100 m/s;
• $G=\rho ·v·S_n$, the mass flow rate of the plasma-forming gas, then the gas velocity $v$ is in the range from 50 to 200 m/s;
• The Reynolds number Re (respectively, the nature of the flow of the gaseous medium under consideration) is a calculated parameter for each case, and has a significant impact on the value of the parameter α;
• The arc current $I$ is in the range from 100 to 200 A.

The functional limitations of this experiment are as follows:

• A constant spraying time;
• A constant value of the power in the experiments on the study of laminar and turbulent flows;
• The average mass temperature of the plasma arc $T_{ave}$ = 6000 K (see Figure 8, Figure 9 and Figure 10);
• The Prandtl number $\mathrm{Pr}=0.54$.

A laboratory experiment aimed to identify the optimal modes of the technological process, consisting of coating deposition (Figure 12) by plasma spraying (described in detail in [35]) to metal substrates made of stainless steel, with equal dimensions and weights as fixed technological parameters (

Table 4. Technological parameters.

Technological Process Parameters
Distance to the surface of the workpiece	$l_w$, l, mm	350
Operating electrical power	$P_{el}$, W	24,000
Average plasma temperature	$T_{ave}$, K	6000
Spraying time	$t_{spr}$, s	8

). Then, the mass gain of the plates was measured for each case and the values of the Reynolds number, productivity, and process efficiency were calculated [36,37].

In the course of experiment No. 1, the coatings were deposited at a constant powder supply rate (0.076 g/s) and a variable mass flow rate of the plasma-forming gas, the air supply rate (

Table 5. Results of experiment No. 1 ($P_{el}$ = 24,000 W, $v_{pow}$ = 70 m/s).

$\mathit{G}$, g/s	$\mathit{v}$, m/s	${\mathit{m}}_1$, g	${\mathit{m}}_2$, g	$\mathit{\Delta }{\mathit{m}}_{\mathit{s}\mathit{b}}$, g	W, g/s	${\mathit{v}}_{\mathit{r}}$, m/s	Re	${\mathit{\eta }}_{\mathit{t}}$, %
0.500	103.821	81.390	82.062	0.672	0.084	125.215	551.234	84.00
0.550	114.203	101.114	101.706	0.592	0.074	133.949	589.684	74.00
0.600	124.585	103.820	104.364	0.544	0.068	142.903	629.105	68.00
0.650	134.967	109.430	109.941	0.511	0.064	152.040	669.326	64.00
0.700	145.349	103.190	103.653	0.463	0.058	161.327	710.210	58.00
0.750	155.731	101.210	101.632	0.422	0.053	170.740	751.650	53.00
0.800	166.113	105.790	106.175	0.385	0.048	180.260	793.559	48.00
0.850	176.495	103.760	104.110	0.350	0.044	189.870	835.866	44.00
0.900	186.877	103.920	104.243	0.323	0.040	199.557	878.513	40.00
0.950	197.259	105.670	105.976	0.306	0.038	209.311	921.453	38.00
1.000	207.641	103.190	103.478	0.288	0.036	219.123	964.648	36.00

).

In the course of experiment No. 2, the coatings were deposited at a constant mass flow rate of the plasma-forming gas (0.75 g/s), air supply rate, and variable mass flow rate of the powder material (

Table 6. Results of experiment No. 2 ($P_{el}$ = 24,000 W, $v$ = 170 m/s).

Al, %	${\mathit{G}}_{\mathit{p}\mathit{o}\mathit{w}}$, g/s	${\mathit{v}}_{\mathit{p}\mathit{o}\mathit{w}}$, m/s	${\mathit{m}}_1$, g	${\mathit{m}}_2$, g	$\mathit{\Delta }{\mathit{m}}_{\mathit{s}\mathit{b}}$, g	W, g/s	${\mathit{v}}_{\mathit{r}}$, g/s	Re	${\mathit{\eta }}_{\mathit{t}}$, %
100.000	0.050	46.531	106.308	106.510	0.202	0.025	172.507	759.430	50.00
93.750	0.056	52.255	107.124	107.354	0.230	0.029	174.138	766.611	51.79
87.500	0.063	57.951	110.026	110.298	0.272	0.034	175.931	774.505	53.97
81.250	0.069	63.615	104.110	104.440	0.330	0.041	177.877	783.072	59.42
75.000	0.075	69.243	106.102	106.482	0.380	0.048	179.967	792.271	64.00
68.750	0.081	74.831	108.666	109.106	0.440	0.055	182.190	802.057	67.90
62.500	0.088	80.373	101.380	101.903	0.523	0.065	184.536	812.383	73.86
56.250	0.094	85.863	103.881	104.491	0.610	0.076	186.992	823.197	80.85
50.000	0.1	91.293	103.490	104.260	0.710	0.089	189.547	834.443	89.00

).

In experiments No. 3 and No. 4, te coatings were also applied at a constant mass flow rate of the plasma-forming gas (1 g/s and 1.4 g/s, respectively). The results of the experiments are presented in the form of graphs (Figure 13). In each of the cases, a dependence was obtained, the nature of which is close to logarithmic.

To exclude the influence of an increase in the amount of the material supplied on the results in the course of this experiment, a mixture of aluminum and refractory silicon oxide that did not settle on the substrate was used for each measurement (Figure 12), with a proportional content of elements calculated on the basis of the flow rate of the mixture. A large difference in the melting points of the raw material of the powder (aluminum) and the silicon oxide eliminated the loss of heat energy for heating the refractory material. At the same time, the nature of the turbulence of the flow with a constant flow rate of the plasma-forming gas was ensured by loading the jet with powder with a commensurate flow rate of aluminum powder and silicon oxide.

From the results obtained, it can be seen that the efficiency of the technological process increased dramatically due to the improvement in the heat transfer processes between plasma and aluminum powder (experiments 2, 3, and 4). When the plasma flow cooled with an increase in the flow rate of the plasma-forming gas, the dependencies shifted towards the need to increase the turbulence of the flow (experiments 3 and 4) by increasing the flow rate of the refractory filling of the source powder material load.

The results of the laboratory study demonstrated that the drop in the productivity of the process in the first case was due to the fact that the generalized effect of a significant reduction in the trajectory of the particles (fixed channel sizes, fixed position of the plasma torch, and reduction in the angle between the flight path and the central axis of the plasma jet) and an increase in the speed of their movement led to the time the particles spent in the jet becoming insufficient for the melting of the aluminum particles, which entailed a decrease in the mass growth with an increase in the rate of supply of the plasma-forming gas (longitudinal velocity). At the same time, it should be noted that, at the transition point to the turbulent flow, there was a slight reduction in the steepness of the drop of the characteristic under study (experiment 1).

In the case of the powder material flow rate increase (transverse velocity), the trajectory of the particles became elongated, which resulted in an increase in the time spent by the particles in the plasma jet, and, together with a positive influence of the transition to the turbulent regime one (in the area of the transition of the jet flow to the turbulent mode, a sharp increase in studied characteristics’ steepness growth was observed), this led to an increase in the process productivity, and therefore the efficiency. In addition, according to the obtained results, it was possible to determine the nature of the heat transfer coefficient change, taking into account the coefficient of the heat transfer efficiency of the plasma and the surface of the powder material ${\eta }_t$ (Table 6).

Since the power of the plasma jet was used to heat the supplied powder, which was then sprayed to the part forming a coating, it can be assumed that the efficiency in Formula (22) is the technological efficiency defined by Formula (24).

Then, based on Formula (22), the formula of the heat transfer coefficient α is:

$$\alpha =\frac{{\eta }_t·k_{jet}·U·I·m_{part}·\left|\overrightarrow{v_{pow}}-\overrightarrow{v}\right|}{\Delta T·S_{part}·G_{pow}·l_{jet}},$$

(25)

Based on the values of the mass flow rate of the plasma-forming gas and powder material, the value of the heat transfer coefficient α for the technological process in experiment 2 varied, on average, from 3.4 W/(cm²·K) to 8.1 W/(cm²·K), and in experiments 3 and 4, from 2.6 W/(cm²·K) to 5.8 W/(cm²·K) and from 2.0 W/(cm²·K) to 4.0 W/(cm²·K), respectively.

To check the correctness of the found values for the heat transfer coefficient α, a calculation was performed according to the method described in [38]:

$$\mathsf{\alpha }=\mathrm{Nu}·\frac{\overline{\lambda }}{d_{part}},$$

(26)

where $\mathrm{Nu}$ is the Nusselt number, determined by the formula $\mathrm{Nu}=2+0.6·{\mathrm{Re}}^{0.5}·{\mathrm{Pr}}^{0.33}$, and $\overline{\lambda }$ is the plasma thermal conductivity averaged over the boundary layer. As a result, the calculated values of the heat transfer coefficient α are of the same order of magnitude as those found experimentally.

Based on the results of the laboratory research, it can be concluded that the turbulent nature of the flow of the plasma jet has a positive effect on the heat transfer between the plasma and the powder material, and the most effective parameters of the plasma-spraying process (positively affecting the performance of the process) are the processes in the boundary layer between the plasma and particles. The low thermal conductivity in this case is due to the presence of a sublimating powder material in the boundary layer, which can be eliminated by the turbulence of the plasma flow.

5. Conclusions

The results of laboratory and mathematical experiments indicated the influence of the turbulent nature of the movement of the gaseous medium on the heat transfer processes; however, the optimal operating modes of the plasma torches in the process of plasma spraying should take into account the need to keep molten particles in the plasma flow for a certain time (sufficient to melt the largest possible particles from the fractions used). The optimal modes of operation are those with a transient nature of the movement of the gaseous medium in the boundary layer around the particles, where the turbulence of the powder-loaded plasma jet scatters the sublimating material of the aluminum particles and ensures a temperature gradient between the plasma and the particle for a more efficient heat transfer. At the same time, in order to maintain this efficient heat transfer between the plasma and powder, a Reynolds number value of 750–900 must be achieved with a corresponding heat transfer coefficient from 2.0 W/(cm²·K) to 8.0 W/(cm²·K). It should be noted that, with an increase in the material fed into the plasma jet, the flow turbulence degree increases and a need to increase the flow rate of the plasma-forming gas arises.

According to the correlation of the results of the mathematical and laboratory experiments, to a first approximation, the ratio of the supply rates of the plasma-forming gas and the sprayed material being set as equal to 1:1.5 is optimal.

Based on the calculations, it becomes clear that the dimensions of the plasma torch (nozzle sections and channel length) also exert a large degree of influence on the processes under consideration. To find the most efficient trajectories of particle motion, it is necessary to conduct a series of additional experiments that take into account the geometry of the channel and the distance to the substrate.

The developed method will help, in the future, to establish the laws of heat transfer processes depending on the gas flow rate and the parameters of the plasma torch with inter-electrode inserts, which was the basis for this research. Furthermore, in the future, it seems important to establish the effect of plasma flow turbulence on heat transfer processes with various powder materials.