Optimal Power Flow Using Improved Cross-Entropy Method
Abstract
1. Introduction
- The improved cross-entropy method is presented for solving the optimal power flow problem.
- The constraint handling technique named superiority of feasible solution is introduced into proposed method, simulation results confirm that proposed method can obtain no constraints violation solution with assists of this method.
- The chaotic operator is introduced into proposed method to speed up the convergence speed and exploration capability.
- The Archive is introduced into proposed method to preserved the global best solution.
2. Problem Formulation
2.1. Control Variables
2.2. State Variables
2.3. Equality Constraint
2.4. Inequality Constraints
- Generator constraints:
- Transformer constraints:
- Shunt VAR compensator constraints:
- Security constraints:
3. Proposed Method
3.1. The Cross-Entropy Method
3.2. Cross-Entropy Method with Chaotic Operator (CGSCE)
3.2.1. Principle of CE Method
| Algorithm 1 CE method for Continuous Optimization Problem |
|
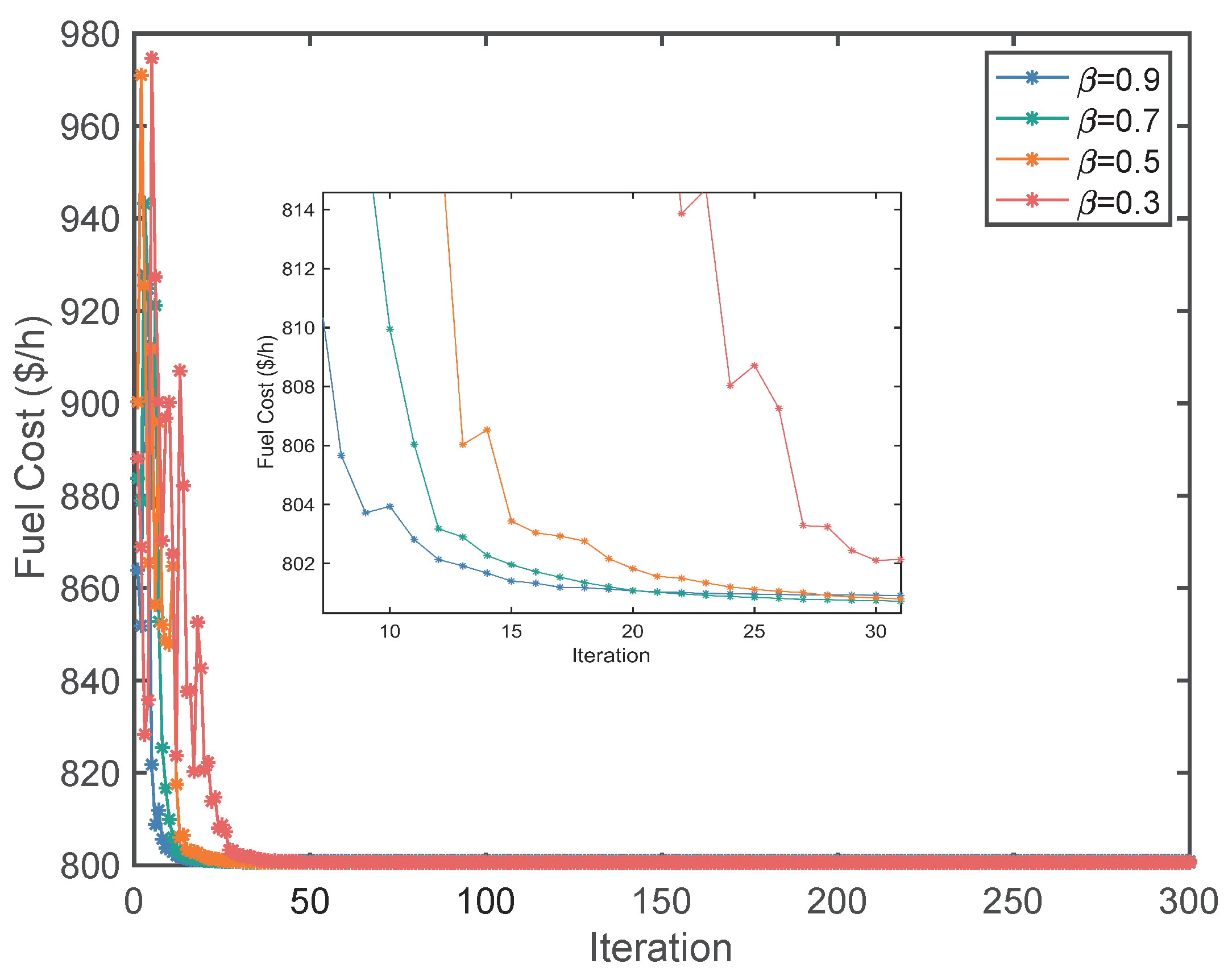
3.2.2. Chaotic Operator
- In the initial stage of the algorithm, CGSCE has chance to acquire a big value of due to the probabilistic selection of (41) to renew while in GSCE is limited to , so CGSCE has chance to converge faster than GSCE in initial stage.
- In the final stage of the algorithm, CGSCE has chance to acquire a bigger value of than that in CE method given by (41).
- A large perturbation of generated by chaotic operator can improve the exploration ability of CGSCE.
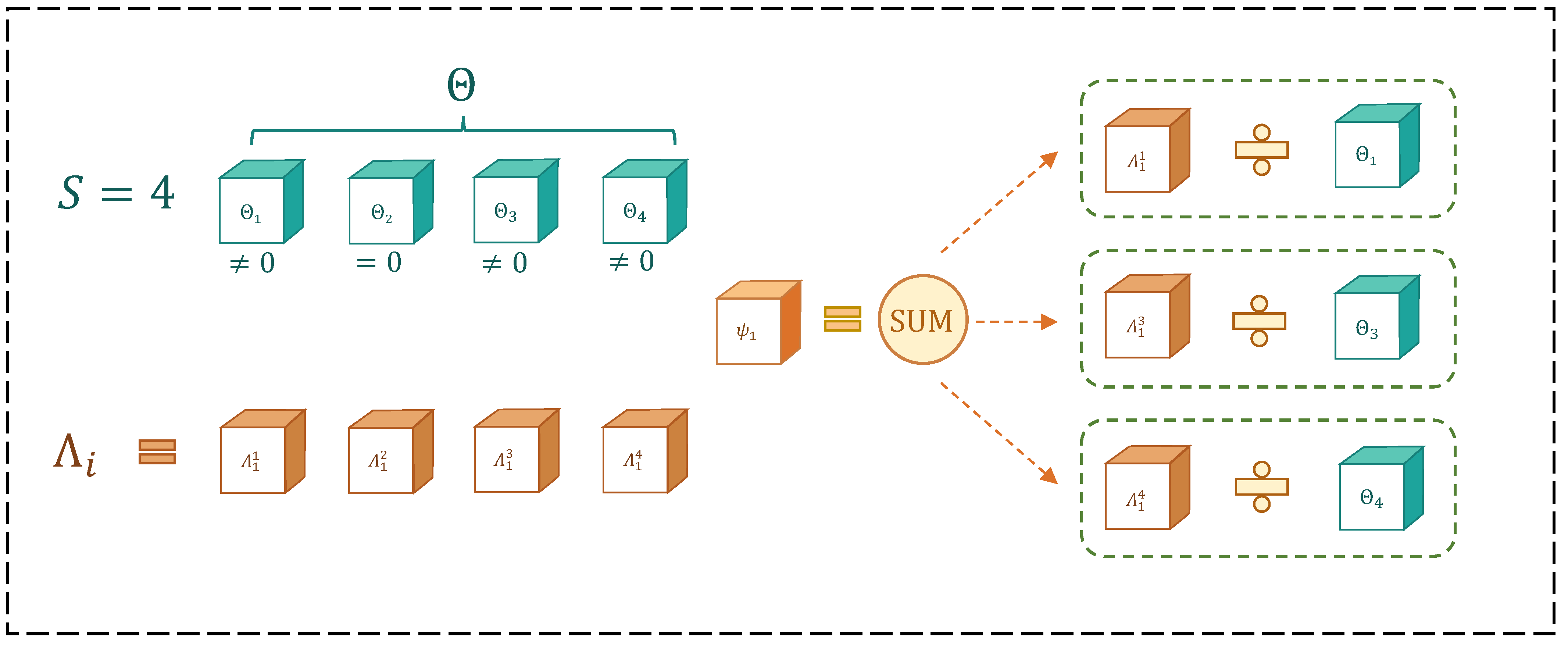
3.2.3. Archive
3.3. Constraints Handling
3.3.1. Constraints Handling for Control variables
3.3.2. Calculation of Total Constraints Violation
| Algorithm 2 Algorithm for Calculating Total Constraints Violation (totalViolation) |
|
3.3.3. Superiority of Feasible Solutions
| Algorithm 3 Algorithm for Superiority of Feasible Solutions (SF) |
|
3.4. CGSCE for Solving OPF Problem
- initialize. The initialize function is used to initialize the parameters of the algorithm including: N: population size, : number of elite individuals, : maximum function evaluations, : current function evaluations, , , , : iteration number and is the initial value of chaotic operator.
- mpoption. The mpoption is a function of matpower used to set and retrieve a MATPOWER options variable. More details information about mpoption, please refer to the source code of MATPOWER.
- loadcase. The loadcase is a function of MATPOWER used to load the data of a specific test system. This function return a structure variable contains the information control variables, state vaiables and other information used to calculate power flow.
- runpf. The runpf is a function of MATPOWER used to run a power flow, it returns a variable contains the control variables X and state variables V.
| Algorithm 4 CGSCE for Solving OPF Problem |
|
4. Study Cases and Simulation Results
4.1. Study Cases for IEEE-30 Bus System
4.1.1. Case1: Minimization of Fuel Cost
4.1.2. Case 2: Minimization of Fuel Cost Considering Multiple Fuels
4.1.3. Case 3: Minimization of L-Index
4.1.4. Case 4: Minimization of Emission
4.1.5. Case5: Minimization of Active Power Loss
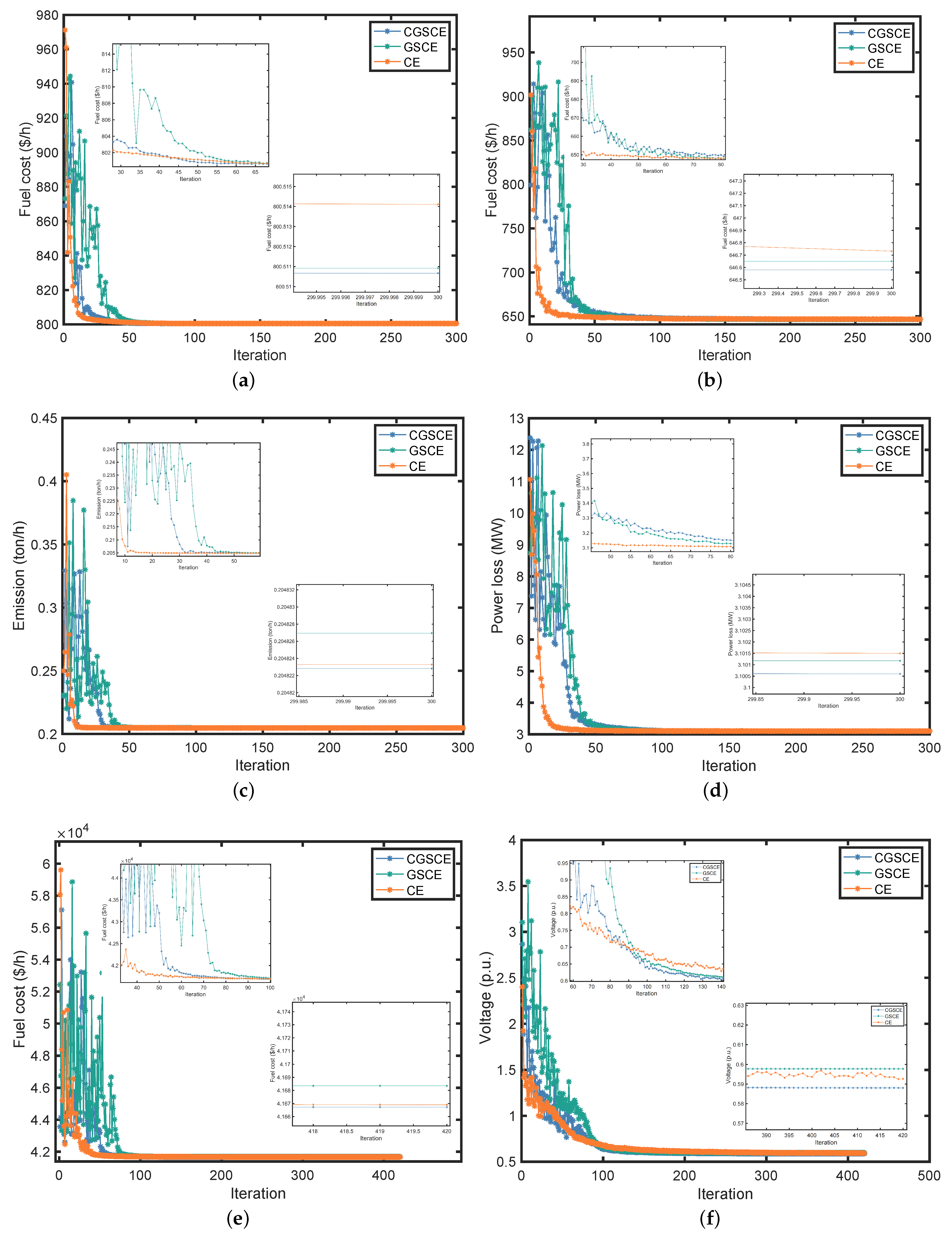
4.2. IEEE-30 Bus System Simulation Results
Simulation Results of CGSCE, GSCE and CE for IEEE-30 Bus System
4.3. Study Cases for IEEE-57 Bus System
4.3.1. Case 6: Minimization of Fuel Cost
4.3.2. Case 7: Minimization of Voltage Deviation
4.4. IEEE-57 Bus System Simulation Results
4.4.1. Simulation Results of CGSCE, GSCE and CE for IEEE-57 Bus System
4.4.2. Comparision of The Simulation Results for IEEE-57 Bus System
4.5. Comparison of Convergence Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OPF | Optimal power flow |
| CE | Cross-entropy method |
| CGSCE | Improved cross-entropy method assisted with a chaotic operator |
| GSCE | Golden stochastic linear cross-entropy method |
| SOPF | Security-constrained optimal power flow |
| DOPF | Dynamic optimal power flow |
| CH | Constraints handling |
| SF | Superiority of feasible solution |
| GA | Genetic Algorithm |
| DE | Differential Evolution |
| PSO | Particle Swarm Optimization |
| HSA | Harmony Search Algorithm |
| TLBO | Teaching-learning-Based Optimization |
| ABC | Artificial Bee Colony Optimization |
| MSLFA | Shuffle Frog Leaping Algorithm |
| MICA | Modified Imperialist Competitive Algorithm |
| ARCBBO | Adaptive Real Coded Biogeography-based Optimization |
| ASP | Associated stochastic problem |
| MLE | Maximum likelihood estimation |
| CDF | Cumulative distribution function |
Appendix A
| Generator | Bus | a | b | c | d | e | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 2 | 0.00375 | 18 | 0.037 | 4.091 | −5.554 | 6.49 | 0.0002 | 2.857 | |
| 2 | 0 | 1.75 | 0.0175 | 16 | 0.038 | 2.543 | −6.047 | 5.638 | 0.0005 | 3.333 | |
| 5 | 0 | 1 | 0.0625 | 14 | 0.04 | 4.258 | −5.094 | 4.586 | 0.000001 | 8 | |
| 8 | 0 | 3.25 | 0.00834 | 12 | 0.045 | 5.326 | −3.55 | 3.38 | 0.002 | 2 | |
| 11 | 0 | 3 | 0.025 | 13 | 0.042 | 4.258 | −5.094 | 4.586 | 0.000001 | 8 | |
| 13 | 0 | 3 | 0.025 | 13.5 | 0.041 | 6.131 | −5.555 | 5.151 | 0.00001 | 6.667 |
| Generator | Bus | a | b | c | a | b | c | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 140 | 55 | 0.7 | 0.005 | 140 | 200 | 82.5 | 1.05 | 0.0075 | |
| 2 | 20 | 55 | 40 | 0.3 | 0.01 | 55 | 80 | 80 | 0.6 | 0.02 |
References
- Abou El Ela, A.A.; Abido, M.A.; Spea, S.R. Optimal power flow using differential evolution algorithm. Electr. Power Syst. Res. 2010, 80, 878–885. [Google Scholar] [CrossRef]
- Zhang, J.R.; Tang, Q.H.; Li, P.; Deng, D.X.; Chen, Y.L. A modified MOEA/D approach to the solution of multi-objective optimal power flow problem. Appl. Soft Comput. 2016, 47, 494–514. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Multi-objective optimal power flow solutions using a constraint handling technique of evolutionary algorithms. Appl. Soft Comput. 2020, 24, 2999–3023. [Google Scholar] [CrossRef]
- Frank, S.; Steponavice, I.; Rebennack, S. Optimal power flow: A bibliographic survey I. Energy Syst. 2012, 3, 221–258. [Google Scholar] [CrossRef]
- Vaisakh, K.; Srinivas, L.R. Evolving ant direction differential evolution for OPF with non-smooth cost functions. Eng. Appl. Artif. Intell. 2011, 24, 426–436. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 1 December 1995; pp. 1942–1948. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 2, 60–68. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-TR06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Niknam, T.; Narimani, M.R.; Jabbari, M.; Malekpour, A.R. A modified shuffle frog leaping algorithm for multi-objective optimal power flow. Energy 2011, 36, 6420–6432. [Google Scholar] [CrossRef]
- Narimani, M.R.; Azizipanah-Abarghooee, R.; Zoghdar-Moghadam-Shahrekohne, B.; Gholami, K. A novel approach to multi-objective optimal power flow by a new hybrid optimization algorithm considering generator constraints and multi-fuel type. Energy 2013, 49, 119–136. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Rahmani, S.; Roosta, A.; Falah, H. A novel hybrid algorithm of imperialist competitive algorithm and teaching learning algorithm for optimal power flow problem with non-smooth cost functions. Eng. Appl. Artif. Intell. 2014, 29, 54–69. [Google Scholar] [CrossRef]
- Adaryani, M.R.; Karami, A. Artificial bee colony algorithm for solving multi-objective optimal power flow problem. Int. J. Electr. Power Energy Syst. 2013, 53, 219–230. [Google Scholar] [CrossRef]
- Roy, R.; Jadhav, H.T. Optimal power flow solution of power system incorporating stochastic wind power using Gbest guided artificial bee colony algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 562–578. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R.; Niknam, T. A modified teaching-learning based optimization for multi-objective optimal power flow problem. Energy Convers. Manag. 2014, 77, 597–607. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Gitizadeh, M.; Akbari, E. An improved teaching-learning-based optimization algorithm using Levy mutation strategy for non-smooth optimal power flow. Int. J. Electr. Power Energy Syst. 2015, 65, 375–384. [Google Scholar] [CrossRef]
- Kumar, A.R.; Premalatha, L. Optimal power flow for a deregulated power system using adaptive real coded biogeography-based optimization. Int. J. Electr. Power Energy Syst. 2015, 73, 393–399. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Optimal power flow solutions using differential evolution algorithm integrated with effective constraint handling techniques. Eng. Appl. Artif. Intell. 2018, 68, 81–100. [Google Scholar] [CrossRef]
- Warid, W.; Hizam, H.; Mariun, N.; Abdul-Wahab, N.I. Optimal Power Flow Using the Jaya Algorithm. Energies 2016, 9, 678. [Google Scholar] [CrossRef]
- Chen, G.G.; Lu, Z.M.; Zhang, Z.Z. Improved Krill Herd Algorithm with Novel Constraint Handling Method for Solving Optimal Power Flow Problems. Energies 2018, 11, 76. [Google Scholar] [CrossRef]
- Rubinstein, R. The Cross-Entropy Method for Combinatorial and Continuous Optimization. Methodol. Comput. Appl. 1999, 1, 127–190. [Google Scholar] [CrossRef]
- Wang, G.B.; Zha, Y.X.; Wu, T.; Qiu, J.; Peng, J.C.; Xu, G. Cross entropy optimization based on decomposition for multi-objective economic emission dispatch considering renewable energy generation uncertainties. Energy 2020, 193, 982–997. [Google Scholar] [CrossRef]
- Selvakumar, A.I. Enhanced cross-entropy method for dynamic economic dispatch with valve-point effects. Int. J. Electr. Power Energy Syst. 2011, 33, 783–790. [Google Scholar] [CrossRef]
- Carvalho, L.D.; da Silva, A.M.L.; Miranda, V. Security-Constrained Optimal Power Flow via Cross-Entropy Method. IEEE Trans. Power Syst. 2018, 33, 6621–6629. [Google Scholar] [CrossRef]
- Sarda, J.; Pandya, K.; Lee, K.Y. Dynamic optimal power flow with cross entropy covariance matrix adaption evolutionary strategy for systems with electric vehicles and renewable generators. Int. J. Energy Res. 2021, 45, 10869–10881. [Google Scholar] [CrossRef]
- Marcelino, C.G.; Perez-Aracil, J.; Wanner, E.F.; Jimenez-Fernandez, S.; Leite, G.M.C.; Salcedo-Sanz, S. Cross-entropy boosted CRO-SL for optimal power flow in smart grids. Soft Comput. 2023, 27, 6549–6572. [Google Scholar] [CrossRef]
- Hui, K.P.; Bean, N.; Kraetzl, M.; Kroese, D.P. The Cross-Entropy Method for Network Reliability Estimation. Ann. Oper. Res. 2005, 134, 101–118. [Google Scholar] [CrossRef]
- Beruvides, G.; Quiza, R.; Haber Guerra, R.E. Multi-objective optimization based on an improved cross-entropy method. A case study of a micro-scale manufacturing process. Inf. Sci. 2015, 334–335, 161–173. [Google Scholar] [CrossRef]
- Tang, Q.; Ma, L.; Zhao, D.; Lei, J.; Wang, Y. A multi-objective cross-entropy optimization algorithm and its application in high-speed train lateral control. Appl. Soft Comput. 2022, 115, 108151. [Google Scholar] [CrossRef]
- Tessema, B.; Yen, G.G. A self adaptive penalty function based algorithm for constrained optimization. In Proceedings of the IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 6–21 July 2006; pp. 246–253. [Google Scholar]
- Mallipeddi, R.; Jeyadevi, S.; Suganthan, P.N.; Baskar, S. Efficient constraint handling for optimal reactive power dispatch problems. Swarm Evol. Comput. 2012, 5, 28–36. [Google Scholar] [CrossRef]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Method Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Kessel, P.; Glavitsch, H. Estimating the Voltage Stability of a Power System. IEEE Trans. Power Deliv. 1986, 186, 346–354. [Google Scholar] [CrossRef]
- Mohamed, A.A.; Mohamed, Y.S.; El-Gaafary, A.A.M.; Hemeida, A.M. Optimal power flow using moth swarm algorithm. Electr. Power Syst. Res. 2017, 142, 190–206. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Chaib, A.E.; Abido, M.A.; El-Sehiemy, R.A. Optimal power flow using an Improved Colliding Bodies Optimization algorithm. Appl. Soft Comput. 2016, 42, 119–131. [Google Scholar] [CrossRef]
- Kroese, D.P.; Porotsky, S.; Rubinstein, R.Y. The cross-entropy method for continuous multi-extremal optimization. Methodol. Comput. Appl. 2006, 8, 383–407. [Google Scholar] [CrossRef]
- De Boer, P.T.; Kroese, D.P.; Mannor, S.; Rubinstein, R.Y. A tutorial on the cross-entropy method. Ann. Oper. Res. 2005, 134, 19–67. [Google Scholar] [CrossRef]
- Rubinstein, R.Y. Optimization of computer simulation models with rare events. Eur. J. Oper. Res. 1997, 99, 89–112. [Google Scholar] [CrossRef]
- Zhang, Y. Research on Load Dispatch of Power Systems Based on Improved Cross-Entroy Methods. Master’s Thesis, Shanghai University, Shanghai, China, 2019. [Google Scholar]
- Caponetto, R.; Fortuna, L.; Fazzino, S.; Xibilia, M.G. Chaotic sequences to improve the performance of evolutionary algorithms. IEEE Trans. Evol. Comput. 2003, 7, 289–304. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Appl. Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Li, S.J.; Gong, W.Y.; Hu, C.Y.; Yan, X.S.; Wang, L.; Gu, Q. Adaptive constraint differential evolution for optimal power flow. Energy 2021, 235, 121362. [Google Scholar] [CrossRef]
- Daryani, N.; Hagh, M.T.; Teimourzadeh, S. Adaptive group search optimization algorithm for multi-objective optimal power flow problem. Appl. Soft Comput. 2016, 38, 1012–1024. [Google Scholar] [CrossRef]
- Khunkitti, S.; Siritaratiwat, A.; Premrudeepreechacharn, S. Multi-Objective Optimal Power Flow Problems Based on Slime Mould Algorithm. Sustainability 2021, 13, 7448. [Google Scholar] [CrossRef]
- Bouchekara, H.; Abido, M.A.; Boucherma, M. Optimal power flow using Teaching-Learning-Based Optimization technique. Electr. Power Syst. Res. 2014, 114, 49–59. [Google Scholar] [CrossRef]
- Abaci, K.; Yamacli, V. Differential search algorithm for solving multi-objective optimal power flow problem. Int. J. Electr. Power Energy Syst. 2016, 79, 1–10. [Google Scholar] [CrossRef]
- Kumari, M.S.; Maheswarapu, S. Enhanced Genetic Algorithm based computation technique for multi-objective Optimal Power Flow solution. Int. J. Electr. Power Energy Syst. 2010, 32, 736–742. [Google Scholar] [CrossRef]
- Reddy, S.S.; Bijwe, P.R.; Abhyankar, A.R. Faster evolutionary algorithm based optimal power flow using incremental variables. Int. J. Electr. Power Energy Syst. 2014, 54, 198–210. [Google Scholar] [CrossRef]
- Warid, W. Optimal power flow using the AMTPG-Jaya algorithm. Appl. Soft Comput. 2020, 91, 106252. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Gharibzadeh, M.; Vahed, A.A. Multi-objective optimal power flow considering the cost, emission, voltage deviation and power losses using multi-objective modified imperialist competitive algorithm. Energy 2014, 78, 276–289. [Google Scholar] [CrossRef]
- Duman, S.; Guvenc, U.; Sonmez, Y.; Yorukeren, N. Optimal power flow using gravitational search algorithm. Energy Convers. Manag. 2012, 59, 86–95. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Farrag, S.M. Solving multi-objective optimal power flow problem via forced initialised differential evolution algorithm. IET Gener. Transm. Distrib. 2016, 10, 1634–1647. [Google Scholar] [CrossRef]
- Roy, P.K.; Paul, C. Optimal power flow using krill herd algorithm. Int. Trans. Electr. Energy Syst. 2015, 25, 1397–1419. [Google Scholar] [CrossRef]
- Braund, M. Security constrained optimal power flow solution using new adaptive partitioning flower pollination algorithm. Appl. Soft Comput. 2016, 46, 501–522. [Google Scholar]
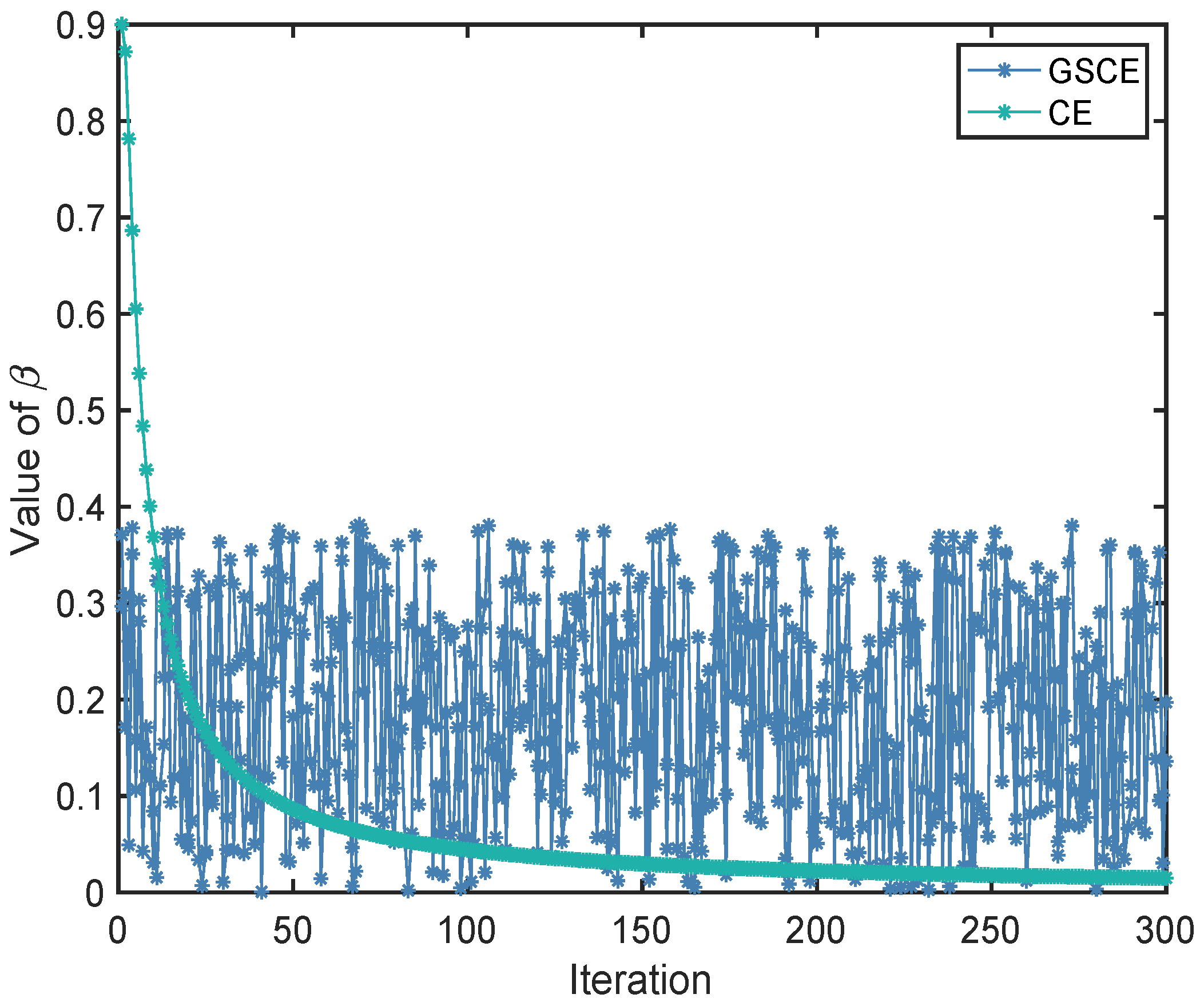
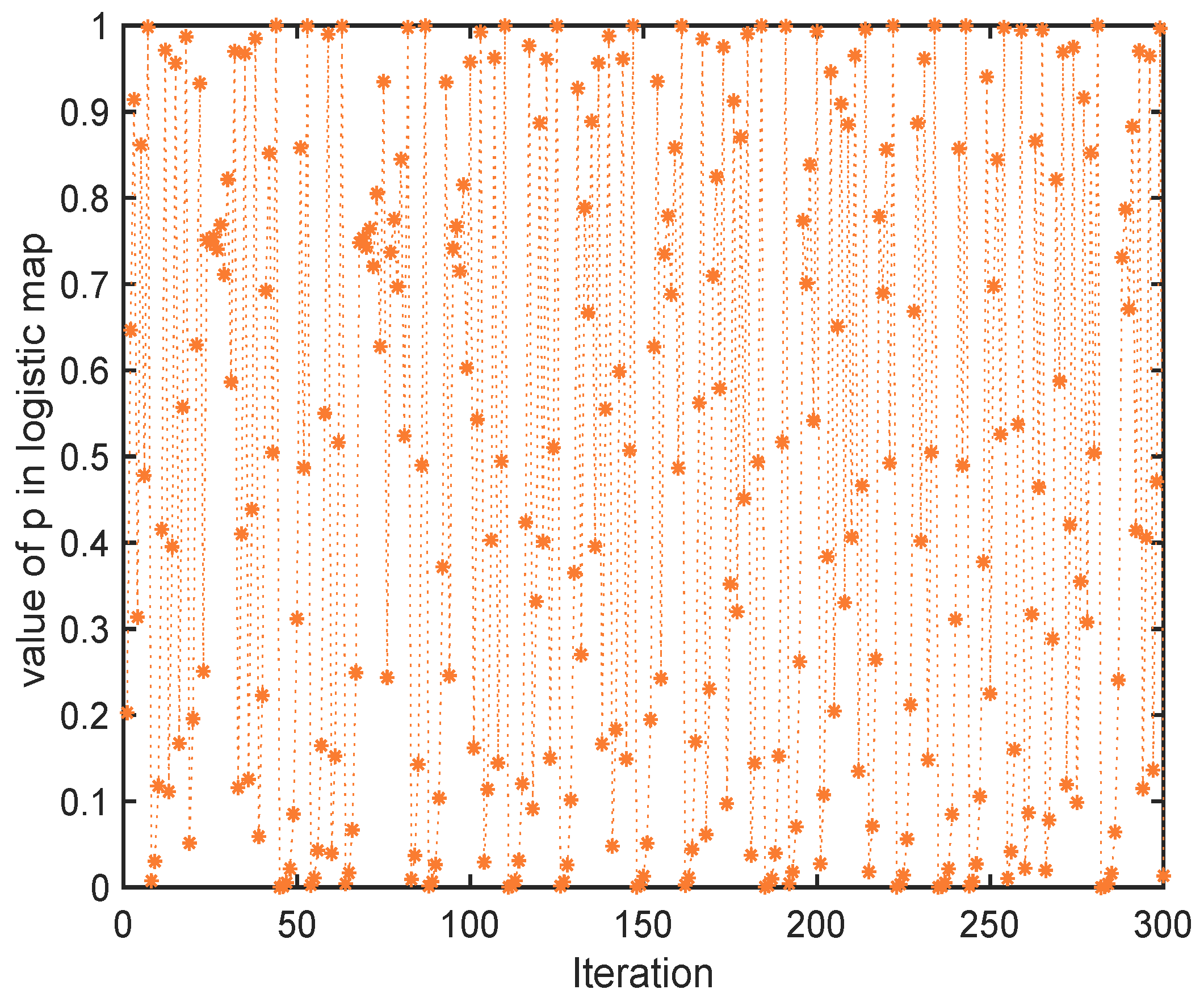
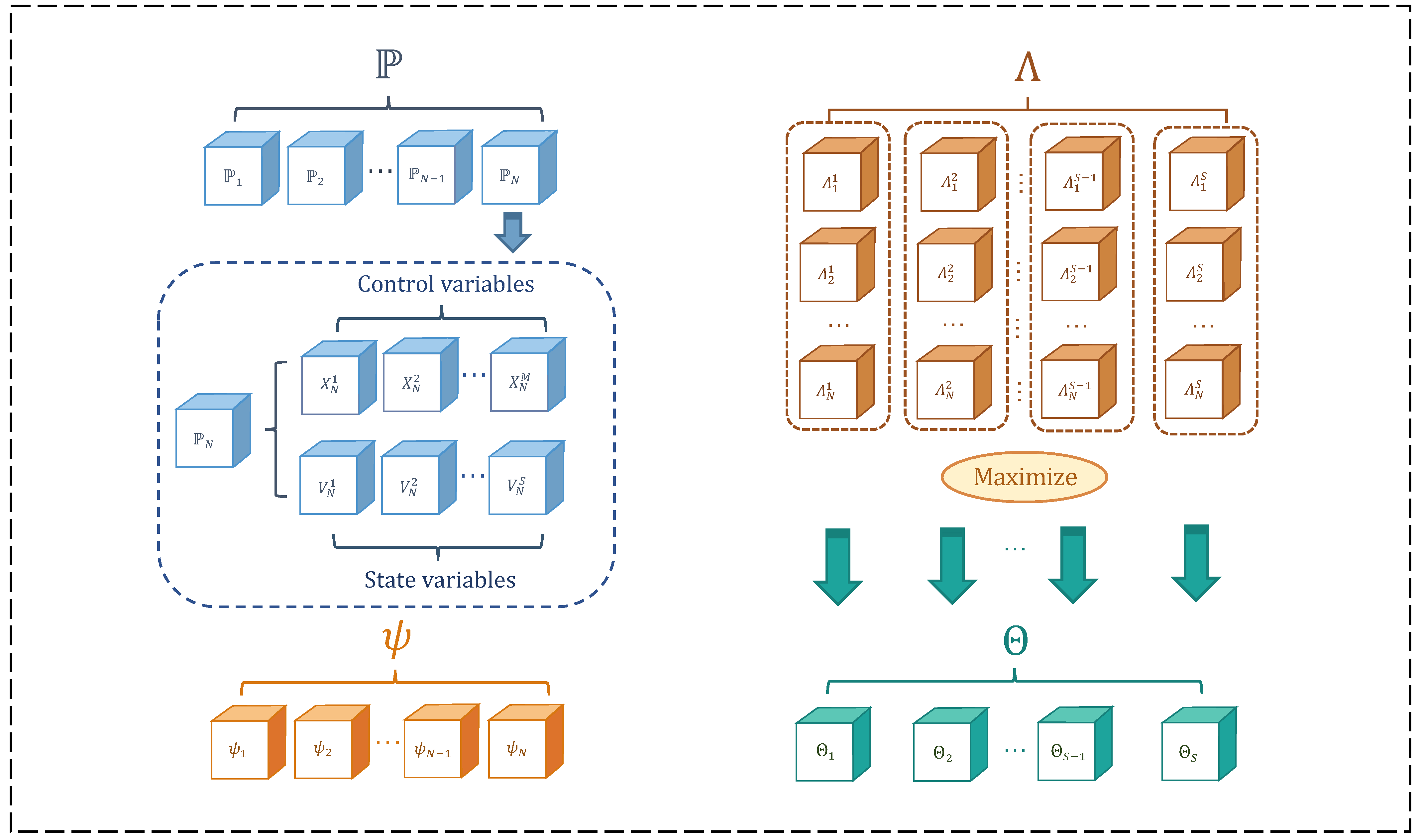




| Study Case | Basic Fuel Cost | Multi-Fuel Option | L-Index | Emission | Power Loss |
|---|---|---|---|---|---|
| Case 1 | √ | ||||
| Case 2 | √ | √ | |||
| Case 3 | √ | ||||
| Case 4 | √ | ||||
| Case 5 | √ |
| Algorithm | Population Size | Number of Elites | q | ||
|---|---|---|---|---|---|
| CGSCE | 100 | 10 | - | 0.9 | 5 |
| GSCE | 100 | 10 | - | - | - |
| CE | 100 | 10 | 0.8 | 0.9 | 5 |
| Study | CGSCE | GSCE | CE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Case | Min | Avg | Max | Min | Avg | Max | Min | Avg | Max |
| Case 1 | 800.5106 | 800.5118 | 800.5150 | 800.5109 | 800.5214 | 800.5416 | 800.5154 | 800.5196 | 800.5353 |
| Case 2 | 646.5803 | 650.8642 | 667.2889 | 646.6502 | 660.6629 | 726.0109 | 646.7323 | 657.4860 | 725.7435 |
| Case 3 | 0.13667 | 0.13713 | 0.13755 | 0.13701 | 0.13764 | 0.13824 | 0.13657 | 0.13716 | 0.13775 |
| Case 4 | 0.204823 | 0.204831 | 0.204854 | 0.204823 | 0.204844 | 0.20487 | 0.204823 | 0.204824 | 0.204824 |
| Case 5 | 3.10060 | 3.10727 | 3.17311 | 3.10117 | 3.13434 | 3.20255 | 3.10150 | 3.10719 | 3.14864 |
| Study | CGSCE | GSCE | CE | |||
|---|---|---|---|---|---|---|
| Case | Std | Simulation Time (s) | Std | Simulation Time (s) | Std | Simulation Time (s) |
| Case 1 | 0.000978 | 81.43 | 0.007665 | 77.59 | 0.002033 | 77.69 |
| Case 2 | 9.189230 | 79.68 | 49.234060 | 78.77 | 26.995089 | 76.75 |
| Case 3 | 0.000397 | 80.07 | 0.000302 | 78.52 | 0.000341 | 78.86 |
| Case 4 | 76.30 | 77.33 | 74.57 | |||
| Case 5 | 0.018013 | 77.89 | 0.032825 | 79.16 | 0.001334 | 78.07 |
| Parameter | Min | Max | CGSCE | GSCE | CE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 1 | Case 2 | Case 3 | Case 1 | Case 2 | Case 3 | |||
| 20 | 80 | 48.6931 | 54.9987 | 66.7369 | 48.6898 | 55.0000 | 41.5293 | 48.8815 | 54.9727 | 52.1764 | |
| 15 | 50 | 21.3708 | 24.1160 | 37.3786 | 21.3849 | 24.01850 | 40.3876 | 21.3515 | 23.6581 | 44.2338 | |
| 10 | 35 | 21.2720 | 34.9820 | 27.5947 | 21.2687 | 34.8902 | 27.1502 | 21.1956 | 34.7845 | 33.1755 | |
| 10 | 30 | 11.9708 | 18.6707 | 18.4351 | 11.9460 | 18.8850 | 17.2777 | 11.9446 | 18.8265 | 28.6691 | |
| 12 | 40 | 12.0011 | 17.3935 | 27.8162 | 12.0000 | 17.3846 | 13.3757 | 12.0107 | 17.9545 | 17.5278 | |
| 0.95 | 1.1 | 1.0848 | 1.0752 | 1.0572 | 1.0845 | 1.0725 | 1.0806 | 1.0845 | 1.0748 | 1.0545 | |
| 0.95 | 1.1 | 1.0653 | 1.0593 | 1.0520 | 1.0650 | 1.0571 | 1.0623 | 1.0651 | 1.0595 | 1.0474 | |
| 0.95 | 1.1 | 1.0338 | 1.0303 | 1.0646 | 1.0336 | 1.0281 | 1.0675 | 1.0337 | 1.0330 | 1.0644 | |
| 0.95 | 1.1 | 1.0384 | 1.0388 | 1.0445 | 1.0383 | 1.0377 | 1.0321 | 1.0383 | 1.0417 | 1.0524 | |
| 0.95 | 1.1 | 1.0993 | 1.0890 | 1.0999 | 1.0969 | 1.0651 | 1.0800 | 1.0858 | 1.0685 | 1.0977 | |
| 0.95 | 1.1 | 1.0462 | 1.0613 | 1.0863 | 1.0464 | 1.0775 | 1.0760 | 1.0484 | 1.0491 | 1.0894 | |
| 0 | 5 | 1.5896 | 3.9445 | 1.4690 | 0.4296 | 3.9626 | 0.4221 | 4.2222 | 4.5480 | 2.1011 | |
| 0 | 5 | 1.1263 | 2.2350 | 2.1954 | 2.3180 | 0.1755 | 0.0553 | 0.9207 | 2.1659 | 1.7148 | |
| 0 | 5 | 4.2301 | 3.3483 | 0.6751 | 3.7287 | 4.1427 | 0.7924 | 4.2812 | 4.1504 | 0.0000 | |
| 0 | 5 | 4.9719 | 3.8243 | 2.1731 | 4.9989 | 4.0545 | 1.5682 | 4.9687 | 3.6805 | 0.3894 | |
| 0 | 5 | 4.0218 | 4.0751 | 3.0847 | 4.0196 | 3.9496 | 3.0796 | 3.7656 | 5.0000 | 1.3733 | |
| 0 | 5 | 4.9972 | 4.1547 | 0.0023 | 4.9982 | 3.8881 | 0.0971 | 4.9573 | 3.7002 | 0.3308 | |
| 0 | 5 | 2.9141 | 4.2729 | 0.0073 | 3.0651 | 3.8867 | 1.4134 | 2.9248 | 3.5028 | 0.0112 | |
| 0 | 5 | 5.0000 | 3.5121 | 0.0145 | 5.0000 | 4.9975 | 0.1129 | 4.9812 | 4.6211 | 0.0000 | |
| 0 | 5 | 2.4753 | 3.0479 | 0.0140 | 2.4203 | 1.0545 | 0.0044 | 2.3190 | 3.7993 | 0.0644 | |
| 0.9 | 1.1 | 1.0377 | 1.0145 | 1.0352 | 1.0654 | 1.0034 | 1.0065 | 1.0520 | 1.0406 | 1.0415 | |
| 0.9 | 1.1 | 0.9539 | 0.9865 | 0.9002 | 0.9162 | 0.9535 | 0.9001 | 0.9390 | 0.9479 | 0.9036 | |
| 0.9 | 1.1 | 0.9687 | 0.9968 | 1.0367 | 0.9713 | 1.0242 | 1.0029 | 0.9710 | 0.9981 | 1.0308 | |
| 0.9 | 1.1 | 0.9741 | 0.9780 | 0.9550 | 0.9737 | 0.9644 | 0.9490 | 0.9754 | 0.9869 | 0.9594 | |
| 50 | 200 | 177.1200 | 139.9995 | 111.3297 | 177.1394 | 140.0000 | 150.7777 | 177.0473 | 139.9892 | 112.9882 | |
| −20 | 150 | 6.5671 | 3.2187 | −19.3636 | 6.3058 | 0.5595 | 7.9395 | 6.3123 | 1.8150 | −18.0799 | |
| −20 | 60 | 25.4217 | 16.7715 | −4.2206 | 25.1212 | 16.5131 | 4.9374 | 25.1998 | 16.3314 | −13.9467 | |
| −15 | 62.5 | 27.5702 | 26.3271 | 60.1374 | 27.7012 | 26.5695 | 60.7670 | 27.7206 | 28.6213 | 58.0778 | |
| −15 | 48.7 | 29.2298 | 25.9939 | 35.9228 | 29.6774 | 30.8777 | 22.5960 | 29.6117 | 31.4906 | 47.1502 | |
| −10 | 40 | 27.1932 | 20.9029 | 26.7080 | 29.7154 | 9.2955 | 15.8414 | 23.6927 | 17.0266 | 26.9806 | |
| −15 | 44.7 | −2.7332 | 9.2131 | 28.6934 | −2.5981 | 21.4015 | 20.0612 | −1.0751 | 5.1479 | 30.8721 | |
| Fuel cost ($/h) | 800.5106 | 646.5803 | 851.1982 | 800.5109 | 646.6502 | 830.2833 | 800.5141 | 646.7323 | 863.1420 | ||
| Emission(t/h) | 0.366195 | 0.283511 | 0.243275 | 0.366253 | 0.283475 | 0.300648 | 0.366033 | 0.283371 | 0.241214 | ||
| 9.02776 | 6.76042 | 5.89136 | 9.02888 | 6.77829 | 7.09840 | 9.03114 | 6.78541 | 5.37070 | |||
| 0.91661 | 0.86997 | 0.88245 | 0.90823 | 0.91271 | 0.86297 | 0.89005 | 0.77869 | 0.87184 | |||
| 0.13809 | 0.13886 | 0.13667 | 0.13809 | 0.13781 | 0.13701 | 0.13857 | 0.14018 | 0.13657 |
| Parameter | Min | Max | CGSCE | GSCE | CE | |||
|---|---|---|---|---|---|---|---|---|
| Case 4 | Case 5 | Case 4 | Case 5 | Case 4 | Case 5 | |||
| 20 | 80 | 67.5762 | 79.9997 | 67.5737 | 80.0000 | 67.5926 | 79.9843 | |
| 15 | 50 | 50.0000 | 50.0000 | 50.0000 | 50.0000 | 49.9999 | 49.9996 | |
| 10 | 35 | 35.0000 | 34.9999 | 35.0000 | 35.0000 | 35.0000 | 35.0000 | |
| 10 | 30 | 30.0000 | 30.0000 | 30.0000 | 30.0000 | 30.0000 | 29.9999 | |
| 12 | 40 | 40.0000 | 40.0000 | 40.0000 | 39.9993 | 40.0000 | 40.0000 | |
| 0.95 | 1.1 | 1.0629 | 1.0621 | 1.0628 | 1.0617 | 1.0635 | 1.0621 | |
| 0.95 | 1.1 | 1.0568 | 1.0579 | 1.0566 | 1.0575 | 1.0575 | 1.0577 | |
| 0.95 | 1.1 | 1.0374 | 1.0385 | 1.0372 | 1.0379 | 1.0370 | 1.0384 | |
| 0.95 | 1.1 | 1.0438 | 1.0448 | 1.0436 | 1.0442 | 1.0443 | 1.0445 | |
| 0.95 | 1.1 | 1.0787 | 1.0791 | 1.0830 | 1.0783 | 1.0794 | 1.0887 | |
| 0.95 | 1.1 | 1.0594 | 1.0558 | 1.0621 | 1.0561 | 1.0530 | 1.0573 | |
| 0 | 5 | 1.3367 | 2.1245 | 0.2767 | 2.6559 | 3.0746 | 0.3799 | |
| 0 | 5 | 1.5171 | 2.1490 | 0.4263 | 3.4914 | 3.6423 | 0.8590 | |
| 0 | 5 | 4.2271 | 4.2533 | 3.7370 | 4.3011 | 4.1017 | 4.5878 | |
| 0 | 5 | 4.9853 | 4.9964 | 4.9993 | 4.9994 | 4.8266 | 4.8344 | |
| 0 | 5 | 3.8746 | 3.9417 | 3.9839 | 3.8621 | 3.7185 | 3.9194 | |
| 0 | 5 | 4.9973 | 5.0000 | 5.0000 | 5.0000 | 4.9278 | 5.0000 | |
| 0 | 5 | 2.9117 | 2.9168 | 3.2087 | 2.9968 | 3.0725 | 2.9412 | |
| 0 | 5 | 4.9992 | 4.9992 | 4.9996 | 5.0000 | 4.9662 | 4.9682 | |
| 0 | 5 | 2.3353 | 2.3996 | 2.3606 | 2.3741 | 2.0545 | 2.2758 | |
| 0.9 | 1.1 | 1.0708 | 1.0824 | 1.0469 | 1.0535 | 1.0568 | 1.0672 | |
| 0.9 | 1.1 | 0.9066 | 0.9017 | 0.9303 | 0.9298 | 0.9270 | 0.9183 | |
| 0.9 | 1.1 | 1.0000 | 0.9956 | 1.0013 | 0.9999 | 0.9943 | 0.9954 | |
| 0.9 | 1.1 | 0.9762 | 0.9772 | 0.9764 | 0.9767 | 0.9752 | 0.9774 | |
| 50 | 200 | 64.0586 | 51.5010 | 64.0616 | 51.5020 | 64.0434 | 51.5177 | |
| −20 | 150 | −2.0884 | −2.1765 | −2.1445 | −2.5592 | −1.8719 | −1.9032 | |
| −20 | 60 | 12.1524 | 12.0002 | 12.1074 | 11.8771 | 13.7125 | 11.4035 | |
| −15 | 62.5 | 23.8599 | 23.9426 | 23.8397 | 23.7576 | 22.8818 | 23.9256 | |
| −15 | 48.7 | 29.6258 | 29.7577 | 29.3823 | 29.2612 | 30.0832 | 28.9347 | |
| −10 | 40 | 23.7034 | 25.1457 | 22.5345 | 21.3193 | 22.1543 | 27.2559 | |
| −15 | 44.7 | 8.1376 | 5.3813 | 10.1862 | 5.5953 | 3.3150 | 6.5615 | |
| Fuel cost ($/h) | 944.3944 | 967.663 | 944.3917 | 967.6631 | 944.4232 | 967.6297 | ||
| Emission(t/h) | 0.204823 | 0.207267 | 0.204823 | 0.207267 | 0.204823 | 0.207261 | ||
| (MW) | 3.23471 | 3.10060 | 3.23525 | 3.10117 | 3.23581 | 3.10150 | ||
| VD (p.u.) | 0.88808 | 0.89096 | 0.89338 | 0.89745 | 0.89314 | 0.89192 | ||
| L-index(max) | 0.13859 | 0.13857 | 0.13858 | 0.13856 | 0.13856 | 0.13861 |
| Algorithm | Fuel Cost | Emission | Power Loss | Voltage Deviation | L-Index |
|---|---|---|---|---|---|
| CGSCE | 800.5106 | 0.366033 | 9.03114 | 0.89005 | 0.13857 |
| GSCE | 800.5109 | 0.366253 | 9.02888 | 0.90832 | 0.13809 |
| CE | 800.5154 | 0.36663 | 9.0384 | 0.90525 | 0.13829 |
| MSFLA [12] | 802.287 | 0.3723 | - | - | - |
| SFLA [12] | 802.5092 | 0.372 | - | - | - |
| Hybrid MPSO-SFLA [13] | 801.75 | 0.377 | 9.54 | - | - |
| ABC [15] | 800.66 | 0.365141 | 9.0328 | 0.9209 | 0.1381 |
| TLBO [17] | 801.9908 | 0.3668 | - | - | - |
| MTLBO [17] | 801.8925 | 0.3665 | - | - | - |
| ARCBBO [19] | 800.5159 | 0.3663 | 0.8867 | 0.1385 | |
| MICA-TLA [14] | 801.0488 | 0.3666 | 9.1895 | - | - |
| AGSO [45] | 801.75 | 0.3703 | - | - | - |
| SMA [46] | 802.5449 | 0.363552 | 9.5232 | - | - |
| Algorithm | Fuel Cost | Emission | Power Loss | Voltage Deviation | L-Index |
|---|---|---|---|---|---|
| CGSCE | 646.5803 | 0.283511 | 6.76042 | 0.86997 | 0.13886 |
| GSCE | 646.6502 | 0.283475 | 6.77829 | 0.91271 | 0.13781 |
| CE | 646.7323 | 0.283371 | 6.78541 | 0.77869 | 0.14018 |
| DE [1] | 650.8224 | 0.2831 | 7.6333 | 0.5733 | 0.1366 |
| SFLA [12] | 654.47 | 0.2902 | - | - | - |
| Hybrid MPSO-SFLA [13] | 647.55 | 0.2834 | - | - | - |
| ABC [15] | 649.0855 | 0.282563 | 7.2526 | 0.6665 | 0.1383 |
| GABC [16] | 647.03 | 0.2835 | 6.816 | 0.801 | - |
| TLBO [47] | 647.9202 | - | 7.1064 | 1.4173 | 0.1211 |
| LTLBO [18] | 647.4315 | 0.2835 | 6.9347 | 0.8896 | - |
| MICA-TLA [14] | 647.1002 | 0.2835 | 6.8945 | - | - |
| MSA [36] | 646.8364 | 0.28352 | 6.8001 | 0.84479 | 0.13867 |
| Algorithm | L-Index | Fuel Cost | Emission | Voltage Deviation | Power Loss |
|---|---|---|---|---|---|
| CGSCE | 0.13667 | 851.1982 | 0.243275 | 0.88245 | 5.89136 |
| GSCE | 0.13701 | 830.2833 | 0.300648 | 0.86297 | 7.09840 |
| CE | 0.13657 | 863.142 | 0.241214 | 0.87184 | 5.37070 |
| ABC [15] | 0.1379 | 801.665 | 0.364295 | 0.938 | 9.2954 |
| MICA-TLA [14] | 0.1369 | 801.8076 | 0.3628 | 0.8521 | 9.229 |
| SF-DE [20] | 0.13671 | 875.8929 | 0.22801 | 0.90387 | 4.6412 |
| Algorithm | Emission | Fuel Cost | Power Loss | Voltage Deviation | L-Index |
|---|---|---|---|---|---|
| CGSCE | 0.204823 | 944.3944 | 3.23471 | 0.88808 | 0.13859 |
| GSCE | 0.204823 | 944.3917 | 3.23525 | 0.89338 | 0.13858 |
| CE | 0.204823 | 944.4232 | 3.23581 | 0.89314 | 0.13856 |
| SFLA [12] | 0.2063 | 951.5106 | - | - | - |
| MSFLA [12] | 0.2056 | 960.1911 | - | - | - |
| Hybrid MPSO-SFLA [13] | 0.2052 | - | - | - | - |
| GSO [45] | 0.206 | 954.9512 | - | - | - |
| AGSO [45] | 0.2059 | 953.629 | - | - | - |
| DSA [48] | 0.2058255 | 944.4086 | 3.24373 | - | 0.12734 |
| MSA [36] | 0.20482 | 944.5003 | 3.2358 | 0.87393 | 0.13888 |
| SF-DE [20] | 0.20482 | 944.3242 | 3.2179 | 0.89617 | 0.13844 |
| Algorithm | Power Loss | Fuel Cost | Emission | Voltage Deviation | L-Index |
|---|---|---|---|---|---|
| CGSCE | 3.10060 | 967.6630 | 0.207267 | 0.89096 | 0.13857 |
| GSCE | 3.10117 | 967.6631 | 0.207267 | 0.89745 | 0.13856 |
| CE | 3.10150 | 967.6297 | 0.207261 | 0.89192 | 0.13861 |
| EGA [49] | 3.2008 | 967.86 | - | - | 0.12178 |
| ABC [15] | 3.1078 | 967.681 | 0.207268 | 0.9008 | 0.1386 |
| EEA [50] | 3.2823 | 952.3785 | 0.206735 | - | 0.1533 |
| TLBO [51] | 3.11389 | 967.49149 | - | - | 0.12651 |
| Study | CGSCE | GSCE | CE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Case | Min | Avg | Max | Min | Avg | Max | Min | Avg | Max |
| Case 6 | 41,667.2777 | 41,700.4722 | 41,765.477 | 41,683.5695 | 41,718.7954 | 41,830.2288 | 41,669.0222 | 41,681.0337 | 41,696.1114 |
| Case 7 | 0.5880 | 0.6055 | 0.6322 | 0.5978 | 0.6259 | 0.6731 | 0.5927 | 0.6014 | 0.6238 |
| Study | CGSCE | GSCE | CE | |||
|---|---|---|---|---|---|---|
| Case | Std | Simulation Time (s) | Std | Simulation Time (s) | Std | Simulation Time (s) |
| Case 6 | 31.301284 | 126.09 | 30.840003 | 128.71 | 8.274621 | 128.82 |
| Case 7 | 0.012038 | 129.75 | 0.020917 | 129.31 | 0.006462 | 129.73 |
| Parameter | Min | Max | CGSCE | GSCE | CE | |||
|---|---|---|---|---|---|---|---|---|
| Case 6 | Case 7 | Case 6 | Case 7 | Case 6 | Case 7 | |||
| 30 | 100 | 90.6551 | 35.0310 | 88.4697 | 72.9556 | 88.2449 | 51.1308 | |
| 40 | 140 | 45.0428 | 112.0647 | 45.0614 | 82.7747 | 44.6113 | 64.7434 | |
| 30 | 100 | 71.7058 | 30.1082 | 72.9811 | 46.4756 | 73.4628 | 32.4851 | |
| 100 | 550 | 460.4218 | 295.5435 | 460.2346 | 259.9944 | 458.7908 | 277.3415 | |
| 30 | 100 | 94.9459 | 99.9859 | 95.6720 | 99.9999 | 96.8078 | 97.2581 | |
| 100 | 410 | 360.1364 | 297.4539 | 360.9547 | 375.5547 | 360.266 | 341.5521 | |
| 0.95 | 1.1 | 1.0658 | 1.0110 | 1.0343 | 1.0190 | 1.0588 | 1.0119 | |
| 0.95 | 1.1 | 1.0635 | 1.0084 | 1.0330 | 1.0175 | 1.0568 | 1.0082 | |
| 0.95 | 1.1 | 1.0555 | 1.0152 | 1.0294 | 1.0176 | 1.0520 | 1.0101 | |
| 0.95 | 1.1 | 1.0623 | 1.0017 | 1.0453 | 0.9997 | 1.0593 | 1.0038 | |
| 0.95 | 1.1 | 1.0725 | 1.0197 | 1.0580 | 1.0078 | 1.0743 | 1.0252 | |
| 0.95 | 1.1 | 1.0460 | 1.0070 | 1.0265 | 0.9994 | 1.0468 | 1.0122 | |
| 0.95 | 1.1 | 1.0448 | 1.0134 | 1.0214 | 1.0265 | 1.0459 | 1.0383 | |
| 0 | 20 | 9.4015 | 5.9546 | 11.8672 | 16.7208 | 6.3064 | 1.6996 | |
| 0 | 20 | 14.0329 | 19.4092 | 15.6236 | 16.9527 | 14.9721 | 19.7239 | |
| 0 | 20 | 12.6535 | 19.9999 | 12.9959 | 20.0000 | 12.7782 | 20.0000 | |
| 0.9 | 1.1 | 0.9784 | 1.0762 | 0.9293 | 0.9818 | 0.9768 | 0.9395 | |
| 0.9 | 1.1 | 1.0006 | 0.9476 | 1.0129 | 1.0700 | 1.0000 | 1.0137 | |
| 0.9 | 1.1 | 1.0094 | 0.9689 | 1.0112 | 0.9716 | 1.0070 | 0.9722 | |
| 0.9 | 1.1 | 1.0739 | 1.0710 | 1.0908 | 1.0977 | 1.0310 | 1.0650 | |
| 0.9 | 1.1 | 0.9630 | 1.0576 | 0.9681 | 0.9889 | 1.0371 | 1.0610 | |
| 0.9 | 1.1 | 1.0281 | 1.0038 | 1.0252 | 0.9992 | 1.0286 | 1.0056 | |
| 0.9 | 1.1 | 0.9962 | 0.9941 | 0.9829 | 0.9848 | 0.9971 | 0.9959 | |
| 0.9 | 1.1 | 0.9613 | 0.9190 | 0.9643 | 0.9179 | 0.9629 | 0.9211 | |
| 0.9 | 1.1 | 0.9083 | 0.9000 | 0.9000 | 0.9000 | 0.9056 | 0.9009 | |
| 0.9 | 1.1 | 0.9789 | 0.9296 | 0.9539 | 0.9303 | 0.9786 | 0.9309 | |
| 0.9 | 1.1 | 0.9633 | 0.9812 | 0.9400 | 0.9674 | 0.9632 | 0.9902 | |
| 0.9 | 1.1 | 0.9703 | 1.0011 | 0.9494 | 1.0028 | 0.9713 | 1.0090 | |
| 0.9 | 1.1 | 0.9348 | 0.9000 | 0.9130 | 0.9000 | 0.9321 | 0.9000 | |
| 0.9 | 1.1 | 0.9697 | 0.9568 | 0.9476 | 0.9599 | 0.9801 | 0.9648 | |
| 0.9 | 1.1 | 0.9947 | 1.0088 | 0.9938 | 0.9886 | 0.9980 | 1.0064 | |
| 0.9 | 1.1 | 0.9672 | 0.9001 | 0.9676 | 0.9026 | 0.9621 | 0.9014 | |
| 0.9 | 1.1 | 0.9928 | 0.9880 | 0.9709 | 0.9812 | 0.9978 | 0.9954 | |
| 0 | 576 | 142.7851 | 404.2220 | 142.6836 | 331.5767 | 143.5011 | 409.7128 | |
| −140 | 200 | 52.0709 | −30.4481 | 36.8008 | −8.2358 | 40.0044 | −32.0001 | |
| −17 | 50 | 49.9950 | 49.8081 | 49.9993 | 49.9986 | 48.3663 | 47.4032 | |
| −10 | 60 | 32.6551 | 59.9857 | 30.4656 | 58.5273 | 37.5336 | 56.6139 | |
| −8 | 25 | −0.2248 | −7.8937 | 3.5300 | −7.8941 | −5.2681 | −5.5796 | |
| −140 | 200 | 46.6276 | 42.4393 | 58.4780 | 28.1540 | 54.6803 | 50.5760 | |
| −3 | 9 | 8.9994 | 8.9983 | 9.0000 | 8.9997 | 8.1877 | 8.9706 | |
| −150 | 155 | 46.8299 | 154.4379 | 51.7570 | 117.2250 | 56.6570 | 152.5423 | |
| Fuel cost ($/h) | 41,667.2777 | 49,522.9283 | 41,683.5695 | 46,244.2043 | 41,669.0222 | 48,776.4802 | ||
| Emission(t/h) | 1.920768 | 1.616655 | 1.921051 | 1.468387 | 1.904056 | 1.703746 | ||
| 14.89291 | 23.60915 | 15.25705 | 18.53159 | 14.88469 | 23.42392 | |||
| 1.69590 | 0.58803 | 1.45795 | 0.59778 | 1.56697 | 0.59268 | |||
| 0.27916 | 0.30138 | 0.28163 | 0.30063 | 0.28233 | 0.30072 |
| Algorithm | Fuel Cost | Emission | Power Loss | Voltage Deviation | L-Index |
|---|---|---|---|---|---|
| CGSCE | 41,667.2777 | 1.920768 | 14.89291 | 1.69590 | 0.27916 |
| GSCE | 41,683.5695 | 1.921051 | 15.25705 | 1.45795 | 0.28163 |
| CE | 41,669.0222 | 1.904056 | 14.88469 | 1.56697 | 0.28233 |
| ABC [15] | 41,693.9589 | - | - | - | - |
| GSA [53] | 41,695.8717 | - | - | - | - |
| ARCBBO [19] | 41,686 | - | 15.3769 | - | - |
| MO-DEA [54] | 41,683 | 15.2727 | 1.5033 | 0.2816 | |
| KHA [55] | 41,709.2647 | - | - | 1.6893 | 0.2733 |
| TLBO [18] | 41,695.6626 | 1.980488 | 15.7469 | - | - |
| LTLBO [18] | 41,679.5451 | 1.930676 | 15.1589 | - | - |
| DSA [48] | 41,686.82 | - | - | 1.083267 | 0.24353 |
| ICBO [37] | 41,697.3324 | 1.917903 | 15.547 | 1.3173 | 0.2776 |
| MSA [36] | 41,673.72 | 1.9526 | 15.0526 | 1.5508 | 0.28392 |
| Algorithm | Voltage Deviation | Fuel Cost | Emission | Power Loss | L-Index |
|---|---|---|---|---|---|
| CGSCE | 0.58803 | 49,522.9283 | 1.616655 | 23.60915 | 0.30138 |
| GSCE | 0.59778 | 46,244.2043 | 1.468387 | 18.53159 | 0.30063 |
| CE | 0.59268 | 48,776.4802 | 1.703746 | 23.42392 | 0.30072 |
| APFPA [56] | 0.8909 | 43,485.933 | - | 12.1513 | - |
| SP-DE [20] | 0.59267 | 45,549.49 | 1.2898 | 18.4275 | 0.30052 |
| SF-DE [20] | 0.59584 | 45,246.02 | 1.23453 | 18.4697 | 0.30135 |
| ESCHT-DE [20] | 0.60416 | 46,813.22 | 1.3379 | 19.0821 | 0.3008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, H.; Niu, Q.; Yang, Z. Optimal Power Flow Using Improved Cross-Entropy Method. Energies 2023, 16, 5466. https://doi.org/10.3390/en16145466
Su H, Niu Q, Yang Z. Optimal Power Flow Using Improved Cross-Entropy Method. Energies. 2023; 16(14):5466. https://doi.org/10.3390/en16145466
Chicago/Turabian StyleSu, Hao, Qun Niu, and Zhile Yang. 2023. "Optimal Power Flow Using Improved Cross-Entropy Method" Energies 16, no. 14: 5466. https://doi.org/10.3390/en16145466
APA StyleSu, H., Niu, Q., & Yang, Z. (2023). Optimal Power Flow Using Improved Cross-Entropy Method. Energies, 16(14), 5466. https://doi.org/10.3390/en16145466





