Performance Evaluation and Optimization of Series Flow Channel Water-Cooled Plate for IGBT Modules
Abstract
1. Introduction
2. Methodology
2.1. Physical Model
2.2. Mathematical Model
2.2.1. Model Assumptions
- The fluid in the cold plate is a Newtonian fluid with no internal heat source and is incompressible;
- The effects of volume forces and thermal radiation are neglected;
- The various physical parameters of the cold plate material and fluid are invariant with the temperature change.
2.2.2. Equations
2.2.3. Cold Plate Heat Transfer Model
2.3. Numerical Simulation
2.3.1. Boundary Condition Setting
2.3.2. Grid Independence Test
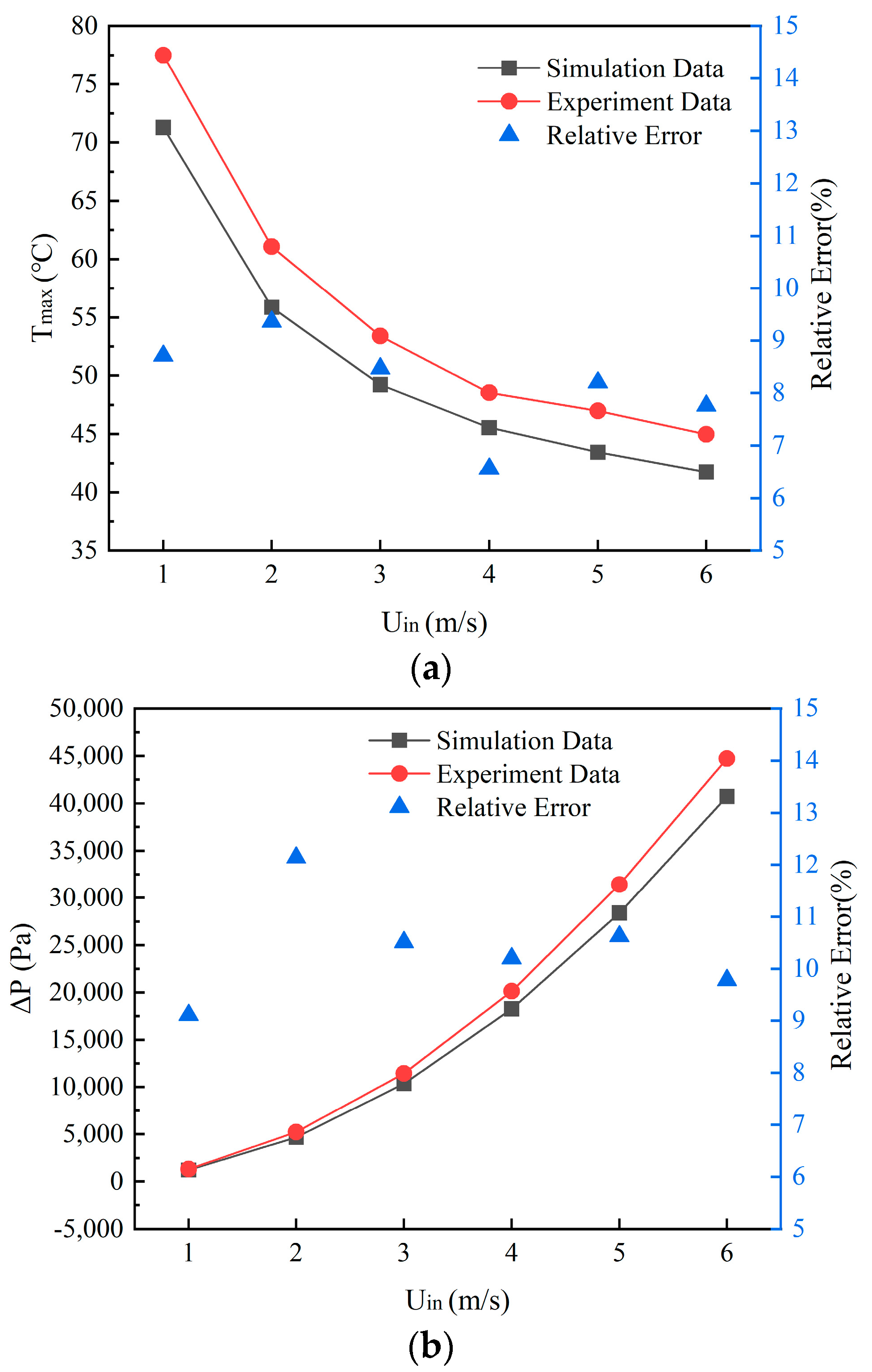
2.3.3. Model Validation
3. Results and Discussion
3.1. Simulation Analysis
3.1.1. Analysis of Channel Performance under Different Parameter Combinations
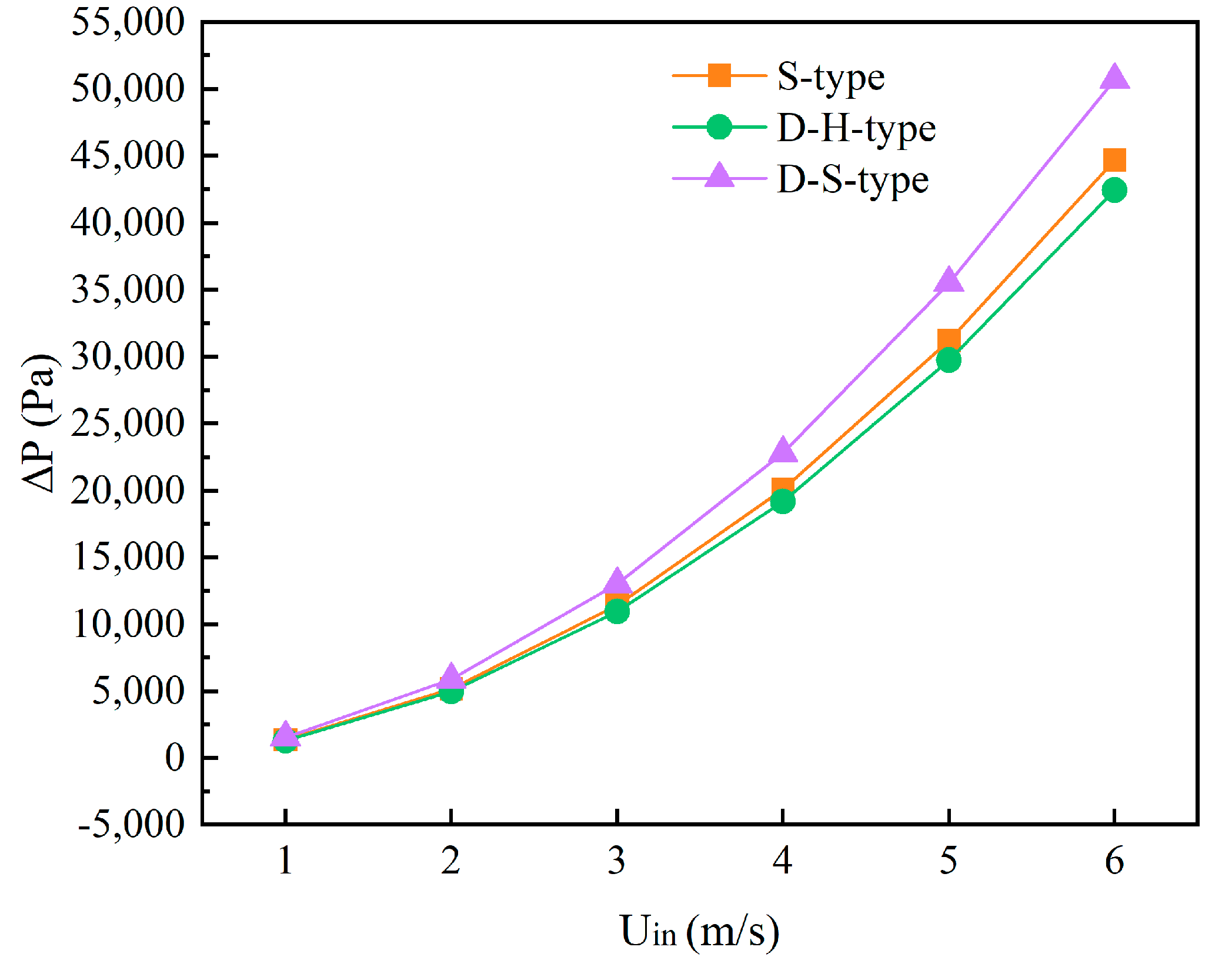
3.1.2. Analysis of Channel Performance at the Same Flow Velocities
3.1.3. Analysis of Channel Performance at Different Flow Velocities
3.2. Multivariate Analysis
3.2.1. Orthogonal Experimental Design
3.2.2. Analysis Results of Maximum Temperature and Pressure Drop
3.2.3. Optimization Effect Analysis
4. Conclusions
- (1)
- The analysis of the numerical simulation results shows that the double-helical-type channel has the best comprehensive performance among the three series-type flow channel structures.
- (2)
- The corner spacing of the flow channel is also an important factor affecting the flow characteristics of the cold plate. Under the same conditions, the larger the corner spacing, the better the flow characteristics of the cold plate.
- (3)
- The importance of the influencing factors (channel width, channel height, and cold plate wall thickness) on the maximum IGBT temperature is ranked as follows: channel height > channel width > cold plate wall thickness. Among them, the level variation of the three factors has a significant effect on the maximum IGBT temperature.
- (4)
- The importance of the influencing factors (channel width, channel height, and cold plate wall thickness) on the pressure drop is ranked as follows: channel height > channel width > cold plate wall thickness. Among them, the level variation of channel height and channel width has a significant effect on the pressure drop at the inlet and outlet, and the effect of the wall thickness of the cold plate is negligible.
- (5)
- Through orthogonal test analysis, the comprehensive performance of the double-helical-type cold plate is the best when the channel width is 30 mm, the channel height is 10 mm, and the wall thickness of the cold plate is 5 mm. The maximum IGBT temperature, overall thermal resistance, and pressure drop of this cold plate decreased by 3.13%, 5.78%, and 18.87%, respectively, compared with the double-S-type structure in parameter case one. This combination was verified to be the optimal channel structure parameter configuration in the parameter study range. This paper has certain guiding significance for the cold plate design of series flow channel structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variables | Greek Symbols | ||
| A | area (m2) | Δ | heat conduction thickness (m) |
| Cp | specific heat capacity (kJ/(kg·k)) | Λ | fluid thermal conductivity (W/m·K) |
| d | inlet diameter (mm) | Μ | fluid dynamic viscosity (Pa·s) |
| Hb | cold plate wall thickness (mm) | Ρ | density (kg/m3) |
| Hc | channel height (mm) | Φ | heat conduction (W) |
| L | length (mm) | ||
| P | pressure (Pa) | ||
| ΔP | pressure drop (Pa) | Subscripts | |
| Rj | range of factor j, (for j = A, B, C) | C | channel |
| SS | sum of squared deviations | f | fluid |
| t | temperature (°C) | In | inlet |
| tin | inlet temperature (°C) | max | maximum value |
| Tmax | maximum surface temperature (°C) | Out | outlet |
| u, v, w | velocity in the x, y, z directions, respectively (m/s) | W | wall |
| Uin | inlet velocity (m/s) | ||
| W | width (mm) | ||
| Wc | channel width (mm) | ||
| x,y,z | Cartesian coordinates | ||
References
- Alptekin, E. Emission, injection and combustion characteristics of biodiesel and oxygenated fuel blends in a common rail diesel engine. Energy 2017, 119, 44–52. [Google Scholar] [CrossRef]
- Jake, Y. A multifaceted future for wind power. Science 2019, 366, 6464. [Google Scholar]
- Chen, Y.; Li, B.; Wang, X.; Yan, Y.; Wang, Y.; Qi, F. Investigation of heat transfer and thermal stresses of novel thermal management system integrated with vapour chamber for IGBT power module. Therm. Sci. Eng. Prog. 2019, 10, 73–81. [Google Scholar] [CrossRef]
- Carroll, J.; Alasdair, M.D.; David, M.M. Failure rate, repair time and unscheduled O&M cost analysis of offshore wind turbines. Wind Energy 2016, 19, 1107–1119. [Google Scholar]
- Fischer, K.; Wenske, J. Towards reliable power converters for wind turbines: Field-data based identification of weak points and cost drivers. In Proceedings of the Ewea Conference & Exhibition, Paris, France, 17–20 November 2015. [Google Scholar]
- Bartschat, A. Reliability of power converters in wind turbines: Results of a comprehensive field study. In Proceedings of the Wind Europe Summit, Hamburg, Germany, 27–29 September 2016. [Google Scholar]
- Valenzuela, J.; Jasinski, T.; Sheikh, Z. Liquid cooling for high-power electronics. Power Electron. Technol. 2005, 31, 50–56. [Google Scholar]
- Anandan, S.S.; Ramalingam, V. Thermal management of electronics: A review of literature. Therm. Sci. 2008, 12, 5–26. [Google Scholar] [CrossRef]
- Choi, U.M.; Blaabjerg, F.; Lee, K.B. Study and Handling Methods of Power IGBT Module Failures in Power Electronic Converter Systems. IEEE Trans. Power Electron. 2015, 30, 2517–2533. [Google Scholar] [CrossRef]
- Ko, Y.; Andresen, M.; Buticchi, G.; Liserre, M. Discontinuous-modulation-based active thermal control of power electronic modules in wind farms. IEEE Trans. Power Electron. 2019, 34, 301–310. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, L.; Zhang, Y.; Wang, K.; Du, X.; Sun, P. Active junction temperature control of IGBT based on adjusting the turn-off trajectory. IEEE Trans. Power Electron. 2018, 33, 5811–5823. [Google Scholar] [CrossRef]
- Alhmoud, L. Reliability improvement for a high-power IGBT in wind energy applications. IEEE Trans. Ind. Electron. 2018, 65, 7129–7137. [Google Scholar] [CrossRef]
- Teng, H.; Yeow, K. Design of direct and indirect liquid cooling systems for high-capacity, high-power lithiumion battery packs. SAE Int. J. Altern. Pow. 2012, 1, 525–536. [Google Scholar]
- Yeo, D.Y.; No, H.C. Modeling film boiling within chimney-structured porous media and heat pipes. Int. J. Heat Mass Transf. 2018, 124, 576–585. [Google Scholar] [CrossRef]
- Mira-Hernandez, C.; Clark, M.D.; Weibel, J.A.; Garimella, S.V. Development and validation of a semi-empirical model for two-phase heat transfer from arrays of impinging jets. Int. J. Heat Mass Transf. 2018, 124, 782–793. [Google Scholar] [CrossRef]
- Lyu, Y.; Siddique, A.R.M.; Majid, S.H.; Biglarbegian, M.; Gadsden, S.A.; Mahmud, S. Electric vehicle battery thermal management system with thermoelectric cooling. Energy Rep. 2019, 5, 822–827. [Google Scholar] [CrossRef]
- Wang, S.; Li, K.; Tian, Y.; Wang, J.; Wu, Y.; Ji, S. Improved thermal performance of a large laminated lithium-ion power battery by reciprocating air flow. Appl. Therm. Eng. 2019, 152, 445–454. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery thermal models for hybrid vehicle simulations. J. Power Sources 2002, 110, 377–382. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Hayner, C.N. Liquid Cooled Cold Plates for Industrial High-Power Electronic Devices—Thermal Design and Manufacturing Considerations. Heat Transfer Eng. 2009, 30, 918–930. [Google Scholar] [CrossRef]
- Deng, Y.; Feng, C.; Jiaqiang, E.; Zhu, H.; Chen, J.; Wen, M.; Yin, H. Effects of different coolants and cooling strategies on the cooling performance of the power lithium ion battery system: A review. Appl. Therm. Eng. 2018, 142, 10–29. [Google Scholar]
- Avram, B.C.; Patrick, M.C.; Wang, P. Two-Phase Liquid Cooling for Thermal Management of IGBT Power Electronic Module. J. Electron. Packag. 2013, 135, 021001. [Google Scholar]
- Chen, S.; Bao, N.; Gao, L.; Peng, X.; Garg, A. An experimental investigation of liquid cooling scheduling for a battery module. Int. J. Energy Res. 2020, 44, 3020–3032. [Google Scholar] [CrossRef]
- Lu, M.; Wang, C. Effect of the inlet location on the performance of parallel-channel cold-plate. IEEE Trans. Compon. Packag. Technol. 2006, 29, 30–38. [Google Scholar]
- Shang, Z.; Qi, H.; Liu, X.; Ouyang, C.; Wang, Y. Structural optimization of lithium-ion battery for improving thermal performance based on a liquid cooling system. Int. J. Heat Mass Transf. 2019, 130, 33–41. [Google Scholar] [CrossRef]
- Liu, X.; Yu, J. Numerical study on performances of mini-channel heat sinks with non-uniform inlets. Appl. Therm. Eng. 2016, 93, 856–864. [Google Scholar] [CrossRef]
- Ahmed, F.A.; Nikil, K.; Jonathan, S.; Harvey, M.T. Thermal management of GaN HEMT devices using serpentine minichannel heat sinks. Appl. Therm. Eng. 2018, 140, 622–636. [Google Scholar]
- Jarrett, A.; Kim, I. Design optimization of electric vehicle battery cooling plates for thermal performance. J. Power Sources 2011, 196, 10359–10368. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, B.; Hao, X.; Xie, G. Fast approach of Pareto-optimal solution recommendation to multi-objective optimal design of serpentine-channel heat sink. Appl. Therm. Eng. 2014, 70, 263–273. [Google Scholar] [CrossRef]
- Zheng, X.; Hu, X.; Zhang, L.; Zhang, X.; Chen, F.; Mai, C. Study on the Effect of Spoiler Columns on the Heat Dissipation Performance of S-Type Runner Water-Cooling Plates. Energies 2022, 15, 3085. [Google Scholar] [CrossRef]
- Ambreen, T.; Kim, M.H. Effect of fin shape on the thermal performance of nanofluid-cooled micro pin-fin heat sinks. Int. J. Heat Mass Transf. 2018, 126, 245–256. [Google Scholar] [CrossRef]
- Rezaee, M.; Khoshvaght-Aliabadi, M.; Arani, A.; Mazloumi, S.H. Heat transfer intensification in pin-fin heat sink by changing pin-length/longitudinal-pitch. Chem. Eng. Process. 2019, 141, 107544. [Google Scholar] [CrossRef]
- Nabeel, S.M.; Hayder, M.J.; Ahmed, A.I. Performance evaluation of serpentine and multi-channel heat sinks based on energy and exergy analyses. Appl. Therm. Eng. 2021, 186, 116475. [Google Scholar]
- Ahmed, A.; Shanks, K.; Sundaram, S.; Mallick, T. Energy and exergy analyses of new cooling schemes based on a serpentine configuration for a high concentrator photovoltaic system. Appl. Therm. Eng. 2021, 199, 117528. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, S.; Pan, M.; Xu, J. Experimental investigation on thermal management of lithium-ion battery with roll bond liquid cooling plate. Appl. Therm. Eng. 2022, 206, 118106. [Google Scholar] [CrossRef]





| Parameters | L | L1 | W | W1 | W2 | d |
|---|---|---|---|---|---|---|
| Dimension (mm) | 335 | 295 | 330 | 30 | 10 | 10 |
| Material | Density (kg/m3) | Specific Heat (J/(kg.k)) | Thermal Conductivity (w/m.k) | Dynamic Viscosity (Ps.s) |
|---|---|---|---|---|
| 6063 Al | 2710 | 902 | 218 | - |
| Coolant | 997.0 | 4200 | 0.609 | 9.028 × 10−4 |
| Mesh | Elements (Million) | T (°C) | Difference (%) | ΔP (Pa) | Difference (%) |
|---|---|---|---|---|---|
| Mesh1 | 0.60 | 54.41 | −2.5581 | 4876 | 4.5903 |
| Mesh2 | 1.28 | 55.84 | 0.5868 | 4662 | 1.4360 |
| Mesh3 | 1.67 | 55.52 | 0.1879 | 4596 | 0.1962 |
| Mesh4 | 2.08 | 55.41 | - | 4587 | - |
| Case 1 | Case 2 | Case 3 | |
|---|---|---|---|
| Wc (mm) | 24 | 30 | 21 |
| Hc (mm) | 12 | 12 | 16 |
| Hb (mm) | 3 | 4 | 2 |
| Models | S-Type | D-H-Type | D-S-Type |
|---|---|---|---|
| Channel length (mm) | 1900 | 1980 | 1980 |
| Horizontal length (mm) | 240 | 640 | 640 |
| Horizontal average length (mm) | 48 | 128 | 106.67 |
| Vertical length (mm) | 1660 | 1340 | 1340 |
| Vertical average length (mm) | 276.67 | 223.33 | 191.43 |
| Combined average length (mm) | 162.34 | 175.67 | 149.05 |
| Levers | Factors | ||
|---|---|---|---|
| A (mm) | B (mm) | C (mm) | |
| 1 | 10 | 21 | 2 |
| 2 | 12 | 24 | 3 |
| 3 | 16 | 27 | 4 |
| 4 | 20 | 30 | 5 |
| Test Number | Test Factors | Test Results | |||
|---|---|---|---|---|---|
| A (mm) | B (mm) | C (mm) | Tmax (°C) | △P (Pa) | |
| 1 | 10 | 21 | 2 | 51.7422 | 6175 |
| 2 | 10 | 24 | 3 | 51.8447 | 5543 |
| 3 | 10 | 27 | 4 | 52.2739 | 5326 |
| 4 | 10 | 30 | 5 | 52.6885 | 5042 |
| 5 | 12 | 21 | 3 | 52.5431 | 5384 |
| 6 | 12 | 24 | 2 | 55.6067 | 4913 |
| 7 | 12 | 27 | 5 | 53.9930 | 4742 |
| 8 | 12 | 30 | 4 | 55.4061 | 4601 |
| 9 | 16 | 21 | 4 | 55.5149 | 4949 |
| 10 | 16 | 24 | 5 | 57.1487 | 4735 |
| 11 | 16 | 27 | 2 | 61.6008 | 4595 |
| 12 | 16 | 30 | 3 | 61.1789 | 4584 |
| 13 | 20 | 21 | 5 | 58.7400 | 4513 |
| 14 | 20 | 24 | 4 | 61.4269 | 4645 |
| 15 | 20 | 27 | 3 | 64.1011 | 4659 |
| 16 | 20 | 30 | 2 | 67.8940 | 4645 |
| Levers | Factors | ||
|---|---|---|---|
| A (mm) | B (mm) | C (mm) | |
| 52.1373 | 54.6351 | 59.2109 | |
| 54.3872 | 56.5068 | 57.4170 | |
| 58.8608 | 57.9922 | 56.1555 | |
| 63.0405 | 59.2919 | 55.6426 | |
| 10.9032 | 4.6568 | 3.5684 | |
| Importance of factors | 1 | 2 | 3 |
| Best solution | A1 B1 C4 | ||
| Levers | Factors | ||
|---|---|---|---|
| A (mm) | B (mm) | C (mm) | |
| 5522 | 5255 | 5082 | |
| 4910 | 4959 | 5043 | |
| 4716 | 4831 | 4880 | |
| 4616 | 4718 | 4758 | |
| 906 | 537 | 324 | |
| Importance of factors | 1 | 2 | 3 |
| Best solution | A4 B4 C4 | ||
| Factors | f | SS | MS | F |
|---|---|---|---|---|
| A | 3 | 281.509 | 93.8362 | 546.83 |
| B | 3 | 48.112 | 16.0375 | 93.46 |
| C | 3 | 30.291 | 10.0968 | 58.84 |
| E | 6 | 1.030 | 0.1716 | |
| T | 15 | 360.941 | ||
| Fα | F0.05(3,6) = 4.757 | F0.01(3,6) = 9.780 | ||
| Factors | f | SS | MS | F |
|---|---|---|---|---|
| A | 3 | 1,978,515 | 659,505 | 17.10 |
| B | 3 | 644,064 | 214,688 | 5.57 |
| C | 3 | 269,450 | 89,817 | 2.33 |
| E | 6 | 231,395 | 38,566 | |
| T | 15 | 3,123,423 | ||
| Fα | F0.05(3,6) = 4.757 | F0.01(3,6) = 9.780 | ||
| Models | S-Type | D-H-Type | D-S-Type | Optimal |
|---|---|---|---|---|
| Tmax (°C) | 54.32 | 53.94 | 54.38 | 52.68 |
| θ (°C/KW) | 6.74 | 6.65 | 6.75 | 6.36 |
| ΔP (Pa) | 5511 | 5313 | 6216 | 5043 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Hu, X.; Zhang, L.; Xing, T.; Jin, Z. Performance Evaluation and Optimization of Series Flow Channel Water-Cooled Plate for IGBT Modules. Energies 2023, 16, 5205. https://doi.org/10.3390/en16135205
He L, Hu X, Zhang L, Xing T, Jin Z. Performance Evaluation and Optimization of Series Flow Channel Water-Cooled Plate for IGBT Modules. Energies. 2023; 16(13):5205. https://doi.org/10.3390/en16135205
Chicago/Turabian StyleHe, Liyi, Xue Hu, Lixin Zhang, Tongtong Xing, and Zemin Jin. 2023. "Performance Evaluation and Optimization of Series Flow Channel Water-Cooled Plate for IGBT Modules" Energies 16, no. 13: 5205. https://doi.org/10.3390/en16135205
APA StyleHe, L., Hu, X., Zhang, L., Xing, T., & Jin, Z. (2023). Performance Evaluation and Optimization of Series Flow Channel Water-Cooled Plate for IGBT Modules. Energies, 16(13), 5205. https://doi.org/10.3390/en16135205





