1. Introduction
Our work addresses challenges at the intersection of two important tropes. One is the increasing attention given to the optimisation of the energy consumption of buildings, both for economical and ecological reasons. For instance, the residential sector is known to represent about 25% of the European energy consumption [
1]. One way to lower this consumption is to improve the thermal isolation of buildings. Another way is linked with the second trope, which is the increasing usage of renewable energies in energy systems [
2]. Among the main renewable sources are wind, and solar, energy. While they may help lower global consumption, reduce carbon emissions, and create local generation–consumption loops, they come with specificities, with respect to traditional systems, which make taking full advantage of their potentialities a challenge. Chief among these specificities is the intermittent nature of the resulting production. This is the point we focus on in our study.
One ever more common situation, nowadays, is that of a household with photovoltaic panels on its rooftop. Consumption which is not covered by the panels is provided by the regular distribution network. It is more interesting for the household to use the solar production, rather than that brought by the energy provider. Therefore, there is much value in aligning consumption with solar production as best as possible [
3]. However, alignment is not straightforward to reach.
There are two ways to improve consumption-production alignment in a building: direct and indirect flexibilities [
4]. The first one refers to the automated activation or deactivation of electrical appliances through the addition of hardware and software in the consumption loop. The second refers to changes in the consumption behaviour of the users of the building. Arguably, the latter is more cost friendly and energy friendly, as it does not require the addition of equipment in the building. Moreover, it is efficient: Twum-Duah et al. [
4] estimate that self-consumption could be improved by as much as
in the case of a smart building, where users can reload their electrical vehicles. And Shadid [
5] estimates that the intervention of nudge signal results in approximately 18% energy conservation during the orange periods when people are nudged not to consume. Additionally, during the green periods, there is an increase of over 11% in the energy self-consumption. However, while it is possible for households to try to align their consumption with solar production on their own, this often represents time-consuming work. Indeed, studies have shown that retired households more actively reduce their consumption upon receiving feedback, likely because they have more time available than working households [
6]. Moreover, households may improperly assess their own consumption [
7].
Therefore, there is a case for recommendation services discharging the user of most of this work and presenting them with ready-made and sharp consumption advice, like, for instance “consume on Wednesday afternoon, but not on Friday evening”. Indeed, mere feedback about consumption have already shown some efficiency in helping users reduce their energy consumption [
8]. More generally, nudges [
9] can be used to entice users to adopt renewable friendly consumption patterns.
The recommendations could be either provided by humans or automation. Automation, through the use of information communication technologies (ICTs) (information and communications technology refers to the use of digital technologies to manage and process information, as well as to communicate, share, and access information), is scalable, contrary to human-provided services. Indeed, it allows fast processing of the large amounts of data needed, and the concurrent generation of recommendations for all households using the service. Therefore, we use ICT nudging pipelines to construct our service. The aim of this study is to introduce two information and communication technology (ICT) nudging pipelines aimed at helping households integrated in energy communities with solar panels to improve their self-consumption rates, and to evaluate their efficiency on semi-real data. ICT pipelines designate the chain of technologies, be it hardware of software, which collect information, process it, and produce an output. In our case, they collect consumption and weather data, make algorithmic computations on those, and output advice in the form of nudges, suggesting to users when to use energy-consuming appliances.
To design the recommendations, we would ideally like to know in advance which part of their consumption the households would be willing to shift. However, this knowledge is practically impossible to obtain in real-world settings, if only because household people may not know it themselves, in advance. We therefore introduce two nudging pipelines using only information accessible in real life: aggregate past consumption of the household and weather forecasts for the future. One pipeline merely signals sunny periods, while the other predicts available production (that is, excess production with respect to the predicted consumption), thanks to load-forecasting techniques.
We show that our pipelines are efficient, even with them using real, and therefore incomplete, information, by validating them on semi-real data, coming from several publicly available datasets, coupled with a simulation environment. We intend to validate them on a real-world setting in the future but, due to the many constraints in setting-up a real-world experiment, we wanted to first test our pipeline in a simulated setting. Under reasonable user behaviour assumption, the simulator provides a first validation of our pipeline.
Our work takes place as part of ongoing efforts to help energy communities, using renewable energies, reach their full potential. This requires shifts in consumption patterns, with respect to usages linked with traditional energy sources. These changes in habit will only be possible if efforts are made to increase general consciousness about the culture changes implied and by providing accurate information to the users. We elaborate on these goals in the discussion section.
3. Model
We start by by presenting our household model (
Section 3.1). Next, we define the self-consumption, and self-sufficiency, rates (
Section 3.2). We then define the format of the nudges we use (
Section 3.3) before introducing the controllers, which compute the nudges (
Section 3.4). Finally, we can describe the entire nudging pipeline (
Section 3.5). All main notations are gathered in
Table 1.
3.1. Household
Let be the time scale at which the load is sampled, that is, a sequence of positive real numbers representing moments in time (or timestamps).
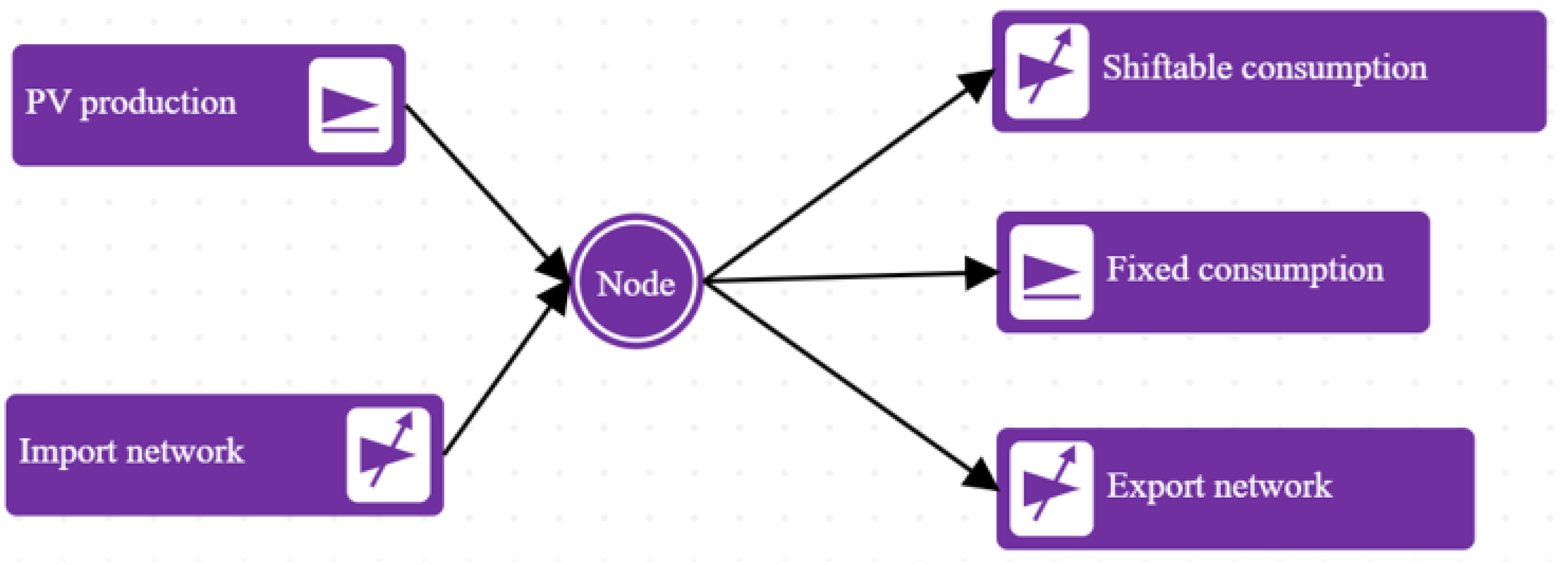
Household consumption. We consider a household which possesses several electrical appliances. Each appliance consumes energy as it is used. The consumption of an appliance is a positive sequence , together with a finite family of non-overlapping intervals , with bounds in . The are the times of the beginning of the appliance usages, and the are the ends of the usages. The load is non-zero if, and only if, there is a k (uniquely defined) such that . All residual consumption of all appliances is gathered in the “mains” appliance. The household consumption is the family of appliance consumptions. The aggregate load at time t, , is the sum over all appliances of the load at time t of each appliance, .
Shiftable appliances. An appliance may be as follows:
Shiftable, meaning the household may be willing to shift its usage intervals, provided these periods are not too far away from the base use time, which depends on the appliance; the length of usage intervals, that is, the values , remain fixed.
Not shiftable, meaning the times at which the appliance are used are fixed.
For instance, people in the household may be willing to shift their use of the washing machine by two to three days at most, while the time at which they use heating is fixed (when there is no demand restraint, the study of which is beyond the scope of this paper). For every shiftable appliance, there is a maximum time delay that the household people are willing to shift this appliance consumption by. The length by which appliance usages may be deferred has been estimated, for instance, by Kwon and ∅stergaard [
40] or Lucas et al. [
41].
Table 2 shows the time delays we assumed for every shiftable appliance. The fact that the lengths of usage intervals are fixed means, for instance, that the washing machine takes 2.5 h per usage, irrespective of when it is used.
Solar energy production. Photovoltaic panels provide the building with the energy at time t. If it is not enough to cover , the building feeds itself on the regular network to cover . If , excess production is “lost”. No storage capacity is used. At each time , a smart meter measures the aggregate load , as well as the solar production.
3.2. Self-Consumption and Self-Sufficiency Rates
We assess the energy-consumption efficiency with the two following metrics. For each
, the self-consumption at time
t equals
: if the household consumes more (
) than it produces, then it self-consumes only what it has produced, that is
, while if it consumes less, then it has self-consumed the amount
. Let us now recall the standard definitions of the self-consumption and the self-sufficiency rates [
42,
43].
Definition 1 (Self-consumption rate, self-sufficiency rate)
. For a household consumption , and two dates , we call the self-consumption rate between and the ratio of self-consumption to the total production:We call the self-sufficiency rate between and the ratio of self-consumption to the total consumption: The self-consumption rate measures the ratio of the solar production which has been consumed, and the self-sufficiency rate measures the ratio of consumption which has used solar production.
3.3. Nudge
We first define the notion of nudge we use, before explicating the model of human behaviour we assume, upon the reception of a nudge. The concept of green period is inspired from Salman Shadid et al. [
19].
Definition 2 (Green period, nudge). We call the green period a tuple , where are the beginning points and are the end points of the period, and is the strength of the period. A nudge is a set of green periods. We write for the set of nudges.
The number of green periods in a nudge is decided by the recommendation service. The strength of the green periods is used to rank them. The user tries to shift their consumption first to periods with high strength, as we explain below.
Model of human behaviour upon nudge reception. We use an ideal model, to evaluate the maximum ideal potential of our ICT pipelines. Upon reception of a nudge, the household people try to shift their consumption as follows. For every shiftable appliance, the following occurs:
They check whether there are use intervals outside of the green periods;
If so, for every green period, ranked according to their strength, they check whether shifting the use of the appliance to the green period is admissible (the new use interval is not too far away from the old use interval);
If so, the consumption is shifted; else, nothing is done.
This behaviour upon nudge reception is ideal in the sense that the user makes full use of the information provided. Indeed, our study aims at evaluating the potential of ICT pipelines to help improve consumption. Explicitly modelling realistic behaviour upon nudge reception, and assessing its impact, represents a following step for our research.
3.4. Controllers
We define a controller as a function which computes nudges as follows, each Sunday just before midnight. Assume it is Sunday, in the evening. Let be midnight of the incoming Monday. Let be 11:30 p.m., the following Sunday. Let be the set of weather forecasts for the incoming week: this is a set with weather forecast data for the sunshine coefficient, the temperature, and other likewise data, which the controller might use to compute the nudge. Let be the set of past household data available upon nudge computation: these are the past aggregate load and the past production.
Definition 3 (Controller)
. A controller is a function taking as arguments weather forecasts and past household aggregate consumption data, and outputting a nudge, that is, a function On Monday, the household receives the nudge, and the user adapts or not their consumption for the week.
Designing good controllers is not straightforward. Indeed, write
as the household consumption once modified from
according to the nudge. Then, find the best possible nudge amounts for solving either of the optimisation problems (which are equivalent when production is fixed):
which means maximising either the self-consumption rate or the self-sufficiency rate of the household, over the coming week, for the nudged consumption
. What complicates matters is that the effect that the nudge has on the consumption is unknown to the controller. Therefore, they have to make guesses as to what would lend itself to efficient nudges. Conversely, the household people know the effect that a nudge has on them; however, the optimisation problem they would have to solve would be too burdensome for us to expect most households to solve it every week. Therefore, to compute nudges, we do not solve these optimisation problems, but introduce the following two heuristic controllers. We validate their efficiency in our numerical simulations.
Weather controller: The first one is called “weather controller”. It takes as input the sunshine coefficient forecast for the coming week. It averages the predicted sunshine coefficient over 2 h periods. The strength parameter is set to these values. Namely, if
is the forecast of the sunshine coefficient at time
, then the strength parameter at time
equals
(There are four half-hours in two hours, and we use a time scale of 30 min steps.) Then, it ranks the periods according to their strength, and outputs the three (say) best periods. The weather controller therefore signals the periods when it is most sunny, as they are those with the most solar production.
Combined controller: The second controller is called “combined controller”. It takes as inputs the sunshine coefficient forecast for the coming week, together with past aggregate consumption data, and past production data. It then uses load forecasting techniques to forecast excess production, that is, the difference between forecast production and forecast consumption (see
Appendix C for details). It averages the predicted excess over 2 h periods, and sets the strength parameter to these averages. Finally, it outputs the three (say) best periods. Precisely, writing
the forecast load at time
t, and
the forecast production at the same time, the predicted excess is
Then, the strength parameter at time
equals
The combined controller therefore signals periods when there will be (if the forecast is accurate) the most excess. The idea is that there may be sunny periods where consumption will be high. In these periods, spare solar production will be low. As a result, shifting more consumption to these periods will not help. Therefore, by forecasting excess production, the combined controller manages to identify periods, shifting consumption to which is profitable.
3.5. Nudging Pipeline
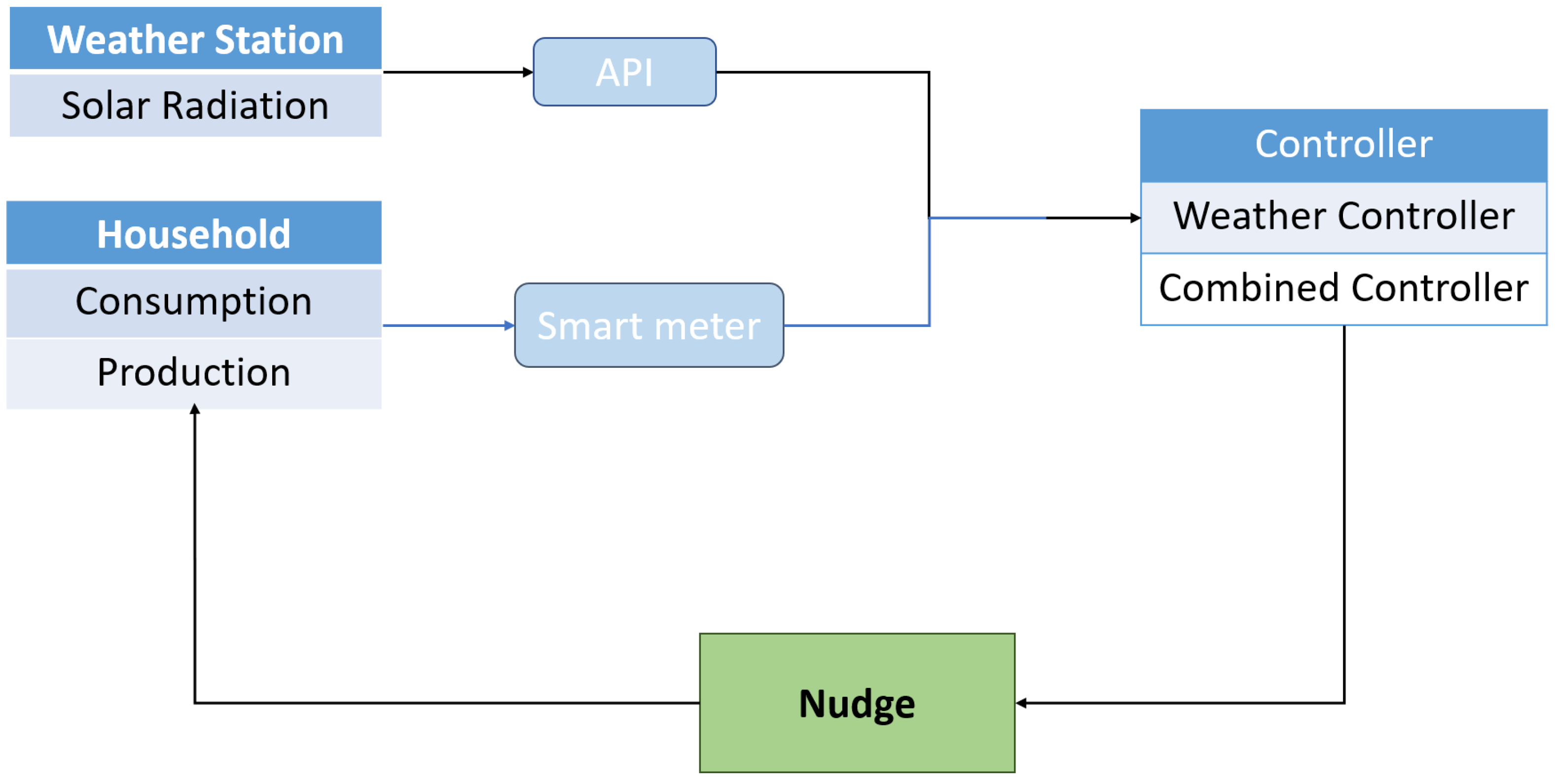
Therefore, the system “household + controller” is a controlled system, illustrated on
Figure 1. The nudging pipeline, which represents the system, save for the human behaviour part, consists of the following several components. Production and consumption data are monitored by a smart sensor located on the household premises. Weather APIs provide us with accurate forecasts for the upcoming days, in particular, concerning solar irradiance. All information is gathered by the controllers, which use it to compute solar consumption-friendly periods. These periods are gathered into nudges, which are sent to the household people through emails, for instance. Finally, upon receiving the nudge, the household people update their consumption accordingly.
4. Numerical Simulations
We first describe our numerical simulations set-up (
Section 4.1). Then, we show the results of simulations on synthetic data (
Section 4.2 and
Section 4.3) and the results of simulations on semi-real data (
Section 4.4 and
Section 4.5). Finally, we study the influence of the capacity of production installed (
Section 4.6) and of the number of green periods in the nudges (
Section 4.7) on the nudging pipeline efficiency.
4.1. Numerical Simulations Set-Up
Synthetic data preparation. We generated two synthetic datasets, representing two use cases: a commuting household (a commuting household refers to a group of individuals who live together in the same residence but travel to different locations for work or school, typically on a regular basis), and a non-commuting household (a non-commuting household refers to a group of individuals who live and work in the same place, without the need for regular travel to a workplace or school). The commuting household represents, for instance, the household of people going to work away from home but who have equipped their domestic electrical appliances with sensors, allowing them to launch, or stop, these appliances, remotely. The non-commuting household represents, for instance, the household of people working remotely.
For each household, we use as fixed consumption (that is, not shiftable), the not-shiftable part of the consumption of a real energy profile (which is part of the Iris dataset [
38]). To create shiftable consumption, we add real dishwasher consumption to the data every day in the morning, real washing machine consumption every three days in the evening, and a real water heater for domestic hot water consumption every day in the evening. Therefore, the shiftable part of the consumption occurs in the morning or in the evening, and is thus representative of that of a commuting household.
For the “non-commuting household”, we add an additional electric cooker every day between 12 p.m. and 1:30 p.m., and an additional air conditioner between 12 p.m. and 4 p.m. As the people of the household are present during the day, they must cook their lunch, and they may use air conditioning to maintain agreeable temperatures within the house in the afternoon. This may be the case, for instance, for a French household, endowed with air conditioning. While it is common in France to cook at lunch, air conditioning is not as widespread as in the United States of America, for instance, but its usage is nonetheless increasing. We classify air conditioning as non-shiftable in this context of someone working from home during the afternoon in a potentially badly isolated building. In such conditions, in order to maintain cool temperatures, the air conditioning system may need to run continuously.
Real datasets preparation. For the simulations using real datasets, we select a subset of appliances, which we define to be “shiftable”, and we fix their maximum shifting delay (see
Table 2 for details). We divide each dataset into past data, on which we train our model, and future data, on which we conduct the simulation. Finally, we renormalise the data sampling steps to 30 min steps.
The AMPds (Almanac of Minutely Power dataset) [
39] is a publicly available dataset created by Simon Fraser University’s (SFU) Electricity and Power Research Centre in Canada. It offers high-resolution energy consumption data collected from residential households. The dataset covers the period from 2012 to 2014 and includes measurements of electricity, water, and natural gas usage at one-minute intervals for an individual building in Canada. It can be found on the project’s official website
http://ampds.org/ (accessed on 30 June 2023) or through various data repositories and academic platforms.
The Iris dataset is a subset of a European database of residential consumption collected as part of the REMODECE (Residential Monitoring to Decrease Energy Consumption) project [
38]. The REMODECE project is an initiative focused on monitoring and reducing energy consumption in residential buildings. It aims to develop innovative solutions and technologies to promote energy efficiency and sustainability in the residential sector. The Iris dataset contains the energy consumption data of 98 houses for a span of one year. The data sampling step is 10 min. We make the appliance names homogeneous between the houses, as there are sometimes small variations in the terminology.
Solar energy production. As part of our simulator, we generate an artificial solar production as follows. We first simulate a sunshine coefficient as the product between the following:
A value taking into account the time of day (representing the fact there is no sun at night);
A value taking into account the month of year (representing the fact that the sun shines brighter during summer than winter);
A value taking into account the amount of clouds (representing the fact that more clouds implies less light for photovoltaic panels).
The process giving the amounts of clouds is simulated by Markov Chain transitioning between five levels of clouds, from “sunny” to “awful weather”. The chain is designed so that periods of sunshine alternate with cloudy periods. Precisely, write
P as the stochastic matrix such that each coordinate
is the probability of the chain going to state
j, given that it is currently in
i. Therefore, each line
is a probability distribution. The chain is a discrete time chain, and for each
,
represents the weather between the times
hours and
hours. As a result, to simulate trajectories of the chain, we start at
, and for
, we simulate
according to
Finally, the solar production generated by the panels from this synthetic sunshine coefficient is simulated as a linear function of the sunshine coefficient, that was renormalised before to the segment . The maximum power possible, that is, the capacity of the solar panels, is 3000 W.
Controllers. We use three controllers and an upper-bounding optimiser:
The weather controller and combined controller, defined in
Section 3.4, whose performance we want to assess.
The “no control” controller, and the “OMEGAlpes” optimiser, described below, which we use as references.
The “no control” controller represents the worst case, when there are no nudges. We call it “reference” in the plots. OMEGAlpes [
15] provides an upper-bound for the best possible case. It is a linear optimisation energy system modelling tool (see
Appendix A for details). It computes the best possible shifting of the consumption. However, it uses data, like detailed knowledge of the shiftable consumption of the household, and therefore cannot be used in real life. Moreover, OMEGAlpes has no restrictions on the number of the formal equivalent of green periods it uses. Therefore, OMEGAlpes is not a controller in the sense of Definition 3 but provides an upper bound on the possible performance of the controllers. We provide some context about the way OMEGAlpes computes its solution in
Appendix A. The nudges sent by our controllers each contain four green periods.
Simulation. The simulations run over one month. For each setting, we run 20 simulations to account for the stochasticity of the production generation.
Metrics displayed. We display the self-consumption rates of the household, for the different controllers and OMEGAlpes. We also display the improvement of our controllers (self-consumption rate with the controller minus the self-consumption rate with no controller), as a percentage of the improvement of OMEGAlpes (self-consumption rate with OMEGAlpes minus self-consumption rate with no controller). For each statistic, we show its mean, as well as the 10–90% interval of values. The results for the self-production rates are similar to those with the self-consumption rate. We present them in
Appendix B.
4.2. Synthetic Data, Commuting Household
We first present the results for the synthetic commuting household. We show in
Table 3 the self-consumption rate of the household, under the different controllers, and OMEGAlpes. We see both the weather and combined controllers improve the self-consumption rate, with respect to the “no control” reference. In average, with “no control”, the rate is 67.4%, while it is 77.35% for the weather controller and 77.63% for the combined controller. We also show the performance of our controllers as percentages of that of OMEGAlpes. They range between 45.9% and 47.25%. Clearly, we cannot obtain the full improvements of OMEGAlpes with our nudges, but we can still obtain a significant part of it.
4.3. Synthetic Data, Non-Commuting Household
In the non-commuting scenario, a large, not-shiftable consumption (due to the electric cooker and the air conditioner) takes place in the afternoons, when solar production is potentially at its maximum. Therefore, even if there is a lot of production in the afternoons, there is not a lot of excess production. As a consequence, looking at the sunshine coefficient to identify green periods will be misleading, as we now see. In
Table 4, we see that the self-consumption rate with the intervention of the Combined Controller (93.82% on average) is significantly higher than that with the Weather Controller (90.9% on average). Indeed, the percentage of improvement, with respect to the OMEGAlpes reference, of the Combined Controller, is more than 29% that of the Weather Controller (average of 47.94% against 18.53%). This happens because the Weather Controller only considers periods when the weather is favourable for production, but does not take into account the household’s consumption patterns. As a result, it may identify a green period when there is a high production, without noticing there is also a high consumption taking place. It may therefore encourage people to shift consumption to a moment where production is already saturated. On the other hand, by forecasting consumption as well as production, the Combined Controller is able to identify moments where there is likely to be excess production. Shifting consumption to these moments therefore helps improve the self-consumption rate.
4.4. Iris Dataset and AMPds Dataset, Individual Building Simulation
We first run a simulation for an individual building of Iris and the AMPds building. We show on
Table 5 the results of the simulation for Iris and AMPds. We see that both the weather and the combined controllers manage to improve the self-consumption rate of the building, taking it from 63.13% to more than 66.77% (weather) and 67.9% (combined). Results are comparable for AMPds: we see that both the controllers improve the self-consumption rates from 70.86% to more than 70.92%. The fact that the performance results of the two controllers are close is probably due to the fact that excess production occurs mainly when the absolute production is high (contrary to the use case of
Section 4.3). We note that even the worse results of the controllers are better than all but the very best results of the reference situation, in which there is no control, which shows the value of our procedure.
4.5. Iris Dataset, Collective Runs
Then, we conduct simulations for all the buildings of the Iris dataset, and show the results on
Table 6. The mean, and mean of the percentage of improvement, are averaged on all the buildings. We see that, on average, the weather and combined controllers improve the self-consumption rate by about 2%. This corresponds to roughly 17–22% of the OMEGAlpes performance. While the results of OMEGAlpes are much higher than that of the controllers, we believe it is mainly due to the limitless number of shifts in consumption it can perform and the fact that it uses per-appliance knowledge of the true consumption. Therefore, given these advantages, we believe reaching 22% of its performance, in the case of the combined controller, still shows the reasonable efficiency of our nudging pipelines.
To look at the influence of energy flexibility on the enhancements in the self-consumption rate, we conducted simulations on three distinct subsets of the Iris dataset, based on the numbers of shiftable appliances in each house: 1, 2, or 3. We show on
Table 7 the results of the simulations. Unsurprisingly, the greater the number of shiftable appliances within the houses, the greater the self-consumption rate increases when nudges are sent (going from 1% for the first dataset, to 4% for the third one), under similar conditions, such as weather and house type.
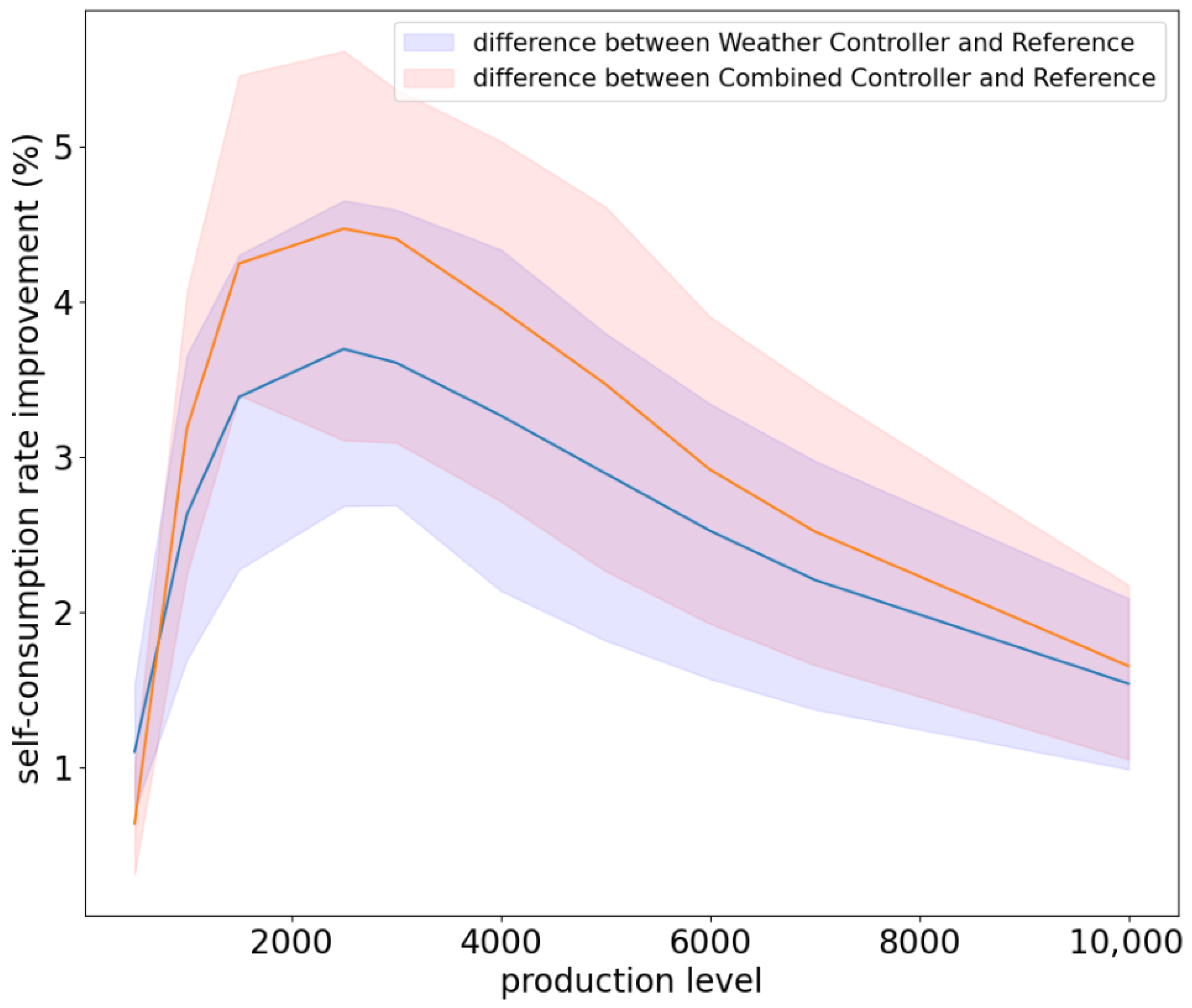
4.6. Influence of the Amount of Production
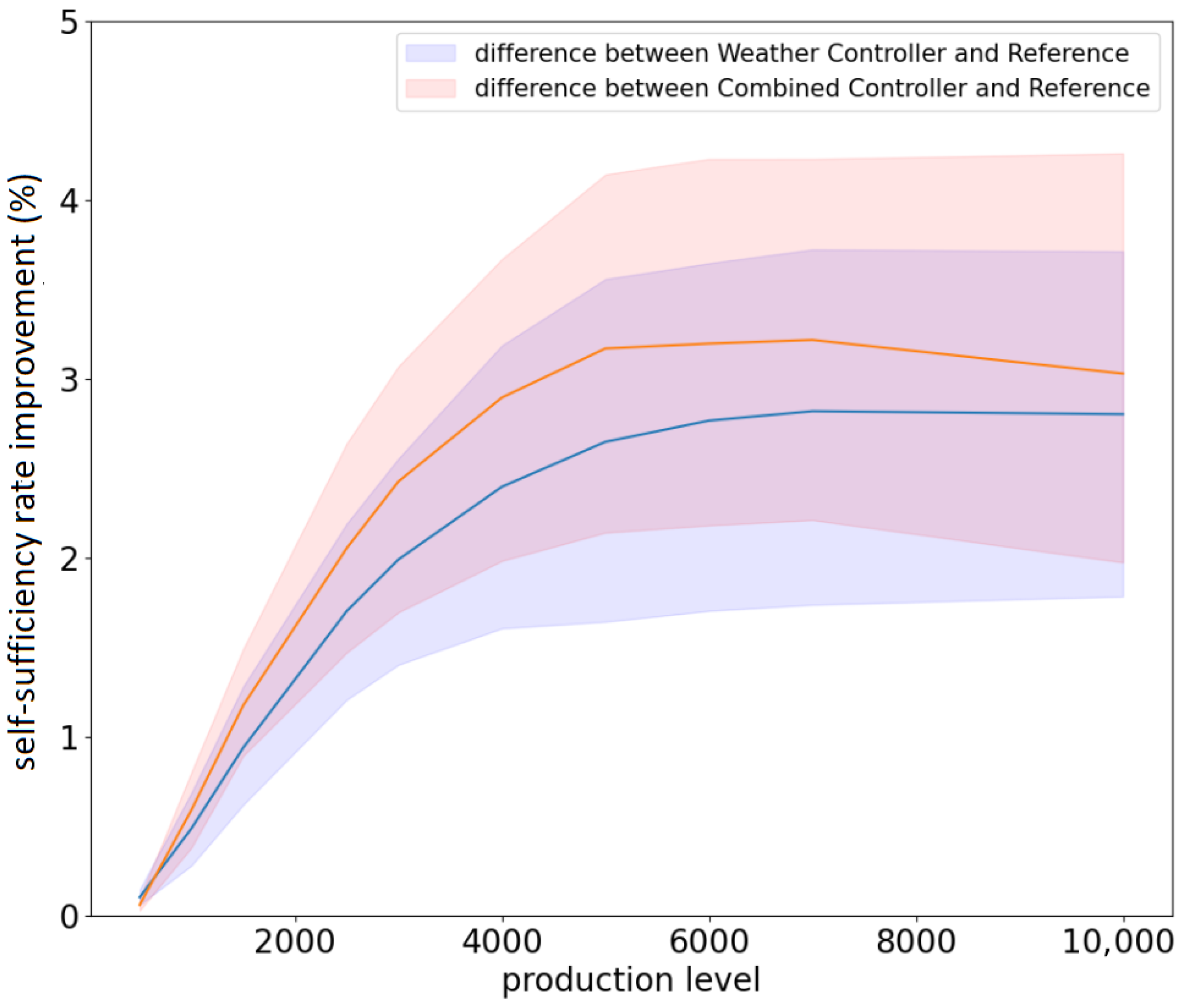
We show on
Figure 2 the increase in the self-consumption rate, for the Iris household, as a function of the amount of maximum possible production (this amount increases when more solar panels are installed). We see that the increase in the self-consumption rate is maximal for a production between 2000 and 3000 W for both cases of controllers and that it decreases for lower, and larger, values of production. Indeed, when there is very little production, there are not many gains to target by shifting consumption; therefore, nudging does not help a lot. Likewise, when there is a lot of production, all consumption already takes place when solar production is high, and therefore, there is no need to shift consumption. On the contrary, for intermediate values of production, shifting may help improve self-consumption, and therefore nudging proves valuable. Finally, we see that the superiority of the combined controller over the weather controller is highest in the production range where nudges are most efficient. This strengthens the case for using the combined controller.
4.7. Influence of the Number of Green Periods
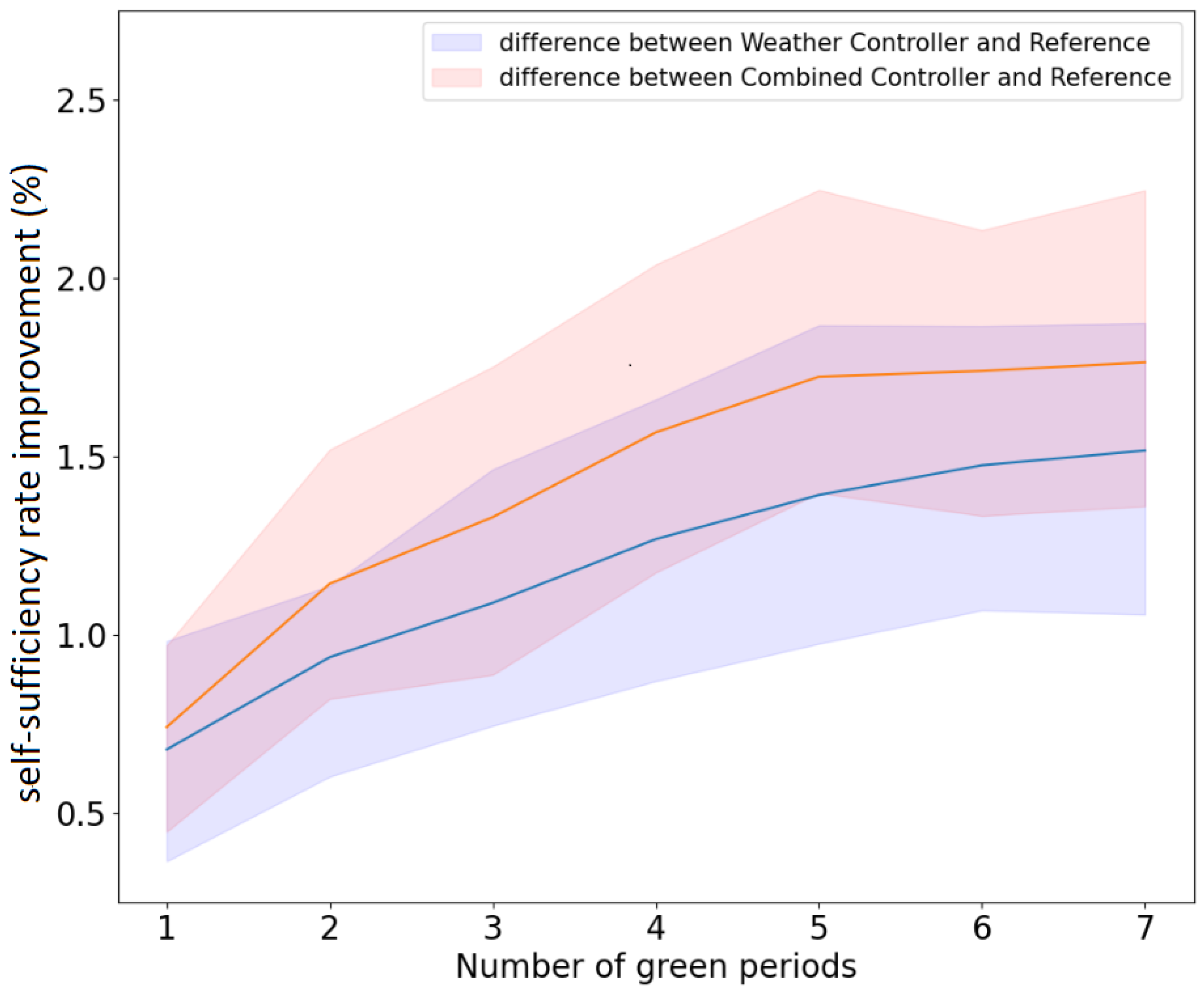
We show on
Figure 3 the efficiency of nudges as a function of the number of green periods in each nudge. This matters, as, realistically, users will tire if presented with too much information. Therefore, we should strive to send nudges with as few green periods as possible. However, we must make sure the efficiency of the nudge remains satisfying. The augmentation of the self-consumption rate increases with the number of green periods of a week, which is expected. However, the slope of the curve decreases as the number of green periods increases. This means that every supplementary green period helps to increase the self-consumption rate less than the previous. As a result, we see that most gains are concentrated on the left of the plot, from 0 to 4 green periods by nudge, and that gains realised by adding more green periods are lower and lower. This is probably due to the fact that the most easily shiftable consumption is already shifted with fewer nudges. We therefore recommend that each weekly nudge contains three or four green periods, as it strikes a good compromise between having an efficient procedure and avoiding user fatigue.
5. Discussion and Conclusions
We showed on semi-real data, in a simulated environment, that our ICT nudging pipelines using real-world accessible information were efficient in helping households improve their self-consumption. We showed that forecasting excess production, and constructing nudges based on this, beats merely providing weather forecasts when maximum solar production and excess production do not take place at the same time. We observed that the more flexibility there is in a household, the more profitable sending nudges is. Moreover, we saw that there is a sweet spot in production, for which nudging is most efficient. Indeed, when production is too small, or too large, there are few improvements to obtain by shifting consumption. Finally, we saw that most gains in self-consumption take place with few “green periods” by nudge, which is encouraging, as limiting their number helps prevent user fatigue.
While our results show that we can obtain reasonable performance with respect to the OMEGAlpes reference, we also saw that absolute improvements in the self-consumption and self-sufficiency rates, by merely shifting some part of the consumption upon nudge reception, are not enough to reach close to one rates. This probably entails that selectively reducing usage may be somewhat necessary for households willing to reach much better rates. Note that this may not necessarily mean a reduction in the “comfort” provided by appliances usage, as “unnecessary” usages, like appliances left in sleep mode instead of being turned off, may be removed, without diminishing the benefits one obtains from the appliance.
One takeaway of our study is the importance of assessing both the hardware and the “human”, so to speak, components of the household to identify settings where nudging will be efficient. Indeed, on the one hand, the photovoltaic capacity must be in the “sweet spot” we identified. On the other hand, the household people must be willing to shift enough of their consumption for these shifts to truly weigh on the part of solar energy used, with respect to the standard energy. In turn, making these assessments requires patient ground work, collecting individual information about photovoltaic capacity and consumption usages. This may seem like time-consuming effort, while nudge pipelines are supposed to be easy to set-up, but they can be viewed as a “one-off”, initial investment before letting the nudging pipeline run automatically.
We intend to pursue our work by testing our nudge scheme in real-world situations. Thanks to our simulations, we can have some confidence that it will be efficient, without overburdening users with information. Indeed, one important take of our simulations is the fact we can restrict our weekly nudges to three or four green periods, while still achieving satisfying results. It seems reasonable to imagine users mentally flagging these three to four periods during the week, and attempt to shift some consumption to these. Of course, we will have to test this assumption, first by directly asking the users, and second, by monitoring the key consumption metrics to quantify the effect our pipelines have on user consumption. As far as the controller choice is concerned, we will deploy the weather adviser for households where solar production and excess production tend to be correlated, and the combined controller for the others. Of course, we might also attempt to shift controllers as time goes on. Finally, before deploying a nudging scheme, we will assess whether the solar panel capacity is indeed in the range where nudging might be profitable, as our simulations showed that there would be no interest in doing so, should it be insufficient, or too large.
However, two main limitations of our work will need to be addressed for our pipelines to prove efficient in real-world settings. The first limitation stems from the complexity of human behaviour in real-life situations, as individuals vary in their reception and response to information. In our simulations, we assumed idealised human behaviour, whereby the household people would try their utmost to comply with the suggestions in the nudge. This may not be the case in real life, not for all individuals, in any case. Thus, future research directions should focus on estimating the “compliance” rate of users receiving nudge, and devising ways to make this rate improve. The second limitation pertains to the energy and weather forecasting modules. We used a simple energy forecasting module, which will probably require enhancing to remain relevant in real-world situations. Fortunately, there are many possible models available in the literature, which we may use. However, even state-of-the-art weather forecasts may prove inaccurate, especially a few days down the line. The prediction errors, about energy usage, and weather, can potentially result in incorrect information about green periods. This may lead to bad consumption shifts from the users, and potentially discourage them from further using the scheme. One way to make the forecast more robust would be to use ensemble models, which gather forecast from several models, and construct an aggregated forecast from these, which often proves more reliable than any one taken separately.
We have so far based our recommendations on the aggregate knowledge of the building consumption. Now, we could formulate better nudges if we had finer knowledge of the building consumption (the energy flexibility in the building). Non-intrusive load monitoring is the field concerned with gaining knowledge about the inner consumption of a building, without having to equip all its devices with ad hoc sensors [
44]. In spite of its inherent difficulty, as a blind source separation problem, valuable results have been obtained through numerous procedures (see, for instance, Zhong et al. [
45], which uses hidden Markov models, or Zhang et al. [
46] which uses neural networks, for machine learning approaches). Branching one such procedure in our nudging pipeline would likely improve it.
In our work, we considered the case of an individual building. Now, thanks to recent legislation (see Commission de Régulation de l’énergie [
47] for the case of France, Di Silvestre et al. [
48] for that of Italy, and Solar Power Europe [
49] for a broader view of the European Union), it is possible for building owners to create an association and share their production with the members: this is called collective self-consumption. Now, the alignment of consumption with production is made more complex by the fact that there are several consumers. Designing efficient nudging strategies also becomes more complex. For instance, telling everyone that there will be a sunny afternoon may result in excess consumption, due to all members shifting their production at the same time. We intend to further our work in this interesting and challenging direction in order to try to contribute to realising the potential that these communities have to get close to zero net energy consumption. This means that all energy used within the community is also produced within the community (the equivalent, in the case of the community, to “zero consumption on the meter” for an individual household) and is one of the very important potential benefits of these communities.
We believe there are two main difficulties in deploying solar energy, related to user adoption. The first is the cultural shift required to fully exploit it. Indeed, people are not used to looking at the weather before using their washing machine, for instance. Adapting behaviours accordingly will require time. This will only be possible through the adoption of this energy. However, this runs into the second difficulty: user experience is, at least in the beginning, downgraded when one gives up using “standard” energy sources and starts to use solar energy. Indeed, consuming whenever one sees fit is more convenient than taking into account the new constraint that one must pay attention to the sun. Of course, there are advantages to doing this, of economical and environmental kinds, but these are not immediately apparent, contrary to the inconvenience of having to take into account the sun. The widespread adoption of solar energy will therefore require efforts in order to make the transition as seamless as possible. We believe that deploying recommendation services, providing just enough information to help users take advantage of the solar energy, in as non-intrusive of a way as possible, will play a huge part in reaching this aim.