Thermal Performance of a Novel Non-Tubular Absorber with Extended Internal Surfaces for Concentrated Solar Power Receivers
Abstract
1. Introduction
- The non-tubular alternative design needs to balance heat transfer enhancement, pressure drop, and downsized geometry. The feasibility of fabricating the extended surface in the absorber must be considered. Meanwhile, careful design is required to ensure that the removal of the tubular structure does not negatively impact the structural integrity of the system.
- Further research is needed to explore the feasibility and potential of pressurized air in downsized applications and identify strategies to overcome the limitations associated with the low heat transfer capability of air.
- The proposed structure is inspired by the design of a heat sink. Instead of ambient air, which transfers heat through passive convection, in our case the working fluid is pressurized directional air flow. Thus, the parameters that affect the heat transfer in heat sinks must be re-evaluated. This research gap highlights the need for further exploration and analysis in this area.
2. Numerical Modeling of the Novel Absorber
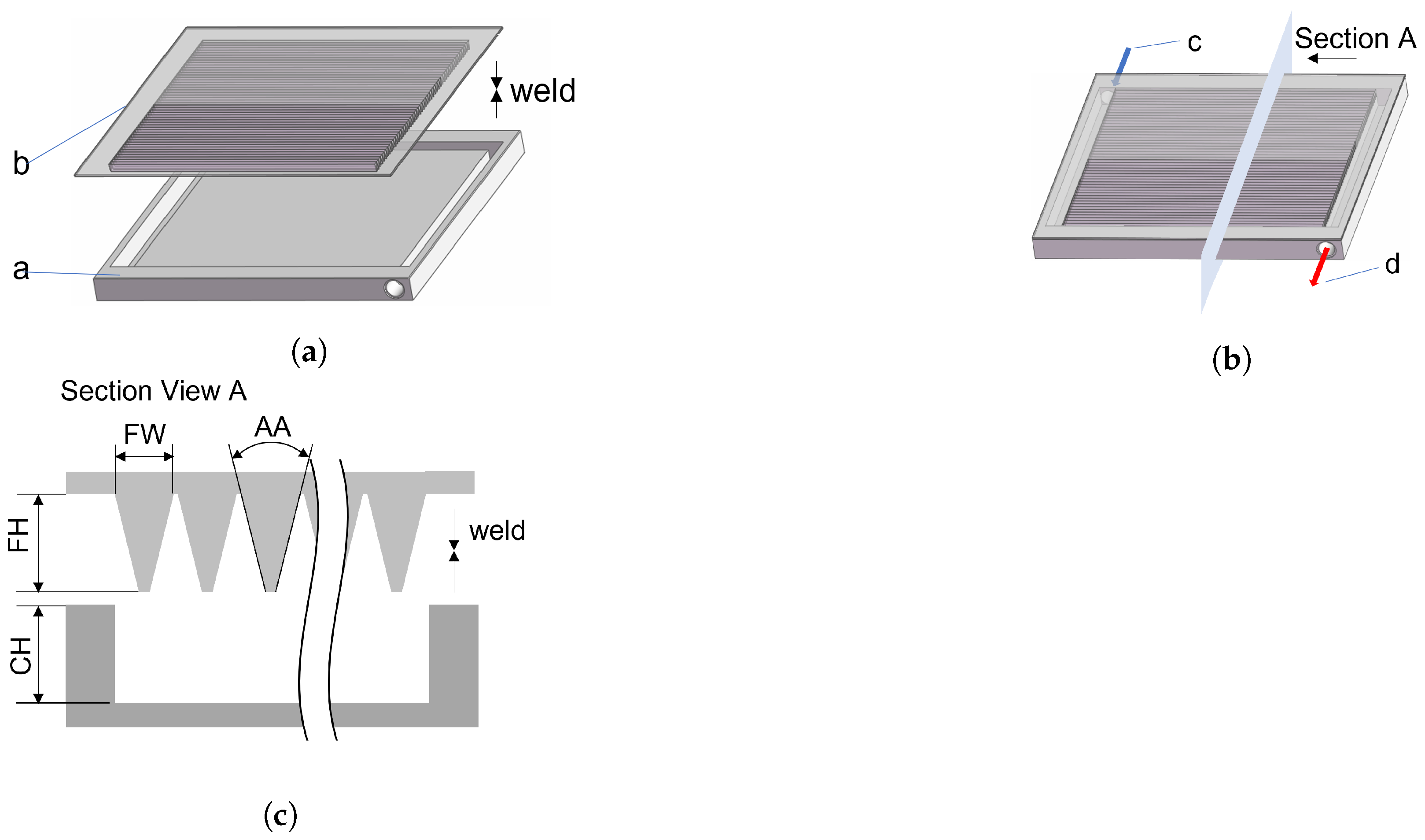
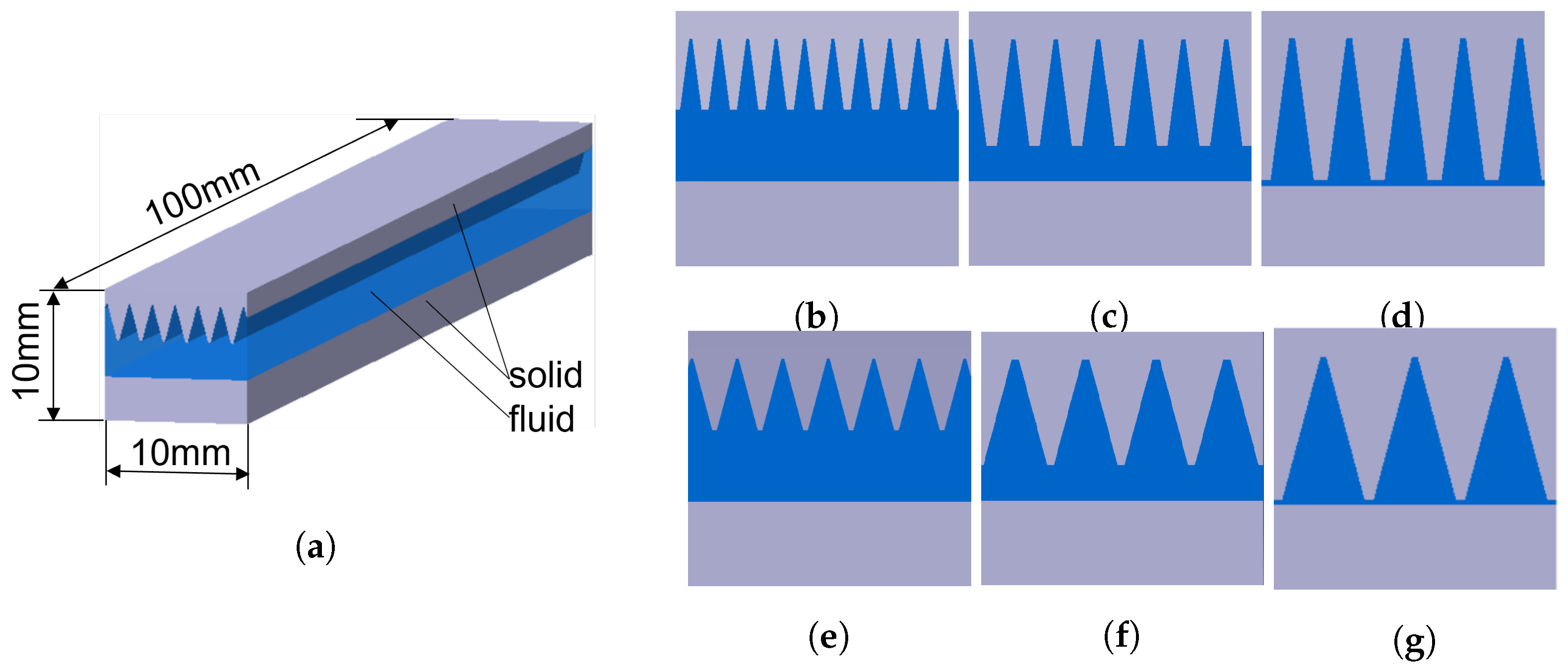
2.1. Design Description
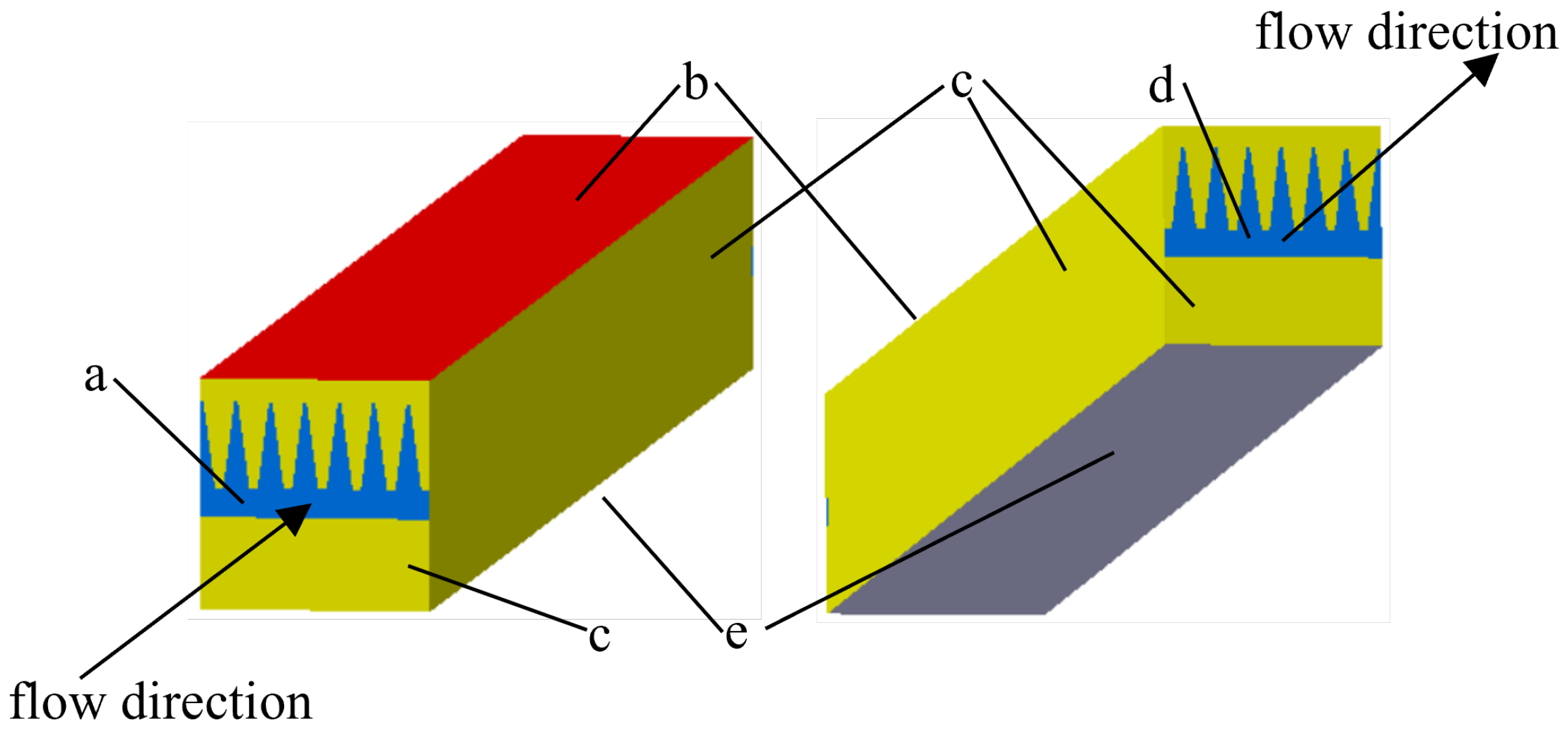
2.2. Numerical Model
3. Numerical Method
3.1. Governing Equations
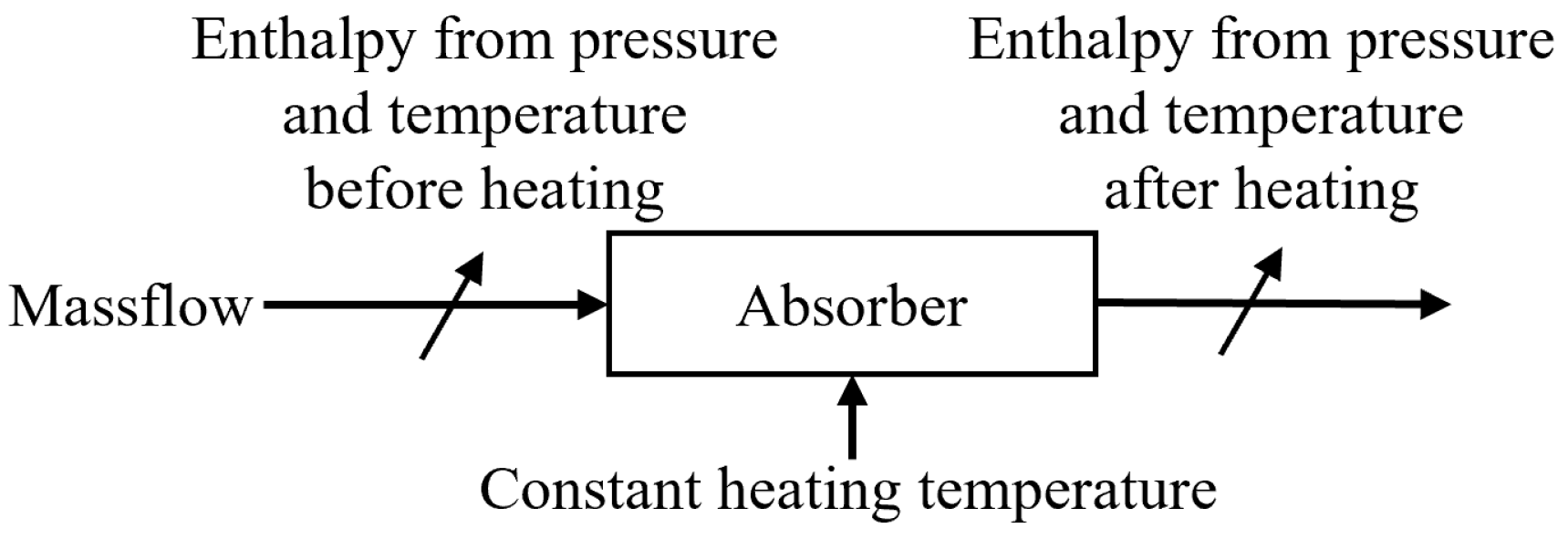
3.2. Boundary Conditions and Numerical Methods
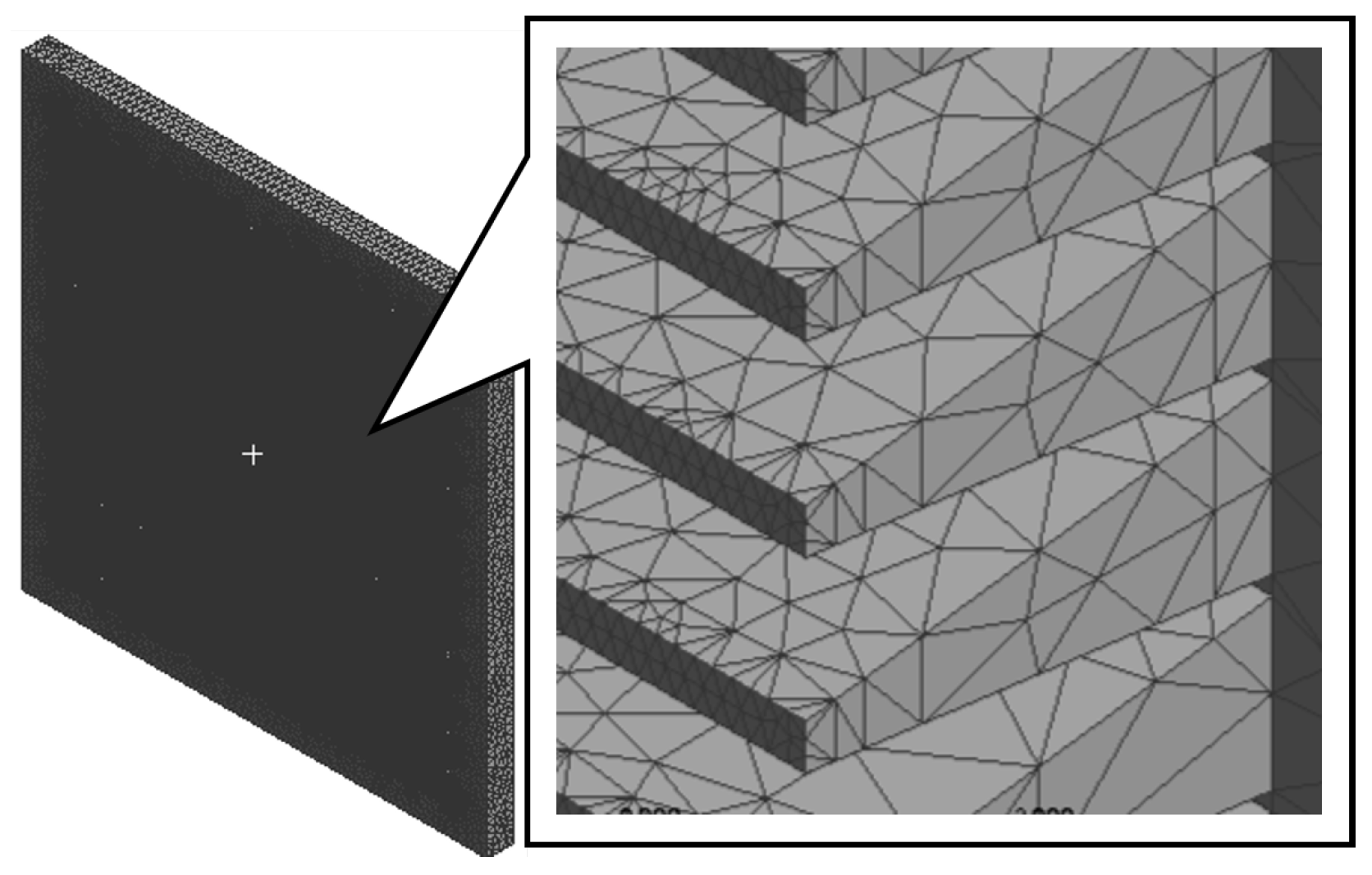
3.3. Grid Generation
3.4. Additional Numerical Analysis
3.4.1. Additional CFD Analysis
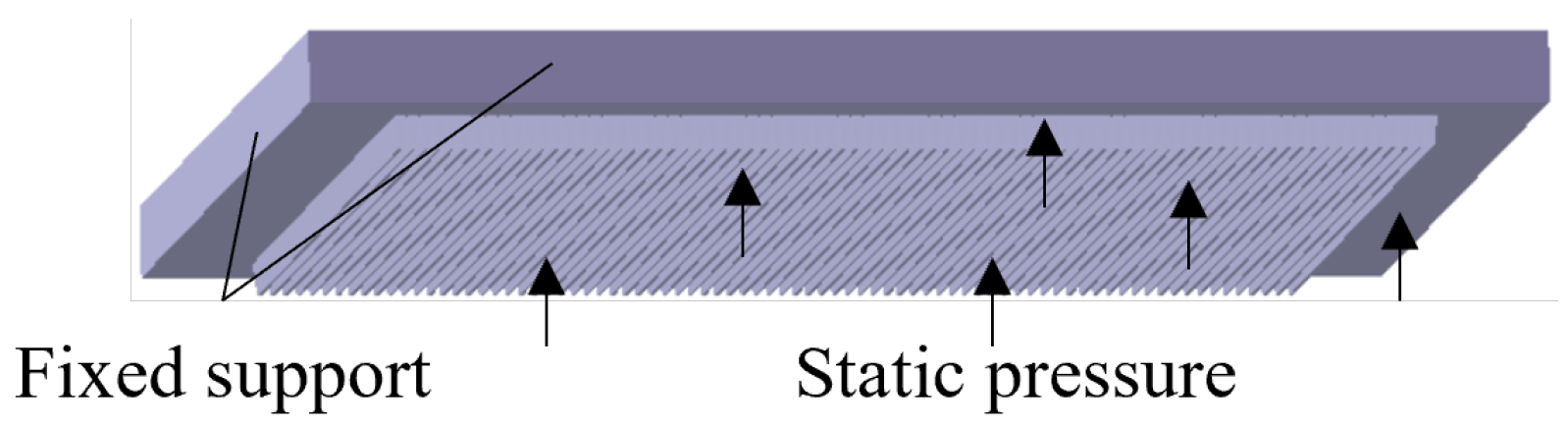
3.4.2. Static Structural Analysis
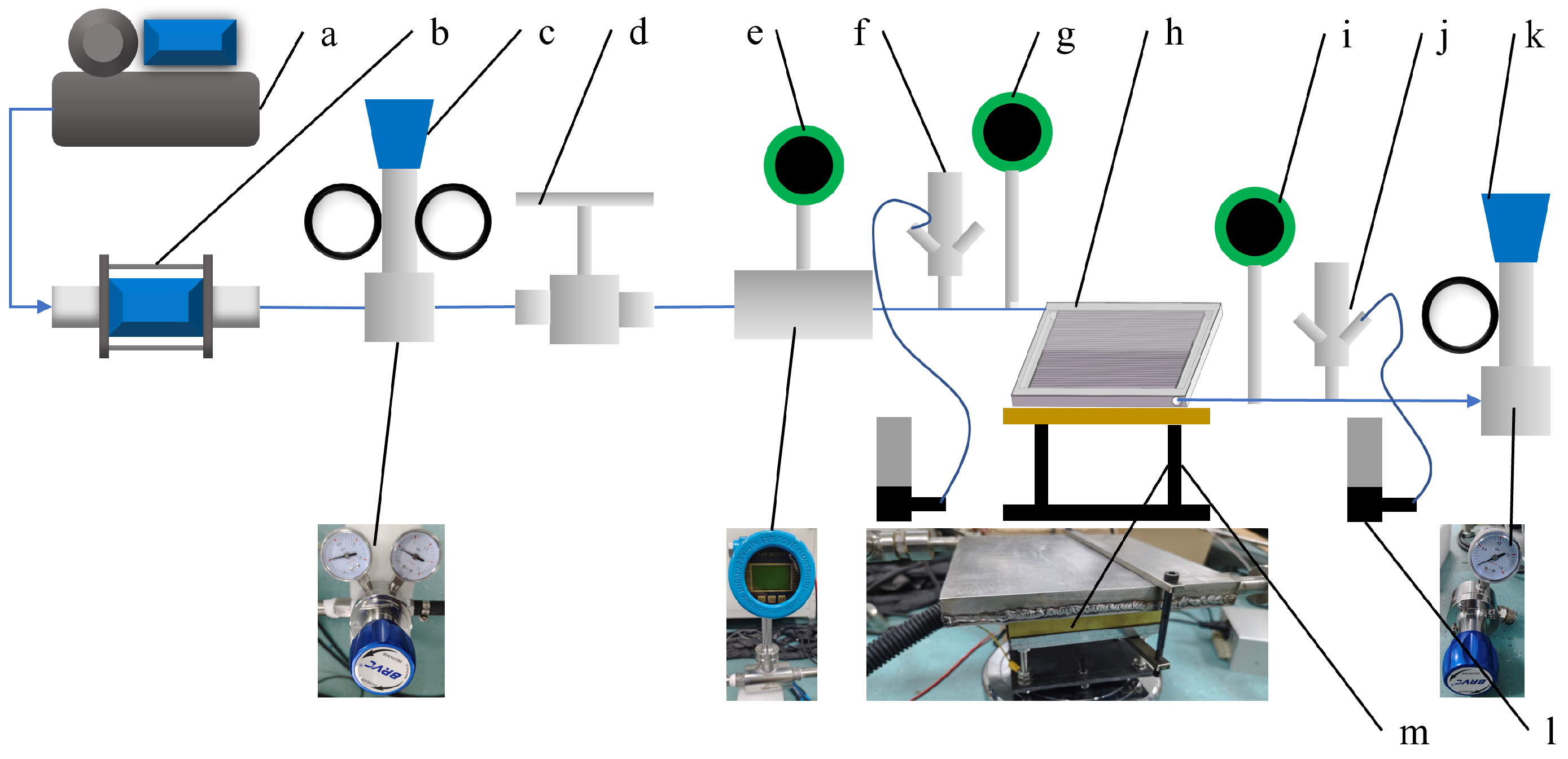
4. Experimental Investigations
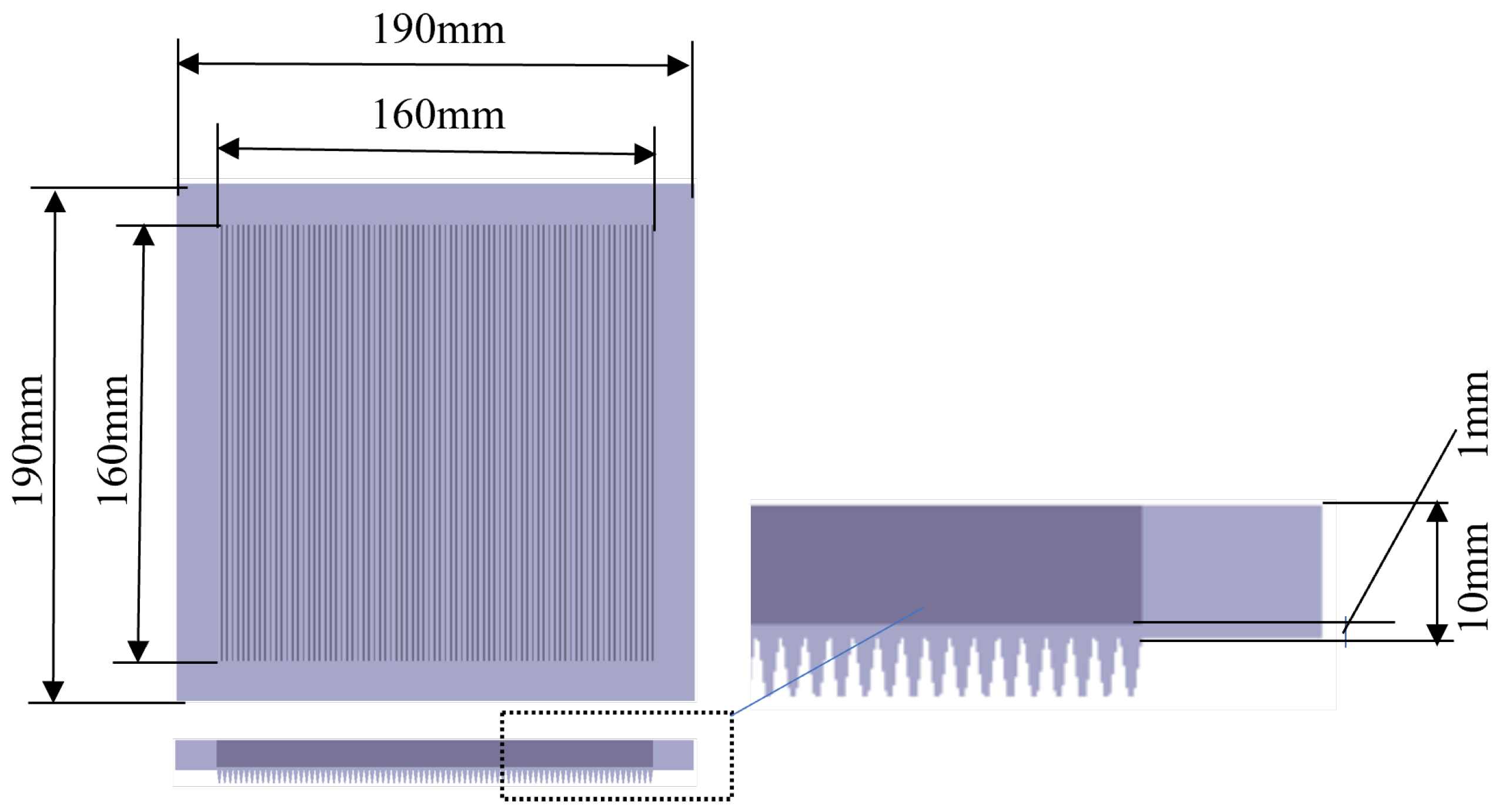
4.1. The Novel Absorber with Extended Internal Surfaces
4.2. Experimental System and Procedures
5. Results and Discussion
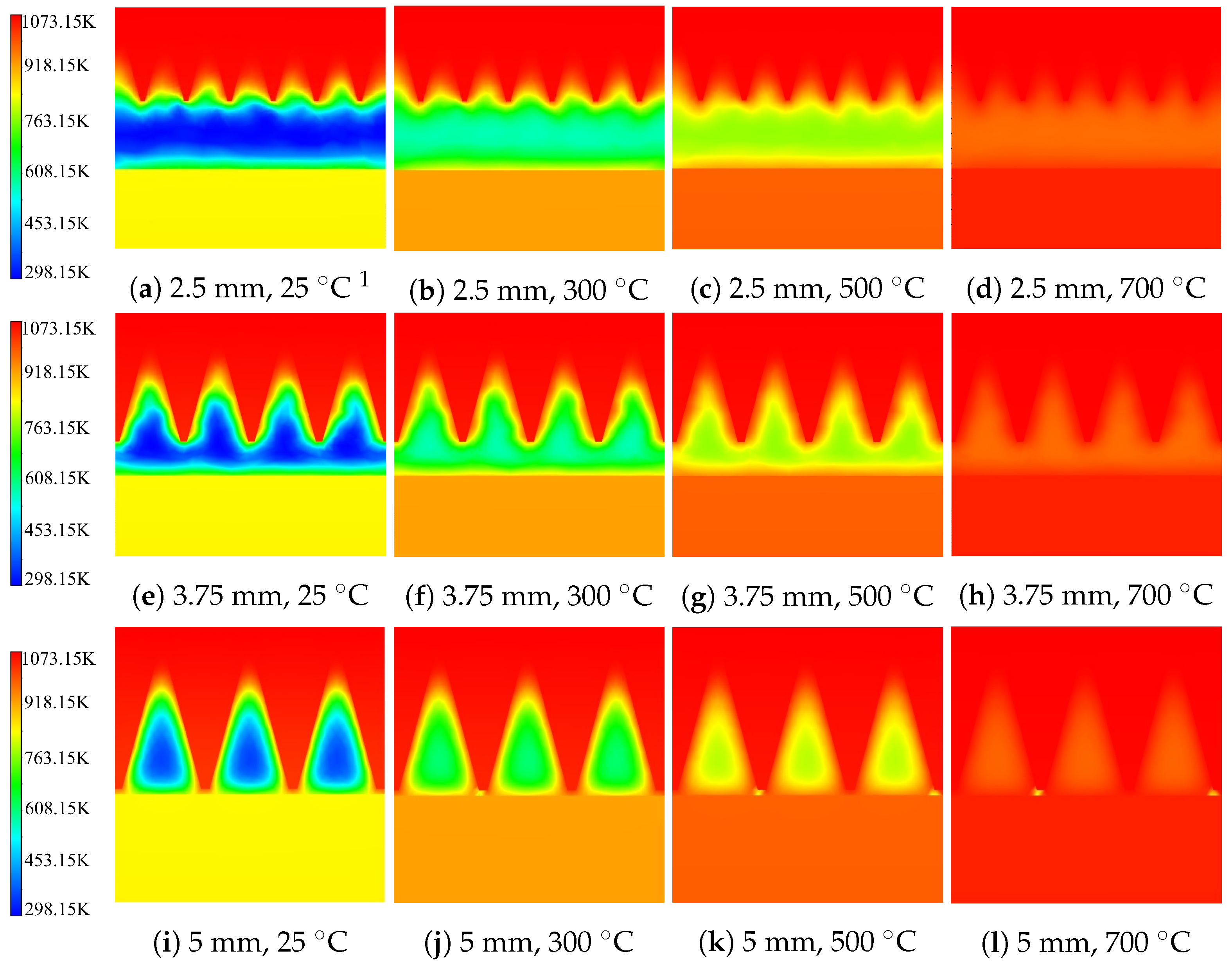
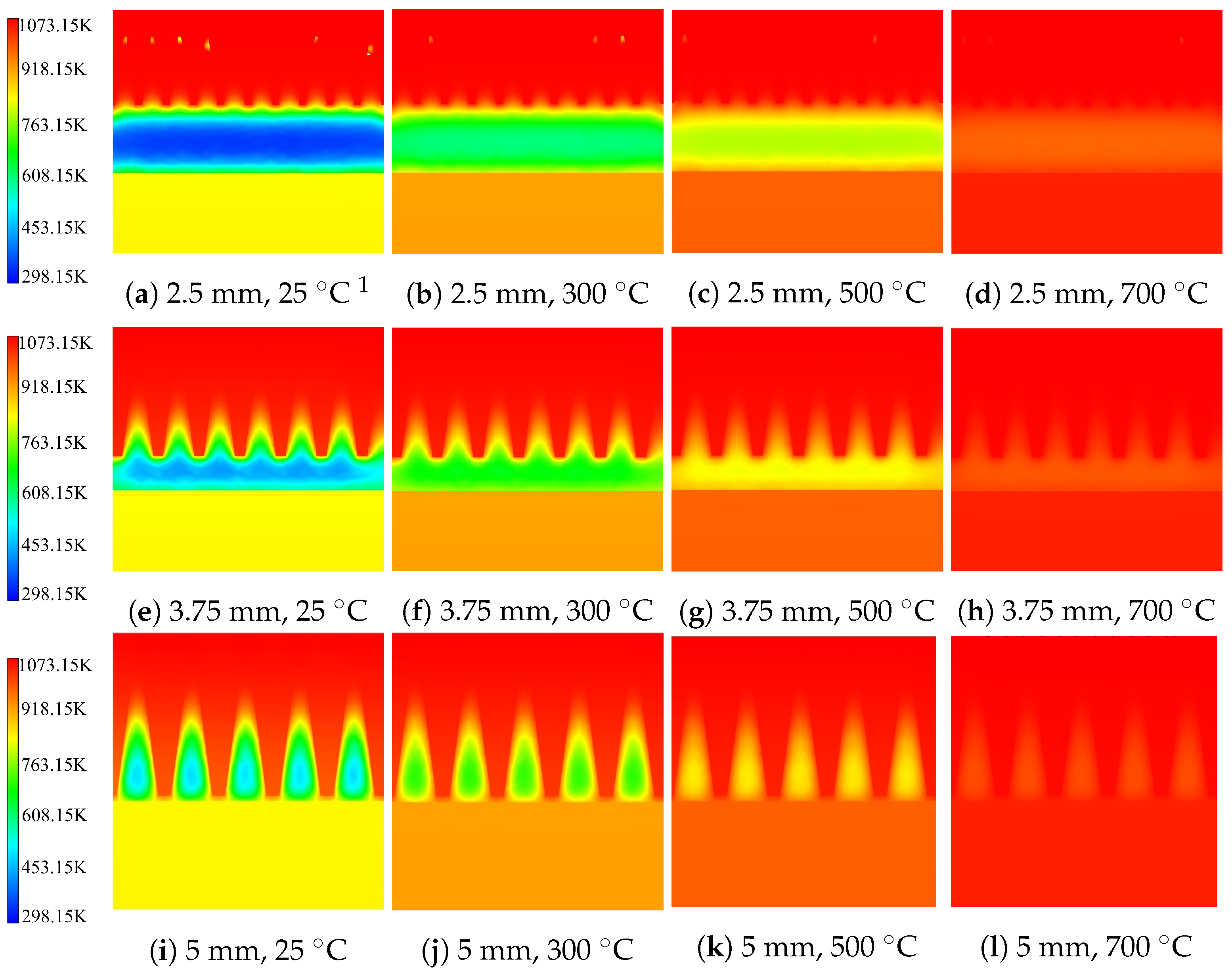
5.1. Fluid Flow and Temperature
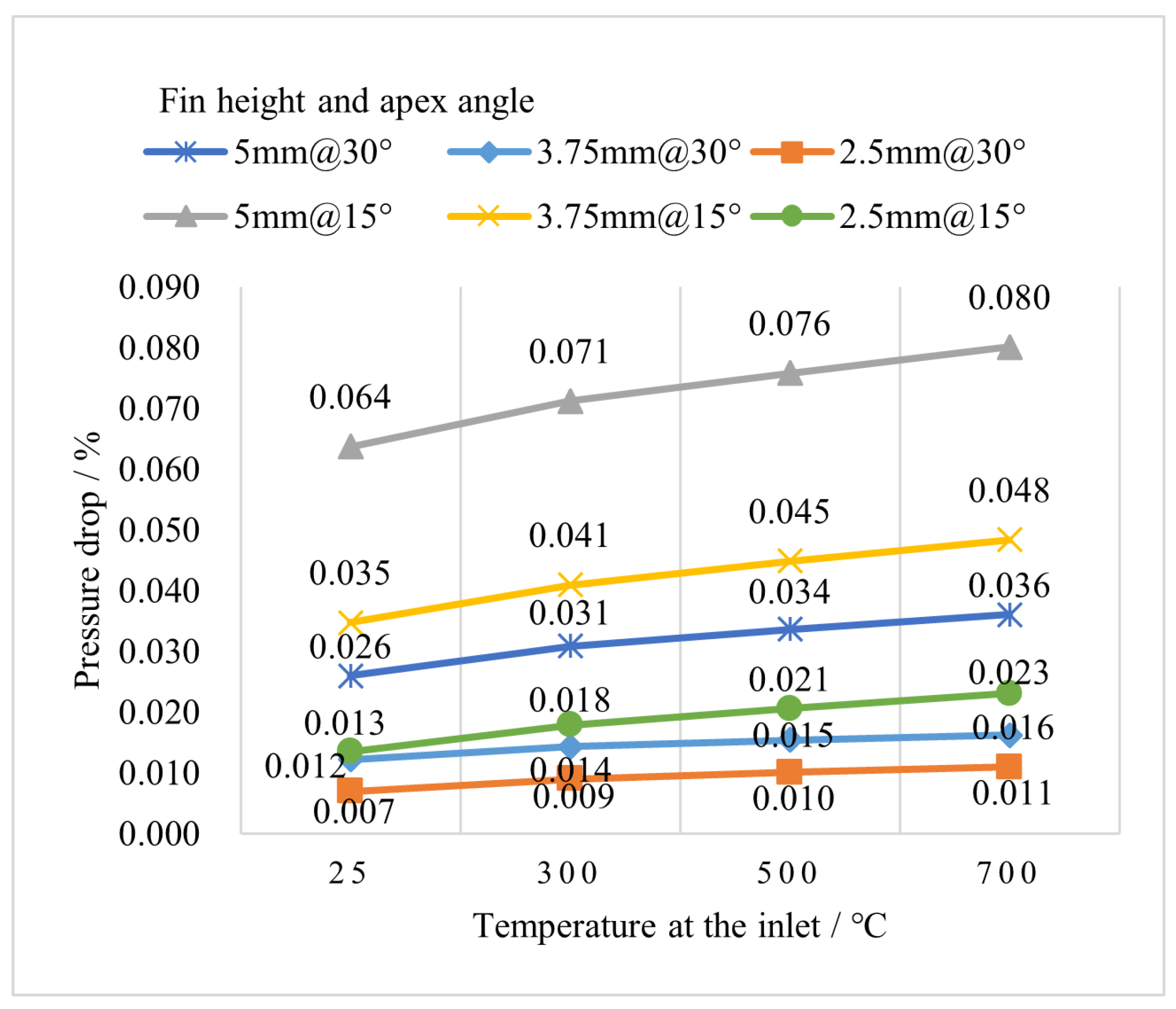
5.2. Pressure Drop
5.2.1. Effect of Fin Dimensions in Different Heating Stages
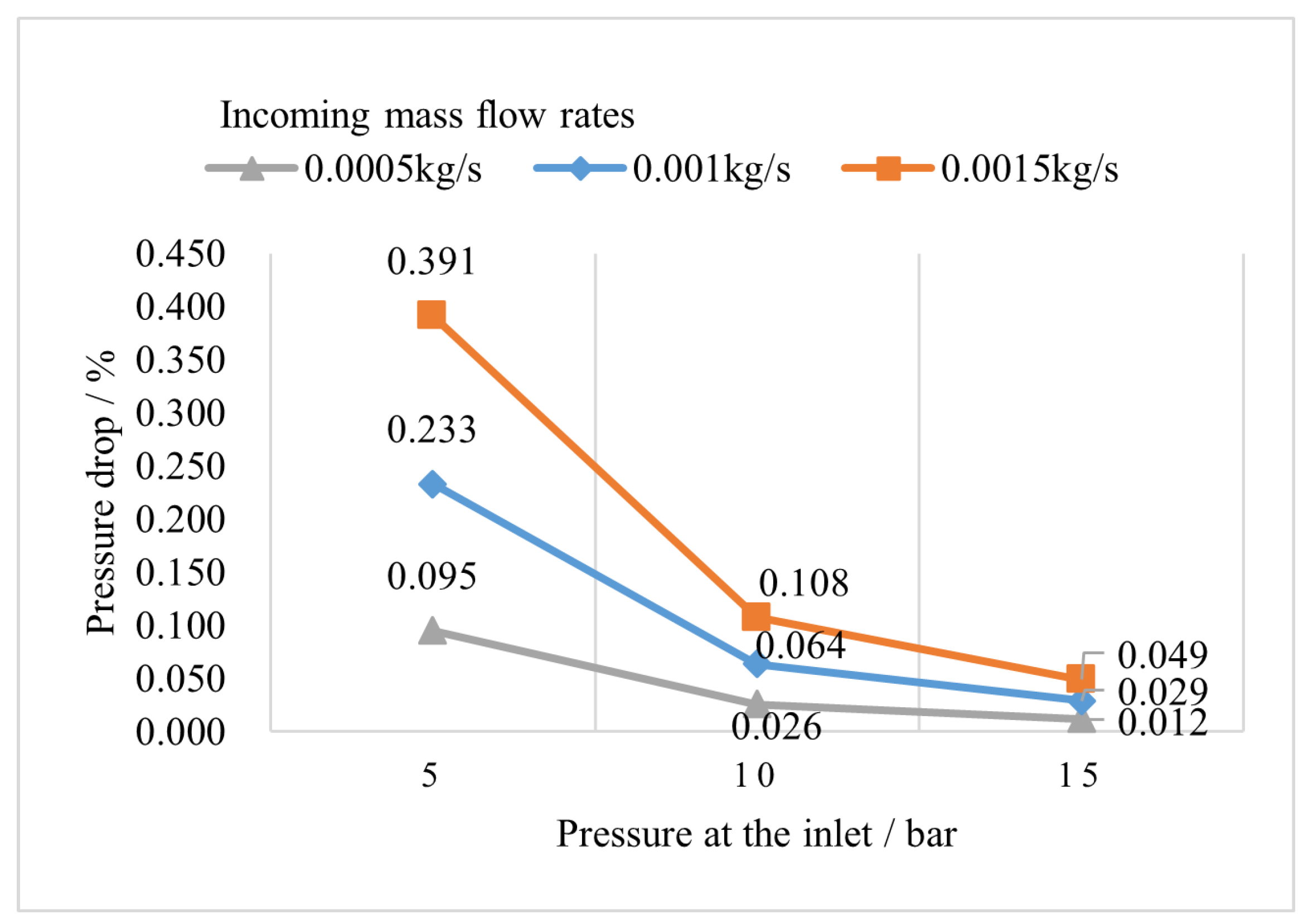
5.2.2. Effect of Pressure and Mass Flow Rates
5.2.3. Summary of Pressure Drop Results
5.3. Heat Transfer
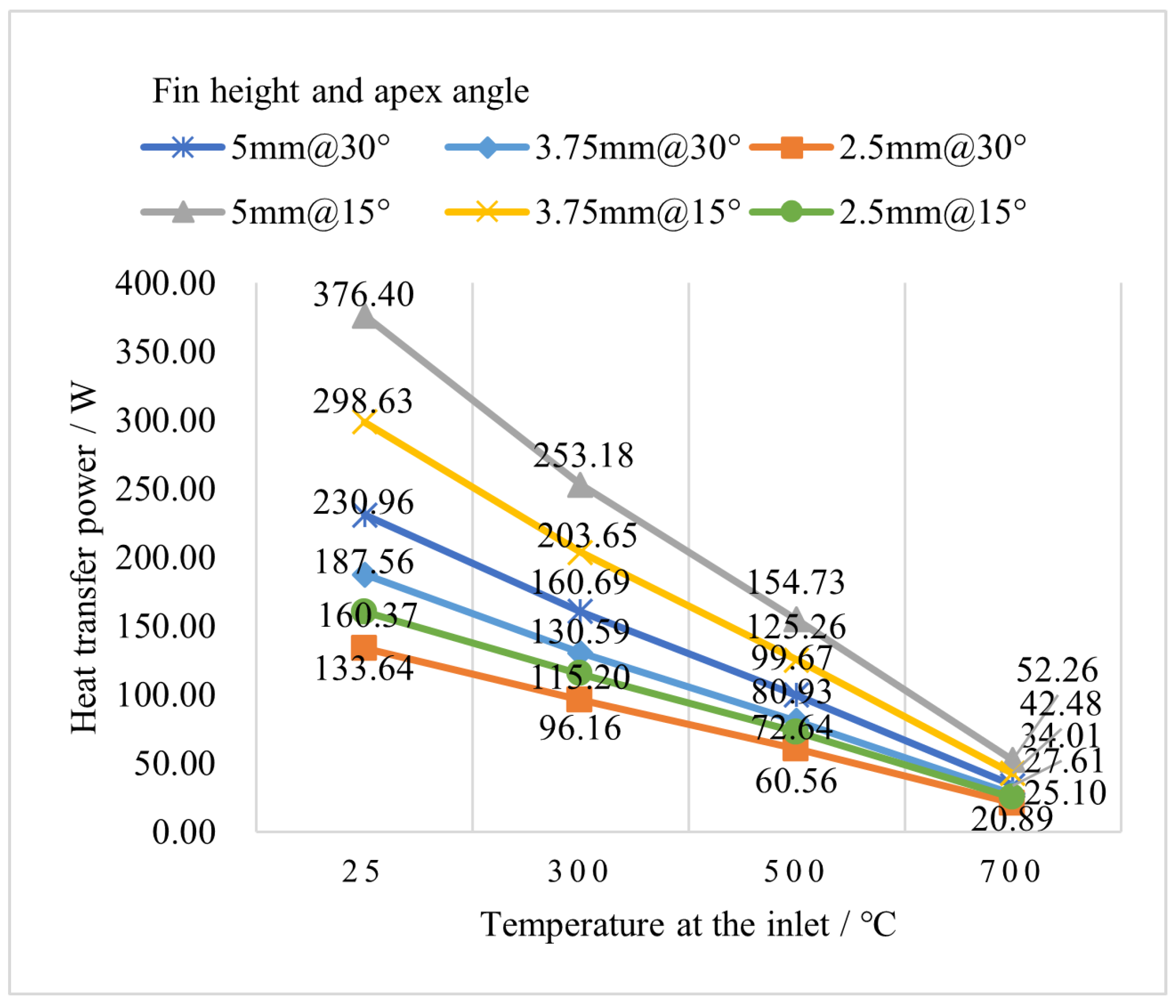
5.3.1. Effect of Fin Dimensions in Different Heating Stages
5.3.2. Effect of Mass Flow Rates
5.3.3. Summary of Numerical Results of Heat Transfer
5.4. Static Structural Results
5.5. Experimental Results
Uncertainties
- An additional error might exist when combining the numerical results acquired in 10 mm wide domains. Adjacent boundaries are set as adiabatic walls (flux = 0) when calculated separately, and these boundaries do not actually exist.
- After reaching the designated heating temperature at constant C, there is a time interval before the heater resumes heating after detecting a temperature drop. The temperature drop in this interval may reach C.
- The high temperature thermocouple was installed about 100 mm away from the exit of the absorber, which may have affected the measured temperature value even with proper insulation.
- Before and after the pressurized air is heated in the finned channels, it passes through two smooth channels in the absorber with 7 mm × 10 mm sections, respectively. These two smooth channels could have an effect on the fluid temperature.
5.6. Comparison with Previous Research
5.6.1. CFD Results
5.6.2. Experimental Results
6. Conclusions
- The implementation of extended surfaces in cavity receiver absorbers can significantly improve heat transfer by reducing thermal resistance in the solid material, expanding the fluid–solid interface, and decreasing the distance between the flow center and the interface. In comparison to conventional tubular absorbers without fins, the novel absorber proposed in this paper demonstrates superior heat transfer performance and temperature distribution at the exit when the structures occupy comparable volumes.
- As the heating temperature increases beyond a certain point, the heat transfer to the working fluid decreases due to a significant increase in heat loss. However, the novel absorber has a smaller external surface area and is more able to apply insulation compared to conventional tubular absorbers, resulting in lower heat loss. This means that the heat transfer degradation with rising temperature is slower when occupying the same volume.
- At the typical working pressure of 10 bar, the pressure drop caused by friction in the fin surfaces along the working flow direction does not exceed 0.06% per 100 mm in the designs studied in this research, and this percentage decreases with increasing pressure. This suggests that the novel absorber’s length could be customized to meet the demands of state-of-the-art CSP applications.
- In addition to their heat transfer function, the extended surfaces in the novel absorber act as stiffeners, improving the compressive strength of the heat transfer plane. The compressive strength of the absorber experimentally tested in this study (160 mm × 160 mm) is capable of withstanding pressures comparable to those present in conventional tubular absorbers.
- Meshing of multi-scale structures generates an excessive number of elements, which may have exceeded 100 million in the studied case. The adapted calculation domains are only representative subsets of the entire absorber structure.
- The flat panel heaters’ heating power generation was limited, and was unable to reach the maximum heat transfer rate acquired in numerical investigations at higher temperatures. In order to fully compare the numerical and experiment results, an additional CFD investigation with lower performance must be performed.
- The absorber in the novel modular collector has not yet been tested under real solar radiation.
- The intended use of the absorber is for either a novel CSP system, such as the one mentioned in [24], or a traditional tower system. The present research only considered the former case, as the geometric dimensions of the scheme were more suitable for laboratory experiments. However, the latter case is more practical for rel-world application.
- The absorber should be installed in a CSP testing system under real solar rediation;
- The channel height, fin height, and fin width should be optimized, especially for systems operating at higher temperatures;
- The fin surfaces can be fabricated with specific microstructures or painted to enhance heat transfer;
- It is expected that the absorber will be redesigned and investigated for application in tower systems.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AA | Apex Angle |
| CSP | Concentrated Solar Power |
| CFD | Computational Fluid Dynamics |
| FEM | Finite Element Method |
| FH | Fin Height |
| FW | Fin Width |
| WEDM | Wire Electrical Discharge Machining |
Appendix A. Governing Equations in ANSYS Fluent
Appendix B. Additional CFD Investigations
Appendix B.1. Fluid Flow Characteristics

- Modeling: no solid body, additional channel added
- Governing equations: no energy equation
- Boundary conditions: same inlet and outlet, no heat transfer on walls
- Numerical method: same
- Grid generation: same.
Appendix B.2. Temperature Distribution in the Channel
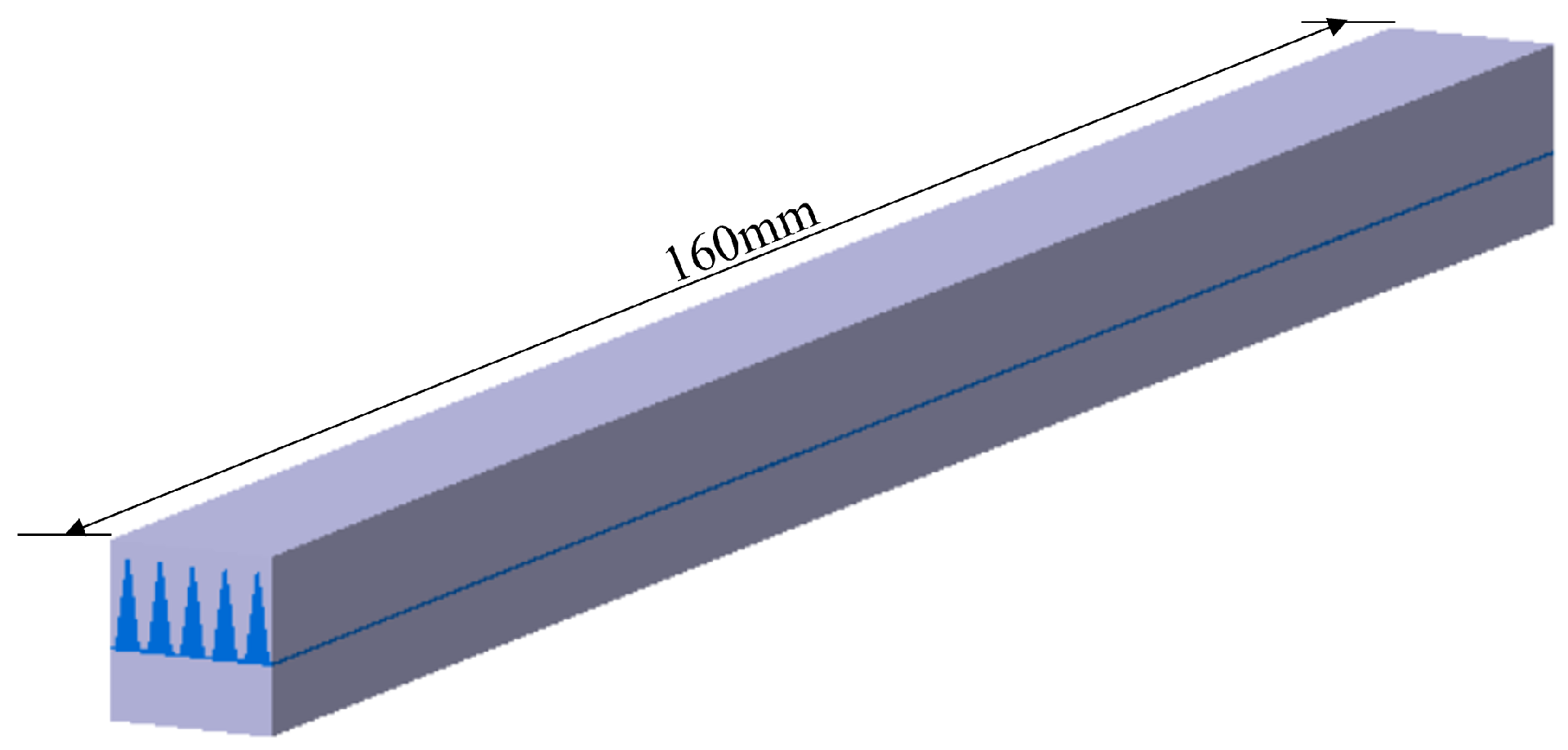
- Modeling: length extended to 160 mm
- Governing equations: same
- Boundary conditions: same
- Numerical method: same
- Grid generation: same.
Appendix C. The Heat Transfer Plate’s Static Structural Properties
References
- Zhou, Y. Worldwide Carbon Neutrality transition? Energy efficiency, renewable, Carbon Trading and Advanced Energy Policies. Energy Rev. 2023, 2, 100026. [Google Scholar] [CrossRef]
- Poživil, P.; Aga, V.; Zagorskiy, A.; Steinfeld, A. A Pressurized Air Receiver for Solar-driven Gas Turbines. Energy Procedia 2014, 49, 498–503. [Google Scholar] [CrossRef]
- Mousavi Ajarostaghi, S.S.; Zaboli, M.; Javadi, H.; Badenes, B.; Urchueguia, J.F. A Review of Recent Passive Heat Transfer Enhancement Methods. Energies 2022, 15, 986. [Google Scholar] [CrossRef]
- Nada, S.; Said, M. Effects of Fins geometries, arrangements, Dimensions and Numbers on Natural Convection Heat Transfer Characteristics in finned-horizontal Annulus. Int. J. Therm. Sci. 2019, 137, 121–137. [Google Scholar] [CrossRef]
- Ammar Ali, M.; Sajid, M.; Uddin, E.; Bahadur, N.; Ali, Z. Numerical Analysis of Heat Transfer and Pressure Drop in Helically Micro-Finned Tubes. Processes 2021, 9, 754. [Google Scholar] [CrossRef]
- Lin, Y.; Li, J.; Chen, Z.; Li, W.; Ke, Z.; Ke, H. Two-Phase Flow Heat Transfer in Micro-Fin Tubes. Heat Transf. Eng. 2019, 42, 369–386. [Google Scholar] [CrossRef]
- Wei, L. Study on Comprehensive Performance Evaluation for Condensation Heat Transfer inside the micro-fin Tube. Adv. Mech. Eng. 2020, 12, 168781402094009. [Google Scholar] [CrossRef]
- Tang, W.; Li, W.; Minkowycz, W.J. A Numerical Investigation of Convective Condensation in micro-fin Tubes of Different Geometries. Numer. Heat Transf. Part Appl. 2020, 78, 697–705. [Google Scholar] [CrossRef]
- Zhang, J.N.; Cheng, M.; Ding, Y.D.; Fu, Q.; Chen, Z.Y. Influence of Geometric Parameters on the gas-side Heat Transfer and Pressure Drop Characteristics of three-dimensional Finned Tube. Int. J. Heat Mass Transf. 2019, 133, 192–202. [Google Scholar] [CrossRef]
- Duan, L.; Ling, X.; Peng, H. Flow and Heat Transfer Characteristics of a double-tube Structure Internal Finned Tube with Blossom Shape Internal Fins. Appl. Therm. Eng. 2018, 128, 1102–1115. [Google Scholar] [CrossRef]
- Kim, T.; Choi, B.I.; Han, Y.S.; Do, K.H. Experimental and Analytical Investigation of a Wavy Fin Recuperator for a Micro Gas Turbine. Int. J. Heat Mass Transf. 2020, 148, 118998. [Google Scholar] [CrossRef]
- Lotfi, B.; Zeng, M.; Sundén, B.; Wang, Q. 3D Numerical Investigation of Flow and Heat Transfer Characteristics in Smooth Wavy fin-and-elliptical Tube Heat Exchangers Using New Type Vortex Generators. Energy 2014, 73, 233–257. [Google Scholar] [CrossRef]
- Zhou, Y. Demand Response Flexibility with Synergies on Passive PCM walls, BIPVs, and Active air-conditioning System in a Subtropical Climate. Renew. Energy 2022, 199, 204–225. [Google Scholar] [CrossRef]
- Zheng, X.; Zhou, Y. A three-dimensional Unsteady Numerical Model on a Novel aerogel-based PV/T-PCM System with Dynamic heat-transfer Mechanism and Solar Energy Harvesting Analysis. Appl. Energy 2023, 338, 120899. [Google Scholar] [CrossRef]
- Dastmalchi, M.; Sheikhzadeh, G.; Arefmanesh, A. Optimization of micro-finned Tubes in Double Pipe Heat Exchangers Using Particle Swarm Algorithm. Appl. Therm. Eng. 2017, 119, 1–9. [Google Scholar] [CrossRef]
- Freegah, B.; Hussain, A.A.; Falih, A.H.; Towsyfyan, H. CFD Analysis of Heat Transfer Enhancement in plate-fin Heat Sinks with Fillet profile: Investigation of New Designs. Therm. Sci. Eng. Prog. 2020, 17, 100458. [Google Scholar] [CrossRef]
- Hussain, A.A.; Freegah, B.; Khalaf, B.S.; Towsyfyan, H. Numerical Investigation of Heat Transfer Enhancement in Plate-Fin Heat sinks: Effect of Flow Direction and Fillet Profile. Case Stud. Therm. Eng. 2019, 13, 100388. [Google Scholar] [CrossRef]
- Sahel, D.; Bellahcene, L.; Yousfi, A.; Subasi, A. Numerical Investigation and Optimization of a Heat Sink Having Hemispherical Pin Fins. Int. Commun. Heat Mass Transf. 2021, 122, 105133. [Google Scholar] [CrossRef]
- Yan, Y.; Zhao, T.; He, Z.; Yang, Z.; Zhang, L. Numerical Investigation on the Characteristics of Flow and Heat Transfer Enhancement by Micro pin-fin Array Heat Sink with fin-shaped Strips. Chem. Eng. Process. Process Intensif. 2021, 160, 108273. [Google Scholar] [CrossRef]
- Singh, P.; Patil, A.K. Experimental Investigation of Heat Transfer Enhancement through Embossed Fin Heat Sink under Natural Convection. Exp. Therm. Fluid Sci. 2015, 61, 24–33. [Google Scholar] [CrossRef]
- Özbektas, S.; Sungur, B.; Topaloglu, B. Numerical Investigation of the Effect of Heat Sinks with Various Fin Geometries on the Performance of a Thermoelectric Generator. J. Therm. Sci. Eng. Appl. 2022, 15, 031004. [Google Scholar] [CrossRef]
- Xu, R.; Wang, G.; Jiang, P. Spray Cooling on Enhanced Surfaces: A Review of the Progress and Mechanisms. J. Electron. Packag. 2021, 144, 010802. [Google Scholar] [CrossRef]
- Pai, Y.W.; Yeh, R.H. Experimental Investigation of Heat Transfer and Pressure Drop Characteristics of Internal Finned Tubes. Int. J. Heat Mass Transf. 2022, 183, 122183. [Google Scholar] [CrossRef]
- Na, X.; Yao, Y.; Zhao, C.; Du, J. Heat Loss Reduction Approach in Cavity Receiver Design Based on Performance Investigation of a Novel Positive Conical Scheme. Energies 2022, 15, 784. [Google Scholar] [CrossRef]
- Li, Y.; Xia, G.; Ma, D.; Jia, Y.; Wang, J. Characteristics of Laminar Flow and Heat Transfer in Microchannel Heat Sink with Triangular Cavities and Rectangular Ribs. Int. J. Heat Mass Transf. 2016, 98, 17–28. [Google Scholar] [CrossRef]
- Lei, Y.; Li, Y.; Jing, S.; Song, C.; Lyu, Y.; Wang, F. Design and Performance Analysis of the Novel shell-and-tube Heat Exchangers with Louver Baffles. Appl. Therm. Eng. 2017, 125, 870–879. [Google Scholar] [CrossRef]
- Gheith, R.; Hachem, H.; Aloui, F.; Nasrallah, S.B. Experimental and Theoretical Investigation of Stirling Engine heater: Parametrical Optimization. Energy Convers. Manag. 2015, 105, 285–293. [Google Scholar] [CrossRef]
- Xiao, G.; Chen, C.; Shi, B.; Cen, K.; Ni, M. Experimental Study on Heat Transfer of Oscillating Flow of a Tubular Stirling Engine Heater. Int. J. Heat Mass Transf. 2014, 71, 1–7. [Google Scholar] [CrossRef]
- García, D.; Prieto, J. A non-tubular Stirling Engine Heater for a Micro Solar Power Unit. Renew. Energy 2012, 46, 127–136. [Google Scholar] [CrossRef]




| Fin Height (mm) | Fin Width (+Internal, mm) | L/ (mm/mm) | /Int.V. * (mm/mm) | /Ext.V. ** (mm/mm) | |
|---|---|---|---|---|---|
| Apex angle 15 C | 5 | 1.8 (+0.2) | 2.80 | 2.51 | 1.81 |
| 3.75 | 1.35 (+0.15) | 2.28 | 1.87 | ||
| 2.5 | 0.9 (+0.1) | 1.76 | 1.51 | ||
| Apex angle 30 C | 5 | 3 (+0.2) | 4.13 | 1.41 | 1.14 |
| 3.75 | 2.25 (+0.25) | 3.39 | 1.05 | ||
| 2.5 | 1.5 (+0.1) | 2.64 | 0.92 | ||
| No fins | – | – | 3.91 | 0.2 | 0.34 |
| Tubes | – | 1.5 + 0.75 *** | 1.78 | 0.92 | 1.14 |
| Mass Flow Rate/kg | 0.0005 | 0.001 | 0.0015 |
| Heat flux/W | 239.6 | 376.0 | 482.7 |
| Final temperature/C | 502.97 | 400.24 | 346.31 |
| Experimental | Numerical | |
|---|---|---|
| Temperature (heat source)/C | 400 | 400 |
| Temperature (inlet)/C | 21.7 | 21.7 |
| Temperature (outlet)/C | 346.5 | 358.484 |
| Pressure (inlet, gauge)/Pa | ||
| Pressure (outlet, gauge)/Pa | ||
| Massflow rate/kg/h | 12 | 12 |
| Heat transfer/W | 1113.033 (96.6741%) | 1151.326 (100%) |
| Gauge | Uncertainty | Impact on Heat Transfer |
|---|---|---|
| Flow meter | 1 | |
| Thermocouple (inlet) | – 2 | |
| Thermocouple (outlet) | – 2 | |
| Thermocouple (heater) | C | 1 |
| Pressure gauge (inlet) | – 2 | |
| Pressure gauge (outlet) | – 2 |
| This Research | Research 1 [27] | Research 2 [28] | Research 3 [29] | |
| Working fluid | Air | Air | Nitrogen | Air |
| Pressure/bar | 8 | 5–7.5 | 6.9 | |
| Heating temperature/C | 400 | 300–500 | 205 | 100–400 |
| Heater volume/mm | 1 | 2 | 3 | 4 |
| Heat transfer/W | 1113 | 5 | 231 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, X.; Yao, Y.; Du, J. Thermal Performance of a Novel Non-Tubular Absorber with Extended Internal Surfaces for Concentrated Solar Power Receivers. Energies 2023, 16, 5055. https://doi.org/10.3390/en16135055
Na X, Yao Y, Du J. Thermal Performance of a Novel Non-Tubular Absorber with Extended Internal Surfaces for Concentrated Solar Power Receivers. Energies. 2023; 16(13):5055. https://doi.org/10.3390/en16135055
Chicago/Turabian StyleNa, Xinchen, Yingxue Yao, and Jianjun Du. 2023. "Thermal Performance of a Novel Non-Tubular Absorber with Extended Internal Surfaces for Concentrated Solar Power Receivers" Energies 16, no. 13: 5055. https://doi.org/10.3390/en16135055
APA StyleNa, X., Yao, Y., & Du, J. (2023). Thermal Performance of a Novel Non-Tubular Absorber with Extended Internal Surfaces for Concentrated Solar Power Receivers. Energies, 16(13), 5055. https://doi.org/10.3390/en16135055







