State-Space Load Flow Calculation of an Energy System with Sector-Coupling Technologies
Abstract
1. Introduction
2. Sector-Coupling Technologies
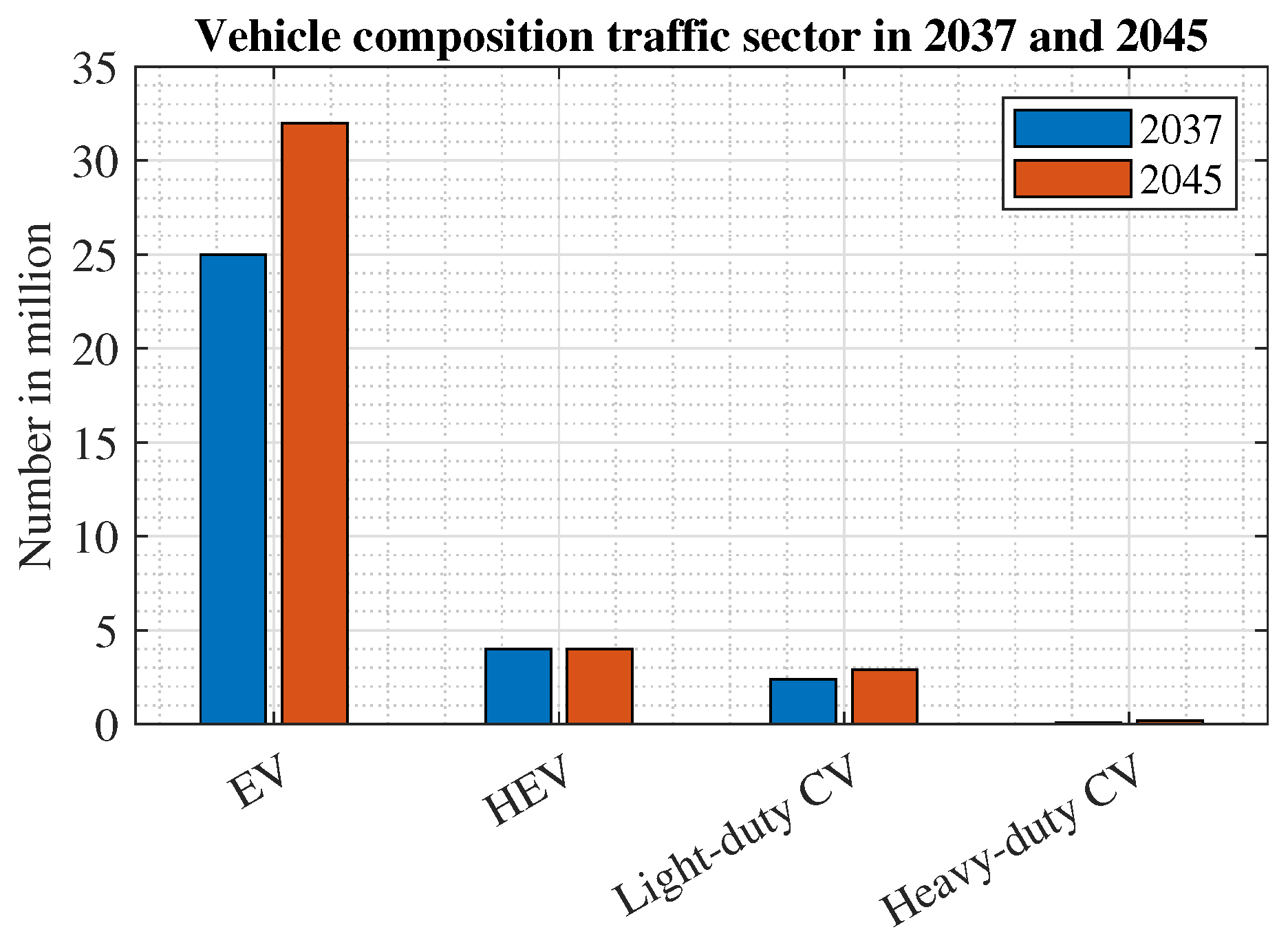
2.1. Mobility
2.2. Heat
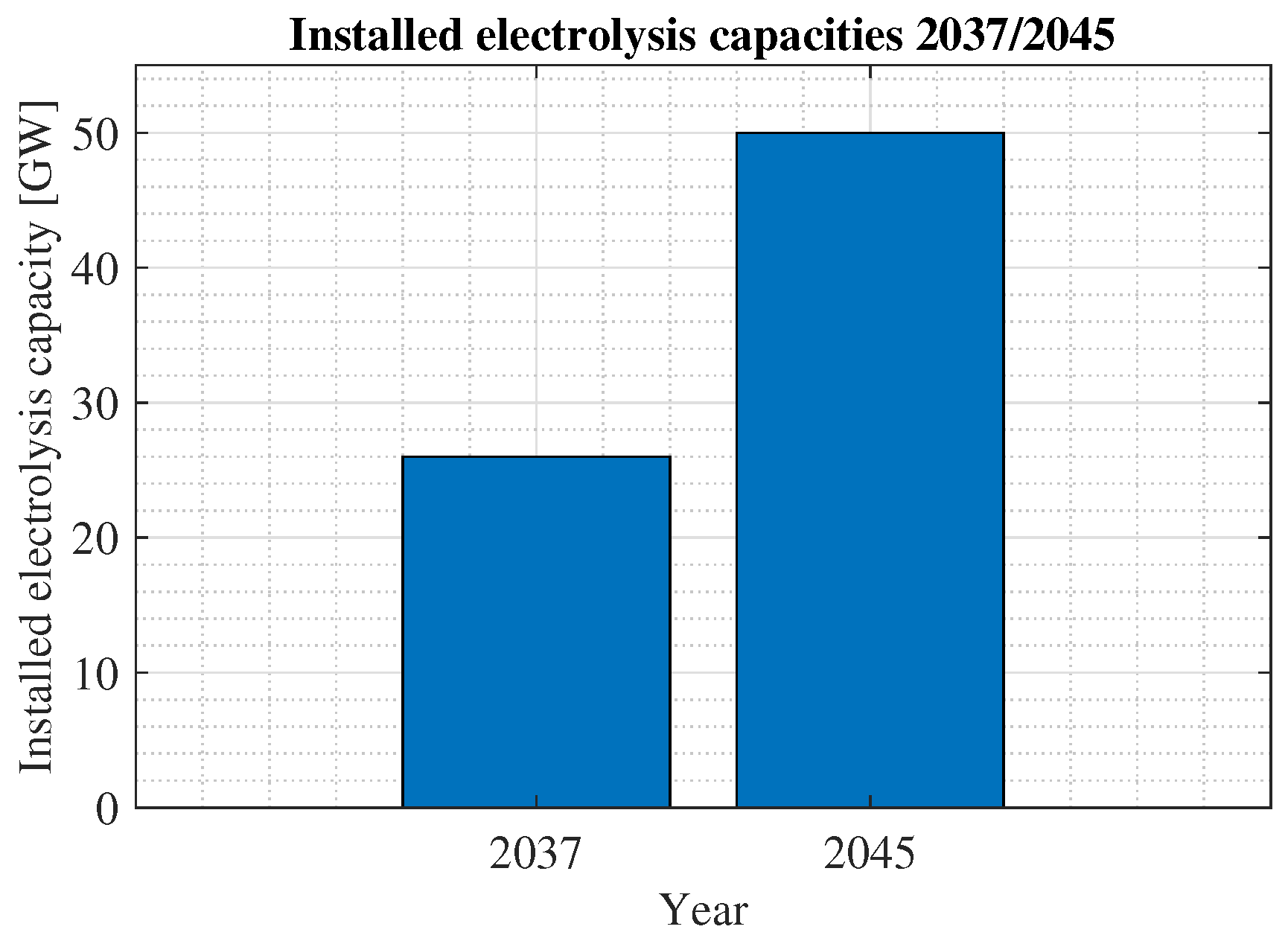
2.3. Gas
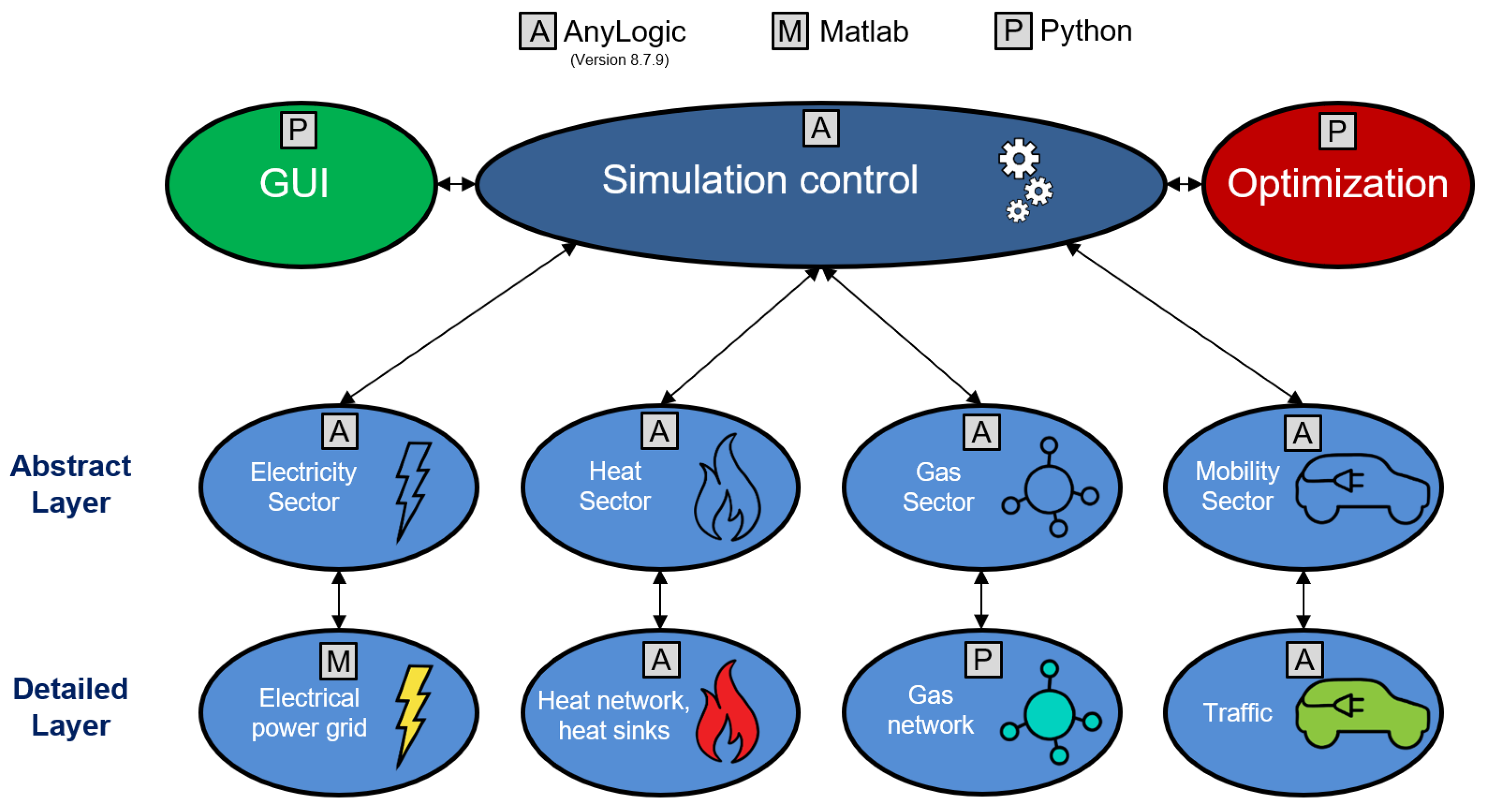
2.4. Derivation of Simulation Scenarios
3. Electricity Sector
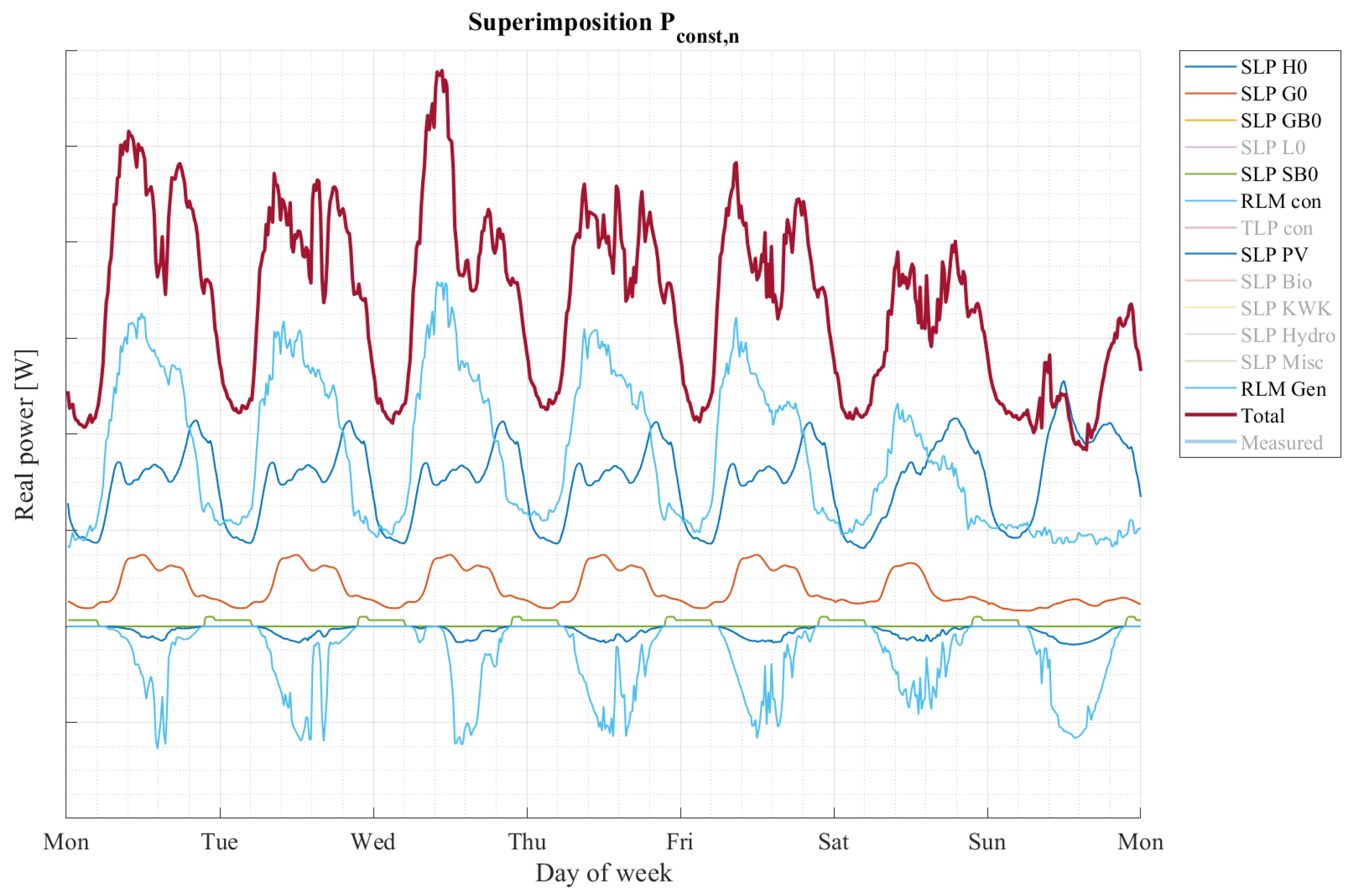
3.1. Principles for Calculating Load–Flow Using the State-Space Representation
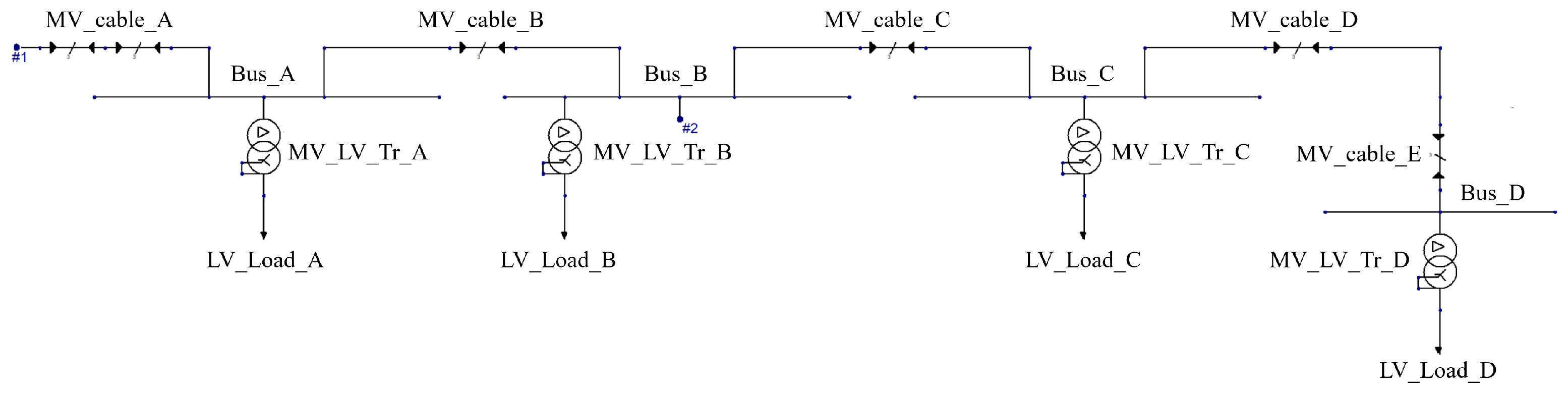
3.2. Network Model
3.3. Energy Storage Systems
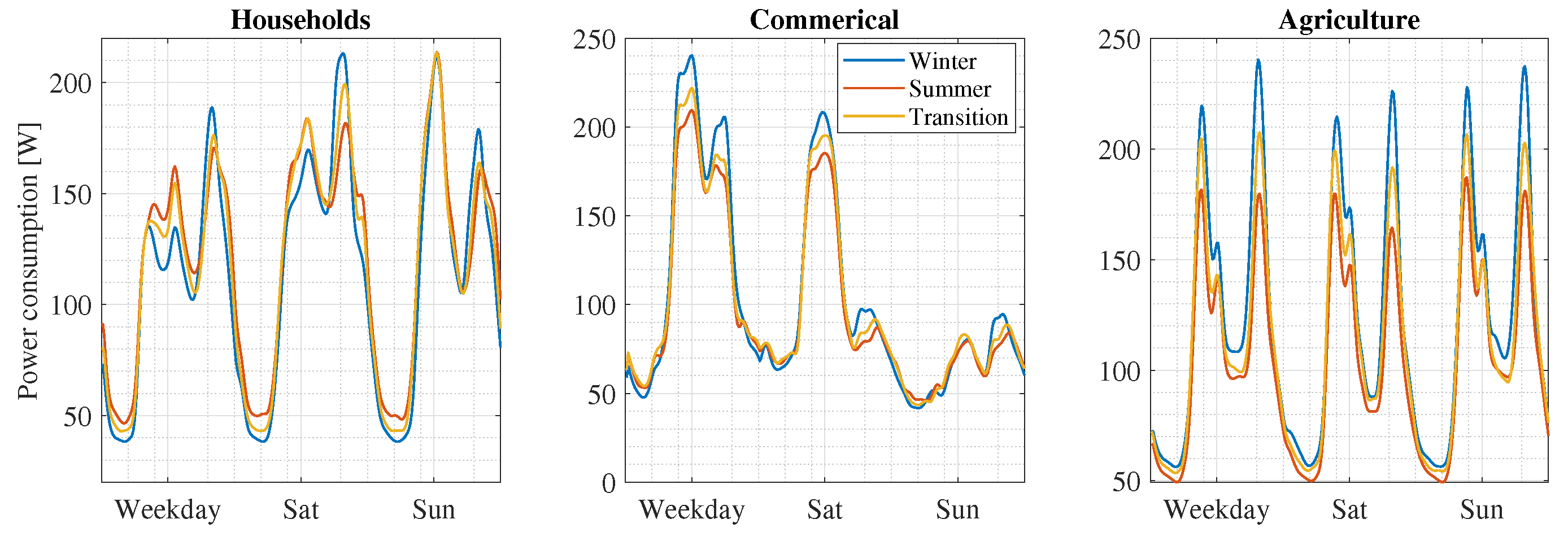
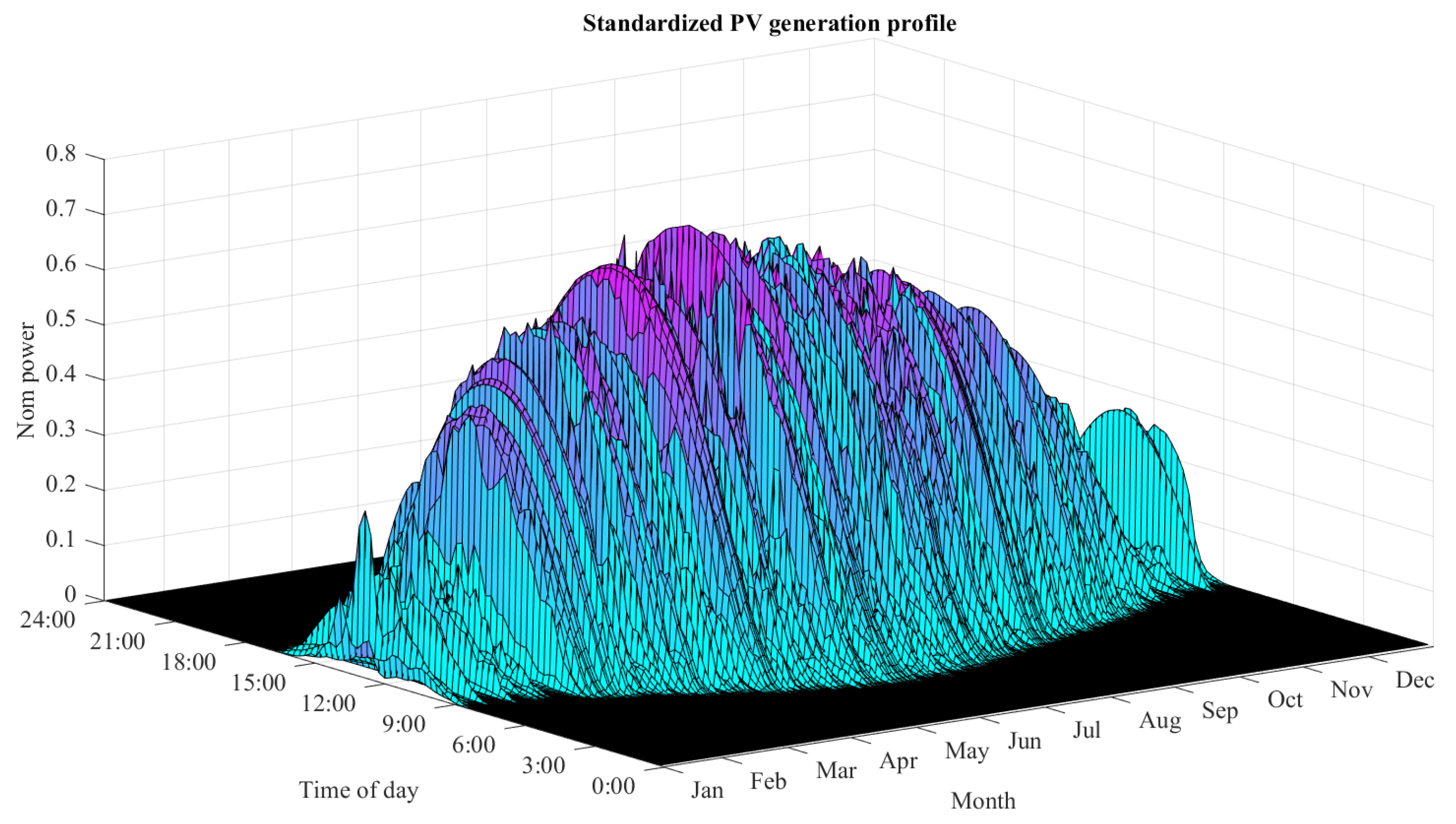
3.4. Load Modeling
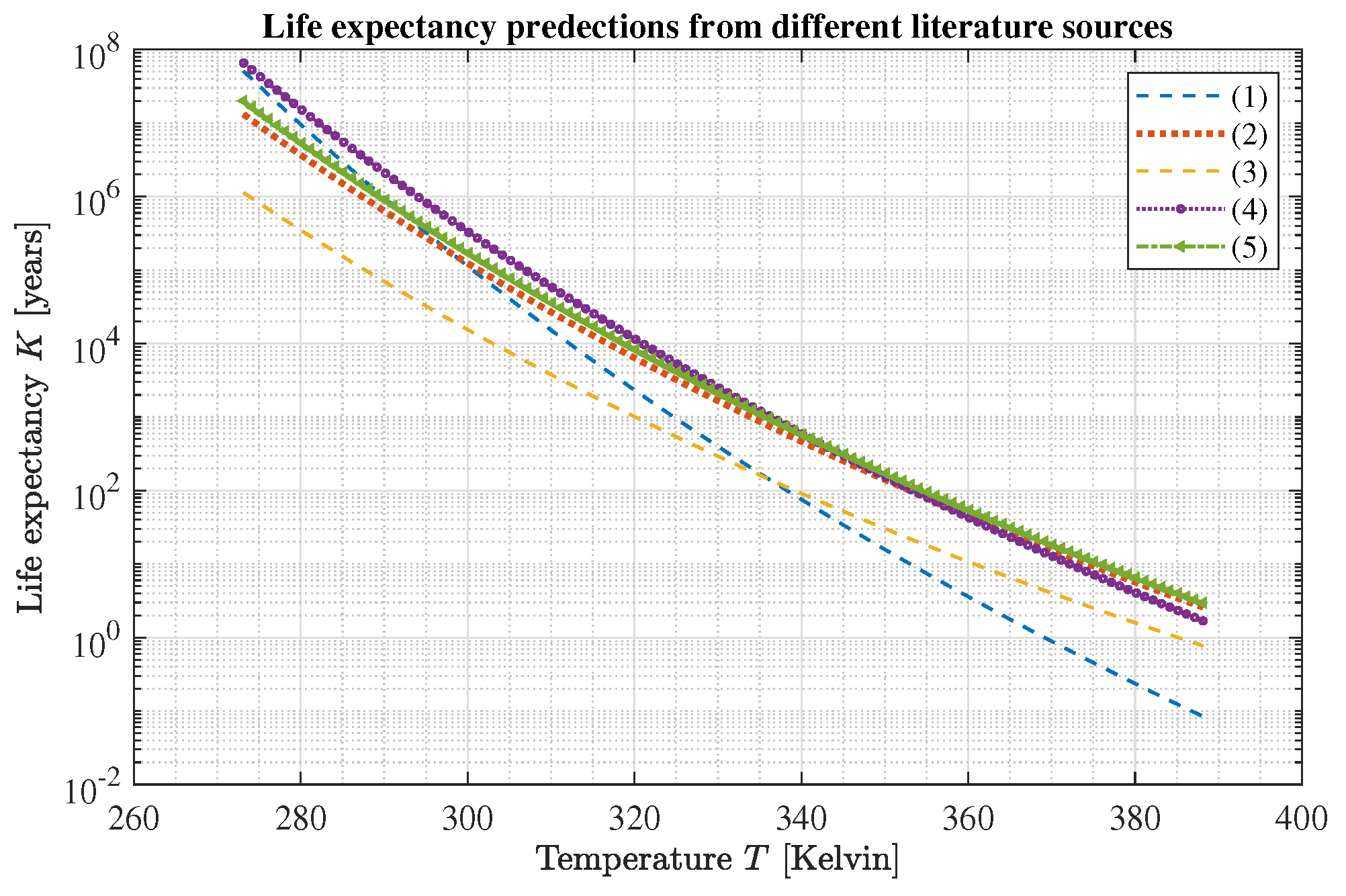
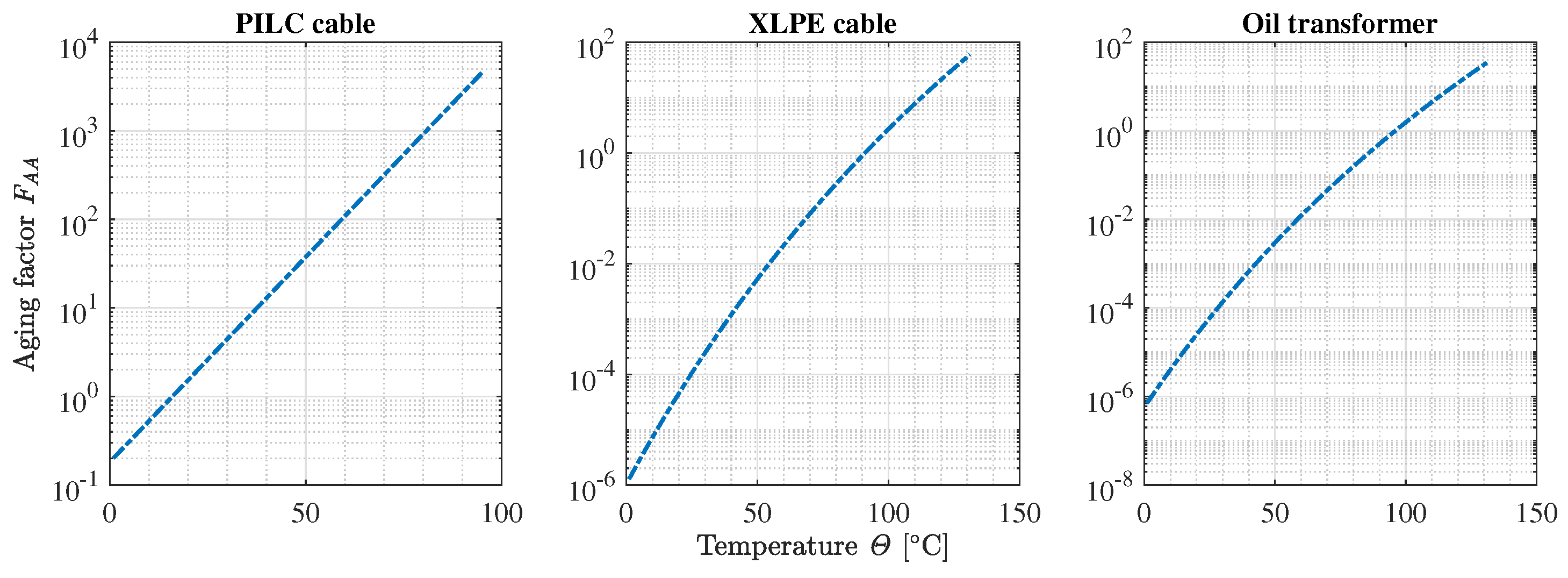
3.5. Thermal Aging of Operating Equipment
4. Conclusions
5. Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohajan, H. The Second Industrial Revolution has brought Brought Modern Social and Economic Developments. J. Sci. Humanit. 2020, 6, 7. [Google Scholar]
- The European Green Deal; European Union: Brussels, Belgium, 2019.
- Climate Action Plan for 2050 Principles and Goals of the German Government’s Climate Policy; Federal Ministry for the Environment, Nature Conservation, Building and Nuclear Safety: Berlin, Germany, 2016.
- Bundesnetzagentur, Genehmigung des Szenarienrahmens 2023–2037/2045. Available online: https://www.netzentwicklungsplan.de/sites/default/files/2023-01/Szenariorahmen_2037_Genehmigung.pdf (accessed on 13 April 2023).
- Mohajan, H.; Schmietendorf, K.; Peinke, J.; Kamps, O. The impact of turbulent renewable energy production on power grid stability and quality. Eur. Phys. J. B 2017, 90, 222. [Google Scholar]
- Tavakoli, A.; Saha, S.; Arif, M.T.; Haque, M.E.; Mendis, N.; Oo, A.M.T. Impacts of grid integration of solar PV and electric vehicle on grid stability, power quality and energy economics: A review. IET Energy Syst. Integr. 2020, 2, 243–260. [Google Scholar] [CrossRef]
- DIN IEC 60216-7; Elektroisolierstoffe-Eigenschaften Hinsichtlich des Thermischen Langzeitverhaltens. IEC: Geneva, Switzerland, 2015.
- Gellings, C.W. The concept of demand-side management for electric utilities. Proc. IEEE 1985, 73, 1468–1470. [Google Scholar] [CrossRef]
- Model Project ESM-Regio: Optimization of the Energy System via Sector Coupling, Model Project for the Energy System in a Sample Bavarian Region. Available online: https://www.bayern-innovativ.de/de/seite/esm-regio-en (accessed on 14 April 2023).
- Daniel Scharrer, Reinhard German, Beiratstreffen ESM-Regio. Available online: https://www.bayern-innovativ.de/uwao-api/faila/files/bypath/pdf-dokumente/cluster-energietechnik/esm-regio/2022-04-06-zwischenberichte-beiratstreffen.pdf?mod=2022-05-18T07:30:14.637Z&published=false (accessed on 14 April 2023).
- Schwab, A.J. Elektro-Energiesysteme, 2. Auflage; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-92226-1. [Google Scholar]
- Schäfer, K.F. Netzberechnung; Springer: Wiesbaden, Germany, 2020; ISBN 978-3-658-26732-2. [Google Scholar]
- Albadi, M. ‘Power Flow Analysis’, Computational Models in Engineering; IntechOpen: London, UK, 2020. [Google Scholar]
- Risi, B.-G.; Riganti-Fulginei, F.; Laudani, A. Modern Techniques for the Optimal Power Flow Problem: State of the Art. Energies 2022, 15, 6387. [Google Scholar] [CrossRef]
- Coutinho de Oliveira, C.; Bonini Neto, A.; Alves, D.A.; Minussi, C.R.; Castro, C.A. Alternative Current Injection Newton and Fast Decoupled Power Flow. Energies 2023, 16, 2548. [Google Scholar] [CrossRef]
- Varghese, J.P.; Sundaramoorthy, K.; Sankaran, A. Development and Validation of a Load Flow Based Scheme for Optimum Placing and Quantifying of Distributed Generation for Alleviation of Congestion in Interconnected Power Systems. Energies 2023, 16, 2536. [Google Scholar] [CrossRef]
- Mišurović, F.; Mujović, S. Numerical Probabilistic Load Flow Analysis in Modern Power Systems with Intermittent Energy Sources. Energies 2022, 15, 2038. [Google Scholar] [CrossRef]
- Blenk, T.; Weindl, C. Characteristics and Advantages of a State-Space Orientated Calculation in Regenerative Energy Systems. In Proceedings of the 2022 International Conference on Diagnostics in Electrical Engineering (Diagnostika), Pilsen, Czech Republic, 6 September 2022. [Google Scholar]
- Luc VAN NUFFEL, Sector Coupling: How Can It Be Enhanced in the EU to Foster Grid Stability and Decarbonize. Available online: https://www.europarl.europa.eu/RegData/etudes/STUD/2018/626091/IPOL_STU(2018)626091_EN.pdf (accessed on 14 April 2023).
- Anteil der Elektroautos Am Bestand der Personenkraftwagen in Deutschland von 2013 Bis 2023, KBA. 2023. Available online: https://de.statista.com/statistik/daten/studie/784986/umfrage/marktanteil-von-elektrofahrzeugen-in-deutschland/ (accessed on 14 April 2023).
- Mwasilu, F.; Justo, J.J.; Kim, E.K.; Do, T.D.; Jung, J.W. Electric vehicles and smart grid interaction: A review on vehicle to grid and renewable energy sources integration. Renew. Sustain. Energy Rev. 2014, 34, 501–516. [Google Scholar] [CrossRef]
- Ravi, S.S.; Aziz, M. Utilization of Electric Vehicles for Vehicle-to-Grid Services: Progress and Perspectives. Energies 2022, 15, 589. [Google Scholar] [CrossRef]
- Agentur Für Erneuerbare Energien, Endenergieverbrauch in Deutschland im Jahr 2019 Nach Strom, Wärme und Verkehr. Available online: https://www.unendlich-viel-energie.de/media/image/54221.AEE_Endenergieverbrauch_Strom_Waerme_Kraftstoffe_2019.jpg (accessed on 17 April 2023).
- AGEB Infographik Endenergieverbrauch Deutschland. Available online: https://ag-energiebilanzen.de/wp-content/uploads/2023/01/AGEB_Infografik_07_2023_Anwendungsbilanzen_2021.pdf (accessed on 17 April 2023).
- AEE Endenergieverbrauch füR Wärme und Kälte in Deutschland (Nach Energieträger) Grafik. Available online: https://www.unendlich-viel-energie.de/mediathek/grafiken/in-der-waermeversorgung-dominiert-in-deutschland-erdgas-mit-einem-anteil-von-fast-43-prozent-im-jahr-2020 (accessed on 17 April 2023).
- BMWk: Aktuelle Informationen. Erneuerbare Energien im Jahr 2022. Available online: https://www.erneuerbare-energien.de/EE/Navigation/DE/Service/Erneuerbare_Energien_in_Zahlen/Aktuelle-Informationen/aktuelle-informationen.html (accessed on 17 April 2023).
- BDEW, Beheizungsstruktur des Wohnungsbestandes in Deutschland, Anteile der Genutzten Energieträger, July 2022. Available online: https://www.bdew.de/service/daten-und-grafiken/beheizungsstruktur-wohnungsbestand/#:~:text=Seit%201995%20hat%20sich%20die,um%202%20%25%2DPunkte%20zu (accessed on 17 April 2023).
- Umweltbundesamt, Arbeitsgemeinschaft Energiebilanzen, KWK-Nettostromerzeugung Nach Energieträngern. 2022. Available online: https://www.umweltbundesamt.de/daten/energie/kraft-waerme-kopplung-kwk#kwk-anlagen (accessed on 17 April 2023).
- BDEW, BDEW-Gaspreisanalyse Januar 2023, Haushalte. 2023. Available online: https://www.bdew.de/media/original_images/2023/02/09/bdew-gaspreisanalyse_januar-2023.pdf (accessed on 17 April 2023).
- Bundesregierung Energiesicherheit: Klimafreundliche und Krisensichere Energieversorgung. Available online: https://www.bundesregierung.de/breg-de/themen/klimaschutz/energieversorgung-sicherheit-2040098 (accessed on 17 April 2023).
- BMWK, Dritter Fortschrittsbericht Energiesicherheit, Berlin. 2022. Available online: https://www.bmwk.de/Redaktion/DE/Downloads/Energie/20220720_dritter-fortschrittsbericht_energiesicherheit.pdf?__blob=publicationFile&v=12 (accessed on 17 April 2023).
- Zapf, M. Stromspeicher und Power-to-Gas im Deutschen Energiesystem; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2017. [Google Scholar]
- Clegg, S.; Mancarella, P. Storing renewables in the gas network: Modelling of power-to-gas seasonal storage flexibility in low-carbon power systems. IET Gener. Transm. Distrib. 2016, 10, 566–575. [Google Scholar] [CrossRef]
- Herz, G.; Rix, C.; Jacobasch, E.; Müller, N.; Reichelt, E.; Jahn, M.; Michaelis, A. Economic assessment of Power-to-Liquid processes—Influence of electrolysis technology and operating conditions. Appl. Energy 2021, 292, 116655. [Google Scholar] [CrossRef]
- Stiftung Klimaneutralität, Agora Energiewende, Agora Verkehrswende, BDI, Dena, BMWK, Ariadna-Kopernikus-Projekte, Vergleich der “Big” Klimaneutralitätsszenarien. 2022. Available online: https://ariadneprojekt.de/media/2022/03/2022-03-16-Big5-Szenarienvergleich_final.pdf (accessed on 17 April 2023).
- Braun, A. Dynamische Systeme Modellierung Mit den Methoden der Laplace-Transformation; Springer: Wiesbaden, Germany, 2019; pp. 103–104. [Google Scholar]
- Rowell, D. 2 . 14 Analysis and Design of Feedback Control Systems State-Space Representation of LTI Systems. 2002. Available online: http://web.mit.edu/2.14/www/Handouts/StateSpace.pdf (accessed on 16 June 2023).
- Blenk, T.; Weindl, C. Fundamentals of state-space based load flow calculation of modern energy systems. Energies, 2023; in press. [Google Scholar]
- Stadtwerke Bayreuth, Veröffentlichung Netzrelevanter Daten STROM Nach dem Energiewirtschaftsgesetz (EnWG). 2021. Available online: https://www.stadtwerke-bayreuth.de/fileadmin/user_upload/netz/Netzinformation/strom-netzrelevanter-daten.pdf (accessed on 17 April 2023).
- BVES, BVES Branchenanalyse 2022, Entwicklung und Perspektiven der Energiespeicherbranche in Deutschland, Berlin. 2022. Available online: https://www.bves.de/wp-content/uploads/2022/12/BVES-Branchenanalyse-2022_v1.pdf (accessed on 15 March 2023).
- Rasmus, L.; Joakim, W.; Daniel, N.; Jenny, P. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef]
- Figgener, J.; Stenzel, P.; Kairies, K.-P.; Linßen, J.; Haberschusz, D.; Wessels, O.; Robinius, M.; Stolten, D.; Sauer, D.U. The development of stationary battery storage systems in Germany—Status 2020. J. Energy Storage 2021, 33, 101982. [Google Scholar] [CrossRef]
- Thakkar, R.R. Electrical equivalent circuit models of lithium-ion battery. Manag. Appl. Energy Storage Devices 2022. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Analog Devices, Coulomb Counting. Available online: https://www.analog.com/media/en/technical-documentation/technical-articles/a-closer-look-at-state-of-charge-and-state-health-estimation-techniques.pdf (accessed on 15 March 2023).
- Meier, H.; Fünfgeld, C.; Adam, T.; Schieferdecker, B. Repräsentative VDEW-Lastprofile. 1999. Available online: https://www.bdew.de/media/documents/1999_Repraesentative-VDEW-Lastprofile.pdf (accessed on 17 April 2023).
- Verordnung üBer den Zugang zu Elektrizitätsversorgungsnetzen (Stromnetzzugangsverordnung—StromNZV). 2005. Available online: https://www.gesetze-im-internet.de/stromnzv/BJNR224300005.html (accessed on 17 April 2023).
- Bajenescu, T. Zuverlässige Bauelemente Für Elektronische Systeme: Fehlerphysik, Ausfallmechanismen, Prüffeldpraxis, Qualitätsüberwachung; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2020. [Google Scholar] [CrossRef]
- DIN EN 60505 VDE 0302-1; Bewertung und Kennzeichnung von elektrischen Isoliersystemen. IEC: Geneva, Switzerland, 2012.
- Hedir, A.; Slimani, F.; Moudoud, M.; Lamrous, O.; Durmus, A.; Fofana, I. Effects of electrical aging on the structural and physicochemical properties of crosslinked polyethylene (XLPE) cable insulation material. Eng. Res. Express 2022, 4, 015038. [Google Scholar] [CrossRef]
- Li, W.; Zheng, W.; Ren, L.; Li, H.; Zhao, X.; Wang, C.; Li, J. A Comparative Study on the Insulation Ageing of 10 kV XLPE Cable via Accelerated Electrical Test and Accelerated Water Tree Test. J. Electr. Eng. Technol. 2022, 17, 475–484. [Google Scholar] [CrossRef]
- Mecheri, Y.; Bouazabia, S.; Boubakeur, A.; Lallouani, M. Effect of thermal Ageing on the Properties of XLPE as an Insulating Material for HV Cables. In Proceedings of the International Electrical Insulation Conference; IET Centre: Birmingham, UK, 2013. [Google Scholar]
- Lawson, W.G.; Simmons, M.A.; Gale, P.S. Thermal Ageing of Cellulose Paper Insulation. IEEE Trans. Electr. Insul. 1977, EI-12, 61–66. [Google Scholar] [CrossRef]
- Alghamdi, A.S.; Desuqi, R.K. A study of expected lifetime of XLPE insulation cables working at elevated temperatures by applying accelerated thermal ageing. Heliyon 2020, 6, e03120. [Google Scholar] [CrossRef]
- Choudhary, M.; Shafiq, M.; Kiitam, I.; Hussain, A.; Palu, I.; Taklaja, P. A Review of Aging Models for Electrical Insulation in Power Cables. Energies 2022, 15, 3408. [Google Scholar] [CrossRef]
- Montsinger, V.M. Loading Transformers By Temperature. Trans. Am. Inst. Electr. Eng. 1930, 49, 776–790. [Google Scholar] [CrossRef]
- DIN EN 50160; Merkmale der Spannung in öffentlichen Elektrizitätsversorgungsnetzen. IEC: Geneva, Switzerland, 2020.
- IEEE Std C57.91-2011; IEEE Guide for Loading Mineral-Oil-Immersed Transformers and Step-Voltage Regulators. IEEE: Toulouse, France, 2012; pp. 1–123, Revision of IEEE Std C57.91-1995. [CrossRef]
- DIN IEC 60076-7; Leistungstransformatoren: Leitfaden für die Belastung von mineralölgefüllten Transformatoren. IEC: Geneva, Switzerland, 2023. IEC: Geneva, Switzerland, 2023.
- Zapf, M.; Blenk, T.; Müller, A.-C.; Pengg, H.; Mladenovic, I.; Weindl, C. Lifetime Assessment of PILC Cables with Regard to Thermal Aging Based on a Medium Voltage Distribution Network Benchmark and Representative Load Scenarios in the Course of the Expansion of Distributed Energy Resources. Energies 2021, 14, 494. [Google Scholar] [CrossRef]
- Huifei, J. Application of Dielectric Loss Measurements for Life Consumption and Future Life Estimation Modeling of Oil-Impregnated Paper Insulation in HV Power Cables. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- DIN EN 60811-401; Kabel, isolierte Leitungen und Glasfaserkabel - Prüfverfahren für nichtmetallene Werkstoffe. IEC: Geneva, Switzerland, 2012.
- Lin, J.; Cai, L. Research on the thermal aging life prediction of XLPE cable. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1570, p. 012050. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Lan, R.; Wei, Y.; Nie, Y.; Li, S.; Lei, Q. The lifetime prediction and insulation failure mechanism of XLPE for high voltage cable. IEEE Trans. Dielectr. Electr. Insul. 2022, 30, 761–768. [Google Scholar] [CrossRef]
- Sun, C.; Wang, C. Assessment Study of Aging Life for Typical Defects in XLPE Cable Joints. In Proceedings of the 2020 3rd International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE), Shenzhen, China, 24–26 April 2020; pp. 772–777. [Google Scholar] [CrossRef]
- Mutepe, R.M.; Thango, B.A.; Bokoro, P.N. Practical Study on the Lifetime Prediction of High Voltage Cross-Linked Polyethylene Cable (XLPE) using Thermal Aging. In Proceedings of the 2023 31st Southern African Universities Power Engineering Conference (SAUPEC), Johannesburg, South Africa, 24–26 January 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Neier, T.; Knauel, J.; Bawart, M.; Antipov, D.; Kim, S. A statistical method for stastical appraisal of the power cable conditions based on the TD and PD diagsnostics result. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2019; Volume 124, p. 02014. [Google Scholar] [CrossRef]
- Bottler, S.; Blenk, T.; Weindl, C. An approach for determining load-dependent monetary assessment factors for PILC and XLPE cables within a load flow simulation. In Proceedings of the 2022 Global Energy Conference (GEC), Batman, Turkey, 26–29 October 2022; pp. 58–64. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bottler, S.; Weindl, C. State-Space Load Flow Calculation of an Energy System with Sector-Coupling Technologies. Energies 2023, 16, 4803. https://doi.org/10.3390/en16124803
Bottler S, Weindl C. State-Space Load Flow Calculation of an Energy System with Sector-Coupling Technologies. Energies. 2023; 16(12):4803. https://doi.org/10.3390/en16124803
Chicago/Turabian StyleBottler, Sebastian, and Christian Weindl. 2023. "State-Space Load Flow Calculation of an Energy System with Sector-Coupling Technologies" Energies 16, no. 12: 4803. https://doi.org/10.3390/en16124803
APA StyleBottler, S., & Weindl, C. (2023). State-Space Load Flow Calculation of an Energy System with Sector-Coupling Technologies. Energies, 16(12), 4803. https://doi.org/10.3390/en16124803







