The Dynamics of US Gasoline Demand and Its Prediction: An Extended Dynamic Model Averaging Approach
Abstract
1. Introduction
2. Research Methodology
- Step 1: Choose a curve fitting function. Equations (16) and (18) may be combined to create the following function:whereas recursive prediction operates using predictive distributions in the following manner:
- Step 2. Arrange the greatest quantity of repetitions (MNC), the total number of bees (N), and LIMIT.
- Step 3. Create random numbers for all bees for whom the optimization procedure begins with a preliminary estimate of their food supply, , source using Equation (21).where SN represents the food supply in total. and represent the top and lower limits of the design variable, while is a random real value between zero and one.
- Step 4. Calculate the objected function for all bees using Equation (19).
- Step 5. Select fifty percent of the finest feeding places and appoint the bee who frequented these areas as the engaged bee.
- Step 6. Set .
- Step 7. Traverse each source of food
- (a)
- Create new options for an employed bee using the following equation, where a new candidate food source () is identified using two prior food source locations remembered by an employed bee () and a randomly chosen neighborhood of a food source ():
- (b)
- The old superscript displays the value of the preceding iteration’s design variable, but the new superscript displays existing design variables, where is a random positive integer between −1 and 1. is a number that is chosen at random and is not equal to s.
- (c)
- Select the ideal dietary intake for each food source. The new place becomes the food source if there are more food sources there than there were at the previous location; otherwise, the previous location remains the food source.
- Step 8. Estimate probability () using the following equation:where represents a measure of the solution’s fitness i, as determined by the employed bee. This corresponds to the nectar content in the food supply at location i.
- Step 9. Traverse each source of food .
- (a)
- Employ unemployed bees.
- (b)
- Utilizing Equation (21), develop novel employment strategies for jobless bees.
- (c)
- Check to see whether the amount of food sources has improved. If there is a considerable change, the observer bee will be promoted to the hired bee position; if there is no change, the candidate food source that the observer bee visited will not be selected.
- Step 10. When the best food spot has not improved after a certain number of cycles (LIMIT), the hired bee switches to scout mode and uses Equation (20) to look for a new food source.
- Step 11. = 1 + cycle.
- Step 12. Stop the operation if the cycle is ; otherwise, go on to Step.
3. The Estimated Model and Data
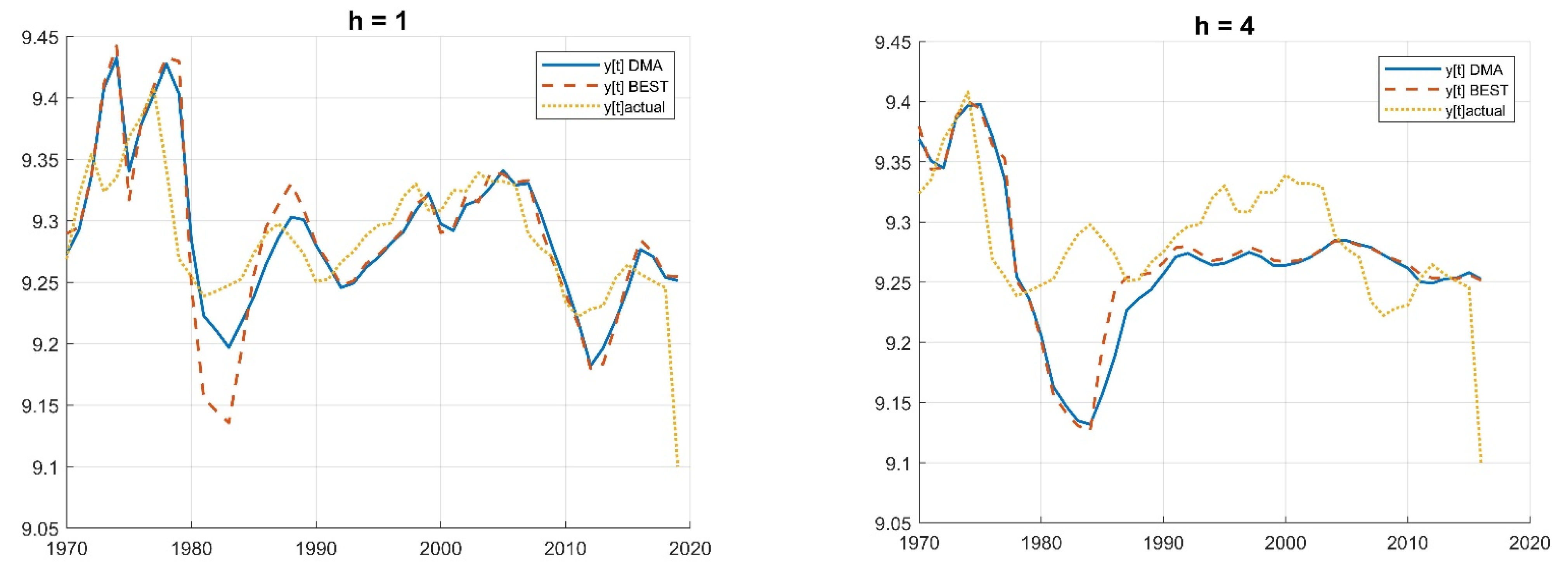
4. Results
5. Conclusions and Implications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- EIA. Annual Energy Outlook (AEO) Retrospective Review: Evaluation of AEO 2020 and Previous Reference Case Projections. Anal. Proj. U.S. Energy Inf. Adm. 2020, 92010, 1–15. [Google Scholar]
- McCarthy, P.S. Market Price and Income Elasticities of New Vehicle Demands. Rev. Econ. Stat. 1996, 78, 543. [Google Scholar] [CrossRef]
- Shen, C.; Linn, J. The Effect of Income on Vehicle Demand: Evidence from China’S New Vehicle Market; Resources for the Future: Washington, DC, USA, 2021. [Google Scholar]
- Dargay, J.; Gately, D.; Sommer, M. Vehicle ownership and income growth, worldwide: 1960–2030. Energy J. 2007, 28, 143–170. [Google Scholar] [CrossRef]
- Huo, H.; Wang, M. Modeling Future Vehicle Sales and Stock in China. Energy Policy 2012, 43, 17–29. [Google Scholar] [CrossRef]
- Oladosu, G. An Almost Ideal Demand System Model of Household Vehicle Fuel Expenditure Allocation in the United States. Energy J. 2003, 24, 1–21. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, S. Forecasting Charging Demand of Electric Vehicles Using Time-Series Models. Energies 2021, 14, 1487. [Google Scholar] [CrossRef]
- Fouquet, R. Trends in Income and Price Elasticities of Transport Demand (1850-2010). Energy Policy 2012, 50, 62–71. [Google Scholar] [CrossRef]
- Graham, D.J.; Glaister, S. Road Traffic Demand Elasticity Estimates: A Review. Transp. Rev. 2004, 24, 261–274. [Google Scholar] [CrossRef]
- Bento, A.M.; Goulder, L.H.; Jacobsen, M.R.; Von Haefen, R.H. Distributional and Efficiency Impacts of Increased US Gasoline Taxes. Am. Econ. Rev. 2009, 99, 667–699. [Google Scholar] [CrossRef]
- Goetzke, F.; Vance, C. An Increasing Gasoline Price Elasticity in the United States? Energy Econ. 2021, 95, 104982. [Google Scholar] [CrossRef]
- Dimitropoulos, A.; Oueslati, W.; Sintek, C. The Rebound Effect in Road Transport: A Meta-Analysis of Empirical Studies. Energy Econ. 2018, 75, 163–179. [Google Scholar] [CrossRef]
- Ghysels, E.; Plazzi, A.; Valkanov, R.; Torous, W. Forecasting Real Estate Prices. Handb. Econ. Forecast. 2013, 2, 509–580. [Google Scholar] [CrossRef]
- Plakandaras, V.; Gupta, R.; Gogas, P.; Papadimitriou, T. Forecasting the U.S. Real House Price Index. Econ. Model. 2015, 45, 259–267. [Google Scholar] [CrossRef]
- Próchniak, M.; Witkowski, B. Time Stability of the Beta Convergence among EU Countries: Bayesian Model Averaging Perspective. Econ. Model. 2013, 30, 322–333. [Google Scholar] [CrossRef]
- Man, G. Competition and the Growth of Nations: International Evidence from Bayesian Model Averaging. Econ. Model. 2015, 51, 491–501. [Google Scholar] [CrossRef]
- Raftery, A.E.; Kárný, M.; Ettler, P. Online Prediction under Model Uncertainty via Dynamic Model Averaging: Application to a Cold Rolling Mill. Technometrics 2010, 52, 52–66. [Google Scholar] [CrossRef]
- Koop, G.; Korobilis, D. Forecasting Inflation Using Dynamic Model Averaging. Int. Econ. Rev. 2012, 53, 867–886. [Google Scholar] [CrossRef]
- Koop, G.; Korobilis, D. UK Macroeconomic Forecasting with Many Predictors: Which Models Forecast Best and When Do They Do So? Econ. Model. 2011, 28, 2307–2318. [Google Scholar] [CrossRef]
- Del Negro, M.; Primiceri, G.E. Time Varying Structural Vector Autoregressions and Monetary Policy: A Corrigendum. Rev. Econ. Stud. 2010, 82, 1342–1345. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Timmermann, A. A Recursive Modelling Approach to Predicting UK Stock Returns. Econ. J. 2000, 110, 159–191. [Google Scholar] [CrossRef]
- Bork, L.; Møller, S.V. Forecasting House Prices in the 50 States Using Dynamic Model Averaging and Dynamic Model Selection. Int. J. Forecast. 2015, 31, 63–78. [Google Scholar] [CrossRef]
- Wei, Y.; Cao, Y. Forecasting House Prices Using Dynamic Model Averaging Approach: Evidence from China. Econ. Model. 2017, 61, 147–155. [Google Scholar] [CrossRef]
- Dong, X.; Yoon, S.M. What Global Economic Factors Drive Emerging Asian Stock Market Returns? Evidence from a Dynamic Model Averaging Approach. Econ. Model. 2019, 77, 204–215. [Google Scholar] [CrossRef]
- Naser, H.; Alaali, F. Can Oil Prices Help Predict US Stock Market Returns? Evidence Using a Dynamic Model Averaging (DMA) Approach. Empir. Econ. 2018, 55, 1757–1777. [Google Scholar] [CrossRef]
- Drachal, K. Forecasting Spot Oil Price in a Dynamic Model Averaging Framework—Have the Determinants Changed over Time? Energy Econ. 2016, 60, 35–46. [Google Scholar] [CrossRef]
- Byrne, J.P.; Cao, S.; Korobilis, D. Forecasting the Term Structure of Government Bond Yields in Unstable Environments. J. Empir. Financ. 2017, 44, 209–225. [Google Scholar] [CrossRef]
- Beckmann, J.; Koop, G.; Korobilis, D.; Schüssler, R.A. Exchange Rate Predictability and Dynamic Bayesian Learning. J. Appl. Econom. 2020, 35, 410–421. [Google Scholar] [CrossRef]
- Byrne, J.P.; Korobilis, D.; Ribeiro, P.J. On the Sources of Uncertainty in Exchange Rate Predictability. Int. Econ. Rev. 2018, 59, 329–357. [Google Scholar] [CrossRef]
- Ma, F.; Liu, J.; Wahab, M.I.M.; Zhang, Y. Forecasting the Aggregate Oil Price Volatility in a Data-Rich Environment. Econ. Model. 2018, 72, 320–332. [Google Scholar] [CrossRef]
- Avramov, D. Stock Return Predictability and Model Uncertainty. J. Financ. Econ. 2002, 64, 423–458. [Google Scholar] [CrossRef]
- Koop, G.; Potter, S. Forecasting in Dynamic Factor Models Using Bayesian Model Averaging. Econom. J. 2004, 7, 550–565. [Google Scholar] [CrossRef]
- Hughes, J.E.; Knittel, C.R.; Sperling, D. Evidence of a Shift in the Short-Run Price Elasticity of Gasoline Demand. Energy J. 2008, 29, 113–134. [Google Scholar] [CrossRef]
- Wadud, Z.; Graham, D.J.; Noland, R.B. Gasoline Demand with Heterogeneity in Household Responses. Energy J. 2010, 31, 47–74. [Google Scholar] [CrossRef]
- Rentziou, A.; Gkritza, K.; Souleyrette, R.R. VMT, Energy Consumption, and GHG Emissions Forecasting for Passenger Transportation. Transp. Res. Part A Policy Pract. 2012, 46, 487–500. [Google Scholar] [CrossRef]
- Lin, C.Y.C.; Prince, L. Gasoline Price Volatility and the Elasticity of Demand for Gasoline. Energy Econ. 2013, 38, 111–117. [Google Scholar] [CrossRef]
- Wang, T.; Chen, C. Impact of Fuel Price on Vehicle Miles Traveled (VMT): Do the Poor Respond in the Same Way as the Rich? Transportation (Amst) 2014, 41, 91–105. [Google Scholar] [CrossRef]
- Dillon, H.S.; Saphores, J.D.; Boarnet, M.G. The Impact of Urban Form and Gasoline Prices on Vehicle Usage: Evidence from the 2009 National Household Travel Survey. Res. Transp. Econ. 2015, 52, 23–33. [Google Scholar] [CrossRef]
- Hymel, K.M.; Small, K.A. The Rebound Effect for Automobile Travel: Asymmetric Response to Price Changes and Novel Features of the 2000s. Energy Econ. 2015, 49, 93–103. [Google Scholar] [CrossRef]
- Levin, L.; Lewis, M.S.; Wolak, F.A. High Frequency Evidence on the Demand for Gasoline. Am. Econ. J. Econ. Policy 2017, 9, 314–347. [Google Scholar] [CrossRef]
- Taiebat, M.; Stolper, S.; Xu, M. Corrigendum to “Forecasting the Impact of Connected and Automated Vehicles on Energy Use: A Microeconomic Study of Induced Travel and Energy Rebound”. Appl. Energy 2019, 256, 297–308. [Google Scholar] [CrossRef]
- Gillingham, K.T. The rebound effect and the proposed rollback of U.S. fuel economy standards. Rev. Environ. Econ. Policy 2020, 14, 136–142. [Google Scholar] [CrossRef]
- Chakraborty, D.; Hardman, S.; Tal, G. Integrating plug-in electric vehicles (PEVs) into household fleets-factors influencing miles traveled by PEV owners in California. Travel Behav. Soc. 2022, 26, 67–83. [Google Scholar] [CrossRef]



| Author | Type | Dep. Variable | Ind. Variable |
|---|---|---|---|
| Hughes et al. [33] | Time series OLS | Fuel demand/capita | Gas price |
| Wadud et al. [34] | RE panel (quarterly) | Fuel demand | Gas price |
| Rentziou et al. [35] | SURE panel model (annual) | State VMT | Gas price |
| Lin & Prince [36] | Dynamic times series | Fuel demand/capita | Gas price |
| Wang & Chen [37] | SEM (daily) | Household VMT | Gas price |
| Dillon et al. [38] | SEM (daily) | Household VMT | Gas price |
| Hymel & Small [39] | Simultaneous equations | State VMT | Fuel cost/mile |
| Levin et al. [40] | FE panel (daily/monthly) | Fuel demand/capita | Gas price |
| Dimitropoulos et al. [12] | Lit. review/meta-analysis | Fuel demand & VMT | Gas price |
| Taiebat et al. [41] | microeconomic model (daily) | Household VMT | Gas price |
| Gillingham [42] | Lit. review/Lit. survey | US VMT | gas price |
| Goetzke & Vance [11] | pooled OLS | Household VMT | Gas price |
| Chakraborty et al. [43] | OLS regression | TOT hh VMT | fuel cost (non-PEV) |
| Variable | Definition | Source |
|---|---|---|
= Motor gasoline total end-use consumption | EIA | |
= Disposable personal income, Billions of Dollars | FRED | |
= Unleaded Regular Gasoline, U.S. City Average Retail Price | EIA | |
= All Motor Vehicles Fuel Efficiency (Miles per Gallon) | EIA | |
= Total Licensed Drivers | FHWA | |
= Total Motor Vehicle Registrations For All Motor Vehicles | FHWA | |
= Public Road Mileage | FHWA |
| Mean | Median | Maximum | Minimum | Std. Dev. | |
|---|---|---|---|---|---|
| 9.252 | 9.269 | 9.408 | 8.995 | 0.095 | |
| 2.587 | 2.857 | 3.970 | 0.737 | 1.006 | |
| 0.048 | 0.152 | 1.293 | −1.191 | 0.783 | |
| 2.708 | 2.797 | 2.901 | 2.477 | 0.158 | |
| −0.462 | −0.401 | −0.359 | −0.727 | 0.112 | |
| −0.381 | −0.290 | −0.173 | −0.889 | 0.208 | |
| 9.655 | 9.655 | 9.888 | 9.453 | 0.142 |
| Prediction Method | MAFE | MSFE | MAFE | MSFE | |||||
|---|---|---|---|---|---|---|---|---|---|
| h = 1 | h = 4 | ||||||||
| DMA-ABC | 0.55 | 3.60 | 1.01 | 0.98 | DMA-ABC | 0.71 | 4.86 | 0.96 | 0.96 |
| DMS-ABC | 0.47 | 3.02 | 0.86 | 0.82 | DMS-ABC | 0.58 | 3.87 | 0.78 | 0.76 |
| DMA = 0.9662; = 0.9449 | 0.53 | 3.60 | 0.98 | 0.98 | DMA = 0.9698; = 0.9556 | 0.71 | 4.85 | 0.95 | 0.96 |
| DMS = 0.9662; = 0.9449 | 0.44 | 3.00 | 0.81 | 0.81 | DMS = 0.9698; = 0.9556 | 0.58 | 3.87 | 0.78 | 0.76 |
| DMA = = 0.99 | 0.54 | 3.65 | 0.99 | 0.99 | DMA = = 0.99 | 0.73 | 5.03 | 0.98 | 0.99 |
| DMS = = 0.99 | 0.45 | 3.04 | 0.82 | 0.83 | DMS = = 0.99 | 0.60 | 3.98 | 0.80 | 0.79 |
| DMA = = 0.95 | 0.55 | 3.57 | 1.01 | 0.97 | DMA = = 0.95 | 0.72 | 4.98 | 0.97 | 0.98 |
| DMS = = 0.95 | 0.46 | 2.99 | 0.85 | 0.81 | DMS = = 0.95 | 0.60 | 3.98 | 0.80 | 0.79 |
| DMA = 0.95; = 0.99 | 0.55 | 3.56 | 1.01 | 0.97 | DMA = 0.95; = 0.99 | 0.72 | 4.95 | 0.97 | 0.98 |
| DMS = 0.95; = 0.99 | 0.46 | 2.99 | 0.85 | 0.81 | DMS = 0.95; = 0.99 | 0.60 | 3.93 | 0.80 | 0.78 |
| DMA = 0.99; = 0.95 | 0.54 | 3.66 | 0.99 | 1.00 | DMA = 0.99; = 0.95 | 0.74 | 5.04 | 0.99 | 0.99 |
| DMS = 0.99; = 0.95 | 0.45 | 3.04 | 0.82 | 0.83 | DMS = 0.99; = 0.95 | 0.60 | 3.98 | 0.80 | 0.79 |
| TVP- BMA ( = 1) | 0.55 | 3.68 | 1.00 | 1.00 | TVP- BMA ( = 1) | 0.75 | 5.08 | 1.00 | 1.00 |
| BMA ( = = 1) | 0.54 | 3.68 | 1.00 | 1.00 | BMA ( = = 1) | 0.75 | 5.07 | 1.00 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamza, S.H.; Li, Q. The Dynamics of US Gasoline Demand and Its Prediction: An Extended Dynamic Model Averaging Approach. Energies 2023, 16, 4795. https://doi.org/10.3390/en16124795
Hamza SH, Li Q. The Dynamics of US Gasoline Demand and Its Prediction: An Extended Dynamic Model Averaging Approach. Energies. 2023; 16(12):4795. https://doi.org/10.3390/en16124795
Chicago/Turabian StyleHamza, Sakar Hasan, and Qingna Li. 2023. "The Dynamics of US Gasoline Demand and Its Prediction: An Extended Dynamic Model Averaging Approach" Energies 16, no. 12: 4795. https://doi.org/10.3390/en16124795
APA StyleHamza, S. H., & Li, Q. (2023). The Dynamics of US Gasoline Demand and Its Prediction: An Extended Dynamic Model Averaging Approach. Energies, 16(12), 4795. https://doi.org/10.3390/en16124795





