On the Remote Calibration of Instrumentation Transformers: Influence of Temperature †
Abstract
1. Introduction
2. Aspects of Metrology as a Context to the Calibration of Instrumentation Transformers
2.1. Different Types of Errors
2.2. Synchrophasor Measurement Uncertainty
2.3. Instrument Transformer Error
3. Principles of Remote Calibration
4. Instrumentation Errors
4.1. IEEE C57.13.5-2008
4.2. IEC 61869
5. Contribution of Temperature to Measurement Uncertainty
5.1. Test Setup
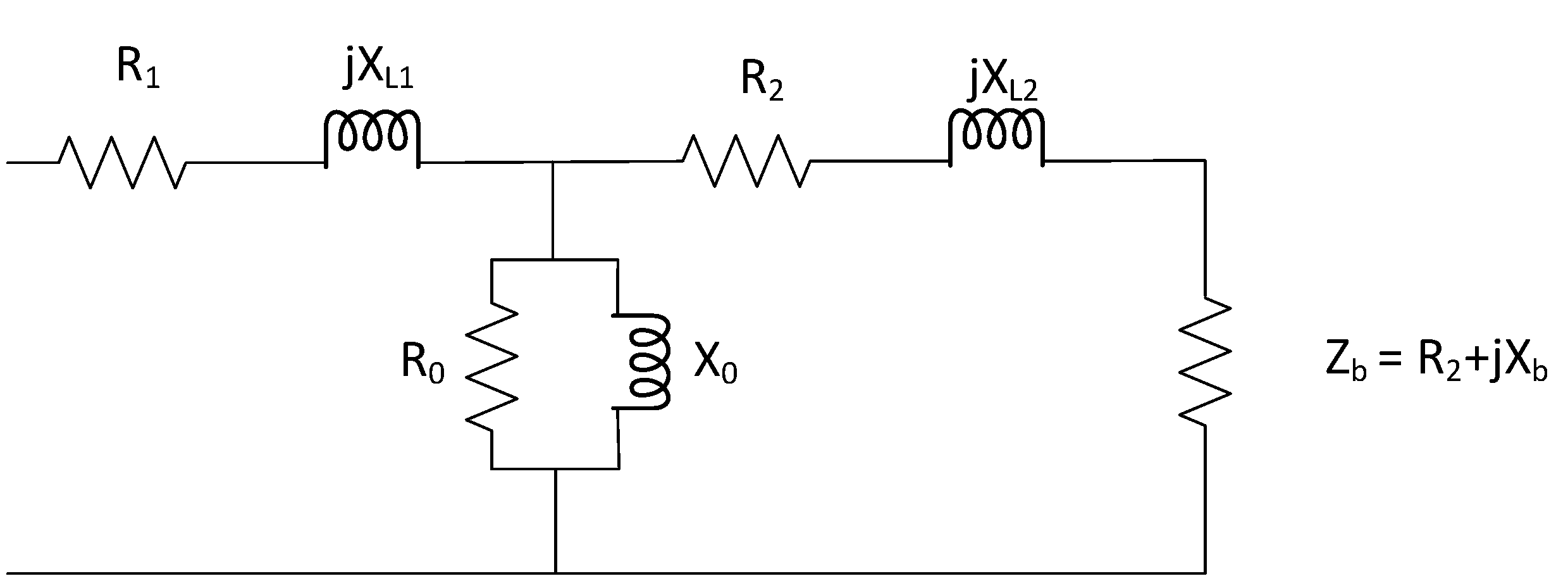
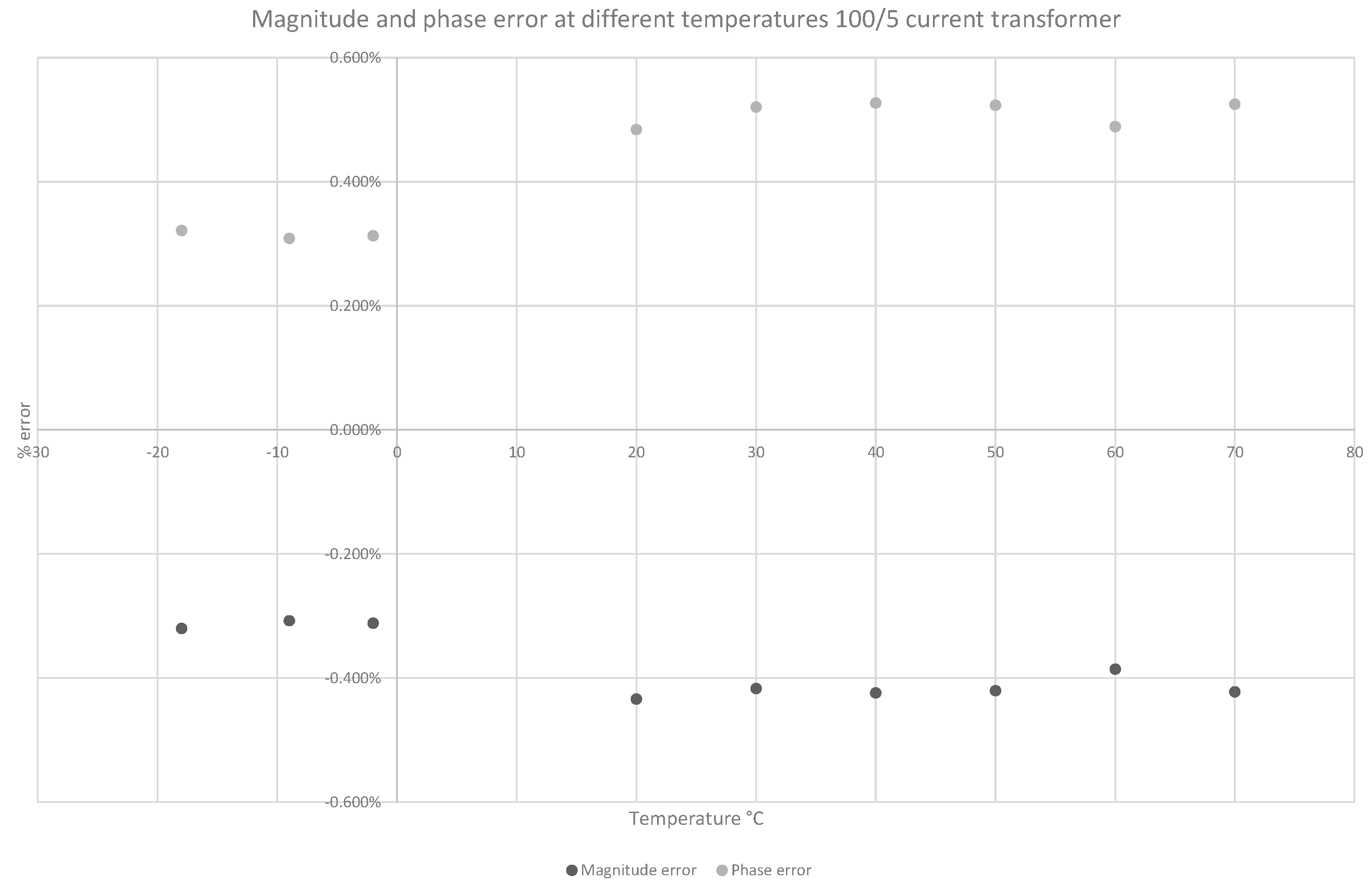
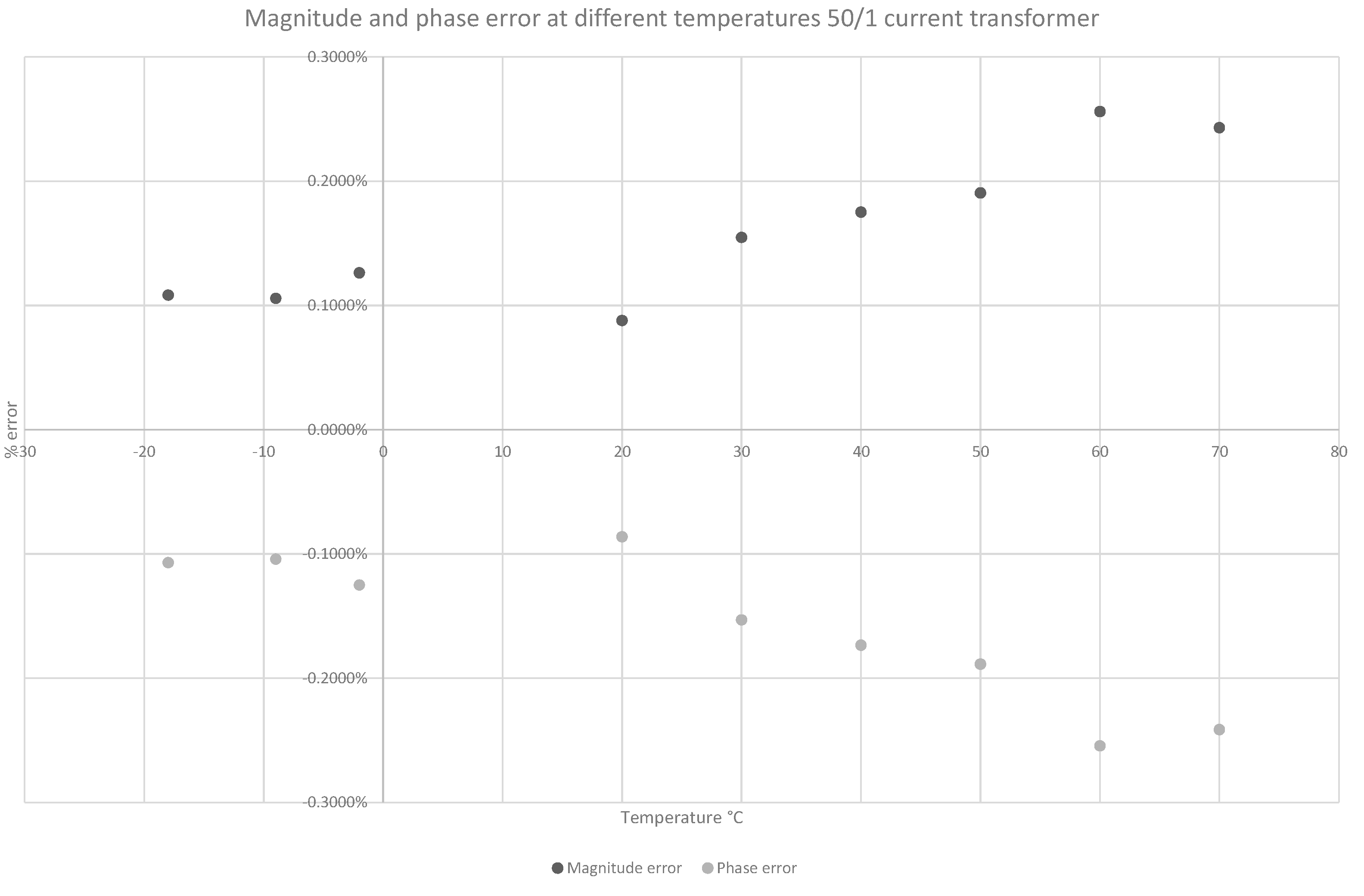
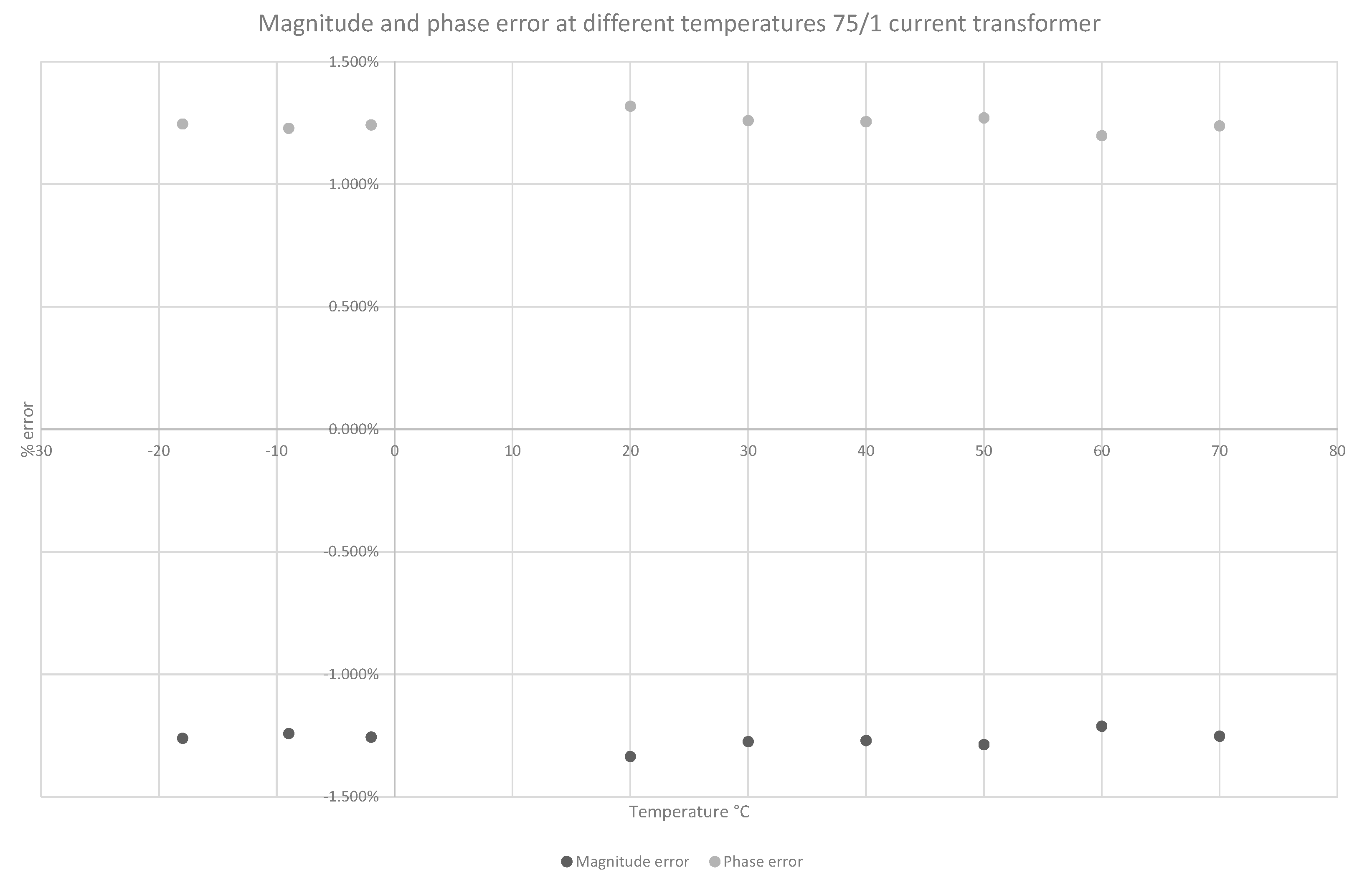
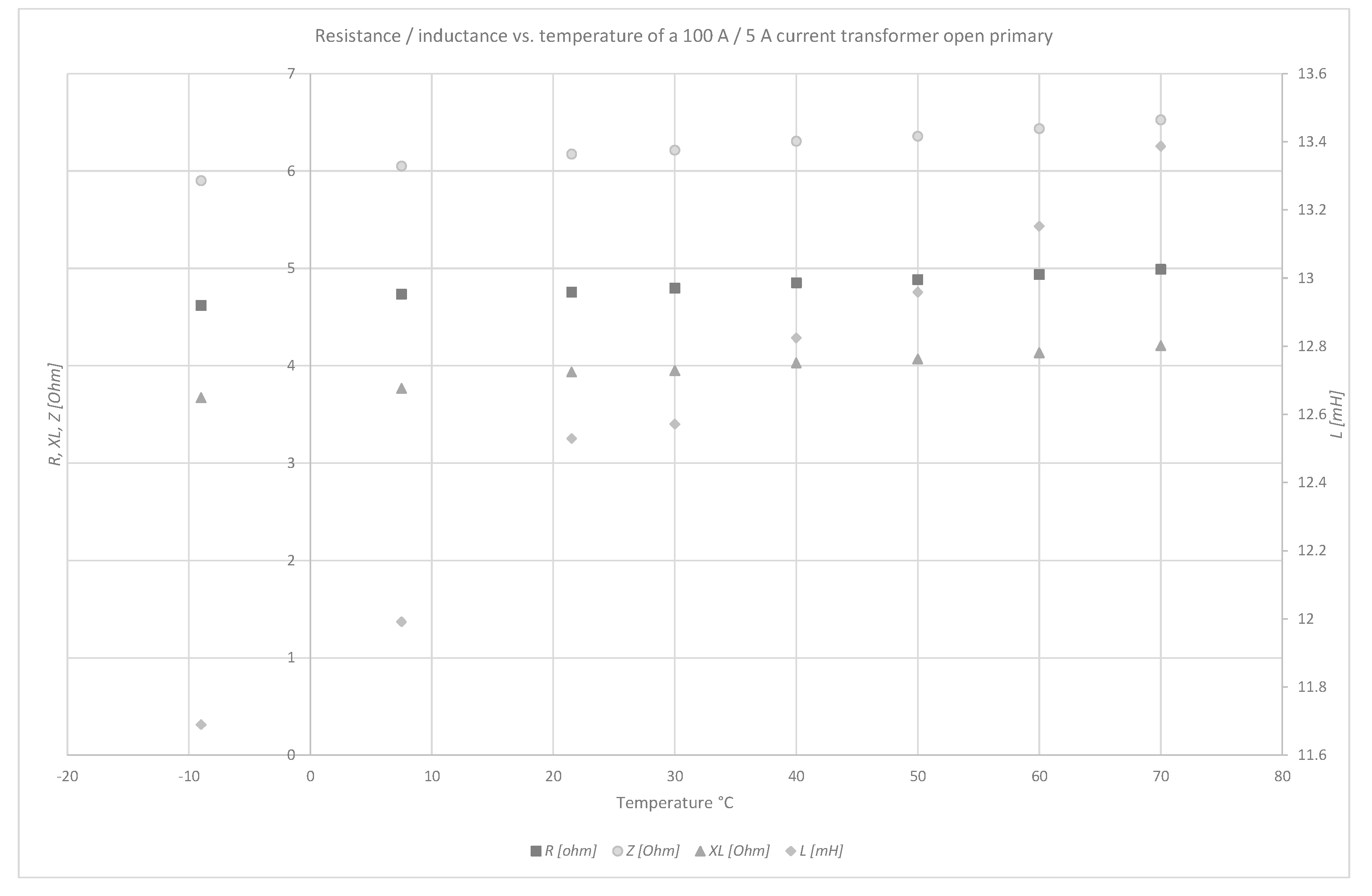
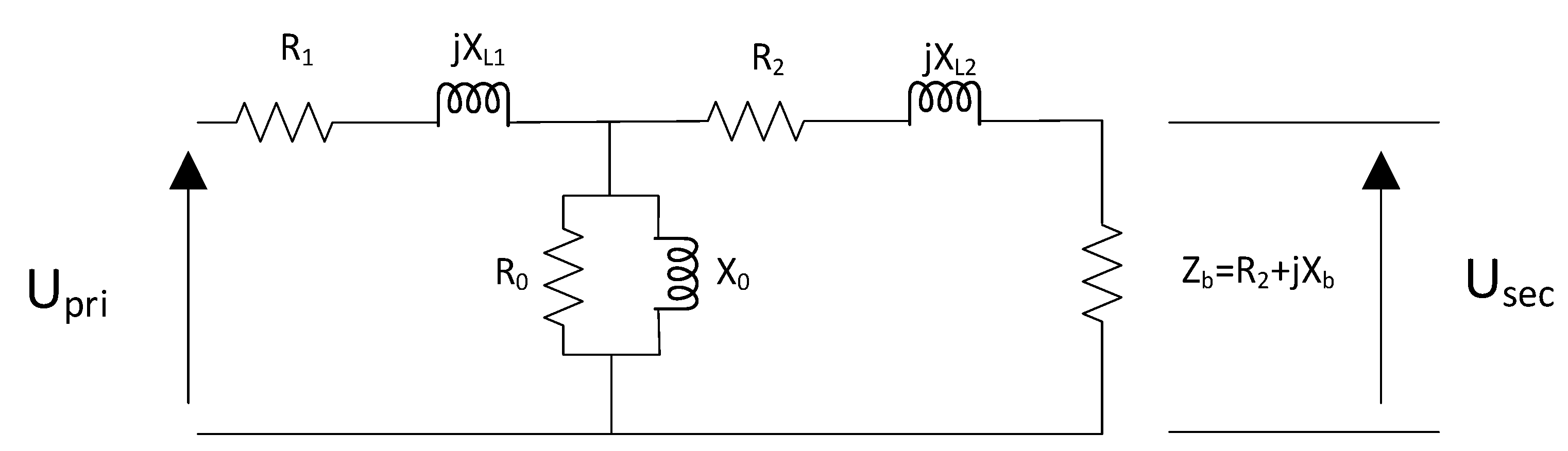
5.2. Magnetic Current Transformers
- core losses (resistance R0);
- magnetizing inductance (X0);
- primary leakage resistance (R1) and reactance (Xl1);
- secondary leakage resistance (R2);
- secondary leakage reactance (Xl2);
- the complex impedance of the burden (Zb).
5.3. Inductive Voltage Transformer
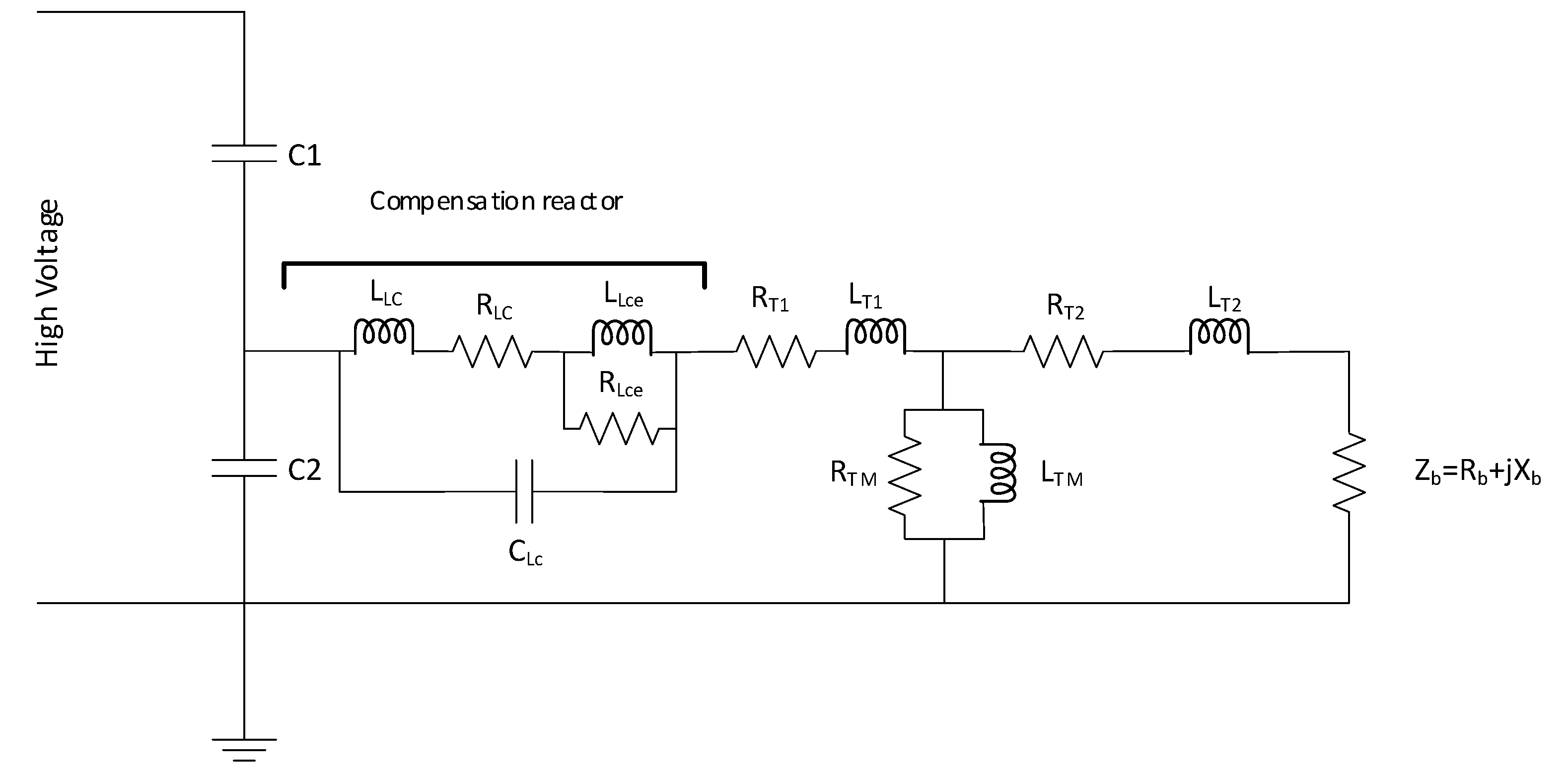
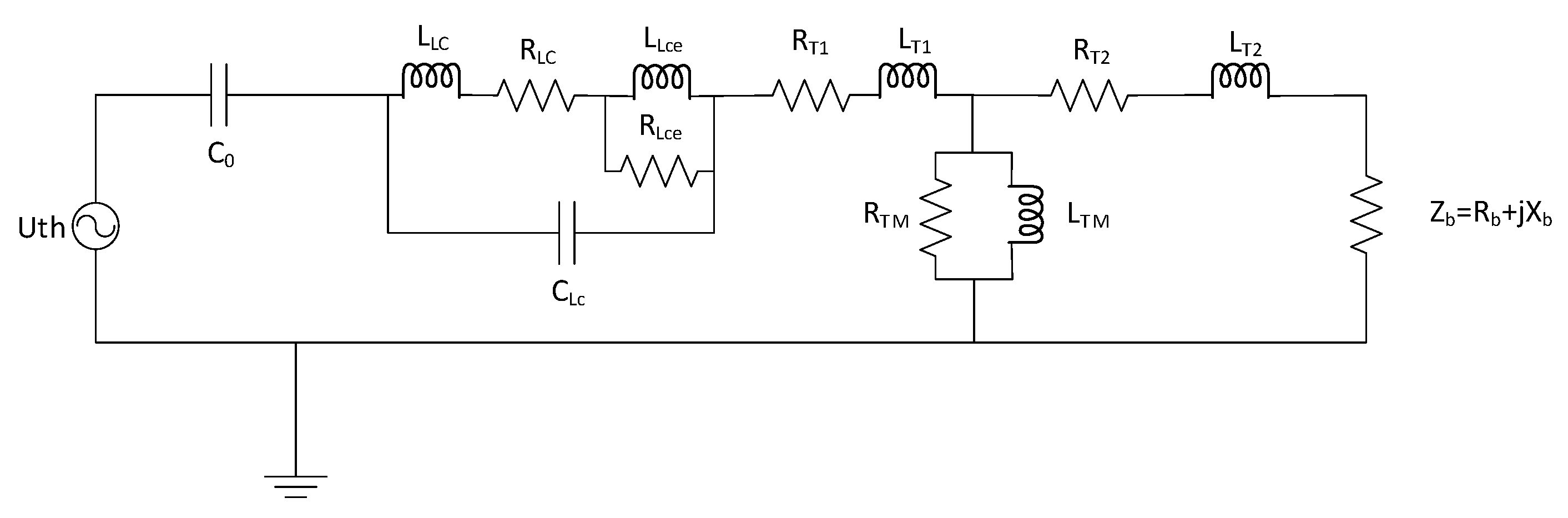
5.4. Capacitive Voltage Transformer
- capacitance;
- reactance;
- impedance.
6. Conclusions on the Opportunity for Instrument Transformer Remote Calibration
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brandolini, A.; Faifer, M.; Ottoboni, R. A Simple Method for the Calibration of Traditional and Electronic Measurement Current and Voltage Transformers. IEEE Trans. Instrum. Meas. 2009, 58, 1345–1353. [Google Scholar] [CrossRef]
- Suomalainen, E.P.; Hallstrom, J.K. Onsite Calibration of a Current Transformer Using a Rogowski Coil. IEEE Trans. Instrum. Meas. 2009, 58, 1054–1058. [Google Scholar] [CrossRef]
- Corney, A. Simple absolute method for current transformer calibration. IEEE Trans. Instrum. Meas. 2001, 50, 278–281. [Google Scholar] [CrossRef]
- Adibi, M.M.; Thorne, D.K. Remote Measurement Calibration. IEEE Trans. Power Syst. 1986, PWRS-1, 194–199. [Google Scholar] [CrossRef]
- Adibi, M.; Clements, K.; Kafka, R.; Stovall, J. Remote measurement calibration. IEEE Comput. Appl. Power 1990, 3, 37–42. [Google Scholar] [CrossRef]
- Pal, A. On-line Calibration of Voltage Transformers Using Synchrophasor Measurements. IEEE Trans. Power Deliv. 2016, 31, 370–380. [Google Scholar] [CrossRef]
- Wu, Z. Synchronized Phasor Measurement Applications in Three-phase Power Systems; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2013. [Google Scholar]
- Rens, J.; Rens, S.; Gerhard, B.; Desmet, J. On the Remote Calibration of Voltage Transformers: Validation of Opportunity. In Proceedings of the 2018 IEEE 9th International Workshop on Applied Measurements for Power Systems (AMPS), Bologna, Italy, 26–28 September 2018. [Google Scholar]
- Mingotti, A.; Peretto, L.; Tinarelli, R. Uncertainty Analysis of an Equivalent Synchronization Method for Phasor Measurements. IEEE Trans. Instrum. Meas. 2018, 67, 2444–2452. [Google Scholar] [CrossRef]
- BIPM. Evaluation of Measurement—Guide to the Expression of Uncertainty in Measurement; Bureau International des Poids et Mesures: Sèvres, France, 2008. [Google Scholar]
- Ferrero, A. The Pillars of Metrology. IEEE Instrum. Meas. Mag. 2015, 18, 7–11. [Google Scholar] [CrossRef]
- IEEE C57.13-2016; Standard Requirements for Instrument Transformers. IEEE: Piscataway, NJ, USA, 2008.
- IEC 61869-1:2007; Instrument Transformers—Part 1: General Requirements. IEC: Geneva, Switzerland, 2007.
- IEC 61869-2:2012; Instrument Transformers—Part 2: Additional Requirements for Current Transformers. IEC: Geneva, Switzerland, 2012.
- IEC 61869-5:2011; Instrument Transformers—Part 5: Additional Requirements for Capacitor Voltage Transformers. IEC: Geneva, Switzerland, 2011.
- Salicone, S. Measurement Uncertainty. In An Approach via the Mathematical Theory of Evidence; Springer Science + Business Media: New York, NY, USA, 2007; pp. 1–15. [Google Scholar]
- Pegoraro, P.A.; Brady, K.; Castello, P.; Muscas, C.; Meier, A.V. Compensation of Systematic Measurement Errors in a PMU-Based Monitoring System for Electric Distribution Grids. IEEE Trans. Instrum. Meas. 2019, 68, 3871–3882. [Google Scholar] [CrossRef]
- Mingotti, A.; Pasini, L.P.G.; Tinarelli, R. Effect of Temperature on the Accuracy of Inductive Current Transformers. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 4–17 May 2018. [Google Scholar]
- Ivano, G.; Mingotti, A.; Peretto, L.; Tinarelli, R.; Mauri, F. Assessment of Metrological Characteristics of Calibration Systems for Accuracy vs. Temperature Verification of Voltage Transformer. In Proceedings of the 2017 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Liverpool, UK, 20–22 September 2017. [Google Scholar]
- IEEE-C37.118; Standard for Synchrophasor Measurements for Power Systems. IEEE: Piscataway, NJ, USA, 2011.
- Wu, Z.; Thomas, K.; Sun, R.; Centeno, V.A.; Phadke, A.G. Three-Phase Instrument Transformer Calibration with Sunchronized Phasor Measurements; Innovative Smart Grid Technologies: Washington, DC, USA, 2012. [Google Scholar]
- Zhou, M. Advanced Systems Monitoring with Phasor Measurements; VT: Blacksburg, VA, USA, 2008. [Google Scholar]
- Hinge, T.P.; Dambhare, S.S. A novel approach for calibration of Instrument Transformers using synchro-phasors. In Proceedings of the 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19–21 December 2016. [Google Scholar]
- Wu, Z.; Zora, L.T.; Phadke, A.G. Simultaneous transmission line parameter and PMU measurement calibration. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Bell, S. A Beginner’s Guide to Uncertainty of Measurement; National Physical Laboratory: Teddington, UK, 2001. [Google Scholar]
- IEC 61869-3:2011; Instrument Transformers—Part 3: Additional Requirements for Inductive Voltage Transfromers. IEC: Geneva, Switzerland, 2011.
- IEEE C57.13.5-2009; Standard for Performance and Test Requirements for Instrument Transformers of a Nominal System Voltage of 115 kV and above. IEEE: Piscataway, NJ, USA, 2009.
- ABB AB High Voltage Products. Instrument Transformers Application Guide; ABB AB High Voltage Products: Ludvika, Sweden, 2015. [Google Scholar]
- Groszkowski, J. The temperature coefficient of inductance. Proc. Inst. Radio Eng. 1937, 25, 448–464. [Google Scholar] [CrossRef]
- Ansari, M.; Saxena, J.; Saxena, A.K. Comparison of Temperature Coefficent of Standard Inductor by Measuring Change in Inductance and Resistance; National Physical Laboratory India: New Delhi, India, 2010. [Google Scholar]
- Texas Instruments. LDC 1000 Temperature Compensation; Texas Instruments: Dallas, TX, USA, 2013. [Google Scholar]
- Kunde, K.; Däumling, H.; Huth, R.; Schlierf, H.-W.; Schmid, J. Frequency Response of Instrument Transformers in the kHz range. Compon. Peripher. 2012, 6, 1–4. [Google Scholar]
- Hu, H.-B.; Zhou, Y.; Ji, Z. The steady—State error Analyis of new type high voltage EVT and its modification. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012. [Google Scholar]
- Wang, D.; Wang, J. Study on error characteristics of capacitor voltage transformer. High Volt. Appar. 2001, 37. [Google Scholar]
- He, M.-C.; Zhang, J.-P.; Zhao, J.-T. Influence of the Temperature Changes on CVT’s Accuracy. Power Capacit. 2006, 1, 13–17. [Google Scholar]
- Jian, L.; Hao, Z.; Chao, G.; Qian, Z. Harmonic voltage measurement error of the capacitor voltage transformer. PLoS ONE 2018, 13, e0205231. [Google Scholar]
- Chen, B.; Du, L.; Liu, K.; Chen, X.; Zhang, F.; Yang, F. Measurement error estimation for Capacitive Voltage Transformer by Insulation Parameters. Energies 2017, 10, 357. [Google Scholar] [CrossRef]




| Accuracy Class | Ratio Error +/− % | Phase Displacement | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| +/− Minutes | +/− Centiradians | |||||||||||
| At Current (% of Rated) | At Current (% of Rated) | At Current (% of Rated) | ||||||||||
| 5 | 20 | 100 | 120 | 5 | 20 | 100 | 120 | 5 | 20 | 100 | 120 | |
| 0.1 | 0.4 | 0.2 | 0.1 | 0.1 | 15 | 8 | 5 | 5 | 0.45 | 0.24 | 0.15 | 0.15 |
| 0.2 | 0.75 | 0.35 | 0.2 | 0.2 | 30 | 15 | 10 | 10 | 0.9 | 0.45 | 0.3 | 0.3 |
| 0.5 | 1.5 | 0.75 | 0.5 | 0.5 | 90 | 45 | 30 | 30 | 2.7 | 1.35 | 0.9 | 0.9 |
| 1 | 3.0 | 1.5 | 1.0 | 1.0 | 180 | 90 | 60 | 60 | 5.4 | 2.7 | 1.8 | 1.8 |
| Metering Accuracy Class | Voltage Transformers (at 90% to 110% Rated Voltage) | Current Transformers | ||||||
|---|---|---|---|---|---|---|---|---|
| Minimum | Maximum | At 100% Rated Current a | At 10% Rated Current | At 5% Rated Current | ||||
| Minimum | Maximum | Minimum | Maximum | Minimum | Maximum | |||
| 0.15S b | - | - | 0.9985 | 1.0015 | - | - | 0.9985 | 1.0015 |
| 0.15 | 0.9985 | 1.0015 | 0.9985 | 1.0015 | - | - | 0.9970 | 1.0030 |
| 0.15N | - | - | 0.9985 | 1.0015 | 0.9970 | 1.0030 | - | - |
| 0.3S | - | - | 0.9970 | 1.0030 | - | - | 0.9970 | 1.0030 |
| 0.3 | 0.9970 | 1.0030 | 0.9970 | 1.0030 | 0.9940 | 1.0060 | - | - |
| 0.6 | 0.9940 | 1.0060 | 0.9940 | 1.0060 | 0.9880 | 1.0120 | - | - |
| 1.2 | 0.9880 | 1.0120 | 0.9880 | 1.0120 | 0.9760 | 1.0240 | - | - |
| High-voltage capacitance C1 | 3.18 nF |
| Medium-voltage capacitance C2 | 54 nF |
| Winding resistance RLC | 766 Ω |
| Core resistance RLce | 9.288 MΩ |
| Winding inductance LLc | 24.71 H |
| Core inductance LLce | 148.9 H |
| Stray capacitance CLc | 61.17 pF |
| Leakage resistance RT1 | 1403 Ω |
| Leakage inductance LT1 | 1.27 H |
| Leakage resistance RT2 | 1054 Ω |
| Leakage inductance LT2 | 6.95 H |
| Excitation resistance RTM | 1070 Ω |
| Excitation inductance LTM | 53 kH |
| Rated burden resistance Rb | 645.2 kΩ |
| Rated burden inductance Xb | 1.54 kΩ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verhelst, B.; Rens, S.; Rens, J.; Knockaert, J.; Desmet, J. On the Remote Calibration of Instrumentation Transformers: Influence of Temperature. Energies 2023, 16, 4744. https://doi.org/10.3390/en16124744
Verhelst B, Rens S, Rens J, Knockaert J, Desmet J. On the Remote Calibration of Instrumentation Transformers: Influence of Temperature. Energies. 2023; 16(12):4744. https://doi.org/10.3390/en16124744
Chicago/Turabian StyleVerhelst, Bart, Sané Rens, Johan Rens, Jos Knockaert, and Jan Desmet. 2023. "On the Remote Calibration of Instrumentation Transformers: Influence of Temperature" Energies 16, no. 12: 4744. https://doi.org/10.3390/en16124744
APA StyleVerhelst, B., Rens, S., Rens, J., Knockaert, J., & Desmet, J. (2023). On the Remote Calibration of Instrumentation Transformers: Influence of Temperature. Energies, 16(12), 4744. https://doi.org/10.3390/en16124744







