Reliable Thermal-Physical Modeling of Lithium-Ion Batteries: Consistency between High-Frequency Impedance and Ion Transport
Abstract
1. Introduction
- Moreover, these models usually consider the several elements independently of one other, potentially leading to physical inconsistencies, as in the case of electrolyte conductivity and diffusivity. According to the relevance of these two parameters for lithium-ion simulations, their relation [18] has to be ensured to provide a physically reliable simulation.
- usually reproduce discharge curves with satisfactory accuracy; however, to provide physical consistency when simulating LIB operation and dynamics, the reliability should be challenged using EIS, as recently pointed out by several research groups [16,17]. The simulation of EIS, and specifically of HFR, can guide the calibration by providing additional constraints to the solution.
- One interesting topic specific to HFR is the need to take into account the role of current collectors, which are often regarded as negligible [14,17]. Indeed, this choice can lead to wrong overestimation of electrolyte resistivity. In some conditions, the contribution of current collectors may be the major part of the pure response of the device, especially in high-energy designs; thus, the assumption of infinite conductivity applied in many models such as DFN is not valid.
2. Methodology
2.1. Battery Samples
2.2. Experimental Testbench
2.3. Physical Model
3. Focus on Cell High-Frequency Resistance
3.1. High-Frequency Resistance at Different SoC and Temperatures
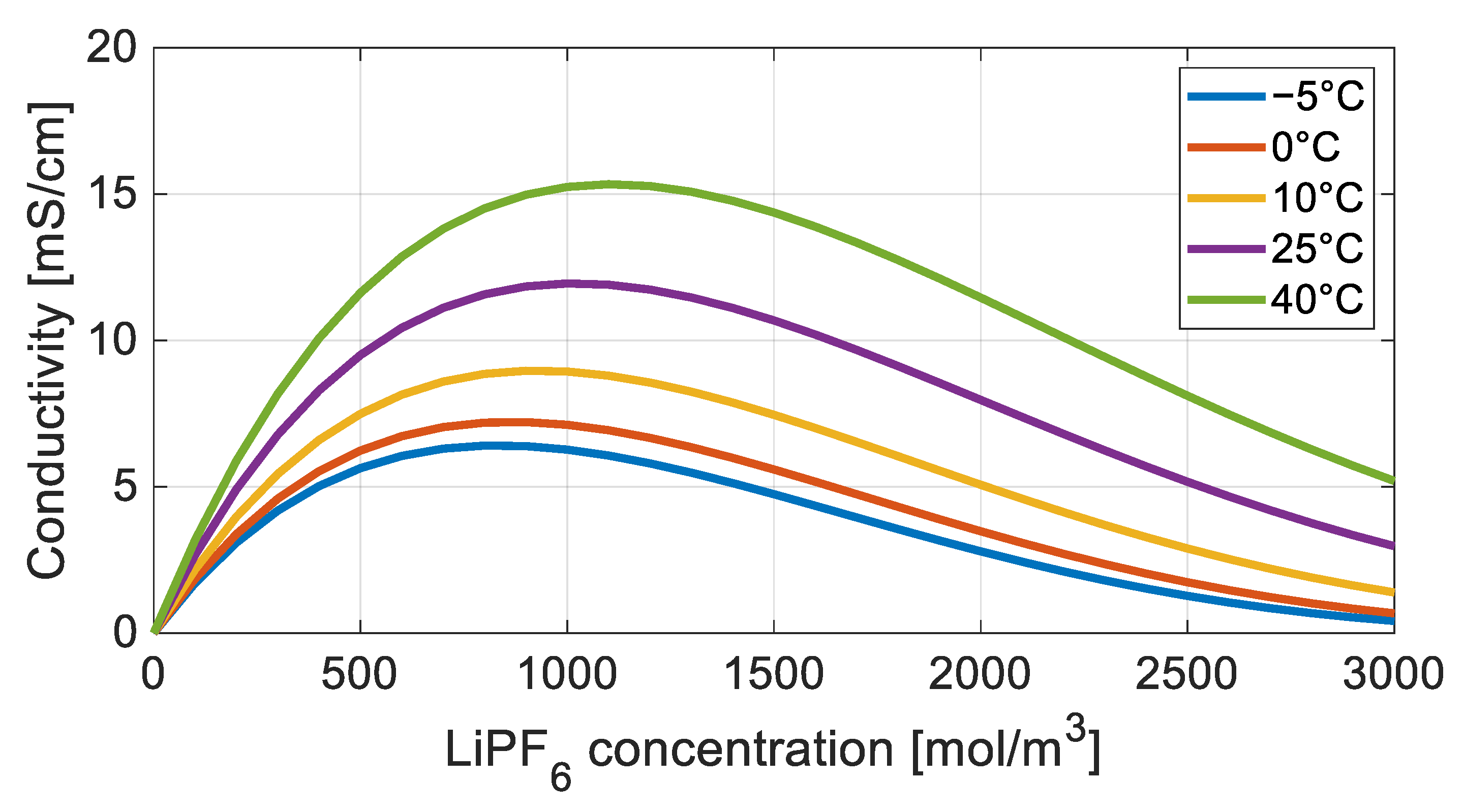
3.2. Electrolyte Ionic Resistance
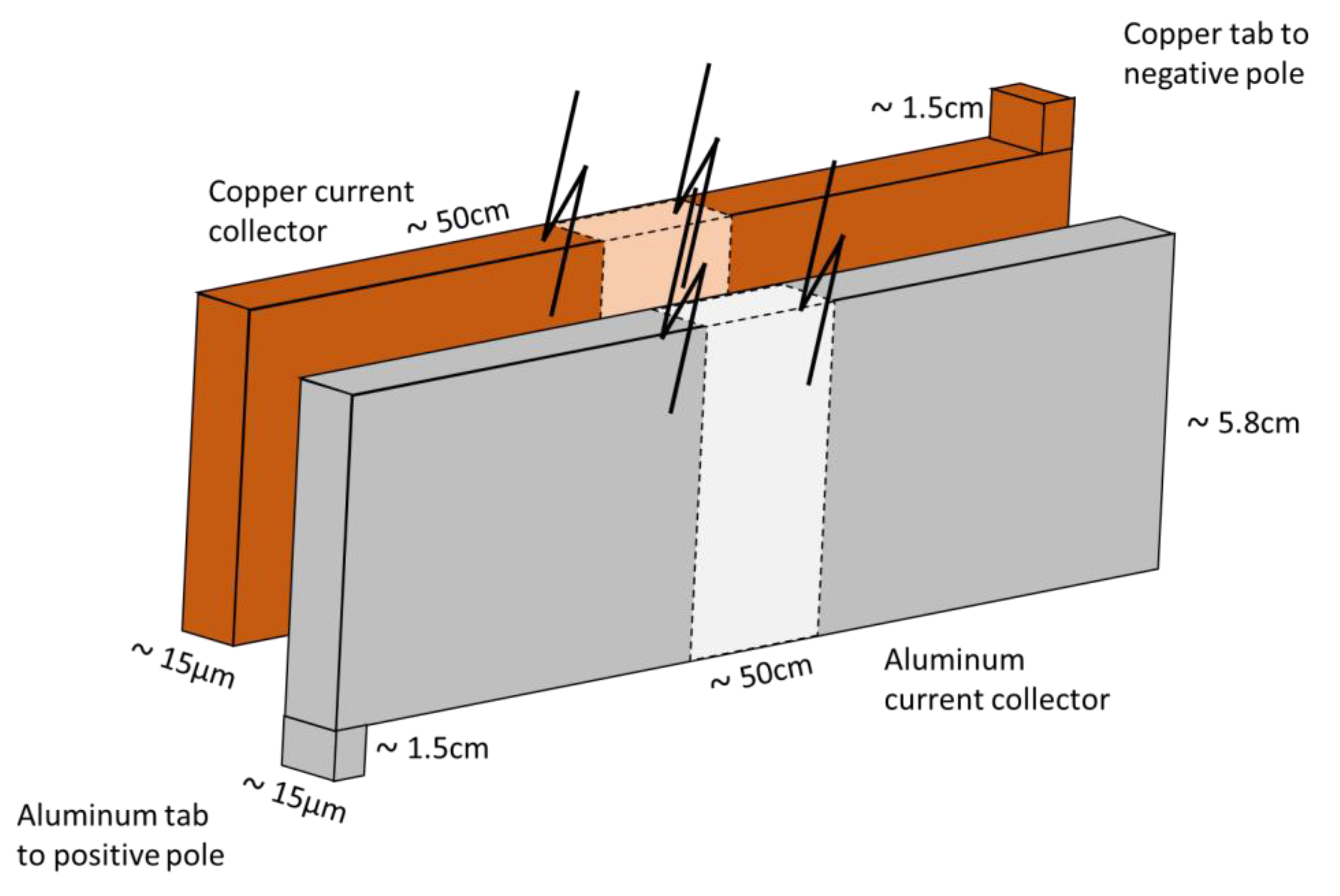
3.3. Current Collectors’ Electrical Resistance
3.4. Modelling the Current Collectors’ Resistance
4. Results and Discussion
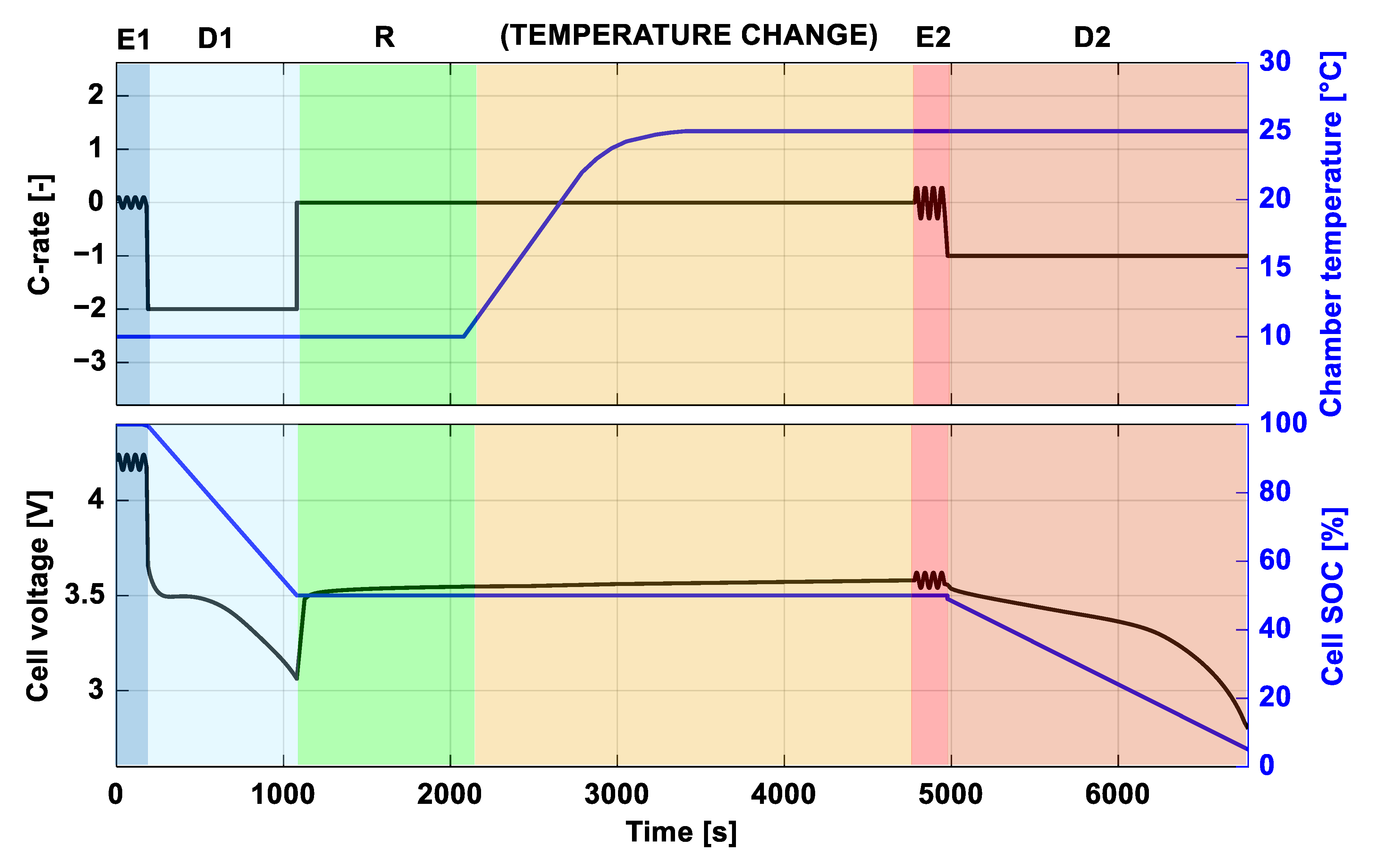
4.1. Diagnostic Protocol
- Measuring EIS spectra is of great importance, at least at two opposite states of charge, to enable a distinction between positive and negative electrode contributions, and at two temperature levels, to enable the calibration of temperature-related parameters.
- The discharge test is mainly sensitive to diffusion-related phenomena, both in electrodes’ bulk and the electrolyte. Two combinations of C-rates and temperatures are advised to be covered with this technique, spanning the entire battery capacity.
- (E1) EIS testing on the battery at SoC 100%, 10 °C is performed at 20 logarithmically spaced frequencies in the range 4000–1 Hz;
- (D1) the battery is discharged at 2C with a DoD 50%;
- (R) a relaxation test of 1000 s follows the discharge. During this test, voltage and temperature are recorded;
- (E2) after the relaxation, the climate chamber temperature of 25 °C is set, and when the temperature is reached, an EIS at SoC 50% within the same frequency interval as the first is performed;
- (D2) the battery is discharged at 1C until the lower voltage limit is reached (theoretical DoD 50%).
4.2. Optimized EIS Simulation and Parameter Identification Procedure
- Optimized domain
- Optimized mesh resolution
- Optimized thermal model
Stepwise Single-Measurement Calibration
- Step 1: the model is calibrated against the two impedance spectra (E1) and (E2) simultaneously, by optimizing the kinetic constants () and double-layer capacitances values (). In this step, only the charge transfer resistance is considered; hence, the HFR value is neglected, and the remaining parameters are fixed at a proper literature value, as listed in Table 4. The other parameters are fixed to an intermediate value within the literature’s range, as a first guess. Since solid diffusivities and (to a certain extent) electrolyte properties have a minor effect on EIS, this solution is viable and will be corroborated Step 3. At this stage, the current collectors’ contribution is estimated according to Equation (5), presented in Section 3.4, corresponding to an intermediate value of electrolyte conductivity from the literature.
- Step 2: the model is then calibrated on partial discharges (D1) and (D2) by optimizing the solid diffusivities () and electrolyte conductivity ().
- Step 3: finally, Step 1 is repeated, employing the solid diffusivities and electrolyte conductivity computed in Step 2.
4.3. Obtained Solution
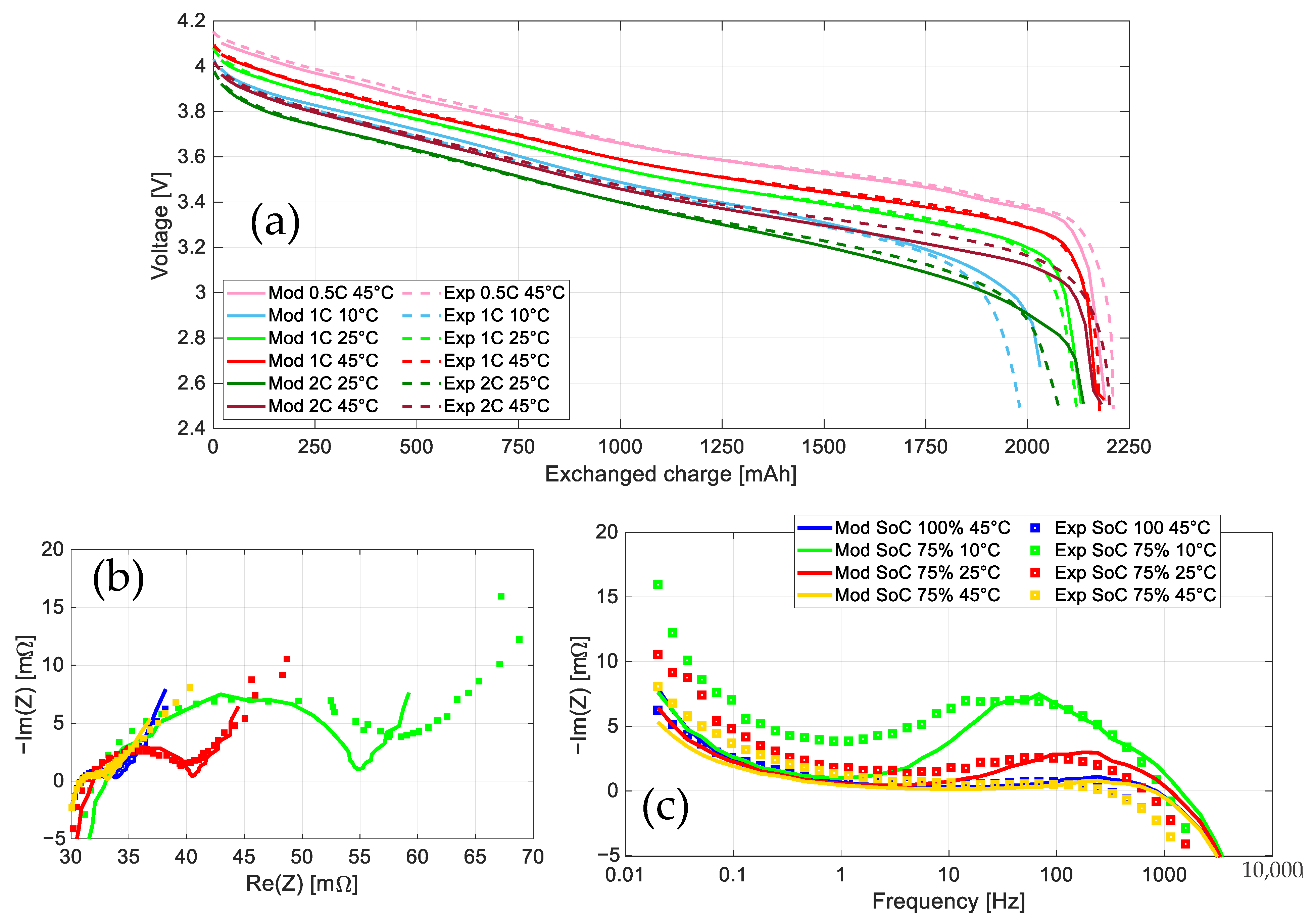
4.4. Validation
- Full discharges at
- ○
- 0.5C at 45 °C
- ○
- 1C, 10–25–45 °C
- ○
- 2C, 25–45 °C
- EIS spectra performed from 4 kHz to 20 mHz, with 40 logarithmically spaced points:
- ○
- At SoC 75% and 10–25–45 °C
- ○
- At 100% SoC and 45 °C;
- The application of the IEC 62660-1:2018 BEV cycle life profile [28], as a highly dynamic profile, at 25 °C, from SoC 100% to the lower voltage threshold.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Acronyms
| Acronym | Description |
| CC | Constant current |
| D1 | First discharge of the developed diagnostic protocol |
| D2 | Second discharge of the developed diagnostic protocol |
| DFN | Doyle–Fuller–Newman physical model |
| DOD | Depth of discharge |
| E1 | First EIS of the developed diagnostic protocol |
| E2 | Second EIS of the developed diagnostic protocol |
| ECM | Equivalent circuit model |
| EIS | Electrochemical impedance spectroscopy |
| FFT | Fast Fourier transform |
| FR | Fast relaxation time |
| GITT | Galvanostatic intermittent titration technique |
| HF | High frequency |
| HFR | High-frequency resistance |
| LF | Low frequency |
| LIB | Lithium-ion battery |
| LMO | Lithium–manganese-oxide battery |
| MF | Medium frequency |
| MR | Mid relaxation time |
| NMC | Lithium–nickel–manganese–cobalt oxide battery |
| OC | Operating condition |
| OCP | Open circuit potential |
| OCV | Open circuit voltage |
| OFAT | One factor at a time |
| PDE | Partial–differential equation |
| PSO | Particle swarm optimization |
| R | Relaxation of the developed diagnostic protocol |
| RMSE | Root mean square error |
| SD | Standard deviation |
| SEI | Solid electrolyte interphase |
| SoC | State of charge |
| SoH | State of health |
| SR | Slow relaxation time |
List of Symbols
| Symbol | Unit of Measure | Description | Symbol | Unit of Measure | Description |
| Latin | Greek | ||||
| Specific active area | Transfer coefficient | ||||
| Electrode area | Material fraction | ||||
| Lithium concentration | Overpotential | ||||
| Heat capacity | Ionic conductivity | ||||
| Double layer capacitance | Density | ||||
| Lithium diffusion coefficient | Electric potential | ||||
| Rate constant activation energy | Subscript | ||||
| Solid diffusion activation energy | Reference | ||||
| Electrode open circuit potential | Anodic | ||||
| Faraday constant | Active material | ||||
| Ionic conductivity factor | Axial | ||||
| Heat transfer coefficient | Cathodic | ||||
| H | Battery height | Electrolyte | |||
| Current density | Inactive material | ||||
| Exchange current density | Maximum | ||||
| I | Current | Minimum | |||
| Lithium molar flux | Mandrel | ||||
| Rate constant | Negative | ||||
| Thermal conductivity | Nominal | ||||
| L | Cell component length | Positive | |||
| Volumetric heat | Reaction | ||||
| Capacity | Radial | ||||
| Battery radius | Solid | ||||
| Particle radius | Steel can | ||||
| Universal gas constant | Separator | ||||
| External resistance | Superscript | ||||
| Film resistance | Effective | ||||
| Electrode state of charge | “ | Absolute | |||
| Battery state of charge | Coordinate | ||||
| Lithium transference number | Linear coordinate | ||||
| Temperature | Radial coordinate | ||||
| Cell voltage | Time | ||||
| Z | Impedance | Axial coordinate |
References
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The Lithium-Ion Battery: State of the Art and Future Perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Stampatori, D.; Raimondi, P.P.; Noussan, M. Li-Ion Batteries: A Review of a Key Technology for Transport Decarbonization. Energies 2020, 13, 2638. [Google Scholar] [CrossRef]
- Messing, M.; Shoa, T.; Habibi, S. Estimating Battery State of Health Using Electrochemical Impedance Spectroscopy and the Relaxation Effect. J. Energy Storage 2021, 43, 103210. [Google Scholar] [CrossRef]
- Zhang, Y.; Wik, T.; Bergström, J.; Pecht, M.; Zou, C. A Machine Learning-Based Framework for Online Prediction of Battery Ageing Trajectory and Lifetime Using Histogram Data. J. Power Sources 2022, 526, 231110. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of Electrochemical Impedance Spectroscopy to Commercial Li-Ion Cells: A Review. J. Power Sources 2020, 480, 228742. [Google Scholar] [CrossRef]
- Beltran, H.; Ayuso, P.; Vicente, N.; Beltrán-Pitarch, B.; García-Cañadas, J.; Pérez, E. Equivalent Circuit Definition and Calendar Aging Analysis of Commercial Li(NixMnyCoz)O2/Graphite Pouch Cells. J. Energy Storage 2022, 52, 104747. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.; Li, D.; Cui, X.; Wang, L.; Li, L.; Wang, K. Electrochemical Impedance Spectroscopy: A New Chapter in the Fast and Accurate Estimation of the State of Health for Lithium-Ion Batteries. Energies 2023, 16, 1599. [Google Scholar] [CrossRef]
- Li, D.; Yang, D.; Li, L.; Wang, L.; Wang, K. Electrochemical Impedance Spectroscopy Based on the State of Health Estimation for Lithium-Ion Batteries. Energies 2022, 15, 6665. [Google Scholar] [CrossRef]
- Fan, M.; Geng, M.; Yang, K.; Zhang, M.; Liu, H. State of Health Estimation of Lithium-Ion Battery Based on Electrochemical Impedance Spectroscopy. Energies 2023, 16, 3393. [Google Scholar] [CrossRef]
- Tran, M.K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A Comprehensive Equivalent Circuit Model for Lithium-Ion Batteries, Incorporating the Effects of State of Health, State of Charge, and Temperature on Model Parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Wang, J.; Jia, Y.; Yang, N.; Lu, Y.; Shi, M.; Ren, X.; Lu, D. Precise Equivalent Circuit Model for Li-Ion Battery by Experimental Improvement and Parameter Optimization. J. Energy Storage 2022, 52, 104980. [Google Scholar] [CrossRef]
- Iurilli, P.; Brivio, C.; Wood, V. On the Use of Electrochemical Impedance Spectroscopy to Characterize and Model the Aging Phenomena of Lithium-Ion Batteries: A Critical Review. J. Power Sources 2021, 505, 229860. [Google Scholar] [CrossRef]
- Krewer, U.; Röder, F.; Harinath, E.; Braatz, R.D.; Bedürftig, B.; Findeisen, R. Review—Dynamic Models of Li-Ion Batteries for Diagnosis and Operation: A Review and Perspective. J. Electrochem. Soc. 2018, 165, A3656–A3673. [Google Scholar] [CrossRef]
- Xu, L.; Lin, X.; Xie, Y.; Hu, X. Enabling High-Fidelity Electrochemical P2D Modeling of Lithium-Ion Batteries via Fast and Non-Destructive Parameter Identification. Energy Storage Mater 2022, 45, 952–968. [Google Scholar] [CrossRef]
- Rabissi, C.; Innocenti, A.; Sordi, G.; Casalegno, A. A Comprehensive Physical-Based Sensitivity Analysis of the Electrochemical Impedance Response of Lithium-Ion Batteries. Energy Technol. 2021, 9, 2000986. [Google Scholar] [CrossRef]
- Rabissi, C.; Sordi, G.; Innocenti, A.; Casalegno, A. Fast and Reliable Calibration of Thermal-Physical Model of Lithium-Ion Battery: A Sensitivity-Based Method. J. Energy Storage 2023, 59, 106435. [Google Scholar] [CrossRef]
- Laue, V.; Röder, F.; Krewer, U. Practical Identifiability of Electrochemical P2D Models for Lithium-Ion Batteries. J. Appl. Electrochem. 2021, 51, 1253–1265. [Google Scholar] [CrossRef]
- Park, M.; Zhang, X.; Chung, M.; Less, G.B.; Sastry, A.M. A Review of Conduction Phenomena in Li-Ion Batteries. J. Power Sources 2010, 195, 7904–7929. [Google Scholar] [CrossRef]
- Valo̸en, L.O.; Reimers, J.N. Transport Properties of LiPF6-Based Li-Ion Battery Electrolytes. J. Electrochem. Soc. 2005, 152, A882. [Google Scholar] [CrossRef]
- Edouard, C.; Petit, M.; Forgez, C.; Bernard, J.; Revel, R. Parameter Sensitivity Analysis of a Simplified Electrochemical and Thermal Model for Li-Ion Batteries Aging. J. Power Sources 2016, 325, 482–494. [Google Scholar] [CrossRef]
- Zhang, L.; Lyu, C.; Hinds, G.; Wang, L.; Luo, W.; Zheng, J.; Ma, K. Parameter Sensitivity Analysis of Cylindrical LiFePO 4 Battery Performance Using Multi-Physics Modeling. J. Electrochem. Soc. 2014, 161, A762–A776. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Rahe, C.; Ecker, M.; Sauer, D.U. Full Cell Parameterization of a High-Power Lithium-Ion Battery for a Physico-Chemical Model: Part I. Physical and Electrochemical Parameters. J. Electrochem. Soc. 2018, 165, A3799–A3810. [Google Scholar] [CrossRef]
- Ong, J.; Newman, J. Double-Layer Capacitance in a Dual Lithium-Ion Insertion Cell. J. Electrochem. Soc. 1999, 146, 4360–4365. [Google Scholar] [CrossRef]
- Flamme, B.; Rodriguez Garcia, G.; Weil, M.; Haddad, M.; Phansavath, P.; Ratovelomanana-Vidal, V.; Chagnes, A. Guidelines to Design Organic Electrolytes for Lithium-Ion Batteries: Environmental Impact, Physicochemical and Electrochemical Properties. Green Chem. 2017, 19, 1828–1849. [Google Scholar] [CrossRef]
- Carlier, D.; Ménétrier, M.; Delmas, C. 7Li MAS NMR Study of Electrochemically Deintercalated LixNi0.30Co0.70O2 Phases: Evidence of Electronic and Ionic Mobility, and Redox Processes. J. Mater Chem 2001, 11, 594–603. [Google Scholar] [CrossRef]
- Marzec, J.; Przewoźnik, J.P.; Molenda, J.; Simon, D.R.; Kelder, E.M.; Schoonman, J. Conduction Mechanism in Operating a LiMn2O4 Cathode. Solid State Ion. 2002, 146, 225–237. [Google Scholar] [CrossRef]
- Funabiki, A.; Inaba, M.; Ogumi, Z.; Yuasa, S.-I.; Otsuji, J.; Tasaka, A. Impedance Study on the Electrochemical Lithium into Natural Graphite Powder. J. Electrochem. Soc. 1998, 145, 172. [Google Scholar] [CrossRef]
- IEC 62660-1:2018; Secondary Lithium-Ion Cells for the Propulsion of Electric Road Vehicles-Part 1: Performance Testing. International Electrotechnical Commission: Geneva, Switzerland, 2018.
- Park, S.; Kato, D.; Gima, Z.; Klein, R.; Moura, S. Optimal Experimental Design for Parameterization of an Electrochemical Lithium-Ion Battery Model. J. Electrochem. Soc. 2018, 165, A1309–A1323. [Google Scholar] [CrossRef]
- Li, J.; Zou, L.; Tian, F.; Dong, X.; Zou, Z.; Yang, H. Parameter Identification of Lithium-Ion Batteries Model to Predict Discharge Behaviors Using Heuristic Algorithm. J. Electrochem. Soc. 2016, 163, A1646–A1652. [Google Scholar] [CrossRef]
- Yang, X.; Chen, L.; Xu, X.; Wang, W.; Xu, Q.; Lin, Y.; Zhou, Z. Parameter Identification of Electrochemical Model for Vehicular Lithium-Ion Battery Based on Particle Swarm Optimization. Energies 2017, 10, 1811. [Google Scholar] [CrossRef]
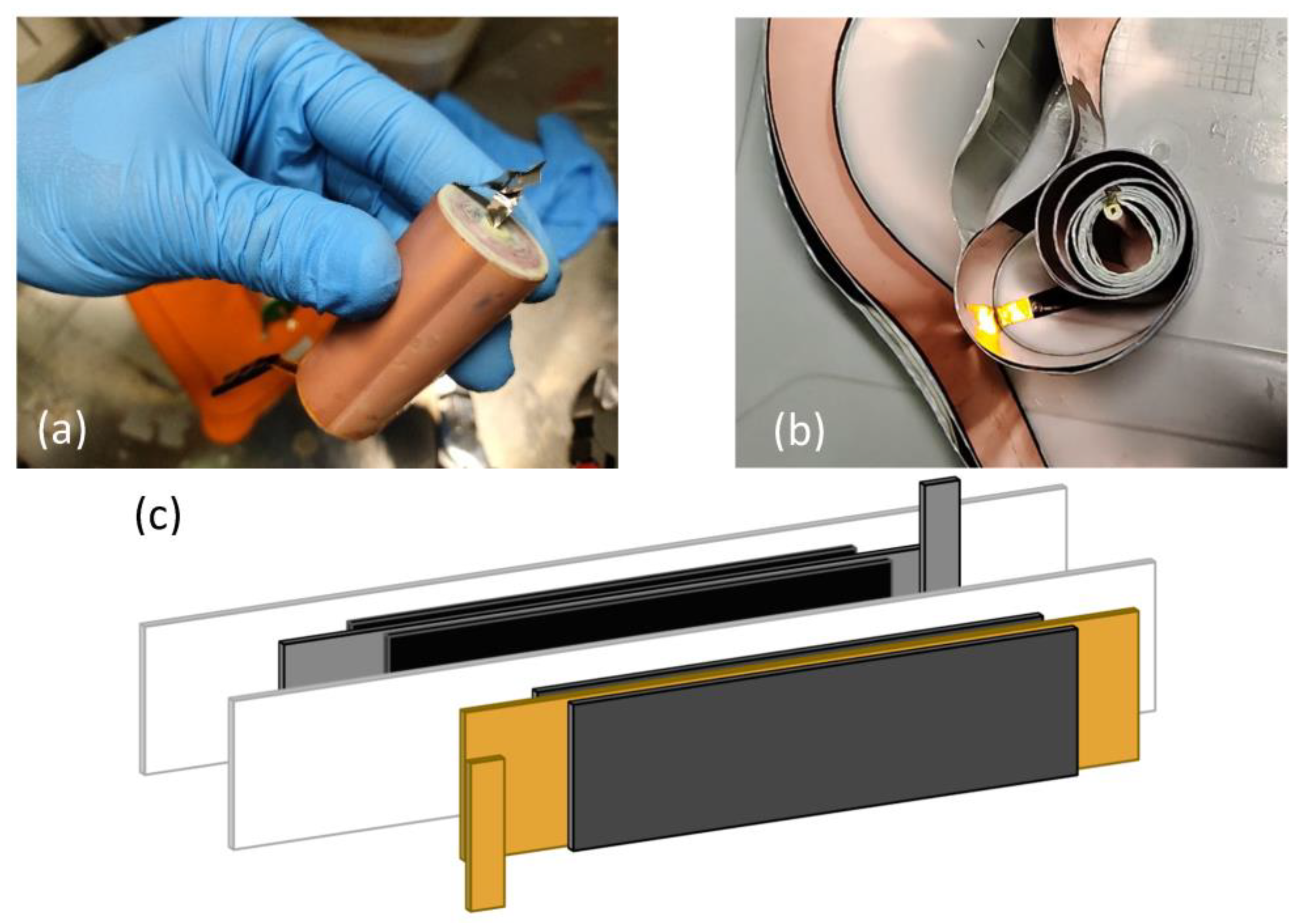




| Model | SONY US18650V3 |
|---|---|
| Geometry | Cylindrical 18650 |
| Anode chemistry | Graphite |
| Cathode chemistry | NMC |
| Nominal capacity | 2250 mAh |
| Maximum current (C-rate) | Charge: 2.25 A (1C) Discharge: 10 A (4.5C) |
| Operative voltage range | 4.2 V–2.5 V |
| Temperature range charge/discharge | Charge: 0–45 °C Discharge: −20 °C/60 °C |
| Weight | 44 g |
| US18650V3 | |||||
|---|---|---|---|---|---|
| Component | Layers | L (cm) | H (cm) | W (µm) | |
| Negative | Current collector (Copper) | 1 | 66.5 | 5.7 | 15 |
| Active layer (Graphite) | 2 | 58.5 | 5.7 | 70 | |
| Positive | Current collector (Aluminum) | 1 | 65.8 | 5.7 | 20 |
| Active layer (NMC) | 2 | 56.5 | 5.7 | 65 | |
| Separator | 2 | 80.3 | 5.7 | 15 | |
| Active area (cm2) | 644.10 | ||||
| Current Collector Material | Tab Number and Position | Half CC Only | Overall (Full CC, Tabs and Cap) | ||
|---|---|---|---|---|---|
| Total [mΩ] | Specific [Ωcm2] | Total [mΩ] | Specific [Ωcm2] | ||
| Copper | 1, outer edge | 11.5 | 7407 | 28 | 18,035 |
| Aluminum | 1, inner edge | 11.3 | 7278 | 24 | 15,458 |
| Parameters | Symbol | Variability Interval Employed in This Work | References |
|---|---|---|---|
| Kinetic rate constant of the cathode | [20,21] | ||
| Kinetic rate constant of the anode | [20,21] | ||
| Double layer of the cathode | [22,23] | ||
| Double layer of the anode | [22,23] | ||
| Ionic conductivity factor | [19,24] | ||
| Solid diffusivity of the cathode | [18,25,26] | ||
| Solid diffusivity of the anode | [18,27] |
| Parameter | Value |
|---|---|
| Technique | Operating Condition | |
|---|---|---|
| Discharge curve | , , | |
| , , | ||
| , 25 , | ||
| , 45 , | ||
| , 25 , | ||
| , 45 , | ||
| EIS | 45 °C, 100% | |
| 10 °C, 75% | ||
| 25 °C, 75% | ||
| 45 °C, 75% | ||
| IEC 62660-1:2018 | 25 °C, 100%−0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sordi, G.; Rabissi, C.; Casalegno, A. Reliable Thermal-Physical Modeling of Lithium-Ion Batteries: Consistency between High-Frequency Impedance and Ion Transport. Energies 2023, 16, 4730. https://doi.org/10.3390/en16124730
Sordi G, Rabissi C, Casalegno A. Reliable Thermal-Physical Modeling of Lithium-Ion Batteries: Consistency between High-Frequency Impedance and Ion Transport. Energies. 2023; 16(12):4730. https://doi.org/10.3390/en16124730
Chicago/Turabian StyleSordi, Gabriele, Claudio Rabissi, and Andrea Casalegno. 2023. "Reliable Thermal-Physical Modeling of Lithium-Ion Batteries: Consistency between High-Frequency Impedance and Ion Transport" Energies 16, no. 12: 4730. https://doi.org/10.3390/en16124730
APA StyleSordi, G., Rabissi, C., & Casalegno, A. (2023). Reliable Thermal-Physical Modeling of Lithium-Ion Batteries: Consistency between High-Frequency Impedance and Ion Transport. Energies, 16(12), 4730. https://doi.org/10.3390/en16124730







