Proactive Frequency Stability Scheme: A Distributed Framework Based on Particle Filters and Synchrophasors
Abstract
1. Introduction and Motivation
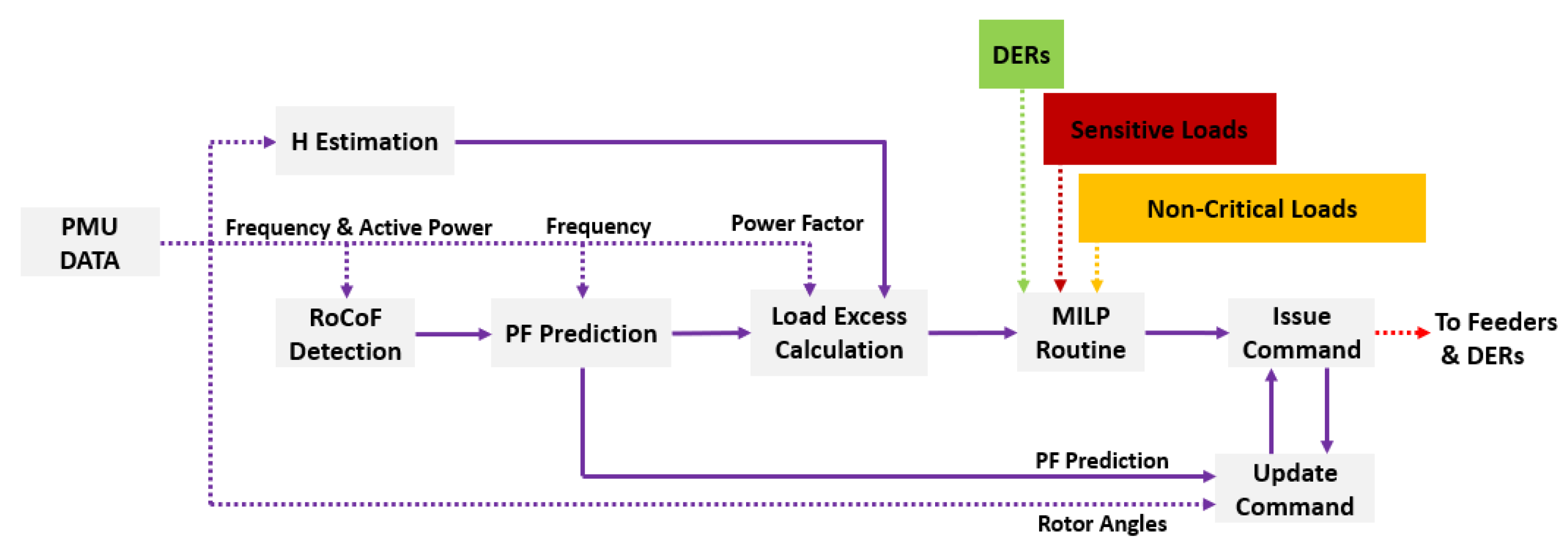
- Disturbances are detected using the rate of change of frequency (RoCoF).
- The state of frequency is predicted one to three seconds into the future.
- A load excess factor is determined using the predicted state of frequency.
- Using loading data collected at the feeder level, the method finds a suitable combination of load (feeders) that will be dropped in stages to meet the excess load factor and regain load-generation balance.
2. State-of-the-Art
3. Background
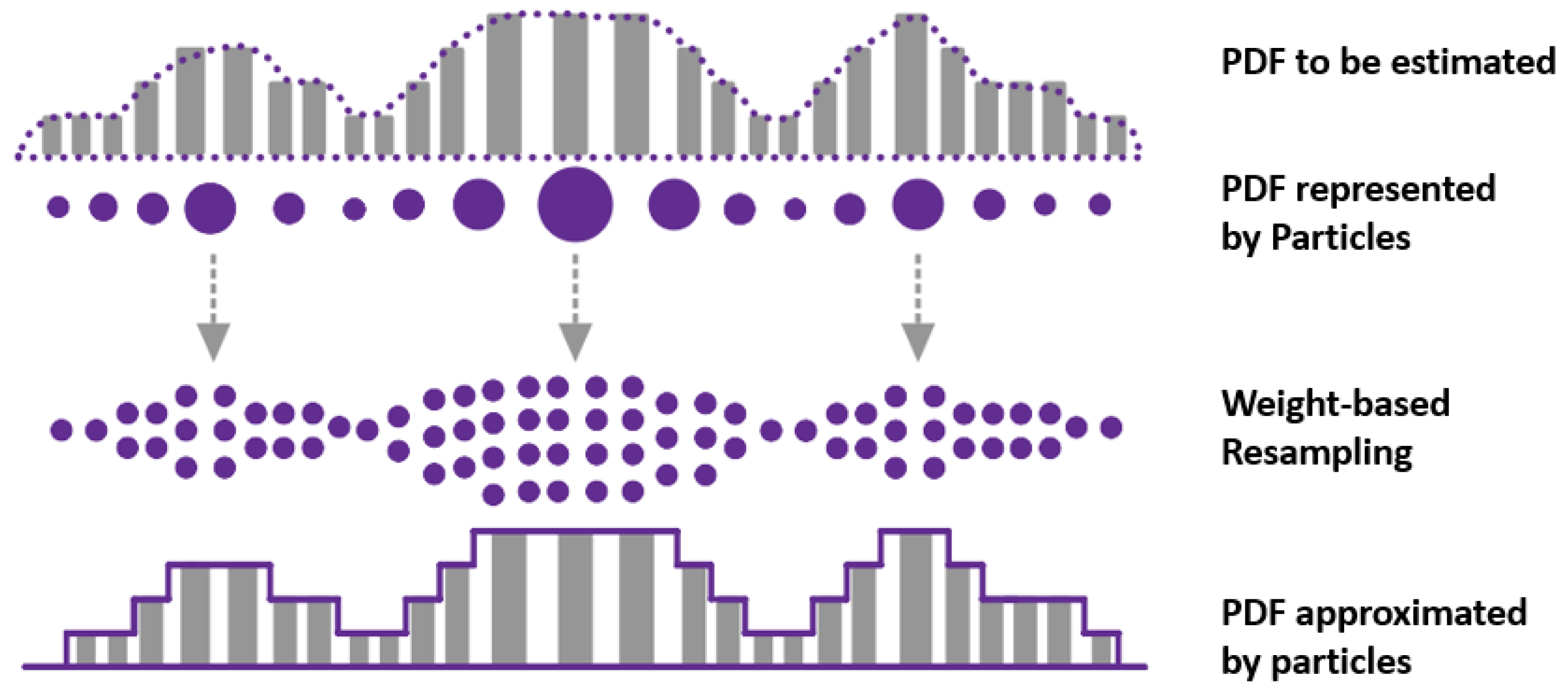
3.1. Particle Filter
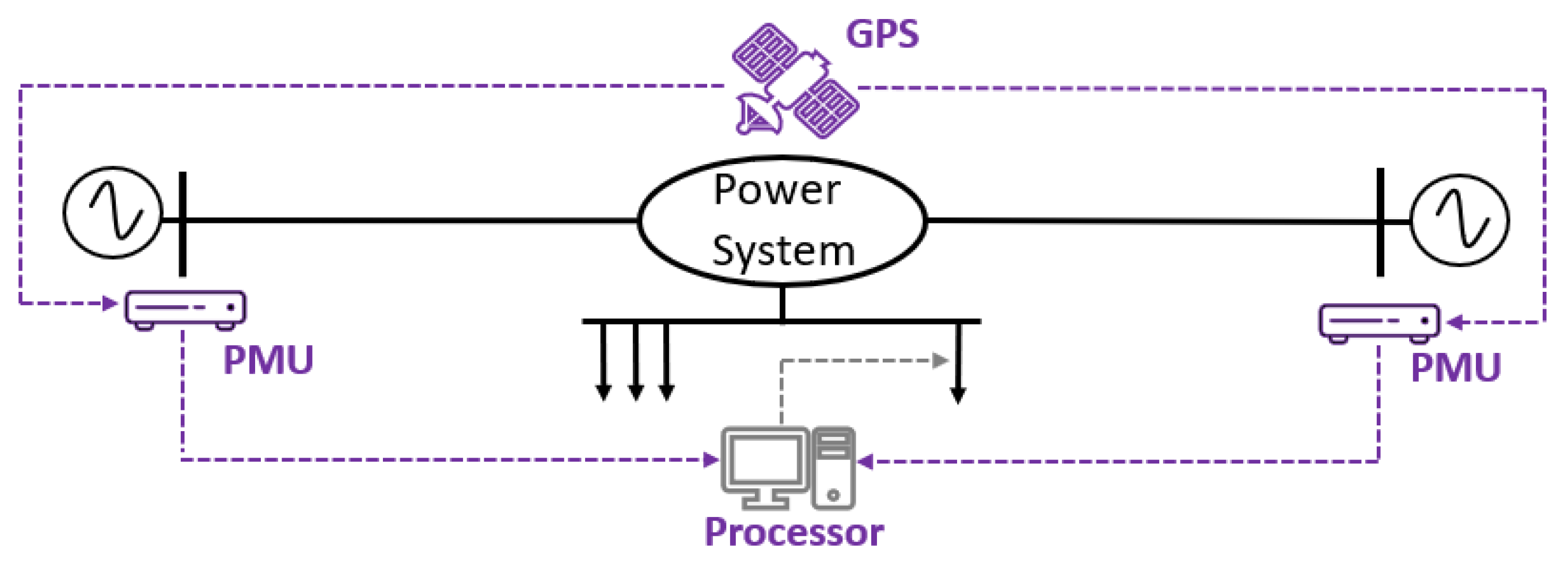
3.2. Synchrophasors
3.3. Disturbance Detection
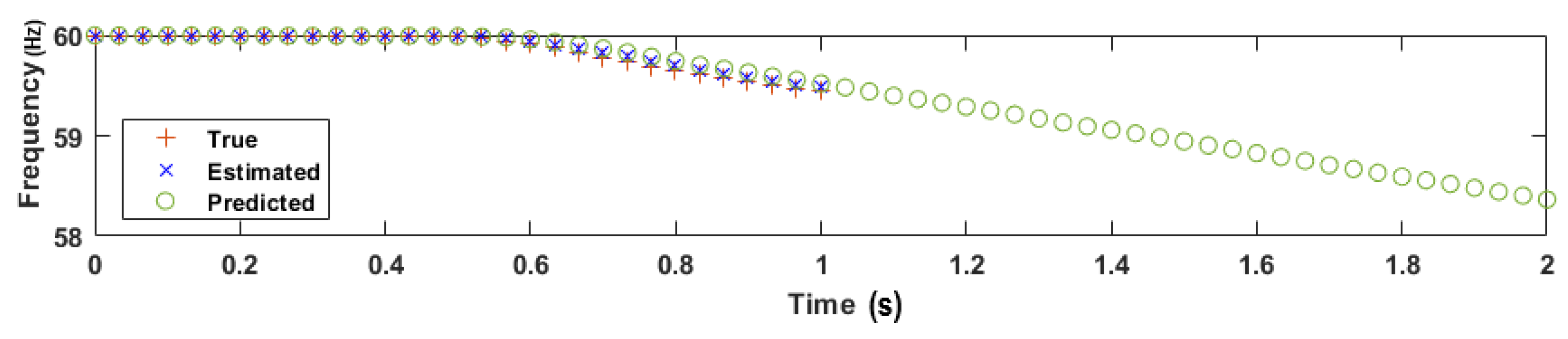
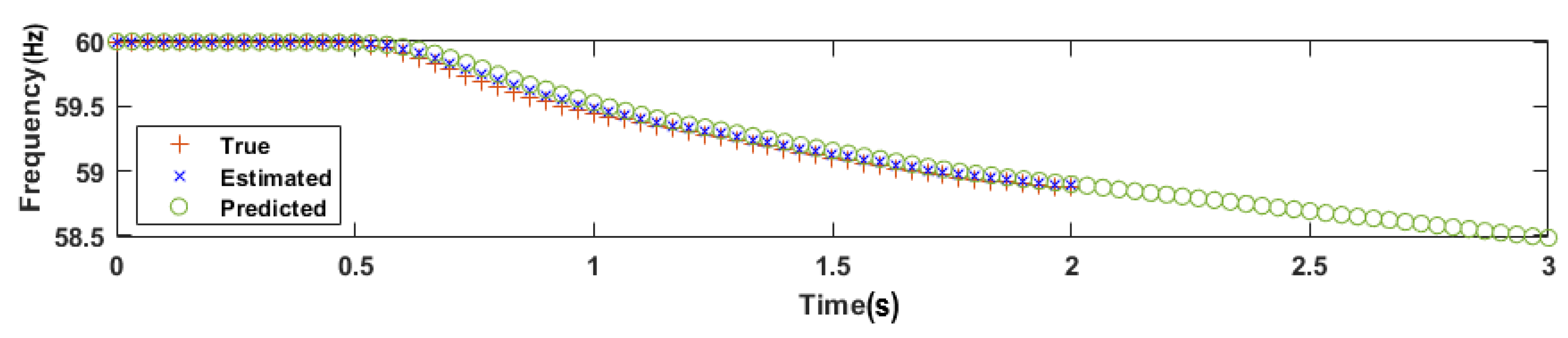
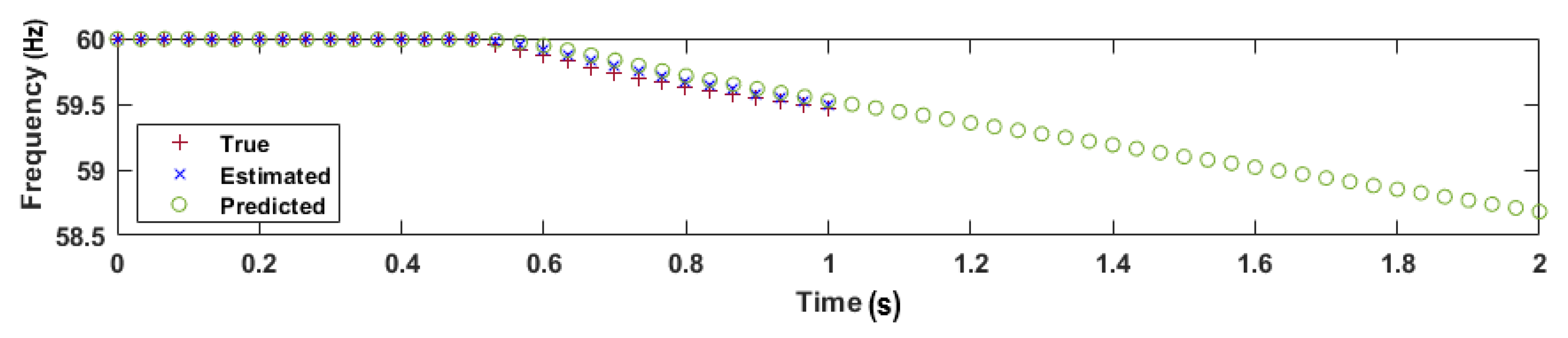
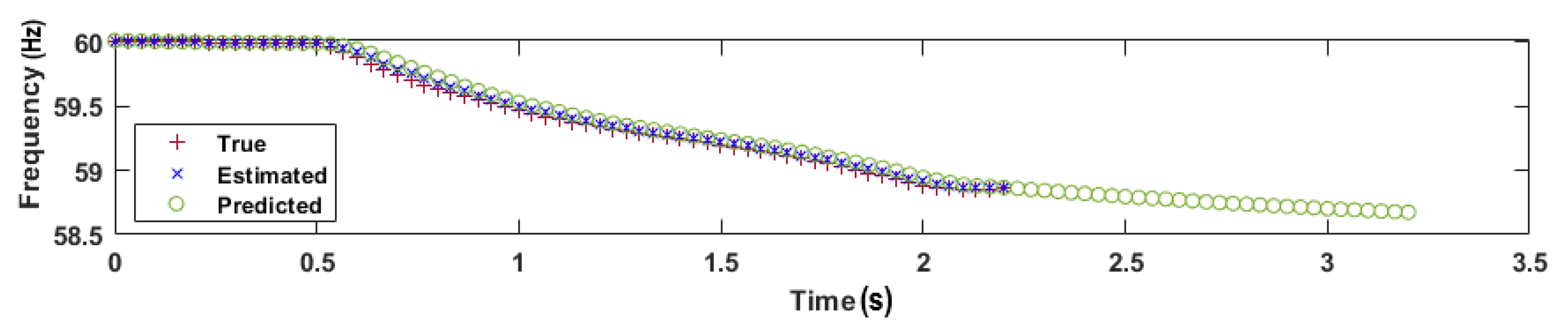
3.4. Prediction
| Algorithm 1 ADP Generation |
|
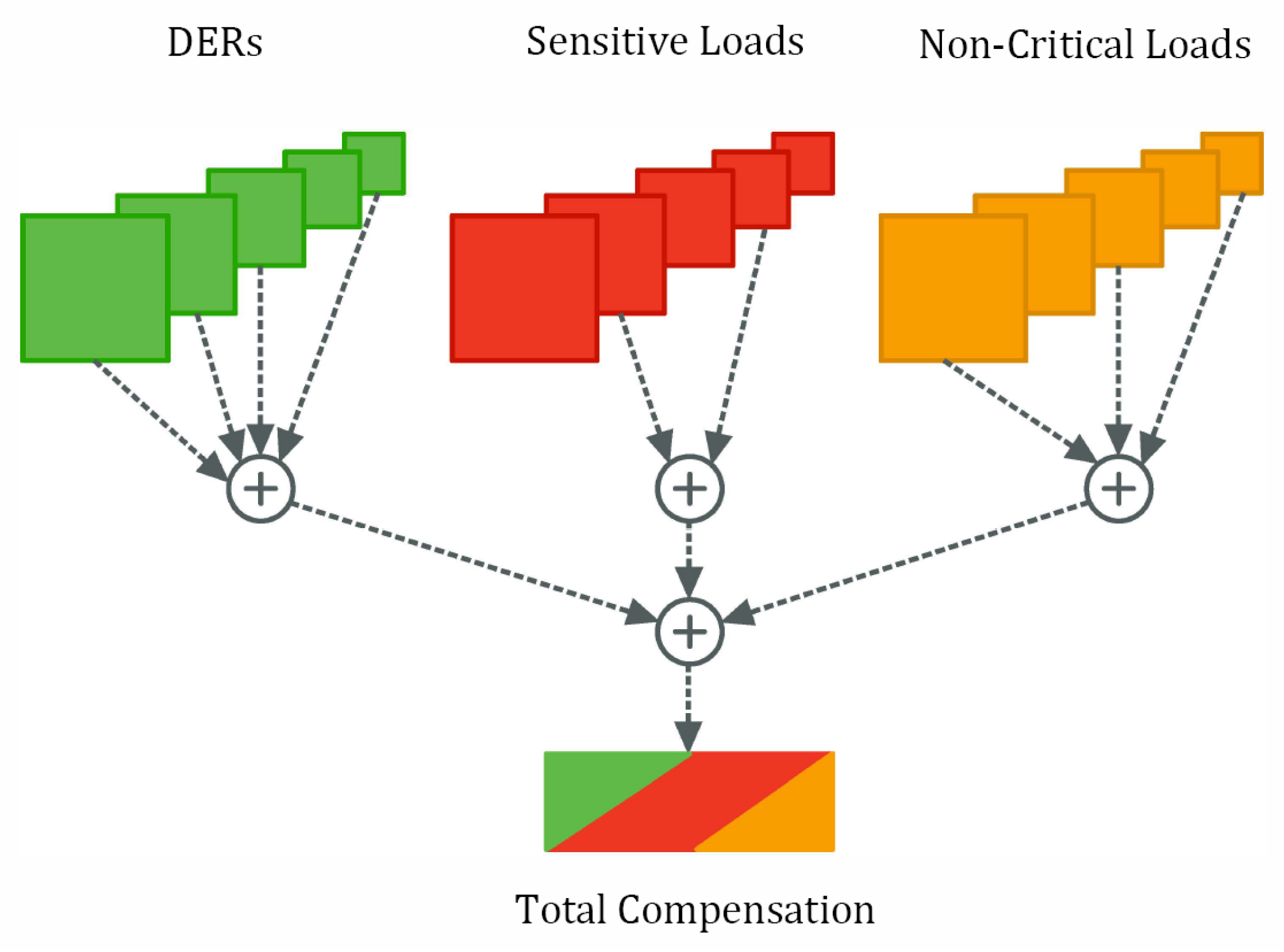
3.5. Excess Loading Equations
3.6. Online H Estimation
- Estimation of H is carried out periodically as opposed to in real-time. Historical data and forecasts can be used to reduce the number of times H is estimated. This work uses dynamic loading (modeled from real life data available at [41]), and the procedure is run the equivalent of six times per day. For the case studies presented on Section 5, H is assumed to have been estimated roughly two hours before the events take place.
3.7. Optimizing the Response
| Algorithm 2 Load Balance Optimization |
|
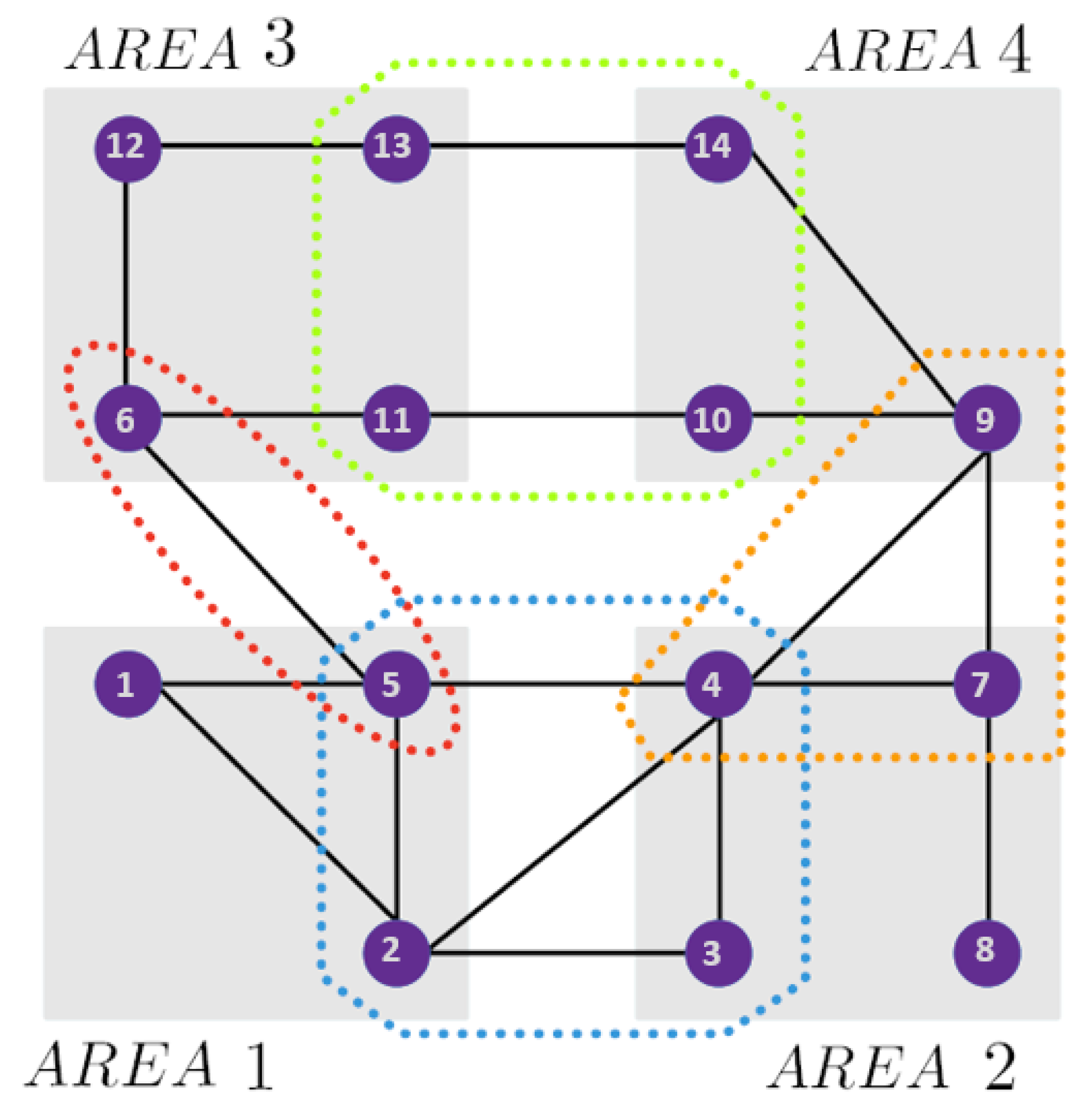
4. Overview in Distributed Form
- Adjustable frequency thresholds.
- Adjustable number of load-shedding stages.
- Customizable islands (based on PMU availability).
- Additional parameters such as voltage levels, frequency overshoot, rotor angles, breaker status, and loading of power lines can be integrated as constraints as long as the networks can support it.
- This method eliminates the need for simulations to establish underfrequency load-shedding (UFLS) contingencies.
5. Case Studies
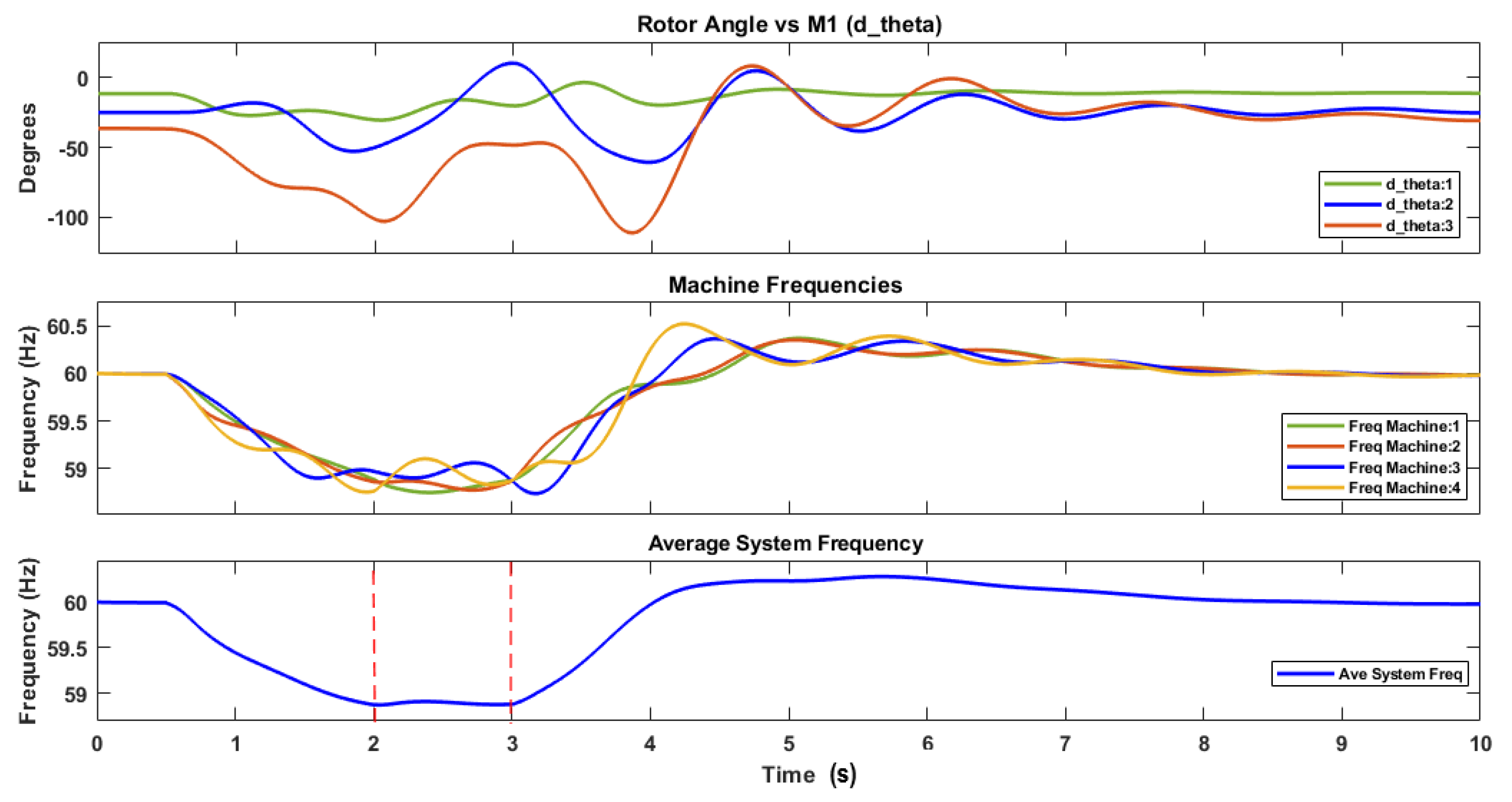
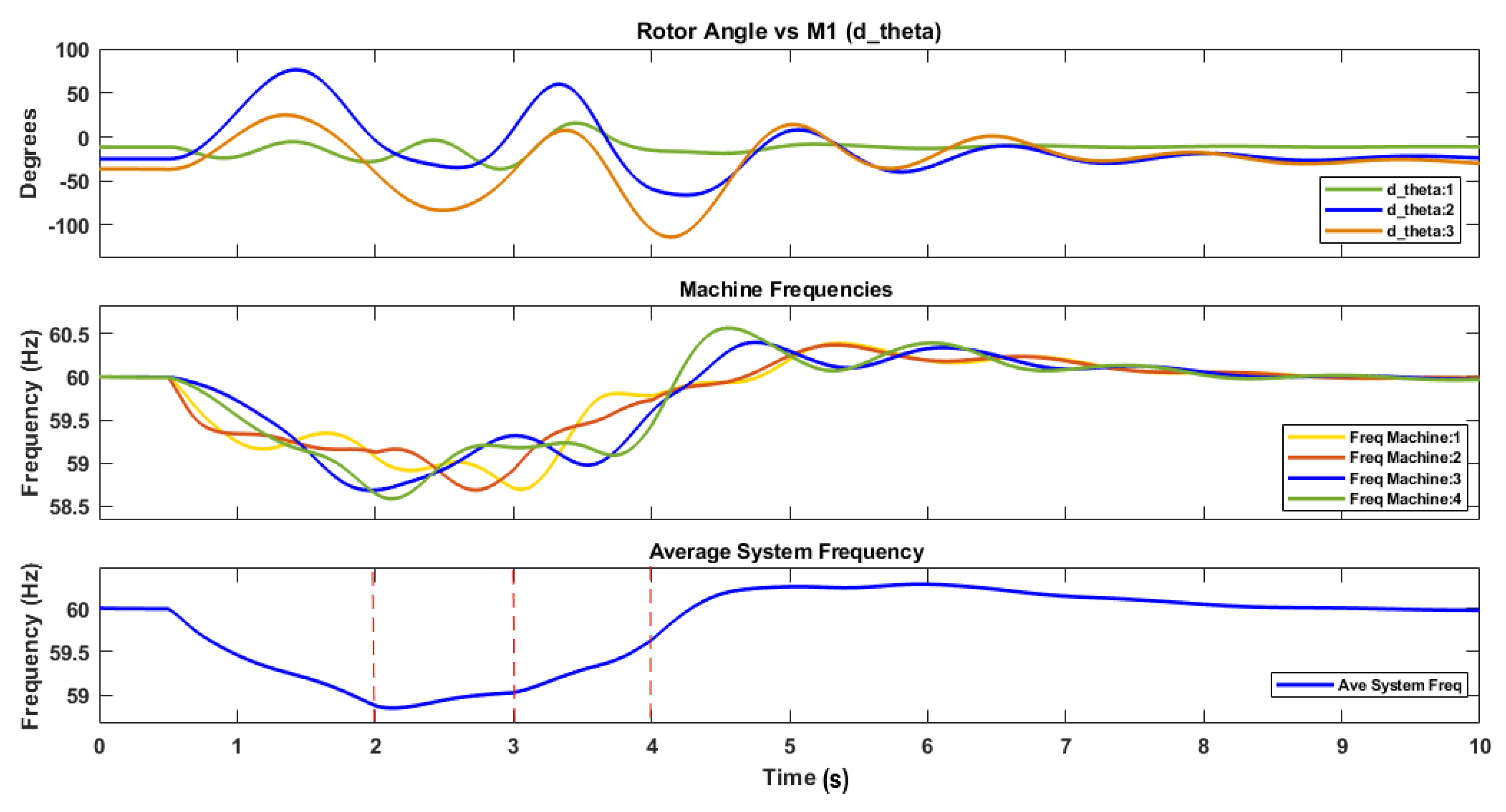
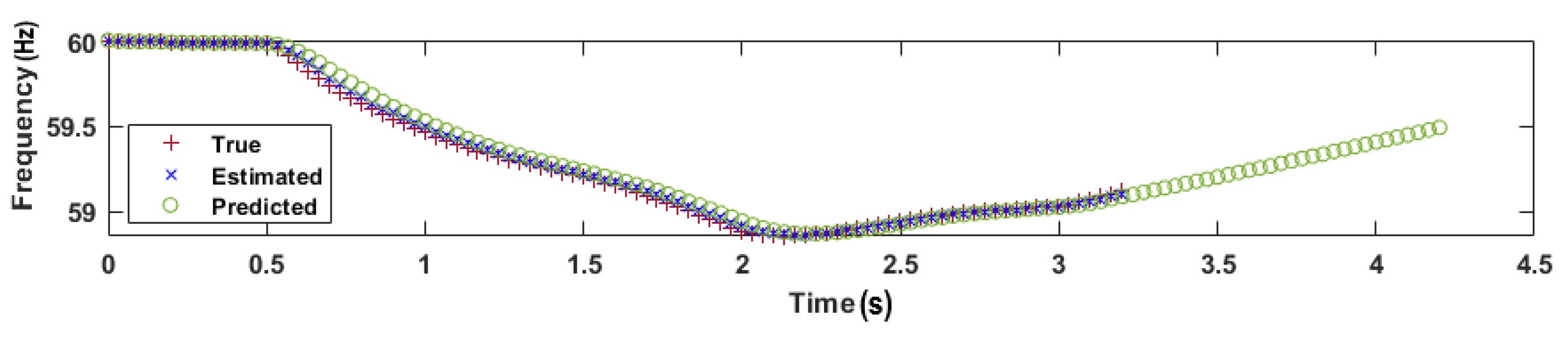
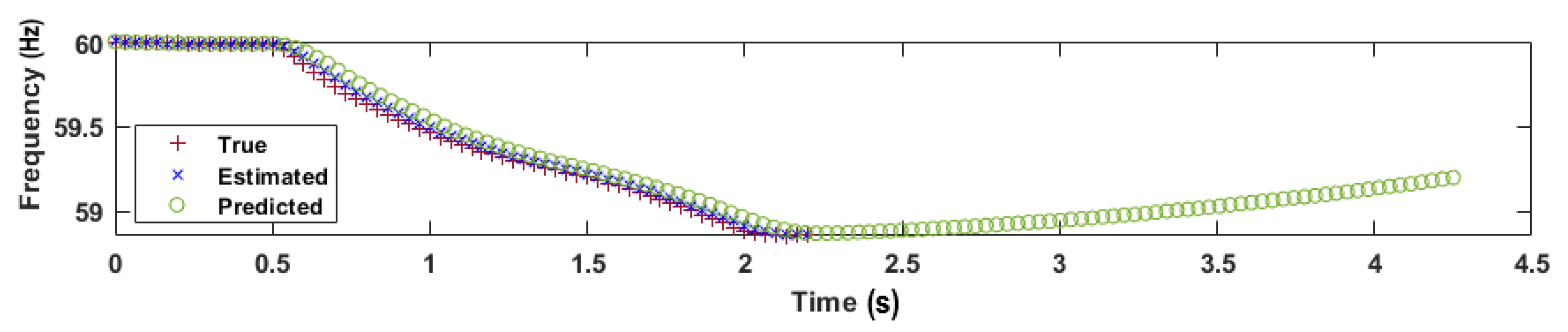
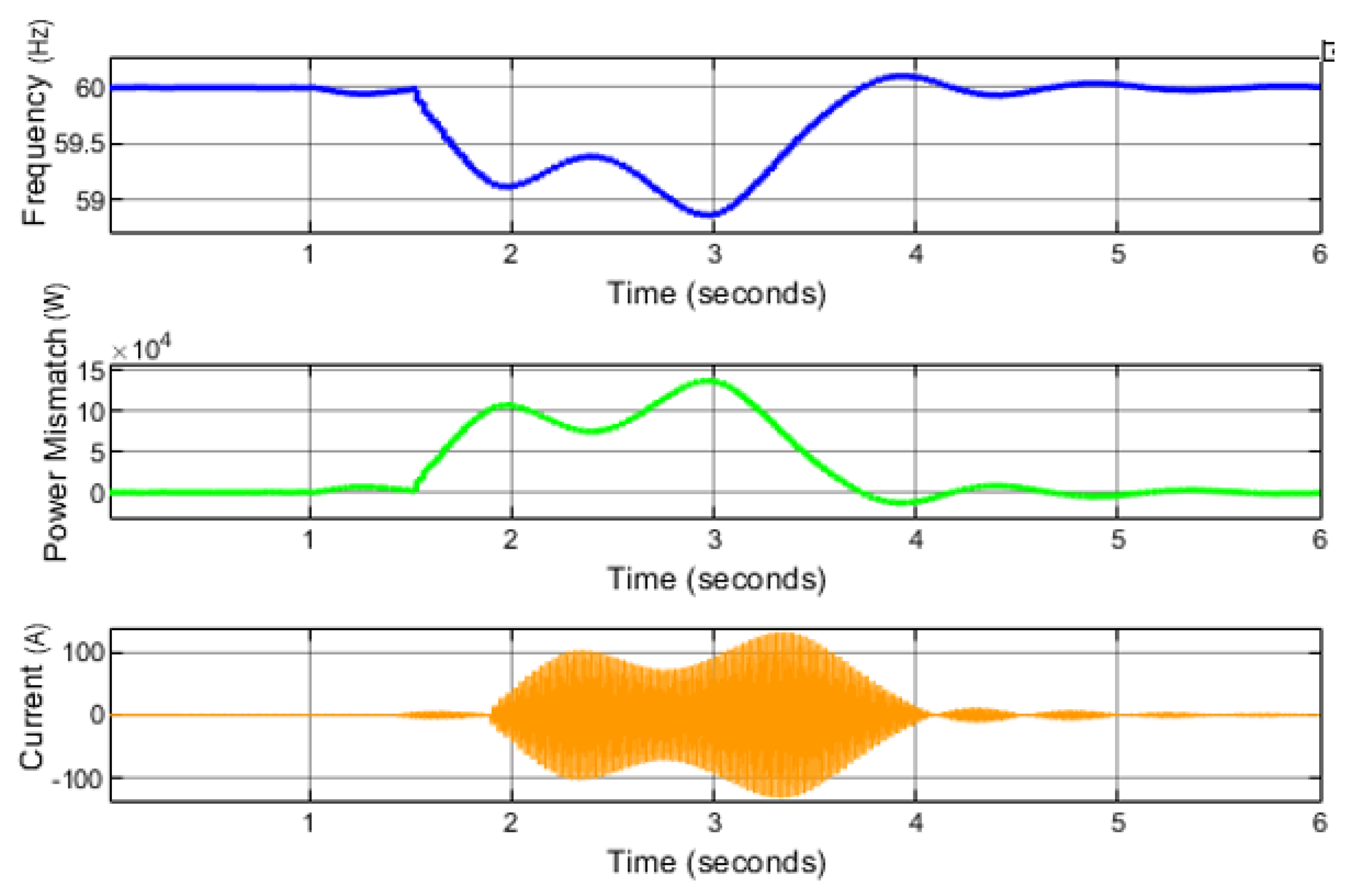
5.1. Illustrative Example
- The PF predicts a rise in frequency.
- The RoCoF is positive.
- Machine synchronization is stable.
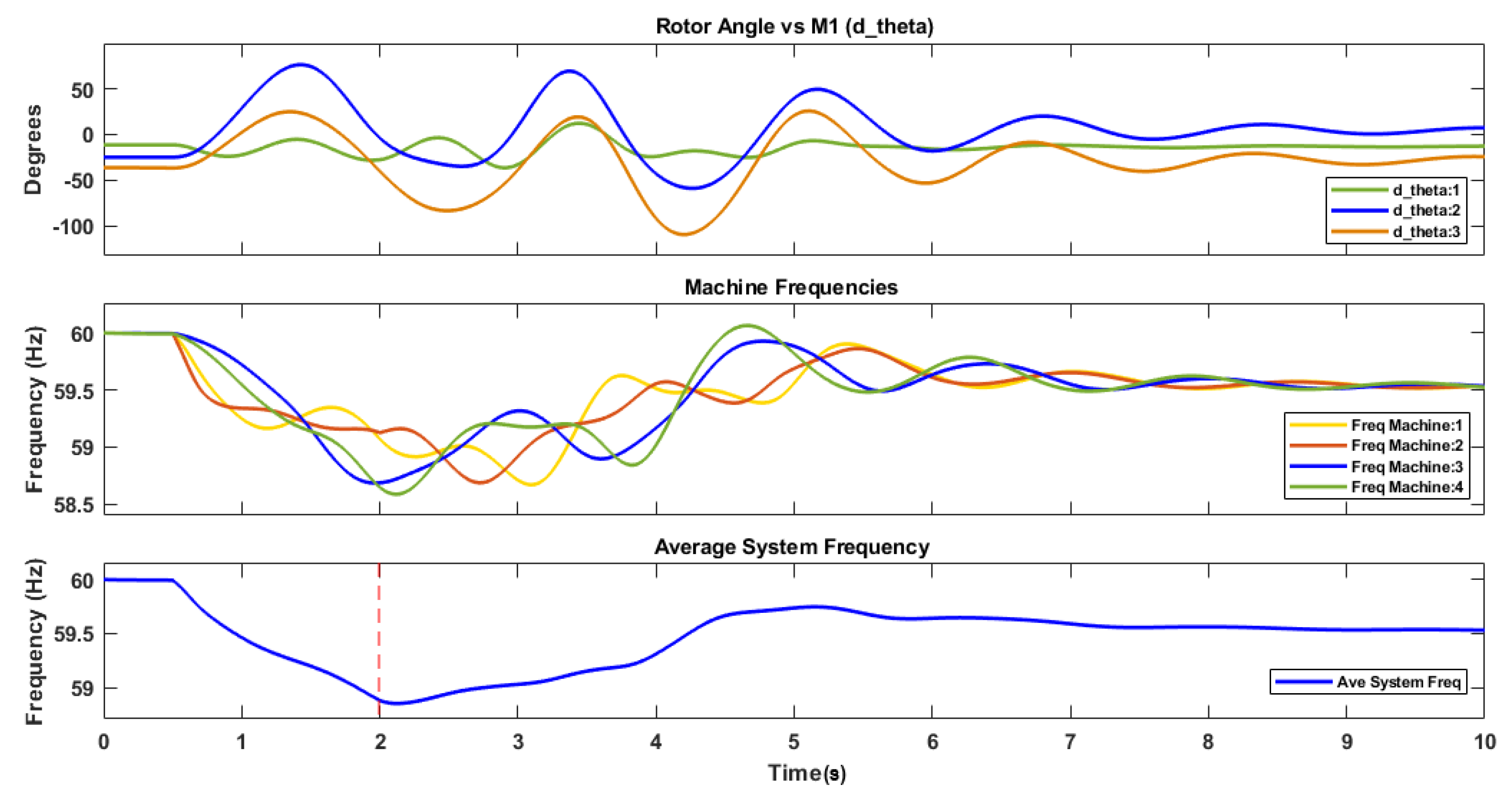
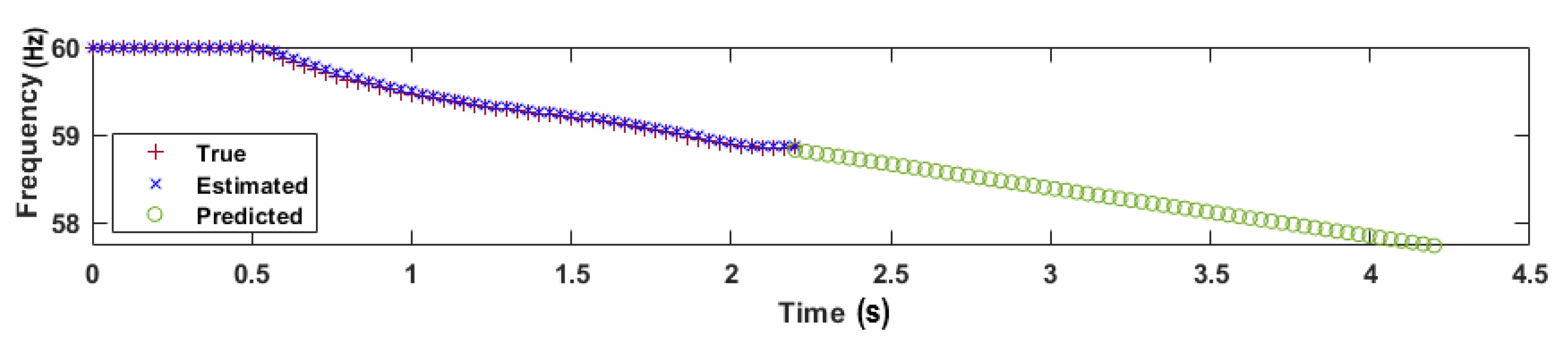
5.2. Case Study I
5.3. Case Study II
5.4. Case Study III
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DER | Distributed Energy Resource |
| KF | Kalman Filter |
| MILP | Mixed Integer Linear Programming |
| PMU | Phasor Measurement Unit |
| PF | Particle Filter |
| RoCoF | Rate of Change of Frequency |
| UFLS | Underfrequency Load-Shedding |
Appendix A
| Disturbance Location | Total DER Capacity | Excess Loading |
|---|---|---|
| 1 | 5% | 18% |
| 2 | 3% | 21% |
| 3 | 6% | 20% |
| 4 | 8% | 22% |
| Disturbance Location | Machine | Loading % | Total DER Capacity | Excess Loading |
|---|---|---|---|---|
| 1 | 1 | 80% | 5% | 17% |
| 2 | 85% | |||
| 3 | 88% | |||
| 4 | 90% | |||
| 5 | 85% | |||
| 2 | 1 | 80% | 4% | 21% |
| 2 | 90% | |||
| 3 | 85% | |||
| 4 | 85% | |||
| 5 | 80% | |||
| 3 | 1 | 90% | 5% | 19% |
| 2 | 88% | |||
| 3 | 80% | |||
| 4 | 80% | |||
| 5 | 85% | |||
| 4 | 1 | 85% | 2% | 20% |
| 2 | 85% | |||
| 3 | 85% | |||
| 4 | 85% | |||
| 5 | 85% |
References
- Sigrist, L.; Rouco, L.; Echavarren, F.M. A review of the state of the art of UFLS schemes for isolated power systems. Int. J. Electr. Power Energy Syst. 2018, 99, 525–539. [Google Scholar] [CrossRef]
- NERC Standards PRC-006-SERC-02; NERC Standards PRC-006-SERC-02. NERC: New York, NY, USA, 2017. Available online: https://www.nerc.com/pa/Stand/Pages/PRC006SERC02RI.aspx (accessed on 14 February 2023).
- IEEE Std. C37.117-2007; IEEE Guide for the Application of Protective Relays Used for Abnormal Frequency Load Shedding and Restoration. IEEE: New York, NY, USA, 2007; p. c1.
- Rudez, U.; Mihalic, R. A novel approach to underfrequency load shedding. Electr. Power Syst. Res. 2011, 81, 636–643. [Google Scholar] [CrossRef]
- Sigrist, L.; Egido, I.; Rouco, L. Principles of a Centralized UFLS Scheme for Small Isolated Power Systems. IEEE Trans. Power Syst. 2013, 28, 1779–1786. [Google Scholar] [CrossRef]
- Larsson, M.; Rehtanz, C. Predictive frequency stability control based on wide-area phasor measurements. IEEE Power Eng. Soc. Summer Meet. 2005, 1, 233–238. [Google Scholar] [CrossRef]
- Rudez, U.; Mihalic, R. WAMS-Based Underfrequency Load Shedding with Short-Term Frequency Prediction. IEEE Trans. Power Deliv. 2016, 31, 1912–1920. [Google Scholar] [CrossRef]
- Bose, A. Smart Transmission Grid Applications and Their Supporting Infrastructure. IEEE Trans. Smart Grid 2010, 1, 11–19. [Google Scholar] [CrossRef]
- Li, C.; Wu, Y.; Sun, Y.; Zhang, H.; Liu, Y.; Liu, Y.; Terzija, V. Continuous Under-Frequency Load Shedding Scheme for Power System Adaptive Frequency Control. IEEE Trans. Power Syst. 2020, 35, 950–961. [Google Scholar] [CrossRef]
- Yao, W.; You, S.; Wang, W.; Deng, X.; Li, Y.; Zhan, L.; Liu, Y. A Fast Load Control System Based on Mobile Distribution-Level Phasor Measurement Unit. IEEE Trans. Smart Grid 2020, 11, 895–904. [Google Scholar] [CrossRef]
- Li, Q.; Xu, Y.; Ren, C. A Hierarchical Data-Driven Method for Event-Based Load Shedding Against Fault-Induced Delayed Voltage Recovery in Power Systems. IEEE Trans. Ind. Inform. 2021, 17, 699–709. [Google Scholar] [CrossRef]
- Wang, C.; Yu, H.; Chai, L.; Liu, H.; Zhu, B. Emergency Load Shedding Strategy for Microgrids Based on Dueling Deep Q-Learning. IEEE Access 2021, 9, 19707–19715. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.-H.; Kim, H.-M. An Effort-Based Reward Approach for Allocating Load Shedding Amount in Networked Microgrids Using Multiagent System. IEEE Trans. Ind. Inform. 2020, 16, 2268–2279. [Google Scholar] [CrossRef]
- Dehghanpour, E.; Karegar, H.K.; Kheirollahi, R. Under Frequency Load Shedding in Inverter Based Microgrids by Using Droop Characteristic. IEEE Trans. Power Deliv. 2021, 36, 1097–1106. [Google Scholar] [CrossRef]
- Brown, W.E.; Moreno-Centeno, E. Transmission-Line Switching for Load Shed Prevention via an Accelerated Linear Programming Approximation of AC Power Flows. IEEE Trans. Power Syst. 2020, 35, 2575–2585. [Google Scholar] [CrossRef]
- Pulendran, S.; Tate, J.E. Energy Storage System Control for Prevention of Transient Under-Frequency Load Shedding. IEEE Trans. Smart Grid 2017, 8, 927–936. [Google Scholar] [CrossRef]
- Sauhats, A.; Utans, A.; Silinevics, J.; Junghans, G.; Guzs, D. Enhancing Power System Frequency with a Novel Load Shedding Method Including Monitoring of Synchronous Condensers’ Power Injections. Energies 2021, 14, 1490. [Google Scholar] [CrossRef]
- Farantatos, E.; Huang, R.; Cokkinides, G.J.; Meliopoulos, A.P. A Predictive Generator Out-of-Step Protection and Transient Stability Monitoring Scheme Enabled by a Distributed Dynamic State Estimator. IEEE Trans. Power Deliv. 2016, 31, 1826–1835. [Google Scholar] [CrossRef]
- Sun, M.; Liu, G.; Popov, M.; Terzija, V.; Azizi, S. Underfrequency Load Shedding Using Locally Estimated RoCoF of the Center of Inertia. IEEE Trans. Power Syst. 2021, 36, 4212–4222. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, K.; Wan, J.; Xiong, Z.; Li, Y. Research on Particle Filter Tracking Method Based on Kalman Filter. In Proceedings of the IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 1564–1568. [Google Scholar] [CrossRef]
- Li, T.; Sattar, T.P.; Sun, S. Deterministic resampling: Unbiased sampling to avoid sample impoverishment in particle filters. Signal Process. 2012, 92, 1637–1645. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, J.; Huang, Z.; Diao, R. Assessing Gaussian Assumption of PMU Measurement Error Using Field Data. IEEE Trans. Power Deliv. 2018, 33, 3233–3236. [Google Scholar] [CrossRef]
- Yang, T.; Mehta, P.G.; Meyn, S.P. Feedback particle filter with mean-field coupling. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 7909–7916. [Google Scholar] [CrossRef]
- Yang, T.; Laugesen, R.S.; Mehta, P.G.; Meyn, S.P. Multivariable feedback particle filter. Automatica 2016, 10–23. [Google Scholar] [CrossRef]
- Yang, T.; Mehta, P.G.; Meyn, S.P. A mean-field control-oriented approach to particle filtering. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 2037–2043. [Google Scholar] [CrossRef]
- Elfring, J.; Torta, E.; van de Molengraft, R. Particle Filters: A Hands-On Tutorial. Sensors 2021, 21, 438. [Google Scholar] [CrossRef] [PubMed]
- Arulampalam, M.S.; Maskell, S.; Gordo, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 139, 174–188. [Google Scholar] [CrossRef]
- IEEE Std C37.118.1-2011 (Revision of IEEE Std C37.118-2005); IEEE Standard for Synchrophasor Measurements for Power Systems. IEEE: New York, NY, USA, 2011; pp. 1–61. [CrossRef]
- Paramo, G.; Bretas, A.; Meyn, S. Research Trends and Applications of PMUs. Energies 2022, 15, 5329. [Google Scholar] [CrossRef]
- Paramo, G.; Bretas, A.; Meyn, S. High-Impedance Non-Linear Fault Detection via Eigenvalue Analysis with low PMU Sampling Rates. In Proceedings of the 2023 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 21–24 November 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Anderson, P.M.; Mirheydar, M. An adaptive method for setting underfrequency load shedding relays. IEEE Trans. Power Syst. 1992, 7, 647–655. [Google Scholar] [CrossRef]
- Rudez, U.; Mihalic, R. Monitoring the First Frequency Derivative to Improve Adaptive Underfrequency Load-Shedding Schemes. IEEE Trans. Power Syst. 2011, 26, 839–846. [Google Scholar] [CrossRef]
- SEL-751. Available online: https://selinc.com/products/751 (accessed on 1 July 2022).
- Zhao, J.; Gómez-Expósito, A.; Netto, M.; Mili, L.; Abur, A.; Terzija, V.; Kamwa, I.; Pal, B.; Singh, A.K.; Qi, J.; et al. Power System Dynamic State Estimation: Motivations, Definitions, Methodologies, and Future Work. IEEE Trans. Power Syst. 2019, 34, 3188–3198. [Google Scholar] [CrossRef]
- Horowitz, S.H.; Phadke, A.G. Power System Relaying, 4th ed.; Wiley: London, UK, 2014. [Google Scholar]
- Paramo, G.; Bretas, A.S. WAMS Based Eigenvalue Space Model for High Impedance Fault Detection. Appl. Sci. 2021, 11, 12148. [Google Scholar] [CrossRef]
- Nezam Sarmadi, S.A.; Venkatasubramanian, V.; Thomas, R.J. Electromechanical Mode Estimation Using Recursive Adaptive Stochastic Subspace Identification. IEEE Trans. Power Syst. 2014, 29, 349–358. [Google Scholar] [CrossRef]
- Kim, J.; Tong, L.; Thomas, R.J. Subspace Methods for Data Attack on State Estimation: A Data Driven Approach. IEEE Trans. Signal Process. 2015, 63, 1102–1114. [Google Scholar] [CrossRef]
- Zeng, F.; Zhang, J.; Chen, G.; Wu, Z.; Huang, S.; Liang, Y. Online Estimation of Power System Inertia Constant Under Normal Operating Conditions. IEEE Access 2020, 8, 101426–101436. [Google Scholar] [CrossRef]
- Naduvathuparambil, B.; Valenti, M.C.; Feliachi, A. Communication delays in wide area measurement systems. In Proceedings of the Thirty-Fourth Southeastern Symposium on System Theory (Cat. No.02EX540), Huntsville, AL, USA, 19 March 2002; pp. 118–122. [Google Scholar] [CrossRef]
- ERCOT. Grid Info: Load, Loading Data. 2022. Available online: http://www.ercot.com/gridinfo/load (accessed on 8 October 2022).
- Carrion, M.; Arroyo, J.M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Floudas, C.A.; Lin, X. Mixed Integer Linear Programming in Process Scheduling: Modeling, Algorithms, and Applications. Ann. Oper. Res. 2005, 139, 131–162. [Google Scholar] [CrossRef]
- Schweitzer, E.O.; Whitehead, D.; Zweigle, G.; Ravikumar, K.G.; Rzepka, G. Synchrophasor-based power system protection and control applications. In Proceedings of the 2010 Modern Electric Power Systems, Wroclaw, Poland, 20–22 September 2010; pp. 1–10. [Google Scholar] [CrossRef]
- Bretas, A.; Bretas, N.; London, J.; Carvalho, B. Cyber-Physical Power Systems State Estimation; Elsevier: Amsterdam, The Netherlands, 2021; Available online: https://www.sciencedirect.com/book/9780323900331/cyber-physical-power-systems-state-estimation (accessed on 1 November 2022).
- Kundur, P. Simplified Synchronous Machine—Speed Regulation. MathWorks. Available online: https://www.mathworks.com/help/sps/ug/pmu-pll-based-positive-sequence-kundur-s-two-area-system.html;jsessionid=9f7bc00182f35350d6b467d0cb3c (accessed on 1 November 2022).



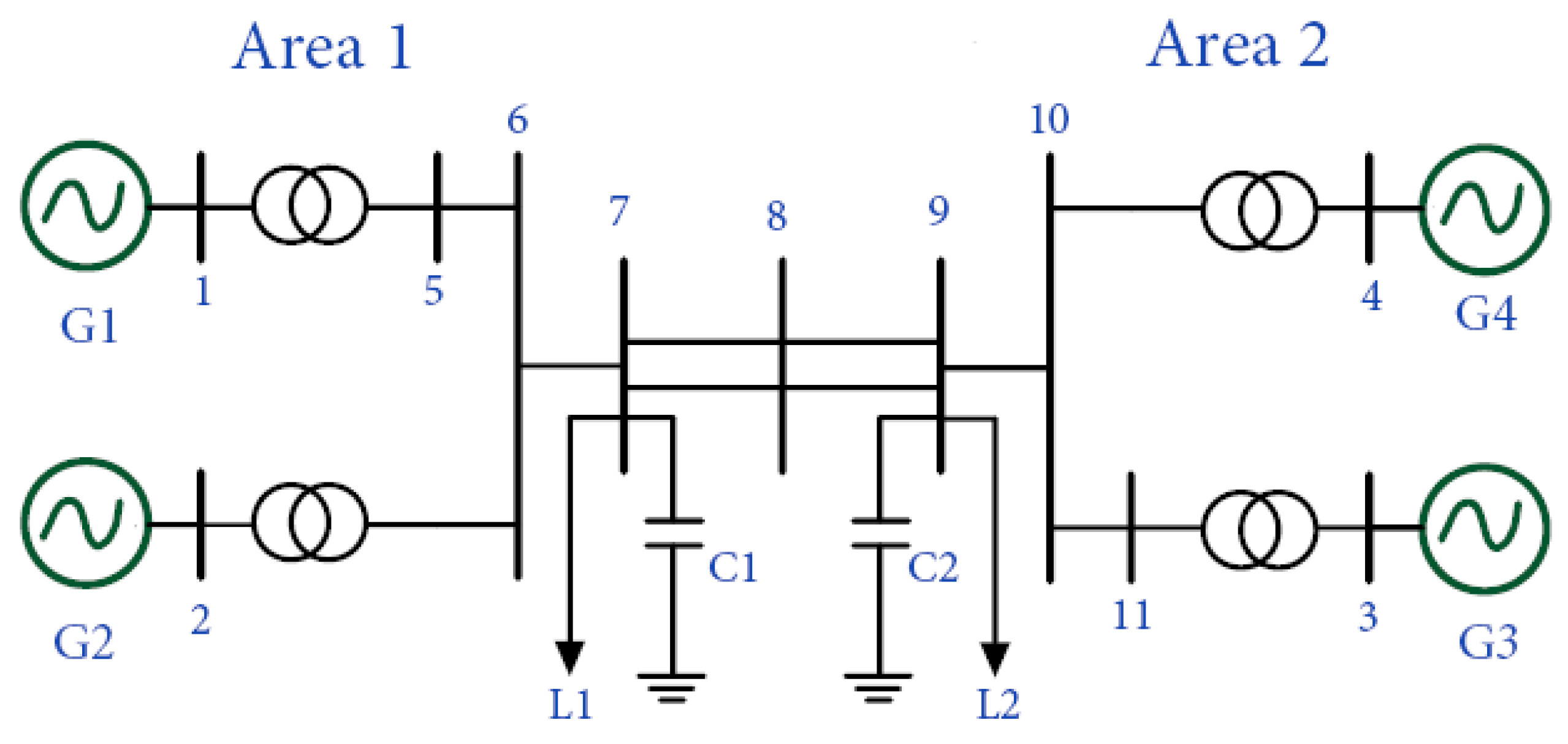
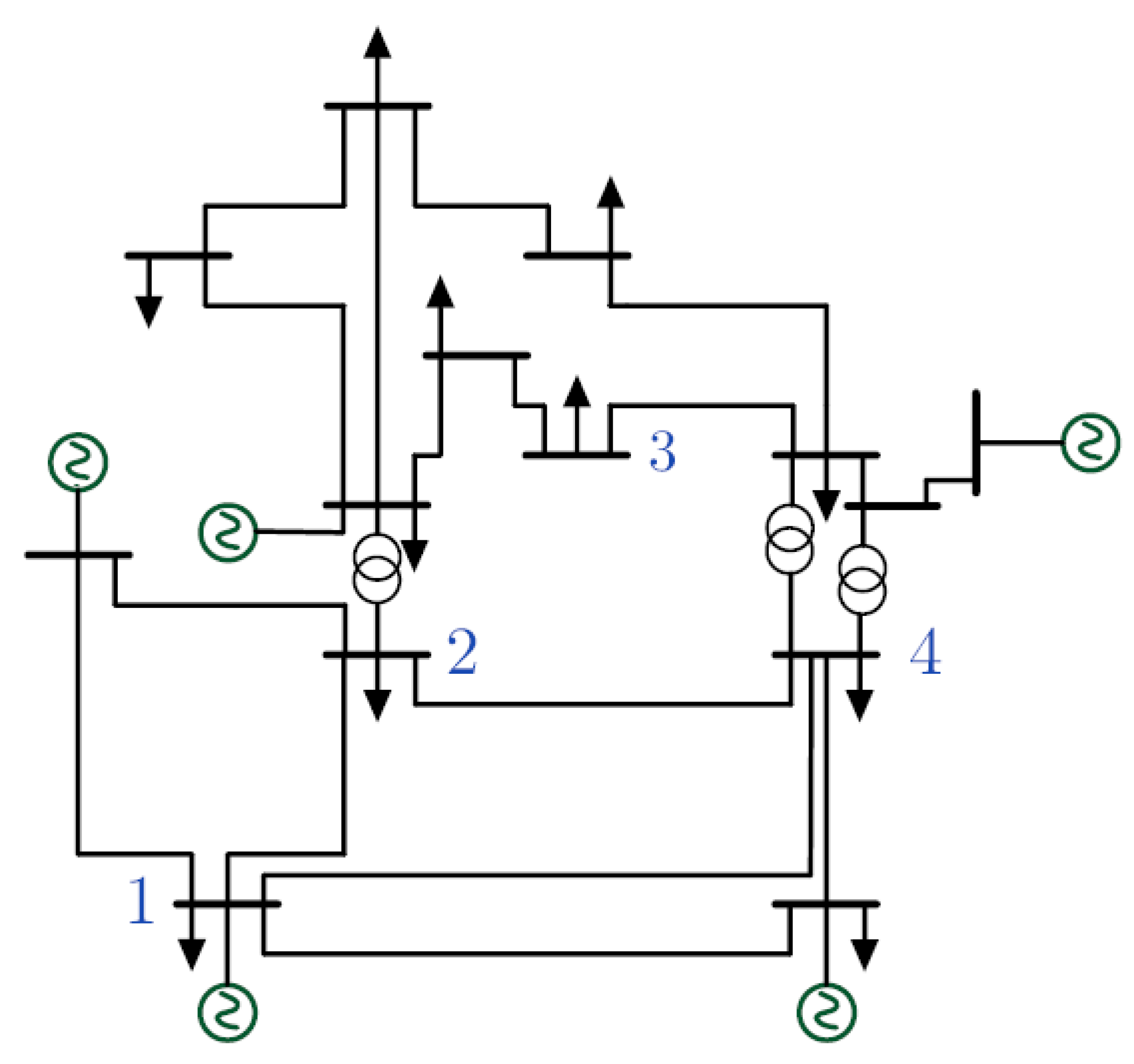
| Bus | V (pu) | (MW) | (MW) | (MVar) | (MW) |
|---|---|---|---|---|---|
| 1 | 1.03 | 615 | - | - | - |
| 2 | 1.01 | 700 | - | - | - |
| 3 | 1.03 | 719 | - | - | - |
| 4 | 1.01 | 700 | - | - | - |
| 7 | - | - | 967 | 100 | 200 |
| 9 | - | - | 1767 | 100 | 350 |
| Generator | Rating | H | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (MVA) | (pu) | (pu) | (pu) | (s) | (s) | (pu) | (pu) | (s) | (s) | (s) | |
| G1 | 900 | 1.8 | 0.3 | 0.25 | 8 | 0.03 | 1.7 | 0.25 | 0.4 | 0.05 | 6.5 |
| G2 | 900 | 1.8 | 0.3 | 0.25 | 8 | 0.03 | 1.7 | 0.25 | 0.4 | 0.05 | 6.5 |
| G3 | 900 | 1.8 | 0.3 | 0.25 | 8 | 0.03 | 1.7 | 0.25 | 0.4 | 0.05 | 6.175 |
| G4 | 900 | 1.8 | 0.3 | 0.25 | 8 | 0.03 | 1.7 | 0.25 | 0.4 | 0.05 | 6.175 |
| Disturbance Location | Method | Number of Stages | % of Load Excess Compensated |
|---|---|---|---|
| 1 | PF | 1 | 50% |
| PCF | 3 | 100% | |
| 2 | PF | 2 | 75% |
| PCF | 3 | 100% | |
| 3 | PF | 2 | 75% |
| PCF | 3 | 100% | |
| 4 | PF | 1 | 50% |
| PCF | 3 | 100% |
| Disturbance Location | Number of Stages | Overshoot |
|---|---|---|
| 1 | 1 | −0.83% |
| 2 | 2 | 1.13% |
| 3 | 2 | 0.91% |
| 4 | 1 | 2.1% |
| Disturbance Location | Method | Number of Stages | % of Load Excess Compensated |
|---|---|---|---|
| 1 | PF | 1 | 50% |
| PCF | 3 | 100% | |
| 2 | PF | 2 | 75% |
| PCF | 3 | 100% | |
| 3 | PF | 1 | 50% |
| PCF | 3 | 100% | |
| 4 | PF | 1 | 50% |
| PCF | 3 | 100% |
| Disturbance Location | Number of Stages | Overshoot |
|---|---|---|
| 1 | 1 | 2.3% |
| 2 | 2 | 0.84% |
| 3 | 1 | −1.72% |
| 4 | 1 | 1.93% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paramo, G.; Bretas, A. Proactive Frequency Stability Scheme: A Distributed Framework Based on Particle Filters and Synchrophasors. Energies 2023, 16, 4530. https://doi.org/10.3390/en16114530
Paramo G, Bretas A. Proactive Frequency Stability Scheme: A Distributed Framework Based on Particle Filters and Synchrophasors. Energies. 2023; 16(11):4530. https://doi.org/10.3390/en16114530
Chicago/Turabian StyleParamo, Gian, and Arturo Bretas. 2023. "Proactive Frequency Stability Scheme: A Distributed Framework Based on Particle Filters and Synchrophasors" Energies 16, no. 11: 4530. https://doi.org/10.3390/en16114530
APA StyleParamo, G., & Bretas, A. (2023). Proactive Frequency Stability Scheme: A Distributed Framework Based on Particle Filters and Synchrophasors. Energies, 16(11), 4530. https://doi.org/10.3390/en16114530






