Optimal Configuration of Hybrid Energy Storage Capacity in a Microgrid Based on Variational Mode Decomposition
Abstract
1. Introduction
- (1)
- Combining the energy mapping relationship between the frequency domain and time domain, the decomposition mode number of VMD is determined based on the principle of minimum total mode aliasing energy, which can completely decouple the original signal and effectively solve the problem of mode aliasing and the boundary effect.
- (2)
- Comprehensively considering the smoothing fluctuation characteristics of different energy storage components and the state of charge (SOC), the dividing point N of high frequency and low frequency in the unbalanced power between the source and load in the microgrid is selected to allocate charging and discharging power instructions for the battery and supercapacitor in order to obtain the best smoothing fluctuation effectiveness.
- (3)
- Taking the annual comprehensive cost of the HESS as the objective function, a hybrid energy storage capacity optimization configuration model is established, and the dividing point N is used as the optimization variable to solve the model and obtain the optimal configuration results. We analyze the advantages of VMD compared to EMD and of hybrid energy storage compared to single energy storage through the case study results.
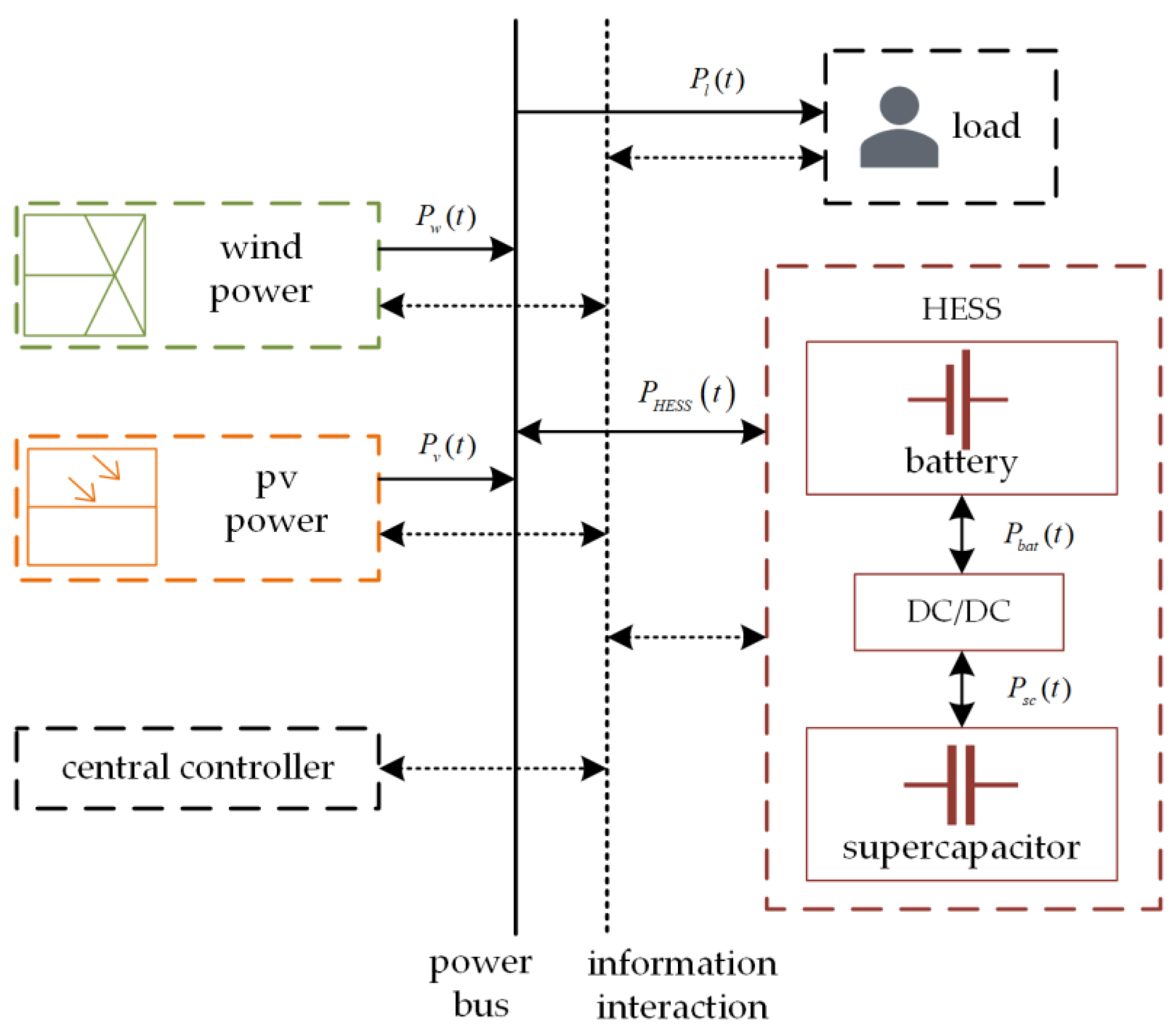
2. Structure of the Microgrid
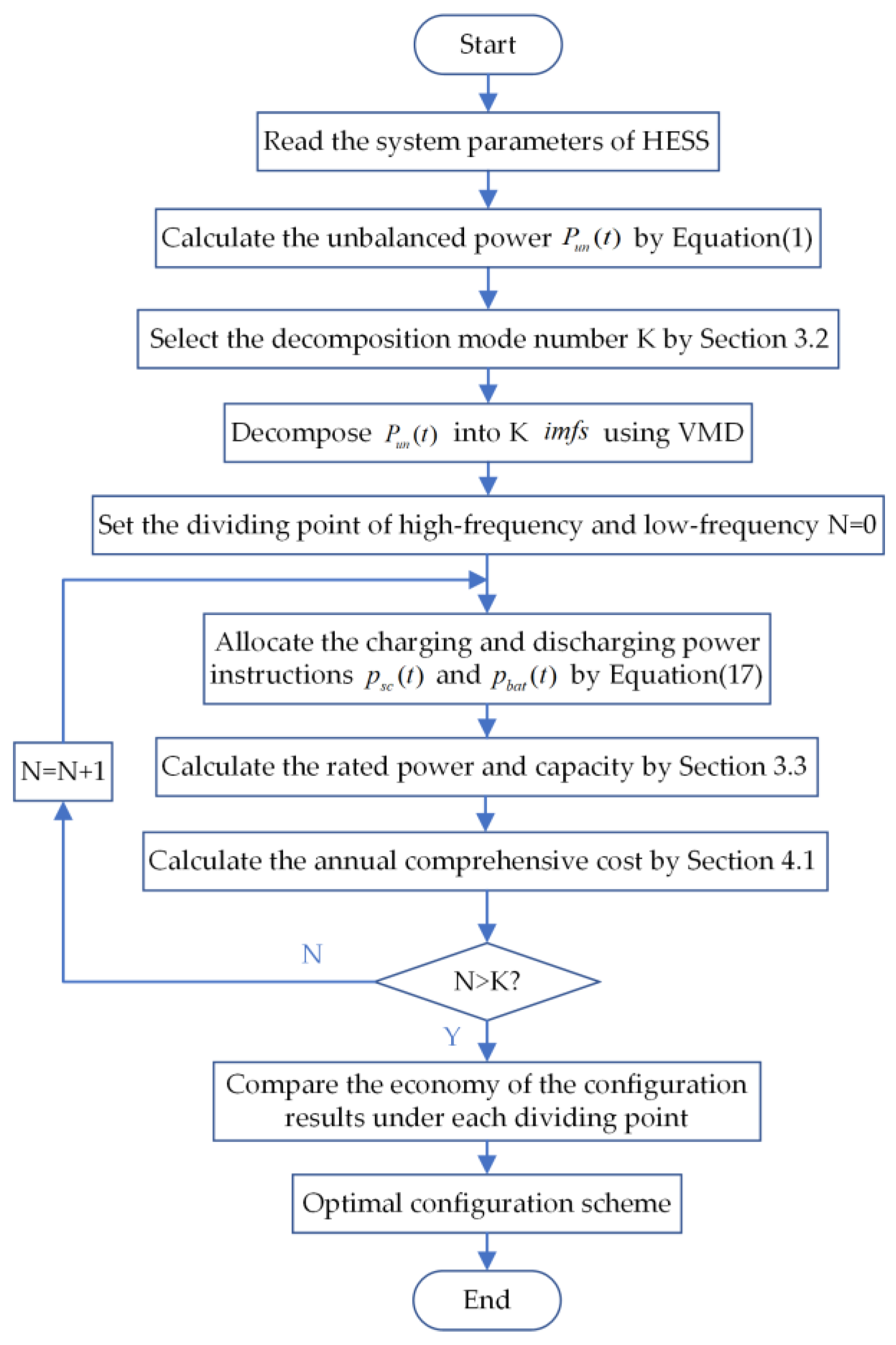
3. VMD for Capacity Configuration
3.1. Mathematical Model of VMD
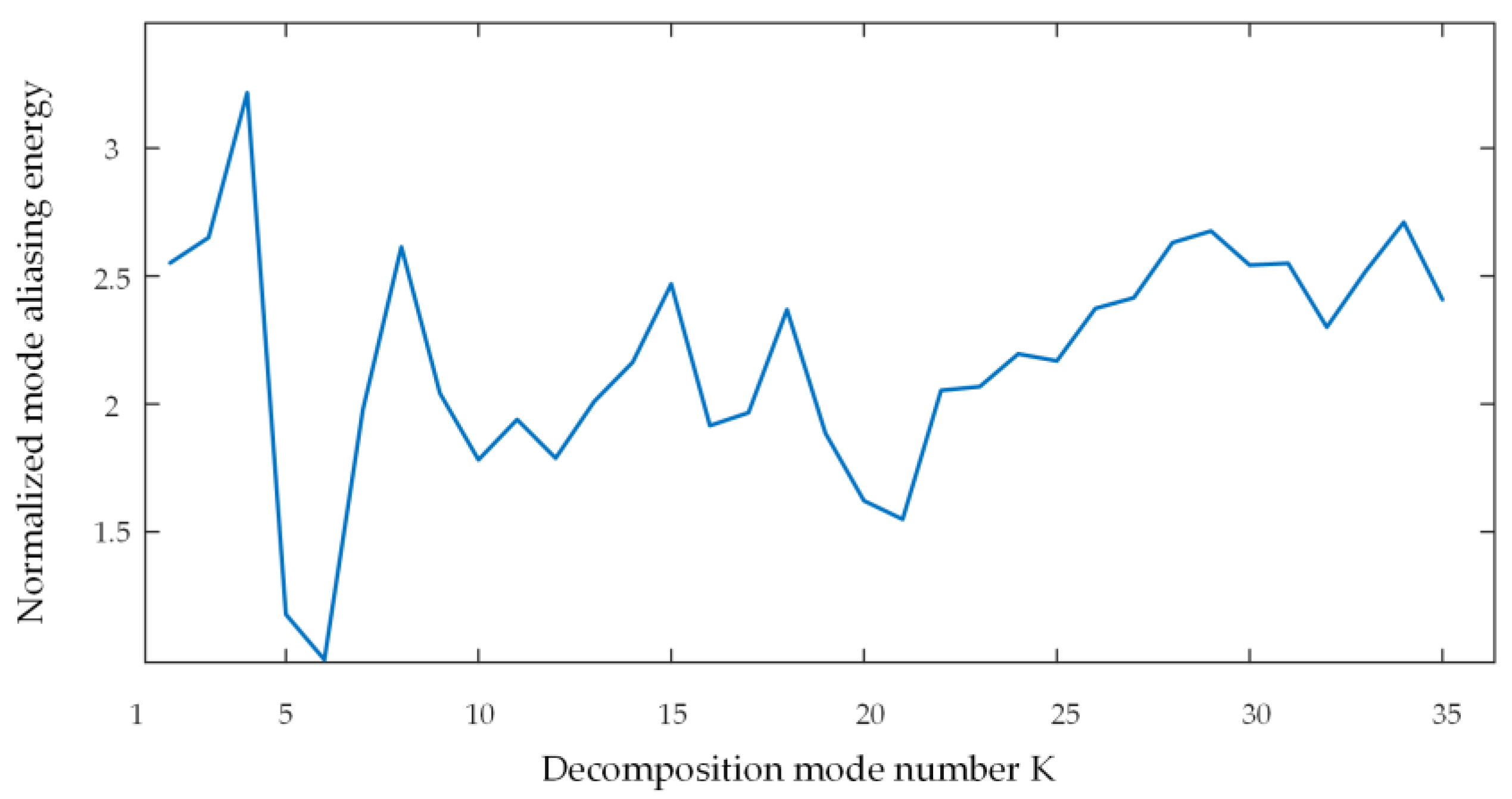
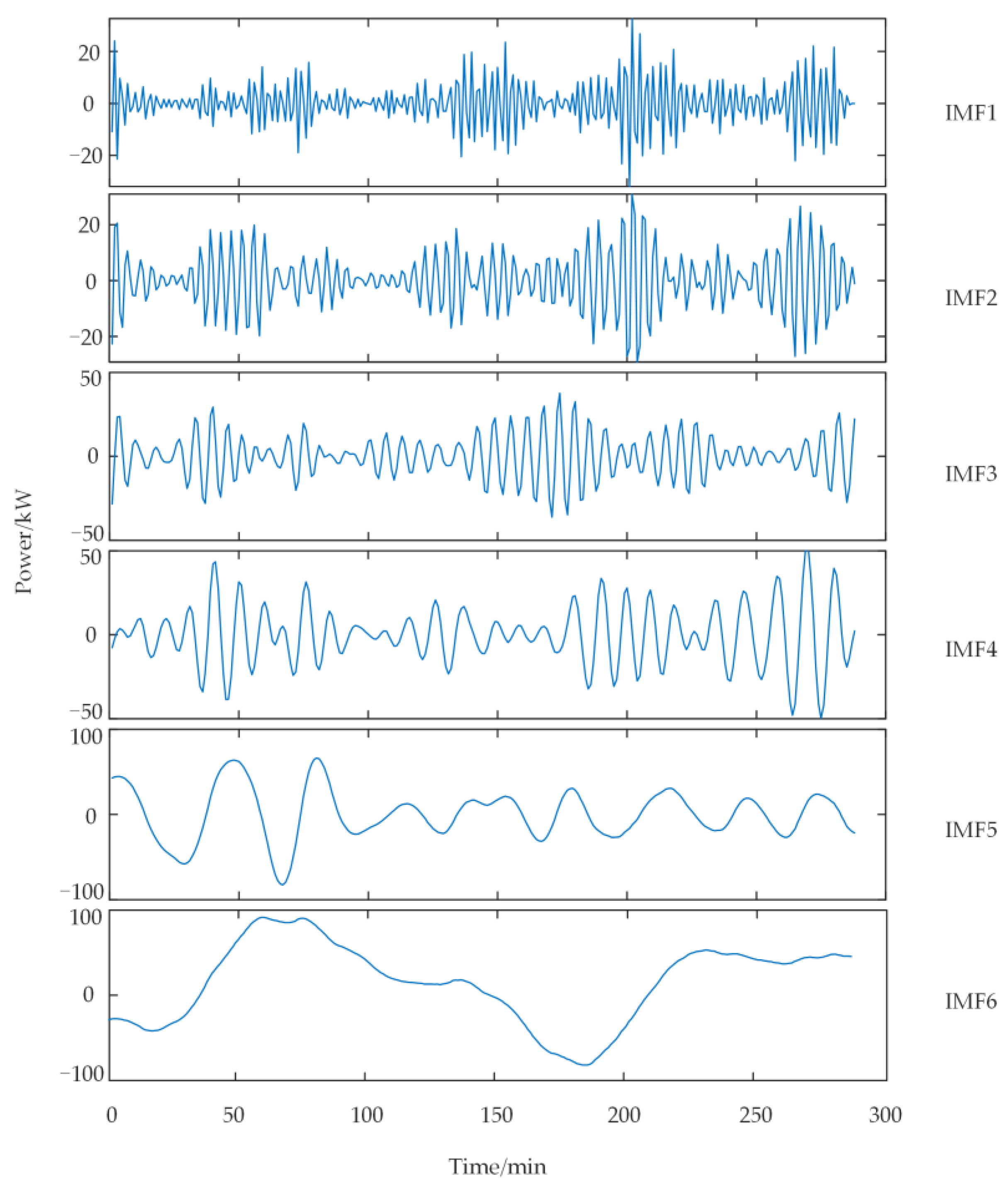
3.2. Selection of the Decomposition Mode Number
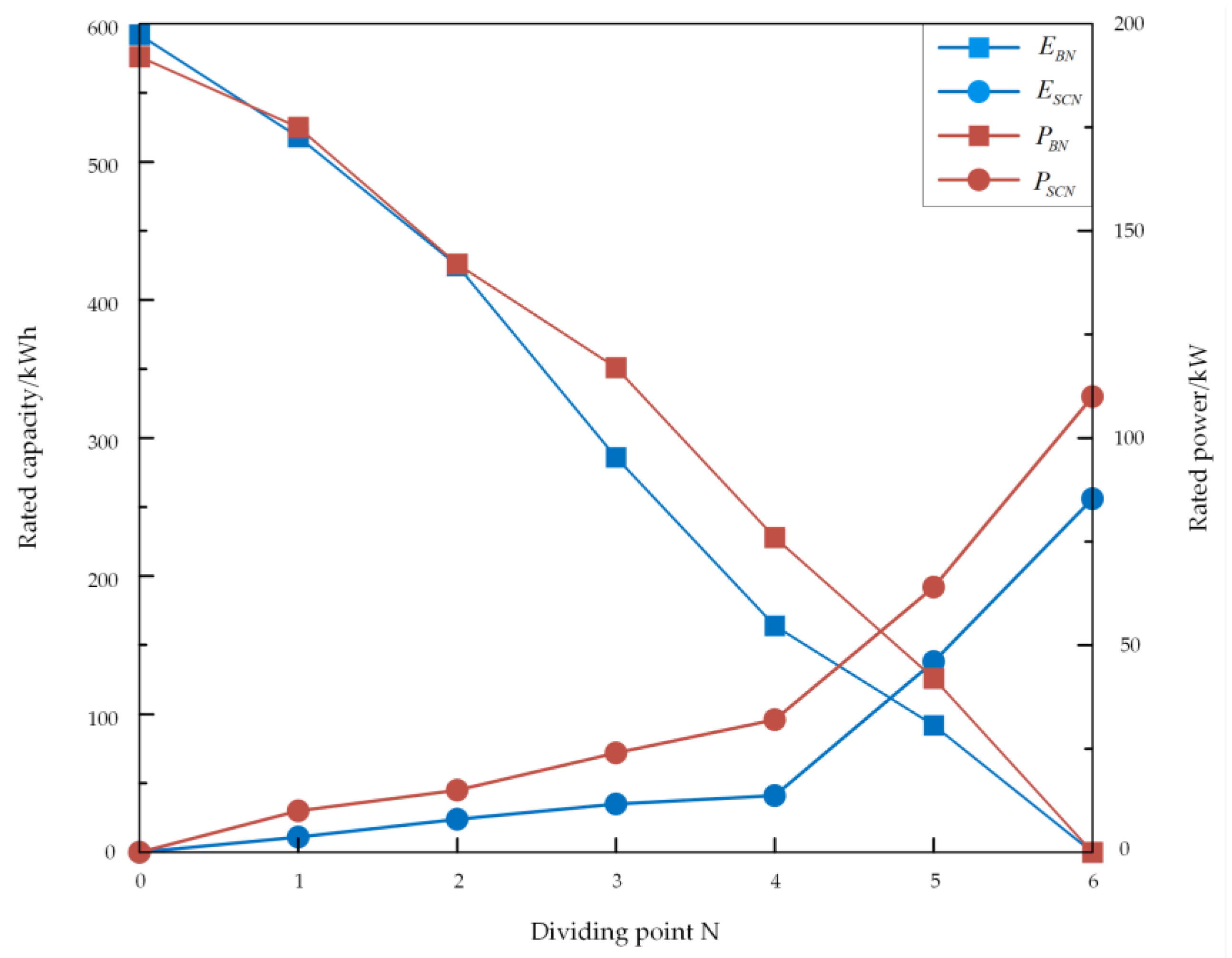
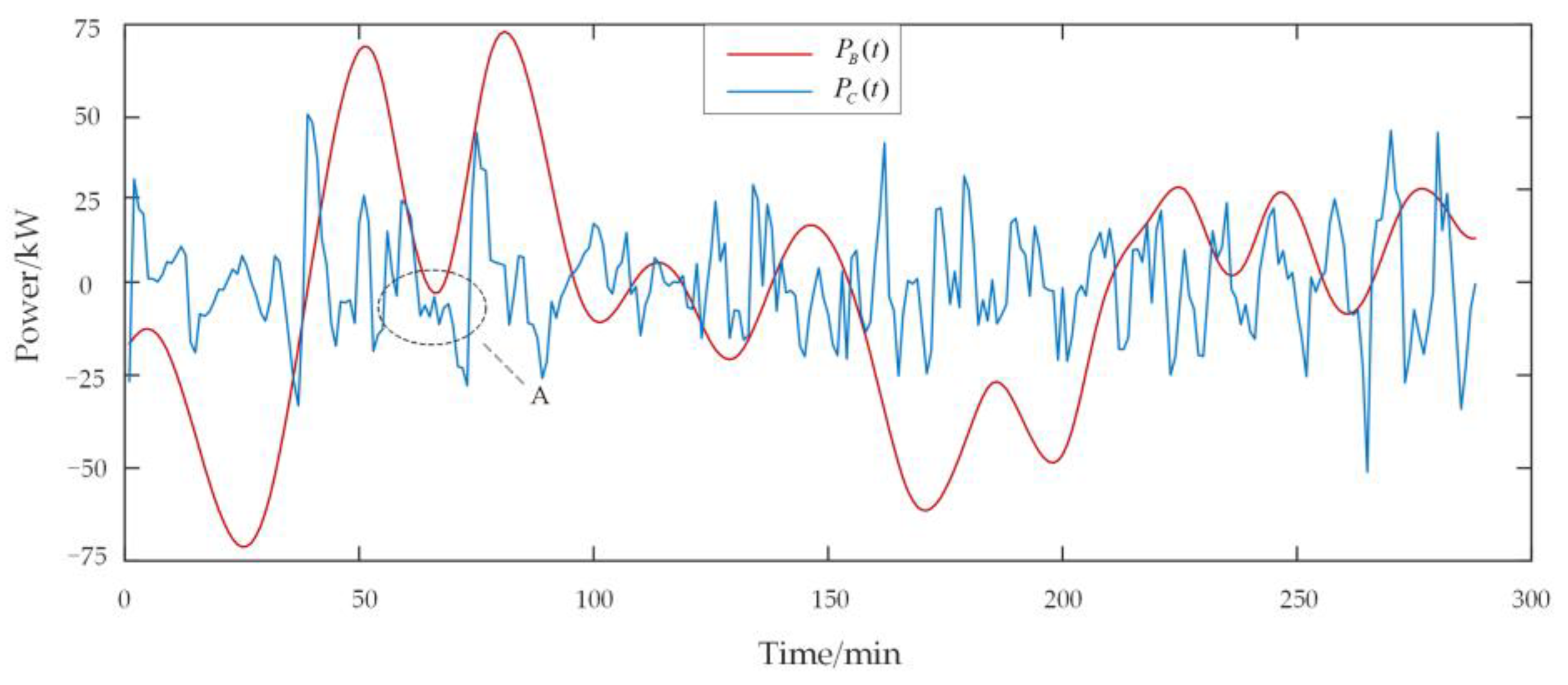
3.3. Rated Power and Rated Capacity of HESS
4. Optimal Configuration Model of the HESS
4.1. Objective Function
- (1)
- The initial investment cost of HESS is shown in Equation (25):
- (2)
- The operation and maintenance costs of the HESS are shown in Equation (27):
- (3)
- The replacement cost of the HESS is shown in Equation (28):
4.2. Constraint
- (1)
- Power balance constraint. Ensure that the HESS can always smooth out the unbalanced power in the microgrid.
- (2)
- Charging and discharging power constraints for batteries and supercapacitors. Ensure that the power and capacity of the HESS are within the rated range.
- (3)
- constraints for batteries and supercapacitors. Ensure the safe and stable operation of the HESS.
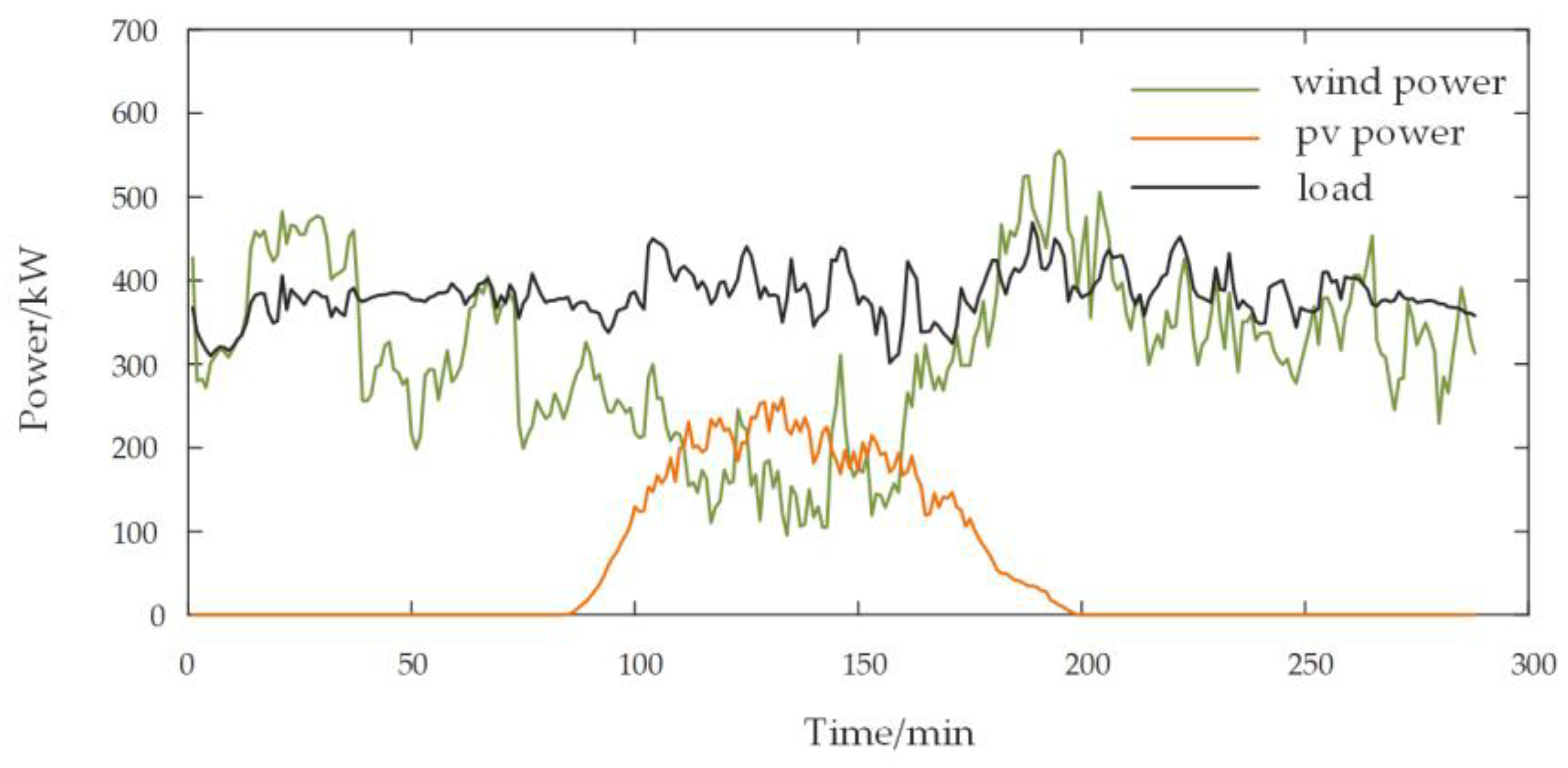
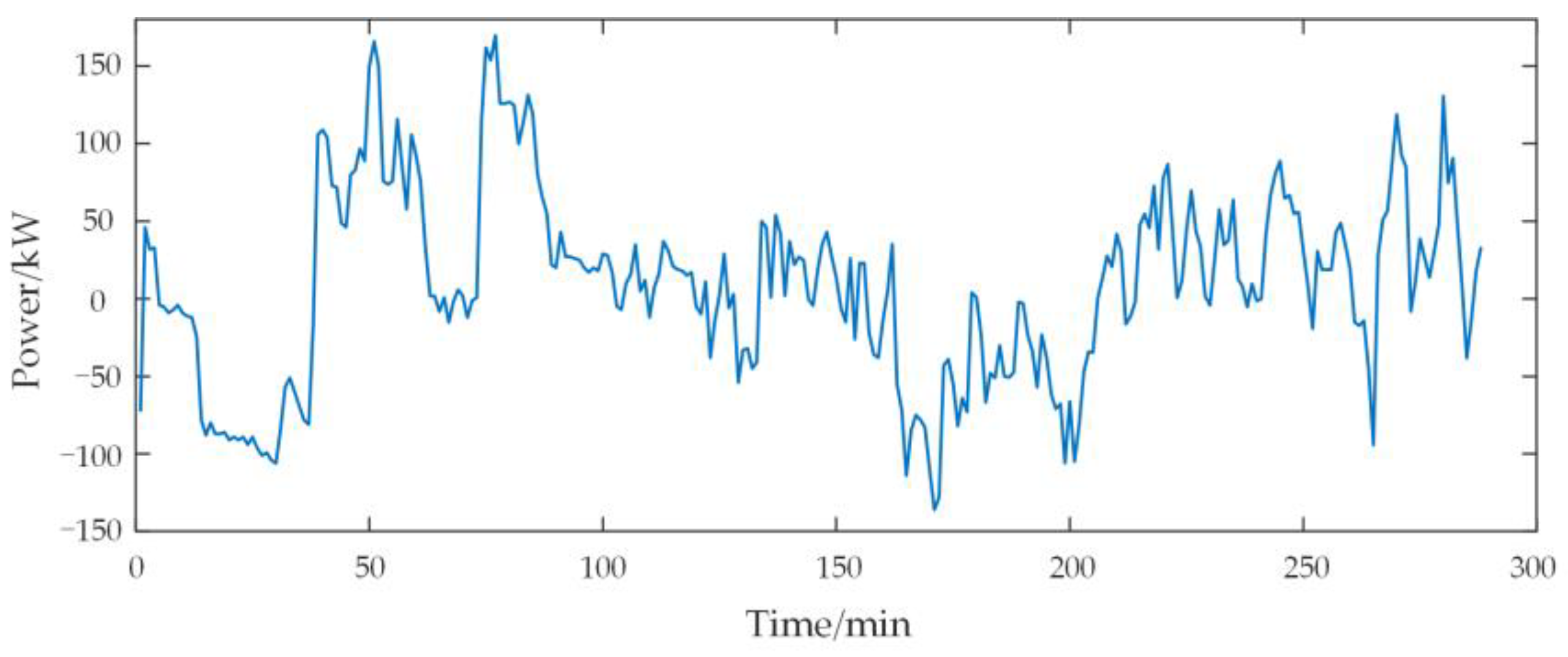
5. Case Study
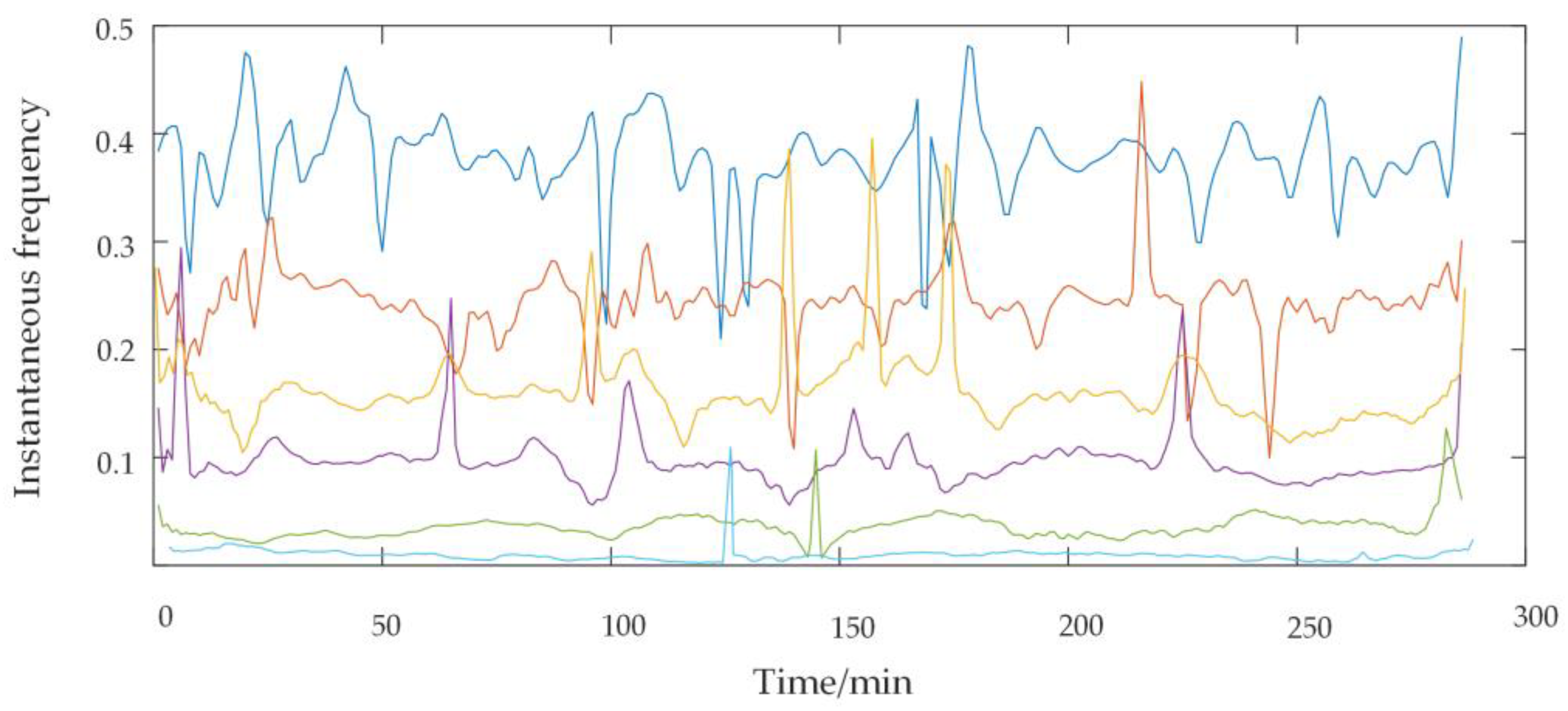
5.1. Decomposition Mode Number
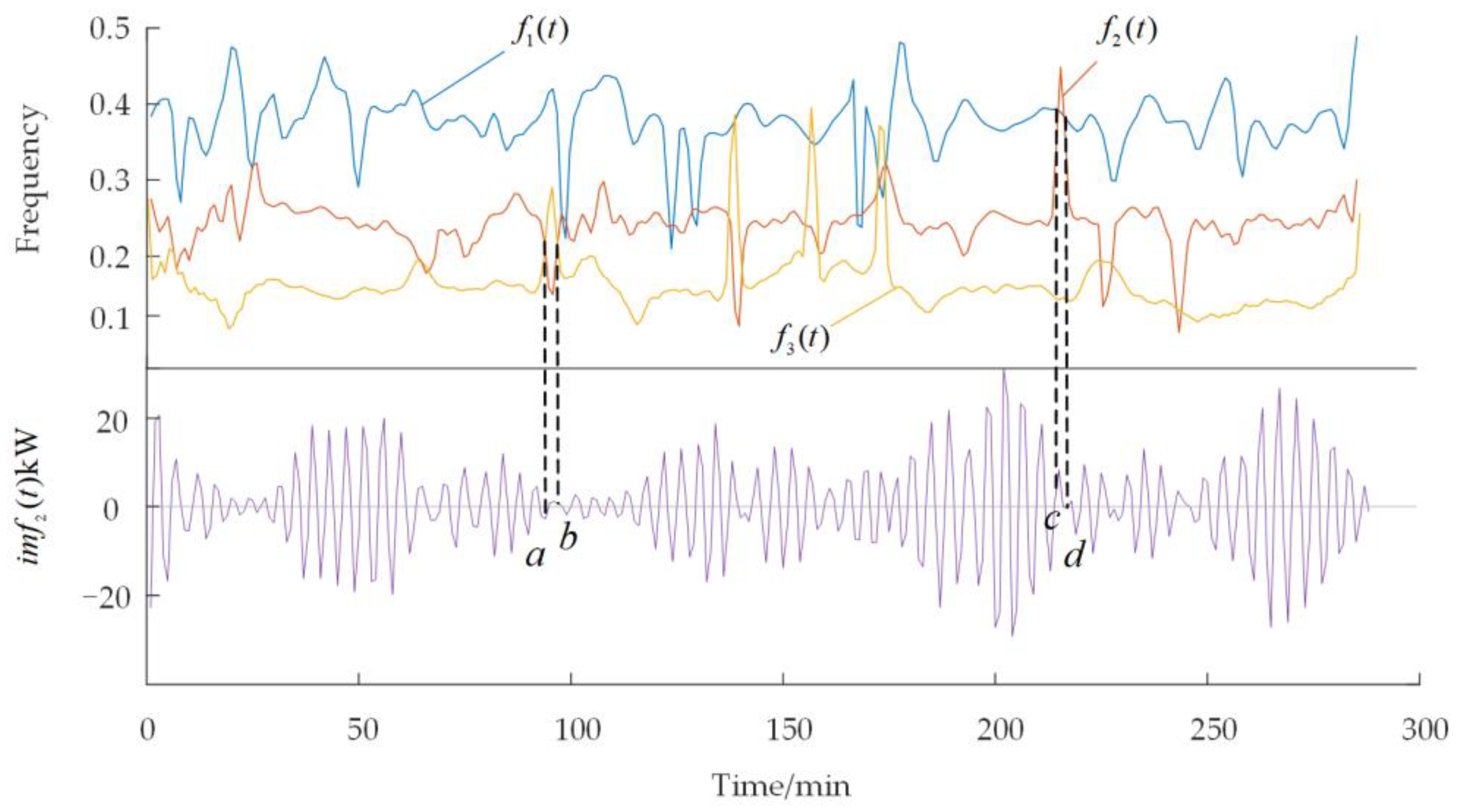
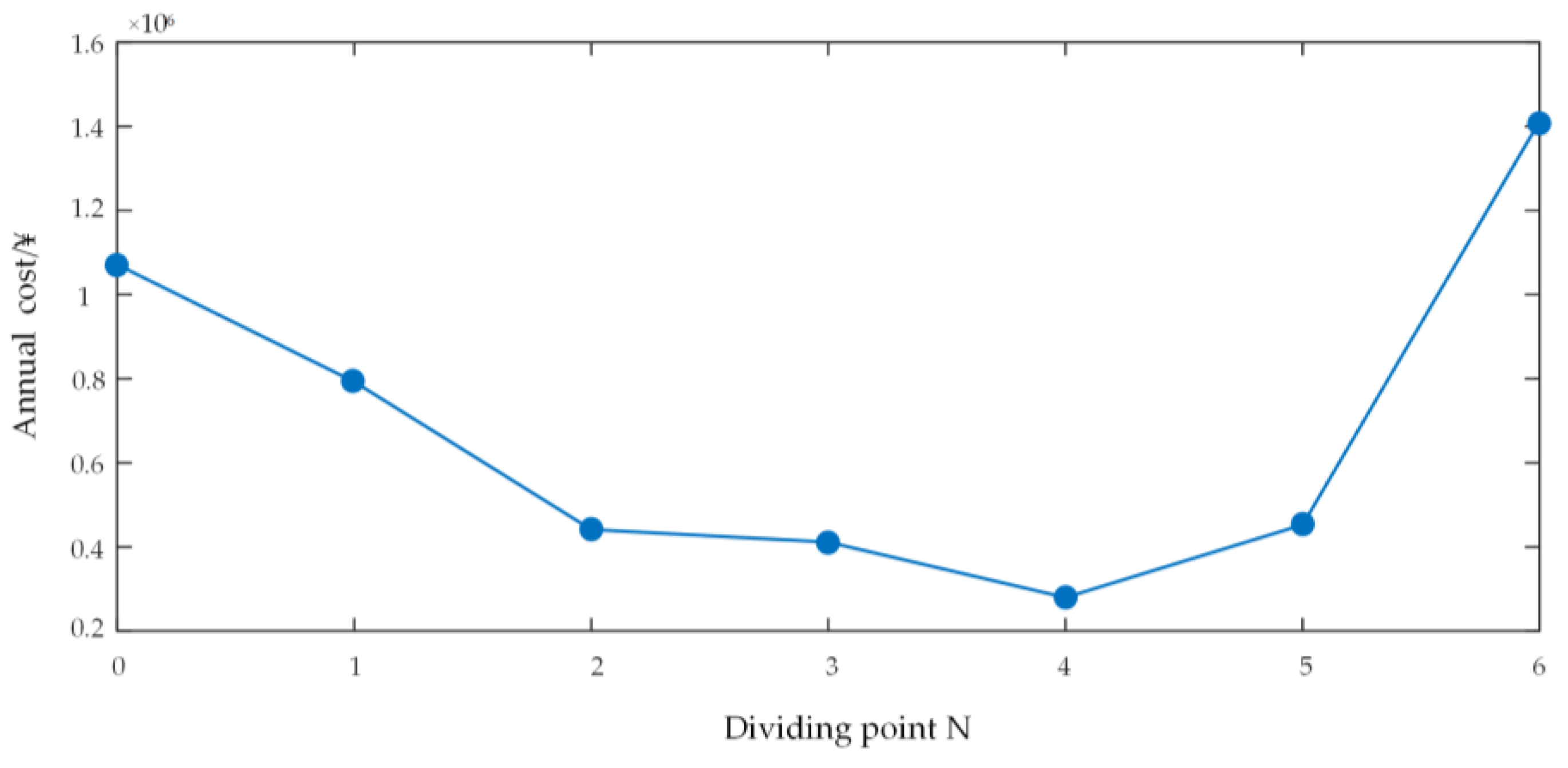
5.2. Frequency-Dividing Point
5.3. Configuration Result Analysis
- (1)
- Analysis of the Cost
- (2)
- Analysis of VMD over EMD
6. Conclusions
- (1)
- In order to take full advantage of the energy storage of the battery and supercapacitor, VMD is used to decompose the unbalanced power in the microgrid. The proposed decomposition mode number selection method, which is based on the principle of minimizing the total energy of modal aliasing, can prevent the configuration results from being influenced by subjective settings and significantly improve the applicability of VMD.
- (2)
- With the annual comprehensive cost of the HESS as the objective function and the high-frequency and low-frequency dividing points of the unbalanced power as the optimization variables, an optimal configuration model of the HESS capacity can be established. The unbalanced power is decoupled into two parts, low-frequency and high-frequency, as the charging and discharging power instructions for the battery and supercapacitor to obtain reasonable capacity configuration results. The service life of the battery in the HESS is 124.63% higher than that of the single energy storage battery. The annual comprehensive cost of the HESS is 31.68% lower than that of the single energy storage supercapacitor and 22.1% lower than that of the single energy storage battery. This indicates that the VMD-based hybrid energy storage capacity optimization configuration model proposed in this paper can not only realize the complementary advantages of power-type energy storage and energy-type energy storage but also improve the lifetime of the battery and the cost-effectiveness of the HESS.
- (3)
- By comparing the configuration costs, charging and discharging power curves, and SOC under both the EMD and VMD algorithms, it can be concluded that VMD is superior to EMD. The annual comprehensive cost of VMD is 15.9% lower than that of EMD. VMD can solve the problems of mode aliasing and SOC limit crossing that exist in EMD.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anvari, M.; Werther, B.; Lohmann, G.; Wächter, M.; Peinke, J.; Beck, H.P. Suppressing power output fluctuations of photovoltaic power plants. Sol. Energy 2017, 157, 735–743. [Google Scholar] [CrossRef]
- Renewable Energy Generation—Our World in Data. Available online: https://ourworldindata.org/grapher/modern-renewable-energy-consumption (accessed on 12 May 2023).
- Low-Emissions Sources Are Set to Cover Almost All the Growth in Global Electricity Demand in the Next Three Years—News—IEA. Available online: https://www.iea.org/news/low-emissions-sources-are-set-to-cover-almost-all-the-growth-in-global-electricity-demand-in-the-next-three-years (accessed on 12 May 2023).
- Rahman, S.; Saha, S.; Haque, M.E.; Islam, S.N.; Arif, M.T.; Mosadeghy, M.; Oo, A.M.T. A framework to assess voltage stability of power grids with high penetration of solar PV systems. Int. J. Electr. Power Energy Syst. 2022, 139, 107815. [Google Scholar] [CrossRef]
- Peng, Q.; Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. Grid-friendly power control for smart photovoltaic systems. Sol. Energy 2020, 210, 115–127. [Google Scholar] [CrossRef]
- Li, J.; Chen, S.; Wu, Y.; Wang, Q.; Liu, X.; Qi, L.; Lu, X.; Gao, L. How to make better use of intermittent and variable energy? A review of wind and photovoltaic power consumption in China. Renew. Sustain. Energy Rev. 2021, 137, 110626. [Google Scholar] [CrossRef]
- Khalilpour, K.R.; Vassallo, A. A generic framework for distributed multi-generation and multi-storage energy systems. Energy 2016, 114, 798–813. [Google Scholar] [CrossRef]
- Kerdphol, T.; Fuji, K.; Mitani, Y.; Watanabe, M.; Qudaih, Y. Optimization of a battery energy storage system using particle swarm optimization for stand-alone microgrids. Int. J. Electr. Power Energy Syst. 2016, 81, 32–39. [Google Scholar] [CrossRef]
- Yuan, H.; Ye, H.; Chen, Y.; Deng, W. Research on the optimal configuration of photovoltaic and energy storage in rural microgrid. Energy Rep. 2022, 8, 1285–1293. [Google Scholar] [CrossRef]
- Hesaroor, K.; Das, D. Optimal sizing of energy storage system in islanded microgrid using incremental cost approach. J. Energy Storage 2019, 24, 100768. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Arévalo, P.; Jurado, F. An optimization framework for planning wayside and on-board hybrid storage systems for tramway applications. J. Energy Storage 2021, 43, 103207. [Google Scholar] [CrossRef]
- Hernández, J.C.; Gomez-Gonzalez, M.; Sanchez-Sutil, F.; Jurado, F. Optimization of battery/supercapacitor-based photovoltaic household-prosumers providing self-consumption and frequency containment reserve as influenced by temporal data granularity. J. Energy Storage 2021, 36, 102366. [Google Scholar] [CrossRef]
- Choi, M.; Kim, S.; Seo, S. Energy Management Optimization in a Battery/Supercapacitor Hybrid Energy Storage System. IEEE Trans. Smart Grid 2012, 3, 463–472. [Google Scholar] [CrossRef]
- Wu, T.; Shi, X.; Liao, L.; Zhou, C.; Zhou, H.; Su, Y. A Capacity Configuration Control Strategy to Alleviate Power Fluctuation of Hybrid Energy Storage System Based on Improved Particle Swarm Optimization. Energies 2019, 12, 642. [Google Scholar] [CrossRef]
- Roy, P.; He, J.; Liao, Y. Cost Minimization of Battery-Supercapacitor Hybrid Energy Storage for Hourly Dispatching Wind-Solar Hybrid Power System. IEEE Access 2020, 8, 210099–210115. [Google Scholar] [CrossRef]
- Lin, L.; Zhu, L.; Yang, R.; Gao, Y.; Wu, Q. Capacity Optimization of Hybrid Energy Storage for Smoothing Power Fluctuations Based on Spectrum Analysis. In Proceedings of the 2017 2nd International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 20–23 September 2017; pp. 61–65. [Google Scholar]
- Li, B.; Zhang, J.; He, Y.; Wang, Y. Short-Term Load-Forecasting Method Based on Wavelet Decomposition with Second-Order Gray Neural Network Model Combined with ADF Test. IEEE Access 2017, 5, 16324–16331. [Google Scholar] [CrossRef]
- Santos, Y.A.; Nunes, M.P.; Lemes, L.A.; Bortoni, E.C. Evaluation of Hybrid Energy Storage Systems Using Wavelet and Stretched-Thread Methods. IEEE Access 2020, 8, 171882–171891. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, X.; Ma, H.; Ma, S. Wavelet Packet-fuzzy Control of Hybrid Energy Storage Systems for PV Power Smoothing. Proc. CSEE 2014, 34, 317–324. [Google Scholar] [CrossRef]
- He, Z.; Wang, Q.; Shen, Y.; Sun, M. Kernel Sparse Multitask Learning for Hyperspectral Image Classification with Empirical Mode Decomposition and Morphological Wavelet-Based Features. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5150–5163. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Fan, W.; Ma, P. A new chaotic time series hybrid prediction method of wind power based on EEMD-SE and full-parameters continued fraction. Energy 2017, 138, 977–990. [Google Scholar] [CrossRef]
- Sanabria-Villamizar, M.; Bueno-López, M.; Hernández, J.C.; Vera, D. Characterization of household-consumption load profiles in the time and frequency domain. J. Electr. Power Energy Syst. 2022, 137, 107756. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Yang, N.; Paire, D.; Gao, F.; Miraoui, A. Power management strategies for microgrid-A short review. In Proceedings of the 2013 IEEE Industry Applications Society Annual Meeting, Lake Buena Vista, FL, USA, 6–11 October 2013; pp. 1–9. [Google Scholar] [CrossRef]
- Jin, M.; Feng, W.; Marnay, C.; Spanos, C. Microgrid to enable optimal distributed energy retail and end-user demand response. Appl. Energy 2018, 210, 1321–1335. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, J.; Xu, K.; Sun, J.; Wang, Y. Optimal Allocation Method of Source and Storage Capacity of PV-Hydrogen Zero Carbon Emission Microgrid Considering the Usage Cost of Energy Storage Equipment. Energies 2022, 15, 4916. [Google Scholar] [CrossRef]
- Wu, T.; Ye, F.; Su, Y.; Wang, Y.; Riffat, S. Coordinated control strategy of DC microgrid with hybrid energy storage system to smooth power output fluctuation. Int. J. Low-Carbon Technol. 2020, 15, 46–54. [Google Scholar] [CrossRef]
- Lin, X.; Zamora, R. Controls of hybrid energy storage systems in microgrids: Critical review, case study and future trends. J. Energy Storage 2022, 47, 103884. [Google Scholar] [CrossRef]
- Hoang, K.D.; Lee, H. Accurate Power Sharing with Balanced Battery State of Charge in Distributed DC Microgrid. IEEE Trans. Ind. Electron. 2019, 66, 1883–1893. [Google Scholar] [CrossRef]
- Ghadimi, E.; Teixeira, A.; Shames, I.; Johansson, M. Optimal Parameter Selection for the Alternating Direction Method of Multipliers (ADMM): Quadratic Problems. IEEE Trans. Autom. Control 2015, 60, 644–658. [Google Scholar] [CrossRef]
- Deng, M.; Deng, A.; Zhu, J.; Sun, W. Adaptive Bandwidth Fourier Decomposition Method for Multi-Component Signal Processing. IEEE Access 2019, 7, 109776–109791. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Pan, G.; Zhao, Y. A novel hybrid model based on VMD-WT and PCA-BP-RBF neural network for short-term wind speed forecasting. Energy Convers. Manag. 2019, 195, 180–197. [Google Scholar] [CrossRef]
- Achlerkar, P.D.; Samantaray, S.R.; Sabarimalai Manikandan, M. Variational Mode Decomposition and Decision Tree Based Detection and Classification of Power Quality Disturbances in Grid-Connected Distributed Generation System. IEEE Trans. Smart Grid 2018, 9, 3122–3132. [Google Scholar] [CrossRef]
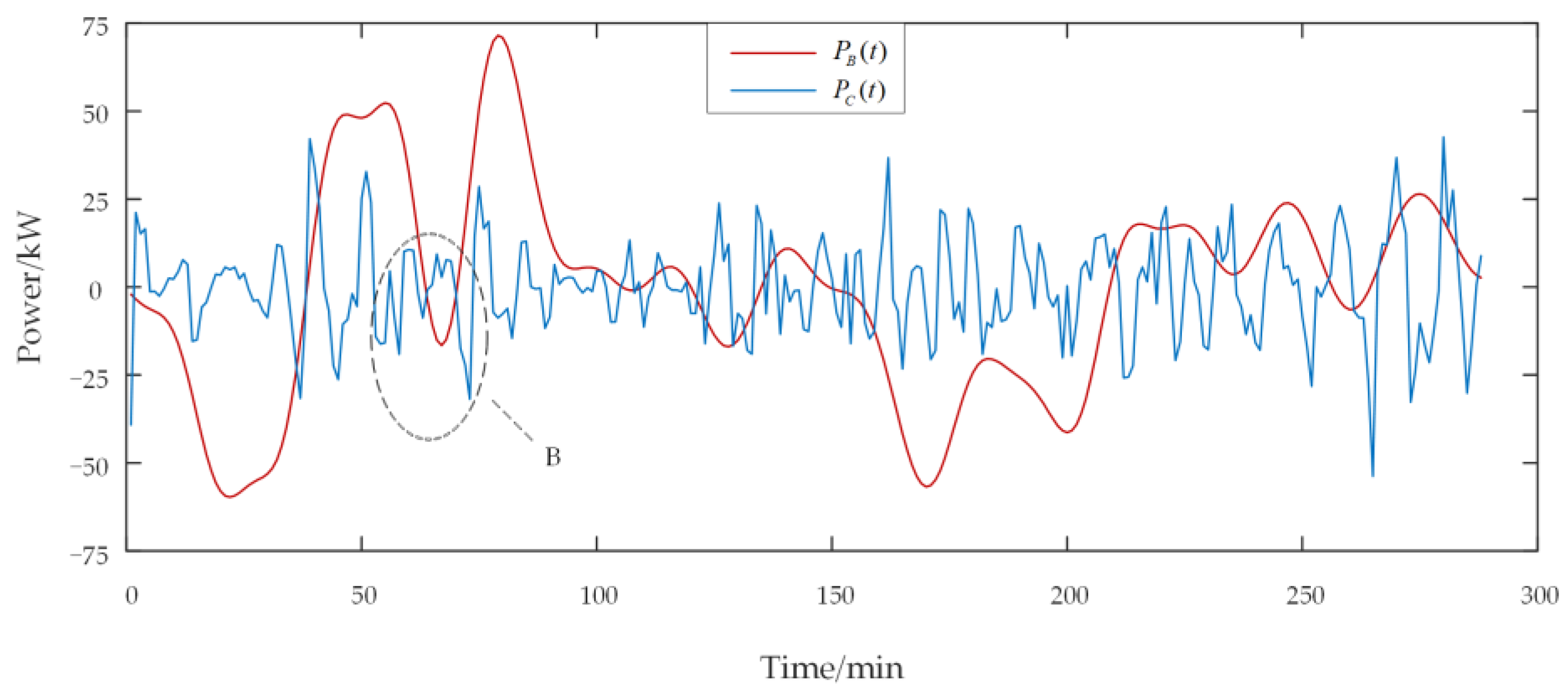
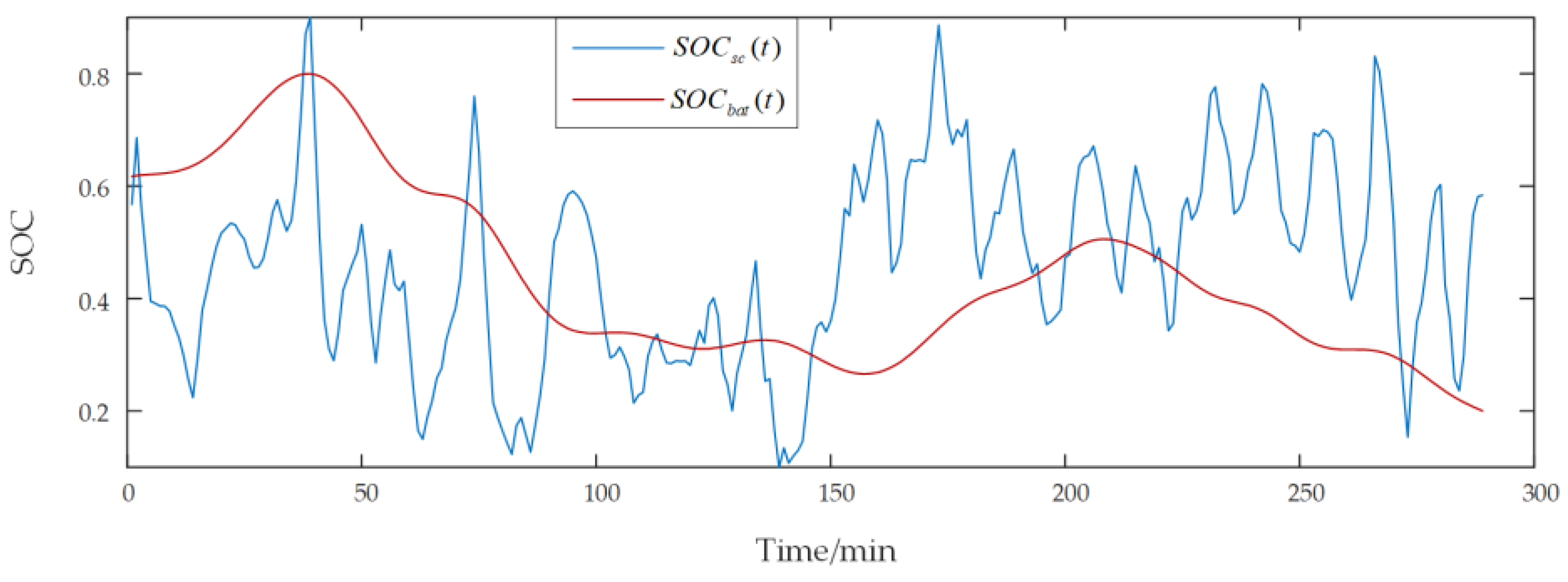

| Component | Parameter | Value |
|---|---|---|
| Battery | (%) | 20 |
| (%) | 80 | |
| (%) | 90 | |
| (¥/kWh) | 0.05 | |
| (¥/kW) | 2700 | |
| (¥/kWh) | 640 | |
| (year) | 5 | |
| (%) | 6 | |
| Supercapacitor | (%) | 10 |
| (%) | 90 | |
| (%) | 95 | |
| (¥/kWh) | 0.05 | |
| (¥/kW) | 1500 | |
| (¥/kWh) | 27,000 | |
| (year) | 20 | |
| (%) | 6 |
| K | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| Total | 10,571.69 | 10,980.57 | 13,326.62 | 5083.28 | 4142.25 | 8196.95 | 10,829.16 |
| 4128.84 | 385.94 | 343.63 | 71.03 | 68.87 | 556.01 | 482.24 | |
| 6442.85 | 3221.96 | 875.91 | 512.65 | 483.74 | 972.09 | 762.07 | |
| 7372.67 | 3050.49 | 861.57 | 655.75 | 1090.66 | 775.68 | ||
| 9056.59 | 947.28 | 713.41 | 1164.48 | 1660.26 | |||
| 2690.75 | 618.63 | 1177.05 | 1477.69 | ||||
| 1601.85 | 1777.64 | 1103.81 | |||||
| 1459.02 | 1986.94 | ||||||
| 2580.47 |
| Component | Rated Power/kW | Rated Capacity/kWh |
|---|---|---|
| Battery | 76 | 164 |
| Supercapacitor | 32 | 41 |
| Parameter | Scheme I | Scheme II | Scheme III | Scheme IV |
|---|---|---|---|---|
| (kW) | 110 | - | 38 | 32 |
| (kWh) | 256 | - | 46 | 41 |
| (¥) | 424,620 | - | 270,192 | 228,700 |
| (kW) | - | 192 | 87 | 76 |
| (kWh) | - | 592 | 196 | 164 |
| (year) | - | 2.68 | 5.84 | 6.20 |
| (¥) | - | 372,371 | 74,951 | 61,412 |
| (¥) | 12.8 | 29.6 | 12.1 | 10.25 |
| (¥) | 424,632.8 | 372,400.6 | 345,155.1 | 290,122.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, S.; He, Y.; Zhang, J.; Deng, K. Optimal Configuration of Hybrid Energy Storage Capacity in a Microgrid Based on Variational Mode Decomposition. Energies 2023, 16, 4307. https://doi.org/10.3390/en16114307
Lei S, He Y, Zhang J, Deng K. Optimal Configuration of Hybrid Energy Storage Capacity in a Microgrid Based on Variational Mode Decomposition. Energies. 2023; 16(11):4307. https://doi.org/10.3390/en16114307
Chicago/Turabian StyleLei, Shuang, Yu He, Jing Zhang, and Kun Deng. 2023. "Optimal Configuration of Hybrid Energy Storage Capacity in a Microgrid Based on Variational Mode Decomposition" Energies 16, no. 11: 4307. https://doi.org/10.3390/en16114307
APA StyleLei, S., He, Y., Zhang, J., & Deng, K. (2023). Optimal Configuration of Hybrid Energy Storage Capacity in a Microgrid Based on Variational Mode Decomposition. Energies, 16(11), 4307. https://doi.org/10.3390/en16114307







