Improved Prediction of the Higher Heating Value of Biomass Using an Artificial Neural Network Model Based on the Selection of Input Parameters
Abstract
1. Introduction
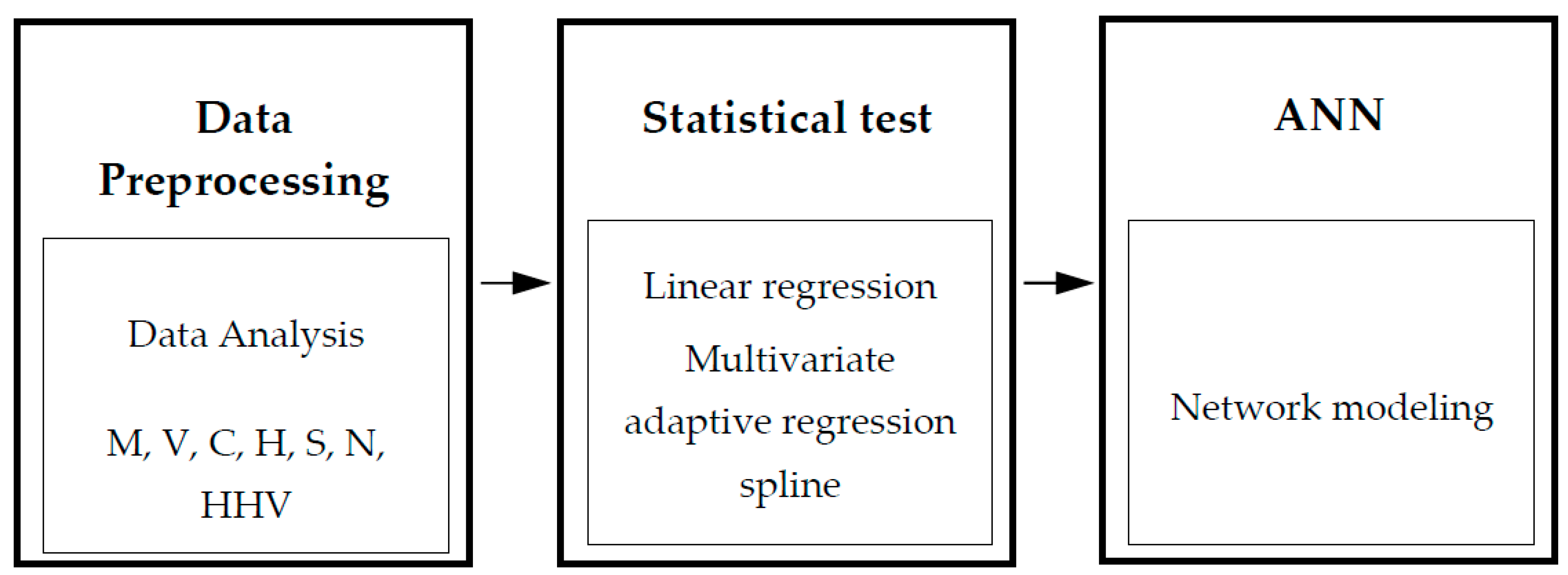
2. Materials and Methods
3. Results
3.1. Dataset
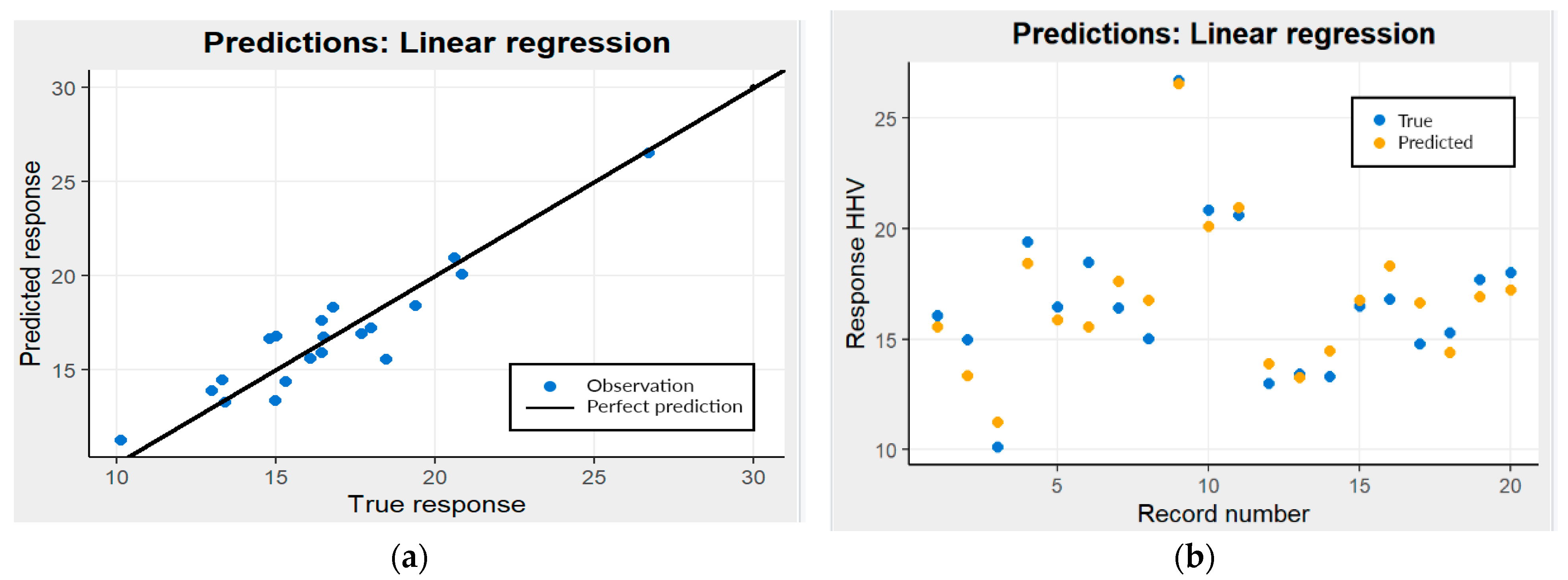
3.2. Linear Regression
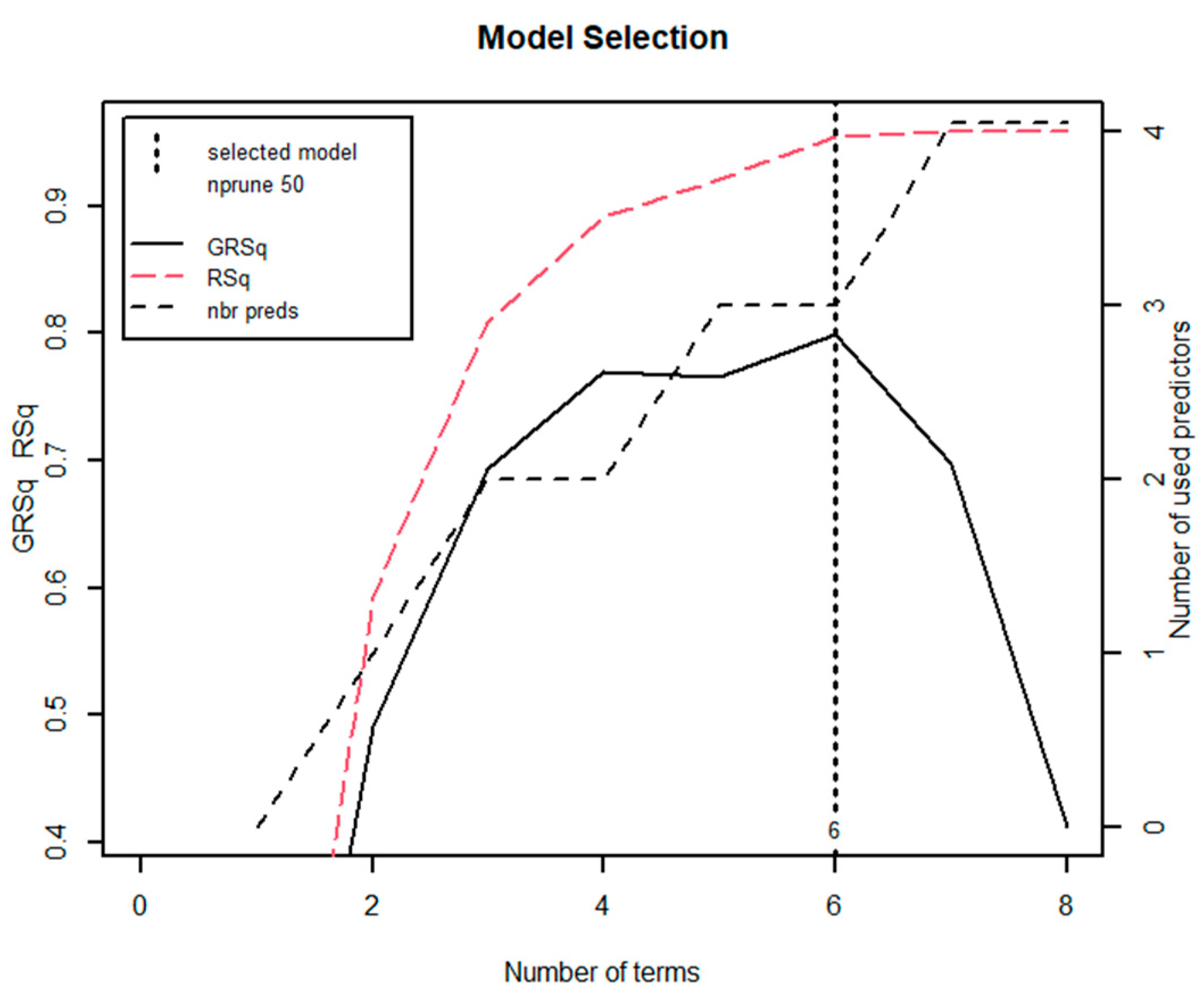
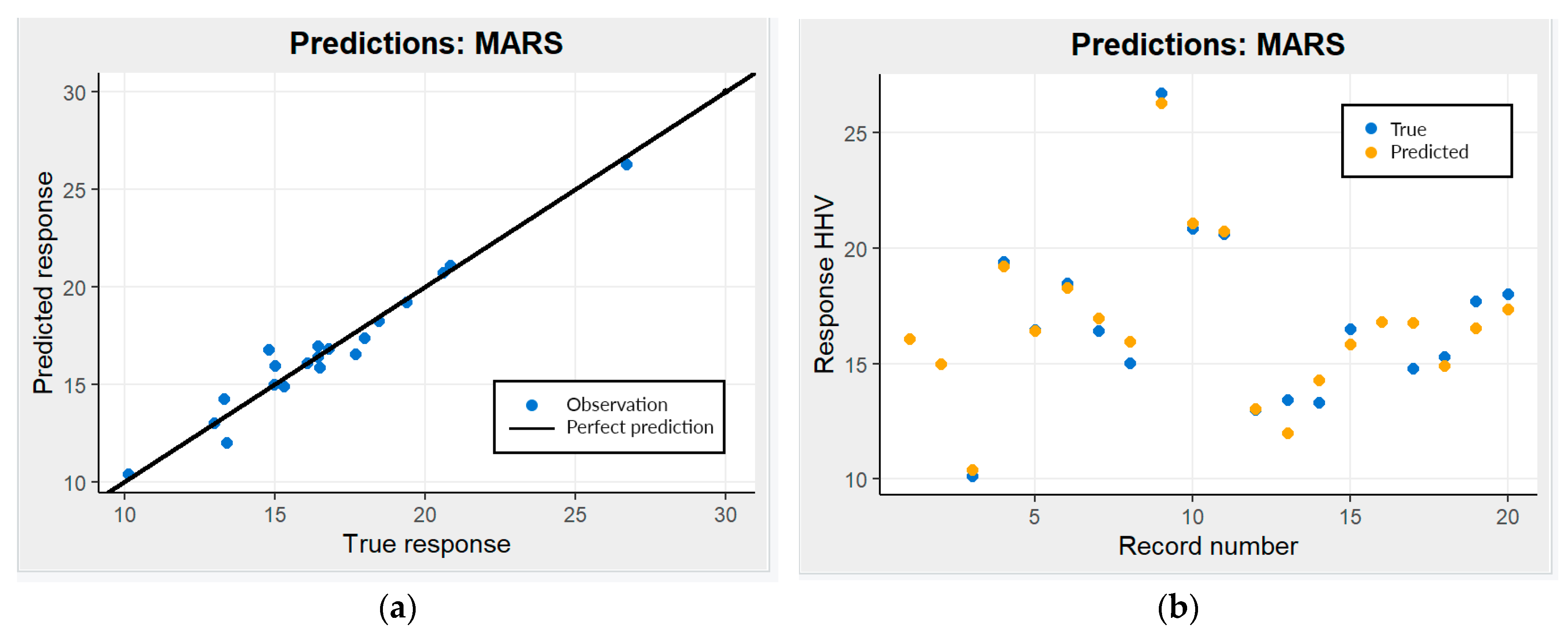
3.3. Multivariate Adaptive Regression Spline
−1.54⋅h(4.17−H) − 0.86⋅h(H-4.17) + 17.47⋅h(S−0.12),
3.4. ANN Simulation
4. Discussion
| Model | RMSE | MAE | R2 | References |
|---|---|---|---|---|
| A correlation for calculating HHV from proximate analysis | 1.043 | 0.502 | 0.359 | Parikh et al. (2005) [46] |
| A correlation for calculating HHV from proximate analysis | 1.431 | 0.679 | 0.456 | Nhuchhen and Salam (2012) [47] |
| Genetic programming | 0.808 | 0.485 | 0.934 | Ghugare et al. (2014) [45] |
| Support Vector Machines (SVR) model | 3.962 | 6.172 | 0.912 | Ghugare et al. (2014) [45] |
| Our model with 2 inputs | 0.6223 | 0.3577 | 0.968 | This study |
| Our model with 3 inputs | 0.5398 | 0.3794 | 0.976 | This study |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Ash content |
| ANN | Artificial neural network |
| BR | Bayesian regularization algorithm |
| C | Carbon |
| FC | Combustible solid content |
| H | Hydrogen |
| HHV | Heating value |
| L-M | Levenberg-Marquardt |
| LR | Linear regression |
| M | Moisture |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MARS | Multivariate adaptive regression spline |
| Max () | Maximum function |
| MLP | Multilayer perception |
| MLR | Multiple linear regression |
| MSE | Mean squared error |
| N | Nitrogen |
| O | Oxygen |
| R | Regression value |
| R2 | Coefficient of determination |
| RMSE | Root Mean Square Error |
| S | Sulfur |
| SCG | Scaled conjugate gradient algorithm |
| V | Volatile matter |
References
- Directive 2009/28/EC of the European Parliament and of the Council of 23 April 2009 on the Promotion of the use of Energy from Renewable Sources and Amending and Subsequently Repealing Directives 2001/77/EC and 2003/30/EC (Text with EEA relevance). Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=celex%3A32009L0028 (accessed on 5 March 2023).
- Runge, T.M. Economic and Environmental Impact of Biomass Types for Bioenergy Power Plants. Environmental and Economic Research and Development Program of Wisconsin’s Focus on Energy, Final Report August. 2013. Available online: https://s3.us-east-1.amazonaws.com/focusonenergy/staging/2018-06/1010RungeFinalReportx.pdf (accessed on 5 March 2023).
- Chen, W.H.; Lin, B.J.; Lin, Y.Y.; Chu, Y.S.; Ubando, A.T.; Show, P.L.; Ong, H.C.; Chang, J.S.; Ho, S.H.; Culaba, A.B.; et al. Progress in biomass torrefaction: Principles, applications and challenges. Prog. Energy Combust. Sci. 2021, 82, 100887. [Google Scholar] [CrossRef]
- Sivabalan, K.; Hassan, S.; Ya, H.; Pasupuleti, J. A review on the characteristic of biomass and classification of bioenergy through direct combustion and gasification as an alternative power supply. J. Phys. Conf. Ser. 2021, 1831, 012033. [Google Scholar] [CrossRef]
- McKendry, P. Energy production from biomass (part 1): Overview of biomass. Bioresour. Technol. 2002, 83, 37–46. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Yuan, J. Online identification of the lower heating value of the coal entering the furnace based on the boiler-side whole process models. Fuel 2015, 161, 68–77. [Google Scholar] [CrossRef]
- Callejón-Ferre, A.J.; Carreño-Sánchez, J.; Suárez-Medina, F.J.; Pérez-Alonso, J.; Velázquez-Martí, B. Prediction models for higher heating value based on the structural analysis of the biomass of plant remains from the greenhouses of Almería (Spain). Fuel 2014, 116, 377–387. [Google Scholar] [CrossRef]
- Via, B.K.; Adhikari, S.; Taylor, S. Modeling for proximate analysis and heating value of torrefied biomass with vibration spectroscopy. Bioresour. Technol. 2013, 133, 1–8. [Google Scholar] [CrossRef]
- Khunphakdee, P.; Korkerd, K.; Soanuch, C.; Chalermsinsuwan, B. Data-driven correlations of higher heating value for biomass, waste and their combination based on their elemental compositions. Energy Rep. 2022, 8, 36–42. [Google Scholar] [CrossRef]
- Hasan, M.; Haseli, Y.; Karadogan, E. Correlations to predict elemental compositions and heating value of torrefied biomass. Energies 2018, 11, 2443. [Google Scholar] [CrossRef]
- Erol, M.; Haykiri-Acma, H.; Küçükbayrak, S. Calorific value estimation of biomass from their proximate analyses data. Renew. Energy 2010, 35, 170–173. [Google Scholar] [CrossRef]
- Uzun, H.; Yıldız, Z.; Goldfarb, J.L.; Ceylan, S. Improved prediction of higher heating value of biomass using an artificial neural network model based on proximate analysis. Bioresour. Technol. 2017, 234, 122–130. [Google Scholar] [CrossRef]
- Nhuchhen, D.R.; Afzal, M.T. HHV predicting correlations for torrefied biomass using proximate and ultimate analyses. Bioengineering 2017, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Lee, S.; Soto, A.M.; Chen, G. Regression model to predict the higher heating value of poultry waste from proximate analysis. Resources 2018, 7, 39. [Google Scholar] [CrossRef]
- Zagórski, I.; Kulisz, M.; Kłonica, M.; Matuszak, J. Trochoidal milling and neural networks simulation of magnesium alloys. Materials 2019, 12, 70. [Google Scholar] [CrossRef] [PubMed]
- Kulisz, M.; Kujawska, J. Prediction of municipal waste generation in poland using neural network modeling. Sustainability 2020, 12, 10088. [Google Scholar] [CrossRef]
- Kulisz, M.; Kujawska, J.; Przysucha, B.; Cel, W. Forecasting water quality index in groundwater using artificial neural network. Energies 2021, 14, 875. [Google Scholar] [CrossRef]
- Zhou, L.; Song, Y.; Ji, W.; Wei, H. Machine learning for combustion. Energy AI 2022, 7, 100128. [Google Scholar] [CrossRef]
- Elbeltagi, E.; Wefki, H. Predicting energy consumption for residential buildings using ANN through parametric modeling. Energy Rep. 2021, 7, 2534–2545. [Google Scholar] [CrossRef]
- Çamur, H.; Al-Ani, A.M.R. Prediction of Oxidation Stability of Biodiesel Derived from Waste and Refined Vegetable Oils by Statistical Approaches. Energies 2022, 15, 407. [Google Scholar] [CrossRef]
- Patel, S.U.; Jeevan Kumar, B.; Badhe, Y.P.; Sharma, B.K.; Saha, S.; Biswas, S.; Chaudhury, A.; Tambe, S.S.; Kulkarni, B.D. Estimation of gross calorific value of coals using artificial neural networks. Fuel 2007, 86, 334–344. [Google Scholar] [CrossRef]
- Huang, C.; Han, L.; Liu, X.; Yang, Z. Models Predicting Calorific Value of Straw from the Ash Content. Int. J. Green Energy 2008, 5, 533–539. [Google Scholar] [CrossRef]
- Estiati, I.; Freire, F.B.; Freire, J.T.; Aguado, R.; Olazar, M. Fitting performance of artificial neural networks and empirical correlations to estimate higher heating values of biomass. Fuel 2016, 180, 377–383. [Google Scholar] [CrossRef]
- Liao, M.; Yao, Y. Applications of artificial intelligence-based modeling for bioenergy systems: A review. GCB Bioenergy 2021, 13, 774–802. [Google Scholar] [CrossRef]
- Chou, S.M.; Lee, T.S.; Shao, Y.E.; Chen, I.F. Mining the breast cancer pattern using artificial neural networks and multivariate adaptive regression splines. Expert Syst. Appl. 2004, 27, 133–142. [Google Scholar] [CrossRef]
- ISO 18134; Solid Biofuels. Determination of Moisture Content. Dryer Method. Part 2: Total Moisture. Simplified Method. International Organization for Standardization: Geneva, Switzerland, 2017.
- ISO 18122; Solid Biofuels. Determination of Ash Content. International Organization for Standardization: Geneva, Switzerland, 2016.
- ISO 16948; Solid Biofuels. Determination of Total Carbon, Hydrogen and Nitrogen Content. International Organization for Standardization: Geneva, Switzerland, 2015.
- ISO 18125; Solid Biofuels. Determination of Calorific Value. International Organization for Standardization: Geneva, Switzerland, 2015.
- Lalak, J.; Martyniak, D.; Kasprzycka, A.; Żurek, G.; Moroń, W.; Chmielewska, M.; Wiącek, D.; Tys, J. Comparsion of selected parameters of biomass and coal. Int. Agrophys. 2016, 30, 475–482. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivarite adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar]
- Milborrow, S. Derived from mda:mars by Trevor Hastie and Rob Tibshirani. Uses Alan Miller’s Fortran utilities with Thomas Lumley’s leaps wrapper. Multivariate Adaptive Regression Splines. Available online: https://cran.r-project.org/web/packages/earth/earth.pdf (accessed on 5 March 2023).
- Aghelpour, A.; Bagheri-Khalili, Z.; Varshavian, V.; Mohammadi, B.; Marquardt, D. Evaluating Three Supervised Machine Learning Algorithms (LM, BR, and SCG) for Daily Pan Evaporation Estimation in a Semi-Arid Region. Water 2022, 14, 3435. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M. Training feed-forward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. Available online: https://www.mathworks.com/help/deeplearning/ref/trainlm.html (accessed on 12 May 2023). [CrossRef]
- Burden, F.; Winkler, D. Bayesian regularization of neural networks. Artif. Neural Netw. 2008, 458, 23–42. [Google Scholar]
- Wali, A.S.; Tyagi, A. Comparative study of advance smart strain approximation method using levenberg-marquardt and bayesian regularization backpropagation algorithm. Mater. Today Proc. 2020, 21, 1380–1395. [Google Scholar] [CrossRef]
- Møller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. Available online: https://www.mathworks.com/help/deeplearning/ref/trainscg.html (accessed on 12 May 2023). [CrossRef]
- Baghirli, O. Comparison of Lavenberg-Marquardt, Scaled Conjugate Gradient and Bayesian Regularization Backpropagation Algorithms for Multistep Ahead Wind Speed Forecasting Using Multilayer Perceptron Feedforward Neural Network. Master’s Thesis, Uppsala University, Uppsala, Sweden, 2015. Available online: https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A828170&dswid=6956 (accessed on 12 May 2023).
- Manatura, K.; Chalermsinsuwan, B.; Kaewtrakulchai, N.; Kwon, E.E.; Chen, W.H. Machine learning and statistical analysis for biomass torrefaction: A review. Bioresour. Technol. 2023, 369, 128504. [Google Scholar] [CrossRef]
- Adil, M.; Ullah, R.; Noor, S.; Gohar, N. Effect of number of neurons and layers in an artificial neural network for generalized concrete mix design. Neural Comput. Appl. 2022, 11, 8355–8363. [Google Scholar] [CrossRef]
- Aniza, R.; Chen, W.H.; Yang, F.C.; Pugazhendh, A.; Singh, Y. Integrating Taguchi method and artificial neural network for predicting and maximizing biofuel production via torrefaction and pyrolysis. Bioresour. Technol. 2022, 343, 126140. [Google Scholar] [CrossRef]
- Rashid, T.; Taqvi, S.A.A.; Sher, F.; Rubab, S.; Thanabalan, M.; Bilal, M.; ul Islam, B. Enhanced lignin extraction and optimisation from oil palm biomass using neural network modelling. Fuel 2021, 293, 120485. [Google Scholar] [CrossRef]
- Chen, W.H.; Aniza, R.; Arpia, A.A.; Lo, H.J.; Hoang, A.T.; Goodarzi, V.; Gao, J. A comparative analysis of biomass torrefaction severity index prediction from machine learning. Appl. Energy 2022, 324, 119689. [Google Scholar] [CrossRef]
- Jakŝić, O.M.; Jakŝić, Z.; Guha, K.; Silva, A.G. Comparing artificial neural network algorithms for prediction of higher heating value for different types of biomass. Soft Comp. 2023, 901, 5933–5950. [Google Scholar] [CrossRef]
- Ghugare, S.B.; Tiwary, S.; Elangovan, V.; Tambe, S.S. Prediction of Higher heating value of solid biomass fuels using artificial intelligence formalisms. Bioenergy Res. 2014, 7, 681–692. [Google Scholar] [CrossRef]
- Parikh, J.; Channiwala, S.A.; Ghosal, G.K. A correlation for calculating HHV from proximate analysis of solid fuels. Fuel 2005, 84, 487–494. [Google Scholar] [CrossRef]
- Nhuchhen, D.R.; Salam, P.A. Estimation of higher heating value of biomass from proximate analysis: A new approach. Fuel 2012, 99, 55–63. [Google Scholar] [CrossRef]
- Gong, S.; Sasanipour, J.; Shayesteh, M.R.; Eslami, M.; Baghban, M. Radial basis function artificial neural network model to estimate higher heating value of solid wastes. Energy Sources Part A Recover. Util. Environ. Eff. 2017, 39, 1778–1784. [Google Scholar] [CrossRef]
- Pattanayak, S.; Loha, C.; Hauchhum, L.; Sailo, L. Application of MLP-ANN models for estimating the higher heating value of bamboo biomass. Biomass Convers. Biorefinery 2021, 11, 2499–2508. [Google Scholar] [CrossRef]
- Brandić, I.; Pezo, L.; Bilandžija, N.; Peter, A.; Šuri´c, J.; Voća, N. Artificial Neural Network as a Tool for Estimation of the Higher Heating Value of Miscanthus Based on Ultimate Analysis. Mathematics 2022, 10, 3732. [Google Scholar] [CrossRef]
- Veza, I.; Irianto, B.; Panchal, H.; Paristiawan, P.A.; Idri, M.; Fattah, I.M.R.; Purta, N.R.; Silambarasan, R. Improved prediction accuracy of biomass heating value using proximate analysis with various ANN training algorithms. Results Eng. 2022, 16, 100688. [Google Scholar] [CrossRef]
- Kartal, F.; Özveren, U. Prediction of torrefied biomass properties from raw biomass. Renew. Energ. 2022, 182, 578–591. [Google Scholar] [CrossRef]
- Xing, J.; Luo, K.; Wang, H.; Gao, Z.; Fan, J. A comprenhesive study on estaming higher heating value of biomass from proximate and ultimate analysis with machine learning approaches. Energy 2019, 188, 116077. [Google Scholar] [CrossRef]


| Determined Parameters | Device | Standard |
|---|---|---|
| Moisture M (%) | Laboratory dryer | ISO 18134 (2017) [26] |
| Volatile matter V (%), ash content A (%) | FCF 2,5S electric muffle furnace made by Czylok with SM-946 electronic controller and temperature display (Warsaw, Poland) | ISO 18122 (2016) [27] |
| Determination of total carbon, hydrogen and nitrogen (%) | CHNS Flash EA 1112 Series Elemental Analyzer (Thermo Finnigan, Walthman, MA, USA) | ISO 16948 (2015) [28] |
| Higher heating value (HHV) (kJ/kg) | Mikado Calorimeter (Warsaw, Poland) | ISO 18125 (2015) [29] |
| The content of other combustible solid fractions FC (%) | FC was determined from the difference FC = 100-A-W-V | [30] |
| Quality Indicator | Formula | Meaning of Symbols |
|---|---|---|
| Regression value R | σy′—standard deviation of reference values of HHV, σy*—standard deviation of predicted values HHV, yi is the actual value of HVV, denotes the value of the HVV for the i-th observation obtained from the model | |
| Mean Squared Error (MSE) | ||
| Root Mean Square Error (RMSE) | ||
| Mean Absolute Percentage Error (MAPE) | ||
| Mean Absolute Error (MAE) |
| Fuel Type | Industrial Analysis (%) | Elemental Analysis (%) | HHV MJ/kg | ||||||
|---|---|---|---|---|---|---|---|---|---|
| M | A | V | FC | C | H | N | S | ||
| Oak Bark | 7.93 | 1.57 | 71.50 | 19 | 41.20 | 3.73 | 0.84 | 7.93 | 16.08 |
| Pine | 6.88 | 1.46 | 64.10 | 27.56 | 36.41 | 3.51 | 0.17 | 6.88 | 14.98 |
| Hornbeam | 5.88 | 1.14 | 41.10 | 51.88 | 31.47 | 2.89 | 0.23 | 5.88 | 10.13 |
| Alder | 10.39 | 1.97 | 79.10 | 18.54 | 44.86 | 4.17 | 0.39 | 10.39 | 19.39 |
| Oat Straw | 6.03 | 4.32 | 43.20 | 46.45 | 42.20 | 3.80 | 0.51 | 6.03 | 16.45 |
| Wheat Straw | 6.16 | 3.15 | 71.34 | 19.35 | 43.26 | 4.03 | 0.64 | 6.16 | 18.47 |
| Maize Straw | 7.02 | 4.20 | 81.80 | 16.98 | 46.00 | 6.00 | 0.56 | 7.02 | 16.43 |
| Rape Straw | 9.05 | 5.50 | 76.54 | 18.91 | 45.00 | 2.80 | 0.47 | 9.05 | 15.02 |
| Douglas Fir Bark | 6.6 | 3.0 | 68.65 | 21.75 | 66.45 | 7.26 | 1.31 | 6.6 | 26.70 |
| Spruce | 5.9 | 1.37 | 73.10 | 19.63 | 54.00 | 5.70 | 0.5 | 5.9 | 20.84 |
| Larch | 7.2 | 0.5 | 52.10 | 40.2 | 51.60 | 5.60 | 0.8 | 0.16 | 20.61 |
| Rye Straw | 5.9 | 4.0 | 76.4 | 13.7 | 46.60 | 0.6 | 0.6 | 0.09 | 13 |
| Triticale Straw | 6.1 | 2.1 | 75.2 | 16.6 | 43.90 | 0.59 | 0.4 | 0.11 | 13.42 |
| Barley Straw | 5.8 | 4.0 | 77.3 | 12.9 | 47.50 | 0.59 | 0.5 | 0.15 | 13.32 |
| Reed Pulp | 5.8 | 11.4 | 70.78 | 12.02 | 43.50 | 5.93 | 3.42 | 0.01 | 16.5 |
| Roegrass Haughty | 7.8 | 2.7 | 69.66 | 19.84 | 38.38 | 8.84 | 0.44 | 0.03 | 16.8 |
| Wooly Spikelet | 6.2 | 9.1 | 79.65 | 17.05 | 44.98 | 5.66 | 1.86 | 0.01 | 14.8 |
| Reed Fescue | 6.5 | 9.2 | 77.56 | 16.74 | 39.47 | 5.07 | 1.2 | 0.02 | 15.3 |
| Gigant Miscanthus | 7.6 | 9.2 | 79.78 | 13.42 | 42.86 | 4.81 | 3.62 | 0.12 | 17.7 |
| Hay | 6.9 | 8.9 | 85.36 | 16.4 | 46.58 | 5.87 | 0.47 | 0.12 | 18 |
| No. of Network | 1 | 2 | 3 |
|---|---|---|---|
| Training algorithm | Levenberg-Marquardt | Scaled Conjugate Gradient | Bayesian Regularization |
| Epoch | 13 | 27 | 76 |
| Performance | 1.15*10−21 | 0.573 | 1.81 |
| Best training performance | 1.4215 at epoch 8 | 1.1868 at epoch 21 | 1.8125 at apoch 73 |
| Gradient | 9.19*10−10 | 0.993 | 1.02 |
| Levenberg-Marquardt | Scaled Conjugate Gradient | Bayesian Regularization | |
|---|---|---|---|
| R (all data) | 0.98453 | 0.96794 | 0.91375 |
| MSE | 0.3873 | 0.7789 | 2.0084 |
| RMSE | 0.6223 | 0.8826 | 1.4172 |
| MAPE | 0.0210 | 0.0428 | 0.0768 |
| MAE | 0.3577 | 0.6894 | 1.1896 |
| No. of Network | 1 | 2 | 3 |
|---|---|---|---|
| Training algorithm | Levenberg-Marquardt | Scaled Conjugate Gradient | Bayesian Regularization |
| Epoch | 11 | 26 | 904 |
| Performance | 0.118 | 0.624 | 1.25 |
| Best training performance | 0.61523 at epoch 5 | 1.0617 at epoch 20 | 1.2438 at epoch 159 |
| Gradient | 0.296 | 1.18 | 0.617 |
| Levenberg-Marquardt | Scaled Conjugate Gradient | Bayesian Regularization | |
|---|---|---|---|
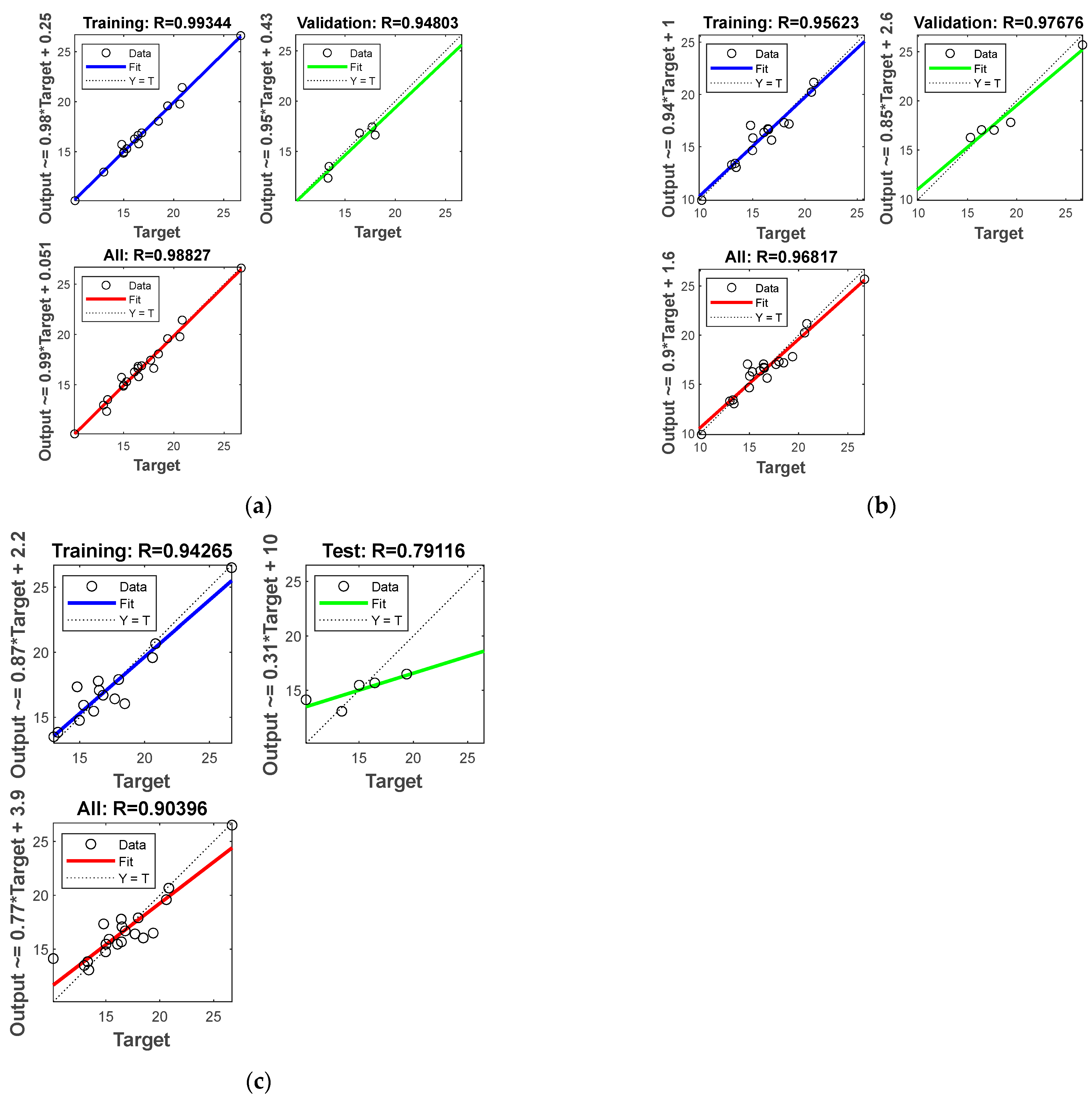
| R (all data) | 0.98827 | 0.96817 | 0.90396 |
| MSE | 0.2914 | 0.7672 | 2.1978 |
| RMSE | 0.5398 | 0.8759 | 1.4825 |
| MAPE | 0.0226 | 0.0411 | 0.0694 |
| MAE | 0.3794 | 0.6896 | 1.0359 |
| Quality Indicators | Model with 2 Inputs (C, H) | Model with 3 Inputs (C, H, S) |
|---|---|---|
| Model 1 | Model 2 | |
| R (all data) | 0.98453 | 0.98827 |
| MSE | 0.3873 | 0.2914 |
| RMSE | 0.6223 | 0.5398 |
| MAPE | 0.0210 | 0.0226 |
| MAE | 0.3577 | 0.3794 |
| Input Variables | Type of ANN | ANN Architecture | R2 | Activation Functions | Authors |
|---|---|---|---|---|---|
| FC, V, M, A | Levenberg-Marquardt | 3-7-1 | 0.9852 | Sigmoid symmetry | [23] |
| FC, V, M, A | Levenberg-Marquardt | 1-23-1-1 | 0.9591 | Hyperbolic tangent sigmoid and linear | [47] |
| C, H, N, S, O, A, H2O | Radial basis function combined with Levenberg- Marquardt | 0.997 | Radial basis function | [48] | |
| V, FC, A, M, C, H, N, S, and O | Levenberg- Marquardt | 9-10-1 | 0.985 | Tangent sigmoid | [49] |
| C, H, N, S, O | Levenberg- Marquardt | 5-11-1 | 0.77 | Tangent sigmoid | [50] |
| FC, V, A | Levenberg- Marquardt | 3-10-1 | 0.966 | Hyperbolic tangent sigmoid transfer function | [51] |
| Temperature, Time, FC, V, A, C, O, H | Levenberg- Marquardt | 5-10-1 | 0.8321 | Tangent sigmoid | [52] |
| V, FC, A, M, C, H, N, S, and O | Levenberg- Marquardt | 9-10-1 | 0.909 | Tangent sigmoid | [53] |
| C, H, S | Levenberg-Marquardt | 3-9-1 | 0.976 | Hyperbolic tangent sigmoid transfer function | This study |
| C, H | Levenberg-Marquardt | 2-8-1 | 0.968 | Hyperbolic tangent sigmoid transfer function | This study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kujawska, J.; Kulisz, M.; Oleszczuk, P.; Cel, W. Improved Prediction of the Higher Heating Value of Biomass Using an Artificial Neural Network Model Based on the Selection of Input Parameters. Energies 2023, 16, 4162. https://doi.org/10.3390/en16104162
Kujawska J, Kulisz M, Oleszczuk P, Cel W. Improved Prediction of the Higher Heating Value of Biomass Using an Artificial Neural Network Model Based on the Selection of Input Parameters. Energies. 2023; 16(10):4162. https://doi.org/10.3390/en16104162
Chicago/Turabian StyleKujawska, Justyna, Monika Kulisz, Piotr Oleszczuk, and Wojciech Cel. 2023. "Improved Prediction of the Higher Heating Value of Biomass Using an Artificial Neural Network Model Based on the Selection of Input Parameters" Energies 16, no. 10: 4162. https://doi.org/10.3390/en16104162
APA StyleKujawska, J., Kulisz, M., Oleszczuk, P., & Cel, W. (2023). Improved Prediction of the Higher Heating Value of Biomass Using an Artificial Neural Network Model Based on the Selection of Input Parameters. Energies, 16(10), 4162. https://doi.org/10.3390/en16104162







