Localization and Sizing of Distributed Generation through a Genetic Algorithm to Improve Voltage Profile Using Ecuadorian Standards

Abstract

The approach proposed for the development of this research work was based on the integration of Distributed Energy Generation (DG) into an energy distribution network, improving the voltage profile by establishing an optimal location and sizing of DG power plants, for which the use of a heuristic optimization method known as Genetic Algorithm (GA), which has several restrictions to limit its operation and thus achieve an optimal solution to the planned optimization problem, was resorted to. The development of a power flow allowed having the voltage measurement in the bars of the network before incorporating DG, allowing to verify that the voltage fluctuations present an improvement after the incorporation one by one of each DG central defined by the GA. The systems in which the voltage measurement was performed, as well as the verification of its fluctuations with and without DG once the GA was used, were the IEEE systems of 9 and 14 busbars, the latter the one used to demonstrate the scalability of the GA to locate and dimension DG without considering the number of busbars in a system.

1. Introduction

Over the last few years, the Electric Power System (EPS) has experienced increased demand due to population growth. Unfortunately, this growth has resulted in several generation and system load issues, as reported in [1]. Additionally, the conventional generation plants have been deteriorating, which has made it difficult to meet current demand [2,3]. The system is poorly maintained and located far from users, causing voltage levels to exceed the limits of flawless operation. These factors have reduced the system’s quality and reliability, as stated in [4,5].

Due to traditional power plants’ high cost and environmental impact, new methods and technologies have been developed to meet user demand, improve voltage, and reduce line losses without causing pollution. For example, a binary particle swarm algorithm can reconfigure the distribution network, reducing feeder load and improving the voltage profile along the system’s bars, as proposed in [1]. Other studies, such as [3,6], have also explored ways to achieve these goals.

Using a more economical and efficient generation is more convenient due to the advanced control, monitoring, and communication of EPS elements. This generation type offers higher reliability, technical adequacy regarding voltage profile, and environmental benefits such as reduced pollution. Such benefits surpass those obtained from other technologies and conventional generation, as stated in [7,8]. When considering DG, focusing on utilizing natural energy sources or those with low carbon dioxide emissions is essential. It addresses issues that cannot be immediately resolved through conventional generation, as suggested in [9].

When deciding to use DG plants, various factors, including size, location, type, and variability, are considered to ensure that the plants can be integrated into the system correctly and prevent voltage fluctuations. As explained in a study by [3], a genetic algorithm was used to determine the optimal size and capacity of the DG plants to improve the voltage profile. The model also considered limitations on voltage fluctuations and the capacity of each CGD plant that can be installed.

In a study referenced as [6], a process was developed to control reactive power for each CGD (Combined Generation and Distribution) installation. This was achieved through a remote station that allows for selecting which plant to use and how much power to inject, ultimately preventing irregular voltage fluctuations. However, for this particular study, the approach was based on [10], which verifies the voltage profile in the system after incorporating several DG (Distributed Generation) plants that only inject active power with a unity power factor. These plants are referred to as Distributed Photovoltaic Generation (DPG).

Based on the given information, Figure 1 demonstrates how to integrate the DG into the system using a GA. To achieve a stable system, it is essential to consider the existing regulations governing the installation of the DG in Ecuador. Genetic algorithms are preferred over other optimization methods for optimal location problems due to their numerous advantages [11].

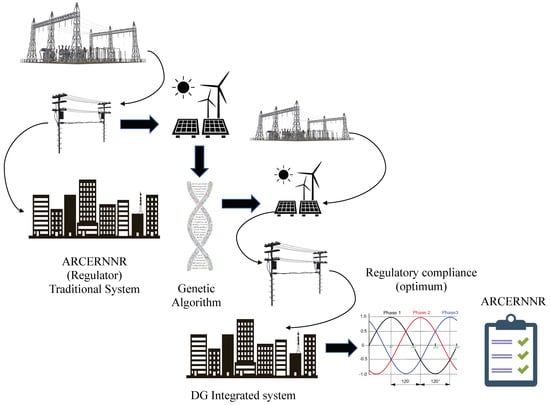
Figure 1. Application of a GA to assign DG in the DS (author).

Genetic algorithms are a powerful tool for solving real-world optimization problems. They excel at handling non-linear and non-differentiable objective functions, which are common in these problems. Unlike other methods, genetic algorithms can find global optima rather than becoming stuck in local optima. Additionally, they can handle multiple objectives and constraints, making them ideal for complex optimization problems [12]. Genetic algorithms are versatile and can be applied to various optimization problems. They can also efficiently handle large-scale optimization problems through parallel processing and distributed computing. As a result, genetic algorithms have proven effective in solving optimal location problems across different fields, including electrical engineering.

Finally, genetic algorithms are powerful tools for optimization problems, including the optimal placement of distributed generation in an electrical system. The algorithm mimics the natural selection process, where the fittest individuals are selected for reproduction and offspring inherit their parents’ traits with slight variations. In locating distributed generation, the algorithm evaluates potential locations based on factors such as voltage regulation, loss reduction, and system stability. Using a genetic algorithm, we can quickly identify the optimal location for distributed generation, leading to improved system efficiency, reduced energy costs, and increased reliability. Therefore, using genetic algorithms to localize distributed generation in electrical systems is critical to modern power system planning and design [13].

2. Background and Related Works

For this paper’s development, several theoretical contributions focused on the integration of DG to the DS must be made, in addition to having terms that allow defining the necessary concepts for the application of the optimization model seeking to improve the voltage profile present in the system busbars when certain limits are established for the correct operation of the systems analyzed during the development of this study [14].

2.1. Distribution Systems (DS)

The DS is one of the essential parts of the EPS, being in charge of carrying the medium voltage (MV) electric power supply from the distribution substation to the end users connected to the EPS [1] and composed of different elements such as primary and secondary distribution lines, distribution transformers, connections, and loads. All these previously specified elements are established within a mesh system and a radial system; however, it should be considered that the radial approach is the most used to represent the DS because it allows better management of the system protections [15]. If the previously established premises are considered, the DS can be represented simply through a single-line diagram specifying each element’s location and connection, regardless of their configuration. A simplified representation can be made, through which the main elements that make up the DS can be established; this process is shown in Figure 2.

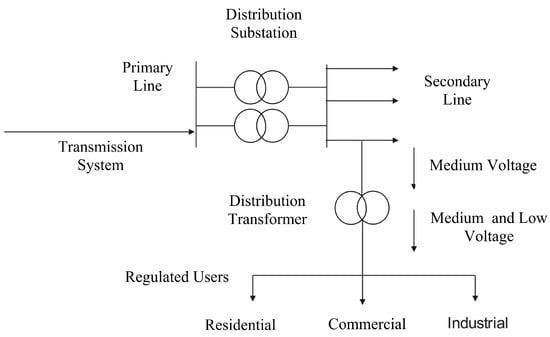
Figure 2. Representation of a simplified DS (author).

2.2. Voltage Profile

When referring to the voltage profile, it is inevitable not to refer to voltage stability since having adequate strength implies keeping the bus voltage within limits established by regulation after the occurrence of a fault, looking for the system to have a more efficient, economic, and reliable behavior [16]. When analyzing the voltage profile, it should be taken into account that its alteration is caused by the variation of loads, changes in the structure of the network due to the presence of several faults, the performance of maintenance within the network, and the fact of presenting a difference in the generation that provides energy to the system [17]. Improving the voltage profile in the DS is essential to ensure an ideal voltage for the user, i.e., the system must have a process to reduce voltage instability while increasing the quality and reliability of the system [6].

2.2.1. Voltage Profile Limits

Each country defines its voltage limits to be able to work without inconveniences through a regulation, considering within its analysis the various technical factors that characterize the system of that country; however, internationally, it is established that for a correct operation of the EPS, the voltage profile must be between 0.95 [p.u] and 1.05 [p.u], while for the DS, the values must be between 0.9 [p.u] and 1.1 [p.u] [18]. In Ecuador, according to regulation No. ARCONEL 005/18, voltage variations depend on the voltage level present in the EPS systems [19]; in that sense, according to the analysis of this regulation, Table 1 quantifies the permissible range allowed for voltage variations within the EPS.

Table 1. Permissible range for voltage variations.

Voltage Level	Permissible Range
High Voltage	$\pm 5\%$
Medium Voltage	$\pm 6\%$
Low Voltage	$\pm 8\%$

2.2.2. Techniques to Conserve the Voltage Profile

The application of several techniques allows keeping the voltage profile within the limits established by a standard, among which we can find [1,6]:

i.

DS reconfiguration.

ii.

Use of voltage controllers and regulators.

iii.

Installation of on-load tap changers.

iv.

Installation of capacitive compensation banks (shunt capacitors).

v.

Installation of FACS.

vi.

The design and integration of DG.

In addition, these last two are considered as the techniques that present the greatest benefits when developed in the DS.

2.3. Distributed Generation (DG)

Talking about DG is a challenging task since, internationally, there is no general definition to categorize it within a single purpose, having to resort to the criteria established by several authors to reach an accurate and commonly used depiction within several texts [18,20]. Considering this premise, DG is defined as a renewable and small electric generator that can be connected to the transmission system and more frequently to the DS [21], being the appropriate generation to reduce environmental pollution and the most suitable for installation near the consumers [3,7]. The energy obtained through photovoltaic, wind, biomass, geothermal, and hydraulic generation (small-scale) is the most referenced when planning the development and installation of DG within a system; however, currently, it has been chosen to use technologies from non-renewable sources of low pollution as sources of DG, the same that are obtained by micro-turbines and combustion turbines, among others [9,18,20].

Figure 3 shows a diagram identifying the most common EPS systems incorporating DG. It shows the conventional generation, high voltage transmission system, medium voltage distribution system, where the DG will be placed, and finally, the low voltage distribution system.

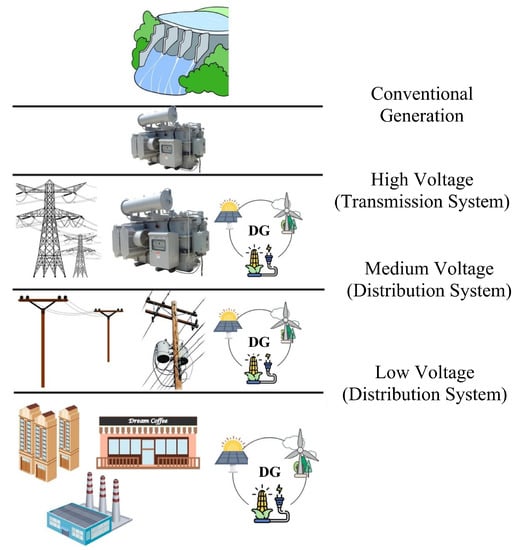
Figure 3. DG integration to the different EPS (author).

The maximum generation that DG can offer depends on the source from which the energy is extracted, which is why not all DG plants have the same capacity, so Table 2 below shows the maximum sizing that can be offered by the primary DG plants [22].

Table 2. Maximum generation depends on the type of DG power plant [22].

DG Power Plants	Generation Range
Diesel or Natural Gas Generator	30 [kW]–6 [MW]
Micro-turbine	30 [kW]–400 [kW]
Photovoltaic	1 [kW]–1 [MW]
Wind	600 [kW]–2.5 [MW]

In Ecuador, according to the Agency for Regulation and Control of Energy and Non-Renewable Natural Resources (ARCERNNR), several regulations have been developed regarding the installation of a CGD; the most used and current is the regulation ARCERNNR 002/21, which establishes a law for a CGD designed for self-supply, as well as for a CGD developed by an Enabled Distributed Generation Company (EDGC).

Ref. [23] Using the regulation specified above, it is possible to define the maximum value of active power that a DG plant in Ecuador can deliver; such limits are determined by Table 3.

Table 3. Rated power of a CGD, established by ARCERNNR—Ecuador.

Adjustments	Nominal Power
ARCERNNR 002/21 (Self-supply)	<1 [MW]
ARCERNNR 002/21 (EDGC)	Between 100 [kW] and 10 [MW]

2.4. Integration of DG into the Power System

To obtain an ideal integration of DG, it is necessary to take into account its location, sizing, type, and the way of installing the DG [9]; in this case, when considering both the location and the sizing, it is possible to maximize the capacity of the DG without causing a decrease in the performance of the system, keeping the voltage profile within the admissible standard ranges [3,6]. Due to a lack of previous knowledge when installing DG, a random installation is sought, that is, without developing a previous study that shows its benefits, scope, and difficulties, incurring an inadequate structure of the DG power plants [21], which makes it necessary to define several restrictions so that the integration of the DG to the DS is developed in an adequate way [18]. In this sense, several strategies seek to optimally solve the problem of optimal placement and sizing of DG, improving the voltage profile [24,25].

If an inadequate DG integration is performed, there will be several negative impacts within the system since the intermittency of the DG during the day is not being considered in the study [3], in addition to thinking that if a high-power DG is installed, it can also cause blackouts throughout the network [26]. If the integration problems are not solved, the system will suffer from voltage fluctuations, damage to its protections, generation of harmonics, need for more reactive power, and a decrease in the system’s reliability [20,27].

Challenges of DG System Integration

Due to the increase in DG installation, it is essential to analyze the main challenges that DG must overcome to maximize its use without damaging the system [20,27]. Correct planning and the development of an ideal design allow for optimal integration between the DS and the DG, decreasing the occurrence of the problems specified previously [18].

Trying to meet the different challenges produced by the installation of DG is of vital importance when designing a project, that is why the following are the main challenges that must be overcome so that the DG can have an optimal integration [20,28,29].

(a)

Technical challenges

i.

Power quality: appearance and propagation of harmonics when using inverters throughout the system, which affects power quality; however, the development of new technologies reduces the appearance of this problem [30].

ii.

Voltage increase: occurs when the power factor is high or when the power generated through the DG is higher than the load, producing a voltage outside the established ranges, being one of the main limitations when integrating DG [30].

iii.

System protection: due to the appearance of the bidirectional flow when integrating DG, during a fault, the short-circuit current increases when supplied by the two types of generation present in the system (conventional and DG), causing the capacity of the protections to be insufficient to protect the system in the event of a fault [20,27].

(b)

Environmental challenges

i.

Using non-renewable sources in DG causes environmental pollution; however, using wind turbines also causes environmental pollution, noise, visual impacts, and climate change, among others [28,31].

(c)

Regulatory challenges

i.

Create a regulation that incentivizes the EDGC since these companies reduce environmental pollution without harming the user’s consumption [28,31].

2.5. Methods to Perform Optimal DG Integration

It is crucial to find several mathematical methods when looking for optimal DG integration, which allows us to identify the best bar to install the established DG into. Crucially, two ways allow searching for this type of integration, which are specified below [24,28,29,30,31,32].

(a)

Classical methods

Mathematical method, used to perform a specific search with convex programming, which is why they are used to solve the problem of assignment and sizing of DG mathematically [29,33].

(b)

Heuristic methods

Intelligent search methods that use different types of algorithms based on nature are considered evolutionary techniques that allow us to obtain an almost optimal solution to the search for the most suitable bar to connect the DG to [29,32].

i.

The Genetic Algorithm (GA): This algorithm was developed several years ago; its name refers to the theory developed by Charles Darwin [29].

ii.

The Simulated Walkthrough (SA): It allows for the development of a probability function, by which the solution established by this method is assumed or discarded [32].

iii.

Bacterial Feed Optimization Algorithm (BFOA): it was developed based on the behavior of a bacterium; its modeling allows the search for a better convergence through a more efficient path [28].

2.6. Genetic Algorithm (GA)

A genetic algorithm (GA) is a simple, fast, and accurate heuristic method based on natural selection and inheritance [34,35]. By applying the adaptation of the individual within a population, it is achieved that the individuals best adapted to an environment will evolve through generations, so it can be said that this algorithm is based on the theory of natural selection created by Charles Darwin [29,36].

To obtain the best solutions (individuals), through the evolution of future generations, a process is performed that allows assigning a single fitness value, being this value is always positive and different for each individual because it is defined through an objective function specified for each individual [34]. A population within the GA is represented as a set of chromosomes [34,37], where the first population is obtained randomly, this being the basis for the evolution of future generations influenced by a mutation, which is why the selection is performed until a solution is found according to the analyzed problem or until the specified iterations are fulfilled [29].

In representing a chromosome, there are different processes; one of the most common is the representation of the chromosome through a binary chain, through which the position of each chromosome (locus) is established, which has two possible variant genes (alleles) represented by the values 0 and 1 [34,37].

Processes of a GA

Modifying a genetic algorithm involves adjusting various parameters to achieve better performance. One of the most critical aspects of a genetic algorithm is the fitness function. It is essential to choose a suitable fitness function that accurately reflects the problem being solved, for this case, the localization and sizing of DG. Modifying the fitness function requires careful consideration and analysis to ensure that it provides the necessary guidance to the algorithm to produce the desired result. This involves changing the weights assigned to specific variables, for this research, we considered the sizing of distributed generation or incorporating new evaluation criteria. The fitness function may also be dynamically adjusted during the optimization process to adapt to changing conditions or constraints. Ultimately, modification of the fitness function can have a significant impact on the efficiency and effectiveness of the genetic algorithm. To better understand how a GA works, several processes have been developed to determine a solution to the optimization problem in which the GA is used. In this sense, each of the fundamental processes within the analysis and application of a GA is identified below.

(a)

Coding scheme For the GA, being an intelligent search method and being based on genetics, it is crucial that for its analysis, the encoded information of each of the established chromosomes must be obtained, a process that can be developed using a bit string, which can be binary, octal, or hexadecimal [34].

When several encoding strings are used within the GA, the aim is to solve problems with more complex numbers, considering that the binary string cannot do it, despite being the most used when using a GA [37].

(b)

Selection of individuals

When performing the selection process within a GA, the possible participation of the chain in the procreation of individuals is determined, which is why, for a better convergence of the GA, it is necessary to have a better selection pressure, that is, not all established individuals can be considered as the best option to enter the crossing process, only the best individuals can participate in this process, especially when it is sought that future generations have better characteristics than those presented by previous generations [37].

(c)

Crossing generations

To produce a new generation, it is necessary to make a cross between two or more parents, using part of the coded information offered by the chromosomes of these parents; therefore, if the coding is not so complex, the choice of the cross will be simple [34]. As there are several crossover types, the single-point crossover is the simplest since it allows the choice of a random crossover point, where the coded information of two parents present after the chosen end can be exchanged [37].

In addition to the representation of a crossover found in Figure 4, Equation (1) is specified as the crossover formula for two generations, which is based on the process that develops the current generation to obtain several future generations [37].

$$R=\frac{(G+2\sqrt{g}))}{3G}$$

(1)

where:

g represents the number of generations involved within the crossover.

G represents the total number of future generations, established by means of a current generation specified in the study.

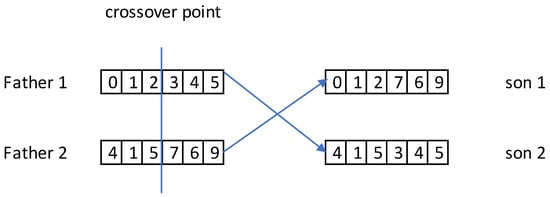
Figure 4. Crossover point of a coded scheme (author).

By having a genetic scheme established by several previous generations, it is sought to maintain order; for this, it is proposed that at the beginning of the simulation, the quantification of the value of R should not be very high; however, as the simulation progresses, the value of R will continue to increase until the simulation concludes, where a very high value of R is presented, caused by the remarkable similarity of the individuals at the end of the simulation [37]. Generation crossover is a process by which the previous generation is modified, due to the sudden alteration, causing the creation of a new generation [34,35]. As established for the selection process, mutation requires the coding shown so that the chromosome can develop [34]. When analyzing the mutation process, it should be taken into account that it can increase or reduce the space where the solution of a problem is found, counting within its operators with a coded mutation and simple inversion [37]. Taking this into account, Figure 5 is developed, through which it is sought to present the alteration that a mutation exerts when applied within a binary chain.

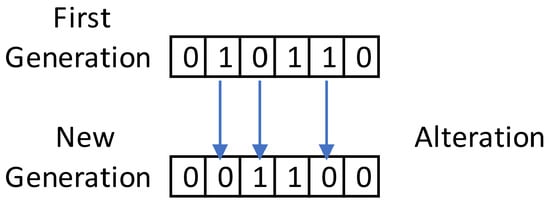
Figure 5. Mutation of a binary string (author).

The development of a GA is based on the application of the aforementioned processes in a specific order. In this sense, Figure 6 shows the flow diagram that establishes the different processes in an orderly manner when applying a GA.

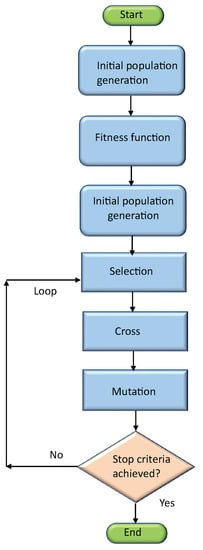
Figure 6. Flow diagram representing the operation of a GA (author).

2.7. Development of the Objective Function (OF)

Developing an OF is paramount in developing the analyzed system; therefore, in Equation (2), the OF is expressed, which is based on the decrease of the voltage drops present inside each bus of the analyzed system. In this case, in [27], both the OF and the adapted constraints to be implemented in this paper are found.

$$FO=\sum _{t=1}^n{\left(V_i\left[p.u\right]-V_{ref}[p.u]\right)}^2$$

(2)

where:

$V_i$ represents the voltage defined at a particular bus.

$V_{ref}$ represents the reference voltage set on the system, by which the analysis can be developed.

n represents the number of busbars of the analyzed IEEE system.

2.8. OF Restrictions

To define the optimal location and sizing of the DG, an OF must be defined and several restrictions that limit the algorithm operation must be detailed. For this work, only two constraints will be available, one for bus voltage and the other for active power injection, the latter being based on using unitary power factor plants, known as GDF plants. Both restrictions are specified below.

2.8.1. Voltage Limit Established for the Busbars of a System

To comply with the limits established for the correct operation of the system after incorporating DG, a voltage restriction must be established to maintain the system’s adequate quality. It should be emphasized that the values in this restriction are specified in [p.u] and are expressed in Equation (3).

$$V_{Lmin}\le V_i\le V_{Lmax}$$

(3)

where:

$V_{Lmin}$ represents the minimum voltage limit set by the above regulation, it has a value of 0.9 [p.u] or 0.95 [p.u].

$V_{Lmax}$ represents the maximum voltage limit set by the above regulation, it has a value of 1.05 [p.u] or 1.1 [p.u].

The different voltages in [p.u] presented in this constraint, depends on the type of system analyzed since, in several cases, from the system without GDF, the defined range is already exceeded [38]. Based on this, the variable $V_i$ is analyzed with GDF when it is desired to verify that the voltage fluctuations do not exceed the limits and without GDF to establish which limits to use in the system.

2.8.2. Active Power Limit of GDF Power Plants

To define the minimum and maximum limits in this constraint, the minimum value generated by photovoltaic technology was considered. In contrast, for the full value, it was established to approximate the value to the results presented in [10], in which GDF power plants are used similarly. In addition, as a guide to visualize the number of panels that make up a GDF power plant to be incorporated in each system, a TSM-DEG20C.20 mono-crystalline bi-facial double glass solar panel is used, which has a maximum power of 600 [w] with 120 cells., Considering the power this panel can deliver and that photovoltaic generation cannot produce less than 1 [kW], the minimum limit for this system will be 1.2 [kW] or two TSM-DEG20C—20 panels in serial connection. According to the guide article, the maximum power for a 33-bus system is 300 [kW]; therefore, for the methods used in this work, the total initial power for each GDF power plant is estimated at 260 [kW], which is within the range established by the ARCERNNR 002/21 regulation and would consist of almost 434 TSM-DEG20C.20 panels in serial connection. However, because two different systems are used in this work, the maximum power could present variations, considering the number of busbars in the system. Considering the premises established above, within Equation (4), the restriction that refers to the limits of active power that can be injected by the GDF power plants to be used within the work is presented.

$$PGD{F}_{Lmin}\le PGDF\le PGD{F}_{Lmax}$$

(4)

where:

PGDF represents the active power obtained by a GDF power plant to be installed within the system.

$PGD{F}_{Lmin}$ represents the minimum active power that the GDF power plant can inject, it has a value of 1.2 [kW].

$PGD{F}_{Lmax}$ represents the maximum active power that can be injected by the GDF power plant depending on the system, initially it will be 260 [kW].

3. Problem Formulation and Methodology

Because conventional generation is deteriorating year after year, preserving the voltage profile in a system has become a challenge, even though several techniques can significantly improve the voltage at the system busbars. In this case, when looking for a technique that offers both technical and environmental benefits during its use in a system, the use of DG has been increasing, considering that its use is focused on obtaining energy from renewable sources. The power injection by a GDF power plant can be established according to the type of technology used. This technique is one of the outstanding ones to satisfy the user’s demand and improve the voltage profile.

For this paper, the first thing to look for is two systems with different numbers of bars, such as the IEEE 9- and 14-bars systems, for which, as a first point, the power flow of each design is simulated, thus obtaining the voltage profile of the system without GDF. Finally, after implementing a GA, the optimal location and sizing for each GDF plant are obtained, establishing the active power to be injected into the system to improve the voltage profile of each system studied and verifying the operation of the GA and its scalability.

3.1. IEEE Test Systems

These systems are used to perform the optimal integration of GDF. Therefore, the proper incorporation of DG to the DS after the application of a GA is established through the IEEE 9-bus system as the primary case later to verify its scalability within an IEEE 14-bus system; therefore, in the following subsections, each of the designs is specified.

3.1.1. IEEE 9-Bus System

The model that is taken as a basis for the development of this study is the IEEE 9-bus system. Therefore, it is necessary to have its single-line diagram, while all its data are defined in [38], while the single-line diagram is developed in Figure 7.

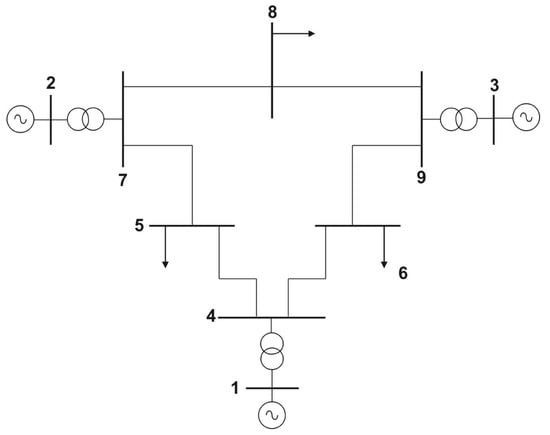
Figure 7. Single-line diagram of the IEEE 9-bus system.

3.1.2. IEEE 14-Bus System

To demonstrate the scalability of the GA, its application is proposed within a 14-bus IEEE system, which has a greater number of elements, which are specified in [38], while Figure 8 shows its single-line diagram.

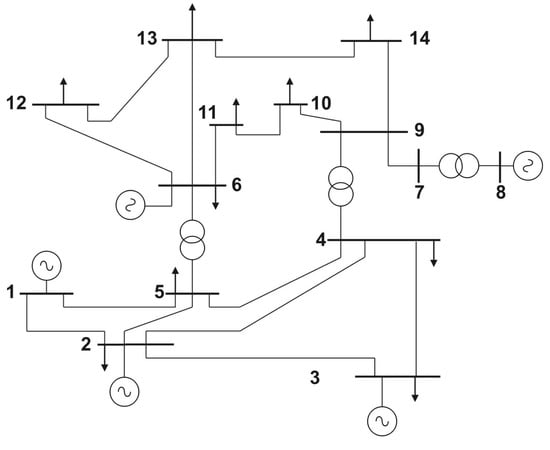
Figure 8. Single-line diagram of the IEEE 14-bus system.

3.2. Pseudo-Code Development

3.2.1. Development of the Power Flow of Systems without GDF

Obtaining the power flow of the 9-bus and 14-bus systems without GDF is considered the base case within this work since they allow quantifying the voltage fluctuations caused by optimally incorporating GDF. Table 4 shows the structure of the pseu-docode.

Table 4. Pseudo-code applied to the solution (author).

Application of GA to Optimally Locate and Size GDFs
Step 1:	Definition of the models, in which the GA will be applied.
Step 2:	Specify the data of the elements of the models used.
Step 3:	Take the voltage at the busbars of the initial model.
Step 4:	Algorithm for optimal location and sizing of GDF.
Step 5:	Assignment of the variables within the algorithm.
	n, $V_{ref},PGDF.$
	target function input
	$FO={\sum }_{t=1}^n{\left(V_i\left[p.u\right]-V_{ref}[p.u]\right)}^2$
	restriction input
	$V_{Lmin}\le V_i\le V_{Lmax}$
	$PGD{F}_{Lmin}\le PGDF\le PGD{F}_{Lmax}$
Step 6:	Application of the GA results to the initial model.
Step 7:	The procedure is performed again for a model with more elements.
Step 8	Verification of GA scalability for the new model.

3.2.2. Voltage Profile of the IEEE 9-Bus System without GDF

The simulation of the power flow of this system developed through an IEEE test model simulator such as DIgSILENT Power Factory allows obtaining the voltage in [p.u] of each of its busbars without the influence of GDF. Table 5 details the quantification of the obtained voltages.

Table 5. Voltage profile of the IEEE 9-bus system without GDF integration (author).

Busbars	Voltage [p.u] without GDF
1	1.0400
2	1.0108
3	1.0225
4	1.0100
5	1.0402
6	0.9885
7	1.0147
8	1.0100
9	1.0305

The values represented in Table 5 allow for establishing the voltage limits that the system should have after incorporating GDF; for this system, the ideal voltage range is between 0.95 [p.u] and 1.05 [p.u].

3.2.3. Voltage Profile of the 14-Bus IEEE System without GDF

As in the previous system, obtaining the voltage profile in [p.u] is necessary to verify the fluctuations that may appear in the system; that is why the power flow is performed again, considering this time the characteristics of this system. Table 6 details the obtained voltages’ quantification.

Table 6. Voltage profile of the 14-bus IEEE system without GDF integration [author].

Busbars	Voltage [p.u] without GDF
1	1.0600
2	1.0450
3	1.010
4	1.0203
5	1.0244
6	1.0600
7	1.0623
8	1.0800
9	1.0419
10	1.0405
11	1.0540
12	1.0573
13	1.0504
14	1.0272

Unlike the 9-bus system, this system, according to the values established in Table 6, allows setting the voltage limits that the system should have after incorporating GDF; for this case, the ideal voltage range is between 0.9 [p.u] and 1.1 [p.u].

4. Analysis of Results

The application of the optimization algorithm used to locate optimally and size GDFs is tested within the following cases specified below:

4.1. 9-Bus IEEE System with and without GDF

Connecting photovoltaic panels in series for distributed generation is a popular technique used in solar power systems. This approach involves connecting multiple panels in a series circuit to produce a higher voltage output. By doing this, the system’s overall efficiency is increased, and the power generated can be used to meet the needs of a larger load. Additionally, this method reduces the amount of wiring and components required, making installation and maintenance more straightforward. Overall, connecting panels in series is a cost-effective way to generate and distribute solar power, making it a popular choice for distributed generation systems. For the IEEE 9-bus system established as a base case of the study, the first thing done was its construction by entering the values taken from the information provided by the IEEE to obtain their voltage profiles before establishing the location and sizing of GDF power plants. The minimum power to be incorporated into this system is 1.2 [kW]. In contrast, due to the smaller number of busbars, a maximum active power value of 120 [kW] can be established, considering that voltages are very close to the one defined for this system. When determining the maximum value of active power that a GDF power plant can inject and using the TSM-DEG20C.20 solar panel as a guide, the use of 200 panels in serial connection can be established, which, during the GA simulation, could undergo several changes since the power delivered by the GDF could be lower than this defined value. As a first case, the incorporation of GDF with the established active power is performed to increase the voltage profile values of the 9-bus system up to a value very close to 1.05 [p.u].

4.2. IEEE 14-Bus System with and without GDF

For the 14-bus IEEE system, once the bus voltages have been established, a limit between 0.9 and 1.1 [p.u] is considered to perform the analysis since the system without GDF exceeds the 1.05 [p.u] established by the range used in the previous system. As in the previous case, the minimum power is 1.2 [kW], while being the system with the most significant number of busbars, it is established that the maximum fuel to be injected by each of the GDF power plants is 260 [kW], contemplating the use of 434 TSM-DEG20C.20 panels.

As a second case, incorporating GDF with the established active power is carried out to increase the voltage profile values of the 14-busbar system to a value very close to 1.1 [p.u]. Finally, if the results obtained allow for an improvement in the voltage profile after incorporating GDF, the scalability of the GA for systems with more busbars than those found within a 9-bus system can be verified.

After performing the GA simulation in Matlab, the location and sizing of each of the GDF power plants focused on improving the voltage profile of each system used is obtained, which is established in the following subsections of this work. Similarly, within the analysis, the simulation time taken by the GA developed in Matlab to find an optimal solution must be specified, using in this process a personal computer consisting of the following features: an AMD Ryzen 3 3300U processor with Radeon Vega Mobile Gfx 2.10 GHz, a 930 GB hard disk and a RAM of 8 GB.

4.3. Voltage Profile of the IEEE 9-Bus System with GDF

As a first step to establish the voltage profile of the system with GDF, we proceed to simulate the GA in Matlab, obtaining through this process the location and sizing of each of the GDF power plants established as the optimal solution for this system. In this sense, the solutions for the location and sizing of the GDF power plants provided by the GA simulation are detailed in Table 7.

Table 7. Location and sizing of GDF power plants—9-bus system (author).

GDF Power Plants	Location	Active P. [kW]
GDF 1	Bar 2	100
GDF 2	Bar 6	57.8

The proposed solution establishes the location of two GDF plants in bars 4 and 6 of the system, with sizing for both plants that are not less than 1.2 [kW] and not more than 120 [kW], allowing to establish that each plant is within the power range defined for the 9-bus system. Using the solar panel guide for the first GDF power plant, it can be estimated that its conformation consists of 167 TSM-DEG20C.20 panels in serial connection. For the second GDF power plant, the number of meetings that can be counted is 97. With the location and sizing of the two GDF power plants, we proceed to enter one by one each power plant into the system, seeking to verify the validity of the solutions established by the GA. Table 8 quantifies the voltage profiles after this incorporation, which will allow comparing them with the voltage profile established by the power flow of this system without GDF.

Table 8. Voltage profile comparison—IEEE 9-bus system with GDF 1–2 (author).

Bar	GDF 1	GDF 2
1	1.0400	1.0400
2	1.0148	1.0149
3	1.0411	1.0416
4	1.0100	1.0100
5	1.0465	1.0467
6	1.0416	1.0433
7	1.0188	1.0189
8	1.0100	1.0100
9	1.0496	1.0500

When reviewing bars 2, 3, 5, 6, 7, and 9, it can be established that there is an increase in their voltage after incorporating each of the defined GDF power plants; however, to achieve a voltage closer to the 1.05 [p.u] established for this system, it is required to incorporate both GDF power plants simultaneously. The comparison of the voltage profile of the system with and without integration of the two GDF power plants is developed in a graph represented in Figure 9.

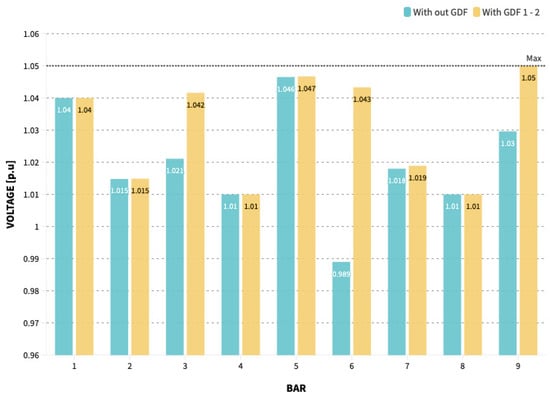
Figure 9. Voltage profile—IEEE 9-bus system with optimum GDF (author).

When reviewing Figure 9, it can be affirmed that the results determining the location and sizing for both GDF plants are optimal, especially when the voltage profile is desired. Finally, due to the fact of performing several processes, among which are the sizing and location of the GDF power plants, the voltage profile by incorporating one by one the established power plants, and the comparative graph of the voltages in the system with and without GDF integration, the GA simulation in Matlab through the computer above takes a time of 304.24145 s or 5.07069 min.

4.4. Voltage Profile of the 14-Bus IEEE System with GDF

The procedure applied to this system is similar to that developed for the previous system. After performing the GA simulation in Matlab, the location and sizing of each GDF power plant was established as the optimal solution for this system. Thus, the solutions provided by the GA simulation for the location and sizing of the GDF power plants are shown in Table 9.

Table 9. Location and sizing of GDF power plants—14-bus system (author).

GDF Power Plants	Location	Active P. [kW]
GDF 1	Bar 3	253.4
GDF 2	Bar 7	140
GDF 3	Bar 10	48.2

The proposed solution establishes the location of three GDF plants in the system’s bars 3, 7, and 10. In contrast, the sizing for each plant did not exceed the 260 [kW] established for this system, in addition to being higher than the 1.2 [kW] specified as minimum power. Using the solar panel guide for the first GDF plant, it can be estimated that it consists of 423 parallel panels; for the second plant, the use of 234 panels is established; and finally, for the third plant, the approximate value would be 81 panels in parallel. Considering the location and sizing of the three power plants, they are incorporated into the 14-bus system, and Table 10 shows the voltage profiles after this incorporation.

Table 10. Voltage profile comparison—IEEE 14-bus system with GDF 1–2–3 (author).

Bar	GDF 1	GDF 1 GDF 2	GDF 1 GDF2 GDF3
1	1.060	1.060	1.060
2	1.045	1.045	1.045
3	1.0100	1.0100	1.0100
4	1.025	1.0187	1.0345
5	1.028	1.0231	1.0421
6	1.0600	1.0600	1.0600
7	1.076	1.0739	1.0920
8	1.0800	1.0800	1.0800
9	1.0643	1.0558	1.0726
10	1.0710	1.0525	1.0884
11	1.0707	1.0607	1.0806
12	1.0588	1.0580	1.0590
13	1.0538	1.0527	1.0554
14	1.0411	1.0360	1.0465

When reviewing buses 4, 5, 6, 7, 9, 10, 11, 12, 13, and 14, an increase in the voltage profile during the whole process can be verified; taking into account this, the incorporation of three GDF power plants established by the GA allows having a voltage profile closer to the 1.1 [p.u] defined for this system. The comparison of the voltage profile of the system with and without the integration of the GDF power plants established to improve the voltage at the busbars is developed in Figure 10.

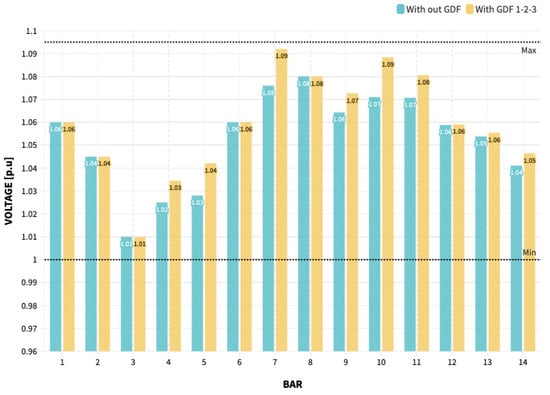
Figure 10. Voltage profile—IEEE 14-bus system with optimum GDF (author).

Focusing on the results obtained in the simulation, the scalability of the GA is fully proven since it presented an improvement in the voltage profile in the IEEE system of 9 and 14 bars without considering that both systems have a different number of bars. Finally, to conclude the analysis of the results presented in this work, it is considered that the simulation of the GA for a 14-busbar system in Matlab using the computer mentioned above had a simulation time of 4664.1609 s or 77.736015 min. In this research, the performance was approximated to 95%, mainly because of the time for smaller scale instances. Here, in Table 11, is a comparison of some related works on genetic algorithms that emphasize performance.

Table 11. Some performance comparisons [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37].

Works	Approach	Problem Type	Problem Size	Success Rate	Execution Time
A	Genetic algorithms with improved mutation and crossover operators	Mathematical function optimization	0–100 variables	95%	1–10 s
B	Genetic algorithms with elite selection and adaptive crossover	Mathematical function optimization	50–500 variables	98%	10–60 s
C	Genetic algorithms with dynamic selection and mutation operators	Production planning problems	Up to 100 tasks	90%	1–5 min
D	Genetic algorithms with multiple populations and hybrid fitness function	Vehicle routing problems	Up to 50 locations	95%	5–20 min
This paper	Genetic algorithms with multiple populations	Function optimization with constraints	10–15 variables	95%	5–8 min

5. Conclusions

After analyzing the results obtained from this study, it has been concluded that a genetic algorithm can effectively design and optimize distributed power generation systems for maximum efficiency and reliability. Using a genetic algorithm allows for the simultaneous optimization of multiple parameters, such as the size and number of generators, fuel types, and network configurations, resulting in the most optimal combination of these factors for generating electricity in a distributed manner. Furthermore, genetic algorithms can adapt and evolve, making them particularly useful in dynamic and changing environments, such as in distributed power generation, where demand and supply can vary depending on location and time of day.

Genetic algorithms can search for the best solutions in complex and non-linear systems. They can optimize the performance of distributed generation systems by identifying the most effective combination of system parameters. These algorithms are useful in solving various problems related to distributed generation, such as system design, control, and optimization.

To ensure that the size of the system does not limit the GA, it is essential to test its scalability in systems with various busbars. This will help verify that the GA can be used in different plans as long as constraints establish an optimal solution.

The significance of genetic algorithm research in electrical engineering cannot be overstated. As the field progresses, new obstacles that call for innovative solutions to intricate problems will emerge. Genetic algorithms are a potent tool for exploring vast solution spaces, optimizing system performance, and lowering computational expenses. With electrical systems growing increasingly complex and increasing efficiency demands, genetic algorithms are becoming more crucial than ever. Ongoing studies in this field will lead to significant progress in electrical engineering, with applications spanning from power distribution and control systems to renewable energy and smart grid technologies. Ultimately, developing more sophisticated genetic algorithms will play a pivotal role in shaping the future of the electrical engineering industry.

Future Works

For the development of future works, several options can be researched based on the optimal sizing of multiple DG units for their incorporation into the DS with variations in the system load. The DG allocation within a system is performed, in general, at full load. However, the load over the years presents a variation due to the increase in users, requiring that the DG power plants previously incorporated must be resized, considering that the size of the DG must increase to meet the required demand, especially when there is a voltage limit that must be met without considering the variation of the loads.