A Bridge-Level Junction Temperature Estimation Method for SiC MOSFETs Combining Transient Voltage and Current Peaks

Abstract

Accurate measurement of the junction temperature T_j is crucial for ensuring safe operation and evaluating the performance of silicon carbide (SiC) metal–oxide–semiconductor field-effect transistors (MOSFETs). In this paper, the junction temperature of a half-bridge is monitored by combining transient voltage and current peaks across the lower device. Both theoretical analysis and switch tests validate that the peak induced voltage and peak reversed current during the commutation transient exhibit a linear relationship with the temperature of the corresponding devices. The impact of load current and bus voltage on the measurement results is also investigated. Moreover, the effectiveness of the proposed method is confirmed by carrying out tests at different temperatures, and the feasibility of online implementation is discussed. The experimental results show that the proposed method has high linearity and sensitivity and can simultaneously provide temperature information for both devices of a half-bridge.

1. Introduction

The silicon carbide metal–oxide–semiconductor field-effect transistor (SiC MOSFET), as a typical representative of wide-bandgap semiconductor devices, has superior properties, such as high switching frequency, high voltage withstanding capability, and low on-resistance. With the widespread application of silicon carbide devices in fields such as rail transportation, aviation and aerospace, automotive, and new energy generation in recent years [1,2], the requirements for their reliability are increasing. Temperature is one of the main causes of power device failure [3], so temperature measurement is of great significance for the safe and reliable operation and thermal management of power electronic devices [4,5].

At present, temperature measurement methods mainly comprise thermal network, physical contact, optical, and temperature-sensitive electrical parameter (TSEP). The accuracy of the thermal network method has been improved [6,7]; based on the power loss of the device under testing and the transient thermal impedance model, the junction temperature can be calculated. However, obtaining the real-time loss of SiC MOSFET can be challenging. Additionally, the thermal impedance network is subject to the effects of device aging and environmental factors, which can influence the accuracy of the calculated junction temperature. The physical contact and optical methods require the decapsulation of power devices, which reduces system reliability [8,9]. Conversely, the TSEP method is advantageous due to its low cost, fast response, and ability to measure junction temperature without causing damage to the package. It is currently the most widely used temperature measurement method.

The temperature-sensitive electrical parameters of SiC MOSFET devices can be categorized into static and dynamic parameters based on different measure timings. The static electrical parameters include internal gate resistance [10], on-state voltage drop [11], on-state resistance [12], and body diode voltage drop [13]. The sensitivity of the internal gate resistance is relatively low, making its measurement difficult. The on-state voltage drop shows a positive correlation with temperature under a high current, although it requires high-resolution voltage clamp circuits during switching transients. The voltage drop across the body diode is also sensitive to temperature changes and remains stable during device aging; however, online application of this parameter is challenging, since its measurement requires injecting a small current into the source-drain.

The dynamic temperature-sensitive electrical parameters consist of dynamic threshold voltage [14], turn on/off delay [15,16], and peak gate current, et cetera. A measurement scheme proposed in [16] enables online measurement of the device’s turn-on delay during inverter operation. However, the sensitivity is at the picosecond level, thus necessitating intelligent driving circuits for improved accuracy. Reference [17] obtains the gate peak current by measuring the voltage across the external drive resistor, which can be easily measured online and integrated, as it is not affected by the load current. Nonetheless, this method is not suitable for gate drive topologies with inductors or push–pull structure.

Regarding bridge-level TSEPs, reference [18] utilized the voltage oscillation on the DC bus caused by the current change rate to extract the temperature of the half-bridge. This method needs to combine the switching timing of the upper and lower switches and cannot simultaneously reflect the bridge temperature in one switching period. Furthermore, real-time digital acquisition of the transient process requires the use of high-precision ADC and signal-processing circuits.

In summary, the existing TSEP methods for SiC MOSFET devices have certain limitations, such as difficult measurement, low linearity, and low sensitivity. Furthermore, research on the dynamic TSEPs of SiC MOSFET devices has typically only focused on device-level parameters, instead of using bridge- or system-level parameters to estimate temperature. The conventional single-TSEP can be influenced by the temperature of other devices in practical applications [19]. Additionally, multiple floating grounds at bridge midpoints bring common mode interference issues [20], requiring additional isolation design of the measurement circuit to monitor the upper switch.

In contrast to traditional device-level TSEPs, this paper proposes a novel method for measuring junction temperature at the bridge level, using the transient reverse recovery current peak and the voltage peak induced by the current change rate as combined TSEPs. The proposed method overcomes the need for measurement circuits at floating grounds, as it only requires one measuring unit at the lower switch of the phase leg. Moreover, it can reflect the temperature of the phase leg simultaneously within one same switching period. The switching process of each SiC MOSFET device during the commutation stage is explained specifically, and the correlation between the proposed TSEPs and the corresponding device temperature is analyzed. Subsequently, a dynamic switching characteristics platform is established to calibrate the peak induced voltage and peak reverse recovery current at different temperatures. The effects of load current and bus voltage on the temperature calibration curve are also evaluated, and the online feasibility of the proposed method is discussed. This method utilizes the inherent parasitic inductance of the SiC MOSFET discrete device itself, without the need for external sensors, making it non-intrusive and suitable for bridge-level temperature estimation of the SiC MOSFET device.

2. Theoretical Analysis of Combining Transient Peaks as a Bridge-Level TSEP

2.1. Commutation Process of SiC MOSFETs in a Phase Leg Structure

The schematic diagram of the half-bridge test circuit considering parasitic parameters is shown in Figure 1a. S₁ is the upper switch, which is actively controlled by a double-pulse drive to the gate, and S₂ is the lower switch, with a constant negative bias on the gate to ensure the channel is completely turned off. The body diode of S₂ is used to provide a freewheeling loop for the load current. The main parasitic parameters in the circuit include: external and internal gate resistance R_g, external and internal gate loop parasitic inductance L_g, drain-source parasitic inductance L_d, power source drain parasitic inductance L_sp, Kelvin source drain parasitic inductance L_sk, and the sum of the parasitic resistance in series between the power source drain and Kelvin source drain, R_s.

The main switch waveforms of S₁ and S₂ are shown in Figure 1b, and the specific commutation process analysis is as follows:

① (t₀~t₁): This stage is the delay period for S₁ to turn on. The gate voltage v_gs1 rises from the negative voltage V_EE to the threshold voltage V_th with a time constant of R_g (C_gs + C_gd). During this stage, v_gs1 < V_th, and the load current flows through the body diode of S₂.

② (t₁~t₂): In this stage, the load current is commutated from the body diode of S₂ to the channel of S₁. After the gate voltage v_gs1 rises to the threshold voltage V_th, the channel current i_d1 of S₁ rises to the load current I_L at a rate of di_d1/dt, and i_d2 decreases to zero at the same rate.

At this time, v_ds1 >> (V_GG − V_th), S₁ is in a saturation region, and the drain-source current i_d1 can be expressed as:

$$i_{\mathrm{d}1}=\frac{\beta }{2}{(v_{\mathrm{gs}1}-V_{\mathrm{th}})}^2$$

(1)

$$\beta =\frac{W_{\mathrm{CH}}{\mu }_{\mathrm{CH}}{C}_{\mathrm{OX}}}{L}$$

(2)

where β is the gain coefficient, W_CH is the channel width of the inversion layer, and μ_CH is the effective carrier mobility of the channel.

The current change rate during this commutation stage can be calculated as:

$$\frac{\mathrm{d}{i}_{\mathrm{d}1}}{\mathrm{d}t}=\beta (v_{\mathrm{gs}1}-V_{\mathrm{th}})\frac{V_{\mathrm{GG}}}{R_{\mathrm{g}}(C_{\mathrm{gs}}+C_{\mathrm{gd}})}{e}^{-\frac{t}{R_{\mathrm{g}}(C_{\mathrm{gs}}+C_{\mathrm{gd}})}}$$

(3)

③ (t₂~t₃): This stage is the charge storage stage. The current of S₁ continues to rise from I_L to I_L + I_rrm, while the current of S₂ continues to decrease from zero to a negative value. During this process, the free carriers in the drift region are swept away. At t₂, the free carriers are zero, and the depletion region begins to form. At t₃, the reverse recovery current reaches the negative peak value I_rrm.

The peak reverse recovery current has the following relationship with the distribution of free carrier concentration [21]:

$$I_{\mathrm{rrm}}=2q{D}_{\mathrm{a}}\frac{\mathrm{d}n}{\mathrm{d}x}=2q{D}_{\mathrm{a}}\frac{n_{\mathrm{a}}}{h}$$

(4)

where D_a is the bipolar diffusion coefficient, q is electron charge, and h is defined as the distance between the maximum and minimum carrier concentrations.

The carrier concentration n_a can be expressed as:

$$n_{\mathrm{a}}=\frac{I_{\mathrm{L}}{\tau }_{\mathrm{HL}}}{2qd}$$

(5)

where τ_HL is the minority carrier lifetime, and d is half of the drift region width.

④ (t₃~t₄): This stage is the reverse recovery stage. S₂ begins to withstand voltage, and at the same time, the parasitic capacitance of S₁ begins to discharge, while the parasitic capacitance of S₂ begins to charge. The current of S₂ during this stage consists of two parts: the actual reverse recovery current caused by the formation of the depletion region and the current charging the parasitic capacitance.

⑤ (t₄~t₅): In this stage, the reverse recovery process of S₂ ends, and S₁ enters the linear ohmic region.

2.2. Temperature Dependence Analysis

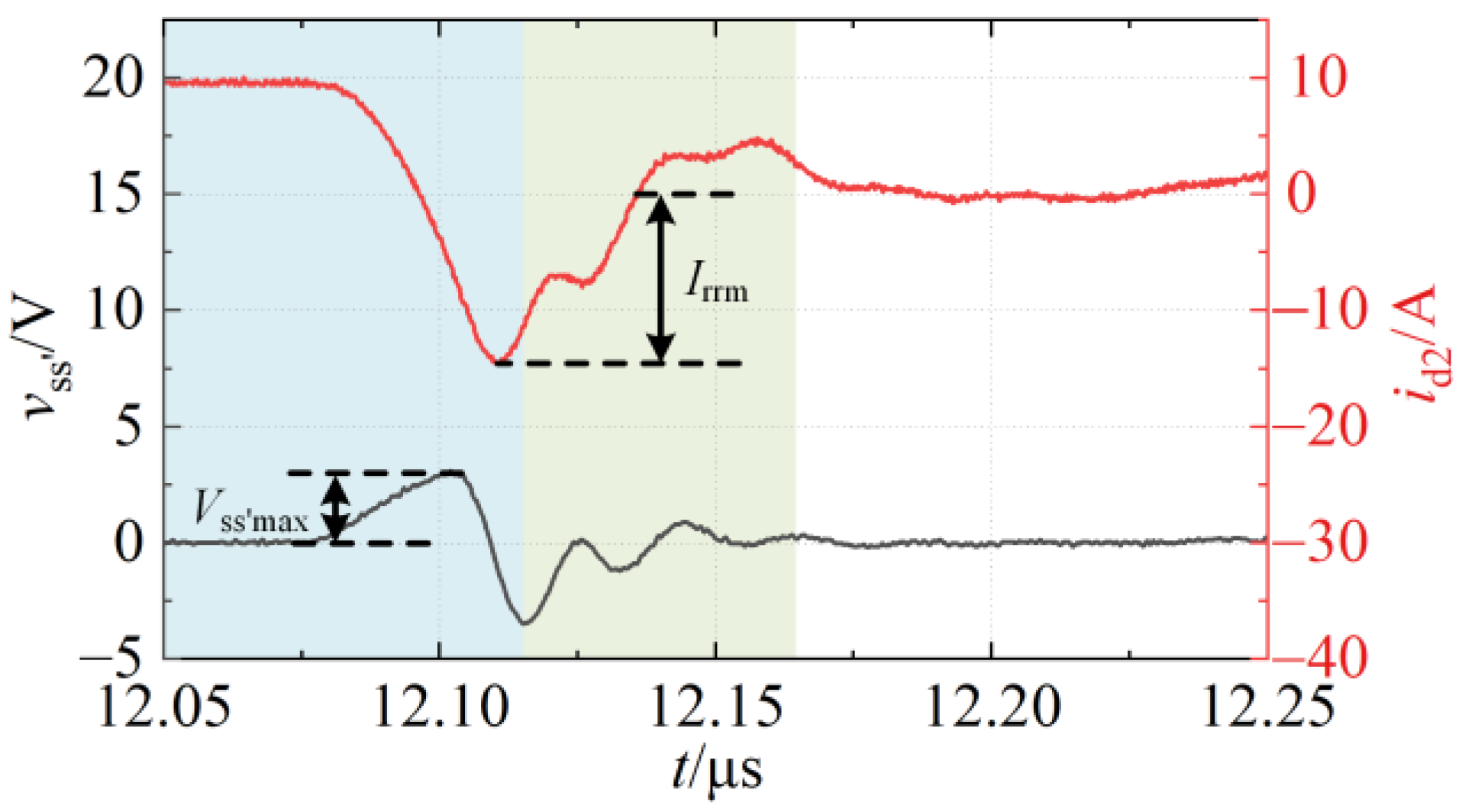
2.2.1. Peak Induced Voltage

From Figure 1a, it is evident that there exist a parasitic inductance L_sk and a parasitic inductance L_sp between the power source s and the auxiliary source s’ of the discrete SiC MOSFET device with a Kelvin package. The induced voltage v_ss′ at the two source terminals can be utilized to reflect the current change rate di_d2/dt. In the commutation process as depicted in Figure 1b, the channel of S₂ is completely turned off; the induced voltage v_ss′ is only influenced by the power loop and can be given by:

$$v_{{\mathrm{ss}}^{\prime }}=L_{\mathrm{sp}}\left(\frac{\mathrm{d}{i}_{\mathrm{d}2}}{\mathrm{d}t}\right)+R_{\mathrm{s}}{i}_{\mathrm{d}2}$$

(6)

As analyzed in Section 2.1, during t₁ to t₃, the current of S₂ drops from the load current at a speed of di_d1/dt, and the induced voltage at this time can be further expressed as:

$$v_{{\mathrm{ss}}^{\prime }}=-L_{\mathrm{sp}}\left(\frac{\mathrm{d}{i}_{\mathrm{d}1}}{\mathrm{d}t}\right)+R_{\mathrm{s}}{i}_{\mathrm{d}2}, t_1<t<t_3$$

(7)

Owing to the wide bandgap property of SiC MOSFET devices, di_d1/dt exhibits a positive temperature coefficient under the dominating influence of the device threshold voltage V_th [22].

The induced voltage peak V_ss′max appears at the moment when the current change rate reaches its maximum value. From Equations (1) and (3), during t₁ to t₂, the drive voltage rises approximately linearly, and the drain-source current increases in a quadratic function form, indicating that the maximum current change rate occurs at t₂. At this moment, the peak induced voltage can be expressed as:

$$V_{{\mathrm{ss}}^{\prime }\max }=-L_{\mathrm{sp}}{\left(\frac{\mathrm{d}{i}_{\mathrm{d}1}}{\mathrm{d}t}\right)}_{\max }+R_{\mathrm{s}}{i}_{\mathrm{d}2}$$

(8)

According to the device datasheet and manufacturer Spice model, the typical value of the source parasitic resistor R_s is usually in the range of 3 to 5 mΩ, while the parasitic inductance L_sp is about a few nH, and the switching current change rate of SiC MOSFET devices is around 0.5–3 A/ns. Therefore, v_ss′ is mainly composed of induced voltage drop caused by parasitic inductance, and the changes caused by the temperature drift of parasitic resistance R_s is negligible. Upon determining the internal factors, such as the doping process and the physical size of the device during manufacturing, the parasitic parameter L_sp can be considered a fixed value [14]. Thus, under the influence of the positive temperature characteristic of (di_d1/dt)_max, V_ss′max has a positive correlation with temperature and is only affected by the temperature of S₁.

2.2.2. Peak Reverse Recovery Current

Based on Equations (4) and (5), it is apparent that the peak reverse recovery current of a SiC MOSFET device is affected by the minority carrier recombination rate in the drift region, which is closely related to the minority carrier lifetime τ_HL and the bipolar diffusion coefficient D_a, with D_a exhibiting a negative temperature coefficient [21]. Furthermore, the relationship between the minority carrier lifetime and temperature can be described mathematically, as given by Equation (9) [21]. The minority carrier lifetime in the drift region increases exponentially with temperature, causing an increase in I_rrm. Thus, I_rrm is affected by the temperature of S₂.

$${\tau }_{HL}={\tau }_0{(\frac{T_j}{300})}^k$$

(9)

In the current commutation process, the body diode of S₂ is turned off by active controlling of the complementary switch S₁. When the external switch speed di_d1/dt is decreased, the gradient of the minority carrier concentration in the drift region is reduced, causing a decline in the peak reverse recovery current of the body diode. Additionally, di_d1/dt is also impacted by the temperature of the upper switch S₁, as discussed in Section 2.2.1. Therefore, the temperature of S₁ also has an impact on I_rrm.

The positive peak voltage V_ss′max and the negative peak current I_rrm both occur at the same switching transient. While V_ss′max is affected independently by the junction temperature of S₁, I_rrm is affected by the temperature of S₁ and S₂. Consequently, it is possible to establish the two electrical parameters as functions of T_j1 (junction temperature of S₁) and T_j2 (junction temperature of S₂), as shown in Equations (10) and (11), if the correlation is highly linear, which would be calibrated in later experiments.

$$V_{{\mathrm{ss}}^{\prime }\max }=f_{v_{{\mathrm{ss}}^{\prime }\max }}(T_{\mathrm{j}1})=a{T}_{\mathrm{j}1}+b$$

(10)

$$I_{\mathrm{rrm}}=g_{I_{\mathrm{rrm}}}(T_{\mathrm{j}1},T_{\mathrm{j}2})=c{T}_{\mathrm{j}1}+d{T}_{\mathrm{j}2}+e$$

(11)

By carrying out offline calibration experiments under fixed operating voltage and current, and various junction temperatures, the values of V_ss′max and I_rrm can be determined. Subsequently, the functions of the two TSEPs with respect to device temperatures can be established using mathematical tools such as MATLAB. This approach offers a feasible solution for determining the temperature of devices in a phase leg configuration simultaneously, by only sampling the electrical parameters of the lower switch.

3. Experimental Results

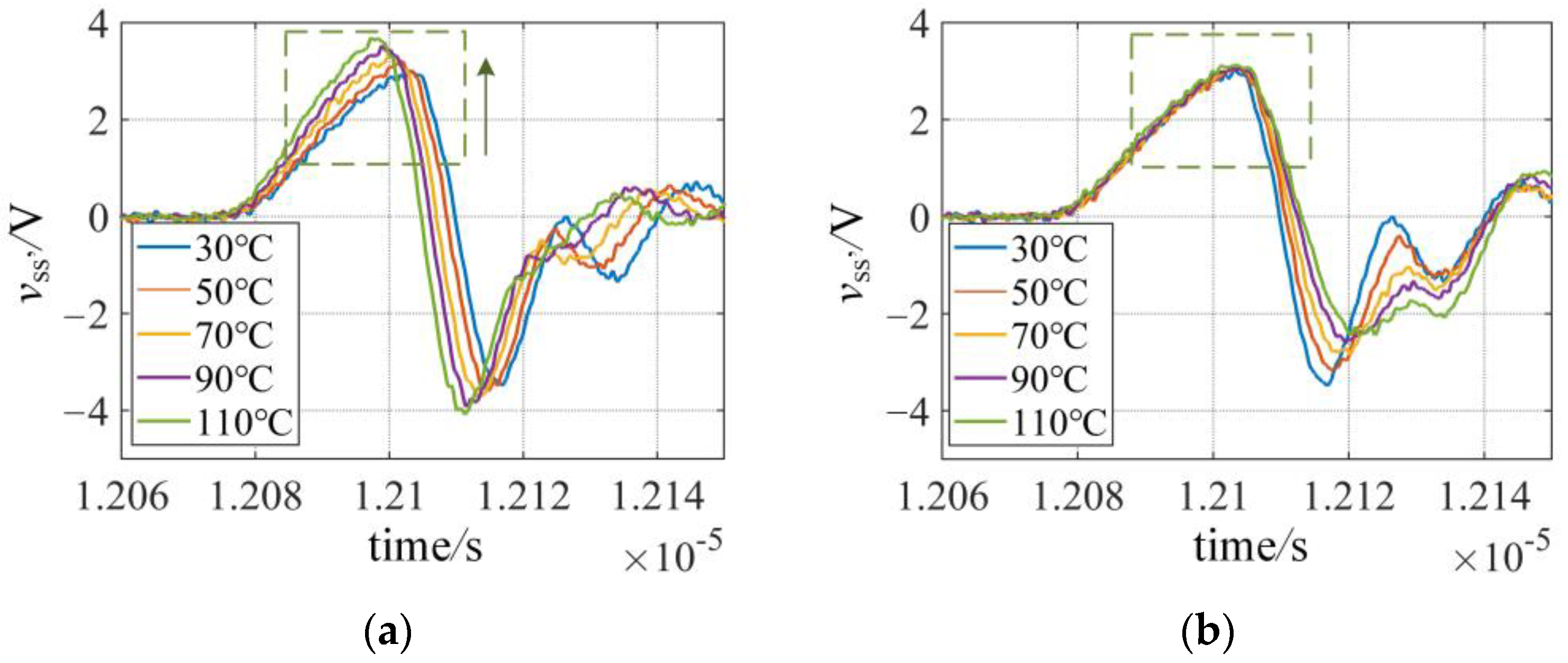
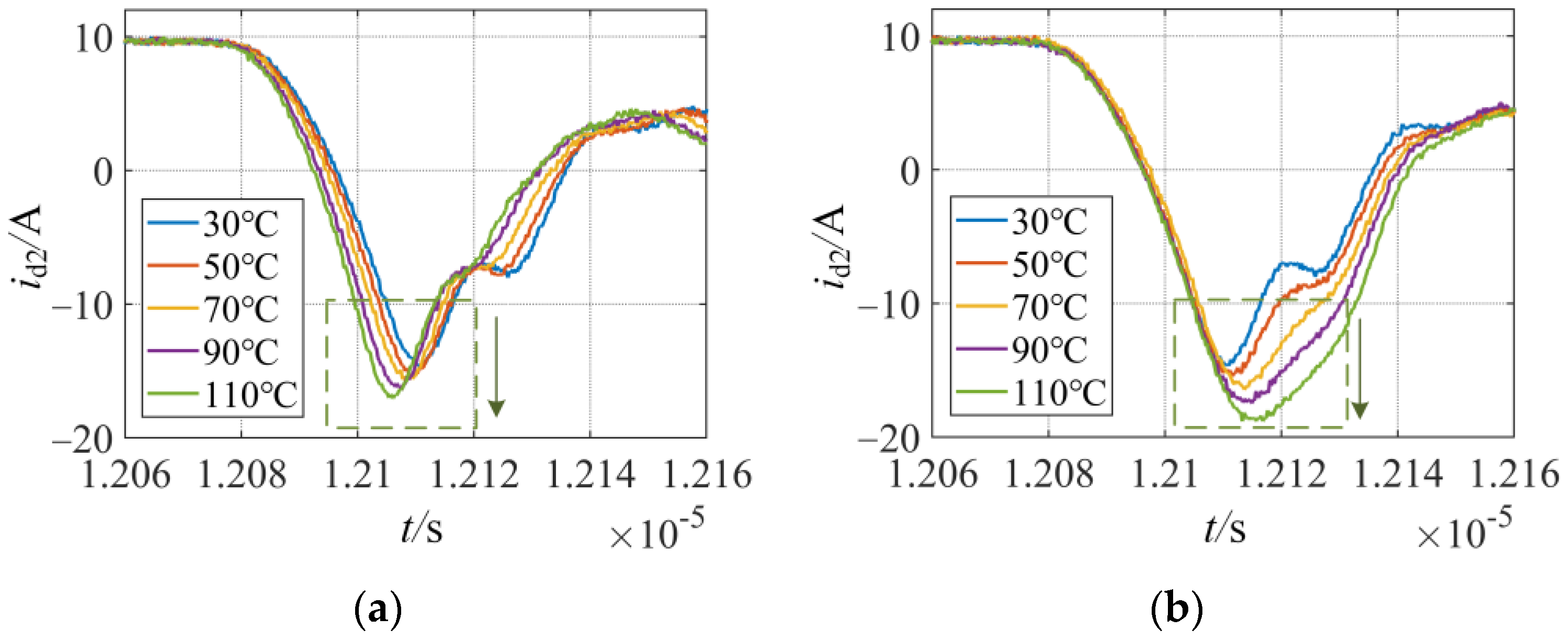
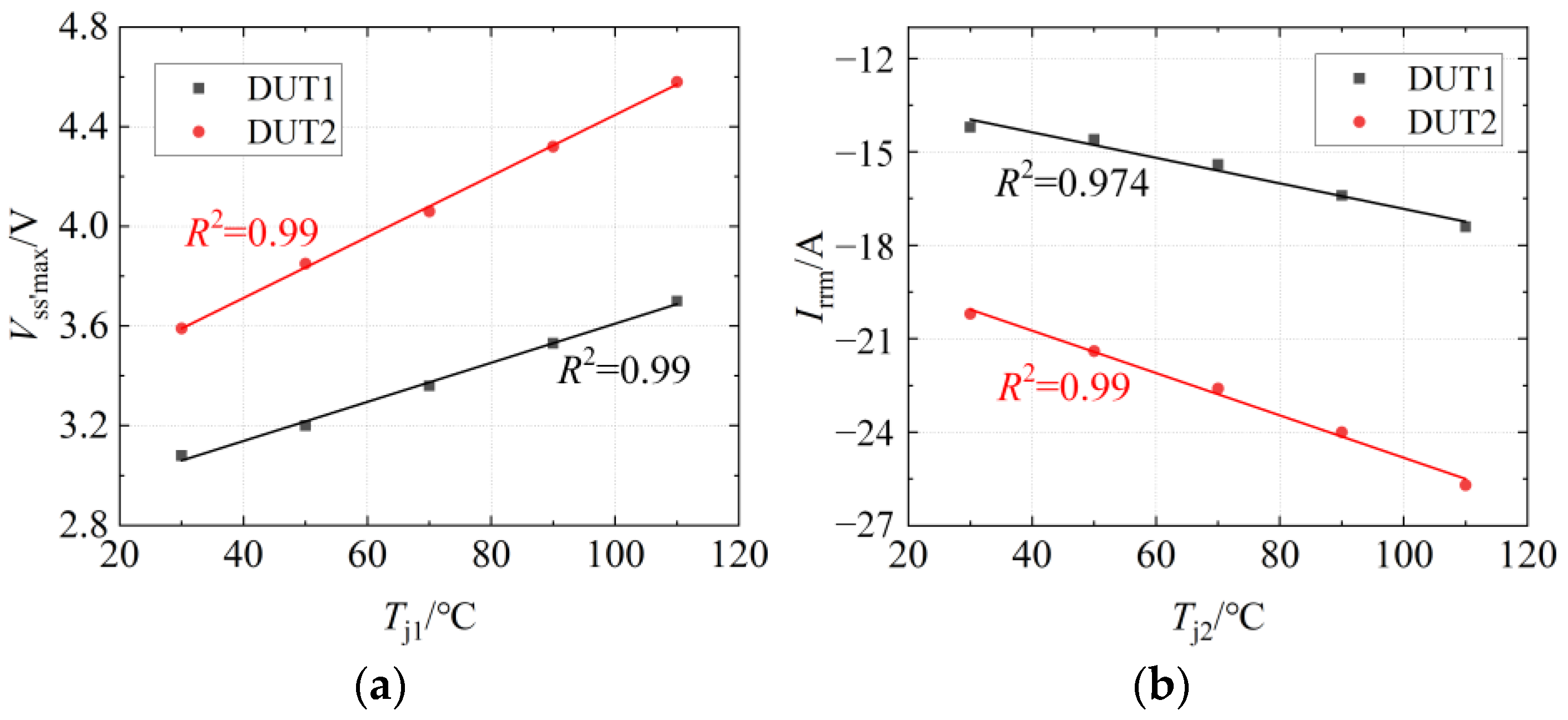
3.1. Temperature Dependence

The double-pulse test platform shown in Figure 2 is built to verify the temperature characteristics of the proposed TSEPs. The test is performed under the operating conditions of a bus voltage of 300 V and a load current of 10 A, with both upper and lower switches in the phase leg being Wolfspeed’s discrete SiC MOSFET devices C2M0045170P (Wolfspeed, Durham, NC, USA), rated for a voltage and current level of 1700 V/72 A.

Due to the switching speed of SiC MOSFET devices being in the nanosecond range, high-bandwidth measuring equipment is required to ensure accurate measurements. Specifically, the bandwidth margin should be designed to be three to five times greater than the calculated value. According to signal theory, the effective bandwidth of the signal rise time t_r or fall time t_f should be [23]:

$$f_{\mathrm{BW}}=\frac{0.35}{\min (t_{\mathrm{r}},t_{\mathrm{f}})}$$

(12)

For instance, as calculated by Formula (12), a 3dB bandwidth of at least 35 MHz is required to measure the turn-on current during a ten-nanosecond period. Considering a margin of five times, the measuring equipment should have a bandwidth of at least 175 MHz. Therefore, device voltage and current measurements in this paper are conducted using a 500 MHz passive voltage probe and a 1 GHz shunt resistor, respectively, and the oscilloscope used is Tektronix’s DPO7104C (Beaverton, OR, USA).

The transient experimental waveforms are illustrated in Figure 3. As the current change rate of i_d2 in the commutation process begins to drop, a voltage with a peak value of approximately 3 V is generated at the parasitic inductance L_sp of the lower switch. Considering the propagation delay of about three to five nanoseconds between the voltage waveform measured by the passive probe and the current waveform measured by the coaxial shunt resistor [24], the peak induced voltage appears around the moment when the load current crosses zero, which is the S₂ temperature insensitive region, and is consistent with the theoretical analysis.

During the test, a PID temperature controller is utilized to control the device under testing. The temperature of the heating pad is set to 30 °C, 50 °C, 70 °C, 90 °C, 110 °C, and 130 °C to observe i_d2 and v_ss′ waveforms. Figure 4a displays the waveform when S₁ is heated and S₂ is maintained at room temperature. In contrast, Figure 4b shows the waveform with S₂ heated and S₁ at room temperature.

As illustrated in Figure 4, under the same operating conditions, V_ss′max rises with the increasing temperature due to the positive correlation between (di_d1/dt)_max and T_j1. The temperature change of T_j2 does not impact the current change rate before its body diode enters the reverse recovery process. Hence, V_ss′max remains unaffected within the tested temperature range of S₂. The experimental results align with the theoretical analysis.

The same testing approach is employed to capture i_d2 waveforms when the upper and lower switches operate at different temperatures, as shown in Figure 5. It is apparent that I_rrm is dependent on both S₁ and S₂ and increases with the rising temperature, owing to the impact of the device carrier lifetime and the switch speed of the complementary device.

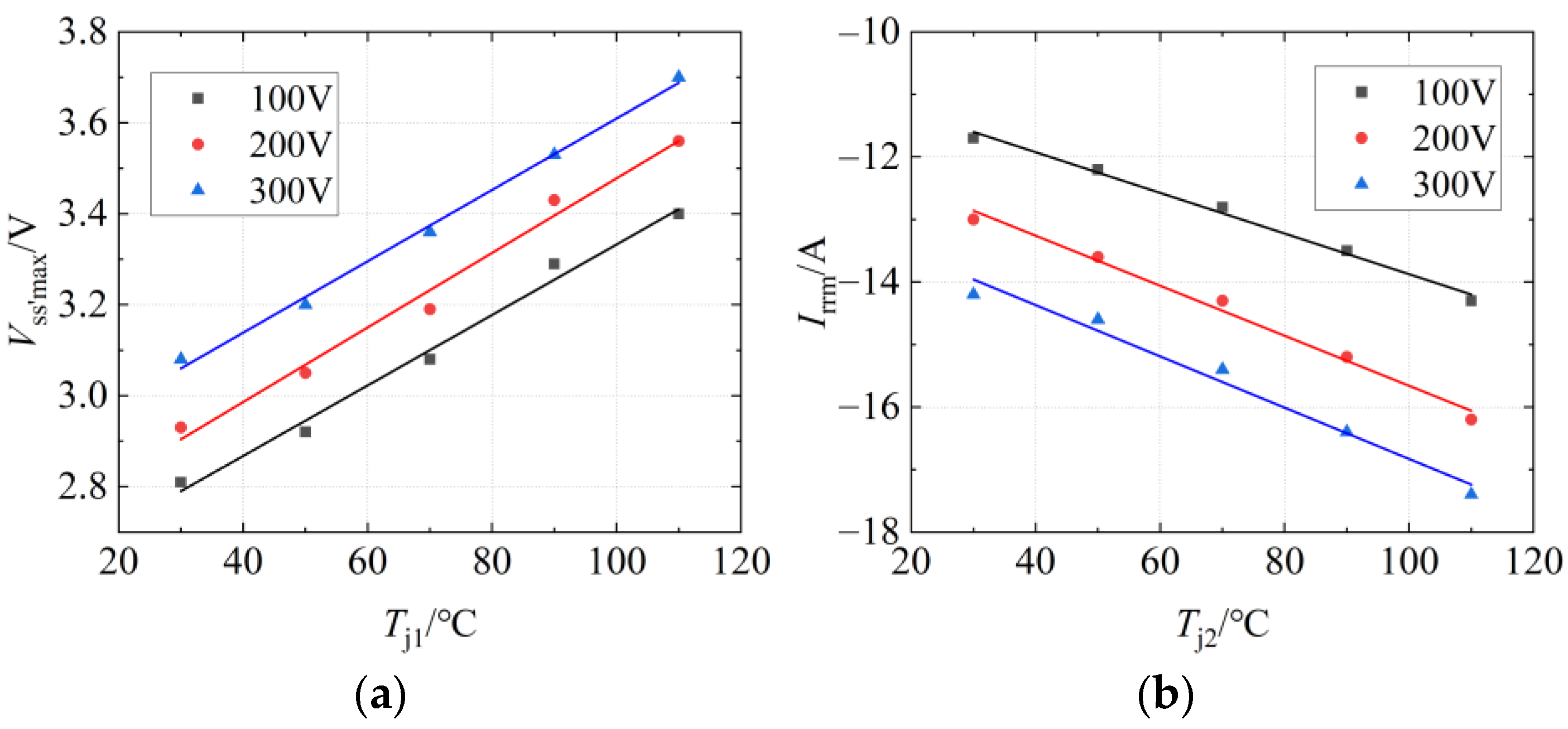
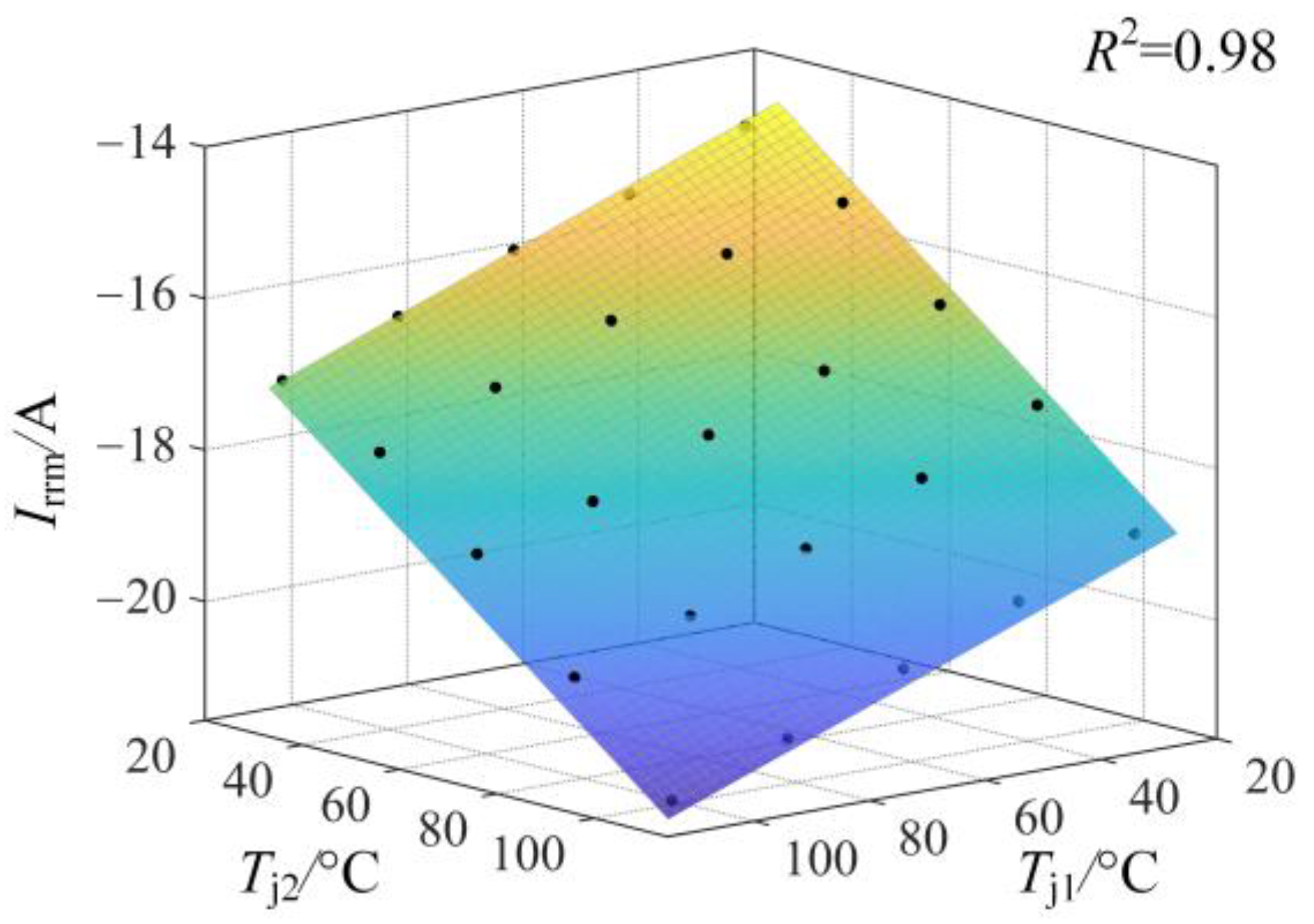
3.2. Operating Conditions Dependence

The relationship between V_ss′max and I_rrm, with junction temperature obtained under different load currents and a fixed bus voltage, is shown in Figure 6. The results demonstrate that both V_ss′max and I_rrm exhibit high temperature sensitivity at any load current. The increase in load current results in a greater number of free charge carriers in the drift region, leading to a larger reverse recovery process. Therefore, the temperature sensitivity of I_rrm increases with increasing load current and is approximately −53 mA/°C, −62 mA/°C, and −86 mA/°C for load currents of 10 A, 15 A, and 20 A, respectively.

Figure 7 displays the relationship between V_ss′max and I_rrm with the junction temperature under different bus voltages. The depletion layer of the device widens with an increase in bus voltage, which decreases the depletion layer capacitance C_dep and accelerates the switching transient. Meanwhile, the device needs to produce a wider space charge region at higher bus voltages. The value of the combined TSEPs will thereby be affected by bus voltage. The fitted results in Figure 7 indicate that the temperature characteristic displays a similar trend under the tested bus voltage of 100 V, 200 V, and 300 V, and the absolute values of V_ss′max and I_rrm increase with an increase in bus voltage.

To validate the universality of the proposed method, a different discrete SiC MOSFET device C3M0030090K from Wolfspeed (Durham, NC, USA), rated at 900 V/73 A, is selected for the same experimental verification. The junction temperature calibration curves for the two different types of devices are shown in Figure 8. The experimental results demonstrate that the combined TSEPs exhibit a similar temperature variation trend for different devices.

Based on the obtained experimental results, it can be observed that the device junction temperature T_j, peak induced voltage V_ss′max, and peak reverse recovery current I_rrm exhibit a nearly linear relationship, with a fitting coefficient R square over 0.97. Specifically, at a bus voltage of 300 V and a load current of 10 A, an increase of 1 °C in T_j1 leads to a rise of approximately 10 mV in V_ss′max, while a temperature rise of 1 °C in T_j2 results in an absolute value increase of 44 mA in I_rrm. The combined TSEPs demonstrate high sensitivity and linearity. In addition, since the sensitivity of I_rrm increases with a larger load current, the accuracy of the proposed method will be further improved in higher current applications. The calibrated relationship between I_rrm and the junction temperature of S₁ and S₂ is presented in Figure 9.

By substituting the experimental data into Equations (10) and (11) and employing MATLAB for linear fitting, the value of the coefficients a, b, c, d, and e can be mathematically obtained:

$$V_{{\mathrm{ss}}^{\prime }\max }=f_{v_{{\mathrm{ss}}^{\prime }\max }}(T_{\mathrm{j}1})=0.007895T_{\mathrm{j}1}+2.822$$

(13)

$$I_{\mathrm{rrm}}=f_{I_{\mathrm{rrm}}}(T_{\mathrm{j}1},T_{\mathrm{j}2})=-0.02895T_{\mathrm{j}1}-0.05317T_{\mathrm{j}2}+12.24594$$

(14)

The function between the phase leg temperature and the combined TSEPs under given working conditions can be derived as:

$$\{\begin{array}{l}{T}_{\mathrm{j}1}=126.6624V_{{\mathrm{ss}}^{\prime }\max }-357.4414\\ T_{\mathrm{j}2}=-68.9656V_{{\mathrm{ss}}^{\prime }\max }-18.8076I_{\mathrm{rrm}}-35.6959\end{array}$$

(15)

where in Equations (13)–(15), the units of voltages, currents, and temperatures are given in volts, amperes, and Celsius degrees, respectively.

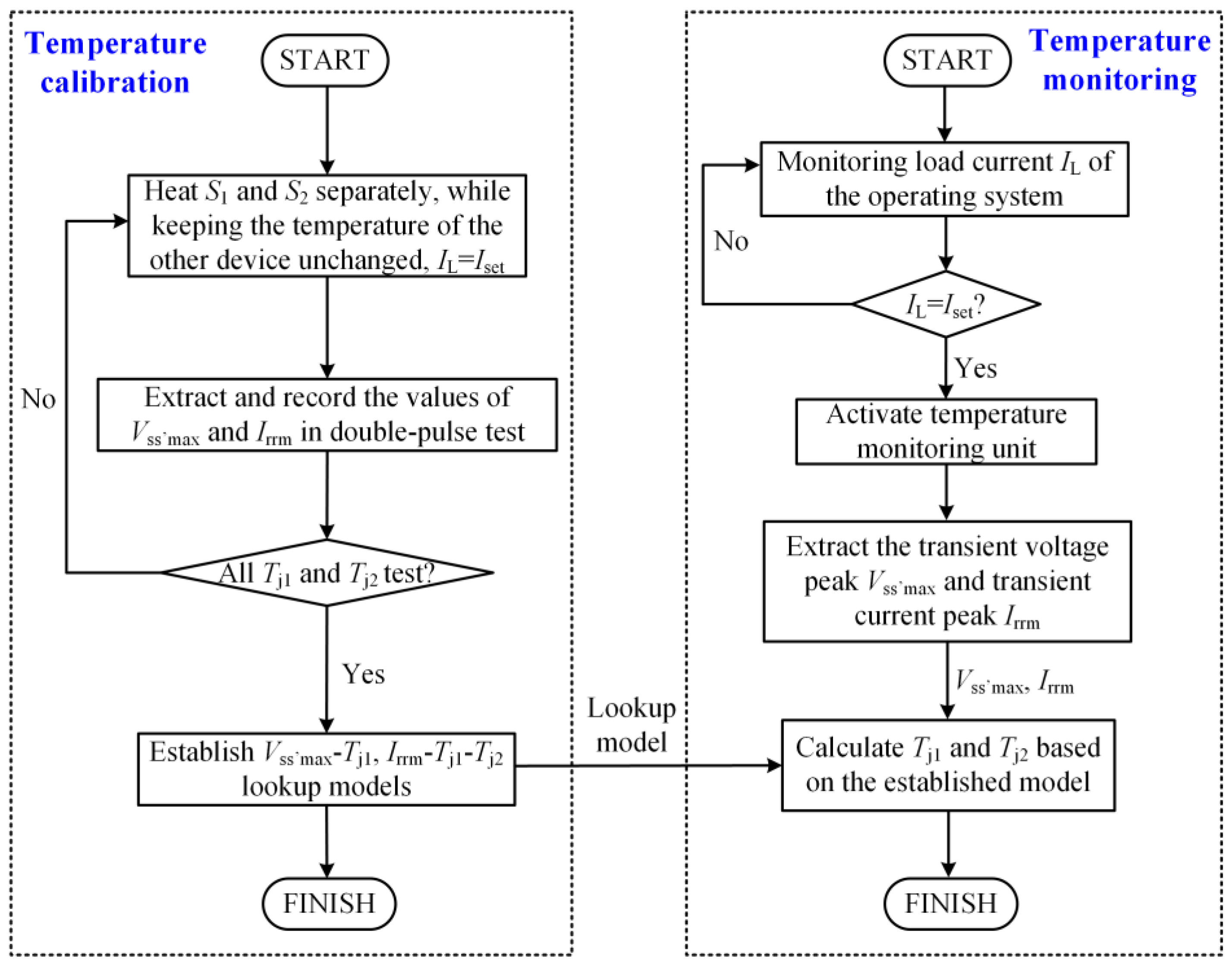
4. Temperature Verification and Online Measurement Discussion

To validate the accuracy of the proposed method, experimental verification is conducted by heating both S₁ and S₂ to another temperature of 130 °C. At this time, the peak reverse recovery current and the peak induced voltage are 23 A and 3.85 V, respectively, as shown in Figure 10. The derived Equation (12) is then utilized to calculate the temperature of the upper and lower switches, which are found to be 130.2 °C and 131.4 °C, with an error of less than 1.5 °C.

When the proposed method is applied to actual systems, offline calibration of the SiC MOSFET device is performed beforehand. According to the experimental results, the variation in bus voltage affects the combined TSEPs. Hence, the proposed method is best suited for applications where the bus voltage remains constant. When extracting the junction temperature in the actual converter, only the current sensor needs to capture the specific load current I_set to trigger the temperature monitoring unit. Subsequently, the measurement circuit can be employed to extract V_ss′max and I_rrm at the lower switch, and the bridge temperature could be obtained based on the established lookup model.

The peak induced voltage V_ss′max can be directly obtained by using a peak detection circuit. Similarly, the peak reverse recovery current I_rrm can be obtained by sampling v_ss′ and applying an integrator to the s and s’ lead [25]. The complete measurement flowchart is illustrated in Figure 11.

It is worth noting that both parameters, V_ss′max and I_rrm, can be obtained with the help of parasitic inductance. The accuracy of the method is solely dependent on the measurement accuracy of voltage V_{ss’ max} and current I_rrm. However, accurate determination of parasitic inductance can just as well avoid the repetitive offline calibration process for different devices in the same circuit, which can be realized by the methods suggested in [26,27]. As a result, the proposed method is non-intrusive and can ensure the normal operation of the system.

Device degradation is a common challenge for the majority of the existing TSEPs utilized for SiC MOSFETs [28]. Specifically, the reliability of gate oxide affects the peak induced voltage V_ss′max, as bias temperature instability (BTI) stress can cause a shift in di/dt [29]. Additionally, device package degradation has an effect on both peak induced voltage V_ss′max and peak reverse recovery current I_rrm. To mitigate estimation errors resulting from device degradation, it is necessary to periodically recalibrate the TSEP of the SiC MOSFET with respect to temperature.

5. Conclusions

This paper proposes a novel bridge-level junction temperature measurement method for SiC MOSFETs by combining the transient voltage and current peaks across the lower switch. It is found that in a half-bridge commutation process, the peak induced voltage has a positive temperature coefficient with the upper switch, and the peak reverse recovery current has a positive temperature coefficient with both upper and lower devices.

A DPT platform is used for switching characteristic analysis. Both peak induced voltage V_ss′max and peak reverse recovery current I_rrm demonstrate a desirable linear relationship with temperature at a steady state. The temperature sensitivity of V_ss′max to the upper switch is about 8 mV/°C, while that of I_rrm to the lower switch is about −53 mA/°C when the bus voltage is 300 V and the load current is 10 A.

The accuracy of the proposed method is verified by testing at another temperature point through the DPT platform, where the bridge temperature can be independently monitored with an error margin of less than 1.5 °C. All the parameters required for this method can be extracted through the parasitic inductance L_sp between the source and auxiliary source of the device with a Kelvin connection, making it non-intrusive and online feasible. Moreover, only a temperature measurement circuit at the lower switch is necessary, which simplifies the design of the circuit isolation stage and reduces the number of measurement circuits.

Future work includes the development of an online temperature monitoring unit for the proposed temperature-sensitive parameters in practical converters and aging compensation strategies.