Prediction of Friction Factor and Heat Transfer Coefficient for Single-Phase Forced Convection Inside Microfin Tubes
Abstract
1. Introduction
2. Experimental Data Bank
3. New Experimental Friction Factor Data Points
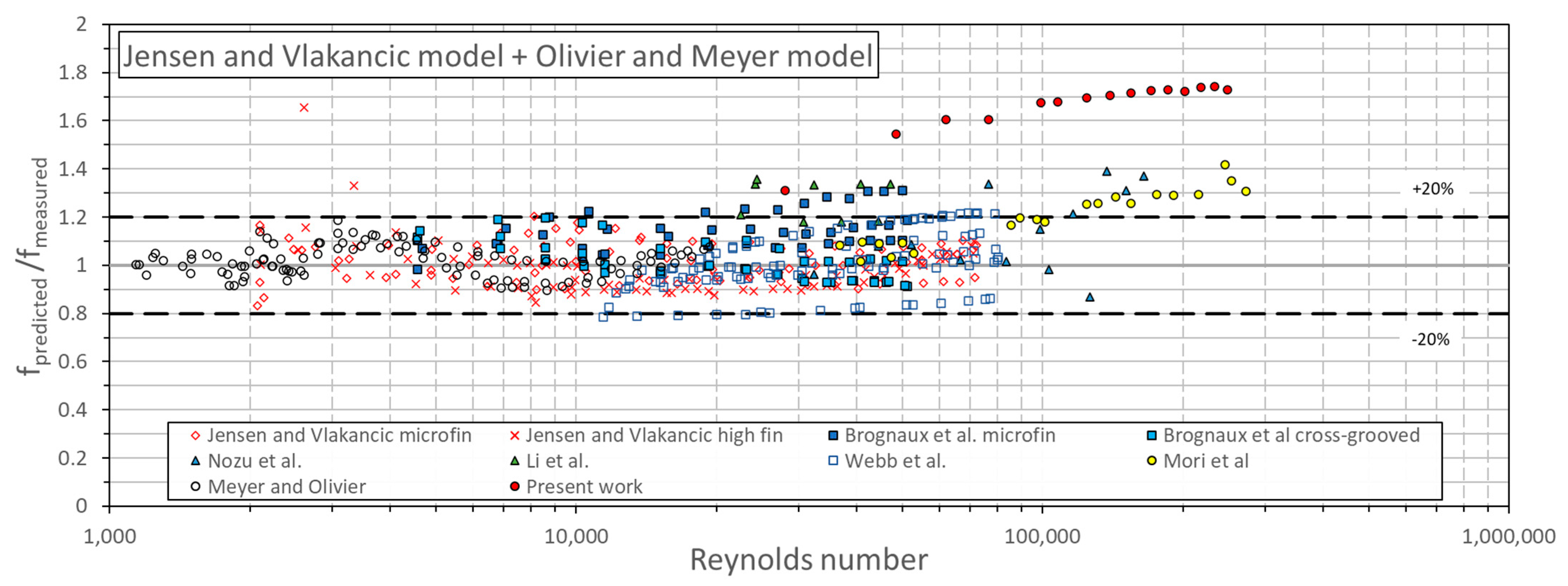
4. Friction Factor Modeling and Comparison of Predictions with Experimental Data
5. Heat Transfer Coefficient Modeling and Comparison of Predictions with Experimental Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| An | Nominal flow area (m2) An = 0.25 π |
| c | Specific heat capacity (J kg−1 K−1) |
| Dev | Deviation |
| di | Inner diameter at the fin root (m) |
| do | Outer tube diameter (m) |
| DP | Friction factor data set |
| e | Fin height (m) |
| f | Fanning friction factor |
| G | Mass velocity (kg m−2 s−1) G = /An |
| H | 2 e/di |
| HT | Heat transfer coefficient data set |
| HTC | Heat transfer coefficient (W m−2 K−1) |
| JK | Jensen and Vlakancic |
| L | Length (m) between pressure taps |
| LHT | Length (m) for heat transfer |
| Mass flow rate (kg s−1) | |
| N | Number of fins (-) |
| Np | Number of data points (-) |
| Nu | Nusselt number Nu = HTC di/λ |
| OD | Outer diameter (m) |
| p | Pressure (bar) |
| pa | Axial rib pitch (=pf/tanβ) (m) |
| pf | Fin pitch (=π di/N) (m) |
| pn | Transverse rib pitch, viewed normal to the ribs (=pf cosβ) (m) |
| Pr | Prandtl number Pr = c μ/λ |
| q | Heat flow rate (W) |
| Re | Reynolds number Re= G di/μ |
| s | Mean fin thickness (m) |
| SA | Inside heat transfer area (m2) |
| t | Temperature (°C) |
| ∆T | Temperature difference (K) |
| y | Physical quantity |
| Greek symbols | |
| β | Helix angle (°) |
| ∆ | Difference |
| γ | Fin apex angle (°) |
| λ | Thermal conductivity (W m−1 K−1) |
| μ | Dynamic viscosity (Pa s) |
| ρ | Density (kg m−3) |
| Subscripts | |
| abs | Absolute |
| act | Actual |
| b | Bulk |
| calc | Calculated |
| cp | Constant property |
| crit | Critical |
| exp | Experimental |
| f | Friction |
| HT | Heat transfer |
| lam | Laminar |
| n | Nominal (based on tube inside diameter at the fin root) |
| rel | Relative |
| st | Smooth tube |
| trans | Transition region |
| w | Wall |
References
- Jensen, M.K.; Vlakancic, A. Experimental investigation of turbulent heat transfer and fluid flow in internally finned tubes. Int. J. Heat Mass Transf. 1999, 42, 1343–1351. [Google Scholar] [CrossRef]
- Carnavos, T.C. Heat transfer performance of internally finned tubes in turbulent flow. Heat Transf. Eng. 1980, 1, 32–37. [Google Scholar] [CrossRef]
- Ravigururajan, T.S.; Bergles, A.E. Development and verification of general correlations for pressure drop and heat transfer in single-phase turbulent flow in enhanced tubes. Exp. Therm. Fluid Sci. 1996, 13, 55–70. [Google Scholar] [CrossRef]
- Webb, R.L.; Narayanamurthy, R.P.; Thors, P. Heat transfer and friction characteristics of internal helical-rib roughness. ASME J. Heat Transf. 2000, 122, 134–142. [Google Scholar] [CrossRef]
- Zdaniuk, G.J.; Chamra, L.M.; Mago, P.J. Experimental determination of heat transfer and friction in helically-finned tubes. Exp. Therm. Fluid Sci. 2008, 32, 761–775. [Google Scholar] [CrossRef]
- Meyer, J.P.; Olivier, J.A. Transitional flow inside enhanced tubes for fully developed and developing flow with different types of inlet disturbances: Part I—Adiabatic pressure drops. Int. J. Heat Mass Transf. 2011, 54, 1587–1597. [Google Scholar] [CrossRef]
- Meyer, J.P.; Olivier, J.A. Transitional flow inside enhanced tubes for fully developed and developing flow with different types of inlet disturbances: Part II-heat transfer. Int. J. Heat Mass Transf. 2011, 54, 1598–1607. [Google Scholar] [CrossRef]
- Tam, H.K.; Tam, L.M.; Ghajar, A.J.; Sun, C.; Leung, H.Y. Experimental investigation of the single-phase friction factor and heat transfer inside the horizontal internally micro-fin tubes in the transition region. In Proceedings of the ASME-JSME-KSME Joint Fluids Engineering Conference, Hamamatsu, Japan, 24–29 July 2011. [Google Scholar]
- Brognaux, L.J.; Webb, R.L.; Chamra, L.M.; Chung, B.Y. Single-phase heat transfer in micro-fin tubes. Int. J. Heat Mass Transf. 1997, 40, 4345–4357. [Google Scholar] [CrossRef]
- Li, X.W.; Meng, J.A.; Li, Z.X. Experimental study of single-phase pressure drop and heat transfer in a micro-fin tube. Exp. Therm. Fluid Sci. 2007, 32, 641–648. [Google Scholar] [CrossRef]
- Raj, R.; Lakshman, N.S.; Mukkamala, Y. Single phase flow heat transfer and pressure drop measurements in doubly enhanced tubes. Int. J. Therm. Sci. 2015, 88, 215–227. [Google Scholar] [CrossRef]
- Siddique, M.; Alhazmy, M. Experimental study of turbulent single-phase flow and heat transfer inside a micro-finned tube. Int. J. Refrig. 2008, 31, 234–241. [Google Scholar] [CrossRef]
- Wang, Y.H.; Zhang, J.L.; Ma, Z.X. Experimental determination of single-phase pressure drop and heat transfer in a horizontal internal helically-finned tube. Int. J. Heat Mass Transf. 2017, 104, 240–246. [Google Scholar] [CrossRef]
- Wang, C.C.; Chiou, C.B.; Lu, D.C. Single-phase heat transfer and flow friction correlations for microfin tubes. Int. J. Heat Fluid Flow 1996, 17, 500–506. [Google Scholar] [CrossRef]
- Biancon Copetti, J.; Macagnan, M.H.; De Souza, D.; De Césaro Oliveski, R. Experiments with micro-fin tube in single phase. Int. J. Refrig. 2004, 27, 876–883. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Ma, Z. Experimental study of single-phase flow and heat transfer characteristics for a horizontal internal helically-finned tube. Procedia Eng. 2017, 205, 1370–1375. [Google Scholar] [CrossRef]
- Li, G.Q.; Wu, Z.; Li, W.; Wang, Z.K.; Wang, X.; Li, H.X.; Ya, S.C. Experimental investigation of condensation in micro-fin tubes of different geometries. Exp. Therm. Fluid Sci. 2012, 37, 19–28. [Google Scholar] [CrossRef]
- Eckels, S.J.; Holthaus, G.; Hildenbrand, K. Single-Phase Refrigerant Heat Transfer and Pressure Drop Characterization of High Reynolds Number Flow for Internally Finned Tubes Including the Effects of Miscible Oils; ASHRAE RP-1067; ASHRAE: Peachtree Corners, GA, USA, 2003; 310p. [Google Scholar]
- Diani, A.; Campanale, M.; Cavallini, A.; Rossetto, L. Low GWP refrigerants condensation inside a 2.4 mm ID microfin tube. Int. J. Refrig. 2018, 86, 312–321. [Google Scholar] [CrossRef]
- Diani, A.; Cavallini, A.; Rossetto, L. R1234yf condensation inside a 3.4 mm ID horizontal microfin tube. Int. J. Refrig. 2017, 75, 178–189. [Google Scholar] [CrossRef]
- Diani, A.; Liu, Y.; Wen, J.; Rossetto, L. Experimental investigation on the flow condensation of R450A, R515B, and R1234ze(E) in a 7.0 mm OD micro-fin tube. Int. J. Heat Mas. Transf. 2022, 196, 123260. [Google Scholar] [CrossRef]
- Mori, H.; Yoshida, S.; Ohishi, K.; Kakimoto, Y. Dryout quality and post-dryout heat transfer coefficient for a refrigerant flowing in horizontal evaporator tubes. In Proceedings of the 20th International Congress of Refrigeration, IIR/IIF, Sydney, Australia, 19–24 September 1999; Volume II, p. 311. [Google Scholar]
- Nozu, S.; Katayama, H.; Nakata, H.; Honda, H. Condensation of a refrigerant CFC11 in horizontal microfin tubes (Proposal of a correlation equation for frictional pressure gradient). Exp. Therm. Fluid Sci. 1998, 18, 82–96. [Google Scholar] [CrossRef]
- Lee, H.S.; Kim, H.J.; Yoon, J.I.; Choi, K.H.; Son, C.H. The cooling heat transfer characteristics of the supercritical CO2 in micro-fin tube. Heat Mass Transf. 2013, 49, 173–184. [Google Scholar] [CrossRef]
- Kuwahara, K.; Higashiiue, S.; Ito, D.; Koyama, S. Experimental study on cooling heat transfer of supercritical carbon dioxide inside horizontal micro-fin tubes. Trans. JSRAE 2007, 24, 173–181. [Google Scholar]
- Wu, Z.; Sundén, B.; Wadekar, V.V.; Li, W. Heat Transfer Correlations for Single-Phase Flow, Condensation, and Boiling in Microfin Tubes. Heat Transf. Eng. 2015, 36, 582–595. [Google Scholar] [CrossRef]
- Wang, H.S.; Rose, J.W. Prediction of effective friction factors for single-phase flow in horizontal microfin tubes. Int. J. Refrig. 2004, 27, 904–913. [Google Scholar] [CrossRef]
- Vlakancic, A. Experimental Investigation of Internally Finned Tube Geometries on Turbulent Heat Transfer and Fluid Flow. Master’s Thesis, Rensselaer Polytechnic Institute, Troy, NY, USA, 1996. [Google Scholar]
- Kline, S.J.; McClintock, F.A. Describing the uncertainties in single-sample experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Shome, B.; Jensen, M.K. Experimental investigation of laminar flow and heat transfer in internally finned tubes. Enhanc. Heat Transf. 1996, 4, 53–70. [Google Scholar] [CrossRef]
- Cavallini, A.; Del Col, D.; Doretti, L.; Longo, G.A.; Rossetto, L. Pressure drop during condensation and vaporisation of refrigerants inside enhanced tubes. Heat Technol. 1997, 15, 3–10. [Google Scholar]
- Filonenko, G.K. Hydraulic resistance in pipes. Teploergetica 1954, 1, 40–44. [Google Scholar]
- Gnielinski, V. On heat transfer in tubes. Int. J. Heat Mass Transf. 2013, 63, 134–140. [Google Scholar] [CrossRef]
- Petukhov, B.S. Heat transfer and friction factor in turbulent pipe flow with variable properties. In Advances in Heat Transfer; Hartnett, J., Irvine, T., Eds.; Academic: New York, NY, USA, 1970; Volume 6, pp. 504–564. [Google Scholar]
- Petukhov, B.S.; Popov, V.N. Theoretical calculation of heat exchange and frictional resistance in turbulent flow in tubes of an incompressible fluid with variable physical properties. High Temp. Heat Phys. 1963, 1, 69–83. [Google Scholar]
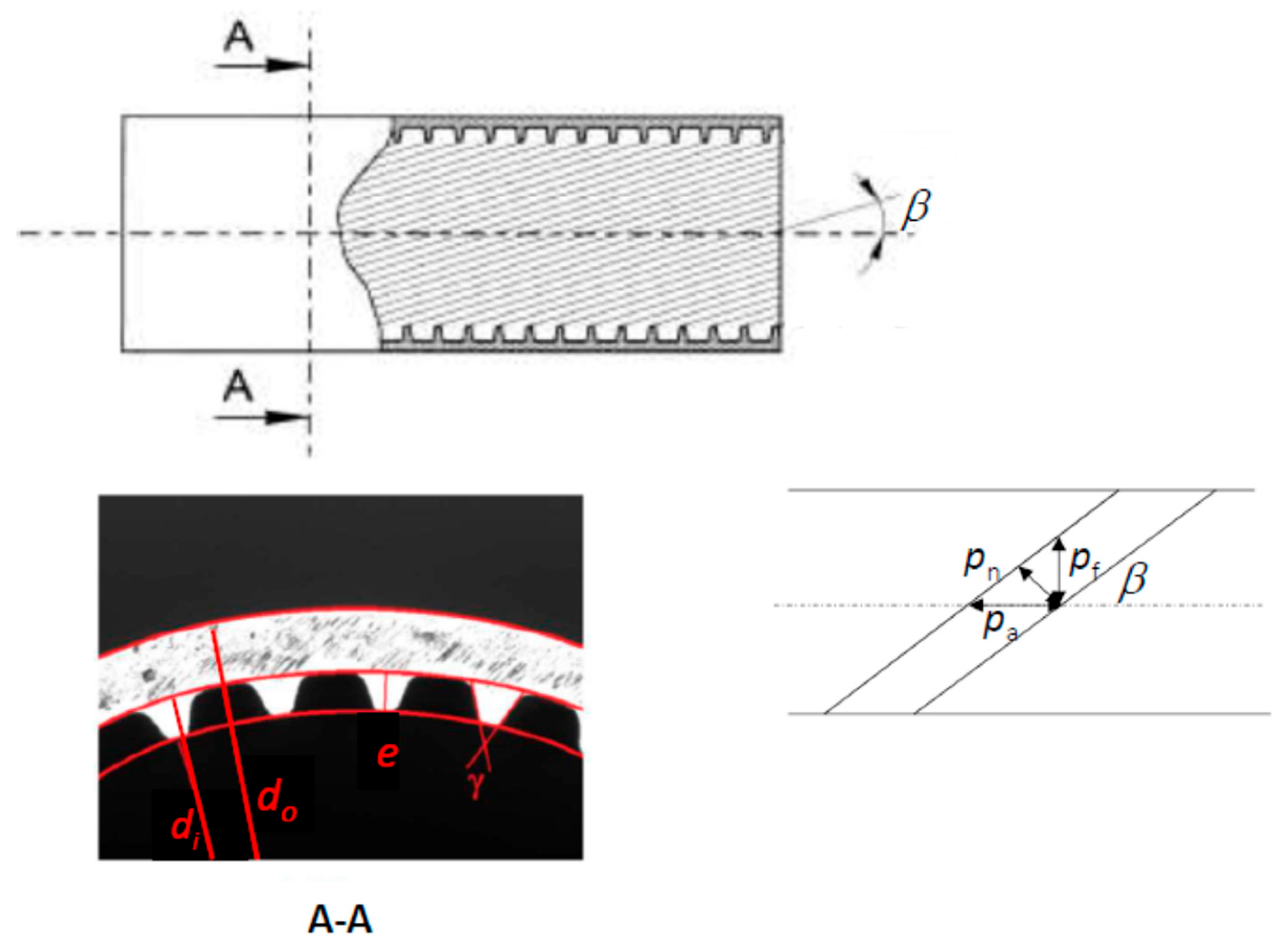




| Reference | Fluid | N (-) | β (°) | e (mm) | di (mm) | s (mm) | γ (°) | H (-) | DP, HT |
|---|---|---|---|---|---|---|---|---|---|
| Jensen and Vlakancic [1], Vlakancic [28] | Water/ ethyl. glycol | 54 | 45 | 0.44 | 22.08 | 0.54 | 40 * | 0.0399 | DP, HT |
| 54 | 45 | 0.33 | 24.13 | 0.9 | 40 * | 0.0274 | DP, HT | ||
| 54 | 45 | 0.22 | 22.1 | 0.58 | 40 * | 0.0199 | DP, HT | ||
| 30 | 30 | 0.36 | 24.18 | 0.64 | 40 * | 0.0298 | HT | ||
| 54 | 30 | 0.18 | 24.03 | 0.4 | 40 * | 0.015 | HT | ||
| 54 | 30 | 0.36 | 24.41 | 0.7 | 40 * | 0.0295 | HT | ||
| 54 | 15 | 0.36 | 24.05 | 0.62 | 40 * | 0.03 | HT | ||
| 36 | 25 | 0.68 | 23.00 | 1.14 | 40 * | 0.0591 | HT | ||
| 8 | 30 | 1.16 | 23.64 | 1.0 | 40 * | 0.0981 | DP, HT | ||
| 14 | 30 | 1.2 | 23.78 | 1.02 | 40 * | 0.1 | DP, HT | ||
| 30 | 30 | 1.3 | 23.70 | 0.82 | 40 * | 0.11 | DP, HT | ||
| 14 | 30 | 2.06 | 24.28 | 0.64 | 40 * | 0.17 | HT | ||
| 14 | 15 | 1.18 | 23.72 | 0.92 | 40 * | 0.0995 | HT | ||
| 14 | 0 | 1.18 | 23.64 | 0.70 | 40 * | 0.0998 | HT | ||
| 22 | 25 | 0.62 | 21.86 | 1.84 | 40 * | 0.0567 | HT | ||
| Brognaux et al. [9] | Water | 78 | 27 | 0.35 | 14.86 | 0.2 | 30 | 0.0471 | DP, HT |
| 78 | 17.5 | 0.35 | 14.86 | 0.2 | 30 | 0.0471 | DP, HT | ||
| 78 | 20 | 0.35 | 14.86 | 0.2 | 30 | 0.0471 | DP, HT | ||
| Nozu et al. [23] | R11 | 47 | 20 | 0.24 | 8.44 | 0.2 | 63 | 0.0569 | DP |
| 65 | 24 | 0.16 | 8.82 | 0.19 | 87.1 | 0.0363 | DP | ||
| Li et al. [17] | R22 | 35 | 18 | 0.12 | 4.54 | 0.036 *** | 25 | 0.0529 | DP, HT |
| 40 | 18 | 0.15 | 4.6 | 0.073 *** | 40 | 0.0652 | DP, HT | ||
| Webb et al. [4] | Water | 45 | 45 | 0.327 | 15.54 | 0.1345 | 41 | 0.0421 | DP, HT |
| 30 | 45 | 0.398 | 15.54 | 0.136 | 41 | 0.0512 | DP, HT | ||
| 10 | 45 | 0.43 | 15.54 | 0.1405 | 41 | 0.0553 | DP, HT | ||
| 40 | 35 | 0.466 | 15.54 | 0.1355 | 41 | 0.0600 | DP, HT | ||
| 25 | 35 | 0.493 | 15.54 | 0.136 | 41 | 0.0635 | DP, HT | ||
| 25 | 25 | 0.532 | 15.54 | 0.136 | 41 | 0.0685 | DP, HT | ||
| 18 | 25 | 0.554 | 15.54 | 0.136 | 41 | 0.0713 | DP, HT | ||
| Mori et al. [22] | R134a | 50 | 18 | 0.21 | 6.5 | 0.09 *** | 35 ** | 0.0646 | DP |
| Meyer and Olivier [6,7] | Water | 25 | 18 | 0.399 | 14.648 | 0.231 *** | 46.97 | 0.0545 | DP, HT |
| 35 | 27 | 0.395 | 14.56 | 0.212 *** | 43.93 | 0.0543 | DP, HT | ||
| 25 | 18 | 0.48 | 17.66 | 0.223 *** | 38.49 | 0.0544 | DP, HT | ||
| 35 | 27 | 0.467 | 17.82 | 0.239 *** | 41.92 | 0.0524 | DP, HT | ||
| Eckels et al. [18] | R134a, R410A, R407C | 60 | 18 | 0.2 | 9.12 | 0.095 | 51 | 0.0440 | HT |
| 50 | 18 | 0.2 | 7.54 | 0.11 | 57 | 0.0531 | HT | ||
| 72 | 0 | 0.2 | 8.88 | 0.093 | 50 **** | 0.0451 | HT | ||
| 60 | 0 | 0.19 | 7.21 | 0.089 | 50 **** | 0.0527 | HT | ||
| Diani et al. [19,20,21] | R1234ze(E) | 50 | 18 | 0.18 | 6.5 | 0.092 *** | 42 | 0.0554 | HT |
| R1234yf | 40 | 18 | 0.12 | 3.64 | 0.063 *** | 43 | 0.066 | HT | |
| R1234yf | 40 | 7 | 0.12 | 2.64 | 0.063 *** | 43 | 0.091 | HT | |
| Present work | R1234ze(E) | 54 | 30 | 0.15 | 4.58 | 0.021 | 0.0655 | DP |
| Reference | Fluid | N (-) | β (°) | e (mm) | di (mm) | s (mm) | γ (°) | e (mm) Second Groove |
|---|---|---|---|---|---|---|---|---|
| Brognaux et al. [9] | Water | 78 | 17.5 | 0.35 | 14.86 | 0.2 | 30 | 0.14 |
| 0.21 | ||||||||
| 0.28 |
| Reference | Friction Factor Uncertainty | HTC Uncertainty |
|---|---|---|
| Vlakancic [28] | ±3.3% | ±19.5% |
| Brognaux et al. [9] | ±4.9% | ±9.65% |
| Nozu et al. [23] | ±17% for (−Δp/L)f | - |
| Li et al. [15] | - | ±9.6% |
| Webb et al. [4] | ±5% * | ±8% ** |
| Mori et al. [22] | ±7% * | - |
| Meyer and Olivier [6] | 0.58–55.7% | 1.04–1.22% |
| Eckels et al. [18] | 2–12% (Re > 100,000) | 4.86–18.6% (Re > 100,000) |
| Diani et al. [19,20,21] | - | 1.9–7.2% |
| Present work | ±5.0% | - |
| Model | Relative Deviation (%) | Absolute Deviation (%) | Np |
|---|---|---|---|
| Equations (1)–(15) model | 5.24 | 10.5 | 536 |
| Equation (18) model | −0.317 | 7.9 | 536 |
| Model | Relative Deviation (%) Equation (16) | Absolute Deviation (%) Equation (17) | Np |
|---|---|---|---|
| Present model Equations (20)–(23) | 3.3 | 13.9 | 648 |
| Jensen and Vlakancic [1] Equations (24)–(26) | −18.9 | 21.4 | 648 |
| Carnavos [2] Equation (2) | 23.0 | 31.4 | 648 |
| Ravigururajan and Bergles [3] Equations (28) and (29) | 22.1 | 24.9 | 590 |
| Webb et al. [4] Equation (30) | 9.84 | 17.3 | 590 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossetto, L.; Diani, A. Prediction of Friction Factor and Heat Transfer Coefficient for Single-Phase Forced Convection Inside Microfin Tubes. Energies 2023, 16, 4053. https://doi.org/10.3390/en16104053
Rossetto L, Diani A. Prediction of Friction Factor and Heat Transfer Coefficient for Single-Phase Forced Convection Inside Microfin Tubes. Energies. 2023; 16(10):4053. https://doi.org/10.3390/en16104053
Chicago/Turabian StyleRossetto, Luisa, and Andrea Diani. 2023. "Prediction of Friction Factor and Heat Transfer Coefficient for Single-Phase Forced Convection Inside Microfin Tubes" Energies 16, no. 10: 4053. https://doi.org/10.3390/en16104053
APA StyleRossetto, L., & Diani, A. (2023). Prediction of Friction Factor and Heat Transfer Coefficient for Single-Phase Forced Convection Inside Microfin Tubes. Energies, 16(10), 4053. https://doi.org/10.3390/en16104053








