Abstract
Among developing countries in Asia, Indonesia has realized the importance of transitioning from fossil fuels to renewable energy sources such as solar power. Careful consideration must be given to the strategic placement of solar power installations to fully leverage the benefits of solar energy. This study proposes a methodology to optimize the site selection of solar power plants in Indonesia by integrating Data Envelopment Analysis (DEA), Fuzzy Analytic Hierarchy Process (F-AHP), and Fuzzy Measurement of Alternatives and Ranking according to Compromise Solution (F-MARCOS) models. The proposed methodology considers quantitative and qualitative criteria to evaluate potential locations for solar power plants. In the first stage, DEA is used to identify the most efficient locations based on quantitative measures such as solar radiation, land availability, and grid connectivity. In the second stage, qualitative factors such as technological, economic, environmental, and socio-political aspects are evaluated using F-AHP to prioritize the most important criteria for site selection. Finally, F-MARCOS ranks potential locations based on the selected criteria. The methodology was tested using data from Indonesia as a case study. The results show that the proposed hybrid model optimizes Indonesia’s solar power plant site selection. The optimal locations can contribute to a cost-effective long-term renewable energy supply nationwide. The findings from this study are relevant to policymakers, industry stakeholders, and researchers interested in renewable energy development and site selection. However, to promote sustainable solar energy development, governments and local authorities must also enact supportive policies and mechanisms that encourage the adoption and growth of renewable energy technologies in Indonesia.
1. Introduction
The availability of energy significantly impacts global economic and industrial progress. More than 80% of the world’s energy is produced through coal, oil, and natural gas [1]. With 270 million people, Indonesia has the fastest-growing power demand in Asia-Pacific, highlighting the urgent need for a secure, affordable, and long-term energy transition in Southeast Asia [2]. Power demand has been growing at a rate of 6.1% per year, and infrastructure is under pressure to capitalize on the growth potential of the growing economy [3]. Solar photovoltaic projects of utility, commercial, and industrial scale have a tremendous chance to rapidly establish economies of scale to meet the 23% renewable energy goal by 2025 [4]. By 2030, projections anticipate a potential installed capacity of 47 GW, a significant increase compared to just over 9 GW estimated in the Reference Case. In light of this, plans are underway to utilize solar photovoltaic (PV) technology to power approximately 1.1 million off-grid households. Rooftop and utility-scale solar PV systems can be expanded significantly in Indonesia, particularly in Java-Bali (which accounts for 70% of power demand in Indonesia) due to the ample area, robust infrastructure, and growing need for electricity in the region [5]. In addition, these types of resources are numerous and excellent for local development and utilization. Unlike the possible depletion of fossil fuels, renewable energy can be naturally replenished. Multiple countries have enacted legislation for renewable energy development, and various applications for renewable energy have evolved. It is projected that renewable energy sources will play a significant part in the global energy supply in the future [6,7]. Solar energy development in Indonesia is promising, but progress is slow despite the country’s significant potential. Various factors contribute to this slow growth, such as limited financial and human resources, institutional challenges, market-controlled processes, unclear policies, and inconsistent norms, despite the availability of modern technology. The public and government agencies know the country’s situation and resources. The three primary challenges for utility-scale solar PV are inadequate transmission grid capacity, complex administrative procedures, and insufficient engagement with local communities. According to the available research, solar site selection in Indonesia has yet to be thoroughly investigated regarding sustainable development [8,9].
A reliable, systematic, and effective decision-making framework is required to aid policymakers in selecting optimal locations for solar power facilities [10]. Sites that could be better can save time and money, cause trouble for local citizens and harm the environment. This study was undertaken to determine the best places in Indonesia to build solar PV systems for long-term sustainability. In-depth literature reviews and interviews with industry professionals help identify potential sites for solar installations and other parameters that will affect the deployment of these systems [11,12]. Due to the numerous factors that must be considered, experts have turned to multi-criteria decision-making (MCDM) approaches [13]. These methods use the strengths of techniques such as the Data Envelopment Analysis (DEA), Fuzzy Analytic Hierarchy Process (F-AHP), and Fuzzy Measurement Alternatives and Ranking according to the Compromise Solution (F-MARCOS) to determine the most suitable locations for solar energy generation prioritization. Among the many firsts of this study is its in-depth examination of a topic that has yet to be previously discussed in the literature: solar site selection in Indonesia. The evaluation criteria are broad and thorough, covering quantifiable and qualitative aspects of identifying priority areas for sustainable development. In addition, this is the first time that DEA, F-AHP, and F-MARCOS have been combined to form a single appropriate and successful methodology for site selection. The developed model aims to provide decision-makers with a comprehensive aid tool for selecting the best site for solar power plants.
The structure of this paper is organized as follows: Section 2 presents a review of relevant research on solar power plant site selection techniques. Section 3 discusses the Data Envelopment Analysis (DEA), Fuzzy Analytic Hierarchy Process (F-AHP), and Fuzzy Multi-Attribute Rating Comparison System (F-MARCOS) methodologies. Section 4 discusses the Indonesian case study, which demonstrates the practical application of the proposed hybrid approach. Finally, Section 5 provides conclusions and highlights potential directions for future research in this area.
2. Literature Review
The growth of solar energy production in many countries has drawn the attention of universities, governments, and organizations worldwide [14]. However, one of the significant challenges in deploying large-scale solar systems is determining the priorities of different regions on a national level. Establishing new solar farms requires substantial real estate, capital, and labor. Thus, identifying technological, technical, economic, environmental, societal, risk-aspect, and political factors is crucial to avoid delays in central and government approval procedures and establishing new solar farms [15]. Prioritizing appropriate areas before investing in costly solar farms can result in optimal production, lower socioeconomic costs, reduced negative environmental impacts, and progress in concerned regions. In order to make informed decisions, criteria are derived from a review of relevant literature and consensus among experts on environmental, technological, financial, and societal factors, as outlined in Table 1.

Table 1.
Considered primary criteria and parameters that determine the suitability for solar PV implementation.
The planning of renewable energy sources (RES) often involves the use of multi-criteria decision-making (MCDM) techniques, which assist decision-makers in selecting the best option from competing alternatives in site selection challenges [30]. Although numerous MCDM techniques are available, few have been applied when combining DEA with MCDM [9]. The fuzzy set theory incorporates uncertainty and ambiguity into the evaluation process. Uyan [31] used GIS and the AHP technique to identify promising areas for solar farms in the Karapinar region of Konya, Turkey. Sindhu et al. [16] investigated solar site selection in India using a combination of AHP and fuzzy TOPSIS analysis. Lee et al. [32] also used AHP and fuzzy TOPSIS analysis for solar site selection in India. Al Garni & Awasthi [33] used a GIS-AHP-based approach to select solar PV power plant sites in Saudi Arabia; their study contributes to SDG 7 (Affordable and Clean Energy) and SDG 13 (Climate Action). Seyed Alavi et al. [34] employed multi-criteria decision-making methods to identify optimal locations for wind power plants in eastern Iran. Wu et al. [35] also improved site selection for solar power installations in China by employing an MCDM framework based on fuzzy Preference Ranking Organization Methods for Enrichment Evaluations (PROMETHEE) II. Table 2 summarizes how MCDM methods have been applied to solar site selection research. These studies demonstrate the importance of integrating MCDM techniques with DEA for RES planning and provide valuable insights into selecting optimal solar sites.

Table 2.
The literature review on MCDM techniques.
After conducting a comprehensive review of the literature across multiple fields and methodologies, it has become clear that there is a lack of studies focused on selecting optimal solar locations in Indonesia. This research fills this gap by combining DEA, F-AHP, and F-MARCOS methodologies to identify the most suitable locations for solar PV installations. DEA is a powerful tool for comparing energy industry options based on measurable criteria, as it enables comparisons of locations in terms of their efficiency in converting inputs to outputs. F-AHP and F-MARCOS are flexible techniques incorporating human evaluations of immeasurable variables. Stankovi’c et al. [47] created the fuzzy MARCOS in 2019 to provide a strong sorting of alternatives in the fuzzy environment irrespective of the scale, which generates a basic, comprehensive decision-making information scheme using the ratio method and the reference point method. The fuzzy MARCOS approach is an effective tool for maximizing a number of objectives. By proposing an algorithm for examining the link between alternatives and reference points, fuzzy MARCOS revitalizes the MCDM domain. In order to make a strong decision, the fuzzy MARCOS method integrates the following elements: defining reference points (fuzzy ideal and fuzzy anti-ideal values), figuring out how alternatives relate to these values, and defining the utility level of alternatives concerning fuzzy ideal and fuzzy anti-ideal solutions. Because the results of the ratio approach and reference point sorting approach were combined, the results obtained by the fuzzy MARCOS method are more logical. In the research of Stević et al. [48] on sustainable supplier selection, it was proven that the robustness and stability of MARCOS outperformed TOPSIS in assessing the decision-making units. By combining DEA, F-AHP, and F-MARCOS, this study aims to provide a comprehensive approach to identifying optimal solar locations in Indonesia.
3. Methods
This section outlines the photovoltaic (PV) power plant site selection methodology, as illustrated in Figure 1. The proposed approach combines Data Envelopment Analysis (DEA), Analytic Hierarchy Process (AHP), and Fuzzy Measurement Alternatives and Ranking according to the Compromise Solution (MARCOS) to develop a comprehensive decision-making framework for selecting optimal sites for PV power plants in Indonesia.
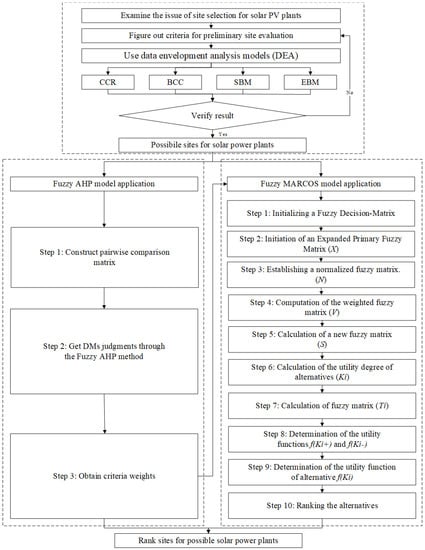
Figure 1.
The process of the research.
3.1. Data Envelopment Analysis (DEA)
Data Envelopment Analysis (DEA) is a commonly used mathematical approach to measure the efficiency of Decision Making Units (DMUs) based on multiple inputs and outputs. This study uses DEA to screen and select the most efficient locations to host solar installations. The CCR, BCC, SBM, and EBM models are examples of DEA models that can assess DMU efficiency. These models differ in terms of the assumptions they make about inputs and outputs, as well as the type of efficiency measured [49].
3.1.1. Charnes, Cooper, Rhodes Model (CCR)
The CCR model is a DEA model commonly used to evaluate the efficiency of Decision-Making Units (DMUs) based on multiple inputs and outputs. This model measures the technical effectiveness of a DMU, assuming that each DMU can be represented by a set of inputs and outputs specified in the model (1).
The CCR model measures the technical efficiency of a DMU by comparing its input-output ratio with those of other DMUs in the dataset. A DMU is considered efficient if its efficiency score equals 1, indicating that the DMU is operating on the efficient frontier. Conversely, a DMU is considered inefficient if its efficiency score is less than 1, implying that the DMU is operating below the efficient frontier and could potentially improve its efficiency by adjusting its input-output ratio.
3.1.2. Banker, Charnes, and Cooper Model (BCC)
The Banker, Charnes, and Cooper (BCC) model, developed by Banker et al. [50], extends the DEA model to account for variable returns to scale (VRS). This model introduces a non-Archimedean element (ε), and and represent the input and output slack variables, respectively.
The BCC model evaluates DMUs based on their technical efficiency at various operational scales. This allows for the differentiation between technical inefficiency and scale inefficiency. The model recognizes growth, decline, constant return scales, and other scale types. The BCC model’s efficiency metric is sometimes called “pure technical efficiency” to highlight its focus on technical performance independent of scale effects.
3.1.3. Slacks-Based Measure Model (SBM)
The effectiveness of a DMU is determined by a ratio known as the “slacks-based measure” (SBM) score. This value is determined by dividing the DMU’s actual output by the minimal number of inputs required to achieve that output, depending on the inputs and outputs of the other DMUs included in the analysis. A DMU with an SBM score of 1 is technically efficient, while a DMU with an SBM score of less than 1 is inefficient.
In this model, represents the SBM score, and is the weight assigned to each DMU. The input and output variables are represented by and , respectively. The input slack variables, , represent the excess inputs that can be reduced without affecting the output. The objective of the SBM model is to minimize the sum of the input slacks relative to the input levels, thus maximizing the efficiency of the DMU. This model provides a more accurate efficiency measure, directly incorporating input and output slack variables into the efficiency evaluation.
3.1.4. Epsilon-Based Measure Model (EBM)
The Epsilon-Based Measure (EBM) [51] model is a variant of Data Envelopment Analysis (DEA) that accounts for the diversity or dispersion of the observed data set by calculating a scalar epsilon. This model aims to address the limitations of the CCR and SBM models by combining the radial and non-radial approaches, which emphasize proportional changes in inputs and outputs and incorporate slack, respectively. The input-oriented EBM model with a constant return to scale is formulated as follows:
In this model, represents the EBM score, is the weight assigned to each DMU, and the subscript “o” represents the DMU under evaluation. The input slack variables, , indicate the excess inputs that can be reduced without affecting the output, and denotes the weight assigned to the i-th input. The parameter specifies the radial qualities and is determined by the degree of input dispersion.
3.2. F-AHP
Table 3 shows that the fuzzy triangular numbers are the linguistic terms for the pairwise comparison scale and the fuzzy scale assigned. The relative importance of the two criteria is ranked on a scale from 1 to 9 based on the linguistic variables provided. A tilde sign () is placed above the parameter symbol to indicate uncertainty. Thus, the following are the details of the F-AHP process [16].

Table 3.
Explanation of the F-AHP scale.
Step 1: To produce the integrated fuzzy pairwise comparison matrix used in the FAHP calculation, we apply the geometrical integration seen in Equation (5). denotes the importance of the criterion over the criterion.
Step 2: Equation to determine the fuzzy geometric mean of each criterion (6).
where approximated by the fuzzy geometric mean, and is a fuzzy comparison value generated by a panel of decision–makers based on the criterion over the criterion.
Step 3: The fuzzy preference weight for each criterion is determined using the following Equation (7).
where is the fuzzy weight of the criterion.
Step 4: To obtain a clear result, we need to defuzzify the preference weights using the average weight criterion , as shown in Equation (8).
where is the fuzzy weight of the criterion, which can be presented as , such that are the lower-bound, middle-bound, and upper-bound of , respectively.
Step 5: The relative importance of each criterion, as determined by the normalized preference weight , as seen by Equation (9).
3.3. F-MARCOS
For multi-criteria decision-making (MCDM) situations with a set of criteria and potential solutions, fuzzy measurement of alternatives and ranking based on compromise solutions (F-MARCOS) can help reduce the uncertainty. Decision-makers can improve the stability of MCDM in fuzzy situations by using this strategy, which has three pillars: reference points, relationships between choices, and alternative utility levels [47]. The process of F-MARCOS is as below.
Step 1: Defining an initial fuzzy decision-making matrix including n criteria (i.e., criteria) and m alternatives.
Step 2: Defining an extended initial fuzzy decision-making matrix by introducing the fuzzy ideal and anti-ideal solutions
The fuzzy is an alternative with the best performance, while the fuzzy is the worst alternative. Depending on the type of the criteria, and are defined by applying Equations (11) and (12):
where B and C are a set of benefit and cost criteria, respectively.
Step 3: Determining the normalization of the extended initial fuzzy decision-making matrix, which is using Equations (13) and (14):
where elements , , , and , , represent the elements of the matrix .
Step 4: Determining the weighted fuzzy matrix , calculated by multiplying matrix with the fuzzy weight coefficients of the criteria as follows.
where represents the elements of the fuzzy weight of the criteria.
Step 5: Calculating the fuzzy matrix using Equation (16) below.
where is the sum of the elements of the weighted fuzzy matrix .
Step 6: Calculating the utility degree of alternative using Equations (17) and (18):
Step 7: To determine the fuzzy matrix , we use Equation (19):
Then, a new fuzzy number is determined by Equation (20):
Following that, it is necessary to defuzzify the number using the expression obtaining the number .
Step 8: Determining the utility function to the ideal and anti-ideal solutions using Equations (21) and (22):
Finally, calculating the defuzzification of , , , and values using the same defuzzification formula.
Step 9: Alternative utility functions can be calculated with Equation (23):
Step 10: The order of the alternatives is determined by the final values of the utility degree function. Favored is the alternative with the superior utility function value.
As shown in Table 4, a new linguistic scale has been established for assessing alternatives in addition to the F-MARCOS method. There are nine words in total, and each assigned its fuzzy triangular number.

Table 4.
The linguistic equivalent of a rating system for alternatives.
4. A Case Study in Indonesia
In this subsection, we put into action the aggregated technique proposed for determining which of Indonesia’s 32 provinces would best host solar power installations (Figure 2). The evaluation’s criterion system and examined alternatives were created by consultation with experts and subsequent interactive conversations, in addition to reviewing the relevant literature.
Figure 2.
The map of solar radiation in Indonesia.
4.1. Using DEA Models to Screen Prospective Locations
As seen in Table 5, the initial stage of the DEA model-based research considered 32 provincial locations as decision-making units (DMUs). As illustrated in Figure 3, five inputs (air temperature, wind speed, relative humidity, rainfall, and air pressure) and three outputs (hours of sunshine, solar irradiance, and altitude) were analyzed to identify DMUs with ideal efficiency ratings (equal to 1).

Table 5.
List of Indonesian locations (DMUs).
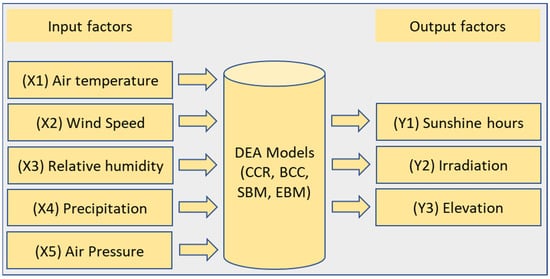
Figure 3.
The input and output factors used in DEA models.
Input factors:
- (X1)
- Air temperature (°C): Solar panel performance is affected by the panels’ temperatures, which are affected by the surrounding temperature and the amount of sunlight they are exposed to. Simply put, solar panels produce more electricity when the temperature is lower. When the panel’s operating temperature rises, the voltage it produces drops, and its efficiency drops.
- (X2)
- Wind speed (m/s): The ability to withstand wind uplift and loads is essential for solar installations. Damage to machinery and increased wear and tear on operating components have been linked to the wind. Having more dust settles on the solar modules’ surfaces due to increased wind speeds is another factor that can reduce production.
- (X3)
- Relative humidity (%): Due to the absorption of short-wave solar radiation by atmospheric water vapor, locations with high humidity have limited potential for solar energy harvesting. In addition to diminishing power production, excessive humidity can cause dew to collect on the surfaces of solar panels, making it easier for airborne dust to settle on the modules.
- (X4)
- Precipitation (mm/year): Precipitation, whether rain, snow, sleet, or hail. When clouds block out the sun, solar power plants are less efficient in producing electricity.
- (X5)
- Air Pressure (Hpa): Air pressure is the force that air’s weight exerts on the earth’s surface. Air pressure decreases with increasing height. The ambient temperature decreases as altitude increases, allowing the solar system to function more efficiently. Due to fewer air layers that scatter, absorb, and reflect sunlight, there is more direct sunlight.
Output factors:
- (Y1)
- Sunshine hour (hour/year): The sunshine hour of irradiation describes the duration of sunlight in a given area over a given period (year). Solar radiation of at least 120 W/m2 is considered sunlight.
- (Y2)
- Irradiation (kWh//m2/year): The quantity of energy produced by the sun during a given period (in kWh) and surface area (in m2) (year).
- (Y3)
- Elevation (m): Solar potential characteristics are modified by a region’s elevation above sea level. Specifically, solar panels can capture more energy from the sun at higher altitudes due to the thinner atmosphere’s reduced absorption of solar radiation.
Statistical analysis of input and output factors is presented in Table 6.

Table 6.
Factor statistical analysis.
The data collection on input and output factors of 32 locations are collected, as can be seen in Table A1 (Appendix A). According to the results presented in Table 7 of the journal, the DEA analysis shows that a total of 11 DMUs have attained perfect efficiency scores of 1. This suggests that these DMUs are operating at the highest level of efficiency possible given the inputs and outputs used in the analysis, which are Jawa Barat (DMU-09), Jawa Timur (DMU-11), Lampung (DMU-16), Maluku (DMU-17), Maluku Utara (DMU-18), Nusa Tenggara Barat (DMU-19), Nusa Tenggara Timur (DMU-20), Papua (DMU-21), Riau (DMU-23), Sulawesi Selatan (DMU-25), and Sulawesi Utara (DMU-28). In the second step, 11 DMUs are chosen for analysis because they are deemed the most promising locations for solar projects.

Table 7.
The DEA score for efficiency.
4.2. Rank the Remaining Locations Using F-AHP and F-MARCOS Values
In the second part of the study, F-AHP and F-MARCOS models are used to conduct additional analysis and rank the locations that were given efficiency scores of 1. F-AHP is utilized to assign relative importance to criteria, and F-MARCOS is then used to order the rank of potential sites. The criteria and their performance grade are assessed based on expert judgment.
4.2.1. Weighting the Criteria with F-AHP
In the process of using F-AHP, relative preference weights for each criterion are calculated. This involves dividing the criteria into categories, such as technical, economic, social, and environmental, and evaluating the relative importance of each criterion within each category. In order to calculate the consistency ratio and relative weights (eigenvectors) of the main factors, the assessment criteria are usually written down in depth in a table, such as Table 8. This table can help illustrate the steps involved in calculating the consistency ratio and relative weight of each factor. Overall, using F-AHP can help decision-makers consider various factors in the site selection process and make more informed decisions regarding the location of solar power plants or other developments. It makes evaluating the relative importance of different criteria and can help to ensure that decisions are made consistently and transparently.

Table 8.
The criteria and their respective definitions.
The integrated fuzzy comparison matrix of F-AHP is shown in Table A3 (Appendix A). Table 9 and Figure 4 present the results of the F-AHP analysis. Based on the information provided, it can be seen that the top three impact criteria identified through the F-AHP analysis are “Facilitating factors,” “Benefits of conserving energy,” and “Terms of network accessibility.” These criteria are particularly important in certain decisions, such as site selection for solar power plants or the development of energy conservation programs. It is important to note that the specific criteria and their relative importance depend on the specific context of the decision or project and may vary depending on the decision maker’s goals and objectives. F-AHP helps decision-makers to consider multiple factors in the decision-making process and make more informed decisions based on a comprehensive evaluation of the relative importance of various criteria.

Table 9.
The relative significant fuzzy weights of F-AHP.

Figure 4.
The significant level of criteria of F-AHP.
4.2.2. Ranking the Locations with F-MARCOS
The integrated normalized fuzzy decision matrix of F-MARCOS is shown in Table A3 (Appendix A). The F-MARCOS model has been used to evaluate the efficiency ranking of 11 different locations in Indonesia: Jawa Barat (DMU-09), Jawa Timur (DMU-11), Lampung (DMU-16), Maluku (DMU-17), Maluku Utara (DMU-18), Nusa Tenggara Barat (DMU-19), Nusa Tenggara Timur (DMU-20), Papua (DMU-21), Riau (DMU-23), Sulawesi Selatan (DMU-25), and Sulawesi Utara (DMU-28). The decision hierarchy tree for selecting solar power plant locations is depicted in Figure 5. The integrated matrix and linguistic matrix calculations of the experts’ assessments can be seen in Table 10. The utility function and the final ranking of locations are shown in Table 11. Based on these results, the top three ranked locations are {DMU-09, DMU-20, DMU-23}, which occupy the first, second, and third positions with utility function values of 0.8272, 0.8211, and 0.8201, respectively. These locations are considered suitable for solar power generation based on the factors evaluated by the MARCOS fuzzy model. Figure 6 displays the final location ranking from the MARCOS fuzzy model. It is important to note that the ranking and utility function scores will depend on the attributes and criteria considered in the F-MARCOS analysis and the relative importance given to each attribute. F-MARCOS helps decision makers to consider various factors in the site selection process and make more informed decisions based on a comprehensive evaluation of the relative suitability of various sites.
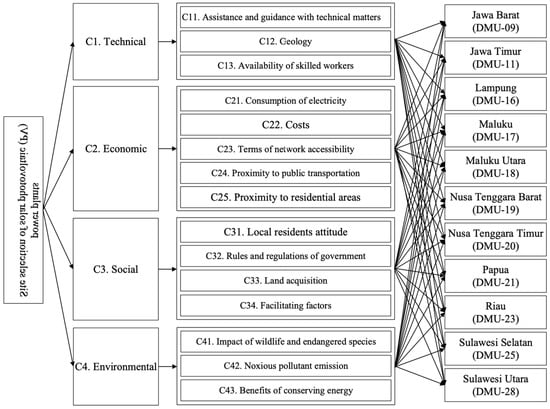
Figure 5.
The hierarchy tree for selecting solar PV power plants.

Table 10.
Utility degree and fuzzy matrix of .

Table 11.
Utility functions and final ranking of locations.
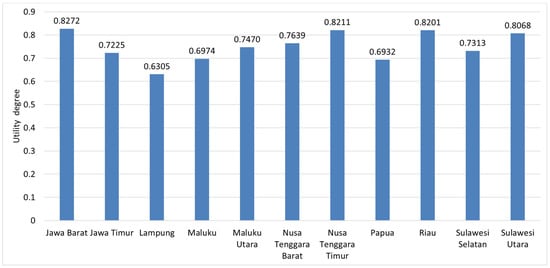
Figure 6.
The final location ranking.
In order to validate the location ranking, four different fuzzy MCDM models are considered, which are the fuzzy multi-attributive border approximation area comparison (fuzzy MABAC) [52], the fuzzy weighted aggregated sum product assessment (fuzzy WASPAS) [53], the fuzzy combined compromise solution (fuzzy CoCoSo) [54], and the fuzzy simple additive weighting (fuzzy SAW) [55]. During the comparative analysis, the same weight of criteria is used, and the results are provided in Table 12 and Figure 7. The findings show that there is no significant difference in the top three rankings of the solar location (Jawa Barat, Nusa Tenggara Timur, Riau). Hence, the proposed model is validated and applicable.

Table 12.
Comparative analysis of MCDM methods.
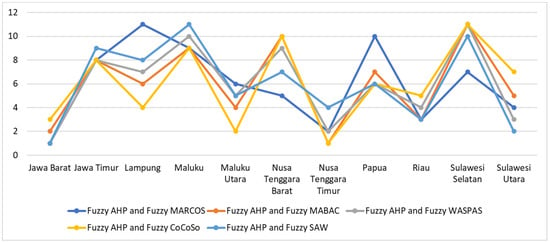
Figure 7.
Comparison of proposed model with other MCDM methods.
5. Conclusions
This study identifies the most suitable locations for solar power plants in Indonesia. This study uses data envelopment analysis (DEA) to identify areas of high efficiency based on measured inputs and outputs. These areas were further evaluated using F-AHP to weigh the evaluation criteria and F-MARCOS to rank the provinces. Based on the analysis, this study identified 32 provinces in Indonesia that are excellent for solar power generation. These provinces have favorable conditions for solar power generation, such as high levels of solar radiation, availability of suitable land, and adequate infrastructure. DEA, F-AHP, and F-MARCOS allow for a comprehensive evaluation of the relative suitability of various locations for solar power generation based on several criteria. The most significant findings and achievements of this research are as follows:
- The potential for solar deployment in Indonesia was evaluated based on 23 criteria, and suitable locations were identified using a novel combination of DEA, F-AHP, and F-MARCOS techniques.
- According to F-AHP, the three most important elements were “Facilitating factors,” “Benefits of conserving energy,” and “Terms of network accessibility.” Figure 4 displays the results of applying this technique to calculate the weights.
- Based on the final F-MARCOS ranking, the three best provinces in Indonesia to install solar power plants are Jawa Barat, Nusa Tenggara Timur, and Riau.
Future researchers are recommended to continue exploring the potential of renewable energy sources in Indonesia and other countries. Renewable energy sources such as solar, wind, and hydropower have the potential to play an important role in meeting the growing demand for energy while reducing the environmental impact of energy production. In addition to these established renewable energy sources, researchers are encouraged to explore the potential of newer technologies such as wave, geothermal, tidal, and hybrid systems (e.g., solar-wind and solar-biomass PV) in Indonesia and other countries. These technologies have the potential to provide additional sources of clean, renewable energy and can help diversify the energy mix. Assessing the ability to generate diverse renewable energy sources is also an important issue in the energy market, as decision-makers need to weigh the relative costs and benefits of different technologies to determine the best energy source. By continuing to research and develop new renewable energy technologies, researchers are improving the sustainability of energy systems and supporting the transition to a more renewable energy future.
Author Contributions
Conceptualization, T.-T.D.; data curation, F.D.W.; formal analysis, F.D.W.; funding acquisition, F.D.W.; investigation, N.-A.-T.N.; methodology, F.D.W.; project administration, C.-N.W.; software, T.-T.D.; validation, Y.-C.C.; writing—original draft, F.D.W.; writing—review and editing, N.-A.-T.N. and Y.-C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors appreciate the support from the National Kaohsiung University of Science and Technology, Taiwan; Hong Bang International University, Vietnam; and FPT University, Vietnam.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Data of input and output of the DEA model.
Table A1.
Data of input and output of the DEA model.
| No. | Location | DMU | X1 | X2 | X3 | X4 | X5 | Y1 | Y2 | Y3 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Aceh | DMU-01 | 26.81 | 1.50 | 89.28 | 3648.40 | 1010.70 | 1670.70 | 1686.30 | 3 |
| 2 | Bali | DMU-02 | 27.31 | 3.10 | 81.68 | 2992.80 | 1011.30 | 2658.00 | 1799.45 | 4 |
| 3 | Bangka Belitung | DMU-03 | 26.45 | 1.75 | 89.32 | 3012.90 | 1011.40 | 1646.50 | 1653.45 | 6 |
| 4 | Banten | DMU-04 | 27.80 | 1.77 | 81.49 | 2290.50 | 1010.60 | 1710.50 | 1679.00 | 14 |
| 5 | Bengkulu | DMU-05 | 27.01 | 2.52 | 83.59 | 3691.80 | 1011.00 | 2327.40 | 1708.20 | 12 |
| 6 | Gorontalo | DMU-06 | 27.24 | 1.53 | 85.50 | 2285.50 | 1011.00 | 1931.40 | 1803.10 | 33 |
| 7 | Jakarta | DMU-07 | 28.40 | 1.48 | 77.18 | 2394.60 | 1011.00 | 1532.00 | 1726.45 | 4 |
| 8 | Jambi | DMU-08 | 27.01 | 0.72 | 86.23 | 3218.40 | 1011.40 | 1574.20 | 1627.90 | 24 |
| 9 | Jawa Barat | DMU-09 | 26.06 | 1.09 | 84.16 | 3786.60 | 924.10 | 1862.40 | 1737.40 | 207 |
| 10 | Jawa Tengah | DMU-10 | 28.12 | 1.99 | 81.06 | 2476.80 | 1011.90 | 2274.90 | 1806.75 | 6 |
| 11 | Jawa Timur | DMU-11 | 24.10 | 1.93 | 79.53 | 2447.80 | 1011.80 | 2060.70 | 1879.75 | 590 |
| 12 | Kalimantan Barat | DMU-12 | 26.80 | 1.26 | 87.70 | 3281.20 | 1011.80 | 1788.30 | 1682.65 | 15 |
| 13 | Kalimantan Selatan | DMU-13 | 27.07 | 1.42 | 87.08 | 2996.20 | 1013.10 | 1418.70 | 1657.10 | 2 |
| 14 | Kalimantan Tengah | DMU-14 | 26.96 | 1.29 | 87.02 | 4132.20 | 1013.90 | 1799.40 | 1679.00 | 10 |
| 15 | Kalimantan Timur | DMU-15 | 27.60 | 1.89 | 83.52 | 2902.00 | 1012.90 | 1203.80 | 1668.05 | 3 |
| 16 | Lampung | DMU-16 | 26.84 | 1.12 | 84.18 | 2063.50 | 1012.10 | 1810.60 | 1708.20 | 71 |
| 17 | Maluku | DMU-17 | 26.58 | 0.97 | 89.08 | 2695.90 | 1012.40 | 1960.20 | 1679.00 | 10 |
| 18 | Maluku Utara | DMU-18 | 26.35 | 0.67 | 90.59 | 3928.20 | 1013.00 | 1724.20 | 1737.40 | 130 |
| 19 | Nusa Tenggara Barat | DMU-19 | 27.26 | 2.58 | 80.25 | 1770.40 | 1014.20 | 2687.60 | 1941.80 | 10 |
| 20 | Nusa Tenggara Timur | DMU-20 | 19.92 | 2.02 | 87.55 | 4493.40 | 1011.00 | 2062.10 | 2014.80 | 1070 |
| 21 | Papua | DMU-21 | 19.72 | 2.38 | 83.30 | 1933.50 | 1011.10 | 1751.60 | 1631.55 | 1653 |
| 22 | Papua Barat | DMU-22 | 27.52 | 1.81 | 82.66 | 2891.60 | 1011.50 | 1433.00 | 1679.00 | 3 |
| 23 | Riau | DMU-23 | 26.75 | 0.35 | 83.44 | 3072.20 | 1010.50 | 1502.90 | 1649.80 | 15 |
| 24 | Sulawesi Barat | DMU-24 | 27.59 | 1.72 | 81.79 | 2268.10 | 1012.50 | 2122.00 | 1708.20 | 29 |
| 25 | Sulawesi Selatan | DMU-25 | 26.98 | 1.16 | 84.00 | 4448.20 | 1013.10 | 2178.60 | 1777.55 | 14 |
| 26 | Sulawesi Tengah | DMU-26 | 27.25 | 0.97 | 85.56 | 2372.80 | 1011.90 | 1653.00 | 1700.90 | 10 |
| 27 | Sulawesi Tenggara | DMU-27 | 28.04 | 1.51 | 80.61 | 2420.80 | 1012.80 | 1831.30 | 1755.65 | 14 |
| 28 | Sulawesi Utara | DMU-28 | 23.15 | 1.24 | 87.69 | 2220.40 | 1012.30 | 1518.50 | 1755.65 | 204 |
| 29 | Sumatera Barat | DMU-29 | 26.70 | 1.83 | 85.02 | 4878.50 | 1010.90 | 2007.20 | 1646.15 | 6 |
| 30 | Sumatera Selatan | DMU-30 | 27.21 | 2.13 | 82.76 | 2297.90 | 1011.00 | 1716.60 | 1689.95 | 10 |
| 31 | Sumatera Utara | DMU-31 | 27.25 | 1.72 | 84.22 | 2543.40 | 1010.60 | 1623.20 | 1671.70 | 25 |
| 32 | Yogyakarta | DMU-32 | 26.37 | 2.04 | 82.40 | 2456.70 | 1014.90 | 1896.20 | 1861.50 | 182 |

Table A2.
The integrated fuzzy comparison matrix of F-AHP.
Table A2.
The integrated fuzzy comparison matrix of F-AHP.
| Criteria | C11 | C12 | C13 | C21 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C11 | 1.0000 | 1.0000 | 1.0000 | 0.8920 | 1.1107 | 1.4241 | 0.4663 | 0.5776 | 0.7496 | 0.2245 | 0.2716 | 0.3425 |
| C12 | 0.7022 | 0.9003 | 1.1211 | 1.0000 | 1.0000 | 1.0000 | 0.6507 | 0.8116 | 1.0532 | 0.6507 | 0.8116 | 1.0532 |
| C13 | 1.3341 | 1.7313 | 2.1446 | 0.9494 | 1.2321 | 1.5368 | 1.0000 | 1.0000 | 1.0000 | 0.6711 | 1.0371 | 1.4902 |
| C21 | 2.9196 | 3.6814 | 4.4541 | 0.9494 | 1.2321 | 1.5368 | 0.6711 | 0.9642 | 1.4902 | 1.0000 | 1.0000 | 1.0000 |
| C22 | 0.9349 | 1.2099 | 1.5029 | 0.9494 | 1.2321 | 1.5368 | 0.9883 | 1.4788 | 2.2442 | 0.7017 | 1.0000 | 1.5368 |
| C23 | 0.7242 | 0.9338 | 1.1722 | 0.6654 | 0.8610 | 1.0770 | 0.7708 | 1.1534 | 1.7826 | 0.8060 | 1.1962 | 1.8384 |
| C24 | 0.7242 | 0.9338 | 1.1722 | 0.6654 | 0.8610 | 1.0770 | 0.7708 | 1.1534 | 1.7826 | 0.8060 | 1.1962 | 1.8384 |
| C25 | 0.9494 | 1.2321 | 1.5368 | 0.9349 | 1.2099 | 1.5029 | 1.8206 | 2.7629 | 3.8043 | 2.9612 | 4.0774 | 5.1412 |
| C31 | 2.8552 | 3.6149 | 4.3860 | 1.4963 | 2.0180 | 2.6586 | 1.0481 | 1.4368 | 1.9871 | 1.0334 | 1.5337 | 2.3144 |
| C32 | 0.9521 | 1.2372 | 1.5468 | 2.3868 | 3.1469 | 4.2117 | 1.2671 | 1.8421 | 2.6531 | 1.0334 | 1.5337 | 2.3144 |
| C33 | 2.0009 | 2.5262 | 3.0737 | 0.5296 | 0.6935 | 1.0118 | 1.0184 | 1.3797 | 1.8541 | 1.0334 | 1.5337 | 2.3144 |
| C34 | 0.9669 | 1.2599 | 1.5817 | 1.3580 | 2.1161 | 3.0837 | 1.8206 | 2.7629 | 3.8043 | 1.8206 | 2.7629 | 3.8043 |
| C41 | 0.9669 | 1.2599 | 1.5817 | 1.3580 | 2.1161 | 3.0837 | 1.8206 | 2.7629 | 3.8043 | 0.9330 | 1.3636 | 1.9537 |
| C42 | 0.9669 | 1.2599 | 1.5817 | 0.7490 | 1.1076 | 1.6632 | 1.8206 | 2.7629 | 3.8043 | 0.9330 | 1.3636 | 1.9537 |
| C43 | 1.4022 | 1.7654 | 2.1540 | 0.7490 | 1.1076 | 1.6632 | 0.9756 | 1.4142 | 2.0148 | 0.6711 | 0.9642 | 1.4902 |
| Criteria | C22 | C23 | C24 | C25 | ||||||||
| C11 | 0.6654 | 0.8265 | 1.0696 | 0.8531 | 1.0709 | 1.3808 | 0.8531 | 1.0709 | 1.3808 | 0.6507 | 0.8116 | 1.0532 |
| C12 | 0.6507 | 0.8116 | 1.0532 | 0.9285 | 1.1614 | 1.5029 | 0.9285 | 1.1614 | 1.5029 | 0.6654 | 0.8265 | 1.0696 |
| C13 | 0.4456 | 0.6762 | 1.0118 | 0.5610 | 0.8670 | 1.2973 | 0.5610 | 0.8670 | 1.2973 | 0.2629 | 0.3619 | 0.5493 |
| C21 | 0.6507 | 1.0000 | 1.4251 | 0.5439 | 0.8360 | 1.2407 | 0.5439 | 0.8360 | 1.2407 | 0.1945 | 0.2453 | 0.3377 |
| C22 | 1.0000 | 1.0000 | 1.0000 | 0.5330 | 0.7548 | 1.0960 | 0.5551 | 0.7768 | 1.1207 | 1.4200 | 1.8684 | 2.3144 |
| C23 | 0.9124 | 1.3249 | 1.8760 | 1.0000 | 1.0000 | 1.0000 | 1.0718 | 1.5436 | 1.9977 | 0.7222 | 1.0371 | 1.4933 |
| C24 | 0.8923 | 1.2873 | 1.8015 | 0.5006 | 0.6478 | 0.9330 | 1.0000 | 1.0000 | 1.0000 | 1.1161 | 1.4902 | 2.0123 |
| C25 | 0.4321 | 0.5352 | 0.7042 | 0.6697 | 0.9642 | 1.3847 | 0.4969 | 0.6711 | 0.8960 | 1.0000 | 1.0000 | 1.0000 |
| C31 | 0.4321 | 0.5352 | 0.7042 | 0.6697 | 0.9642 | 1.3847 | 0.9479 | 1.3259 | 1.6843 | 0.7832 | 1.0718 | 1.6174 |
| C32 | 0.7995 | 1.1207 | 1.6141 | 0.4693 | 0.6084 | 0.7687 | 0.7017 | 1.0098 | 1.4758 | 1.4614 | 2.0939 | 3.0539 |
| C33 | 0.8414 | 1.2011 | 1.8015 | 0.4693 | 0.6084 | 0.7687 | 0.5318 | 0.6881 | 1.0021 | 0.7832 | 1.0718 | 1.6174 |
| C34 | 1.3195 | 2.0320 | 2.8772 | 0.4621 | 0.5974 | 0.7517 | 0.5318 | 0.6881 | 1.0021 | 1.4614 | 2.0939 | 3.0539 |
| C41 | 0.6418 | 0.9103 | 1.3741 | 0.5345 | 0.7146 | 0.9502 | 0.5318 | 0.6881 | 1.0021 | 0.5574 | 0.7277 | 1.0740 |
| C42 | 0.6418 | 0.9103 | 1.3741 | 0.3335 | 0.4234 | 0.5676 | 0.8394 | 1.1390 | 1.6174 | 0.7832 | 1.0718 | 1.6174 |
| C43 | 1.2873 | 1.8541 | 2.5832 | 0.4512 | 0.5949 | 0.7628 | 0.8394 | 1.1390 | 1.6174 | 1.4614 | 2.0939 | 3.0539 |
| Criteria | C31 | C32 | C33 | C34 | ||||||||
| C11 | 0.2280 | 0.2766 | 0.3502 | 0.6465 | 0.8083 | 1.0503 | 0.3253 | 0.3959 | 0.4998 | 0.6322 | 0.7937 | 1.0342 |
| C12 | 0.3761 | 0.4955 | 0.6683 | 0.2374 | 0.3178 | 0.4190 | 0.9883 | 1.4420 | 1.8882 | 0.3243 | 0.4726 | 0.7364 |
| C13 | 0.5032 | 0.6960 | 0.9541 | 0.3769 | 0.5428 | 0.7892 | 0.5394 | 0.7248 | 0.9819 | 0.2629 | 0.3619 | 0.5493 |
| C21 | 0.4321 | 0.6520 | 0.9677 | 0.4321 | 0.6520 | 0.9677 | 0.4321 | 0.6520 | 0.9677 | 0.2629 | 0.3619 | 0.5493 |
| C22 | 1.4200 | 1.8684 | 2.3144 | 0.6196 | 0.8923 | 1.2508 | 0.5551 | 0.8326 | 1.1885 | 0.3476 | 0.4921 | 0.7579 |
| C23 | 0.7222 | 1.0371 | 1.4933 | 1.3010 | 1.6438 | 2.1308 | 1.3010 | 1.6438 | 2.1308 | 1.3303 | 1.6740 | 2.1639 |
| C24 | 0.5937 | 0.7542 | 1.0549 | 0.6776 | 0.9903 | 1.4251 | 0.9979 | 1.4532 | 1.8805 | 0.9979 | 1.4532 | 1.8805 |
| C25 | 0.6183 | 0.9330 | 1.2769 | 0.3274 | 0.4776 | 0.6843 | 0.6183 | 0.9330 | 1.2769 | 0.3274 | 0.4776 | 0.6843 |
| C31 | 1.0000 | 1.0000 | 1.0000 | 0.6183 | 0.9330 | 1.2769 | 0.3274 | 0.4776 | 0.6843 | 0.6183 | 0.9330 | 1.2769 |
| C32 | 0.7832 | 1.0718 | 1.6174 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.3830 | 1.8303 | 0.6084 | 0.8569 | 1.1548 |
| C33 | 1.4614 | 2.0939 | 3.0539 | 0.5464 | 0.7231 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.2288 | 0.3026 | 0.4592 |
| C34 | 0.7832 | 1.0718 | 1.6174 | 0.8659 | 1.1671 | 1.6438 | 2.1778 | 3.3051 | 4.3700 | 1.0000 | 1.0000 | 1.0000 |
| C41 | 0.6711 | 0.9642 | 1.4902 | 0.5464 | 0.7231 | 1.0000 | 1.8206 | 2.7629 | 3.8043 | 1.0334 | 1.5337 | 2.3144 |
| C42 | 0.6711 | 0.9642 | 1.4902 | 0.5464 | 0.7231 | 1.0000 | 1.0334 | 1.5337 | 2.3144 | 0.7017 | 1.0000 | 1.5368 |
| C43 | 0.9883 | 1.4788 | 2.2442 | 1.1598 | 1.5332 | 2.0927 | 1.0334 | 1.5337 | 2.3144 | 0.5296 | 0.6790 | 0.9622 |
| Criteria | C41 | C42 | C43 | |||||||||
| C11 | 0.6322 | 0.7937 | 1.0342 | 0.6322 | 0.7937 | 1.0342 | 0.4642 | 0.5665 | 0.7132 | |||
| C12 | 0.3243 | 0.4726 | 0.7364 | 0.6012 | 0.9029 | 1.3351 | 0.6012 | 0.9029 | 1.3351 | |||
| C13 | 0.2629 | 0.3619 | 0.5493 | 0.2629 | 0.3619 | 0.5493 | 0.4963 | 0.7071 | 1.0250 | |||
| C21 | 0.5119 | 0.7334 | 1.0718 | 0.5119 | 0.7334 | 1.0718 | 0.6711 | 1.0371 | 1.4902 | |||
| C22 | 0.7277 | 1.0986 | 1.5582 | 0.7277 | 1.0986 | 1.5582 | 0.3871 | 0.5394 | 0.7768 | |||
| C23 | 1.0524 | 1.3994 | 1.8708 | 1.7617 | 2.3618 | 2.9987 | 1.3110 | 1.6808 | 2.2162 | |||
| C24 | 0.9979 | 1.4532 | 1.8805 | 0.6183 | 0.8780 | 1.1914 | 0.6183 | 0.8780 | 1.1914 | |||
| C25 | 0.9311 | 1.3741 | 1.7941 | 0.6183 | 0.9330 | 1.2769 | 0.3274 | 0.4776 | 0.6843 | |||
| C31 | 0.6711 | 1.0371 | 1.4902 | 0.6711 | 1.0371 | 1.4902 | 0.4456 | 0.6762 | 1.0118 | |||
| C32 | 1.0000 | 1.3830 | 1.8303 | 1.0000 | 1.3830 | 1.8303 | 0.4778 | 0.6522 | 0.8622 | |||
| C33 | 0.2629 | 0.3619 | 0.5493 | 0.4321 | 0.6520 | 0.9677 | 0.4321 | 0.6520 | 0.9677 | |||
| C34 | 0.4321 | 0.6520 | 0.9677 | 0.6507 | 1.0000 | 1.4251 | 1.0392 | 1.4727 | 1.8882 | |||
| C41 | 1.0000 | 1.0000 | 1.0000 | 0.2629 | 0.3619 | 0.5493 | 0.4321 | 0.6520 | 0.9677 | |||
| C42 | 1.8206 | 2.7629 | 3.8043 | 1.0000 | 1.0000 | 1.0000 | 0.2629 | 0.3619 | 0.5493 | |||
| C43 | 1.0334 | 1.5337 | 2.3144 | 1.8206 | 2.7629 | 3.8043 | 1.0000 | 1.0000 | 1.0000 | |||

Table A3.
The integrated normalized fuzzy decision matrix of F-MARCOS.
Table A3.
The integrated normalized fuzzy decision matrix of F-MARCOS.
| Location | C11 | C12 | C13 | C21 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | l | m | u | l | m | u | l | m | u | |
| DMU-09 | 0.5603 | 0.7284 | 0.8401 | 0.1901 | 0.2050 | 0.2486 | 0.8521 | 1.0335 | 1.1144 | 0.8064 | 0.9780 | 1.0546 |
| DMU-11 | 0.2922 | 0.4690 | 0.5746 | 0.5508 | 0.9963 | 1.0485 | 0.2126 | 0.3300 | 0.4956 | 0.2012 | 0.2012 | 0.3765 |
| DMU-16 | 0.4618 | 0.6154 | 0.7466 | 0.3485 | 0.5796 | 0.6420 | 0.3655 | 0.4709 | 0.6502 | 0.3287 | 0.3459 | 0.5950 |
| DMU-17 | 0.2777 | 0.5194 | 0.5556 | 0.7221 | 0.7997 | 1.1702 | 0.2649 | 0.2934 | 0.5489 | 0.1713 | 0.2507 | 0.2777 |
| DMU-18 | 0.7290 | 0.8340 | 0.9780 | 0.2750 | 0.3425 | 0.4201 | 0.6186 | 0.7703 | 0.8813 | 0.4772 | 0.5854 | 0.7290 |
| DMU-19 | 0.2945 | 0.4094 | 0.5654 | 0.6809 | 1.3061 | 1.3061 | 0.1622 | 0.3112 | 0.4326 | 0.1535 | 0.1535 | 0.2945 |
| DMU-20 | 0.6262 | 0.7928 | 0.8770 | 0.3202 | 0.3732 | 0.5465 | 0.5677 | 0.6617 | 0.8377 | 0.3668 | 0.5372 | 0.6262 |
| DMU-21 | 0.4736 | 0.5654 | 0.7409 | 0.4234 | 0.6809 | 0.7541 | 0.3112 | 0.5004 | 0.5974 | 0.2659 | 0.2945 | 0.4736 |
| DMU-23 | 0.8340 | 0.9222 | 1.0815 | 0.1854 | 0.2174 | 0.2404 | 0.6186 | 0.7703 | 0.8813 | 0.1232 | 0.2134 | 0.3312 |
| DMU-25 | 0.1447 | 0.1447 | 0.2593 | 0.6809 | 1.3061 | 1.3061 | 0.1622 | 0.3112 | 0.4326 | 0.1535 | 0.1535 | 0.2945 |
| DMU-28 | 0.8626 | 1.0285 | 1.1090 | 0.2140 | 0.2366 | 0.3073 | 0.6893 | 0.8953 | 0.9900 | 0.8626 | 1.0285 | 1.1090 |
| Location | C22 | C23 | C24 | C25 | ||||||||
| DMU-09 | 0.2896 | 0.3960 | 0.5277 | 0.4226 | 0.5824 | 0.7700 | 0.2511 | 0.2925 | 0.4000 | 0.2892 | 0.3955 | 0.5269 |
| DMU-11 | 0.4976 | 0.9000 | 0.9472 | 0.2354 | 0.2478 | 0.4482 | 0.3900 | 0.5025 | 0.9089 | 0.4969 | 0.8987 | 0.9458 |
| DMU-16 | 0.3148 | 0.5237 | 0.5800 | 0.3845 | 0.4405 | 0.7084 | 0.2973 | 0.3179 | 0.5288 | 0.3144 | 0.5229 | 0.5791 |
| DMU-17 | 0.6523 | 0.7225 | 1.0572 | 0.2109 | 0.3087 | 0.3419 | 0.3521 | 0.6588 | 0.7296 | 0.6514 | 0.7215 | 1.0557 |
| DMU-18 | 0.2485 | 0.3094 | 0.3795 | 0.5876 | 0.7208 | 0.8976 | 0.2193 | 0.2509 | 0.3125 | 0.2611 | 0.3089 | 0.4230 |
| DMU-19 | 0.7662 | 1.1800 | 1.1800 | 0.1890 | 0.1890 | 0.3626 | 0.4468 | 0.7738 | 1.1916 | 0.6803 | 1.1783 | 1.4678 |
| DMU-20 | 0.2893 | 0.3372 | 0.4938 | 0.4517 | 0.6614 | 0.7710 | 0.2307 | 0.2921 | 0.3405 | 0.3199 | 0.3367 | 0.6142 |
| DMU-21 | 0.4269 | 0.6151 | 0.6813 | 0.3274 | 0.3626 | 0.5831 | 0.3235 | 0.4311 | 0.6212 | 0.4930 | 0.6142 | 1.1783 |
| DMU-23 | 0.5469 | 0.8487 | 1.4699 | 0.1517 | 0.2628 | 0.4078 | 0.2193 | 0.2509 | 0.3125 | 0.2481 | 0.3255 | 0.3790 |
| DMU-25 | 0.6151 | 1.1800 | 1.1800 | 0.1890 | 0.1890 | 0.2910 | 0.7055 | 1.2638 | 1.2638 | 0.6142 | 1.0638 | 1.1783 |
| DMU-28 | 0.1933 | 0.2138 | 0.2777 | 0.8032 | 1.0432 | 1.1536 | 0.1649 | 0.1779 | 0.2121 | 0.1930 | 0.2135 | 0.2773 |
| Location | C31 | C32 | C33 | C34 | ||||||||
| DMU-09 | 0.6609 | 0.7697 | 0.9342 | 0.3432 | 0.4573 | 0.6254 | 0.8521 | 1.0335 | 1.1144 | 0.8521 | 1.0335 | 1.1144 |
| DMU-11 | 0.3846 | 0.4956 | 0.6725 | 0.1912 | 0.2012 | 0.3640 | 0.2021 | 0.2126 | 0.3846 | 0.2021 | 0.2126 | 0.3846 |
| DMU-16 | 0.6079 | 0.6502 | 0.8738 | 0.3123 | 0.3459 | 0.5753 | 0.3300 | 0.3655 | 0.6079 | 0.3300 | 0.3655 | 0.6079 |
| DMU-17 | 0.2934 | 0.5677 | 0.5871 | 0.1713 | 0.2507 | 0.2777 | 0.2498 | 0.3250 | 0.3476 | 0.1453 | 0.2373 | 0.2957 |
| DMU-18 | 0.7703 | 0.7967 | 1.0335 | 0.4772 | 0.6927 | 0.7290 | 0.2649 | 0.4111 | 0.5489 | 0.4518 | 0.5542 | 0.7319 |
| DMU-19 | 0.3112 | 0.4627 | 0.5974 | 0.1535 | 0.1535 | 0.2945 | 0.1796 | 0.1796 | 0.3328 | 0.2255 | 0.3136 | 0.5043 |
| DMU-20 | 0.8521 | 1.0335 | 1.1144 | 0.8064 | 0.9780 | 1.0546 | 0.3250 | 0.5677 | 0.6279 | 0.2788 | 0.3658 | 0.5086 |
| DMU-21 | 0.5004 | 0.6609 | 0.7829 | 0.2659 | 0.2945 | 0.4736 | 0.2911 | 0.3627 | 0.5346 | 0.2021 | 0.2498 | 0.4792 |
| DMU-23 | 0.4792 | 0.5769 | 0.7448 | 0.4772 | 0.6927 | 0.7290 | 0.8813 | 0.9745 | 1.1428 | 0.8813 | 0.9745 | 1.1428 |
| DMU-25 | 0.1529 | 0.1529 | 0.2740 | 0.1447 | 0.1447 | 0.2593 | 0.1302 | 0.1302 | 0.2255 | 0.2255 | 0.3136 | 0.5043 |
| DMU-28 | 0.6893 | 0.8953 | 0.9900 | 0.8626 | 1.0285 | 1.1090 | 0.6893 | 0.8953 | 0.9900 | 0.2788 | 0.3658 | 0.5086 |
| Location | C41 | C42 | C43 | |||||||||
| DMU-09 | 0.3197 | 0.3447 | 0.4181 | 0.2211 | 0.2385 | 0.2892 | 0.7887 | 0.9185 | 1.1149 | |||
| DMU-11 | 0.7189 | 0.9263 | 1.6755 | 0.6407 | 1.1589 | 1.2197 | 0.4825 | 0.6326 | 0.8368 | |||
| DMU-16 | 0.5479 | 0.5861 | 0.9748 | 0.4054 | 0.6743 | 0.7468 | 0.7494 | 0.8300 | 1.0780 | |||
| DMU-17 | 0.6491 | 1.2143 | 1.3450 | 0.8400 | 0.9303 | 1.3613 | 0.4148 | 0.7494 | 0.7880 | |||
| DMU-18 | 0.4043 | 0.4625 | 0.5759 | 0.4887 | 0.8908 | 1.0928 | 0.6550 | 0.8035 | 0.9749 | |||
| DMU-19 | 0.7065 | 0.9823 | 1.5798 | 0.5185 | 0.6795 | 0.6795 | 0.3972 | 0.5522 | 0.7497 | |||
| DMU-20 | 0.5484 | 0.7316 | 1.0172 | 0.3725 | 0.4341 | 0.6358 | 0.7494 | 0.9997 | 1.0780 | |||
| DMU-21 | 0.7435 | 0.9192 | 1.7633 | 0.4157 | 0.5740 | 0.6358 | 0.6380 | 0.7887 | 0.9905 | |||
| DMU-23 | 0.4043 | 0.4625 | 0.5759 | 0.4490 | 0.5995 | 0.9303 | 0.6614 | 0.8735 | 0.9993 | |||
| DMU-25 | 0.7065 | 0.9823 | 1.5798 | 0.3203 | 0.3790 | 0.5223 | 0.8300 | 1.0169 | 1.1531 | |||
| DMU-28 | 0.3599 | 0.3979 | 0.5169 | 0.2489 | 0.2753 | 0.3575 | 0.6774 | 0.7896 | 0.9997 | |||
References
- Aleixandre-Tudó, J.L.; Castelló-Cogollos, L.; Aleixandre, J.L.; Aleixandre-Benavent, R. Renewable Energies: Worldwide Trends in Research, Funding and International Collaboration. Renew. Energy 2019, 139, 268–278. [Google Scholar] [CrossRef]
- International Energy Agency [IEA]. 2022, p. 98. Available online: https://www.iea.org/reports/world-energy-outlook-2022 (accessed on 18 August 2022).
- Secretary General of National Energy Council. 2019, p. 51. Available online: https://www.esdm.go.id/assets/media/content/content-indonesia-energy-outlook-2019-english-version (accessed on 18 August 2022).
- Asian Development Bank. 2020, pp. 17–18. Available online: https://www.adb.org/sites/default/files/publication/575626/ado2020.pdf (accessed on 18 August 2022).
- International Renewable Energy Agency (IRENA) 2017. Available online: https://www.irena.org/publications/2017/Jul/Renewable-Energy-Statistics-2017 (accessed on 20 August 2022).
- Rose, A.; Stoner, R.; Pérez-Arriaga, I. Prospects for Grid-Connected Solar PV in Kenya: A Systems Approach. Appl. Energy 2016, 161, 583–590. [Google Scholar] [CrossRef]
- Tang, J.; Ni, H.; Peng, R.-L.; Wang, N.; Zuo, L. A Review on Energy Conversion Using Hybrid Photovoltaic and Thermoelectric Systems. J. Power Sources 2023, 562, 232785. [Google Scholar] [CrossRef]
- Ruiz, H.S.; Sunarso, A.; Ibrahim-Bathis, K.; Murti, S.A.; Budiarto, I. GIS-AHP Multi Criteria Decision Analysis for the Optimal Location of Solar Energy Plants at Indonesia. Energy Rep. 2020, 6, 3249–3263. [Google Scholar] [CrossRef]
- Wang, C.-N.; Dang, T.-T.; Nguyen, N.-A.-T.; Wang, J.-W. A Combined Data Envelopment Analysis (DEA) and Grey Based Multiple Criteria Decision Making (G-MCDM) for Solar PV Power Plants Site Selection: A Case Study in Vietnam. Energy Rep. 2022, 8, 1124–1142. [Google Scholar] [CrossRef]
- Al Garni, H.Z.; Awasthi, A. Solar PV Power Plants Site Selection. In Advances in Renewable Energies and Power Technologies; Elsevier: Amsterdam, The Netherlands, 2018; pp. 57–75. [Google Scholar]
- Deveci, M.; Cali, U.; Pamucar, D. Evaluation of Criteria for Site Selection of Solar Photovoltaic (PV) Projects Using Fuzzy Logarithmic Additive Estimation of Weight Coefficients. Energy Rep. 2021, 7, 8805–8824. [Google Scholar] [CrossRef]
- Khan, M.F.; Pervez, A.; Modibbo, U.M.; Chauhan, J.; Ali, I. Flexible Fuzzy Goal Programming Approach in Optimal Mix of Power Generation for Socio-Economic Sustainability: A Case Study. Sustainability 2021, 13, 8256. [Google Scholar] [CrossRef]
- Modibbo, U.M.; Hassan, M.; Ahmed, A.; Ali, I. Multi-Criteria Decision Analysis for Pharmaceutical Supplier Selection Problem Using Fuzzy TOPSIS. Manag. Decis. 2022, 60, 806–836. [Google Scholar] [CrossRef]
- Jurasz, J.; Canales, F.A.; Kies, A.; Guezgouz, M.; Beluco, A. A Review on the Complementarity of Renewable Energy Sources: Concept, Metrics, Application and Future Research Directions. Sol. Energy 2020, 195, 703–724. [Google Scholar] [CrossRef]
- Burke, M.J.; Stephens, J.C. Political Power and Renewable Energy Futures: A Critical Review. Energy Res. Soc. Sci. 2018, 35, 78–93. [Google Scholar] [CrossRef]
- Sindhu, S.; Nehra, V.; Luthra, S. Investigation of Feasibility Study of Solar Farms Deployment Using Hybrid AHP-TOPSIS Analysis: Case Study of India. Renew. Sustain. Energy Rev. 2017, 73, 496–511. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, N.-A.-T.; Dang, T.-T.; Bayer, J. A Two-Stage Multiple Criteria Decision Making for Site Selection of Solar Photovoltaic (PV) Power Plant: A Case Study in Taiwan. IEEE Access 2021, 9, 75509–75525. [Google Scholar] [CrossRef]
- Doorga, J.R.S.; Rughooputh, S.D.D.V.; Boojhawon, R. Multi-Criteria GIS-Based Modelling Technique for Identifying Potential Solar Farm Sites: A Case Study in Mauritius. Renew. Energy 2019, 133, 1201–1219. [Google Scholar] [CrossRef]
- Potić, I.; Golić, R.; Joksimović, T. Analysis of Insolation Potential of Knjaževac Municipality (Serbia) Using Multi-Criteria Approach. Renew. Sustain. Energy Rev. 2016, 56, 235–245. [Google Scholar] [CrossRef]
- Liu, J.; Xu, F.; Lin, S. Site Selection of Photovoltaic Power Plants in a Value Chain Based on Grey Cumulative Prospect Theory for Sustainability: A Case Study in Northwest China. J. Clean. Prod. 2017, 148, 386–397. [Google Scholar] [CrossRef]
- Gherboudj, I.; Ghedira, H. Assessment of Solar Energy Potential over the United Arab Emirates Using Remote Sensing and Weather Forecast Data. Renew. Sustain. Energy Rev. 2016, 55, 1210–1224. [Google Scholar] [CrossRef]
- Watson, J.J.W.; Hudson, M.D. Regional Scale Wind Farm and Solar Farm Suitability Assessment Using GIS-Assisted Multi-Criteria Evaluation. Landsc. Urban Plan. 2015, 138, 20–31. [Google Scholar] [CrossRef]
- Qolipour, M.; Mostafaeipour, A.; Shamshirband, S.; Alavi, O.; Goudarzi, H.; Petković, D. Evaluation of Wind Power Generation Potential Using a Three Hybrid Approach for Households in Ardebil Province, Iran. Energy Convers. Manag. 2016, 118, 295–305. [Google Scholar] [CrossRef]
- Zoghi, M.; Houshang Ehsani, A.; Sadat, M.; javad Amiri, M.; Karimi, S. Optimization Solar Site Selection by Fuzzy Logic Model and Weighted Linear Combination Method in Arid and Semi-Arid Region: A Case Study Isfahan-IRAN. Renew. Sustain. Energy Rev. 2017, 68, 986–996. [Google Scholar] [CrossRef]
- Wu, Y.; Geng, S.; Zhang, H.; Gao, M. Decision Framework of Solar Thermal Power Plant Site Selection Based on Linguistic Choquet Operator. Appl. Energy 2014, 136, 303–311. [Google Scholar] [CrossRef]
- Jun, D.; Tian-tian, F.; Yi-sheng, Y.; Yu, M. Macro-Site Selection of Wind/Solar Hybrid Power Station Based on ELECTRE-II. Renew. Sustain. Energy Rev. 2014, 35, 194–204. [Google Scholar] [CrossRef]
- Ozdemir, S.; Sahin, G. Multi-Criteria Decision-Making in the Location Selection for a Solar PV Power Plant Using AHP. Measurement 2018, 129, 218–226. [Google Scholar] [CrossRef]
- Vafaeipour, M.; Hashemkhani Zolfani, S.; Morshed Varzandeh, M.H.; Derakhti, A.; Keshavarz Eshkalag, M. Assessment of Regions Priority for Implementation of Solar Projects in Iran: New Application of a Hybrid Multi-Criteria Decision Making Approach. Energy Convers. Manag. 2014, 86, 653–663. [Google Scholar] [CrossRef]
- Do, T.N.; Burke, P.J.; Baldwin, K.G.H.; Nguyen, C.T. Underlying Drivers and Barriers for Solar Photovoltaics Diffusion: The Case of Vietnam. Energy Policy 2020, 144, 111561. [Google Scholar] [CrossRef]
- Rigo, P.D.; Rediske, G.; Rosa, C.B.; Gastaldo, N.G.; Michels, L.; Neuenfeldt Júnior, A.L.; Siluk, J.C.M. Renewable Energy Problems: Exploring the Methods to Support the Decision-Making Process. Sustainability 2020, 12, 10195. [Google Scholar] [CrossRef]
- Uyan, M. GIS-Based Solar Farms Site Selection Using Analytic Hierarchy Process (AHP) in Karapinar Region, Konya/Turkey. Renew. Sustain. Energy Rev. 2013, 28, 11–17. [Google Scholar] [CrossRef]
- Lee, A.; Kang, H.-Y.; Liou, Y.-J. A Hybrid Multiple-Criteria Decision-Making Approach for Photovoltaic Solar Plant Location Selection. Sustainability 2017, 9, 184. [Google Scholar] [CrossRef]
- Al Garni, H.Z.; Awasthi, A. Solar PV Power Plant Site Selection Using a GIS-AHP Based Approach with Application in Saudi Arabia. Appl. Energy 2017, 206, 1225–1240. [Google Scholar] [CrossRef]
- Seyed Alavi, S.M.; Maleki, A.; Khaleghi, A. Optimal Site Selection for Wind Power Plant Using Multi-Criteria Decision-Making Methods: A Case Study in Eastern Iran. Int. J. Low-Carbon Technol. 2022, 17, 1319–1337. [Google Scholar] [CrossRef]
- Janke, J.R. Multicriteria GIS Modeling of Wind and Solar Farms in Colorado. Renew. Energy 2010, 35, 2228–2234. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Henggeler Antunes, C.; García-Cascales, M.S.; Dias, L.C. GIS-Based Photovoltaic Solar Farms Site Selection Using ELECTRE-TRI: Evaluating the Case for Torre Pacheco, Murcia, Southeast of Spain. Renew. Energy 2014, 66, 478–494. [Google Scholar] [CrossRef]
- Aragonés-Beltrán, P.; Chaparro-González, F.; Pastor-Ferrando, J.-P.; Pla-Rubio, A. An AHP (Analytic Hierarchy Process)/ANP (Analytic Network Process)-Based Multi-Criteria Decision Approach for the Selection of Solar-Thermal Power Plant Investment Projects. Energy 2014, 66, 222–238. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; García-Cascales, M.S.; Lamata, M.T. Evaluation of Suitable Locations for the Installation of Solar Thermoelectric Power Plants. Comput. Ind. Eng. 2015, 87, 343–355. [Google Scholar] [CrossRef]
- Tavana, M.; Santos Arteaga, F.J.; Mohammadi, S.; Alimohammadi, M. A Fuzzy Multi-Criteria Spatial Decision Support System for Solar Farm Location Planning. Energy Strategy Rev. 2017, 18, 93–105. [Google Scholar] [CrossRef]
- Anwarzai, M.A.; Nagasaka, K. Utility-Scale Implementable Potential of Wind and Solar Energies for Afghanistan Using GIS Multi-Criteria Decision Analysis. Renew. Sustain. Energy Rev. 2017, 71, 150–160. [Google Scholar] [CrossRef]
- Akkas, O.P.; Erten, M.Y.; Cam, E.; Inanc, N. Optimal Site Selection for a Solar Power Plant in the Central Anatolian Region of Turkey. Int. J. Photoenergy 2017, 2017, 7452715. [Google Scholar] [CrossRef]
- Rezaei, M.; Mostafaeipour, A.; Qolipour, M.; Tavakkoli-Moghaddam, R. Investigation of the Optimal Location Design of a Hybrid Wind-Solar Plant: A Case Study. Int. J. Hydrog. Energy 2018, 43, 100–114. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, B.; Wu, C.; Zhang, T.; Liu, F. Optimal Site Selection for Parabolic Trough Concentrating Solar Power Plant Using Extended PROMETHEE Method: A Case in China. Renew. Energy 2019, 143, 1910–1927. [Google Scholar] [CrossRef]
- Badi, I.; Pamucar, D.; Gigović, L.; Tatomirović, S. Optimal Site Selection for Sitting a Solar Park Using a Novel GIS- SWA’TEL Model: A Case Study in Libya. Int. J. Green Energy 2021, 18, 336–350. [Google Scholar] [CrossRef]
- Heidary Dahooie, J.; Husseinzadeh Kashan, A.; Shoaei Naeini, Z.; Vanaki, A.S.; Zavadskas, E.K.; Turskis, Z. A Hybrid Multi-Criteria-Decision-Making Aggregation Method and Geographic Information System for Selecting Optimal Solar Power Plants in Iran. Energies 2022, 15, 2801. [Google Scholar] [CrossRef]
- Jbaihi, O.; Ouchani, F.; Alami Merrouni, A.; Cherkaoui, M.; Ghennioui, A.; Maaroufi, M. An AHP-GIS Based Site Suitability Analysis for Integrating Large-Scale Hybrid CSP+PV Plants in Morocco: An Approach to Address the Intermittency of Solar Energy. J. Clean Prod. 2022, 369, 133250. [Google Scholar] [CrossRef]
- Stanković, M.; Stević, Ž.; Das, D.K.; Subotić, M.; Pamučar, D. A New Fuzzy MARCOS Method for Road Traffic Risk Analysis. Mathematics 2020, 8, 457. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable Supplier Selection in Healthcare Industries Using a New MCDM Method: Measurement of Alternatives and Ranking According to COmpromise Solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, N.-A.-T.; Dang, T.-T.; Trinh, T.-T.-Q. A Decision Support Model for Measuring Technological Progress and Productivity Growth: The Case of Commercial Banks in Vietnam. Axioms 2021, 10, 131. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Tone, K. A Slacks-Based Measure of Efficiency in Data Envelopment Analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Božanić, D.; Tešić, D.; Kočić, J. Multi-Criteria FUCOM—Fuzzy MABAC Model for the Selection of Location for Construction of Single-Span Bailey Bridge. Decis. Mak. Appl. Manag. Eng. 2019, 2, 132–146. [Google Scholar] [CrossRef]
- Agarwal, S.; Kant, R.; Shankar, R. Evaluating Solutions to Overcome Humanitarian Supply Chain Management Barriers: A Hybrid Fuzzy SWARA—Fuzzy WASPAS Approach. Int. J. Disaster Risk Reduct. 2020, 51, 101838. [Google Scholar] [CrossRef]
- Ecer, F.; Pamucar, D. Sustainable Supplier Selection: A Novel Integrated Fuzzy Best Worst Method (F-BWM) and Fuzzy CoCoSo with Bonferroni (CoCoSo’B) Multi-Criteria Model. J. Clean. Prod. 2020, 266, 121981. [Google Scholar] [CrossRef]
- Roszkowska, E.; Kacprzak, D. The Fuzzy Saw and Fuzzy TOPSIS Procedures Based on Ordered Fuzzy Numbers. Inf. Sci. N. Y. 2016, 369, 564–584. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).