Surrogate Models for Efficient Multi-Objective Optimization of Building Performance

Abstract

Nowadays, the large set of available simulation tools brings numerous benefits to urban and architectural practices. However, simulations often take a considerable amount of time to yield significant results, particularly when performing many simulations and with large models, as is typical in complex urban and architectural endeavors. Additionally, multiple objective optimizations with metaheuristic algorithms have been widely used to solve building optimization problems. However, most of these optimization processes exponentially increase the computational time to correctly produce outputs and require extensive knowledge to interpret results. Thus, building optimization with time-consuming simulation tools is often rendered unfeasible and requires a specific methodology to overcome these barriers. This work integrates a baseline multi-objective optimization process with a widely used, validated building energy simulation tool. The goal is to minimize the energy use and cost of the construction of a residential building complex. Afterward, machine learning and optimization techniques are used to create a surrogate model capable of accurately predicting the simulation results. Finally, different metaheuristics with their tuned hyperparameters are compared. Results show significant improvements in optimization results with a decrease of up to 22% in the total cost while having similar performance results and execution times up to 100 times faster.

1. Introduction

One of the largest shares of energy consumption is associated with the building stock (in Europe, it is responsible for 40% of the total energy consumption). In this context, the European Parliament established the “Energy Performance of Buildings Directive”, which promotes policies to help to achieve the energy efficiency and decarbonization of buildings by 2050 [1,2]. This directive highlights the need to improve the existing building stock and establishes guidelines and frameworks to achieve this. Since a building’s lifetime can exceed 100 years, it is important to improve regulations and specific instruments that promote energy efficiency and the reduction of greenhouse gas emissions while improving the thermal comfort and quality of life of occupants [3].

To obtain information regarding the building stock and define strategies to improve it via these directives, Building Performance Simulation (BPS) tools can help to predict building design and rehabilitation impacts in multiple aspects of a building’s performance [4]. BPS tools predict these results through models described by specific inputs that yield the desired outputs. With these simulations, it is possible to integrate iterative Building Performance Optimization (BPO) into building design, planning, and rehabilitation processes [5].

Unfortunately, the use of BPS tools with BPO is still out of reach for most practitioners and presents several limitations:

• BPS tools are not portable and require different model formats and descriptions. This forces practitioners to develop models with different descriptions and inputs for each simulation, which is error-prone [6,7].
• Most BPS is time-consuming and still requires a considerable amount of time to perform the calculations for multiple or large models. This constitutes a significant limitation, particularly for BPO that requires testing of multiple iterations of a project [8,9].
• The use of BPS tools requires extensive knowledge regarding building physics and performed calculations to understand and process the inputs and results [10,11].

BPO typically entails multiple objectives, which are often conflicting [5]. Additionally, most building performance indicators are outputs of BPS or extensive calculations performed by field experts [12]. Because of this, optimization problems that are focused outside the practitioner’s realm of knowledge are usually treated as multi-objective optimization (MOO) problems with derivative-free functions [5,13,14,15]. Metaheuristics, a class of optimization algorithms, have been widely used in the field of optimization for the built environment with positive results. These algorithms guide the search based on biological heuristics such as evolutionary ones and swarms of different kinds, among others [16]. Furthermore, Wolpert and Macready state with the “No Free Lunch” theorem that no algorithm outperforms all others for all problems. This means that one has to either know from experience which algorithms yield better performance for each BPO problem or test multiple metaheuristics to find the best one [17]. Moreover, these algorithms have variables that define how they search for the optimal space, called hyperparameters. These need to be fine-tuned to provide optimum results [18]. To fine-tune optimization algorithms, one must optimize the combination of hyperparameters that yield the best indicators of their performance. The most commonly used evaluation metric for multi-objective optimization algorithms is the hypervolume [19,20,21].

Pereira et al. [13] evaluated multiple optimization algorithms and benchmarked their hypervolumes for a daylighting and a structural optimization problem. This study established that algorithms that performed worse in one problem performed best in the other. This highlights the need to benchmark multiple algorithms according to their hypervolumes for different building optimization problems.

BPO functions that are outputs of BPS are significantly time-consuming [10,11,22], and when integrating them with the above-mentioned pipeline of activities for a derivative-free MOO problem, it usually renders the process unfeasible. Thus, emerging research in this field has been studying alternatives and approaches that allow us to overcome these barriers.

Algorithmic Design (AD) emerged as a way to solve the portability issue of BPS tools. AD allows practitioners to describe a design project with a single algorithm. With this design process, it is possible to swiftly change parameters or design heuristics and obtain the respective model without effort. Additionally, some AD tools are either capable of supporting BPS tools or exporting models that are able to be read by them. Consequently, with AD, it is possible to integrate BPO to automatically explore a design space, a process often referred to as Algorithmic Design and Analysis (ADA) [23].

The use of ADA constitutes a trade-off, since it allows practitioners to obtain higher portability between their projects’ design, performance analysis, and optimization, at the cost of having to learn programming languages that have a high learning curve [23]. Moreover, ADA does not address the remaining limitations of BPS processes, which still require significant computation time, expertise, and testing to be successfully applied [9,13].

Coincidentally, recent advances in research have been demonstrating the advantages of surrogate models (SM) developed with machine learning (ML) techniques to help practitioners to execute their projects that integrate BPO [24]. SM are capable of predicting a target output after being trained with a database that illustrates its variation according to specific training features. In particular, SM developed with a building database can help to reduce the number of required inputs and features while significantly improving BPS and BPO’s computational times [12,25,26].

The resulting research is intended to support practitioners and stakeholders to make better-informed project decisions in the following ways.

• Tackling portability issues by deploying the developed SM for a widely used BPS tool and a common BPO problem.
• Significantly improving the required computational time to use BPS and BPO.
• Providing SM that are easier to grasp than the respective BPS inputs and do not require as much knowledge and expertise.
• Providing workflows capable of addressing the current limitations regarding the use of BPS tools and BPO.

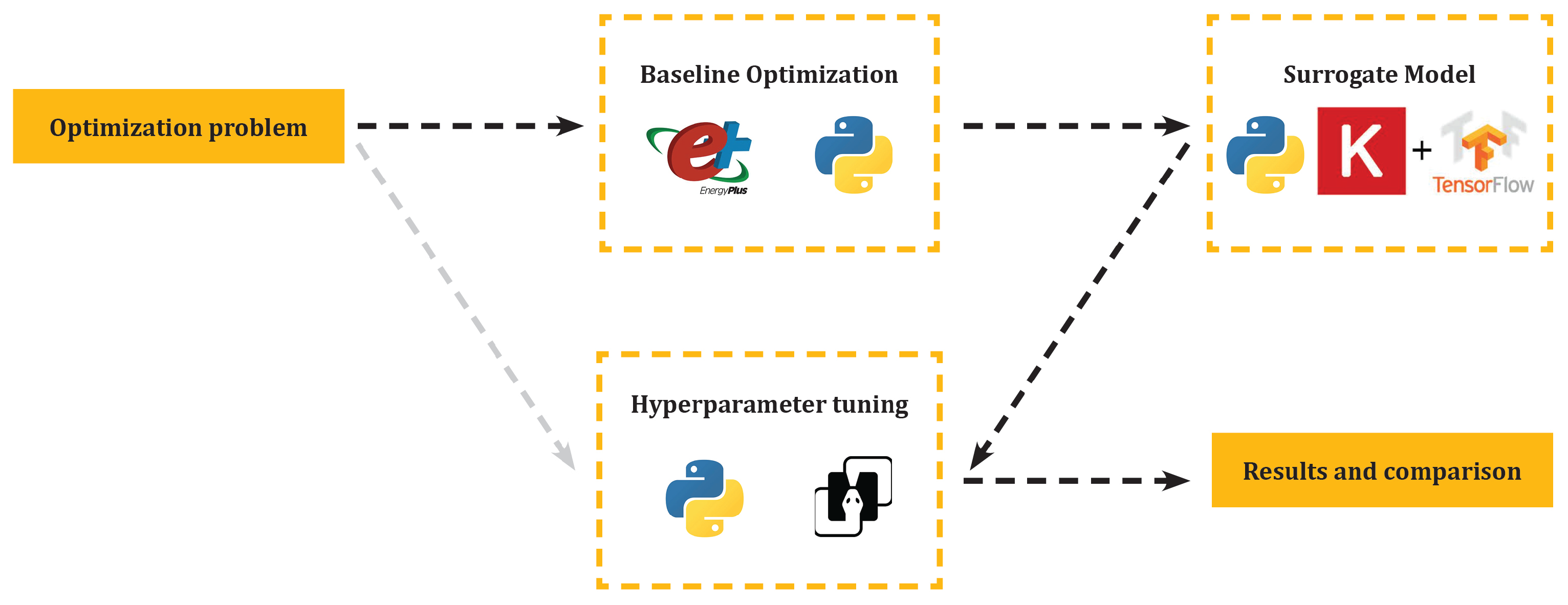
In this sense, this work documents the processes required to perform a standard pipeline of activities for a BPO of time-consuming functions. Initially, an ADA approach is used to integrate a baseline MOO problem with a metaheuristic and a widely used BPS tool. The obtained results are coupled with machine learning techniques and regression algorithms to generate a surrogate model capable of yielding significantly faster simulation results based on the BPO decision variables. With this surrogate model, it is then feasible to fine-tune the metaheuristics hyperparameters, compare their performance for a specific BPO problem, and benchmark their results. This process is applied to a case study of a residential complex construction composed of six buildings in Lisbon, Portugal.

2. Materials and Methods

The methodology for this work can be further subdivided into four sections: baseline optimization, surrogate model, hyperparameter tuning, and results and discussion (Figure 1). In the baseline optimization section, the optimization objectives and decision variables are described, and a simulation-based optimization with EnergyPlus [27] in a Python environment [28] is integrated to compile a training database. This database is used in the surrogate model section to train a convolutional neural network (CNN) with the Keras and TensorFlow packages [29], capable of predicting the total energy use of the 6 buildings and their standard deviations. The CNN layers’ nodes are optimized with a Bayesian optimization using Gaussian processes [30]. In the hyperparameter tuning section, four metaheuristics are selected to be compared. Each algorithm’s hyperparameters are fine-tuned with a Bayesian optimization as well. Finally, the metaheuristics are compared regarding their performance indicators, and optimization results are discussed for this particular class of BPO problems.

2.1. Baseline Optimization

Our BPO problem is to find the best combination of constructions for each building’s surface type that minimizes the construction cost and total energy use. The case study comprises a standard midrise apartment program from LadybugTools for building operation, usage, and schedules [31] applied to a geometric model of 6 buildings in Lisbon, Portugal, illustrated in Figure 2. LadybugTools integrates the Rhino3D tool with EnergyPlus by translating geometrical representations and weather files into a file folder and format that is readable by EnergyPlus. In this case study, a simulation of each building’s total heating and cooling energy (J) is performed with an ideal air load system for one year with residential occupation schedules (

Table 1. Simulation setting values for the proposed case study.

Simulation Setting	Value
Period	1 year
Timestep	1 timestep per hour
Program and schedules	Midrise apartment
Window-to-wall ratio	0.2
Outputs	Zone Ideal Load Supply Air Total Heating Energy (J)
	Zone Ideal Load Supply Air Total Cooling Energy (J)

).

Each building can have one out of three different constructions for each surface type: exterior walls, interior floors, roofs, and windows. Thus, our optimization problem comprises the walls, roofs, floors, and windows of 6 buildings, with a total of 24 variables with 3 possible constructions each (

Table 2. Materials for each surface type construction solution.

Construction Type	Total Area ${\mathbf{m}}^2$	x	Cost [€/m${}^2$]	Materials
Walls	8699.94	0	20	Plaster—2 cm
				Bored brick—11 cm
				Air gap—6 cm
				Bored brick—11 cm
				Stucco—1.5 cm
		1	25	Plaster—2 cm
				Bored brick—15 cm
				Air gap—6 cm
				Bored brick—11 cm
				Stucco—1.5 cm
		2	35	Plaster—2 cm
				Bored brick—11 cm
				Air gap—6 cm
				XPS—4 cm
				Bored brick—11 cm
				Stucco—1.5 cm
Interior floors	9327.27	0	10	Wood panels—12 cm
				Stucco—1.5 cm
		1	25	Ceramics—1 cm
				Screed—8 cm
				Lightweight slab—15 cm
				Stucco—1.5 cm
		2	30	Ceramics—1 cm
				Screed—8 cm
				Concrete slab—15 cm
				Stucco—1.5 cm
Roofs	1216.67	0	20	Screed—8 cm
				Waterproofing—0.2 cm
				Screed—8 cm
				Lightweight slab—15 cm
				Stucco—1.5 cm
		1	30	Screed—8 cm
				Waterproofing—0.2 cm
				XPS—4 cm
				Screed—8 cm
				Lightweight slab—15 cm
				Stucco—1.5 cm
		2	35	Screed—8 cm
				Waterproofing—0.2 cm
				XPS—4 cm
				Screed—8 cm
				Concrete slab—15 cm
				Stucco—1.5 cm
				$\mathbf{U}[\mathbf{W}/{\mathbf{m}}^{\mathbf{2}}\mathbf{K}]$	${\mathbf{\tau }}_{\mathbf{sol}}$	${\mathbf{\tau }}_{\mathbf{vis}}$
Windows	2174.98	0	50	2.69	0.75	0.80
		1	80	1.70	0.38	0.70
		2	100	1.25	0.20	0.70

). The opaque materials’ properties are represented from their outermost layer to their innermost, and the window materials are defined using a simple glazing system definition with the window U-value, solar (${\tau }_{sol}$), and visible transmittance (${\tau }_{vis}$). Each simulation takes ≈25 (s).

The optimization variables and goals are described in Equations (1) to (4). $E_n$ (Equation (1)) represents the total energy use of building n, $f_1$ (Equation (2)) is the total energy use of all buildings, $f_2$ (3) is the standard deviation of the building sample, and $f_3$ (4) is the total cost of construction. The BPO problem objectives are to minimize these functions to guarantee the minimum total energy use ($f_1$), the best fairness of performance among buildings ($f_2$), and minimum costs ($f_3$). The Non-Dominated Sorting Genetic Algorithm II (NSGAII) [32] was the chosen algorithm to run for 1000 iterations.

$$E_n(x_0,\dots ,x_{n\times 4})={Heating}_n+{Cooling}_n\mathrm{kW}\mathrm{h}/{\mathrm{m}}^2$$

(1)

$$f_1\left(x_0,\dots ,x_{n\times 4}\right)=\sum E_n(x_0,\dots ,x_{n\times 4})\mathrm{kW}\mathrm{h}/{\mathrm{m}}^2$$

(2)

$$f_2\left(x_0,\dots ,x_{n\times 4}\right)=\sigma \left(E_n(x_0,\dots ,x_{n\times 4})\right)\mathrm{kW}\mathrm{h}/{\mathrm{m}}^2$$

(3)

$$f_3\left(x_0,\dots ,x_{n\times 4}\right)=Cost(x_0,\dots ,x_{n\times 4})€$$

(4)

$$\begin{array}{c}x\in \{0,1,2\}—Numberofconstructiontypes\\ n=Numberofbuildings\end{array}$$

2.2. Surrogate Model

The SM was developed using the simulation-based optimization data as a training set. Afterward, the data were split into a train and test set with a ratio of 67/33, and the variables were used to train a sequential neural network with 1 dense layer, 4 convolutional layers, and 1 dense output layer. To optimize the layers’ filters (number of nodes), a Bayesian optimization using Gaussian processes with 100 iterations was integrated to maximize the CNN coefficient of variation ($R^2$ score) between the test set results and the model predictions (Equation (5)). Finally, this process was employed to train two CNN models that predicted $f_1$ and $f_2$ (Equations (2) and (3)), with an early stopping callback to avoid over-fitting. The optimized CNN structure’s final $R^2$ score and Root Mean Squared Error (RMSE) are documented in

Table 3. Optimum convolutional neural network structure and performance for surrogate model of Equation (2).

Layer (Type)	Filters	Kernel Size
Dense	300	1
1D-Convolutional	157	2
1D-Convolutional	6	2
1D-Convolutional	290	2
1D-Convolutional	70	1
Dense	1	1
R${}^{\mathbf{2}}$ score	0.96
RMSE (kWh/m${}^{\mathbf{2}}$)	0.54

and

Table 4. Optimum convolutional neural network structure and performance for a surrogate model of Equation (3).

Layer (Type)	Filters	Kernel Size
Dense	300	1
1D-Convolutional	300	2
1D-Convolutional	300	2
1D-Convolutional	6	2
1D-Convolutional	100	1
Dense	1	1
R${}^{\mathbf{2}}$ score	0.97
RMSE (kWh/m${}^{\mathbf{2}}$)	0.01

. The SM obtained an $R^2$ score of 0.96 and 0.97, and an RMSE of 0.54 and 0.01, for $f_1$ and $f_2$, respectively. Additionally, the SM prediction execution time was ≈0.25 (s) for each iteration, which is 100 times faster than the simulation computation time.

$$f_4\left(i_0,\dots ,i_n\right)=R^2\left(test,predictions\right)$$

(5)

$$\begin{array}{c}i\in [6,300]—Numberoffilters\\ n=Numberoflayers\end{array}$$

2.3. Hyperparameter Tuning

This section describes the selected metaheuristics and the optimization problem that fine-tunes each algorithm’s hyperparameters. Two evolutionary (EA) and two particle swarm optimization (PSO) algorithms were selected. From the EA class of algorithms, we selected NSGAII and the Indicator-Based Evolutionary Algorithm (IBEA) [33]. From the PSO class, the Speed-Constrained Multi-Objective PSO (SMPSO) [34] and the OMOPSO [35] were selected. The algorithms were run for 500 iterations and, besides each one’s default hyperparameters, a polynomial mutation and an SBX crossover were added [36].

Table 5. Considered hyperparameters and their ranges for all the optimization algorithms.

Algorithm	Iterations	Hyperparameters	Range
NSGAII	500	Population size $P_s$	[30 .. 200]
		SBX crossover S	[0, 1]
		Polynomial mutation $P_m$	[0, 1]
IBEA	500	$P_s$	[30 .. 200]
		S	[0, 1]
		$P_m$	[0, 1]
SMPSO	500	Swarm size $S_s$	[30 .. 200]
		Leader size $L_s$	[30 .. 200]
		Max iterations i	[30 .. 200]
		S	[0, 1]
		$P_m$	[0, 1]
OMOPSO	500	$S_s$	[30 .. 200]
		$L_s$	[30 .. 200]
		i	[30 .. 200]
		S	[0, 1]
		$P_m$	[0, 1]
		Epsilon $ϵ$	[0.0001, 1]

documents each algorithm’s considered hyperparameters.

To evaluate an optimization model’s performance for MOO, most performance metrics are calculated regarding the optimum solutions found by the algorithm. These solutions are called non-dominated solutions. They represent solutions that cannot improve more in one objective, without harming the other/s [37]. In this case study, the problem’s non-dominated solutions illustrate the trade-offs between the total energy use of the buildings ($f_1$), the fairness of performance among buildings ($f_2$), and the cost of construction ($f_3$) (Equations (2) to (4)). Thus, an algorithm that explores the largest solution space tends to perform better for this particular problem. To measure this, the hypervolume of each algorithm’s non-dominated solutions is calculated as a means of describing the area/volume of the solutions obtained in a ratio of a specific boundary domain [19,20]. In this case, our boundary domain represents the highest and lowest possible thresholds for the minimum total energy use ($f_1$), standard deviation ($f_2$), and costs of construction ($f_3$).

The fine-tuning of the algorithms’ hyperparameters can be described as a single objective optimization problem to find the combination of parameters that yields the maximum hypervolume in $f_{NSGAII}$, $f_{IBEA}$, $f_{SMPSO}$, and $f_{OMOPSO}$ (Equations (6) to (9)). Thus, a Bayesian optimization with 100 iterations is integrated to find the best combination of hyperparameters for each algorithm’s settings.

$$f_{NSGAII}\left(P_s,S,P_m\right)=H(f_1,f_2,f_3)$$

(6)

$$f_{IBEA}\left(P_s,S,P_m\right)=H(f_1,f_2,f_3)$$

(7)

$$f_{SMPSO}\left(S_s,L_{s}i,S,P_m\right)=H(f_1,f_2,f_3)$$

(8)

$$f_{OMOPSO}\left(S_s,L_{s}i,S,P_m,\epsilon \right)=H(f_1,f_2,f_3)$$

(9)

$$\begin{array}{c}H—Hypervolume;\\ BoundariesforHcalculation:\\ f_1\in \left[30,60\right]\text{-}\mathrm{kW}\mathrm{h}/{\mathrm{m}}^2\\ f_2\in \left[0.25,0.50\right]\text{-}\mathrm{kW}\mathrm{h}/{\mathrm{m}}^2\\ f_3\in \left[\mathrm{400,000},\mathrm{900,000}\right]\text{-}€\end{array}$$

3. Results and Discussion

After the optimizations with the fine-tuned metaheuristics, the algorithms’ non-dominated solutions are calculated and plotted according to the results of each objective. Afterward, the algorithms’ hypervolumes are compared and the best-performing algorithm is selected for the final optimization process. Results are presented and discussed.

3.1. Results

The solution space explored by each algorithm is illustrated in Figure 3. It is visible that the algorithms obtained different results regarding the exploration of the objective space. SMPSO and OMOPSO explored a wider range of values, while IBEA focused more on one area of the solution space. NSGAII explored an acceptable area but failed to find solutions with higher total energy use ($f_1$, Equation (2)), a lower standard deviation ($f_2$, Equation (3)), and lower construction costs ($f_3$, Equation (4)), in contrast to the PSO algorithms. In total, the algorithms explored a solution space with values of $f_1$ between ≈45 and ≈55 kWh/m${}^2$, $f_2$ between ≈0.30 and ≈0.40 kWh/m${}^2$, and $f_3$ between ≈400,000 and ≈600,000 €.

Table 6. Optimum metaheuristics hyperparameters and respective hypervolumes.

	Hyperparameter	Value	Hypervolume
NSGAII	$P_s$	30	0.53
	S	1
	$P_m$	0.59
IBEA	$P_s$	32	0.54
	S	0.66
	$P_m$	1
SMPSO	$S_s$	68	0.52
	$L_s$	59
	i	67
	S	0.43
	$P_m$	0.35
OMOPSO	$S_s$	30	0.52
	$L_s$	200
	i	200
	S	1
	$P_m$	0
	$ϵ$	0.001

documents the algorithms’ hypervolumes for the optimum values of their hyperparameters. The IBEA algorithm ($f_{IBEA}$, Equation (7)) obtained the best hypervolume of 0.54, followed by NSGAII, with 0.53 ($f_{NSGAII}$, Equation (6)), and SMPSO and OMOPSO, with 0.52 ($f_{SMPSO}$ and $f_{OMOPSO}$ Equations (8) and (9)). Additionally, it is visible in Figure 3 that IBEA obtained the higher hypervolume because it focused on a specific area, not because it explored the largest solution space. Thus, IBEA successfully found better optimum solutions but ultimately failed in the exploration of the solution space and its inherent trade-offs between the buildings’ energy usage, standard deviation, and cost of construction. For these reasons, the NSGAII algorithm, which obtained the highest hypervolume and explored a balanced solution space, was chosen to perform the final optimization.

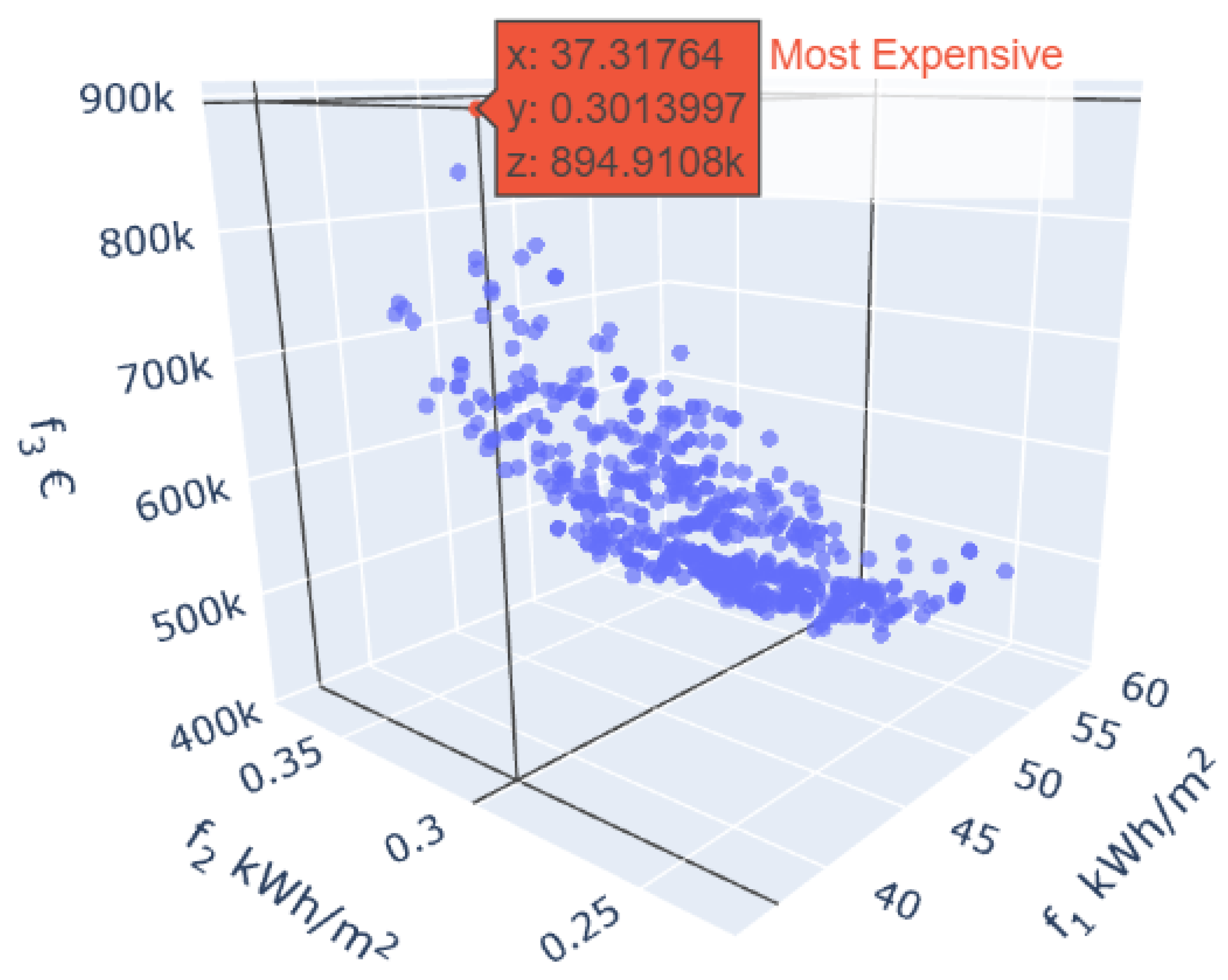
The NSGAII algorithm was run with the optimum hyperparameters found for 10,000 iterations and the non-dominated solutions found were simulated to validate the surrogate model predictions. Results show a hypervolume of 0.60, which is significantly larger when compared with the values obtained for the 500 iterations in Table 6. Additionally, Figure 4 shows that the algorithm explored values between 40 and 60 kWh/m${}^2$, 0.2 and 0.5 kWh/m${}^2$, and 400,000 and 900,000 €. With these results, it is possible to discern the existing trade-offs between energy consumption, fairness of performance among buildings, and the total cost of construction. Moreover, assuming that this construction has a fixed budget, it is possible to find the best available solution with a minimum $f_1$ and $f_2$. Finally, Figure 4 also shows how a solution with the most expensive construction for all surfaces is not necessarily the best solution, with the algorithm finding a significant number of cheaper solutions with lower $f_1$ and $f_2$, which can allow savings of up to 22% (200,000 €) on the total cost of construction while maintaining the same performance ($f_1$) and fairness of performance among buildings ($f_2$).

3.2. Discussion

The use of SM to estimate building energy use speeds up a building simulation process exponentially. Additionally, SM can be deployed in a single platform (e.g., web applications, programming environments, mobile applications, among others), and because they use only optimization problem variables as inputs, they reduce the simulation complexity and provide a more accessible analysis to users with any expertise level. As an example, the optimization process performed in this study can be integrated into a web application where the user specifies variables and costs and performs the optimization with the selected algorithm. Afterward, the algorithm’s hypervolume is calculated and a figure illustrates the obtained optimum solutions.

The comparison of the optimization algorithms shows that, for this particular BPO problem, different algorithms explored different solution spaces. These can be more or less suitable for the practitioner’s decision-making goals. Additionally, they show that the algorithm with the highest hypervolume obtained the best solutions, but did not explore the desired solution space. In particular, the PSO algorithms excelled in exploring a wide solution space, the IBEA algorithm obtained the highest hypervolume and best solution, and NSGAII showed an even balance between the hypervolume and solution space.

The comparison of the four MOO algorithms’ hypervolumes (Table 6) and solution spaces (Figure 3) provided a confident selection of the most suitable algorithm for the proposed optimization problem, with results that allowed us to save up to 22% of the total construction cost while maintaining acceptable energy performance. In the future, an extensive comparison of optimization algorithms for different aspects of building performance can provide a comprehensive foundation regarding the algorithms’ performance for different building performance optimization problems.

4. Conclusions

Most building and urban optimization problems typically have objectives that are outputs of analysis and simulation tools. These tools are prone to errors, take significant time to yield results, and lack model portability among tools (different building models must be developed for each tool). Because of this, it is often unfeasible to perform a correct optimization process. This work integrates a surrogate model approach in the optimization structure that allows us to perform a standard pipeline of activities for the optimization of a time-consuming function in an acceptable timeframe. This approach is illustrated with the optimization of a six-building residential complex in Lisbon, Portugal.

The optimization problem is described as the best combination of construction materials that yield the minimum annual total energy use, construction cost, and standard deviation (to guarantee the fairness of performance among buildings). Four different optimization algorithms were compared and NSGAII was selected to perform the optimization. Results of this case study show that adjusting building materials with this approach can result in savings of up to 22% in the construction cost, while showing the minimum energy use and standard deviation. The processes required for the optimization are integrated with a surrogate model developed with a convolutional neural network, with $R^2$ scores of ≈0.96 in the prediction of the simulation results, and being 100 times faster than a simulation.

Surrogate models are efficient in not only reducing the time taken for simulations to run but also in reducing the number of input features required to obtain results. Additionally, they are portable and can be deployed easily within a single platform. In spite of this methodology focusing on a particular problem, research shows that these approaches are efficient and can be applicable transversely to other time-consuming optimization problems within the building performance realm, such as computational fluid dynamics, agent-based modeling, daylighting, and structural analysis, among others. By developing and deploying multiple surrogate models that predict aspects of building performance, it is possible to obtain a broader understanding of a building’s performance and tackle portability issues associated with the use of multiple simulation tools.

Future work must focus on (1) the benchmarking of specific algorithms for optimization problems, and (2) the development of end-user interfaces with automated optimization and surrogate model development. In (1), multiple algorithms must be extensively compared regarding their hypervolumes and solution spaces for optimization problems that encompass different building performance aspects. In (2), the surrogate model development and optimization must be automated according to the benchmarked algorithms and problems, while a user defines the variables and objectives. These studies are extremely relevant in order to bridge the existing gap between practitioners and building performance analysis and optimization processes such as the one portrayed in this study.