MODELING of Rarefied Gas Flows Inside a Micro-Nozzle Based on the DSMC Method Coupled with a Modified Gas–Surface Interaction Model
Abstract
1. Introduction
2. Mathematical Models
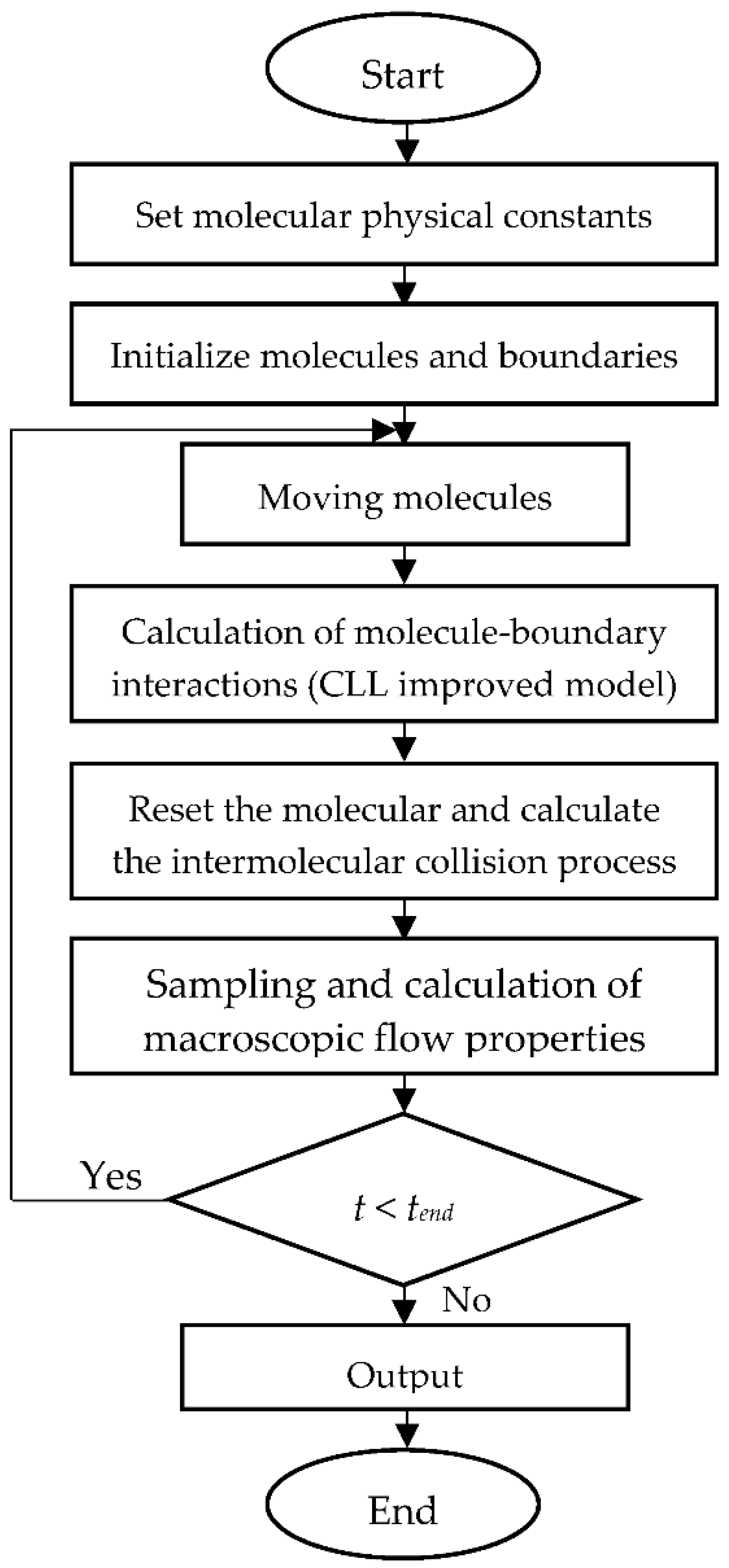
2.1. Molecular Collision Model
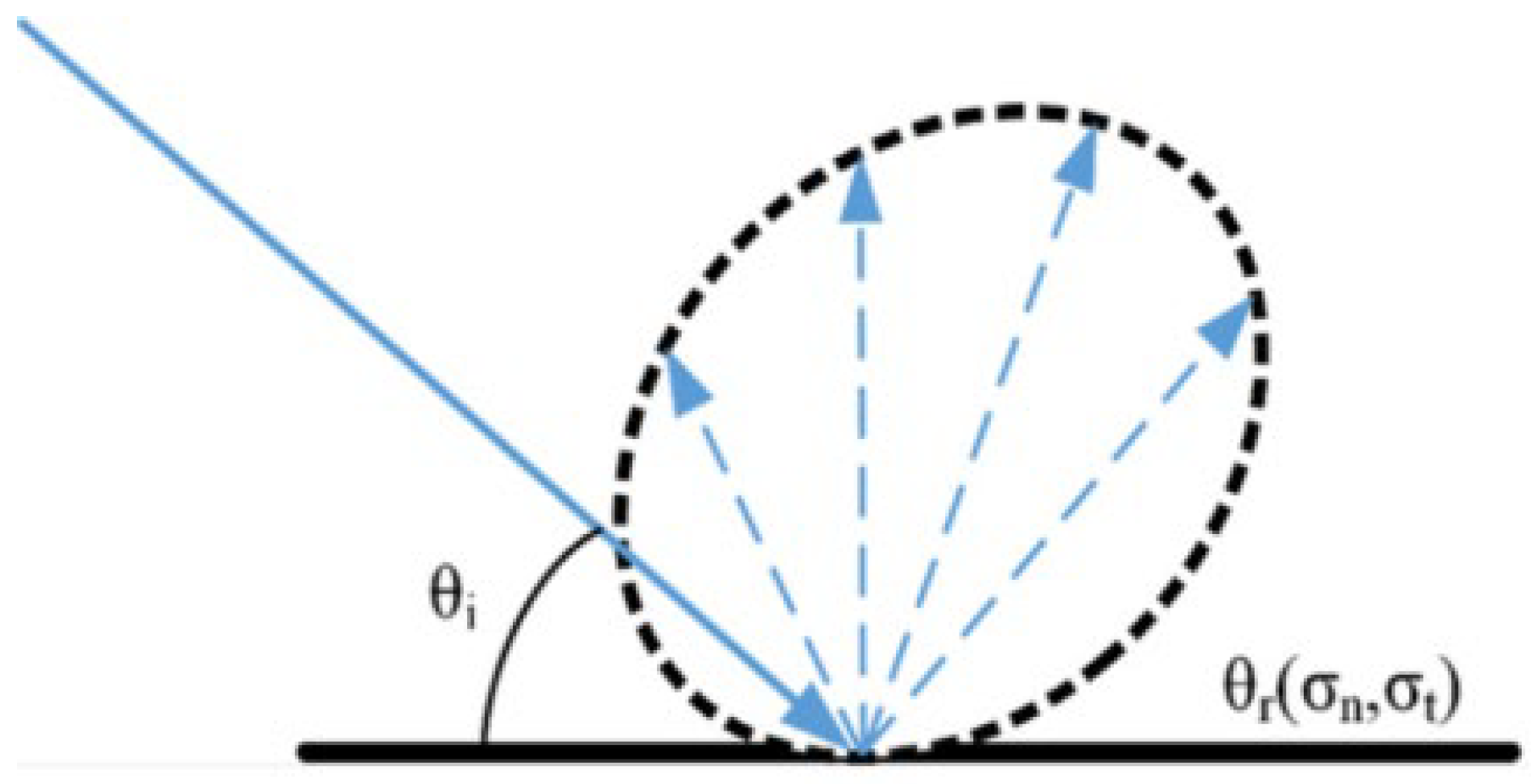
2.2. Cercignanie–Lampise–Lord (CLL) Gas–Surface Interaction Model
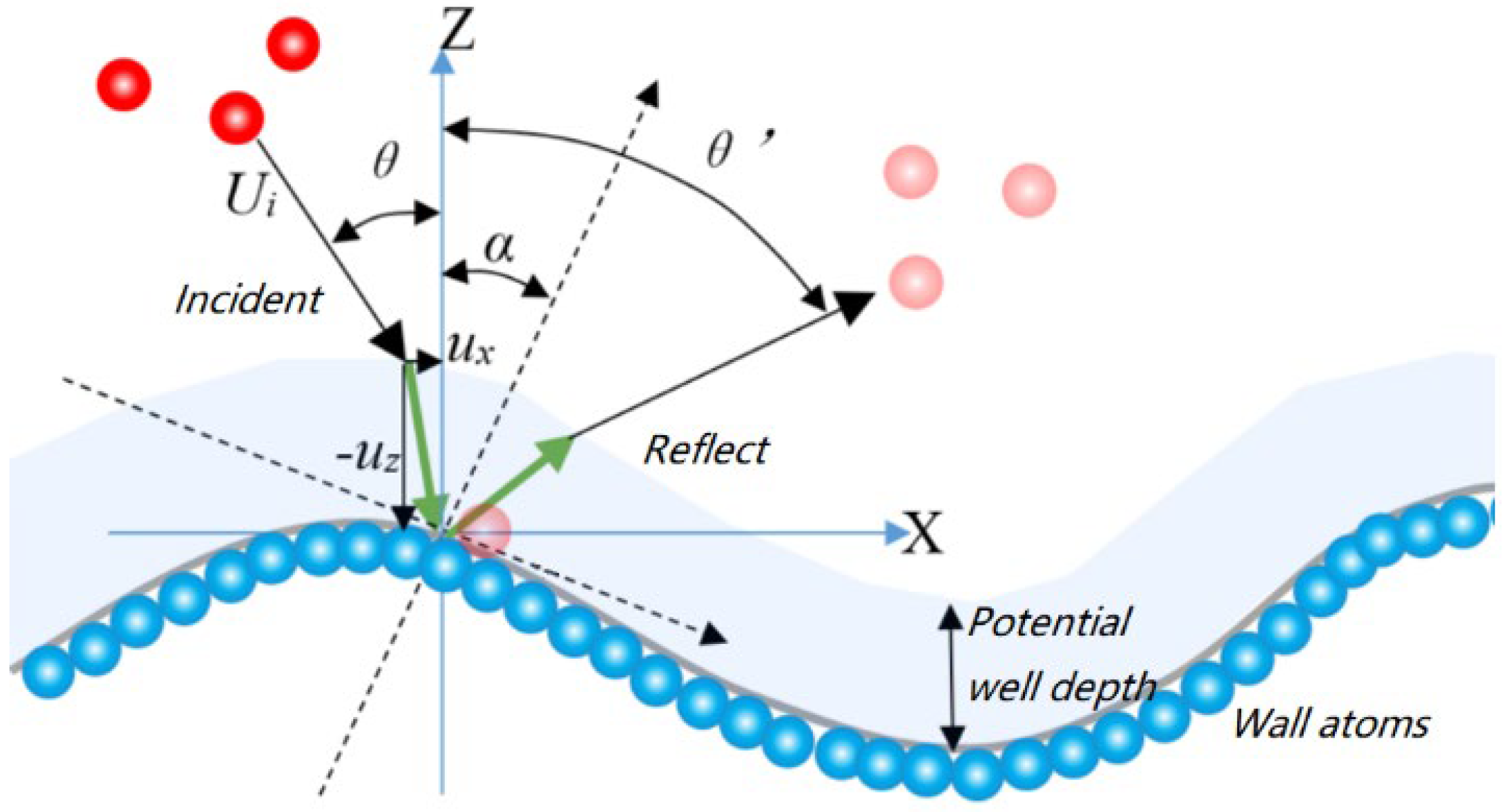
2.3. Modified CLL Gas–Surface Interaction Model
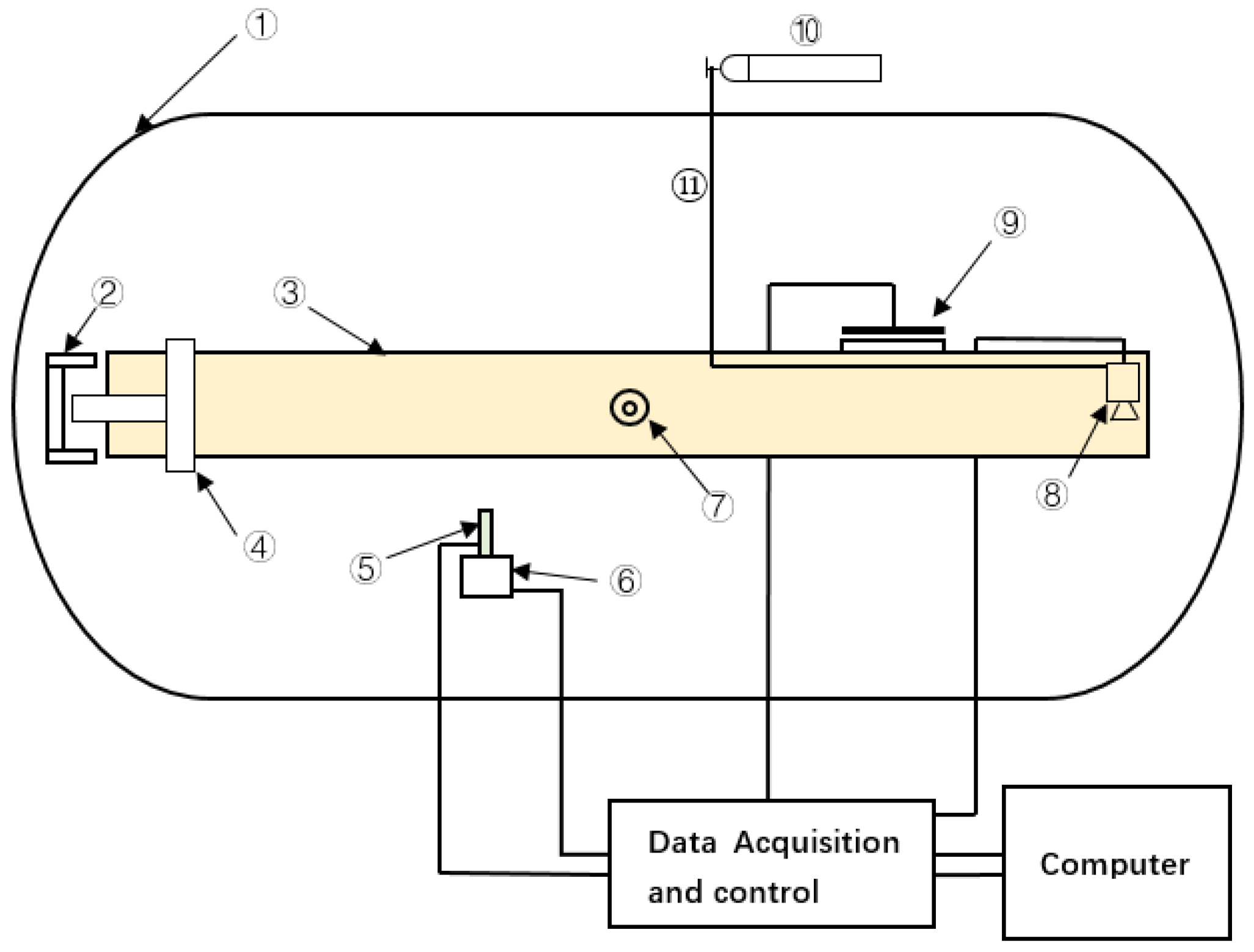
3. Experiment Setup
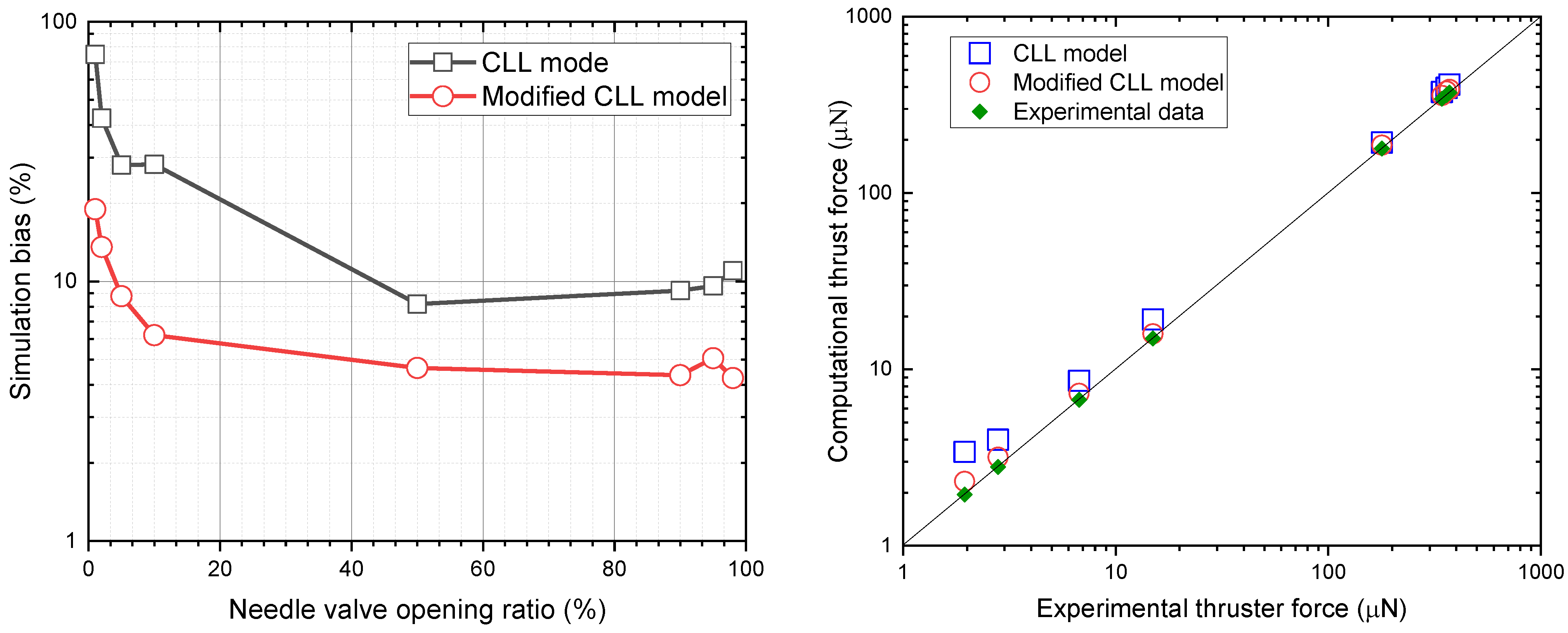
4. Model Validation
5. Results and Discussion
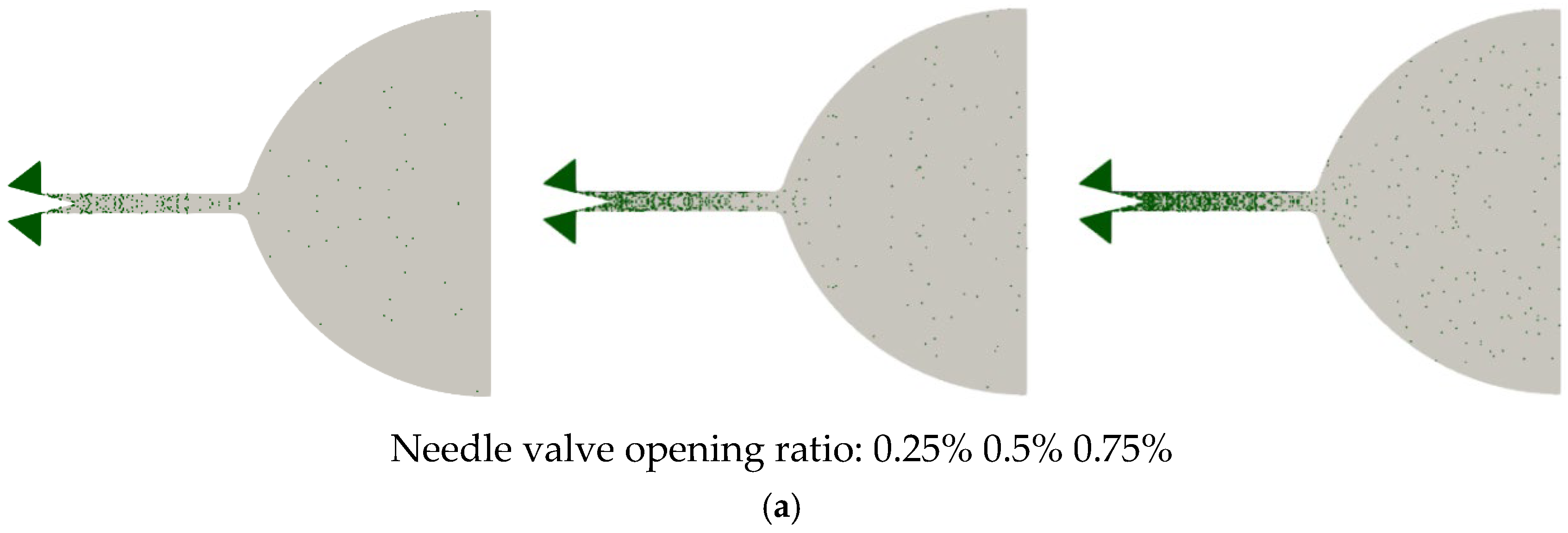
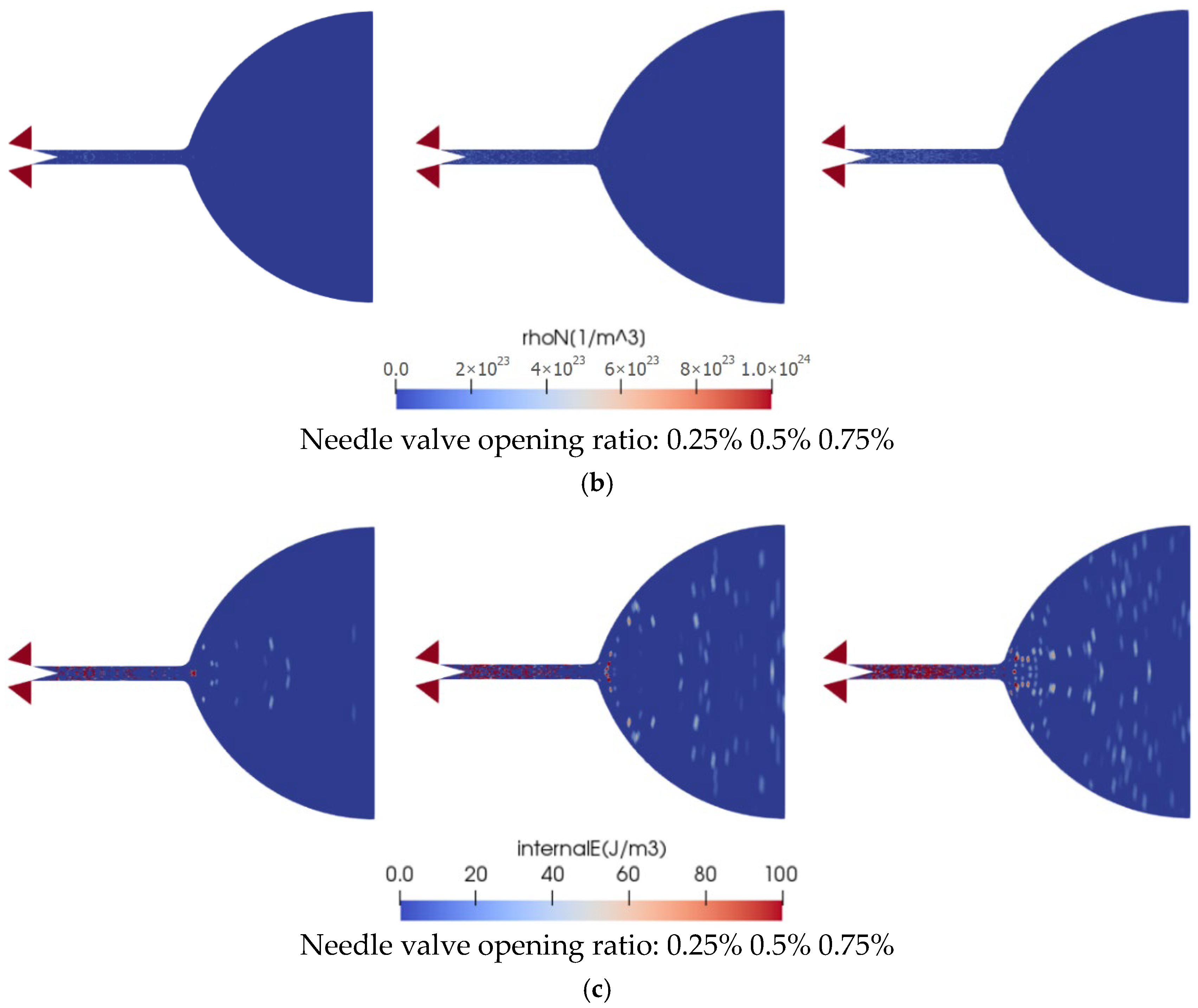
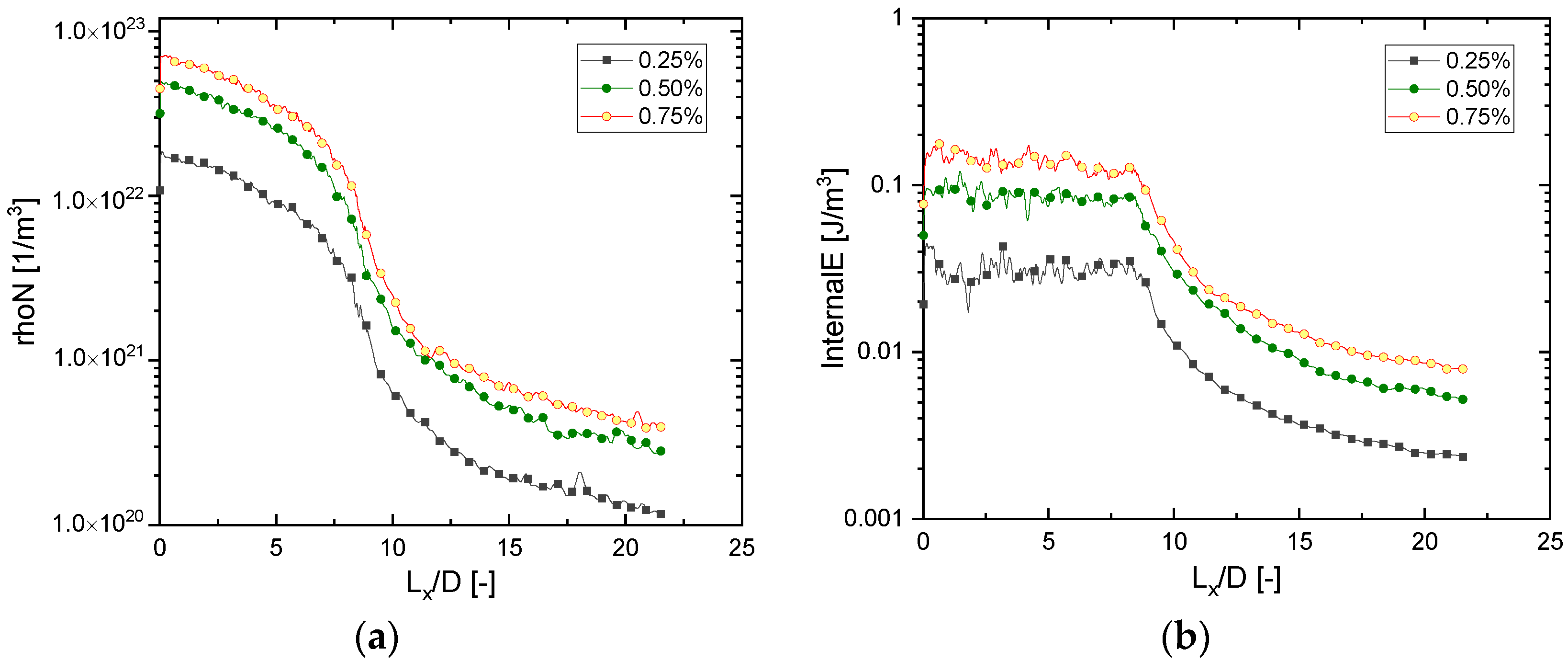
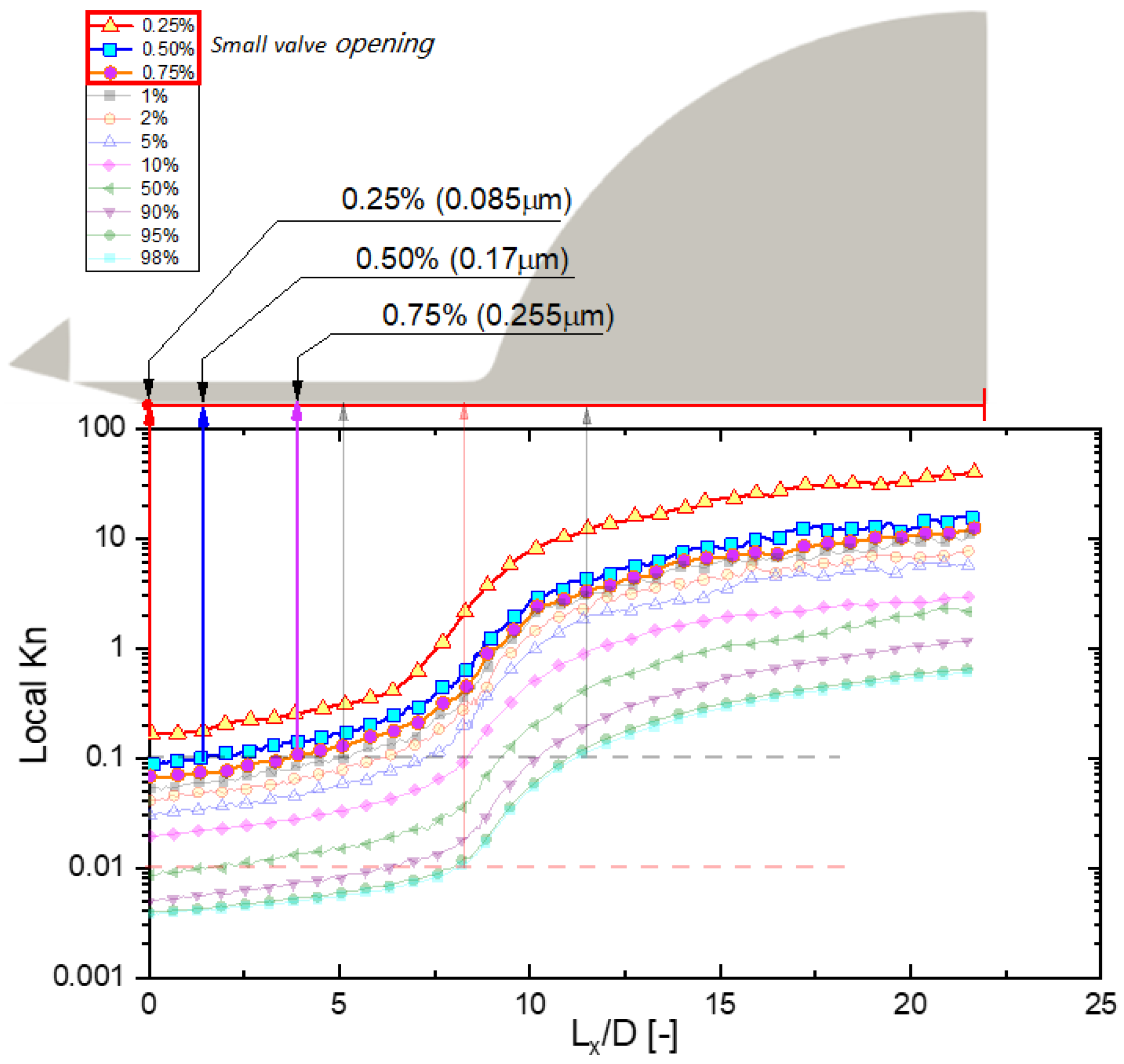
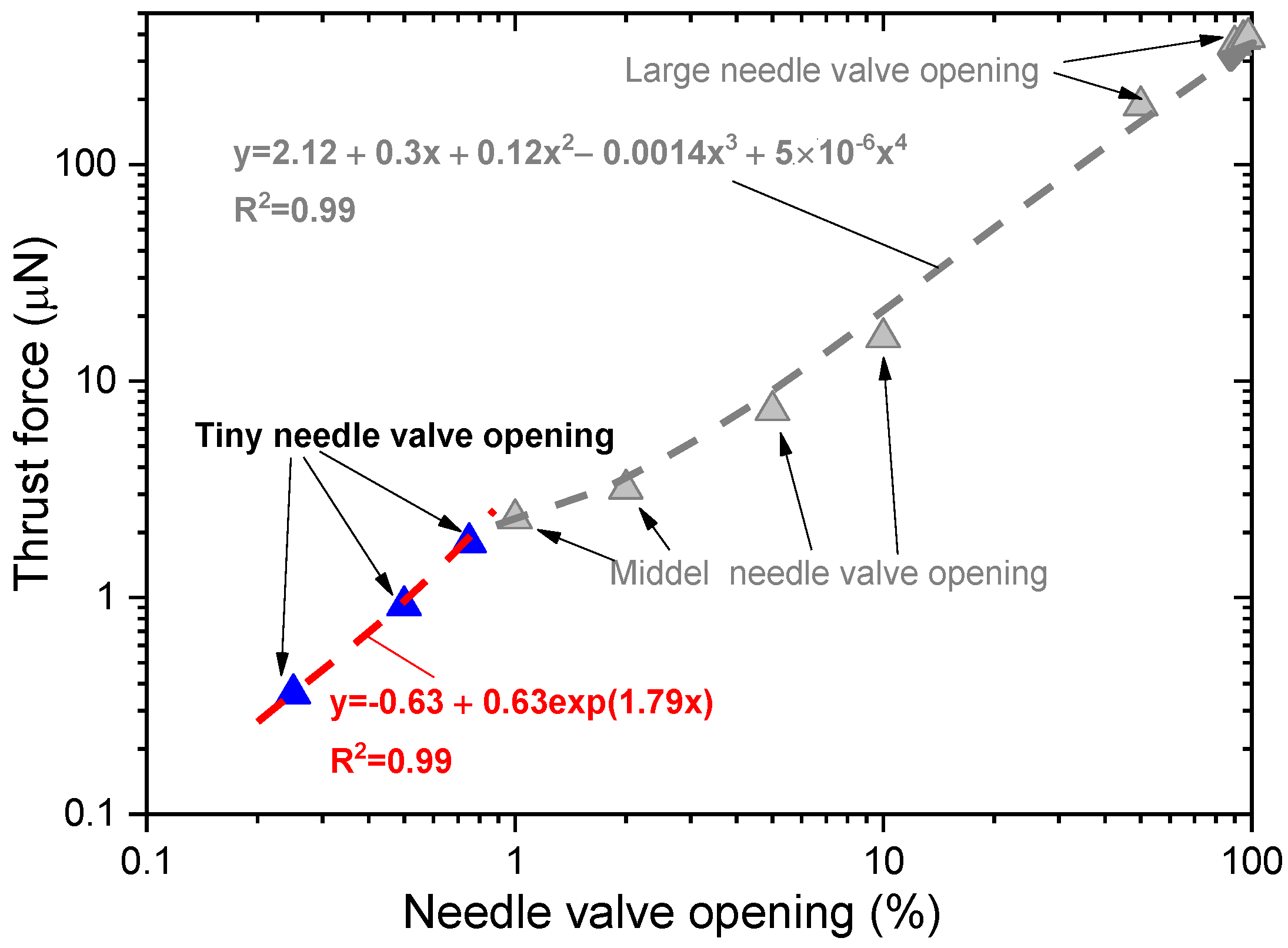
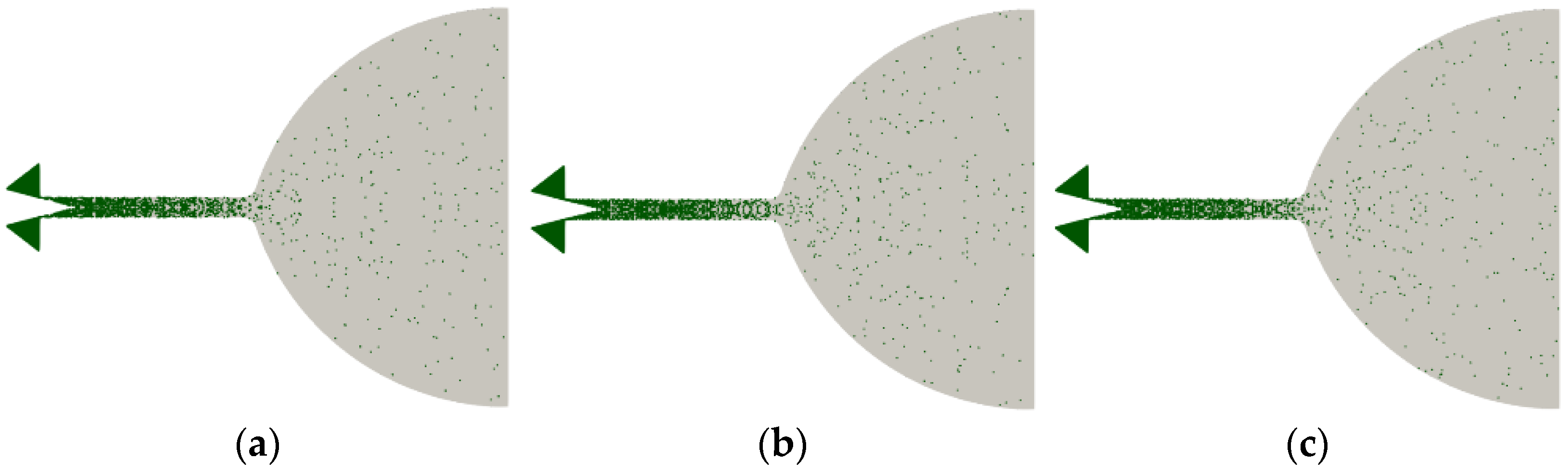
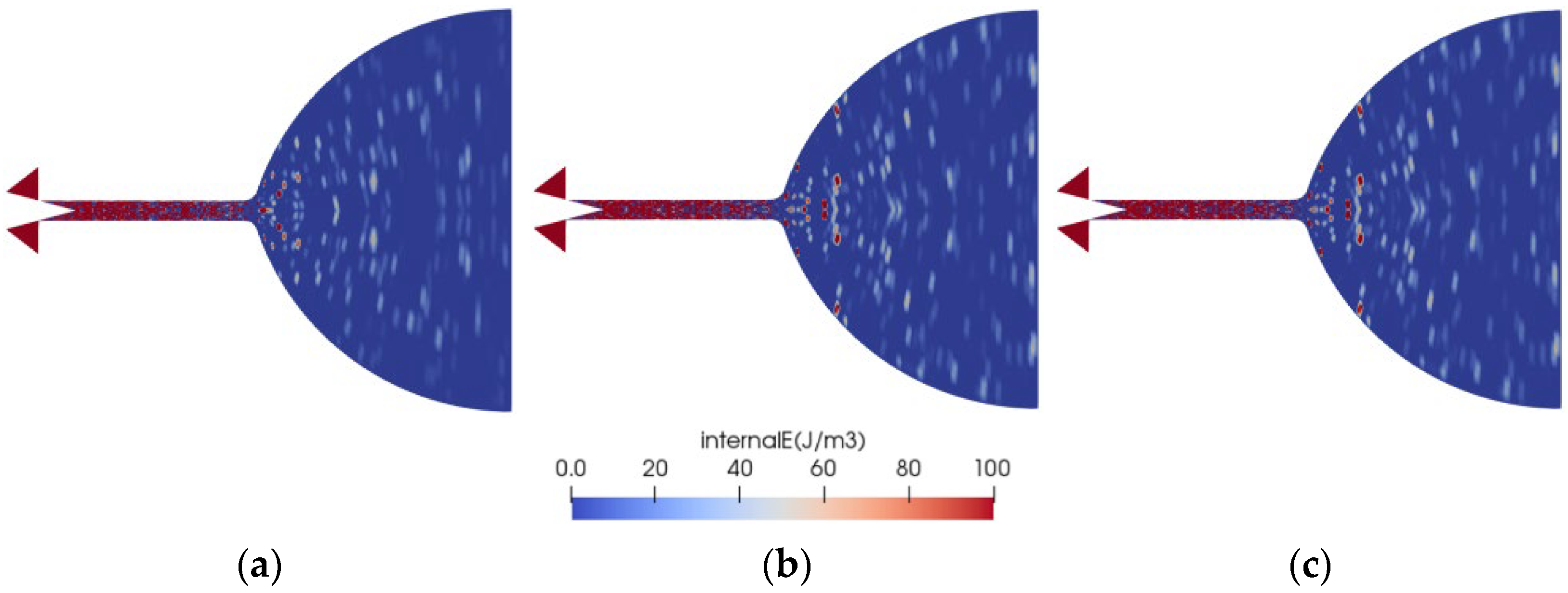
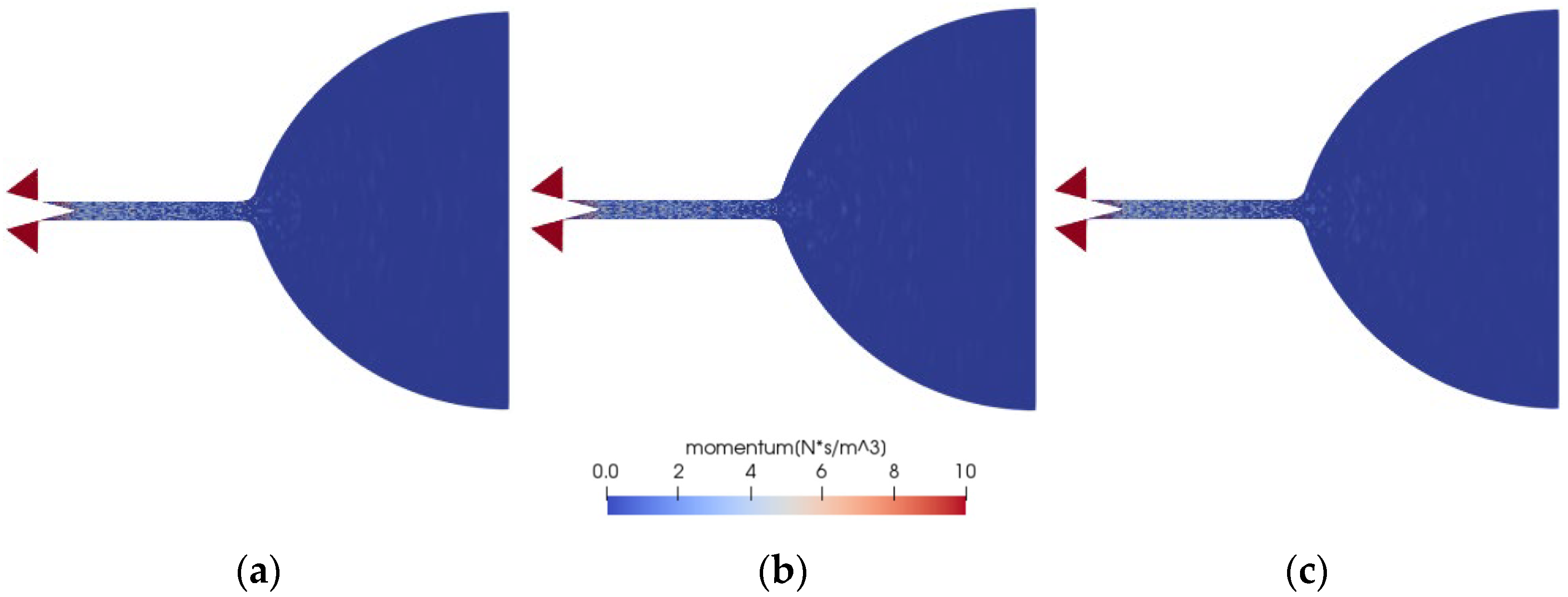
5.1. Flow Characteristics at a Gas Temperature of 300 K and a Needle Valve Opening of Less Than 1%
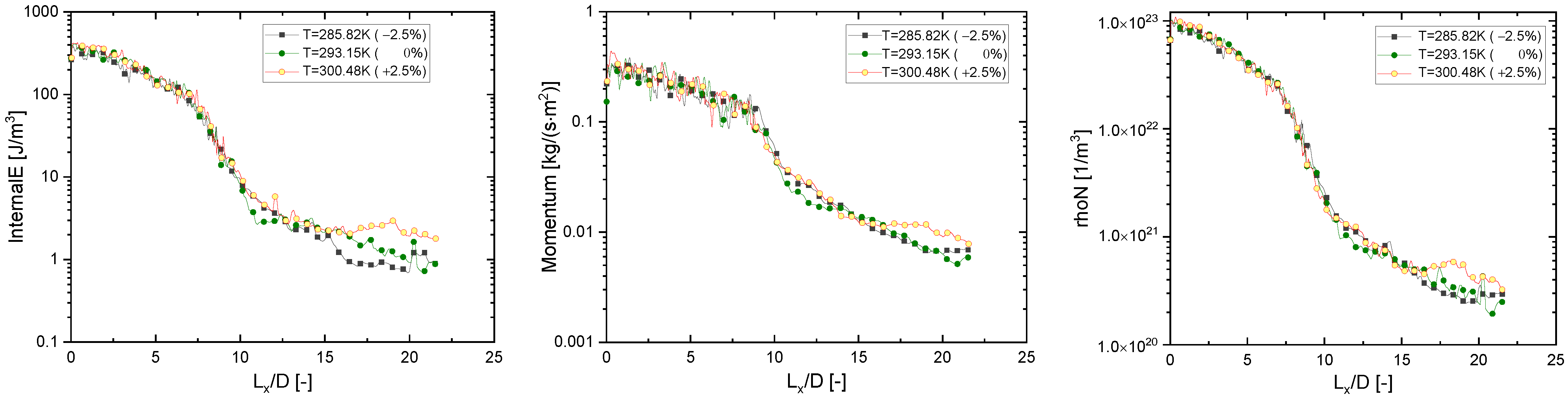
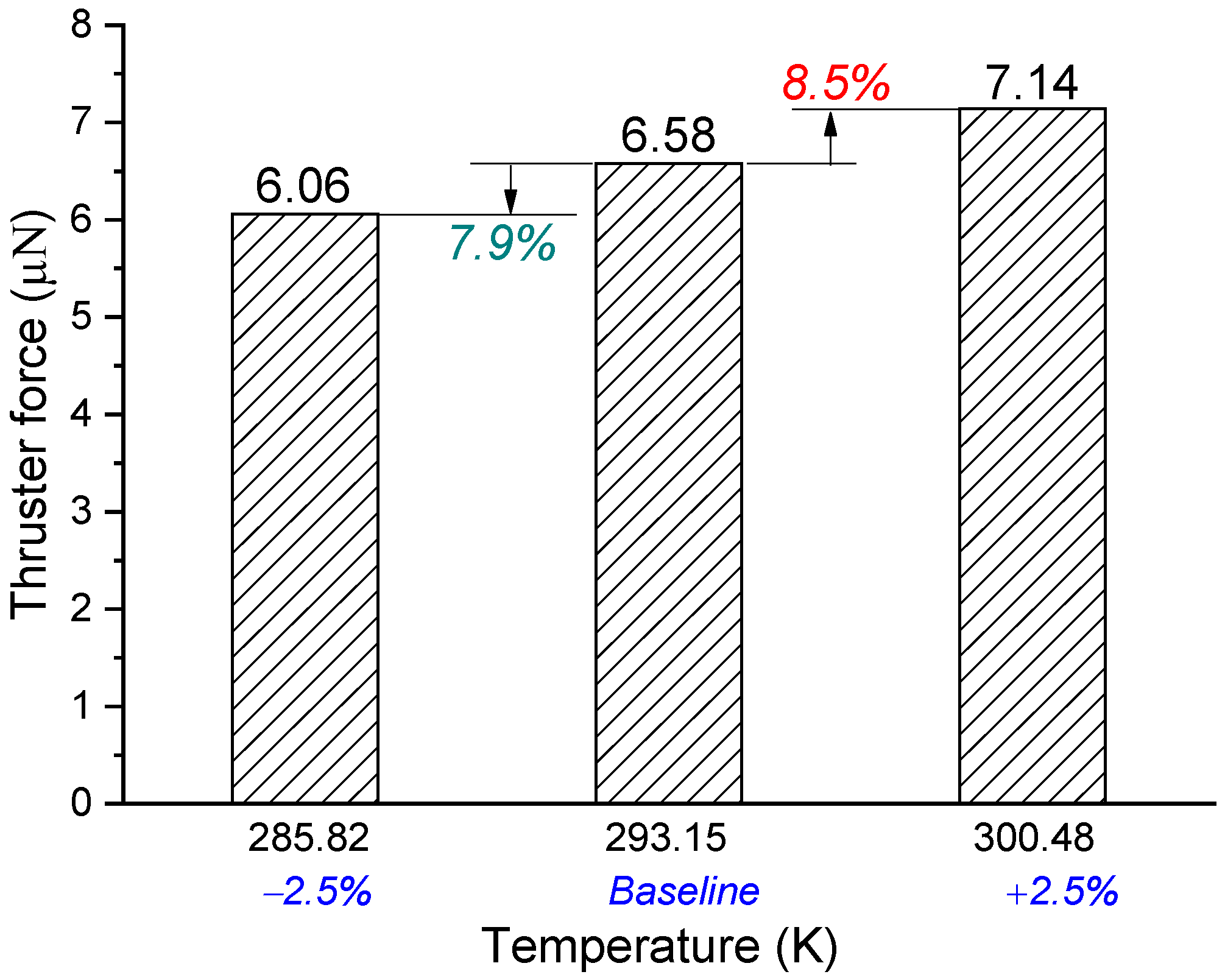
5.2. Effect of Gas Temperature on Flow Characteristics
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Niu, X.; Zeng, M.; Wang, S.; Cui, K.; Yu, D. Review of micro propulsion technology for space gravitational waves detection. Acta Astronaut. 2022, 193, 496–510. [Google Scholar] [CrossRef]
- Hitt, D.L.; Zakrzwski, C.M.; Thomas, M.A. MEMS-based satellite micropropulsion via catalyzed hydrogen peroxide decomposition. Smart Mater. Struct. 2001, 10, 1163. [Google Scholar] [CrossRef]
- Luo, J.; Bai, Y.-Z.; Cai, L.; Cao, B.; Chen, W.-M.; Chen, Y.; Cheng, D.-C.; Ding, Y.-W.; Duan, H.-Z.; Gou, X.; et al. The first round result from the TianQin-1 satellite. Class. Quantum Gravity 2020, 37, 185013. [Google Scholar] [CrossRef]
- Bayt, R.L. Analysis, Fabrication and Testing of a MEMS-Based Micropropulsion System; Massachusetts Institute of Technology: Cambridge, MA, USA, 1999. [Google Scholar]
- Merkowitz, S.M.; Maghami, P.G.; Sharma, A.; Willis, W.D.; Zakrzwski, C.M. A μNewton thrust-stand for LISA. Class. Quantum Gravity 2002, 19, 1745. [Google Scholar] [CrossRef]
- Louisos, W.F.; Hitt, D.L. Viscous effects on performance of three-dimensional supersonic micronozzles. J. Spacecr. Rocket. 2012, 49, 51–58. [Google Scholar] [CrossRef]
- Louisos, W.F.; Hitt, D.L. Numerical studies of supersonic flow in bell-shaped micronozzles. J. Spacecr. Rocket. 2014, 51, 491–500. [Google Scholar] [CrossRef]
- Bird, G.A. Molecular gas dynamics. NASA STI/Recon Tech. Rep. A 1976, 76, 40225. [Google Scholar]
- Bird, G.A. Approach to translational equilibrium in a rigid sphere gas. PhyFluids 1963, 6, 1518–1519. [Google Scholar] [CrossRef]
- He, X.; He, B.; Cai, G. Simulation of rocket plume and lunar dust using DSMC method. Acta Astronaut. 2012, 70, 100–111. [Google Scholar] [CrossRef]
- Lee, K.H. Plume simulation of liquid apogee engine for GEO satellite using parallel DSMC method. Comput. Fluids 2020, 208, 104612. [Google Scholar] [CrossRef]
- Rosa, P.; Karayiannis, T.G.; Collins, M.W. Single-phase heat transfer in microchannels: The importance of scaling effects. Appl. Therm. Eng. 2009, 29, 3447–3468. [Google Scholar] [CrossRef]
- Le, N.T.P.; Roohi, E.; Tran, T.N. Comprehensive assessment of newly-developed slip-jump boundary conditions in high-speed rarefied gas flow simulations. Aerosp. Sci. Technol. 2019, 91, 656–668. [Google Scholar] [CrossRef]
- Michalis, V.; Kalarakis, A.; Skouras, E.; Burganos, V.N. Rarefaction effects on gas viscosity in the Knudsen transition regime. Microfluid. Nanofluidics 2010, 9, 847–853. [Google Scholar] [CrossRef]
- Darbandi, M.; Roohi, E. Study of subsonic–supersonic gas flow through micro/nanoscale nozzles using unstructured DSMC solver. Microfluid. Nanofluidics 2011, 10, 321–335. [Google Scholar] [CrossRef]
- Varade, V.; Duryodhan, V.; Agrawal, A.; Pradeep, A.; Ebrahimi, A.; Roohi, E. Low Mach number slip flow through diverging microchannel. Comput. Fluids 2015, 111, 46–61. [Google Scholar] [CrossRef]
- Renksizbulut, M.; Niazmand, H.; Tercan, G. Slip-flow and heat transfer in rectangular microchannels with constant wall temperature. Int. J. Therm. Sci. 2006, 45, 870–881. [Google Scholar] [CrossRef]
- Li, C.; Jia, L.; Zhang, T. The entrance effect on gases flow characteristics in micro-tube. J. Therm. Sci. 2009, 18, 353–357. [Google Scholar] [CrossRef]
- Zhang, T.; Jia, L.; Li, X. Numerical research on entrance effect on internal flow characteristics in micro-scale. Prog. Comput. Fluid Dyn. Int. J. 2009, 9, 67–76. [Google Scholar] [CrossRef]
- Sobhan, C.B.; Garimella, S.V. A comparative analysis of studies on heat transfer and fluid flow in microchannels. Microscale Thermophys. Eng. 2001, 5, 293–311. [Google Scholar] [CrossRef]
- Palm, B. Heat transfer in microchannels. Microscale Thermophys. Eng. 2001, 5, 155–175. [Google Scholar] [CrossRef]
- Lu, H.; Xu, M.; Gong, L.; Duan, X.; Chai, J.C. Effects of surface roughness in microchannel with passive heat transfer enhancement structures. Int. J. Heat Mass Transf. 2020, 148, 119070. [Google Scholar] [CrossRef]
- Shams, M.; Khadem, M.H.; Hossainpour, S. Direct simulation of roughness effects on rarefied and compressible flow at slip flow regime. Int. Commun. Heat Mass Transf. 2009, 36, 88–95. [Google Scholar] [CrossRef]
- Alexeenko, A.; Fedosov, D.; Gimelshein, S.; Levin, D.; Collins, R. Transient heat transfer and gas flow in a MEMS-based thruster. J. Microelectromechanical Syst. 2006, 15, 181–194. [Google Scholar] [CrossRef]
- Hameed, A.H.; Kafafy, R.; Asrar, W.; Idres, M. Two-dimensional flow properties of micronozzle under varied isothermal wall conditions. Int. J. Eng. Syst. Model. Simul. 2013, 5, 174–180. [Google Scholar] [CrossRef]
- Rafi, K.M.M.; Deepu, M.; Rajesh, G. Effect of heat transfer and geometry on micro-thruster performance. Int. J. Therm. Sci. 2019, 146, 106063. [Google Scholar] [CrossRef]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Balaj, M.; Roohi, E.; Akhlaghi, H.; Myong, R.S. Investigation of convective heat transfer through constant wall heat flux micro/nano channels using DSMC. Int. J. Heat Mass Transf. 2014, 71, 633–638. [Google Scholar] [CrossRef]
- Shoja-Sani, A.; Roohi, E.; Kahrom, M.; Stefanov, S. Investigation of aerodynamic characteristics of rarefied flow around NACA 0012 airfoil using DSMC and NS solvers. Eur. J. Mech. B/Fluids 2014, 48, 59–74. [Google Scholar] [CrossRef]
- Bird, G.A. Molecular Gas Dynamics; Clarendon Press: Oxford, UK, 1976. [Google Scholar]
- Ivanov, M.S.; Rogasinsky, S.V. Analysis of numerical techniques of the direct simulation Monte Carlo method in the rarefied gas dynamics. Sov. J. Numer. Anal. Math. Model. 1988, 3, 453–466. [Google Scholar] [CrossRef]
- Goshayeshi, B.; Roohi, E.; Stefanov, S. DSMC simulation of hypersonic flows using an improved SBT-TAS technique. J. Comput. Phys. 2015, 303, 28–44. [Google Scholar] [CrossRef]
- Roohi, E.; Stefanov, S.; Shoja-Sani, A.; Ejraei, H. A generalized form of the Bernoulli Trial collision scheme in DSMC: Derivation and evaluation. J. Comput. Phys. 2018, 354, 476–492. [Google Scholar] [CrossRef]
- Taheri, E.; Roohi, E.; Stefanov, S. A symmetrized and simplified Bernoulli trial collision scheme in direct simulation Monte Carlo. Phys. Fluids 2022, 34, 012010. [Google Scholar] [CrossRef]
- Stefanov, S.; Roohi, E.; Shoja-Sani, A. A novel transient-adaptive subcell algorithm with a hybrid application of different collision techniques in direct simulation Monte Carlo (DSMC). Phys. Fluids 2022, 34, 092003. [Google Scholar] [CrossRef]
- Sazhin, O.V.; Borisov, S.F. Influence of the state of a surface on the formation of a rarefied gas flow in a channel. J. Eng. Phys. Thermophys. 2001, 74, 1232–1238. [Google Scholar] [CrossRef]
- Sharipov, F.; Seleznev, V. Data on internal rarefied gas flows. J. Phys. Chem. Data 1998, 27, 657–706. [Google Scholar] [CrossRef]
- Maxwell, J.C. On stresses on rarefied gases arising from inequalities of temperature. Philos. Trans. R. Soc. Lond. 1965, 170, 231–256. [Google Scholar] [CrossRef]
- Cercignani, C.; Lampis, M. Kinetic models for gas-surface interactions. Transp. Theory Stat. Phys. 1971, 1, 101–114. [Google Scholar] [CrossRef]
- Hurkmans, A.; Overbosch, E.G.; Olander, D.R.; Los, J. The trapping of potassium atoms by a polycrystalline tungsten surface as a function of energy and angle of incidence. Surf. Sci. 1976, 54, 154. [Google Scholar] [CrossRef]
- John, C.T. Washboard model of gas–surface scattering. J. Chem. Phys. 1990, 92, 680. [Google Scholar] [CrossRef]
- He, L.; Ma, W.; Guo, P.; Sheng, T. Developments of attitude determination and control system of microsats: A survey. Proceedings of the Institution of Mechanical Engineers, Part I. J. Syst. Control. Eng. 2021, 235, 1733–1750. [Google Scholar] [CrossRef]



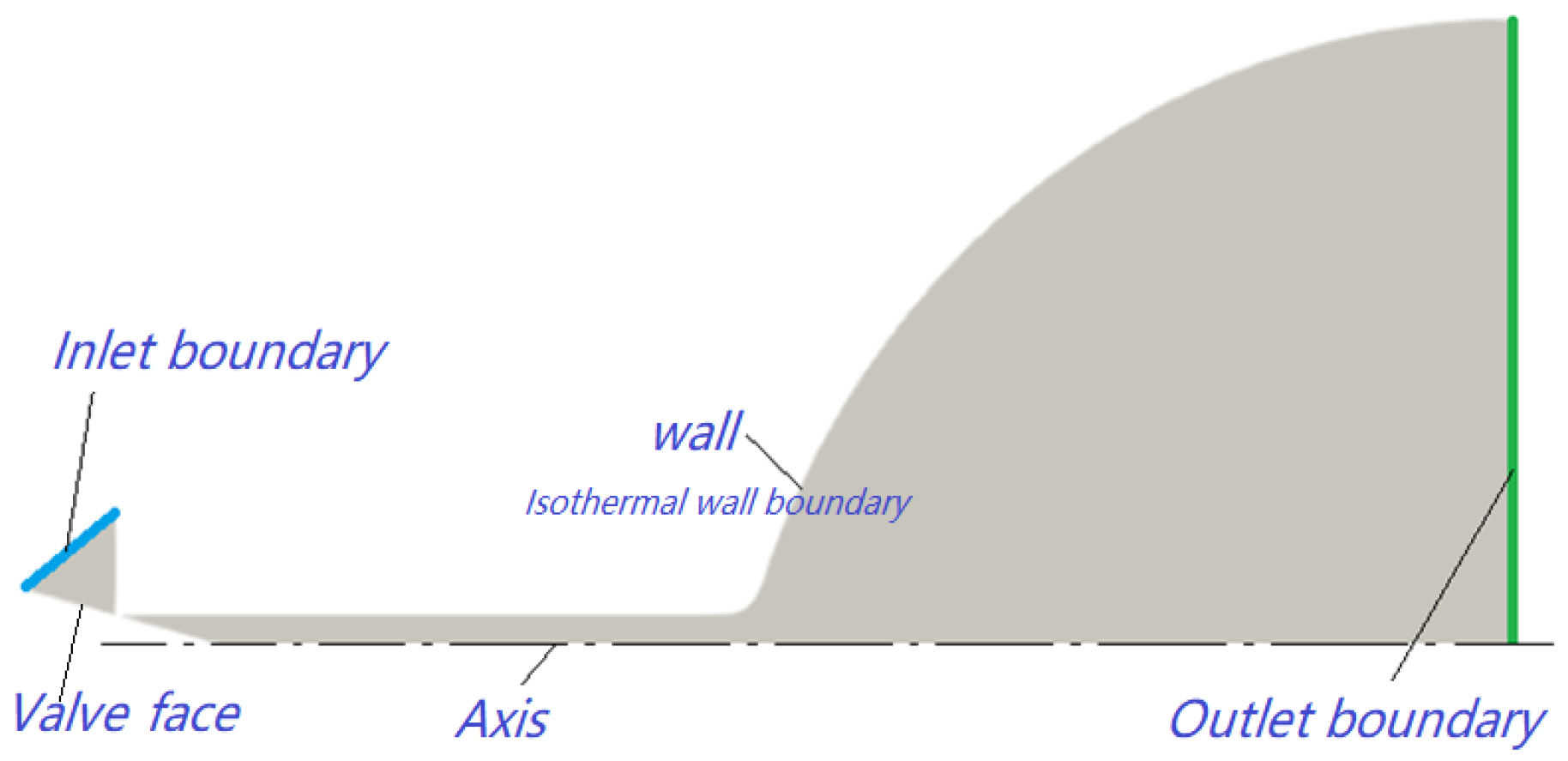

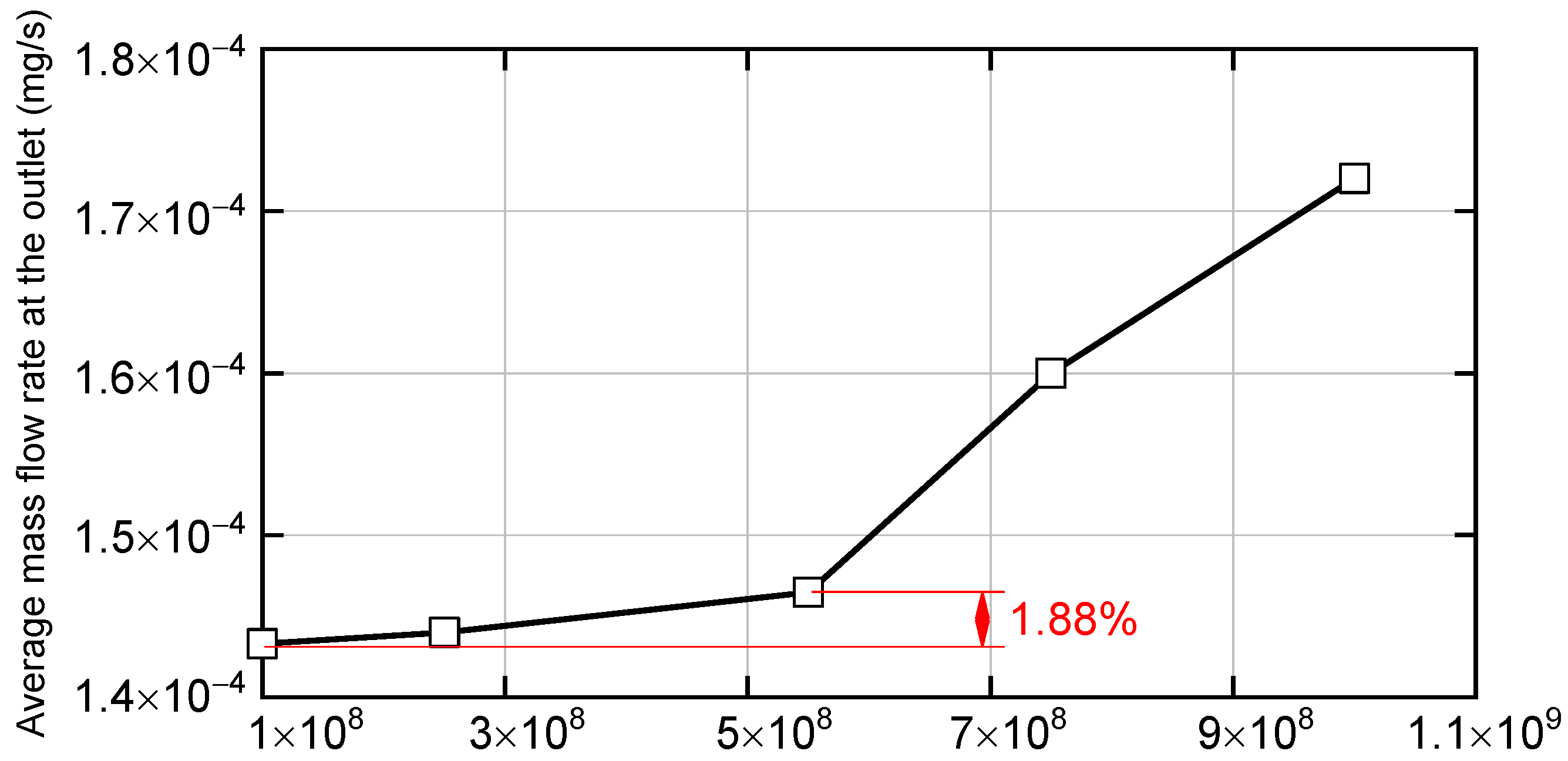
| Number of Axial Grids | Number of Radial Grids | Number of Circumferential Grids | Average Flow Velocity (m/s) | Relative Deviation % | |
|---|---|---|---|---|---|
| Case 1 | 30, 40, 120, 60 | 20 | 1 | 435.6 | 13.05 |
| Case 2 | 30, 40, 120, 60 | 20 | 2 | 421.2 | 9.32 |
| Case 3 | 30, 60, 140, 80 | 20 | 2 | 402.3 | 3.41 |
| Case 4 | 30, 60, 140, 80 | 40 | 2 | 392.2 | 1.79 |
| Case 5 | 50, 80, 160, 100 | 40 | 2 | 390.1 | 1.25 |
| Case 6 | 70, 120, 200, 150 | 40 | 4 | 385.3 | 0.00 |
| Needle Valve Displacement (μm) | Needle Valve Opening | Experimental Thrust Results (μN) | Original CLL Model | Modified CLL Model | ||
|---|---|---|---|---|---|---|
| Thrust Force (μN) | Simulation Bias (%) | Thrust Force (μN) | Simulation Bias (%) | |||
| 0.34 | 1% | 1.95 | 3.41 | 73.87 | 2.32 | 18.97 |
| 0.68 | 2% | 2.80 | 3.99 | 42.50 | 3.18 | 13.57 |
| 1.70 | 5% | 6.73 | 8.62 | 28.08 | 7.32 | 8.77 |
| 3.40 | 10% | 13.98 | 19.21 | 28.24 | 15.91 | 6.21 |
| 17.00 | 50% | 178.82 | 193.45 | 8.18 | 187.12 | 3.64 |
| 30.60 | 90% | 342.73 | 373.32 | 9.22 | 357.64 | 3.35 |
| 32.30 | 95% | 360.22 | 393.82 | 9.61 | 378.45 | 5.06 |
| 33.32 | 98% | 371.56 | 412.43 | 10.99 | 387.32 | 3.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Li, D.; Fu, X.; Gao, Y.; Wang, X. MODELING of Rarefied Gas Flows Inside a Micro-Nozzle Based on the DSMC Method Coupled with a Modified Gas–Surface Interaction Model. Energies 2023, 16, 505. https://doi.org/10.3390/en16010505
Liu X, Li D, Fu X, Gao Y, Wang X. MODELING of Rarefied Gas Flows Inside a Micro-Nozzle Based on the DSMC Method Coupled with a Modified Gas–Surface Interaction Model. Energies. 2023; 16(1):505. https://doi.org/10.3390/en16010505
Chicago/Turabian StyleLiu, Xuhui, Dong Li, Xinju Fu, Yong Gao, and Xudong Wang. 2023. "MODELING of Rarefied Gas Flows Inside a Micro-Nozzle Based on the DSMC Method Coupled with a Modified Gas–Surface Interaction Model" Energies 16, no. 1: 505. https://doi.org/10.3390/en16010505
APA StyleLiu, X., Li, D., Fu, X., Gao, Y., & Wang, X. (2023). MODELING of Rarefied Gas Flows Inside a Micro-Nozzle Based on the DSMC Method Coupled with a Modified Gas–Surface Interaction Model. Energies, 16(1), 505. https://doi.org/10.3390/en16010505






