A Modified Particle Swarm Optimization Algorithm for Power Sharing and Transient Response Improvement of a Grid-Tied Solar PV Based A.C. Microgrid
Abstract
1. Introduction
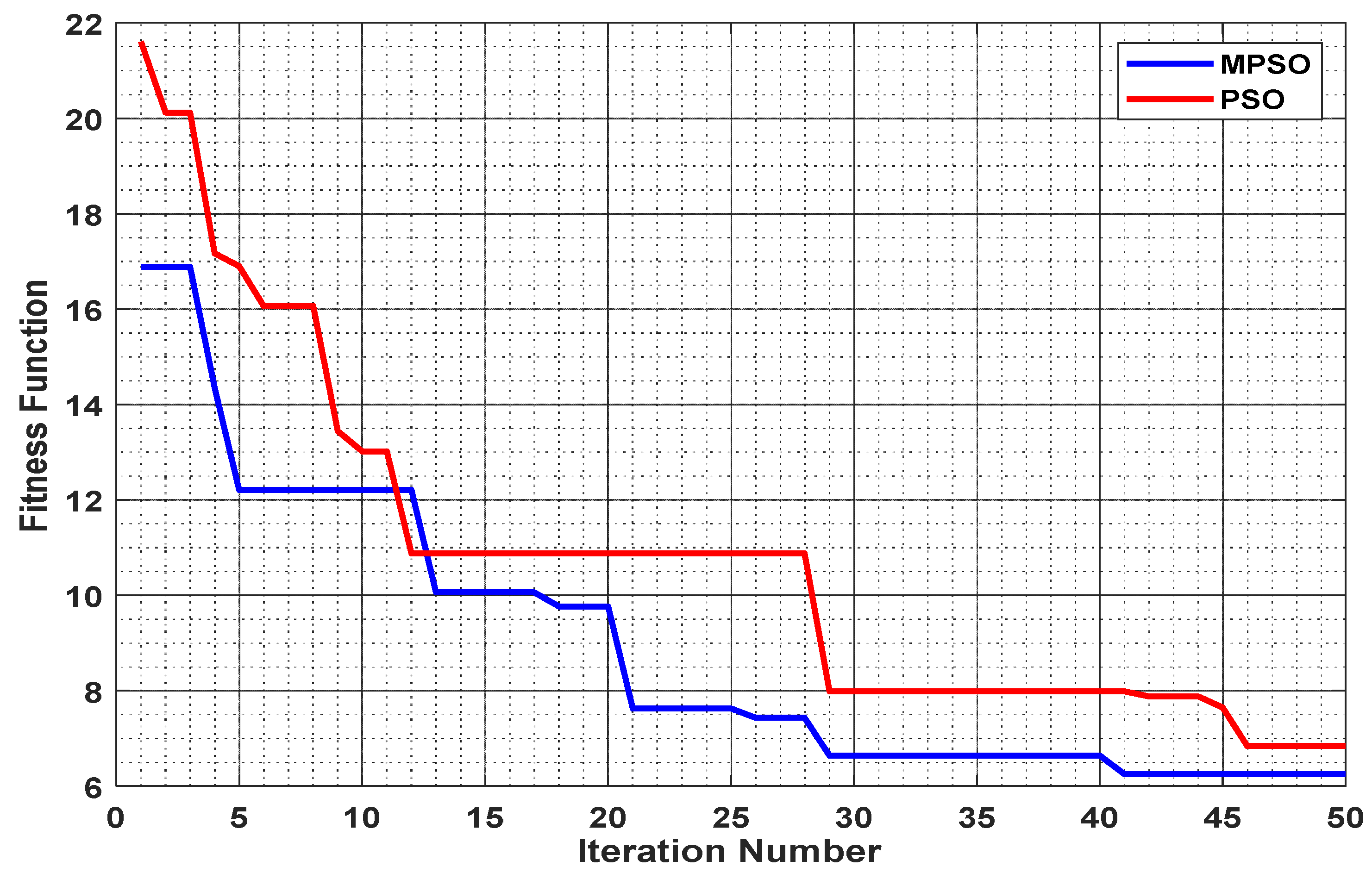
- To avoid the stated problems associated with conventional PSO, an improved version of the same algorithm called modified particle swarm optimization (MPSO) has been incorporated in the M.G. control structure for minimization of fitness function (F.F.) which is ITAE in this case.
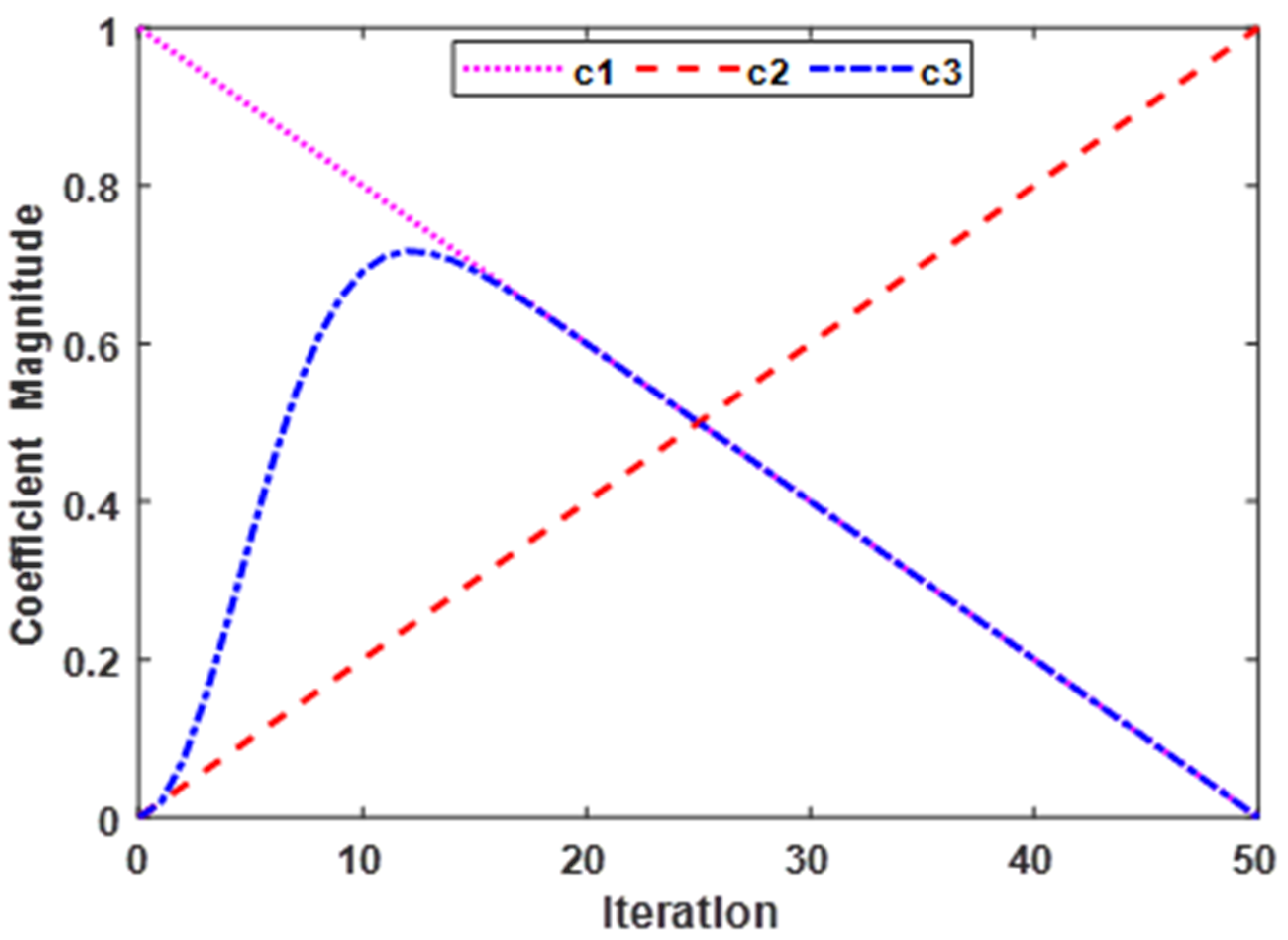
- Contrary to the original version, the proposed MPSO algorithm includes an additional parameter named best neighbor particles (rbest) in the velocity updating equation to convey additional information to every individual particle about all its neighbor particles, consequently leading to increased exploration capability of the algorithm.
- Thus, the optimized control parameters obtained at the end of the simulation ensure improved transient response and power-sharing during the M.G. connection and load changes.
- Furthermore, the performance of the proposed controller with the optimal parameters has been examined through the nonlinear time-domain simulation.
- The results show the proposed approach’s effectiveness in minimizing the overshoot, settling time, and extracting the reference power.
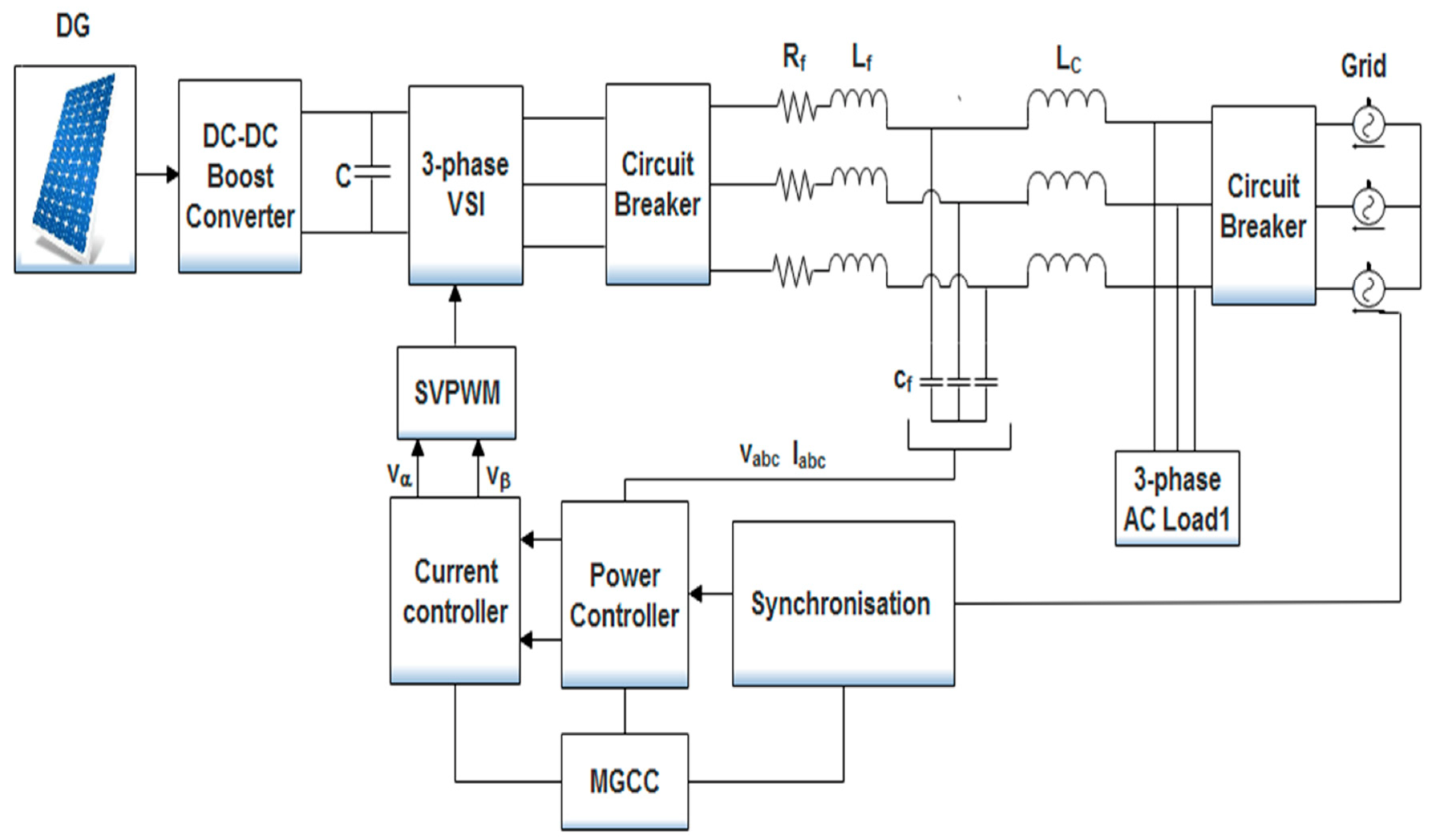
2. Modeling of the Grid-Tied Microgrid along with the Proposed V.S.I. Control Architecture
Proposed Power Control Strategy
3. Methodology
3.1. MPSO and Its Justification
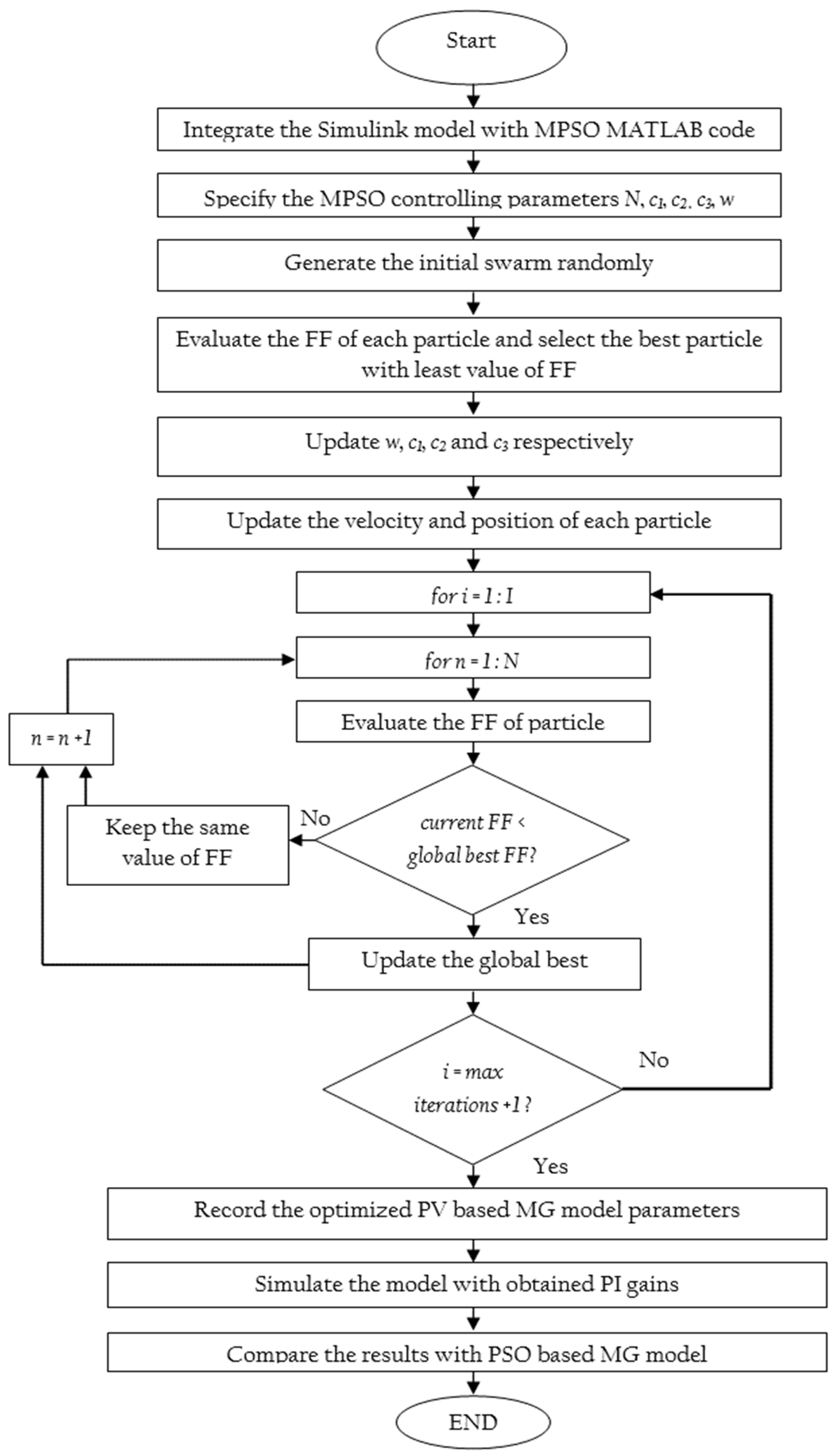
3.2. MPSO Implementation in Developed Grid-Tied MG Model
4. Results and Discussion
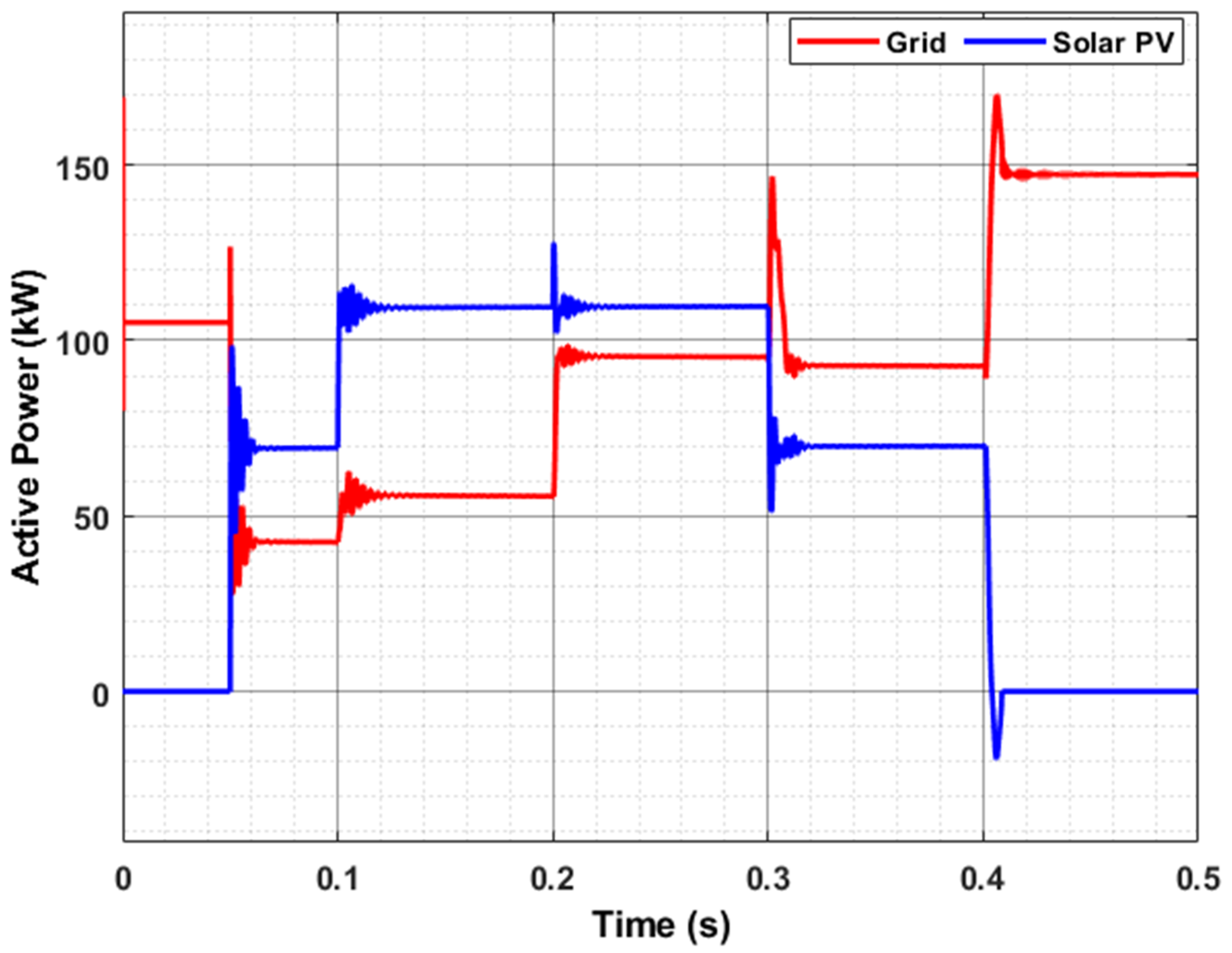
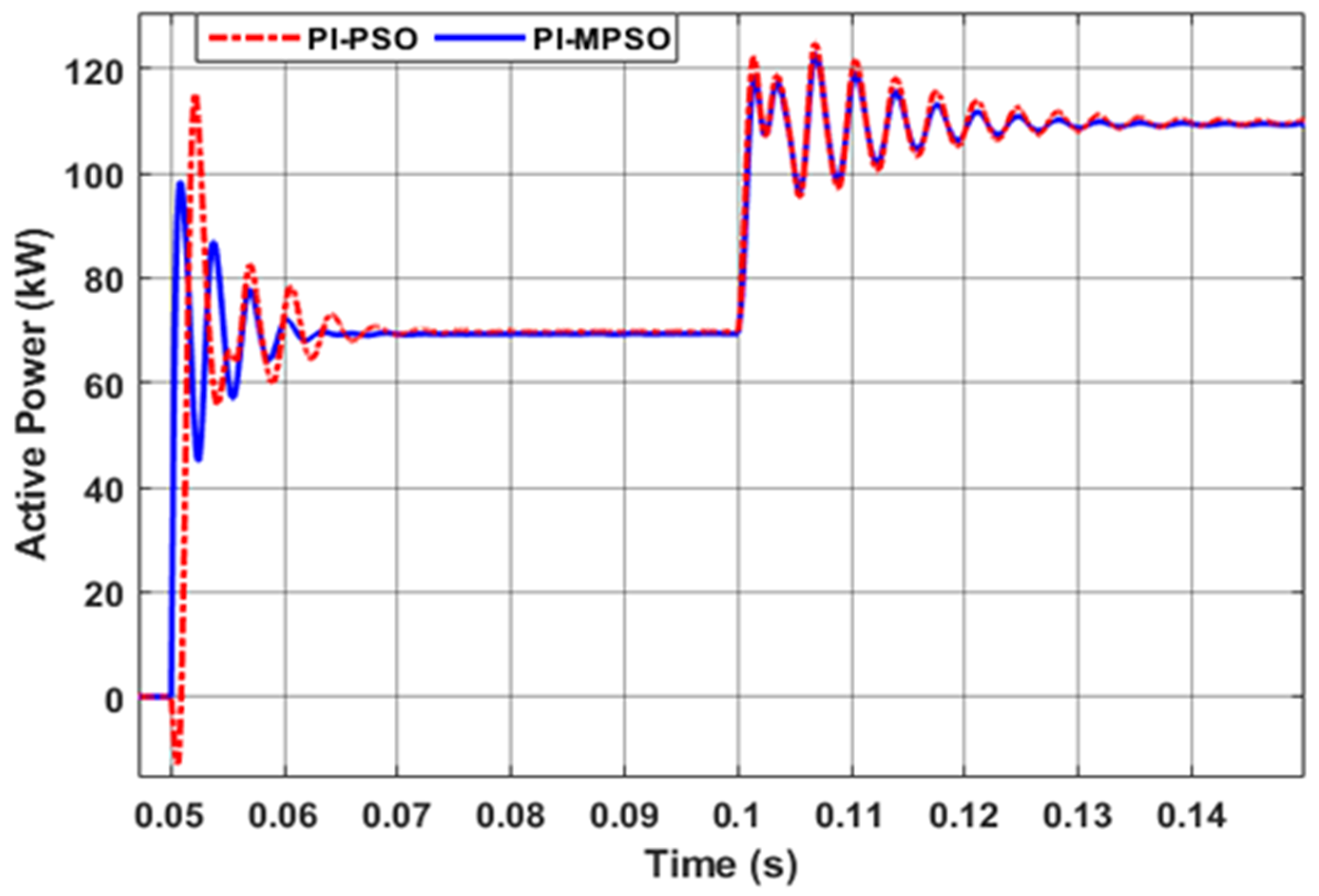
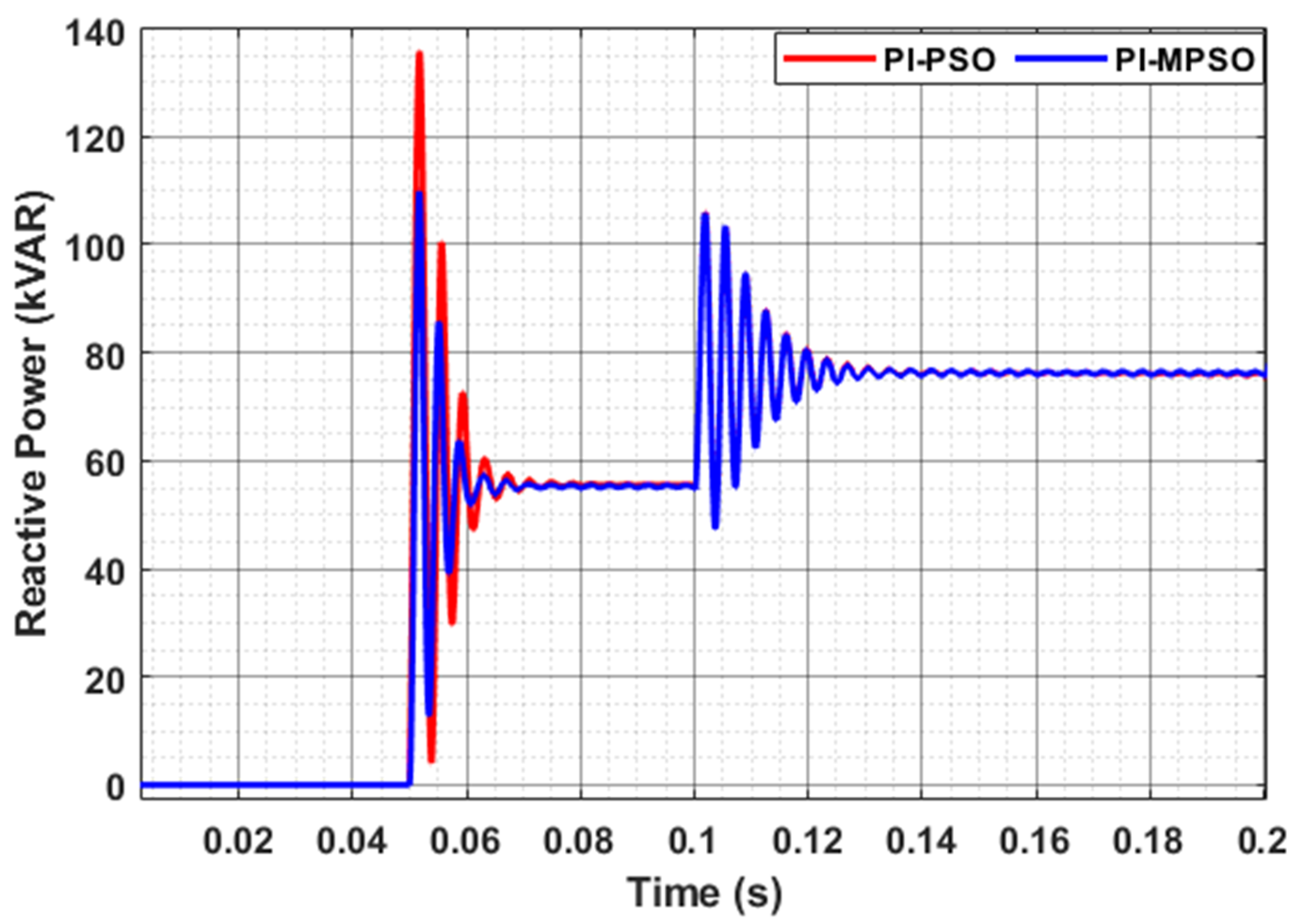
4.1. Power-Sharing Evaluation during D.G. Insertion and Abrupt Load Changes
4.2. Comparison between PSO and MPSO-Based Control Designs
4.3. Fitness Function Convergence Behavior
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| D.G. | Distributed Generation |
| MPSO | Modified Particle Swarm Optimization |
| PSO | Particle Swarm Optimization |
| M.G. | Microgrid |
| ITAE | Integral Time Absolute Error |
| F.F. | Fitness Function |
| SVPWM | Space vector pulse width modulation |
| IGBT | Insulated gate bipolar transistor |
| P.I. | Proportional Integral |
| GA | Genetic Algorithm |
| V.S.I. | Voltage Source Inverter |
References
- Jumani, T.A.; Mustafa, M.W.; Rasid, M.M.; Mirjat, N.H.; Leghari, Z.H.; Saeed, M.S. Optimal Voltage and Frequency Control of an Islanded Microgrid using Grasshopper Optimization Algorithm. Energies 2018, 11, 3191. [Google Scholar] [CrossRef]
- Aziz, S.; Peng, J.; Wang, H.; Jiang, H. ADMM-Based Distributed Optimization of Hybrid MTDC-AC Grid for Determining Smooth Operation Point. IEEE Access 2019, 7, 74238–74247. [Google Scholar] [CrossRef]
- Jumani, T.A.; Mustafa, M.W.; Rasid, M.M.; Mirjat, N.H.; Baloch, M.H.; Salisu, S. Optimal Power Flow Controller for Grid-Connected Microgrids using Grasshopper Optimization Algorithm. Electronics 2019, 8, 111. [Google Scholar] [CrossRef]
- Zhang, R.; Li, G.; Bu, S.; Aziz, S.; Qureshi, R. Data-driven cooperative trading framework for a risk-constrained wind integrated power system considering market uncertainties. Int. J. Electr. Power Energy Syst. 2023, 144, 108566. [Google Scholar] [CrossRef]
- Aziz, S.; Wang, H.; Liu, Y.; Peng, J.; Jiang, H. Variable Universe Fuzzy Logic-Based Hybrid L.F.C. Control With Real-Time Implementation. IEEE Access 2019, 7, 25535–25546. [Google Scholar] [CrossRef]
- Saeed, M.S.; Mustafa, M.W.; Sheikh, U.U.; Jumani, T.A.; Mirjat, N.H. Ensemble Bagged Tree Based Classification for Reducing Non-Technical Losses in Multan Electric Power Company of Pakistan. Electronics 2019, 8, 860. [Google Scholar] [CrossRef]
- Jumani, T.A.; Mustafa, M.; Rasid, M.M.; Anjum, W.; Ayub, S. Salp Swarm Optimization Algorithm-Based Controller for Dynamic Response and Power Quality Enhancement of an Islanded Microgrid. Processes 2019, 7, 840. [Google Scholar] [CrossRef]
- Arfeen, Z.A.; Kermadi, M.; Azam, M.K.; Siddiqui, T.A.; Akhtar, Z.U.; Ado, M.; Abdullah, M.P. Insights and trends of optimal voltage-frequency control DG-based inverter for autonomous microgrid: State-of-the-art review. Int. Trans. Electr. Energy Syst. 2020, 30, e12555. [Google Scholar] [CrossRef]
- Chung, I.-Y.; Liu, W.; Cartes, D.A.; Collins, E.G.; Moon, S.-I. Control methods of inverter-interfaced distributed generators in a microgrid system. IEEE Trans. Ind. Appl. 2010, 46, 1078–1088. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Coordinated design of PSS and SVC damping controller using CPSO. In Proceedings of the 2011 5th International Power Engineering and Optimization Conference, Shah Alam, Malaysia, 6–7 June 2011; pp. 11–16. [Google Scholar] [CrossRef]
- Habib, S.; Abbas, G.; Jumani, T.A.; Bhutto, A.A.; Mirsaeidi, S.; Ahmed, E.M. Improved Whale Optimization Algorithm for Transient Response, Robustness, and Stability Enhancement of an Automatic Voltage Regulator System. Energies 2022, 15, 5037. [Google Scholar] [CrossRef]
- Jumani, T.A.; Mustafa, M.W.; Hamadneh, N.N.; Atawneh, S.H.; Rasid, M.M.; Mirjat, N.H.; Bhayo, M.A.; Khan, I. Computational Intelligence-Based Optimization Methods for Power Quality and Dynamic Response Enhancement of ac Microgrids. Energies 2020, 13, 4063. [Google Scholar] [CrossRef]
- Khan, I.A.; Alghamdi, A.S.; Jumani, T.A.; Alamgir, A.; Awan, A.B.; Khidrani, A. Salp Swarm Optimization Algorithm-Based Fractional Order P.I.D. Controller for Dynamic Response and Stability Enhancement of an Automatic Voltage Regulator System. Electronics 2019, 8, 1472. [Google Scholar] [CrossRef]
- Jumani, T.A.; Mustafa, M.W.; Rasid, M.M.; Memon, Z.A. Dynamic response enhancement of grid-tied ac microgrid using slap swarm optimization algorithm. Int. Trans. Electr. Energy Syst. 2019, 30, e12321. [Google Scholar]
- Ali, A.; Abbas, G.; Keerio, M.U.; Koondhar, M.A.; Chandni, K.; Mirsaeidi, S. Solution of Constrained mixed-integer multi-objectiveoptimal power flow problem considering the hybridmulti-objective evolutionary algorithm. IET Gener. Transm. Distrib. 2022, 1–25. [Google Scholar] [CrossRef]
- Abbas, G.; Ali, B.; Chandni, K.; Koondhar, M.A.; Chandio, S.; Mirsaeidi, S. A Parametric Approach to Compare the Wind Potential of Sanghar and Gwadar Wind Sites. IEEE Access 2022, 10, 110889–110904. [Google Scholar] [CrossRef]
- Wu, Z.; Zhuang, Y.; Zhou, S.; Xu, S.; Yu, P.; Du, J.; Luo, X.; Abbas, G. Bi-Level Planning of Multi-Functional Vehicle Charging Stations Considering Land Use Types. Energies 2020, 13, 1283. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Damping controller design for power system oscillations using hybrid GA-SQP. Int. Rev. Electr. Eng. 2011, 6, 888–896. [Google Scholar]


| Parameter Names | Value and Unit |
|---|---|
| DG rating | 120 kW |
| Load 1 | 110 kW, 38 kVAR |
| Load 2 | 55 kW, 12 kVAR |
| Load 3 | 40 kW, 18 kVAR |
| DC link capacitor | 50 mF |
| R.L.C. Filter | 0.002 Ω, 0.63388 mH, 2500 µF |
| Switching frequency | 10 kHz |
| Sampling frequency | 500 kHz |
| Current controller P.I. gains | Kp = 12.656, Ki = 0.00215 |
| Time (s) | Operating Condition | Total Load Injected or Shared | D.G. Reference Power Values (Power Shared) | Grid Shared Power |
|---|---|---|---|---|
| 0–0.04 | Grid operation | 110 kW, 38 kVAR | 0 kW, 0 kVAR | 110 kW, 38 kVAR |
| 0.05 | DG injection | - | 70 kW, 55 kVAR | 40 kW, −10 kVAR |
| 0.1 | Load insertion | 55 kW, 20 kVAR | 40 kW, 20 kVAR | 15 kW, 0 kVAR |
| 0.2 | Load insertion | 40 kW, 18 kVAR | 0 kW, 0 kVAR | 40 kW, 18 kVAR |
| 0.3 | Load detachment | 55 kW, 12 kVAR | 55 kW, 2 kVAR | 0 kW, 10 kVAR |
| 0.4 | DG detachment | - | - | 147.5 kW, 68 kVAR |
| Kpp | Kip | Kpq | Kiq | |
|---|---|---|---|---|
| PI-PSO MG | 16.273 | 6.654 | 30.250 | 5.839 |
| MPSO-PI MG | 1.088 | 9.650 | 22.769 | 2.150 |
| Active Power | Reactive Power | |||
|---|---|---|---|---|
| % Mp | ts (ms) | % Mp | ts (ms) | |
| PI-PSO MG | 64.71 | 14.8 | 146.91 | 21.74 |
| MPSO-PI MG | 40.71 | 10.5 | 100.0 | 17.37 |
| % Improvement | 37.08 | 29.05 | 31.93 | 20.10 |
| Active Power | Reactive Power | |||
|---|---|---|---|---|
| % Mp | ts (ms) | % Mp | ts (ms) | |
| PI-PSO MG | 13.63 | 27.0 | 39.21 | 27.1 |
| MPSO-PI MG | 11.54 | 20.0 | 39.47 | 27.1 |
| % Improvement | 15.33 | 25.92 | 0.66 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, G.; Bhutto, A.A.; Jumani, T.A.; Mirsaeidi, S.; Tunio, M.A.; Alnuman, H.; Alshahir, A. A Modified Particle Swarm Optimization Algorithm for Power Sharing and Transient Response Improvement of a Grid-Tied Solar PV Based A.C. Microgrid. Energies 2023, 16, 348. https://doi.org/10.3390/en16010348
Abbas G, Bhutto AA, Jumani TA, Mirsaeidi S, Tunio MA, Alnuman H, Alshahir A. A Modified Particle Swarm Optimization Algorithm for Power Sharing and Transient Response Improvement of a Grid-Tied Solar PV Based A.C. Microgrid. Energies. 2023; 16(1):348. https://doi.org/10.3390/en16010348
Chicago/Turabian StyleAbbas, Ghulam, Aqeel Ahmed Bhutto, Touqeer Ahmed Jumani, Sohrab Mirsaeidi, Mohsin Ali Tunio, Hammad Alnuman, and Ahmed Alshahir. 2023. "A Modified Particle Swarm Optimization Algorithm for Power Sharing and Transient Response Improvement of a Grid-Tied Solar PV Based A.C. Microgrid" Energies 16, no. 1: 348. https://doi.org/10.3390/en16010348
APA StyleAbbas, G., Bhutto, A. A., Jumani, T. A., Mirsaeidi, S., Tunio, M. A., Alnuman, H., & Alshahir, A. (2023). A Modified Particle Swarm Optimization Algorithm for Power Sharing and Transient Response Improvement of a Grid-Tied Solar PV Based A.C. Microgrid. Energies, 16(1), 348. https://doi.org/10.3390/en16010348








