Short-Term Electricity Prices Forecasting Using Functional Time Series Analysis
Abstract
:1. Introduction
2. Functional Modeling
2.1. Preliminaries
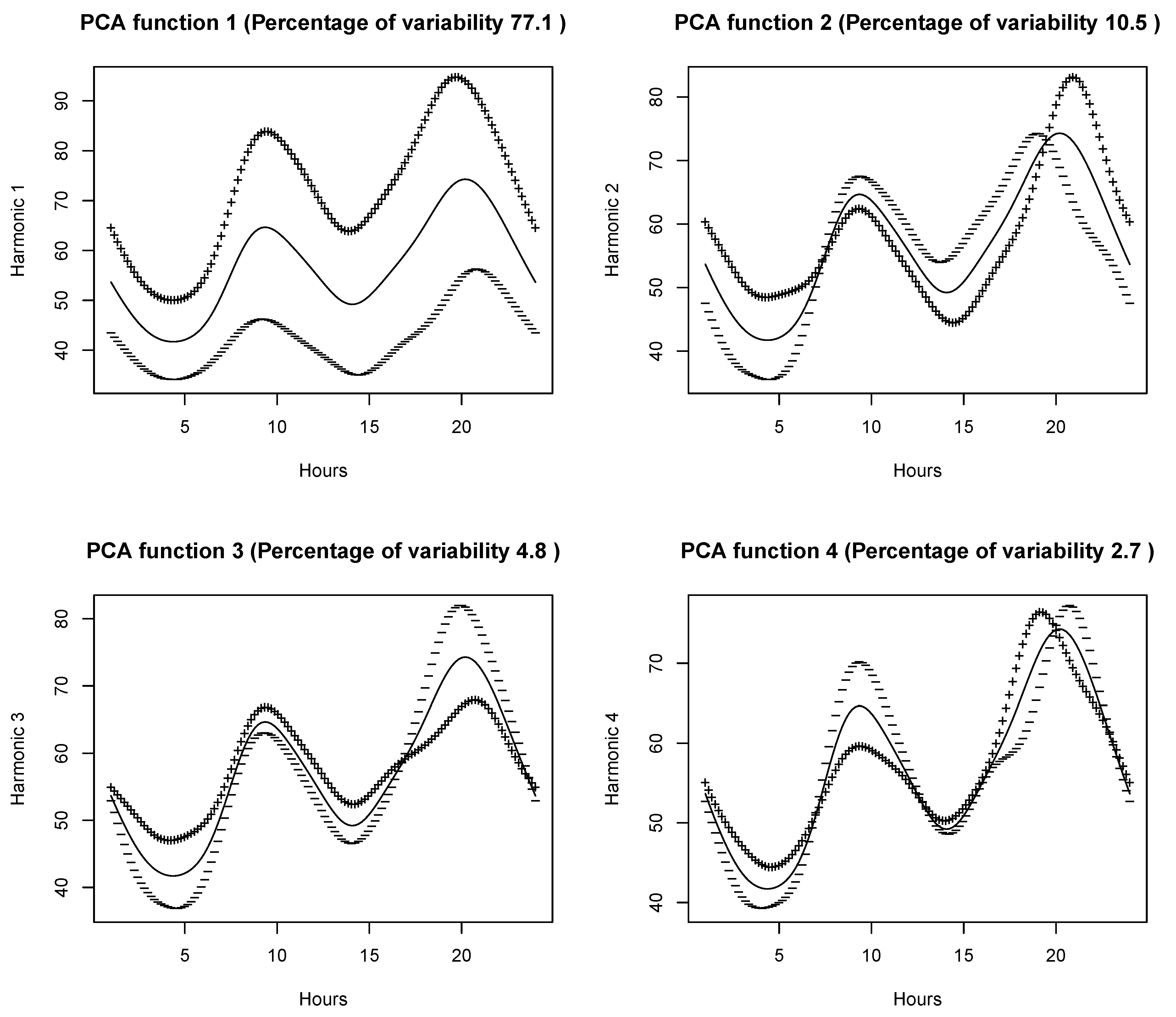
2.2. Functional Autoregressive Model
- First, the dimension which is denoted by is fixed by using the method described in Section 2.3, and the estimated FPC scores are obtained as for each observation , and the estimated j-variate FPC scores vectors .
- Next, the order is fixed using the technique described in Section 2.3 and we fit the vector AR model, VAR(), as for eigenscores vectors to produce forecasting . Durbin–Levinson and innovations algorithm can be readily applied here, given the vectors .
- In the last step, the multivariate time series are converted back to functional version using the KL theorem . The FPC scores and sample eigenfunctions result in , which is then used as a one-step-ahead forecast of .
2.3. Selection of Order and Dimension of FAR()
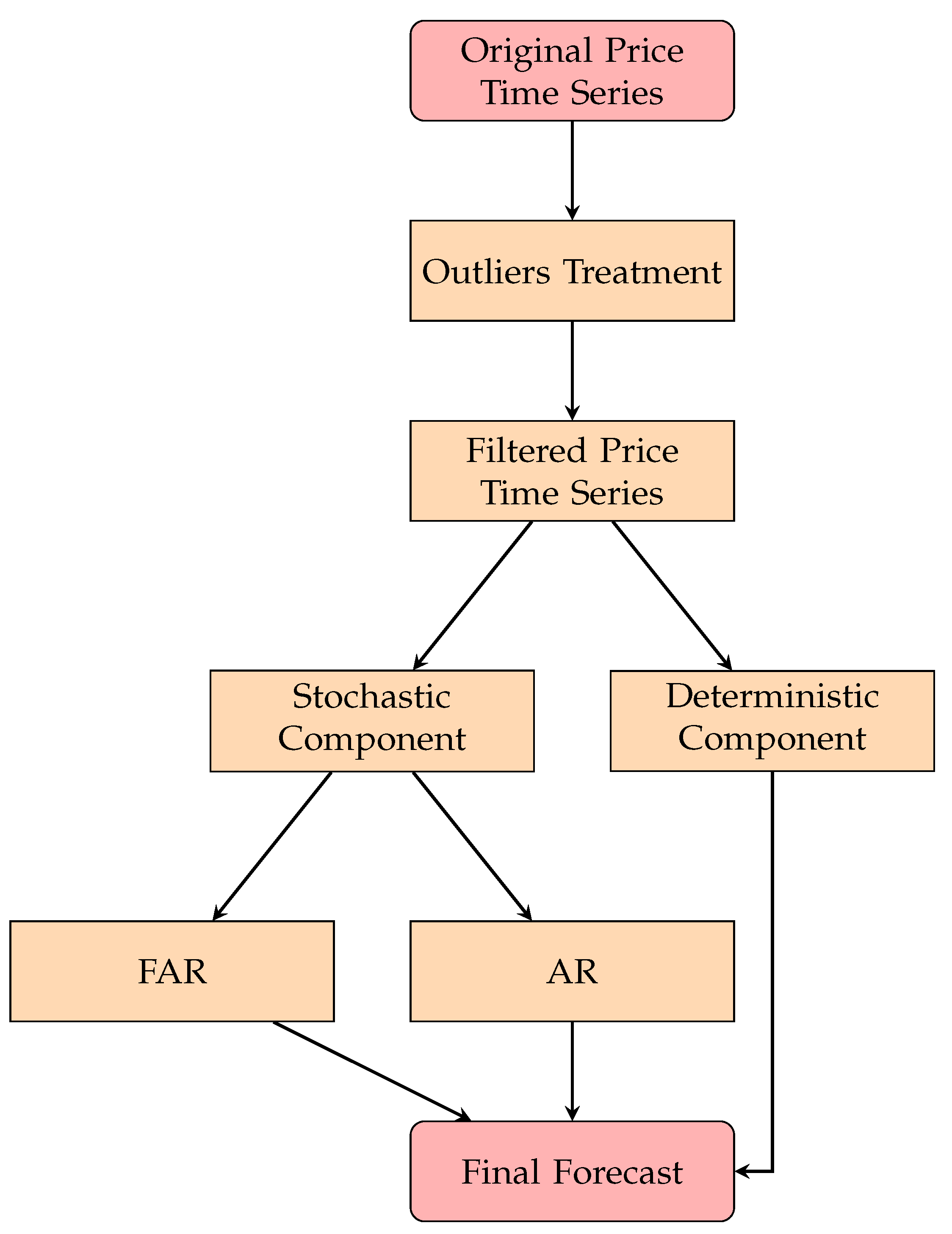
3. Modeling Framework
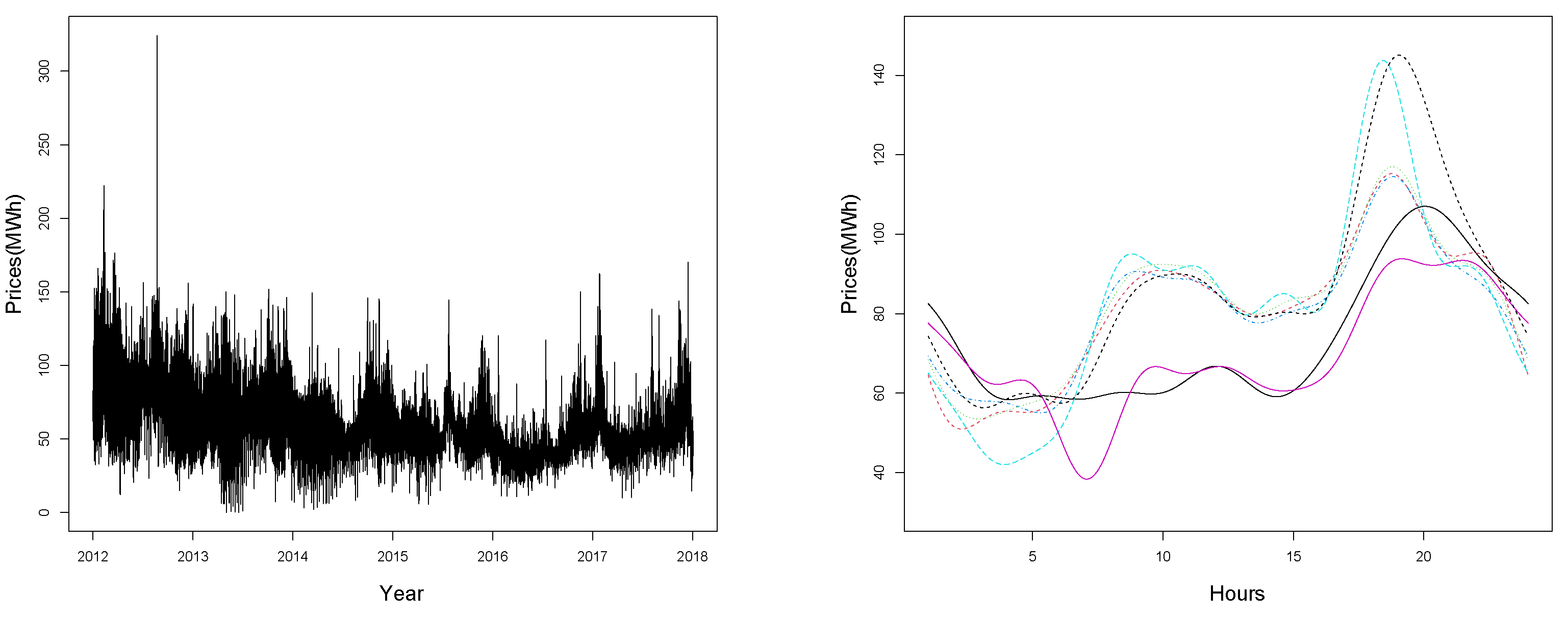
3.1. Moving Window Filter on Prices
3.2. The Model
3.2.1. Autoregressive (AR) Model
3.2.2. The Naïve Benchmark
- To forecast a given day, for example, Thursday, select the day before Thursday, which is Wednesday, and denote it by .
- From the validation dataset, select all the Wednesdays (except ) and compare them with using the mean absolute error (MAE).
- Obtain a value of the MAE for each comparison that will result in a vector of the MAE values.
- Find and locate the smallest value of the MAE in the vector. Once the Wednesday having the lowest MAE is located, use its next day, i.e., Thursday, as the forecast for the concerned Thursday. This process is repeated for all the remaining days of the week.
4. Out-of-Sample Forecast
5. Conclusions and Future Direction
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bunn, D.W. Modelling Prices in Competitive Electricity Markets; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Shah, I.; Bibi, H.; Ali, S.; Wang, L.; Yue, Z. Forecasting one-day-ahead electricity prices for italian electricity market using parametric and nonparametric approaches. IEEE Access 2020, 8, 123104–123113. [Google Scholar] [CrossRef]
- Lisi, F.; Nan, F. Component estimation for electricity prices: Procedures and comparisons. Energy Econ. 2014, 44, 143–159. [Google Scholar] [CrossRef]
- Misiorek, A.; Trueck, S.; Weron, R. Point and interval forecasting of spot electricity prices: Linear vs. non-linear time series models. Stud. Nonlinear Dyn. Econom. 2006, 10, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Debnath, K.B.; Mourshed, M. Forecasting methods in energy planning models. Renew. Sustain. Energy Rev. 2018, 88, 297–325. [Google Scholar] [CrossRef] [Green Version]
- Shah, I. Modeling and Forecasting Electricity Market Variables. Ph.D. Thesis, University of Padova, Padua, Italy, 2016. [Google Scholar]
- Li, W.; Yang, X.; Li, H.; Su, L. Hybrid forecasting approach based on GRNN neural network and SVR machine for electricity demand forecasting. Energies 2017, 10, 44. [Google Scholar] [CrossRef]
- Contreras, J.; Espinola, R.; Nogales, F.J.; Conejo, A.J. ARIMA models to predict next-day electricity prices. IEEE Trans. Power Syst. 2003, 18, 1014–1020. [Google Scholar] [CrossRef]
- Conejo, A.J.; Plazas, M.A.; Espinola, R.; Molina, A.B. Day-ahead electricity price forecasting using the wavelet transform and ARIMA models. IEEE Trans. Power Syst. 2005, 20, 1035–1042. [Google Scholar] [CrossRef]
- Babu, C.N.; Reddy, B.E. A moving-average filter based hybrid ARIMA–ANN model for forecasting time series data. Appl. Soft Comput. 2014, 23, 27–38. [Google Scholar] [CrossRef]
- González, J.P.; San Roque, A.M.; Perez, E.A. Forecasting functional time series with a new Hilbertian ARMAX model: Application to electricity price forecasting. IEEE Trans. Power Syst. 2017, 33, 545–556. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Li, R. Forecasting energy demand in China and India: Using single-linear, hybrid-linear, and non-linear time series forecast techniques. Energy 2018, 161, 821–831. [Google Scholar] [CrossRef]
- Diongue, A.K.; Guégan, D. The k-Factor Gegenbauer Asymmetric Power GARCH Approach for Modelling Electricity Spot Price Dynamics; Universite Pantheon-Sorbonne: Paris, France, 2008. [Google Scholar]
- Garcia, R.C.; Contreras, J.; Van Akkeren, M.; Garcia, J.B.C. A GARCH forecasting model to predict day-ahead electricity prices. IEEE Trans. Power Syst. 2005, 20, 867–874. [Google Scholar] [CrossRef]
- Qu, H.; Duan, Q.; Niu, M. Modeling the volatility of realized volatility to improve volatility forecasts in electricity markets. Energy Econ. 2018, 74, 767–776. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Electricity consumption forecasting in Italy using linear regression models. Energy 2009, 34, 1413–1421. [Google Scholar] [CrossRef]
- Su, M.; Zhang, Z.; Zhu, Y.; Zha, D. Data-driven natural gas spot price forecasting with least squares regression boosting algorithm. Energies 2019, 12, 1094. [Google Scholar] [CrossRef] [Green Version]
- Karakatsani, N.V.; Bunn, D.W. Forecasting electricity prices: The impact of fundamentals and time-varying coefficients. Int. J. Forecast. 2008, 24, 764–785. [Google Scholar] [CrossRef]
- He, Y.; Liu, R.; Li, H.; Wang, S.; Lu, X. Short-term power load probability density forecasting method using kernel-based support vector quantile regression and Copula theory. Appl. Energy 2017, 185, 254–266. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Li, S.; Li, W.; Qu, M. Power load probability density forecasting using Gaussian process quantile regression. Appl. Energy 2018, 213, 499–509. [Google Scholar] [CrossRef]
- Lebotsa, M.E.; Sigauke, C.; Bere, A.; Fildes, R.; Boylan, J.E. Short term electricity demand forecasting using partially linear additive quantile regression with an application to the unit commitment problem. Appl. Energy 2018, 222, 104–118. [Google Scholar] [CrossRef] [Green Version]
- Taylor, J.W.; McSharry, P.E. Short-term load forecasting methods: An evaluation based on european data. IEEE Trans. Power Syst. 2007, 22, 2213–2219. [Google Scholar] [CrossRef] [Green Version]
- De Livera, A.M.; Hyndman, R.J.; Snyder, R.D. Forecasting time series with complex seasonal patterns using exponential smoothing. J. Am. Stat. Assoc. 2011, 106, 1513–1527. [Google Scholar] [CrossRef] [Green Version]
- Taylor, J.W. Triple seasonal methods for short-term electricity demand forecasting. Eur. J. Oper. Res. 2010, 204, 139–152. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Srinivasan, D.; Zhang, D. Electricity Demand Forecasting Using HWT Model with Fourfold Seasonality. In Proceedings of the 2017 International Conference on Control, Artificial Intelligence, Robotics & Optimization (ICCAIRO), Prague, Czech Republic, 20–22 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 254–258. [Google Scholar]
- Jiang, W.; Wu, X.; Gong, Y.; Yu, W.; Zhong, X. Holt–Winters smoothing enhanced by fruit fly optimization algorithm to forecast monthly electricity consumption. Energy 2020, 193, 116779. [Google Scholar] [CrossRef]
- Trull, O.; García-Díaz, J.C.; Troncoso, A. Initialization Methods for Multiple Seasonal Holt–Winters Forecasting Models. Mathematics 2020, 8, 268. [Google Scholar] [CrossRef] [Green Version]
- Amor, S.B.; Boubaker, H.; Belkacem, L. Forecasting Electricity Spot Price with Generalized Long Memory Modeling: Wavelet and Neural Network. Int. J. Econ. Manag. Eng. 2018, 11, 2307–2323. [Google Scholar]
- Gürbüz, F.; Öztürk, C.; Pardalos, P. Prediction of electricity energy consumption of Turkey via artificial bee colony: A case study. Energy Syst. 2013, 4, 289–300. [Google Scholar] [CrossRef]
- Ugurlu, U.; Oksuz, I.; Tas, O. Electricity price forecasting using recurrent neural networks. Energies 2018, 11, 1255. [Google Scholar] [CrossRef] [Green Version]
- Urolagin, S.; Sharma, N.; Datta, T.K. A combined architecture of multivariate LSTM with Mahalanobis and Z-Score transformations for oil price forecasting. Energy 2021, 231, 120963. [Google Scholar] [CrossRef]
- Gholipour Khajeh, M.; Maleki, A.; Rosen, M.A.; Ahmadi, M.H. Electricity price forecasting using neural networks with an improved iterative training algorithm. Int. J. Ambient. Energy 2018, 39, 147–158. [Google Scholar] [CrossRef]
- Dordonnat, V.; Koopman, S.J.; Ooms, M.; Dessertaine, A.; Collet, J. An hourly periodic state space model for modelling French national electricity load. Int. J. Forecast. 2008, 24, 566–587. [Google Scholar] [CrossRef] [Green Version]
- Rigatos, G.G. State-Space Approaches for Modelling and Control in Financial Engineering; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Li, T.; Qian, Z.; Deng, W.; Zhang, D.; Lu, H.; Wang, S. Forecasting crude oil prices based on variational mode decomposition and random sparse Bayesian learning. Appl. Soft Comput. 2021, 113, 108032. [Google Scholar] [CrossRef]
- Laouafi, A.; Mordjaoui, M.; Laouafi, F.; Boukelia, T.E. Daily peak electricity demand forecasting based on an adaptive hybrid two-stage methodology. Int. J. Electr. Power Energy Syst. 2016, 77, 136–144. [Google Scholar] [CrossRef]
- Yang, Z.; Ce, L.; Lian, L. Electricity price forecasting by a hybrid model, combining wavelet transform, ARMA and kernel-based extreme learning machine methods. Appl. Energy 2017, 190, 291–305. [Google Scholar] [CrossRef]
- Chang, Z.; Zhang, Y.; Chen, W. Electricity price prediction based on hybrid model of adam optimized LSTM neural network and wavelet transform. Energy 2019, 187, 115804. [Google Scholar] [CrossRef]
- Bibi, N.; Shah, I.; Alsubie, A.; Ali, S.; Lone, S.A. Electricity Spot Prices Forecasting Based on Ensemble Learning. IEEE Access 2021, 9, 150984–150992. [Google Scholar] [CrossRef]
- Hahn, H.; Meyer-Nieberg, S.; Pickl, S. Electric load forecasting methods: Tools for decision making. Eur. J. Oper. Res. 2009, 199, 902–907. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B.W. Applied Functional Data Analysis: Methods and Case Studies; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Shah, I.; Lisi, F. Forecasting of electricity price through a functional prediction of sale and purchase curves. J. Forecast. 2020, 39, 242–259. [Google Scholar] [CrossRef]
- Bosq, D. Modelization, nonparametric estimation and prediction for continuous time processes. In Nonparametric Functional Estimation and Related Topics; Springer: Berlin/Heidelberg, Germany, 1991; pp. 509–529. [Google Scholar]
- Andersson, J.; Lillestøl, J. Modeling and forecasting electricity consumption by functional data analysis. J. Energy Mark. 2010, 3, 3. [Google Scholar] [CrossRef]
- Aneiros-Pérez, G.; Cao, R.; Vilar-Fernández, J.M. Functional methods for time series prediction: A nonparametric approach. J. Forecast. 2011, 30, 377–392. [Google Scholar] [CrossRef] [Green Version]
- Shah, I.; Lisi, F. Day-ahead electricity demand forecasting with nonparametric functional models. In Proceedings of the 12th International Conference on the European Energy Market (EEM), Lisbon, Portugal, 19–22 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Lisi, F.; Shah, I. Forecasting next-day electricity demand and prices based on functional models. Energy Syst. 2020, 11, 947–979. [Google Scholar] [CrossRef]
- Shang, H.L. Functional time series approach for forecasting very short-term electricity demand. J. Appl. Stat. 2013, 40, 152–168. [Google Scholar] [CrossRef]
- Horváth, L.; Kokoszka, P. Inference for Functional Data with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 200. [Google Scholar]
- Bosq, D. Linear Processes in Function Spaces: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000; Volume 149. [Google Scholar]
- Indritz, J. Methods in Analysis; Macmillan: New York, NY, USA, 1963. [Google Scholar]
- Karhunen, K. Under Lineare Methoden in der Wahr Scheinlichkeitsrechnung; Annales Academiae Scientiarun Fennicae Series A1: Mathematia Physica; Universitat Helsinki: Helsinki, Finland, 1947; Volume 47. [Google Scholar]
- Loeve, M. Functions aleatoires du second ordre. Process. Stoch. Mouv. Brownien 1948, 366–420. [Google Scholar]
- Ramsay, J.; Silverman, B. Functional Data Analysis-Methods and Case Studies; Springer: New York, NY, USA, 2002. [Google Scholar]
- Shang, H.L. A survey of functional principal component analysis. AStA Adv. Stat. Anal. 2014, 98, 121–142. [Google Scholar] [CrossRef] [Green Version]
- Chiou, J.M. Dynamical functional prediction and classification, with application to traffic flow prediction. Ann. Appl. Stat. 2012, 6, 1588–1614. [Google Scholar] [CrossRef] [Green Version]
- Yao, F.; Müller, H.G.; Wang, J.L. Functional data analysis for sparse longitudinal data. J. Am. Stat. Assoc. 2005, 100, 577–590. [Google Scholar] [CrossRef]
- Rice, J.A.; Silverman, B.W. Estimating the mean and covariance structure nonparametrically when the data are curves. J. R. Stat. Soc. Ser. B (Methodol.) 1991, 53, 233–243. [Google Scholar] [CrossRef]
- Hall, P.; Vial, C. Assessing the finite dimensionality of functional data. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2006, 68, 689–705. [Google Scholar] [CrossRef]
- Hörmann, S.; Kokoszka, P. Weakly dependent functional data. Ann. Stat. 2010, 38, 1845–1884. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Koch, T.; Lim, K.G.; Xu, X.; Zakiyeva, N. A review study of functional autoregressive models with application to energy forecasting. Wiley Interdiscip. Rev. Comput. Stat. 2021, 13, e1525. [Google Scholar] [CrossRef]
- Jiao, S.; Aue, A.; Ombao, H. Functional time series prediction under partial observation of the future curve. J. Am. Stat. Assoc. 2021, 1–12. [Google Scholar] [CrossRef]
- Lutkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Aue, A.; Norinho, D.D.; Hörmann, S. On the prediction of stationary functional time series. J. Am. Stat. Assoc. 2015, 110, 378–392. [Google Scholar] [CrossRef] [Green Version]
- Jau, Y.M.; Su, K.L.; Wu, C.J.; Jeng, J.T. Modified quantum-behaved particle swarm optimization for parameters estimation of generalized nonlinear multi-regressions model based on Choquet integral with outliers. Appl. Math. Comput. 2013, 221, 282–295. [Google Scholar] [CrossRef]
- Bardwell, L.; Fearnhead, P. Bayesian detection of abnormal segments in multiple time series. Bayesian Anal. 2017, 12, 193–218. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A review on outlier/anomaly detection in time series data. arXiv 2020, arXiv:2002.04236. [Google Scholar] [CrossRef]
- Lai, K.H.; Zha, D.; Wang, G.; Xu, J.; Zhao, Y.; Kumar, D.; Chen, Y.; Zumkhawaka, P.; Wan, M.; Martinez, D.; et al. TODS: An Automated Time Series Outlier Detection System. arXiv 2020, arXiv:2009.09822. [Google Scholar]
- Borovkova, S.; Permana, F.J. Modelling electricity prices by the potential jump-diffusion. In Stochastic Finance; Springer: Berlin/Heidelberg, Germany, 2006; pp. 239–263. [Google Scholar]
- Shah, I.; Akbar, S.; Saba, T.; Ali, S.; Rehman, A. Short-term forecasting for the electricity spot prices with extreme values treatment. IEEE Access 2021, 9, 105451–105462. [Google Scholar] [CrossRef]
- Shah, I.; Iftikhar, H.; Ali, S.; Wang, D. Short-term electricity demand forecasting using components estimation technique. Energies 2019, 12, 2532. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Wang, S.; Lai, K.K. Forecasting crude oil price with an EMD-based neural network ensemble learning paradigm. Energy Econ. 2008, 30, 2623–2635. [Google Scholar] [CrossRef]
- Petrella, A.; Sapio, S. No PUN Intended: A Time Series Analysis of the Italian Day-Ahead Electricity Prices; Florence School of Regulation: Florence, Italy, 2010. [Google Scholar]
- Petrella, A.; Sapio, S. A time series analysis of day-ahead prices on the Italian power exchange. In Proceedings of the 6th International Conference on the European Energy Market, Porto, Portugal, 6–9 June 2016; IEEE: Piscataway, NJ, USA, 2009; pp. 1–6. [Google Scholar]
- Cervone, A.; Santini, E.; Teodori, S.; Romito, D.Z. Electricity price forecast: A comparison of different models to evaluate the single national price in the Italian energy exchange market. Int. J. Energy Econ. Policy 2014, 4, 744–758. [Google Scholar]
| Model | MAE | MAPE | RMSE | Dstat (%) | SAME | UP | DOWN |
|---|---|---|---|---|---|---|---|
| FAR() | 5.16485 | 8.99009 | 8.65032 | 88.34342 | 1525 | 3743 | 3492 |
| AR(7) | 5.65833 | 10.09469 | 9.20305 | 82.95525 | 1272 | 4084 | 3404 |
| Naive | 6.86278 | 12.63467 | 10.09929 | 53.63626 | 385 | 4137 | 4238 |
| Model | Error | Days of a Week | ||||||
|---|---|---|---|---|---|---|---|---|
| Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday | ||
| FAR() | MAE | 5.63112 | 5.87795 | 6.53440 | 5.00897 | 4.88412 | 4.06196 | 4.17448 |
| AR(7) | 6.16619 | 6.34358 | 6.95023 | 5.86286 | 5.45145 | 4.54586 | 4.31402 | |
| Naive | 7.58172 | 7.38245 | 6.39990 | 6.93643 | 6.40897 | 6.86697 | 6.47056 | |
| FAR() | MAPE | 9.87044 | 9.23202 | 9.30545 | 7.72602 | 7.85736 | 8.58661 | 10.32703 |
| AR(7) | 11.14407 | 10.06261 | 10.35827 | 9.02434 | 8.86721 | 9.91458 | 11.26919 | |
| Naive | 13.82605 | 12.47558 | 11.01666 | 10.93947 | 11.04299 | 13.52881 | 18.26894 | |
| FAR() | RMSE | 8.72362 | 9.56184 | 11.93833 | 9.59608 | 7.97935 | 5.43820 | 5.36185 |
| AR(7) | 9.34377 | 10.08267 | 11.97317 | 10.87680 | 8.79962 | 5.86412 | 5.60787 | |
| Naive | 11.60842 | 10.63521 | 10.37988 | 10.76548 | 8.88560 | 9.54221 | 8.54465 | |
| Model | Hour | MAE | MAPE | RMSE | Hour | MAE | MAPE | RMSE |
|---|---|---|---|---|---|---|---|---|
| FAR() | 1 | 3.17448 | 10.32703 | 5.36185 | 13 | 5.03299 | 9.77343 | 7.50008 |
| AR(7) | 4.09499 | 8.20630 | 5.48352 | 5.50527 | 10.81530 | 8.32688 | ||
| Naive | 2.99810 | 5.71016 | 4.35740 | 5.89142 | 10.72254 | 8.54265 | ||
| FAR() | 2 | 5.63112 | 9.87044 | 8.72362 | 14 | 5.13495 | 10.97364 | 7.45864 |
| AR(7) | 3.90162 | 8.62680 | 5.04521 | 5.69565 | 12.52584 | 8.52711 | ||
| Naive | 3.99566 | 8.14583 | 5.04110 | 5.15640 | 10.87232 | 7.39582 | ||
| FAR() | 3 | 5.87795 | 9.23202 | 6.46184 | 15 | 4.91392 | 10.19534 | 9.29372 |
| AR(7) | 3.82670 | 9.05766 | 4.96036 | 6.52555 | 13.92227 | 10.37498 | ||
| Naive | 3.66855 | 8.12195 | 4.42199 | 5.40823 | 11.21776 | 7.62226 | ||
| FAR() | 4 | 3.39714 | 8.41575 | 4.46110 | 16 | 6.20807 | 11.99534 | 9.73345 |
| AR(7) | 3.97490 | 10.11668 | 5.28032 | 6.91072 | 13.74287 | 10.63356 | ||
| Naive | 3.52617 | 8.48418 | 4.64024 | 6.07377 | 11.75996 | 9.43945 | ||
| FAR() | 5 | 3.39652 | 8.35320 | 4.46989 | 17 | 6.63385 | 10.73122 | 10.96537 |
| AR(7) | 3.89939 | 9.77731 | 5.18900 | 7.02079 | 11.61225 | 11.34363 | ||
| Naive | 6.33318 | 12.83398 | 9.91261 | 6.47302 | 10.62784 | 10.48912 | ||
| FAR() | 6 | 4.88413 | 7.85736 | 7.97935 | 18 | 6.95788 | 9.73444 | 12.11111 |
| AR(7) | 3.73582 | 8.64474 | 5.02575 | 7.32959 | 10.47554 | 12.35075 | ||
| Naive | 7.59001 | 8.59831 | 4.74848 | 7.04453 | 13.45730 | 10.9536 | ||
| FAR() | 7 | 4.06196 | 8.58661 | 5.43820 | 19 | 7.83811 | 9.91660 | 14.00040 |
| AR(7) | 4.27194 | 8.50246 | 5.79461 | 7.99731 | 10.31619 | 13.91400 | ||
| Naive | 4.98340 | 11.28051 | 6.28747 | 7.35881 | 11.86122 | 11.68502 | ||
| FAR() | 8 | 4.94668 | 8.16684 | 7.92432 | 20 | 7.35007 | 9.7326 | 11.80230 |
| AR(7) | 5.60254 | 9.18891 | 9.23695 | 7.40072 | 9.98525 | 11.66830 | ||
| Naive | 6.25091 | 11.78682 | 8.76700 | 8.46851 | 12.49491 | 13.42239 | ||
| FAR() | 9 | 7.28609 | 10.34856 | 12.47580 | 21 | 6.28777 | 9.03979 | 9.63504 |
| AR(7) | 8.17881 | 11.92595 | 13.42361 | 6.26023 | 9.14635 | 9.46692 | ||
| Naive | 7.14544 | 11.18423 | 11.62178 | 8.05637 | 12.35241 | 11.55807 | ||
| FAR() | 10 | 6.73647 | 9.88567 | 11.63280 | 22 | 5.11291 | 7.86378 | 8.41742 |
| AR(7) | 7.67803 | 11.57003 | 12.60697 | 5.18257 | 8.05526 | 8.48756 | ||
| Naive | 6.95444 | 10.27270 | 11.25744 | 7.08351 | 10.66474 | 10.11036 | ||
| FAR() | 11 | 6.09630 | 9.80792 | 9.88950 | 23 | 3.86946 | 6.64648 | 6.09351 |
| AR(7) | 6.80914 | 11.15632 | 10.81531 | 3.93445 | 9.78030 | 6.12057 | ||
| Naive | 6.40122 | 10.11695 | 9.80316 | 6.14502 | 9.13875 | 9.47691 | ||
| FAR() | 12 | 5.79828 | 10.13717 | 8.84841 | 24 | 3.55292 | 6.70792 | 5.27639 |
| AR(7) | 6.45438 | 11.43950 | 9.81589 | 3.55885 | 6.69256 | 5.32193 | ||
| Naive | 5.94363 | 10.01007 | 8.73133 | 4.49332 | 7.98897 | 6.5533 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jan, F.; Shah, I.; Ali, S. Short-Term Electricity Prices Forecasting Using Functional Time Series Analysis. Energies 2022, 15, 3423. https://doi.org/10.3390/en15093423
Jan F, Shah I, Ali S. Short-Term Electricity Prices Forecasting Using Functional Time Series Analysis. Energies. 2022; 15(9):3423. https://doi.org/10.3390/en15093423
Chicago/Turabian StyleJan, Faheem, Ismail Shah, and Sajid Ali. 2022. "Short-Term Electricity Prices Forecasting Using Functional Time Series Analysis" Energies 15, no. 9: 3423. https://doi.org/10.3390/en15093423
APA StyleJan, F., Shah, I., & Ali, S. (2022). Short-Term Electricity Prices Forecasting Using Functional Time Series Analysis. Energies, 15(9), 3423. https://doi.org/10.3390/en15093423







