A Review of Aging Models for Electrical Insulation in Power Cables
Abstract
:1. Introduction
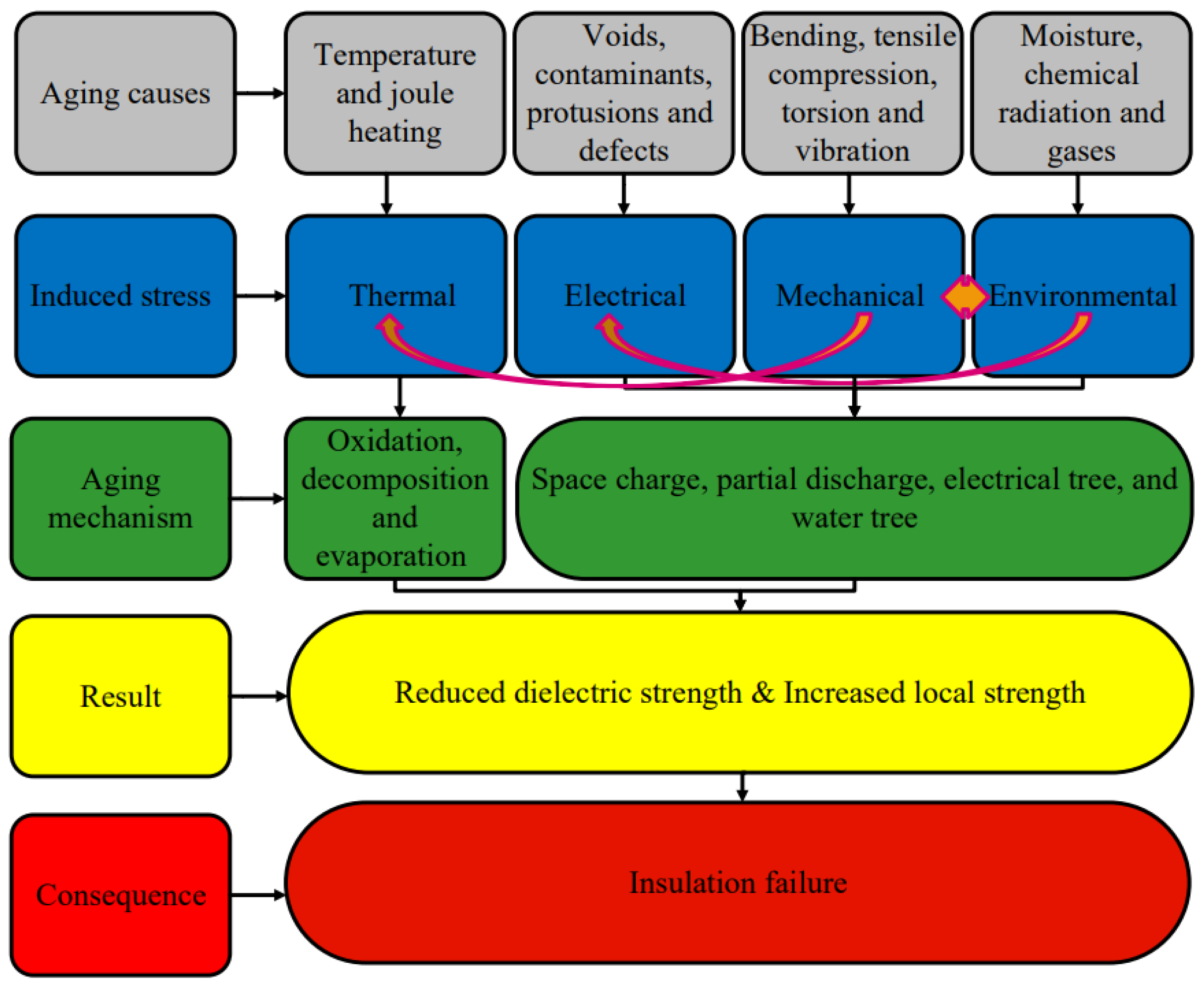
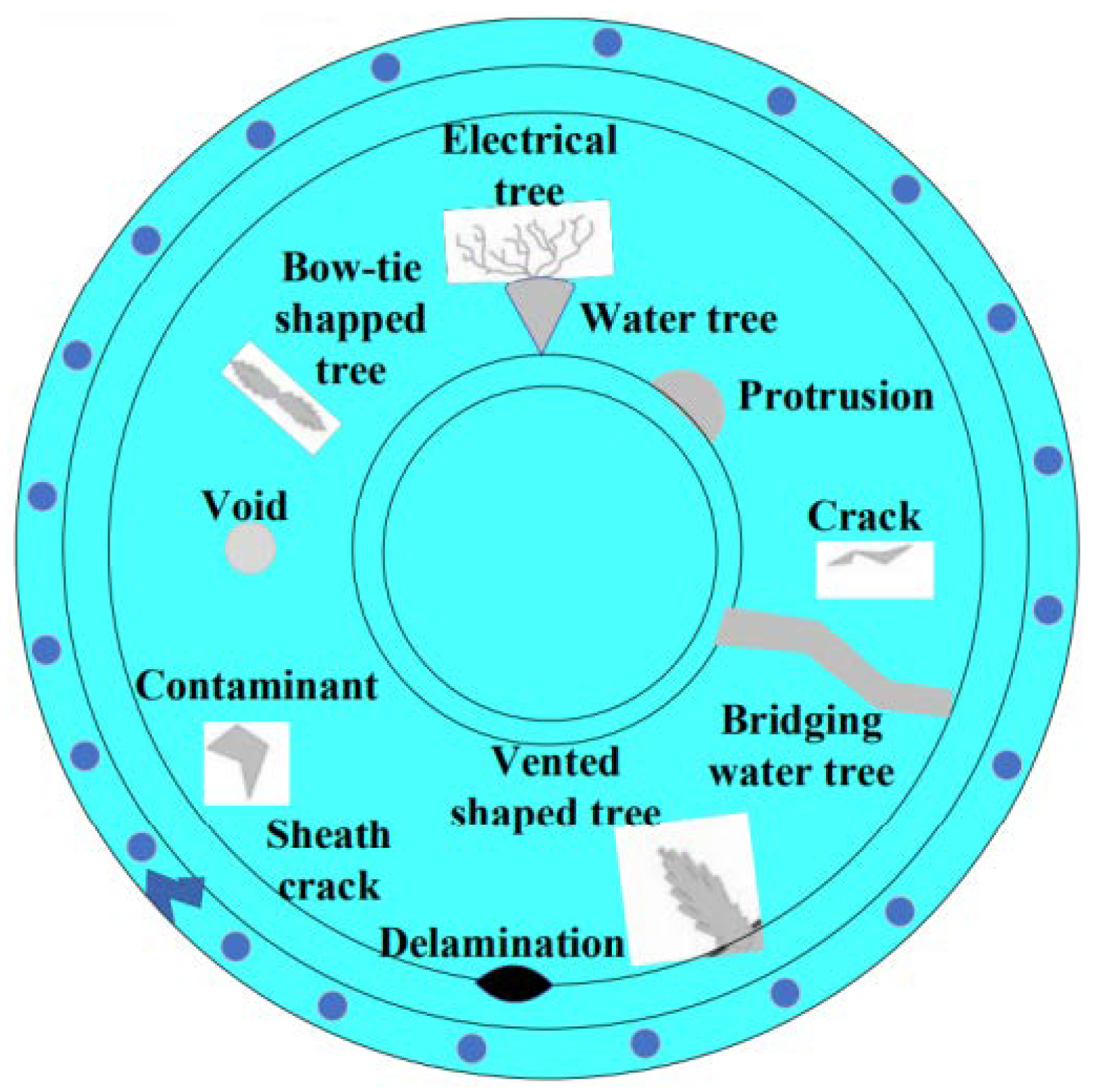
2. Insulation Degradation in Solids and Aging Models
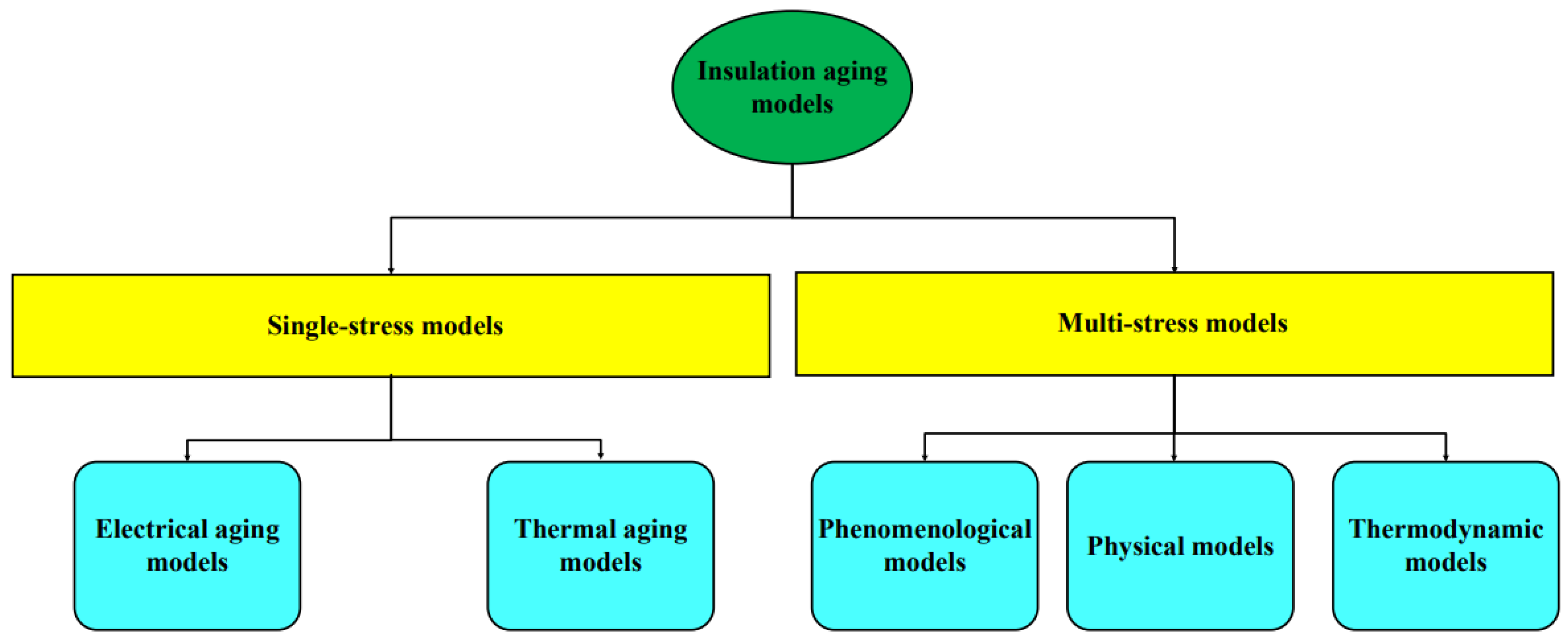
3. Single-Stress Aging Models
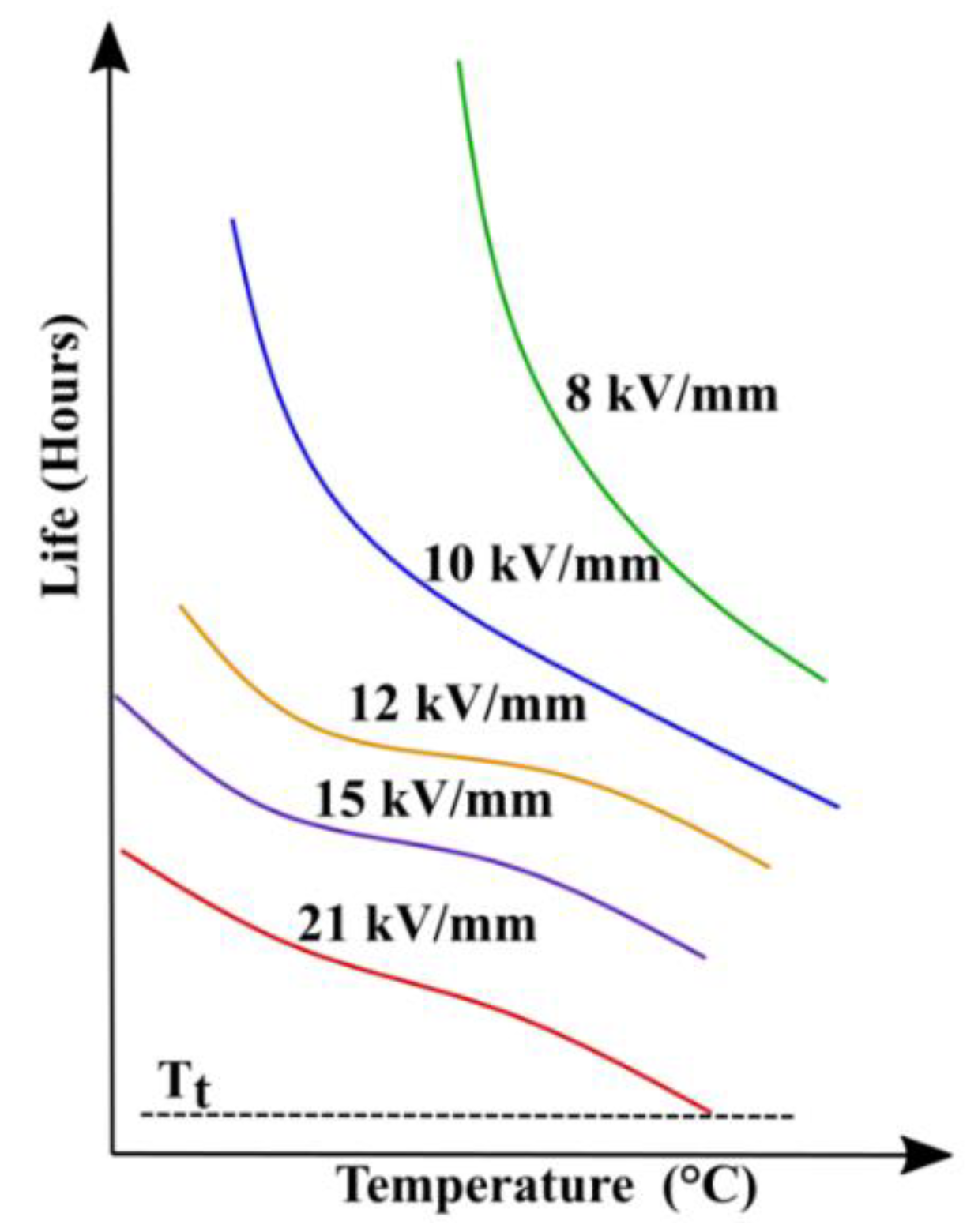
3.1. Electrical-Aging Models
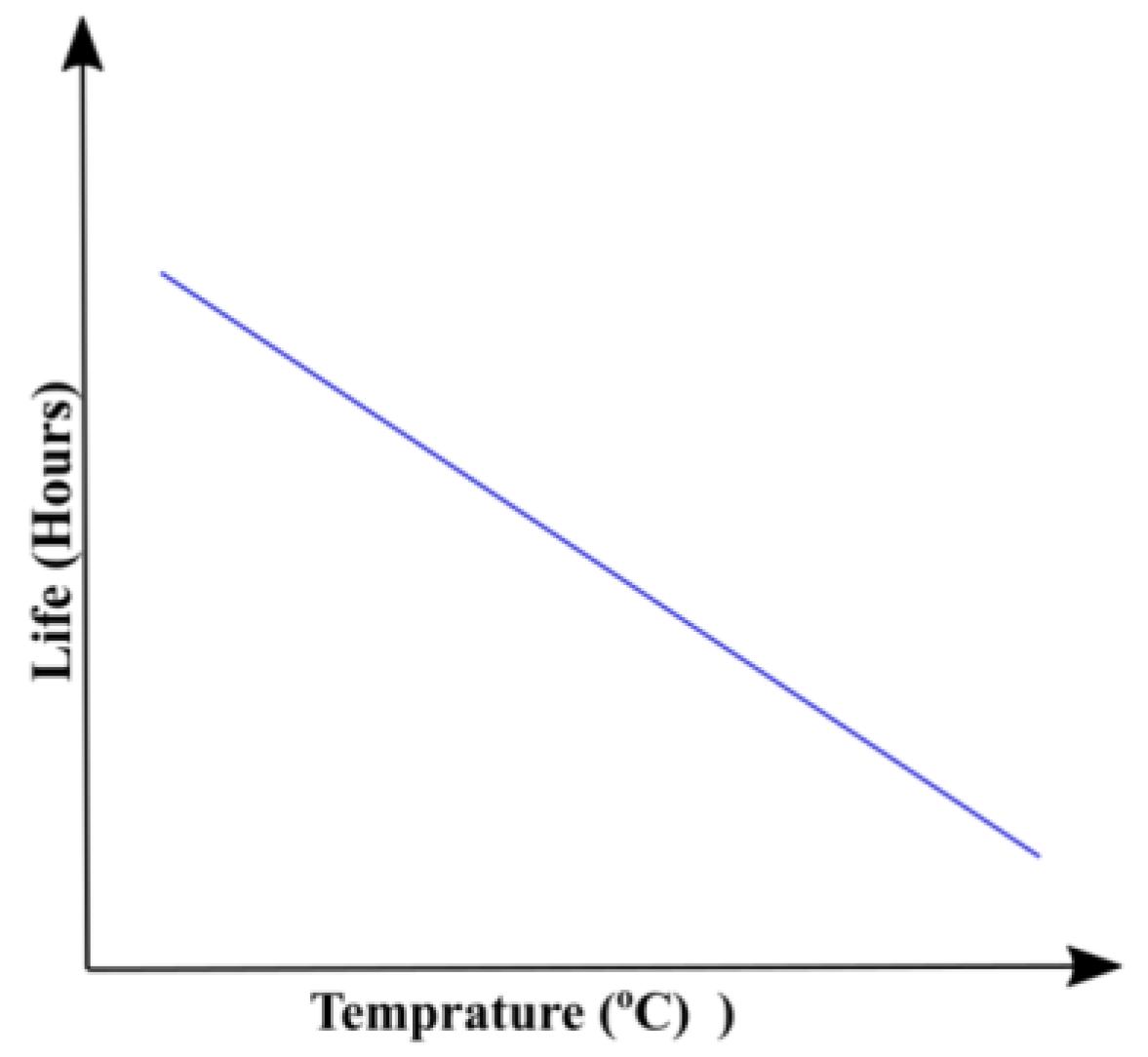
3.2. Thermal-Aging Models
- increase in dissipation factor and conductance due to oxidation.
- brittle hardening of the insulation due to reduction in the plasticizer effect.
- depolarization of plastic insulation at elevated temperatures.
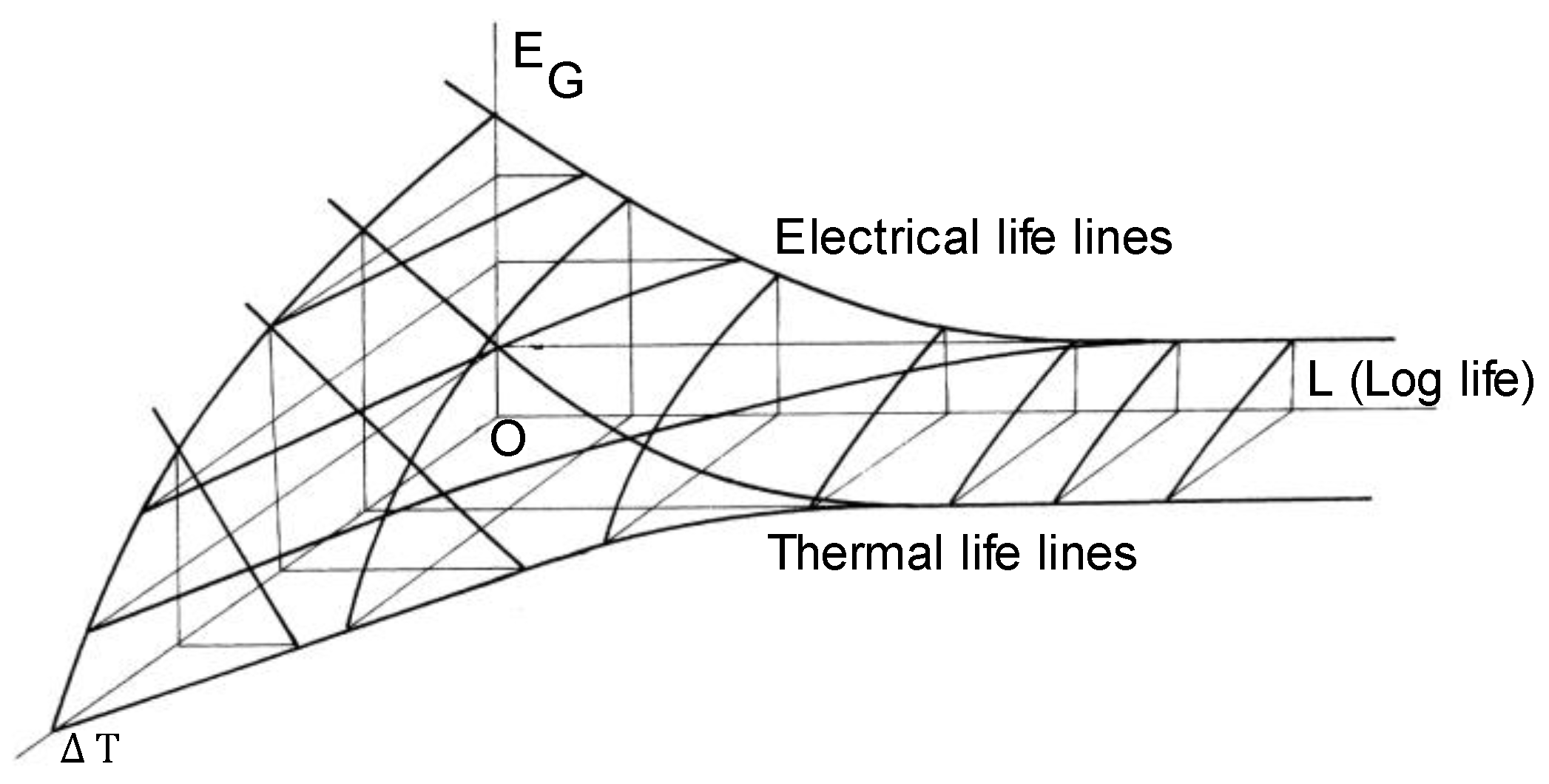
4. Multistress Aging Models
- Phenomenological Models.
- Thermodynamic Models.
- Physical Models.
4.1. Phenomenological Models
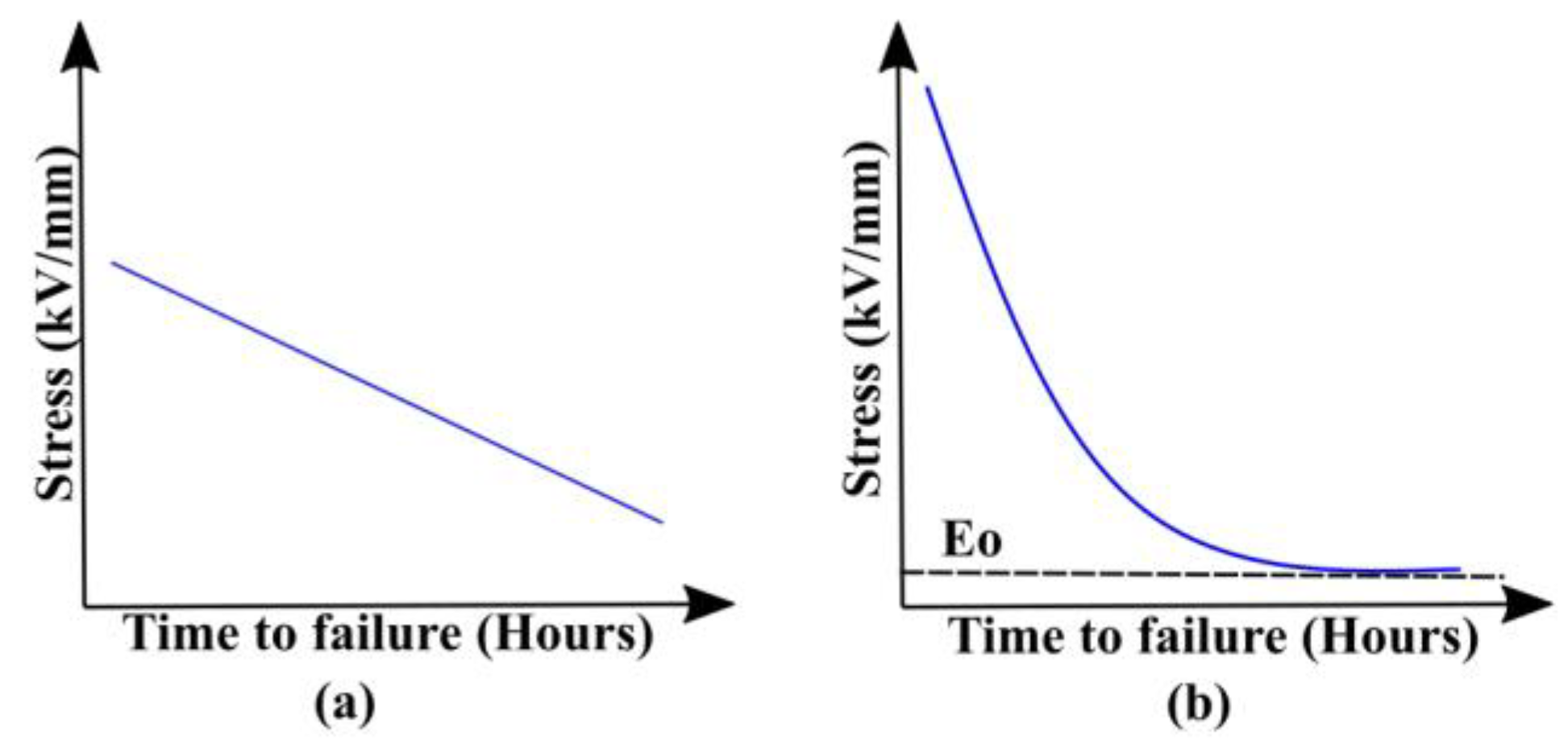
- Depicts the relationship between stress (es) and life of the equipment based on the experimental data;
- Characterizes insulating materials based on experimental evidence rather than physical properties;
- Predicts life at any stage through extrapolation of the test data;
- Statistical and statistical or probabilistic approaches can be used to find model parameters.
- In absence of electrical stress in other words (E ≤ EGto), the model must tend to the thermal model; however, at T ≤ Tto, the life function must tend to infinity.
- Likewise, in the absence of thermal stress the model must tend to the electrical model and at lower value of electrical stress (E ≤ Eto), the life must follow upward curvature (tend to infinity).
4.2. Physical Models
4.3. Thermodynamic Models
5. Discussion
- It has been observed that most of the models are material-oriented, as their validity is examined on certain materials. It can be seen in Table 1 that most of the models are tested on XLPE and ethylene-propylene rubber (EPR) cables. However, insulation characteristics or aging behavior varies with material type, manufacturing techniques, operating environments, and level of stress applied. The life of cables with the same insulation installed in different networks is different. This depends on the environment and operational conditions. As the operational conditions keep on changing, the degradation rate changes hence the time to failure will change. This challenges the general validity of models.
- Experimental surveys [43,68] show a wide variation in the life graphs of various insulation materials when they come under single or multiple stress. Due to randomness in experimental data points, the graph does not follow a clear pattern. Thus, it is quite unwieldy to fit data accurately in one model. Although the model in [33] is valid for threshold and non-threshold behavior of dielectric materials, the life equation relies on several parameters. Almost all models contain parameters, indicated in Table 1, that can be found by different statistical methods such as maximum likelihood, linear regression, etc. The parameter resembles variables in an equation. It is cumbersome to handle multiple variables when it comes to experimental analysis of combined thermal and electrical stress.
- Considering the operation of the new components being proliferated in the modern grid, such as power electronics converters (PEC), it is found that available models do not incorporate their effect. A model proposed in [69] considers the impact of PEC and describes overall aging or degradation rate as the sum of electrical stress (peak-to-peak value of voltages) at nominal frequency (50 Hz) and the impulse frequency expressed as
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Saleem, M.Z.; Akbar, M. Review of the Performance of High-Voltage Composite Insulators. Polymers 2022, 14, 431. [Google Scholar] [CrossRef]
- Campo, E.A. 4—Electrical Properties of Polymeric Materials. In Selection of Polymeric Materials; Plastics Design Library, Willian Andrew Inc.: Norwich, NY, USA, 2008; pp. 141–173. [Google Scholar] [CrossRef]
- Garros, B. Ageing and reliability testing and monitoring of power cables: Diagnosis for insulation systems: The ARTEMIS program. IEEE Electr. Insul. Mag. 1999, 15, 10–12. [Google Scholar] [CrossRef]
- Bertling, L.; Eriksson, R.; Allan, R.N.; Gustafsson, L.Å.; Åhlén, M. Survey of causes of failures based on statistics and practice for improvements of preventive maintenance plans. In Proceedings of the 14th Power Systems Computation Conference, Seville, Spain, 24–28 June 2002; pp. 1–7. [Google Scholar]
- Dakin, T.W. Electrical Insulation Deterioration Treated as a Chemical Rate Phenomenon. Cond. Affect. Success Main Line Electrif. 1948, 67, 113–122. [Google Scholar] [CrossRef]
- Mazzanti, G.; Montanari, G.C.; Dissado, L.A. Electrical aging and life models: The role of space charge. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 876–890. [Google Scholar] [CrossRef]
- Densley, J. Ageing mechanisms and diagnostics for power cables—An overview. IEEE Electr. Insul. Mag. 2001, 17, 14–22. [Google Scholar] [CrossRef]
- Van der Wielen, P.C.J.M. On-Line Detection and Location of Partial Discharges in Medium-Voltage Power Cables. Ph.D. Dissertation, Eindhoven University of Technology, Eindhoven, The Netherlands, 2005. [Google Scholar]
- Yaacob, M.M.; Alsaedi, M.A.; Rashed, J.R.; Dakhil, A.M.; Atyah, S.F. Review on partial discharge detection techniques related to high voltage power equipment using different sensors. Photon Sens. 2014, 4, 325–337. [Google Scholar] [CrossRef] [Green Version]
- Tshiloz, K.; Smith, A.C.; Mohammed, A.; Djurović, S.; Feehally, T. Real-time insulation lifetime monitoring for motor windings. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 2335–2340. [Google Scholar] [CrossRef] [Green Version]
- Zaeni, A.; Khayam, U.; Viviantoro, D. Methods for Remaining Life Prediction of Power Cable based on Partial Discharge with Regard to Loading Factor Calculation and Voltage Variation. In Proceedings of the 2019 2nd International Conference on High Voltage Engineering and Power Systems (ICHVEPS), Denpasar, Indonesia, 1–4 October 2019; pp. 180–185. [Google Scholar]
- Srinivasan, M.; Krishnan, A. Prediction of Transformer Insulation Life with an Effect of Environmental Variables. Int. J. Comput. Appl. 2012, 55, 43–48. [Google Scholar] [CrossRef]
- Bahadoorsingh, S.; Rowland, S. A Framework Linking Knowledge of Insulation Aging to Asset Management. IEEE Electr. Insul. Mag. 2008, 24, 38–46. [Google Scholar] [CrossRef]
- Shafiq, M.; Kauhaniemi, K.; Robles, G.; Isa, M.; Kumpulainen, L. Online condition monitoring of MV cable feeders using Rogowski coil sensors for PD measurements. Electr. Power Syst. Res. 2019, 167, 150–162. [Google Scholar] [CrossRef]
- Hovonen, P. Prediction of Insulation Degradation of Distribution Power Cables Based on Chemical Analysis and Electrical Measurements. Ph.D. Dissertation, Aalto University, Espoo, Finland, 2008. [Google Scholar]
- Shafiq, M.; Kiitam, I.; Kauhaniemi, K.; Taklaja, P.; Kütt, L.; Palu, I. Performance Comparison of PD Data Acquisition Techniques for Condition Monitoring of Medium Voltage Cables. Energies 2020, 13, 4272. [Google Scholar] [CrossRef]
- Ahmed, Z. Development of a Continuous Condition Monitoring System Based on Probabilistic Modelling of Partial Discharge Data for Polymeric Insulation Cables. Ph.D. Dissertation, Mississippi State University, Starkville, MS, USA, 2019. [Google Scholar]
- Choudhary, M.; Suwanasri, T.; Kumpalavalee, S.; Fuangpian, P.; Suwanasri, C. Condition Assessment of Synchronous Generator Using Fuzzy Logic. IEET Int. Electr. Eng. Trans. 2018, 4, 27. [Google Scholar]
- David, E.; Parpal, J.-L.; Crine, J.-P. Aging of XLPE cable insulation under combined electrical and mechanical stresses. In Proceedings of the 1996 IEEE International Symposium on Electrical Insulation, Montreal, QC, Canada, 16–19 June 1996. [Google Scholar] [CrossRef]
- Zhou, C.; Yi, H.; Dong, X. Review of Recent Research Towards Power Cable Life Cycle Management. High Volt. 2017, 2, 179–187. [Google Scholar] [CrossRef]
- Higinbotham, W. Review of Medium-Voltage Asset Failure Investigations. Prem. Electr. Maint. Saf. Event 2018, 1, 17. [Google Scholar]
- Toshikatsu, T.; Greenwood, A. Advanced Power Cable Technology: Present and Future; CRC Press Inc.: Boca Raton, FL, USA, 1983; Volume 2, pp. 57–94. [Google Scholar]
- Su, J.; Du, B.; Li, J.; Li, Z. Electrical tree degradation in high-voltage cable insulation: Progress and challenges. High Volt. 2020, 5, 353–364. [Google Scholar] [CrossRef]
- Helleso, S.; Benjaminsen, J.T.; Selsjord, M.; Hvidsten, S. Water tree initiation and growth in XLPE cables under static and dynamic mechanical stress. In Proceedings of the 2012 IEEE International Symposium on Electrical Insulation, San Juan, PR, USA, 10–13 June 2012; pp. 623–627. [Google Scholar] [CrossRef]
- IEEE 1407; IEEE Guide for Accelerated Aging Tests for Medium-Voltage (5 kV–35 kV) Extruded Electric Power Cables Using Water-Filled Tanks. IEEE: Piscataway, NJ, USA, 2017.
- IEEE 98; IEEE Standard for the Preparation of Test Procedures for the Thermal Evaluation of Solid Electrical Insulating Materials. IEEE: Piscataway, NJ, USA, 2016; pp. 1–32.
- Montanari, G.; Motori, A. Short-term thermal endurance characterization of polymeric cable insulating materials. Use of oxidative stability measurements. IEEE Trans. Dielectr. Electr. Insul. 1996, 3, 561–566. [Google Scholar] [CrossRef]
- IEC-60270:2000+AMD1; High-Voltage Test Techniques-Partial Discharge Measurements. IEC: Geneva, Switzerland, 2015.
- Hussain, G.A.; Shafiq, M.; Lehtonen, M.; Hashmi, M. Online Condition Monitoring of MV Switchgear Using D-Dot Sensor to Predict Arc-Faults. IEEE Sens. J. 2015, 15, 7262–7272. [Google Scholar] [CrossRef]
- Simoni, L. A General Approach to the Endurance of Electrical Insulation under Temperature and Voltage. IEEE Trans. Electr. Insul. 1981, 16, 277–289. [Google Scholar] [CrossRef]
- Simoni, L. General Equation of the Decline in the Electric Strength for Combined Thermal and Electrical Stresses. IEEE Trans. Electr. Insul. 1984, 19, 45–52. [Google Scholar] [CrossRef]
- Simoni, L.; Mazzanti, G.; Montanari, G.; Lefebre, L. A general multi-stress life model for insulating materials with or without evidence for thresholds. IEEE Trans. Electr. Insul. 1993, 28, 349–364. [Google Scholar] [CrossRef]
- Dissado, L.; Mazzanti, G.; Montanari, G.C. The incorporation of space charge degradation in the life model for electrical insulating materials. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 1147–1158. [Google Scholar] [CrossRef]
- IEEE Dielectrics and Electrical Insulation Society; Multifactor Stress Committee. IEEE Guide for Multifactor Stress Functional Testing of Electrical Insulation Systems; IEEE: Piscataway, NJ, USA, 1991. [Google Scholar]
- Edwards, V. Electrons Theory; Edtech Press: London, UK, 2018; Chapter 1; pp. 1–15. [Google Scholar]
- Fisher, L.E.; Haries, C.D.; Lehr, J.M. Initiation and Growth of the Secondary Electron Avalanche along High-Gradient Insulators in Vacuum. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 972–980. [Google Scholar] [CrossRef]
- IEC 61251; Electrical Insulating Materials and Systems-AC Voltage Endurance Evaluation. IEC: Geneva Switzerland, 2015.
- IEEE 930-1987; IEEE Guide for the Statistical Analysis of Electrical Insulation Voltage Endurance Data. IEEE: Piscataway, NJ, USA, 1995.
- Stone, G.C.; Lawless, J.F. The Application of Weibull Statistics to Insulation Aging Tests. IEEE Trans. Electr. Insul. 1979, 14, 233–239. [Google Scholar] [CrossRef]
- Cygan, P.; Laghari, J.R. Models for insulation aging under electrical and thermal multistress. IEEE Trans. Electr. Insul. 1990, 25, 923–934. [Google Scholar] [CrossRef]
- Pattini, G.; Simoni, L. Discussion on modeling of voltage endurance. In Proceedings of the 1980 IEEE International Conference on Electrical Insulation, Boston, MA, USA, 9–11 June 1980. [Google Scholar] [CrossRef]
- Dakin, T.W. The Endurance of Electrical Insulation. In Proceedings of the 4th Symposium Electrical Insulation Materials, JIEE, Saclay, France, 21–23 April 1971. [Google Scholar]
- Montanari, G.C.; Simoni, L. Aging phenomenology and modeling. IEEE Trans. Electr. Insul. 1993, 28, 755–776. [Google Scholar] [CrossRef]
- Hirose, H. A Method to Estimate the Lifetime of Solid Electrical Insulation. IEEE Trans. Electr. Insul. 1987, 22, 745–753. [Google Scholar] [CrossRef]
- Montsinger, V.M. Loading Transformers by Temperature. Cond. Affect. Success Main Line Electrif. 1930, 49, 776–790. [Google Scholar] [CrossRef]
- Brancato, E. Insulation Aging a Historical and Critical Review. IEEE Trans. Electr. Insul. 1978, 13, 308–317. [Google Scholar] [CrossRef]
- IEEE Std 101-1987; IEEE Guide for the Statistical Analysis of Thermal Life Test Data. IEEE: Piscataway, NJ, USA, 1988.
- Endicott, H.S.; Hatch, B.D.; Sohmer, R.G. Application of the Eyring Model to capacitor aging data. In Proceedings of the Annual Report 1962 Conference on Electrical Insulation, Hershey, PA, USA, 15–17 October 1962; pp. 47–50. [Google Scholar]
- Simoni, L. Application of a new geometrical approach to determination of combined stress endurance of insulating materials. IEEE Trans. Electr. Insul. 1988, 23, 489–492. [Google Scholar] [CrossRef]
- IEC 60216–3; Electrical Insulating Materials—Thermal Endurance Properties—Part 3: Instructions for Calculating Thermal Endurance Characteristics. IEC: Geneva, Switzerland, 2021.
- Nelson, W. Analysis of Accelerated Life Test Data—Part I: The Arrhenius Model and Graphical Methods. IEEE Trans. Electr. Insul. 1971, 6, 165–181. [Google Scholar] [CrossRef]
- Mazzanti, G.; Montanari, G. A comparison between XLPE and EPR as insulating materials for HV cables. IEEE Trans. Power Deliv. 1997, 12, 15–28. [Google Scholar] [CrossRef]
- Montanari, G.C.; Pattini, G.; Simoni, L. Long—Term Behavior of XLPE Insulated Cable Models. IEEE Trans. Power Deliv. 1987, 2, 596–602. [Google Scholar] [CrossRef]
- Ramu, T.S. On the estimation of life of power apparatus insulation under combined electrical and thermal stress. IEEE Trans. Electr. Insul. 1985, EI-20, 70–78. [Google Scholar] [CrossRef]
- Montanari, G.C. Insulation Aging Models. In Encyclopedia of Electrical and Electronics Engineering; J. Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Fallou, B.; Burguiere, C. First Approach on Multiple Stress Accelerated Life Testing of Electrical insulation. Annu. Rep. Proc. CEIDP 1979, 621–628. [Google Scholar]
- Cacciari, M.; Montanari, G. Optimum design of life tests for insulating materials, systems and components. IEEE Trans. Electr. Insul. 1991, 26, 1112–1123. [Google Scholar] [CrossRef]
- Cacciari, M.; Montanari, G.C. Probabilistic models for life prediction of insulating materials. J. Phys. D Appl. Phys. 1990, 23, 1592–1598. [Google Scholar] [CrossRef]
- Montanari, G.; Cacciari, M. A probabilistic life model for insulating materials showing electrical thresholds. IEEE Trans. Electr. Insul. 1989, 24, 127–134. [Google Scholar] [CrossRef]
- Bahder, G.; Garrity, T.; Sosnowski, M.; Eaton, R.; Katz, C. Physical Model of Electric Aging and Breakdown of Extruded Pplymeric Insulated Power Cables. IEEE Trans. Power Appar. Syst. 1982, 101, 1379–1390. [Google Scholar] [CrossRef]
- Montanari, G. Aging and life models for insulation systems based on PD detection. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 667–675. [Google Scholar] [CrossRef]
- Zhang, Y.; Lewiner, J.; Alquie, C.; Hampton, N. Evidence of strong correlation between space-charge buildup and breakdown in cable insulation. IEEE Trans. Dielectr. Electr. Insul. 1996, 3, 778–783. [Google Scholar] [CrossRef]
- Crine, J.-P.; Parpal, J.-L.; Lessard, G. A model of aging of dielectric extruded cables. In Proceedings of the 3rd International Conference on Conduction and Breakdown in Solid Dielectrics, Trondheim, Norway, 3–6 July 1989; pp. 347–351. [Google Scholar]
- Sanche, L. Electronic aging and related electron interactions in thin-film dielectrics. IEEE Trans. Electr. Insul. 1993, 28, 789–819. [Google Scholar] [CrossRef]
- Griffiths, C.; Freestone, J.; Hampton, R. Thermoelectric aging of cable grade XLPE. In Proceedings of the Conference Record of IEEE International Symposium on Electrical Insulation, Arlington, VA, USA, 7–10 June 1998; Volume 2, pp. 578–582. [Google Scholar]
- Dissado, L.A.; Mazzanti, G.; Montanari, G.C. The role of trapped space charges in the electrical aging of insulating materials. IEEE Trans. Dielectr. Electr. Insul. 1997, 4, 496–506. [Google Scholar] [CrossRef]
- Mazzanti, G.; Montanari, G.; Dissado, L. A space-charge life model for ac electrical aging of polymers. IEEE Trans. Dielectr. Electr. Insul. 1999, 6, 864–875. [Google Scholar] [CrossRef]
- Gubanski, S.M. Analysis of lifetime estimation methods based on data for electro-thermally aged PET films. In Proceedings of the Conference Record of IEEE International Symposium on Electrical Insulation, Toronto, ON, Canada, 3–6 June 1990; pp. 27–30. [Google Scholar] [CrossRef]
- Cavallini, A.; Fabiani, D.; Montanari, G.C. Power electronics and electrical insulation systems—Part 2: Life modeling for insulation design. IEEE Electr. Insul. Mag. 2010, 26, 33–39. [Google Scholar] [CrossRef]
- Frigione, M.; Rodríguez-Prieto, A. Can Accelerated Aging Procedures Predict the Long Term Behavior of Polymers Exposed to Different Environments? Polymers 2021, 13, 2688. [Google Scholar] [CrossRef] [PubMed]


| Model No. | Model Equation | Model Type and No. of Parameters | Validity Tested On | References |
|---|---|---|---|---|
| 1. | Phenomenological 4 | Poly propylene-oil system | [56] | |
| 2. | Phenomenological 6 | Composite (Nomex-Mylar-Nomex), cycloaliphatic epoxy resin and polyurethane resin | [31] | |
| 3. | Phenomenological 7 | XLPE Cables and (Composite N-M-N) | [33] | |
| 4. | Phenomenological 5 | XLPE Cables | [59] | |
| 5. | Physical 5 | XLPE, PE (Polyethylene) and (EPR) Cables | [60] | |
| 6. | Physical 4 | XLPE Cables | [61] | |
| 7. | Thermodynamic 1 | Polyethene (HMW-PE), Cross linked PE, XLPE and EPR | [63] | |
| 8. | Thermodynamic 2 | XLPE Cables | [65] | |
| 9. | Thermodynamic 8 | PET and PP Specimen and XLPE cables | [6] | |
| 10. | Phenomenological 1 | Enameled Wires | [69] |
| Model No. | Pros | Cons |
|---|---|---|
| 1. |
| Only valid for non-threshold materials. |
| 2. |
|
|
| 3. |
| Increased number of parameters can increase the complexity of model. |
| 4. |
| The model doesn’t represent the impact of individual stress. There is no separate term for thermal or electrical stress. |
| 5. |
|
|
| 6. |
| Model parameters rely on occurrence of electrical tree. Thus, life prediction prior to tree is not possible. |
| 7. |
|
|
| 8. |
|
|
| 9. |
|
|
| 10. |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choudhary, M.; Shafiq, M.; Kiitam, I.; Hussain, A.; Palu, I.; Taklaja, P. A Review of Aging Models for Electrical Insulation in Power Cables. Energies 2022, 15, 3408. https://doi.org/10.3390/en15093408
Choudhary M, Shafiq M, Kiitam I, Hussain A, Palu I, Taklaja P. A Review of Aging Models for Electrical Insulation in Power Cables. Energies. 2022; 15(9):3408. https://doi.org/10.3390/en15093408
Chicago/Turabian StyleChoudhary, Maninder, Muhammad Shafiq, Ivar Kiitam, Amjad Hussain, Ivo Palu, and Paul Taklaja. 2022. "A Review of Aging Models for Electrical Insulation in Power Cables" Energies 15, no. 9: 3408. https://doi.org/10.3390/en15093408
APA StyleChoudhary, M., Shafiq, M., Kiitam, I., Hussain, A., Palu, I., & Taklaja, P. (2022). A Review of Aging Models for Electrical Insulation in Power Cables. Energies, 15(9), 3408. https://doi.org/10.3390/en15093408








