Assessing the Benthic Response to Climate-Driven Methane Hydrate Destabilisation: State of the Art and Future Modelling Perspectives

Abstract

Modern observations and geological records suggest that anthropogenic ocean warming could destabilise marine methane hydrate, resulting in methane release from the seafloor to the ocean-atmosphere, and potentially triggering a positive feedback on global temperature. On the decadal to millennial timescales over which hydrate-sourced methane release is hypothesized to occur, several processes consuming methane below and above the seafloor have the potential to slow, reduce or even prevent such release. Yet, the modulating effect of these processes on seafloor methane emissions remains poorly quantified, and the full impact of benthic methane consumption on ocean carbon chemistry is still to be explored. In this review, we document the dynamic interplay between hydrate thermodynamics, benthic transport and biogeochemical reaction processes, that ultimately determines the impact of hydrate destabilisation on seafloor methane emissions and the ocean carbon cycle. Then, we provide an overview of how state-of-the-art numerical models treat such processes and examine their ability to quantify hydrate-sourced methane emissions from the seafloor, as well as their impact on benthic biogeochemical cycling. We discuss the limitations of current models in coupling the dynamic interplay between hydrate thermodynamics and the different reaction and transport processes that control the efficiency of the benthic sink, and highlight their shortcoming in assessing the full implication of methane release on ocean carbon cycling. Finally, we recommend that current Earth system models explicitly account for hydrate driven benthic-pelagic exchange fluxes to capture potential hydrate-carbon cycle-climate feed-backs.

1. Introduction

Methane hydrate sequesters vast amounts of carbon within continental margin, and subsea-permafrost bearing shelf sediments. In these locations, changes in atmospheric-ocean temperatures and sea-level associated with global climate change may perturb the hydrate stability field and lead to methane release into deep sediments, the overlying water column, and ultimately, the atmosphere [1,2].

Hydrate reservoirs located on upper continental slopes and those associated with thawing subsea permafrost beneath the shallow Arctic Ocean shelves are the most vulnerable to climate change [2]. Assessing the environmental implications of hydrate destabilisation in these settings requires accounting for both benthic and pelagic methane sinks. This review focuses on describing the physical and biogeochemical benthic processes dominating the fate of methane released from hydrates in marine reservoirs. Although the main processes at play in marine environments are similar to those in subsea permafrost settings, the latter, are characterized by very specific and, still poorly known environmental conditions (e.g., the reactivity of thawing permafrost organic matter, rates of methanogenesis, and dominant modes of methane transport) [3], that are beyond the scope of this review.

Marine sediments store about 99% of the global hydrate inventory (e.g., [4]). Size estimates of this reservoir range from 100 to 530,000 gigatons of carbon (GtC), with most likely values around 1800–2000 GtC [2,5,6]. On geological timescales, ocean warming may have caused the destabilisation of marine hydrate, resulting in methane leakage to the seafloor and arguably the atmosphere (e.g., [2,7,8,9,10,11,12]). The large negative carbon isotopic excursion (CIE) recorded in both marine and terrestrial sediments during past hyper-thermal events, have been widely interpreted as a widespread release of isotopically-light (i.e., microbial) carbon from dissociating marine methane gas hydrates [13,14]. However, whether methane from hydrates was indeed the source of the atmospheric carbon that drove additional warming in past hyper-thermal events still remains controversial [15,16,17,18].

Recent modelling efforts (e.g., [19,20,21,22]) and field observations (e.g., [1,23,24,25,26,27]) suggest that anthropogenic ocean warming may be causing hydrate destabilisation in the contemporary ocean. Given the strong global warming potential of methane (i.e., 25 times higher than that of carbon dioxide [28]), a major concern is that the accelerating rates of ocean warming might release large amounts of methane stored in hydrates, further amplifying anthropologically driven global warming and accelerating the destabilisation of remaining hydrates [29]. However, on a global scale, hydrate-sourced methane emissions are forecast to have a minor impact on climate during this century [30] (neglecting contributions from abrupt methane release events such as those triggered by submarine slumps), in part owing to a highly efficient consumption of methane within the sediment-ocean continuum [2,12,20,31,32] (Figure 1).

The benthic methane sink, mostly dominated by anaerobic oxidation of methane (AOM), and to a lesser extent by aerobic oxidation of methane (AeOM) [34,35,36], has long been recognized as an extremely efficient microbial filter for upward migrating methane. In particular, in diffusion dominated settings, the AOM is estimated to be capable of mitigating up to 100% of methane from reaching the seafloor [37,38,39]. However, the efficiency of AOM in consuming methane can be highly variable (ranging from 80% to 20% in cold seep settings with slow to high fluid flow, respectively [38]), and is strongly controlled by the balance between multiphase methane transport and microbial dynamics [27,40,41,42]. Environmental factors, such as high sedimentation rates [39], active fluid flow [43], or factors that enable methane to by-pass the AOM and AeOM zones in form of methane gas [43] or through preferential transport paths like fractures [44], reduce the efficiency of the benthic sink, thus, promoting methane emissions to the ocean. In addition, the delayed response of the microbial community to a sudden onset or changes in methane fluxes, caused by the need to build-up a sufficient biomass (e.g., [27,43]), can reduce the AOM efficiency to less than 10% during a transient period of up to a century [38]. Thus, creating important temporal windows of opportunity for methane escape to the ocean [40,41,45].

The current knowledge gap in our quantitative understanding of the dynamic interplay between the numerous factors controlling the efficiency of the benthic methane sink, results in low confidence predictions of methane emissions from the seafloor (particularly those enhanced by hydrate destabilisation) [2,46], and related benthic biogeochemical impacts (e.g., the influence of methane turnover across the sediment column on pore-water chemistry). Indeed, numerical models developed to assess the impact of transport processes on biomass distributions, AOM rates, and methane release from the seafloor, show that when disregarding the variable efficiency of the benthic methane sink, the uncertainty in predicted methane emissions may be much larger than the uncertainty associated with methane emissions predicted using different models of future climate (Figure 2).

Reducing uncertainty in model predictions is important for two reasons. Firstly, the assessment of how much methane is injected into the ocean, and ultimately the atmosphere, is crucial for future climate projections. Secondly, the AOM zone acts as a biogeochemical interface in the global carbon cycle, with an important, yet largely overlooked, impact on regional dissolved inorganic carbon (DIC) budgets, ocean acidification, deoxygenation, and nutrients imbalance [47,48,49,50,51,52,53,54]. The recent work by Akam et al. [55] shows that AOM in contemporary diffusion-dominated marine sediments, supports globally important return fluxes of DIC to the ocean, as well as a significant burial flux of authigenic carbonate. Yet, the importance of this AOM carbon pump and of its potential implications for ocean pH and carbon emissions in response to future methane hydrate destabilisation remains unconstrained [47,56]. In particular, and similar to what is expected to result from increases of atmospheric carbon dioxide, pH decrease resulting from hydrate destabilisation may impact many marine organisms and biological processes [57,58,59,60], including composition of communities and food webs, alter ocean atmospheric carbon dioxide uptake [61,62], and increase the toxicity of certain heavy metals and organic pollutants [63].

Here, we review our current knowledge of the benthic methane sink, as well as important knowledge gaps concerning the benthic biogeochemical response to methane hydrate destabilisation. We illustrate how the benthic methane sink provides a globally important, yet extremely dynamic and poorly quantified barrier for the vast amounts of methane that are generated in marine sediments (see Section 2.3). As a consequence, benthic methane efflux and its benthic biogeochemical impact remain poorly constrained (see Section 2.4). Because of the large amount of methane stored in hydrate reservoirs, the high warming potential of methane gas, and the amplification of climate change in high latitudes that host large amounts of hydrate, this knowledge gap is particularly critical (e.g., [2,27,56]. Therefore, a thorough assessment of the fate of hydrate-related methane in marine sediments that accounts for the full range of interacting physical, biogeochemical and microbial processes is urgently needed to evaluate their impact on climate evolution and provide robust estimates for the design of climate policies.

Numerical models allow the disentangling of the complex and dynamic interplay of transport and reaction processes active in marine sediments for a wide range of environmental conditions. Therefore, they are ideal tools to assess the evolution of hydrate reservoirs in the context of climate change and evaluate the benthic response to related methane fluxes. Here, we review the state-of-the-art numerical models used to simulate the response of hydrate systems to climate change (Section 3). We examine how current models describe, and to what level of detail, the different physical and biogeochemical processes governing methane formation, release, and consumption within the sediment column. In particular, we discuss the limitations of current models at coupling the dynamic interplay between hydrate thermodynamics and the different reaction and transport processes controlling the efficiency of the benthic sink and highlight their shortcoming in considering biogeochemical implications of methane turnover. We also examine the different spatial and temporal scales required on their simulations and evaluate the ability of these models at quantifying methane release, consumption and escape to the ocean. Finally, we examine potential carbon cycle feed-backs associated with climate-driven methane hydrate destabilisation and discuss the need to incorporate these into current Earth System Models (Section 4).

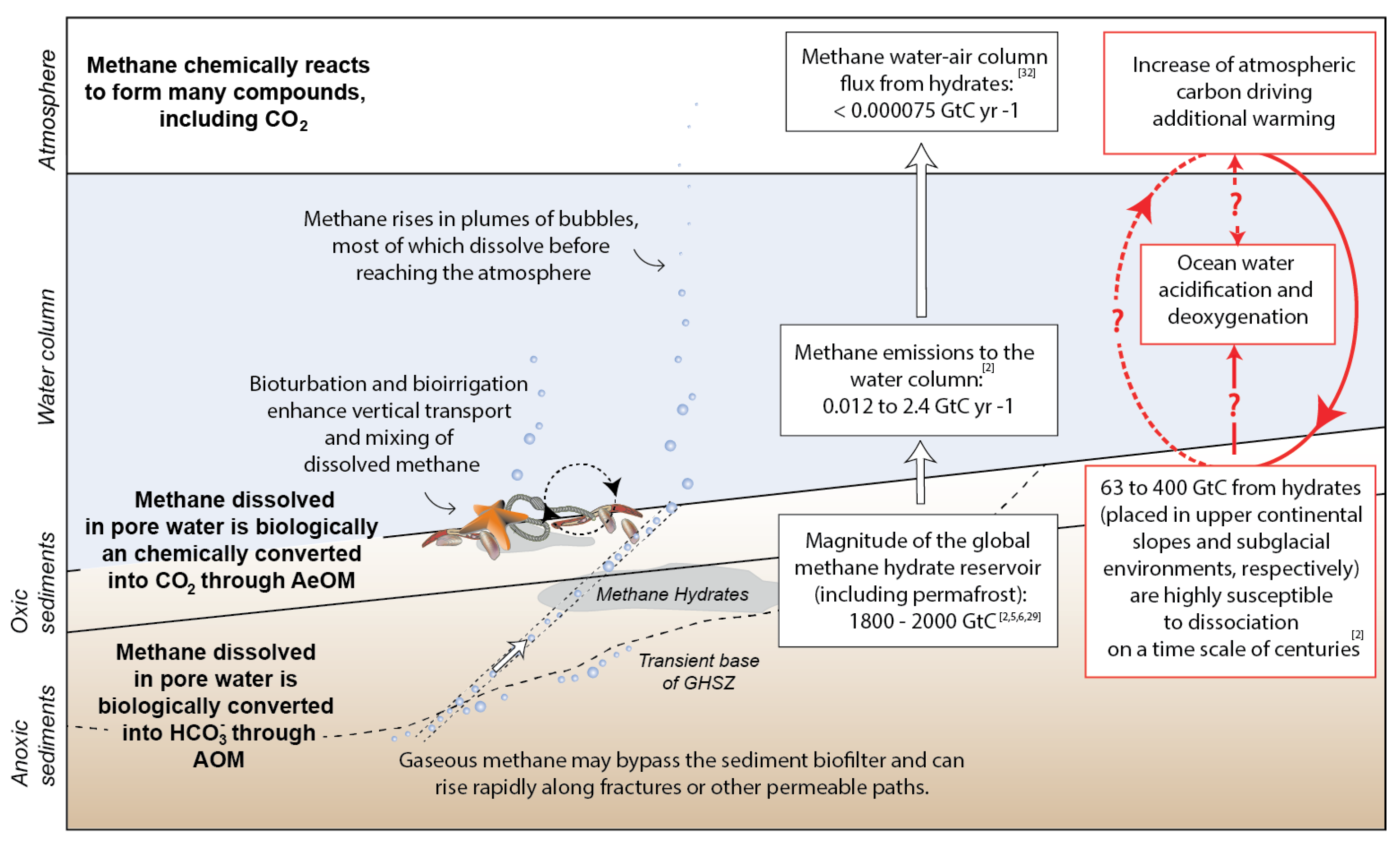
2. Marine Hydrate Destabilisation and Methane Fate within Sediments

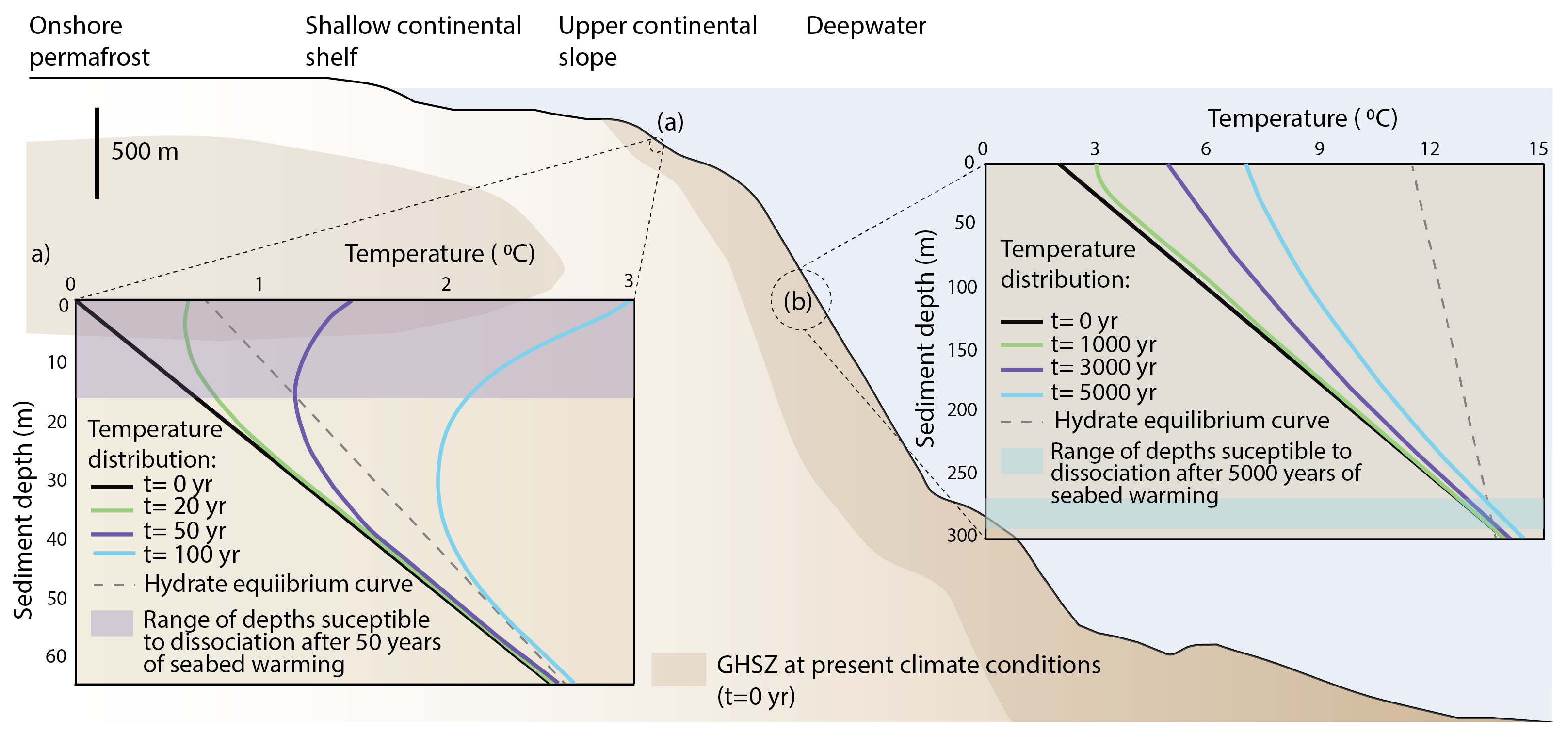
2.1. Hydrate Vulnerability to Climate Perturbations

The stability of marine methane hydrate is highly vulnerable to an increase in ocean bottom-water temperatures and/or sea-level changes (i.e., pressure changes) associated with global climate change [2,33,51,64,65]. In the context of accelerating global warming, central to the discussion is quantifying how sensitive marine methane hydrate systems are to climate perturbations, and thus, what fraction of the hydrate inventory may destabilise, and how fast.

Ruppel et al. [66] estimate that shallow marine systems (Figure 3), corresponding to ∼3.5% of the global gas hydrate inventory (∼63 GtC, assuming an inventory of 1800 GtC), could destabilize in response to ocean warming on a time scale of centuries. Deep-water reservoirs instead are forecast to contribute little to no methane to the ocean even over the next 3000 years (Figure 3). Their contribution to benthic emissions is only forecast on millennial to longer time scales [33,47,66,67]. However, global warming can also promote changes in sea-level that might locally affect the stability of hydrates. In particular, global warming may induce sea-level fall in places where the isostatic response to melting ice sheets outpaces the eustatic sea-level rise. The resulting local reservoir shallowing and lowering of hydrostatic pressure can force hydrate destabilisation [68]. On the other hand, projected sea-level rise related to ice melting and ocean expansion [69] is estimated to exert a minor effect on hydrate stability, generally insufficient to balance for the the destabilising effect of increasing bottom water temperatures (e.g., [51,70]).

A time lag is expected between the onset of the climate perturbation triggering hydrate destabilisation and the emission of methane to the ocean. This time lag can reach centuries to millennia in the deep ocean and depends, among other factors, on (i) thermal diffusion, (ii) hydrate distribution and concentration within the sediment column, (iii) multiphase transport of methane through the sediment dynamically controlled by the pore size distribution, the presence of connected fractures, and interactions between the different fluids, (iv) input of methane into the base of the system, and (v) hydrate phase transition kinetics [65,71,72].

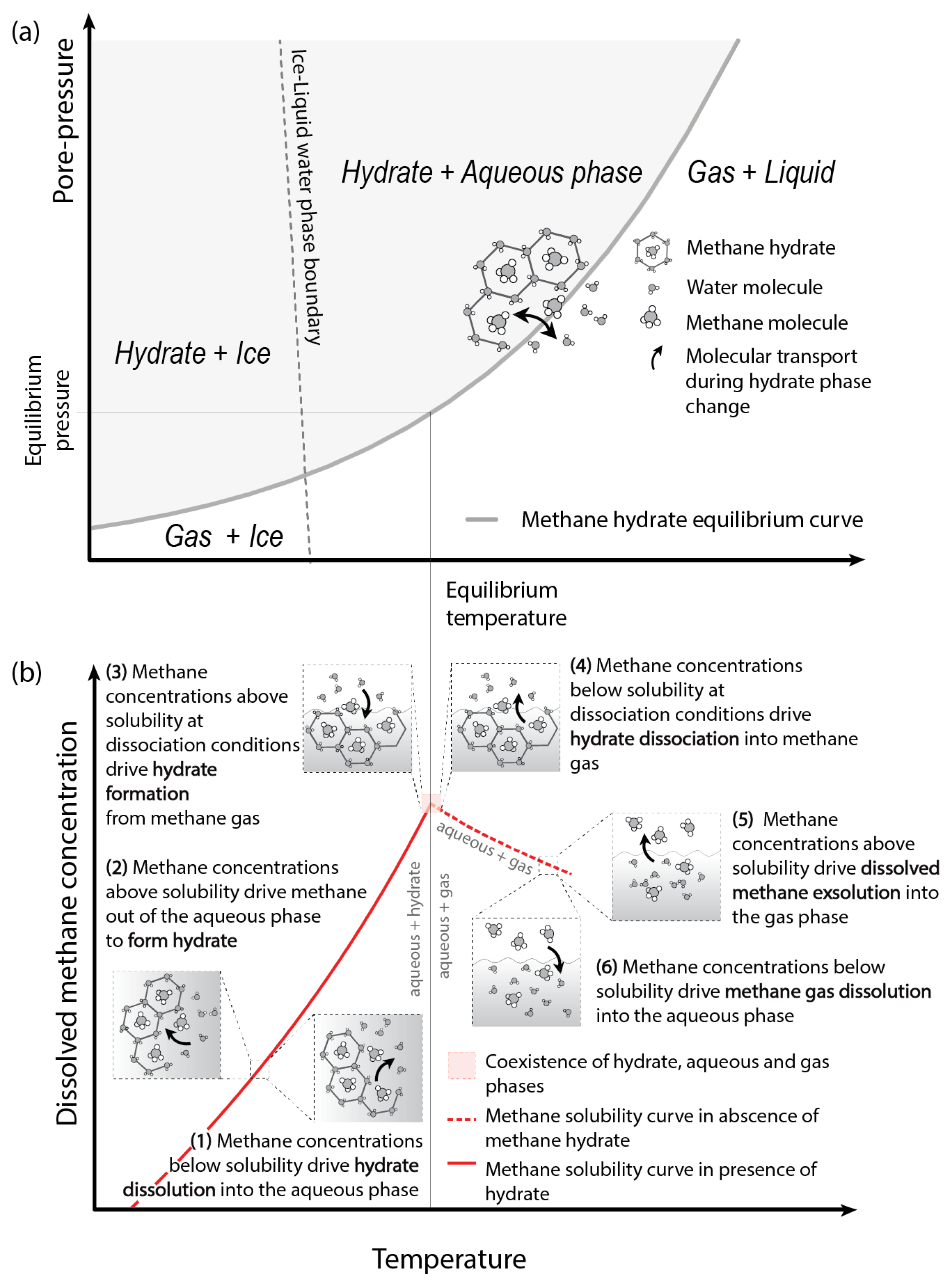
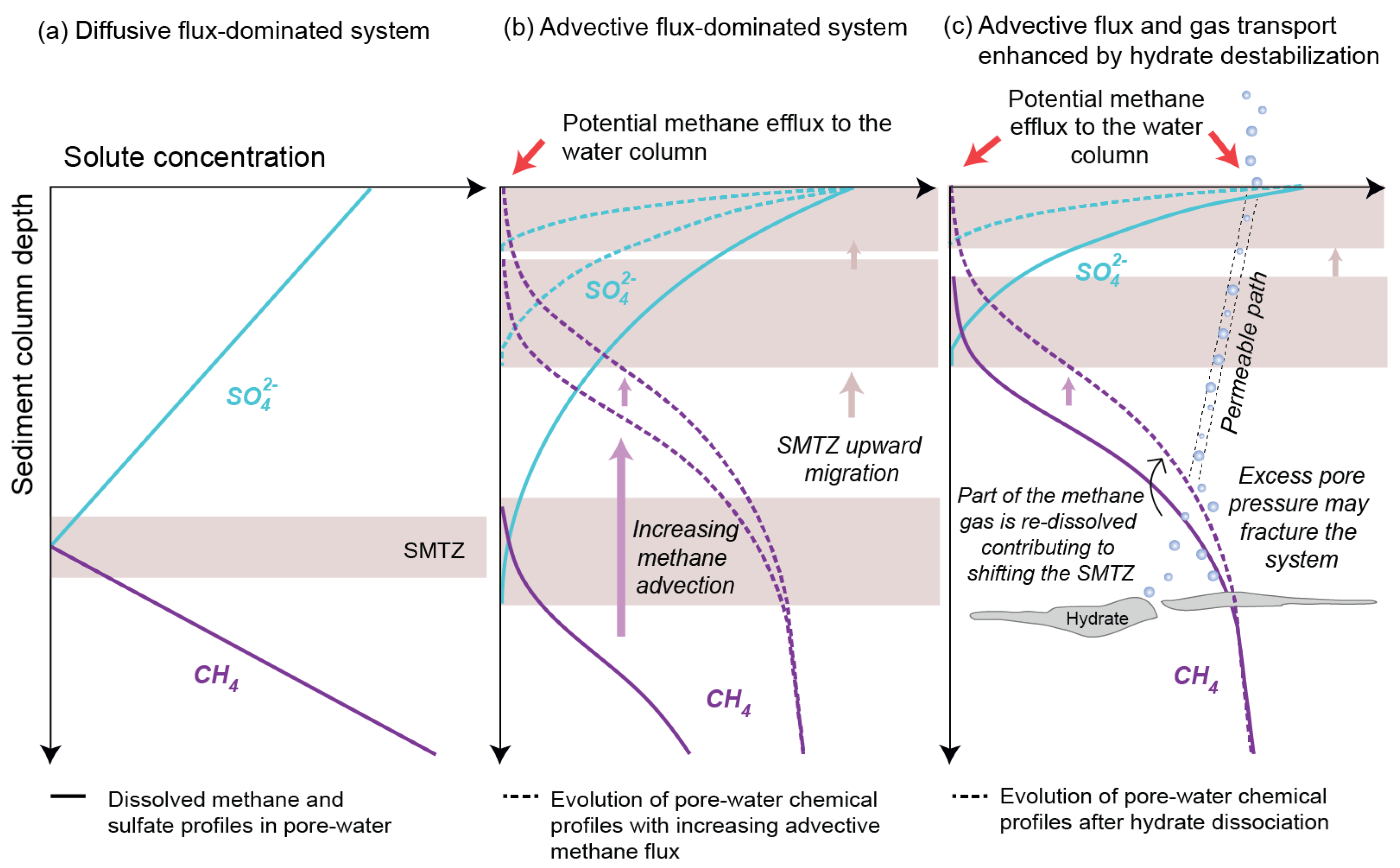
2.2. Hydrate Destabilisation and Multiphase Transport of Methane

Methane hydrate destabilisation into liquid water and methane (either dissolved or in gas phase) includes both dissociation and dissolution processes, and is a multi-physics problem that modifies the structure and mechanical response of the porous medium [73], and enhances methane transport towards the seafloor by either advective flux, bubble ebullition or eventually, fracture generation and propagation [20,21,65].

Hydrate destabilisation is generally driven by pressure and temperature perturbations (i.e., pressure-temperature shifts towards the right side of the hydrate equilibrium curve, solid grey line in Figure 4a), pore-water under-saturation in dissolved methane (Figure 4b) or an increase in water salinity [74]. During this process, the local temperature of the system decreases due to the endothermic nature of the reaction and the pore-water salinity decreases due to the release of fresh water. This cooling, together with the pore-water freshening may result in secondary hydrate or ice formation, which reduces the permeability of the reservoir [75] and may favour short-term hydrate self-preservation against warming. In addition, and depending on the sediment’s permeability and its ability to dissipate pore pressure, the release of liquid water and methane gas (in the case of dissociation) may increase the sediment pore pressure [76]. Pore-pressure increase can play two different roles in the reservoir. On one hand, it may favour hydrate stability. On the other, especially in low-permeability, fine-grained sediments, excess pore-pressure can lead to sediment fracturing (e.g., [77,78]), thus facilitating methane escape towards the seafloor [44,46]. In addition, as hydrate destabilisation progresses, the pore-scale distribution of phases (i.e., pore-volume ratio occupied by the different solid, aqueous and gas phases) evolves, leading to large changes in the reservoir’s permeability and the multiphase flow behaviour [79]. The resulting flow characteristics will control methane transport and significantly influence the amount of dissolved methane available for microbial consumption [56].

Once hydrate breaks-down, the methane released can be transported through the sediment column dissolved in water or as free gas. Dissolved methane is commonly transported through the diffusion and advection of pore water. Diffusive transport is driven by methane concentration gradients in the aqueous phase according to Fick’s law [80]. Advective transport is driven by pressure gradients, typically described by Darcy’s law [81] and thus, influenced by sediment permeability and fluid viscosity [56]. Methane gas is transported by pressure gradients including those generated by buoyancy in the form of individual bubbles or as a continuous gas phase. During its transport towards the seafloor, methane gas can be retained within the sediments due to capillary entry pressure (i.e., pore size restrictions) [21,71]; be recycled within the gas hydrate stability zone (GHSZ) by hydrate re-formation (e.g., [82,83]); be re-dissolved into the aqueous phase [84], thus, contributing to the total flux of dissolved methane; or rapidly escape towards the seafloor through sediment fractures [44].

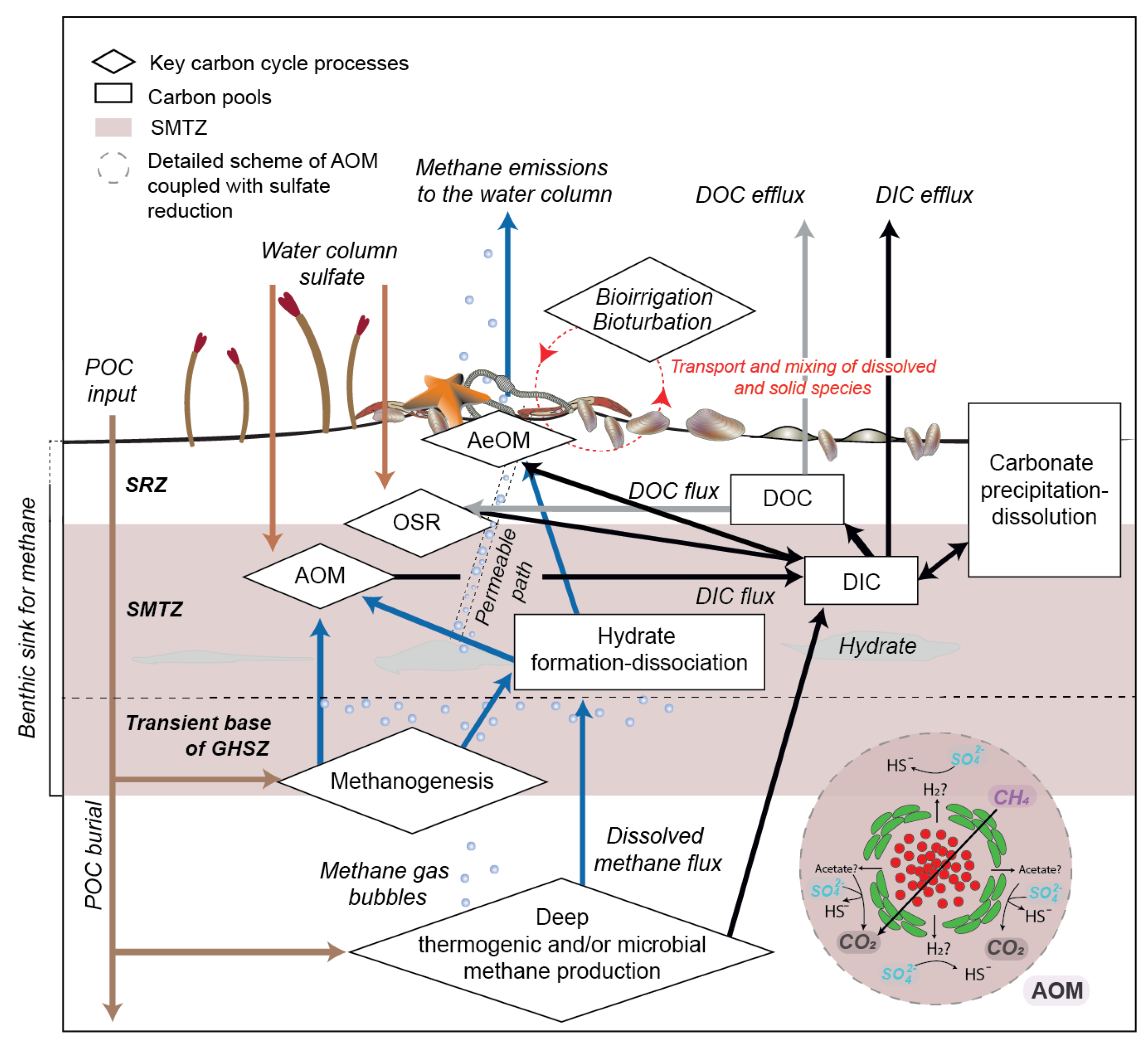
2.3. The Benthic Methane Sink: The Variable Efficiency of the AOM Bio-Filter

Once methane is released from hydrates, several biogeochemical processes can consume the upward migrating methane (i.e., converting it into different carbon pools [86], as summarized in Figure 1). AOM and AeOM, carried out by consortia of methanotrophic archaea (ANME groups) and sulfate-reducing bacteria [87,88], and methanotrophic bacteria [89], respectively, constitute the so-called “benthic sink for methane” [90,91] (Figure 5). Their efficiency is quantified as the proportion of total methane oxidised to the total methane influx at the base of Sulfate-Methane Transition Zone (SMTZ) [38].

As a general rule, AOM dominates methane consumption within the sediments, while AeOM dominates its consumption within the water column [35,89]. In particular, in shelf and upper continental slope sediments, which are generally depleted in oxygen below the well mixed sediment layer (ca. <10 cm), the consumption of methane via AOM is the main process controlling methane emissions across the seafloor [36]. AOM may be carried out using several terminal electron acceptor pathways to oxidize methane (e.g., coupled to nitrate or nitrite, Equations (1) and (2), respectively) [92,93,94].

$$5C{H}_{4_{\left(aq\right)}}+8N{O}_3^{-}+8H^{+}\to 5C{O}_2+4N_2+14H_{2}O$$

(1)

$$3C{H}_{4_{\left(aq\right)}}+8N{O}_2^{-}+8H^{+}\to 3C{O}_2+4N_2+10H_{2}O$$

(2)

However, in marine sediments where sulfate is more abundant than the alternative terminal electron acceptors (TEAs), sulfate-driven AOM is the main methane consumption process [36,43,95,96] (also referred to here as AOM bio-filter, Equation (3)):

$$C{H}_{4_{\left(aq\right)}}+S{O}_4^{2-}\to H{S}^{-}+HC{O}_3^{-}+H_{2}O$$

(3)

Within the often oxygenated shallow mixed layer of the sediment, AeOM may also contribute to the benthic sink through:

$$C{H}_{4_{\left(aq\right)}}+2O_2\to C{O}_2+H_{2}O$$

(4)

Nonetheless, even in oxygenated sediments, AeOM represents a weak barrier for methane fluxes because it competes with aerobic organic matter degradation as well as secondary redox reactions that also consume oxygen (e.g., nitrification or sulfate re-oxidation). In addition, within the mixed sediment layer bio-mixing can enhance methane export to the ocean and favour methane to bypass the AeOM sink (see Section 2.3.3) [45].

In a warming world, AOM is an important barrier for the transfer of hydrate-derived methane to the ocean. However, the efficiency of AOM in response to hydrate destabilisation is still a poorly constrained issue and its benthic biogeochemical impact is largely overlooked [2,27,36,46,55]. At a global scale, the AOM bio-filter is highly efficient, consuming a total of ∼45–61 Tg of methane per year, which approximately balances the cumulative production of methane by methanogenesis in marine sediments [39]. In particular, the AOM bio-filter has been estimated to consume up to 100% of the dissolved methane transported upwards in diffusive dominated systems [35,37]. However, its efficiency can be reduced to up to 20% at cold seep and advective dominated systems, depending on the fluid flow regime [38]. Moreover, in marine settings where methanotrophic fauna and bacterial mats are absent, the AOM efficiency is estimated to be less than 10% [90] and consequently, active gas ebullition is generally observed.

In the following subsections, we describe the main factors that are thought to control AOM efficiency and discuss their role in facilitating methane efflux to the ocean.

2.3.1. Influence of Fluid Flow Regime on the AOM

The different ways in which methane is transported through the sediment column (Section 2.2) exerts an important influence on the efficiency of the AOM bio-filter. In settings dominated by diffusive transport, upward migrating methane is typically quantitatively consumed (>50–90%) by the sulfate diffusing downwards from seawater (Figure 6a). However, in settings characterised by active fluid flow, a greater fraction of the methane flux is transported upwards by advection, pushing the SMTZ up towards shallower depths (Figure 6b).

The upward migration of the SMTZ has two main implications. First, it results in a steepening of the solute gradients. At high advective rates and especially when the SMTZ is pushed into the mixed layer, the downward diffusive sulfate flux may not be able to consume all of the upward migrating methane flux [36,41,100,101]. As a result, methane can more easily escape the seafloor (red arrow in Figure 6b). Second, and because advection does not necessarily transport the microbial community upwards (although it might via gas bubble-mediated transport [102]), at the new SMTZ location, the resident AOM community will first have to build up sufficient biomass to operate at full capacity, thus, delaying the response of the methane sink.

At cold seeps and in other gas-rich sediments, the efficiency of the AOM bio-filter is generally considerably reduced because the AOM consortia cannot access methane in its gaseous phase. In addition, the possibility of fracture generation and propagation due to pore fluid over-pressure may also favour both dissolved and gas methane to by-pass the benthic sink. Therefore, these settings are often characterised by methane emissions to the ocean (e.g., [27,42,103]). Nonetheless, not all methane gas migrating through the sediment column by-passes the AOM bio-filter. Within the SMTZ where methane consumption starts to under-saturate pore-water, some of the gas can re-dissolve and thus contribute to the flux of dissolved methane accessible to microbes [43]. Such re-dissolution close to the SMTZ may lead to higher AOM rates but also drive the vertical displacement of the SMTZ (Figure 6b). Hydrate destabilisation would act as an additional source of methane gas in the system that contributes to the described behaviour [84,104,105,106]. Thus, weakening the AOM bio-filter efficiency, favouring sediment fracturing and promoting methane escape to the seafloor (red arrow in Figure 6c) [21,99,107,108]. Furthermore, hydrate destabilisation can also unlock gas accumulations at and below the base of the GHSZ, which would enhance gas transport to the seafloor [68,82].

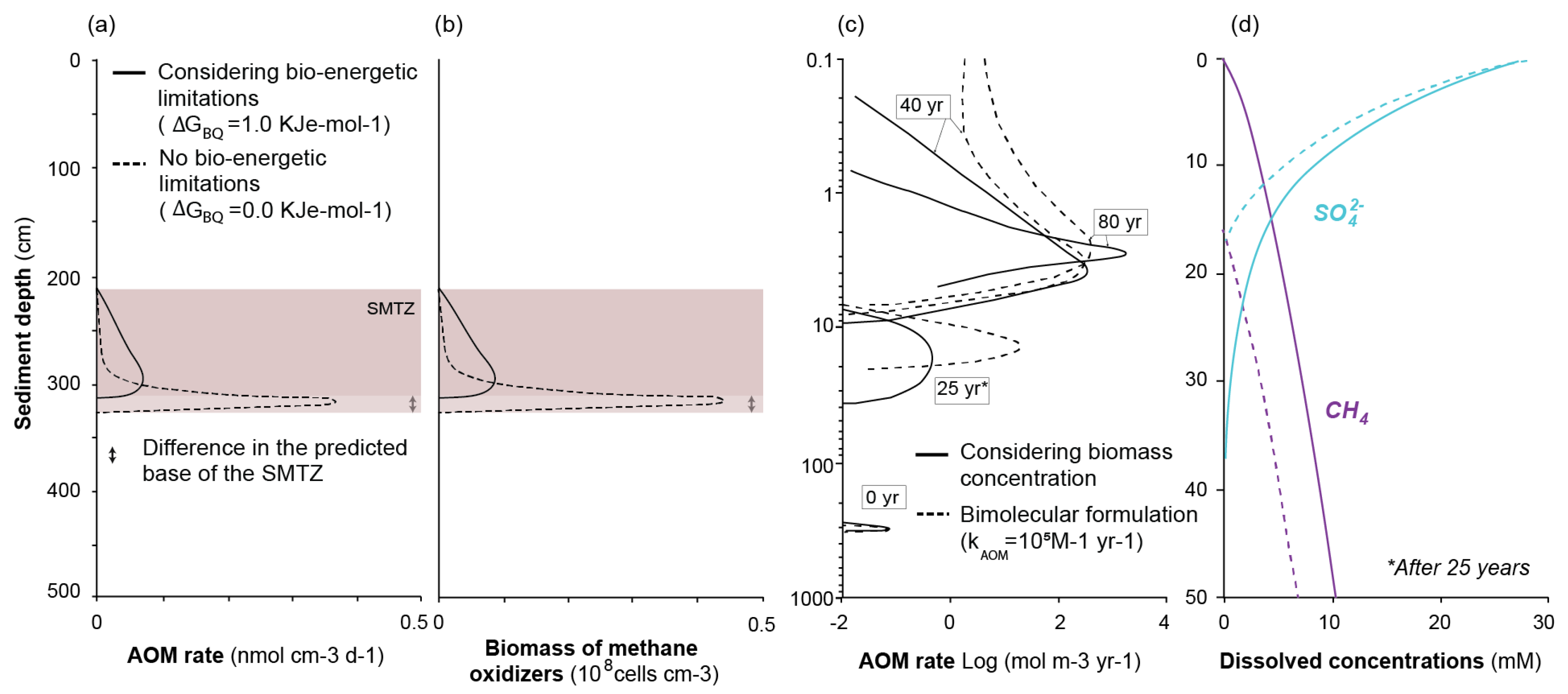
2.3.2. Kinetic and Bio-Energetic Limitations to Biomass Growth

In situ measurements of methane efflux by Thurber et al. [27] in the High Antarctic provide recent evidence of a significant microbial control on the efficiency of the AOM bio-filter. Their work show that, faced with a new deep source of methane, the local microbial community took up to 5 years to establish an efficient bio-filter.

The very small energetic yields and the low growth rates of the AOM microbial consortia are likely to play a significant role in this delayed response of the AOM bio-filter to changes in methane fluxes [41]. Microbial growth is a slow dynamic process (with generation times of months to years [27,43]), that depends on the catabolic energy-generating reaction between an electron donor and an acceptor (

Table 1. Main microbially-mediated reactions related to biomass growth. The catabolic reactions provide the energy to synthesise biomass ($C_5{H}_7{O}_{2}N$). Adapted from [41].

Sulfate Reduction
Catabolic reaction:	$0.5H_2+0.125S{O}_4^{2-}+0.125H^{+}\to 0.125H{S}^{-}+0.5H_{2}O$
Biomass growth:	$9.5S{O}_4^{2-}+0.2N{H}_4^{+}+10.3H^{+}+HC{O}_3^{-}+40H_2\to 0.2C_5{H}_7{O}_{2}N+9.5H{S}^{-}+40.6H_{2}O$
Methanogenesis
Catabolic reaction:	$0.5H_2+0.125HC{O}_3^{-}+0.125H^{+}\to 0.125C{H}_4+0.375H_{2}O$
Biomass growth:	$10.5HC{O}_3^{-}+0.2N{H}_4^{+}+10.1H^{+}+40H_2\to 0.2C_5{H}_7{O}_{2}N+9.5C{H}_4+31.1H_{2}O$
AOM
Catabolic reaction:	$0.125C{H}_4+0.375H_{2}O\to 0.5H_2+0.125HC{O}_3^{-}+0.125H^{+}$
Biomass growth:	$10C{H}_4+0.2N{H}_4^{+}+27.4H_{2}O\to 0.2C_5{H}_7{O}_{2}N+9.2H^{+}+38H_2+9HC{O}_3^{-}$

), the rate of which is, in turn, a function of kinetic and thermodynamic factors [41]. AOM is limited when the sulfate reducers do not consume enough hydrogen ($H_2$) for the oxidation to become thermodynamically viable [40,41]. In addition, the net growth rate of a given biomass group is controlled by kinetic forces that are proportional to the concentration of both electron donor and acceptor [40] (see Section 3.2).

Several numerical models have investigated how temporal changes in the active biomass of methane oxidisers triggered by kinetic and bio-energetic limitations may affect the AOM rate and thus, the efficiency of this sink. In particular, the bio-energetic yield for microbial growth has found to exert an important control on AOM rates. Models considering a minimum bio-energetic yield for microbial growth ($\Delta G_{BQ}$, see Section 3.2) predict a much lower amount of biomass available for methane consumption than those that do not, and therefore, a reduced AOM rate (Figure 7a,b) (e.g., [41]).

A similar behaviour can be predicted by models accounting for both the kinetic and bio-energetic driving forces governing the net growth rate of biomass (Figure 7c,d) (see Section 3.2). In particular, Regnier et al. [43], show that the reduction of the AOM rate due to biomass dynamics is more pronounced just after the onset of the fluid flow (i.e., 25 years after the initiation of the simulation in Figure 7c) because of the movement of the SMTZ to shallower depths. These results also evidence how the decrease in the AOM rate translates into an increase of sulfate and methane concentrations in pore-water in the sediment column (Figure 7d), which can favour methane efflux to the ocean.

2.3.3. Bioirrigation and Bioturbation

Bioirrigation and bioturbation are important mechanisms of solute/solid transfer between the ocean and the shallow layers of the sediment through channels and dwellings and the mixing of sediment by macrofaunal activity [109,110,111,112]. In active settings, where the SMTZ is generally pushed into the mixed sediment layer, the presence of bioturbation and bioirrigation activity seems to favour a rapid increase in methane efflux to the ocean [45]. However, in passive settings, where the SMTZ is usually located well below the mixed sediment layer [41], bio-mixing slightly increases AOM methane consumption when the down transport of TEAs is enhanced [45,113].

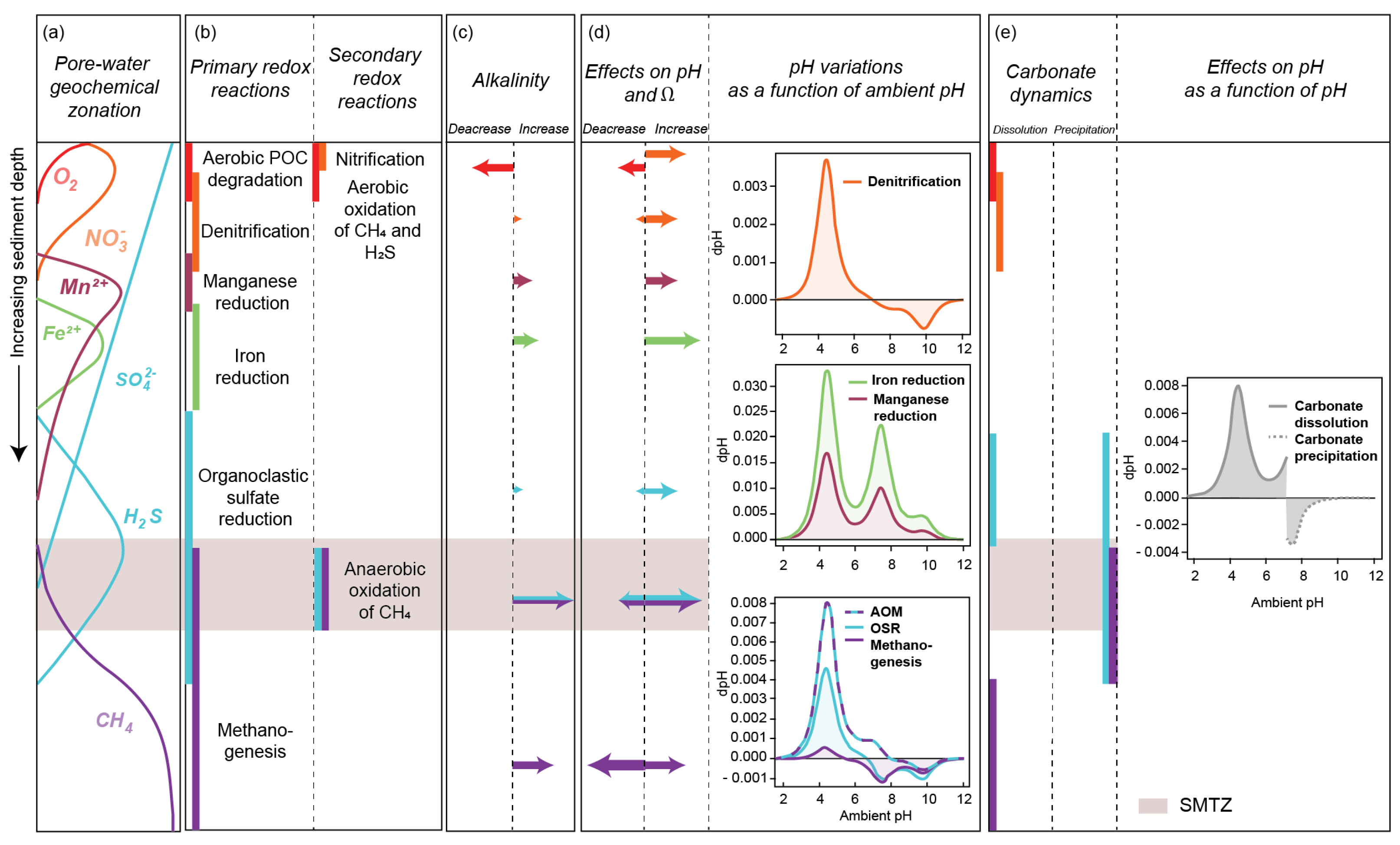
2.4. Benthic Biogeochemical Impact of Methane Consumption through the Sediment Column

Only a fraction of the methane released by hydrate destabilisation is forecast to reach the ocean due to intense AOM. However, methane consumption can have substantial impacts on oceanic carbon cycling on timescales of hundreds to thousands of years [29,55,114], with potential, yet difficult to predict, atmospheric climate feed-backs (e.g., AOM could enhance, or not, ocean-atmosphere GHG exchange and ocean carbon burial).

Among other properties, AOM can exert important changes in benthic DIC/alkalinity/ pH, and thus also carbonate saturation state (Figure 8). However, the overall impact of these changes in the benthic environment depends on the consumption of the AOM by-products (i.e., bicarbonate and sulfide, R4 in

Table 2. Main secondary reactions impacting on pore-water alkalinity, pH and oxygen concentration in methane-rich marine sediments. $N{H}_4^{+}$: Ammonium, $O_2$: Oxygen, $HC{O}_3^{-}$: Bicarbonate, $N{O}_3^{-}$: Nitrate, $C{O}_2$: Carbon dioxide, $H_{2}O$: Water, $H_{2}S$: Hydrogen sulfide, $S{O}_4^{2-}$: Sulfate, $C{H}_4$: Methane, $H{S}^{-}$: Sulfide, $C{a}^{2+}$: Calcium, $CaC{O}_3$: Calcium carbonate, $F{e}^{2+}$: Iron, $FeS$: Iron sulfide, $Fe{S}_2$: Iron bisulfide.

Secondary Redox Reactions
R1: Nitrification	$N{H}_4^{+}+2O_2+2HC{O}_3^{-}\to N{O}_3^{-}+2C{O}_2+3H_{2}O$
R2: Sulfide Oxidation	$H_{2}S+2O_2+2HC{O}_3^{-}\to S{O}_4^{2-}+2C{O}_2+2H_{2}O$
R3: AeOM	$C{H}_4+2O_2\to C{O}_2+2H_{2}O$
R4: AOM	$C{H}_4+S{O}_4^{2-}\to H{S}^{-}+HC{O}_3^{-}+H_{2}O$
Precipitation Reactions
R5: Carbonate precipitation	$2HC{O}_3^{-}+C{a}^{2+}\to CaC{O}_3+C{O}_2+H_{2}O$
R6: Sulfide precipitation	$F{e}^{2+}+2HC{O}_3^{-}+H_{2}S\to FeS+2C{O}_2+2H_{2}O$
	$FeS+2HC{O}_3^{-}+H_{2}S\to Fe{S}_2+2C{O}_2+2H_{2}O$

). Therefore, on the entire, complex, and dynamic interplay of redox, equilibrium and mineral precipitation/dissolution reactions, as well as transport processes active in marine sediments, which in turn, are controlled by the environmental conditions of the depositional environment.

AOM can contribute significantly to the total ocean DIC pool, defined as the sum of the aqueous species of inorganic carbon in solution (Equation (5)), via the conversion of methane carbon into bicarbonate ($HC{O}_3^{-}$ in R4, Table 2).

$$DIC=\left[C{O}_2\right]+\left[HC{O}_3^{-}\right]+\left[C{O}_3^{2-}\right]$$

(5)

The amount of DIC produced by AOM mostly depends on methane and sulfate availability in pore-waters and the upward and downward movements of the SMTZ (see Section 2.3) (e.g., [115,116]). That is, it will be strongly influenced by deep methane emissions associated with hydrate destabilisation, as well as by the variable efficiency of the AOM bio-filter. The work of Akam et al. [55] shows that DIC outflux through the SMTZ in diffusive settings is comparable to ∼20% of global riverine DIC flux to oceans, and is estimated to contribute, in different proportions, to alkalinity and carbon dioxide emissions to the ocean depending on the rates of nitrification, sulfide oxidation and authigenic carbonate precipitation (R1, R2 and R5 in Table 2, respectively).

In oxygenated sediments, methane escaping the AOM bio-filter may still contribute to the DIC pool by the conversion of methane carbon into carbon dioxide ($C{O}_2$) via AeOM (R3 in Table 2). The produced $C{O}_2$ combines with water to form carbonic acid ($H_{2}C{O}_3$), which dissociates into hydrogen ions ($H^{+}$), and thus, may contribute to decrease the pore-water pH (Equation (6)), favouring ocean acidification [117].

$$pH=-log\left[H^{+}\right]$$

(6)

Nonetheless, the resulting decrease in ocean pH could, in turn, promote weathering of silicate minerals in shallow sediments, and thus, favour alkalinity production and eventually buffering ambient pH [55,118].

Ambient pH (secondary columns in Figure 8d,e) regulate the impact of most redox and equilibrium reactions on the rate of change in pH ($dpH$ in Figure 8d). The resulting net effect of methane turnover on ambient pH can shift the regime of some of these reactions, thus influencing the net benthic biogeochemical response to hydrate-related methane emissions [53]. For example, at contemporaneous ocean pH (∼8.1), the AOM should have a minimum impact on ocean pH changes. However, if pore-water pH decreases below ∼8 AOM would contribute to increase ambient pH, while at higher pH it would reduce it, promoting acidification (bottom inset at additional column in Figure 8d).

In addition to DIC and pH changes, the production of sulfide ($H{S}^{-}$) via AOM (R3 in Table 2) enhances the total alkalinity (TA) of pore-water (Equation (7)). TA, commonly described as the excess of proton acceptors over donors, plays a major role in ocean chemistry with important effects in pH buffering and calcium carbonate precipitation and dissolution. Thus, understanding alkalinity dynamics is pivotal to quantify changes in ocean carbon dioxide uptake [119,120].

In a typical global ocean carbon cycle model, total alkalinity may commonly be approximated by [121]:

$$TA=HC{O}_3^{-}+2C{O}_3^{2-}+H{S}^{-}+O{H}^{-}-H^{+}+B{\left(OH\right)}_4^{-}$$

(7)

Including borate species $\left(B{\left(OH\right)}_4^{-}\right)$.

The net flux of alkalinity from the seafloor is, however, difficult to predict and depends, ultimately, on the rates of authigenic carbonate precipitation, as well as sulfide oxidation and precipitation (R5, R2 and R6 in Table 2, respectively) [122].

Authigenic carbonate precipitation (R5 in Table 2), i.e., carbonate precipitating inorganically at the sediment-water interface or within the SMTZ, is stimulated by high alkalinity produced by AOM [53,97,123]. During authigenic carbonate precipitation, the consumption of bicarbonate sequesters a portion of total DIC entering the SMTZ, thus, reducing the TA by a factor of two (Equation (7)). Diagenetic models have estimated that approximately 10–20% of the carbon in the form of methane oxidized by AOM can precipitate as authigenic carbonates [104]. This result suggests that in the case of methane emissions enhance by hydrate destabilisation, authigenic carbonates can become a significant component of marine carbon burial, especially in settings dominated by diffusive methane fluxes [55,124,125,126]. However, authigenic carbonates do not precipitate in all methane flux settings. In settings characterised by high-intensity fluxes, low dissolved methane concentrations, intense bioturbation or high sedimentation rates, carbonate precipitation is significantly hindered (e.g., [55,127,128]). Furthermore, authigenic carbonates can also experience dissolution (Figure 8e), reversing the effect of carbonate precipitation on the carbon-cycle. For example, carbon dioxide production via AeOM (e.g., [129]) or sulfide oxidation (e.g., [130]) can acidify pore-waters to a pH below ∼7, thus, promoting carbonate dissolution. Nonetheless, processes like marine silicate weathering can reverse such effect on ambient pH and promote further carbonate precipitation [131].

In addition, is worth noting that authigenic carbonate precipitation can favour the formation of carbonate cap rocks that can seal hydrocarbon systems [132]. Hence, carbonate dynamics (i.e., precipitation/dissolution) can affect the hydrodynamic behaviour of the system and so methane fluid flow towards the seafloor (e.g., [133,134,135]), and disrupt the AOM-driven sequestration process [47].

3. Modelling the Benthic Response to Climate-Driven Methane Hydrate Destabilisation

Numerical models are ideal tools to quantify the evolution of hydrate reservoirs in the context of global climate change, evaluate their contribution to sediment-ocean methane exchange, and ultimately, assess related benthic biogeochemical implications. In this section, we define the scientific questions that models should answer in order to assess these issues. We also review the state-of-the-art numerical models used to simulate the response of hydrate systems to climate change. In particular, we examine how current models describe, and to what level of detail, the different physical and biogeochemical processes governing methane formation, release, and consumption within the sediment column. We then evaluate their ability to provide high confidence predictions of benthic methane emissions associated with hydrate destabilisation and related benthic biogeochemical impacts.

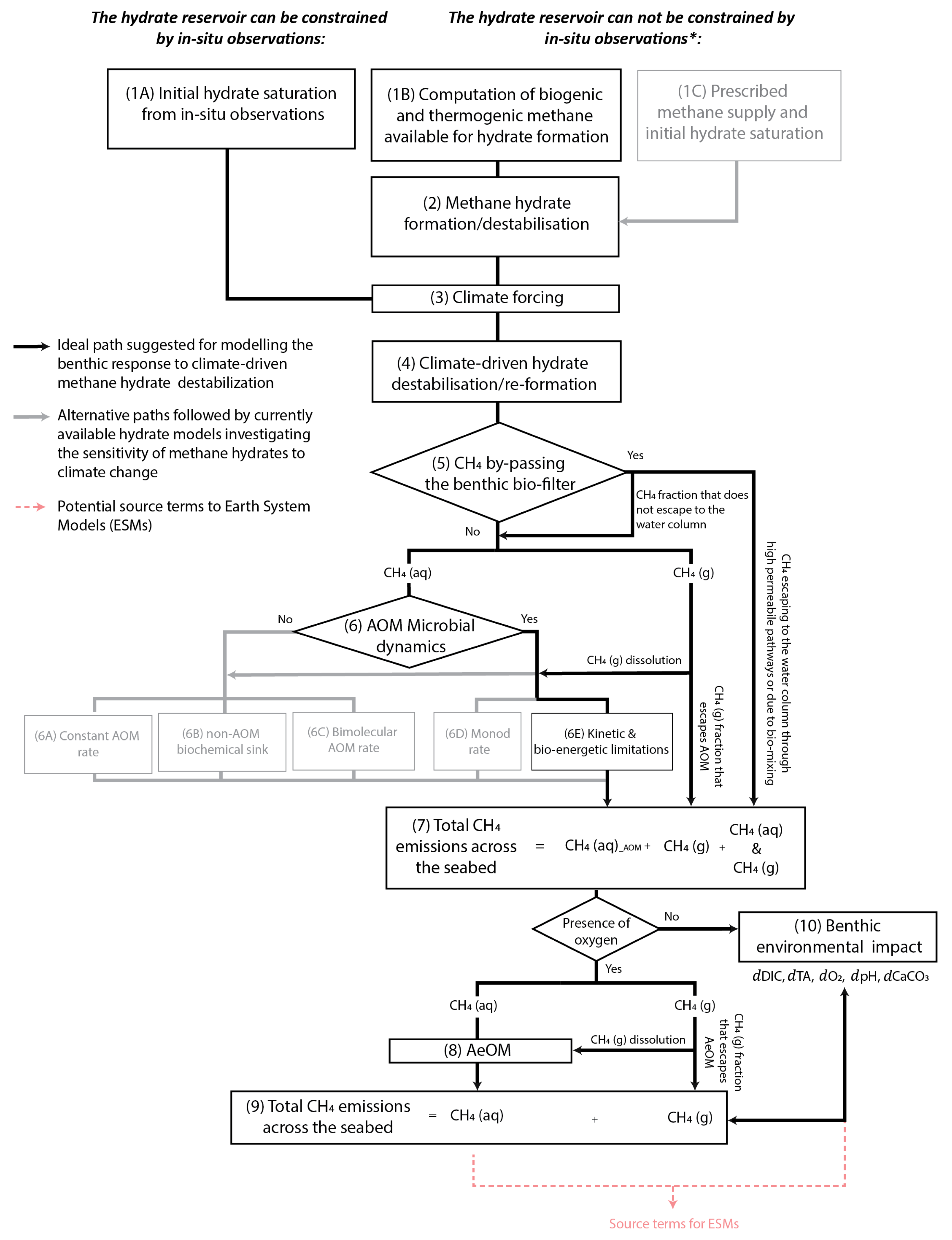
3.1. What the Scientific Questions Numerical Models Should Answer

The key questions raised in this review are whether methane released from hydrate due to climate change is consumed by the benthic methane sink before it reaches the ocean, and how the corrresponding methane turnover by AOM impacts benthic pore-water chemistry. To address this issues, numerical models should answer the following questions:

• How much methane is stored in methane hydrate and how much of it could be released in response to climate perturbations?
• How efficient is the benthic methane sink and thus, how much, at what rate and for how long hydrate-sourced methane can be actually emitted to the ocean?
• What are the implications of methane turnover across AOM on benthic biogeochemical dynamics and fluxes?

To answer these questions, numerical models should first constrain the hydrate inventory. For cases where reliable in situ data about hydrate saturation exist, this step is straightforward. Conversely, when there is no available data or when simulating past scenarios, the hydrate inventory can be constrained either by prescribing a reasonable methane supply and an initial hydrate inventory (box 1C in Figure 9), or by simulating how much methane was available in the sediment for the formation of methane hydrate (box 1B in Figure 9). The last, will require modelling the burial history of deep marine sediments and associated phenomena (e.g., sediment compaction and reduction in sediment porosity and permeability, fluid expulsion, heat flux…), in situ generation of biogenic methane from buried organic carbon, deep influx of thermogenic methane, and multiphase flow through a deformable porous media.

Then, both model approaches should estimate how much of this methane is sequestered in the form of hydrate. This requires considering the thermodynamics governing methane hydrate phase transformations (box 2 in Figure 9), and then for a more sophisticated modelling approach, multiphase methane transport.

Once the hydrate inventory is constrained, numerical models should estimate how much of it could be affected by climate perturbations. Models should account for the slow heat penetration through the sediment column and/or pressure changes with depth related to ocean bottom warming and/or sea-level changes and assess their effect on the stability of hydrate (see Section 2, and boxes 3 and 4 in Figure 9), while accounting for potential hydrate self-stabilization, multiphase methane transport, as well as changes in sediment mechanical (e.g., compressibility, porosity), hydraulic (e.g., intrinsic permeability) and thermal (e.g., thermal conductivity) properties.

Finally, models should estimate how much of the methane from within or beneath hydrates could actually reach the seafloor and what are the benthic biogeochemical implications of its consumption within the sediment column. For that, numerical models should account for preferential paths for methane to by-pass the AOM bio-filter (e.g., high permeability pathways including fractures, and/or sediment bio-mixing, box 5 in Figure 9), as well as the existence of a benthic sink (boxes 6 and 8 in Figure 9). Rates of methane consumption within the sediment can be modeled in more or less detail depending on the problem setting considered. For example, a bimolecular AOM rate could be suitable to simulate steady-state methane flux scenarios but it is insufficient for transient scenarios (Section 3.2). Finally, models should be able to trace the chemical impact of methane turnover via AOM and AeOM by considering the full chemical reaction network characterising carbon cycling within the upper layer of the sediment column (Table 2 and box 10 in Figure 9).

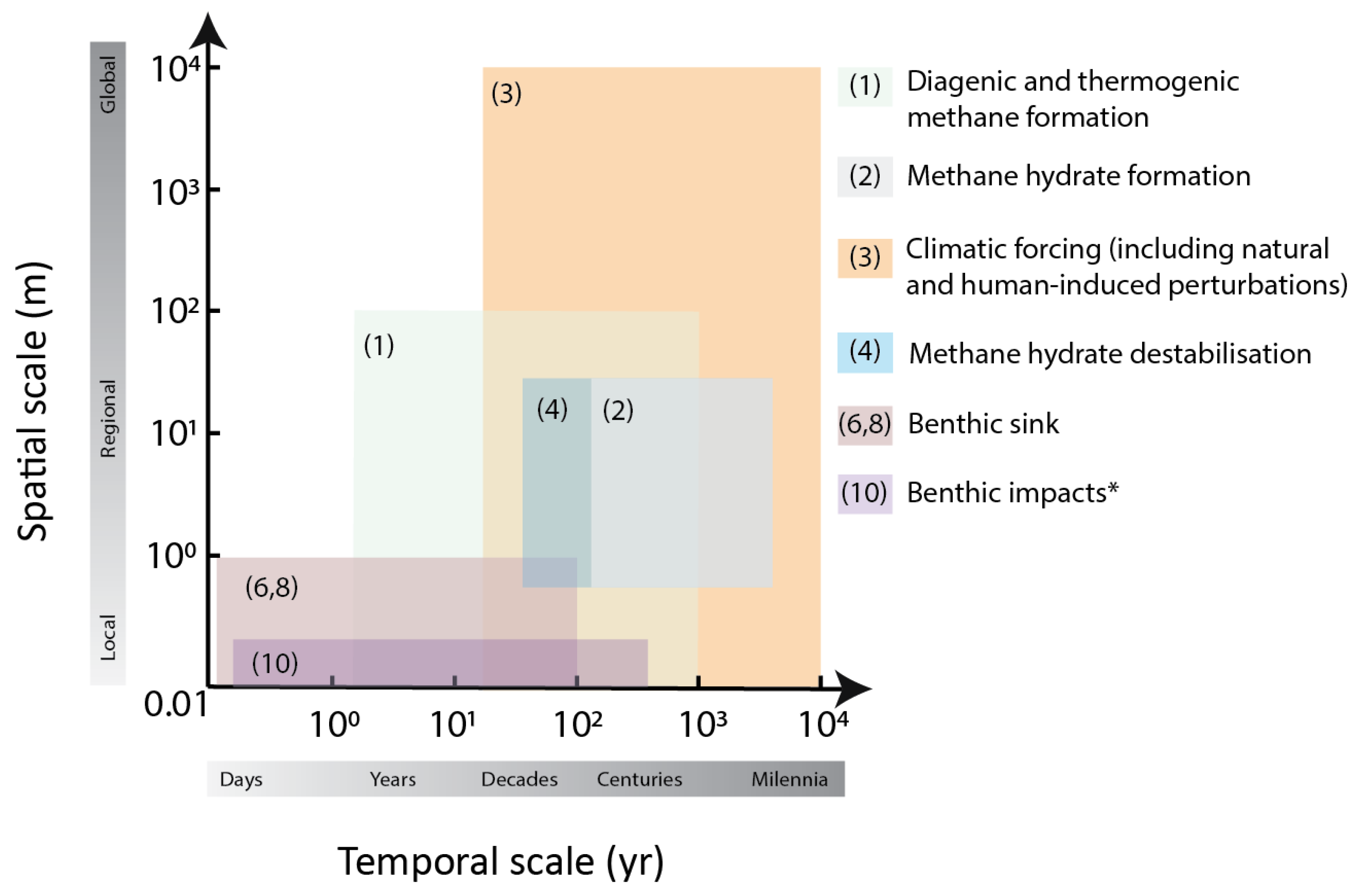
Temporal and Spatial Scales

Representing the geological, chemical, physical, and biological processes characterising the benthic response to climate-driven methane hydrate destabilisation requires numerical simulations that consider a large variety of processes occurring on a wide range of scales (Figure 10).

Hydrate destabilisation driven by climate perturbations and the related methane leakage to our oceans is a long-term process that can last for several centuries [20]. Thus, numerical simulations assessing hydrate-sourced methane emissions at the seafloor use computational domains of meters to hundreds of the meters (because of the depth of the methane hydrate phase boundary), and simulation times ranging from decades to millennia (see Section 2.1). However, the simulation scales required to simulate the fate of hydrate-sourced methane within the sediment are different. Numerical studies assessing benthic biogeochemical and transport processes typically limit their simulations to the upper 10–100 cm of the sediment column (where the main biogeochemical reactions take place), and only require simulation times of days to a maximum of hundreds of years to reach steady-state conditions (e.g., [41,43,45,119]).

Thus, simulating the benthic response to climate-driven methane hydrate destabilisation require a spatial discretization of the computational domain and simulation times suitable to capture the dynamic interplay between hydrate dynamics and benthic biogeochemical processes (Figure 9 and Figure 10). To do so, the computational mesh should, ideally, be spaced a maximum of a few meters in the part of the reservoir where hydrate is present (so that the destabilisation front is well constrained, e.g., [73,82]), and from centimeters to millimeters in the very top few centimeters below the seafloor (to capture well the gradients of solutes) [43]. In addition, time scales should be long enough to capture the time lag between the climate perturbation and the emission of hydrate-related methane across the seafloor, as well as those biogeochemical processes with significant physical and chemical implications at long-term scales. For example, Luff et al. [127] reveals that thick carbonate crusts (>10–20 cm), which have important impacts on carbon sequestration and the sediment hydraulic conductivity (e.g., [135]), typically require centuries to form. In the same line, the results from Garcia-Tigreros et al. [136] suggest that the effect of methane oxidation at enhancing ocean acidification may become more noticeable over decadal or longer time scales.

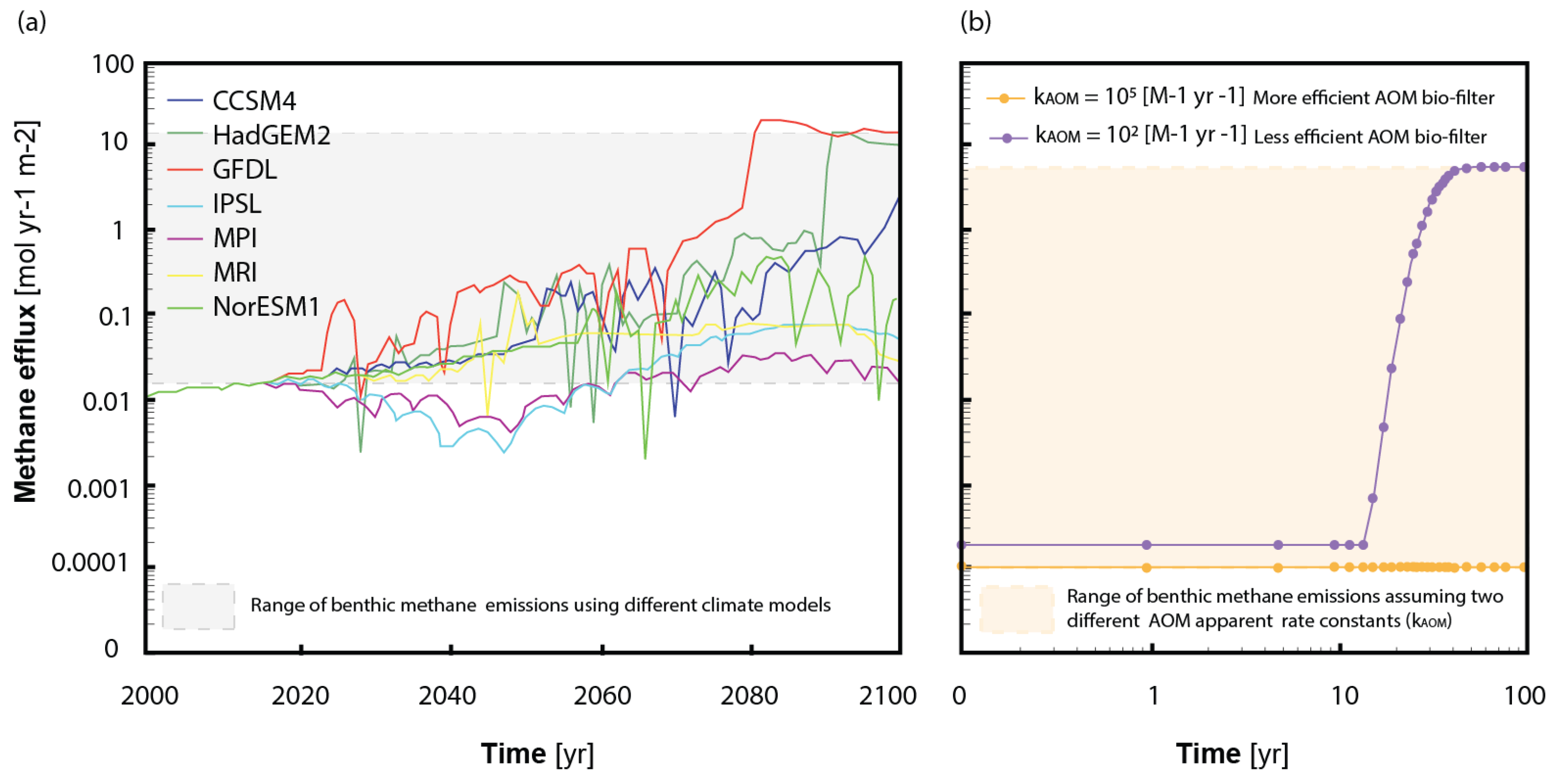
3.2. State-of-the-Art

An extensive set of numerical studies have examined the climate sensitivity of methane hydrate reservoirs in different study areas and geological settings (

Table 3. Notable numerical studies investigating the sensitivity of marine methane hydrate to climate change. The "x" shows the level of complexity (increasing towards the right in the different sub-columns) in which the numerical models used in these studies simulate the different physical and biogeochemical processes involved in the 2 first scientific questions (see Section 3.1). Morover, the third main column details a broad range of chemical species and solid phases that models should trace in order to assess the benthic biogeochemical impact of hydrate-sourced methane turnover. Note that the numbers on the table can be related to those in Figure 9. Notation: ${}^A$ AOM is considered for estimating the initial hydrate inventory but is disregard when assessing methane efflux after hydrate destabilisation, ${}^B$ the AOM rate is formulated based on pore-space methane dissolution principles that do not consider biochemical processes. DIC: Dissolved Inorganic Carbon, TA: Total Alkalinity, $O_2$: Dissolved oxygen, $CaC{O}_3$: Authigenic carbonates.

Numerical Study	Model Reference	Scientific Question 1				Scientific Question 2								Scientific Question 3
		(1,2) Estimation of the Hydrate Inventory		(3,4) Climate-Driven Hydrate Destabilisation/Re-Formation		(5) Methane by-Passing AOM			(6) AOM Rate					(8, 10) Benthic Environmental Impact
		(1C) Prescribed Methane Supply and Initial Hydrate Saturation	(1B) Diagenetic Approach for Methane Sources	Changes in GHSZ Thickness	Hydrate Thermodynamics	Gas Phase Escapes the AOM	Hydraulic Fractures or Permeable Paths	Bio-Mixing	(6A) Constant Rate	(6B) ${}^B$ Non- Biochemical Sink	(6C) Bimolecular	(6D) Monod Rate	(6E) Kinetic & Bio-Energetic limitations	DIC	TA	${\mathit{O}}_{\mathbf{2}}$	pH	${\mathit{CaCO}}_{\mathbf{3}}$
Xu et al. [139]	Xu and Ruppel [144]	x			x					x
Reagan and Moridis [47]	TOUGH+Hydrate [145] C.CANDI [146,147]	x			x	x		x			x							x
Biastoch [49]	Biastoch [49]	x		x
Archer et al. [29]	Davie and Buffet [148]		x	x		x				x
Reagan et al. [140]	TOUGH+Hydrate [149]	x			x
Hunter et al. [51]	Tishchenko et al. [150]	x	x	x
Thatcher et al. [65]	TOUGH+Hydrate [149].	x			x
Darnell and Flemings [141]	Liu and Flemings [151]	x			x
Kretschmer et al. [20] ${}^A$	Wallmann et al. [152]		x	x
Marin-Moreno et al. [31]	TOUGH+Hydrate [153]	x			x
Mestdagh et al. [12]	Xu and Ruppel [144]	x			x
Wallmann et al. [68]	Wallmann et al. [68]	x		x		x						x
Stranne et al. [46]	TOUGH+Hydrate -GeoMech [44,154]	x			x		x			x
Braga et al. [22]	TOUGH+Hydrate [154]	x			x

). The numerical models used in these studies span a wide range of complexities, from the simplest approaches where methane gas escaping from the seafloor is estimated as a function of changes in the thickness of the GHSZ (e.g., [20,49,51,137,138]), to more sophisticated models that include the coupled hydraulic–thermodynamic behaviour and multiphase fluid flow characterising hydrate-bearing porous media (e.g., [12,19,21,22,31,46,47,65,68,139,140,141,142]).

Simplistic models calculate changes in the vertical extension of the GHSZ either according to a new steady-state of temperature and pressure at the seabed, or as a function of time, assuming conductive heat and pressure transfer through the sediment column. Then, by combining estimates of sediment porosity and hydrate saturations, these models translate changes in GHSZ thickness into an amount of destabilized hydrate and thus, to a specific volume of methane gas that can potentially escape to the ocean. However, these models neglect important dynamic processes and factors that decrease the rate of hydrate destabilisation as well as the amount of methane that can escape the sediment column.

Neglected aspects include the increase in pore pressures and pore water freshening during hydrate destabilisation [76]; the endothermic nature of the dissociation reaction [143]; factors limiting the movement of the gas phase through the sediment column [44,47]; the amount of gas that can be recycled into hydrate within the GHSZ [82,83]; and the role of the benthic methane sink [2] (see Section 2). Thus, these models can overestimate the amount of hydrate-sourced methane injected into the ocean [21] and predict greater rates of GHSZ thinning during warming events [2,51].

More sophisticated models successfully capture the dynamic behaviour of hydrate systems and simulate multiphase flow and transport processes in porous media (see [155] for review). Although these models may have notable differences among their formulations, they all have a similar conceptual framework, in general consisting of: multiple components (methane, water, salt); multiple phases (aqueous, gas, ice, and hydrate); multiphase fluid flow; hydrate phase equilibrium; mass balance of all components in the phases where they exist; and a thermal balance equation including hydrate destabilisation and formation. Occasionally, they also incorporate sediment geomechanics capable of capturing sediment fracturing induced by pore over-pressure during hydrate destabilisation (e.g., [21]). Nonetheless, these models rarely account for methane consumption by the AOM bio-filter, or fully consider its dynamic response.

Regardless of their complexity, hydrate models require prescribing an initial methane supply and hydrate saturation that characterize the initial state of the simulation. This data can be derived from in situ data (box 1A in Figure 9), or approximated for the study case (box 1C in Figure 9). However, it does not account for the source of methane (i.e., biogenic or thermogenic) or how this source is changed through time, for example due to changes in particulate organic carbon accumulation/degradation, and in sedimentation rates. To overcome such limitation, diagenetic models, mainly developed to simulate the dynamics of the key constituents of the sediment involved in early diagenesis [156,157], have been extended to hydrate systems (e.g., [6,148,152,158,159,160]) or coupled to existing hydrate models (e.g., [119,161]). The resulting formulations are able to estimate a hydrate inventory based on the global distribution of organic carbon in sediments and the environmental variables of the study area (box 1 in Figure 9). Yet, these models have been mostly limited to investigate the inventory of marine hydrate, and have rarely been extended to evaluate the response of hydrate reservoirs to climate change (e.g., [148,152]).

Even when hydrate models assume a reasonable hydrate inventory, they can only be used for robust predictions of hydrate-sourced methane emissions across the seafloor, when their formulation gives full consideration to the variable efficiency of the benthic sink (boxes 5 and 6 in Figure 9). Generally, hydrate models either ignore methane consumption by AOM or account for it by considering that the top meters below the seafloor are a hydrate-free region (e.g., [31,65,141]). Some models approach this geochemical sinks by assuming that AOM prevents a certain fraction of hydrate-sourced methane from reaching the overlying ocean (e.g., [49]). Others, selectively incorporate non-AOM geochemical sinks based on methane dissolution in the pore space (e.g., [29,46,139]) (see Table 3). Thus, these models ignore the dynamic interplay of different reaction and transport processes that control the depth of the SMTZ and the efficiency of the AOM bio-filter.

Diagenetic models instead have been widely used to study the AOM bio-filter in methane-rich settings (e.g., [41,43,45,53,104,142,162]). These models generally simulate changes on dissolved species through a a set of coupled advection-diffusion reaction equations in porous media which are solved simultaneously [163,164].

$$\frac{\delta {\varphi }_{\left(z\right)}{C}_{i_{(z,t)}}}{\delta t}=-\frac{F_{i_{(z,t)}}}{\delta z}+S_{{ij}_{(z,t)}}$$

(8)

where $\varphi$ is the sediment porosity at a given depth, $C_i$ is the concentration of the dissolved specie “i”, $F_i$ correspond to fluxes related to the transport processes (i.e., molecular diffusion, fluid advection and potentially bioturbation and bioirrigation flux), and $S_{ij}$ refers to the sources/sinks of specie “i” related to the biogeochemical reaction “j”.

The reaction term $S_{ij}$ can be written as:

$$S_{ij}=\sum _j{\lambda }_{ij}{R}_j$$

(9)

where ${\lambda }_{ij}$ is the stoichiometric coefficient of production/consumption of specie “i” by the reaction “j”, and $R_j$ is the rate of the reaction “j”. In particular, the AOM rate ($R_{AOM}$) in these models has been expressed via different formulations with various levels of detail at describing the complexity of the process. The simplest phenomenological expression that they use is a bimolecular rate law:

$$R_{AOM}=k_{AOM}\left[C{H}_4\right]\left[S{O}_4^{2-}\right]$$

(10)

where $k_{AOM}$ is an apparent second-order rate constant (concentration⁻¹ time⁻¹) and the square brackets refer to concentrations of dissolved methane and sulfate, respectively. This expression has been extensively used in the literature to simulate the AOM rate as it only involves one fitting parameter ($k_{AOM}$) and therefore, it can be easily calibrated to measured pore-water profiles (see [43] for review). However, the compilation of published bimolecular AOM rate constants by Regnier et al. [43] reveals that fitted values of $k_{AOM}$ may vary by six orders of magnitude between different study sites. This suggests that $k_{AOM}$ implicitly accounts for factors that are not explicitly described in a simple bimolecular expression [40,165,166]. In fact, Luff et al. [104] recall that the biogeochemical measurements used for model calibrations can only represent a snapshot of the system, which may be completely different few meters away or a few days later. Consequently, fitted values of $k_{AOM}$ are useful to simulate specific time-space scenarios and geological settings (e.g., [45]), but cannot be directly generalise to distinct hydrate systems and cannot represent transient scenarios where changes in the localised supply of methane may trigger large changes in biomass density [167,168].

For transient scenarios, diagenetic models suggest that the very small energetic yields and low growth rates of the microbial consortia are likely to play a major role in the response of AOM to changes in the fluid flow regime and methane transport rates [41]. In particular, the consumption of methane and sulfate by microorganisms generally exhibits saturation kinetics, which can be well captured by the Michaelis–Menten model for enzymatically-catalyzed reactions [169]. For AOM, saturation kinetics with respect to both the electron donor and the acceptor can be expressed as a Monod rate:

$$R_{AOM}=v_{max}\left(\frac{\left[C{H}_4\right]}{K_m^{C{H}_4}+\left[C{H}_4\right]}\right)\left(\frac{\left[S{O}_4^{2-}\right]}{K_m^{S{O}_4^{2-}}+\left[S{O}_4^{2-}\right]}\right)$$

(11)

where $K_m$ is referred to as the half-saturation constant and $v_{max}$ is the maximum rate that AOM will reach with increasing the concentration of methane and sulfate, provided that the microbial biomass is time-invariant.

Moreover, it is known that by catalysing the AOM reaction (Equation (3)), microorganisms channel the catabolic energy into microbial metabolism and growth. However, AOM can only proceed when the energy yield for the catabolic reaction exceeds a minimum metabolic threshold [40]. According to Regnier et al. [43], the kinetically limited expression for the AOM (Equation (11)) can be extended to account for bio-energetic limitations through a functional dependency on the thermodynamic driving force for the reaction, which depends on the Gibbs energy yield $\Delta G_r$:

$$R_{AOM}=v_{max}\left(\frac{\left[C{H}_4\right]}{K_m^{C{H}_4}+\left[C{H}_4\right]}\right)\left(\frac{\left[S{O}_4^{2-}\right]}{K_m^{S{O}_4^{2-}}+\left[S{O}_4^{2-}\right]}\right)\left(1-exp\left(\frac{\Delta G_r+\Delta G_{BQ}}{\chi RT}\right)\right)$$

(12)

where $\Delta G_{BQ}$ is the minimum energy required to sustain metabolism and growth, $\chi$ is the average stoichiometric number of the reaction [170], and R and T are the gas constant and absolute temperature of the system, respectively. Equation (12) captures well the complexity of the dynamic response of the microbial consortia and therefore it is the best alternative to describe the entire spectrum of boundary conditions that could be encountered at hydrate-bearing systems, which are often characterised by sudden onset of methane and changes in methane transport rates.

An early attempt to consider the role of the benthic sink in numerical studies of the fate of the methane released by hydrate is the work presented by Reagan and Moridis [47]. Their study estimates methane released from hydrate due to ocean warming using the well-established hydrate model TOUGH+HYDRATE [145]. Then, the estimates are used as an initial condition for the reactive-transport model C.CANDI [146,147], which incorporates a bimolecular AOM rate (Equation (10)), and is used to model the top 1 m of the sediment column. Their work represents a key step forward at improving predictions of the benthic biogeochemical response to climate-driven hydrate destabilisation and concludes that under the most favourable conditions for AOM (which may be considered unrealistic), over 90% of the methane escapes into the ocean. However, their work has important limitations. Firstly, the C.CANDI model does not account for multiple phases, meaning that the simulation of methane efflux across the seafloor is restricted to chemistry within the aqueous phase, so that methane transported as gas is assumed to fully escape the AOM bio-filter. Secondly, the bimolecular rate expression used in C.CANDI might not capture the complex response of the AOM bio-filter to transient changes in methane influx to the SMTZ. Finally, the version of the TOUGH+HYDRATE used in their study lacks a sediment geomechanics module capable of describing preferential paths for the methane escape to the ocean.

More recently, Stranne et al. [46] integrated a fully coupled, yet idealized, AOM module to the TOUGH+HYDRATE-GeoMech code [44,154], which accounts for hydraulic fracturing induced by hydrate destabilisation. This model is the first to investigate how the efficiency of the microbial filter varies as a function of the intrinsic permeability of the sediment, which is enhanced by hydraulic fracturing (box 5 in Figure 9). Their results show that AOM efficiency during fracture-dominated flow can be significantly reduced (to less than 50%). However, this model greatly simplifies the AOM rate expression, which is modelled as a linear function of the methane supply, with an upper (maximum) imposed AOM rate limit. The lack of biomass dynamics, together with the assumption of a static SRZ are important limitations of the model.

A less explored aspect by existing relevant models is the environmental implications of methane turnover by AOM within the sediment column. While complex diagenetic models (e.g., [45,53,162]) and extended diagenetic models for hydrate systems (e.g., [119,159]) have been widely used to explore this aspect in detail, to the best of our knowledge, the work presented by Reagan and Moridis [47] is the only numerical study assessing this in the context of hydrate destabilisation driven by climate perturbations (see Table 3). In particular, this model investigates the effect of methane consumption by AOM on authigenic carbonate dynamics. Their long term simulations show the potential for methane carbon sequestration in authigenic carbonates when in situ conditions promote their precipitation. However, this model overlooks the effects of methane turnover on total alkalinity, total sulfide, dissolved inorganic carbon, dissolved oxygen and pore-water pH (see Section 2.4).

For a range of spatial and temporal scales, existing models can still be successfully applied to answer some of the scientific questions linked to the full benthic impact of hydrate destabilisation. However, typically they simplify the transport and/or reaction term of the benthic methane sink and they rarely explicitly account for microbial dynamics. In addition, they generally fail to assess the benthic biogeochemical impact of methane turnover by AOM. Their lack of complexity hinders them from making robust predictions of climate-driven methane efflux across the seafloor, particularly for transient scenarios of methane influx to the SMTZ, and limit their capacity to assess related benthic biogeochemical implications.

3.3. Future Modelling Perspectives

AOM in marine sediments is rarely fully considered when assessing ocean-warming-induced seafloor methane release from hydrates. However, this review cites a wealth of studies suggesting that the AOM does not only represents a generally efficient, yet highly variable benthic sink for methane, but that also has important, yet difficult to predict, implications for hydrate-derived carbon dioxide emissions and carbon burial fluxes. Thus, playing a prominent role in assessing hydrate destabilisation-climate feed-backs, predicting climate evolution and designing climate policies. This review also highlights that explicit modelling of the evolution of microbial biomass under transient conditions may be critical for assessing methane release from marine sediments on decadal to millennial time scales. In line with these studies, with previous reviews on the role of methane hydrate in past and future climate change [2,36], and with the recent call for the inclusion of microbial dynamics in models exploring the response of the Earth system to climate change [171], we stress that improving our quantitative understanding of the benthic methane sink and benthic carbon cycle-climate feed-backs in response to climate-driven methane hydrate destabilisation is urgent. To do so, we suggest that future modelling efforts should be directed towards:

• Applying existing numerical models that so far have been only used to assess the hydrate inventory, to investigate the response of hydrate systems to climate perturbations. For instance, the models developed by Chatterjee et al. [119] and Tian et al. [161] could be well suited to exploring the benthic response to hydrate destabilisation but they have not been applied to examine scenarios of climate change. Chatterjee et al. [119] updated a 1D numerical model for the formation of hydrate in marine sediment [172,173] to couple it with mass balance equations for methane, sulfate, dissolved inorganic carbon, dissolved calcium ($C{a}^{2+}$) and carbon isotopes in pore water. They examined changes in these species due to methane cycling, including sediment burial, methane production from organic carbon, upward fluxes of methane, and significant loss of methane by AOM. However, they neglected hydrate and free gas phases in their calculations, only solving the dissolved methane concentrations and assuming that methane concentrations exceeding solubility do not form gas hydrate or free gas. In addition, they simplified the AOM rate to a bimolecular law. On the other hand, Tian et al. [161] coupled the TOUGH + HYDRATE model [154] with TOUGHREACT [174] to integrate reactive transport with the behaviour of hydrate-bearing systems. However, they focused on evaluating the resource of natural gas hydrate and quantifying the contribution of methane sources constrained by site-specific data.
• Extending current diagenetic formulations developed for hydrate systems to explicitly resolve AOM microbial dynamics and incorporate the full reaction-network driving the production/consumption of methane, total alkalinity, total sulfide, and dissolved inorganic carbon and controlling carbonate saturation and water pH (e.g., [160]). Burwicz et al. [160] developed a numerical model to investigate different scenarios of gas hydrate formation from both single and mixed methane sources (i.e., in situ biogenic and deep thermogenic sources). Although their model reproduces well the hydrate inventory, the AOM rate considered is too simplistic and the formulation ignores other key chemical reactions controlling benthic pore-water chemistry, for example, organoclastic sulfate consumption or authigenic carbonate precipitation/dissolution. In addition, this model has not been applied yet to explore hydrate destabilisation driven by climate perturbations. In the case of more sophisticated hydrate models (e.g., [46,47]), it would be key also to incorporate diagenetic processes for organic carbon accumulation and microbial degradation.
• Extending reactive-transport models to incorporate hydrate dynamics and consider multiphase transport. Among others reactive-transport models, the Biogeochemical Reaction Network Simulator (BRNS) [175,176,177] has been widely used to quantitatively explore the fluxes and transformations of methane carbon in the sediment column. This type of model is well suited to assessing the benthic response to hydrate destabilisation as it traces a wide range of chemical species dissolved in pore-water (e.g., [45,53]).
• Developing new models capable of fully coupling the dynamic interplay between hydrate thermodynamics, the different reaction and transport processes, and biomass dynamics, and which are particularly designed to assess the biogeochemical impact of methane turnover via AOM in the benthic environment (see flow path suggested in black in Figure 9). The development of new numerical schemes will avoid issues related to generalising or modifying existing formulations and can facilitate direct coupling with Earth system models (red dashed line in Figure 9, see Section 3.3.1).
• Implementing carbon isotope fractionation in fully coupled hydrate models to trace methane sources and simulate quantitative proxies of methane emissions, such as authigenic carbonates [53,178]. This will help reconstruct the activity of hydrate systems in past hyper-thermal events and establish a baseline for understanding the system response in future climate predictions.

3.3.1. The Need to Integrate Benthic Hydrate-Related Carbon Feed-Backs into Earth System Models (ESMs)

On a global scale, the impact of hydrate destabilisation on climate is generally simplified to whether the methane carbon released into the ocean reaches the atmosphere in the form of methane (either dissolved or in the form of gas bubbles). That is, the impact is approached by equating the totality or a fraction of the hydrate-sourced methane released to the ocean to the ocean-atmosphere flux. Yet, this approach is based on weak estimates of hydrate-sourced benthic methane emissions (see Section 3.2) and overlooks potential effects of methane turnover on greenhouse gas (GHG) emissions, ocean chemistry, ocean ecosystems, and biogeochemical cycles at different temporal and spatial scales [29,49,55,179,180].

As described in Section 2.4, the fraction of methane that escapes the benthic bio-filter, thus entering the ocean, has strong chemical implications in the benthic environment. AOM influences regional carbon dioxide budgets, pore-water oxygen levels and pH in a way that is difficult to predict. In addition, methane efflux across the seafloor is exposed to many biological and chemical processed within the ocean [180] which may also contribute to locally changing ocean chemistry.

The ocean plays a major role in the global carbon cycle and storage of anthropogenic carbon dioxide [62]. This key function is related to the dissolution of atmospheric carbon dioxide to form bicarbonate ($HC{O}_3^{-}$), and minor quantities of carbonic acid ($H_{2}C{O}_3$) and carbonate ($C{O}_3^{2-}$):

$$\begin{array}{c}\hfill C{O}_{2_{\left(g\right)}}+H_2{O}_{\left(l\right)}⟺H_{2}C{O}_{3_{\left(aq\right)}}\\ \hfill H_{2}C{O}_{3_{\left(aq\right)}}⟺HC{O}_{3_{\left(aq\right)}}^{-}+H_{\left(aq\right)}^{+}\\ \hfill HC{O}_{3_{\left(aq\right)}}^{-}⟺C{O}_3^{2-}+H_{\left(aq\right)}^{+}\end{array}$$

(13)

Intense methane consumption across the sediment-ocean continuum can trigger local changes in ocean chemistry that may perturb its capacity at regulating global climate. Alkalinity governs the efficiency at which carbon dioxide dissolves into the ocean (Equation (13)), and provides buffering capacity towards acidification [62]. Thus, the enhancement of alkalinity by intense AOM (see Section 2.4) could contribute to reducing ocean acidification and increasing the capacity of carbon dioxide absorption in surface waters [55,122,181]. On the contrary, AeOM (mainly across the water column) tends to increase ocean acidification. Regional hydrate-induced acidification would occur in addition to the ocean-wide acidification caused by the uptake of anthropogenic carbon dioxide [30]. Their combined effect would accelerate ocean acidification in parts of the ocean that otherwise would have experienced acidification with a considerable time delay. Moreover, hydrate-induced ocean acidification is accompanied by the depletion of oxidants/nutrients specific to methanotrophic metabolism, which may have important ecological implications for marine ecosystems and methane transfer to the atmosphere [52,182]. In particular, oxygen depletion is suggested to allow methane accumulation in deep basins, favouring methane transfer to the atmosphere via diffusion [50].

Quantifying benthic carbon feed-backs when assessing the evolution of global climate is highly challenging and requires the use of sophisticated Earth System Models (ESMs) [179]. However, with the exception of carbon dioxide, the biogeochemical transformations and physical processes that affect the distributions of other climatically active gases in the oceans (e.g., methane) are poorly represented in ESMs [183]. Moreover, the role of sea-bed processes is rarely considered. Current ESMs generally define sea-bed methane concentrations as prescribing lower boundary conditions [184]. To date, only a few studies have coupled ocean models (or Lagrangian analysis of the oceanic currents) with the methane fluxes across the seafloor estimated via hydrate models [29,49,50] (see Table 3 for details). Their simulations indicate that despite much of the methane released at the seafloor remaining deep in the water column, this methane still has significant biogeochemical and climatic implications. Archer et al. [29] and Biastoch et al. [49] simulate arbitrary scenarios in which a distinct fraction of the hydrate-source methane released at the seafloor is oxidized at the water column (100% and 50%, respectively). In particular, Archer et al. [29] estimate that eventually ∼25% of the by-product carbon dioxide is emitted to the atmosphere adding about 0.4–0.5 °C to the long-term impact of anthropogenic carbon on temperature. Biastoch et al. [49] show that intense AeOM results in lowering ocean pH (acidification) and depleting dissolved oxygen. A more complex study examining global hydrate-climate implications is that presented by Elliott et al. [50]. Their work introduces hydrate-related methane fluxes estimated by Reagan et al. [140] to a version of the global Parallel Ocean Program specifically extended for eco-dynamic and dissolved trace gas computations [185,186]. This is the first attempt at modelling the response of hydrate-derived methane injections into a biologically active ocean environment. Their simulations explore the possibility of intense AeOM causing oxygen depletion in deep-sea basins and conclude that this process is sufficient to cause regional acidification in the range 0.1–0.2 pH units and that allows the occurrence of hypoxia. All these models evidence important carbon feed-backs related to the fate of hydrate-methane emissions before reaching the atmosphere.

Existing global analyses suggest a limited direct impact on climate from hydrate destabilisation, at least as a fast positive feedback. Nonetheless, they point out the existence of significant carbon cycle-climate feed-backs that should be carefully examined and incorporated when assessing long-term climate predictions. That is, even if rapid or “catastrophic” feed-backs are not forecast to occur by climate-driven hydrate destabilisation on human time scales, the long-term biochemical and chemical consequences of methane efflux to the oceans demand further investigation. To date, methane climate feed-backs derived from hydrate destabilisation remain poorly quantified [32,56], and consequently, have not received much attention in the recent IPCC special report [30]. A good start towards a better understanding of the impact of hydrate destabilisation in the global climate would be to improve current numerical models used to evaluate the fate of hydrate-related methane through the sediment column (see Section 3.3). Then, the corresponding estimates of methane emissions across the seafloor, together with related changes in pore-water chemistry should be used as source terms to characterize the bottom boundary conditions in ESMs (red dashed line in Figure 9). That would feed the various processes at play in the ocean (e.g., AeOM, horizontal and vertical transport mechanisms, …) and allow introducing important feed-backs that may alter the ultimate air-sea carbon exchange.

4. Conclusions

Current estimates of hydrate-related methane emissions to the atmosphere are considered insignificant in relation to anthropogenic emissions. Yet, given the large volume of hydrate susceptible to destabilisation due to climate perturbations, these relatively minimal emissions may indicate active methane consumption within the sediment-ocean continuum. Marine methane fluxes are mostly prevented from entering the atmosphere by microbial interactions in shallow sediments and biochemical consumption across the water column. These processes convert methane carbon to inorganic and organic carbon pools preventing a direct impact of methane carbon in the climate system. Microbially mediated anaerobic oxidation of methane (AOM) is the major biological sink of methane in marine sediments, developing a crucial role of maintaining a sensitive balance of our atmosphere’s greenhouse gas content. Yet, the efficiency of this benthic bio-filter to the onset of methane fluxes caused by hydrate destabilisation remains poorly constrained, and its impact on the ocean carbon budget is still to be explored.

Past modelling efforts examining the evolution of hydrate systems in response to climate perturbation have largely ignore the role of the benthic sink in their simulations, thus ignoring potential effects of intense AOM in the global carbon cycle. More particularly, numerical models for hydrate systems rarely resolve the dynamics of the microbial community and thus fail to represent transient changes in AOM bio-filter efficiency and windows of opportunity for methane escape that arise due to slow microbial growth dynamics. Furthermore, none of these models has fully assessed yet the influence of hydrate-derived methane fluxes on benthic-pelagic alkalinity and DIC fluxes. We conclude that numerical modelling of the interaction between climate and methane hydrate should be improved to account more thoroughly for (i) realistic distributions of hydrate, (ii) transient changes on the benthic sink efficiency, and (iii) the transfer of methane-carbon to other carbon pools. In addition, we suggest that future lines of work should focus on using the seafloor methane fluxes, pore-water pH and oxygen levels predicted by improved hydrate models as ocean bottom boundary conditions in ESMs to better constrain mechanistic controls on the marine carbon budget and capture large-scale environmental impacts related to hydrate destabilisation on decadal to millennial timescales.