A Galerkin Method for the Simulation of Laminar Boundary Layers on Heated Walls
Abstract
1. Introduction
2. Laminar Boundary-Layer Energy Equation
3. Solution Method
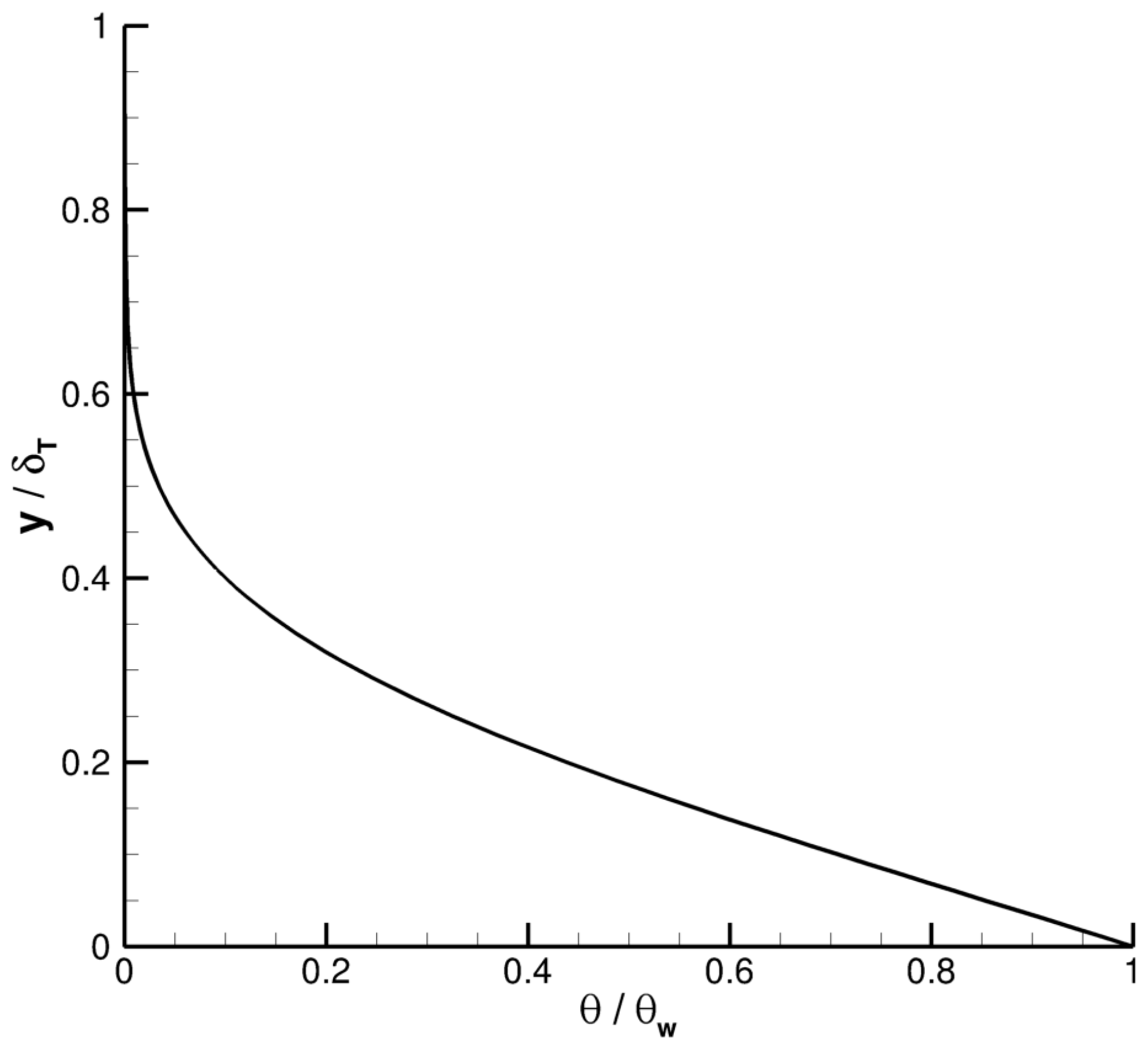
3.1. Galerkin Method with Respect to the y Variable
3.2. Finite Volume Method with Respect to the x Variable
- Solution initialization: in each cell, set: , where is the dynamic boundary layer thickness and , .
- End of the computation: Iterate until convergence to the steady state, i.e., until a given norm of the residual drops below a predefined threshold.
4. Results and Discussion
4.1. Test Case Definition
4.2. Convergence of the Method
4.2.1. Description of the Investigated Test Case
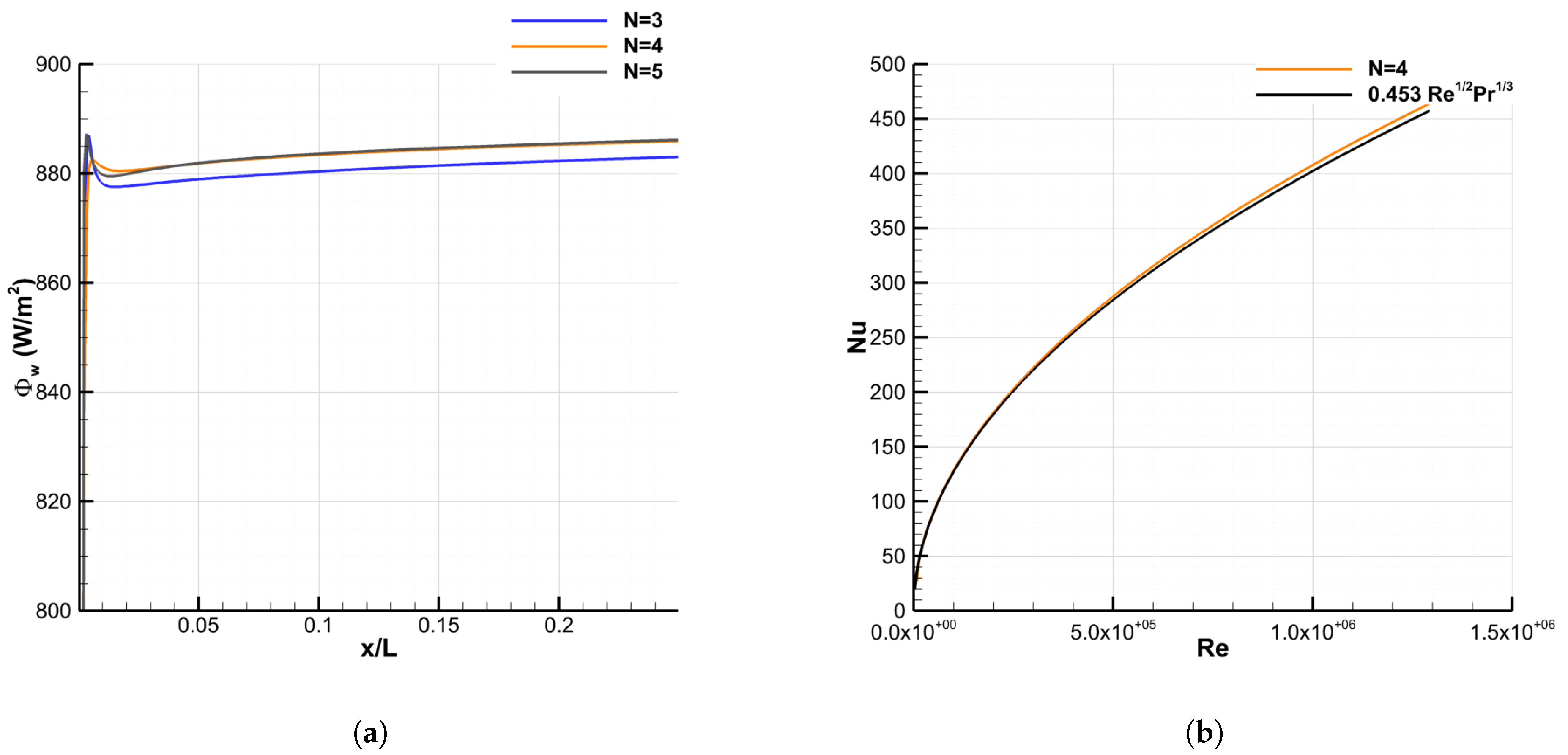
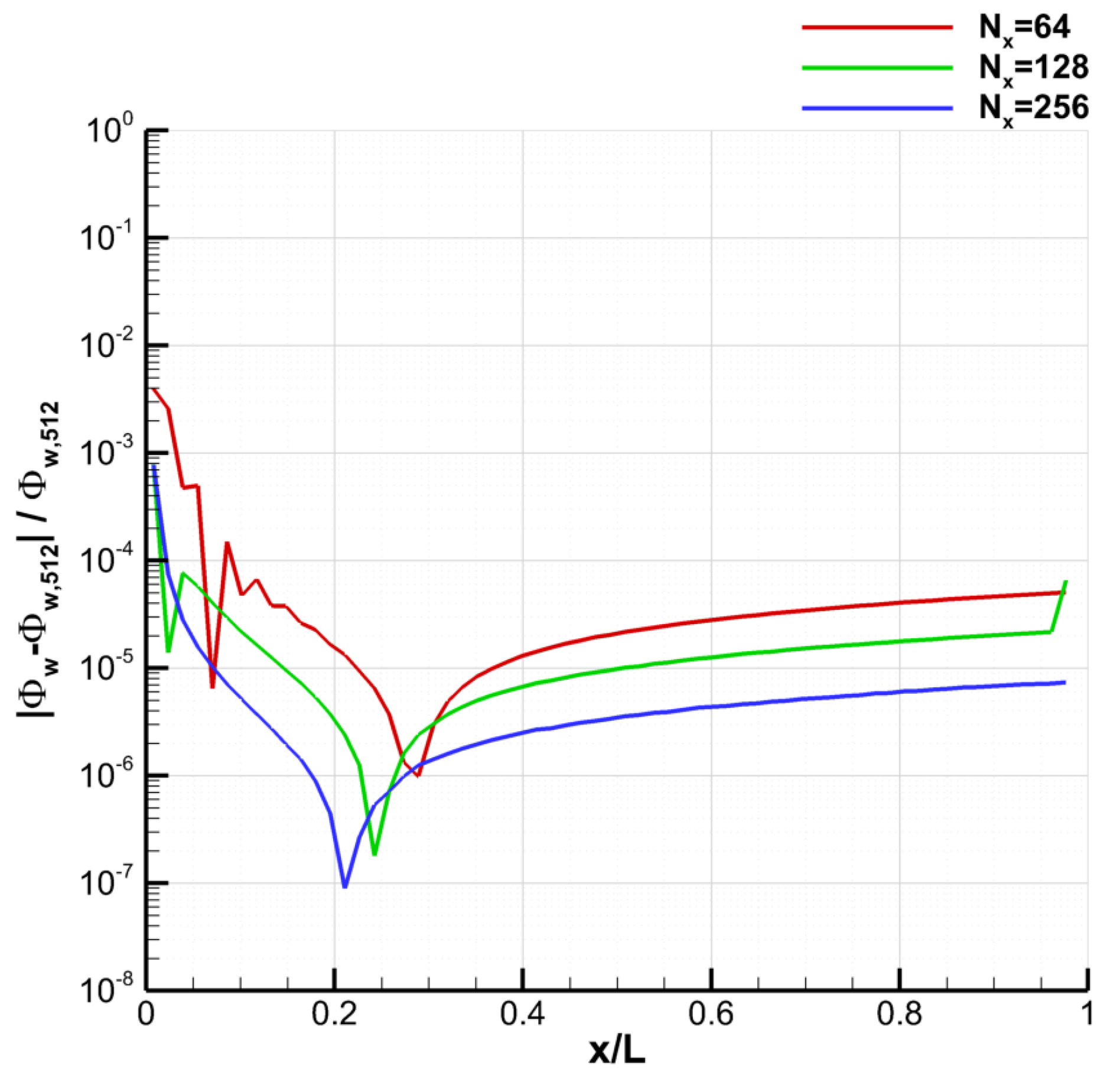
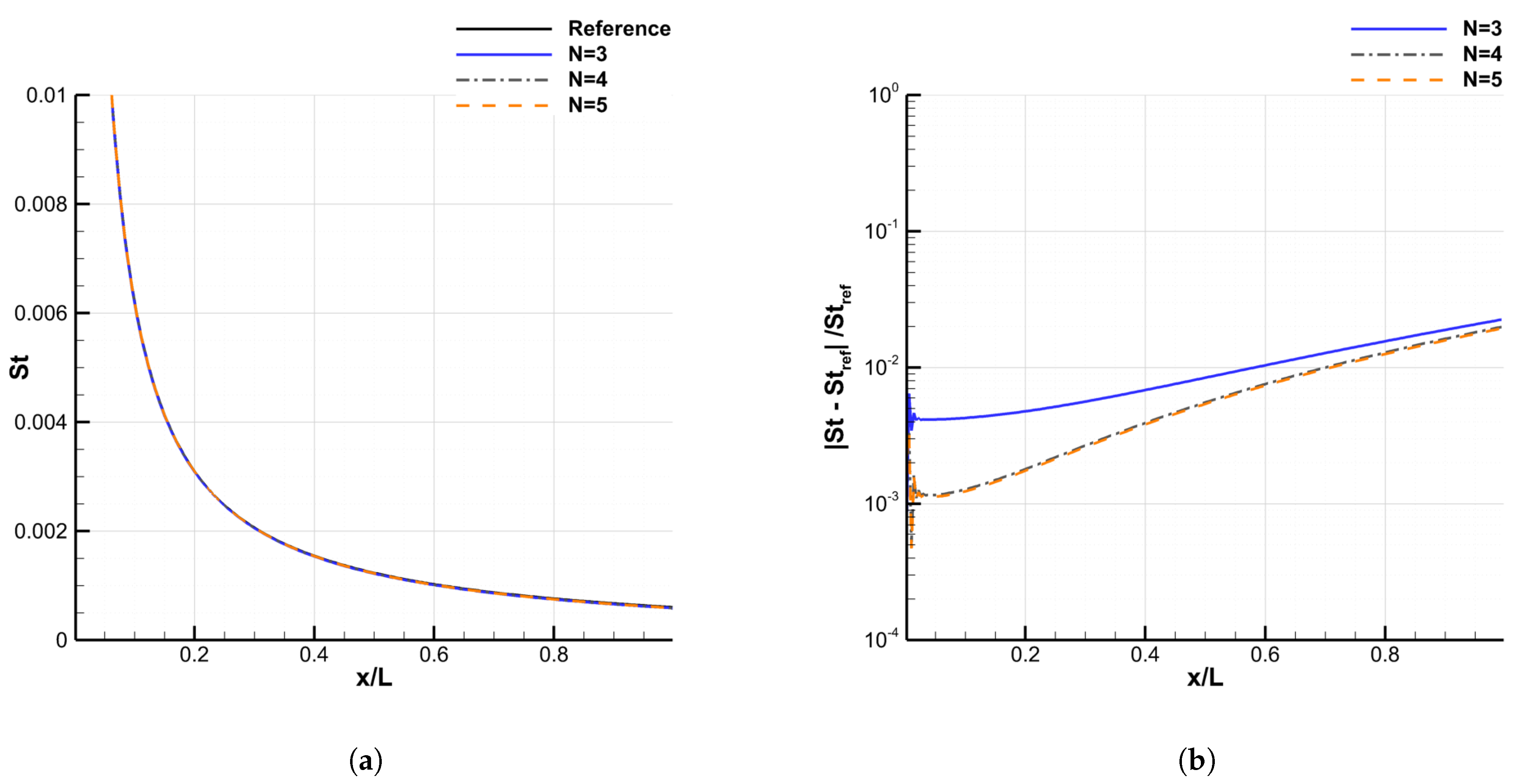
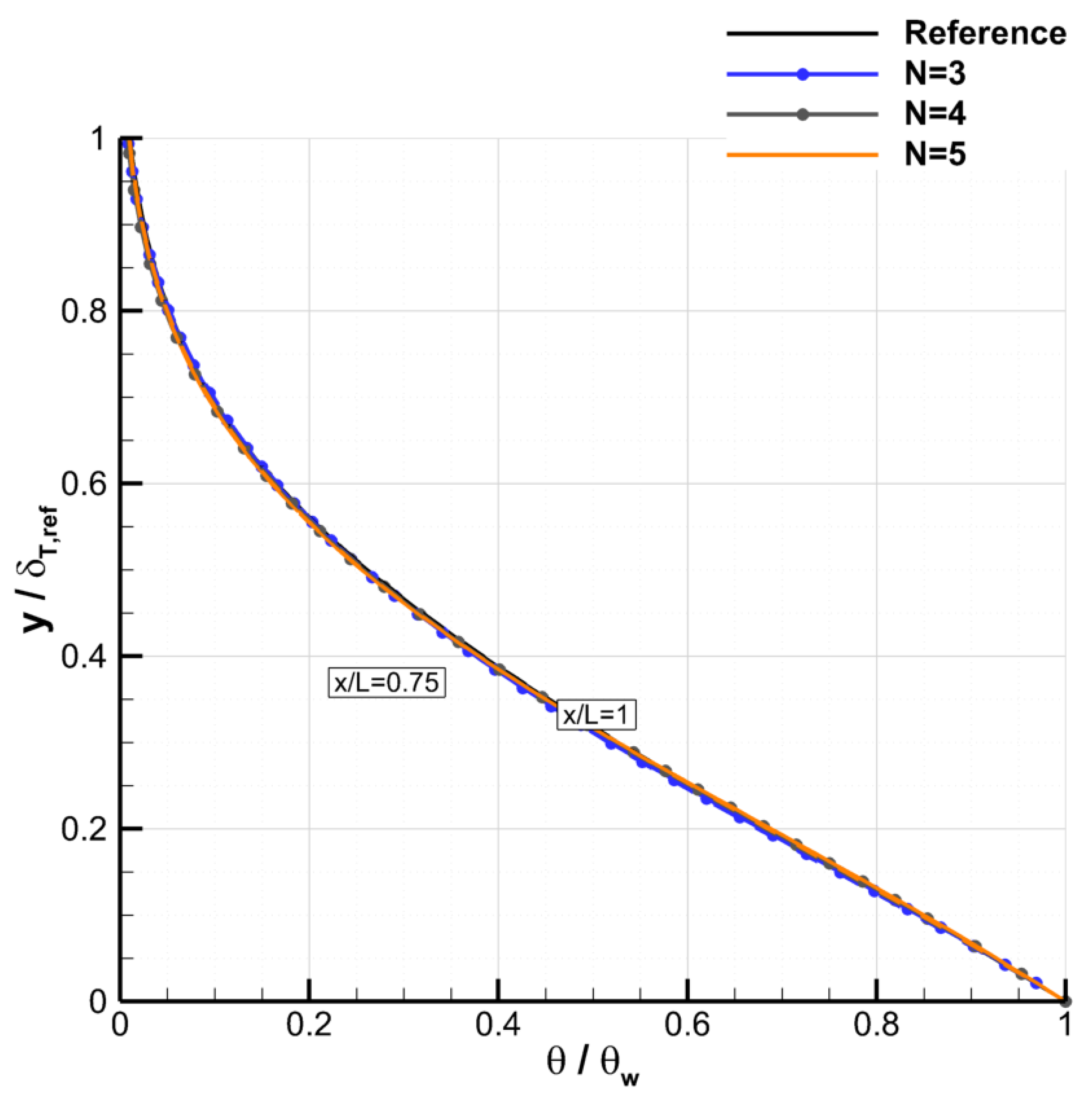
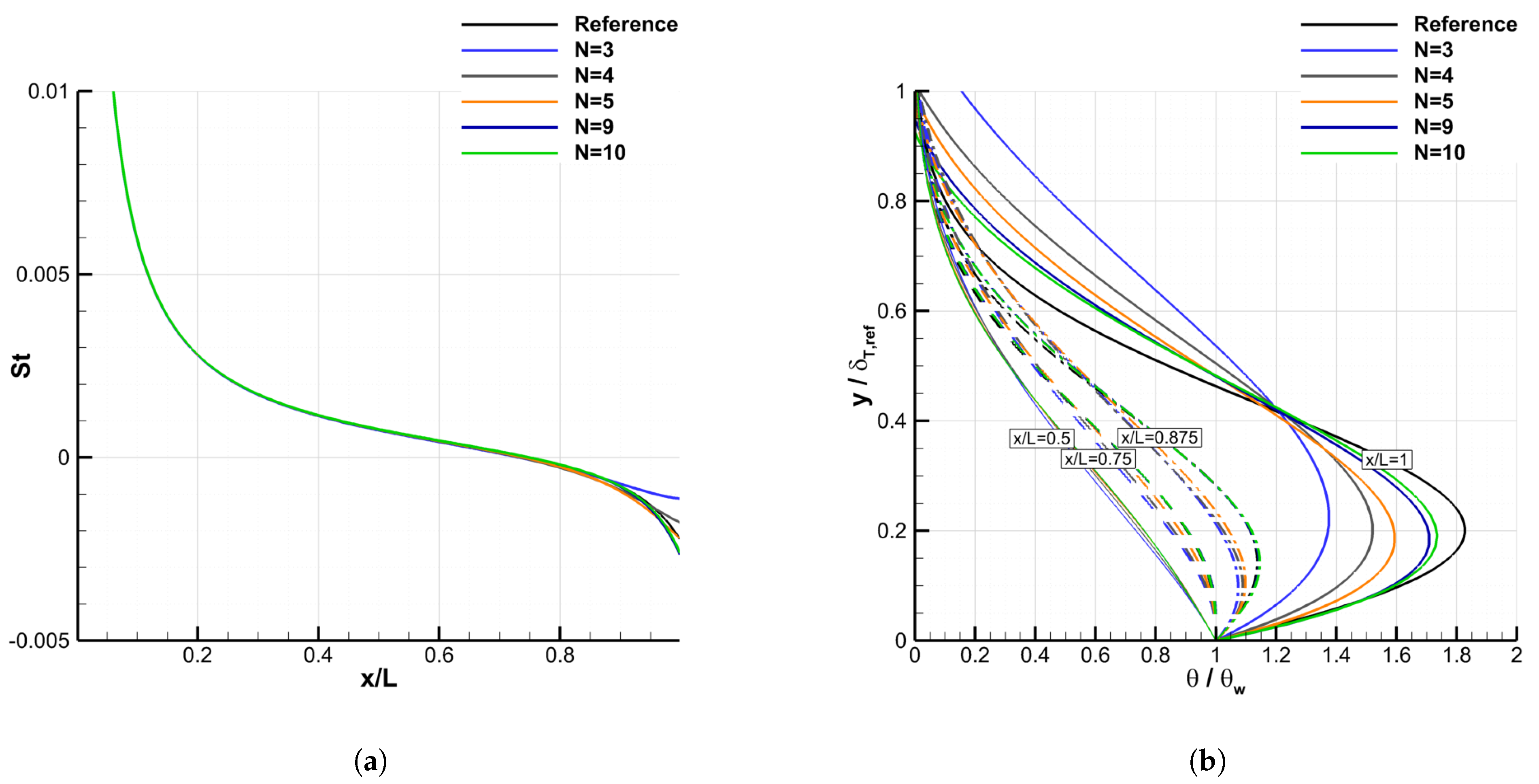
4.2.2. Grid Convergence
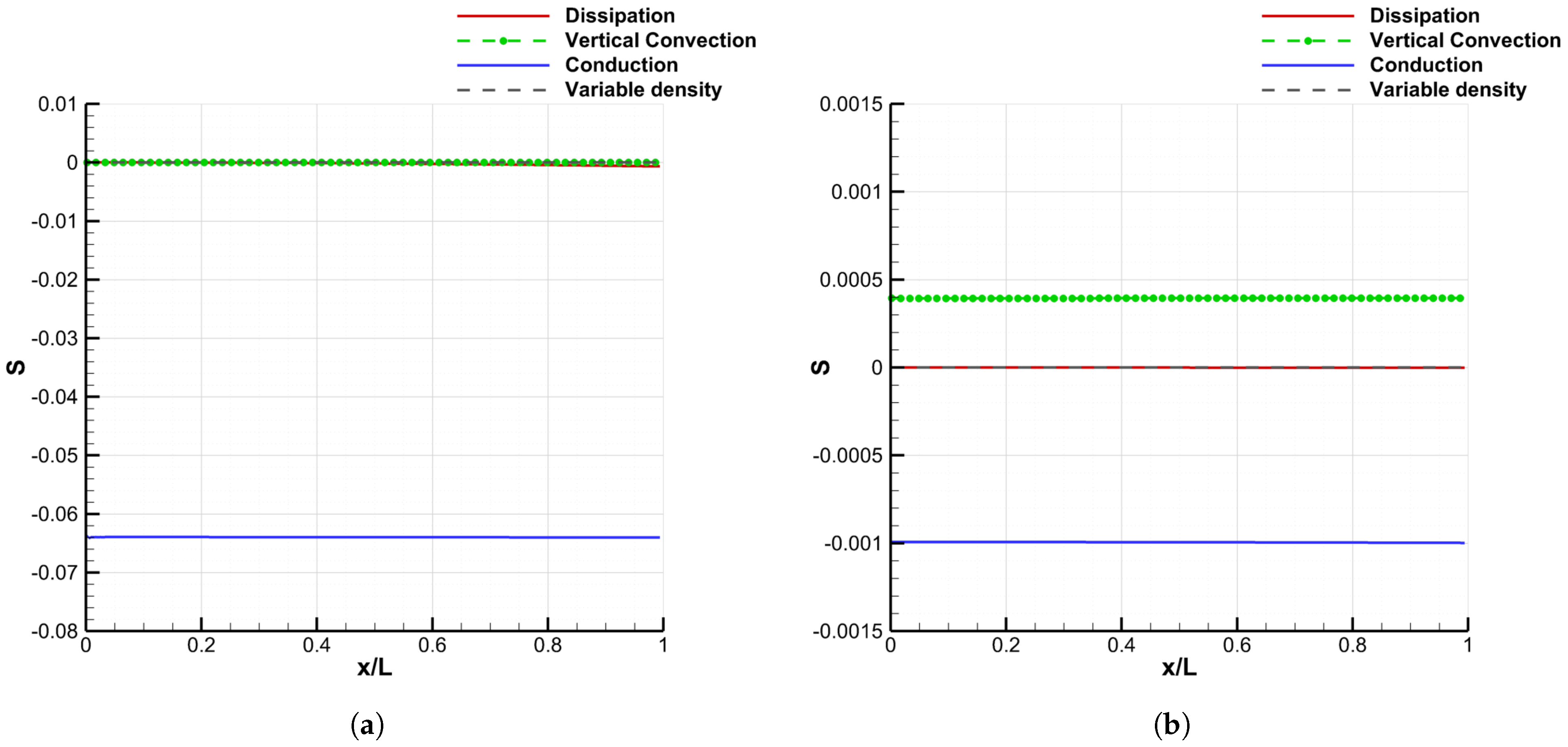
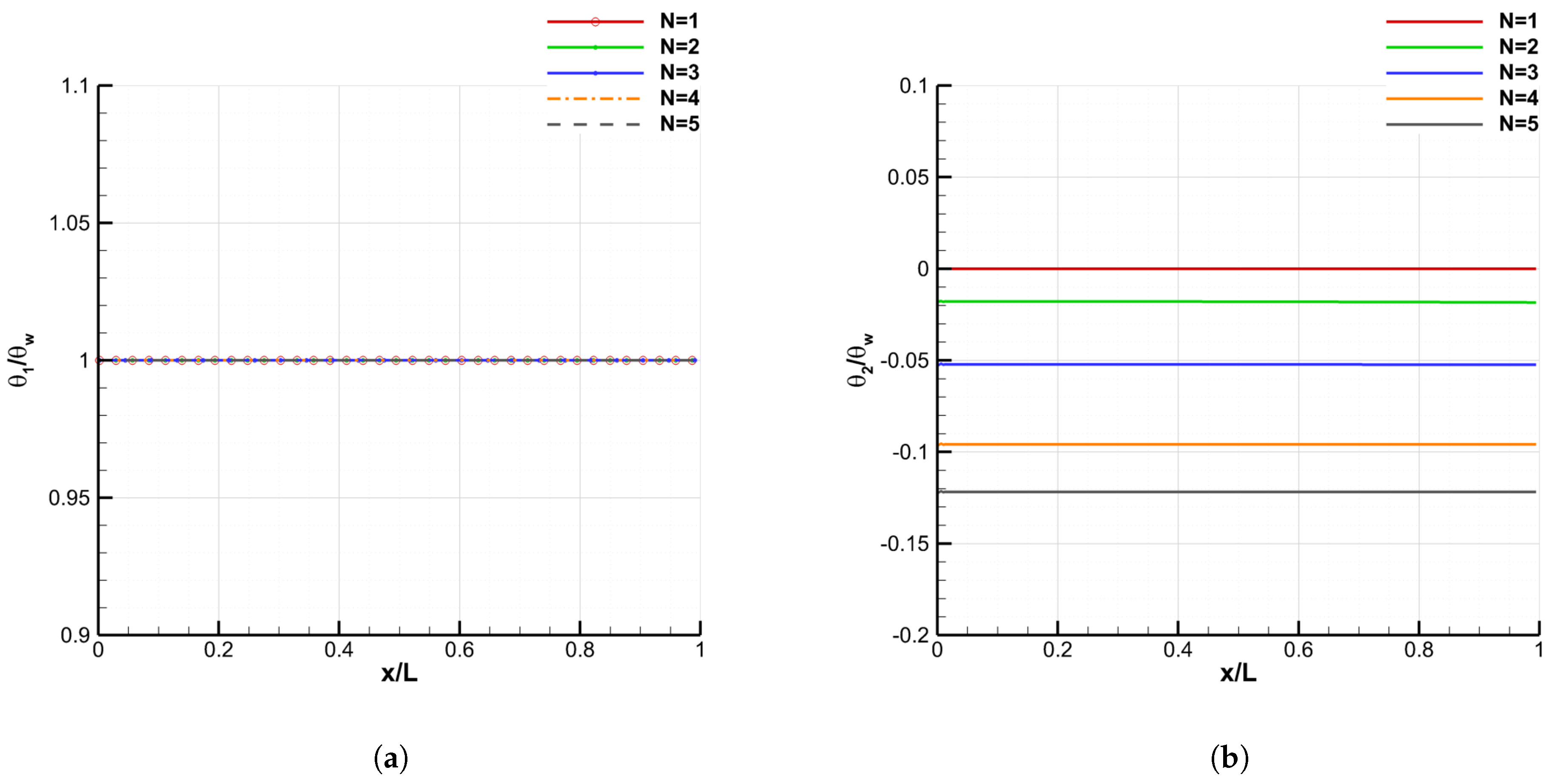
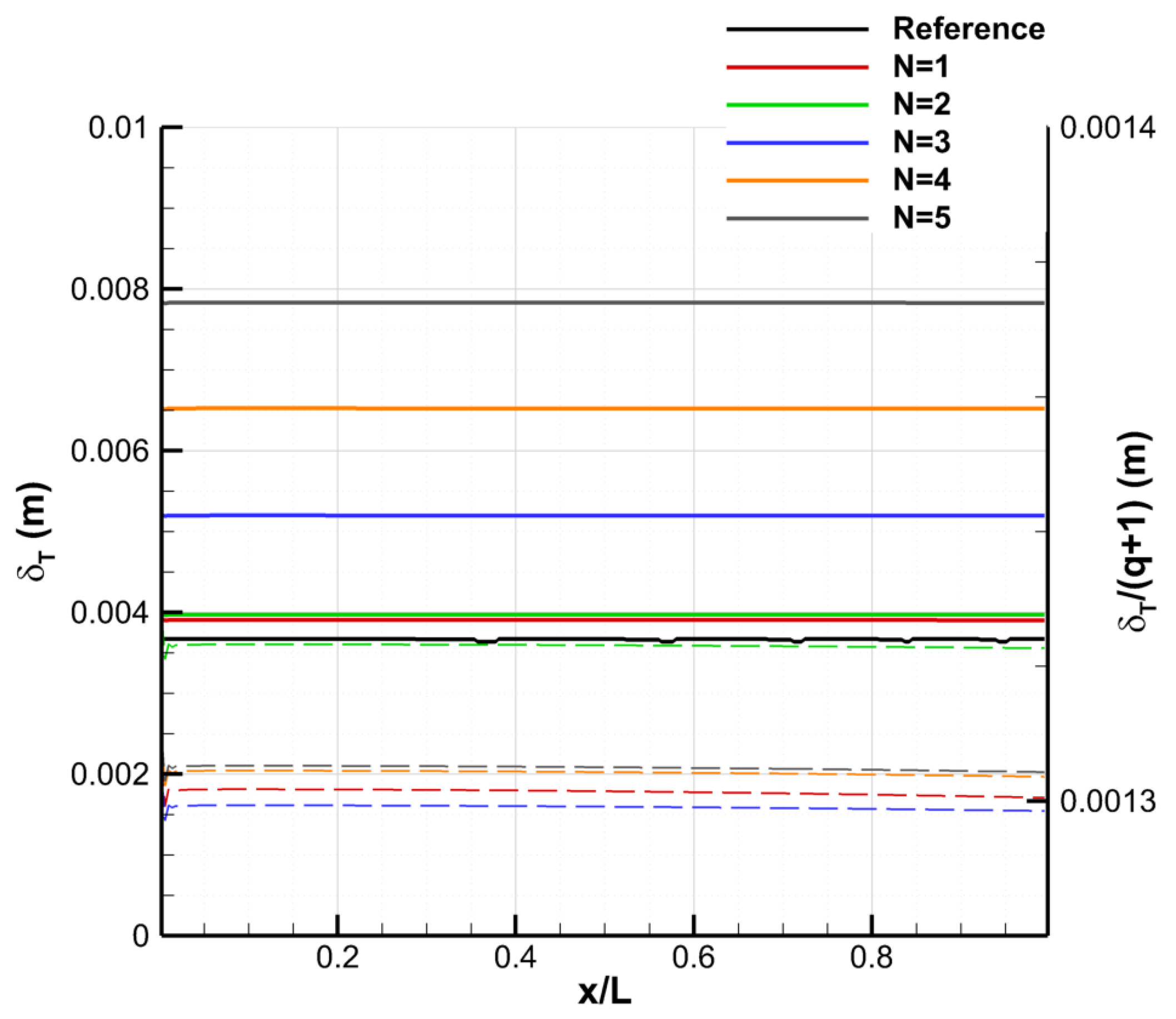
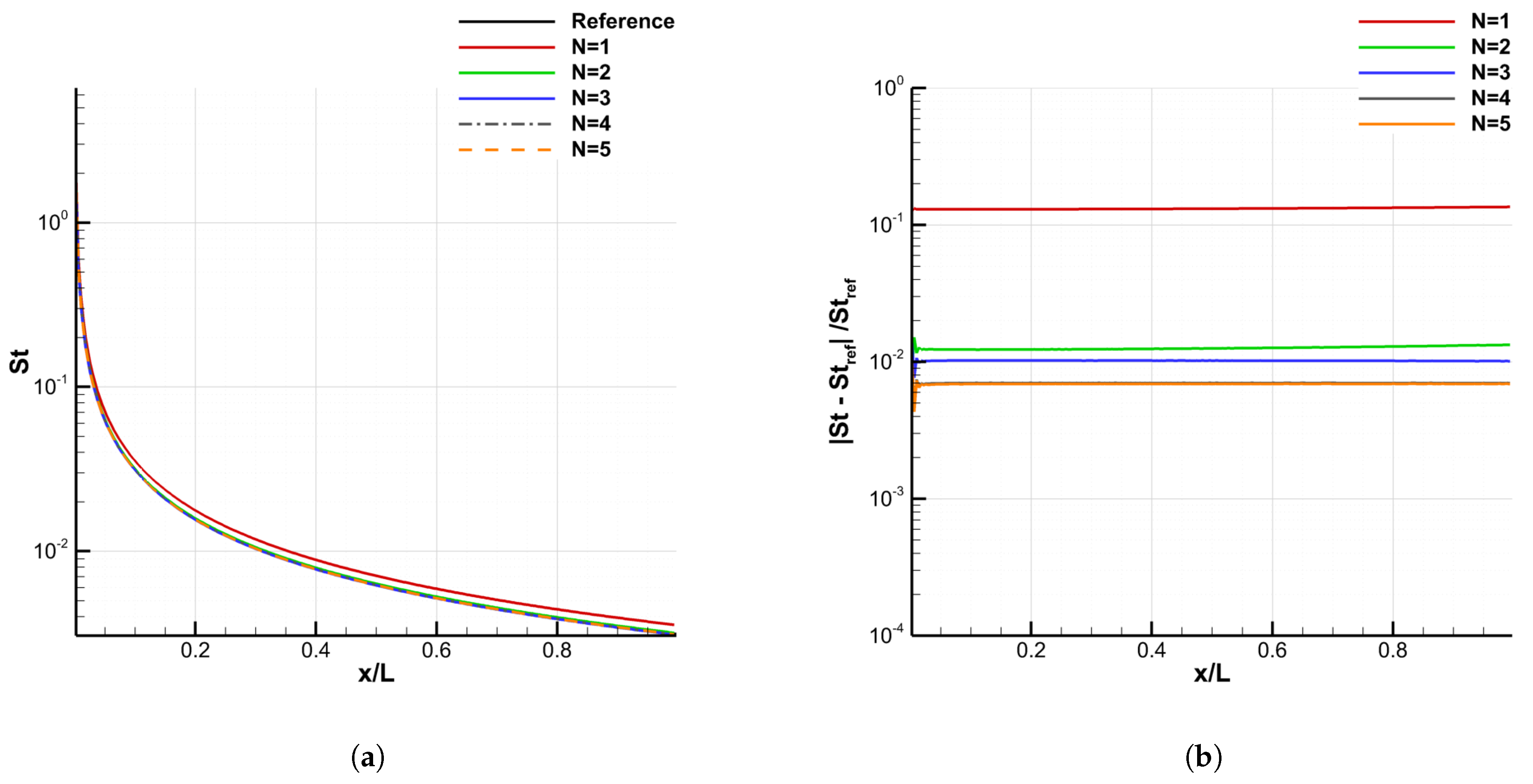
4.2.3. Convergence of the Galerkin Method
4.3. Influence of the Wall to Free-Stream Temperature Ratio
4.3.1. Influence on the Velocity Profile
4.3.2. Consequences on the Wall Heat Flux
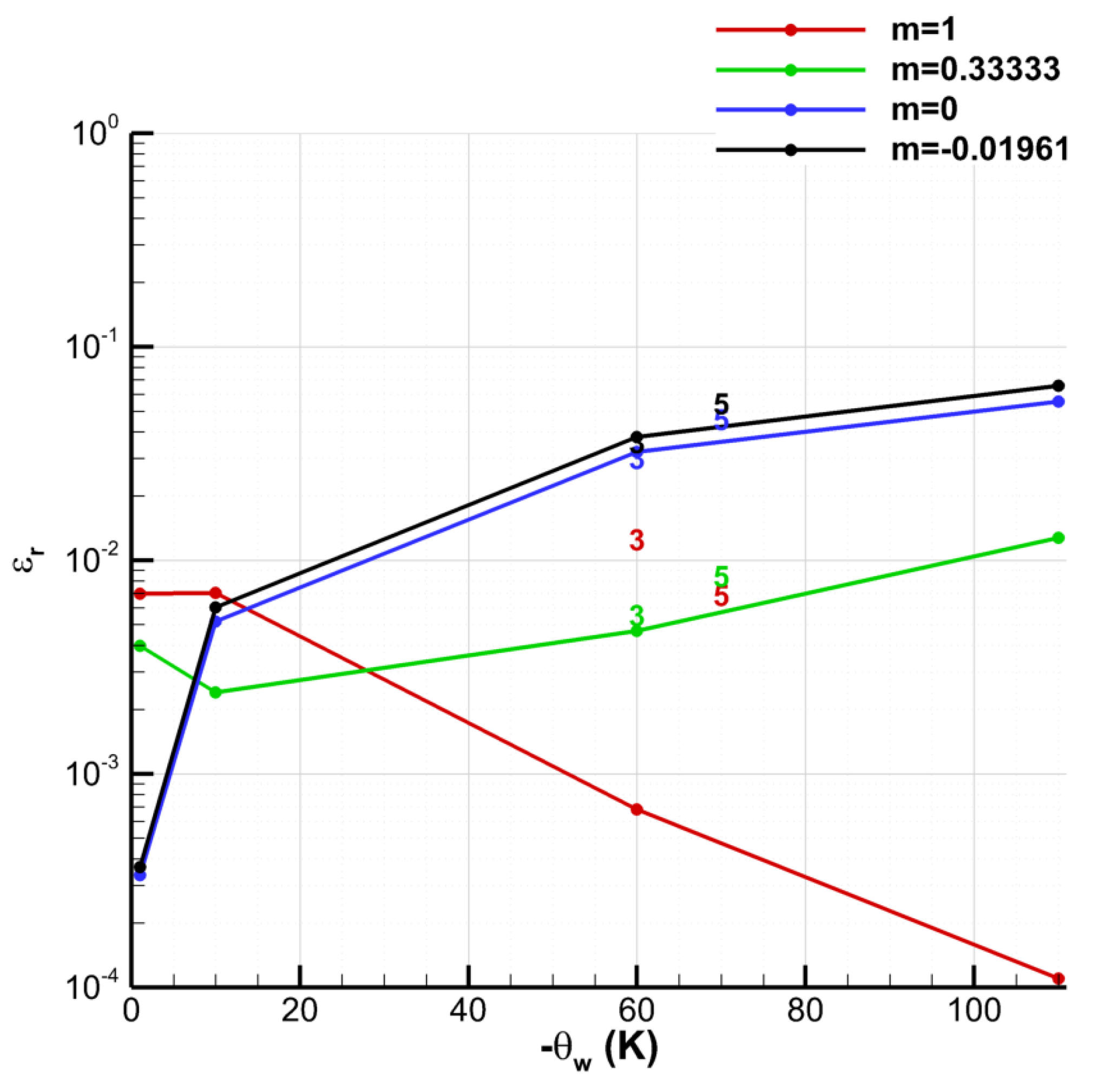
4.4. Influence of the Wall Temperature Gradient
4.4.1. Uniform Temperature, m = 1
4.4.2. Uniform Temperature Gradient −400 K/m, m = 1
4.4.3. Uniform Temperature Gradient +400 K/m, m = 1
4.4.4. Uniform Temperature, m = −0.01961
4.4.5. Uniform Temperature Gradient −400 K/m, m = −0.01961
4.5. Discussion about the Computational Time
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Short Description of the Resolution of the Dynamic Boundary Layer in the Solver BLIM2D
Appendix B. Validation of the Model against an Empiric Relation
References
- Morency, F.; Tezok, F.; Paraschivoiu, I. Anti-icing system simulation using CANICE. J. Aircr. 1999, 36, 999–1006. [Google Scholar] [CrossRef]
- Al-Khalil, K.M.; Horvath, C.; Miller, D.R.; Wright, W. Validation of NASA Thermal Ice Protection Computer Codes Part 3: Validation of ANTICE; Technical Report, NASA TM 2001-210907; Glenn Research Center: Cleveland, OH, USA, 2001.
- da Silva, G.A.L.; de Mattos Silvares, O.; de Jesus Zerbini, E.J.G. Numerical Simulation of Airfoil Thermal Anti-Ice Operation. Part 1: Mathematical Modeling. J. Aircr. 2007, 44, 627–633. [Google Scholar] [CrossRef]
- Wright, W. User’s Manual for LEWICE Version 3.2; Technical Report, NASA/CR-2008-214255; Glenn Research Center: Cleveland, OH, USA, 2008.
- Bu, X.; Lin, G.; Yu, J.; Yang, S.; Song, X. Numerical simulation of an airfoil electrothermal anti-icing system. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2013, 227, 1608–1622. [Google Scholar] [CrossRef]
- Morency, F.; Tezok, F.; Paraschivoiu, I. Heat and Mass Transfer in the Case of Anti-Icing System Simulation. J. Aircr. 2000, 37, 245–252. [Google Scholar] [CrossRef]
- Croce, G.; Beaugendre, H.; Habashi, W. CHT3D-FENSAP-ICE conjugate heat transfer computations with droplet impingement and runback effects. In Proceedings of the 40th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar] [CrossRef]
- Bu, X.; Lin, G.; Shen, X.; Hu, Z.; Wen, D. Numerical simulation of aircraft thermal anti-icing system based on a tight-coupling method. Int. J. Heat Mass Transf. 2020, 148, 119061. [Google Scholar] [CrossRef]
- Henry, R. Development of an electrothermal de-icing/anti-icing model. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]
- Chauvin, R.; Villedieu, P.; Trontin, P.; Bennani, L. A robust coupling algorithm applied to thermal ice protection system unsteady modeling. In Proceedings of the 6th AIAA Atmospheric and Space Environments Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar] [CrossRef]
- Aupoix, B. Couches Limites Bidimensionnelles Compressibles; Descriptif et Mode d’emploi du Code CLICET—Version 2015; Technical Report; ONERA: Toulouse, France, 2015. [Google Scholar]
- Bayeux, C.; Radenac, E.; Villedieu, P. Theory and Validation of a 2D Finite-Volume Integral Boundary-Layer Method for Icing Applications. AIAA J. 2019, 57, 1092–1112. [Google Scholar] [CrossRef]
- Bayeux, C. Méthode Intégrale pour la Couche Limite Tridimensionnelle. Applications au Givrage. Ph.D. Thesis, Institut Superieur de l’Aeronautique et de l’Espace (ISAE), Toulouse, France, 2017. [Google Scholar]
- Radenac, E.; Bayeux, C.; Villedieu, P. Use of a Two-Dimensional Finite Volume Integral Boundary-Layer Method for Ice-Accretion Calculations. AIAA J. 2020, 58, 1592–1606. [Google Scholar] [CrossRef]
- Radenac, E.; Kontogiannis, A.; Bayeux, C.; Villedieu, P. An extended rough-wall model for an integral boundary layer model intended for ice accretion calculations. In Proceedings of the 10th AIAA Atmospheric and Space Environments Conference—AVIATION 2018 ATLANTA, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Harry, R.; Radenac, E.; Blanchard, G.; Villedieu, P. Heat Transfer modeling by integral boundary-layer methods towards icing applications. In Proceedings of the AIAA Aviation 2021 Forum, Virtual, 2–6 August 2021. [Google Scholar] [CrossRef]
- Graebel, W.P.; Hsu, C. A Galerkin method for calculation of laminar thermal boundary layers. Int. J. Heat Mass Transf. 1981, 24, 771–774. [Google Scholar] [CrossRef][Green Version]
- Ozdemir, H.; Boogaard, E. Solving the integral boundary layer equations with a discontinuous Galerkin method. In Proceedings of the European Wind Energy Conference and Exhibition 2011, Brussels, Belgium, 13–17 March 2011. [Google Scholar]
- Sunden, B.; Wu, Z. On Heat Transfer Issues for Wind Energy Systems. J. Energy Resour. Technol. 2017, 139, 051201. [Google Scholar] [CrossRef]
- Lokatt, M.; Eller, D. Finite-volume scheme for the solution of integral boundary layer equations. Comput. Fluids 2016, 132, 62–71. [Google Scholar] [CrossRef]
- Prieling, D.; Steiner, H. Analysis of the wall mass transfer on spinning disks using an integral boundary layer method. Chem. Eng. Sci. 2013, 101, 109–119. [Google Scholar] [CrossRef]
- Cousteix, J. Aérodynamique et Couche Limite Laminaire; Cepadues Editions: Toulouse, France, 1989. [Google Scholar]
- Papadakis, M.; Wong, S.H.; Yeong, H.W.; Wong, S.C. Icing Tunnel Experiments with a Hot Air Anti-Icing System. In Proceedings of the 46th AIAA Aerospace Science Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar] [CrossRef]
- Aupoix, B. Roughness corrections for the k-ω shear stress transport model: Status and proposals. J. Fluids Eng. 2015, 137, 021202. [Google Scholar] [CrossRef]
- Chedevergne, F. Analytical wall function including roughness corrections. Int. J. Heat Fluid Flow 2018, 73, 258–269. [Google Scholar] [CrossRef]
- Radenac, E.; Gaible, H.; Bezard, H.; Reulet, P. IGLOO3D Computations of the Ice Accretion on Swept-Wings of the SUNSET2 Database; SAE Technical Paper 2019-01-1935; SAE: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Bempedelis, N.; Bayeux, C.; Blanchard, G.; Radenac, E.; Villedieu, P. A 3D Finite-Volume Integral Boundary Layer method for icing applications. In Proceedings of the 9th AIAA Atmospheric and Space Environments Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef][Green Version]
- Lienhard, J.H. Heat Transfer in Flat-Plate Boundary Layers: A Correlation for Laminar, Transitional, and Turbulent Flow. J. Heat Transf. 2020, 142, 061805. [Google Scholar] [CrossRef]
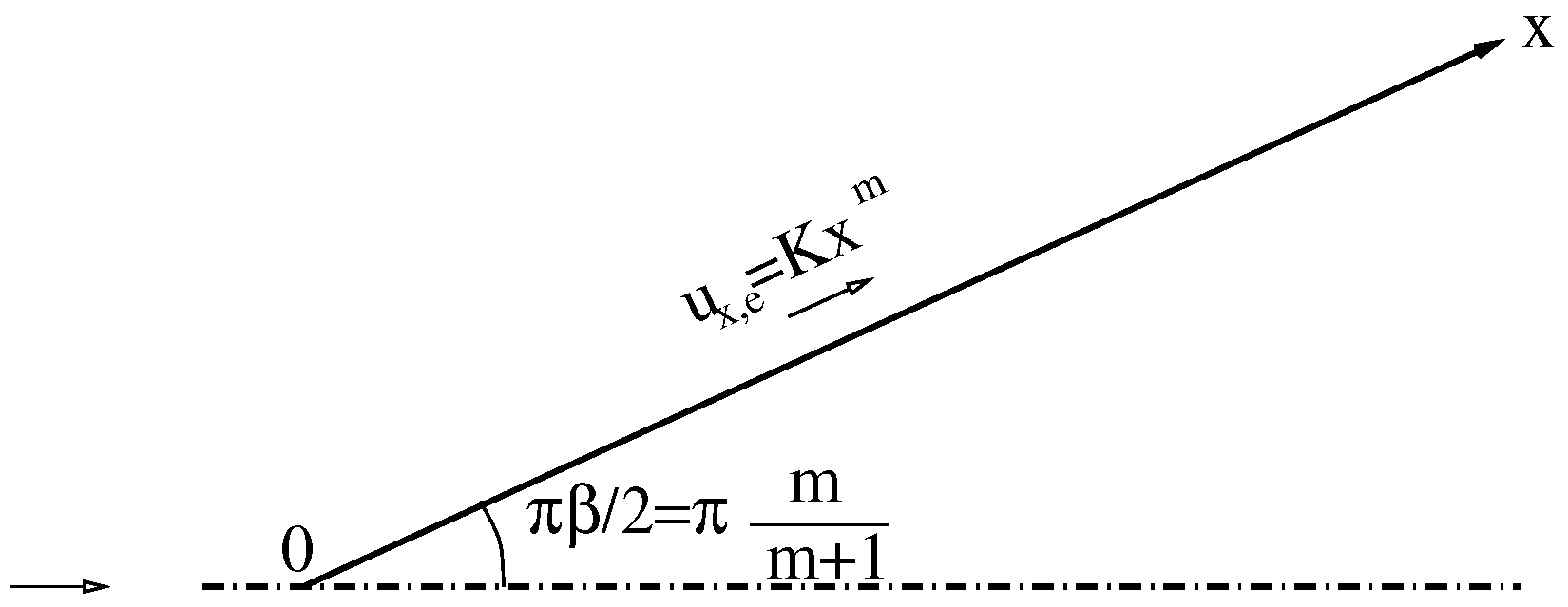




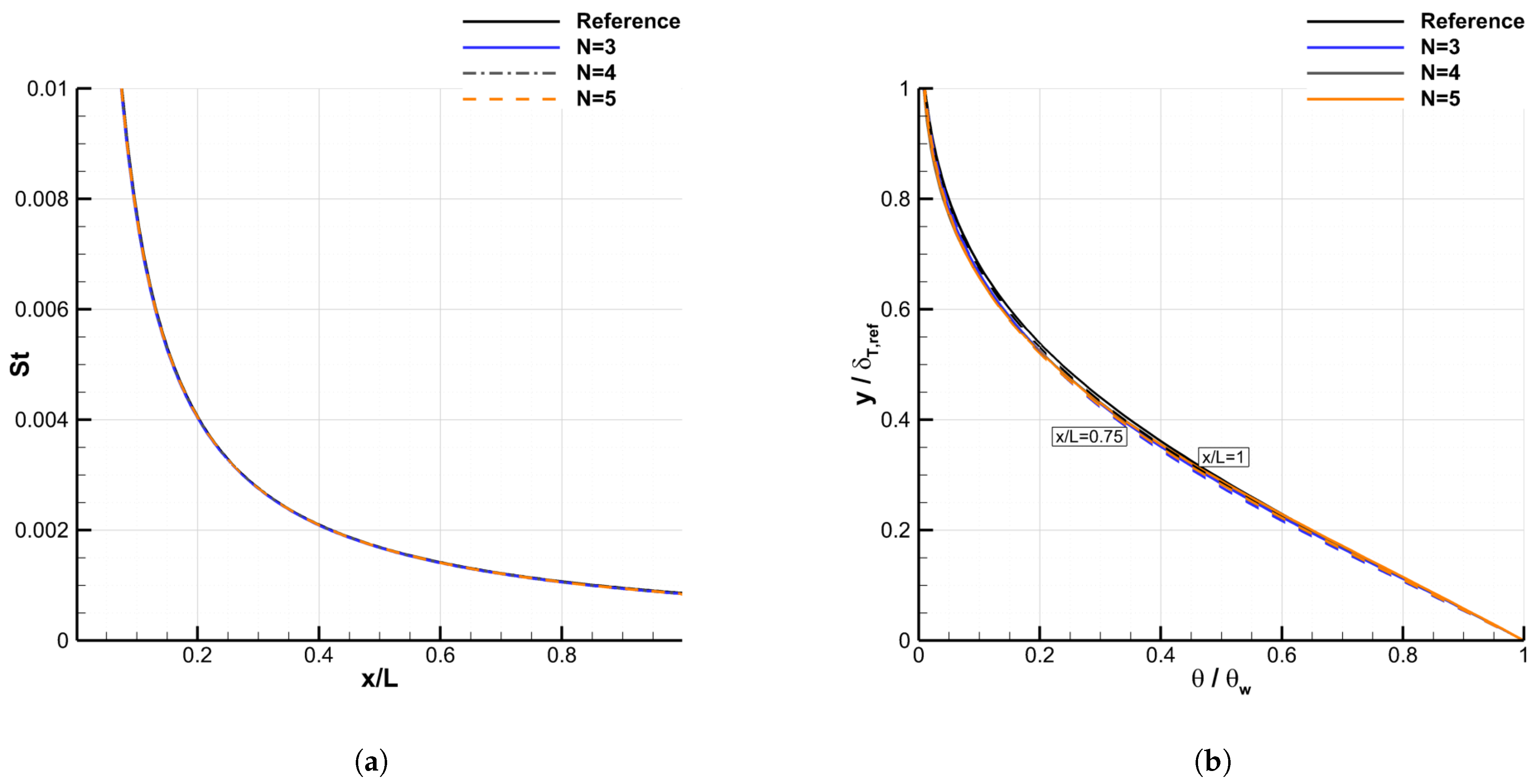
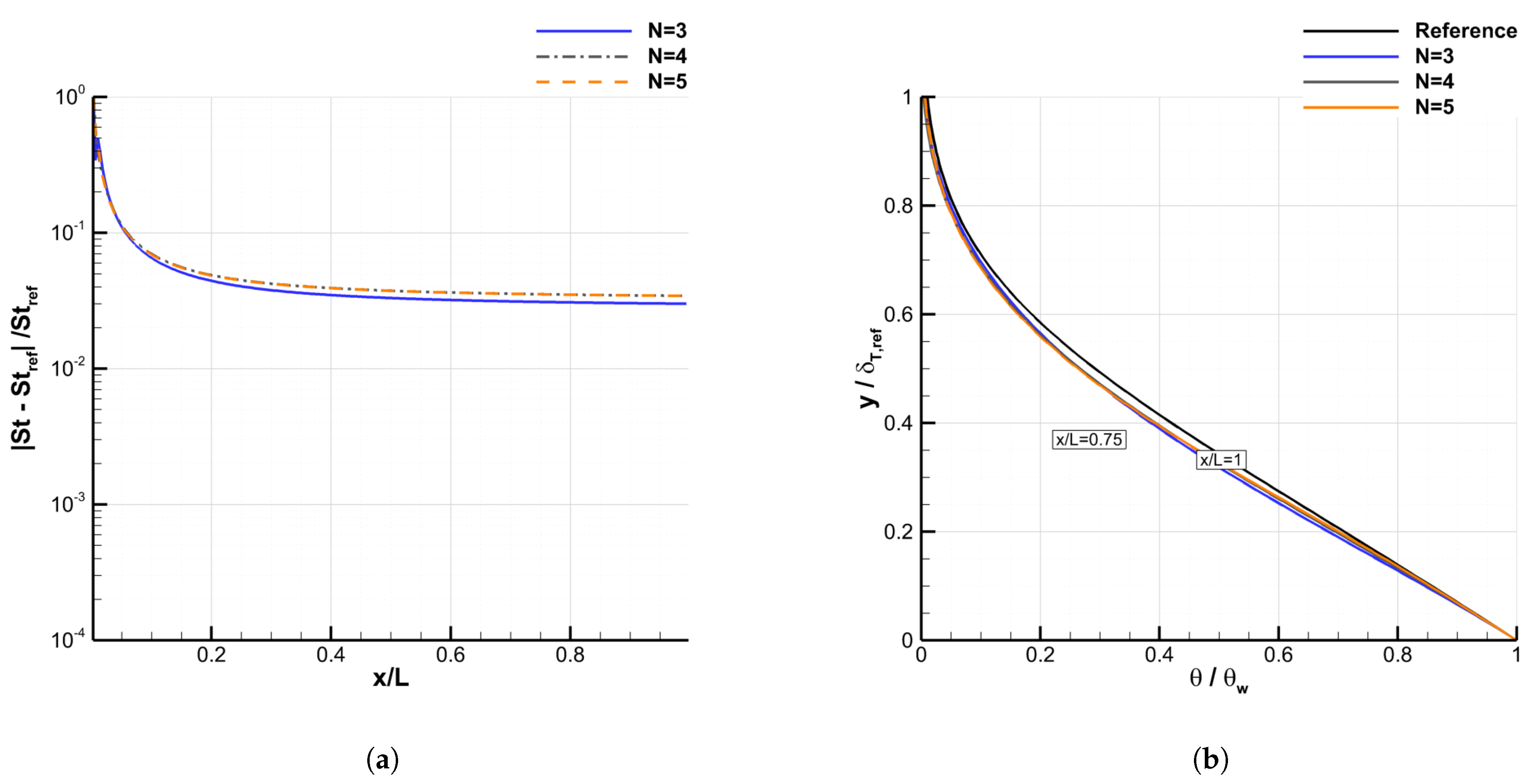
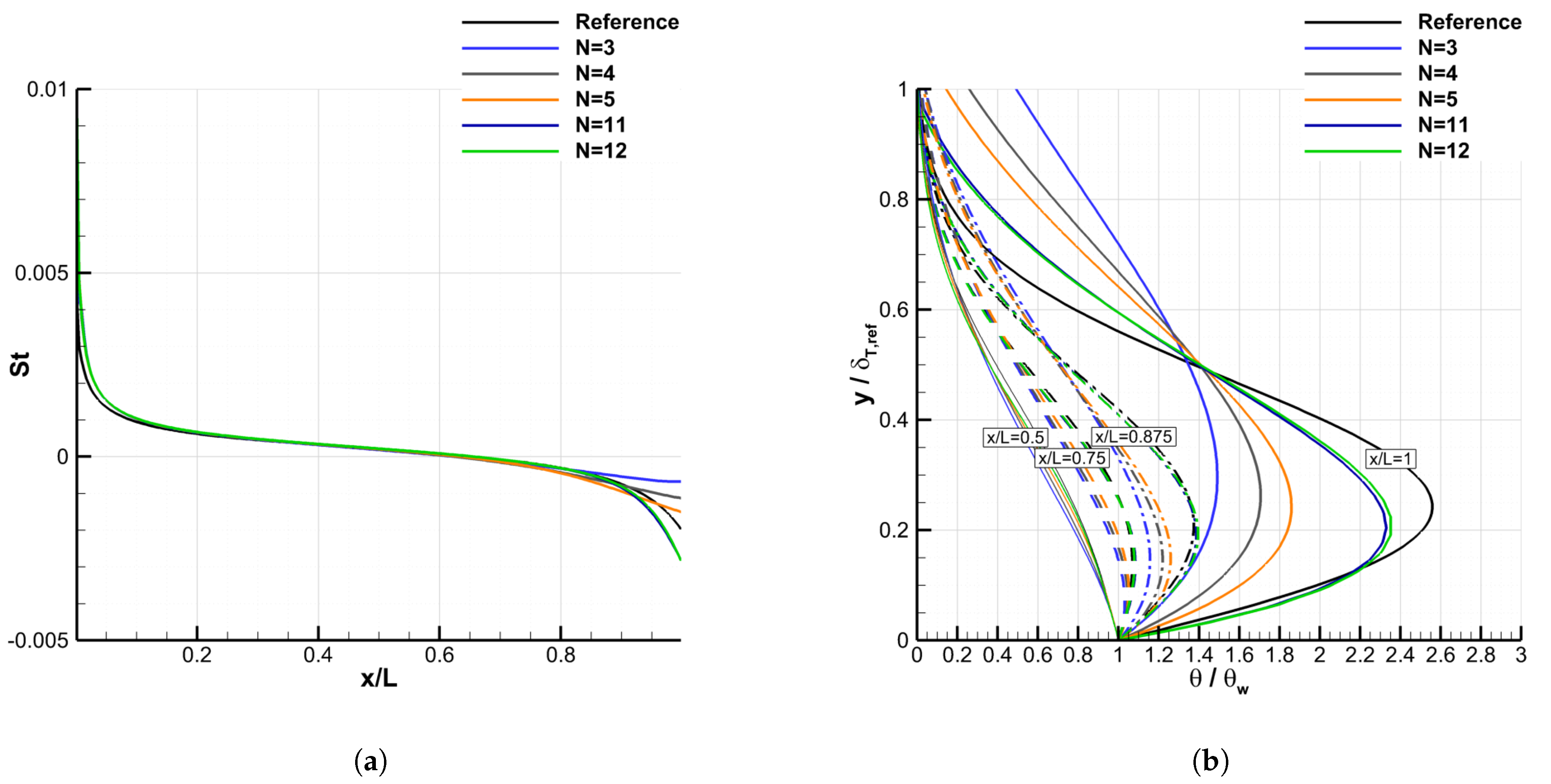
| Test-Case | L (m) | m | M | (Pa) | (K) | (K) | (K/m) |
|---|---|---|---|---|---|---|---|
| 1 | 0.25 | 1 | 0.01 | 80,005 | 263.155 | 264.15 | 0 |
| 2 | 0.25 | −0.01961, 0, 1/3, 1 | 0.01 | 80,005 | 263.155 | 264.15, 273.15, 323.15, 373.15 | 0 |
| 3 | 0.25 | −0.01961, 0, 1/3, 1 | 0.25 | 83,555 | 266.439 | 323.15 | 0 |
| 4 | 0.25 | −0.01961, 0, 1/3, 1 | 0.25 | 83,555 | 266.439 | 373.15 | −400 |
| 5 | 0.25 | −0.01961, 0, 1/3, 1 | 0.25 | 83,555 | 266.439 | 273.15 | 400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radenac, E.; Harry, R.; Villedieu, P. A Galerkin Method for the Simulation of Laminar Boundary Layers on Heated Walls. Energies 2022, 15, 3267. https://doi.org/10.3390/en15093267
Radenac E, Harry R, Villedieu P. A Galerkin Method for the Simulation of Laminar Boundary Layers on Heated Walls. Energies. 2022; 15(9):3267. https://doi.org/10.3390/en15093267
Chicago/Turabian StyleRadenac, Emmanuel, Rémi Harry, and Philippe Villedieu. 2022. "A Galerkin Method for the Simulation of Laminar Boundary Layers on Heated Walls" Energies 15, no. 9: 3267. https://doi.org/10.3390/en15093267
APA StyleRadenac, E., Harry, R., & Villedieu, P. (2022). A Galerkin Method for the Simulation of Laminar Boundary Layers on Heated Walls. Energies, 15(9), 3267. https://doi.org/10.3390/en15093267