Data-Driven Calibration of Rough Heat Transfer Prediction Using Bayesian Inversion and Genetic Algorithm
Abstract
:1. Introduction
2. Test Case Geometry and Setup
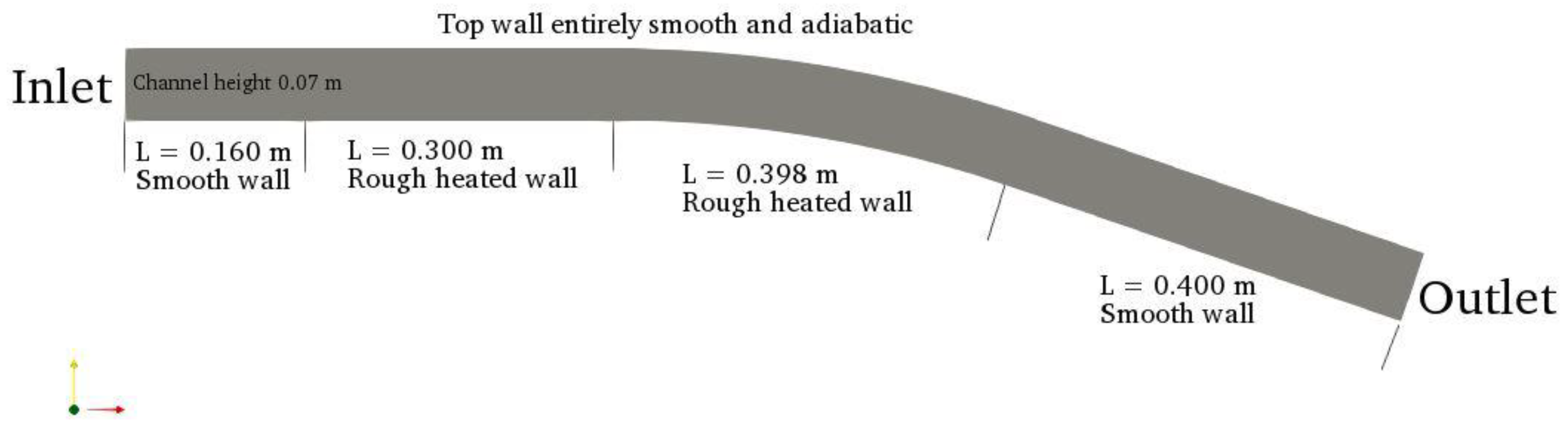
2.1. Physical Geometry and Boundary Conditions
2.2. Mesh and Numerical Setup
3. 2PP Thermal Correction Model
4. PCE Metamodeling
4.1. Design of Experiment (DOE)
4.2. Metamodels Generation
5. Sensitivity Study
- above 80% is very important;
- between 50% and 80% is important;
- between 30% and 50% is unimportant;
- below 30% is negligible.
6. Model Calibration
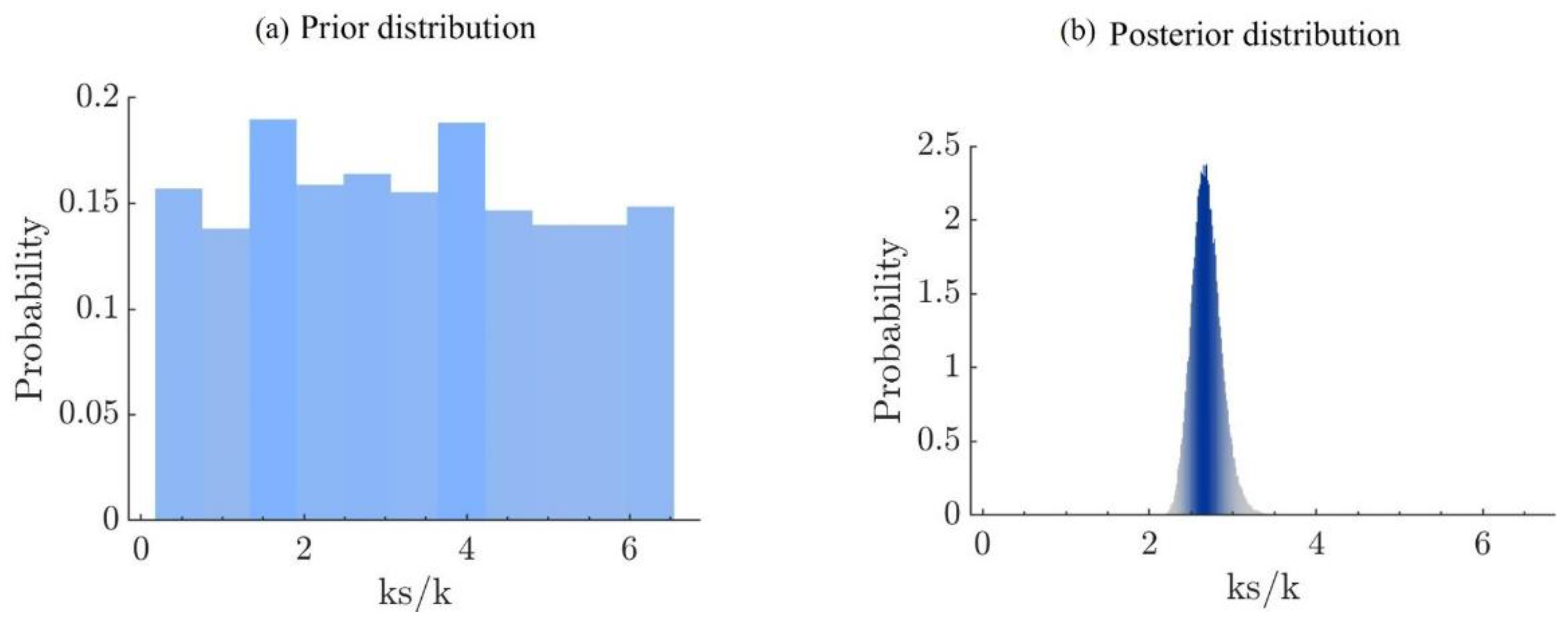
6.1. Bayesian Inversion Calibration
6.2. Calibration Using a Genetic Algorithm
7. Results
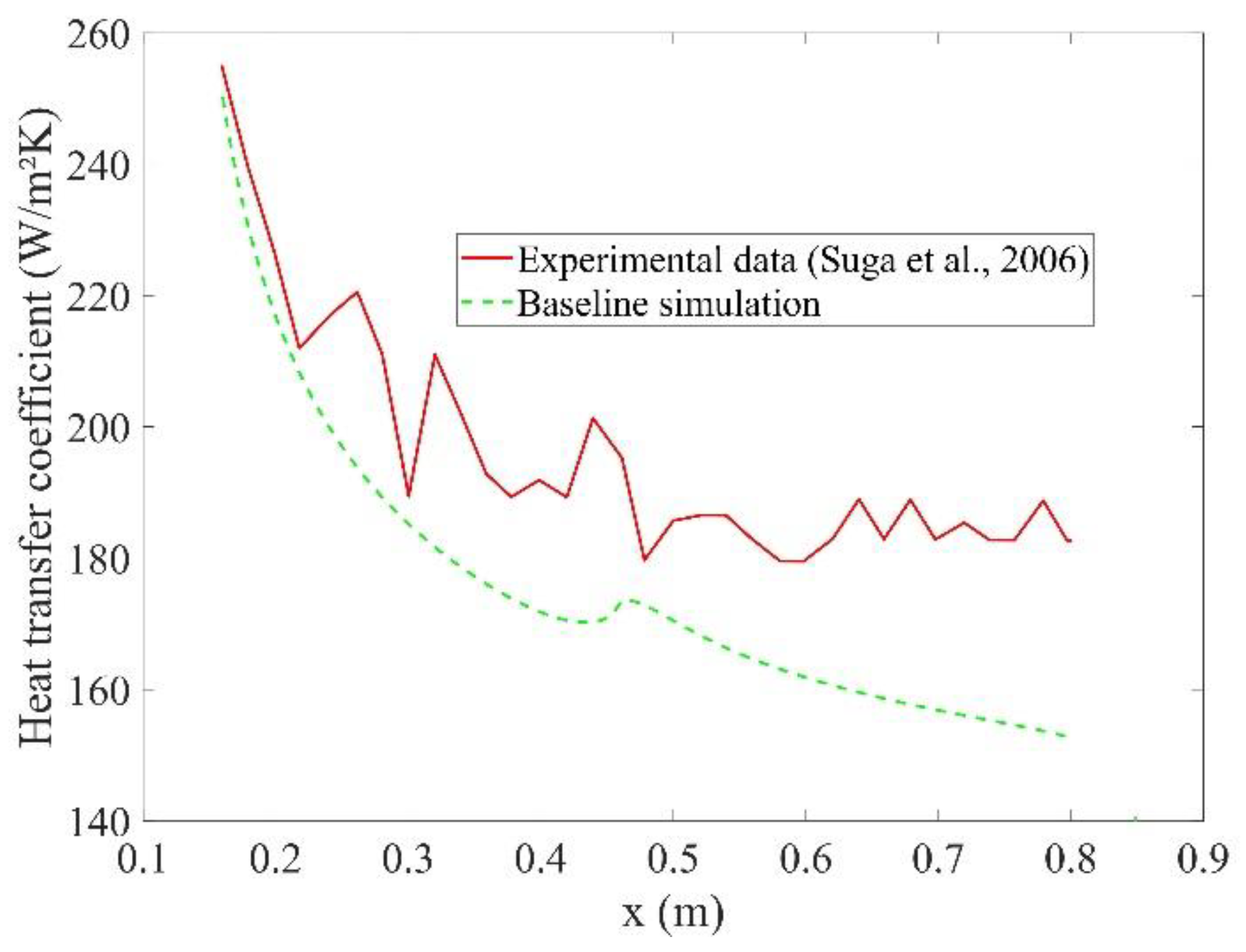
7.1. CFD Results before Calibration
7.2. Visualization of the DOE outputs
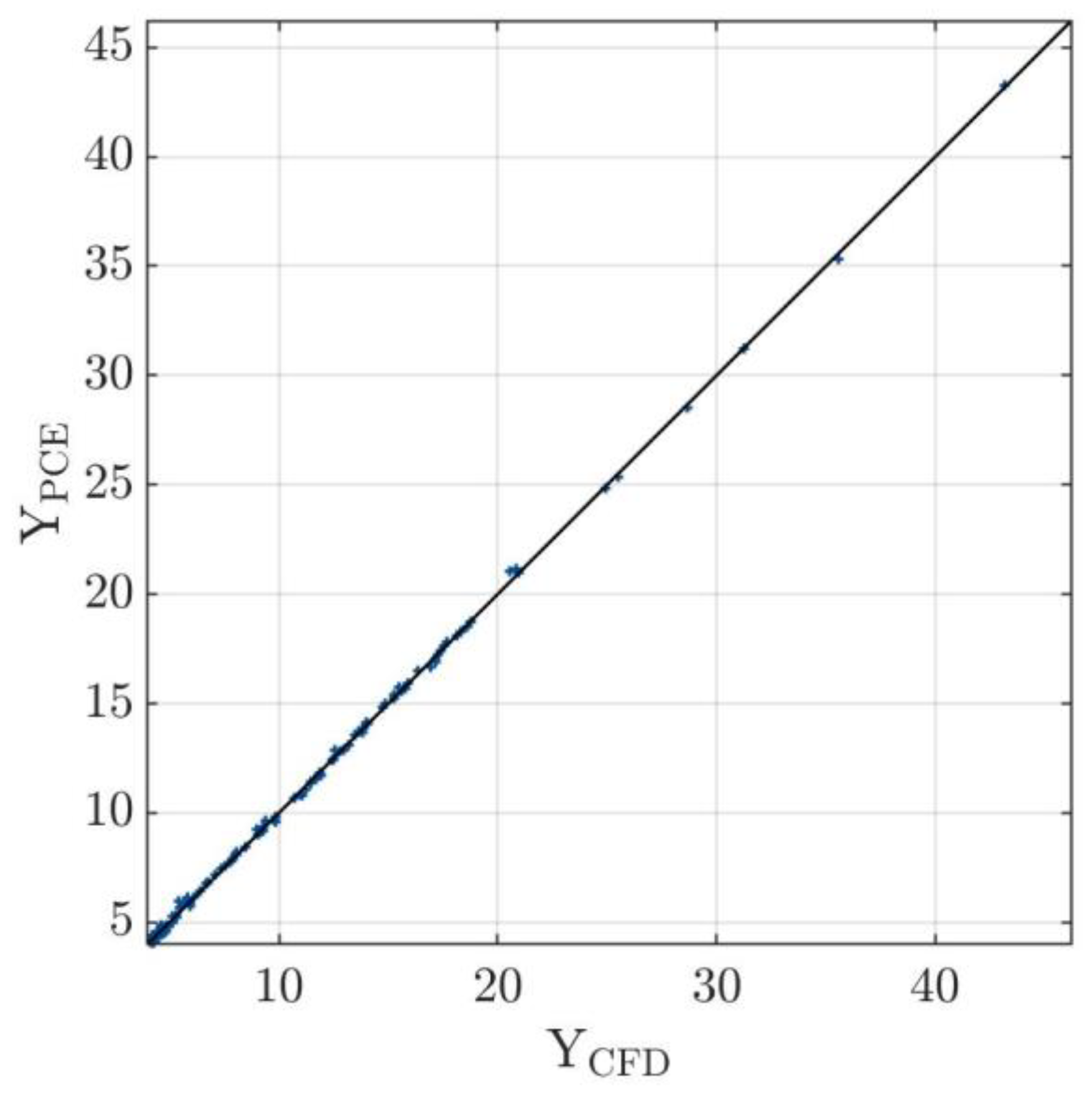
7.3. Characteristics of the Metamodels and Accuracy
7.4. Sensitivity Study
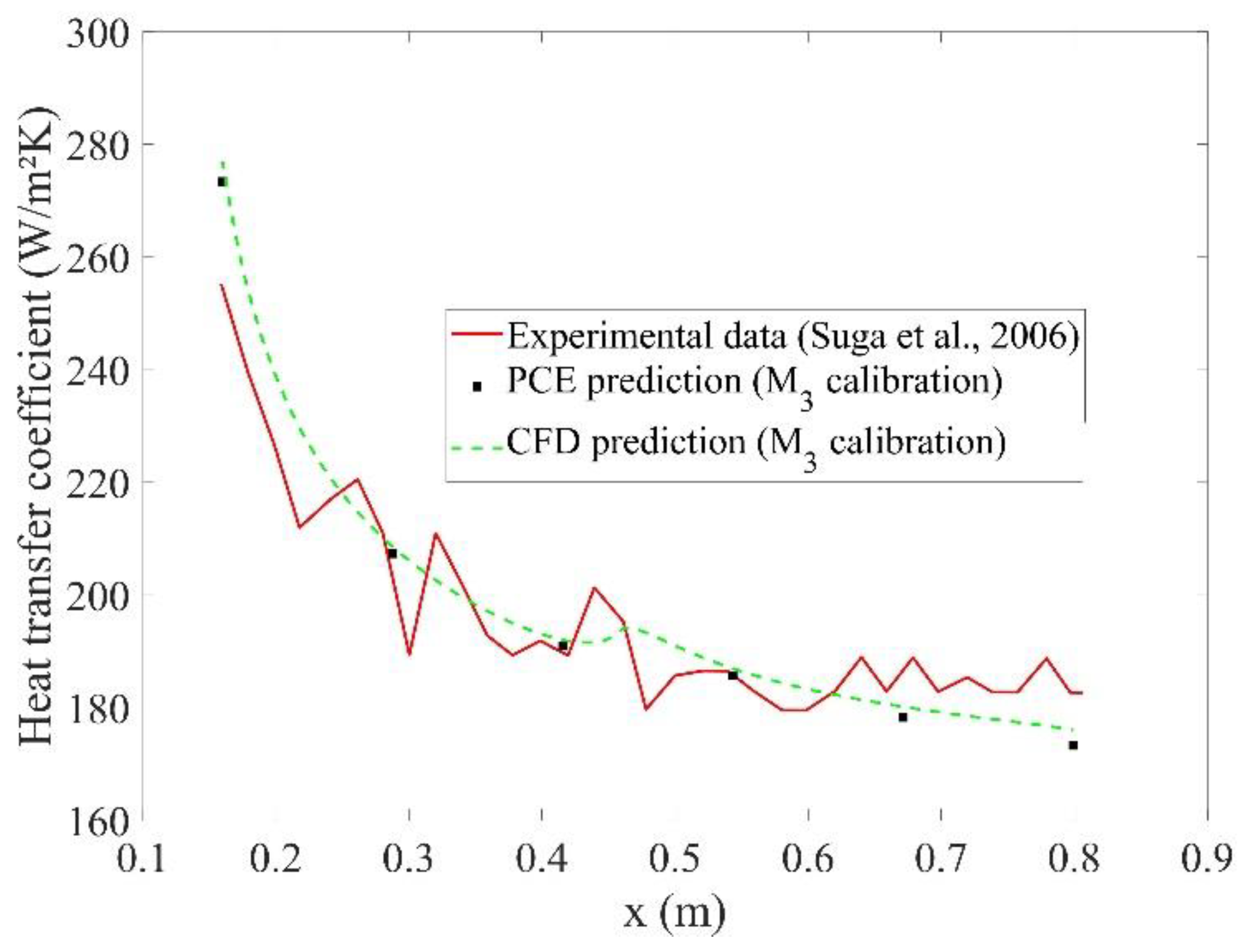
7.5. Bayesian Inversion Calibration
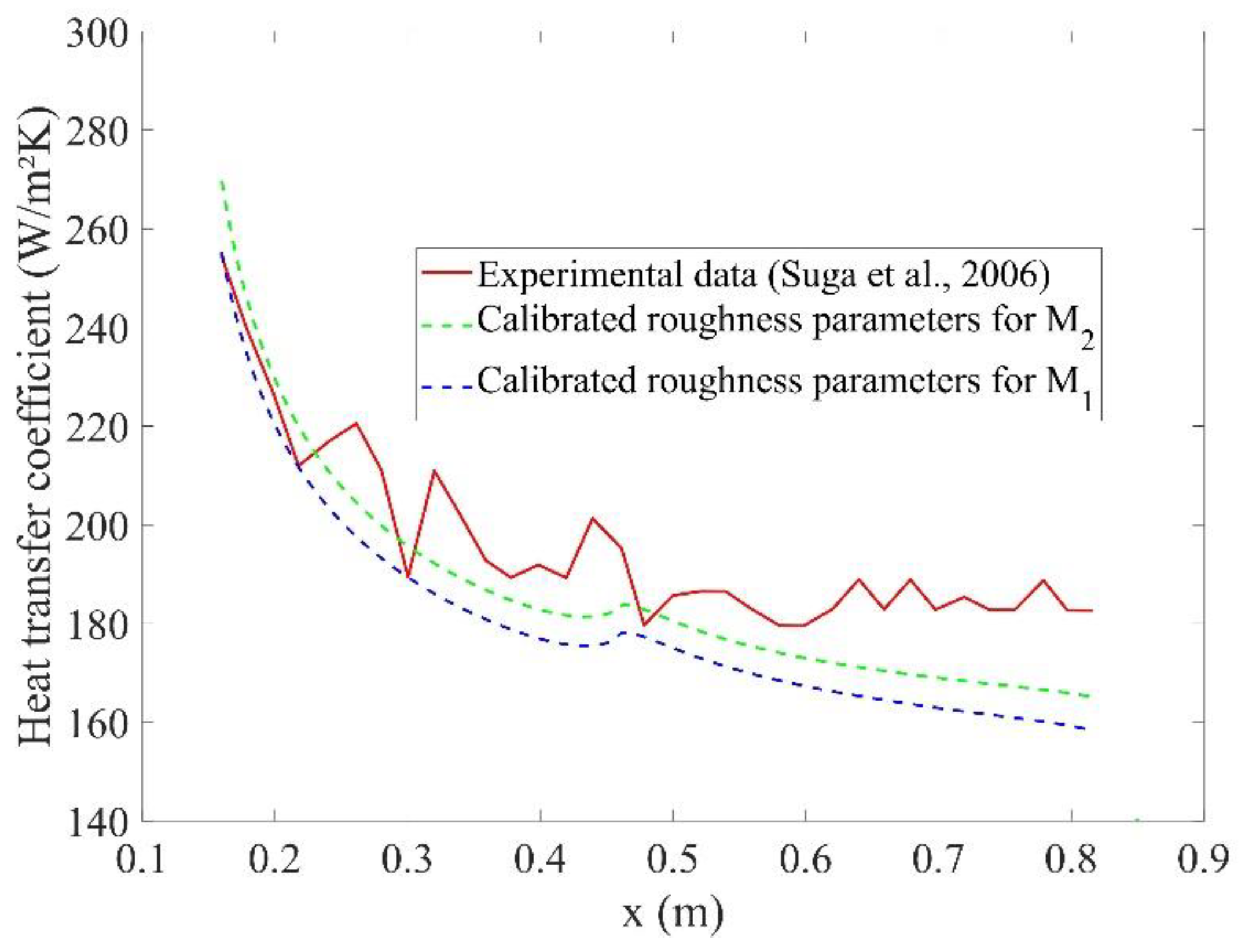
7.6. Genetic Algorithm Calibration
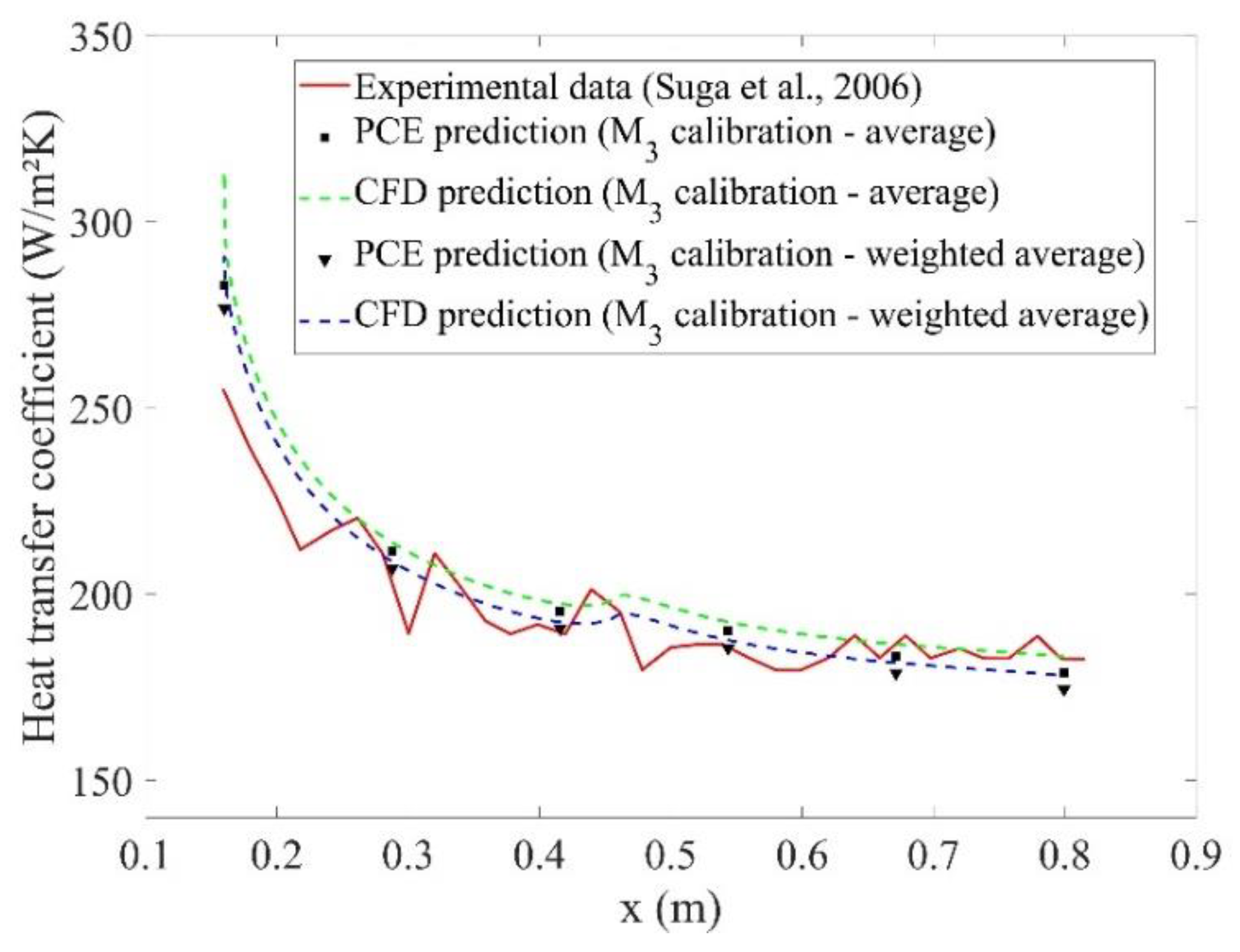
7.7. Comparison of Both Calibration Methods
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| d | Distance to the wall (m) |
| E | Mean value of a dataset |
| Relative error between mesh i and j for a scalar quantity | |
| g | Adimensional factor in the thermal correction model |
| hc | Heat transfer coefficient (W/m2K) |
| k | Roughness height (m) |
| ks | Equivalent roughness (m) |
| l | Mesh characteristic length (m) |
| Mi | Metamodel |
| Npoints | Number of mesh points in the rough wall |
| N | Number of outputs for a multi-output metamodel |
| Laminar Prandtl number | |
| p | Convergence order for mesh study |
| pPCE | Degree of polynomial chaos expansion |
| R2 | Regression coefficient |
| Roughness Reynolds number | |
| Si and Si,j | First and second order Sobol indices |
| STi | Total Sobol index |
| Friction velocity (m/s) | |
| V | Variance of a dataset |
| x | Local abscissa along the channel (m) |
| X = (X1,X2) | Vector of input variables for a metamodel |
| Yi | Output of interest of a metamodel |
| yα | Coefficient of the PCE term of index α |
| Greek letters | |
| α = (α1,α2) | Multi-index of the PCE decomposition |
| Turbulent Prandtl number correction | |
| Kinematic viscosity of air (m2/s) | |
| ε | Mean relative error |
| Multivariate polynomial of index α | |
| Univariate polynomial of index αi | |
| π(θ|Xi) | Posterior distribution of input Xi |
| π(θ) | Prior distribution with parameters θ |
| π(Xi) | Marginal likelihood |
| Subscripts | |
| CFD | CFD-predicted value |
| EXP | Experimental value |
Appendix A
| hc (x = 0.16 m) | hc (x = 0.46 m) | hc (x = 0.8 m) | |
|---|---|---|---|
| p | 0.7 | 1.7 | 2.1 |
| GCI21 | 0.9% | 0.2% | 0.1% |
| GCI32 | 1.4% | 0.7% | 0.5% |
References
- Aupoix, B.; Spalart, P.R. Extensions of the Spalart–Allmaras turbulence model to account for wall roughness. Int. J. Heat Fluid Flow 2003, 24, 454–462. [Google Scholar] [CrossRef]
- Suga, K.; Craft, T.J.; Iacovides, H. An analytical wall-function for turbulent flows and heat transfer over rough walls. Int. J. Heat Fluid Flow 2006, 27, 852–866. [Google Scholar] [CrossRef]
- Aupoix, B. Improved heat transfer predictions on rough surfaces. Int. J. Heat Fluid Flow 2015, 56, 160–171. [Google Scholar] [CrossRef]
- Morency, F.; Beaugendre, H. Comparison of turbulent Prandtl number correction models for the Stanton evaluation over rough surfaces. Int. J. Comput. Fluid Dyn. 2020, 34, 278–298. [Google Scholar] [CrossRef]
- Ignatowicz, K.; Morency, F.; Beaugendre, H. Sensitivity Study of Ice Accretion Simulation to Roughness Thermal Correction Model. Aerospace 2021, 8, 84. [Google Scholar] [CrossRef]
- Dirling, R. A method for computing roughwall heat transfer rates on reentry nosetips. In Proceedings of the 8th Thermophysics Conference, Palm Springs, CA, USA, 16–18 July 1973. [Google Scholar] [CrossRef]
- Shin, J. Characteristics of surface roughness associated with leading-edge ice accretion. J. Aircr. 1996, 33, 316–321. [Google Scholar] [CrossRef]
- Da Ronch, A.; Panzeri, M.; Drofelnik, J.; D’ippolito, R. Sensitivity and calibration of turbulence model in the presence of epistemic uncertainties. CEAS Aeronaut. J. 2020, 11, 33–47. [Google Scholar] [CrossRef] [Green Version]
- Marelli, S.; Sudret, B. UQLab User Manual—Polynomial Chaos Expansions; Chair of Risk, Safety and Uncertainty Quantification, ETH: Zurich, Switzerland, 2019. [Google Scholar]
- Salehi, S.; Raisee, M.; Cervantes, M.J.; Nourbakhsh, A. Efficient uncertainty quantification of stochastic CFD problems using sparse polynomial chaos and compressed sensing. Comput. Fluids 2017, 154, 296–321. [Google Scholar] [CrossRef]
- Hosder, S.; Walters, R.; Perez, R. A Non-Intrusive Polynomial Chaos Method For Uncertainty Propagation in CFD Simulations. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar] [CrossRef]
- Rumpfkeil, M.P.; Beran, P.S. Multifidelity Sparse Polynomial Chaos Surrogate Models Applied to Flutter Databases. AIAA J. 2020, 58, 1292–1303. [Google Scholar] [CrossRef]
- Shahane, S.; Aluru, N.R.; Vanka, S.P. Uncertainty quantification in three dimensional natural convection using polynomial chaos expansion and deep neural networks. Int. J. Heat Mass Transf. 2019, 139, 613. [Google Scholar] [CrossRef] [Green Version]
- Tabatabaei, N.; Raisee, M.; Cervantes, M.J. Uncertainty Quantification of Aerodynamic Icing Losses in Wind Turbine With Polynomial Chaos Expansion. J. Energy Resour. Technol. 2019, 141, 051210. [Google Scholar] [CrossRef]
- Zhang, K.; Li, J.; Zeng, F.; Wang, Q.; Yan, C. Uncertainty Analysis of Parameters in SST Turbulence Model for Shock Wave-Boundary Layer Interaction. Aerospace 2022, 9, 55. [Google Scholar] [CrossRef]
- Najm, H.N. Uncertainty Quantification and Polynomial Chaos Techniques in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 2009, 41, 35–52. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 304. [Google Scholar] [CrossRef]
- Resmini, A.; Peter, J.; Lucor, D. Sparse grids-based stochastic approximations with applications to aerodynamics sensitivity analysis. Int. J. Numer. Methods Eng. 2016, 106, 32–57. [Google Scholar] [CrossRef]
- Wagner, P.-R.; Nagel, J.; Marelli, S.; Sudret, B. UQLab User Manual—Bayesian Inference for Model Calibration and Inverse Problems; Chair of Risk, Safety and Uncertainty Quantification, ETH: Zurich, Switzerland, 2021. [Google Scholar]
- Muehleisen, R.T.; Bergerson, J. Bayesian Calibration—What, Why And How. In Proceedings of the International High Performance Buildings Conference, West Lafayette, IN, USA, 11–14 July 2016. [Google Scholar]
- Guillas, S.; Glover, N.; Malki-Epshtein, L. Bayesian calibration of the constants of the κ-ε turbulence model for a CFD model of street canyon flow. Comput. Methods Appl. Mech. Eng. 2014, 279, 536–553. [Google Scholar] [CrossRef] [Green Version]
- Morita, Y.; Rezaeiravesh, S.; Tabatabaei, N.; Vinuesa, R.; Fukagata, K.; Schlatter, P. Applying Bayesian optimization with Gaussian process regression to computational fluid dynamics problems. J. Comput. Phys. 2022, 449, 110788. [Google Scholar] [CrossRef]
- Reddy, T.A.; Maor, I.; Panjapornpon, C. Calibrating Detailed Building Energy Simulation Programs with Measured Data—Part II: Application to Three Case Study Office Buildings (RP-1051). HVAC&R Res. 2007, 13, 243–265. [Google Scholar] [CrossRef]
- Yang, X.-S. (Ed.) Chapter 6—Genetic Algorithms. In Nature-Inspired Optimization Algorithms, 2nd ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 91–100. [Google Scholar] [CrossRef]
- Khan, A.H.; Islam, M.S.; Sazzad, I.U. Calibration of κ-ε turbulence model for thermal–hydraulic analyses in rib-roughened narrow rectangular channels using genetic algorithm. SN Appl. Sci. 2021, 3, 678. [Google Scholar] [CrossRef]
- Oh, J.; Chien, N.B. Optimization Design by Coupling Computational Fluid Dynamics and Genetic Algorithm. In Computational Fluid Dynamics—Basic Instruments and Applications in Science; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef] [Green Version]
- Owoyele, O.; Pal, P.; Torreira, A.; Probst, D.; Shaxted, M.; Wilde, M.; Senecal, P. Application of an automated machine learning-genetic algorithm (AutoML-GA) approach coupled with computational fluid dynamics simulations for rapid engine design optimization. Int. J. Engine Res. 2021. [Google Scholar] [CrossRef]
- Wagner, P.-R.; Fahrni, R.; Klippel, M.; Frangi, A.; Sudret, B. Bayesian calibration and sensitivity analysis of heat transfer models for fire insulation panels. Eng. Struct. 2019, 205, 110063. [Google Scholar] [CrossRef] [Green Version]
- Ranftl, S.; Von Der Linden, W. Bayesian Surrogate Analysis and Uncertainty Propagation. Phys. Sci. Forum 2021, 3, 6. [Google Scholar]
- Turner, A.B.; Hubbe-Walker, S.E.; Bayley, F.J. Fluid flow and heat transfer over straight and curved rough surfaces. Int. J. Heat Mass Transf. 2000, 43, 251–262. [Google Scholar] [CrossRef]
- Economon, T.D.; Palacios, F.; Copeland, S.R.; Lukaczyk, T.W.; Alonso, J.J. SU2: An Open-Source Suite for Multiphysics Simulation and Design. AIAA J. 2015, 54, 828–846. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Dukhan, N.; Masiulaniec, K.C.; Witt, K.J.D.; Fossen, G.J.V. Experimental Heat Transfer Coefficients from Ice-Roughened Surfaces for Aircraft Deicing Design. J. Aircr. 1999, 36, 948–956. [Google Scholar] [CrossRef]
- Fortin, G. Equivalent Sand Grain Roughness Correlation for Aircraft Ice Shape Predictions; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Stein, M. Large sample properties of simulations using latin hypercube sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Schaefer, J.A.; Cary, A.W.; Mani, M.; Spalart, P.R. Uncertainty Quantification and Sensitivity Analysis of SA Turbulence Model Coefficients in Two and Three Dimensions. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Degennaro, A.M.; Rowley, C.W.; Martinelli, L. Uncertainty Quantification for Airfoil Icing Using Polynomial Chaos Expansions. J. Aircr. 2015, 52, 1404–1411. [Google Scholar] [CrossRef] [Green Version]
- Chan, K.; Saltelli, A.; Tarantola, S. Sensitivity Analysis of Model Output: Variance-based Methods Make the Difference. In Proceedings of the 29th Conference on Winter Simulation, Atalanta, GA, USA, 7–10 December 1997. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Conn, A.R.; Gould, N.I.M.; Toint, P. A Globally Convergent Augmented Lagrangian Algorithm for Optimization with General Constraints and Simple Bounds. SIAM J. Numer. Anal. 1991, 28, 545–572. [Google Scholar] [CrossRef] [Green Version]
- Prince Raj, L.; Yee, K.; Myong, R.S. Sensitivity of ice accretion and aerodynamic performance degradation to critical physical and modeling parameters affecting airfoil icing. Aerosp. Sci. Technol. 2020, 98, 105659. [Google Scholar] [CrossRef]
- Ignatowicz, K.; Morency, F.; Beaugendre, H. Numerical simulation of ice accretion using Messinger-based approach: Effects of surface roughness. In Proceedings of the CASI AERO Conference 2019, Laval, QC, Canada, 14–16 May 2019. [Google Scholar]
- Celik, I.; Ghia, U.; Roache, P.J.; Freitas, C.; Coloman, H.; Raad, P. Procedure of Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef] [Green Version]




| Parameter | Minimum | Maximum | Distribution |
|---|---|---|---|
| k (mm) | 0.41 | 4.32 | Uniform |
| Ratio ks/k | 0.2 | 6.5 | Uniform |
| Metamodel | Output(s) of Interest |
|---|---|
| M1 | hc at the starting point of the rough zone, W/m2K |
| M2 | Mean relative error with experimental hc (%) |
| M3 | hc values at N equally spaced locations along the rough zone (multi-output), W/m2K |
| Metamodel Calibrated | Objective of the Calibration | Sampler | Discrepancy | Experimental Observation Supplied |
|---|---|---|---|---|
| M1 | Recovering the same starting value of hc | AIES | Uniform [0; 15] W/m2K | 255.1 W/m2K |
| M2 | Having a mean relative error with experimental hc of 0% | AIES | Uniform [0; 5]% | 0% |
| M3 | Recovering the same hc values at the N equally spaced locations along the rough zone | MH | Uniform [0; 15] W/m2K | Experimental hc at the N locations (W/m2K) |
| Metamodel Calibrated | Objective of the Calibration | Objective Function Used |
|---|---|---|
| M1 | Recovering the same starting value of hc | |M1 − 255.1| |
| M2 | Having a mean relative error with experimental hc of 0% | |M2| |
| M3 | Recovering the same hc values at the N equally spaced locations along the rough zone | |M3[i] − hc[i]| i = 1…N |
| Metamodel | Output of Interest | PCE Degree pPCE | Number of Terms in Equation (4) | R2 Coefficient |
|---|---|---|---|---|
| M1 | hc at the starting point of the rough zone, W/m2K | 10 | 66 | 0.99994 |
| M2 | Mean relative error with experimental hc (%) | 10 | 66 | 0.99962 |
| M3 | hc values at 6 equally spaced locations along the rough zone (multi-output), W/m2K | Y1:10 | 66 | 0.99994 |
| Y2:9 | 55 | 0.99993 | ||
| Y3:12 | 91 | 0.99999 | ||
| Y4:10 | 66 | 0.99992 | ||
| Y5:12 | 91 | 0.99999 | ||
| Y6:12 | 91 | 0.99997 |
| Metamodel | Total Sobol Indices |
|---|---|
| M1 | k: 0.1445 ks/k: 0.8868 |
| M2 | k: 0.3061 ks/k: 0.9772 |
| M3 | k: 0.1167 ks/k: 0.9061 |
| Calibrated Metamodel | Values Retained | Final Calibrated Roughness Parameters |
|---|---|---|
| M1 | Mean | k = 2.2 mm ks = 6.4 mm |
| M2 | Mean | k = 1.6 mm ks = 4.2 mm |
| M3 | MAP | k = 1.8 mm ks = 5.0 mm |
| Calibrated Metamodel | Values Retained | Final Calibrated Roughness Parameters |
|---|---|---|
| M1 | k = 1.9 mm ks = 3.1 mm | |
| M2 | k = 4.3 mm ks = 8.2 mm | |
| M3 | Average among the N values | k = 3.0 mm ks = 8.3 mm |
| M3 | Weighted average among the N values | k = 2.9 mm ks = 7.1 mm |
| Calibrated Metamodel | hc Mean Relative Error with Experimental Data | |
|---|---|---|
| Bayesian Inversion | Genetic Algorithm * | |
| M1 | 4.7% | 8.2% |
| M2 | 4.8% | 5.7% |
| M3 | 5.4% | Avg: 10% W-Avg: 7.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ignatowicz, K.; Solaï, E.; Morency, F.; Beaugendre, H. Data-Driven Calibration of Rough Heat Transfer Prediction Using Bayesian Inversion and Genetic Algorithm. Energies 2022, 15, 3793. https://doi.org/10.3390/en15103793
Ignatowicz K, Solaï E, Morency F, Beaugendre H. Data-Driven Calibration of Rough Heat Transfer Prediction Using Bayesian Inversion and Genetic Algorithm. Energies. 2022; 15(10):3793. https://doi.org/10.3390/en15103793
Chicago/Turabian StyleIgnatowicz, Kevin, Elie Solaï, François Morency, and Héloïse Beaugendre. 2022. "Data-Driven Calibration of Rough Heat Transfer Prediction Using Bayesian Inversion and Genetic Algorithm" Energies 15, no. 10: 3793. https://doi.org/10.3390/en15103793
APA StyleIgnatowicz, K., Solaï, E., Morency, F., & Beaugendre, H. (2022). Data-Driven Calibration of Rough Heat Transfer Prediction Using Bayesian Inversion and Genetic Algorithm. Energies, 15(10), 3793. https://doi.org/10.3390/en15103793










