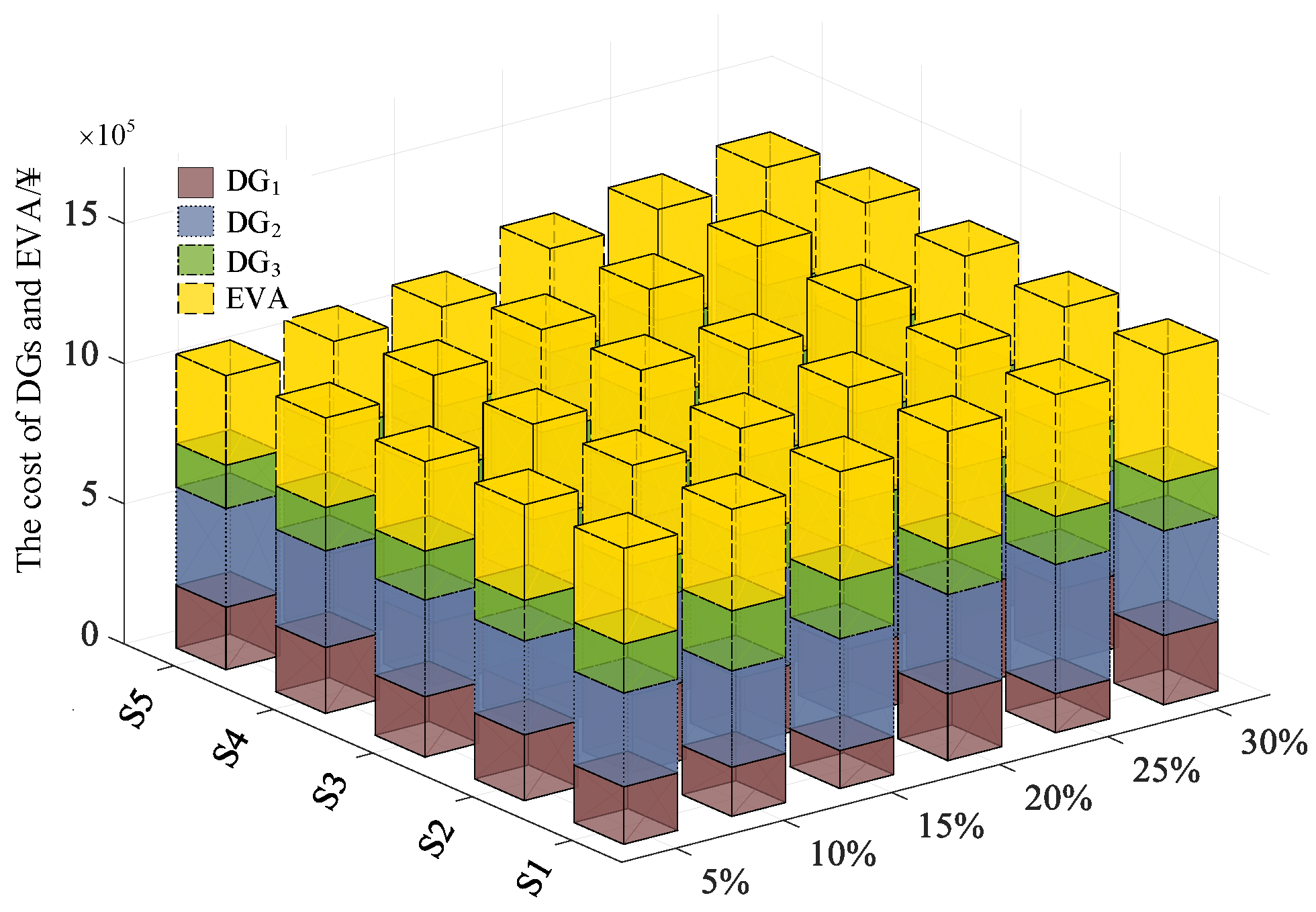
2.3.2. Construction of Robust Optimization Model
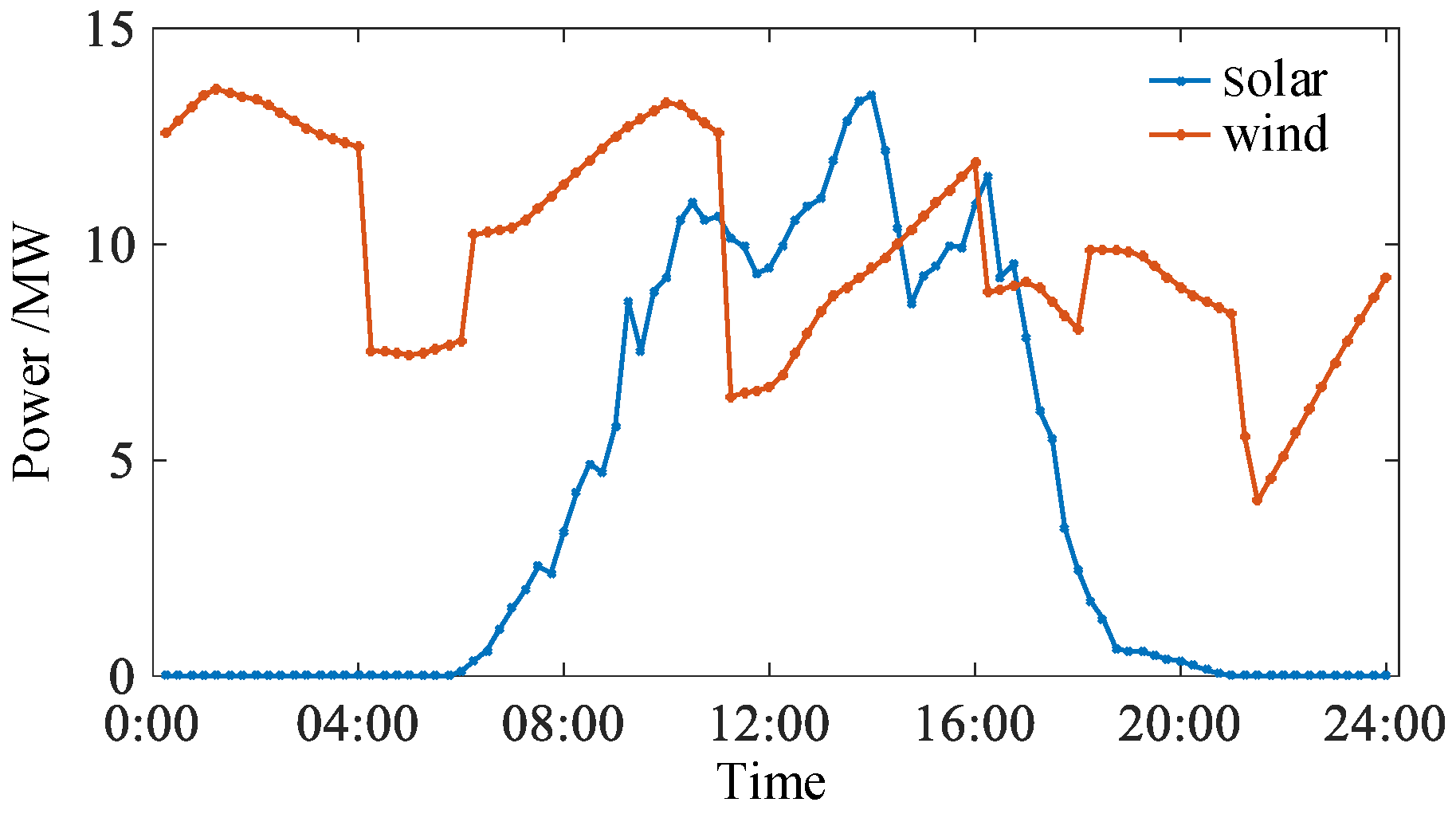
The objective function is constructed with the goal of minimizing costs. The system contains two types of renewable energy: solar and wind power. In order to simplify the complexity of the model and promote the consumption of renewable energy, the cost of abandoning wind and solar is included in the objective function.
The essence of Formula (9) is to minimize the cost on the uncertain set . , , and are the unit power vector, standby power vector, EV cluster power vector, and abandoning renewable power vector, respectively. , , and are the corresponding cost functions; the calculation methods are as follows:
Formula (10) contains two parts of cost: fuel cost and start–stop cost of units, where is the number of units; is the number of optimization periods, ; , and are the cost coefficients of the i-th unit; is the boolean variable that indicates the startup and shutdown of the unit at period ; is the startup and shutdown cost of unit .
(2) Standby power capacity cost:
The essence of Formula (11) is the dispatching cost of standby power capacity, which includes up-regulated and down-regulated costs, where , , and are respectively the up-regulated and down-regulated powers of unit and the corresponding adjusted prices; Formula () restricts and both to be zero or only one to be not zero at the same period.
(3) EV cluster compensation cost:
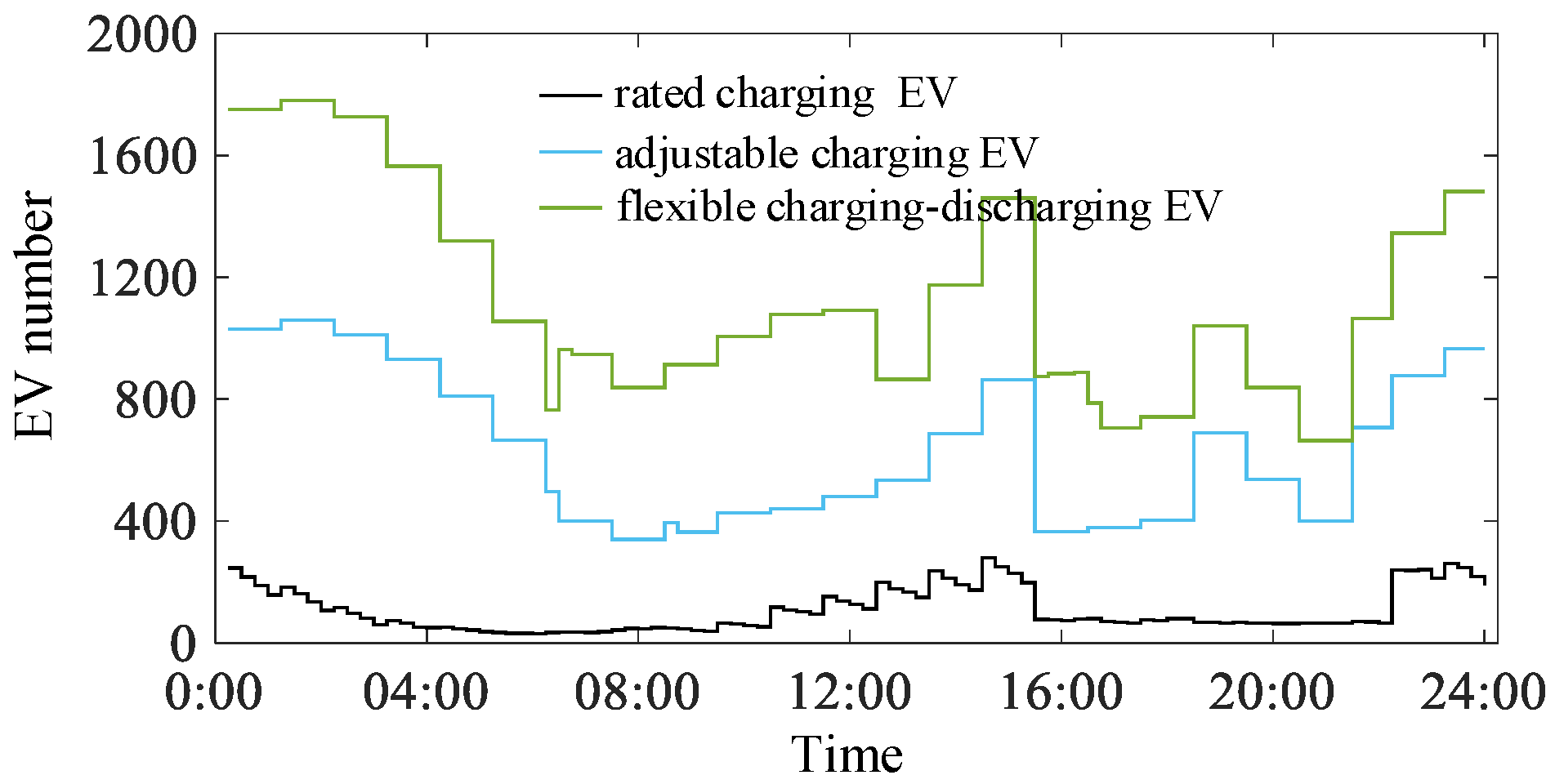
is the compensation cost of the EV cluster, which corresponds to the broken line abc of Type 2 and Type 3 EVs in
Figure 2;
is the power adjustment compensation cost of the EV cluster in response to intermittent fluctuations of renewable energy;
is the compensation factor.
and
are respectively the incentive cost of the
Type 2 EV and the incentive cost of the
Type 3 EV in the
EVA. To calculate the incentive cost
of
, this paper uses the method of reference [
25]:
Formula (13) shows that the closer the charging trajectory of the EV is to the upper boundary, the smaller the compensation cost is, where and are respectively the charging benefit and cost corresponding to the upper boundary of (broken line ); is the charging benefit corresponding to the broken line ; and are respectively the discharging compensation coefficient and the total discharging energy.
(4) Cost of abandoning renewable energy:
where
is the power of abandoning renewable energy;
is the penalty factor;
,
,
and
are the forecast output values and forecast errors of solar and wind power, respectively;
is the actual consumption of renewable energy.
The solution of objective function Equation (9) needs to meet the constraints of unit operation and power balance.
(1) Unit operation constraints:
where
,
,
and
are the maximum and minimum outputs of unit
, and the limit value of output increase and decrease, respectively;
,
,
and
are the continuous start-up and shutdown time, and the minimum start-up and shutdown time of unit
, respectively.
(2) Power balance constraint:
2.3.3. The Description of Output Uncertainty Convex Set
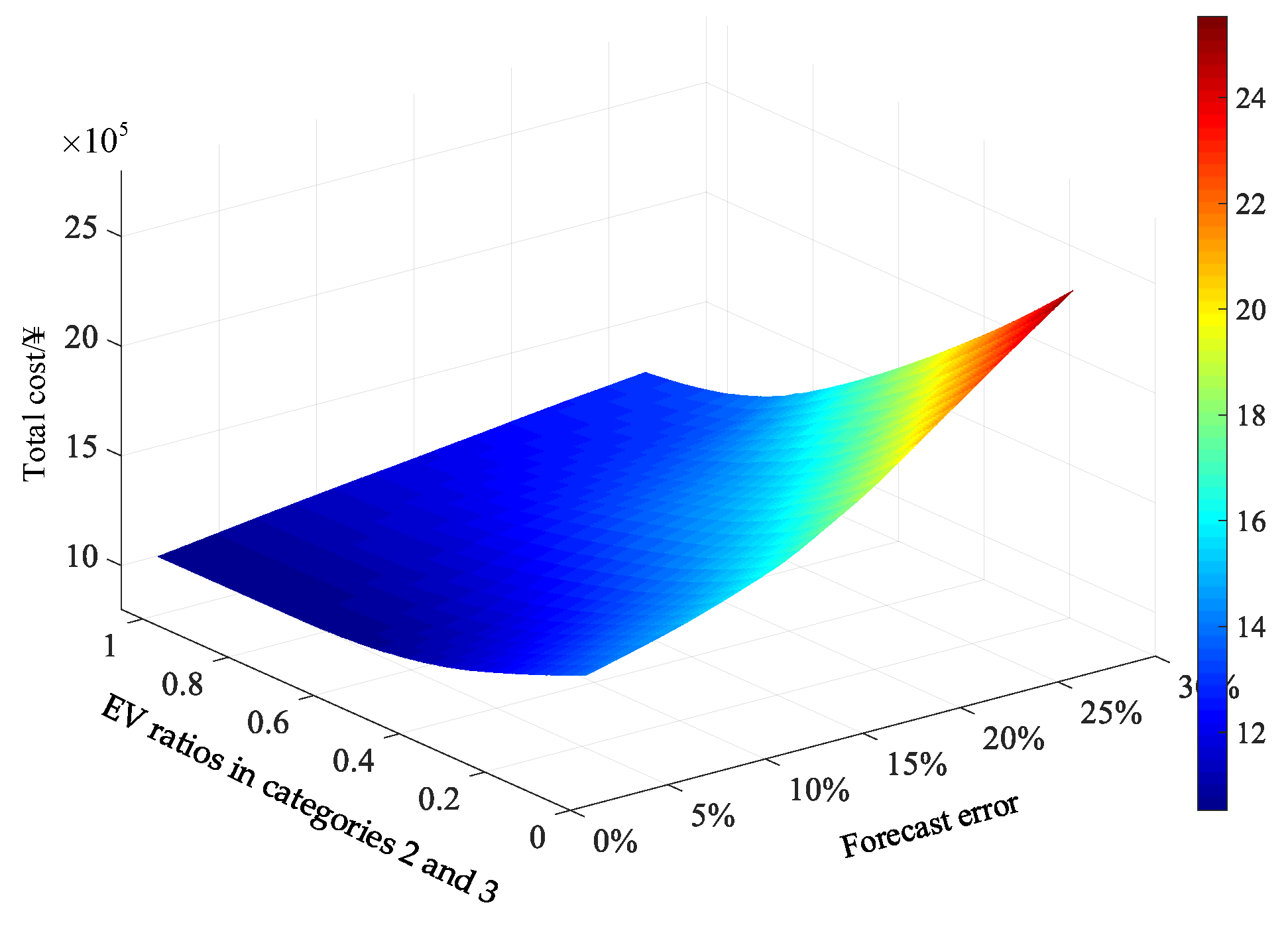
The selection of the uncertain parameter
in Formula (9) has a direct impact on the optimization results. This article uses intervals to describe the volatility of wind and solar output. Let the interval of
and
be:
Formula (13) represents the fluctuation range of uncertain parameters, where and are respectively the upper and lower limits of solar power at period ; and and are respectively the upper and lower limits of wind power at period .
According to the interval calculation rule, the uncertainty interval of renewable energy output
is
. Introducing the
binary auxiliary variable
,
and the robust model conservative degree control parameter
, the uncertainty of renewable energy output under robust control is described by Equation (19):
where
and
are the upper and lower limits of
, respectively;
and
control whether
obtains the upper limit or the lower limit; for
,
,
takes the upper limit of the interval; for
,
,
takes the lower limit of the interval; when both are 0, it means that both wind and solar output take the predicted value (
,
). When
(
), it indicates that the wind and solar output in all periods are predicted values, and the output volatility is not considered, and the model is the most aggressive; when
, it indicates that the upper or lower limit of
is used for all periods, and the model is the most conservative. In practical applications, the conservative degree of the model is controlled by adjusting the value of
.
2.3.4. Decoupled Solving of Robust Optimization Models
The models in
Section 2.2 and
Section 3.2 of this paper can decouple the objective function Equation (9) into two stages. First stage: when volatility is not considered and the forecast output of wind power and solar power is based on the minimum cost, the optimal output of the unit, the power of the EV cluster, and the consumption of renewable energy in the period
are determined with the goal of minimum cost. Second stage: when considering the fluctuation of renewable energy, according to the given
value, the solution value of the first phase is adjusted again with the goal of minimum adjustment cost.
Equation (20) needs to satisfy constraint Equations (1)–(3), (7), (10)–(17).
(1) First stage solution
The first stage is the deterministic minimization problem. , and and are both equal to zero;
are decision variables; let
X be the optimization vector in the whole
period, then
, and the dimension of
X is 2
NgT + 2
T. The matrix form of the min term is as follows:
where
A is the corresponding coefficient matrix;
and
respectively correspond to the inequalities and equality constraints of Equations (1)–(3), (10), (12), (14), (16) and (17);
is a suitable constant vector;
is a zero vector. Equation (21) is a typical mixed integer programming problem, which is solved efficiently by using the commercial solver CPLEX.
(2) Second stage solution
The second stage can be called the reschedule minimization problem,
;
contains the non-convex constraint of Equation (
), and it is difficult to solve directly. In order to relax the constraints of Formula (9), we construct function Formula (22) as follows:
It satisfies constraint Equations (4)–(7), (11), (12), (14)–(19). A brief proof of the constraint of relaxation Formula () is as follows:
Let
,
; suppose the optimal solution in period
is
(
, and
or
). Let
,
, and construct function
as follows:
From the perspective of power balance, if , there are only two possibilities for , values:
(1) ,
(2)
Let , (). and correspond to the above two possibilities, respectively; and are put into Equation (23) to obtain . Obviously, , that is, , so when and , Equation (23) obtains the optimal value. Similarly, if , when , Equation (23) obtains the optimal value.
Therefore, when Formula (23) takes the optimal solution, B = 0 is satisfied during any period, that is, is satisfied for any unit.
and
are decision variables. Let
,
; the dimension of
Y is 2
NgT + 2
T; the dimension of
Z is 2
T. The general form of the matrix of Equation (22) is:
where
B is the corresponding coefficient matrix; both
M and
N are matrices adapted to Formulas (7), (11), (12), (14)–(19);
L is a suitable constant vector;
is a zero vector. Max-min is a two-level optimization problem. According to the duality theory, dual variables
and
are introduced to convert the two-level optimization into a single-level optimization. The dual form of Equation (24) is:
Equation (25) is a linear programming problem, which is solved by using the simplex method. Equation (24) satisfies strong duality; let , and , , be the optimal solutions of Equations (24) and (25), respectively; it meets: .
According to the complementary relaxation in the KKT condition, can be obtained, which can be further accelerated by introducing it into Equation (25).
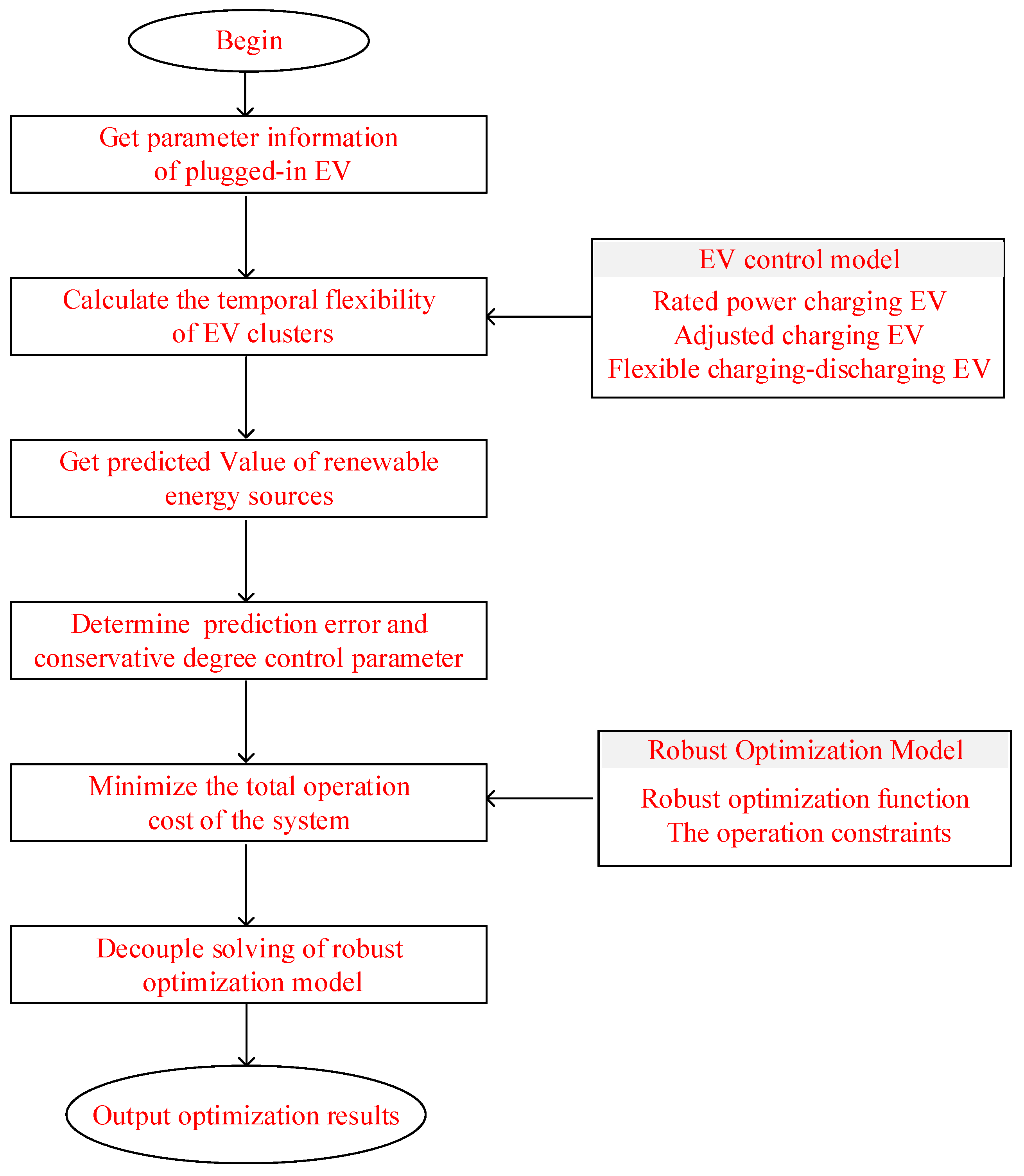
The flowchart in
Figure 3 summarizes the whole process of the proposed model.