Multi-Crack Dynamic Interaction Effect on Oil and Gas Pipeline Weld Joints Based on VCCT
Abstract
:1. Introduction
2. Numerical Simulation Model of Multi-Cracks
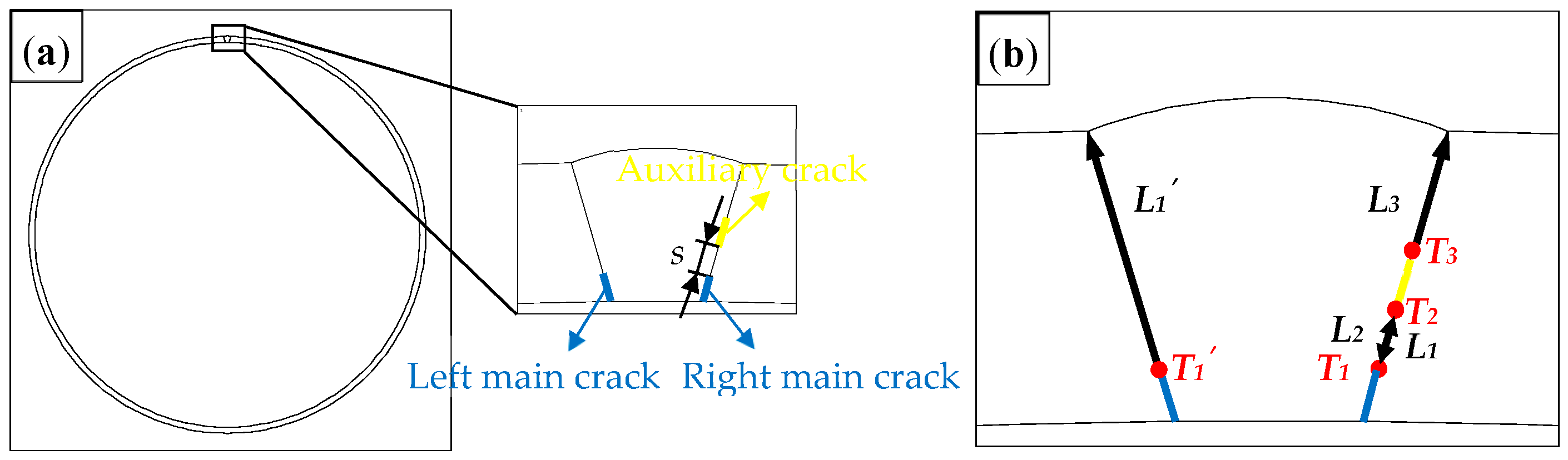
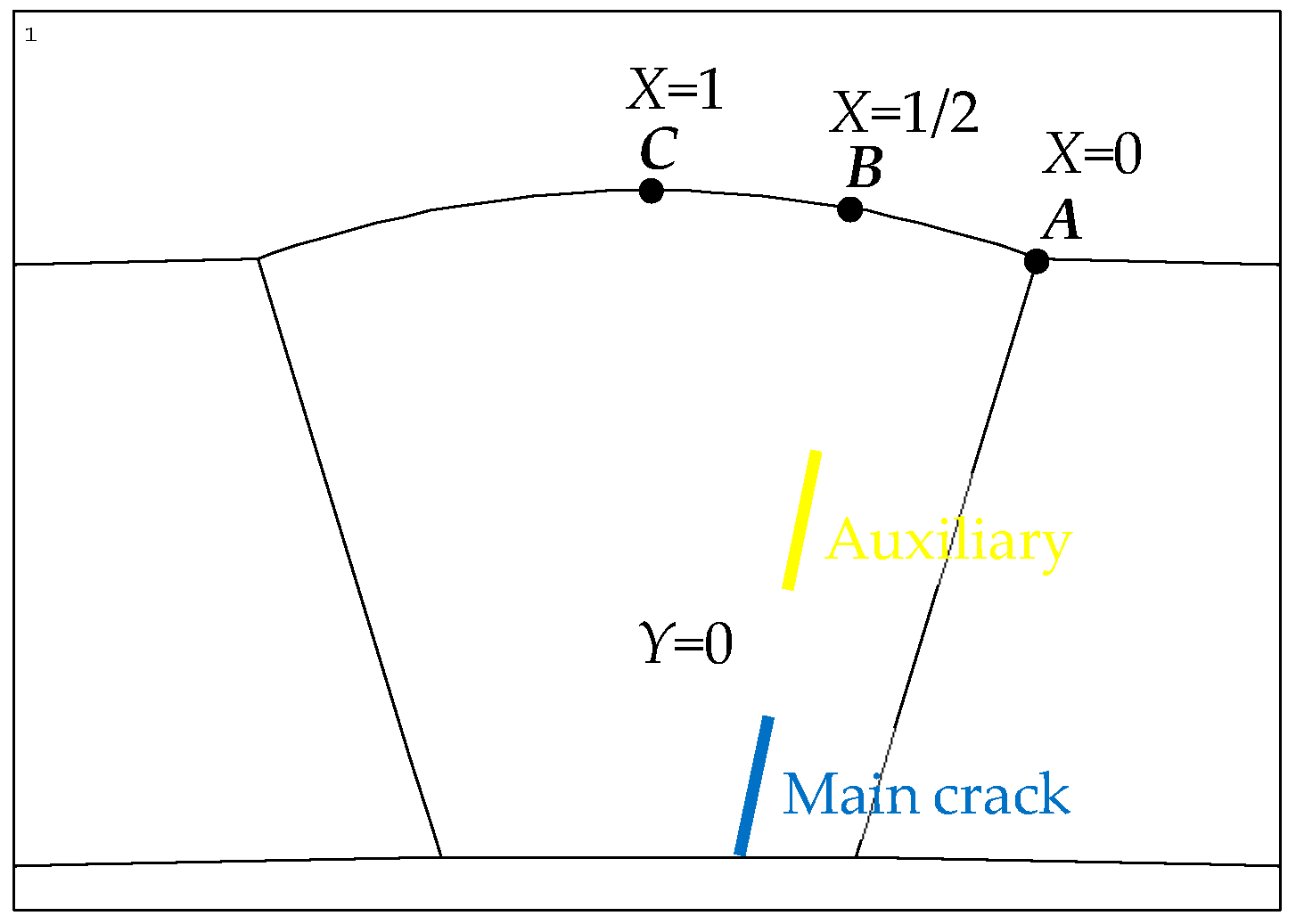
2.1. Geometric Model and Parameter Setting
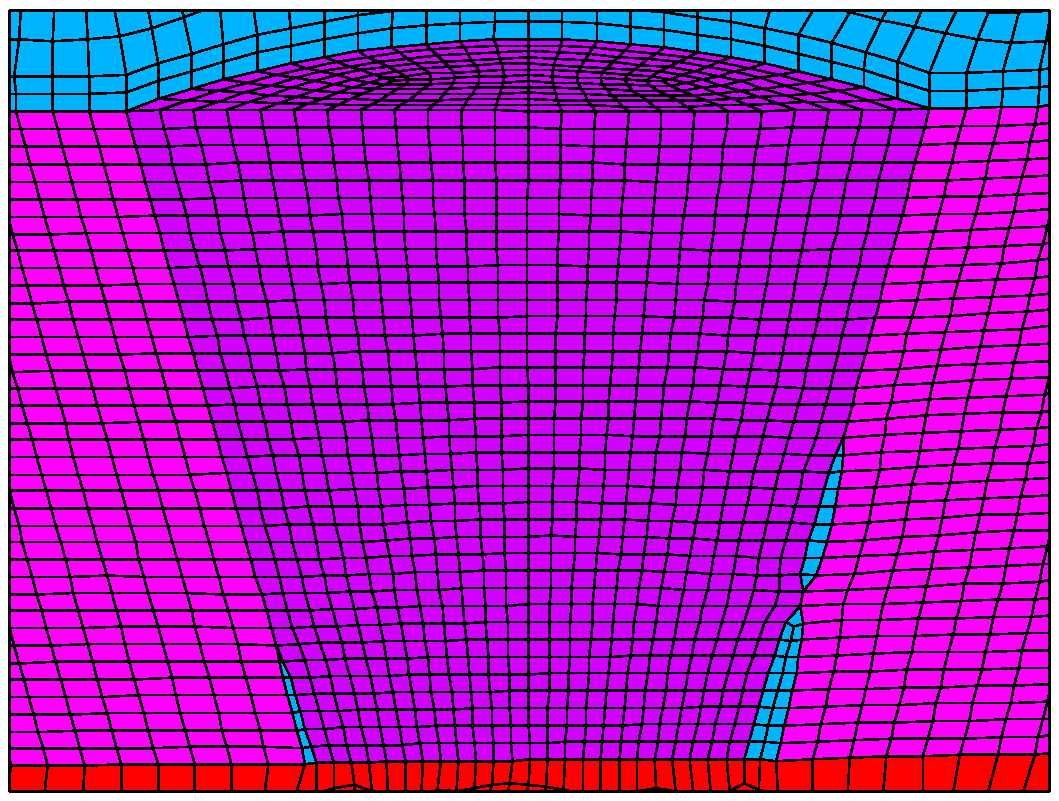
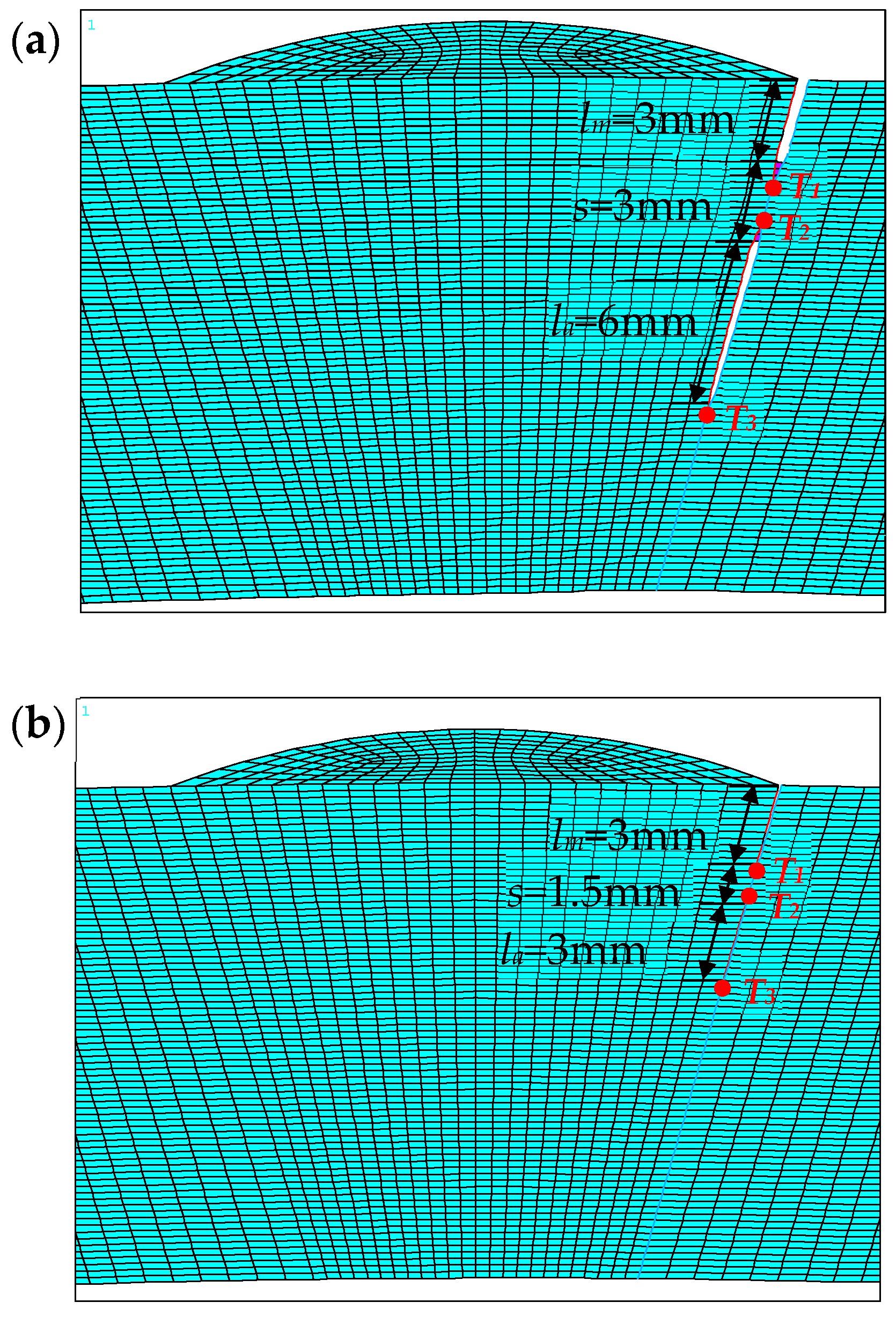
2.2. The Finite Element Model
3. Crack Tip Distance and Size Effect
3.1. Crack Tip Distance Effect
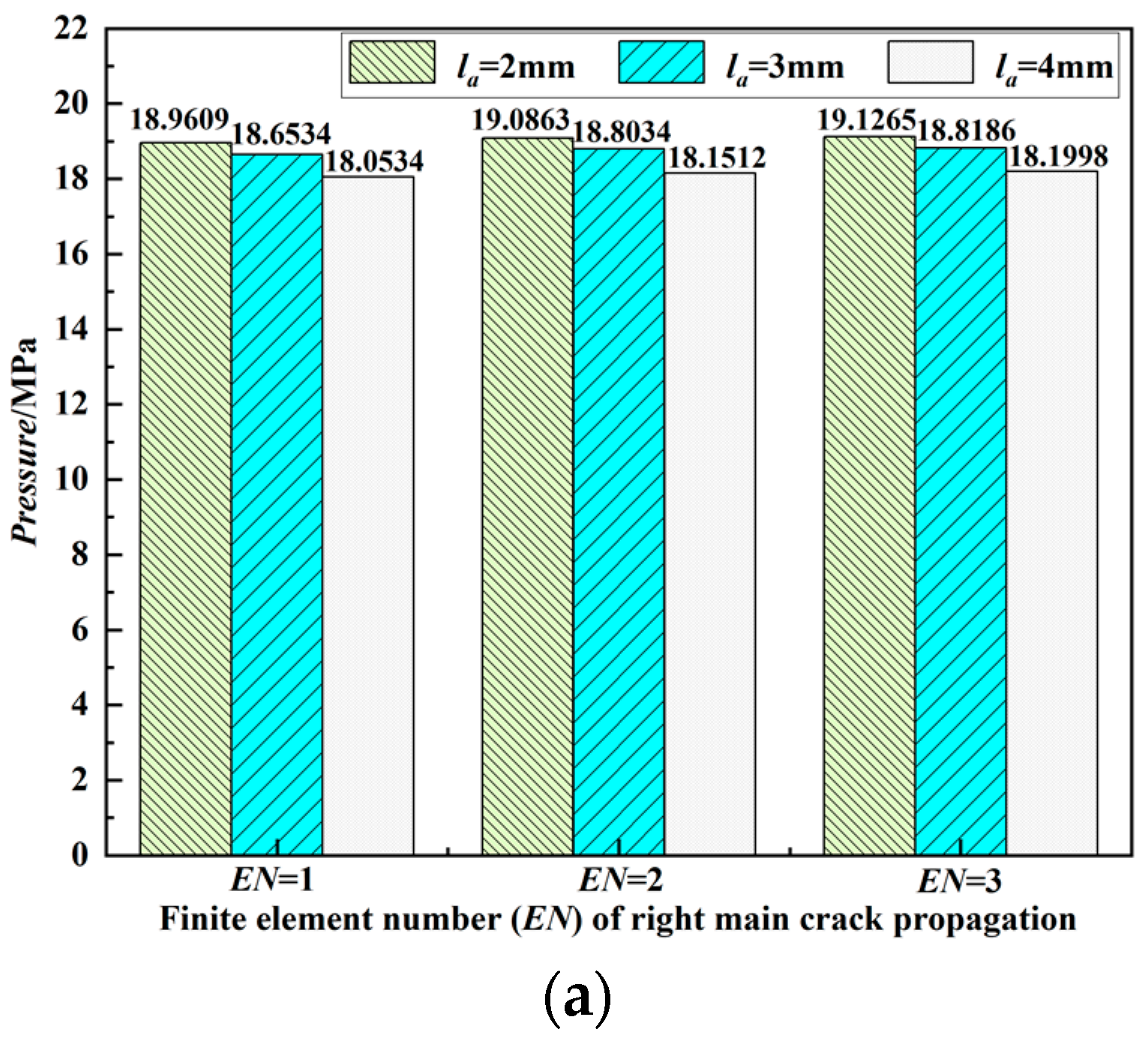
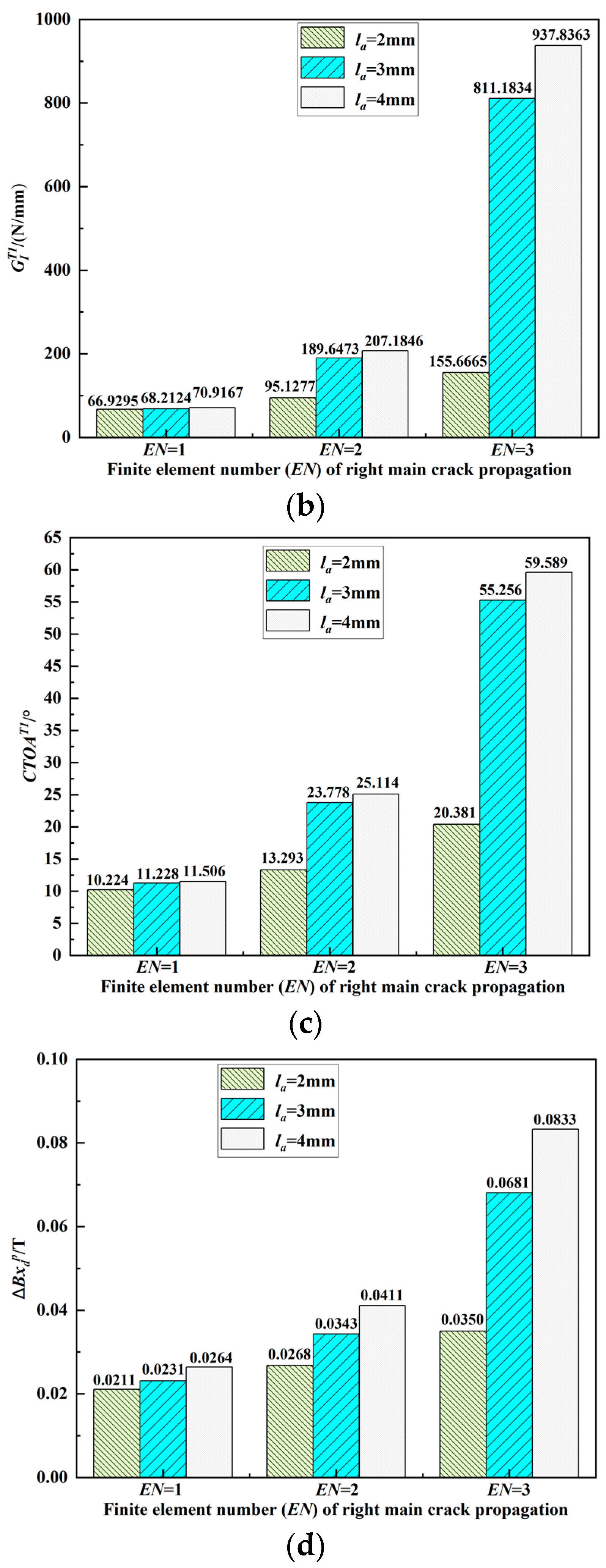
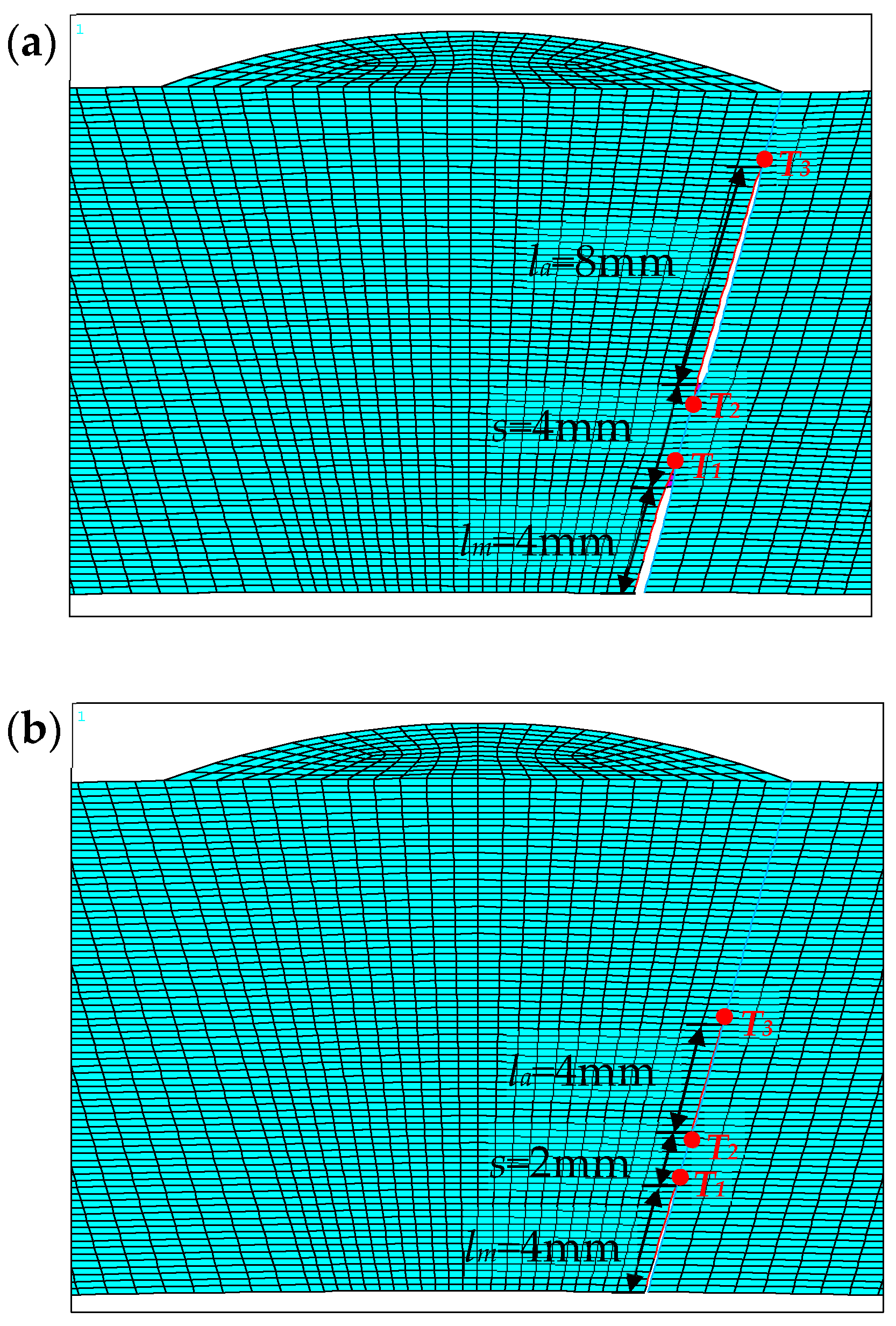
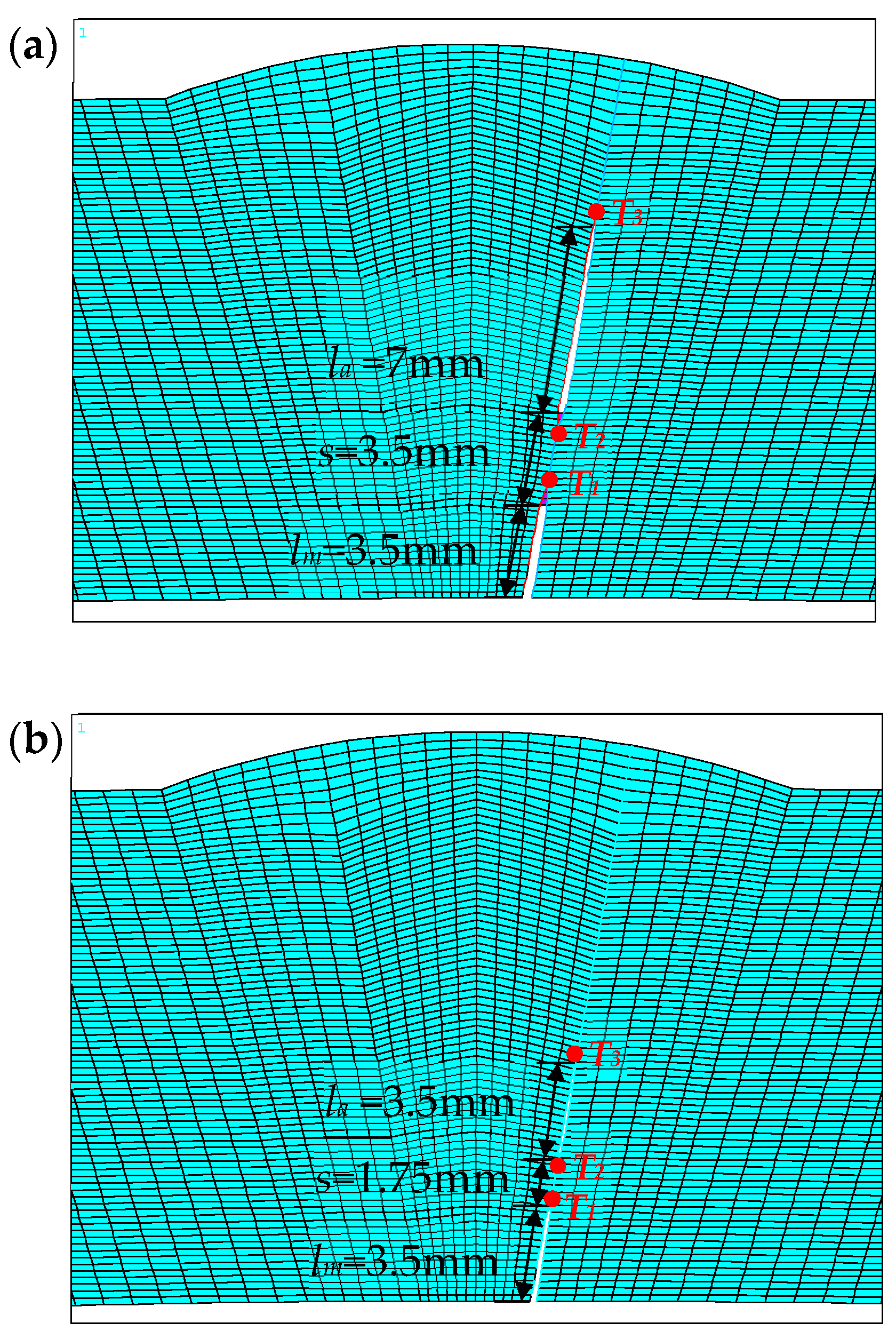
3.2. Influence of the Auxiliary Crack Size on Main Crack
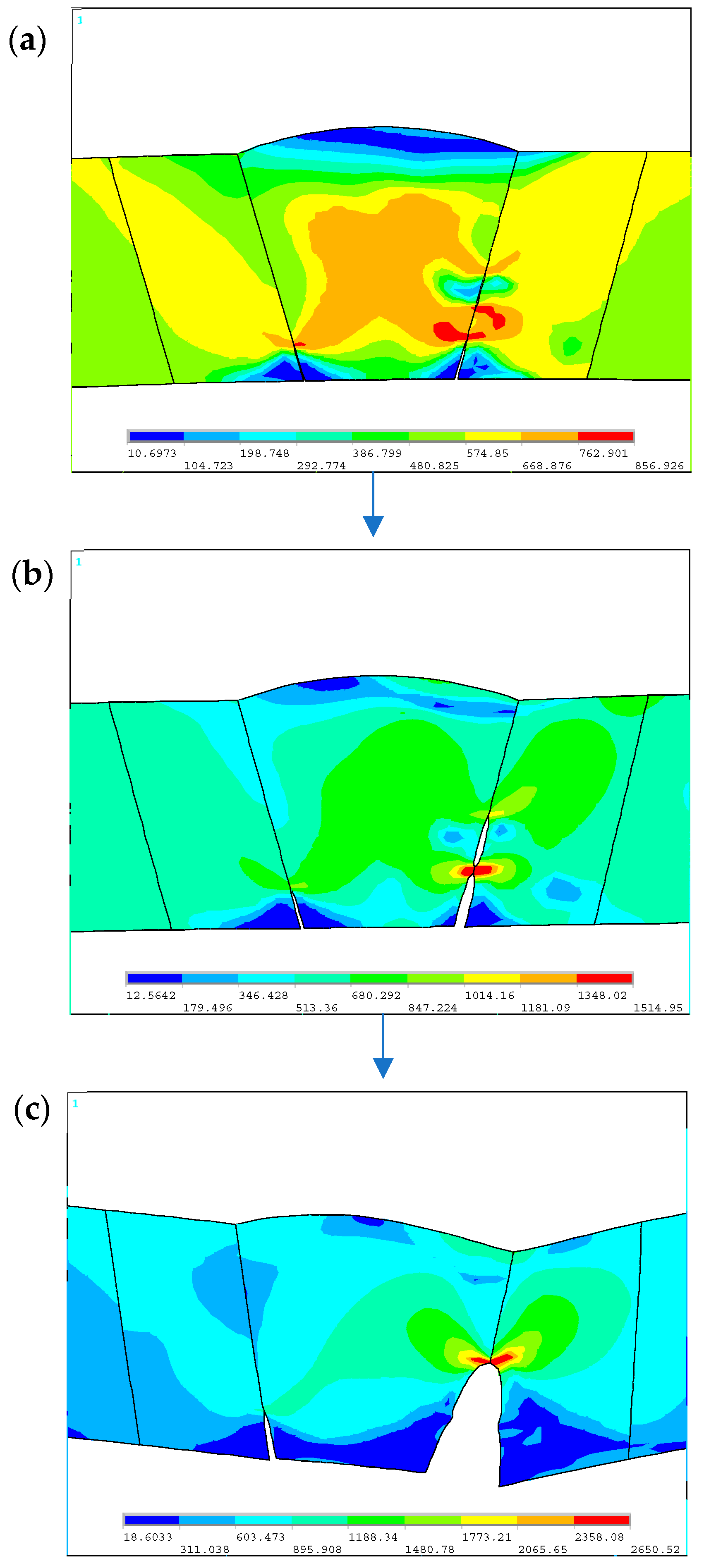
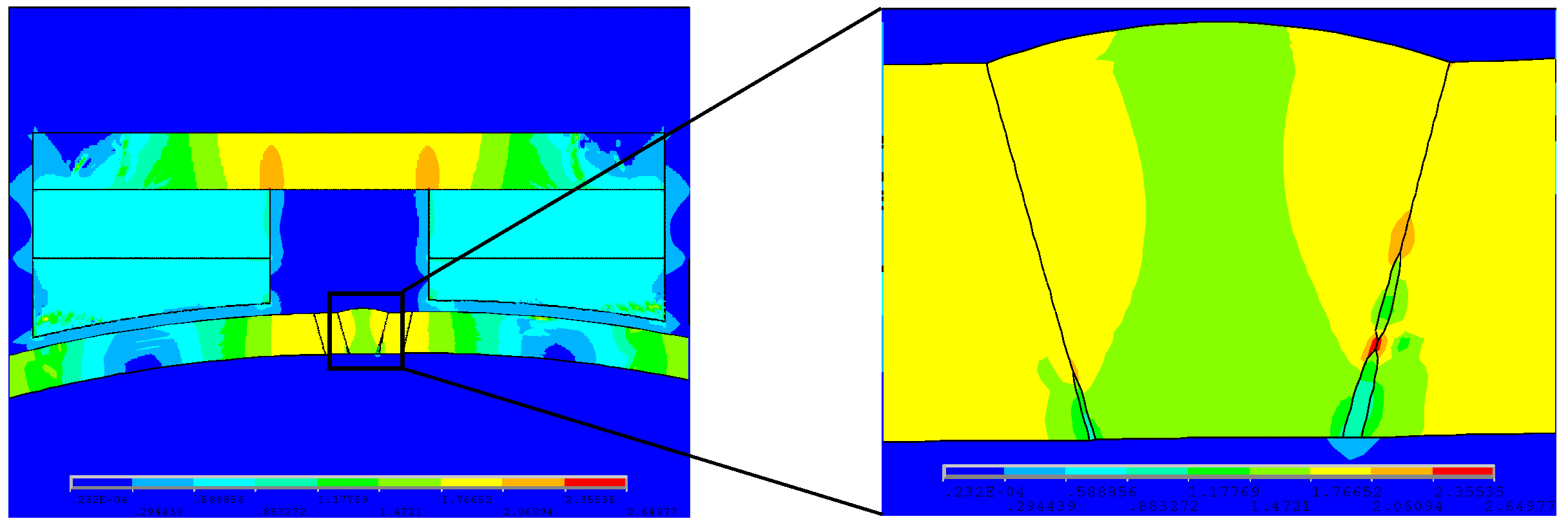
4. Comparative Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Acronym
| Meaning | Units | |
| BKIN | bilinear kinematic | - |
| CTOA | crack tip opening angle | ° |
| CTOAT1 | crack tip opening angle of tip 1 of the right main crack | ° |
| CTOAT1′ | crack tip opening angle of tip 1 of the left main crack | ° |
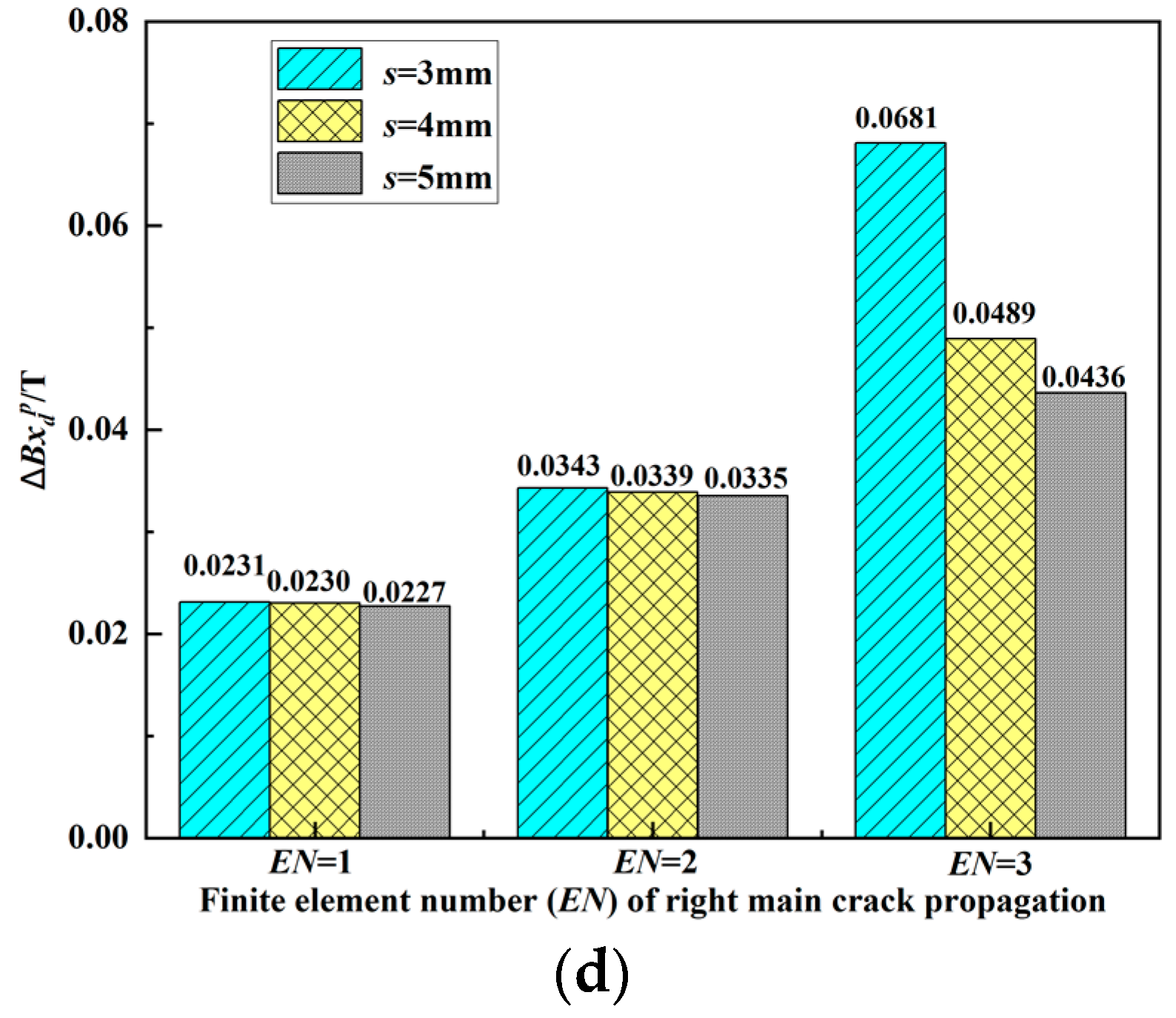
| EN | extended finite element number, and the discrete size of the element on the crack propagation path is 0.5 mm | - |
| EN’ | extended finite element number, and the discrete size of the element on the crack propagation path is 0.25 mm | - |
| GIT1 | crack tip energy release rate of tip 1 of the right main crack | N/mm |
| GIT1′ | crack tip energy release rate of tip 1 of the left main crack | N/mm |
| L1 | crack propagation path of tip 1 of the right main crack | - |
| L2 | crack propagation path of tip 2 of the right auxiliary crack | - |
| L3 | crack propagation path of tip 3 of the right auxiliary crack | - |
| L1′ | crack propagation path of tip 1 of the left main crack | - |
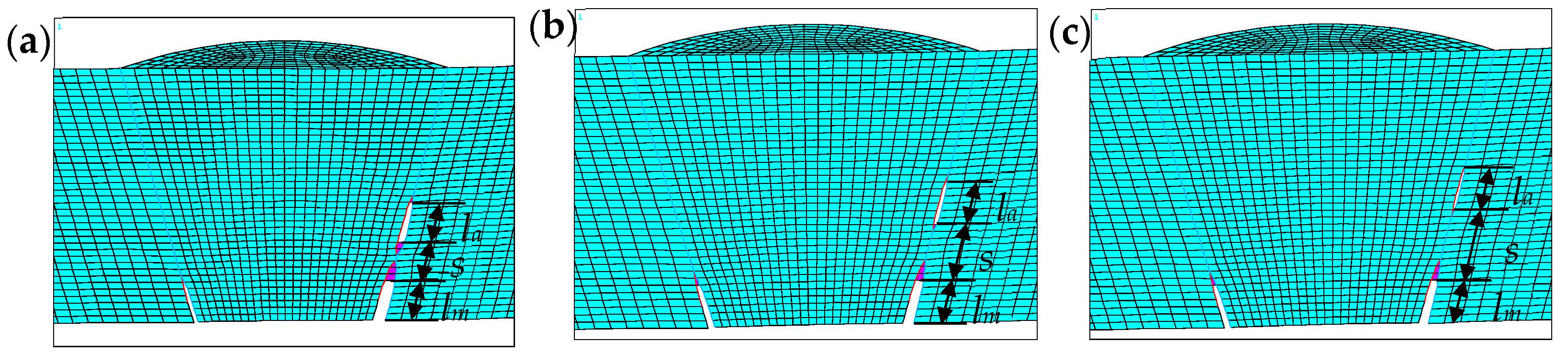
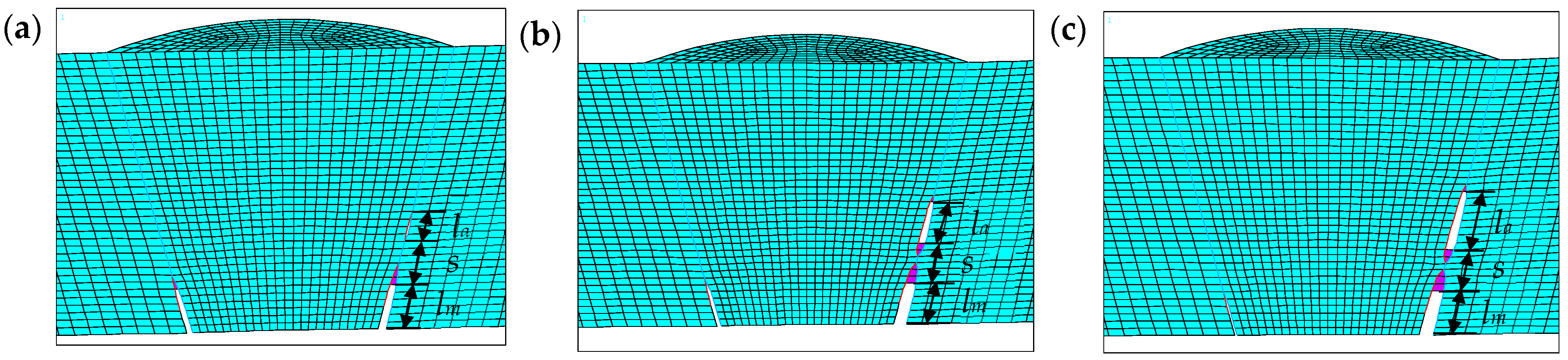
| la | initial length of the auxiliary crack | mm |
| lm | initial length of the main crack | mm |
| P | fluid pressure load | MPa |
| s | initial distance between the right main crack tip and the right auxiliary crack tip | mm |
| T1 | tip 1 of the right main crack | - |
| T1′ | tip 1 of the left main crack | - |
| T2 | tip 2 of the right auxiliary crack | - |
| T3 | tip 3 of the right auxiliary crack | - |
| VCCT | virtual crack closure technique | - |
| X | circumferential position | - |
| Y | radial position | - |
| ratio of the initial length of the main crack lm to the initial length of the auxiliary crack la | - | |
| ratio of the initial distance between the right main crack and the right auxiliary crack tips s to the initial length of the main crack lm | - | |
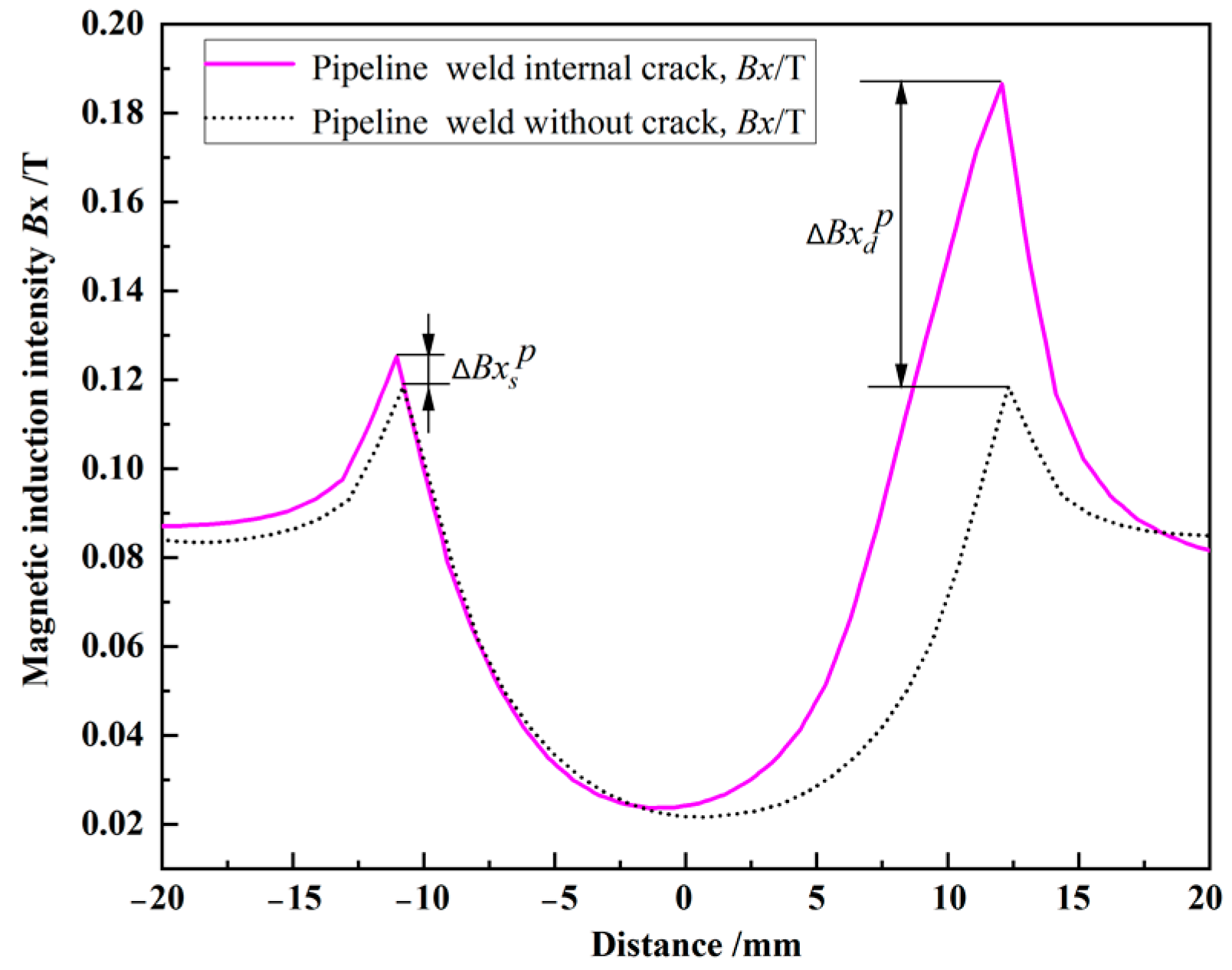
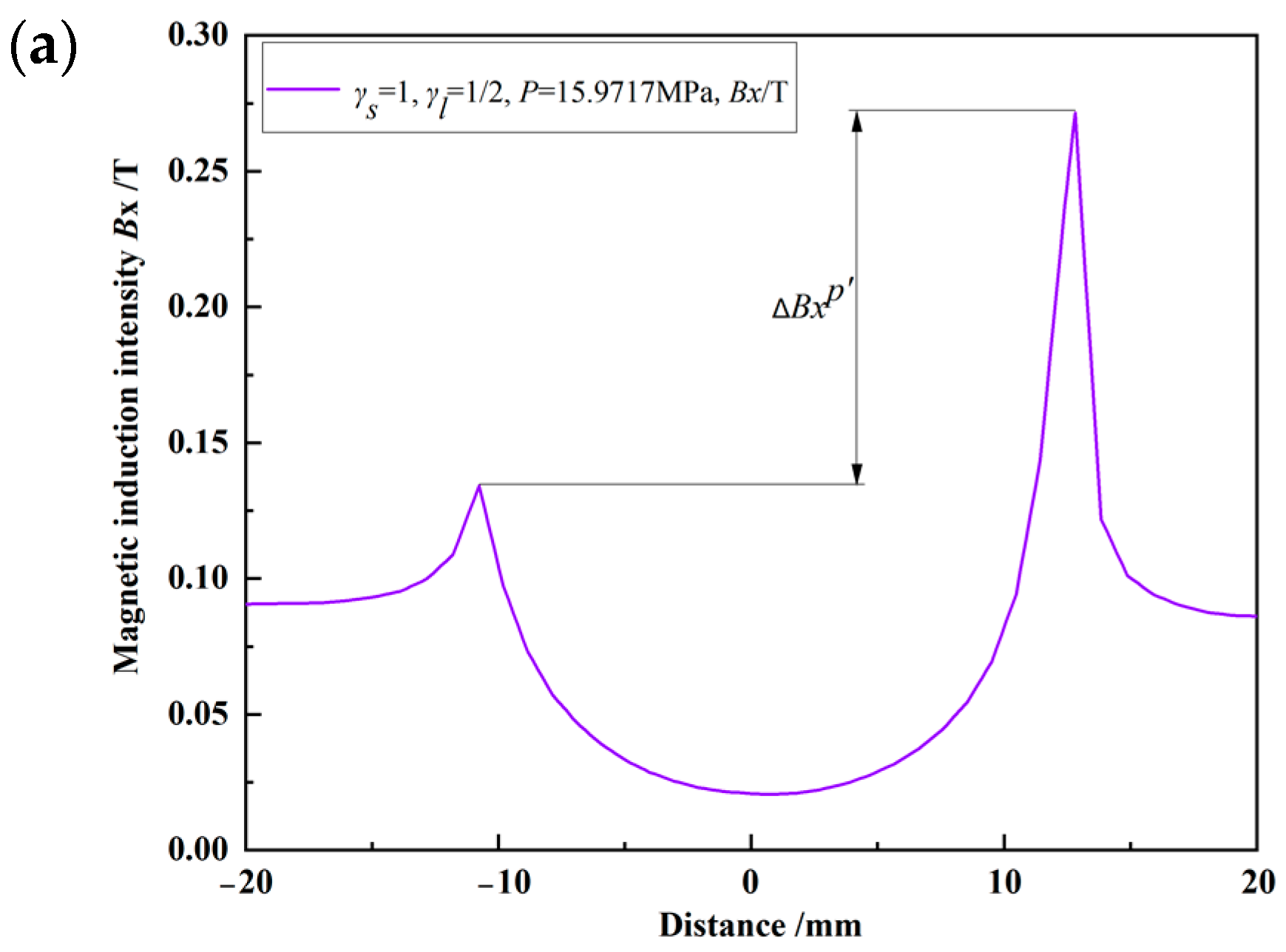
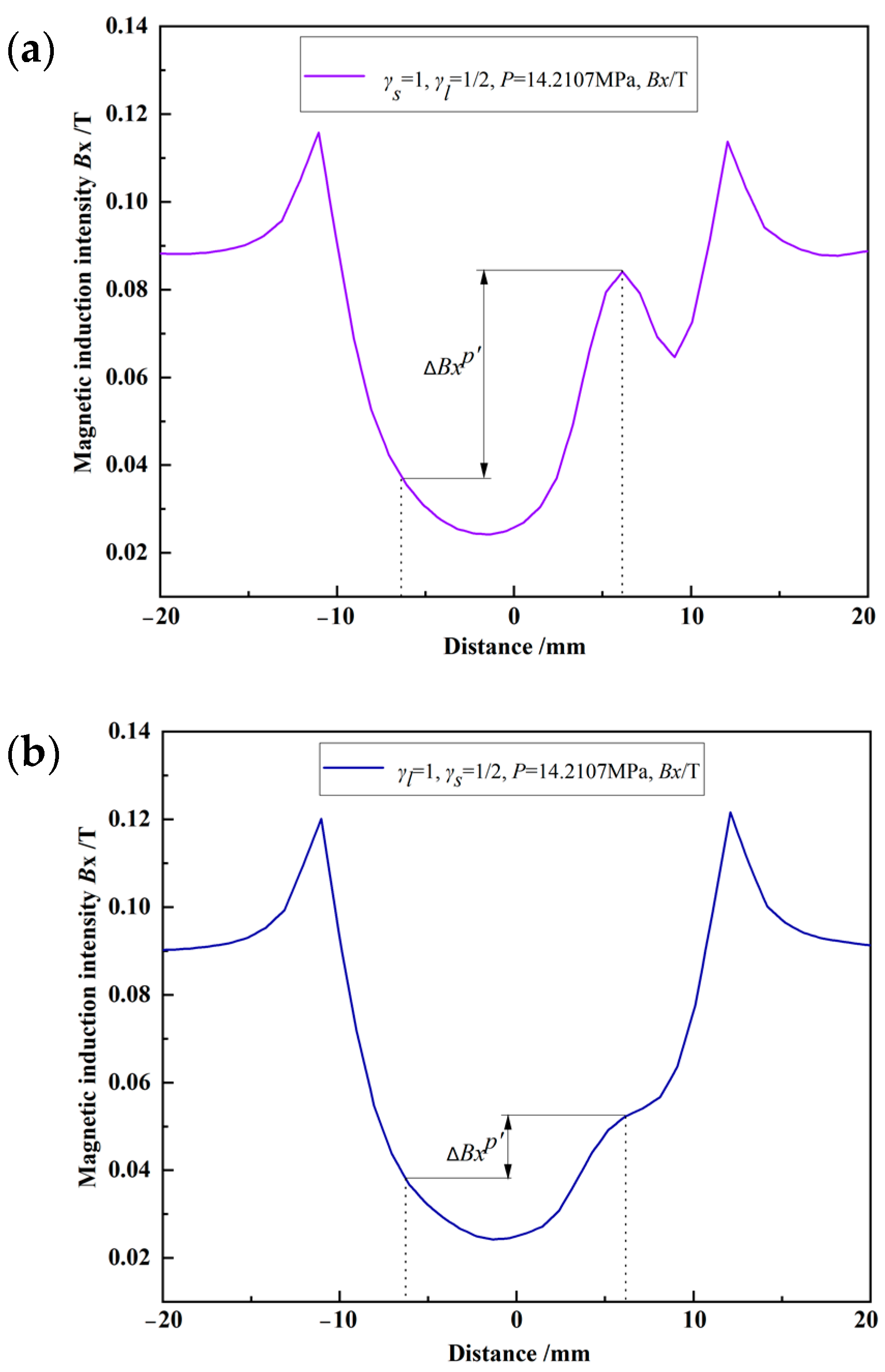
| difference between the peak values of the magnetic induction intensity component for the double crack (on the right side) and the magnetic induction intensity component of the weld without cracks | T | |
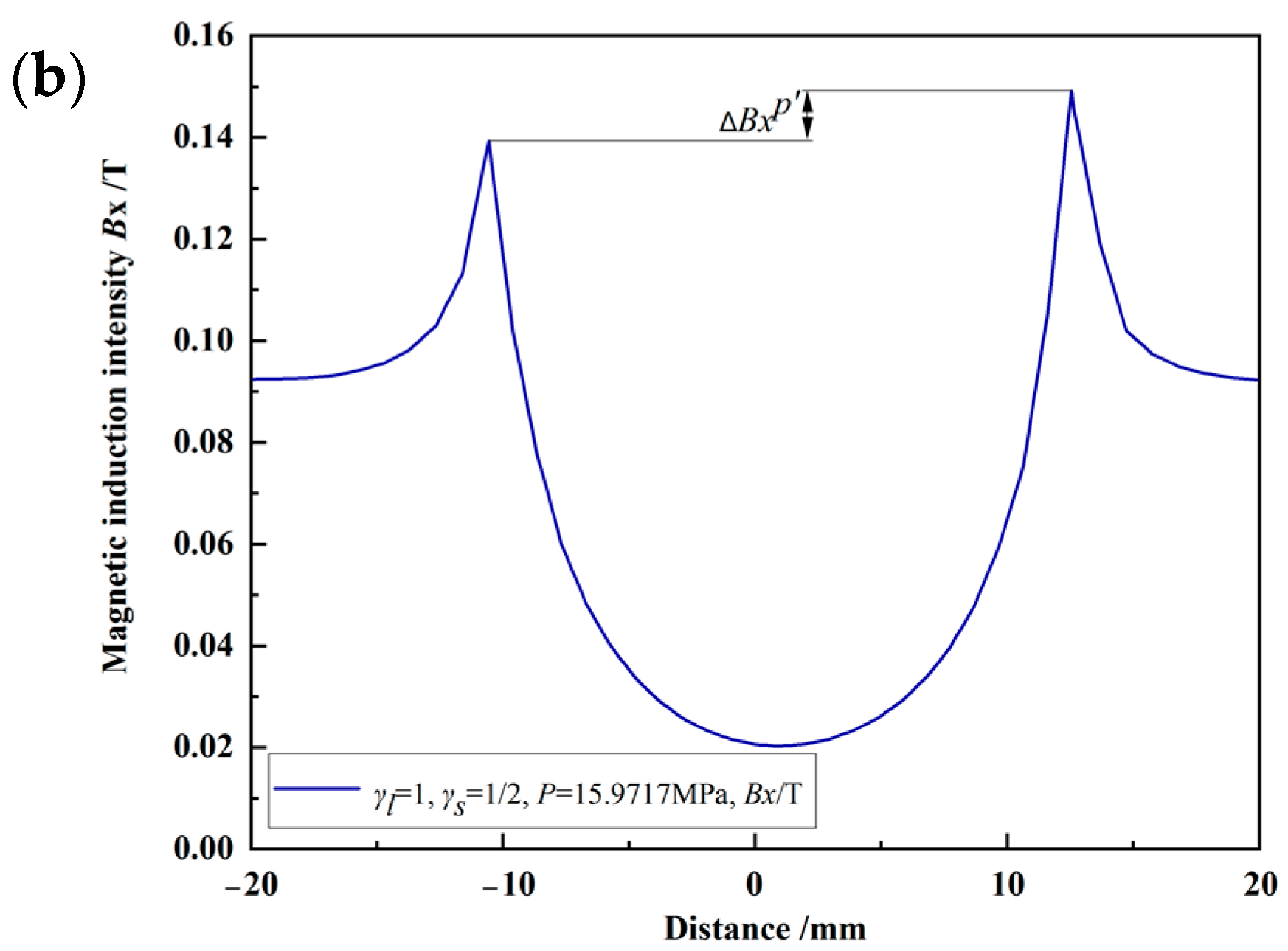
| difference between the peak values of the magnetic induction intensity component of the single crack on the left side and the magnetic induction intensity component of the weld without cracks | T | |
| difference between the peak value of the magnetic induction intensity component at the crack and the magnetic induction intensity component of its symmetrical position | T |
References
- Pozo, A.D.; Torres, A.; Villalobos, J.C.; Villanueva, H.; Fragiel, A.; Rodriguez, J.G.G.; Barquera, S.A.S. Ethanolic media effect on the susceptibility to stress corrosion cracking in an x-70 microalloyed steel with different aging treatments. Energies 2020, 13, 3277. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, X.S.; Fan, C.H. Research on a Safety Assessment Method for Leakage in a Heavy Oil Gathering Pipeline. Energies 2020, 13, 1340. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Z.M.; Yan, J.; Chen, B.J. Electro-elastic stress analysis for a Zener-Stroh crack interacting with a coated inclusion in piezoelectric solid. Acta Mech. 2004, 171, 29–40. [Google Scholar] [CrossRef]
- Ping, X.C.; Wang, C.G.; Cheng, L.P.; Chen, M.C.; Xu, J.Q. A super crack front element for three-dimensional fracture mechanics analysis. Eng. Fract. Mech. 2018, 196, 1–27. [Google Scholar] [CrossRef]
- Du, Y.; Zhou, F.; Hu, W.; Zheng, L.B.; Ma, L.; Zheng, J.Y. Incremental dynamic crack propagation of pipe subjected to internal gaseous detonation-ScienceDirect. Int. J. Impact Eng. 2020, 142, 103580. [Google Scholar] [CrossRef]
- Sun, J.; Cheng, Y.F. Modeling of mechano-electrochemical interaction between circumferentially aligned corrosion defects on pipeline under axial tensile stresses. J. Petrol. Sci. Eng. 2020, 198, 108160. [Google Scholar] [CrossRef]
- Majidi-Jirandehi, A.A.; Hashemi, S.H.; Ebrahimi-Nejad, S.; Kheybari, M. Impact of crack propagation path and inclusion elements on fracture toughness and micro-surface characteristics of welded pipes in DWTT. Mater. Res. Express 2021, 8, 106504. [Google Scholar] [CrossRef]
- Jovanović, M.; Čamagić, I.; Sedmak, S.; Sedmak, A.; Burzić, Z. The effect of material heterogeneity and temperature on impact toughness and fracture resistance of sa-387 gr. 91 welded joints. Materials 2022, 15, 1854. [Google Scholar] [CrossRef]
- Macek, W.; Branco, R.; Korpys’c, M.; Łagoda, T. Fractal dimension for bending–torsion fatigue fracture characterization. Measurement 2021, 184, 109910. [Google Scholar] [CrossRef]
- Bergara, A.; Dorado, J.I.; Martin-Meizoso, A.; Martínez-Esnaola, J.M. Fatigue crack propagation in complex stress fields: Experiments and numerical simulations using the Extended Finite Element Method (XFEM). Int. J. Fatigue 2017, 103, 112–121. [Google Scholar] [CrossRef]
- Ren, Z.J.; Ru, C.Q. Numerical investigation of speed dependent dynamic fracture toughness of line pipe steels. Eng. Fract. Mech. 2013, 99, 214–222. [Google Scholar] [CrossRef]
- Cheng, Y.X.; Zhang, Y.J. Experimental Study of Fracture Propagation: The Application in Energy Mining. Energies 2020, 13, 1411. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.B.; Zhuang, Z.; You, X.C.; Feng, Y.R.; Huo, C.Y.; Zhuang, C.J. Dynamic fracture study by an experiment/simulation method for rich gas transmission X80 steel pipelines. Eng. Fract. Mech. 2008, 75, 5018–5028. [Google Scholar] [CrossRef]
- Pang, J.; Hoh, H.J.; Tsang, K.S.; Low, J.; Kong, S.C.; Wen, G.Y. Fatigue crack propagation analysis for multiple weld toe cracks in cut-out fatigue test specimens from a girth welded pipe. Int. J. Fatigue 2017, 94, 158–165. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Xiao, Z.M.; Luo, J. Fatigue crack growth investigation on offshore pipelines with three-dimensional interacting cracks. Geosci. Front. 2018, 9, 689–1698. [Google Scholar] [CrossRef]
- Dong, S.H.; Zhang, L.B.; Zhang, H.W.; Chen, Y.N.; Zhang, H. Experimental study of unstable crack propagation velocity for X80 pipeline steel. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 805–817. [Google Scholar] [CrossRef]
- Shoheib, M.M.; Shahrooi, S.; Shishehsaz, M.; Hamzehei, M. Fatigue crack propagation of welded steel pipeline under cyclic internal pressure by Bézier extraction based XIGA. J. Pipeline Syst. Eng. Pract. 2022, 13, 04022001. [Google Scholar] [CrossRef]
- Shen, Q.Q.; Rao, Q.H.; Li, Z.; Yi, W.; Sun, D.L. Interacting mechanism and initiation prediction of multiple cracks-ScienceDirect. T. Nonferr. Metal. Soc. 2021, 31, 779–791. [Google Scholar] [CrossRef]
- Wang, S.Y.; Hu, S.W. Experimental study of crack propagation in cracked concrete. Energies 2019, 12, 3854. [Google Scholar] [CrossRef] [Green Version]
- Xiao, X.; Xiao, C. Analysis of Initiation Angle for fracture propagation considering stress interference. Energies 2019, 12, 1841. [Google Scholar] [CrossRef] [Green Version]
- Petrova, V.E.; Schmauder, S. Modeling of thermomechanical fracture of functionally graded materials with respect to multiple crack interaction. Phys. Mesomech. 2017, 20, 241–249. [Google Scholar] [CrossRef]
- Ahmed, T.; Yavuz, A.; Turkmen, H.S. Fatigue crack growth simulation of interacting multiple cracks in perforated plates with multiple holes using boundary cracklet method. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 333–348. [Google Scholar] [CrossRef]
- Gope, P.C.; Bisht, N.; Singh, V.K. Influence of crack offset distance on interaction of multiple collinear and offset edge cracks in a rectangular plate. Theor. Appl. Fract. Mec. 2014, 70, 19–29. [Google Scholar] [CrossRef]
- Menouillard, T.; Belytschko, T. Dynamic fracture with meshfree enriched XFEM. Acta Mech. 2010, 213, 53–69. [Google Scholar] [CrossRef]
- Djokovic, J.M.; Nikolic, R.R.; Sumarac, D.M.; Bujnak, J. Analysis based on the energy release rate criterion of a dynamically growing crack approaching an interface. Int. J. Damage Mech. 2016, 25, 1170–1183. [Google Scholar] [CrossRef]
- Amir, G.; Jaber, T.S.; Amin, S. The distinct element method (DEM) and the extended finite element method (XFEM) application for analysis of interaction between hydraulic and natural fractures. J. Petrol. Sci. Eng. 2018, 171, 422–430. [Google Scholar] [CrossRef]
- Sheng, M.; Li, G.; Sutula, D.; Tian, S.; Bordas, S. XFEM modeling of multistage hydraulic fracturing in anisotropic shale formations. J. Petrol. Sci. Eng. 2018, 162, 801–812. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Sayedain, M. Finite element modeling strategies for 2D and 3D delamination propagation in composite DCB specimens using VCCT, CZM and XFEM approaches. Theor. Appl. Fract. Mec. 2019, 103, 102246. [Google Scholar] [CrossRef]
- Drake, D.A.; Sullivan, R.W. Interfacial fracture energy of a single cantilevered beam specimen using the j-integral method. Int. J. Fracture 2021, 229, 185–194. [Google Scholar] [CrossRef]
- Cui, W.; Zhang, Y.H.; Xiao, Z.M.; Zhang, Q. A new magnetic structural algorithm based on virtual crack closure technique and magnetic flux leakage testing for circumferential symmetric double-crack propagation of X80 oil and gas pipeline weld. Acta Mech. 2020, 231, 1187–1207. [Google Scholar] [CrossRef]
- Cui, W.; Zhang, Y.H.; Zhang, Q.; Feng, Z.M. A fluid-solid-magnetic coupling method for the crack growth in pipe welds considering the fluid permeation pressure. Mater. Rep. 2019, 33, 120–124. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Rajabpour-Shirazi, H.; Heidari-Rarani, M.; Haghpanahi, M. Simulation of mode I delamination propagation in multidirectional composites with R-curve effects using VCCT method. Comp. Mater. Sci. 2012, 65, 66–73. [Google Scholar] [CrossRef]
- Ahn, J.S.; Woo, K.S. Delamination of laminated composite plates by p-convergent partial discrete-layer elements with VCCT. Mech. Res. Commun. 2015, 66, 60–69. [Google Scholar] [CrossRef]
- Li, J.X.; Xiao, W.; Hao, G.Z.; Dong, S.M.; Hua, W.; Li, X.L. Comparison of different hydraulic fracturing scenarios in horizontal wells using XFEM based on the cohesive zone method. Energies 2019, 12, 1232. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.Z.; Zeng, Q.D.; Yao, J.; Liu, Z.Y.; Li, T.L.; Yan, X. Numerical study of elasto-plastic hydraulic fracture propagation in deep reservoirs using a hybrid EDFM–XFEM method. Energies 2021, 14, 2610. [Google Scholar] [CrossRef]
- Burlayenko, V.N.; Altenbach, H.; Sadowski, T.; Dimitrova, S.D. Computational simulations of thermal shock cracking by the virtual crack closure technique in a functionally graded plate. Comp. Mater. Sci. 2016, 116, 11–21. [Google Scholar] [CrossRef]
- Farkash, E.; Banks-Sills, L. Virtual crack closure technique for an interface crack between two transversely isotropic materials. Int. J. Fracture 2017, 205, 189–202. [Google Scholar] [CrossRef]
- Liu, Y.P.; Li, T.J. Application of the virtual crack closure technique (VCCT) using tetrahedral finite elements to calculate the stress intensity factor. Eng. Fract. Mech. 2021, 253, 107853. [Google Scholar] [CrossRef]
- Singh, M.P.; Arora, K.S.; Kumar, R.; Shukla, D.K.; Prasad, S.S. Influence of heat input on microstructure and fracture toughness property in different zones of X80 pipeline steel weldments. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 85–100. [Google Scholar] [CrossRef]
- Yang, Y.H.; Shi, L.; Xu, Z.; Lu, H.S.; Chen, X.; Wang, X. Fracture toughness of the materials in welded joint of X80 pipeline steel. Eng. Fract. Mech. 2015, 148, 337–349. [Google Scholar] [CrossRef]
- Liu, W.Y. Study on Crack Propagation in Heat Affected Zone of Pressure Pipeline Welding; Southwest Petroleum University: Chengdu, China, 2017. [Google Scholar]
- Cao, Y.G.; Zhen, Y.; He, Y.Y.; Zhang, S.H.; Sun, Y.T.; Yi, H.J.; Liu, F. Prediction of limit pressure in axial through-wall cracked X80 pipeline based on critical crack-tip opening angle. J. China Univ. Pet. (Ed. Nat. Sci.) 2017, 41, 139–146. [Google Scholar]
- GB 10854-89, Weld Outer Dimensions for Steel Construction. 1989. Available online: https://wenku.baidu.com/view/e7b14cba86c24028915f804d2b160b4e767f81e4.html (accessed on 30 December 2021).
- Shi, L. A Study on the Fracture Toughness of X80 Pipeline Steel Welded Joint; Tianjin University: Tianjin, China, 2014. [Google Scholar]
- Yao, A.L.; He, W.B.; Xu, T.L.; Jiang, H.Y.; Gu, D.F. A 3D-VCCT based method for the fracture analysis of gas line pipes with multiple cracks. Nat. Gas Ind. 2019, 39, 85–93. [Google Scholar] [CrossRef]
- Wang, X.M.; Mike, W.Z. Design and Calculation of Engineering Pressure Vessel, 2nd ed.; National Defense Industry Press: Beijing, China, 2011; pp. 462–463. [Google Scholar]
- Afzal, M.; Udpa, S. Advanced signal processing of magnetic flux leakage data obtained from seamless gas pipeline. NDT&E Int. 2002, 35, 449–457. [Google Scholar] [CrossRef]
- Mukherjee, D.; Saha, S.; Mukhopadhyay, S. Inverse mapping of magnetic flux leakage signal for defect characterization. NDT&E Int. 2013, 54, 198–208. [Google Scholar] [CrossRef]
- Nara, T.; Fujieda, M.; Gotoh, Y. Non-destructive inspection of ferromagnetic pipes based on the discrete fourier coefficients of magnetic flux leakage. J. Appl. Phys. 2014, 115, 17E509. [Google Scholar] [CrossRef]





| Material Parameters | Geometric Dimensioning | Loading | ||
|---|---|---|---|---|
| ×80 | pipeline diameter (mm) | 1219 | initial internal pressure Ps (MPa) | 1 |
| pipeline wall thickness (mm) | 18.4 | |||
| weld width (mm) | 22 | maximum internal pressure Pe (MPa) | 30 | |
| weld reinforcement (mm) | 2 | |||
| Parameter | Value |
|---|---|
| Elastic Moduli E (GPa) | 180.30 |
| Poisson ratio | 0.3 |
| Fracture toughness | 115 |
| itical strain energy release rate of plane strain model (N/mm) | 66.75 |
| Dimensions | Materials | |
|---|---|---|
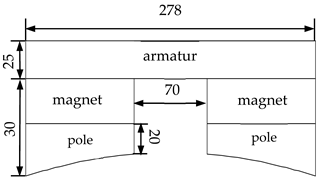 | magnet | Nd-Fe-B |
| armature | armco iron | |
| pole shoe | armco iron | |
| P (MPa) | GIT1 (N/mm) | GIT1′ (N/mm) | EN (Right Main Crack) | EN (Left Main Crack) | CTOAT1 (°) | CTOAT1′ (°) | ||
|---|---|---|---|---|---|---|---|---|
| 18.6534 | 68.2124 | 60.0168 | 1 | — | 11.228 | — | 0.0231 | 0.0017 |
| 18.8034 | 189.6473 | 65.5480 | 2 | — | 23.778 | — | 0.0343 | 0.0047 |
| 18.8186 | 811.1834 | 80.5873 | 3 | 1 | 55.256 | 13.930 | 0.0681 | 0.0068 |
| EN (Right Main Crack) | s (mm) | P (MPa) | GIT1 (N/mm) | CTOAT1 (°) | |
|---|---|---|---|---|---|
| 1 | 3 | 18.6534 | 68.2124 | 11.228 | 0.0231 |
| 4 | 18.8034 | 67.4471 | 10.84 | 0.0230 | |
| 5 | 18.8877 | 67.2119 | 10.804 | 0.0227 | |
| 2 | 3 | 18.8034 | 189.6473 | 23.778 | 0.0343 |
| 4 | 19.068 | 104.3703 | 15.566 | 0.0339 | |
| 5 | 19.1994 | 87.5952 | 15.233 | 0.0335 | |
| 3 | 3 | 18.8186 | 811.1834 | 55.256 | 0.0681 |
| 4 | 19.14 | 300.4616 | 33.346 | 0.0489 | |
| 5 | 19.2381 | 194.8184 | 24.812 | 0.0436 |
| EN (Right Main Crack) | la (mm) | P (MPa) | GIT1 (N/mm) | CTOAT1 (°) | |
|---|---|---|---|---|---|
| 1 | 2 | 18.9609 | 66.9295 | 10.224 | 0.0211 |
| 3 | 18.6534 | 68.2124 | 11.228 | 0.0231 | |
| 4 | 18.0534 | 70.9167 | 11.506 | 0.0264 | |
| 2 | 2 | 19.0863 | 95.1277 | 13.293 | 0.0268 |
| 3 | 18.8034 | 189.6473 | 23.778 | 0.0343 | |
| 4 | 18.1512 | 207.1846 | 25.114 | 0.0411 | |
| 3 | 2 | 19.1265 | 155.6665 | 20.381 | 0.0350 |
| 3 | 18.8186 | 811.1834 | 55.256 | 0.0681 | |
| 4 | 18.1998 | 937.8363 | 59.589 | 0.0833 |
| P (MPa) | EN’ | GIT1 (N/mm) | CTOAT1 (°) | |
|---|---|---|---|---|
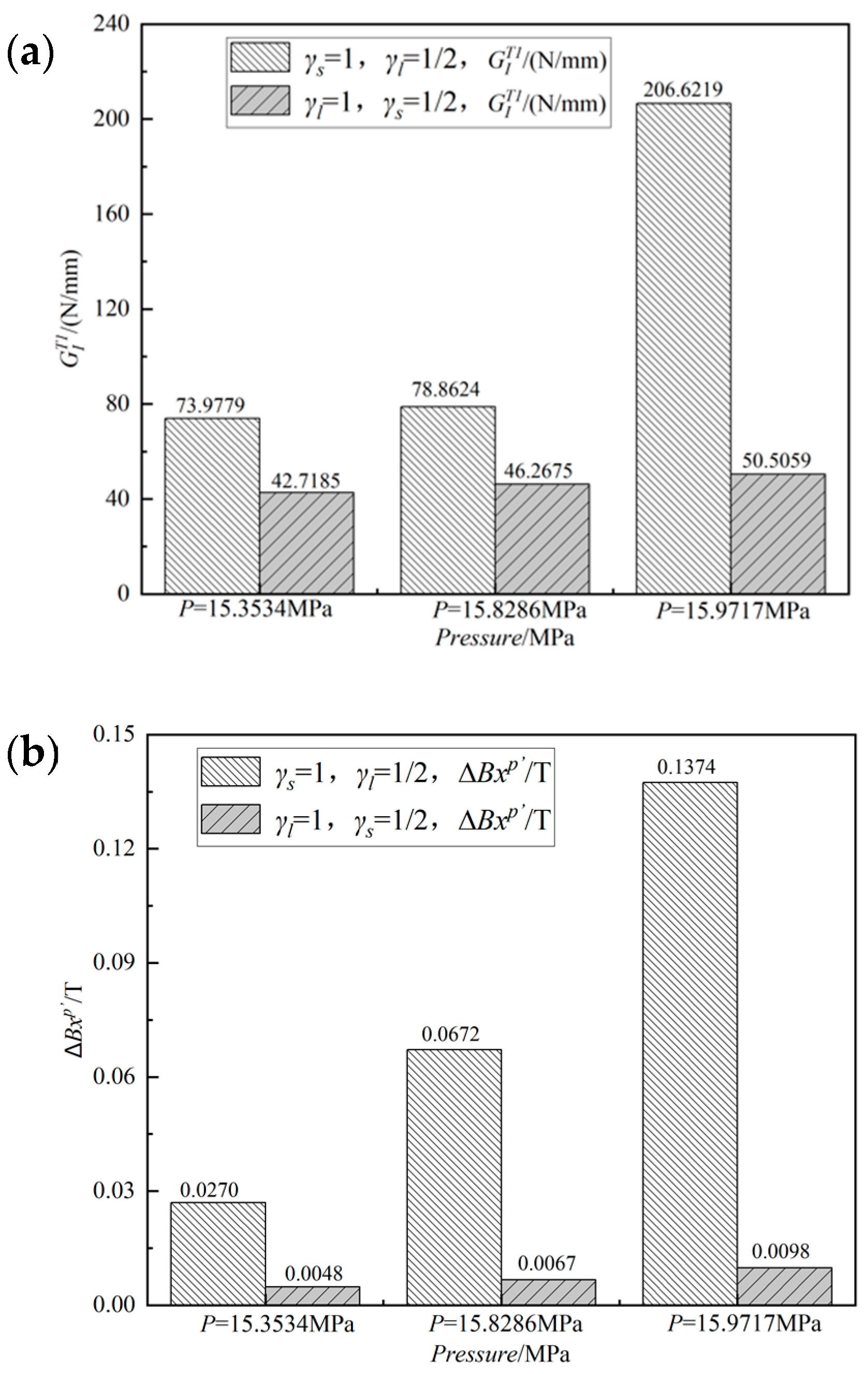
| 15.3534 | : 73.9779 | : 11.942 | : 0.0270 | |
| : 0 | : 42.7185 | : — | : 0.0048 | |
| 15.8286 | : 2 EN′ | : 78.8624 | : 18.305 | : 0.0672 |
| : 0 | : 46.2675 | : — | : 0.0067 | |
| 15.9717 | : 3 EN′ | : 206.6219 | : 36.955 | : 0.1374 |
| : 0 | : 50.5059 | : — | : 0.0098 |
| P (MPa) | EN’ | GIT1 (N/mm) | CTOAT1 (°) | |
|---|---|---|---|---|
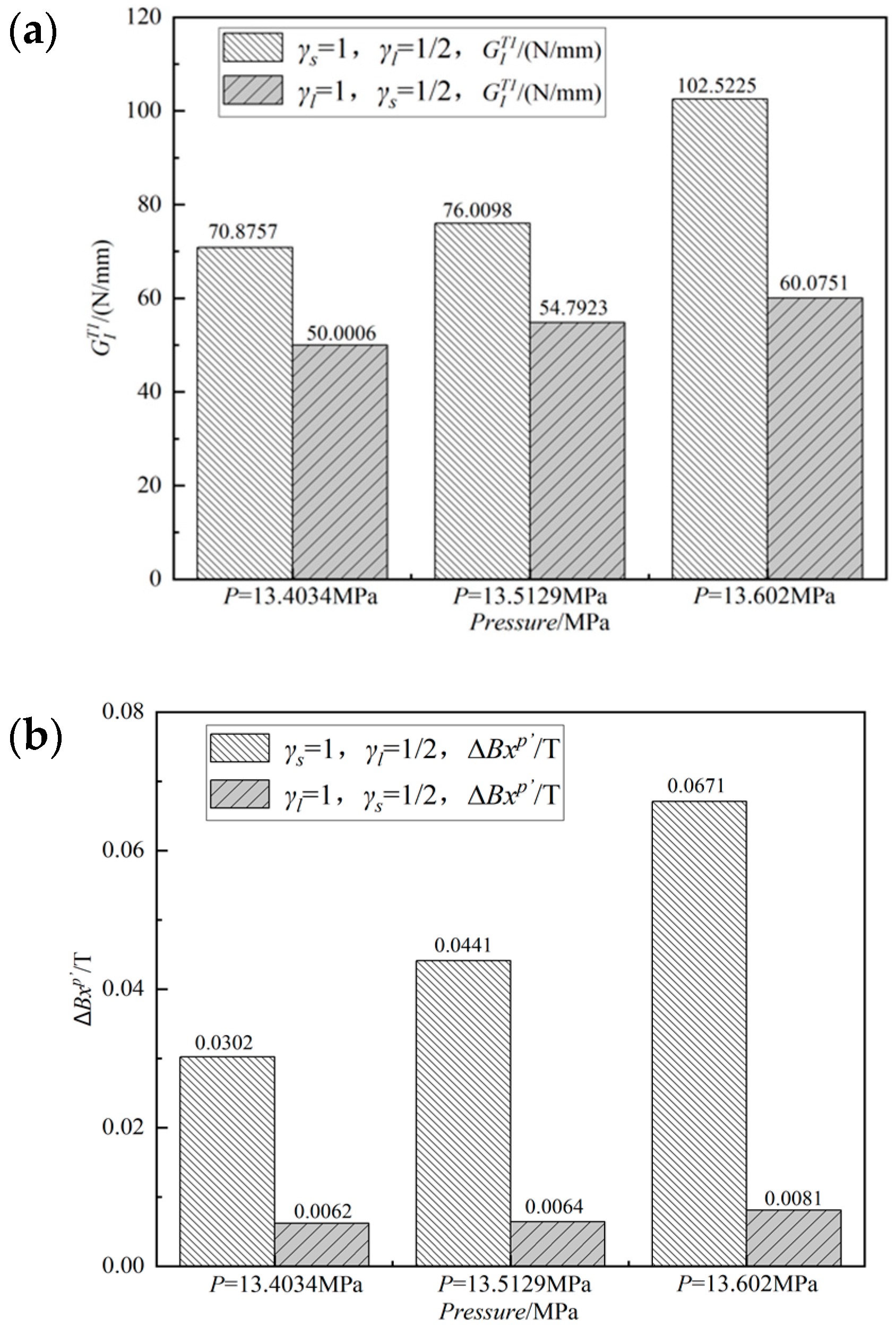
| 13.4034 | : 70.8757 | : 12.279 | : 0.0302 | |
| : 0 | : 50.0006 | : — | : 0.0062 | |
| 13.5129 | : 2 EN′ | : 76.0098 | : 15.372 | : 0.0441 |
| : 0 | : 54.7923 | : — | : 0.0064 | |
| 13.602 | : 3 EN′ | : 102.5225 | : 23.79 | : 0.0671 |
| : 0 | : 60.0751 | : — | : 0.0081 |
| P (MPa) | EN′ | GIT1 (N/mm) | CTOAT1 (°) | |
|---|---|---|---|---|
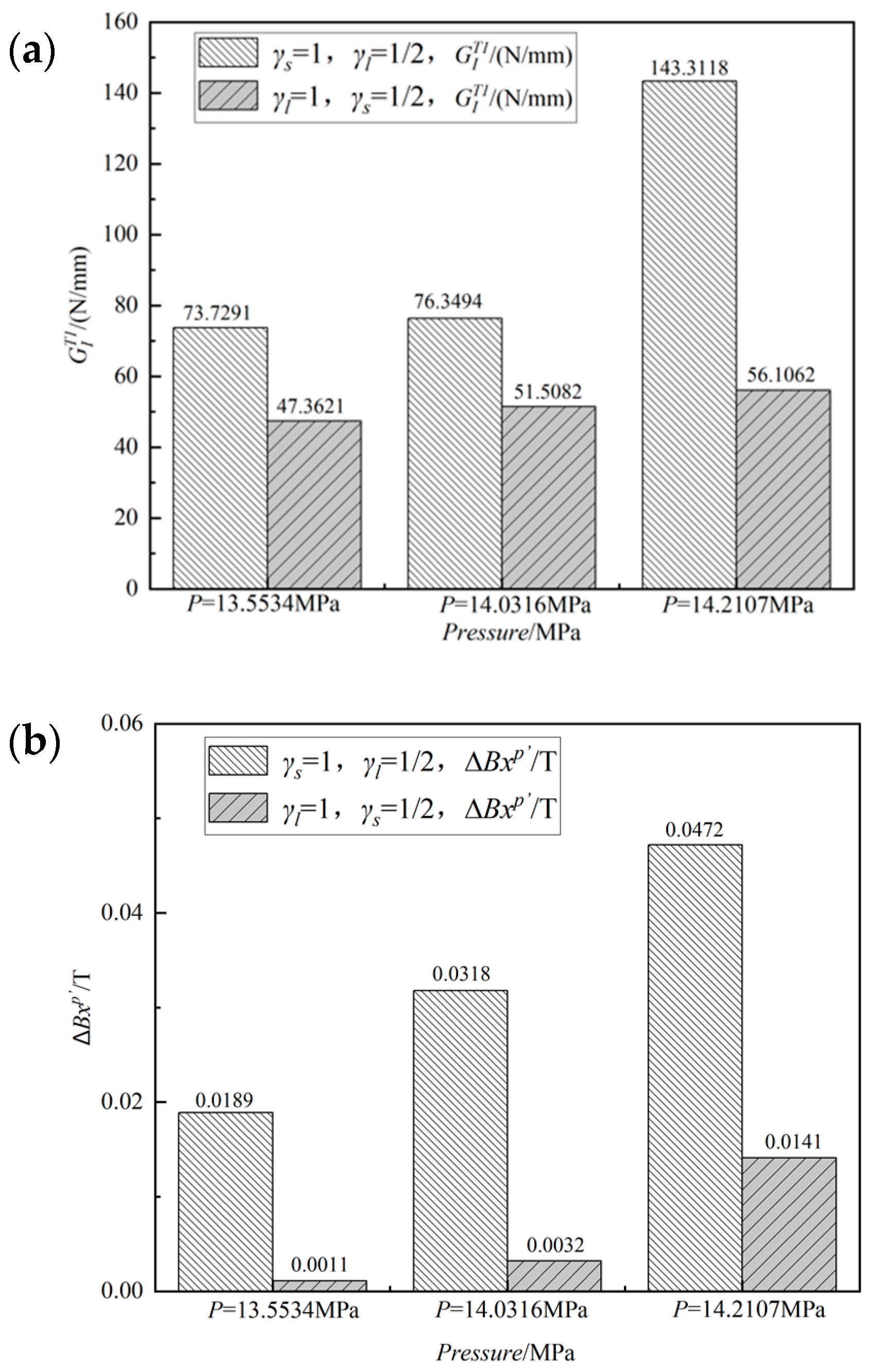
| 13.5534 | : 1 EN′ | : 73.7291 | : 12.328 | : 0.0189 |
| : 0 | : 47.3621 | : — | : 0.0011 | |
| 14.0316 | : 2 EN′ | : 76.3494 | : 16.694 | : 0.0318 |
| : 0 | : 51.5082 | : — | : 0.0032 | |
| 14.2107 | : 3 EN′ | : 143.3118 | : 28.697 | : 0.0472 |
| : 0 | : 56.1062 | : — | : 0.0141 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, W.; Xiao, Z.; Yang, J.; Tian, M.; Zhang, Q.; Feng, Z. Multi-Crack Dynamic Interaction Effect on Oil and Gas Pipeline Weld Joints Based on VCCT. Energies 2022, 15, 2812. https://doi.org/10.3390/en15082812
Cui W, Xiao Z, Yang J, Tian M, Zhang Q, Feng Z. Multi-Crack Dynamic Interaction Effect on Oil and Gas Pipeline Weld Joints Based on VCCT. Energies. 2022; 15(8):2812. https://doi.org/10.3390/en15082812
Chicago/Turabian StyleCui, Wei, Zhongmin Xiao, Jie Yang, Mi Tian, Qiang Zhang, and Ziming Feng. 2022. "Multi-Crack Dynamic Interaction Effect on Oil and Gas Pipeline Weld Joints Based on VCCT" Energies 15, no. 8: 2812. https://doi.org/10.3390/en15082812
APA StyleCui, W., Xiao, Z., Yang, J., Tian, M., Zhang, Q., & Feng, Z. (2022). Multi-Crack Dynamic Interaction Effect on Oil and Gas Pipeline Weld Joints Based on VCCT. Energies, 15(8), 2812. https://doi.org/10.3390/en15082812







