Multi-Objective Optimisation for Large-Scale Offshore Wind Farm Based on Decoupled Groups Operation
Abstract
:1. Introduction
- (1)
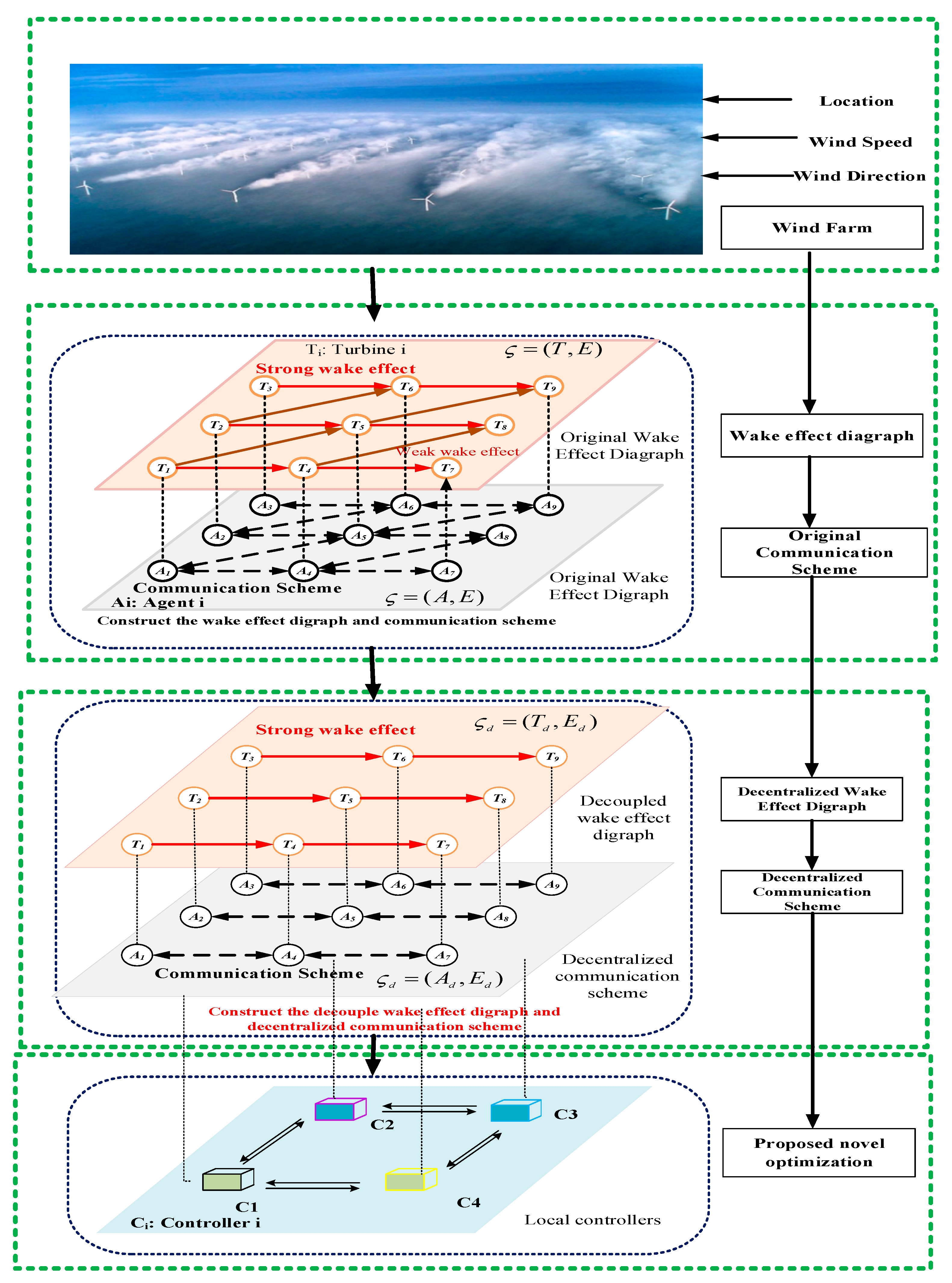
- We propose a decentralized communication construction scheme based on a wake-based digraph that can divide a large-scale wind farm into decoupled groups. Every local controller computes the data of turbines in the same group to reduce the communication burden.
- (2)
- We propose a new multi-objective optimization framework for wind farm profits points, which includes the total output power, the total fatigue load, and the dispatch of the fatigue load on each wind turbine. Our novel method can decrease the maintenance frequency and lower the maintenance cost of the wind farm.
- (3)
- We propose a decentralized CMC-BSO algorithm developed based on a decoupled communication scheme in the wind farm, which combines the advantages of the BSA and PSO algorithms. The algorithm is implemented with a wake steering control to identify the optimized solution on the objectives by controlling the yaw angles and axial factors.
2. Methodology
2.1. Wind Farm Model with Wake Interactions
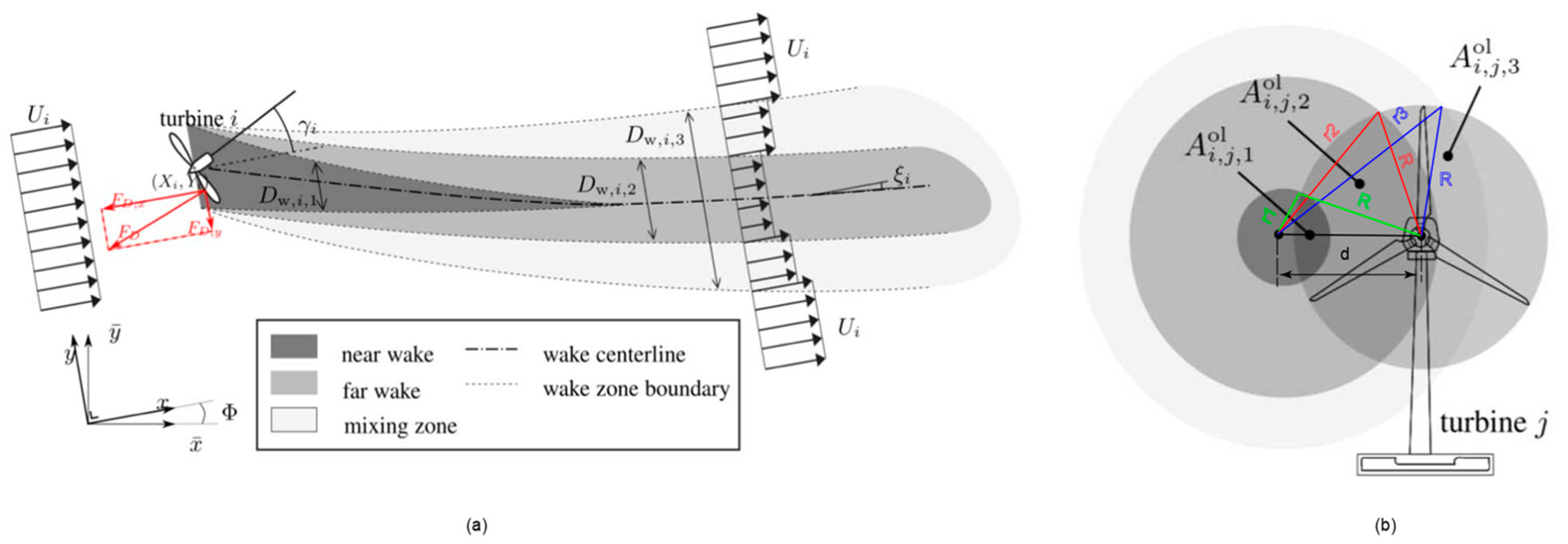
2.1.1. Wind Turbine Wake Model
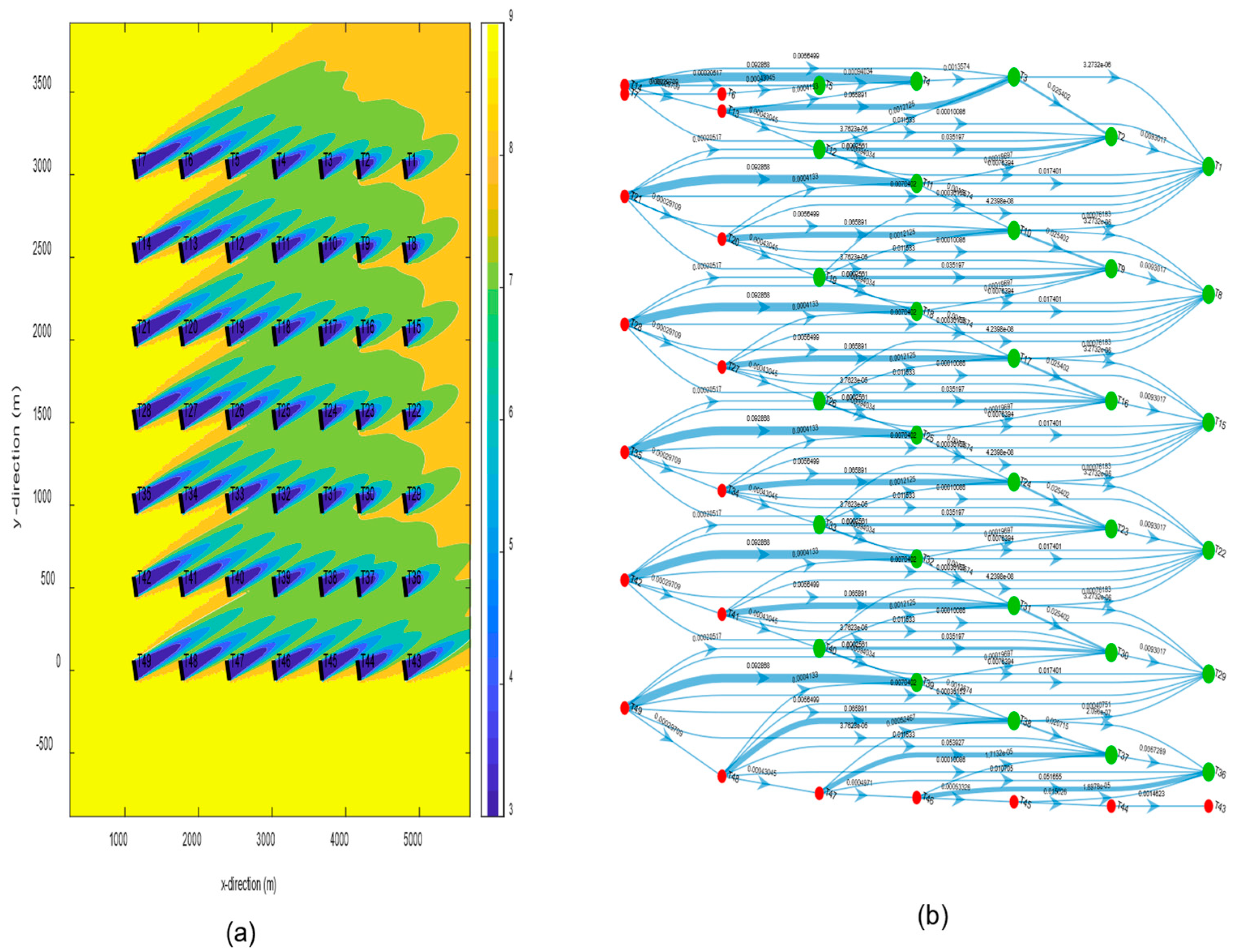
2.1.2. Original Wake Effect Digraph of Offshore Wind Farm
2.2. Decentralized Wake Effect Digraph of Offshore Wind Farm
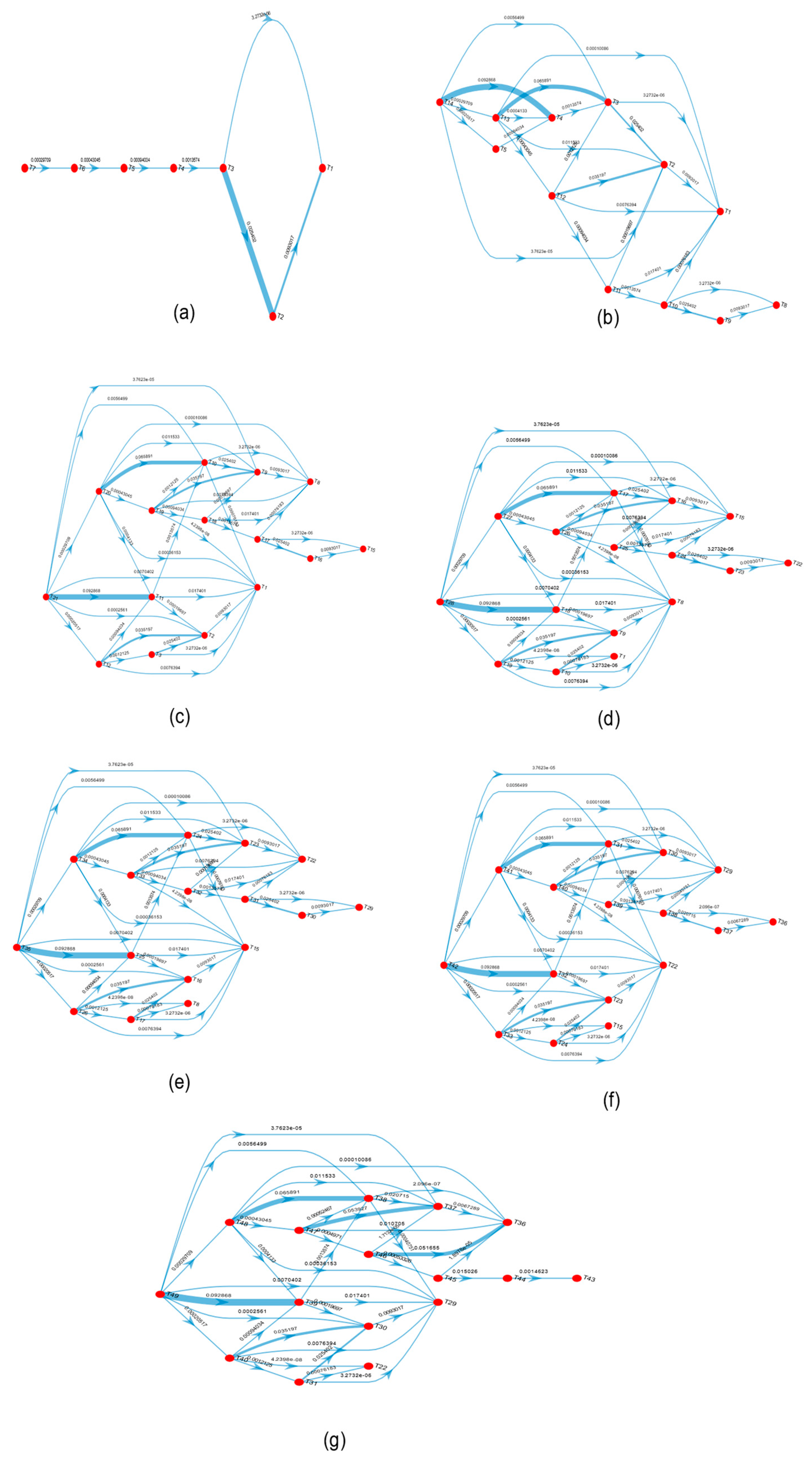
2.2.1. Parallel of Depth-First Search Algorithm to Identify Subgraph
2.2.2. Calculating the HITS Score of Shared Turbines
| Algorithm 1. The HITS algorithm is based on the wake diagram ς. |
| : a collection of v linked turbines |
| i, c: natural numbers |
| , |
| t = 1 |
| do |
| for each v in |
| do |
| Normalize: |
| Normalize: |
| Iteration: i |
| Till |
| Return () |
| Report the nodes with the c largest coordinate in . |
| Report the nodes with the c largest coordinate in . |
2.2.3. The Process of Decoupling Shared Turbines Based on the 12-Turbines
2.3. Multi-Objective Optimization Based on Decoupled Groups
2.3.1. Formulation of Multi-Objective Optimization
2.3.2. CMC-BSO Optimization Algorithm
- (1)
- Update the position on the antennae of individual and group beetles.
- (2)
- Define the movement of beetles.
- (3)
- Define the speed of beetles.
- (4)
- Define the adaptive inertia weight [39]:
- (5)
- Pre-update the right and left antenna beetles.
- (6)
- Implemented solution of the Monte Carlo law.
- (7)
- Step size:
3. Simulation Results and Discussion
3.1. Parameter Setup
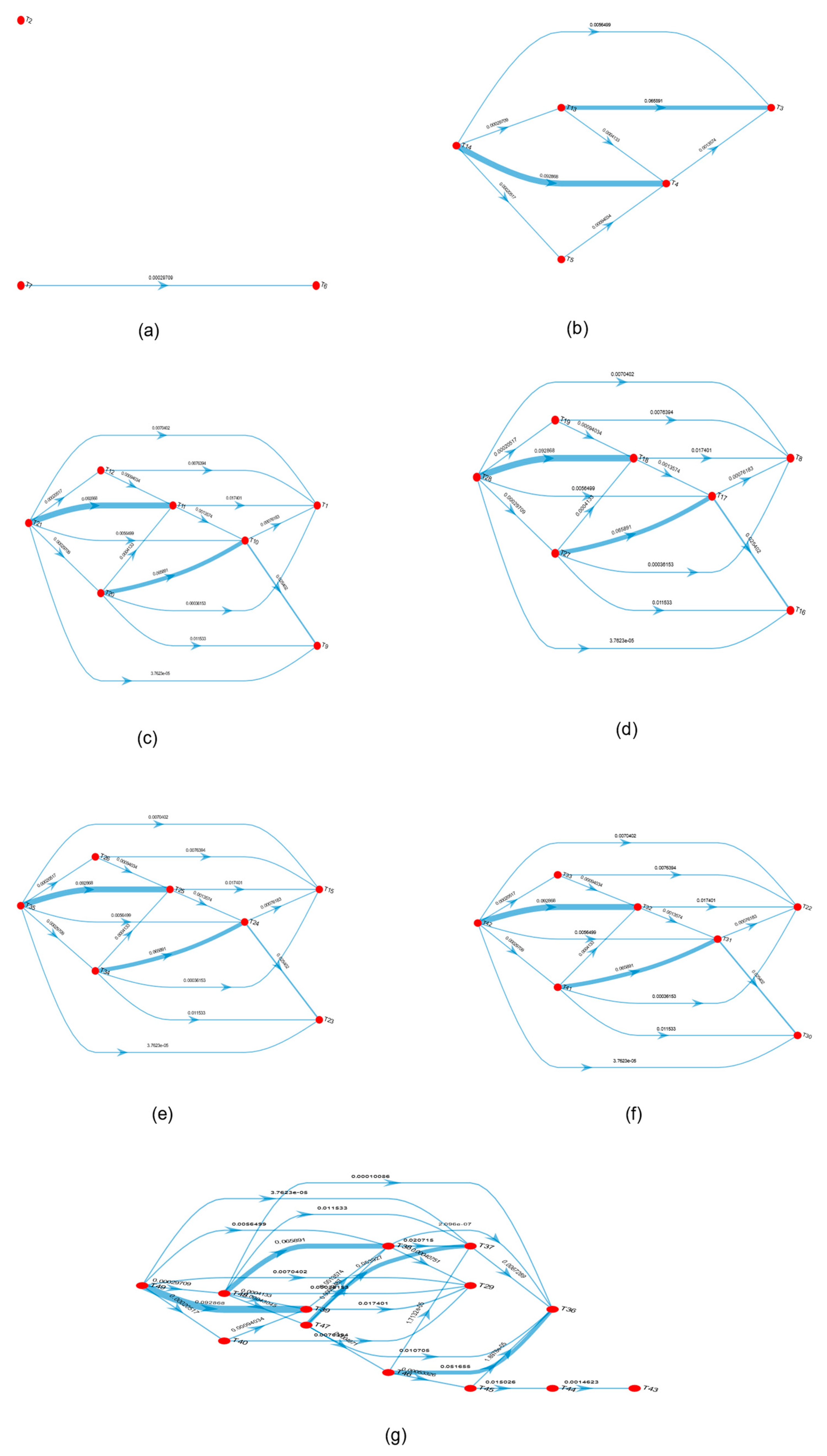
3.2. Process of Decoupling Groups
3.3. Optimization Results
3.3.1. Simulation Results with a Constant Wind Speed
3.3.2. Simulation Results with Constant Wind Directions
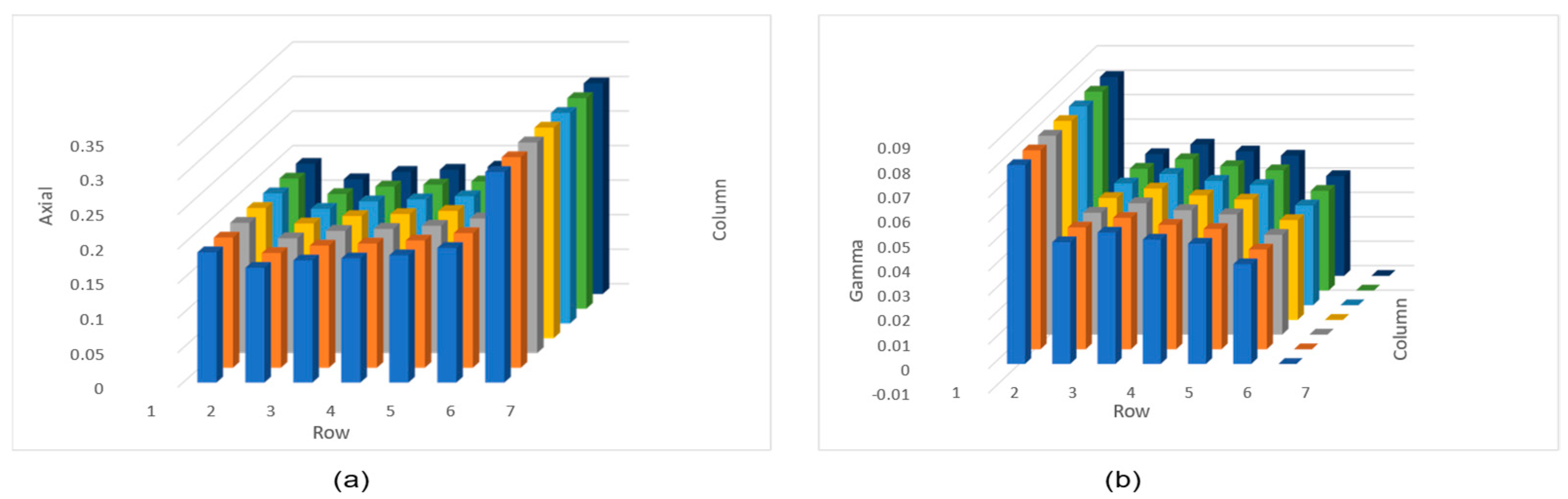
3.3.3. Simulation Results with Different Hyperparameters
- The weight value can decide the relationship between P, F, ΔP, and ΔF.
- 2.
- The with a varying hyperparameters value σ.
- 3.
- The with a varying hyperparameters value .
- (1)
- Weight value is an important weight factor and can be used to adjust the important degree of P or F, and a larger means it is more important to optimize P. If , P and F are optimized at the same degree.
- (2)
- Hyperparameters values σ and can affect the fatigue load of each turbine, The greater σ or , the more the fatigue loads of each subset will decrease (and vice versa). The difference is that hyperparameters are more sensitive than σ.
4. Discussion
- (1)
- The accuracy and control speed of the proposed algorithm. The reaction speed of the proposed algorithm is faster than other methods, and the control time of the CMC-BSO algorithm has been reduced by 9.23% compared to the MC-BAS method in [17] and decreased by 3.98% compared to the traditional multi-objective algorithm in [13] owing to the novel decentralized communication topology.
- (2)
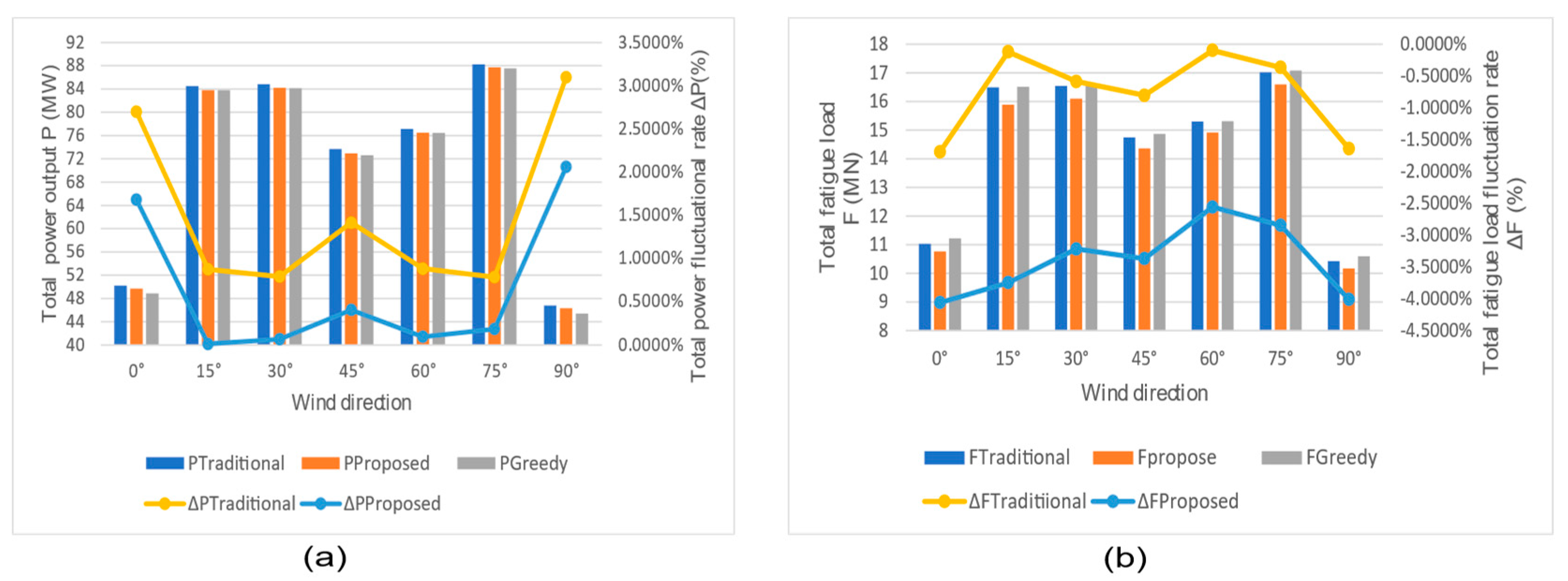
- The performance of the proposed multi-objective function. With different wind speeds and directions, the implementation of the proposed algorithm compared with the other two methods:
- (a)
- Compared with the greedy method, the average power output of the proposed algorithm increased by approximately 0.47%. The proposed algorithm demonstrated superior performance regarding fatigue distribution, with an average fatigue decrease rate for the lead turbine of approximately 13.5%. This means the output power has increased, and the fatigue load has decreased.
- (b)
- Compared with the traditional multi-objective optimization method, the improved performance of the proposed algorithm has also been verified. Although the total output power rate is decreased at 1.5%, the average fatigue decrease rate is 12.3%. Therefore, it can be economically profitable at a low power cost.
- (3)
- The tuning factors. The different tuning factors of the proposed multi-objective function were analyzed. In this case, the tuning factor ranges from 0.4 to 0.9, and the specific value needs to consider the balance between calculation accuracy and speed.
5. Conclusions
- (1)
- The PDFS implemented with the HITS algorithm has been newly proposed in the wake effect digraph of a large-scale OWF, which can be useful for splitting the OWF into decoupled groups. It is of significance and practical importance for us to control the wake effect digraph with a modular and flexible structure.
- (2)
- A novel multi-objective algorithm has been submitted in this study to increase the economic profits of OWF owners. The importance of this algorithm is of good performance on balancing fatigue load dispatch of each wind turbine on the whole OWF. A quantitative analysis has been conducted comparing the result data of the novel algorithm and the traditional algorithm, and its good performance was well verified.
- (3)
- It is a non-negligible key technology to design a solver of controllers. The CMC-BSO algorithm has been proposed first in this paper. The practical importance of this paper is to develop a novel control technique by presenting the CMC-BSO algorithm. We have confirmed that it can decrease the probabilities of the suboptimal solution and improve the active speed, which has been verified by comparing the computation time of the MC-BAS algorithm as in Section 3.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Scheme | Authority Score | Decoupled Subsets |
|---|---|---|
| S1:{T7|T6, T5, T4, T3, T2, T1} | T6 = 0.013756 | SD1:{T2|T6, T5, T4, T3, T2} |
| S2:{T14|T13, T5, T4, T3, T12, T2, T1, T11, T10, T9, T8} | T4 = 0.8660 T5 = 0.0019 T13 = 0.0028 T3 = 0.1134 | SD2:{T14|T13, T3, T4, T5} |
| S3:{T21|T20, T19, T10, T9, T8, T18, T17, T16, T15, T11, T1, T12, T3, T2} | T1 = 0.0656 T9 = 0.0138 T10 = 0.1049 T11 = 0.8008 | SD3:{T21|T12, T11, T10, T1, T20, T9} |
| S4:{T28|T27, T26, T25, T24, T23, T22, T17, T16, T15, T18, T8, T9, T1, T10, T19} | T19 = 0.0018 T18 = 0.8008 T17 = 0.1049 T16 = 0.0138 T8 = 0.0656 | SD4:{T28|T19, T18, T17, T16, T27, T8} |
| S5:{T35|T34, T33, T24, T23, T22, T32, T31, T30, T29, T25, T15, T16, T17, T8, T26} | T15 = 0.065594 T23 = 0.013756 T24 = 0.104902 T25 = 0.800807 T26 = 0.001768 | SD5:{T35|T26, T25, T24, T23, T34, T15} |
| S6:{T42|T41, T40, T31, T30, T29, T39, T38, T37, T36, T32, T22, T23, T33, T24, T15} | T33 = 0.001768 T32 = 0.800808 T22 = 0.065594 T30 = 0.013756 T31 = 0.104902 | SD6:{T42|T33, T32, T22, T31, T41, T30} |
| S7:{T49|T48, T47, T38, T37, T36, T46, T45, T44, T43, T39, T46, T45, T44, T43, T39} | T40 = 0.001758 T39 = 0.796475 T38 = 0.104887 T37 = 0.017292 T29 = 0.065226 T36 = 0.00192 | SD7:{T49|T48, T40, T39, T47, T38, T37, T29, T46, T45, T44, T43, T36} |
| No. of Subsets | Lead | Turbines in Subset |
|---|---|---|
| N1 | T1 | {T1|T2, T3, T4, T5, T6, T7} |
| N2 | T8 | {T8|T9, T10, T11, T12, T13, T14} |
| N3 | T15 | {T15|T16, T17, T18, T19, T20, T21} |
| N4 | T22 | {T22|T23, T24, T25, T26, T27, T28} |
| N5 | T29 | {T29|T30, T31, T32, T33, T34, T35} |
| N6 | T36 | {T36|T37, T38, T39, T40, T41, T42} |
| N7 | T43 | {T43|T44, T45, T46, T47, T48, T49} |
| No. of Subsets | Lead | Turbines in Subset |
|---|---|---|
| N1 | T1 | {T1|T8, T15, T22, T29, T36, T43} |
| N2 | T2 | {T2|T9, T16, T23, T30, T37, T44} |
| N3 | T3 | {T3|T10, T17, T24, T31, T38, T45} |
| N4 | T4 | {T4|T11, T18, T25, T32, T39, T46} |
| N5 | T5 | {T5|T12, T19, T26, T33, T40, T47} |
| N6 | T6 | {T6|T13, T20, T27, T34, T41, T48} |
| N7 | T7 | {T7|T14, T21, T28, T35, T42, T49} |
References
- Mamouri, A.R.; Khoshnevis, A.B.; Lakzian, E. Experimental study of the effective parameters on the offshore wind turbine’s airfoil in pitching case. Ocean Eng. 2020, 198, 106955. [Google Scholar] [CrossRef]
- Song, D.; Li, Z.; Wang, L.; Jin, F.; Huang, C.; Xia, E.; Rizk-Allah, R.M.; Yang, J.; Su, M.; Joo, Y.H. Energy capture efficiency enhancement of wind turbines via stochastic model predictive yaw control based on intelligent scenarios generation. Appl. Energy 2022, 312, 118773. [Google Scholar] [CrossRef]
- Song, D.; Tu, Y.; Wang, L.; Jin, F.; Li, Z.; Huang, C.; Xia, E.; Rizk-Allah, R.M.; Yang, J.; Su, M.; et al. Coordinated optimization on energy capture and torque fluctuation of wind turbines via variable weight NMPC with fuzzy regulator. Appl. Energy 2022, 312, 118821. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; Hassanien, A.E.; Song, D. Chaos-opposition-enhanced slime mould algorithm for minimizing the cost of energy for the wind turbines on high-altitude sites. ISA Trans. 2021, 121, 191–205. [Google Scholar] [CrossRef]
- Chen, X.; Huang, L.; Liu, J.; Song, D.; Yang, S. Peak shaving benefit assessment considering the joint operation of nuclear and battery energy storage power stations: Hainan case study. Energy 2021, 239, 121897. [Google Scholar] [CrossRef]
- Shafiee, M.; Dinmohammadi, F. An FMEA-Based Risk Assessment Approach for Wind Turbine Systems: A Comparative Study of Onshore and Offshore. Energies 2014, 7, 619–642. [Google Scholar] [CrossRef] [Green Version]
- Song, D.; Zheng, S.; Yang, S.; Yang, J.; Dong, M.; Su, M.; Joo, Y.H. Annual Energy Production Estimation for Variable-speed Wind Turbine at High-altitude Site. J. Mod. Power Syst. Clean Energy 2021, 9, 684–687. [Google Scholar] [CrossRef]
- Perveen, R.; Kishor, N.; Mohanty, S.R. Off-shore wind farm development: Present status and challenges. Renew. Sustain. Energy Rev. 2014, 29, 780–792. [Google Scholar] [CrossRef]
- Liao, H.; Hu, W.; Wu, X.; Wang, N.; Liu, Z.; Huang, Q.; Chen, C.; Chen, Z. Active power dispatch optimization for offshore wind farms considering fatigue distribution. Renew. Energy 2020, 151, 1173–1185. [Google Scholar] [CrossRef]
- Ahmad, T.; Basit, A.; Anwar, J.; Coupiac, O.; Kazemtabrizi, B.; Matthews, P.C. Fast Processing Intelligent Wind Farm Controller for Production Maximisation. Energies 2019, 12, 544. [Google Scholar] [CrossRef] [Green Version]
- Knudsen, T.; Bak, T.; Svenstrup, M. Survey of wind farm control-power and fatigue optimization: Survey of wind farm control. Wind Energy 2015, 18, 1333–1351. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Guo, Q.; Sun, H.; Xue, Y. Distributed Model Predictive Control of a Wind Farm for Optimal Active Power ControlPart II: Implementation With Clustering-Based Piece-Wise Affine Wind Turbine Model. IEEE Trans. Sustain. Energy 2015, 6, 840–849. [Google Scholar] [CrossRef] [Green Version]
- Baros, S.; Ilic, M.D. Distributed Torque Control of Deloaded Wind DFIGs for Wind Farm Power Output Regulation. IEEE Trans. Power Syst. 2017, 32, 4590–4599. [Google Scholar] [CrossRef]
- Zhong, S.; Wang, X. Decentralized Model-Free Wind Farm Control via Discrete Adaptive Filtering Methods. IEEE Trans. Smart Grid 2018, 9, 2529–2540. [Google Scholar] [CrossRef]
- Shu, T.; Song, D.; Joo, Y.H. Decentralised optimisation for large offshore wind farms using a sparsified wake directed graph. Appl. Energy 2021, 306, 117986. [Google Scholar] [CrossRef]
- Ghosh, S.; Senroy, N. Balanced truncation based reduced order modeling of wind farm. Int. J. Electr. Power Energy Syst. 2013, 53, 649–655. [Google Scholar] [CrossRef]
- Pulgar-Painemal, H.A.; Sauer, P.W. Towards a wind farm reduced-order model. Electr. Power Syst. Res. 2011, 81, 1688–1695. [Google Scholar] [CrossRef]
- Huang, S.; Wu, Q.; Guo, Y.; Lin, Z. Bi-level decentralized active and reactive power control for large-scale wind farm cluster. Int. J. Electr. Power Energy Syst. 2019, 111, 201–215. [Google Scholar] [CrossRef]
- Chen, Y.; Joo, Y.H.; Song, D. Modified Beetle Annealing Search (BAS) Optimization Strategy for Maxing Wind Farm Power through an Adaptive Wake Digrah Clustering Approach. Energies 2021, 14, 7326. [Google Scholar] [CrossRef]
- Roque, P.; Chowdhury, S.; Huan, Z. Performance Enhancement of Proposed Namaacha Wind Farm by Minimising Losses Due to the Wake Effect: A Mozambican Case Study. Energies 2021, 14, 4291. [Google Scholar] [CrossRef]
- Yang, J.; Wang, L.; Song, D.; Huang, C.; Huang, L.; Wang, J. Incorporating environmental impacts into zero-point shifting diagnosis of wind turbines yaw angle. Energy 2021, 238, 121762. [Google Scholar] [CrossRef]
- Zhao, R.; Shen, W.; Knudsen, T.; Bak, T. Fatigue distribution optimization for offshore wind farms using intelligent agent control: Fatigue distribution optimization for offshore wind farms. Wind Energy 2012, 15, 927–944. [Google Scholar] [CrossRef] [Green Version]
- Kanev, S.; Bot, E.; Giles, J. Wind Farm Loads under Wake Redirection Control. Energies 2020, 13, 4088. [Google Scholar] [CrossRef]
- Zhang, B.; Soltani, M.; Hu, W.; Hou, P.; Chen, Z. A wind farm active power dispatch strategy for fatigue load reduction. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 5879–5884. [Google Scholar]
- Bossanyi, E. Combining induction control and wake steering for wind farm energy and fatigue loads optimisation. J. Phys. Conf. Ser. 2018, 1037, 032011. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Tang, J. On Advanced Control Methods toward Power Capture and Load Mitigation in Wind Turbines. Engineering 2017, 3, 494–503. [Google Scholar] [CrossRef]
- Kirchner-Bossi, N.; Porté-Agel, F. Wind Farm Area Shape Optimization Using Newly Developed Multi-Objective Evolutionary Algorithms. Energies 2021, 14, 4185. [Google Scholar] [CrossRef]
- Lv, J.; Sun, W.; Wang, H.; Zhang, F. Coordinated Approach Fusing RCMDE and Sparrow Search Algorithm-Based SVM for Fault Diagnosis of Rolling Bearings. Sensors 2021, 21, 5297. [Google Scholar] [CrossRef]
- Hasager, C.B.; Rasmussen, L.; Peña, A.; Jensen, L.E.; Réthoré, P.-E. Wind Farm Wake: The Horns Rev Photo Case. Energies 2013, 6, 696–716. [Google Scholar] [CrossRef]
- Chanfreut, P.; Maestre, J.M.; Camacho, E.F. A survey on clustering methods for distributed and networked control systems. Annu. Rev. Control 2021, 52, 75–90. [Google Scholar] [CrossRef]
- Sizhuang, L.; Youtong, F. Analysis of the Jensen’s model, the Frandsen’s model and their Gaussian variations. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 3213–3219. [Google Scholar]
- Gebraad, P.M.O.; Teeuwisse, F.W.; van Wingerden, J.W.; Fleming, P.A.; Ruben, S.D.; Marden, J.R.; Pao, L.Y. Wind plant power optimization through yaw control using a parametric model for wake effects—A CFD simulation study: Wind plant optimization by yaw control using a parametric wake model. Wind Energy 2016, 19, 95–114. [Google Scholar] [CrossRef]
- Ghaffari, M.; Parter, M. Near-Optimal Distributed DFS in Planar Graphs 16. In Proceedings of the 31st International Symposium on Distributed Computing, DISC 2017, Vienna, Austria, 16–20 October 2017. [Google Scholar] [CrossRef]
- Kleinberg, J.M. Authoritative sources in a hyperlinked environment. J. ACM 1999, 46, 604–632. [Google Scholar] [CrossRef]
- Park, J.; Kwon, S.; Law, K.H. Wind farm power maximization based on a cooperative static game approach. SPIE Proc. 2013, 8688, 204–218. [Google Scholar]
- Jiang, X.; Li, S. BAS: Beetle Antennae Search Algorithm for Optimization Problems. 2017. Available online: http://arxiv.org/abs/1710.10724 (accessed on 10 February 2022).
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, J. A Self-Adaptive Particle Swarm Optimization Algorithm with Individual Coefficients Adjustment. In Proceedings of the 2007 International Conference on Computational Intelligence and Security (CIS 2007), Harbin, China, 15–19 December 2007; pp. 133–136. [Google Scholar] [CrossRef]
- Jiang, X.; Li, S. Beetle antennae search without parameter tuning (BAS-WPT) for multi-objective optimization. Filomat 2020, 34, 5113–5119. [Google Scholar] [CrossRef]
- FLORIS. Data-Driven Control (TU Delft). Available online: https://github.com/TUDelft-DataDrivenControl/FLORISSE_M (accessed on 13 February 2022).
- Howland, M.F.; Dabiri, J.O. Wind Farm Modeling with Interpretable Physics-Informed Machine Learning. Energies 2019, 12, 2716. [Google Scholar] [CrossRef] [Green Version]




| T Algorithm (s) | ΔT of Decentralized Algorithm | |||
|---|---|---|---|---|
| Centralized | CMBSA | Proposed | Traditional | |
| 0° | 4129.41 | 7.69% | 7.22% | 7.39% |
| 15° | 3678.35 | 8.32% | 7.57% | 7.92% |
| 30° | 3195.16 | 9.06% | 8.41% | 8.61% |
| 45° | 3579.48 | 7.69% | 6.93% | 7.02% |
| 60° | 2889.57 | 9.06% | 8.02% | 8.59% |
| 75° | 2849.79 | 8.29% | 7.08% | 7.71% |
| 90° | 2708.91 | 7.67% | 7.11% | 7.37% |
| Average | 23,030.67 | 8.23% | 7.47% | 7.78% |
| F Baseline | ΔF of Algorithm (s) | ΔF of Decentralized Algorithm | ||
|---|---|---|---|---|
| Greedy | Centralized | Proposed | Traditional | |
| 0° | 10.6224 | 7.43% | 1.36% | 3.86% |
| 15° | 15.7124 | 6.42% | 1.16% | 4.97% |
| 30° | 16.0009 | 5.40% | 0.66% | 3.39% |
| 45° | 14.1718 | 5.94% | 1.40% | 4.10% |
| 60° | 14.7316 | 5.36% | 1.31% | 3.87% |
| 75° | 16.3864 | 5.54% | 1.30% | 3.89% |
| 90° | 10.0034 | 8.90% | 1.75% | 4.26% |
| Average | 97.6289 | 6.24% | 1.24% | 4.04% |
| P Baseline | ΔP of the Centralized (s) | ΔP of Decentralized Algorithm | ||
|---|---|---|---|---|
| Greedy | Algorithm | Proposed | Traditional | |
| 0° | 48.877 | 4.50% | 1.68% | 2.70% |
| 15° | 83.7846 | 1.58% | 0.01% | 0.88% |
| 30° | 84.1432 | 1.43% | 0.07% | 0.79% |
| 45° | 72.6399 | 1.86% | 0.41% | 1.42% |
| 60° | 76.4526 | 1.82% | 0.10% | 0.88% |
| 75° | 87.5558 | 1.03% | 0.19% | 0.79% |
| 90° | 45.3892 | 3.51% | 2.06% | 3.10% |
| Average | 71.263186 | 2.00% | 0.47% | 1.31% |
| P_Greedy (W) | P_Novel Algorithm (W) | ΔP | |
|---|---|---|---|
| 0.2 | 69,070,174.64 | 72,914,910.21 | 6% |
| 0.3 | 69,768,511.93 | 77,803,254.87 | 12% |
| 0.4 | 69,913,115.76 | 78,815,630.65 | 13% |
| 0.5 | 67,947,711 | 79,137,971.2 | 16% |
| 0.6 | 67,947,711 | 79,137,971.2 | 17% |
| 0.7 | 67,947,711 | 79,922,278.4 | 18% |
| 0.8 | 68,429,385.3 | 82,338,785.5 | 20% |
| 0.9 | 68,429,385.3 | 84,357,546.7 | 23% |
| F_Greedy (N) | F_Novel Algorithm (N) | ΔF | |
|---|---|---|---|
| 0.2 | 13,884,399.2 | 10,530,049.5 | −24% |
| 0.3 | 14,443,457.5 | 12,042,756.6 | −17% |
| 0.4 | 14,443,457.5 | 12,518,335.6 | −13% |
| 0.5 | 14,443,457.5 | 12,822,310.3 | −11% |
| 0.6 | 14,232,568.4 | 12,967,260.6 | −10% |
| 0.7 | 14,443,457.5 | 13,050,097.4 | −9% |
| 0.8 | 14,253,567.5 | 13,948,030.2 | −2% |
| 0.9 | 13,167,647.1 | 13,113,747.1 | 0% |
| ΔFT1 | ΔFT2 | ΔFT3 | ΔFT4 | ΔFT5 | ΔFT6 | ΔFT7 | ΔFS1 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0% | −14% | −9% | −12% | −11% | −8% | 23% | −11% |
| 0.1 | −32% | −15% | −9% | −13% | −12% | −8% | 22% | −12% |
| 0.2 | −32% | −15% | −10% | −13% | −12% | −9% | 22% | −13% |
| 0.3 | −33% | −16% | −11% | −14% | −13% | −10% | 21% | −13% |
| 0.4 | −34% | −17% | −12% | −15% | −14% | −11% | 20% | −14% |
| 0.5 | −35% | −18% | −13% | −16% | −15% | −12% | 20% | −15% |
| 0.6 | −36% | −19% | −14% | −17% | −16% | −12% | 19% | −16% |
| 0.7 | −37% | −20% | −15% | −18% | −17% | −13% | 18% | −17% |
| 0.8 | −38% | −21% | −16% | −19% | −18% | −15% | 17% | −18% |
| 0.9 | −39% | −22% | −17% | −20% | −19% | −16% | 16% | −19% |
| ΔFT1 | ΔFT2 | ΔFT3 | ΔFT4 | ΔFT5 | ΔFT6 | ΔFT7 | ΔFS1 | |
|---|---|---|---|---|---|---|---|---|
| 0.04 | −21% | −8% | −7% | −3% | −6% | −2% | 21% | −6% |
| 0.05 | −24% | −9% | −7% | −3% | −6% | −4% | 19% | −7% |
| 0.06 | −25% | −10% | −9% | −4% | −8% | −9% | 18% | −9% |
| 0.07 | −27% | −12% | −10% | −8% | −9% | −9% | 18% | −10% |
| 0.08 | −33% | −16% | −11% | −14% | −13% | −10% | 21% | −13% |
| 0.09 | −34% | −17% | −11% | −15% | −14% | −11% | 22% | −14% |
| 0.1 | −34% | −17% | −11% | −15% | −17% | −14% | 21% | −14% |
| 0.12 | −35% | −18% | −15% | −18% | −21% | −14% | 21% | −16% |
| 0.13 | −35% | −19% | −15% | −19% | −21% | −14% | 21% | −17% |
| 0.14 | −36% | −20% | −16% | −19% | −22% | −15% | 19% | −18% |
| 0.15 | −36% | −24% | −23% | −22% | −24% | −17% | 19% | −20% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Joo, Y.H.; Song, D. Multi-Objective Optimisation for Large-Scale Offshore Wind Farm Based on Decoupled Groups Operation. Energies 2022, 15, 2336. https://doi.org/10.3390/en15072336
Chen Y, Joo YH, Song D. Multi-Objective Optimisation for Large-Scale Offshore Wind Farm Based on Decoupled Groups Operation. Energies. 2022; 15(7):2336. https://doi.org/10.3390/en15072336
Chicago/Turabian StyleChen, Yanfang, Young Hoon Joo, and Dongran Song. 2022. "Multi-Objective Optimisation for Large-Scale Offshore Wind Farm Based on Decoupled Groups Operation" Energies 15, no. 7: 2336. https://doi.org/10.3390/en15072336
APA StyleChen, Y., Joo, Y. H., & Song, D. (2022). Multi-Objective Optimisation for Large-Scale Offshore Wind Farm Based on Decoupled Groups Operation. Energies, 15(7), 2336. https://doi.org/10.3390/en15072336