Abstract
Power distribution networks at the distribution level are becoming more complex in their behavior and more heavily stressed due to the growth of decentralized energy sources. Demand response (DR) programs can increase the level of flexibility on the demand side by discriminating the consumption patterns of end-users from their typical profiles in response to market signals. The exploitation of artificial intelligence (AI) methods in demand response applications has attracted increasing interest in recent years. Particle swarm optimization (PSO) is a computational intelligence (CI) method that belongs to the field of AI and is widely used for resource scheduling, mainly due to its relatively low complexity and computational requirements and its ability to identify near-optimal solutions in a reasonable timeframe. The aim of this work is to evaluate different PSO methods in the scheduling and control of different residential energy resources, such as smart appliances, electric vehicles (EVs), heating/cooling devices, and energy storage. This review contributes to a more holistic understanding of residential demand-side management when considering various methods, models, and applications. This work also aims to identify future research areas and possible solutions so that PSO can be widely deployed for scheduling and control of distributed energy resources in real-life DR applications.
1. Introduction
The rapidly increasing integration of decentralized energy resources, such as solar photovoltaic (PV) systems, energy storage, and electric vehicles (EVs), along with the use of power-electronic-interfaced loads, such as heat pumps, have increased the complexity of low-voltage (LV) grids. This new set of appliances and domestic loads can distort consumer habits and thus impact typical consumption patterns. Therefore, the balance between intermittent generation in almost real time and unpredictable demand, voltage control, frequency regulation, and power quality monitoring have become more and more crucial for maintaining power system stability and reliability. Traditionally, this burden would fall under the responsibility of power system operators, who in turn should reinforce the grid to tackle these challenges. However, in the smart grid era, power flows are bidirectional, and consumers can actively contribute towards a more reliable, efficient, and flexible power grid. One of the most promising solutions at the distribution level is demand-side management (DSM). Reducing peak electricity demand, shifting the load from peak to off-peak hours, and decreasing/increasing hourly electricity consumption are some of the benefits that DSM can provide [1].
DSM actions can be implemented through demand response (DR) programs. Currently, DR programs can be classified into either price-based or incentive-based [2,3,4]. In the former, customers can modify their electricity consumption based on the electricity tariff applied. A time-of-use (ToU) tariff is the most common price-based DR program, where a fixed set of electricity prices can vary within the hours of the day (e.g., day vs. night tariff) and the days of the week (e.g., weekdays vs. weekend). Other programs include critical peak pricing (higher tariffs applied during peak demand hours) and real-time pricing (tariffs change dynamically within the day, usually on an hourly basis). Incentive-based programs can be further split into voluntary, mandatory, and market-clearing programs [4]. The most popular voluntary scheme in residential and commercial applications is direct load control (DLC), where special incentives (bill credits, discounts, or rewards) are offered to end-users so that they shift their demand during the day. In that case, consumers voluntarily participate either directly, by turning on/off their loads, or indirectly, by collaborating with a third-party (e.g., aggregator) who is responsible for automatically and remotely controlling consumer assets to provide the requested services. Mandatory DR schemes are more applicable to large industrial consumers. During critical hours, when the power network is under stress, industrial consumers might be instructed by system operators to reduce their consumption (load curtailment). Market-clearing programs offer the opportunity to large consumers (industrial or aggregated) to bid and participate in the wholesale electricity market when flexibility products, such as demand reduction, are needed.
This work is focused on residential demand response applications that have attracted increasing interest in the literature in recent years. Using data gathered from smart meters installed at each customer’s point of connection, consumers can keep track of their appliances’ consumption and subsequently change their behavior directly or while collaborating with a third-party service provider. The main benefits of residential demand response applications are [5,6]:
- Economic benefits:
- ◦
- DR can lead to dispatching fewer hours of uneconomical generation units when the power system becomes tight, i.e., when generation cannot meet demand or when the security of supply margins decreases;
- ◦
- End-users profit by either consuming in low-tariff hours, selling power back to the grid with the use of local storage, or other incentives (e.g., bill discount);
- ◦
- DR can decrease distribution network stress and therefore reduce the need for network investments.
- Power system operation:
- ◦
- System reliability increases when providing frequency response, contingency reserves, and flexibility services;
- ◦
- Renewable energy source (RES) curtailment is reduced by modifying demand to match green power generation.
- Reduction in greenhouse gas emissions:
- ◦
- Utilization of distributed resources (EVs, PVs, and local storage) is higher;
- ◦
- Energy efficiency is higher, and thus, energy consumption decreases.
Recent research has shown that computational intelligence (CI) and machine learning (ML) methods can be computationally faster and more accurate than physical models (white-box methods) and statistical methods in numerous residential demand response applications [7,8]. For instance, when predicting energy consumption in buildings with white-box methods, the physical properties of the energy systems need to be modeled using a detailed set of input parameters [7]. These parameters are often hard to retrieve, the mathematical formulation behind the optimization can be quite complex, and the model outputs are highly case-dependent. In black-box models, there is little need for understanding the physical mechanisms of the energy systems. However, there is a requirement for a large set of historical data to train the models. Gray-box methods constitute a combination of the above, where a rather small historical dataset is used to train statistical models that are based on a high-level knowledge of the physical energy systems. Advantages over black-box methods are the need for less data for training the statistical models and the better explainability of the modeling process and results since they are interpreted in physical terms. However, these models are customized to specific applications, such as modeling individual components in residential HVAC systems [9], and cannot easily generalize over a diverse group of energy systems. Additionally, there is still a need to retrieve the physical parameters of the energy systems, and this can increase the complexity in specific applications.
For the above reasons, several AI algorithms, such as reinforcement learning (RL), evolutionary algorithms, swarm AI, and artificial neural networks (ANN), have been suggested for the control, optimization, and scheduling of distributed energy systems. Furthermore, methods that are model-free and highly adaptable, such as particle swarm optimization (PSO), have been recommended when addressing the need for the maximization of end-user comfort along with the minimization of energy consumption and costs [7,10]. Combining these criteria in residential demand response management systems could make DR more appealing to consumers and, thus, increase its applicability in households and commercial buildings.
To date, there have been a few review papers in the area of AI for residential demand response applications. The review in [11] examines the use of reinforcement learning (RL) for demand response applications in buildings covering a wide range of energy systems, such as distributed generation, storage, and HVAC. The applicability of RL to scheduling and control of residential loads was studied, taking into consideration user comfort and satisfaction. However, other methods, such as ANN, swarm AI, and evolutionary algorithms, have also been used in research to solve load scheduling and control from the consumer side, as shown in [10]. On the other hand, [12] provides a more holistic view of the use of deep reinforcement learning in power systems without specifically focusing on demand response applications. The review in [7] focuses on air-conditioning system control strategies, optimization techniques, and thermal modeling (white-, black-, and gray-box methods). Similarly, [8] provides the first survey of ML methods for electric water heater (EWH) optimization and scheduling. Another review that focuses on a specific energy system is [13], which reviews techniques for HVAC system control and optimization. An interesting review is [14], where the AI methods analyzed consider both thermal comfort and energy savings. However, the limitation of [14] is that it investigates only thermal energy systems for residential demand response. In [15], the classification of AI methods was based on the optimization objective (energy, comfort, safety, design, and maintenance). The aforementioned analysis revealed that AI methods in demand response applications are a growing research area with room for further investigation since every author categorizes them differently.
The main attributes of each relevant review paper are summarized in Table 1. Most of the review papers investigate various AI methods based on the optimization objective (energy cost, user comfort, flexibility, and energy consumption). A few reviews have thoroughly analyzed different DR-related energy sub-systems (EVs, energy storage, smart appliances, distributed generation (DG), and HVAC), and [10,11] are currently the most comprehensive works covering most of the selected categories. The review papers are categorized based on the way that their authors classified state-of-the-art AI research for energy applications. The following attribute categories were used to categorize the relevant review papers:

Table 1.
Categorization of the relevant review papers.
- AI group:Some review papers classify demand response applications and investigate only a single group of AI methods. Other papers analyze more than one group of AI methods and thus provide a more holistic review of the state-of-the-art from a computational intelligence (CI) perspective.
- Energy sub-systems:This set of attributes refers to the different energy sub-systems reviewed in the literature for scheduling and control in DR applications. Distributed generation, heating/cooling devices, EVs, local energy storage, and residential appliances are the different areas considered in this category.
- Energy management system (EMS) scheduling and control:Load modeling, scheduling, and control methods in response to signals for DR are reviewed. Additionally, the classification of methods based on demand-side strategies is considered.
- Optimization objectives:AI algorithms in demand response can be used for various optimization objectives, such as the minimization of energy consumption with or without considering user comfort, the minimization of energy cost, and the provision of load balancing.
The above literature review shows that there are no review papers focusing on the classification of PSO methods for the scheduling and control of various residential energy systems (EVs, energy storage, heating/cooling devices, distributed generation, and smart appliances). Therefore, the authors believe that a review in that area could bridge this research gap and be beneficial for future researchers without overlapping with existing work. The reason why PSO was selected over other heuristic methods is, on the one hand, that PSO is the most widely used heuristic algorithm for DR applications [10]. On the other hand, there is an abundance of research publications that can support a review work on PSO for residential demand response provision. A simple search with the use of the well-established research database of SCOPUS led to more than 80 research papers, without considering cross-references, when combining the following attributes:
- Text found in title, abstract, or keyword: “demand AND response” OR “demand AND side AND management”;
- Text found in title, abstract, or keyword: “particle AND swarm”;
- Text found in title, abstract, or keyword: “residential OR household OR home”;
- Text found in title, abstract, or keyword: “controller OR scheduling OR control”.
The contributions of this review paper can be summarized as follows:
- This is the only review paper that classifies PSO methods used specifically for scheduling and control based on the type of the residential energy sub-system (EVs, heating/cooling devices, local storage, residential appliances, and DG);
- It identifies different optimization objectives when using PSO methods, taking into consideration user convenience (in the form of appliances’ operational time delay) but also user thermal comfort (indoor ambient and hot water temperature);
- It discusses the limitations and challenges of PSO methods and models in residential demand response management systems and suggests potential future research areas for investigation.
The structure of this paper is organized as follows. In Section 2, an introduction to the PSO technique is provided. Basic concepts of PSO, such as motivation, structure, and mathematical formulation, as well as a brief description of the most commonly used PSO variants, are presented. Section 3 critically reviews the models used in the selected publications for residential resource scheduling and control using PSO. Research work is classified based on the optimization objective(s) and modeling constraints, as well as the different energy applications considered in the analysis. Section 4 presents the various PSO methods that were used in the reviewed research works. Section 5 focuses on evaluating the accuracy and complexity of the proposed model of each publication. Section 6 proposes future research directions and areas of investigation. Section 7 summarizes the main findings of this work and concludes the paper.
2. Basic Principles of PSO
Particle swarm optimization is a nature-inspired computational intelligence (CI) technique and was first introduced by Kennedy and Eberhard in 1995 [16]. PSO belongs to the wider group of swarm intelligence methods, which in turn is part of evolutionary computation, one of the three pillars of CI [17]. The inspiration behind the design of this algorithm was to mimic the way that a school of fish or a flock of birds navigate or forage. The PSO algorithm shares common principles with a search algorithm, since a large population of individuals, called particles, aims to find the optimal solution in a given multi-dimensional search space. Particles represent possible solutions, and their location is the value of the objective function that needs to be optimized. To identify the optimal result, particles continue searching through the hyperspace under the following guidelines [18,19,20]:
- Record the individual best location found so far with the help of a fitness function that evaluates how close each particle is to the optimal solution;
- Record their current direction and intensity of movement (velocity);
- Be informed about which location is the global best, defined as the optimal location among all particles.
Combining the above information, each particle moves towards a new location with an updated velocity, as shown in Equation (1) [19]:
where and are vectors describing the next and current positions of each particle, respectively, and is the velocity vector that shows the upcoming direction and intensity of movement of each particle.
At each iteration, these velocities are stochastically updated based on the historical optimal positions of individual particles but also based on the historical global best position among all particles, as shown in Equation (2) [19]:
where and are two positive numbers (acceleration constants), and are weight factors in the range of [0, 1], and and are the individual and global best particle positions, respectively. When the weight factor w (inertia weight) equals one, we refer to the original PSO algorithm; otherwise, we refer to the canonical PSO algorithm [20]. The above iterative process continues until either we find a particle location that is close enough to the desired outcome or the threshold of allowed iterations is exceeded. The aforementioned process is illustrated in Figure 1 [20].
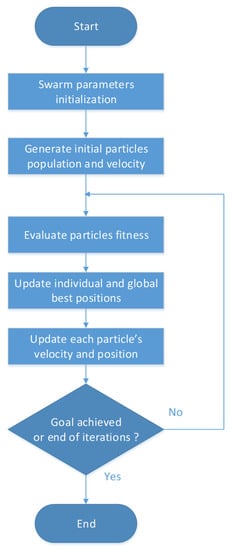
Figure 1.
Simplified flowchart of PSO algorithm.
When analyzing Equation (2), it can be observed that there are three different components being combined to update the distance that each particle moves at each iteration:
- The inertia component w Vi(t): this term tends to maintain the current movement direction (velocity) of each particle;
- The cognitive/individual component : this component describes the distance between each particle’s current position and the individual best location found;
- The social component : this component calculates the distance between the particle’s current position and the best position found by the entire swarm.
The impact of cognitive and social components on velocity in Equation (2) can be modified by tuning factors and . The same applies to the inertia weight w, which impacts the balance between exploration and exploitation in PSO algorithms. Usually, this factor decreases linearly across iterations. It starts from a high value (e.g., 0.9) in order to let the swarm move freely and quickly when exploring the search space for the best solution. As iterations progress, the exploration level of the swarm should decrease, and focus should be placed on the exploitation of the neighborhoods around individual and global optima. Except for the above parameters, which are initialized before running the PSO algorithm, a set of limits need to be selected to ensure convergence of the swarm. The maximum velocity (in absolute terms) needs to be defined, and the maximum aggregated value of the acceleration constants is suggested to be below four [19].
PSO is the most widely used method among heuristics for DR applications [10]. The main advantages of PSO compared to other optimization methods can be summarized as follows [10,19,20]:
- Simple and easy to use;
- Fast convergence and robustness, even in complex and highly constrained multi-dimensional search spaces;
- High applicability since it can be used in various optimization problems;
- High adjustability since it can be easily hybridized and modified to fit the purpose of each problem and improve its performance.
Some of the potential drawbacks that can be seen when using PSO are the following [10,19,20]:
- Risk of suboptimal solutions (local optima) due to either the problem formulation characteristics or a lack of diversity in particle movement that leads to premature convergence;
- No guarantee that PSO will reach the global optimum solution since there is a risk of premature convergence to local optima;
- Lack of interpretability/explainability given that the algorithm is not based on a strong mathematical theoretical basis (lack of mathematical proof of convergence).
It is important to highlight that the poor performance of PSO might be related to the above algorithmic drawbacks but can also be related to problem formulation, modeling inputs, and system constraints. Therefore, better tuning of the method’s initialization and modeling parameters cannot always lead to more optimal results.
3. Models for Residential Load Scheduling and Control Using PSO
Scheduling and control of decentralized energy resources, in practice, is a stochastic mathematical problem, given the intermittency of renewable generation, the uncertainty of users’ consumption patterns, and continuously changing electricity prices, which, in most of the reviewed works, is a key driver. Additionally, the large number and diversity of household appliances and the consideration of user thermal comfort and convenience increase the complexity of optimization, where classical computational techniques such as linear programming (LP), integer linear programming (ILP), and mixed-integer linear programming (MILP) cannot provide feasible solutions within a reasonable timeframe [21]. On the contrary, heuristic optimization techniques, such as PSO, genetic algorithms (GA), ant colony optimization (ACO), and wind-driven optimization (WDO), can support more complex optimization problems with the identification of near-optimal solutions.
In this work, PSO-based resource scheduling models are reviewed given the research “gap” identified in Section 1 but also due to the fact that it presents the following advantages over similar nature-inspired optimization techniques [10,19,20,21,22]:
- It requires fewer parameters for tuning and adjustment;
- Easier implementation and less computational effort are usually needed to reach a near-optimal solution compared to other heuristic algorithms;
- The histories of all particles contribute to the search, while in other methods (e.g., GA), the algorithm’s memory capability is lower due to the replacement of the old population with a new, more efficient one.
In the reviewed research works [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84], different models were designed. They can be classified based on the optimization objectives, the system constraints applied, or the energy system applications. In the latter, the type of energy resources (EVs, distributed generation, energy storage, or appliance type), the number of users (single or multiple), and the type of control (local, decentralized, or centralized) are included.
3.1. Optimization Objectives
One of the main considerations of scheduling and control for demand-side management is the formulation of the objective function that needs to be optimized. Additionally, it is very important to define the system constraints and operational limits of key variables that will collectively shape the boundaries of the optimization search space. Optimization objectives can be categorized into the following three groups based on the number of objectives that are investigated.
- 1.
- Single objective:
In the majority of the reviewed works, the main objective was to optimally schedule different energy resources in order to minimize electricity costs, with or without taking into consideration user comfort, convenience, and peak-to-average (PAR) ratio. Depending on the complexity of the problem, the cost minimization function consists of components such as electricity imports (consumption) and exports back to the main grid [24,30,33,35,42,43,59,66,72,81]. In the case of a microgrid (MG), total cost minimization, investment, operation, and maintenance costs are considered. For instance, in [43,66], the optimization goal was to optimally size microgrid components (DG and ES) by shifting the load to the hours of maximum renewable penetration and therefore minimize total system costs. Some of the reviewed works also present different electricity tariffs based on the customer type (residential, commercial, or industrial).
- 2.
- Single objective with aggregated variables, weights, or penalties:
In this case, more than one objective is combined and aggregated as a single function. In some works, weights are assigned to each optimization parameter, leading to a weighted single-objective optimization problem. In most cases, minimization of electricity costs, maximization of user convenience (appliance operational delay), and/or thermal comfort are considered, as in [22,26,41,44,45,46,51,61,67,68]. In a few research publications, such as in [46,68,83], three different objectives are weighted to form a single objective function. In other research works, the authors do not specify a weight factor, as in [38,62,64,65,76], but assign penalties to non-economic constraints in order to combine them into an aggregated single-objective function.
- 3.
- Multiple objectives:
In [27,29,57,60,63,78], where objectives are conflicting, such as cost minimization and user convenience maximization, the Pareto front, meaning a set of non-dominated solutions, is calculated through the evaluation of different fitness functions that correspond to each objective. The Pareto front consists of compromise solutions. Therefore, a second step, in that case, would be the selection of the best solution from the Pareto set. Additionally, in this review work, bi-level optimization problems are characterized as multi-objective ones. In [48,49,53,69], there is a single “upper level” objective and a single “inner level” objective that need to be optimized hierarchically. The single upper-level objective is initially optimized, and then the output of the upper level is used as an input in the inner-level optimization.
3.2. Constraints
3.2.1. System Constraints
Part of the problem formulation in every work reviewed was to define the system constraints that should be considered in the optimization. The number of constraints differs depending on the system complexity and the type of energy resources considered. The main equality constraint, which can be identified in all works reviewed, is to maintain the energy balance between power supply and demand. The time period and the system boundaries (household, microgrid, or utility level) of such constraints depend on the problem formulation. The constraints that are identified in the reviewed works are the following:
- Power grid thresholds (Egrid):The minimum and/or maximum contracted power of end-users with utility at the connection point. This increases the complexity of the optimization and potentially decreases the amount of energy savings that can be achieved since there is less flexibility to shift more loads to off-peak hours due to constraint violation.
- Storage-related constraints (Estorage):Charging and discharging rates as well as the capacity of storage units are introduced as inequality constraints in works with energy storage, either in the form of batteries or in electric vehicles.
- RES generation capacity (ERES):The maximum generation capacity of renewable sources is constrained, usually as a share of total household demand (e.g., 30% of net demand is met by RES).
- User convenience:Another important consideration is user convenience in the sense of minimizing the operational delay (waiting time) of different household appliances or prioritizing the operation of appliances over others based on consumer preferences. In some works, such as [38], user convenience is introduced as the minimum amount of appliance switching needed during a DR event.
- Thermal comfort:In many works, not only appliance waiting time but also indoor temperature and water heater temperature is considered when using thermostatically controlled loads. To operate appliances within the preferred temperature range, smart sockets and temperature sensors can be installed, as in [23].
- Voltage level:In [38,40,66,76], bus or node voltage constraints are introduced when optimizing the operation of microgrids connected to the main power network.
3.2.2. Electricity Costs and User Convenience/Comfort
From the taxonomy of research work, based on optimization objectives and system constraints, it is clear that user convenience and thermal comfort are key considerations when trying to schedule and control residential resources. Operating according to user preferences will inevitably lead to higher electricity costs and vice versa. However, significant energy savings can still be obtained. In [23], using binary PSO (BPSO), 20–25% energy savings were achieved without jeopardizing user convenience. DR services were provided only in a specific timeframe (4–11 p.m.) in a geographical location with a lack of seasonality, so it would be worth testing the system under more challenging conditions. In [22,26,41,44,45,46,51,61,67,68], user convenience and energy savings were combined in the objective function, leading to a weighted single-objective optimization problem. User convenience was modeled with the use of allowed time periods when appliance operation should be completed. More specifically, in [22,26], GA and BPSO were compared, among others, where GA outperformed BPSO in terms of both electricity costs and energy consumption. In [28,32], the tradeoff between user convenience (appliance waiting time) and energy cost was investigated. PSO has the tendency to heavily shift loads from peak to off-peak hours with lower electricity tariffs in order to decrease electricity costs. However, a greater degree of user convenience is sacrificed in that case. Therefore, it can be concluded that the higher the electricity cost, the less the user discomfort, and vice versa in DR residential applications. While in [28], the single objective was to decrease consumer electricity costs, in [32], a single-objective function was formulated with the aim of minimizing energy costs and average-to-peak ratio. The feasible region of solutions was found, and boundaries were set for the objective function. In [30,33,34,55,59,79,80,81], reducing electricity bills while considering user convenience and thermal comfort was analyzed. The authors concluded that overall costs can be decreased without sacrificing user comfort by setting the indoor temperature at a higher level during low-tariff hours.
3.3. Applications
Each DSM model is characterized by the energy resources that can contribute to demand-side management, the number of users (single or multiple), and the control level (local, microgrid, or utility/aggregator). This review work focuses on residential users. The taxonomy of research works based on the application is illustrated in Figure 2.
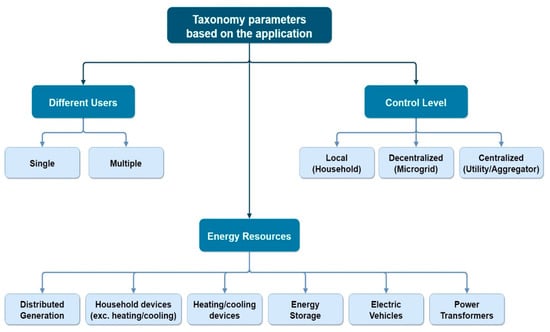
Figure 2.
Taxonomy parameters based on the application.
3.3.1. Energy Systems
Scheduling and control of household appliances is the core focus in the majority of research works. Depending on the flexibility that these appliances can offer for demand-side management, they can be categorized as fixed, shiftable, elastic or interruptible, and power-adjustable. Fixed appliances are characterized by fixed power consumption and a length of operation that cannot be modified. Examples include lights, fans, clothing irons, microwave ovens, toasters, TVs, etc. The operation of shiftable appliances, such as washing machines, dishwashers, and clothes dryers, can be shifted in time but cannot be interrupted while their power consumption is fixed and inelastic. Elastic or interruptible household appliances, such as EVs, can not only be shifted in time but also be interrupted while in operation. This group of appliances can offer flexibility services by shifting their operation in periods of lower electricity tariffs. Last but not least, power-adjustable appliances are interruptible appliances with adjustable power consumption. The majority of these are thermostatically controlled loads (e.g., electric water heaters, ACs, or heat pumps). In research, the above categorization might differ based on the authors’ problem formulation. For instance, EVs can be treated as a shiftable but non-interruptible load in some works, while lights can be considered controllable when using a smart plug. In any case, when using interruptible and power-adjustable appliances for flexibility provision, it is important to ensure that user convenience and thermal comfort are not sacrificed when trying to schedule and control them for demand-side management.
In addition to residential appliances, decentralized energy resources such as EVs, distributed generation (mostly RES), and energy storage can contribute to domestic electricity bill reduction, load balance, and peak shaving. Additionally, a better tradeoff between user comfort and electricity cost reduction can be achieved, given that each household can utilize local or decentralized (microgrid) energy resources instead of consuming from the power grid. For instance, in [28], interruptible loads, including those of an EV and an electric water heater, contributed to achieving a better compromise between user convenience and energy costs. Although EVs are commonly treated as a highly flexible load, their battery-related constraints, such as the charging and discharging rate and maximum energy storage, can set limitations on its storage operation for demand-side management. It can also be observed that renewable power generation is often coupled with local energy storage, which aims at complementing the intermittency of renewable energy resources.
3.3.2. DR Programs—Electricity Tariffs
In addition to the objective function formulation and the constraints introduced for load scheduling, an important parameter is the type of DR program/mechanism that consumers are enrolled in. Time-of-use (ToU) retail tariffs have been extensively used in research, with prices usually ranging among high-, medium-, and low-price periods during the day. In some of the works where ToU is selected, it is highlighted that load is heavily shifted to off-peak hours. Therefore, the load tends to become unbalanced, with spikes occurring after these hours, and the peak-to-average ratio (PAR) remains high. A similar phenomenon can also be spotted when using day-ahead, real-time pricing (RTP) tariffs, which typically fluctuate on an hourly basis. For that reason, tariffs with inclined block rates (IBRs) were used in [22,32,39,44,48,51,84]. In this pricing scheme, when the load surpasses a certain level, a monetary penalty is added to the end-user’s electricity bill. In this way, load shifting from peak to off-peak hours is rather limited, PAR decreases, and load spikes are avoided.
3.4. Taxonomies
In Table 2, the reviewed works are classified based on the optimization objectives for residential load scheduling and control, together with modeling constraints. Table 3 presents the taxonomy of research work based on model applications, including DR programs.

Table 2.
Taxonomy of the reviewed works based on the optimization objectives.

Table 3.
Taxonomy of the reviewed works based on the application.
4. PSO Methods
Controlling a large number of household appliances with unpredictable usage patterns and operational constraints constitutes a non-convex optimization problem. PSO is selected over other methods due to its low computational needs, near-optimal solution identification, the small number of initialization parameters, and the lack of model training prior to implementation. Therefore, this review paper focuses on the computational method of PSO used for scheduling residential resources to provide demand-side management.
In the reviewed research works, not only original/canonical PSO algorithms (presented in Section 2 but also other PSO variants were utilized to attempt to overcome the disadvantages of premature convergence and local optima in both continuous and binary optimization problems. Additionally, hybrid algorithmic methods, where PSO is combined with other computational intelligence methods, were investigated. Other heuristic and metaheuristic methods such as GA, ACO, WDO, bacterial foraging optimization (BFO), and binary backtracking search algorithm (BBSA) were compared in research with PSO-based methods, but analyzing these methods is outside the scope of this review paper. The PSO variants found in the research are the following:
- Canonical/traditional PSO [24,25,35,36,40,42,43,44,48,50,51,64,66,67,70,72,77,82,83,84];
- Multi-objective PSO [29,57,60,78];
- Bi-level PSO (BLPSO) [49,53,69];
- Binary PSO [21,22,23,25,26,27,28,31,32,34,39,41,45,52,54,56,63,65,73,74,76,81];
- Gradient-based PSO [30,33,54,63];
- Hybrid methods:
- ◦
- BPSO–GA [21,45,48,56,74];
- ◦
- PSO–ANN [37];
- ◦
- BPSO–integer linear programming [55];
- ◦
- PSO–evolutionary algorithm [58];
- ◦
- PSO–sequential quadratic programming optimizer (SQP) [59];
- ◦
- PSO–local vortex search [62];
- ◦
- PSO–bacterial foraging (BF) [63];
- ◦
- PSO–fuzzy logic [71];
- ◦
- PSO–sinusoidal and cosine acceleration (SCAC) [75];
- ◦
- BSPO–chaos optimization [76];
- ◦
- PSO–harmony search (HS) [77];
- ◦
- BPSO–gradient-based NLP solver [79];
- ◦
- BPSO–fuzzy Mamdani and fuzzy Sugeno [80].
- Modified PSO [38,61,67,68];
- Quadratic BPSO [41];
- Cooperative PSO:
- ◦
- Stochastic attraction–repulsion of diversity (SARD) [46];
- ◦
- Stochastic repulsion (R) [47].
Binary particle swarm optimization (BPSO) is the most popular PSO variant for energy scheduling optimization problems. BPSO is a PSO variant that is applicable to binary problem spaces, where particle positions can take the discrete values of “0” and “1” instead of continuous values as in the canonical PSO algorithm. Particle velocities are still expressed as continuous values, as shown in Equation (2). Using the sigmoid function, the velocity of each particle is transformed into the probability that this particle’s position will change (“1” or “0”). Equations (3) and (4) describe the way that the position of each particle i in the population is updated:
In the problem of appliance scheduling, BPSO is preferable over canonical PSO since the method aims at determining whether each appliance will be operational or not (ON/OFF) in a given timeframe. Each particle consists of a binary set of values, where each bit represents a household appliance. Therefore, when using BPSO, the possibility of turning the load ON/OFF in a period t can be obtained. From the aforementioned transfer function, it can be seen that in zero velocity of a decision vector (bit), the probability is 50% that the bit will be 0 or 1. When velocities are positive, then the probability that the value will be 1 is higher, while the opposite applies to negative velocities.
Canonical/traditional PSO has been used extensively in RES management problems with the use of local energy storage (batteries). In these problems, the challenge is to optimally schedule the charging and discharging periods of energy storage in order to meet demand with the lowest cost possible.
Gradient-based PSO (GPSO) is often proposed for solving mixed discrete–continuous scheduling problems. GPSO shows improved convergence speed when compared to the canonical PSO algorithm, especially when there are many inequality constraints in the problem. Instead of using a penalty function when constraints are violated, GPSO uses a gradient-based repair method to adjust particle positions. Therefore, faster convergence from infeasible to feasible solutions and lower computational cost can be achieved.
Hybrid and modified PSO methods have been used in research to solve the problems of premature convergence and near-optimal solution identification since PSO is prone to be “trapped” in local optima. For instance, CPSO-SARD and CPSO-R methods were used in [46,47] to increase particles’ exploration capability and thus decrease the chances of premature convergence. In both methods, particles move depending on the phase: in the attraction phase, particles move as in the canonical PSO, but in the repulsion phase, they move in the opposite direction from their previous global best solution, avoiding premature convergence to local optima. Another implementation that aims at increasing the exploration capability of particles was used in [76]. CBPSO increases the exploration of particles at an early stage of the PSO algorithm by applying chaotic motion to particles that are close to the global best. Modified PSO algorithms, such as the improved hybrid discrete PSO developed in [61], introduce methods to identify the particles that fall into local optima based on the frequency of their updated best positions. Hybrid methods have also been developed to combine the advantages of different heuristic algorithms and therefore increase the overall efficiency. For instance, in [21], the authors combined BPSO, which is effective in electricity bill reduction, with GA, which performs better in PAR minimization. It is shown in [63] that BFOA performs better in electricity cost and carbon footprint minimization due to its high exploration capability. On the contrary, BPSO performs better in terms of PAR minimization and user convenience maximization.
5. Evaluation
Various models have been introduced in research for residential load scheduling and control. Different PSO and other heuristic methods have been suggested based on the problem formulation and the level of complexity in the optimization. The accuracy of PSO in load scheduling problems can vary, mostly depending on the design variables, the optimization objectives, and the input data.
5.1. Problem Design
Several features need to be considered when designing the system model and formulating the scheduling problem for residential DR provision. These features can be classified into the following categories based on the reviewed works [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84]:
- System architecture—HEMS design. As the first step, it is important to define the energy system resources and the way that they are connected with other users and the main power grid. It is also useful to describe the flow of data information and the point of control where scheduling will take place: local control, decentralized control of grid-connected or standalone microgrids, or centralized control on a utility/aggregator level.
- Appliance classification and user categorization. Residential household appliances can be characterized as fixed, flexible, interruptible, and power-adjustable. In a microgrid, users can be passive (unidirectional power flow without self-consumption), semi-active (unidirectional power flow with self-consumption and storage), or active (bidirectional power flow with self-consumption and storage).
- Energy consumption. Equality constraints that ensure load balance at each time interval are introduced. In some works, a maximum and/or minimum grid consumption constraint is defined so that load shift to off-peak hours will not lead to demand spikes. Additionally, grid exchange capabilities (selling back to the grid) might increase the problem complexity even further but provide a more realistic modeling approach.
- Local RES generation and energy storage. In some works, local RES generation with coupled energy storage is considered. A set of constraints (charge/discharge rates and maximum energy stored) is essential to properly model local energy storage. Depending on the problem design, either RES production follows a predefined profile or a RES forecasting model is utilized.
- DR program and electricity tariffs. The DR program that each user follows is a crucial feature of the problem design, since in the majority of problems, cost minimization is the main objective. In research, inclined block rates (IBRs) can ensure a smoother load shift from peak to off-peak hours.
- Other considerations. PAR can be introduced as a minimization objective or can be investigated when modeling results are obtained. In other works, a set of constraints is introduced to ensure that model results respect users’ thermal comfort and convenience preferences (appliance operational delay).
- Objectives. The most common objective, as shown in Section 3, is electricity cost minimization. User convenience, thermal comfort, PAR, and emission reduction can also be considered as optimization objectives.
5.2. Complexity
In this review work, the complexity of the proposed models is evaluated based only on the DR scheduling task and does not take into account other modeling blocks, such as price and load forecasting, that authors might have introduced in their works. The time of convergence and the accuracy of modeling results are directly linked to the complexity of the optimization process. A heavily constrained optimization problem, as in [22,32,62,81], with multiple households, local energy storage, RES penetration, and consideration of end-user preferences, increases the modeling complexity and the risk of infeasibilities or slow convergence. High complexity can also be seen in multi-objective optimization problems, as in [29,49,57,78]. Some objectives, such as electricity cost minimization and user comfort maximization, might conflict, and in that case, the Pareto front of acceptable solutions is calculated. Moderate complexity can be seen when energy system participants are interconnected. For instance, in [75], a large number of customers and households are controlled in a microgrid system. Power grid exchange is allowed, and two-stage optimization of consumption and production in an MG is investigated. In [24], grid exchange capability is modeled with the use of three different electricity tariffs, namely, an RTP for the power purchased from the grid, a resell electricity price when excess solar energy is sold to the grid, and a penalty price that represents the avoidable cost when energy storage meets demand. However, in that case, household appliances are not optimally scheduled, since the load is treated in an aggregated way; therefore, the total model complexity decreases. It is clear, though, that the higher the number of parameters involved in the analysis, the more computationally complex the optimization becomes.
Table 2 and Table 3 can help the reader identify the problems with the highest complexity based on the number of parameters considered, the system architecture, and the optimization objectives and constraints.
- High complexity. The problems in [22,28,29,32,46,49,51,57,61,62,66,68,74,78,79,80,81] can be characterized as highly complex, since they have a complex energy system architecture (high number of users); they consider many energy resources, including interruptible and power-adjustable household appliances; they are heavily constrained; and in most cases, the optimization functions involve multiple objectives.
- Moderate complexity. The problems in [21,24,26,27,30,31,33,34,37,38,39,40,41,42,44,45,48,53,54,55,56,59,60,63,64,69,72,75,76,77,82,83,84] show moderate complexity either due to a single objective combined with a large number of constraints and energy resources or due to a combination of more objectives with fewer resources and constraints applied.
- Lower complexity. The problems in [23,25,35,36,43,47,50,52,58,65,67,70,71,73] present lower complexity compared to the research works mentioned above. The smaller number of system constraints, the simpler energy system architecture (small number of users), the lack of power-adjustable and/or interruptible appliances, and the single-objective optimization are the main reasons for this categorization.
5.3. Accuracy
The accuracy of results when using PSO for residential resource scheduling depends on the system design parameters as well as on the actual data used in the model simulations. In many research works, authors tend to compare the simulation results of PSO with other heuristic methods and nature-inspired algorithms, such as GA, WDO, ACO, and others. PSO, or its most common variant, BPSO, leads to electricity bill savings, typically around 20–30%, depending on the electricity tariffs applied. However, even higher savings have been found when RES and energy storage are introduced. When compared to other heuristic methods, such as GA, PSO can either outperform or underperform, depending on the design variables. For instance, in [22], GA shows better PAR, higher cost reduction, and faster convergence when compared to BPSO. On the contrary, in [21], the execution of BPSO is faster than in [22] and results in lower electricity costs but higher PAR. Given that energy resources (DG and storage) are introduced in all of the above problems, the difference lies in the electricity tariffs and in the number of households and resources controlled. The use of BPSO with ToU tariffs leads to a major shift of loads to off-peak hours, where tariffs are lower. Therefore, PAR remains high when compared to an implementation with the use of GA. However, electricity cost reduction is higher in the case of BPSO. When using RTP combined with IBR tariffs, as in [32,39], BPSO can outperform GA in both PAR and electricity costs. In terms of the number of households, [21,26,32] show that BPSO can be computationally faster and perform better for single household modeling. The previous analysis shows that residential scheduling for DR provision is a complex and challenging problem since model performance is affected by numerous parameters and features. Therefore, selecting PSO over other heuristic methods or vice versa cannot be treated as a predefined option. However, PSO can be considered a highly accurate and robust method for such problems, as shown in [35], where results were found to be marginally different when compared to the commercial CPLEX MILP solver from IBM.
6. Future Research
During the last decade, significant work has been carried out in the field of residential scheduling and control algorithms for demand response provision [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84]. However, there are still many areas that need to be investigated so that PSO can be established in real-life DSM applications and end-users can become more engaged with DR programs.
6.1. Advanced and Explainable Methods
From the reviewed research works, it can be noticed that most recent research focuses on the improvement of existing PSO algorithms or the design of new variants to avoid the problem of premature convergence in local optima and increase convergence speed, such as in [85,86], where the hybrid PSO methods of comprehensive learning (CLPSO) PSO, unified PSO (UPSO), and self-regulation PSO (SRPSO) were used to accelerate the exploration of the particles while maintaining strong exploitation capabilities. However, the fact that PSO-related methods generate near-optimal schedules cannot be acceptable on its own in competitive electricity markets, where transparency in dispatching is also required. This creates the need to develop more advanced hybrid methods that can fully justify the dispatching of DR capacities over conventional generation.
In addition, the high autonomy of AI in decision making and EU GDPR’s Article 12, which allows end-users to enquire about AI decisions, make responsible and explainable algorithms not only a research challenge but also a practical necessity. Therefore, increasing the explainability and transparency of scheduling methods can increase consumer understanding and engagement, contributing significantly to the establishment of such methods in real-life applications.
6.2. Consideration of Uncertainties
Models for scheduling and control of residential resources consider various uncertainties in inputs that are being used for the estimation of available flexibility, such as must-run load, electricity price signals, and renewable power generation. From a utility point of view, the difference between realized and scheduled load needs to be defined in order to better estimate the level of DR needed. From the end-user point of view, DR actions are planned based on forecasted electricity tariffs and estimated RES generation. Monte Carlo simulation, chance-constraint, or stochastic optimization can be used to solve such uncertainties. However, in most of the reviewed works, more practical implementations were considered, such as near real-time rescheduling in case of an error in forecasting [33] or the manual addition of a contingency on the expected RES output (e.g., −10%) [21]. In order to assess the value of uncertainty in the optimization results, sensitivity analysis is needed so that end-users or utilities can better estimate the potential range of their savings.
6.3. End-Users as Price Makers
In most of the reviewed works, end-users act as price takers receiving electricity tariffs (ToU, RTP, and CPP) provided by the grid operator in order to optimally schedule their appliances and resources. Only in [38] end-users were modeled as price makers and were provided with the opportunity to tender their participation in a DR event. Assuming that DR is expected to play a role in the emerging energy flexibility markets, it is worth researching how market players can profit by tendering their own distributed energy resources.
6.4. Fully Utilize EV Potential
In the majority of the reviewed works where EVs were considered, they were treated either as interruptible loads or as a source of local energy storage. Only in [66] did the authors model EVs both as a load and as a generator that can sell its energy back to the grid (V2G), unlocking the full potential of EVs. In a smart grid, where peer-to-peer trading will be allowed among prosumers, EVs are a flexible asset that can lead to high energy savings; therefore, it is suggested that V2G be more comprehensively considered in future research.
6.5. Energy Model Scalability
In the most recent publications, the efficiency and applicability of PSO in scheduling were tested in energy models with a large number of households and/or resources, as in [84], where 1000 customers were divided into four clusters based on their load profiles, or in [66], where 2000 vehicles were modeled. The next step would be to increase the penetration of other resources, such as RES, DG, and ES, in order to test the performance of PSO in larger-scale energy models.
6.6. Comprehensive Metrics for DSM Evaluation
The development of comprehensive metrics and indexes that evaluate not only cost savings but also environmental benefits and user satisfaction is a key factor that can contribute towards the wide deployment of DSM schemes in energy markets. Users’ thermal comfort and convenience are extensively addressed in research. However, considering other social aspects, such as user experience during a DR event, social comfort, and method explainability, can improve user satisfaction and consequently increase their engagement and participation in DSM programs.
In addition, it is important to consider the cost of equipment degradation when performing DR actions. As seen in [42], if battery cycling cost is ignored in the optimization model, batteries will undergo unconstrained charge/discharge. This can result in suboptimal operating points for the aggregator. Therefore, the storage cycling cost can be introduced as a metric at any cost-saving estimate when energy storage or EVs are being used to provide DR services.
7. Conclusions
This review paper provides a comprehensive description of models, energy applications, and PSO methods used in residential resource scheduling and control for DR provision. The currently available research is evaluated and classified based on the above criteria, and future research directions in this field are suggested. Research has shown that PSO is a relatively simple computational method that can accurately schedule residential resources for DR provision, even in complex and constrained energy system models, within a reasonable timeframe. In the majority of research works, electricity bill reduction is the main optimization objective, accompanied by user-related considerations (convenience and thermal comfort). Scheduling and control of household appliances under an RTP scheme has been the most preferable energy system model, especially when supported by IBR to avoid high PAR. Although canonical/traditional PSO and BPSO are the most deployed PSO methods, hybrid PSO algorithms have been extensively developed in recent years to suggest solutions to PSO’s main drawback of premature convergence in local optima. Future research areas include the development of more advanced and explainable algorithmic methods, the consideration of load and price forecasting uncertainties in the problem formulation, a more dynamic system approach with end-users as price makers, V2G consideration, and the modeling of more resources, as well as the definition of comprehensive metrics to evaluate the performance of DR scheduling methods.
Author Contributions
C.M.-A.: Conceptualization, methodology, investigation, data curation, formal analysis, and writing—original draft preparation. I.L.: Supervision, funding acquisition, and review. P.S.G.: Methodology, supervision, and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented in this paper has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Action GECKO (Grant agreement No 955422).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC | Air conditioning |
| ACO | Ant colony optimization |
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| BBSA | Binary backtracking search algorithm |
| BFOA | Bacterial foraging optimization algorithm |
| BPSO | Binary particle swarm optimization |
| CI | Computational intelligence |
| CBPSO | Chaotic binary particle swarm optimization |
| CLPSO | Comprehensive learning particle swarm optimization |
| CPSO-R | Cooperative particle swarm optimization with stochastic repulsion |
| CPSO-SARD | Cooperative particle swarm optimization with stochastic attraction–repulsion of diversity |
| DG | Distributed generation |
| DLC | Direct load control |
| DNO | Distribution network operator |
| DR | Demand response |
| DSM | Demand-side management |
| EV | Electric vehicle |
| ES | Energy storage |
| GA | Genetic algorithm |
| HVAC | Heating, ventilation, and air conditioning |
| IBR | Inclined block rates |
| ILP | Integer linear programming |
| LP | Linear programming |
| LS | Local search |
| MG | Microgrid |
| ML | Machine learning |
| MILP | Mixed-integer linear programming |
| PAR | Peak-to-average ratio |
| PSO | Particle swarm optimization |
| PV | Photovoltaic |
| RES | Renewable energy resources |
| RL | Reinforcement learning |
| RTP | Real-time pricing |
| SRPSO | Self-regulated particle swarm optimization |
| ToU | Time of use |
| UPSO | Unified particle swarm optimization |
| V2G | Vehicle-to-grid |
| WDO | Wind-driven optimization |
References
- Shewale, A.; Mokhade, A.; Funde, N.; Bokde, N.D. An overview of demand response in smart grid and optimization techniques for efficient residential appliance scheduling problem. Energies 2020, 13, 4266. [Google Scholar] [CrossRef]
- Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Pallonetto, F.; De Rosa, M.; D’Ettorre, F.; Finn, D.P. On the assessment and control optimisation of demand response programs in residential buildings. Renew. Sustain. Energy Rev. 2020, 127, 109861. [Google Scholar] [CrossRef]
- Khan, A.A.; Razzaq, S.; Khan, A.; Khursheed, F.; Owais. HEMSs and enabled demand response in electricity market: An overview. Renew. Sustain. Energy Rev. 2015, 42, 773–785. [Google Scholar] [CrossRef]
- Aghaei, J.; Alizadeh, M.I. Demand response in smart electricity grids equipped with renewable energy sources: A review. Renew. Sustain. Energy Rev. 2013, 18, 64–72. [Google Scholar] [CrossRef]
- Georgilakis, S.P. Review of Computational Intelligence Methods for Local Energy Markets at the Power Distribution Level to Facilitate the Integration of Distributed Energy Resources: State-of-the-art and Future Research. Energies 2020, 13, 186. [Google Scholar] [CrossRef] [Green Version]
- Rajasekhar, B.; Tushar, W.; Lork, C.; Zhou, Y.; Yuen, C.; Pindoriya, N.M.; Wood, K.L. A survey of computational intelligence techniques for air-conditioners energy management. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 555–570. [Google Scholar] [CrossRef]
- Mabina, P.; Mukoma, P.; Booysen, M.J. Sustainability matchmaking: Linking renewable sources to electric water heating through machine learning. Energy Build. 2021, 246, 111085. [Google Scholar] [CrossRef]
- Afram, A.; Sharifi, F.J. Gray-box modeling and validation of residential HVAC system for control system design. Appl. Energy 2015, 137, 134–150. [Google Scholar] [CrossRef]
- Antonopoulos, I.; Robu, V.; Couraud, B.; Kirli, D.; Norbu, S.; Kiprakis, A.; Flynn, D.; Elizondo-Gonzalez, S.; Wattam, S. Artificial intelligence and machine learning approaches to energy demand-side response: A systematic review. Renew. Sust. Energ. Rev. 2020, 130, 109899. [Google Scholar] [CrossRef]
- Vazquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, D. Deep reinforcement learning for power system application: An overview. CSEE J. Power Energy Syst. 2020, 6, 213–225. [Google Scholar]
- Ahmad, M.W.; Mourshed, M.; Yuce, B.; Rezgui, Y. Computational intelligence techniques for HVAC systems: A review. Build. Simul. 2016, 9, 359–398. [Google Scholar] [CrossRef] [Green Version]
- Merabet, G.H.; Essaaidi, M.; Ben Haddou, M.; Qolomany, B.; Qadir, J.; Anan, M.; Al-Fuqaha, A.; Riduan Abid, M.; Benhaddou, D. Intelligent building control systems for thermal comfort and energy-efficiency: A systematic review of artificial intelligence-assisted techniques. Renew. Sust. Energ. Rev. 2021, 144, 110969. [Google Scholar] [CrossRef]
- Farzaneh, H.; Malehmirchegini, L.; Bejan, A.; Afolabi, T.; Mulumba, A.; Daka, P.P. Artificial intelligence evolution in smart buildings for energy efficiency. Appl. Sci. 2021, 11, 763. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- What Is Computational Intelligence? Available online: https://cis.ieee.org/about/what-is-ci (accessed on 25 February 2022).
- Engelbrecht, A.P. Computational Intelligence: An Introduction, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007; pp. 285–358. [Google Scholar]
- del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.C.; Harley, R.G. Particle Swarm Optimization: Basic Concepts, Variants and Applications in Power Systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Ahmad, A.; Khan, A.; Javaid, N.; Hussain, H.M.; Abdul, W.; Almogren, A.; Alamri, A.; Azim Niaz, I. An Optimized Home Energy Management System with Integrated Renewable Energy and Storage Resources. Energies 2017, 10, 549. [Google Scholar] [CrossRef] [Green Version]
- Rahim, S.; Javaid, N.; Ahmad, A.; Khan, S.A.; Khan, Z.A.; Alrajeh, N.; Qasim, U. Exploiting heuristic algorithms to efficiently utilize energy management controllers with renewable energy sources. Energy Build. 2016, 129, 452–470. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Mohamed, A.; Khatib, T.; Shareef, H.; Homod, R.Z.; Abd Ali, J. Real time optimal schedule controller for home energy management system using new binary backtracking search algorithm. Energy Build. 2017, 138, 215–227. [Google Scholar] [CrossRef]
- Liu, D.; Xu, Y.; Wei, Q.; Liu, X. Residential energy scheduling for variable weather solar energy based on adaptive dynamic programming. IEEE/CAA J. 2018, 5, 36–46. [Google Scholar] [CrossRef]
- Gudi, N.; Wang, L.; Devabhaktuni, V. A demand side management based simulation platform incorporating heuristic optimization for management of household appliances. Int. J. Electr. Power Energy Syst. 2012, 43, 185–193. [Google Scholar] [CrossRef]
- Javaid, N.; Javaid, S.; Abdul, W.; Ahmed, I.; Almogren, A.; Alamri, A.; Niaz, I.A. A Hybrid Genetic Wind Driven Heuristic Optimization Algorithm for Demand Side Management in Smart Grid. Energies 2017, 10, 319. [Google Scholar] [CrossRef] [Green Version]
- Lugo-Cordero, H.M.; Fuentes-Rivera, A.; Guha, R.K.; Ortiz-Rivera, E.I. Particle Swarm Optimization for load balancing in green smart homes. IEEE Congr. Evol. Comput. CEC 2011, 715–720. [Google Scholar] [CrossRef]
- Javaid, N.; Ullah, I.; Akbar, M.; Iqbal, Z.; Ali Khan, F.; Alrajeh, N.; Alabed, M.S. An Intelligent Load Management System With Renewable Energy Integration for Smart Homes. IEEE Access 2017, 5, 13587–13600. [Google Scholar] [CrossRef]
- Aghajani, G.R.; Shayanfar, H.A.; Shayeghi, H. Presenting a multi-objective generation scheduling model for pricing demand response rate in micro-grid energy management. Energy Convers. Manag. 2015, 106, 308–321. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, L.; Guo, W.; Kang, Q.; Wu, Q. Chance Constrained Optimization in a Home Energy Management System. IEEE Trans Smart Grid 2018, 9, 252–260. [Google Scholar] [CrossRef]
- Ullah, I.; Javaid, N.; Khan, Z.A.; Qasim, U.; Khan, Z.A.; Mehmood, S.A. An Incentive-based Optimal Energy Consumption Scheduling Algorithm for Residential Users. Procedia Comput. Sci. 2015, 52, 851–857. [Google Scholar] [CrossRef] [Green Version]
- Javaid, N.; Hafeez, G.; Iqbal, S.; Alrajeh, N.; Alabed, M.S.; Guizani, M. Energy Efficient Integration of Renewable Energy Sources in the Smart Grid for Demand Side Management. IEEE Access 2018, 6, 77077–77096. [Google Scholar] [CrossRef]
- Huang, Y.; Tian, H.; Wang, L. Demand response for home energy management system. Int. J. Electr. Power Ener. 2015, 73, 448–455. [Google Scholar] [CrossRef]
- Mahmood, D.; Javaid, N.; Alrajeh, N.; Khan, Z.A.; Qasim, U.; Ahmed, I.; Ilahi, M. Realistic Scheduling Mechanism for Smart Homes. Energies 2016, 9, 202. [Google Scholar] [CrossRef] [Green Version]
- Faia, R.; Faria, P.; Vale, Z.; Spinola, J. Demand Response Optimization Using Particle Swarm Algorithm Considering Optimum Battery Energy Storage Schedule in a Residential House. Energies 2019, 12, 1645. [Google Scholar] [CrossRef] [Green Version]
- Hassan, S.; Arshad, M.; Chen, M.; Lin, H.; Mohammed, A.; Mohammed, K.; Gohar Rehman, C. Optimization Modeling for Dynamic Price Based Demand Response in Microgrids. J. Clean. Prod. 2019, 222, 231–241. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Mohamed, A.; Homod, R.Z.; Shareef, H. Hybrid LSA-ANN Based Home Energy Management Scheduling Controller for Residential Demand Response Strategy. Energies 2016, 9, 716. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.M.; Arefi, A.; Shafiullah, G.M.; Hettiwatte, S. A new approach to voltage management in unbalanced low voltage networks using demand response and OLTC considering consumer preference. Int. J. Electr. Power Energy Syst. 2018, 99, 11–27. [Google Scholar] [CrossRef]
- Hafeez, G.; Javaid, N.; Iqbal, S.; Khan, F.A. Optimal Residential Load Scheduling Under Utility and Rooftop Photovoltaic Units. Energies 2018, 11, 611. [Google Scholar] [CrossRef] [Green Version]
- Ziadi, Z.; Taira, S.; Oshiro, M.; Funabashi, T. Optimal Power Scheduling for Smart Grids Considering Controllable Loads and High Penetration of Photovoltaic Generation. IEEE Trans. Smart Grid 2014, 5, 2350–2359. [Google Scholar] [CrossRef]
- Rezaee Jordehi, A. Binary particle swarm optimisation with quadratic transfer function: A new binary optimisation algorithm for optimal scheduling of appliances in smart homes. Appl. Soft Comput. 2019, 78, 465–480. [Google Scholar] [CrossRef]
- Correa-Flórez, C.G.; Gerossier, A.; Michiorri, A.; Kariniotakis, G. Stochastic operation of home energy management systems including battery cycling. Appl. Energy 2018, 225, 1205–1218. [Google Scholar] [CrossRef] [Green Version]
- Mohseni, S.; Moghaddas-Tafreshi, S.M. A multi-agent system for optimal sizing of a cooperative self-sustainable multi-carrier microgrid. Sustain. Cities Soc. 2018, 38, 452–465. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Hu, Y.-C. Residential Consumer-Centric Demand-Side Management Based on Energy Disaggregation-Piloting Constrained Swarm Intelligence: Towards Edge Computing. Sensors 2018, 18, 1365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Javaid, N.; Ahmed, F.; Ullah, I.; Abid, S.; Abdul, W.; Alamri, A.; Almogren, A.S. Towards Cost and Comfort Based Hybrid Optimization for Residential Load Scheduling in a Smart Grid. Energies 2017, 10, 1546. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Lin, Y.; Lei, W.; Liu, Y.; Tao, M. Optimal household appliances scheduling of multiple smart homes using an improved cooperative algorithm. Energy 2019, 171, 944–955. [Google Scholar] [CrossRef]
- Pedrasa, M.A.A.; Spooner, T.D.; MacGill, I.F. Coordinated Scheduling of Residential Distributed Energy Resources to Optimize Smart Home Energy Services. IEEE Trans. Smart Grid 2010, 1, 134–143. [Google Scholar] [CrossRef]
- Du, Y.F.; Jiang, L.; Li, Y.; Wu, Q. A Robust Optimization Approach for Demand Side Scheduling Considering Uncertainty of Manually Operated Appliances. IEEE Trans. Smart Grid 2018, 9, 743–755. [Google Scholar] [CrossRef] [Green Version]
- Carrasqueira, P.; Alves, M.J.; Antunes, C.H. Bi-level particle swarm optimization and evolutionary algorithm approaches for residential demand response with different user profiles. Inf. Sci. 2017, 418–419, 405–420. [Google Scholar] [CrossRef] [Green Version]
- Faria, P.; Vale, Z.; Soares, J.; Ferreira, J. Demand Response Management in Power Systems Using Particle Swarm Optimization. IEEE Intell. Syst. 2013, 28, 43–51. [Google Scholar] [CrossRef] [Green Version]
- Hussain, B.; Khan, A.; Javaid, N.; Hasan, Q.U.; Malik, S.A.; Ahmad, O.; Dar, A.H.; Kazmi, A. A Weighted-Sum PSO Algorithm for HEMS: A New Approach for the Design and Diversified Performance Analysis. Electronics 2019, 8, 180. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.; Javaid, N.; Ahmad, A.; Akbar, M.; Khan, Z.A.; Ilahi, M. A priority-induced demand side management system to mitigate rebound peaks using multiple knapsack. J. Ambient Intell. Humaniz. Comput. 2019, 10, 1655–1678. [Google Scholar] [CrossRef]
- Jing, Z.; Zhu, J.; Hu, R. Sizing optimization for island microgrid with pumped storage system considering demand response. J. Mod. Power Syst. Clean Energy 2018, 6, 791–801. [Google Scholar] [CrossRef] [Green Version]
- Hafeez, G.; Wadud, Z.; Khan, I.U.; Khan, I.; Shafiq, Z.; Usman, M.; Khan, M.U.A. Efficient Energy Management of IoT-Enabled Smart Homes Under Price-Based Demand Response Program in Smart Grid. Sensors 2020, 20, 3155. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, Y.; Zhou, Y. Interval number optimization for household load scheduling with uncertainty. Energy Build 2016, 130, 613–624. [Google Scholar] [CrossRef]
- Imran, A.; Hafeez, G.; Khan, I.; Usman, M.; Shafiq, Z.; Qazi, A.B.; Khalid, A.; Thoben, K.D. Heuristic-Based Programable Controller for Efficient Energy Management Under Renewable Energy Sources and Energy Storage System in Smart Grid. IEEE Access 2020, 8, 139587–139608. [Google Scholar] [CrossRef]
- Aghajani, G.R.; Shayanfar, H.A.; Shayeghi, H. Demand side management in a smart micro-grid in the presence of renewable generation and demand response. Energy 2017, 126, 622–637. [Google Scholar] [CrossRef]
- Pinto, R.; Bessa, R.J.; Matos, M.A. Multi-period flexibility forecast for low voltage prosumers. Energy 2017, 141, 2251–2263. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Wang, W.; Hou, B. A hybrid algorithm for mixed integer nonlinear programming in residential energy management. J. Clean. Prod. 2019, 226, 940–948. [Google Scholar] [CrossRef]
- Khan, Z.A.; Khalid, A.; Javaid, N.; Haseeb, A.; Saba, T.; Shafiq, M. Exploiting Nature-Inspired-Based Artificial Intelligence Techniques for Coordinated Day-Ahead Scheduling to Efficiently Manage Energy in Smart Grid. IEEE Access 2019, 7, 140102–140125. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeng, P.; Li, S.; Zang, C.; Li, H. A Novel Multiobjective Optimization Algorithm for Home Energy Management System in Smart Grid. Math. Probl. Eng. 2015, 2015, 807527. [Google Scholar] [CrossRef] [Green Version]
- Lezama, F.; Faia, R.; Faria, P.; Vale, Z. Demand Response of Residential Houses Equipped with PV-Battery Systems: An Application Study Using Evolutionary Algorithms. Energies 2020, 13, 2466. [Google Scholar] [CrossRef]
- Nawaz, A.; Hafeez, G.; Khan, I.; Jan, K.U.; Li, H.; Ali Khan, S.; Wadud, Z. An Intelligent Integrated Approach for Efficient Demand Side Management with Forecaster and Advanced Metering Infrastructure Frameworks in Smart Grid. IEEE Access 2020, 8, 132551–132581. [Google Scholar] [CrossRef]
- Sisodiya, S.; Shejul, K.; Kumbhar, G.B. Scheduling of demand-side resources for a building energy management system. Int. Trans. Electr. Energy Syst. 2017, 29, e2369. [Google Scholar] [CrossRef]
- Pedrasa, M.A.A.; Spooner, T.D.; MacGill, I.F. Scheduling of Demand Side Resources Using Binary Particle Swarm Optimization. IEEE Trans. Smart Grid 2009, 24, 1173–1181. [Google Scholar] [CrossRef]
- Soares, J.; Morais, H.; Sousa, T.; Vale, Z.; Faria, P. Day-Ahead Resource Scheduling Including Demand Response for Electric Vehicles. IEEE Trans. Smart Grid 2013, 4, 596–605. [Google Scholar] [CrossRef] [Green Version]
- Rezaee Jordehi, A. Enhanced leader particle swarm optimisation (ELPSO): A new algorithm for optimal scheduling of home appliances in demand response programs. Artif. Intell. Rev. 2020, 53, 2043–2073. [Google Scholar] [CrossRef]
- Ma, K.; Hu, S.; Yang, J.; Xu, X.; Guan., X. Appliances scheduling via cooperative multi-swarm PSO under day-ahead prices and photovoltaic generation. Appl. Soft Comput. 2018, 62, 504–513. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, D.; Gu, C.; Li, F.J. Bilevel economic operation of distribution networks with microgrid integration. Renew. Sustain. Energy 2015, 7, 023120. [Google Scholar] [CrossRef] [Green Version]
- Chellamani, G.K.; Chandramani, P.V. An Optimized Methodical Energy Management System for Residential Consumers Considering Price-Driven Demand Response Using Satin Bowerbird Optimization. J. Electr. Eng. Technol. 2020, 15, 955–967. [Google Scholar] [CrossRef]
- Parvin, K.; Hannan, M.A.; Al-Shetwi, A.Q.; Ker, P.J.; Roslan, M.F.; Mahlia, T.M.I. Fuzzy Based Particle Swarm Optimization for Modeling Home Appliances Towards Energy Saving and Cost Reduction Under Demand Response Consideration. IEEE Access 2020, 8, 210784–210799. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Yang, R. Intelligent Multiagent Control System for Energy and Comfort Management in Smart and Sustainable Buildings. IEEE Trans. Smart Grid 2012, 3, 605–617. [Google Scholar] [CrossRef]
- Gudi, N.; Wang, L.; Devabhaktuni, V.; Depuru, S.S.S.R. Demand response simulation implementing heuristic optimization for home energy management. In Proceedings of the North American Power Symposium 2010, Arlington, TX, USA, 26–28 September 2010; pp. 1–6. [Google Scholar]
- Rehman, A.U.; Wadud, Z.; Elavarasan, R.M.; Hafeez, G.; Khan, I.; Shafiq, Z.; Alhelou, H.H. An Optimal Power Usage Scheduling in Smart Grid Integrated With Renewable Energy Sources for Energy Management. IEEE Access 2021, 9, 84619–84638. [Google Scholar] [CrossRef]
- Ebrahimi, J.; Abedini, M.; Rezaei, M.M. Optimal scheduling of distributed generations in microgrids for reducing system peak load based on load shifting. Sustain. Energy Grids Netw. 2020, 23, 100368. [Google Scholar] [CrossRef]
- Li, P.; Xu, D.; Zhou, Z.; Lee, W.J.; Zhao, B. Stochastic Optimal Operation of Microgrid Based on Chaotic Binary Particle Swarm Optimization. IEEE Trans. Smart Grid 2016, 7, 66–73. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Zhong, H.; Ma, H. Optimal scheduling model for smart home energy management system based on the fusion algorithm of harmony search algorithm and particle swarm optimization algorithm. Sci. Technol. Built. Environ. 2019, 26, 42–51. [Google Scholar] [CrossRef]
- Esmaeili, S.; Jadid, S. Economic-Environmental Optimal Management of Smart Residential Micro-Grid Considering CCHP System. Electr. Power Compon. Syst. 2019, 46, 1592–1606. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, J.; Mo, Y.; Lu, S.; Ma, J. A Hybrid Optimization Approach for Residential Energy Management. IEEE Access 2020, 8, 225201–225209. [Google Scholar] [CrossRef]
- Javaid, S.; Javaid, N. Comfort evaluation of seasonally and daily used residential load in smart buildings for hottest areas via predictive mean vote method. Sustain. Comput. Inform. Syst. 2020, 25, 100369. [Google Scholar] [CrossRef]
- Kanakadhurga, D.; Prabaharan, N. Demand response-based peer-to-peer energy trading among the prosumers and consumers. Energy Rep. 2021, 7, 7825–7834. [Google Scholar] [CrossRef]
- Zeeshan, M.; Jamil, M. Adaptive Moth Flame Optimization based Load Shifting Technique for Demand Side Management in Smart Grid. IETE J. Res. 2021, 1–12. [Google Scholar] [CrossRef]
- Chen, H.; Gao, L.; Zhang, Z.; Li, H. Optimal Energy Management Strategy for an Islanded Microgrid with Hybrid Energy Storage. J. Electr. Eng. Technol. 2021, 16, 1313–1325. [Google Scholar] [CrossRef]
- Abbasi, A.; Sultan, K.; Aziz, M.A.; Khan, A.U.; Khalid, H.A.; Guerrero, J.M.; Zafar, B.A. A Novel Dynamic Appliance Clustering Scheme in a Community Home Energy Management System for Improved Stability and Resiliency of Microgrids. IEEE Access 2021, 9, 142276–142288. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, H.; Li, W.; Zhou, M.; Zhang, Y.; Chaovalitwongse, W.A. Comprehensive Learning Particle Swarm Optimization Algorithm With Local Search for Multimodal Functions. IEEE Trans. Evol. Comput. 2019, 23, 718–731. [Google Scholar] [CrossRef]
- Lodewijks, G.; Cao, Y.; Zhao, N.; Zhang, H. Reducing CO2 Emissions of an Airport Baggage Handling Transport System Using a Particle Swarm Optimization Algorithm. IEEE Access 2021, 9, 121894–121905. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).