Balancing of Flexible Rotors Supported on Fluid Film Bearings by Means of Influence Coefficients Calculated by the Numerical Assembly Technique
Abstract
1. Introduction
2. Material and Methods
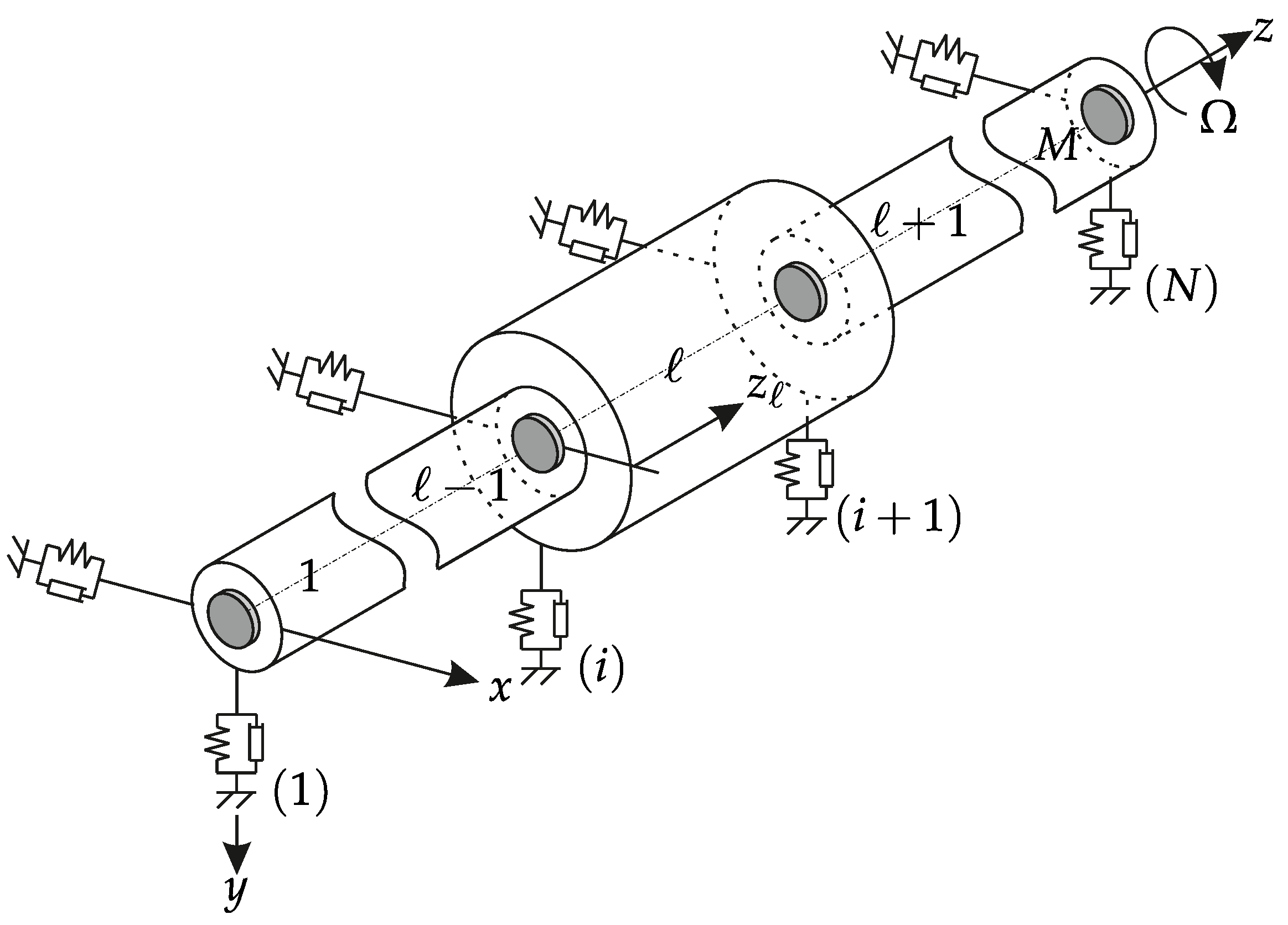
2.1. Equations of Motion
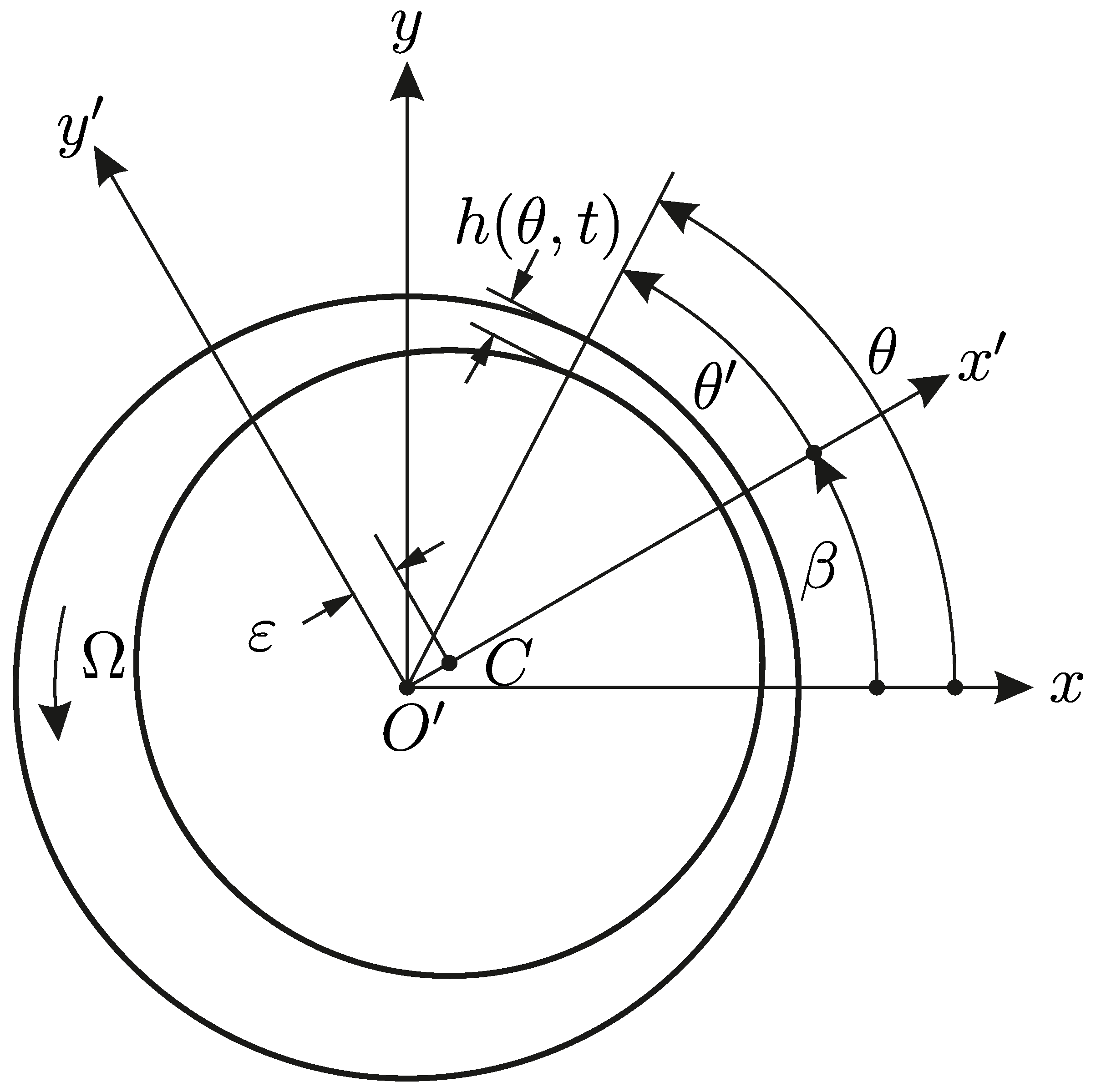
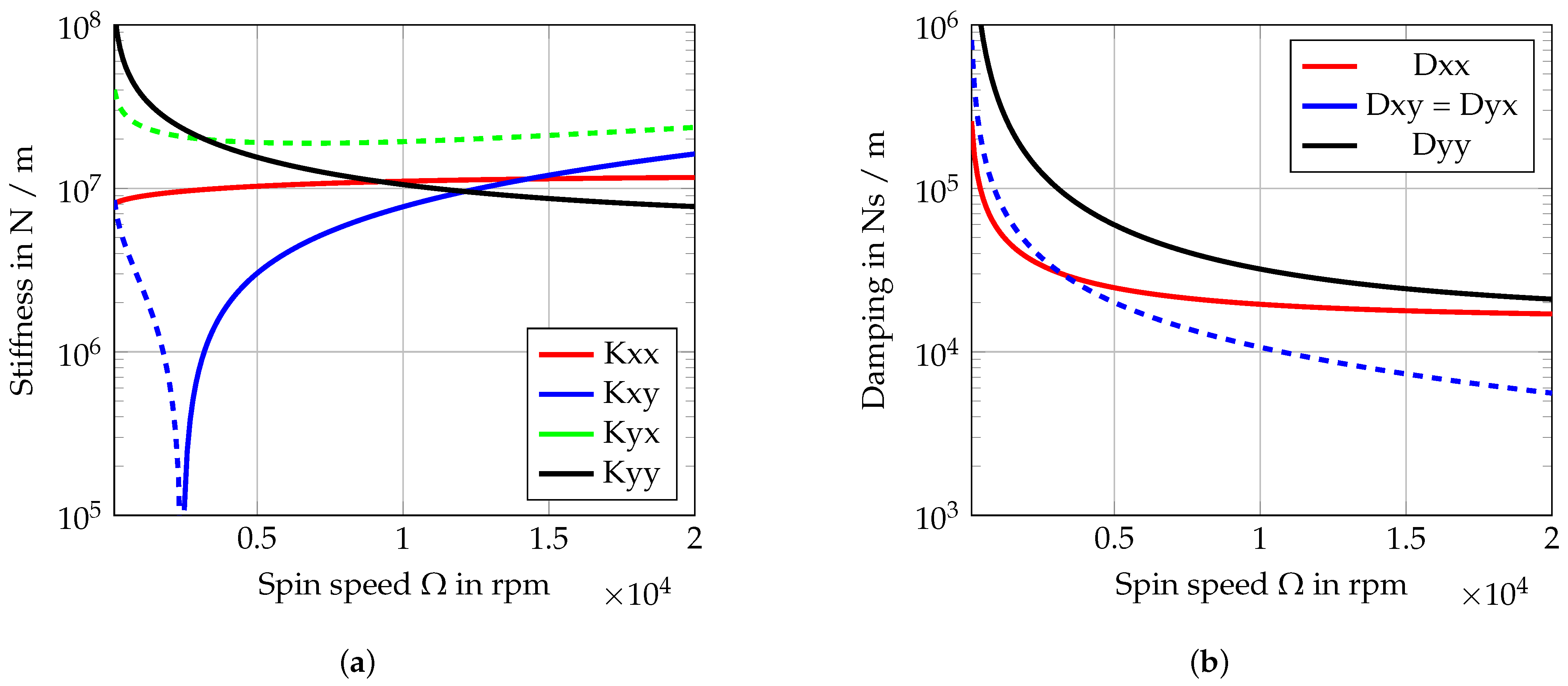
2.2. Speed Dependent Parameters of Fluid Film Bearings
2.3. Boundary and Interface Conditions
2.4. Homogeneous Solution
2.5. Particular Solution
2.6. Assembly and Solution Procedure
2.7. Recursive Eigenvalue Search
2.8. Influence Coefficient Method
3. Results
3.1. Rotor Bearing System
3.2. Influence Coefficient Matrix
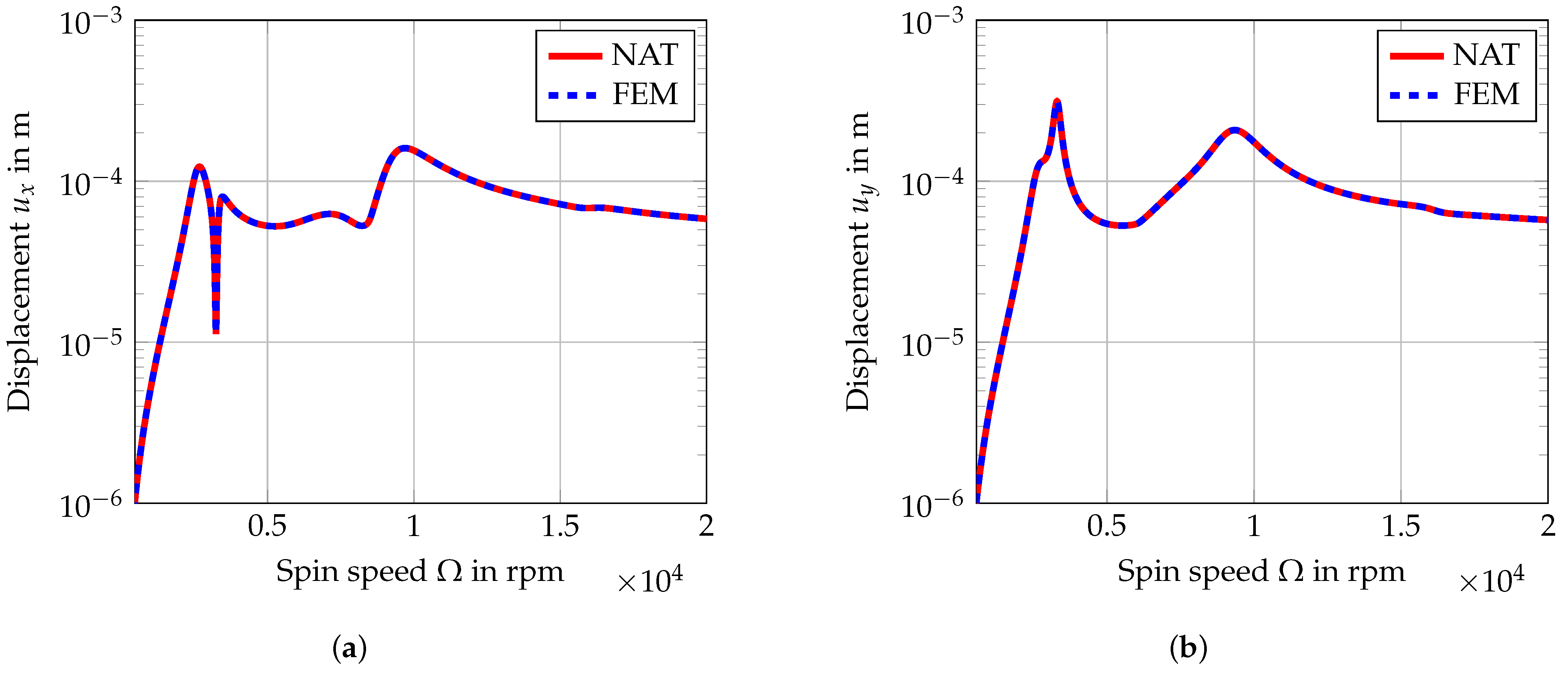
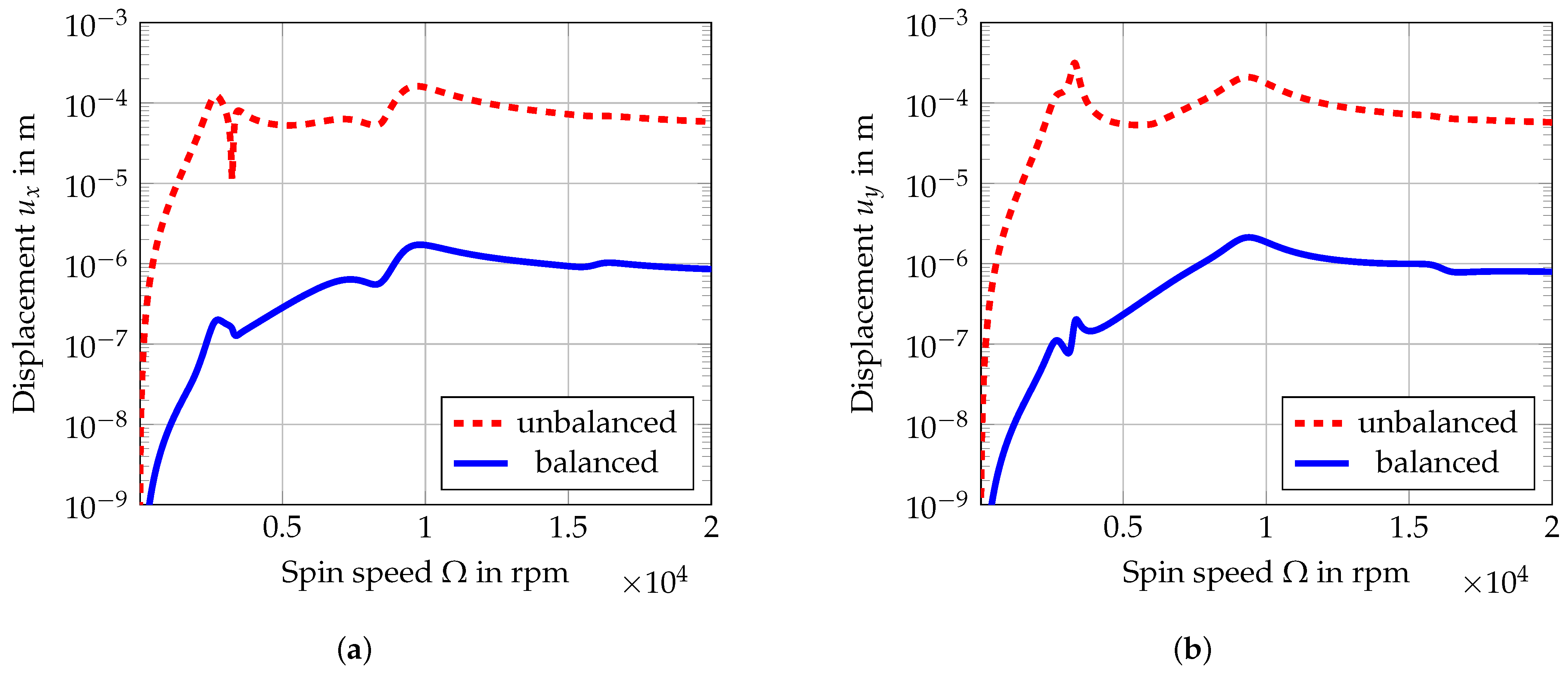
3.3. Concentrated Unbalance
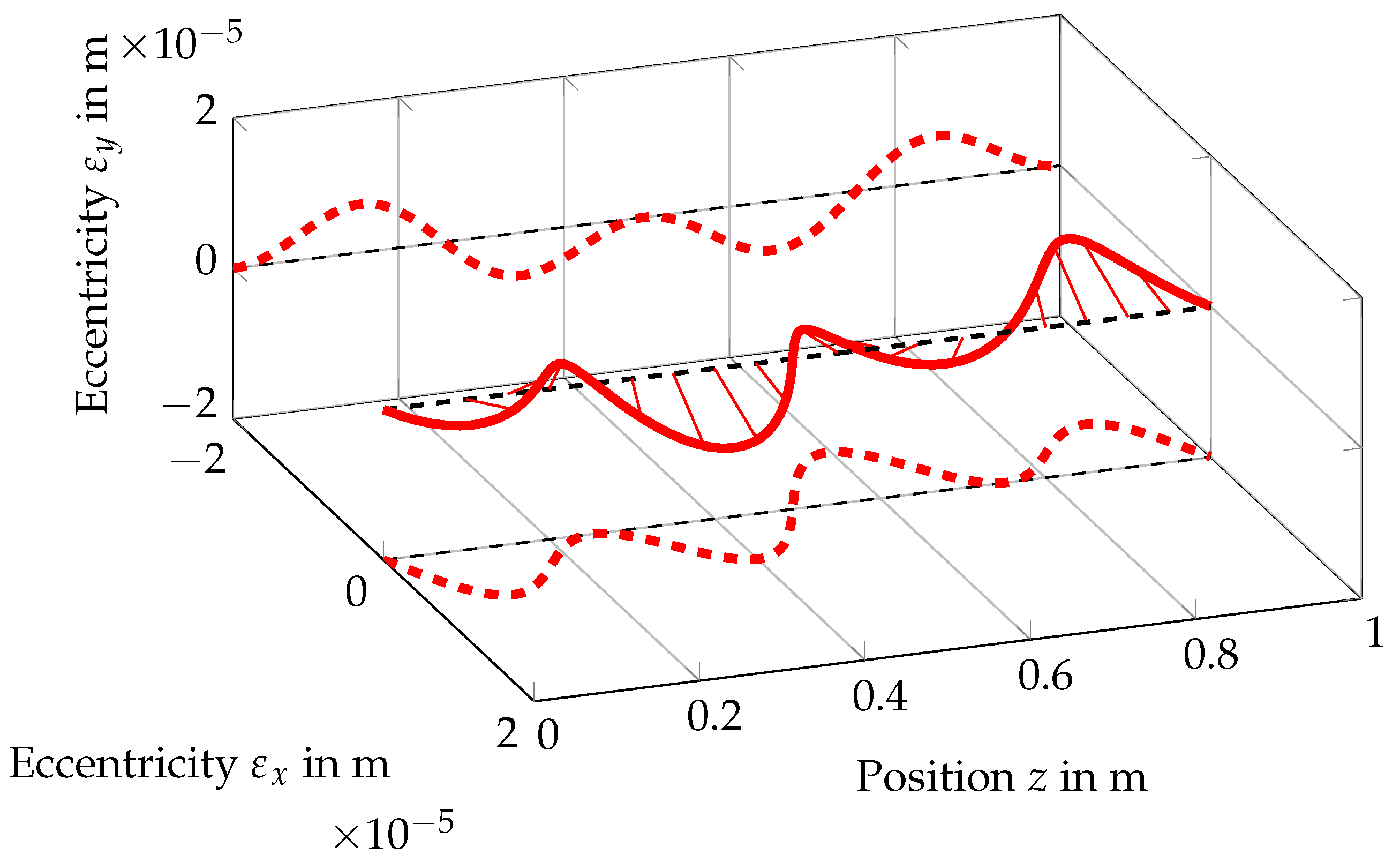
3.4. Distributed Unbalance
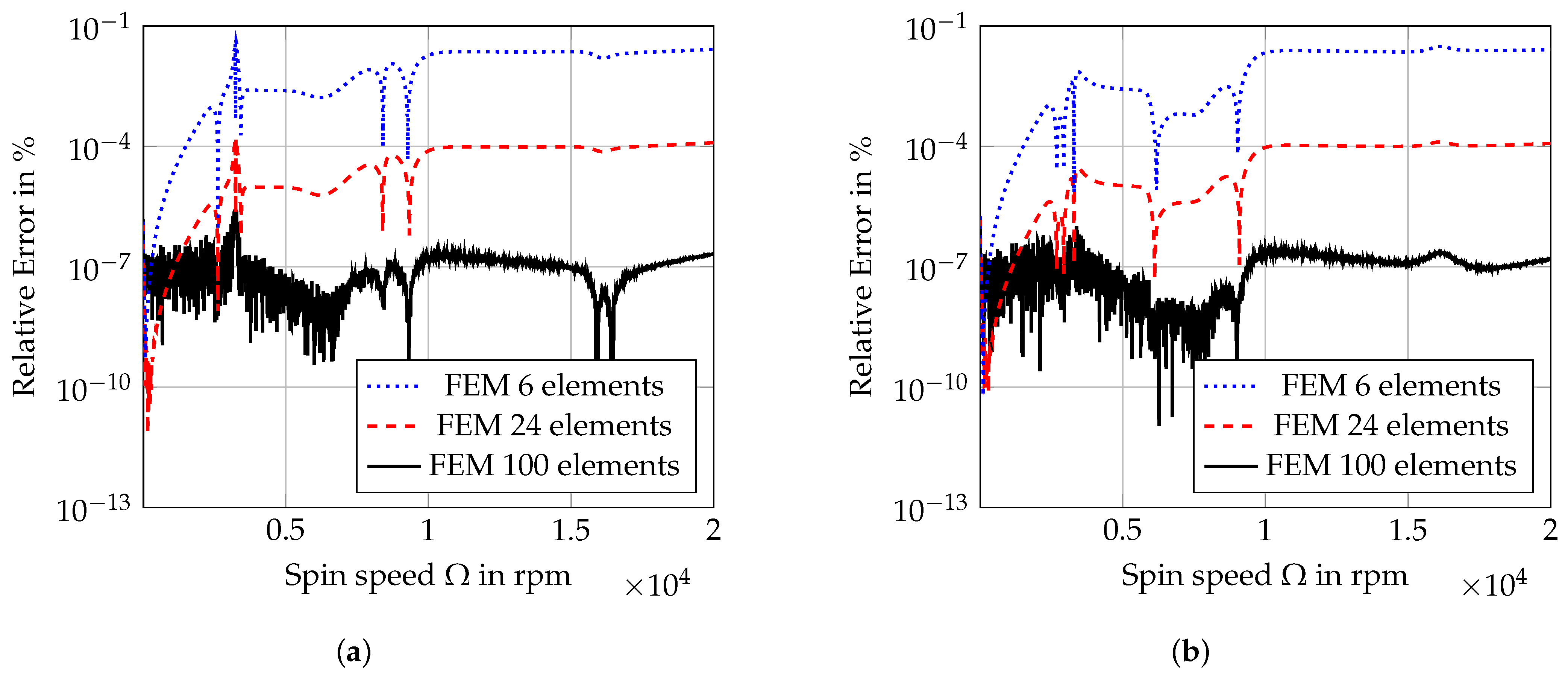
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| FRF | Frequency Response Function |
| NAT | Numerical Assembly Technique |
| rpm | Rotations per minute |
References
- Tessarzik, J.M.; Badgley, R.H.; Anderson, W.J. Flexible Rotor Balancing by the Exact Point-Speed Influence Coefficient Method. J. Eng. Ind. 1972, 94, 145–158. [Google Scholar] [CrossRef]
- Li, L.; Cao, S.; Li, J.; Nie, R.; Hou, L. Review of Rotor Balancing Methods. Machines 2021, 9, 89. [Google Scholar] [CrossRef]
- Bishop, R.E.D.; Gladwell, G.M.L. The Vibration and Balancing of an Unbalanced Flexible Rotor. J. Mech. Eng. Soc. 1959, 1, 66–77. [Google Scholar] [CrossRef]
- Gnielka, P. Modal balancing of flexible rotors without test runs: An experimental investigation. J. Vib. 1982, 90, 152–170. [Google Scholar] [CrossRef]
- Thearle, E.L. Dynamic Balancing of Rotating Machinery in the Field. Trans. ASME 1934, 56, 745–753. [Google Scholar]
- Nordmann, R.; Knopf, E.; Abrate, B. Numerical Analysis of the Influence Coefficient Matrix for On-Site Balancing of Flexible Rotors. In Proceedings of the 10th International Conference on Rotor Dynamics—IFToMM, Rio de Janeiro; Springer: Berlin/Heidelberg, Germany, 2018; pp. 157–172. [Google Scholar]
- Wu, J.-S.; Chou, H.M. A new approach for determining the natural frequency of mode shapes of a uniform beam carrying any number of sprung masses. J. Sound Vib. 1999, 220, 451–468. [Google Scholar] [CrossRef]
- Wu, J.-S.; Chen, D.-W. Free vibration analysis of a Timoshenko beam carrying multiple spring masses by using the numerical assembly technique. Int. J. Numer. Methods Eng. 2001, 50, 1039–1058. [Google Scholar] [CrossRef]
- Chen, D.-W.; Wu, J.-S. The exact solutions for the natural frequencies and mode shapes of non-uniform multi-span beams with multiple spring mass systems. J. Sound Vib. 2002, 225, 299–322. [Google Scholar] [CrossRef]
- Chen, D.-W. The exact solutions for the natural frequencies and mode shapes of non-uniform multi-span beamscarrying multiple various concentrated elements. Strucutural Eng. Mech. Int. J. 2003, 16, 153–176. [Google Scholar] [CrossRef]
- Chen, D.-W. The exact solutions for free vibration of uniform beams carrying multiple two-degree-of-freedom spring-mass systems. J. Sound Vib. 2006, 295, 342–361. [Google Scholar] [CrossRef]
- Lin, H.-Y.; Tsai, Y.-C. On the natural frequencies and mode shapes of a uniform multi-step beam carrying multiple point masses. Struct. Eng. Mech. Int. J. 2005, 21, 351–367. [Google Scholar] [CrossRef]
- Lin, H.-Y.; Tsai, Y.-C. On the natural frequencies and mode shapes of a multi-step beam carrying a number of intermediate lumped masses and rotary inertias. Struct. Eng. Mech. Int. J. 2006, 22, 701–717. [Google Scholar] [CrossRef]
- Lin, H.-Y.; Tsai, Y.-T. Free vibration analysis of a uniform multi-span beam carrying multiple spring-mass systems. J. Sound Vib. 2007, 302, 442–456. [Google Scholar] [CrossRef]
- Wang, J.-R.; Liu, T.-L.; Chen, D.-W. Free vibration analysis of a Timoshenko beam carrying multiple sping mass systems with the effect of shear deformation and rotary inertia. Struct. Eng. Mech. Int. J. 2007, 26, 1–14. [Google Scholar] [CrossRef]
- Lin, H.-Y. On the natural frequencies and mode shapes of a multi-span and multi-step beam carrying a number of concentrated elements. Struct. Eng. Mech. Int. J. 2008, 29, 531–550. [Google Scholar] [CrossRef]
- Lin, H.-Y. On the natural frequencies and mode shapes of a multi-span Timoshenko beam carrying a number of various concentrated elements. J. Sound Vib. 2009, 319, 593–605. [Google Scholar] [CrossRef]
- Yesilce, Y.; Demirdag, O. Effect of axial force on free vibration of Timoshenko multi-span beam carrying multiple spring-mass systems. Int. J. Mech. Sci. 2008, 50, 995–1003. [Google Scholar] [CrossRef]
- Yesilce, Y. Effect of Axial Force on the Free Vibration of a Reddy-Bickford Multi-span Beam Carrying Multiple Spring-mass Systems. J. Vib. Control. 2010, 16, 11–32. [Google Scholar] [CrossRef]
- Yesilce, Y. Free Vibrations of a Reddy-Bickford Multi-span Beam Carrying Multiple Spring-mass Systems. J. Shock Vib. 2011, 18, 709–726. [Google Scholar] [CrossRef][Green Version]
- Wu, J.-S.; Lin, F.-T.; Shaw, H.-J. Analytical Solution for Whirling Speeds and Mode Shapes of a Distributed-Mass Shaft With Arbitrary Rigid Disks. J. Appl. Mech. 2014, 81, 034503. [Google Scholar] [CrossRef]
- Vaz, J.D.C.; de Lima junior, J.J. Vibration anaysis of Euler–Bernoulli beams in multiple steps and different shapes of cross section. J. Vib. Control. 2016, 22, 193–204. [Google Scholar] [CrossRef]
- Farghaly, S.H.; El-Sayed, T.A. Exact free vibration of a multi-step Timoshenko beam system with several attachments. Mech. Syst. Signal Process. 2016, 72, 525–546. [Google Scholar] [CrossRef]
- Klanner, M.; Ellermann, K. Steady-state linear harmonic vibrations of multiple-stepped Euler-Bernoulli beams under arbitrarily distributed loads carrying any number of concentrated elements. Appl. Comput. Mech. 2019, 14, 31–50. [Google Scholar] [CrossRef]
- Klanner, M.; Prem, M.S.; Ellermann, K. Steady-state harmonic vibrations of a linear rotor- bearing system with a discontinuous shaft and arbitrarily distributed mass unbalance. In Proceedings of the ISMA2020 International Conference on Noise and Vibration Engineering and USD2020 International Conference on Uncertainty in Structural Dynamics, Leuven, Belgium, 7–9 September 2020; pp. 1257–1272. [Google Scholar]
- Klanner, M.; Prem, M.S.; Ellermann, K. Steady-State Harmonic Vibrations of Viscoelastic Timoshenko Beams with Fractional Derivative Damping Models. Appl. Mech. 2021, 2, 789–819. [Google Scholar] [CrossRef]
- Quinz, G.; Prem, M.S.; Klanner, M.; Ellermann, K. Balancing of a linear elastic rotor-bearing system with arbitrarily distributed unbalance using the Numerical Assembly Technique. Bull. Pol. Acad. Sci. Tech. Sci. 2021, 69, e138237. [Google Scholar]
- Bauchau, O.A.; Craig, J.I. Structural Analysis-With Applications to Aerospace Structures; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Genta, G. Dynamics of Rotating Systems; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Reynolds, O. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. 1886, 177, 154–234. [Google Scholar]
- Ocvirk, F.W. Short bearing approximation for full journal bearings. In NACA TN 20808; NACA: Cornell, NY, USA, 1952. [Google Scholar]
- Someya, T. Journal Bearings Databook; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Adcock, B.; Huybrechs, D.; Martin-Vaquero, J. On the Numerical Stability of Fourier Extensions. Found. Comput. Math. 2014, 14, 635–687. [Google Scholar] [CrossRef][Green Version]
- Matthysen, R.; Huybrechs, D. Fast Algorithms for the Computation of Fourier Extensions of Arbitrary Length. SIAM J. Sci. Comput. 2016, 38, A899–A922. [Google Scholar] [CrossRef]
- Bestle, D.; Abbas, L.; Rui, X. Recursive eigenvalue search algorithm for transfer matrix method of linear flexible multibody systems. Multibody Syst. Dyn. 2014, 32, 429–444. [Google Scholar] [CrossRef]
- Nordmann, R.; Knopf, E.; Krueger, T.; Abrate, B. Balancing of Flexible Rotors by means of Calculated Influence Coefficients. In Proceedings of the SIRM 2021 International Conference on Dynamics of Rotating Machinery, Gdansk, Poland, 17–19 February 2021; pp. 1–13. [Google Scholar]
- Friswell, M.I.; Penny, J.E.; Garvey, S.D.; Lees, A.W. Dynamics of Rotating Machines; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Teodorescu, P.P. Treatise on Classical Elasticity; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Tessarzik, J.M.; Anderson, W.J. Flexible Rotor Balancing by the Influence Coefficient Method Part 1: Evaluation of the Exact Point-Speed and Least Square Procedure; MTI Technical Report No. MTI-72TR32, NASA Contractor Report No, CR-121107, prepared for NASA-Lewis Research Center under Contract., A-NO. NAS3-14420; NASA: Cleveland, OH, USA, 1972.
- Hajžman, M.; Balda, M.; Polcar, P.; Polach, P. Turbine Rotor Dynamics Models Considering Foundation and Stator Effects. Machines 2022, 10, 77. [Google Scholar] [CrossRef]
- Prem, M.S.; Klanner, M.; Ellermann, K. Model parameter estimation of ball bearings using generalized Polynomial Chaos Expansion. In Proceedings of the SIRM 2021 International Conference on Dynamics of Rotating Machinery, Gdansk, Poland, 17–19 February 2021; pp. 331–340. [Google Scholar]
- Sekhar, M.R.C.; Sekhar, A.S. Application of artificial neural networks for identification of unbalance and looseness in rotor bearing systems. Int. J. Appl. Sci. Eng. 2013, 11, 69–84. [Google Scholar]
- Pavlenko, I.; Neamtu, C.; Verbovyi, A.; Ivanov, J.; Pop, G.; Sekhar, A.S. Using Computer Modeling and Artificial Neural Networks for Ensuring the Vibration Reliability of Rotors. CMIS 2019, 2535, 702–716. [Google Scholar]
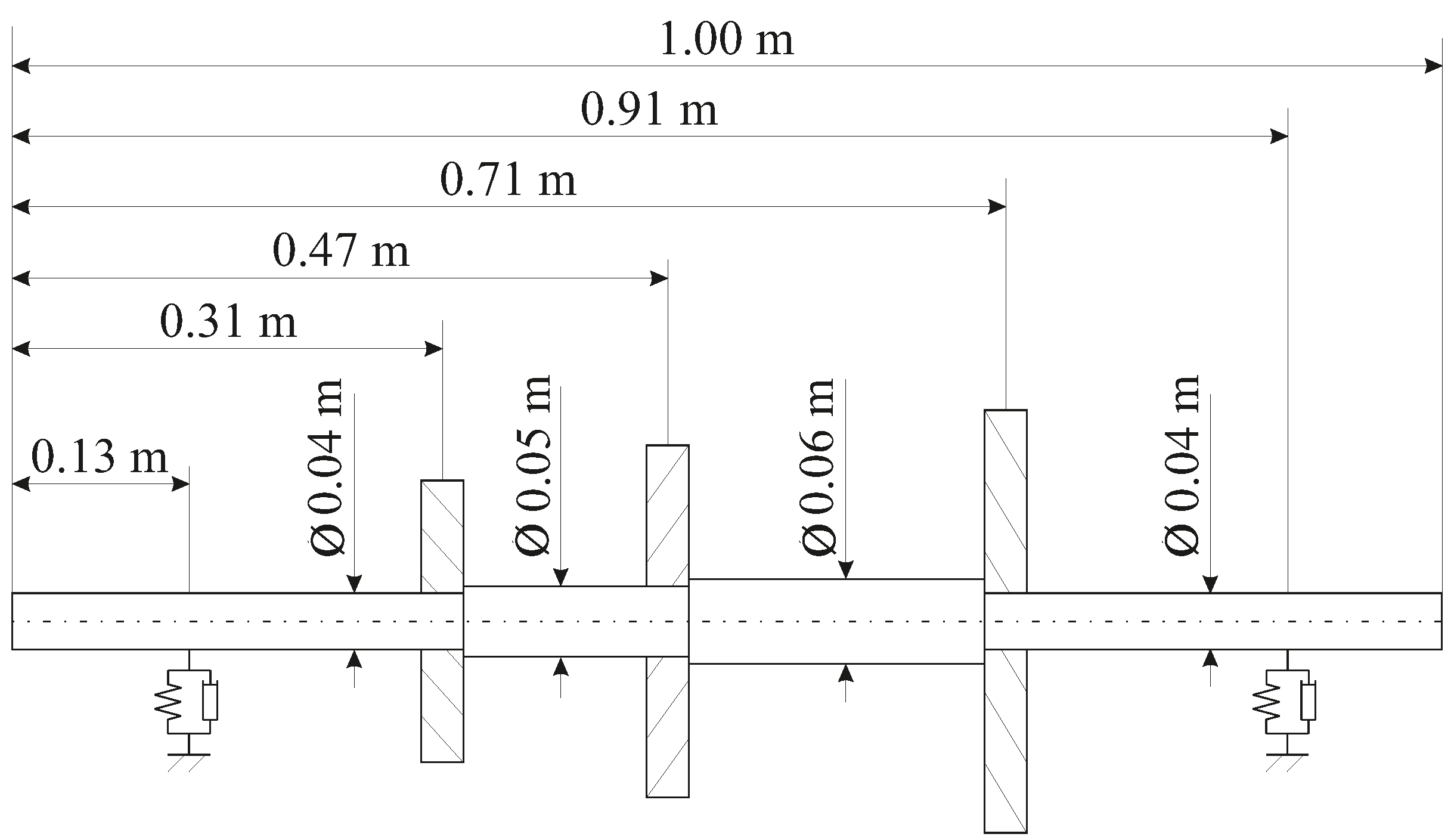

| z | m | F | b | c | ||||
|---|---|---|---|---|---|---|---|---|
| m | kg | N | m | m | m | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.13 | 0 | 0 | 0 | 431 | 0.04 | 0.02 | 0.032 | |
| 0.31 | 14.7 | 0.0412 | 0.0735 | 0 | 0 | 0 | 0 | 0 |
| 0.47 | 23 | 0.0966 | 0.0180 | 0 | 0 | 0 | 0 | 0 |
| 0.71 | 33 | 0.1960 | 0.3722 | 0 | 0 | 0 | 0 | 0 |
| 0.91 | 0 | 0 | 0 | 380 | 0.04 | 0.02 | 0.032 | |
| 1.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NAT | FEM | Relative Error |
|---|---|---|
| 43.014 | 43.015 | |
| 55.059 | 55.060 | |
| 154.28 | 154.29 | |
| 160.75 | 161.76 |
| z | U | |
|---|---|---|
| m | kg m | rad |
| 0.31 | 0 | |
| 0.47 | ||
| 0.71 |
| Number of Elements | x-Direction | y-Direction |
|---|---|---|
| 6 | ||
| 24 | ||
| 100 |
| z | U | |
|---|---|---|
| m | kg m | rad |
| 0.31 | ||
| 0.47 | − | |
| 0.71 | 0 |
| z | U | |
|---|---|---|
| m | kg m | rad |
| 0.31 | −3.0885 | |
| 0.47 | −1.5469 | |
| 0.71 | 0.0060 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quinz, G.; Klanner, M.; Ellermann, K. Balancing of Flexible Rotors Supported on Fluid Film Bearings by Means of Influence Coefficients Calculated by the Numerical Assembly Technique. Energies 2022, 15, 2009. https://doi.org/10.3390/en15062009
Quinz G, Klanner M, Ellermann K. Balancing of Flexible Rotors Supported on Fluid Film Bearings by Means of Influence Coefficients Calculated by the Numerical Assembly Technique. Energies. 2022; 15(6):2009. https://doi.org/10.3390/en15062009
Chicago/Turabian StyleQuinz, Georg, Michael Klanner, and Katrin Ellermann. 2022. "Balancing of Flexible Rotors Supported on Fluid Film Bearings by Means of Influence Coefficients Calculated by the Numerical Assembly Technique" Energies 15, no. 6: 2009. https://doi.org/10.3390/en15062009
APA StyleQuinz, G., Klanner, M., & Ellermann, K. (2022). Balancing of Flexible Rotors Supported on Fluid Film Bearings by Means of Influence Coefficients Calculated by the Numerical Assembly Technique. Energies, 15(6), 2009. https://doi.org/10.3390/en15062009






