Waste Clothing Recycling Channel Selection Using a CoCoSo-D Method Based on Sine Trigonometric Interaction Operational Laws with Pythagorean Fuzzy Information
Abstract
:1. Introduction
1.1. Pythagorean Fuzzy Sets
1.2. Operational Laws
1.3. The ITARA Method
1.4. The CoCoSo Method
1.5. Motivations and Contributions of This Paper
- The STOLs can satisfy DMs’ preference for multi-time phase parameters from a generalized perspective, and the IOLs consider the interaction between membership functions to make the evaluation information processing more objective and truly conform to the actual decision situation. Therefore, this study greatly has theoretical academic significance to combine them and explore novel operation rules (STIOLs) for Pythagorean fuzzy information fusion;
- At present, aggregation operators of STOLs and IOLs have not been considered simultaneously in Pythagorean fuzzy environments. Therefore, we proposed some Pythagorean fuzzy AOs based on STIOLs, that is, STI-PyFWA and STI-PyFWG operators;
- The ITARA approach has not been extended in PyFS. Moreover, the existing ITARA is conducted defuzzification too early in the process of determining the weight, and cannot keep the whole process of vagueness and uncertainty, so we need to improve the ITARA method to make it as much as possible the vagueness and uncertainty of information security evaluation toward the end. Moreover, the ITARA method has not been integrated with the CoCoSo method in Pythagorean fuzzy environment;
- In various decision-making environments, extended CoCoSo methods usually make use of PyFN’s score function to defuzzy the WSM and WPM model values. As the score function does not consider the influence of PyFN’s abstention or hesitancy degree, part of the evaluation information may be lost. In this paper, the proposed AOs are utilized to replace WSM and WPM models, and the distance measure is used to improve the CoCoSo method.
- Currently, there is no suitable decision method to deal with the WCRC selection problem. It is necessary to establish a PyFMAGDM framework to select optimal WCRC in this article.
- The STIOLs of PyFNs are developed for the first time. Compared with the existing AOLs and STOLs of PyFNs, the STIOLs show more efficiency and advantages.
- We propose the STI-PyFWA and STI-PyFWG operators based on the STIOLs and discuss their desirable properties and special cases;
- We extend the ITARA method with PyFNs and use membership function separation and parallel calculation to ensure the vagueness and uncertainty of evaluation information in the process of attribute weight determination;
- We build a new decision framework based on PyF-CoCoSo-D to solve group decision-making issues. The STI-PyFWA and STI-PyFWG operators are used to replace WSM and WPM models, and the defuzzification of different aggregation strategies is realized by distance measure;
- A case study of WCRC selection illustrates the feasibility of the proposed framework, and a sensitivity analysis and comparison study are conducted to verify the advantages of our methods.
2. Materials and Methods
2.1. Preliminaries
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
- (1)
- If ϑ = 1, Equation (3) reduces the Hamming distance DH(α,β).
- (2)
- If ϑ = 2, Equation (3) reduces the Euclidean distance DE(α,β).
- (3)
- If ϑ → +∞, Equation (3) reduces the Chebychev distance.
2.2. The Sine Trigonometric Interaction Operational Laws of PyFNs
- (1)
- (2)
- (3)
- (4)
- (1)
- sin(α1) ⊕ sin(α2) = sin(α2) ⊕ sin(α1);
- (2)
- sin(α1) ⊗ sin(α2) = sin(α2) ⊗ sin(α1);
- (3)
- τ(sin(α1) ⊕ sin(α2)) = τsin(α1) ⊕ τsin(α2), τ ≥ 0;
- (4)
- (sin(α1) ⊗ sin(α2))τ = (sin(α1))τ ⊗ (sin(α2))τ, τ ≥ 0;
- (5)
- τ1 sin(α1) ⊕ τ2 sin(α1) = (τ1+τ2) sin(α1), τ1, τ2 ≥ 0;
- (6)
- (sin(α1))τ1 ⊗ (sin(α1))τ2 = (sin(α1))τ1+τ2, τ1, τ2 ≥ 0.
2.3. The Sine Trigonometric Interaction Pythagorean Fuzzy AOs
2.3.1. STI-PyFWA Operator
- (1)
- Idempotency: If αi = α = (, ) (i = 1, 2, …, n), then STI-PyFWA(α1, α2, …, αn) = sin(α).
- (2)
- Boundedness:, where
- (3)
- Monotonicity: Let βi = (ζi, εi) (i = 1, 2, …, n) be another family of PyFNs, if i ≤ ζi, , then STI-PyFWA(α1, α2, …, αn) ≥ STI-PyFWA(β1, β2, …, βn).
2.3.2. STI-PyFWG Operator
- (1)
- Idempotency: If αi = α = (, ) (i = 1, 2, …, n), then STI-PyFWG(α1, α2, …, αn) = sin(α).
- (2)
- Boundedness: , where
- (3)
- Monotonicity: Let βi = (ξi, εi) (i = 1, 2, …, n) be another set of PyFNs, ifi ≤ εi,, then STI-PyFWA(α1, α2, …, αn) ≤ STI-PyFWA(β1, β2, …, βn).
2.4. The CoCoSo-D Method for MAGDM Problems with PyFNs
3. Results and Discussion
3.1. Case Study: WCRC Selection
3.2. Sensitivity Analysis
3.3. Comparison with Existing Methods
3.3.1. Comparison of Weighting Methods
3.3.2. Compared with Existing Sorting Methods
4. Conclusions
- The process of determining the weight of DMs in this paper is simple and subjective, without considering the correlation of DMs’ preferences.
- This paper does not take into account the interrelationship between attribute variables in the process of attribute weight determination and information aggregation.
- Although the proposed method contains one parameter, its flexibility is limited, and the proposed method cannot better and flexibly express the preferences and attitudes of DMs in information fusion.
Author Contributions
Funding
Conflicts of Interest
References
- Holmes, L. New Lifestyles System Data: 2016 Global Consumer Trends Survey Results. 2016. Available online: https://blog.euromonitor.com/new-lifestyles-system-data-2016-global-consumer-trends-survey-results/ (accessed on 11 October 2020).
- Leal Filho, W.; Ellams, D.; Han, S.; Tyler, D.; Boiten, V.J.; Paco, A.; Moora, H.; Balogun, A.L. A review of the socio-economic advantages of textile recycling. J. Clean. Prod. 2019, 218, 10–20. [Google Scholar] [CrossRef]
- Kerr, J.; Landry, J. Pulse of the Fashion Industry; Global Fashion Agenda: Copenhagen, Sweden, 2017. [Google Scholar]
- United Nations Environment Programme. Putting the Brakes on Fast Fashion. 2018. Available online: https://www.unenvironment.org./news-and-stories/story/putting-brakes-fast-fashion (accessed on 12 November 2018).
- Panwar, R.; Niesten, E. Advancing circular economy. Bus. Strategy Environ. 2020, 29, 2890–2892. [Google Scholar] [CrossRef]
- Brismar, A. Circular Fashion. 2019. Available online: https://circularfashion.com/circular-fashion-definition/ (accessed on 30 September 2019).
- Kaisa, V.; Anne, R.; Pirjo, H.; Ali, H. Consumer attitudes and communication in circular fashion. J. Fash. Mark. Manag. 2018, 22, 286–300. [Google Scholar]
- Ki, C.W.; Chong, S.M.; Ha-Brookshire, J.E. How fashion can achieve sustainable development through a circular economy and stakeholder engagement: A systematic literature review. Corp. Soc. Responsib. Environ. Manag. 2020, 27, 2401–2424. [Google Scholar] [CrossRef]
- Ki, C.W.; Park, S.; Ha-Brookshire, J.E. Toward a circular economy: Understanding consumers’ moral stance on corporations’ and individuals’ responsibilities in creating a circular fashion economy. Bus. Strategy Environ. 2021, 30, 1121–1135. [Google Scholar] [CrossRef]
- Lin, C.W.R.; Chen, M.T.; Tseng, M.L.; Jantarakolica, T.; Xu, H. Multi-objective production programming to systematic sorting and remanufacturing in second-hand clothing recycling industry. Symmetry 2020, 12, 1161. [Google Scholar] [CrossRef]
- Mi, S. Unspoken Crisis: Mounting Textile Waste in China. 2018. Available online: http://www.coresponsibility.com/unspoken-crisis-mounting-textile-waste-in-china/ (accessed on 5 July 2018).
- Zhang, L.; Wu, T.; Liu, S.; Jiang, S.Y.; Wu, H.J.; Yang, J.M. Consumers’ clothing disposal behaviors in Nanjing, China. J. Clean. Prod. 2020, 276, 123184. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 31, 343–349. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Wei, G.W. Pythagorean fuzzy interaction aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 2119–2132. [Google Scholar] [CrossRef]
- Wei, G.W.; Lu, M. Pythagorean fuzzy power aggregation operators in multiple attribute decision making. Int. J. Intell. Syst. 2018, 33, 169–186. [Google Scholar] [CrossRef]
- Gao, H. Pythagorean fuzzy Hamacher Prioritized aggregation operators in multiple attribute decision making. J. Intell. Fuzzy Syst. 2018, 35, 2229–2245. [Google Scholar] [CrossRef]
- Wang, L.; Li, N. Pythagorean fuzzy interaction power Bonferroni mean aggregation operators in multiple attribute decision making. Int. J. Intell. Syst. 2020, 35, 150–183. [Google Scholar] [CrossRef]
- Wang, L.; Garg, H.; Li, N. Pythagorean fuzzy interactive Hamacher power aggregation operators for assessment of express service quality with entropy weight. Soft Comput. 2020, 25, 973–993. [Google Scholar] [CrossRef]
- Wei, G.W. Pythagorean fuzzy Maclaurin symmetric mean operators in multiple attribute decision making. Int. J. Intell. Syst. 2018, 33, 1043–1070. [Google Scholar] [CrossRef]
- Chen, T.Y. Remoteness index-based Pythagorean fuzzy VIKOR methods with a generalized distance measure for multiple criteria decision analysis. Inf. Fusion 2018, 41, 129–150. [Google Scholar] [CrossRef]
- Akram, M.; Ilyas, F.; Garg, H. Multi-criteria group decision making based on ELECTRE I method in Pythagorean fuzzy information. Soft Comput. 2020, 24, 3425–3453. [Google Scholar] [CrossRef]
- Ren, P.J.; Xu, Z.S.; Gou, X.J. Pythagorean fuzzy TODIM approach to multi-criteria decision making. Appl. Soft Comput. 2016, 42, 246–259. [Google Scholar] [CrossRef]
- Gul, M.; Ak, M.F.; Guneri, A.F. Pythagorean fuzzy VIKOR-based approach for safety risk assessment in mine industry. J. Safety Res. 2019, 69, 135–153. [Google Scholar] [CrossRef]
- Peng, X.D.; Yang, Y. Pythagorean fuzzy Choquet integral based MABAC method for multiple attribute Ggroup Ddecision Mmaking. Int. J. Intell. Syst. 2016, 31, 989–1020. [Google Scholar] [CrossRef]
- Akram, M.; Luqman, A.; Alcantud, J.C.R. Risk evaluation in failure modes and effects analysis: Hybrid TOPSIS and ELECTRE I solutions with Pythagorean fuzzy information. Neural Comput. Appl. 2021, 33, 5675–5703. [Google Scholar] [CrossRef]
- Peng, X.D.; Ma, X.L. Pythagorean fuzzy multi-criteria decision making method based on CODAS with new score function. J. Intell. Fuzzy Syst. 2020, 38, 3307–3318. [Google Scholar] [CrossRef]
- Li, P.; Liu, J.; Wei, C.P.; Liu, J. A new EDAS method based on prospect theory for Pythagorean fuzzy set and its application in selecting investment projects for highway. Kybernetes 2021, in press. [Google Scholar] [CrossRef]
- Huang, C.; Lin, M.W.; Xu, Z.S. Pythagorean fuzzy MULTIMOORA method based on distance measure and score function: Its application in multicriteria decision making process. Knowl. Inf. Syst. 2020, 62, 4373–4406. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Hao, W.N.; Yu, X.H.; Chen, G.; Zhang, S.J.; Chen, J.Y. Pythagorean fuzzy preference ranking organization method of enrichment evaluations. Int. J. Intell. Syst. 2019, 34, 1416–1439. [Google Scholar] [CrossRef]
- Molla, M.U.; Giri, B.C.; Biswas, P. Extended PROMETHEE method with Pythagorean fuzzy sets for medical diagnosis problems. Soft Comput. 2021, 25, 4503–4512. [Google Scholar] [CrossRef]
- Zhao, M.W.; Wei, G.W.; Wei, C.; Wu, J. Pythagorean fuzzy TODIM method based on the cumulative prospect theory for MAGDM and its application on risk assessment of science and technology projects. Int. J. Fuzzy Syst. 2021, 23, 1027–1041. [Google Scholar] [CrossRef]
- Akram, M.; Dudek, W.A.; Ilyas, F. Group decision-making based on Pythagorean fuzzy TOPSIS method. Int. J. Intell. Syst. 2019, 34, 1455–1475. [Google Scholar] [CrossRef]
- Sarkar, B.; Biswas, A. Pythagorean fuzzy AHP-TOPSIS integrated approach for transportation management through a new distance measure. Soft Comput. 2021, 25, 4073–4089. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Pardasani, K.R.; Mardani, A.; Liao, H.C.; Streimikiene, D. A novel VIKOR approach based on entropy and divergence measures of Pythagorean fuzzy sets to evaluate renewable energy technologies in India. J. Clean. Prod. 2019, 238, 117936. [Google Scholar] [CrossRef]
- Alrasheedi, M.; Mardani, A.; Mishra, A.R.; Rani, P.; Loganathan, N. An extended framework to evaluate sustainable suppliers in manufacturing companies using a new Pythagorean fuzzy entropy-SWARA-WASPAS decision-making approach. J. Enterp. Inf. Manag. 2021, in press. [Google Scholar] [CrossRef]
- Ayyildiz, E.; Erdogan, M.; Gumus, A.T. A Pythagorean fuzzy number-based integration of AHP and WASPAS methods for refugee camp location selection problem: A real case study for Istanbul, Turkey. Neural Comput. Appl. 2021, 33, 15751–15768. [Google Scholar] [CrossRef]
- Garg, H. New exponential operational laws and their aggregation operators for interval-valued Pythagorean fuzzy multicriteria decision-making. Int. J. Intell. Syst. 2018, 33, 653–683. [Google Scholar] [CrossRef]
- Garg, H. New logarithmic operational laws and their aggregation operators for Pythagorean fuzzy set and their applications. Int. J. Intell. Syst. 2019, 34, 82–106. [Google Scholar] [CrossRef] [Green Version]
- Ashraf, S.; Abdullah, S. Decision aid modeling based on sine trigonometric spherical fuzzy aggregation information. Soft Compu. 2021, 25, 8549–8572. [Google Scholar] [CrossRef]
- Garg, H. Sine trigonometric operational laws and its based Pythagorean fuzzy aggregation operators for group decision-making process. Artif. Intell. Rev. 2021, 54, 4421–4447. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S.; Khan, S. Fuzzy decision support modeling for internet finance soft power evaluation based on sine trigonometric Pythagorean fuzzy information. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 3101–3119. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S.; Zeng, S.; Jin, H.; Ghanin, F. Fuzzy decision support modeling for hydrogen power plant selection based on single value neutrosophic sine trigonometric aggregation operators. Symmetry 2020, 12, 298. [Google Scholar] [CrossRef] [Green Version]
- Garg, H. A novel trigonometric operation-based q-rung orthopair fuzzy aggregation operator and its fundamental properties. Neural Comput. Appl. 2020, 32, 15077–15099. [Google Scholar] [CrossRef]
- He, Y.D.; Chen, H.Y.; Zhou, L.G.; Liu, J.P.; Tao, Z.F. Intuitionistic fuzzy geometric interaction averaging operators and their application to multi-criteria decision making. Inf. Sci. 2014, 259, 142–159. [Google Scholar] [CrossRef]
- Lin, M.W.; Li, X.M.; Chen, L.F. Linguistic q-rung orthopair fuzzy sets and their interactional partitioned Heronian mean aggregation operators. Int. J. Intell. Syst. 2020, 35, 217–249. [Google Scholar] [CrossRef]
- Yang, Z.L.; Garg, H. Interaction power partitioned Maclaurin Symmetric mean operators under q-rung orthopair uncertain linguistic information. Int. J. Fuzzy Syst. 2021, 1–19. (in press). [Google Scholar] [CrossRef]
- Garg, H.; Arora, R. Novel scaled prioritized intuitionistic fuzzy soft interaction averaging aggregation operators and their application to multi criteria decision making. Eng. Appl. Artif. Intell. 2018, 71, 100–112. [Google Scholar] [CrossRef]
- Garg, H. Generalized intuitionistic fuzzy interactive geometric aggregation operators using Einstein t-norm and t-conorm and their application to decision making. Comput. Ind. Eng. 2016, 101, 53–69. [Google Scholar] [CrossRef]
- Liu, P.D.; Chen, S.M.; Liu, J.L. Multiple attribute group decision making based on intuitionistic fuzzy interaction partitioned Bonfereoni mean operators. Inf. Sci. 2017, 411, 98–121. [Google Scholar] [CrossRef]
- Hatefi, M.A. Indifference threshold-based attribute ratio analysis: A method for assigning the weights to the attributes in multiple attribute decision making. Appl. Soft Comput. 2019, 74, 643–651. [Google Scholar] [CrossRef]
- Liu, P.D.; Pan, Q.; Xu, H.X. Multi-attribute border approximation area comparison (MABAC) method based on normal q-rung orthopair fuzzy environment. J. Intell. Fuzzy Syst. 2021, 40, 9085–9111. [Google Scholar] [CrossRef]
- Chang, T.W.; Pai, C.J.; Lo, H.W.; Hu, S.K. A hybrid decision-making model for sustainable supplier evaluation in electronics manufacturing. Comp. Ind. Eng. 2021, 156, 107283. [Google Scholar] [CrossRef]
- Alper Sofuoğlu, M. Development of an ITARA-based hybrid multi-criteria decision-making model for material selection. Soft Comput. 2019, 23, 6715–6725. [Google Scholar] [CrossRef]
- Du, P.L.; Chen, Z.; Gong, X.M. Load response potential evaluation for distribution networks: A hybrid decision-making model with intuitionistic normal cloud and unknown weight information. Energy 2020, 192, 116673. [Google Scholar] [CrossRef]
- Gong, J.W.; Li, Q.; Yin, L.S.; Liu, H.C. Undergraduate teaching audit and evaluation using an extended MABAC method under q-rung orthopair fuzzy environment. Int. J. Intell. Syst. 2020, 35, 1912–1933. [Google Scholar] [CrossRef]
- Ulutas, A.; Karabasevic, D.; Popovic, G.; Stanujkic, D.; Nguyen, P.T.; Karakoy, C. Development of a novel integrated CCSD-ITARA-MARCOS decision-making approach for stackers selection in a logistics system. Mathematics 2020, 8, 1672. [Google Scholar] [CrossRef]
- Lo, H.W.; Hsu, C.C.; Huang, C.N.; Liou, J.J.H. An ITARA-TOPSIS based integrated assessment model to identify potential product and system risks. Mathematics 2021, 9, 239. [Google Scholar] [CrossRef]
- Gong, J.W.; Liu, H.C.; You, X.Y.; Yin, L. An integrated multi-criteria decision-making approach with linguistic hesitant fuzzy sets for E-learning website evaluation and selection. Appl. Soft Comput. 2021, 102, 107118. [Google Scholar] [CrossRef]
- Liu, R.; Zhu, Y.J.; Chen, Y.; Liu, H.C. Occupational health and safety risk assessment using an integrated TODIM-PROMETHEE model under linguistic spherical fuzzy environment. Int. J. Intell. Syst. 2021, 36, 6814–6836. [Google Scholar] [CrossRef]
- Yazdani, M.; Zarate, P.; Zavadskas, E.K.; Turskis, Z. A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar] [CrossRef]
- Ecer, F.; Pamucar, D. Sustainable supplier selection: A novel integrated fuzzy best worst method (F-BWM) and fuzzy CoCoSo with Bonferroni (CoCoSo’B) multi-criteria model. J. Clean. Prod. 2020, 266, 121981. [Google Scholar] [CrossRef]
- Liao, H.C.; Qin, R.; Wu, D.; Yazdani, M.; Zavadskas, E.K. Pythagorean fuzzy combined compromise solution method integrating the cumulative prospect theory and combined weights for cold chain logistics distribution center selection. Int. J. Intell. Syst. 2020, 35, 2009–2031. [Google Scholar] [CrossRef]
- Cui, Y.F.; Liu, W.; Rani, P.; Alrasheedi, M. Internet of things (IoT) adoption barriers for the circular economy using Pythagorean fuzzy SWARA-CoCoSo decision-making approach in the manufacturing sector. Technol. Forecast. Soc. 2021, 171, 120951. [Google Scholar] [CrossRef]
- Peng, X.D.; Huang, H.H. Fuzzy decision making method based on CoCoSo with CRITIC for financial risk evaluation. Technol. Econ. Dev. Econ. 2020, 26, 695–724. [Google Scholar] [CrossRef] [Green Version]
- Yazdani, M.; Wen, Z.; Liao, H.C.; Banaitis, A.; Turskis, Z. A grey combined compromise solution (COCOSO-G) method for supplier selection in construction management. J. Civ. Eng. Manag. 2019, 25, 858–874. [Google Scholar] [CrossRef] [Green Version]
- Erceg, Z.; Starcevic, V.; Pamucar, D.; Mitrovic, G.; Stevic, Z.; Zikic, S. A new model for stock management in order to rationalize costs: ABC-FUCOM-Interval rough CoCoSo model. Symmetry 2019, 11, 1527. [Google Scholar] [CrossRef] [Green Version]
- Yazdani, M.; Chatterjee, P.; Pamucar, D.; Chakraborty, S. Development of an integrated decision making model for location selection of logistics centers in the Spanish autonomous communities. Expert Syst. Appl. 2020, 148, 113208. [Google Scholar] [CrossRef]
- Wen, Z.; Liao, H.C.; Zavadskas, E.K.; Al-Barakati, A. Selection third-party logistics service providers in supply chain finance by a hesitant fuzzy linguistic combined compromise solution method. Econ. Res.-Ekon. Istraz. 2019, 32, 4033–4058. [Google Scholar] [CrossRef]
- Wen, Z.; Liao, H.C.; Ren, R.X.; Bai, C.G.; Al-Barakati, A. Cold chain logistics management of medicine with an integrated multi-criteria decision-making method. Int. J. Environ. Res. Public Health 2019, 16, 4843. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.Y.; Liao, H.C.; Al-Barakati, A.; Zavadskas, E.K.; Antucheviciene, J. Supplier selection for housing development by an integrated method with interval rough boundaries. Int. J. Strateg. Prop. Manag. 2020, 24, 269–284. [Google Scholar] [CrossRef]
- Svadlenka, L.; Simic, V.; Dobrodolac, M.; Lazarevic, D.; Todorovic, G. Picture fuzzy decision-making approach for sustainable last-mile delivery. IEEE Access 2020, 8, 209393. [Google Scholar] [CrossRef]
- Deveci, M.; Pamucar, D.; Gokasar, I. Fuzzy power Heronian function based CoCoSo method for the advantage prioritization of autonomous vehicles in real-time traffic management. Sustain. Cities Soc. 2021, 69, 102846. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Krishankumar, R.; Zavadskas, E.K.; Cavallaro, F.; Ravichandran, K.S. A hesitant fuzzy combined compromise solution framework-based on discrimination measure for ranking sustainable third-party reverse logistic providers. Sustainability 2021, 13, 2064. [Google Scholar] [CrossRef]
- Alrasheedi, M.; Mardani, A.; Mishra, A.R.; Streimikiiene, D.; Liao, H.C.; Al-nefaie, A.H. Evaluating the green growth indicators to achieve sustainable development: A novel extended interval-valued intuitionistic fuzzy-combined compromise solution approach. Sustain. Dev. 2021, 29, 120–142. [Google Scholar] [CrossRef]
- Rani, P.; Ali, J.; Krishankumar, R.; Mishra, A.R.; Cavallaro, F.; Ravichandran, K.S. An integrated single-valued Neutrosophic combined compromise solution methodology for renewable energy resource selection problem. Energies 2021, 14, 5494. [Google Scholar] [CrossRef]
- Liu, P.D.; Rani, P.; Mishra, A.R. A novel Pythagorean fuzzy combined compromise solution framework for the assessment of medical waste treatment technology. J. Clean. Prod. 2021, 292, 126047. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Z.S. Extension of TOPSIS to multi-criteria decision making with Pythagorean fuzzy sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Biswas, A.; Sarkar, B. Pythagorean fuzzy TOPSIS for multicriteria group decision-making with unknown weight information through entropy measure. Int. J. Intell. Syst. 2019, 34, 1108–1128. [Google Scholar] [CrossRef]
- Fu, X.; Zhu, Q.; Sarkis, J. Evaluating green supplier development programs at a telecommunications systems provider. Int. J. Prod. Econ. 2012, 140, 357–367. [Google Scholar] [CrossRef]
- Song, W.Y.; Ming, X.G.; Liu, H.C. Identifying critical risk factors of sustainable supply chain management: A rough strength-relation analysis method. J. Clean. Prod. 2017, 143, 100–115. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Pardasani, K.R. A novel WASPAS approach for multicriteria physician selection problem with intuitionistic fuzzy type-2 sets. Soft Comput. 2020, 24, 2355–2367. [Google Scholar] [CrossRef]
- Sarkar, B.; Biswas, A. Multicriteria decision making approach for strategy formulation using Pythagorean fuzzy MULTIMOORA. Expert Syst. 2022, 39, e12802. [Google Scholar] [CrossRef]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Ullah, K.; Mahmood, T.; Garg, H. Evaluation of the performance of search and rescue robots using T-spherical fuzzy Hamacher aggregation operators. Int. J. Fuzzy Syst. 2020, 22, 570–582. [Google Scholar] [CrossRef]
- Garg, H.; Ullah, K.; Mahmood, T.; Hassan, N.; Jan, N. T-spherical fuzzy power aggregation operators and their applications in multi-attribute decision making. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 9067–9080. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Kousar, Z.; Ullah, K.; Mahmood, T.; Yapici Pehlivan, N.; Ali, Z. Approach to Multi-Attribute Decision-Making Methods for Performance Evaluation Process Using Interval-Valued T-Spherical Fuzzy Hamacher Aggregation Information. Axioms 2021, 10, 145. [Google Scholar] [CrossRef]
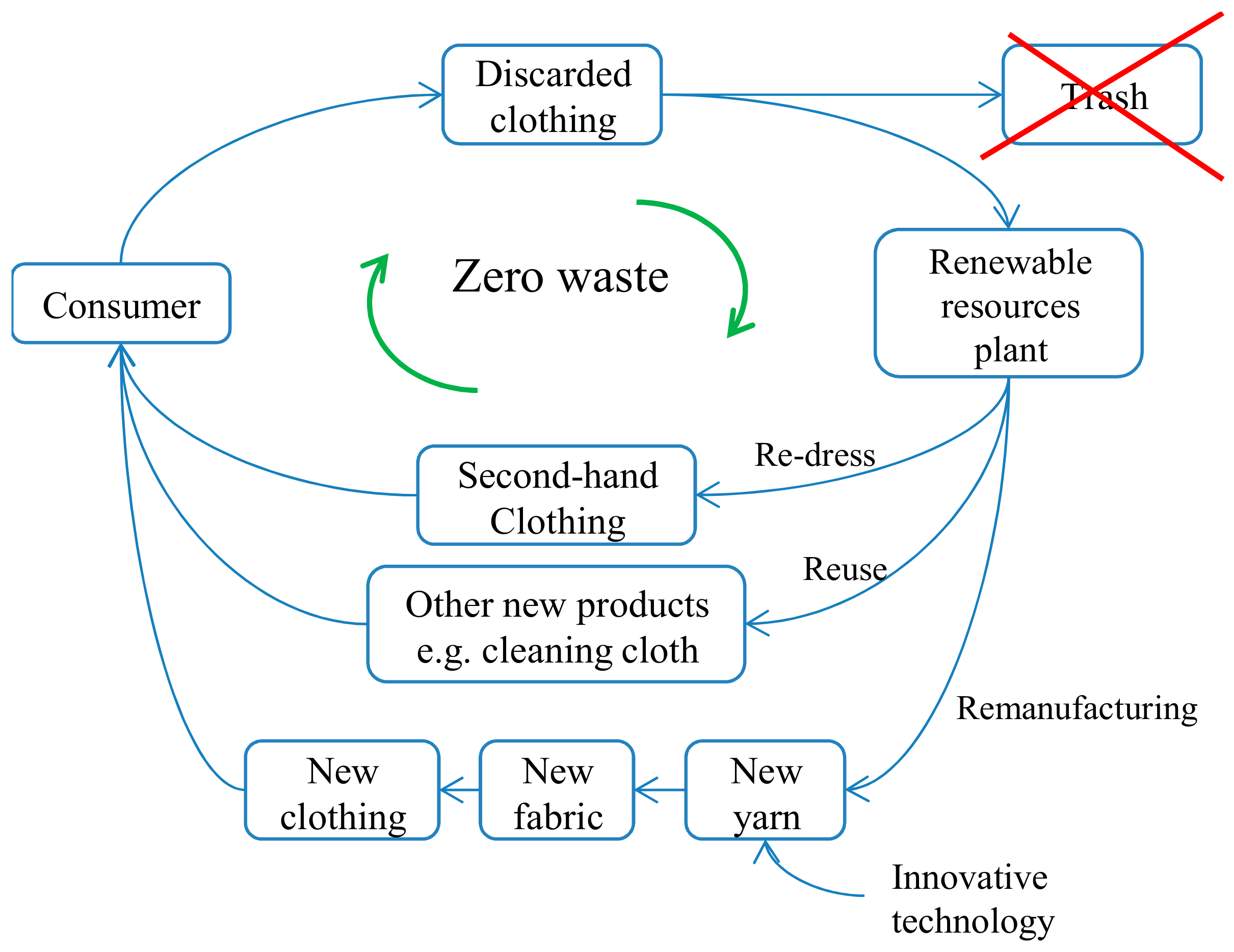

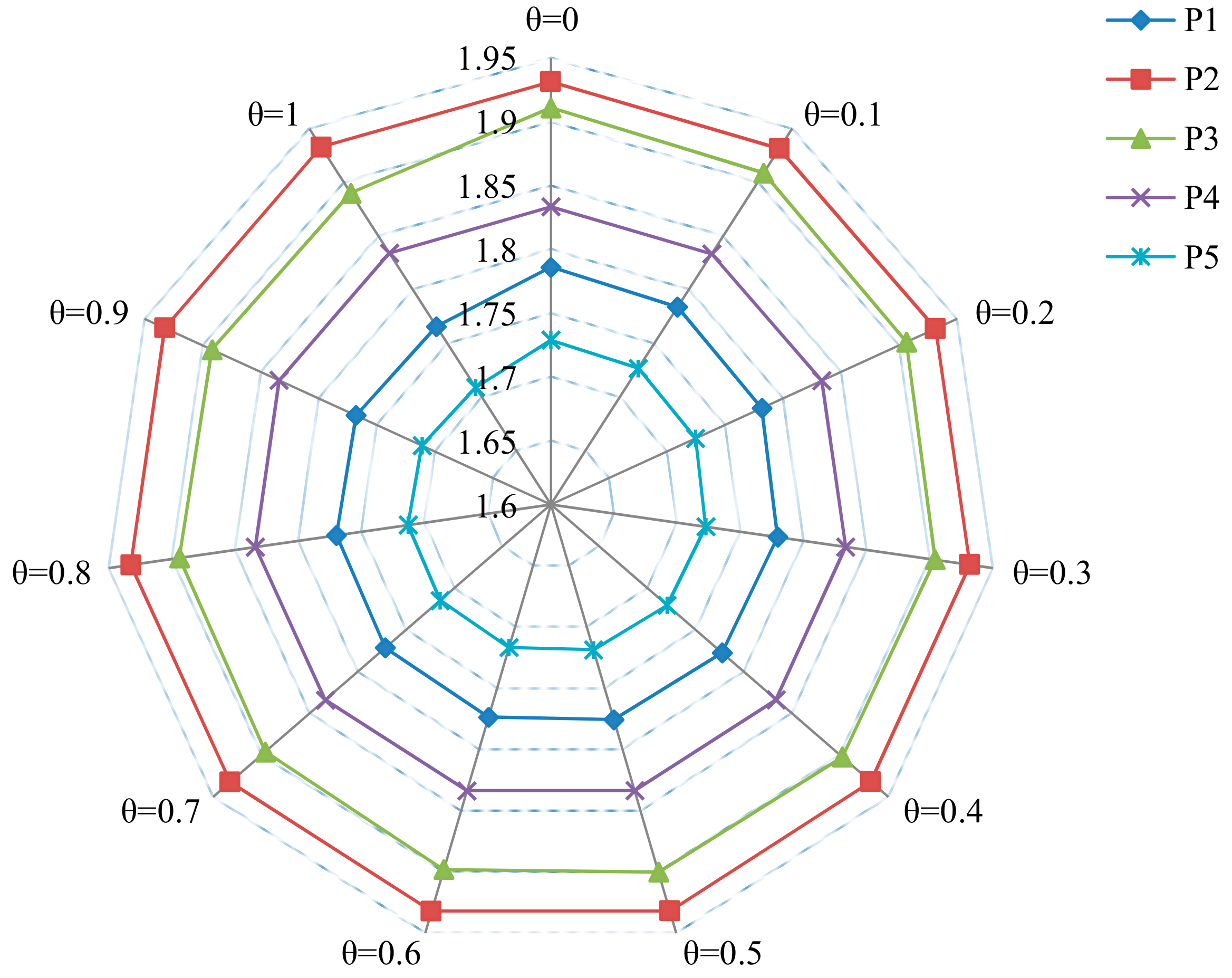

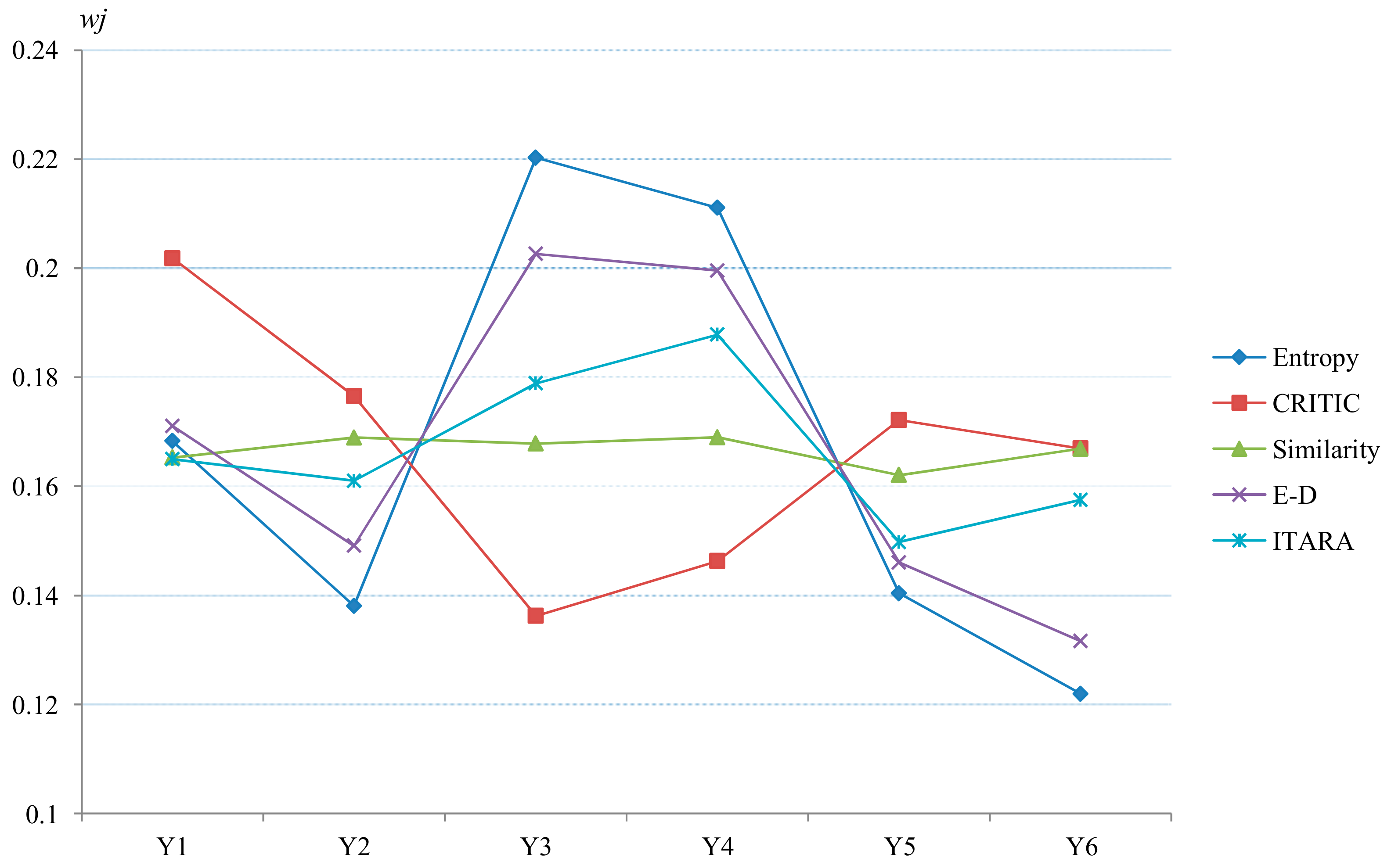
| Refs. | Type of Info. | DMs’ Weight | Weight of Attribute | OLs | Defuzzification | Application Area | |||
|---|---|---|---|---|---|---|---|---|---|
| Subjective | Objective | Combined | Approach | Step in CoCoSo | |||||
| Erceg et al. (2019) [68] | IVRS | Given | FUCOM | - | NO | AOLs | - | - | Stock management |
| Wen et al. (2019) [70] | HFLTS | Hesitant degree | Subjective evaluation | Distance measure | YES | AOLs | Score function | Decision matrix | Service provider selection |
| Wen et al. (2019) [71] | PLTS | Given | SWARA | - | NO | AOLs | Expectation function | Decision matrix | Supplier selection |
| Yazdani et al. (2019) [67] | GS | - | BWM | - | NO | AOLs | - | - | Supplier selection |
| Yazdani et al. (2020) [69] | RS | Given | FUCOM | - | NO | DOLs | - | - | Location selection |
| Zhang et al. (2020) [72] | PLTS | Given | BWM | - | NO | AOLs | Expectation function | Decision matrix | Supplier selection |
| Ecer et al. (2020) [63] | FS | Given | BWM | - | NO | AOLs | Score function | Aggregation strategies | Sustainable supplier selection |
| Liao et al. (2020) [64] | PyFS | Prospect theory | Given | Correlation coefficients | NO | AOLs | Score function | Aggregation strategies | Distribution center selection |
| Svadlenka et al. (2020) [73] | PFS | - | Direct rating | Entropy | YES | DOLs | 2-step defuzzifica -tion method | Aggregation strategies | Sustainable last-mile delivery |
| Deveci et al. (2021) [74] | FS | Given | Logarithmic method | - | NO | AOLs | - | - | Traffic management |
| Mishra et al. (2021) [75] | HFS | Quantized formula | Subjective evaluation | Discrimination measure | YES | AOLs | Score function | Aggregation strategies | 3PRL provider selection |
| Alrasheedi et al. (2021) [76] | IVIFS | Deviation degree | Subjective evaluation | Similarity measure | YES | AOLs | Score function | Aggregation strategies | Sustainable devel. evaluation |
| Cui et al. (2021) [65] | PyFS | Quantized formula | SWARA | - | NO | AOLs | Score function | Aggregation strategies | IoT |
| Rani et al. (2021) [77] | SVNS | Quantized formula | SWARA | - | NO | AOLs | Score function | Aggregation strategies | Renewable energy resource selection |
| Liu et al. (2021) [78] | PyFS | Quantized formula | Subjective evaluation | Similarity measure | YES | AOLs | Score function | Aggregation strategies | MWT technology |
| This paper | PyFS | Quantized formula | Subjective evaluation | ITARA | YES | STIOLs | Distance measure | Aggregation strategies | WCRC selection |
| DMs | PyFNs | Weights |
|---|---|---|
| e1 | (0.6,0.5) | 0.2043 |
| e2 | (0.8,0.3) | 0.3036 |
| e3 | (0.7,0.6) | 0.1996 |
| e4 | (0.7,0.3) | 0.2925 |
| DMs | Alternatives | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 |
|---|---|---|---|---|---|---|---|
| e1 | P1 | (0.8,0.3) | (0.6,0.5) | (0.5,0.6) | (0.6,0.3) | (0.4,0.7) | (0.6,0.5) |
| P2 | (0.7,0.4) | (0.8,0.2) | (0.9,0.0) | (0.8,0.3) | (0.8,0.3) | (0.1,0.9) | |
| P3 | (0.9,0.4) | (0.7,0.5) | (0.8,0.2) | (0.7,0.4) | (0.7,0.3) | (0.4,0.6) | |
| P4 | (0.4,0.7) | (0.5,0.7) | (0.9,0.2) | (0.7,0.4) | (0.3,0.8) | (0.9,0.2) | |
| P5 | (0.5,0.6) | (0.5,0.5) | (0.6,0.6) | (0.8,0.5) | (0.6,0.4) | (0.7,0.5) | |
| e2 | P1 | (0.9,0.0) | (0.7,0.4) | (0.5,0.5) | (0.6,0.5) | (0.4,0.6) | (0.6,0.4) |
| P2 | (0.8,0.3) | (0.7,0.3) | (0.7,0.4) | (0.7,0.4) | (0.7,0.4) | (0.3,0.8) | |
| P3 | (0.6,0.5) | (0.6,0.4) | (0.7,0.4) | (0.7,0.5) | (0.6,0.5) | (0.5,0.5) | |
| P4 | (0.5,0.8) | (0.4,0.6) | (0.6,0.6) | (0.8,0.3) | (0.2,0.9) | (0.8,0.4) | |
| P5 | (0.7,0.5) | (0.6,0.5) | (0.6,0.3) | (0.7,0.4) | (0.6,0.5) | (0.6,0.5) | |
| e3 | P1 | (0.8,0.3) | (0.6,0.3) | (0.5,0.6) | (0.8,0.3) | (0.0,0.9) | (0.7,0.5) |
| P2 | (0.9,0.3) | (0.7,0.4) | (0.8,0.4) | (0.7,0.4) | (0.7,0.5) | (0.5,0.5) | |
| P3 | (0.6,0.6) | (0.7,0.5) | (0.7,0.3) | (0.8,0.0) | (0.4,0.7) | (0.6,0.5) | |
| P4 | (0.4,0.6) | (0.4,0.6) | (0.5,0.5) | (0.5,0.5) | (0.4,0.6) | (0.7,0.3) | |
| P5 | (0.6,0.6) | (0.8,0.5) | (0.6,0.4) | (0.7,0.4) | (0.6,0.6) | (0.6,0.3) | |
| e4 | P1 | (0.5,0.5) | (0.7,0.4) | (0.5,0.4) | (0.5,0.5) | (0.3,0.8) | (0.4,0.7) |
| P2 | (0.6,0.5) | (0.8,0.5) | (0.9,0.0) | (0.7,0.4) | (0.7,0.4) | (0.8,0.4) | |
| P3 | (0.7,0.5) | (0.7,0.3) | (0.9,0.3) | (0.8,0.5) | (0.6,0.6) | (0.6,0.5) | |
| P4 | (0.4,0.6) | (0.5,0.5) | (0.9,0.1) | (0.6,0.4) | (0.4,0.6) | (0.8,0.2) | |
| P5 | (0.5,0.5) | (0.6,0.5) | (0.7,0.5) | (0.9,0.2) | (0.5,0.7) | (0.6,0.5) |
| DMs | Alternatives | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 |
|---|---|---|---|---|---|---|---|
| e1 | P1 | (0.8,0.3) | (0.6,0.5) | (0.5,0.6) | (0.6,0.3) | (0.7,0.4) | (0.6,0.5) |
| P2 | (0.7,0.4) | (0.8,0.2) | (0.9,0.0) | (0.8,0.3) | (0.3,0.8) | (0.1,0.9) | |
| P3 | (0.9,0.4) | (0.7,0.5) | (0.8,0.2) | (0.7,0.4) | (0.3,0.7) | (0.4,0.6) | |
| P4 | (0.4,0.7) | (0.5,0.7) | (0.9,0.2) | (0.7,0.4) | (0.8,0.3) | (0.9,0.2) | |
| P5 | (0.5,0.6) | (0.5,0.5) | (0.6,0.6) | (0.8,0.5) | (0.4,0.6) | (0.7,0.5) | |
| e2 | P1 | (0.9,0.0) | (0.7,0.4) | (0.5,0.5) | (0.6,0.5) | (0.6,0.4) | (0.6,0.4) |
| P2 | (0.8,0.3) | (0.7,0.3) | (0.7,0.4) | (0.7,0.4) | (0.4,0.7) | (0.3,0.8) | |
| P3 | (0.6,0.5) | (0.6,0.4) | (0.7,0.4) | (0.7,0.5) | (0.5,0.6) | (0.5,0.5) | |
| P4 | (0.5,0.8) | (0.4,0.6) | (0.6,0.6) | (0.8,0.3) | (0.9,0.2) | (0.8,0.4) | |
| P5 | (0.7,0.5) | (0.6,0.5) | (0.6,0.3) | (0.7,0.4) | (0.5,0.6) | (0.6,0.5) | |
| e3 | P1 | (0.8,0.3) | (0.6,0.3) | (0.5,0.6) | (0.8,0.3) | (0.9,0.0) | (0.7,0.5) |
| P2 | (0.9,0.3) | (0.7,0.4) | (0.8,0.4) | (0.7,0.4) | (0.5,0.7) | (0.5,0.5) | |
| P3 | (0.6,0.6) | (0.7,0.5) | (0.7,0.3) | (0.8,0.0) | (0.7,0.4) | (0.6,0.5) | |
| P4 | (0.4,0.6) | (0.4,0.6) | (0.5,0.5) | (0.5,0.5) | (0.6,0.4) | (0.7,0.3) | |
| P5 | (0.6,0.6) | (0.8,0.5) | (0.6,0.4) | (0.7,0.4) | (0.6,0.6) | (0.6,0.3) | |
| e4 | P1 | (0.5,0.5) | (0.7,0.4) | (0.5,0.4) | (0.5,0.5) | (0.8,0.3) | (0.4,0.7) |
| P2 | (0.6,0.5) | (0.8,0.5) | (0.9,0.0) | (0.7,0.4) | (0.4,0.7) | (0.8,0.4) | |
| P3 | (0.7,0.5) | (0.7,0.3) | (0.9,0.3) | (0.8,0.5) | (0.6,0.6) | (0.6,0.5) | |
| P4 | (0.4,0.6) | (0.5,0.5) | (0.9,0.1) | (0.6,0.4) | (0.6,04) | (0.8,0.2) | |
| P5 | (0.5,0.5) | (0.6,0.5) | (0.7,0.5) | (0.9,0.2) | (0.7,0.5) | (0.6,0.5) |
| Alternatives | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 |
|---|---|---|---|---|---|---|
| P1 | (0.947,0.070) | (0.864,0.142) | (0.707,0.241) | (0.838,0.153) | (0.935,0.078) | (0.790,0.255) |
| P2 | (0.936,0.119) | (0.927,0.162) | (0.969,0.062) | (0.908,0.117) | (0.596,0.467) | (0.770,0.382) |
| P3 | (0.909,0.244) | (0.871,0.164) | (0.952,0.097) | (0.927,0.182) | (0.766,0.292) | (0.748,0.229) |
| P4 | (0.630,0.488) | (0.654,0.324) | (0.949,0.109) | (0.879,0.122) | (0.939,0.075) | (0.957,0.079) |
| P5 | (0.803,0.257) | (0.844,0.239) | (0.838,0.204) | (0.952,0.125) | (0.788,0.279) | (0.830,0.196) |
| Attributes | e1 | e2 | e3 | e4 | ωj | sc(ωj) | wjs |
|---|---|---|---|---|---|---|---|
| Y1 | (0.5,0.4) | (0.7,0.5) | (0.4,0.6) | (0.3,0.7) | (0.734,0.283) | 0.729 | 0.148 |
| Y2 | (0.7,0.4) | (0.8,0.2) | (0.9,0.3) | (0.7,0.4) | (0.945,0.098) | 0.942 | 0.192 |
| Y3 | (0.8,0.5) | (0.5,0.6) | (0.6,0.5) | (0.5,0.7) | (0.818,0.314) | 0.785 | 0.160 |
| Y4 | (0.5,0.5) | (0.6,0.4) | (0.7,0.4) | (0.8,0.3) | (0.877,0.123) | 0.877 | 0.179 |
| Y5 | (0.9,0.1) | (0.7,0.4) | (0.9,0.2) | (0.7,0.4) | (0.955,0.072) | 0.954 | 0.194 |
| Y6 | (0.4,0.6) | (0.4,0.6) | (0.6,0.4) | (0.3,0.8) | (0.625,0.372) | 0.626 | 0.127 |
| Alternatives | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 |
|---|---|---|---|---|---|---|
| NIS | (0630,0.488) | (0654,0.324) | (0707,0.241) | (0.838,0.182) | (0.596,0.467) | (0.748,0.382) |
| P1 | (0.947,0.070) | (0.864,0.142) | (0.707,0.241) | (0.838,0.153) | (0.935,0.078) | (0.790,0.255) |
| P2 | (0.936,0.119) | (0.927,0.162) | (0.969,0.062) | (0.908,0.117) | (0.596,0.467) | (0.770,0.382) |
| P3 | (0.909,0.244) | (0.871,0.164) | (0.952,0.097) | (0.927,0.182) | (0.766,0.292) | (0.748,0.229) |
| P4 | (0.630,0.488) | (0.654,0.324) | (0.949,0.109) | (0.879,0.122) | (0.939,0.075) | (0.957,0.079) |
| P5 | (0.803,0.257) | (0.844,0.239) | (0.838,0.204) | (0.952,0.125) | (0.788,0.279) | (0.830,0.196) |
| PIS | (0.947,0.070) | (0.927,0.142) | (0.969,0.062) | (0.952,0.117) | (0.939,0.076) | (0.957,0.079) |
| Alternatives | Kia | Kib | Kic | Ki | Ranking | ||||
|---|---|---|---|---|---|---|---|---|---|
| NIS | (0.901,0.104) | (0.898,0.123) | - | - | - | - | - | - | - |
| P1 | (0.980,0.018) | (0.979,0.029) | 0.813 | 0.815 | 0.194 | 2.066 | 0.918 | 1.776 | 4 |
| P2 | (0.988,0.031) | (0.985,0.087) | 0.902 | 0.869 | 0.211 | 2.248 | 0.999 | 1.932 | 1 |
| P3 | (0.985,0.034) | (0.985,0.040) | 0.871 | 0.872 | 0.207 | 2.211 | 0.982 | 1.900 | 2 |
| P4 | (0.984,0.031) | (0.980,0.085) | 0.856 | 0.826 | 0.200 | 2.134 | 0.948 | 1.834 | 3 |
| P5 | (0.977,0.035) | (0.977,0.043) | 0.787 | 0.789 | 0.188 | 2.000 | 0.888 | 1.719 | 5 |
| PIS | (0.997,0.008) | (0.997,0.009) | - | - | - | - | - | - | - |
| Alternatives | θ = 0.0 | θ = 0.1 | θ = 0.2 | θ = 0.3 | θ = 0.4 | θ = 0.5 | θ = 0.6 | θ = 0.7 | θ = 0.8 | θ = 0.9 | θ = 0.9 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1.786 | 1.784 | 1.782 | 1.780 | 1.778 | 1.776 | 1.774 | 1.772 | 1.770 | 1.768 | 1.766 |
| P2 | 1.931 | 1.931 | 1.932 | 1.932 | 1.932 | 1.932 | 1.932 | 1.932 | 1.933 | 1.933 | 1.933 |
| P3 | 1.911 | 1.909 | 1.906 | 1.904 | 1.902 | 1.900 | 1.898 | 1.896 | 1.894 | 1.892 | 1.890 |
| P4 | 1.833 | 1.833 | 1.833 | 1.834 | 1.834 | 1.834 | 1.834 | 1.834 | 1.834 | 1.834 | 1.834 |
| P5 | 1.729 | 1.727 | 1.725 | 1.723 | 1.721 | 1.719 | 1.717 | 1.715 | 1.713 | 1.711 | 1.709 |
| Scenarios | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Ranking |
|---|---|---|---|---|---|---|---|
| #0 | w1 = 0.147 | w2 = 0.185 | w3 = 0.172 | w4 = 0.201 | w5 = 0.175 | w6 = 0.120 | P2 > P3 > P4 > P1 > P5 |
| #1 | w1 = 0.167 | w2 = 0.167 | w3 = 0.167 | w4 = 0.167 | w5 = 0.167 | w6 = 0.167 | P2 > P3 > P4 > P1 > P5 |
| #2 | w1 = 0.500 | w2 = 0.100 | w3 = 0.100 | w4 = 0.100 | w5 = 0.100 | w6 = 0.100 | P2 > P1 > P3 > P5 > P4 |
| #3 | w1 = 0.100 | w2 = 0.500 | w3 = 0.100 | w4 = 0.100 | w5 = 0.100 | w6 = 0.100 | P2 > P3 > P1 > P5 > P4 |
| #4 | w1 = 0.100 | w2 = 0.100 | w3 = 0.500 | w4 = 0.100 | w5 = 0.100 | w6 = 0.100 | P2 > P3 > P4 > P5 > P51 |
| #5 | w1 = 0.100 | w2 = 0.100 | w3 = 0.100 | w4 = 0.500 | w5 = 0.100 | w6 = 0.100 | P5 > P3 > P2 > P4 > P1 |
| #6 | w1 = 0.100 | w2 = 0.100 | w3 = 0.100 | w4 = 0.100 | w5 = 0.500 | w6 = 0.100 | P4 > P1 > P3 > P5 > P4 |
| #7 | w1 = 0.100 | w2 = 0.100 | w3 = 0.100 | w4 = 0.100 | w5 = 0.100 | w6 = 0.500 | P4 > P2 > P5 > P1 > P3 |
| Weighting Approaches | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 |
|---|---|---|---|---|---|---|
| Entropy [20] | 0.168 | 0.138 | 0.220 | 0.211 | 0.140 | 0.122 |
| CRITIC [66] | 0.202 | 0.177 | 0.136 | 0.146 | 0.172 | 0.167 |
| Similarity [78] | 0.165 | 0.169 | 0.168 | 0.169 | 0.162 | 0.167 |
| E-D [36] | 0.171 | 0.149 | 0.203 | 0.200 | 0.146 | 0.132 |
| ITARA | 0.165 | 0.161 | 0.179 | 0.188 | 0.150 | 0.158 |
| Alternatives | CoCoSo-D | TOPSIS [79] | WASPAS [83] | MULTIMOORA [84] | CoCoSo [78] | VIKOR [36] |
|---|---|---|---|---|---|---|
| P1 | Q1 = 1.776 | ξ1 = 0.507 | sc(Q1) = 0.715 | U1 = 0.936 | Q1 = 1.907 | Q1 = 1.000 |
| P2 | Q2 = 1.932 | ξ2 = 0.591 | sc(Q2) = 0.739 | U2 = 1.000 | Q2 = 1.923 | Q2 = 0.202 |
| P3 | Q3 = 1.900 | ξ3 = 0.570 | sc(Q3) = 0.732 | U3 = 0.952 | Q3 = 1.938 | Q3 = 0.355 |
| P4 | Q4 = 1.834 | ξ4 = 0.516 | sc(Q4) = 0.624 | U4 = 0.815 | Q4 = 1.759 | Q4 = 0.545 |
| P5 | Q5 = 1.719 | ξ5 = 0.462 | sc(Q5) = 0.603 | U5 = 0.780 | Q5 = 1.703 | Q5 = 0.230 |
| Ranking | P2 > P3 > P4 > P1 > P5 | P2 > P3 > P4 > P1 > P5 | P2 > P3 > P1 > P4 > P5 | P2 > P3 > P1 > P4 > P5 | P3 > P2 > P1 > P4 > P5 | P2 > P3 > P5 > P4 > P1 |
| Spearman’s correlation | - | 1 | 0.9 | 0.9 | 0.8 | 0.7 |
| Characteristics | This Paper | Zhang and Xu [79] | Rani et al. [83] | Sarkar and Biswas [84] | Liu et al. [78] | Rani et al. [36] |
|---|---|---|---|---|---|---|
| Approaches | CoCoSo-D | TOPSIS | WASPAS | MULTIMOORA | CoCoSo | VIKOR |
| Decision type | Group | Single | Group | Group | Group | Group |
| Experts’ weights | Computed | Not Applicable | Computed | Assumed | Computed | Computed |
| Criteria weights | Combined | Assumed | Combined | Objective | Combined | Combined |
| Weighting methods | Subjective evaluation/ITARA | - | Subjective evaluation/E-D | Entropy | Subjective evaluation/similarity measure | Subjective evaluation/E-D |
| OLs | STIOLs | AOLs | AOLs | AOLs | AOLs | AOLs |
| AOs | STI-PyFWA, STI-PyFWG | PyFWA | PyFWA, PyFWG | PyFWA, PyFWG | PyFWA, PyFWG | PyFWA |
| Defuzzification techniques | Distance measure | Distance measure | Score function | Score function/Distance measure | Score function | Divergence measure |
| Decision mechanism | Compromise | Similarity to ideal solution | Score function | WSM | Compromise | Compromise |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, F.; Ullah, K. Waste Clothing Recycling Channel Selection Using a CoCoSo-D Method Based on Sine Trigonometric Interaction Operational Laws with Pythagorean Fuzzy Information. Energies 2022, 15, 2010. https://doi.org/10.3390/en15062010
Wang H, Zhang F, Ullah K. Waste Clothing Recycling Channel Selection Using a CoCoSo-D Method Based on Sine Trigonometric Interaction Operational Laws with Pythagorean Fuzzy Information. Energies. 2022; 15(6):2010. https://doi.org/10.3390/en15062010
Chicago/Turabian StyleWang, Haolun, Faming Zhang, and Kifayat Ullah. 2022. "Waste Clothing Recycling Channel Selection Using a CoCoSo-D Method Based on Sine Trigonometric Interaction Operational Laws with Pythagorean Fuzzy Information" Energies 15, no. 6: 2010. https://doi.org/10.3390/en15062010
APA StyleWang, H., Zhang, F., & Ullah, K. (2022). Waste Clothing Recycling Channel Selection Using a CoCoSo-D Method Based on Sine Trigonometric Interaction Operational Laws with Pythagorean Fuzzy Information. Energies, 15(6), 2010. https://doi.org/10.3390/en15062010







