Low-Grade Flow Energy Harvesting by Low-Mass-Ratio Oscillating Bent Plate
Abstract
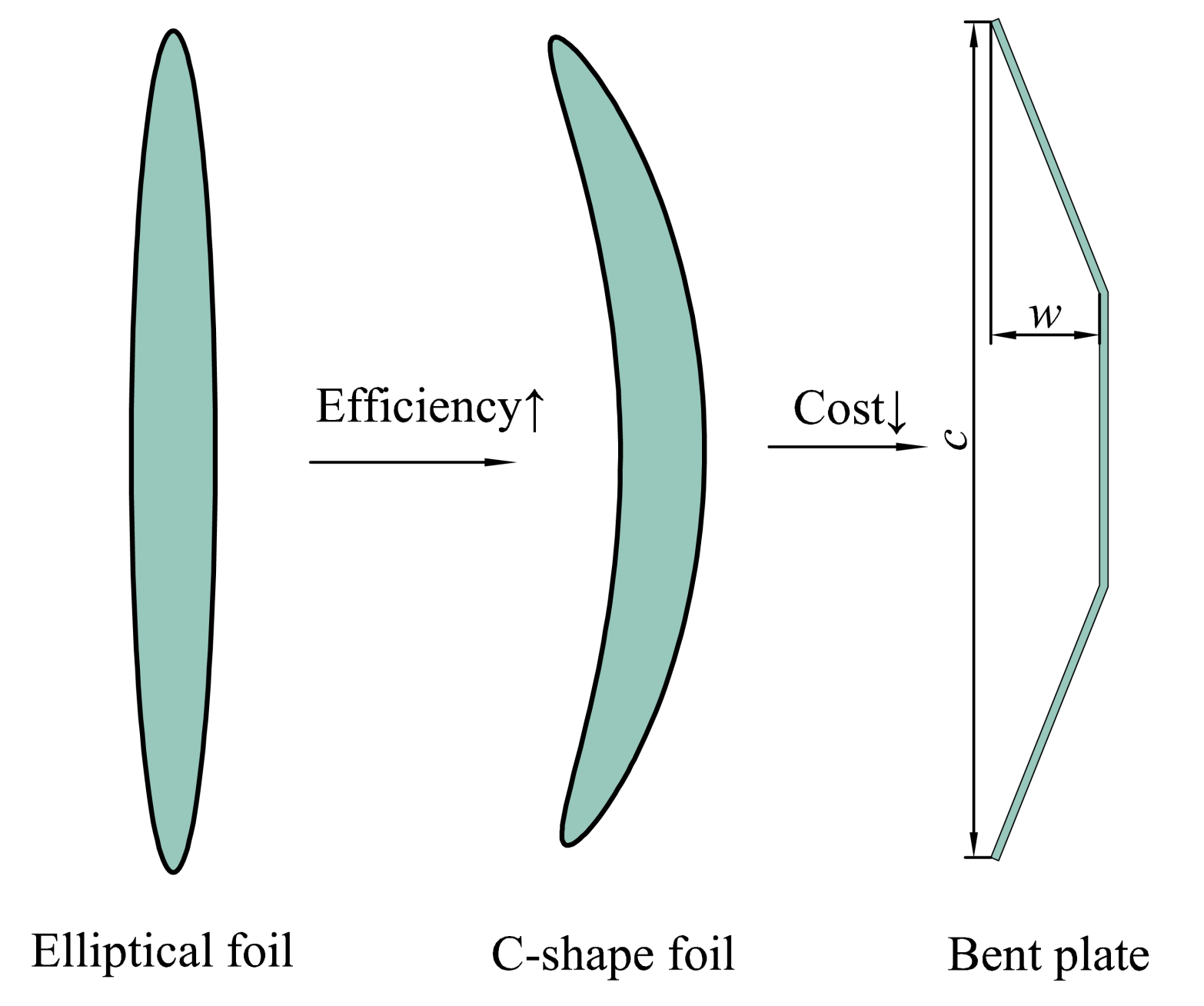
:1. Introduction
2. Method
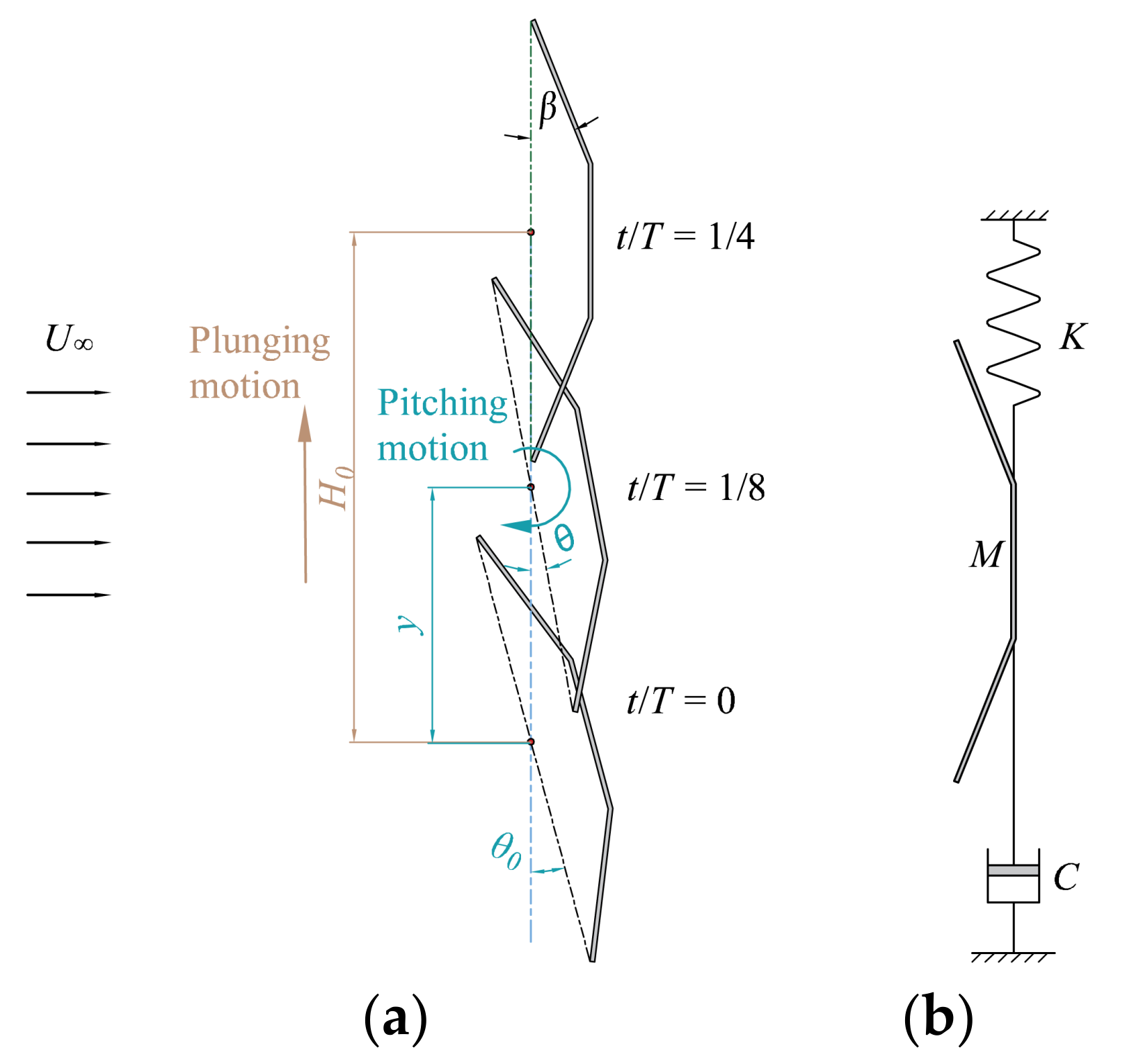
2.1. Problem Description
2.2. Numerics
2.3. Computational Conditions
2.4. Verification and Validation
3. Results and Discussions
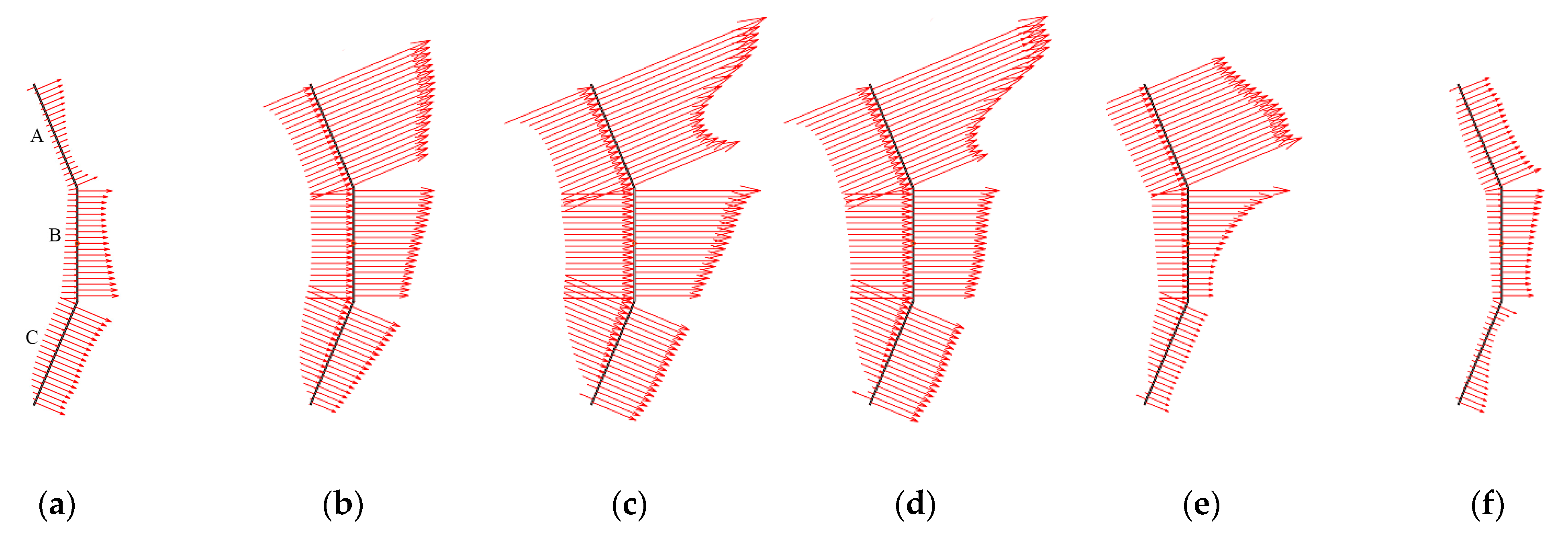
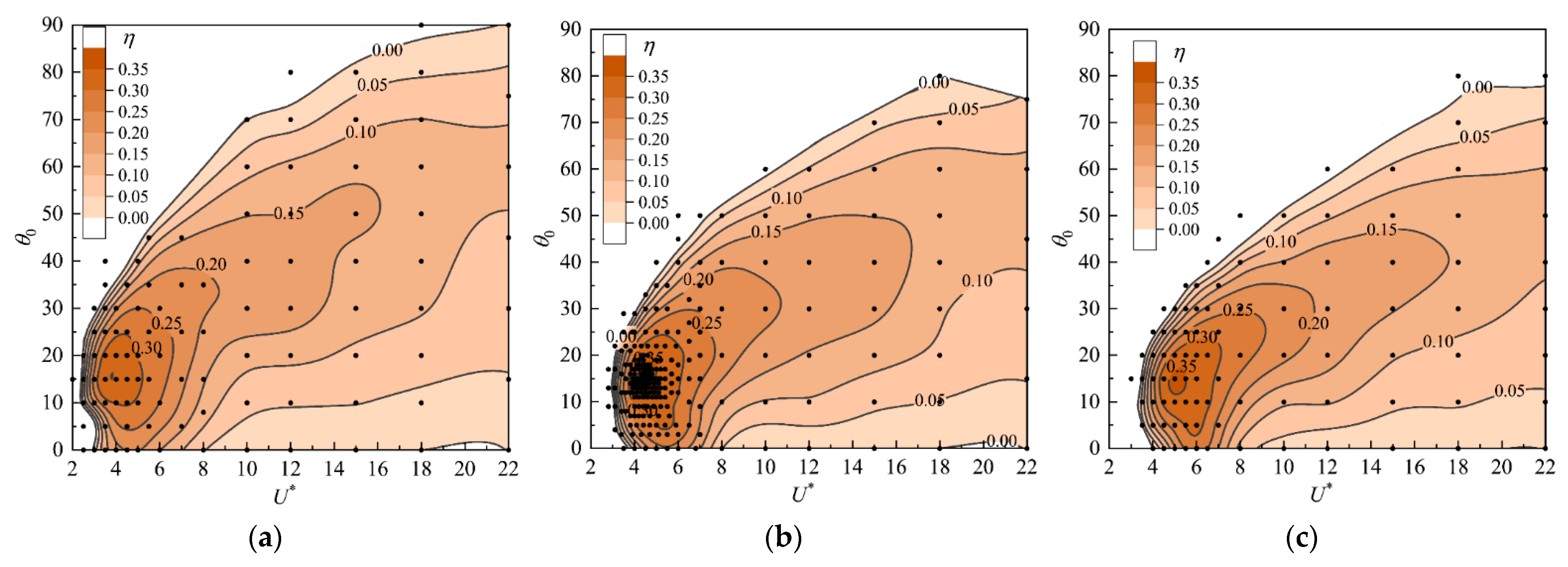
3.1. Prescribed Single-DOF Plunging Oscillation
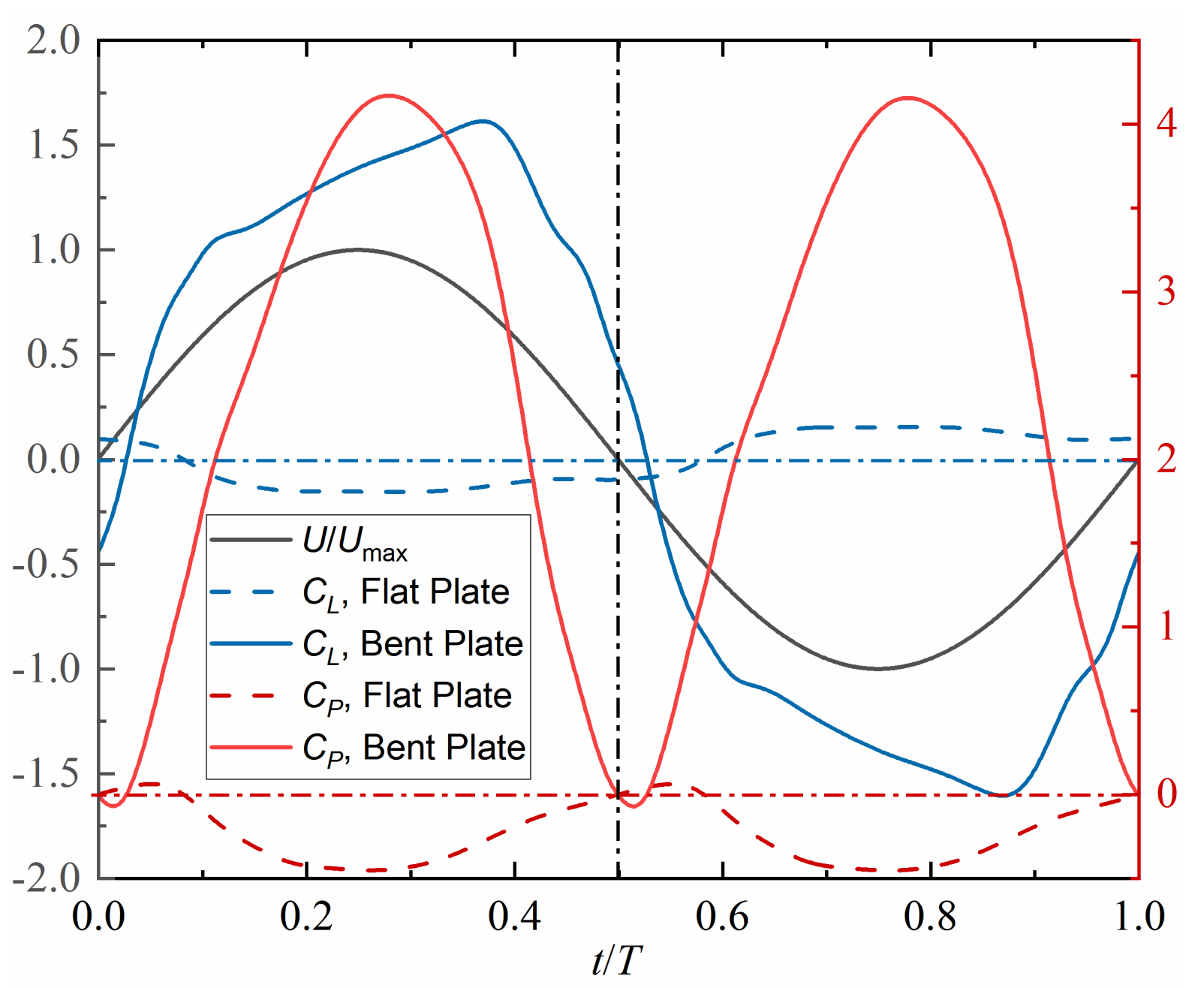
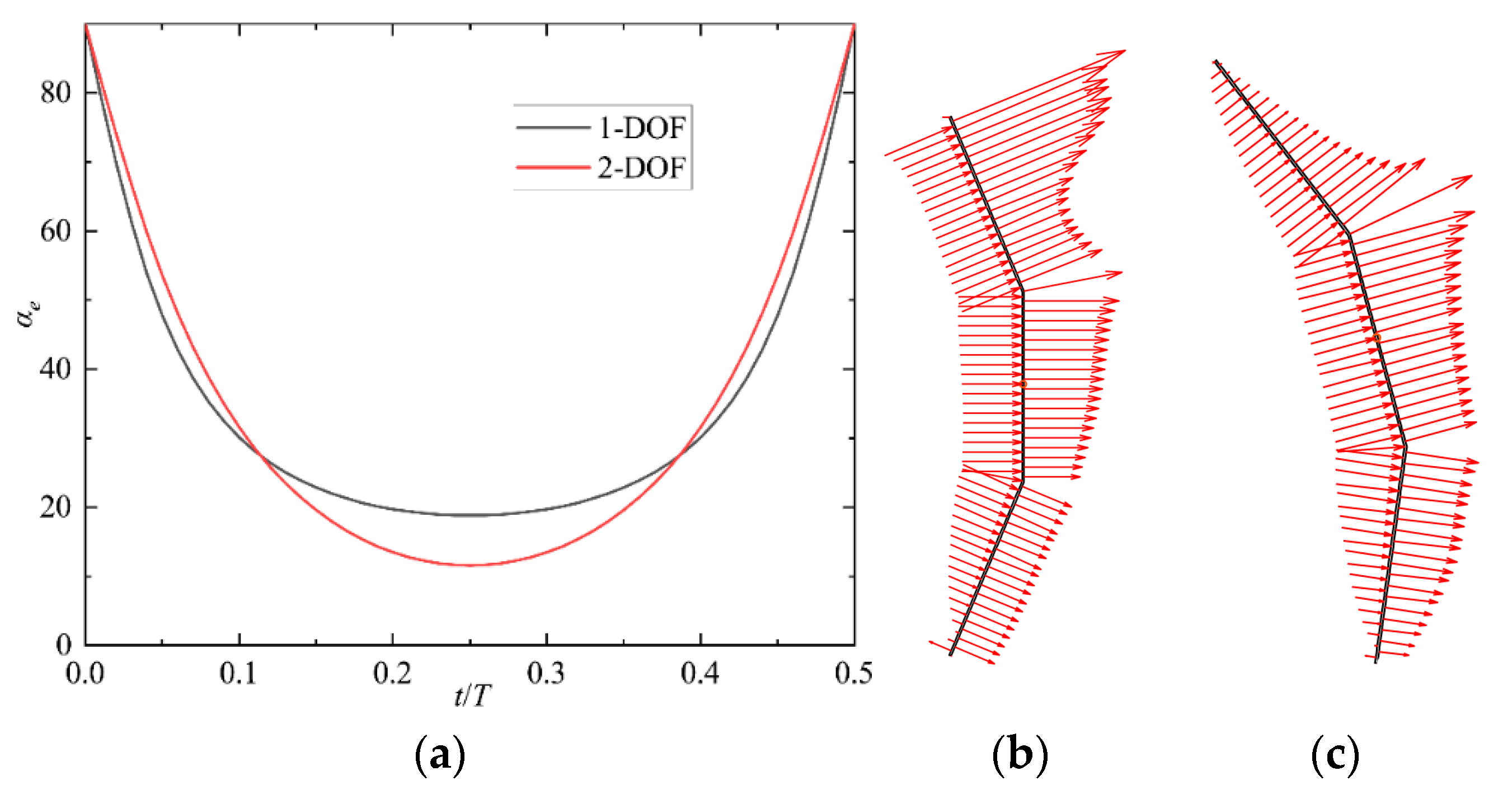
3.2. Prescribed Double-DOF Combined Plunging and Pitching Oscillation
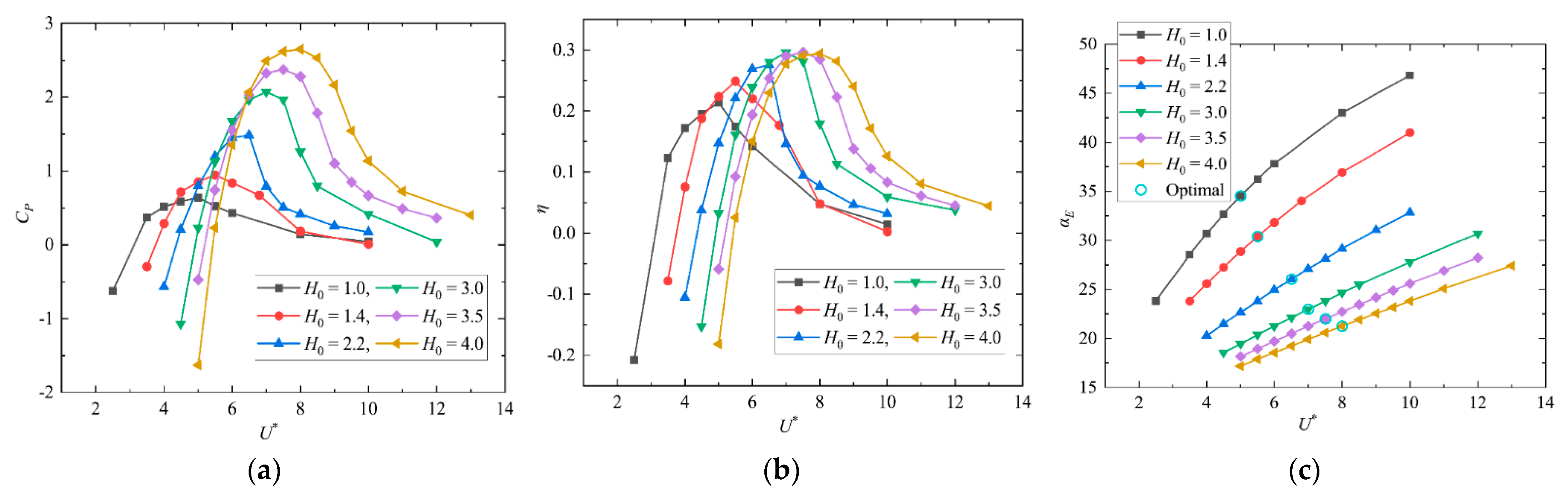
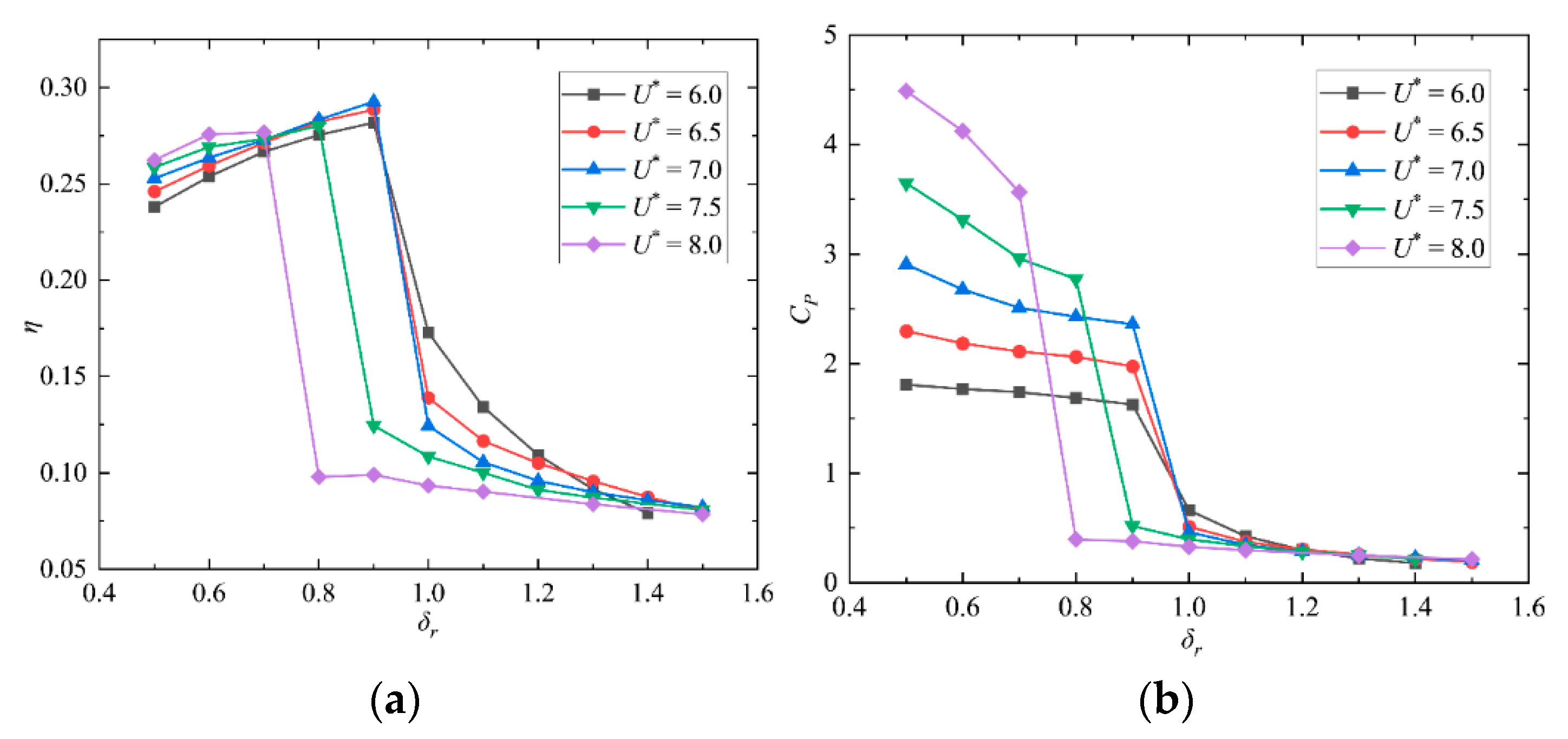
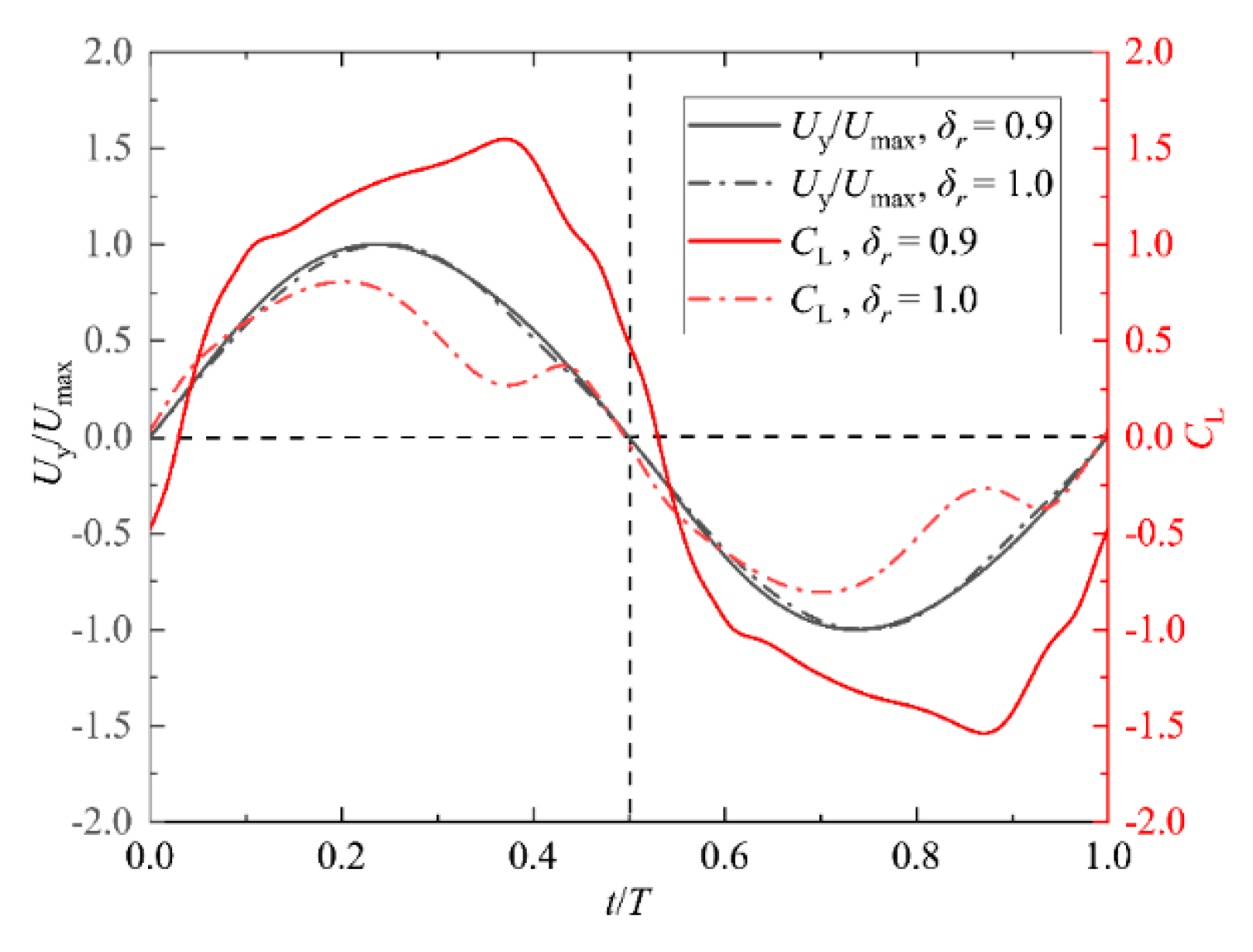
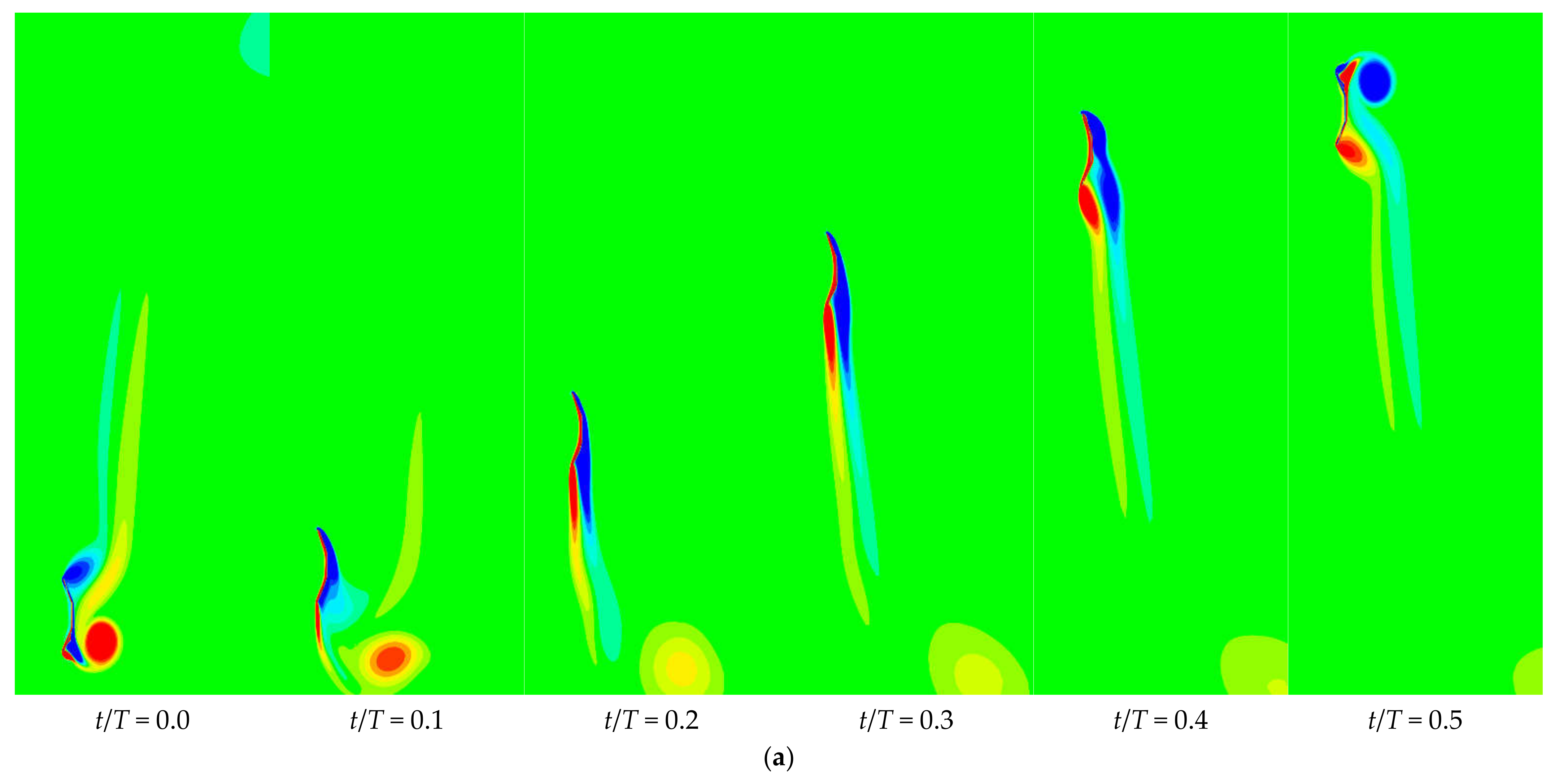
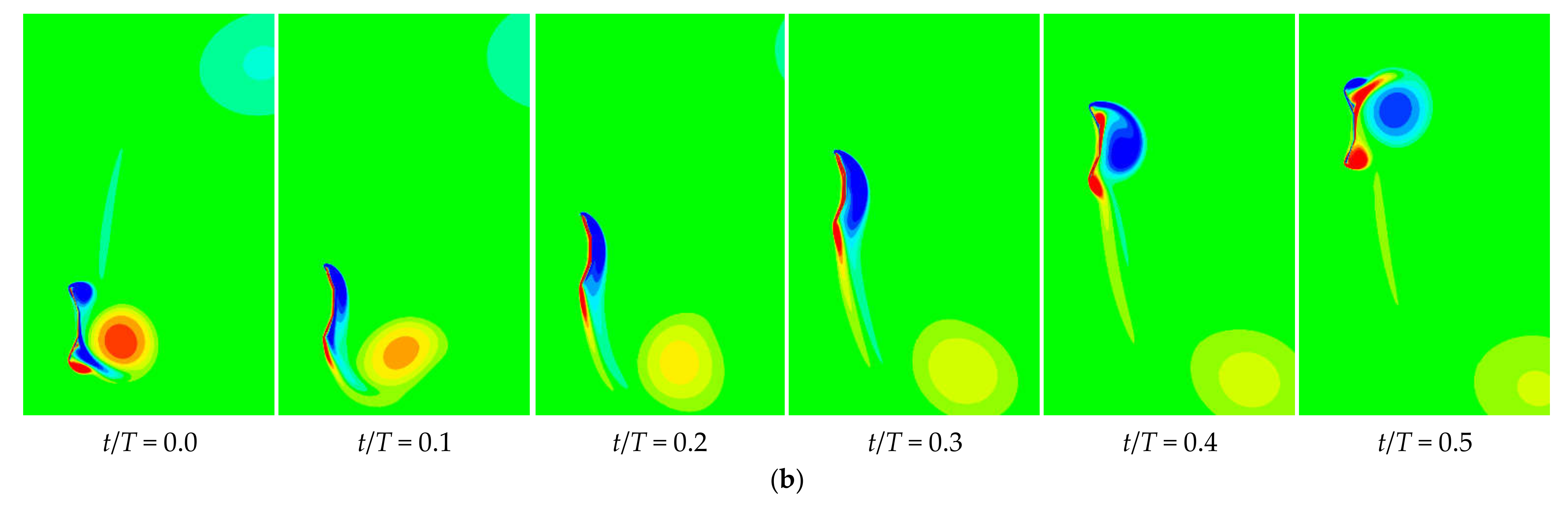
3.3. Flow-Induced Single-DOF Plunging Oscillation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| c | Foil chord length, m |
| C | Damping of the damper, N·s·m−1 |
| CL | Lift coefficient |
| CP | Power coefficient |
| CPmean | Time-averaged power coefficient |
| d | Vertical extent of the foil motion, m |
| f | Oscillation frequency, s−1 |
| Fy | Lift force, N |
| fN | Natural frequency for oscillator, s−1 |
| H0 | Plunging amplitude, m |
| K | Stiffness of the spring, N·m−1 |
| M | Foil mass, kg |
| md | Displaced fluid mass, kg |
| m* | Mass ratio |
| Re | Reynolds number |
| t | Physical time, s |
| T | Oscillating period, s |
| U* | Reduced velocity |
| U∞ | Free stream velocity, m·s−1 |
| Vy | Plunging velocity, m·s−1 |
| w | Camber height, m |
| y(t) | Plunging motion, m |
| αe | Effective angle of attack, ° |
| β | Bending angle of the bent plate, ° |
| δr | Mass-damping parameter |
| φ | Phase difference between the pitching and plunging motions, ° |
| η | Energy extraction efficiency |
| θ0 | Pitching amplitude, ° |
| θ(t) | Pitching motion, ° |
References
- Moriarty, P.; Honnery, D. Can renewable energy power the future? Energy Policy 2016, 93, 3–7. [Google Scholar] [CrossRef]
- Wei, C.; Jing, X. A comprehensive review on vibration energy harvesting: Modelling and realization. Renew. Sustain. Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Lee, Y.J.; Qi, Y.; Zhou, G.; Lua, K.B. Vortex-induced vibration wind energy harvesting by piezoelectric MeMS device in formation. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Abdelkefi, A. Aeroelastic energy harvesting: A review. Int. J. Eng. Sci. 2016, 100, 112–135. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C.H. Investigation of relative effects of mass and damping in vortex-induced vibration of a circular cylinder. J. Wind Eng. Ind. Aerodyn. 1997, 69, 341–350. [Google Scholar] [CrossRef]
- Williamson, C.; Govardhan, R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef] [Green Version]
- Govardhan, R.; Williamson, C. Critical mass in vortex-induced vibration of a cylinder. Eur. J. Mech. B Fluids 2004, 23, 17–27. [Google Scholar] [CrossRef]
- Govardhan, R.; Williamson, C. Resonance forever: Existence of a critical mass and an infinite regime of resonance in vortex-induced vibration. J. Fluid Mech. 2002, 473, 147–166. [Google Scholar] [CrossRef]
- Govardhan, R.; Williamson, C. Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 2000, 420, 85–130. [Google Scholar] [CrossRef]
- Raghavan, K.; Bernitsas, M.M. Experimental investigation of Reynolds number effect on vortex induced vibration of rigid circular cylinder on elastic supports. Ocean Eng. 2011, 38, 719–731. [Google Scholar] [CrossRef]
- Li, T.; Ishihara, T. Numerical study on vortex-induced vibration of circular cylinder with two-degree-of-freedom and geometrical nonlinear system. J. Fluids Struct. 2021, 107, 103415. [Google Scholar] [CrossRef]
- Bernitsas, M.M.; Raghavan, K.; Ben-Simon, Y.; Garcia, E.M.H. VIVACE (Vortex Induced Vibration Aquatic Clean Energy): A New Concept in Generation of Clean and Renewable Energy from Fluid Flow. J. Offshore Mech. Arct. Eng. 2008, 130, 041101. [Google Scholar] [CrossRef]
- Bernitsas, M.M.; Ben-Simon, Y.; Raghavan, K.; Garcia, E. The VIVACE converter: Model tests at high damping and Reynolds number around 105. J. Offshore Mech. Arct. Eng. 2009, 131, 011102. [Google Scholar] [CrossRef]
- Ding, L.; Zhang, L.; Bernitsas, M.M.; Chang, C.-C. Numerical simulation and experimental validation for energy harvesting of single-cylinder VIVACE converter with passive turbulence control. Renew. Energy 2016, 85, 1246–1259. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Abdelkefi, A.; Dai, H.; Naseer, R.; Wang, L. Design and experimental analysis of broadband energy harvesting from vortex-induced vibrations. J. Sound Vib. 2017, 408, 210–219. [Google Scholar] [CrossRef]
- Hover, F.; Techet, A.; Triantafyllou, M. Forces on oscillating uniform and tapered cylinders in a crossflow. J. Fluid Mech. 1998, 363, 19. [Google Scholar] [CrossRef] [Green Version]
- Barrerogil, A.; Pindado, S.; Avila, S.G. Extracting energy from Vortex-Induced Vibrations: A parametric study. Appl. Math. Model. 2012, 36, 3153–3160. [Google Scholar] [CrossRef] [Green Version]
- Ding, L.; Zhang, L.; Wu, C.; Mao, X.; Jiang, D. Flow induced motion and energy harvesting of bluff bodies with different cross sections. Energy Convers. Manag. 2015, 91, 416–426. [Google Scholar] [CrossRef]
- Zhang, B.; Song, B.; Mao, Z.; Tian, W.; Li, B. Numerical investigation on VIV energy harvesting of bluff bodies with different cross sections in tandem arrangement. Energy 2017, 133, 723–736. [Google Scholar] [CrossRef]
- Dai, H.; Abdelkefi, A.; Wang, L. Piezoelectric energy harvesting from concurrent vortex-induced vibrations and base excitations. Nonlinear Dyn. 2014, 77, 967–981. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G. Optimal operating parameters for an oscillating foil turbine at Reynolds number 500,000. AIAA J. 2014, 52, 1885–1895. [Google Scholar] [CrossRef]
- Veilleux, J.-C.; Dumas, G. Numerical optimization of a fully-passive flapping-airfoil turbine. J. Fluids Struct. 2017, 70, 102–130. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, Y.L.; Zhang, D.; Xie, Y.H. Numerical investigation into power extraction by a fully passive oscillating foil with double generators. Renew. Energy 2019, 133, 32–43. [Google Scholar] [CrossRef]
- Boudreau, M.; Dumas, G.; Rahimpour, M.; Oshkai, P. Experimental investigation of the energy extraction by a fully-passive flapping-foil hydrokinetic turbine prototype. J. Fluids Struct. 2018, 82, 446–472. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, Y.; Zhang, D.; Xie, Y. Numerical investigation into the energy extraction characteristics of 3D self-induced oscillating foil. Renew. Energy 2020, 148, 60–71. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, D.; Xie, Y.H. Numerical investigation into energy extraction from self-induced oscillations of an elliptical plate. J. Fluids Struct. 2017, 69, 1–15. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, D.; Xie, Y.H. Numerical investigation into the effects of arm motion and camber on a self-induced oscillating hydrofoil. Energy 2016, 115 Pt 1, 1010–1021. [Google Scholar] [CrossRef]
- Bos, F.M.; Lentink, D.; Van Oudheusden, B.W.; Bijl, H. Influence of wing kinematics on aerodynamic performance in hovering insect flight. J. Fluid Mech. 2008, 594, 341–368. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Mei, Z.Y.; Wu, F.; Han, A.; Xie, Y.H.; Xie, D.M. Effect of shroud on the energy extraction performance of oscillating foil. Energy 2022, 239, 122387. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G. Parametric study of an oscillating airfoil in a power-extraction regime. AIAA J. 2008, 46, 1318–1330. [Google Scholar] [CrossRef]
- Zasso, A.; Belloli, M.; Giappino, S.; Muggiasca, S. On the pressure and force field on a circular cylinder oscillating in the lock-in region at sub-critical Reynolds number. In Proceedings of the ASME Pressure Vessels and Piping Conference, Vancouver, BC, Canada, 23–26 July 2006; pp. 919–927. [Google Scholar]
- Ho, S.; Nassef, H.; Pornsinsirirak, N.; Tai, Y.-C.; Ho, C.-M. Unsteady aerodynamics and flow control for flapping wing flyers. Prog. Aerosp. Sci. 2003, 39, 635–681. [Google Scholar] [CrossRef]
- Sane, S.P. The aerodynamics of insect flight. J. Exp. Biol. 2003, 206, 4191–4208. [Google Scholar] [CrossRef] [PubMed] [Green Version]







| Mesh Size, Cells | Time Step, ms | CLmax | δ, % |
|---|---|---|---|
| 14.8 × 104 | 1.0 | 2.028 | 4.94 |
| 1.5 | 1.958 | 1.35 | |
| 2.3 | 1.929 | −0.16 | |
| 3.5 | 1.925 | −0.36 | |
| 5.2 | 1.932 | - | |
| 4.2 × 104 | 2.3 | 1.965 | 1.85 |
| 8.8 × 104 | 1.959 | 1.57 | |
| 11.4 × 104 | 1.944 | 0.79 | |
| 14.8 × 104 | 1.929 | 0.01 | |
| 21.1 × 104 | 1.929 | - |
| H0 | U* | θ0 | ηmax | U* | θ0 | CPmax |
|---|---|---|---|---|---|---|
| 1.0 | 3.5 | 15 | 33.8% | 3.5 | 15 | 1.02 |
| 1.4 | 4.4 | 15 | 37.4% | 4.4 | 15 | 1.42 |
| 1.8 | 5.0 | 15 | 34.9% | 5.0 | 15 | 1.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Wu, F.; Mei, Z.; Shi, R.; Xie, D. Low-Grade Flow Energy Harvesting by Low-Mass-Ratio Oscillating Bent Plate. Energies 2022, 15, 1606. https://doi.org/10.3390/en15051606
Jiang W, Wu F, Mei Z, Shi R, Xie D. Low-Grade Flow Energy Harvesting by Low-Mass-Ratio Oscillating Bent Plate. Energies. 2022; 15(5):1606. https://doi.org/10.3390/en15051606
Chicago/Turabian StyleJiang, Wei, Fan Wu, Ziyue Mei, Rui Shi, and Danmei Xie. 2022. "Low-Grade Flow Energy Harvesting by Low-Mass-Ratio Oscillating Bent Plate" Energies 15, no. 5: 1606. https://doi.org/10.3390/en15051606
APA StyleJiang, W., Wu, F., Mei, Z., Shi, R., & Xie, D. (2022). Low-Grade Flow Energy Harvesting by Low-Mass-Ratio Oscillating Bent Plate. Energies, 15(5), 1606. https://doi.org/10.3390/en15051606






